Идеальный газ, все формулы и примеры
Это газ, который состоит из материальных точек, имеющих конечную массу, но не имеющих объема. Данные частицы не могут взаимодействовать на расстоянии. Столкновения частиц идеального газа описываются при помощи законов абсолютно упругого соударения шаров. Следует отметить, что имеются в виду законы столкновения именно шаров, так как точечные частицы испытывают только лобовые столкновения, которые не могут изменять направления скоростей на разные углы.
Идеальный газ существует только в теории. В реальной жизни он не может существовать в принципе, так как точечные молекулы и отсутствие их взаимодействия на расстоянии аналогично их существованию вне пространства, то есть их не существованию. Ближе всех по своим свойствам к модели идеального газа приближаются газы при малом давлении (разреженные газы) и (или) высокой температуре. Модель идеального газа подходит для изучения методов исследования систем многих частиц, знакомства с соответствующими понятиями.
В промежутках между столкновениями молекулы идеального газа движется по прямым. Законы столкновений и соударений о стенки сосудов, в которых находится газ, известны. Следовательно, если знать положения и скорости всех частиц идеального газа в какой-то момент времени, то можно найти их координаты и скорости в любой другой момент времени. Эта информация наиболее полно описывает состояние системы частиц. Однако количество частиц столь велико, что динамическое описание системы многих частиц непригодно для теории и бесполезно для практики. Это означает, что для изучения систем многих частиц информация должна быть обобщена, и ее относят не к отдельным частицам, а к их большим совокупностям.
Давление идеального газа
При помощи модели идеального газа удалось качественно и количественно объяснить давление газа на стенки сосуда, в котором он находится. Газ оказывает давление на стенки сосуда потому, что его молекулы взаимодействуют со стенками как упругие тела по законам классической механики. Количественно давление (p) идеального газа получили равным:
где — средняя кинетическая энергия поступательного движения молекул газа; — концентрация молекул газа (N – число молекул газа в сосуде; V – объем сосуда).
Законы идеальных газов
Идеальным называют газы, которые строго подчиняются законам Бойля – Мариотта и Гей – Люссака.
Закон Бойля – Мариотта. Для постоянной массы (m) идеального газа при постоянной температуре (T) произведение давления (p) газа на его объем (V) является постоянной величиной для любых состояний рассматриваемого вещества:
Закон Гей-Люссака. Для постоянной массы газа при неизменном давлении выполняется соотношение:
В поведении реальных газов наблюдают отступления от законов Бойля — Мариотта и Гей-Люссака, и эти отступления различны для разных газов.
Для идеального газа выполняется закон Шарля. Который говорит о том, что для постоянной массы газа, при постоянном объеме, отношение давления газа к температуре, не изменяется:
Для связи параметров идеального газа, часто используют уравнение состояния, которое носит имена двух ученых Клапейрона и Менделеева:
где — молярная масса газа; – универсальная газовая постоянная.
Закон Дальтона. Давление смеси идеальных газов (p) равно сумме парциальных давлений () рассматриваемых газов:
При этом уравнение состояния смеси идеальных газов имеет вид (2), как будто газ является химически однородным.
Примеры решения задач
ru.solverbook.com
Молекулярная физика — Основные формулы
1. Основы молекулярно-кинетической теории. Газовые законы
1.1 Количество вещества
m — масса;
μ — молярная масса вещества;
N — число молекул;
NA = 6,02·1023 моль-1 — число Авогадро
1.2 Основное уравнение молекулярно-кинетической теории идеального газа
p — давление идеального газа;
m — масса одной молекулы;
n = N/V — концентрация молекул;
V — объем газа;
N — число молекул;
— среднее значение квадрата скорости молекул.
1.3 Средняя квадратичная скорость молекул идеального газа
k = 1,38·10-23 Дж/К — постоянная Больцмана;
R = kNA = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T = t+273 — абсолютная температура;
t — температура по шкале Цельсия.
1.4 Средняя кинетическая энергия молекулы одноатомного газа
1.5 Давление идеального газа
n — концентрация молекул;
k — постоянная Больцмана;
T — абсолютная температура.
1.6 Закон Бойля-Мариотта
p — давление;
V — объем газа.
1.7 Закон Шарля
p0 — давление газа при 0 °С;
α = 1/273 °C-1 — температурный коэффициент давления.
1.8 Закон Гей-Люссака
1.9 Уравнение Менделеева-Клапейрона
1.10 Объединенный закон газового состояния (уравнение Клапейрона)
1.11 Закон Дальтона
pi — парциальное давление i-й компоненты смеси газов.
2. Основы термодинамики
2.1 Внутренняя энергия идеального одноатомного газа
ν — количество вещества;
R = 8,31 Дж/(моль·К) — универсальная газовая постоянная;
T — абсолютная температура.
2.2 Элементарная работа, совершаемая газом,
при изменении объема на бесконечно малую величину dV
p — давление газа.
При изменении объема от V1 до V2
2.3 Первый закон термодинамики
ΔQ — количество подведенной теплоты;
ΔA — работа, совершаемая веществом;
ΔU — изменение внутренней энергии вещества.
2.4 Теплоемкость идеального газа
ΔQ — количество переданной системе теплоты на участке процесса;
ΔT — изменение температуры на этом участке процесса.
fizikazadachi.ru
Формула идеального газа в химии
Определение и формулы идеального газа
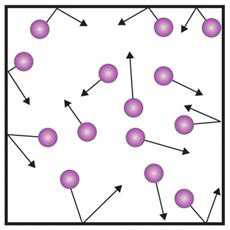
Допущения модели идеального газа:
- объём частиц газа пренебрежимо мал, молекулы – материальные точки;
- молекулы не взаимодействуют между собой, все столкновения абсолютно упругие;
- время взаимодействия между частицами газа пренебрежимо мало по сравнению со средним временем между столкновениями молекул.
К большинству реальных в довольно широком интервале температур и давлений применима модель идеального газа.
Формулы для идеального газа
Формула, связывающая макроскопические параметры идеального газа, называется уравнением состояния идеального газа или уравнением Менделеева Клапейрона :
где р – давление, Па; V – объем, м; m – масса (кг), T – абсолютная температура (К), R – универсальная газовая постоянная, R = 8,314 Дж/(моль • К), М – молярная масса газа (кг/моль).
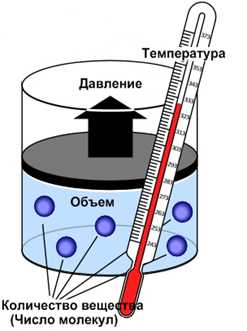
Если масса газа постоянна, то уравнение состояния можно записать в форме объединенного газового закона:
При постоянной температуре объединенный газовый закон переходит в уравнение Бойля Мариотта:
При постоянном давлении объединенный газовый закон переходит в уравнение Гей-Люссака:
При постоянном объеме объединенный газовый закон переходит в уравнение Шарля:
Основное уравнение молекулярно-кинетической теории идеального газа связывает давление газа и среднюю кинетическую энергию его частиц:
где n – число частиц газа в единице объема, m0 – масса одной частицы, υ – скорость частицы.
Средняя кинетическая энергия частиц и абсолютная температура газа связаны уравнением:
где k = 1,38 • 10−23 Дж/К – постоянная Больцмана.
Примеры решения задач
ru.solverbook.com
|
Уравнение состояния идеального газа (уравнение Менделеева – Клапейрона). |
|
|
Уравнением состояния называется уравнение, связывающее параметры физической системы и однозначно определяющее ее состояние. В 1834 г. французский физик Б. Клапейрон, работавший дли тельное время в Петербурге, вывел уравнение состояния идеального газа для постоянной массы газа. В 1874 г. Д. И. Менделеев вывел уравнение для произвольного числа молекул. |
|
|
В МКТ и термодинамике идеального газа макроскопическими параметрами являются: p, V, T, m. Мы знаем, что . Следовательно, . Учитывая, что , получим: . |
|
Произведение постоянных величин есть величина постоянная, следовательно: — универсальная газовая постоянная (универсальная, т.к. для всех газов одинаковая). |
|
|
Таким образом, имеем: — уравнение состояния (уравнение Менделеева – Клапейрона). |
|
|
Другие формы записи уравнения состояния идеального газа. |
|
|
1.Уравнение для 1 моля вещества. Если n=1 моль, то, обозначив объем одного моля Vм, получим: . Для нормальных условий получим: |
|
|
2. Запись уравнения через плотность: — плотность зависит от температуры и давления! |
|
|
3. Уравнение Клапейрона. Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества n=const. Тогда: |
|
|
Эта запись означает, что для данной массы данного газа справедливо равенство: |
|
|
Для постоянной массы идеального газа отношение произведения давления на объем к абсолютной температуре в данном состоянии есть величина постоянная: . |
|
|
Газовые законы. |
|
|
1. Закон Авогадро. В равных объемах различных газов при одинаковых внешних условиях находится одинаковое число молекул (атомов). Условие: V1=V2=…=Vn; p1=p2=…=pn; T1=T2=…=Tn |
|
|
Доказательство:
Следовательно, при одинаковых условиях (давление, объем, температура) число молекул не зависит от природы газа и одинаково. |
|
|
2. Закон Дальтона. Давление смеси газов равно сумме парциальных (частных) давлений каждого газа. Доказать: p=p1+p2+…+pn Доказательство: |
|
|
3. Закон Паскаля. Давление, производимое на жидкость или газ, передается во все стороны без изменения. |
|
www.eduspb.com
| № п/п | Наименование параметра | Формула | Обозначения |
|---|---|---|---|
| 2.1 | Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона) | Р ― давление, V ― объем, ν ― количество молей газа, R = 8,31 Дж/(К∙моль) ― молярная газовая постоянная, Т ― термодинамическая температура | |
| 2.2 | Число молекул, скорости которых находятся в интервале от v до v+dv | N ― количество всех молекул, m ― масса одной молекулы, k ― постоянная Больцмана, Т ― термодинамическая температура, v ― скорость молекулы | |
| 2.3 | Средняя арифметическая скорость молекул | R = 8,31 Дж/(К∙моль) ― молярная газовая постоянная, Т ― термодинамическая температура, М ― молярная масса газа | |
| 2.4 | Средняя квадратичная скорость молекул | R = 8,31 Дж/(К∙моль) ― молярная газовая постоянная, Т ― термодинамическая температура, М ― молярная масса газа | |
| 2.5 | Наиболее вероятная скорость молекул | R = 8,31 Дж/(К∙моль) ― молярная газовая постоянная, Т ― термодинамическая температура, М ― молярная масса газа | |
| 2.6 | Длина свободного пробега молекулы | d ─ эффективный диаметр молекулы, n = p/(kT) ― концентрация молекул газа, k = 1,38∙10–23 Дж/К ― постоянная Больцмана, Т ― термодинамическая температура | |
| 2.7 | Среднее число столкновений в единицу времени | d ― эффективный диаметр молекулы, n ― концентрация газа, <v> ― средняя арифметическая скорость молекул | |
| 2.8 | Cредняя арифметическая скорость молекул | М ― молярная масса молекулы, R ― молярная газовая постоянная, n = P/(kT) ― концентрация молекул газа | |
| 2.9 | Внутренняя энергия молекул газа | i ― число степеней свободы молекулы газа | |
| 2.10 | Показатель адиабаты | СР ― молярная теплоемкость при постоянном давлении, СV ― молярная теплоемкость при постоянном объеме | |
| 2.11 | При изотермическом процессе | ν ― количество газа, R = 8,31 Дж/(К∙моль) ― молярная газовая постоянная, Т ― термодинамическая температура, V1 и V2 ― начальный и конечный объем | |
| 2.12 | При изобарическом процессе: работа A теплота изменение внутренней энергии | или | р ― давление, V1 и V2 ― начальный и конечный объем ν ― количество молей газа, R = 8,31 Дж/(моль∙К) ― молярная газовая постоянная, ΔТ ― разность температур i ― число степеней свободы одной молекулы |
| 2.13 | При изохорном процессе | i ― число степеней свободы молекулы, ν ― количество молей газа, R = 8,31 Дж/(моль∙К) ― молярная газовая постоянная, ΔТ ― разность температур | |
| 2.14 | При адиабатическом процессе | ν ― количество газа, i ― число степеней свободы молекулы, R = 8,31 Дж/(К∙моль) ― молярная газовая постоянная, ΔТ ― разность температур | |
| 2.15 | Распределение Больцмана (частиц в силовом поле) | n ― концентрация частиц; U ― их потенциальная энергия; n0 ― концентрация частиц в точках поля, где U = 0; k ― постоянная Больцмана; Т ― термодинамическая температура газа | |
| 2.15a | Зависимость концентрации газов от высоты, если в качестве уровня, где U = 0, выбрать поверхность Земли | n0 ― концентрация частиц на высоте h = 0; m ― масса молекулы; g ― ускорение свободного падения; h ― высота над поверхностью Земли; k ― постоянная Больцмана; Т ― термодинамическая температура газа | |
| 2.16 | Барометрическая формула | где p — давление газа в слое, расположенном на высоте h, p0 — давление на нулевом уровне h0, M — молярная масса газа, R — газовая постоянная, T — абсолютная температура | |
| 2.17 | Кинетическая энергия, приходящаяся на одну степень свободы молекулы | k = 1,38∙10−23 Дж/К ― постоянная Больцмана, T — абсолютная температура газа | |
| 2.18 | Теплоемкость газа Изменение внутренней энергии газа Приращение работы | dQ ― изменение теплоты газа; dA ― приращение работы, выполненной газом; dU ― изменение внутренней энергии газа; dT ― изменение температуры газа ν ― количество молей газа, i ― число степеней свободы молекулы, R ― молярная газовая постоянная p ― давление газа, dV ― изменение объема | |
| 2.19 | Удельная теплоемкость смеси: при постоянном давлении при постоянном объеме | m1, m2 ― массы составляющих смеси; cp1, cp2 ― удельные теплоемкости составляющих смеси при постоянном давлении; cv1, cv2 ― удельные теплоемкости составляющих смеси при постоянном объеме | |
| 2.20 | Молярная теплоемкость смеси | ν1, ν2 ― количества молей составляющих смеси; Сp1, Сp2 ― молярные теплоемкости составляющих смеси при постоянном давлении; Сv1, Сv2 ― молярные теплоемкости составляющих смеси при постоянном объеме | |
| 2.21 | Изменение энтропии при изотермическом процессе | Q1 ― полученная теплота; T ― термодинамическая температура | |
| 2.22 | Изменение энтропии | Q ― полученная теплота; T ― термодинамическая температура | |
| 2.23 | Распределение молекул по энергиям | k ― постоянная Больцмана, T ― термодинамическая температура, ε ― энергия молекулы | |
| 2.24 | Распределение молекул по скоростям | k ― постоянная Больцмана, T ― термодинамическая температура, m ― масса молекулы, v ― скорость молекулы | |
| 2.25 | Теплота, затраченная на нагревание воды массы m от t1 до t2 равна | св = 4183 Дж/(кг∙К) ― удельная теплоемкость воды, m ― масса воды, t2−t1 ― разность температур | |
| 2.26 | Теплота, затраченная на испарение воды массы m, равна | λв = 2250∙103 Дж/кг ― удельная теплота парообразования для воды, m ― масса воды | |
| 2.27 | Молярная масса смеси газов | m1, m2 ― массы составляющих смеси; M1, M2 ― массы составляющих смеси |
reshenie-zadach.com.ua
Основные формулы термодинамики
В термодинамике изучают самые общие законы и физические процессы преобразований внутренней энергии. При этом считается, что любое материальное тело имеет тепловую энергию $U$, которая зависит от его температур.
Перед тем, как рассмотреть основные термодинамические формулы необходимо дать определение термодинамике.
Определение 1
Термодинамика — это обширный раздел физики, который исследует и описывает процессы, происходящие в системах, а также их состояния.
Указанное научное направление опирается на обобщенные факты, которые были получены опытным путем. Происходящие в термодинамических концепциях явления описываются посредством использования макроскопических величин.
В их список входят такие параметры, как:
- давление;
- температура;
- концентрация;
- энергия;
- объем.
К отдельным молекулам данные параметры неприменимы, а сводятся к детальному описанию системы в общем ее виде. Много решений, которые основаны на термодинамических законах, можно встретить в сфере электроэнергетики и тепловой техники. Что и свидетельствует о понимании фазовых переходов, химических процессов и явлений переноса. В некотором роде термодинамика тесно “сотрудничает” с квантовой динамикой.
Уравнение идеального газа в термодинамике

Рисунок 1. Работа в термодинамике. Автор24 — интернет-биржа студенческих работ
Определение 2
Идеальный газ – это некая идеализация, такая же, как и материальная точка.
Молекулы такого элемента являются материальными точками, а соударения частиц – абсолютно упругие и постоянные. В задачах по термодинамике реальные газы зачастую принимаются за идеальные. Так гораздо легче составлять формулы, и не нужно иметь дела с огромным количеством новых величин в уравнениях.
Итак, молекулы идеального газа движутся, а вот чтобы узнать с какой скоростью и массой, необходимо использовать уравнение состояния идеального газа, или формулу Клапейрона-Менделеева: $PV = \frac{m}{M}RT$. Здесь $m$ – масса исследуемого газа, $M$ – его изначальная молекулярная масса, $R$ – универсальная постоянная, равная 8,3144598 Дж/(моль*кг).
В этом аспекте массу идеального газа также можно вычислить, как произведение объема и плотности $m = pV$. Существует некая связь между средней кинетической энергией $E$ и давлением газа. Эта взаимосвязь называется в физике основным уравнением молекулярно-кинетической теории и имеет вид: $p = \frac{2}{3}nE$, где $n$ – концентрация движущихся молекул по отношению к общему объему, $E$ – коэффициент средней кинетической энергии.
Первое начало термодинамики. Формулы для изопроцессов
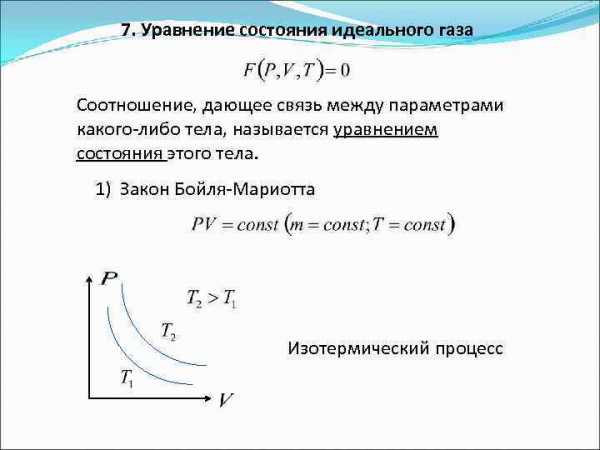
Рисунок 2. Уравнение состояния идеального газа. Автор24 — интернет-биржа студенческих работ
Первый термодинамический закон гласит: количество внутренней теплоты, переданное газу, идёт только на изменение общей энергии газа $U$ и на совершение веществом работы $A$. Формула первого начала термодинамики записывается так: $Q = ΔU + A$.
как известно, с газом в системе всегда что-то происходит, ведь его можно сжать или нагреть. В данном случае необходимо рассмотреть такие процессы, которые протекают при одном стабильном параметре. Первое начало термодинамики в изотермическом случае, который протекает при постоянной температуре, задействует закон Бойля-Мариотта.
В результате изотермического процесса давление газа обратно пропорционально его изначальному объёму: $Q = A.$
Изохорный – наблюдается при постоянном объеме. Для этого явление применим закон Шарля, согласно которому, давление прямо пропорционально общей температуре. В изохорном процессе все подведенное к газу тепло идет на изменение его внутренней энергии и записывается в таком виде: $Q = ΔA.$
Изобарный процесс – происходит при постоянном давлении. Закон Гей-Люссака предполагает, что при неизменном давлении идеального газа его начальный объём прямо пропорционален итоговой температуре. При изобарном процессе тепло идет на совершение газом работы и на изменение внутреннего энергетического потенциала: $Q = \Delta U+p\Delta V.$
Формула теплоемкости и главная формула КПД в термодинамике

Рисунок 3. Количество теплоты. Автор24 — интернет-биржа студенческих работ
Замечание 1
Удельная теплоемкость в термодинамической системе всегда равна количеству теплоты, которое выделяется для нагревания одного килограмма действующего вещества на один градус Цельсия.
Уравнение теплоемкости записывается таким образом: $c = \frac{Q}{m\Delta t}$. Помимо указанного параметра, существует и молярная теплоемкость, которая работает при постоянном объеме и давлении.
Ее действия видно в следующей формуле: $C_v = \frac {i}{2}R$ где $i$ – количество степеней свободы молекул газа.
Тепловая машина, в самом простейшем случае, состоит из холодильника, нагревателя и рабочего материального тела. Нагреватель изначально сообщает тепло физическому веществу и совершает определенную работу, а затем постепенно охлаждается холодильником, и все повторяется по кругу. Типичным примером тепловой машины выступает двигатель внутреннего сгорания.
Коэффициент полезного действия теплового устройства вычисляется по формуле: $n = \frac {Q_h-Q_x }{Q_h }.$
При изучении основ и уравнений термодинамики следует понять, что на сегодняшний день существует два метода описания физических процессов, происходящих в макроскопических материальных телах: статистический и термодинамический.
Методы термодинамики и ее формулы позволяет раскрыть и описать смысл экспериментальных закономерностей в виде закона Менделеева-Клапейрона. Важно понять, что в термодинамических концепциях, в отличие от систем молекулярной физики, не изучаются конкретные взаимодействия, происходящие с определенными молекулами или атомами, а рассматривается постоянные взаимопревращения и связь разнообразных видов теплоты, энергии и работы.
Уравнение состояния и его функции

Рисунок 4. Термодинамические уравнения состояния. Автор24 — интернет-биржа студенческих работ
При исследовании макросостояний применяются функции состояния, которые предполагают показатель, демонстрирующий определённые состояния термодинамического равновесия, независящий от предыстории концепции и метода её перехода в абсолютное состояние.
Основными функциями состояния при грамотном построении термодинамики являются:
- внутренняя энергия;
- энтропия;
- температура;
- термодинамические потенциалы.
Однако функции состояния в термодинамики не являются полностью независимыми, и для однородной системы любой термодинамический принцип может быть записан как выражение двух самостоятельных переменных. Такие функциональные взаимосвязи называются уравнениями общего состояния.
На сегодняшний день различают такие виды уравнений:
- термическое уравнение состояние — определяющее связь между давлением, температурой и объёмом;
- калорическое уравнение — выражающее внутренний энергетический потенциал, как функцию от объёма и температуры;
- каноническое уравнение состояние — записываемое в качестве термодинамического потенциала в соответствующих переменных.
Знание уравнения состояния очень важно для использования на практике общих принципов термодинамики. Для каждой конкретной термодинамической концепции такие выражения определяются из опыта или способами статистической механики, и в пределах термодинамики оно считается заданным при изначальном определении системы.
spravochnick.ru
Идеальный газ
МОЛЕКУЛЯРНАЯ ФИЗИКА
Идеальный газ
Основные понятия
Основные положения молекулярной физики: 1) все вещества состоят из атомов и молекул, 2) они находятся в постоянном хаотическом движении. Поскольку размеры молекул малы, то в макроскопических объемах вещества содержится большое число молекул. Поэтому изучение движения молекул вещества основано на статистическом методе. Законы поведения большого числа молекул основаны на статистических закономерностях. Используются средние значения таких характеристик как скорость, энергия и т.д.
Термодинамикаизучает общие свойства
макроскопических систем, находящихся
в состоянии термодинамического
равновесия, а также процессы между ними.
Основу термодинамики составляют начала
– фундаментальные законы, установленные
опытным путем. Состояние термодинамических
( т/д) систем задается с помощью набора
т/д параметров, которые полностью
описывают свойства системы. К таким
параметрам относятся: давление, объем,
температура и др. Температура –
характеризует состояние т/д равновесия
макроскопической системы. Она имеет
смысл только для системы, находящейся
в состоянии равновесия.Термодинамическая
температурная шкалабазируется на
одной реперной точке – тройная точка
воды. (температура, при которой лед, вода
и насыщенный пар при давленииР=609 Па). Она равна273,16 К. В этой шкале
температура замерзания воды равна273,15 К. Температура в градусах Цельсия, ,
связана с т/д температурой соотношением
,
связана с т/д температурой соотношением
Удельный объем– это объем единицы массы вещества. Любое изменение состояния называется т/д процессом.
Идеаьный газ удовлетворяет следующим условиям:
1) Объем молекул газа пренебрежимо мал по сравнению с объемом сосуда
2) молекулы газа не взаимодействуют
3) столкновения молекул со стенками сосуда являются абсолютно упругими.
Газовые законы
Закон Бойля – Мариотта. Для заданной массы газа при постоянной температуре
дляи.
Графики в переменных
 являются
гиперболами. Каждый график соответствует
одной температуре. Такие кривые называютсяизотермами. Процесс, идущий приназывается изотермическим.
являются
гиперболами. Каждый график соответствует
одной температуре. Такие кривые называютсяизотермами. Процесс, идущий приназывается изотермическим.
Рис 1
Законы Гей – Люссака.
1) прии.
График в переменных
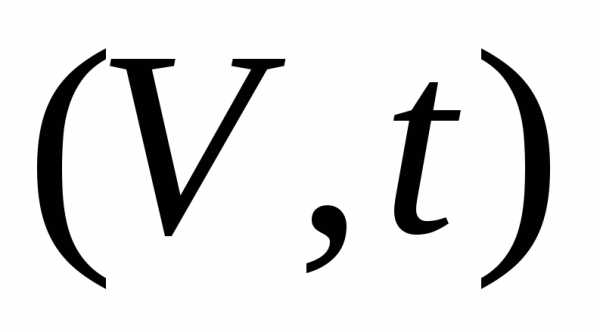 есть прямая линия. Каждая прямая
соответствует одному значению давления.
Такие линии называютсяизобарами.
Процесс, идущий приназывается изобарным.
есть прямая линия. Каждая прямая
соответствует одному значению давления.
Такие линии называютсяизобарами.
Процесс, идущий приназывается изобарным.
Рис
2) прии.
График в переменных
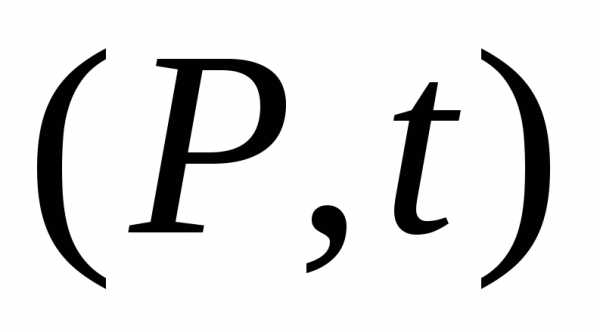 есть прямая линия. Каждая прямая
соответствует одному значению объема.
Такие линии называютсяизохорами.
Процесс, идущий приназывается изохорным.
есть прямая линия. Каждая прямая
соответствует одному значению объема.
Такие линии называютсяизохорами.
Процесс, идущий приназывается изохорным.
Рис
Значение коэффициента
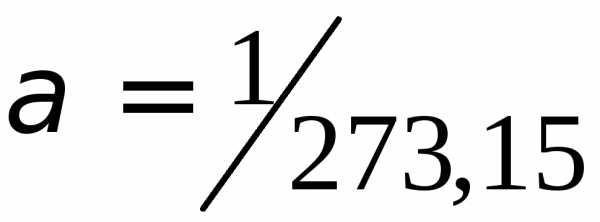
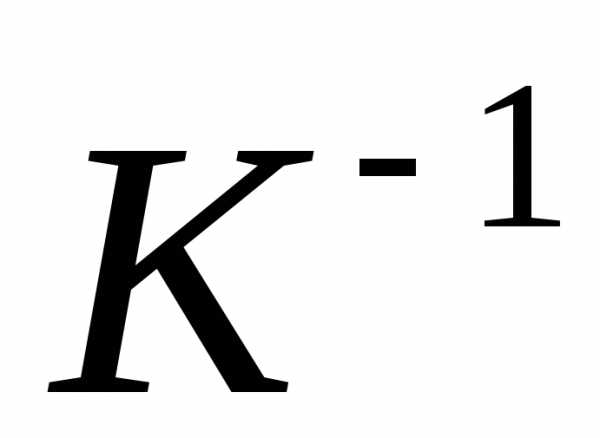 .
Если перейти к термодинамической
температуре,
получим следующие соотношения.
.
Если перейти к термодинамической
температуре,
получим следующие соотношения.
и. Несложно получить следующие соотношения:
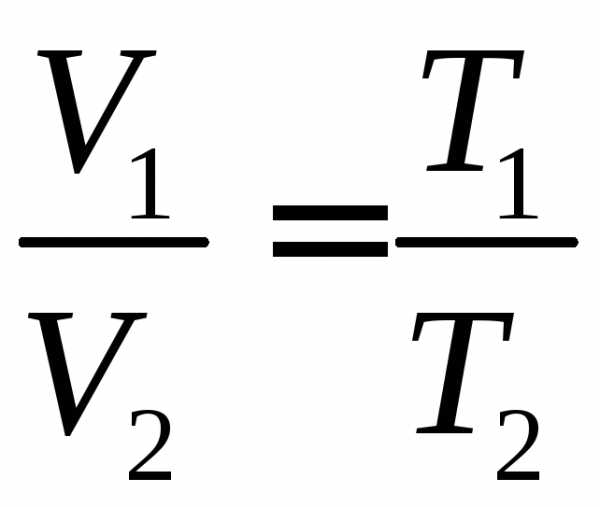 при.
при.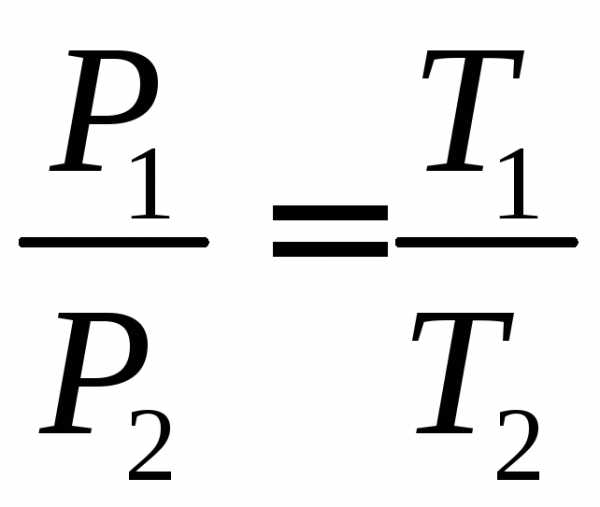 при.
при.
Закон Авогадро.Один моль любого
газа при одинаковых температуре и
давлении занимает одинаковый объем.
При нормальных условиях этот объем
равен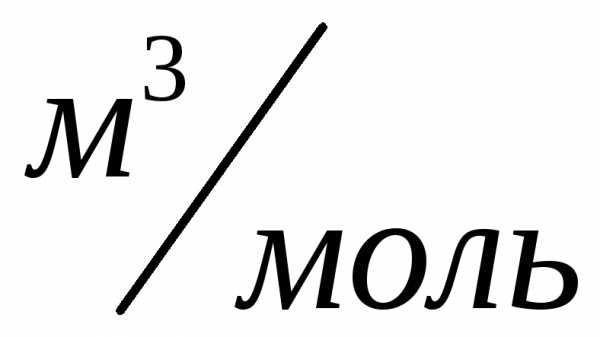 .
Один моль различных веществ содержит
одно и тоже число молекул, которое
называетсяпостоянной Авогадро:
.
Один моль различных веществ содержит
одно и тоже число молекул, которое
называетсяпостоянной Авогадро: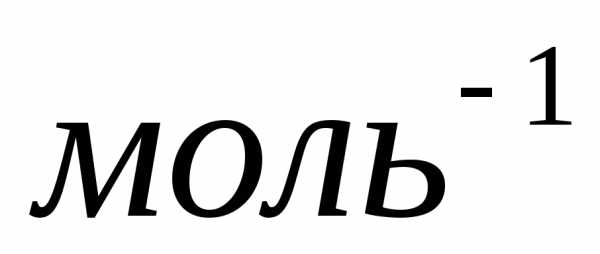 .
.
Нормальные условия: ,,
,,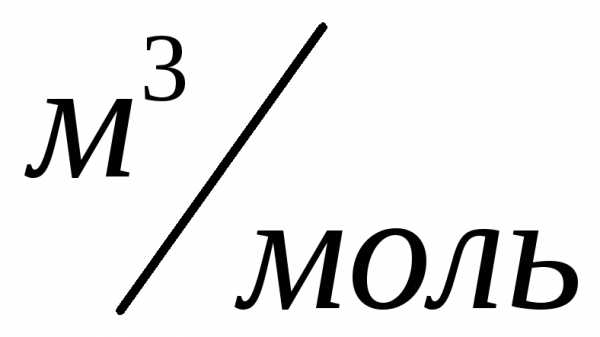 .
.
Закон Дальтона:Полное давление в
газовой смеси:где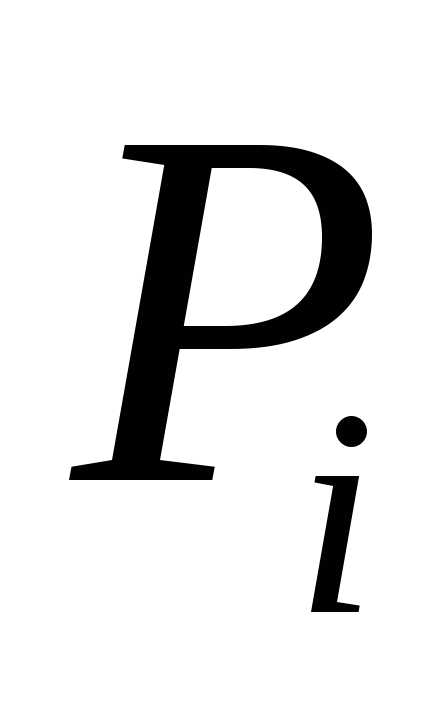 — парциальное давление
— парциальное давление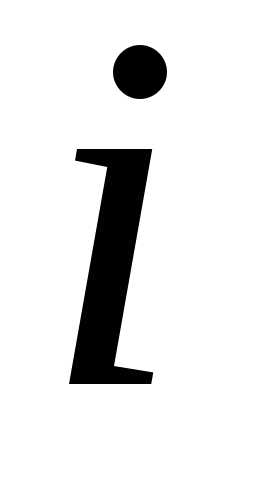 компоненты. Парциальное давление – это
давление одной компоненты газовой
смеси, когда она занимает весь объем
при той же температуре.
компоненты. Парциальное давление – это
давление одной компоненты газовой
смеси, когда она занимает весь объем
при той же температуре.
Уравнение Клапейрона – Менделеева
Уравнение, которые связывают переменные
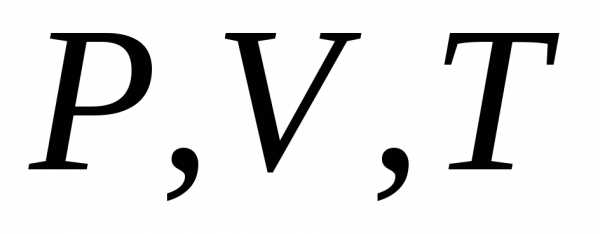 называется уравнением состояния. Оно
имеет вид.
Клапейрон вывел уравнение состояния
идеального газа, на основе законов Бойля
– Мариотта и Гей-Люссака. Рассмотрим
процесс изображенный на рисунке в
координатах
называется уравнением состояния. Оно
имеет вид.
Клапейрон вывел уравнение состояния
идеального газа, на основе законов Бойля
– Мариотта и Гей-Люссака. Рассмотрим
процесс изображенный на рисунке в
координатах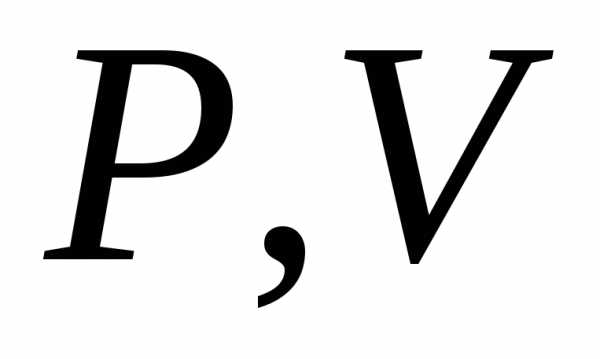 :.
Первый шаг – изотермический, второй –
изохорный процессы.
:.
Первый шаг – изотермический, второй –
изохорный процессы.
Рис
Для изотермического процесса имеем
.
Для изохорного —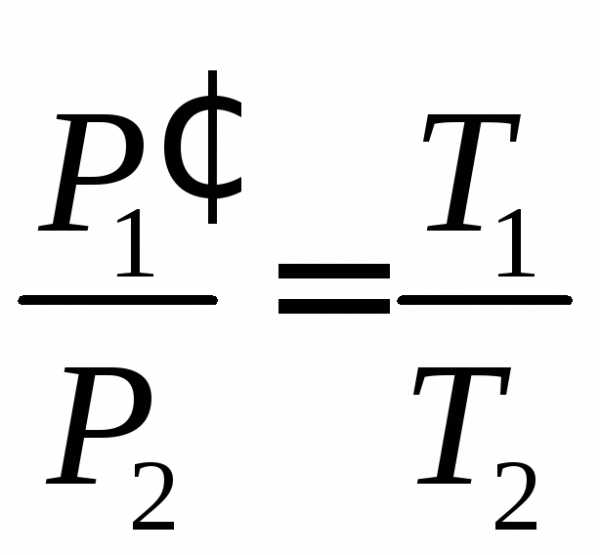 или
или
.
Исключая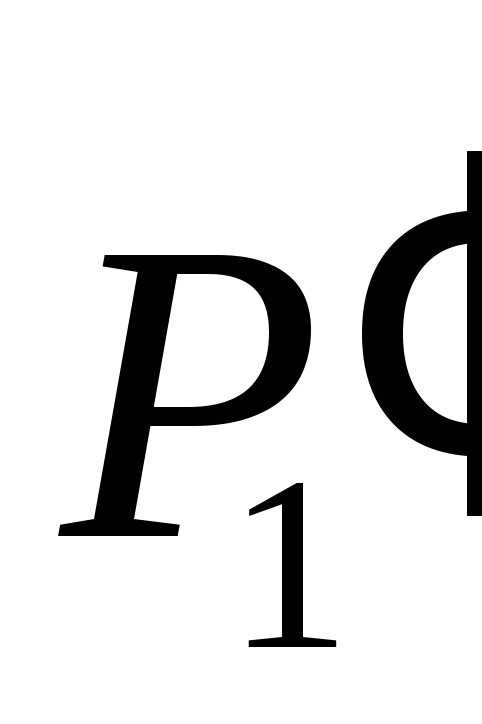 ,
в силу произвольности исходного и
конечного состояний находим
,
в силу произвольности исходного и
конечного состояний находим
 .
(1)
.
(1)
Уравнение (1) – уравнение Клапейрона.
Постоянная является различной для
разных газов. Менделеев, используя закон
Авогадро, переписал уравнение Клапейрона
для одного моля газа. Для этого он
использовал молярный объем,
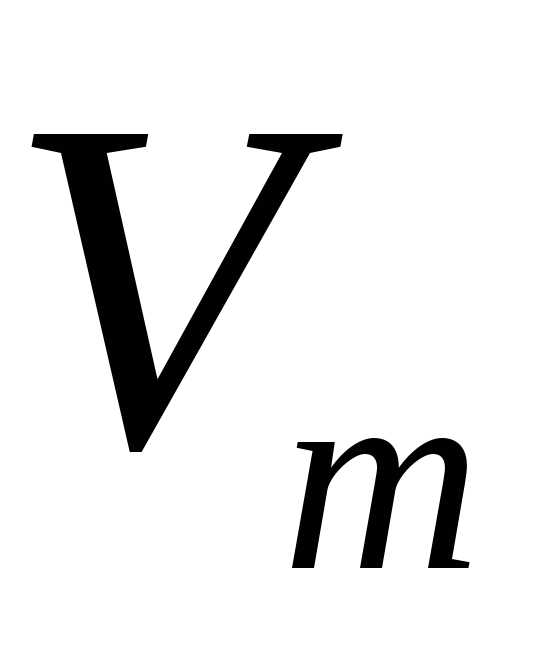 , который одинаков для любого вида газа.
Как следствие этого, постоянная в
уравнении Клапейрона будет одинаковой
для всех газов.
, который одинаков для любого вида газа.
Как следствие этого, постоянная в
уравнении Клапейрона будет одинаковой
для всех газов.
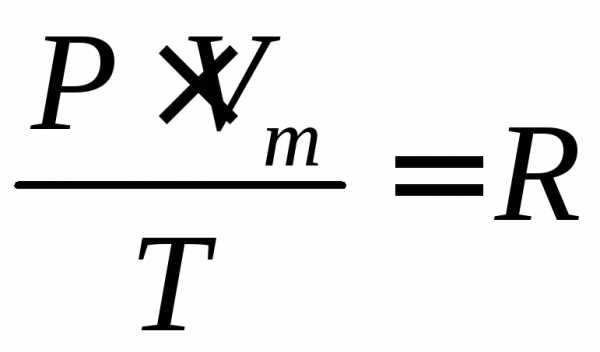 (2)
(2)
 — молярная газовая постоянная.при нормальных условиях. Для произвольной
массы газа
— молярная газовая постоянная.при нормальных условиях. Для произвольной
массы газа
(3)
где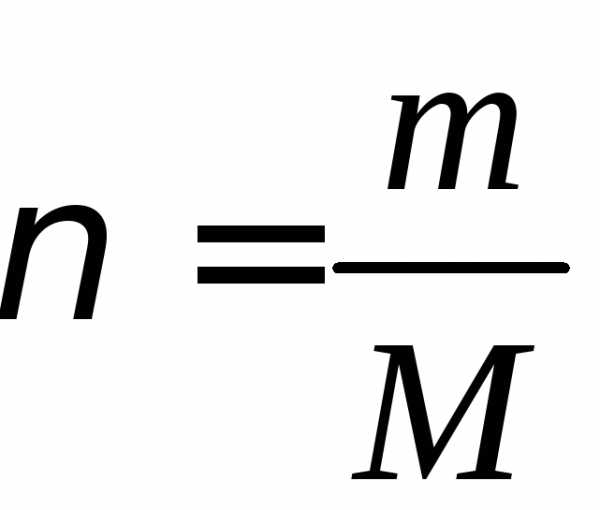 — количество вещества,
— количество вещества,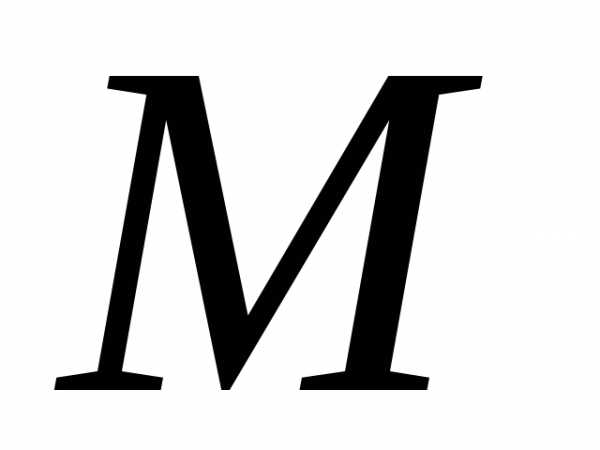 — молярная масса – это масса одного моля
вещества. Уравнения (2) и (3) это ур.
Клапейрона – Менделеева. Молярная масса
— молярная масса – это масса одного моля
вещества. Уравнения (2) и (3) это ур.
Клапейрона – Менделеева. Молярная масса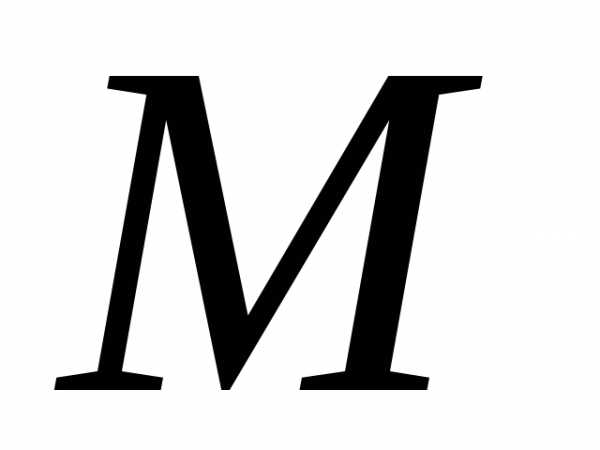 численно равна относительной массе
молекулы.
численно равна относительной массе
молекулы.
Введем постоянную Больцмана
.
Уравнение состояния идеального газа примет вид:
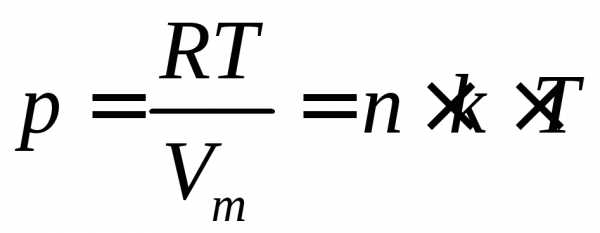
где
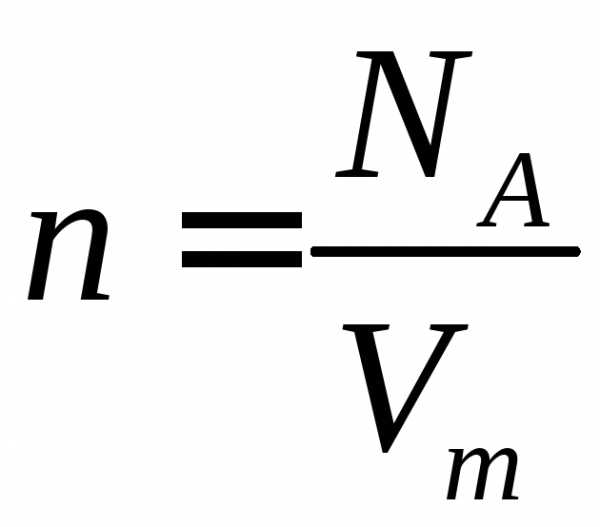 — концентрация молекул.
— концентрация молекул.
Основное уравнение молекулярно-кинетической теории идеальных газов.
Молекулы идеального газа двигаются
хаотично. Предположим, что число
соударений между молекулами газа мало
по сравнению с числом соударений о
стенки сосуда. Удары молекул о стенки
считаем абсолютно упругими. Эти удары
определяют давление в газе. Найдем
давление газа в сосуде. Выделим на стенке
сосуда площадку
 и определим давление газа на эту площадку.
Давление определяется по формуле сила,
деленная на площадь:
и определим давление газа на эту площадку.
Давление определяется по формуле сила,
деленная на площадь:
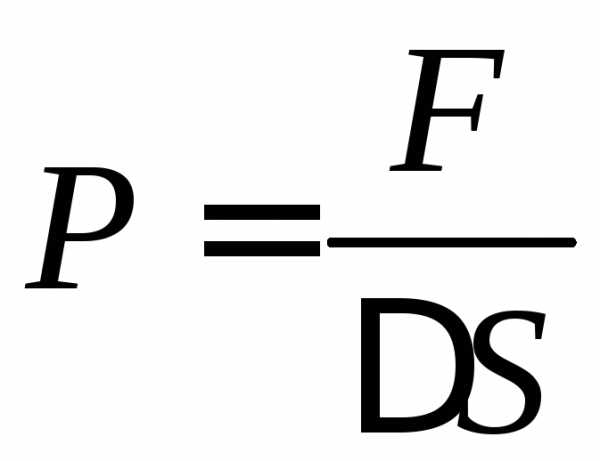 (1)
(1)
Сила определяется согласно второму закону Ньютона:
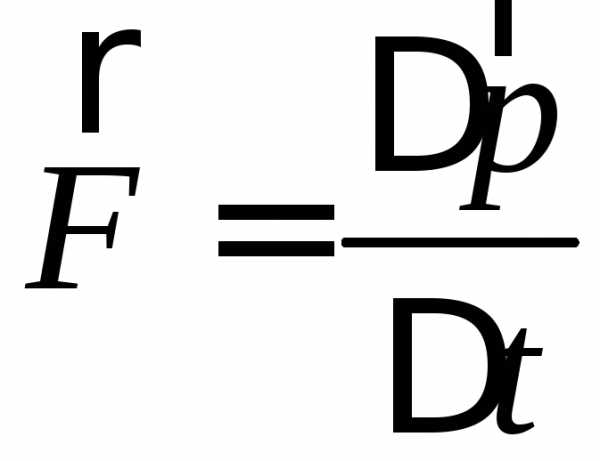 (2)
(2)
Это изменение импульса во времени.
Найдем изменение импульса молекул газа
при соударении со стенкой сосуда. Когда
молекула двигается перпендикулярно
стенке, при упругом ударе стенке
передается импульс:
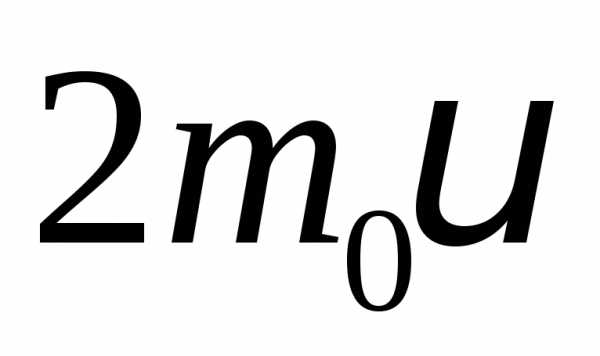 .
.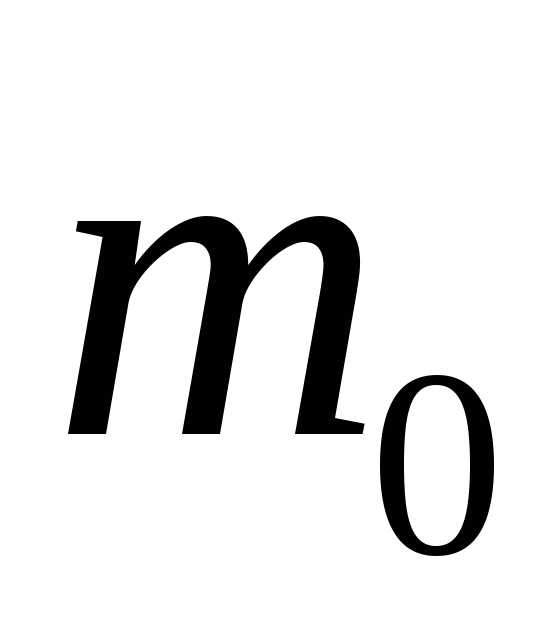 — масса молекулы,
— масса молекулы, — скорость молекулы. За время
— скорость молекулы. За время те молекулы достигнут площадки
те молекулы достигнут площадки ,
которые находятся в объеме.
Число таких молекул равно,
где
,
которые находятся в объеме.
Число таких молекул равно,
где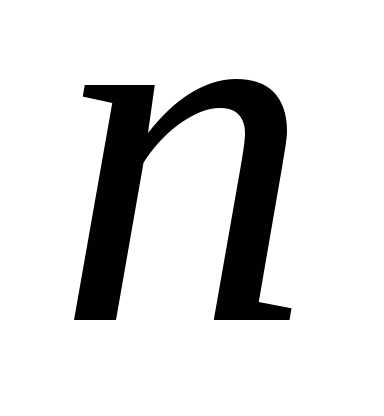 — концентрация молекул. Из-за хаотичного
движения молекулы достигают стенки под
произвольным углом, а не только под
прямым. Чтобы учесть это предположим,
что все молекулы двигаются вдоль трех
взаимно перпендикулярных направлений.
Число молекул двигающихся вдоль каждой
оси одинаково и составляет
— концентрация молекул. Из-за хаотичного
движения молекулы достигают стенки под
произвольным углом, а не только под
прямым. Чтобы учесть это предположим,
что все молекулы двигаются вдоль трех
взаимно перпендикулярных направлений.
Число молекул двигающихся вдоль каждой
оси одинаково и составляет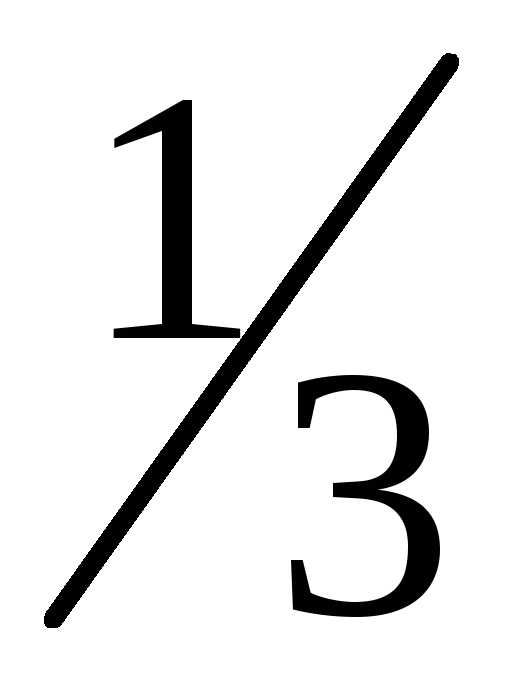 от полного числа молекул. Вдоль каждой
оси молекулы двигаются в двух
противоположных направлениях. Тогда
число ударов о площадку равно
от полного числа молекул. Вдоль каждой
оси молекулы двигаются в двух
противоположных направлениях. Тогда
число ударов о площадку равно
 .
Они передадут стенке импульс
.
Они передадут стенке импульс
(3)
Подставим найденное изменение импульса в определение силы и далее в формулу (1). Найдем давление
(4)
Поскольку молекулы двигаются с различными скоростями, то вводят среднюю квадратичную скорость:
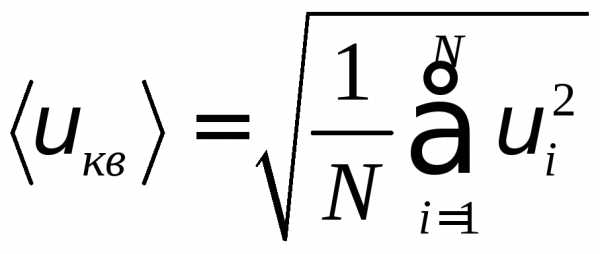 (5)
(5)
где
 — число молекул в газе. Уравнение для
давления газа в сосуде примет вид:
— число молекул в газе. Уравнение для
давления газа в сосуде примет вид:
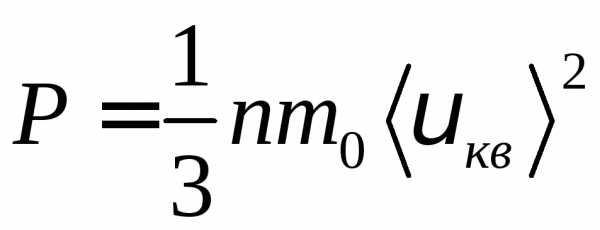 (6)
(6)
Это основное уравнение молекулярно –
кинетической теории (МКТ) газов. Точный
расчет приводит к такой формуле. Придадим
этой фортеле иной вид, используя уравнение
для идеального газа. В ур. (6) подставим
выражение для концентрации
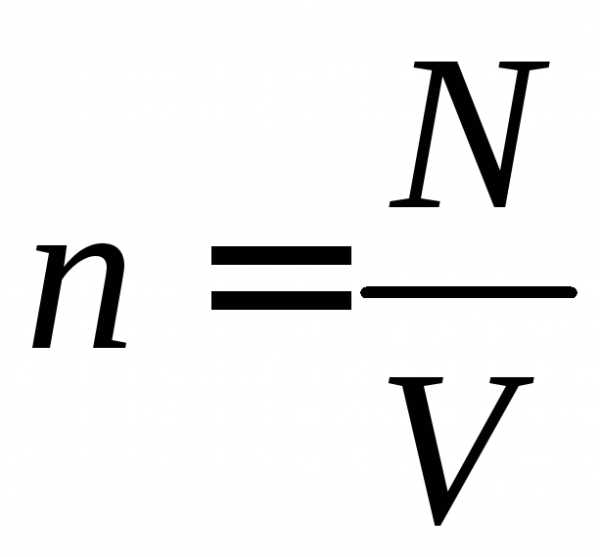 и умножим обе части равенства на объем
и умножим обе части равенства на объем .
.
(7)
где
 — суммариная кинетическая энергия
поступательного движения молекул газа.
Введем массу газа
— суммариная кинетическая энергия
поступательного движения молекул газа.
Введем массу газа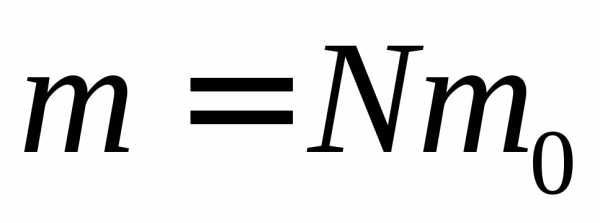 и молярную массу газа
и молярную массу газа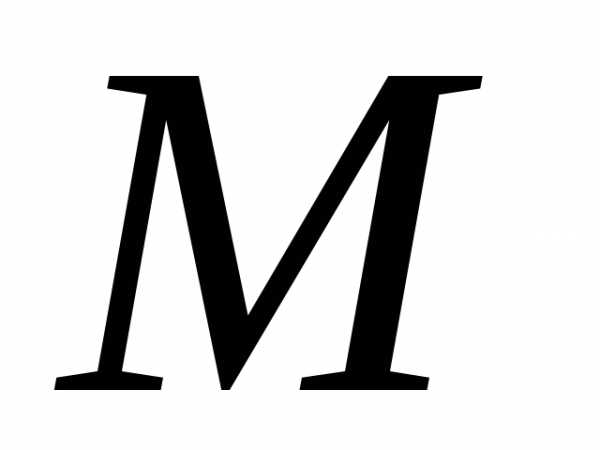 .
Это масса одного моля газа.
.
Это масса одного моля газа.
Для произвольной массы газа:
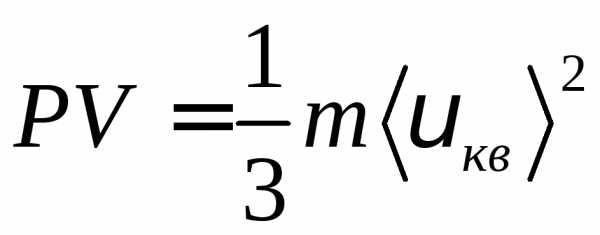 для одного моля газа:
для одного моля газа: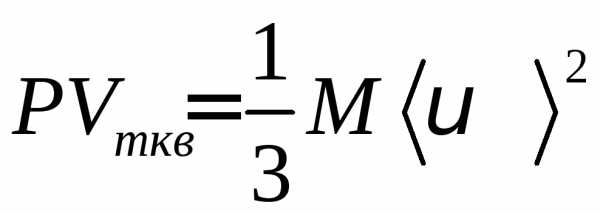 .
Используя это соотношение и уравнение
Менделеева – Клапейрона,,
получаем соотношение
.
Используя это соотношение и уравнение
Менделеева – Клапейрона,,
получаем соотношение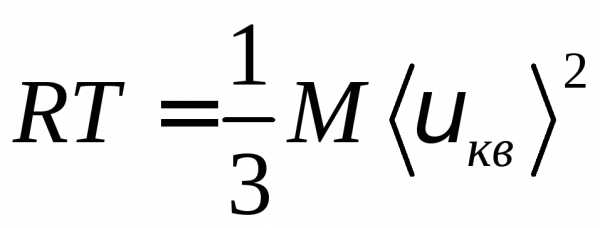 .
Отсюда находим:
.
Отсюда находим:
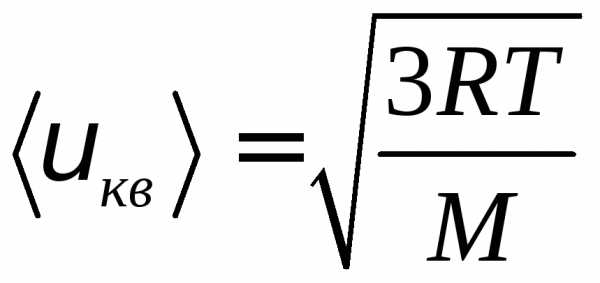 (8)
(8)
Так как молярная масса
,
где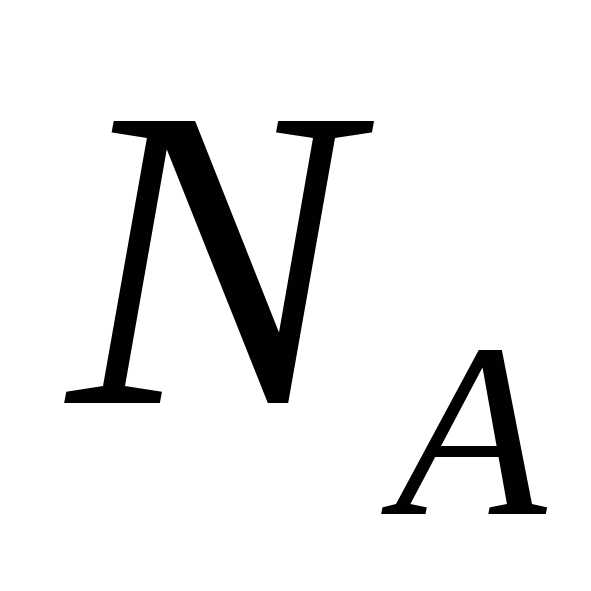 — число Авогадро, можно получить
— число Авогадро, можно получить
(9)
где
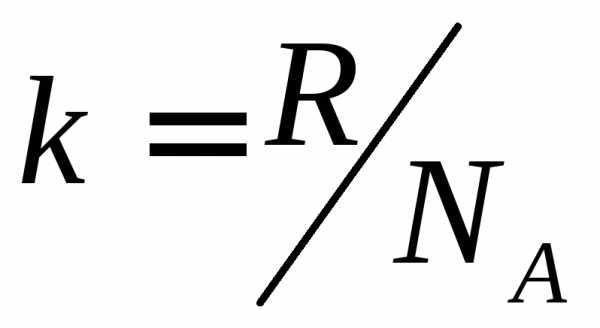 — постоянная Больцмана. Значения
среднеквадратичной скорости для
некоторых газов при комнатной температуре.
— постоянная Больцмана. Значения
среднеквадратичной скорости для
некоторых газов при комнатной температуре.
Кислород —
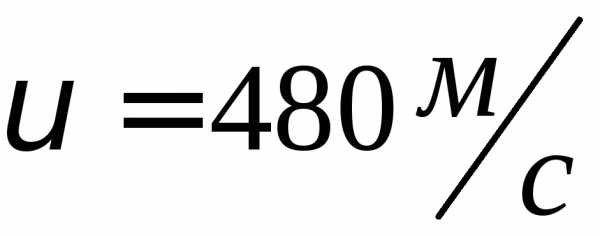 ,
водород —
,
водород —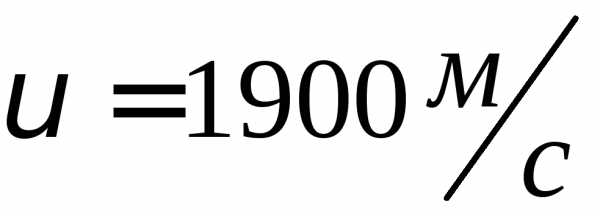 .
.
Средняя кинетическая энергия поступательного движения одной молекулы газа равна
(10)
Из Ур. (10) следует, что при
 кинетическая энергия равна нулю. На
самом деле энергия нулевых колебаний
не равна нулю вследствие квантовых
эффектов.
кинетическая энергия равна нулю. На
самом деле энергия нулевых колебаний
не равна нулю вследствие квантовых
эффектов.
Закон Максвелла о распределении молекул идеального газа по скоростям
Молекулы в газе двигаются хаотично. В
процессе движения они сталкиваются, их
скорости изменяются в широких пределах.
Если система находится в состоянии
термодинамического равновесия, средняя
квадратичная скорость
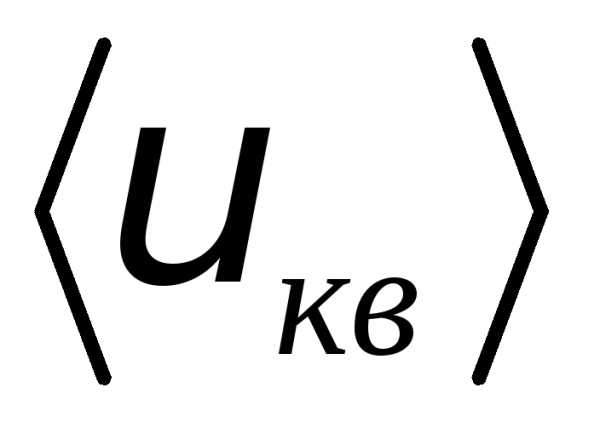 остается постоянной, хотя скорости
различных молекул могут значительно
различаться. Эта ситуация соответствует
стационарному распределению молекул
газа по скоростям. Закон распределения
молекул по скоростям вывел Максвелл в
1859 г. При выводе функции распределения
использовались следующие предположения:
остается постоянной, хотя скорости
различных молекул могут значительно
различаться. Эта ситуация соответствует
стационарному распределению молекул
газа по скоростям. Закон распределения
молекул по скоростям вывел Максвелл в
1859 г. При выводе функции распределения
использовались следующие предположения:
Число молекул в газе
 велико, молекулы тождественны и находятся
в состоянии беспорядочного теплового
движения,,
внешние силовые поля на газ не действуют.
велико, молекулы тождественны и находятся
в состоянии беспорядочного теплового
движения,,
внешние силовые поля на газ не действуют.
Максвелл ввел функцию распределения
молекул по скоростям
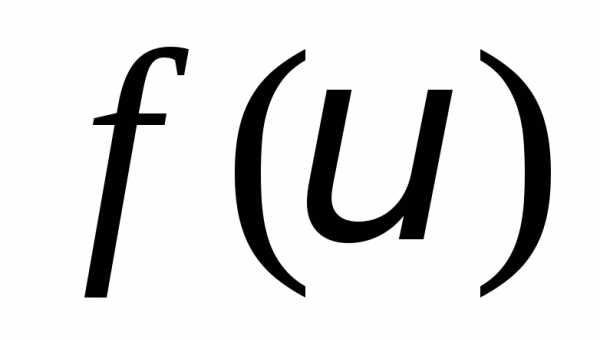 ,
где
,
где — величина скорости молекулы. График
функции
— величина скорости молекулы. График
функции
Выберем интервал скоростей
.
В него попадет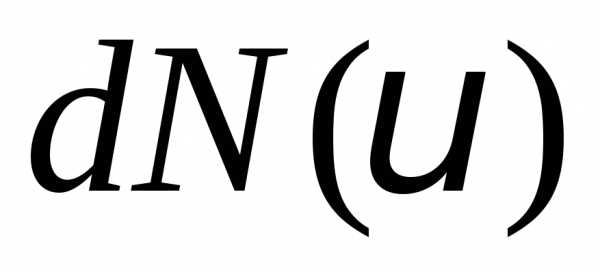 молекул. Смысл функции распрелеления
молекул. Смысл функции распрелеления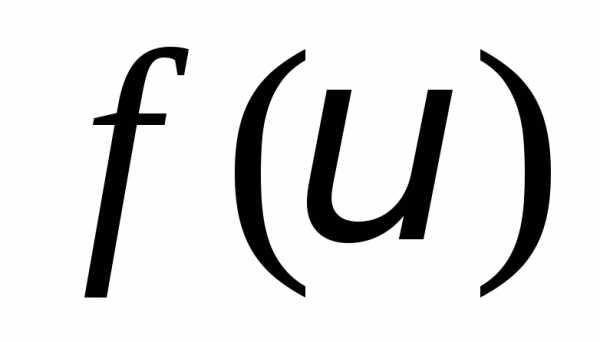 — это относительная доля молекул
— это относительная доля молекул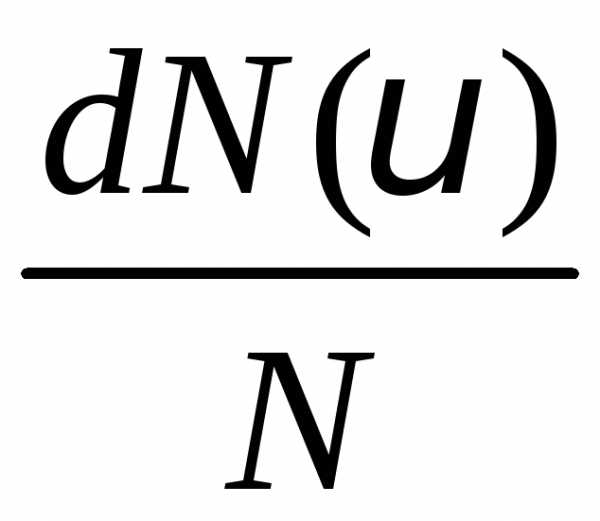 ,
скорости которых лежат в выбранном
интервале. Функция распределения
определяется как
,
скорости которых лежат в выбранном
интервале. Функция распределения
определяется как
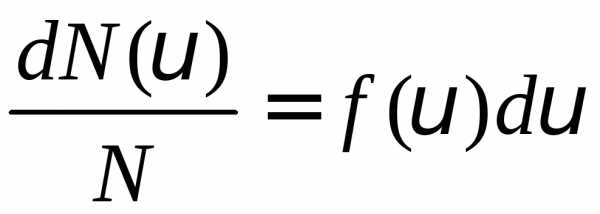 или
или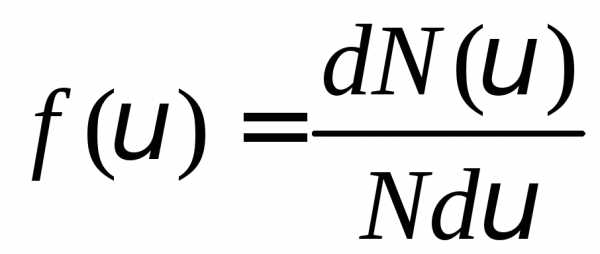 .
(1)
.
(1)
Конкретный вид функции нашел Максвелл
(2)
График функции представлен на рис. Функция (2) нормирована
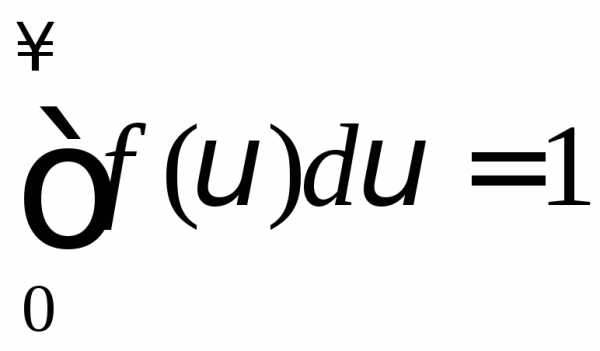 (3)
(3)
Скорость, для которой функция распределения имеет максимальное значение, называется наиболее вероятной скоростью. Для её определения найдем максимум функции распределения.
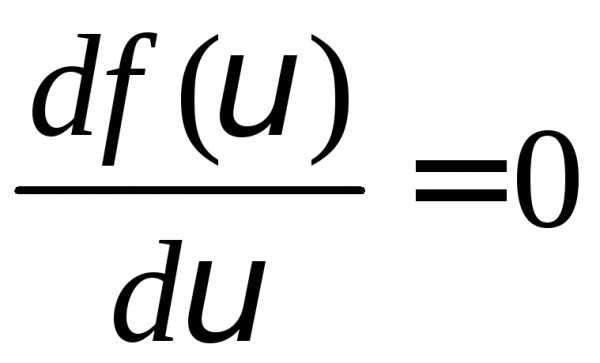 или
или
Из последнего соотношения видим, что
значения
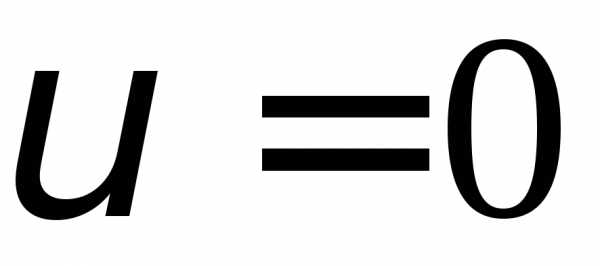 идоставляют минимум функции распределения.
Значение
идоставляют минимум функции распределения.
Значение


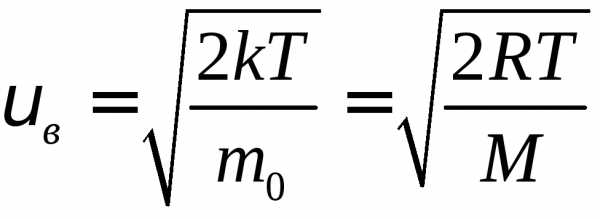 (4)
(4)
studfiles.net
