Видеоуроки по физике — 10 класс
Видеоуроки по физике — 10 класс
- Подробности
- Просмотров: 1702
На этой странице представлены несколько качественных вариантов видеоуроков по физике для 10 класса.
ВИДЕОУРОКИ ФИЗИКА 10 класс — Interneturok.ru
Обновлено — 3.09.2017
1. Механическое движение Кинематика — смотреть
2. Система материальных точек. Центр масс. Закон движения центра масс — смотреть
3. Равномерное движение тела по окружности — смотреть
4. Принцип относительности Галилея — смотреть
5. Вводный урок по теме: «Законы механики Ньютона» — смотреть
6. Закон всемироного тяготения — смотреть
7. Решение задач по динамике. Движение связанных тел — смотреть
8. Механическая работа. Мощность — смотреть
9. Влажность. Измерение влажности — смотреть
10. Второй закон термодинамики. Необратимость тепловых процессов — смотреть
 Электрический заряд. Закон сохранения заряда — смотреть
Электрический заряд. Закон сохранения заряда — смотреть12. Потенциал электрического поля Разность потенциалов — смотреть
13. Электрическое поле, Напряженность, Линии напряженности, проводники в электрическом поле — смотреть
14. Закон Кулона — смотреть
15. Решение задач по теме Закон Кулона, Напряженность электрического поля — смотреть
16. Условия для существования электрического тока — смотреть
17. Эл ток в жидкостях — смотреть
ВИДЕОУРОКИ ФИЗИКА 10 класс — Infourok.ru
Обновлено — 5.06.2021
Кинематика
1. Что такое механика ………. смотреть
2. Движение точки тела. Способы описания движения ………. смотреть
3. Уравнение равномерного прямолинейного движения ………. смотреть
4. Мгновенная скорость. Сложение скоростей ………. смотреть
 …… смотреть
…… смотреть6. Уравнение движения с постоянным ускорением ………. смотреть
7. Равномерное движение точки по окружности ………. смотреть
Динамика
8. Исаак Ньютон ………. смотреть
9. Первый закон Ньютона. Инерциальные системы отсчета ………. смотреть
10. Взаимодействие тел. Второй закон Ньютона ………. смотреть
11. Третий закон Ньютона. Понятие о системе единиц ………. смотреть
12. Силы в природе. Закон всемирного тяготения ………. смотреть
13. Первая космическая скорость. Сила тяжести и вес. Невесомость ………. смотреть
14. Деформация и силы упругости. Закон Гука ………. смотреть
15. Силы трения между соприкасающимися поверхностями твердых тел ………. смотреть
Законы сохранения в механике
16. Другая формулировка второго закона Ньютона ………. смотреть
17. Закон сохранения импульса. Реактивное движение ………. смотреть
Закон сохранения импульса. Реактивное движение ………. смотреть
18. Работа силы. Мощность ………. смотреть
19. Энергия. Кинетическая энергия и её изменение ………. смотреть
20. Работа силы тяжести. Работа силы упругости. Потенциальная энергия ………. смотреть
21. Закон сохранения энергии в механике ………. смотреть
Статика
22. Равновесие тел. Первое условие равновесия твердого тела ………. смотреть
23. Момент силы. Второе условие равновесия твёрдого тела ………. смотреть
Молекулярная физика. Тепловые явления
24. Основные положения молекулярно-кинетической теории ………. смотреть
25. Масса молекул. Количество вещества ………. смотреть
27. Строение газообразных, жидких и твердых тел ………. смотреть
28.
 Идеальный газ в молекулярно-кинетической теории ………. смотреть
Идеальный газ в молекулярно-кинетической теории ………. смотреть29. Решение задач на основное уравнение МКТ идеального газа ………. смотреть
30. Температура и тепловое равновесие. Определение температуры ………. смотреть
31. Абсолютная температура ………. смотреть
32. Измерение скоростей молекул газа ………. смотреть
33. Уравнение состояния идеального газа ………. смотреть
34. Газовые законы. Изопроцессы ………. смотреть
35. Насыщенный пар. Зависимость давления пара от температуры ………. смотреть
36. Влажность воздуха и её измерение ………. смотреть
37. Строение и свойства кристаллических и аморфных тел ………. смотреть
39. Работа в термодинамике ………. смотреть
40. Количество теплоты ………. смотреть
41. Первый закон термодинамики .
 ……… смотреть
……… смотреть42. Необратимость процессов в природе ………. смотреть
43. Принципы действия тепловых двигателей. КПД. КПД тепловых двигателей ………. смотреть
Основы электродинамики
44. Электрический заряд и элементарные частицы ………. смотреть
45. Электрическое поле. Принцип суперпозиции полей ………. смотреть
46. Силовые линии электрического поля ………. смотреть
47. Проводники в электростатическом поле ………. смотреть
48. Диэлектрики в электростатическом поле. Поляризация диэлектриков ………. смотреть
50. Потенциал электростатического поля, разность потенциалов ………. смотреть
51. Связь между напряженностью электростатического поля и напряжением ………. смотреть
52. Электроёмкость. Единицы электроёмкости.
 Конденсаторы ………. смотреть
Конденсаторы ………. смотреть53. Электрический ток. Закон Ома для участка цепи ………. смотреть
54. Электрические цепи. Последовательное и параллельное соединение ………. смотреть
55. Работа и мощность постоянного тока ………. смотреть
56. Электродвижущая сила. Закон Ома для полной цепи ………. смотреть
57. Электрическая проводимость различных веществ ………. смотреть
58. Электрический ток через контакт полупроводников р и n типов ………. смотреть
60. Электрический ток в жидкостях. Закон электролиза ………. смотреть
61. Электрический ток в газах ………. смотреть
Урок физики по теме «Механическое движение». 7-й класс
Пояснительная запискаПредлагаю проект урока физики в 7 классе, с использованием интерактивной игры – образовательного квеста.
В последние годы в реалиях современного образования очевиден недостаток внимания к обучению физике, что может стать началом кризиса научно-технического прогресса. Мне, как современному участнику педагогического процесса, уже с первого года обучения необходимо заинтересовать учащихся изучением физики, развить стремление к поисковой естественнонаучной деятельности. По моему мнению, одними из самых результативных технологий для активизации познавательной деятельности являются игровые и интерактивные технологии обучения. Интерактивную игру считаю очень эффективным видом современных интерактивных технологий, так как она создает оптимальные условия для становления, личностного роста обучающихся.
Являясь классным руководителем в 7 классе, я наблюдала за детьми еще в начальной школе, и вплотную занимаюсь изучением их возрастных особенностей с 5 класса. На подготовительном этапе я разделила класс на три группы. Формируя первую группу, я учитывала личные особенности детей (состояние здоровья, умственные способности). В первую группу вошли «эксперты»: один ученик с познавательной деятельностью ниже среднего и плохой памятью; два учащихся очень плотного телосложения, у которых возникают трудности на уроках физкультуры и которым физически будет трудно бегать в поиске мест постановки задачи; один обучающийся с дефектами речи, но высокой познавательной активностью; один мальчик с замедленностью темпа деятельности, которому необходимо чуть больше времени, чем остальным для нахождения и формулировки верного ответа. Все дети, вошедшие в эту группу, способны к изучению физики и сами изъявили желание на подготовительном этапе выступить моими помощниками. Для них были приготовлены задания на поиск, оформление и презентацию информации (часть этих заданий мы выполняли совместно, часть они делали самостоятельно, но с помощью и под контролем учителя). Формируя вторую и третью группы (на этапе вхождения в игру), я учитывала межличностные интересы детей (они хорошо общаются между собой), стремление к самообразованию и самовоспитанию участников игры, а так же познавательные интересы обучающихся (свойство их памяти и склонность к более плодотворному изучению данного предмета).
В первую группу вошли «эксперты»: один ученик с познавательной деятельностью ниже среднего и плохой памятью; два учащихся очень плотного телосложения, у которых возникают трудности на уроках физкультуры и которым физически будет трудно бегать в поиске мест постановки задачи; один обучающийся с дефектами речи, но высокой познавательной активностью; один мальчик с замедленностью темпа деятельности, которому необходимо чуть больше времени, чем остальным для нахождения и формулировки верного ответа. Все дети, вошедшие в эту группу, способны к изучению физики и сами изъявили желание на подготовительном этапе выступить моими помощниками. Для них были приготовлены задания на поиск, оформление и презентацию информации (часть этих заданий мы выполняли совместно, часть они делали самостоятельно, но с помощью и под контролем учителя). Формируя вторую и третью группы (на этапе вхождения в игру), я учитывала межличностные интересы детей (они хорошо общаются между собой), стремление к самообразованию и самовоспитанию участников игры, а так же познавательные интересы обучающихся (свойство их памяти и склонность к более плодотворному изучению данного предмета).
Большую роль в формировании естественнонаучной деятельности школьников имеют интерактивные игры. Такие игры отличаются значительным эмоциональным оттенком, характеризуются изменчивостью игровых элементов. Игровая ситуация помогает детям выбирать самый подходящий способ решения различных задач. В играх у детей формируется интерес к конкурсным заданиям. В играх дети нередко достигают лучших итогов, чем, просто выполняя задание. Игры – важный процесс коллективного общения детей, их социальной адаптации.
В зависимости от действий игроков игру можно изменить либо путем замены заданий (с расчетных на качественные) на этот случай предусмотрены дополнительные задания, которые позволят продолжить продвижение к заключительному этапу игры, либо игру можно продолжить в классе в виде игры-соревнования.
Игра — это мощный стимул обучения, это разнообразная и сильная мотивация учения. Так как урок построен в форме образовательного квеста, то, конечно, у ребят возникает желание победить, а для этого у них должны быть крепкие знания по теме урока (учащиеся повторяют пройденный материал дома). Поэтому, для создания соревновательной мотивации я выбрала главным мотив «достижение», т.к. он нацеливает учащихся на победу, достижение лучших результатов. В качестве сопутствующих мотивов решила взять: «коммуникативный», так как он прочно связан с общением, сотрудничеством, взаимодействием; «эмоциональный», ведь он вызывается положительными эмоциями: чувством интереса, радости от того, что «Я – не хуже других!», азарта – «Я могу еще лучше!»; «внешний мотив», потому, что данный мотив связан с получением признания в любой форме от товарищей по классу, сверстников и поощрения от учителя. Кроме того, подсознательно возникает установка на соревнование.
Для того чтобы коллективная деятельность стала продуктивной, её навыкам необходимо обучить.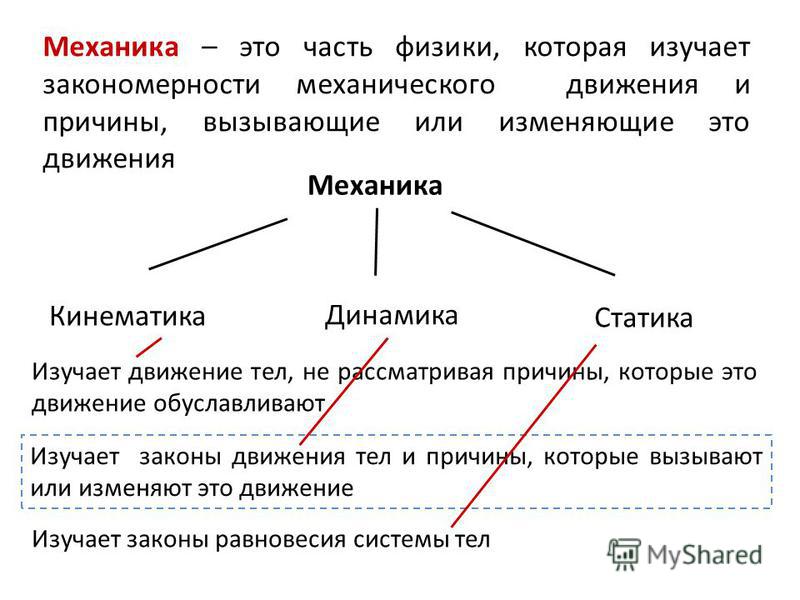 Для этого я использовала такие шаги обучения, как: мозговой штурм при решении задач разного типа на местах постановки задачи, где каждый член группы при обсуждении проблемы предлагает любой, самый неожиданный или «невозможный» вариант ее решения, принцип коллективизма в обучении – это всеобщее сотрудничество всех со всеми, всесторонняя товарищеская взаимопомощь. («Учись сам, учи других, учись у других»), принцип педагогизации деятельности каждого участника учебного процесса (при коллективном обучении все обучают каждого и каждый всех), принцип завершенности (обучаемый должен знать и уметь то, что знает и умеет обучающий по данному вопросу).
Для этого я использовала такие шаги обучения, как: мозговой штурм при решении задач разного типа на местах постановки задачи, где каждый член группы при обсуждении проблемы предлагает любой, самый неожиданный или «невозможный» вариант ее решения, принцип коллективизма в обучении – это всеобщее сотрудничество всех со всеми, всесторонняя товарищеская взаимопомощь. («Учись сам, учи других, учись у других»), принцип педагогизации деятельности каждого участника учебного процесса (при коллективном обучении все обучают каждого и каждый всех), принцип завершенности (обучаемый должен знать и уметь то, что знает и умеет обучающий по данному вопросу).
Игра в образовательном процессе, а особенно интерактивный квест меняет мою роль, как учителя, с активной на несколько других ролей. На подготовительной стадии я принимаю на себя роль «тренера». При этом преследую цель – тренировка игроков первой группы на выполнение их роли «эксперта». Подготавливаю их к решению задач, которые будут предложены двум другим группам на местах постановки задачи. Далее я беру на себя роль «инструктора». Эту роль я исполняю на стадии ввода в игру. Цель – описание правил игры игрокам второй и третьей группы, прогнозирование последствий игровых действий. Следующая роль, исполняемая мной во время игры – это «Судья-рефери». Цель – поддержание хода игры через обеспечение соблюдения игровых правил, и, наконец, я становлюсь «Арбитром» на стадии анализа и оценки результатов игры.
Далее я беру на себя роль «инструктора». Эту роль я исполняю на стадии ввода в игру. Цель – описание правил игры игрокам второй и третьей группы, прогнозирование последствий игровых действий. Следующая роль, исполняемая мной во время игры – это «Судья-рефери». Цель – поддержание хода игры через обеспечение соблюдения игровых правил, и, наконец, я становлюсь «Арбитром» на стадии анализа и оценки результатов игры.
Технологическая карта урока
| Тема урока | «Механическое движение» |
||||||
Тип урока |
комбинированный урок закрепления изученного материала, применения знаний и умений по данной теме, и обобщения и систематизации знаний |
||||||
Формы, приемы, методы |
Форма урока: интерактивной игры – образовательного квеста. |
||||||
Педагогические технологии |
Игровые технологии, интерактивные технологии обучения, информационно-коммуникационные технологии, здоровьесберегающие технологии, технология сотрудничества |
||||||
Цель |
повторение и закрепление основных понятий и формул (механическое движение, траектория, пройденный путь, равномерное и неравномерное движение, скорость, единицы скорости, формула скорости, средняя скорость), применение полученных знаний и умений в новой ситуации (во время прохождения образовательного квеста) |
||||||
Планируемые результаты |
|||||||
Личностные результаты |
Метапредметные результаты |
Предметные результаты |
|||||
Сформированность познавательных интересов учащихся; убежденность в необходимости разумного использования достижений науки и техники; самостоятельность в приобретении новых знаний и практических умений;
|
Формирование следующих универсальных учебных действий (УУД). |
Учащиеся должны знать/понимать: |
|||||
Конспект урока
Движение. Механическое движение — урок. Физика, 9 класс.
Движения в природе имеют особое значение. Можно сказать даже так: движения создали наш мир.
Если бы не было движения элементарных частиц, то и не было бы химических элементов; не было бы химических веществ — не было бы вообще ничего.
Переполнена движениями живая природа. Само понятие живого воспринимается как организованное движение. Стоит только приостановиться этому движению в живой клетке, и она отмирает.
Но и в мёртвой клетке, и в простом камне, лежащем на обочине дороги, сохраняется движение. Если даже не учитывать движения химических элементов внутри этих предметов, то в них всегда имеется так называемое тепловое движение молекул (рис. \(1\)).
Рис. \(1\)
Неспокоен и космос. В результате распада химических элементов внутри звёзд и планет к этим космическим объектам со всех сторон устремляются элементарные частицы. Как утекающая из ванны вода закручивается в водоворот, так и центростремительные потоки частиц звёзд и планет закручиваются в гигантские космические спирали (рис. \(2\)).
Рис. \(2\)
Этим объясняется и то, что наша планета Земля вращается вокруг своей оси, и то, что она летает вокруг Солнца (рис. \(3\)).
Рис. \(3\)
Движения могут быть зримыми, как, например, движение автомобиля, и незримыми — например, тепловое движение. Они могут быть ощущаемыми (тепло на ощупь) и неощущаемыми (движения питательных веществ в растениях).
Движения можно разделить на организованные, например, вихревые движения химических элементов, и на беспорядочные, например, движения камней в горной лавине.
И звук, и свет, и электричество — всё это представляет собой движение в разных видах.
Движения могут переходить из одних видов в другие. Так, трение преобразует видимые движения предметов в их тепловые движения. И наоборот, невидимые тепловые движения химических элементов можно превращать в видимые, например, в двигателе автомобиля. Движение электронов можно превратить в свет, а свет можно превратить в тепловые движения.
Таким образом, говоря о движении, мы имеем в виду изменения, которые происходят в окружающем нас мире.
Из всех видов движения самым простым является механическое движение.
Если тело с течением времени изменяет свое местоположение относительно других тел, то говорят, что это тело движется. А само движение называют механическим.
учитель из Одессы записал 473 урока на YouTube
25 Мая, 2018, 12:45
170996
Преподаватель Ришельевского лицея Павел Виктор создал полный углубленный курс физики для специализированных физико-математических школ. Курс состоит из видео, записанных во время уроков, которые Виктор ежедневно в течение трех лет транслировал в прямом эфире на YouTube. Всего в него вошло 473 урока. Об этом сообщает Mayak со ссылкой на Ришельевский лицей. Редактор AIN.UA детально расспросила преподавателя о его работе с YouTube.
Курс состоит из видео, записанных во время уроков, которые Виктор ежедневно в течение трех лет транслировал в прямом эфире на YouTube. Всего в него вошло 473 урока. Об этом сообщает Mayak со ссылкой на Ришельевский лицей. Редактор AIN.UA детально расспросила преподавателя о его работе с YouTube.
Видео рассортированы по темам и доступны бесплатно на Youtube-канале «РЛ Физика». Как сообщается на сайте лицея, курс Павла Виктора по физике стал наиболее полным из доступных в интернете на сегодня. Курс физики охватывает все темы углубленной программы 9-11 классов от «Механики» до «Физики ядра», также есть избранные темы для 7-8 классов.
Трансляции Виктора суммарно набрали более 7 млн просмотров, на канал подписались почти 60 000 пользователей. Под видео ученики оставляют комментарии и задают вопросы. Чтобы просмотреть их и дать ответы, учитель ежедневно тратит около часа времени. «Иногда дети в комментариях оставляют такие вопросы, над которыми нужно крепко подумать, прежде чем дать ответ. Это вдохновляет меня, потому что интересные осмысленные вопросы дают пищу для размышлений», — заявил Виктор.
Это вдохновляет меня, потому что интересные осмысленные вопросы дают пищу для размышлений», — заявил Виктор.
В 2021 году у Павла Виктора свыше 738 000 подписчиков и более 35,4 млн просмотров. Канал регулярно обновляется. Всего учитель опубликовал более 700 уроков по физики, как для базовой, так и для углубленной школьной программы. Также Павел Виктор выкладывает полнометражные научные фильмы с дикторским текстом и музыкальным сопровождением.
С момента публикации этого материала, Павел Виктор стал популярным блогером, а также выпустил книгу «Физика. Основы и механическое движение». В частности, в ней приведены основные темы по механике, что пригодятся как школьникам, которым нужно закрепить знания по предмету. В издательстве, книгу порекомендовали и взрослым, которые хотят глубже понимать физику.
<span style=»display: inline-block; width: 0px; overflow: hidden; line-height: 0;» data-mce-type=»bookmark» class=»mce_SELRES_start»></span>
Курс Павла Виктора смотрят не только его ученики, как предполагалось изначально, но весь мир. Пользователи приходят со всей Украины, Казахстана, Беларуси, Германии и других стран.
Пользователи приходят со всей Украины, Казахстана, Беларуси, Германии и других стран.
«Что интересно, если посмотреть по возрастным категориям, среди зрителей больше всего не школьников, а студентов — молодых людей 18-24 лет. Есть и зрители старшего поколения. Видимо, учителя. Наверное, они используют это для подготовки к урокам», — поделился Павел Андреевич в комментарии AIN.UA.
Как все начиналось
Идея транслировать уроки возникла спонтанно. Когда ученики болели, они просили Павла Андреевича включить Skype, чтобы виртуально присутствовать на уроке. Учитель согласился, и провел несколько таких уроков, которые просто шли без записи в одном канале для одного ребенка. «Приходилось таскать за собой компьютер, чтобы показать правую часть доски, левую часть доски, а качество изображения там невысокое», — вспоминает преподаватель. Так появились первые формы дистанционного обучения.
Так появились первые формы дистанционного обучения.
Потом в лицее было несколько карантинов. А для физики очень важно не прерывать процесс обучения, потому что преподавателю будет сложно рассказать весь скопившийся материал в сжатые сроки, отмечает Павел Андреевич. Поэтому он начал пробовать снимать уроки на видео и выкладывать в интернет.
Администрация лицея и родители поддержали его идею и помогли установить в аудитории хорошее оборудование, которое позволяет транслировать уроки физики в хорошем качестве. Сейчас в распоряжении Павла Андреевича две видеокамеры (одна для общего плана, другая для демонстрации мелких предметов, страниц учебника или крупных планов графиков на доске), видеомикшер, мощный компьютер и быстрый интернет.
«Появилась возможность транслировать уроки в реальном времени прямо на YouTube, а там они записываются. Попробовали, получилось, вроде понравилось. Тогда я решил записывать все уроки подряд», — рассказал учитель.
Тяжелый труд
Поначалу Павел Андреевич не задумывался о том, во что это выльется — ему понравилось, что можно так легко доносить детям информацию. Но вскоре стало понятно, что это очень тяжелая работа — подготовка к лекциям, ежедневные трансляции, обработка комментариев и ответы на вопросы отнимали много времени. Однако останавливаться было поздно — Виктор решил довести дело до конца.
Но вскоре стало понятно, что это очень тяжелая работа — подготовка к лекциям, ежедневные трансляции, обработка комментариев и ответы на вопросы отнимали много времени. Однако останавливаться было поздно — Виктор решил довести дело до конца.
По словам Павла Виктора, проведя последнюю трансляцию курс физики для старших классов, он поначалу испытал облегчение. Однако вскоре почувствовал опустошенность. «Так бывает после большого и длительного байдарочного похода, когда хочется побыстрее добраться до теплого и уютного дома. Но переступив порог, начинаешь тосковать по природе, туристическому драйву, экстриму, приключениям», — комментирует преподаватель.
Сегодня преподаватель записывает завершающий курс физики для 7 класса, после чего планирует приступить к курсу для 8 класса по просьбе зрителей. «Это напряженная работа, на самом деле, она выматывает. Но если ты уже начал снимать, надо показать побольше. Вложить максимум демонстраций и содержания, все то, что обычно ты из экономии времени мог не рассказывать», — говорит Павел Андреевич.
После успеха эксперимента с трансляциями по физике, администрация лицея решила заняться разработкой курсов дистанционного обучения и по другим предметам. У лицея уже есть Youtube-каналы с уроками по украинскому языку и математике. Сообщается, что Ришельевский лицей стал экспериментальной площадкой по «разработке и внедрению педагогических технологий дистанционного обучения на базе образовательного центра с использованием современных электронных средств коммуникации» согласно специального указа МОН.
Секрет успеха
По мнению Павла Виктора, его курс физики стал успешным, потому что он — полностью естественный и живой. «Почему у меня получилось? Я просто вел уроки, я не шел специально ни на какую студию, моих видео не коснулся монтажер. Это просто эфир. И в этом кроется два преимущества: во-первых, это наименее трудозатратно и поэтому выполнимо, во-вторых, это живой урок, и у зрителей возникает эффект присутствия. К доске выходят дети, общаются с преподавателем, и получается, ты как бы еще один ученик в классе, — пояснил он.
Недавно я читал отзывы и понял, что огромное преимущество в том, что это — живые уроки. Поэтому они лучше воспринимаются, чем спрессованный 10-минутный ролик, который содержит материал урока. Это более естественно».
Напомним, украинский стартап разработал «электронную школу»: дневники, журналы, учебники — все в онлайне.
Техническая механика — Сайт Антона Чиркова
В целях упрощения внеаудиторной самостоятельной работы студентов технических специальностей в 2012-2013 учебном году были сняты и смонтированы шесть видеоуроков по решению основных задач из курса «Техническая механика». Они размещены в свободном доступе на видеохостинге YouTube и в социальной сети ВКонтакте.
За время существования видеоуроков количество просмотров превысило 470 тысяч.
При работе с видеоуроками рекомендуется вести записи.
Видеоурок 1. Определение реакций жёстких стержней в плоской системе сходящихся сил
Раздел дисциплины: Статика.
Продолжительность: 28 минут.
Видеоурок 2. Определение реакций опор двухопорной балки
Раздел дисциплины: Статика.
Продолжительность: 31 минута.
Видеоурок 3. Определение координат центра тяжести сложной плоской фигуры
Раздел дисциплины: Статика.
Продолжительность: 21 минута.
Видеоурок 4. Построение эпюр продольных сил и нормальных напряжений (при деформации растяжения/сжатия)
Раздел дисциплины: Сопротивление материалов.
Продолжительность: 35 минут.
Видеоурок 5. Проектирование вала в условиях деформации кручения
Раздел дисциплины: Сопротивление материалов.
Продолжительность: 28 минут.
Видеоурок 6. Расчёты на прочность и жёсткость при прямом поперечном изгибе
Раздел дисциплины: Сопротивление материалов.
Продолжительность: 49 минут.
10 каналов о физике, на которые стоит подписаться
«Афиша Daily» рекомендует лучшие видеоблоги на русском и английском языках, за которыми стоит следить, чтобы начать разбираться в физике.
Физика от Побединского
174 000 подписчиков
Канал ведет молодой популяризатор науки, выпускник МФТИ Дмитрий Побединский. Он коротко и увлекательно рассказывает о физических явлениях и наглядно показывает, как знание физики может пригодиться в повседневной жизни. Например, объясняет феномен популярности спиннеров и рассказывает о физических лайфхаках — как налить колу без пены, где лучше всего установить колонки и как быстро сделать лед.
Vsauce
12 000 000 подписчиков
Авторы Vsauce с точки зрения физики и других естественных наук отвечают на любопытные, забавные, а порой и парадоксальные вопросы. Что будет, если все жители Земли одновременно подпрыгнут? Каково разрешение человеческого глаза? Сколько весит тень? Отличный канал для повзрослевших почемучек, которые хотят больше узнать о нашем мире. Другие видео от создателей Vsauce можно посмотреть на каналах-последователях Vsauce2 и Vsauce3.
minutephysics
3 900 000 подписчиков
Один из самых популярных каналов англоязычного YouTube о физике: minutephysics идеально подойдет тем, кто хочет быстро разобраться в азах этой науки. В коротких видео авторы при помощи рисунков объясняют сложные на первый взгляд темы — принцип параллельных вселенных, основы гравитации и природу темной материи. Более продвинутым пользователям могут понравиться забавные ролики про то, как путешествовать во времени или почему существование дождевых капель невозможно с точки зрения математики.
Physics Girl
692 000 подписчиков
Молодой ученый из США Дайанна Коверн делится своими знаниями и любовью к физике. Сама Дайанна специализируется на астрофизике, поэтому многие видео посвящены именно этому разделу науки и связанным с ним темам. Среди прочего девушка рассказывает о том, как работает невесомость и в чем разница между солнечным и лунным затмением. Также Дайанна делает видео с простыми и забавными физическими экспериментами, которые зрители при желании могут повторить самостоятельно — скажем, создать ураган на поверхности мыльного пузыря.
PBS Space Time
942 000 подписчиков
Если вы интересуетесь астрофизикой, глубже в тему можно погрузиться благодаря видео с канала PBS Space Time. Создатели разбирают фундаментальные вопросы — уровня «откуда взялись время и пространство», — рассказывают о квантовой теории поля и разъясняют идеи физика Ричарда Фейнмана. Содержание роликов рассчитано на более или менее подготовленного зрителя. Если вы совсем ничего не понимаете в физике, лучше сначала ознакомиться с основами.
DoodleScience
21 000 подписчиков
На этом канале нет видео с забавными экспериментами и ответами на экстраординарные вопросы — зато есть короткие скетчи, которые помогут в кратчайшие сроки вспомнить школьный курс физики и заново усвоить основные формулы. Скетчи минималистичны и наглядны: ничего лишнего, только фундаментальные научные законы.
GetAClass — Физика в опытах и экспериментах
49 000 подписчиков
Русскоязычный канал о физике, который лучше всего подойдет для быстрого изучения науки с нуля. В 4–5-минутных видео авторы емко и доступно объясняют, как работают те или иные физические явления. Есть удобное разделение роликов на тематические плейлисты в соответствии с разделами физики — от аэродинамики и звука до света и тепловых явлений. Новые видео появляются каждую неделю.
В 4–5-минутных видео авторы емко и доступно объясняют, как работают те или иные физические явления. Есть удобное разделение роликов на тематические плейлисты в соответствии с разделами физики — от аэродинамики и звука до света и тепловых явлений. Новые видео появляются каждую неделю.
CrashCourse — Physics
6 200 000 подписчиков
«Физическая» подборка видео от образовательного канала CrashCourse подойдет тем, кому недостаточно просто освежить в памяти школьную программу. Плейлист состоит из сорока шести 10-минутных видео, в которых последовательно раскрываются все ключевые физические законы и явления. CrashCourse проводит зрителя от движения по прямой линии до теории относительности и квантовой механики.
Veritasium
4 300 000 подписчиков
Канал был создан в 2011 году популяризатором науки Дереком Мюллером и с тех пор неоднократно получал положительные отзывы от критиков, а видео Veritasium попадали на Scientific American и CBS News. Создатели Veritasium регулярно развеивают распространенные мифы о науке и проводят эксперименты, чтобы наглядно продемонстрировать те или иные физические эффекты. На Veritasium порой появляются и забавные околонаучные ролики вроде пародии на песню Jet «Are You Gonna Be My Girl?» о том, что такое электричество.
Создатели Veritasium регулярно развеивают распространенные мифы о науке и проводят эксперименты, чтобы наглядно продемонстрировать те или иные физические эффекты. На Veritasium порой появляются и забавные околонаучные ролики вроде пародии на песню Jet «Are You Gonna Be My Girl?» о том, что такое электричество.
brusspup
2 500 000 подписчиков
Автор канала ставит захватывающие физические эксперименты, записывает их на видео и делится с подписчиками. Практического применения большинство из его трюков не имеет, но фанатам оптических иллюзий канал наверняка понравится. Некоторые опыты автора несложно повторить в домашних условиях при помощи подручных средств. Пользы вы из этого, скорее всего, не извлечете, зато интересно проведете время.
Інтерв’ю з українцем, який працює на Великому адронному колайдері: «Фізика – це як секс»
Які експерименти проводяться на Великому адронному колайдері (ВАК)? Що таке Стандартна модель та як вона з’явилася? Що означає відкриття бозона Хіггса? Як впіймати нейтрино та чому ці частинки є новим напрямом у розумінні Всесвіту? Регалії українського фізика Миколи Хандоги досить великі – науковий співробітник Лабораторії ядерної фізики та фізики високих енергій Університету Сорбонни, учасник експерименту ATLAS в CERN, PhD з фізики елементарних частинок. Його участь в експериментах, які проводяться на адронному колайдері (CERN) і великий досвід дозволяють читачеві зрозуміти, що зараз відбувається у фізиці та який великий пристрій побудують після ВАК.
Його участь в експериментах, які проводяться на адронному колайдері (CERN) і великий досвід дозволяють читачеві зрозуміти, що зараз відбувається у фізиці та який великий пристрій побудують після ВАК.
ITC.ua розпочинає серію статей з українськими вченими, котрі працюють у великих наукових інститутах, популяризують науку та можуть розказати, що нас чекає в науковому майбутньому.
Ким ви працювали до співпраці із CERN?
Я дніпрянин, у 2007 році закінчив фізичний факультет Дніпровського національного університету й того ж року вступив до аспірантури за спеціальністю «Теоретична фізика». Мене з дитинства цікавило, як влаштований наш світ, а отже, дуже хотілося і самому докластись до досліджень у цьому напрямі. На жаль, подібно до багатьох своїх друзів, в Україні я не довів справу до захисту, почав працювати в іншій сфері. Але через кілька років тяга до фізики все-таки взяла своє і я поїхав до Парижа, щоб продовжити те, що почав.
Уже у Франції довелося трохи повчитися, щоб скоригувати профіль спеціалізації з теоретичної на експериментальну фізику. Теоретики та експериментатори фактично займаються одними й тими самими речами, але використовують для того різні методи, а отже, і бачать ці речі дещо по-різному. Як на мене, вузьким місцем сучасної фізики є саме недостатня кількість непояснених експериментальних даних. У другій половині ХХ століття теоретики добряче попрацювали, отже тепер м’яч на боці експериментаторів.
Теоретики та експериментатори фактично займаються одними й тими самими речами, але використовують для того різні методи, а отже, і бачать ці речі дещо по-різному. Як на мене, вузьким місцем сучасної фізики є саме недостатня кількість непояснених експериментальних даних. У другій половині ХХ століття теоретики добряче попрацювали, отже тепер м’яч на боці експериментаторів.
Який ваш профіль спеціалізації? Чим ви займаєтеся на Великому адронному колайдері (ВАК)? Розкажіть про свій звичайний робочий день.
ВАК – це експериментальна установка, яка розганяє протони майже до швидкості світла. Collide з англійської означає «стикати», що натякає нам на дуже просту суть роботи колайдера: прискорені частинки стикають між собою, щоб подивитися, що з того буде. Але що значить «подивитись»? Чим на них дивитись? Звісно, що не очима.
На ВАК облаштовано чотири точки зіткнень протонів, навколо яких побудовано чотири експерименти – ATLAS, CMS, LHCb та ALICE. Їх ще називають детекторами, але, наприклад, експеримент ATLAS, на якому працюю я, розміром з восьмиповерхівку – 25 метрів заввишки та 45 метрів завдовжки, нашпигований стійкою до радіації хай-тек-електронікою, надпровідними магнітами тощо. Інші експерименти трохи менші, але цілком співмірні за масштабом.
Інші експерименти трохи менші, але цілком співмірні за масштабом.
У колаборації ATLAS працює понад три тисячі фізиків, і це не рахуючи інженерів, комп’ютерних спеціалістів, технічного персоналу тощо. Це одна з найбільших наукових колаборацій у світі. Усі ці люди не знаходяться весь час у Женеві: вони є співробітниками майже двохсот наукових установ по всьому світі. Проте досить часто ми подорожуємо до ЦЕРНу: інколи на тижні чи місяці, інколи й на кілька років. Сам ЦЕРН – це щось на зразок місця зустрічі: переважна більшість людей, які там знаходяться, є співробітниками інших установ і працюють там тимчасово.
Кожна стаття, яка публікується від імені колаборації, підписується усіма її членами – дехто жартівливо називає подібні статті, де перелік імен може займати декілька сторінок, «братськими могилами».
Звісно, що робота в подібній колаборації, розпорошеній по всій земній кулі, має свою специфіку. Це справжнє перехрестя культур, робочих підходів і звичок.
Працюють науковці, як водиться, у наукових установах. Це можуть бути лабораторії в університетах чи науково-дослідних інститутах (НДІ). Робоче місце науковця, мабуть, найбільше схоже на робоче місце IT-спеціаліста: на столі лаптоп і пара моніторів.
Через те, що наш експеримент такий величезний, спектр діяльності науковця дуже широкий. У цілому можна виділити три великі частини:
- робота над інструментальним оснащенням детектора;
- розробка алгоритмів і програмного забезпечення для обробки даних з детектора;
- аналіз даних для отримання фізичних результатів;
Перший пункт зазвичай передбачає «роботу руками» – тобто з приладами та інструментами у спеціально обладнаних приміщеннях. Фізичне виготовлення та випробування елементів детектора – це часто робота в «чистій кімнаті» – там треба мати спеціальний одяг, дотримуватись правил задля зменшення запиленості і т. ін.
Останні два пункти можна робити просто з робочого комп’ютера, вони часто вимагають певних навичок з програмування та загальної комп’ютерної грамотності. У колайдері кожну секунду відбувається 40 мільйонів зіткнень, ці дані фіксуються, відбираються, записуються. Отже фактично це аналіз великих даних. Ці дані доступні всім учасникам експерименту завдяки розгалуженій системі обміну даними, яка називається CERN GRID. До наших послуг обчислювальний кластер з тисячами ядер CPU та сотнями ядер графічних процесорів GPU.
У колайдері кожну секунду відбувається 40 мільйонів зіткнень, ці дані фіксуються, відбираються, записуються. Отже фактично це аналіз великих даних. Ці дані доступні всім учасникам експерименту завдяки розгалуженій системі обміну даними, яка називається CERN GRID. До наших послуг обчислювальний кластер з тисячами ядер CPU та сотнями ядер графічних процесорів GPU.
Для аналізу цих даних зараз дуже широко використовуються передові статистичні методи, нейромережі, розгалужені обчислення на кластері. Кожен проєкт – це перш за все розробка ПЗ. Для контролю версій використовуємо сервіс GitLab.
Ми інколи жартуємо, що стати фізиком – це неймовірна можливість одночасно зафейлитися як інженер, як математик і як програміст. Бо насправді кожен з нас уміє всього потроху. У певній кількості інженери, звісно ж, присутні, але зазвичай це стосується розробки та підтримки якихось великих систем для усього ЦЕРНу – як-от обчислювальний кластер. Для дрібніших задач інженери не дуже добре пристосовані, і це перш за все пов’язано зі специфікою наукової роботи. Інженери добре справляються в тих випадках, коли мають чітко визначену задачу, яку треба виконати зрозумілим для них способом. У науці ж пріоритети можуть швидко змінюватися в залежності від міркувань, які стосуються саме фізики та її прогресу. Інженери від того шаленіють, бо в них на меті саме розв’язання інженерної задачі.
Інженери добре справляються в тих випадках, коли мають чітко визначену задачу, яку треба виконати зрозумілим для них способом. У науці ж пріоритети можуть швидко змінюватися в залежності від міркувань, які стосуються саме фізики та її прогресу. Інженери від того шаленіють, бо в них на меті саме розв’язання інженерної задачі.
Ось є в нас, наприклад, загальний фреймворк, який для всієї колаборації обробляє дані з детектора та реконструює картину зіткнення частинок. Його архітектуру писали професійні інженери з розробки систем. Але конкретні фічі розробляють уже фізики, бо легше фізика навчити писати програмний код, аніж інженера навчити фізики.
Фото в кімнаті, з якої здійснюється управління експериментом АТЛАСЗвісно, що інженери все роблять якісніше. Пам’ятаю, у ЦЕРНі ми ходили дивитися на експеримент з вироблення антиматерії. Наш гід був якраз інженер, і він наочно показував нам різницю. «Дивіться, оце робили інженери», – і показує акуратно зібрану установку, до якої підходить пучок дротів, дбайливо проведених по стіні. «А оце, – каже, – фізики». І ми бачимо якесь кубло з дротів виду «вибух на макаронній фабриці», за якою ледь проглядається наспіх зібрана установка. З кодом та сама біда – коли його пишуть аспіранти першого року, то краще туди не заглядати. Але в цьому штука – фізики можуть не знати «як», зате знають «що», і це в нашій ситуації важливіше.
«А оце, – каже, – фізики». І ми бачимо якесь кубло з дротів виду «вибух на макаронній фабриці», за якою ледь проглядається наспіх зібрана установка. З кодом та сама біда – коли його пишуть аспіранти першого року, то краще туди не заглядати. Але в цьому штука – фізики можуть не знати «як», зате знають «що», і це в нашій ситуації важливіше.
Мій робочий день виглядає якось так: о восьмій ранку прямо з дому робочий мітинг по відео за участю колег з Азії, у яких уже пізній вечір. Доповіді, обмін результатами, обговорення, пропозиції. Потім їду на роботу: у кампус Jussieu Університету Сорбонни на березі Сени. Там я пару годин працюю над нашим проєктом з використанням графових нейромереж (graph neural network) для класифікації подій на колайдері, у яких формується W-бозон. Далі по обіді я спускаюся на цокольний поверх, одягаю білий халат і проводжу вимірювання нещодавно зібраних силіконових сенсорів – майбутніх пікселів для апгрейду внутрішнього детектора нашого експерименту.
О шостій вечора в мене знову мітинг, тепер уже з колегами з Америки, де ми обговорюємо інший наш проєкт – використання нейромереж для корекції перехресного сигналу з калориметра.
Отже, робочий час розподіляється між роботою з розробки детекторних систем, отриманням нових результатів з аналізу даних та обговоренням усього цього на робочих мітингах.
Як взагалі влаштована робота співробітників на ВАК, ваших колег зокрема?
Кожен працює на якусь наукову установу, але при цьому є певна свобода у виборі роботи. Уся праця обертається навколо внутрішніх проєктів – як я вже казав, це може бути розробка детекторних систем, обробка даних чи їх аналіз. Кожен бере участь у кількох таких проєктах, у кожному з яких можуть бути залученими від кількох осіб до кількох сотень. При цьому майже ніколи ці люди не працюють в одній установі, отже координують свою роботу дистанційно. Через це ми маємо стільки мітингів – від кількох на тиждень до кількох на добу. Інколи, звісно, треба бачитися й особисто. Ось тут допомагають поїздки в ЦЕРН, який є звичайним місцем зустрічі. Але є і традиція їздити «в гості» напряму – так, наприклад, торік я мав тритижневе відрядження у Бразилію.
Ось тут допомагають поїздки в ЦЕРН, який є звичайним місцем зустрічі. Але є і традиція їздити «в гості» напряму – так, наприклад, торік я мав тритижневе відрядження у Бразилію.
Звісно, така велика кількість людей повинна мати певну організаційну структуру та ієрархію – хтось повинен визначати пріоритети, оцінювати роботу колег і робити заяви від імені експерименту. Ця структура існує, усі такі посади є виборними на термін від двох до чотирьох років. Формальним головою експерименту є spokesperson – це і є людина, яка має формальний мандат говорити від імені експерименту. Нинішня голова ЦЕРНу Фабіола Джіанотті раніше була саме головою експерименту ATLAS.
Фото на фоні експерименту CMSЗвісно, що, де є ієрархія, там завжди є і певна політика, внутрішня кухня та якісь кулуарні питання. Але в цілому, як на мене, усе тримається в пристойних межах.
Існує досить сувора (може, навіть занадто сувора) процедура внутрішньої перевірки результатів для публікації. Адже кожна стаття публікується від імені кожного учасника експерименту, тому ніхто не бажає публічно пошитися в дурні, поставивши своє ім’я під помилковим результатом.
Усі добре пам’ятають історію з італійським експериментом OPERA, який досліджував проходження нейтрино від ЦЕРН через італійські Альпи. У 2011 році цей експеримент опублікував приголомшливі результати: стверджувалось, що зафіксовано нейтрино, які подорожують швидше за світло! Новину обговорювали по всьому світі, адже це фактично ламало всі наші уявлення про сучасну фізику і напряму суперечило основам теорії відносності. Справа навіть вийшла за межі спільноти фізиків: про відкриття написали всі провідні газети світу. Проте згодом виявилося, що отриманий результат був хибним: експериментатори неправильно врахували один із сотень факторів, які впливають на точність вимірювань. Звісно, що подібний провал не найкращим чином відбився на кар’єрах тих, хто мав стосунок до експерименту OPERA. Наступного року цей експеримент закрили.
У яких експериментах ви брали участь?
Оскільки я працюю у великому експерименті, який дає змогу спробувати дуже різні речі, майже всю свою кар’єру фізика я працював лише в ATLAS. При цьому фізично можна попрацювати в різних університетах, державах, ба навіть на різних континентах – залишаючись при цьому членом колаборації ATLAS. В ATLAS є брат – експеримент CMS, який теж розташований на ВАК, у протилежній точці кільця колайдера. Там теж працюють під три тисячі науковців. CMS досліджує ті самі речі, але побудований трохи за іншим принципом.
При цьому фізично можна попрацювати в різних університетах, державах, ба навіть на різних континентах – залишаючись при цьому членом колаборації ATLAS. В ATLAS є брат – експеримент CMS, який теж розташований на ВАК, у протилежній точці кільця колайдера. Там теж працюють під три тисячі науковців. CMS досліджує ті самі речі, але побудований трохи за іншим принципом.
Два експерименти порівнюють лише кінцеві результати, при цьому обговорювати між собою способи їх досягнення заборонено. Це зробили для того, щоб результати були максимально незалежними й аби виключити можливе дублювання помилок при їх отриманні. Я працював на CMS протягом кількох місяців перед тим, як почати робити дисертацію на ATLAS. Великі результати типу відкриття бозона Хіггса вимагають незалежного підтвердження від обох експериментів.
Через певну схожість експериментів переходи фізиків з ATLAS у CMS та навпаки – не рідкість. Якось мені довелося доповідати на конференції результати з однієї теми від імені обох експериментів – це теж поширена практика. Менші експерименти можуть мати по кілька десятків учасників, там уся система організації дещо інша.
Менші експерименти можуть мати по кілька десятків учасників, там уся система організації дещо інша.
Що вас найбільше дивує в роботі ВАК?
Мене дивує і захоплює, як люди із зовсім різних культур здатні об’єднуватися, знаходити спільну мову та досягати результатів. За роки роботи в цьому середовищі я жодного разу не бачив навіть натяку на зневагу до когось через стать, країну походження, віру й таке інше. Ми всі колеги, вагу мають лише досвід і здатність досягати результату. Мені б хотілося, щоб такий підхід мав ширше розповсюдження. При цьому, звісно, китайські науковці лишаються китайцями, французи – французами, а українці (і це я знаю точно) – українцями. Але ось ця інтернаціональна культура співпраці – вона справді захоплює.
Які відкриття зробили після бозона Хіггса? Як щодо гравітаційних хвиль? Що є актуальним предметом досліджень у ВАК?
Я гадаю, на це запитання важко буде відповісти без того, щоб дати коротенький огляд стану речей у сучасній фізиці. Сподіваюсь, що після нього стане трошки зрозумілішим, що взагалі вважати відкриттям і де в цій картині знаходяться бозон Хіггса та гравітаційні хвилі.
Сучасна фізика почала формуватись приблизно сто років тому, на початку ХХ століття. Тоді ж окреслилися два головних напрями – квантова фізика та загальна теорія відносності (ЗТВ). Вийшло так, що квантова фізика працює на дуже малих масштабах, а ЗТВ – на дуже великих. Тому інколи говорять, що сучасна фізика – це фізика двох нескінченостей: нескінченно малого та нескінченно великого.
Так виглядає знайдений бозон Хіггса при обробці наукових даних (горбок на графіку)ЗТВ на сьогодні вважається панівною теорією для опису гравітації. Історично ЗТВ здебільшого «дивилась вгору»: її цікавили зірки, галактики, чорні діри й оте все велике. Квантова ж теорія опікувалася рештою взаємодій, а саме електромагнітною, сильною та слабкою. Були цікаві роботи (типу праць Хокінга), які включали квантові ефекти до космологічних явищ, але по-справжньому «помирити» ці дві гілки фізики досі нікому не вдалося. На наше щастя, гравітація на десятки порядків слабша за три інші взаємодії, тому фізиці вдається розвиватися, попри певні негаразди в узгодженні квантової теорії та ЗТВ. Обидві теорії є дуже успішними й чудово підтвердженими експериментально.
Обидві теорії є дуже успішними й чудово підтвердженими експериментально.
Квантова теорія стрімко розвивалася, і десь у 1940-х роках ХХ століття вдалося її «помирити» зі спеціальною теорією відносності, принаймні у випадку електромагнітної взаємодії. Це означало, що фізикам вдалося описувати взаємодії квантових частинок, які рухаються близько до швидкості світла. Це назвали квантовою електродинамікою, і це вже було серйозним поступом. Отриманих знань у цілому було достатньо для розробки у ХХ столітті транзисторів, діодів, лазерів і всього того мотлоху, без якого ми зараз не уявляємо свій день. З усім тим цього було замало задля опису явищ ядерної фізики, оскільки там працювали також дві інші взаємодії – слабка та сильна. Для розвитку успіху потрібно було більше експериментальних даних.
Аж ось після Другої світової у гру вступили прискорювачі частинок й одразу ж показали себе дуже ефективним інструментом для отримання нових даних. У певний час це навіть стало проблемою – бо на кінець 1950-х понавідкривали цілу купу частинок, які взаємодіяли незрозумілим чином, неясно було, звідки вони беруться та як їх класифікувати.
У певний час це навіть стало проблемою – бо на кінець 1950-х понавідкривали цілу купу частинок, які взаємодіяли незрозумілим чином, неясно було, звідки вони беруться та як їх класифікувати.
Якщо за перші відкриття нових елементарних частинок стабільно давали Нобелівську премію, то вже у 1960-х фізики ладні були заволати «Горщик, не вари!», бо частинки сипались наче з рогу достатку. Цю картину тоді називали «зоопарк частинок (particle zoo)». Ось на базі цієї надзвичайно багатої колекції експериментальних даних низці блискучих теоретиків вдалося побудувати теорію, яка б добре описувала три взаємодії і могла систематизувати весь той зоопарк. Це і була стандартна модель, яку загалом сформували в 1970-х роках і яка передбачала існування ряду частинок, що на той час були ще невідомими. Одна за іншою ці частинки були знайдені експериментально, і про останню з них, мабуть, усі чули – це і є славнозвісний бозон Хіггса, який відкрили у 2012 році. Стандартна модель стала чимось на зразок періодичної системи елементів, але для фізики частинок.
Стандартна модель пояснила будову сотень частинок, знайдених на прискорювачах протягом цих років, з допомогою відносно невеликої кількості первісних «кубиків». Ці кубики називаються фундаментальними, або елементарними, частинками. Їх список справді досить короткий: шість кварків, шість лептонів і п’ять бозонів. Зазвичай кажуть, що кварки та лептони складають структуру матерії, а бозони забезпечують їх взаємодію між собою. Стандартна модель дозволяє розраховувати взаємодії між частинками з неймовірною точністю. Загалом її можна назвати чи не найуспішнішою фізичною теорією за всю історію фізики.
Схема Стандартної моделіХоча, звісно, досі залишається чимало запитань. Наприклад, кварків і лептонів спокійно могло б бути всього чотири, а не дванадцять. Щоб побудувати матерію навколо нас, цілком вистачило б двох кварків, електрона та нейтрино. Але природа чомусь вирішила, що кожен з них повинен мати двох «старших братів», які б взаємодіяли так само, але мали б більшу масу. Чому так сталося і чому поколінь частинок саме три, а не два чи п’ять? На сьогодні ми не можемо на це відповісти.
Чому так сталося і чому поколінь частинок саме три, а не два чи п’ять? На сьогодні ми не можемо на це відповісти.
Але тим і цікавий науковий пошук, що результат дуже важко передбачити. Саме в тому і полягає інтрига, що жодна жива душа у світі не знає, що там криється за рогом.
Стандартну модель добре дослідили за ті дев’ять років, які пройшли з відкриття бозона Хіггса. Чимало кількісних передбачень теорії підтвердили експериментально, це, зокрема, стосується і властивостей новознайденого бозона. Власне, саме це й становить предмет досліджень на експериментах ВАК – перевірка Стандартної моделі та пошуки сигналів нової фізики, яка б не вкладалася в устатковану теорію. Поки що можна сказати, що ці пошуки не дали однозначних вказівок на те, де шукати нову фізику.
Іронічно, що Стандартна модель стала жертвою власної успішності – ще недавно фізики дуже раділи кожному її підтвердженню, а зараз витрачають шалені зусилля на пошук умов, за яких вона вже не працює. Отже, тепер важко сказати, чого чекати далі – поки що не вдалося знайти доказів на користь будь-якої більш фундаментальної теорії.
Отже, тепер важко сказати, чого чекати далі – поки що не вдалося знайти доказів на користь будь-якої більш фундаментальної теорії.
Зараз інтернетом шириться кумедна картинка, де в гумористичній формі для IT-працівників перелічені твердження сучасної фізики. Можу трохи пояснити цікаві речі, які виглядають як жарт, але насправді так і є.
- Мова про те, що квантові частинки поводять себе відмінно і від частинок, і від хвиль – інколи проявляючи властивості тих чи інших. Це є прямим наслідком квантових законів і здається нам дивним і контрінтуїтивним, бо наша інтуїція сформована у звичайному, а не квантовому світі.
- Мова про те, що загальна теорія відносності (ЗТВ) і квантова механіка окремо взяті є дуже успішними та чудово підтвердженими теоріями, проте між собою вони не дуже добре узгоджуються. Результатом є певне умовне розгалуження сучасної фізики на «космічну» та «частинкову».
- Енергія фотона – це його енергія руху. Суворо кажучи, якщо фотон не рухається – то він і не існує.
- Квантова теорія вважає всі елементарні частинки однаковими. Один електрон неможливо відрізнити від іншого. Тому можна сказати, що вони всі є копіями один одного.
- Мова про ефект спеціальної теорії відносності – так зване релятивістське уповільнення часу при русі з великою швидкістю.
- Мова про так звану темну матерію – невидиму, проте масивну матерію, яка кількісно пояснює характер обертання галактик. Існування темної матерії (ТМ) в цілому не викликає сумнівів у науковців, програми з пошуку ТМ є також і на ВАК. Проте той факт, що ця матерія не взаємодіє жодним шляхом крім гравітаційного, у багатьох викликає скепсис. Взагалі це окремий вид розваги – знайти в ФБ студентський паблік, присвячений космології, та почати суперечку щодо існування ТМ, використовуючи лише аргументи з фізики частинок (це хуліганство, не робіть так, якщо бережете свою карму 🙂).
- Згідно із сучасними спостереженнями, наш Всесвіт справді розширюється. Залишається чимало запитань щодо подробиць цього ефекту.

- Ну, це в певному сенсі і є милиці. Тобто ми бачимо ці ефекти у спостереженнях і отже повинні якось вводити їх до нашої теорії, навіть якщо це інколи породжує більше запитань, ніж відповідей. Схоже, що природа не надто турбується про те, щоб наші теорії завжди були простими та красивими. Але будемо сподіватися, що з отриманням нових даних ми краще зрозуміємо, як воно все працює.
Вплив ВАК на фізику величезний. А як щодо практичних речей – як колайдери допомогли змінити життя сучасної людини?
Річард Фейнман казав, що фізика – це як секс: ви, звісно, можете досягти певних практичних результатів, але зазвичай люди цим займаються з інших причин. Метою фізики є саме пізнання природи навколишнього світу (бо ж «фізика» – це «природа» в перекладі з грецької). Фізики добувають знання, а вже винахідники, інженери та маркетологи потім вигадують, як з тих знань отримати практичну користь і пояснити це решті людей.
Однак, як це не дивно, нерідко побічним продуктом фізичних досліджень є цілком практичні речі. Наприклад, принцип ядерного магнітного резонансу, який колись відкрили саме задля досліджень з ядерної фізики, ліг в основу магнітно-резонансної томографії – МРТ-установки зараз стоять у кожній сучасній лікарні.
Наприклад, принцип ядерного магнітного резонансу, який колись відкрили саме задля досліджень з ядерної фізики, ліг в основу магнітно-резонансної томографії – МРТ-установки зараз стоять у кожній сучасній лікарні.
Безпосередньо прискорювачі використовують для виготовлення ізотопів з коротким терміном життя, які потрібні для діагностики раку. Так само пучки протонів, отримані на спеціальному прискорювачі, успішно використовують для лікування ракових пухлин.
Синхротронне випромінювання стало незамінним у матеріалознавстві – це найнадійніший спосіб неруйнівного вивчення структури матеріалів. Ви здивуєтеся, але навіть Лувр має свій невеличкий прискорювач – задля вивчення предметів мистецтва та підтвердження їхньої автентичності У 2017 році в Луврі запустили 37-метровий прискорювач частинок, розташований під музеєм, він використовуватиметься для визначення хімічного складу об’єктів без взяття зразків. – Прим. ред..
Є й інші побічні речі. Оскільки ще у 1980-х колайдерна фізика вже оперувала величезними на ті часи обсягами даних, задля швидкого обміну інформації саме в ЦЕРНі в 1989 році розробили структуру World Wide Web і перший інтернет-браузер. Через це британський вчений Тім Бернерс-Лі, який на той час працював у ЦЕРНі, вважається батьком інтернету, яким ми його знаємо.
Через це британський вчений Тім Бернерс-Лі, який на той час працював у ЦЕРНі, вважається батьком інтернету, яким ми його знаємо.
Дрібніших речей перелічувати годі, при ЦЕРНі на постійній основі працює фабрика стартапів.
Зараз активно добудовують інші колайдери. Чи допоможуть вони знайти відповіді щодо темної матерії, загадково малих мас нейтрино і переважання матерії, що спостерігається, над антиматерією у Всесвіті? Які основні виклики в розумінні світобудови стоять перед вченими?
ВАК є важливою складовою сучасної фізики, але, звісно ж, не є єдиним прискорювачем у світі. У певному сенсі ВАК як адронний колайдер наслідував американському колайдеру Tevatron, який закрили у 2011 році. Інші експерименти суттєво розширюють і доповнюють картину, яку бачить ВАК.
Цікавий факт: перший прискорювач у ЦЕРНі, введений в експлуатацію ще в 1950-х, до сьогодні справно працює як передприскорювач для ВАК.
Отже, експерименти ATLAS і CMS головним чином зосереджені на перевірці властивостей Стандартної моделі та можливих її розширень. Працюють також два менші експерименти: LHCb та ALICE. LHCb як раз успішно досліджує процеси, пов’язані з порушенням парності у слабкій взаємодії. Цей ефект вважається можливою причиною приголомшливої переваги матерії над антиматерією у спостережному Всесвіті.
Працюють також два менші експерименти: LHCb та ALICE. LHCb як раз успішно досліджує процеси, пов’язані з порушенням парності у слабкій взаємодії. Цей ефект вважається можливою причиною приголомшливої переваги матерії над антиматерією у спостережному Всесвіті.
Дуже схожими задачами займається експеримент Belle-II, розташований у Японії. Там замість протонних проводять електрон-позитронні зіткнення, що робить експеримент набагато чистішим і легшим для інтерпретації.
Схема колайдера RHICТакож на LHCb та Belle ведуть серйозні дослідження лептонної універсальності. Тут треба пояснити, що це таке. Як було згадано раніше, електрон має двох «старших братів» – мюона і тау-лептона. Вони важчі за електрон і нестабільні – врешті розпадаються, утворюючи електрон. Стандартна модель постулює, що крім маси решта властивостей у них однакова. Проте минулого року американський експеримент Muon g-2 показав, що з високою ймовірністю є суттєві відхилення від теорії. Спостерігається порушення лептонної універсальності – коли різні лептони таки відрізняються за своїми властивостями. Досі вважалося, що вони ідентичні, а виходить, що не зовсім.
Досі вважалося, що вони ідентичні, а виходить, що не зовсім.
ALICE спроєктований для досліджень зіткнень важких іонів свинцю, коли замість двох протонів стикаються сотні протонів і нейтронів. Це дозволяє відтворити стан матерії, у якому Всесвіт перебував у першу мить після Великого вибуху. Такий стан зветься кварк-глюонна плазма.
Взагалі зіткнення важких іонів – це цікава тема, на сьогодні в США працює колайдер RHIC, повністю присвячений такій фізиці. Я певний час працював над цією темою, спочатку як теоретик, а потім під час кількох місяців роботи на CMS. Але це не зовсім «мейнстрім» сучасної фізики частинок. Можливо, тому що теорія там досить складна, а експериментальні результати важко інтерпретувати. Там одночасно діють кілька фізичних ефектів, кожен з яких ми не досить добре розуміємо. Проте якщо вдасться дати тому раду, то ми зможемо багато чого пояснити в сучасній будові Всесвіту.
Попри надзвичайно серйозну роль ВАК у фізиці частинок, він теж має свої обмеження. Наприклад, детектори ВАК геть не здатні бачити нейтрино.
Наприклад, детектори ВАК геть не здатні бачити нейтрино.
Усе через те, що нейтрино взаємодіють виключно через слабку взаємодію – назва, власне, все пояснює. Скажімо, якщо «вистрілити» нейтрино у воду, то воно може пролетіти аж сто світлових років, не зачепивши жодної молекули води!
Нейтринні експерименти складні та проблемні. Джерелом нейтрино може слугувати ядерний реактор чи прискорювач, а детектор інколи розміщують за сотні кілометрів. Нейтрино спокійно проходять крізь гори чи земну кору, майже не взаємодіючи. За рік нейтринний експеримент фіксує лише кілька сотень чи навіть десятків взаємодій – порівняйте це з 40 мільйонами щосекунди на ВАК. З огляду на це вже не здається таким дивним, що у 2011-му вчені з OPERA таки припустилися помилки.
Проте нейтринні експерименти зараз стають усе популярнішими. Одна з головних причин такого інтересу до нейтрино наступна: у 2000-х роках отримали свідчення того, що вони таки мають масу, хоча й дуже малу (за це навіть було присуджено Нобелівську премію). Водночас Стандартна модель стверджує, що нейтрино є безмасовими. Це чи не єдиний випадок, коли Стандартна модель так суттєво помиляється. Висновок очевидний: нейтрино – це ключ до нової фізики.
Водночас Стандартна модель стверджує, що нейтрино є безмасовими. Це чи не єдиний випадок, коли Стандартна модель так суттєво помиляється. Висновок очевидний: нейтрино – це ключ до нової фізики.
Як я вже казав, починаючи із середини ХХ століття прискорювачі були і, мабуть, досі залишаються основними «робочими конячками» для дослідження фізики частинок. А що ж було до того? А до того люди досліджували космічні промені. Кожної секунди атмосферу Землі бомбардують незчисленні частинки з космосу, головним чином протони. На наше щастя, вони більшою мірою розбиваються об атмосферу, інакше ми навряд чи пережили б такий рівень радіації.
У першій половині ХХ століття саме небо над нами слугувало головним джерелом елементарних частинок. Були навіть експерименти з використанням повітряних куль, які показали зростання потоку частинок при підйомі в атмосферу.
Згодом робота з прискорювачами майже повністю замінила подібні спостереження, бо слугувала надійнішим джерелом частинок і дозволяла краще контролювати умови експерименту.
Але космічні промені все ж таки мають певні переваги. Перш за все через дуже широкий спектр енергій частинок, серед яких існують навіть такі, які значно перевищують енергії зіткнень на ВАК. При цьому знання, отримані з допомогою прискорювачів, плідно використовуються для інтерпретації спостережень за космічними променями. Через це зараз збільшується число подібних експериментів. Усе частіше ми згадуємо, що варто підняти голову і подивитись угору.
Ну і, звісно ж, не можна не відзначити прогрес в астрономії, астрофізиці та космології. Саме ці дисципліни мають відповідати на запитання щодо темної матерії та енергії, віку та будови Всесвіту, питань ЗТВ. Буквально днями всі спостерігали за розгортуванням новітнього телескопа Уебб – це справжній тріумф технологій. Ясна річ, ще більше телескопів облаштовується на поверхні Землі.
Важливо відзначити: якщо раніше колайдерна фізика була безперечним лідером у застосуванні передових методів обробки й аналізу даних, то зараз ситуація вирівнялась. Кілька років тому оприлюднили так звані фотографії чорної діри. Для того щоб отримати ці зображення, проаналізували терабайти даних. Це блискуча робота й очевидне підтвердження прогресу.
Кілька років тому оприлюднили так звані фотографії чорної діри. Для того щоб отримати ці зображення, проаналізували терабайти даних. Це блискуча робота й очевидне підтвердження прогресу.
Підсумовуючи, скажу, що останніми 40 роками фізика отримала більше даних, ніж за всю історію людства до того. Тож варто чекати на цікаві новини. Хоча, які саме новини, знатимемо лише тоді, коли їх отримаємо.
| I. Кинематика | |
|---|---|
| Лекция 1 Воспроизвести видео |
Измерения пространства и времени Эта лекция посвящена единицам, измерениям, измерениям и связанным с ними неопределенностям, размерному анализу и аргументам масштабирования. |
| Лекция 2 Воспроизвести видео |
Скорость, скорость и ускорение Эта лекция представляет собой введение в кинематику, которая в конечном итоге приводит (в лекции 4) к траекториям в трех измерениях.  |
| Лекция 3 Воспроизвести видео |
Векторы Эта лекция посвящена единицам измерения, размерам, измерениям и связанным с ними неопределенностям, размерному анализу и аргументам масштабирования. |
| Лекция 4 Воспроизвести видео |
3D-кинематика: движение снарядов В этой видеолекции профессор Уолтер Левин читает лекцию о движении снарядов (если можно игнорировать сопротивление воздуха).Объекты испытывают постоянное вертикальное ускорение из-за ускорения свободного падения (см. также лекцию 12). |
| Лекция 5 Воспроизвести видео |
Круговое движение В этой видеолекции профессор Уолтер Левин рассказывает о круговом движении, движении центрифуг, системах отсчета и воспринимаемой гравитации. |
| Лекция 6 Воспроизвести видео |
Три закона Ньютона В этой видеолекции проф.  Уолтер Левин читает лекции по Первому (инерции), Второму (F=ma) и Третьему (действие=противодействию) законам Ньютона. Уолтер Левин читает лекции по Первому (инерции), Второму (F=ma) и Третьему (действие=противодействию) законам Ньютона. |
| Лекция 7 Воспроизвести видео |
Вес и невесомость В этой видеолекции профессор Уолтер Левин исследует вес, воспринимаемую гравитацию, невесомость, свободное падение, нулевую воспринимаемую гравитацию на орбите. |
| Лекция 8 Воспроизвести видео |
Силы трения В этой видеолекции проф.Уолтер Левин читает лекции исключительно о силах трения. |
| Лекция 9 Воспроизвести видео |
Обзор экзамена В этой видеолекции профессор Уолтер Левин делает обзор избранных тем, ранее затронутых в лекциях с 1 по 5. |
| Лекция 10 Воспроизвести видео |
Закон Гука и простое гармоническое движение В этой видеолекции профессор Уолтер Левин начинает свою лекцию с таких тем, как восстанавливающая сила пружины (закон Гука), которая приводит к уравнению движения, характерному для простого гармонического осциллятора.  (ШО).Используя приближение малых углов, аналогичное выражение получается для маятника. (ШО).Используя приближение малых углов, аналогичное выражение получается для маятника. |
| II. Работа и энергия | |
| Лекция 11 Воспроизвести видео |
Работа и механическая энергия В этой видеолекции профессор Уолтер Левин знакомит с такими понятиями, как работа, консервативные силы, потенциальная энергия, кинетическая энергия, механическая энергия и закон всемирного тяготения Ньютона. |
| Лекция 12 Воспроизвести видео |
Силы сопротивления В этой видеолекции проф.Уолтер Левин читает лекции о силах сопротивления, таких как сопротивление воздуха. Он включает в себя вязкое (линейное по скорости) и давление (квадратичное по скорости) условия. Показаны количественные демонстрации с воздушными шарами и шарикоподшипниками, брошенными в сироп. |
| Лекция 13 Воспроизвести видео |
Консервативные силы и SHO В этой видеолекции профессор Уолтер Левин читает лекцию о сохранении механической энергии, которую можно использовать для вывода уравнения движения для простых гармонических осцилляторов (SHO).  |
| Лекция 14 Воспроизвести видео |
Энергия, мощность и спутниковые орбиты В этой видеолекции профессор Уолтер Левин читает лекции о связанных и несвязанных орбитах; скорость убегания. Также обсуждаются различные источники энергии, хранение энергии, преобразование энергии и потребление энергии в мире. |
| III. Импульс | |
| Лекция 15 Воспроизвести видео |
Столкновения и центр масс В этой видеолекции проф.Уолтер Левин вводит импульс и его сохранение во время столкновений. Кинетическая энергия может уменьшаться или увеличиваться во время столкновений. Когда кинетическая энергия сохраняется, мы называем это упругим столкновением. |
| Лекция 16 Воспроизвести видео |
Упругие и неупругие столкновения В этой видеолекции профессор Уолтер Левин обсуждает одномерные упругие столкновения, головоломки, упругие столкновения со стеной, центр масс (ЦМ), систему отсчета, одномерное неупругое столкновение, внутреннюю энергию и демонстрация колыбели Ньютона.  |
| Лекция 17 Воспроизвести видео |
Изменение импульса, импульс и ракеты В этой видеолекции профессор Уолтер Левин читает лекцию об импульсе отдельных объектов, которые изменяются различными способами. |
| Лекция 18 Воспроизвести видео |
Обзор экзамена В этой видеолекции профессор Уолтер Левин дает обзор экзамена. |
| IV.Небесная механика | |
| Лекция 19 Воспроизвести видео |
Вращательная кинетическая энергия В этой видеолекции профессор Уолтер Левин читает лекции о вращающихся твердых телах, моментах инерции, параллельной оси и теореме о перпендикулярной оси. Вводится момент инерции твердого тела вокруг оси вращения, связанный с его кинетической энергией вращения. Маховики можно использовать для накопления энергии. Планеты и звезды обладают кинетической энергией вращения, и пульсар в Крабовидной туманности представлен как наглядный пример.  |
| Лекция 20 Воспроизвести видео |
Угловой момент В этой видео-лекции профессор Уолтер Левин представляет угловой момент (вектор). Скорость изменения углового момента связана с крутящим моментом (также вектором). В отсутствие внешнего момента момент импульса сохраняется. Обсуждается также спиновой угловой момент (планет, звезд, нейтронных звезд). |
| Лекция 21 Воспроизвести видео |
Крутящие моменты и колеблющиеся тела В этой видеолекции проф.Уолтер Левин обсуждает, как в отсутствие чистого внешнего крутящего момента на объекте сохраняется угловой момент. Он также обсуждает, когда объект колеблется вокруг оси вращения, и как на объект действует переменный восстанавливающий крутящий момент. |
| Лекция 22 Воспроизвести видео |
Законы Кеплера и эллиптические орбиты В этой видеолекции профессор Уолтер Левин читает лекции о законах Кеплера, эллиптических орбитах, изменении орбит и знаменитом прохождении бутерброда с ветчиной.  Три закона Кеплера обобщают движение планет в нашей Солнечной системе. Следуя закону всемирного тяготения Ньютона, сохранение углового момента и механической энергии позволяют вычислить большую полуось эллиптических орбит, период обращения и другие параметры орбиты. Все, что нам нужно знать, это одно положение и связанная с ним скорость планеты и всей орбиты. Три закона Кеплера обобщают движение планет в нашей Солнечной системе. Следуя закону всемирного тяготения Ньютона, сохранение углового момента и механической энергии позволяют вычислить большую полуось эллиптических орбит, период обращения и другие параметры орбиты. Все, что нам нужно знать, это одно положение и связанная с ним скорость планеты и всей орбиты. |
| Лекция 23 Воспроизвести видео |
Доплеровский сдвиг и звездная динамика В этой видеолекции проф.Уолтер Левин читает лекции об эффекте Доплера, двойных звездах, нейтронных звездах и черных дырах. Доплеровский сдвиг вводится со звуковыми волнами, а затем распространяется на электромагнитные волны (излучение). Доплеровский сдвиг звездных спектральных линий и/или частот пульсара обеспечивает меру лучевой (так называемой радиальной) скорости источника относительно наблюдателя. В сочетании с законом всемирного тяготения Ньютона это может привести к параметрам орбиты и массе обеих звезд в двойной звездной системе.  |
| Лекция 24 Воспроизвести видео |
Катящееся движение и гироскопы В этой видеолекции профессор Уолтер Левин читает лекции по вращательному движению и гироскопам. Этот материал очень неинтуитивен. |
| В. Механика твердого тела | |
| Лекция 25 Воспроизвести видео |
Статическое равновесие В этой видеолекции профессор Уолтер Левин читает лекции о статическом равновесии, устойчивости и канатоходцах.Статическое равновесие достигается только тогда, когда чистая внешняя сила И чистый внешний крутящий момент на объекте равны нулю. |
| Лекция 26 Воспроизвести видео |
Эластичность материалов В этой видеолекции профессор Уолтер Левин обсуждает упругость и модуль Юнга. Деформация относительной длины материала (деформация) зависит от силы, приходящейся на единицу площади (напряжения).  Зависимость напряжения от деформации описывается концептуально, а затем исследуется эмпирически. Зависимость напряжения от деформации описывается концептуально, а затем исследуется эмпирически. |
| VI. Гидромеханика | |
| Лекция 27 Воспроизвести видео |
Давление в неподвижной жидкости В этой видеолекции профессор Уолтер Левин обсуждает такие понятия, как газы и несжимаемые жидкости, принцип Паскаля, гидростатическое и барометрическое давление. |
| Лекция 28 Воспроизвести видео |
Выталкивающая сила и уравнение Бернулли В этой видеолекции проф.Уолтер Левин обсуждает такие концепции, как гидростатика, принцип Архимеда, гидродинамика, факторы, заставляющие лодку плавать, и уравнение Бернулли. |
| Лекция 29 Воспроизвести видео |
Обзор экзамена В этой видеолекции профессор Уолтер Левин делает обзор отдельных понятий, ранее рассмотренных в лекциях с 16 по 24.  |
| Лекция 30 Воспроизвести видео |
Прочие колебательные системы В этой видеолекции проф.Уолтер Левин читает лекции о простых гармонических колебаниях (SHO) взвешенных твердых тел, связанных с их геометрией. Он также обсуждает, как крутильный маятник колеблется в горизонтальной плоскости, и SHO НЕ зависит от малоуглового приближения. |
| Лекция 31 Воспроизвести видео |
Вынужденные колебания и резонанс В этой видеолекции профессор Уолтер Левин рассказывает о системах, состоящих из маятников и пружин, и о том, как они могут свободно колебаться на своих собственных частотах (также называемых нормальными модами).Он также обсуждает, что когда мы подвергаем систему воздействию широкого спектра частот, отклик будет очень большим на частотах нормального режима (резонансах) этой системы. Примеры включают музыкальные инструменты (стоячие волны на струнах скрипки и волны давления в духовых инструментах) и крутильные стоячие волны на мосту, движимые сильным ветром.  |
| VII. Теплофизика | |
| Лекция 32 Воспроизвести видео |
Теплопроводность и тепловое расширение В этой видеолекции проф.Уолтер Левин обсуждает, как тепло повышает температуру, и обычно объем материала, который поглощает тепло. Он также читает лекции о линейных и кубических коэффициентах теплового расширения металлов (включая ртуть), которые описаны и продемонстрированы. Лед также рассматривается как частный случай. |
| Лекция 33 Воспроизвести видео |
Теория кинетического газа и фазы В этой видеолекции профессор Уолтер Левин представляет закон идеального газа и скорость передачи импульса от молекул газа к стенкам сосуда, которая связана с давлением.Также вводятся понятия фазовых диаграмм и фазовых переходов, и они исследуются с помощью огнетушителей, кипящей воды и охлаждаемых баллонов, наполненных воздухом.  Закон идеального газа выполняется (приблизительно), когда у вас есть только газ; он не держится всякий раз, когда присутствует какая-либо жидкость. Закон идеального газа выполняется (приблизительно), когда у вас есть только газ; он не держится всякий раз, когда присутствует какая-либо жидкость. |
| VIII. Современная физика | |
| Лекция 34 Воспроизвести видео |
Удивительный квантовый мир В этой видеолекции проф.Уолтер Левин обсуждает классическую механику и, несмотря на всю ее впечатляющую предсказательную силу, не может объяснить многие микроскопические явления. Это привело к развитию квантовой механики, где электроны вращаются вокруг ядер на дискретных уровнях энергии, свет может вести себя как частица, а частицы ведут себя как волны. Местоположение микроскопических частиц может быть выражено только в терминах вероятностей. Принцип неопределенности Гейзенберга также обсуждается и демонстрируется. |
| Лекция 35 Воспроизвести видео |
Рентгеновская астрономия и астрофизика В этой видеолекции проф.  Уолтер Левин рассказывает о некоторых ярких моментах своих первых дней в Массачусетском технологическом институте. Все началось с полетов на воздушном шаре на очень большой высоте для наблюдения за звездами в рентгеновских лучах. Это привело к открытию рентгеновских вспышек и периодического рентгеновского источника (GX 1+4). В семидесятых и восьмидесятых годах он внес важный вклад в наше понимание рентгеновских всплесков (эпизодов термоядерного синтеза на нейтронных звездах). Уолтер Левин рассказывает о некоторых ярких моментах своих первых дней в Массачусетском технологическом институте. Все началось с полетов на воздушном шаре на очень большой высоте для наблюдения за звездами в рентгеновских лучах. Это привело к открытию рентгеновских вспышек и периодического рентгеновского источника (GX 1+4). В семидесятых и восьмидесятых годах он внес важный вклад в наше понимание рентгеновских всплесков (эпизодов термоядерного синтеза на нейтронных звездах). |
| # | Лекция | Проиграть лекцию |
|---|---|---|
| 1 | 0.1 Векторы против скаляров | Воспроизвести видео |
| 2 | 0.2 Векторные операторы | Воспроизвести видео |
| 3 | 0.3 Системы координат и единичные векторы | Воспроизвести видео |
| 4 | 0. 4 Векторы — Величина и направление 4 Векторы — Величина и направление |
Воспроизвести видео |
| 5 | 0.5 Векторная декомпозиция на компоненты | Воспроизвести видео |
| 6 | 0.6 Переход между представлениями | Воспроизвести видео |
| 7 | 1.0 Неделя 1 Введение | Воспроизвести видео |
| I. Урок 1: Одномерная кинематика — положение и скорость | ||
| 8 | 1.1 Системы координат и единичные векторы в 1D | Воспроизвести видео |
| 9 | 1.2 Вектор положения в 1D | Воспроизвести видео |
| 10 | 1.3 Вектор смещения в 1D | Воспроизвести видео |
| 11 | 1. 4 Средняя скорость в 1D 4 Средняя скорость в 1D |
Воспроизвести видео |
| 12 | 1.5 Мгновенная скорость в 1D | Воспроизвести видео |
| 13 | 1.7 Рабочий пример: производные в кинематике | Воспроизвести видео |
| II. Урок 2: 1D-кинематика — ускорение | ||
| 14 | 2.1 Введение в ускорение | Воспроизвести видео |
| 15 | 2.2 Ускорение в 1D | Воспроизвести видео |
| 16 | 2.3 Рабочий пример: ускорение из положения | Воспроизвести видео |
| 17 | 2.4 Интеграция | Воспроизвести видео |
III. Урок 3: 2D-кинематика — положение, скорость и ускорение Урок 3: 2D-кинематика — положение, скорость и ускорение |
||
| 18 | 3.1 Система координат и вектор положения в 2D | Воспроизвести видео |
| 19 | 3.2 Мгновенная скорость в 2D | Воспроизвести видео |
| 20 | 3.3 Мгновенное ускорение в 2D | Воспроизвести видео |
| 21 | 3.4 Движение снаряда | Воспроизвести видео |
| 22 | 3.5 Демонстрация: съемка яблока | Воспроизвести видео |
| 23 | 3.5 Демонстрация: пистолет Relative Motion | Воспроизвести видео |
| IV.Неделя 1 Примеры работы | ||
| 24 | PS. 1.1 Три вопроса перед началом 1.1 Три вопроса перед началом |
Воспроизвести видео |
| 25 | PS.1.2 Съемка яблочного раствора | Воспроизвести видео |
| 26 | P.1.3 Рабочий пример: тормозная тележка | Воспроизвести видео |
| 27 | P.1.4 Эскиз движения | Воспроизвести видео |
| 28 | С.1.5 Рабочий пример: пешеход и велосипедист на перекрестке | Воспроизвести видео |
| 29 | 4.0 Неделя 2 Введение | Воспроизвести видео |
| V. Урок 4: Законы движения Ньютона | ||
| 30 | 4.1 Первый и второй законы Ньютона | Воспроизвести видео |
| 31 | 4. 2 Третий закон Ньютона 2 Третий закон Ньютона |
Воспроизвести видео |
| 32 | 4.3 Базовые кадры | Воспроизвести видео |
| 33 | 4.4 Неинерциальные системы отсчета | Воспроизвести видео |
| VI. Урок 5: Гравитация | ||
| 34 | 5.1 Универсальный закон всемирного тяготения | Воспроизвести видео |
| 35 | 5.2 Рабочий пример: гравитация — суперпозиция | Воспроизвести видео |
| 36 | 5.3 Гравитация на поверхности Земли: Значение g. | Воспроизвести видео |
| VII. Урок 6: Контактные силы | ||
| 37 | 6. 1 Контактные силы 1 Контактные силы |
Воспроизвести видео |
| 38 | 6.2 Статическое трение | Воспроизвести видео |
| VIII.Урок 7: Натяжение и пружины | ||
| 39 | 7.1 Толкание Тяга и натяжение | Воспроизвести видео |
| 40 | 7.2 Идеальная веревка | Воспроизвести видео |
| 41 | 7.3 Решение систем шкивов | Воспроизвести видео |
| 42 | 7.4 Закон Гука | Воспроизвести видео |
| IX.Глубокое погружение: Трение | ||
| 43 | DD.1.1 Трение в наномасштабе | Воспроизвести видео |
X. Примеры работы за 2-ю неделю Примеры работы за 2-ю неделю |
||
| 44 | PS.2.1 Рабочий пример — скользящий блок | Воспроизвести видео |
| 45 | PS.2.2 Рабочий пример — сложенные блоки — бесплатные схемы тел и применение второго закона Ньютона | Воспроизвести видео |
| 46 | шт.2.2 Рабочий пример — сложенные блоки — нахождение максимальной силы | Воспроизвести видео |
| 47 | PS.2.2 Рабочий пример — сложенные блоки — выбор системы из 2 блоков вместе | Воспроизвести видео |
| 48 | PS.2.3 Схемы кузова без стеклоомывателя | Воспроизвести видео |
| 49 | PS.2.3 Средство для мытья окон | Воспроизвести видео |
| 50 | Пара 3-й закон Ньютона | Воспроизвести видео |
| 51 | Внутренние и внешние силы | Воспроизвести видео |
| 52 | Применение второго закона Ньютона | Воспроизвести видео |
| 53 | 8. 0 Неделя 3 Введение 0 Неделя 3 Введение |
Воспроизвести видео |
| XI. Урок 8: Круговое движение — положение и скорость | ||
| 54 | 8.1 Полярные координаты | Воспроизвести видео |
| 55 | 8.2 Круговое движение: векторы положения и скорости | Воспроизвести видео |
| 56 | 8.3 Угловая скорость | Воспроизвести видео |
| XII.Урок 9: Равномерное круговое движение | ||
| 57 | 9.1 Равномерное круговое движение | Воспроизвести видео |
| 58 | 9.2 Равномерное круговое движение: направление ускорения | Воспроизвести видео |
XIII. Урок 10: Круговое движение – ускорение Урок 10: Круговое движение – ускорение |
||
| 59 | 10.1 Круговое движение — ускорение | Воспроизвести видео |
| 60 | 10.2 Угловое ускорение | Воспроизвести видео |
| 61 | 10.3 Рабочий пример — угловое положение от углового ускорения. | Воспроизвести видео |
| XIV. Урок 11: Второй закон Ньютона и движение по окружности | ||
| 62 | 11.1 Второй закон Ньютона и движение по окружности | Воспроизвести видео |
| 63 | 11.2 Рабочий пример — автомобиль на повороте с креном | Воспроизвести видео |
| 64 | 11.3 Демонстрация: вращающийся ковш | Воспроизвести видео |
XV.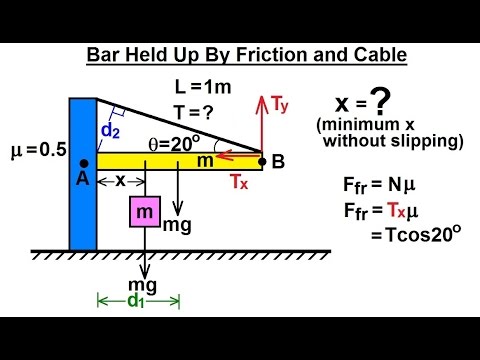 Неделя 3 Примеры работы Неделя 3 Примеры работы |
||
| 65 | PS.3.1 Рабочий пример — орбитальное круговое движение — радиус | Воспроизвести видео |
| 66 | шт.3.1 Рабочий пример — орбитальное круговое движение — скорость | Воспроизвести видео |
| 67 | PS.3.1 Рабочий пример — орбитальное круговое движение — период | Воспроизвести видео |
| 68 | 12.0 Неделя 4 Введение | Воспроизвести видео |
| XVI. Урок 12: Шкивы и ограничения | ||
| 69 | 12.1 Проблемы со шкивом | Воспроизвести видео |
| 70 | 12.2 Условия ограничения | Воспроизвести видео |
| 71 | 12.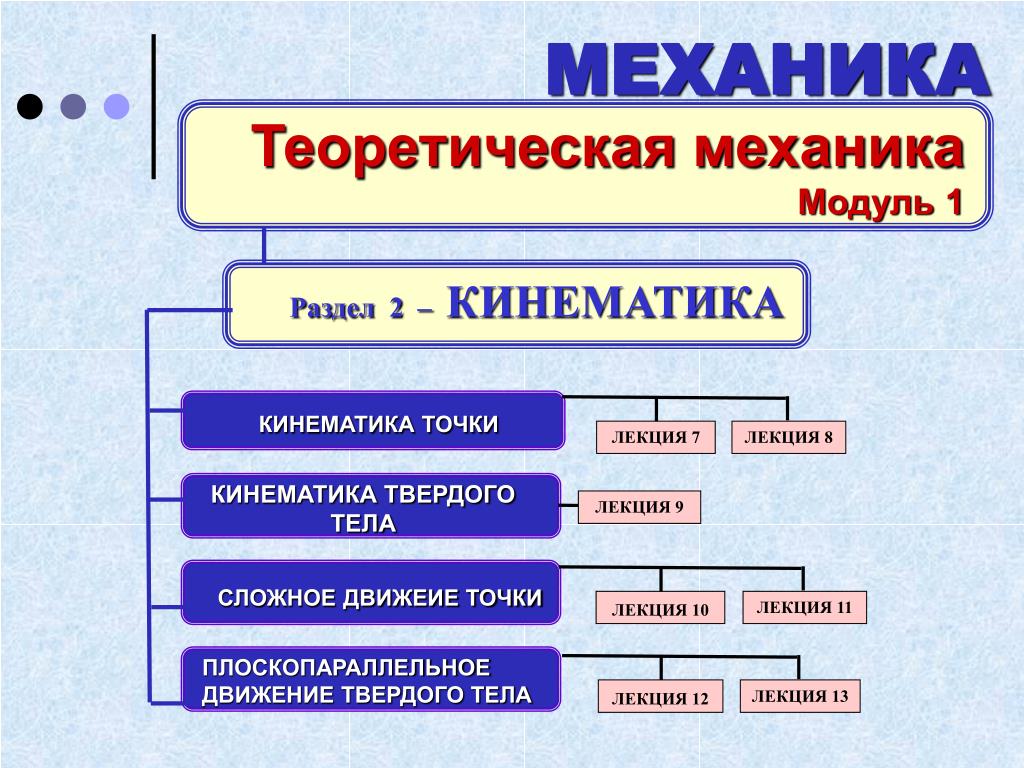 3 Виртуальное смещение 3 Виртуальное смещение |
Воспроизвести видео |
| 72 | 12.4 Решение системы уравнений | Воспроизвести видео |
| 73 | 12.5 Рабочий пример: 2 блока и 2 шкива | Воспроизвести видео |
| XVII. Урок 13: массивная веревка | ||
| 74 | 13.1 Веревка, висящая между деревьями | Воспроизвести видео |
| 75 | 13.2 Дифференциальный анализ массивной веревки | Воспроизвести видео |
| 76 | 13.3 Дифференциальные элементы | Воспроизвести видео |
| 77 | 13.4 Плотность | Воспроизвести видео |
| 78 | 13. 5 Демонстрация: Трение обертывания 5 Демонстрация: Трение обертывания |
Воспроизвести видео |
| 79 | 13.6 Сводка по дифференциальному анализу | Воспроизвести видео |
| XVIII. Урок 14: Силы сопротивления | ||
| 80 | 14.1 Введение в силы сопротивления | Воспроизвести видео |
| 81 | 14.2 Сопротивляющие силы – низкоскоростной корпус | Воспроизвести видео |
| 82 | 14.3 Силы сопротивления — корпус для высоких скоростей | Воспроизвести видео |
| 83 | 15.0 Неделя 5 Введение | Воспроизвести видео |
| XIX. Урок 15: Импульс и импульс | ||
| 84 | 15. 1 Импульс и импульс 1 Импульс и импульс |
Воспроизвести видео |
| 85 | 15.2 Импульс — это Вектор | Воспроизвести видео |
| 86 | 15.3 Рабочий пример — прыгающий мяч | Воспроизвести видео |
| 87 | 15.4 Импульс системы точечных частиц | Воспроизвести видео |
| 88 | 15.5 Влияние на систему частиц | Воспроизвести видео |
| ХХ.Урок 16: Сохранение импульса | ||
| 89 | 16.1 Случаи постоянного импульса | Воспроизвести видео |
| 90 | 16.2 Импульсные диаграммы | Воспроизвести видео |
XXI. Урок 17: Центр масс и движение центра масс Урок 17: Центр масс и движение центра масс |
||
| 91 | 17.1 Определение центра масс | Воспроизвести видео |
| 92 | 17.2 Рабочий пример — центр масс 3 объектов | Воспроизвести видео |
| 93 | 17.3 Центр масс непрерывной системы | Воспроизвести видео |
| 94 | 17.5 Рабочий пример — центр масс однородного стержня | Воспроизвести видео |
| 95 | 17.6 Скорость и ускорение центра масс | Воспроизвести видео |
| 96 | 17.7 Сведение системы к точечной частице | Воспроизвести видео |
| 97 | 18. 0 Неделя 6 Введение 0 Неделя 6 Введение |
Воспроизвести видео |
| XXII. Урок 18: Относительная скорость и отдача | ||
| 98 | 18.1 Относительная скорость | Воспроизвести видео |
| 99 | 18.2 Настройка проблемы отдачи | Воспроизвести видео |
| 100 | 18.3 Решите для скорости в наземной системе координат | Воспроизвести видео |
| 101 | 18.4 Расчет скорости в движущейся системе отсчета | Воспроизвести видео |
| XXIII. Урок 19: Непрерывный массообмен | ||
| 102 | 19.1 Ракетная задача 1 — Настройка задачи | Воспроизвести видео |
| 103 | 19. 2 Ракетная задача 2 — Диаграммы импульса 2 Ракетная задача 2 — Диаграммы импульса |
Воспроизвести видео |
| 104 | 19.3 Ракетная задача 3 — Массовые отношения | Воспроизвести видео |
| 105 | 19.4 Ракетная задача 4 — решение | Воспроизвести видео |
| 106 | 19.5 Ракетная задача 5. Тяга и внешние силы | Воспроизвести видео |
| 107 | 19.6 Ракетная задача 6 — Решение для отсутствия внешних сил | Воспроизвести видео |
| 108 | 19.7 Ракетная задача 7 — решение с внешними силами | Воспроизвести видео |
| XXIV. Неделя 6 Примеры работы | ||
| 109 | Ракетные салазки PS. 6.1 — дифференциальное уравнение 6.1 — дифференциальное уравнение |
Воспроизвести видео |
| 110 | шт.6.1 Ракетные сани — интегрируем уравнение ракеты | Воспроизвести видео |
| 111 | Ракетные салазки PS.6.1 — вычислить начальную скорость | Воспроизвести видео |
| 112 | PS.6.2 Проблема со снегоочистителем | Воспроизвести видео |
| 113 | 20.0 Неделя 7 Введение | Воспроизвести видео |
| ХХV.Урок 20: Кинетическая энергия и работа в 1D | ||
| 114 | 20.1 Кинетическая энергия | Воспроизвести видео |
| 115 | 20.2 Работа с постоянной силой | Воспроизвести видео |
| 116 | 20. 3 Работа непостоянной силы 3 Работа непостоянной силы |
Воспроизвести видео |
| 117 | 20.4 Интеграция adt и adx | Воспроизвести видео |
| 118 | 20.5 Теорема о работе и кинетической энергии | Воспроизвести видео |
| 119 | 20,6 Мощность | Воспроизвести видео |
| ХХVI. Урок 21: Кинетическая энергия и работа в 2D и 3D | ||
| 120 | 21.1 Свойства скалярного произведения | Воспроизвести видео |
| 121 | 21.2 Скалярное произведение в декартовых координатах | Воспроизвести видео |
| 122 | 21.3 Кинетическая энергия как скалярное произведение | Воспроизвести видео |
| 123 | 21. 4 Работа в 2D и 3D 4 Работа в 2D и 3D |
Воспроизвести видео |
| 124 | 21.5 Теорема о работе и кинетической энергии в 2D и 3D | Воспроизвести видео |
| 125 | 21.6 Рабочий пример: Блок, спускающийся по пандусу | Воспроизвести видео |
| XXVII.Урок 22: Консервативные и неконсервативные силы | ||
| 126 | 22.1 Независимость от траектории — Гравитация | Воспроизвести видео |
| 127 | 22.2 Зависимость пути — трение | Воспроизвести видео |
| 128 | 22.3 Консервативные силы | Воспроизвести видео |
| 129 | 22.4 Неконсервативные силы | Воспроизвести видео |
| 130 | 22. 5 Краткий обзор работы и кинетической энергии 5 Краткий обзор работы и кинетической энергии |
Воспроизвести видео |
| XXVIII. Неделя 7 Примеры работы | ||
| 131 | PS.7.1 Рабочий пример — столкновение и скольжение по шероховатой поверхности | Воспроизвести видео |
| 132 | 23.0 Неделя 8 Введение | Воспроизвести видео |
| XXIX. Урок 23: Потенциальная энергия | ||
| 133 | 23.1 Введение в потенциальную энергию | Воспроизвести видео |
| 134 | 23.2 Потенциальная энергия гравитации вблизи поверхности Земли | Воспроизвести видео |
| 135 | 23.3 Эталонное состояние потенциальной энергии | Воспроизвести видео |
| 136 | 23. 4 Потенциальная энергия пружины 4 Потенциальная энергия пружины |
Воспроизвести видео |
| 137 | 23.5 Потенциальная энергия гравитации | Воспроизвести видео |
| ХХХ. Урок 24: Сохранение энергии | ||
| 138 | 24.1 Механическая энергия и энергосбережение | Воспроизвести видео |
| 139 | 24.2 диаграммы энергетического состояния | Воспроизвести видео |
| 140 | 24.3 Рабочий пример — блок, скользящий вниз по круговому склону | Воспроизвести видео |
| 141 | 24.4 Второй закон Ньютона и закон сохранения энергии | Воспроизвести видео |
| XXXI. Урок 25: Диаграммы потенциальной энергии | ||
| 142 | 25. 1 Сила есть производная потенциала 1 Сила есть производная потенциала |
Воспроизвести видео |
| 143 | 25.2 Точки стабильного и неустойчивого равновесия | Воспроизвести видео |
| 144 | 25.3 Чтение диаграмм потенциальной энергии | Воспроизвести видео |
| 145 | 26.0 Неделя 9 Введение | Воспроизвести видео |
| XXXII.Урок 26: Типы столкновений | ||
| 146 | 26.1 Импульс при столкновениях | Воспроизвести видео |
| 147 | 26.2 Кинетическая энергия при столкновениях | Воспроизвести видео |
| 148 | 26.3 Полностью неупругие столкновения | Воспроизвести видео |
XXXIII.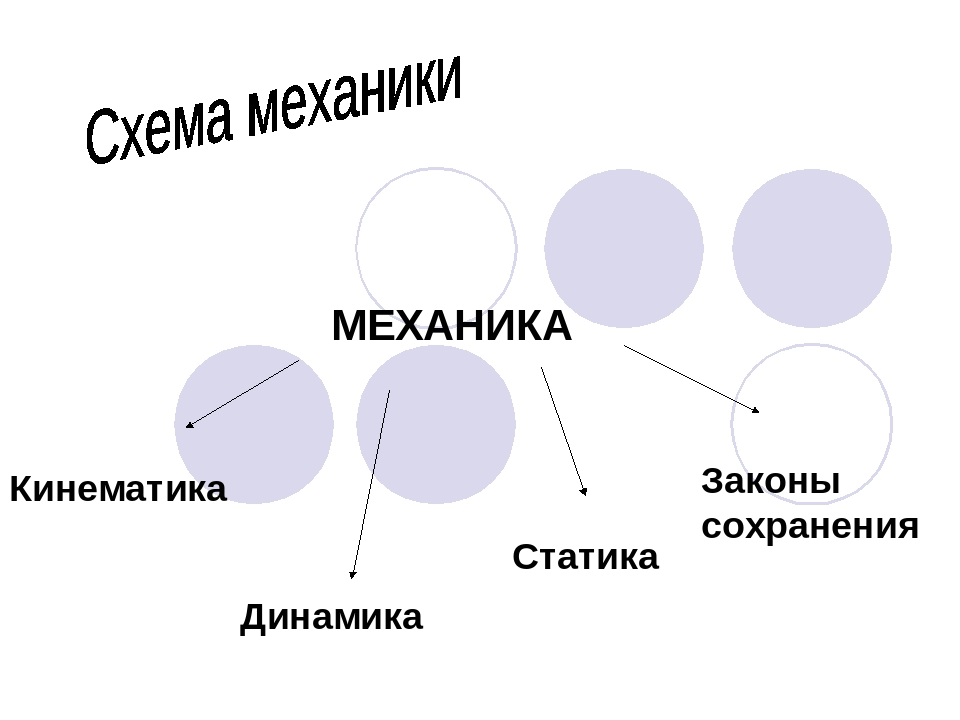 Урок 27: Упругие столкновения Урок 27: Упругие столкновения |
||
| 149 | 27.1 рабочий пример: эластичное одномерное столкновение | Воспроизвести видео |
| 150 | 27.2 Относительная скорость в 1D | Воспроизвести видео |
| 151 | 27.3 Уравнение кинетической энергии и импульса | Воспроизвести видео |
| 152 | 27.4 Рабочий пример: повторное упругое одномерное столкновение | Воспроизвести видео |
| 153 | 27.5 Рабочий пример: гравитационная рогатка | Воспроизвести видео |
| 154 | 27,6 2D-столкновения | Воспроизвести видео |
XXXIV. Глубокое погружение: система отсчета центра масс Глубокое погружение: система отсчета центра масс |
||
| 155 | DD.2.1 Положение в рамке CM | Воспроизвести видео |
| 156 | DD.2.2 Относительная скорость не зависит от системы отсчета | Воспроизвести видео |
| 157 | ДД.2.3 Одномерные упругие скорости столкновения в CM Frame | Воспроизвести видео |
| 158 | DD.2.4 Рабочий пример: одномерное упругое столкновение в раме CM | Воспроизвести видео |
| 159 | DD.2.5 Кинетическая энергия в различных системах отсчета | Воспроизвести видео |
| 160 | DD.2.6 Кинетическая энергия в раме CM | Воспроизвести видео |
| 161 | ДД.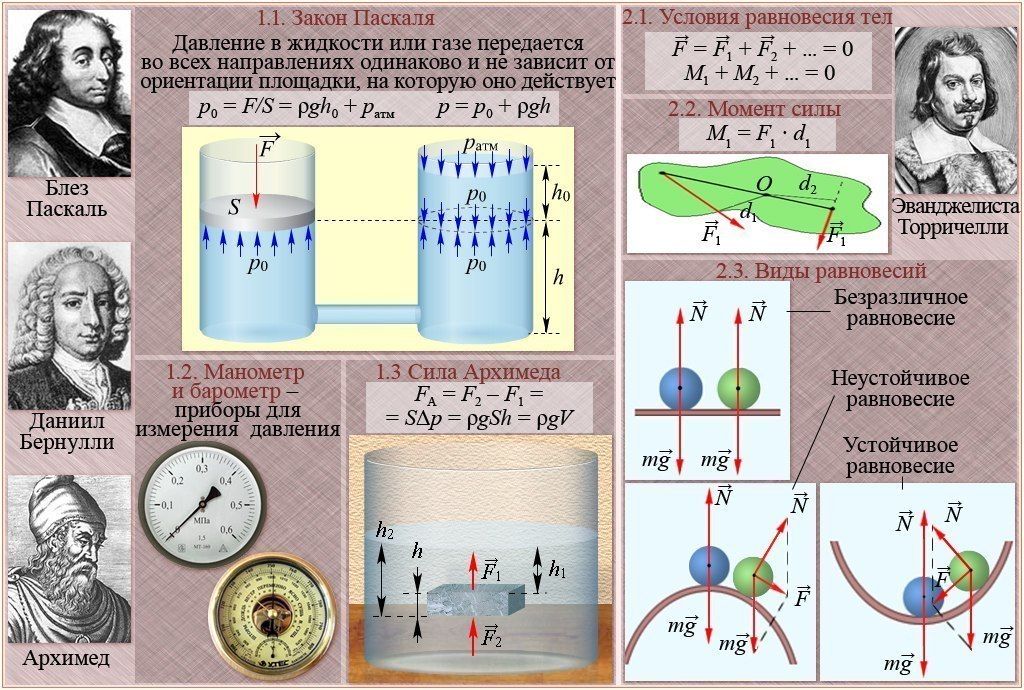 2.7 Изменение кинетической энергии 2.7 Изменение кинетической энергии |
Воспроизвести видео |
| 162 | 28.0 Неделя 10 Введение | Воспроизвести видео |
| XXXV. Урок 28: Движение твердого тела | ||
| 163 | 28.1 Жесткие корпуса | Воспроизвести видео |
| 164 | 28.2 Введение в перенос и вращение | Воспроизвести видео |
| 165 | 28.3 Обзор угловой скорости и ускорения | Воспроизвести видео |
| XXXVI. Урок 29: Момент инерции | ||
| 166 | 29.1 Кинетическая энергия вращения | Воспроизвести видео |
| 167 | 29. |
Воспроизвести видео |
| 168 | 29.3 Момент инерции диска | Воспроизвести видео |
| 169 | 29.4 Теорема о параллельных осях | Воспроизвести видео |
| 170 | 29.5 Глубокое погружение — момент инерции сферы | Воспроизвести видео |
| 171 | 29.6 Глубокое погружение — вывод теоремы о параллельных осях | Воспроизвести видео |
| ХХXVII. Урок 30: Крутящий момент | ||
| 172 | 30.1 Введение в динамику крутящего момента и вращения | Воспроизвести видео |
| 173 | 30.2 Перекрестное произведение | Воспроизвести видео |
| 174 | 30. 3 Перекрестное произведение в декартовых координатах 3 Перекрестное произведение в декартовых координатах |
Воспроизвести видео |
| 175 | 30,4 Крутящий момент | Воспроизвести видео |
| 176 | 30.5 Крутящий момент от гравитации | Воспроизвести видео |
| XXXVIII. Урок 31: Вращательная динамика | ||
| 177 | 31.1 Связь между крутящим моментом и угловым ускорением | Воспроизвести видео |
| 178 | 31.2 Отмена внутренних крутящих моментов в парах | Воспроизвести видео |
| 179 | 31.3 Рабочий пример — нахождение момента инерции диска от падающего груза | Воспроизвести видео |
| 180 | 31. 4 Рабочий пример — машина Atwood 4 Рабочий пример — машина Atwood |
Воспроизвести видео |
| 181 | 31.5 Проблемы с массивным шкивом | Воспроизвести видео |
| 182 | 31.7 Рабочий пример — два блока и шкив, использующий энергию | Воспроизвести видео |
| XXXIX.Неделя 10 Примеры работы | ||
| 183 | PS.10.1 Рабочий пример — блоки с фрикционным и массивным шкивом | Воспроизвести видео |
| 184 | 32.0 Неделя 11 Введение | Воспроизвести видео |
| XL. Урок 32: Угловой момент точечной частицы | ||
| 185 | 32.1 Угловой момент для точечной частицы | Воспроизвести видео |
| 186 | 32. 2 Расчет углового момента 2 Расчет углового момента |
Воспроизвести видео |
| 187 | 32.3 Рабочий пример — угловой момент относительно разных точек | Воспроизвести видео |
| 188 | 32.4 Угловой момент кругового движения | Воспроизвести видео |
| XLI. Урок 33: Момент количества движения твердого тела относительно неподвижной оси | ||
| 189 | 33.1 рабочий пример — угловой момент двух вращающихся частиц | Воспроизвести видео |
| 190 | 33.2 Угловой момент симметричного объекта | Воспроизвести видео |
| 191 | 33.4 Если импульс равен нулю, то угловой момент не зависит от начала координат | Воспроизвести видео |
| 192 | 33. 5 Кинетическая энергия симметричного объекта 5 Кинетическая энергия симметричного объекта |
Воспроизвести видео |
| XLII.Урок 34: Крутящий момент и угловой импульс | ||
| 193 | 34.1 Крутящий момент вызывает изменение углового момента — точечная частица | Воспроизвести видео |
| 194 | 34.2 Крутящий момент вызывает изменение углового момента — система частиц | Воспроизвести видео |
| 195 | 34,3 Угловой импульс | Воспроизвести видео |
| 196 | 34.4 Демонстрация: демонстрация велосипедного колеса | Воспроизвести видео |
| 197 | 34,5 Рабочий пример — попадание частиц в поворотное кольцо | Воспроизвести видео |
| 198 | 35. 0 Неделя 12 Введение 0 Неделя 12 Введение |
Воспроизвести видео |
| XLIII. Урок 35: Кинематика качения | ||
| 199 | 35.1 Перемещение и вращение колеса | Воспроизвести видео |
| 200 | 35.2 Катящееся колесо в центре масс рамы | Воспроизвести видео |
| 201 | 35.3 Катящееся колесо в грунтовой раме | Воспроизвести видео |
| 202 | 35.4 Перекатывание без проскальзывания Проскальзывание и занос | Воспроизвести видео |
| 203 | 35.5 Точка контакта колеса, катящегося без проскальзывания | Воспроизвести видео |
| XLIV.Урок 36: Динамика качения | ||
| 204 | 36.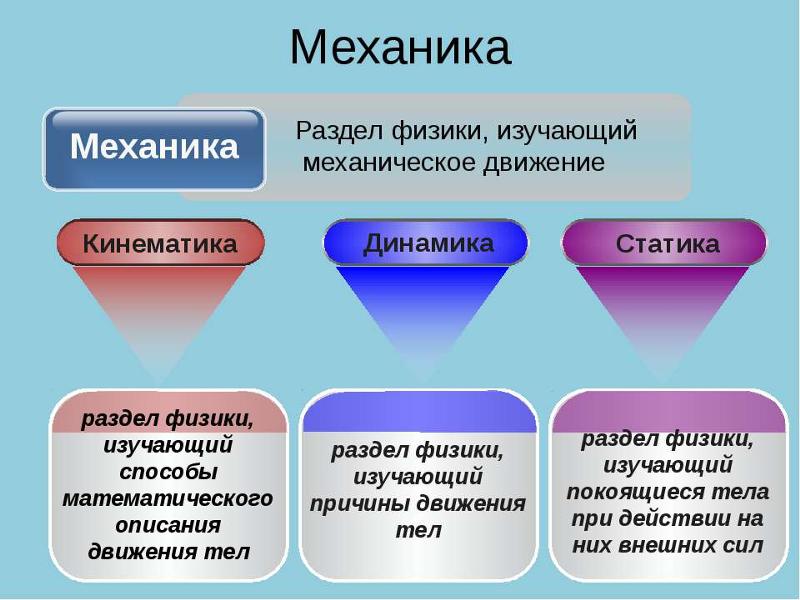 1 Трение на катящемся колесе 1 Трение на катящемся колесе |
Воспроизвести видео |
| 205 | 36.2 Рабочий пример — вращение колеса без проскальзывания вниз по наклонной плоскости — метод крутящего момента | Воспроизвести видео |
| 206 | 36.3 Демонстрация: демонстрация катушки | Воспроизвести видео |
| 207 | 36.4 Рабочий пример — йойо тянут по земле | Воспроизвести видео |
| 208 | 36.5 Анализ силы и крутящего момента в задачах перемещения и вращения | Воспроизвести видео |
| XLV. Урок 37: Кинетическая энергия качения и угловой момент | ||
| 209 | 37.1 Кинетическая энергия поступательного движения и вращения | Воспроизвести видео |
| 210 | 37.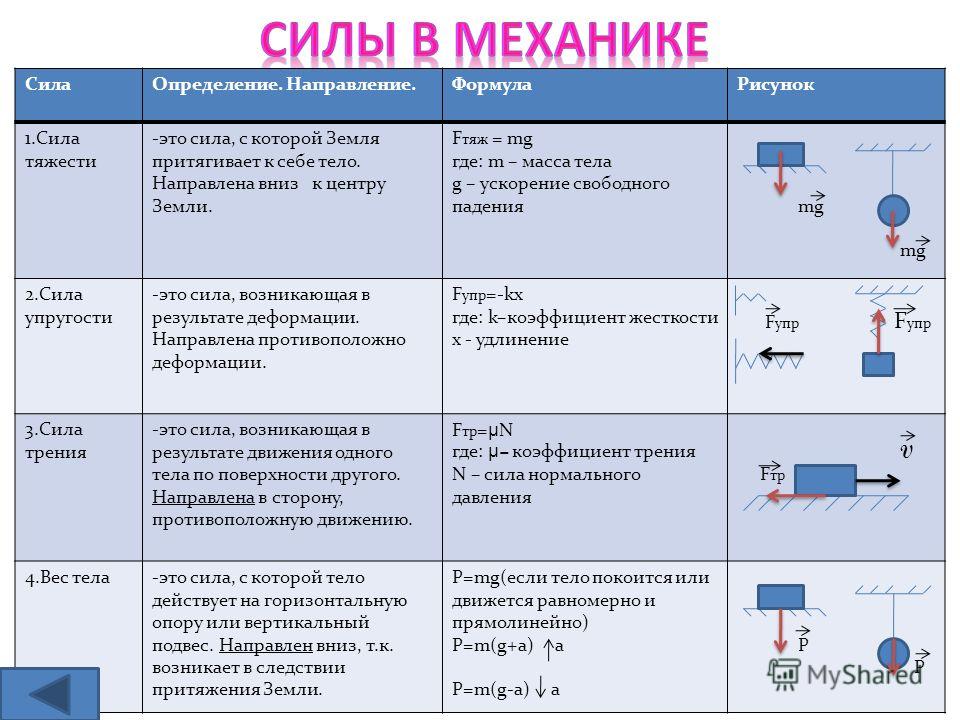 2 Рабочий пример — качение колеса без проскальзывания по наклонной плоскости 2 Рабочий пример — качение колеса без проскальзывания по наклонной плоскости |
Воспроизвести видео |
| 211 | 37.3 Угловой момент поступательного движения и вращения | Воспроизвести видео |
| XLVI. Глубокое погружение: гироскопы | ||
| 212 | DD.3.1 Deep Dive — Гироскопы — Бесплатные диаграммы тела, крутящий момент и векторы вращения | Воспроизвести видео |
| 213 | ДД.3.2 Глубокое погружение — гироскопы — прецессионная угловая скорость и названные гироскопы | Воспроизвести видео |
| 214 | DD.3.3 Deep Dive — Гироскопы — Нутация и полный угловой момент | Воспроизвести видео |
AP Лекции по физике: видео Вирена
A.
 Кинематика (исследование описания движения)
Кинематика (исследование описания движения) видео A1: Расстояние, положение, перемещение, скорость, скорость и ускорение. Быстро объясняет, что подразумевается под каждым из этих терминов, включая среднюю и мгновенную скорость.
видео A2: Вывод кинематических уравнений для прямолинейного равномерного ускорения с использованием графика v-t
видео A2.1: Вывод кинематических уравнений для прямолинейного равномерного ускорения с помощью исчисления. Примечание: для этих выводов используется интегральное исчисление.
видео A3: быстрый и интуитивно понятный способ решения некоторых задач кинематики. В этом видео идея средней скорости используется для быстрого решения некоторых типов задач кинематики. Это хороший способ быстро проверить свои ответы на тестах по кинематике.
видео A4: быстрый и интуитивно понятный способ решения некоторых свободного падения проблем. В этом видео идея средней скорости используется для быстрого решения некоторых типов задач кинематики. Это хороший способ быстро проверить свои ответы на тестах по кинематике.
В этом видео идея средней скорости используется для быстрого решения некоторых типов задач кинематики. Это хороший способ быстро проверить свои ответы на тестах по кинематике.
видео A5: Быстрый и интуитивно понятный способ решения некоторых Движения снаряда Проблемы. В этом видео идея средней скорости используется для быстрого решения некоторых типов задач кинематики. Это хороший способ быстро проверить свои ответы на тестах по кинематике.
видео A6: Основы движения снаряда. Только основы движения снаряда.
видео A7: Относительная скорость . Все скорости относительны, в этом видео показано, как найти скорость одного объекта относительно другого объекта с помощью векторов.
видео A8: основы работы с векторами (часть I) . Только основы векторной записи, включая объяснение единичных векторов.
Только основы векторной записи, включая объяснение единичных векторов.
видео A9: Основы работы с векторами (часть 2) Основы работы с векторами (часть 2). Некоторые основы связи между векторами скорости и ускорения.
видео B1: Решение задач второго закона Ньютона. В этом видеоролике показаны этапы решения задачи второго закона Ньютона с особым вниманием к объекту, движущемуся по наклонной плоскости.
видео B1.1: Основы силы натяжения. В этом видеоролике объясняется, почему струна или веревка незначительной массы обычно имеют одинаковое натяжение по всей длине.
видео B1.2: Сила кинетического трения
видео B1.3: Сила статического трения
видео B2: Наклонные плоскости (продолжение видео B1) : Это видео является продолжением видео B1. Он смотрит на объект на наклонной плоскости, где присутствует трение.
Он смотрит на объект на наклонной плоскости, где присутствует трение.
видео B2.1: Примеры задач на два 2-го закона Ньютона : Мяч, свисающий с потолка грузовика, и ящик в грузовике. В этом видео рассматриваются 2 проблемы второго закона Ньютона. Задача 1. Мяч висит на веревке, прикрепленной к потолку грузовика.Зная угол отклонения каната от вертикали, найти ускорение тележки. Задача 2. Грузовик, перевозящий ящик, движется по дороге с ускорением. Зная коэффициенты статического и кинетического трения, найдите максимальное ускорение, которое может иметь грузовик, прежде чем он начнет скользить по горизонтальному полу грузовика.
видео B3: Решение задач с участием нескольких тел с использованием законов Ньютона: В этом видео показано, как найти ускорение и силы для задачи с участием двух или более тел.
видео B3.1: Машинные проблемы Этвуда. В этом видеоролике показан метод решения задач второго закона Ньютона с участием шкивов.
видео B4: Машинные проблемы Атуда (часть II) . Это видео завершает анализ проблем машин Этвуда, связанных со шкивами.
видео B5: Задачи на круговое движение. В этом видео показано, как законы Ньютона применяются к задачам кругового движения.
видео B6: Задачи на движение по окружности (часть 2). В этом видео показано, как автомобили едут по повороту без уклона.
видео B6.5: Круговое движение для неравномерного кругового движения. Объясняет, как второй закон Ньютона используется для анализа объекта, движущегося в неравномерном круговом движении. (Неравномерное круговое движение — это круговое движение, при котором объект либо ускоряется, либо замедляется.)
видео B7: Виражи и игрушечные самолетики. Это видео подробно описывает физику движения автомобиля по кругу на вираже.
видео B7. 1: Физика поворота с креном (с учетом трения). В этом видео показана физика, когда автомобиль проходит поворот с креном, но ему все еще нужно трение, чтобы пройти поворот. Ему нужно трение, потому что оно движется либо слишком быстро, либо слишком медленно. Если он движется слишком медленно, то сила трения поднимается вверх по насыпи. Если он движется слишком быстро, то сила трения направлена вниз по насыпи. В первом примере автомобиль движется по трассе с уклоном без трения.Во втором примере автомобиль движется по наклонной трассе, которая имеет трение.
1: Физика поворота с креном (с учетом трения). В этом видео показана физика, когда автомобиль проходит поворот с креном, но ему все еще нужно трение, чтобы пройти поворот. Ему нужно трение, потому что оно движется либо слишком быстро, либо слишком медленно. Если он движется слишком медленно, то сила трения поднимается вверх по насыпи. Если он движется слишком быстро, то сила трения направлена вниз по насыпи. В первом примере автомобиль движется по трассе с уклоном без трения.Во втором примере автомобиль движется по наклонной трассе, которая имеет трение.
видео B8: Задачи о лифте и законы Ньютона. В этом видеоролике показано, как решить типичную задачу о лифте, связанную с законами движения Ньютона.
видео B9: Обзор блока B. Законы Ньютона (часть 1). Это видео представляет собой обзор понятий, описанных в разделе B. Попробуйте останавливать видео после каждого вопроса, чтобы посмотреть, сможете ли вы ответить на вопрос самостоятельно.
видео B10: Обзор блока B (часть 2)
видео B11: Обзор блока B (часть 3)
C.Работа, энергия и мощность
видео C0: Часть 1 скалярного произведения или скалярного произведения. Изначально я забыл добавить это. Смотрите это перед D1.
видео C1: Точечный продукт или скалярный продукт. В этом видеоролике объясняется один из двух способов умножения двух векторных величин. О втором методе будет рассказано в другом видео.
видео C2: Интеграл и работа силы. Это видео представляет собой введение в работу, выполняемую переменной силой.
видео C3: Использование исчисления для вывода уравнений кинематики для прямолинейного движения с постоянным ускорением. Это видео пытается сделать именно то, что в нем говорится.
видео C4: Работа, совершаемая над объектом постоянной силой.
видео C5: Работа, совершаемая над объектом переменной силой.
видео C6: Мощность и эффективность
видео C7: Консервативные и неконсервативные силы. В этом видео показана разница между консервативными и неконсервативными силами в отношении работы, выполняемой каждым типом силы.
видео C8: Консервативные и неконсервативные силы (часть 2)
видео C9: Работа, проделанная консервативными силами. В этом видео показано, как работа, совершаемая консервативной силой, например силой гравитации, будет равна отрицательному изменению потенциальной энергии системы.
видео C10: Обзор блока C (часть 1). Это видео представляет собой обзор понятий, описанных в модуле D. Попробуйте останавливать видео после каждого вопроса, чтобы посмотреть, сможете ли вы ответить на вопрос самостоятельно.
видео C11: Обзор блока C (часть 2)
видео C12: Обзор блока C (часть 3)
видео C13: Обзор блока C (часть 4)
D. Импульс, импульс и центр масс
видео D1: Momentum Basics. В этом видео показано, как закон сохранения импульса следует из законов движения Ньютона.
видео D2: Типы столкновений. В этом видео подробно описаны различные типы столкновений между двумя объектами.
видео D3: Типы столкновений (часть 2).
видео D4: Столкновения в двух измерениях. В этом видео подробно описывается физика, которая возникает, когда столкновение происходит не «лоб в лоб», а скорее «не по центру», так что два объекта отклоняются от своих первоначальных прямолинейных траекторий.
видео D5: Проблемы с баллистическим маятником. В этом видео подробно рассматривается физика задачи о баллистическом маятнике. Примером задачи баллистического маятника может быть блок, висящий на веревке, в который попадает пуля, так что система пули-блока поднимается на определенную высоту, прежде чем вернуться в исходное положение.
В этом видео подробно рассматривается физика задачи о баллистическом маятнике. Примером задачи баллистического маятника может быть блок, висящий на веревке, в который попадает пуля, так что система пули-блока поднимается на определенную высоту, прежде чем вернуться в исходное положение.
видео D6: Обзор блока D (часть 1). Это видео представляет собой обзор концепций, рассмотренных в модуле D по Импульсу и Импульсу. Попробуйте ставить видео на паузу после каждого вопроса, чтобы увидеть, сможете ли вы ответить на вопрос самостоятельно.
видео D7: Обзор блока D (часть 2).
видео D8: Обзор блока D (часть 3).
видео E1: Вращательная кинематика. В этом видео объясняется кинематика вращения при постоянном угловом ускорении.
видео E2: Вращательная кинематика (часть 2). Это видео продолжает объяснять кинематику вращения и подробно описывает, как линейные величины связаны с вращательными (или угловыми) величинами при вращении объекта.
видео E3: Вращательная кинематика (часть 3)
видео E4: Крутящий момент и векторное произведение (или векторное произведение): В этом видео немного объясняется крутящий момент и векторное произведение или векторное произведение двух векторы. Итак, это второй способ перемножения двух векторных величин.
видео E5: Крутящий момент и векторное произведение (часть 2)
видео E6: Крутящий момент и векторное произведение (часть 3)
видео E7: Задачи статического равновесия. Это видео, в котором объясняются необходимые условия для поддержания конструкции в статическом равновесии. Статическое равновесие возникает, когда система не имеет линейного ускорения и углового ускорения.
видео E8: Задачи статического равновесия (часть 2)
видео E8.1: Задача о статическом равновесии для Физика человека, поднимающегося по лестнице.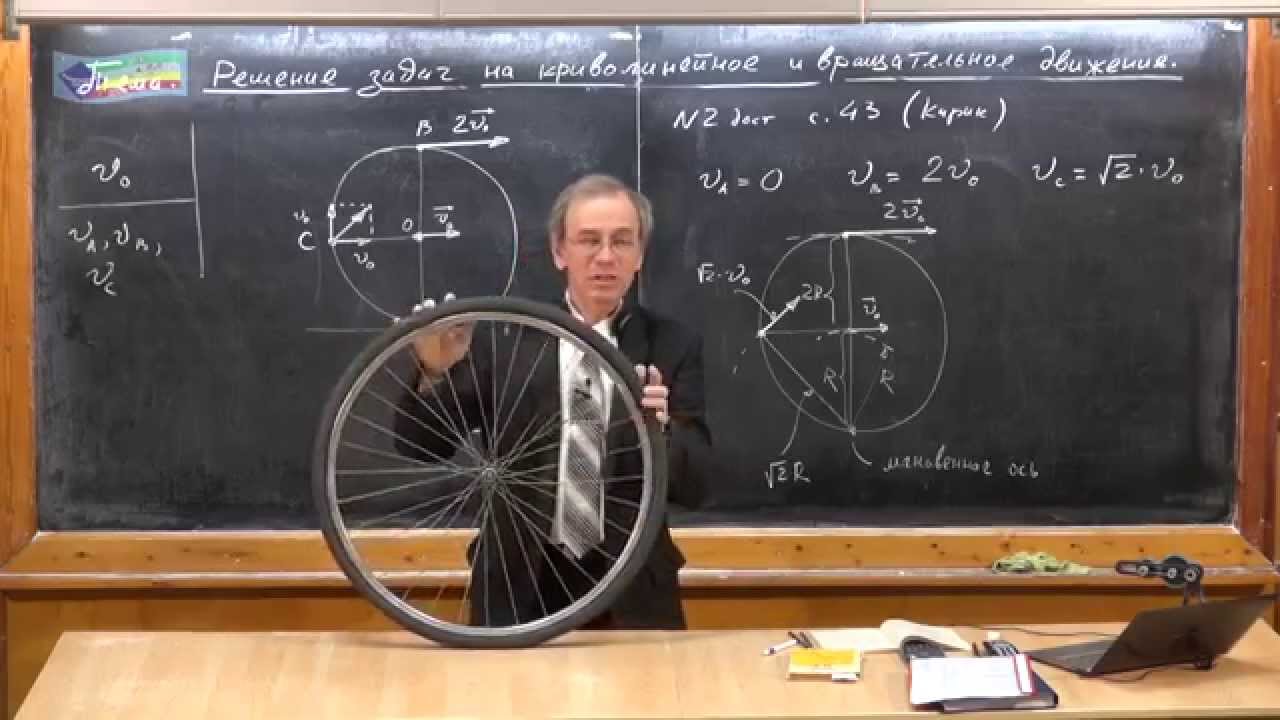 В этом видео объясняется, как анализировать физику человека, поднимающегося по лестнице. Первая часть находит силы на лестнице от земли. Вторая часть находит максимальное расстояние, на которое человек может подняться по лестнице, прежде чем он соскользнет у основания лестницы.
В этом видео объясняется, как анализировать физику человека, поднимающегося по лестнице. Первая часть находит силы на лестнице от земли. Вторая часть находит максимальное расстояние, на которое человек может подняться по лестнице, прежде чем он соскользнет у основания лестницы.
видео E9: Инерция вращения или момент инерции. В этом видео представлена концепция инерции вращения (или медленного вращения, или момента инерции)
видео E9.1: Инерция вращения длинного тонкого стержня. В этом видеоролике определяется момент инерции (I) для длинного тонкого стержня с равномерной линейной плотностью массы.
видео E9.2: Инерция вращения твердого диска. В этом видеоролике определяется момент инерции (I) твердого диска с одинаковой плотностью массы относительно оси, проходящей через его центр и перпендикулярной плоскости диска.
видео E9.3: Инерция вращения сплошного цилиндра.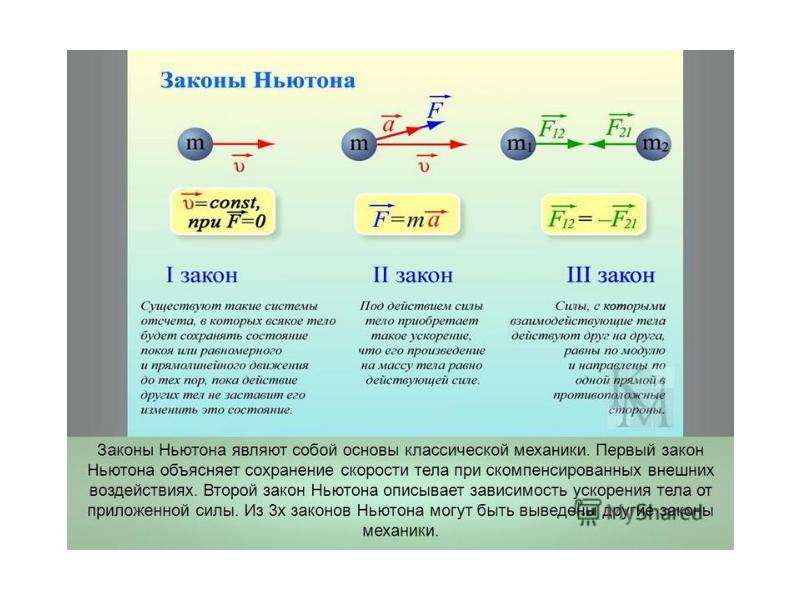 В этом видеоролике определяется момент инерции (I) твердого цилиндра с одинаковой плотностью, ось которого проходит через центр.
В этом видеоролике определяется момент инерции (I) твердого цилиндра с одинаковой плотностью, ось которого проходит через центр.
видео E9.4: Инерция вращения тонкого стержня НЕОДНОРОДНОЙ плотности массы. В этом видео определяется момент инерции (I) для длинного тонкого стержня НЕОДНОРОДНОЙ плотности массы с осью на конце стержня и перпендикулярно ему.
видео E9.5: Инерция вращения твердого цилиндра НЕОДНОРОДНОЙ плотности массы. В этом видеоролике определяется момент инерции (I) твердого цилиндра НЕОДНОРОДНОЙ плотности, ось которого проходит через центр.
видео E10: Теорема о параллельных осях. Если вы знаете инерцию вращения системы относительно оси, проходящей через ее центр масс, то вы можете найти инерцию вращения вокруг второй оси, параллельной исходной оси, используя теорему о параллельных осях.
видео E11: Вращательная динамика (второй закон Ньютона во вращательном движении)
видео E12: Вращательная динамика (часть 2)
видео E13: Вращательная динамика (часть 3): Проблемы с машиной Этвуда, когда шкив имеет значительную массу.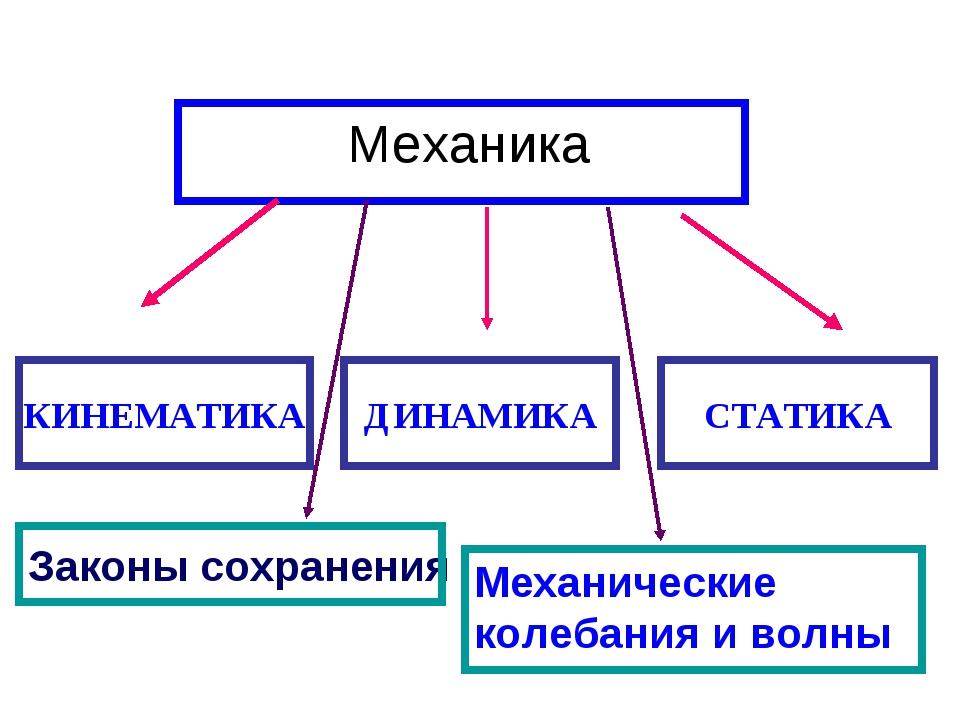
видео E14: Кинетическая энергия вращения (часть 1)
видео E15: Кинетическая энергия вращения (часть 2)
видео E15.1: Пример задачи о машине Этвуда, включающей шкив с непренебрежимо малым значением массой и с трением в его оси.
видео E16: Угловой момент
видео E17: Угловой момент (часть 2)
видео E18: Обзор блока E (часть 1). Это видео представляет собой обзор концепций, изложенных в модуле F по вращательному движению.Попробуйте ставить видео на паузу после каждого вопроса, чтобы увидеть, сможете ли вы ответить на вопрос самостоятельно.
видео E19: Обзор блока E (часть 2)
видео F1: Сила гравитации.
В этом видео представлены несколько различных точек зрения на гравитационную силу, описанную законом всемирного тяготения Ньютона.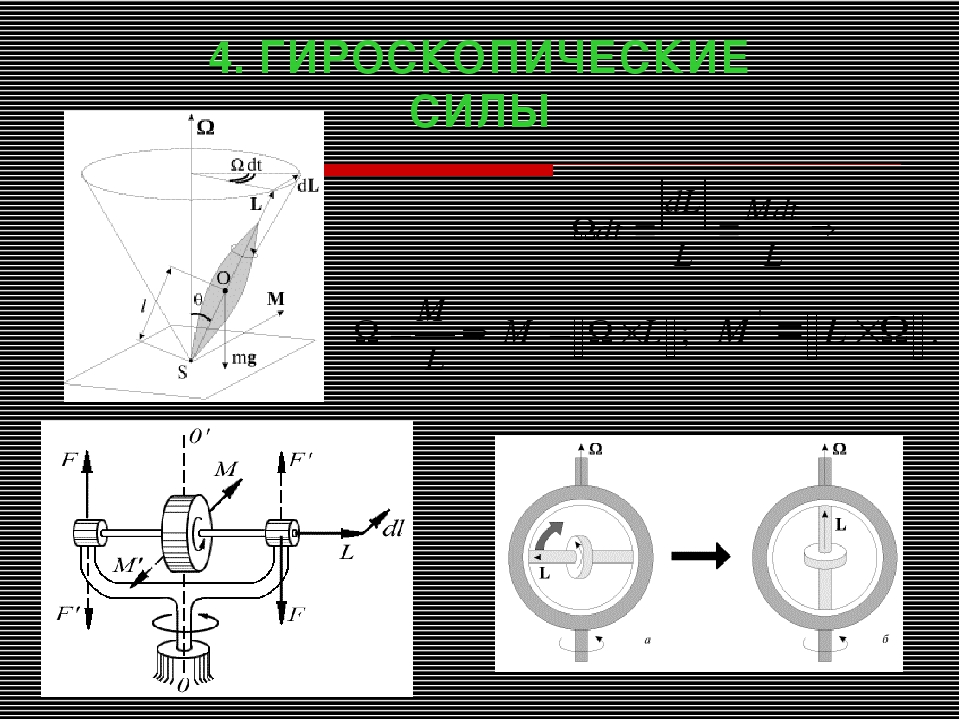
видео F2: Гравитационная потенциальная энергия.
В этом видео представлены несколько различных точек зрения на гравитационную потенциальную энергию. Более подробная информация о гравитационной потенциальной энергии будет дана в модулях D и G.
видео F3: Гравитационные силы и энергии:
В этом видео показано, как универсальные уравнения для гравитационных сил и энергии переходят в более простые формы, когда вы находитесь вблизи земной поверхности.
видео F4: Напряженность гравитационного поля. Это видео о гравитационном поле планеты.
видео F5: Спутники на круговой орбите. Это видео подробно описывает физику спутников на круговой орбите вокруг другого объекта.
видео F6: 3 закона движения планет Кеплера.
видео F7: Эллиптические орбиты и закон сохранения энергии
видео F8: Эллиптические орбиты и закон сохранения углового момента
Видео F9: Скорость убегания.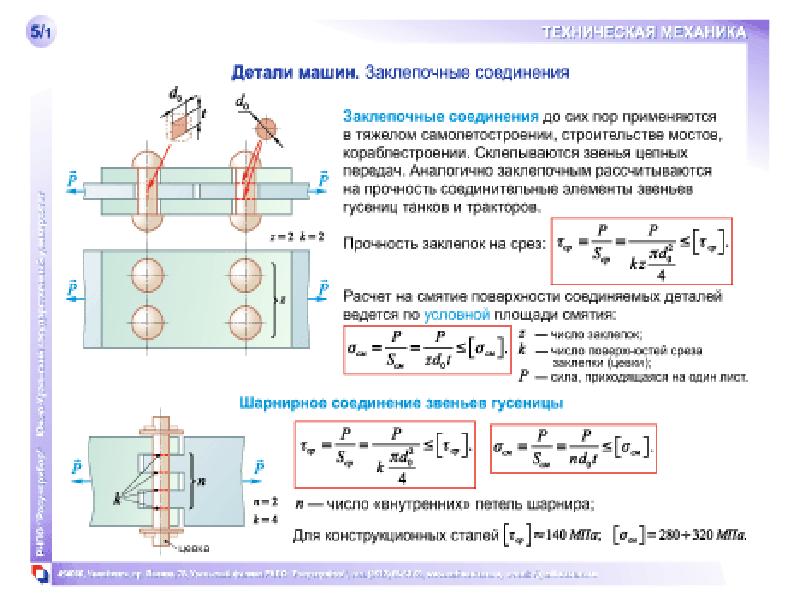 Объясняет, как рассчитать скорость убегания объекта для данной планеты.
Объясняет, как рассчитать скорость убегания объекта для данной планеты.
видео F10: Физика двойных звездных систем
видео F11: Обзор блока F (часть 1) .Это видео представляет собой обзор концепций, рассмотренных в модуле G о планетарном или спутниковом движении. Попробуйте ставить видео на паузу после каждого вопроса, чтобы увидеть, сможете ли вы ответить на вопрос самостоятельно.
видео F12: Обзор блока F (часть 2)
видео F13: Обзор блока F (часть 3)
G. Периодическое движение (гармоническое движение)
видео G1: Кинематика Движение (часть 1): Введение в гармоническое движение. В этом видео сравнивается движение объекта, движущегося в равномерном круговом движении, с объектом, движущимся в простом гармоническом движении.Кинематика изучает ОПИСАНИЕ движения. Динамика изучает ПРИЧИНЫ движения.
видео G2: Кинематика гармонического движения (часть 2)
видео G3: Кинематика гармонического движения (часть 3)
видео G4: Динамика простого гармонического движения (часть 52) 9. Это видео объясняет, как законы Ньютона применяются к простому гармоническому движению.
видео G5: Сохранение энергии и простое гармоническое движение
видео G6: Гармонический осциллятор с ящиком на ящике. В этом видео подробно рассказывается о физике ящика, который прикреплен к пружине, а другой предмет находится поверх первого. Чистая сила на верхнем ящике обеспечивается только силой трения.
видео G7: Пружины последовательно и параллельно. В этом видеоролике объясняется, как найти эквивалентные жесткости пружины для любого набора пружин, соединенных параллельно или последовательно.
видео G8: Период простого маятника.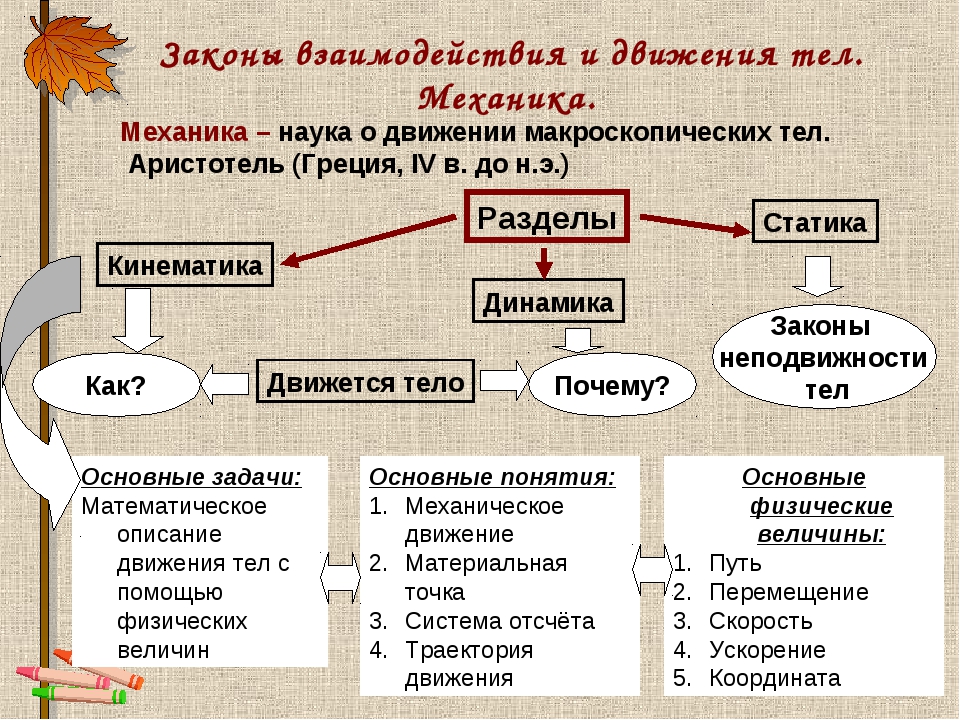 В этом видео описывается вывод периода простого маятника.
В этом видео описывается вывод периода простого маятника.
видео G9: Период физического маятника. В этом видео описывается вывод периода физического маятника.
видео G10: Период физического маятника (часть 2). В этом видео показано, как применить уравнение, полученное в видео G9.
видео G11: Эквивалентность вертикальной массы на пружине горизонтальной массе на пружине. В этом видео делается попытка объяснить, почему физика массы, прикрепленной к горизонтальной пружине, имеет много общего с физикой массы, прикрепленной к вертикальной пружине.
видео G12: Обзор блока G(часть 1). Это видео представляет собой обзор концепций, описанных в модуле H по Harmonic Motion. Попробуйте ставить видео на паузу после каждого вопроса, чтобы увидеть, сможете ли вы ответить на вопрос самостоятельно.
видео G13: Обзор блока G (часть 2).
видео G14: Обзор блока G (часть 3)
видео G15: Обзор блока G (часть 4)
видео G 16: Обзор блока G (часть 5)
0 9.Рост и разрушение в физике (сопротивление воздуха)*
видео N1: Объекты, падающие с сопротивлением воздуха.
видео N2: Объекты, падающие с сопротивлением воздуха (часть 2)
видео N3: Обзор сопротивления воздуха
видео N4: Обзор сопротивления воздуха (часть 2). Только часть этого видео — сопротивление воздуха. Другая часть этого видео посвящена RC-цепям.
видео h2: Общая картина (часть 1): Общая картина.В этом видео разрабатывается концептуальная карта, которая связывает различные темы, затронутые в механике.
видео h3 Общая картина (часть 2): Еще одно обобщение общей картины, связывающей кинематику, законы Ньютона, энергию и мощность.
Видеокурс по механике – охватывает полный блок по механике для уровня A/AS Physics
Видеокурс по механике для A level Physics, подходит для всех экзаменационных комиссий. Это мои предварительно записанные уроки, которые я использую в своем классе A-level, отзывы о них были положительными.Я делюсь ими в надежде, что вы также сможете извлечь пользу из моего огромного опыта преподавания физики уровня A!
Урок 1 – Графики движения
Урок 2 – Векторы
Урок 3 – Уравнения движения
Урок 4 – Движение снаряда
Урок 5 – 1-й и 2-й законы Ньютона
Урок 6. Третий закон Ньютона
Урок 7 – Моменты
Урок 8 – Энергия, мощность и эффективность
Урок 9 – Импульс
Экзаменационные вопросы по механике проходят через
Купить рабочую тетрадь
Полный курс состоит из 10 видео, из них 9 уроков по темам, а экзаменационный вопрос проходит через видео.Идеи вводятся с четкими пояснениями. Есть тренировочные вопросы, которые вы можете попробовать, где вас просят приостановить видео, а затем я прохожу с вами решения, чтобы вы могли укрепить свою уверенность в ответах на вопросы и отточить свою технику экзамена.
Вы сможете комментировать и задавать вопросы по темам в каждом видео.
Полный видеокурс по механике в настоящее время доступен бесплатно только на веб-сайте Physics Tutor Online!
Рекомендуется, чтобы учащиеся приобрели рабочую тетрадь и попробовали ответить на вопросы по каждой теме в условиях времени, прежде чем смотреть видеозапись. Если вы можете купить это, это поможет поддержать веб-сайт PTO, чтобы можно было производить больше бесплатных ресурсов — ваша поддержка будет очень признательна!
Если вы можете купить это, это поможет поддержать веб-сайт PTO, чтобы можно было производить больше бесплатных ресурсов — ваша поддержка будет очень признательна!
Материалы темы видеокурса
Видеокурс «Электрические цепи»
PHYS 200 — Лекция 1 — Введение в курс и ньютоновская механика
PHYS 200 — Лекция 1 — Введение в курс и ньютоновская механика
Глава 1. Введение и организация курса [00:00:00]
Профессор Рамамурти Шанкар: Это первая часть годичного курса, знакомящего вас со всеми основными идеями в физике, начиная с Галилея и Ньютона вплоть до великих революций прошлого века, которые касались теории относительности и квантовой теории. механика.Целевая аудитория этого курса действительно очень широкая. На самом деле, я всегда удивлялся тому, насколько широко это представлено. Я не знаю, какая у вас специальность; Я не знаю, что вы собираетесь делать позже, поэтому я выбрал темы, которые все мы в физике находим интересными. Некоторые могут быть или не быть полезными, но вы просто не знаете. Некоторые из вас, вероятно, станут врачами, и вы не знаете, почему я буду заниматься специальной теорией относительности или квантовой механикой, но вы не знаете, когда это пригодится.Если вы врач и у вас есть пациент, который убегает от вас со скоростью света, вы знаете, что делать. Или, если вы педиатр с очень маленьким пациентом, который не будет сидеть на месте, это потому, что законы квантовой механики не позволяют объекту иметь определенное положение и импульс. Так что это все вещи, о которых вы просто не знаете, когда они пригодятся, и я учу их, потому что это то, что меня заводит и заставляет меня заниматься физикой, и независимо от того, пойдете ли вы в физику, вам обязательно нужно научиться о самых больших и интересных революциях вплоть до современной физики.
Некоторые могут быть или не быть полезными, но вы просто не знаете. Некоторые из вас, вероятно, станут врачами, и вы не знаете, почему я буду заниматься специальной теорией относительности или квантовой механикой, но вы не знаете, когда это пригодится.Если вы врач и у вас есть пациент, который убегает от вас со скоростью света, вы знаете, что делать. Или, если вы педиатр с очень маленьким пациентом, который не будет сидеть на месте, это потому, что законы квантовой механики не позволяют объекту иметь определенное положение и импульс. Так что это все вещи, о которых вы просто не знаете, когда они пригодятся, и я учу их, потому что это то, что меня заводит и заставляет меня заниматься физикой, и независимо от того, пойдете ли вы в физику, вам обязательно нужно научиться о самых больших и интересных революциях вплоть до современной физики.
Хорошо. Вот какова будет тема, и я собираюсь немного рассказать вам о том, как организован курс. Во-первых, в этом году он будет записан на пленку.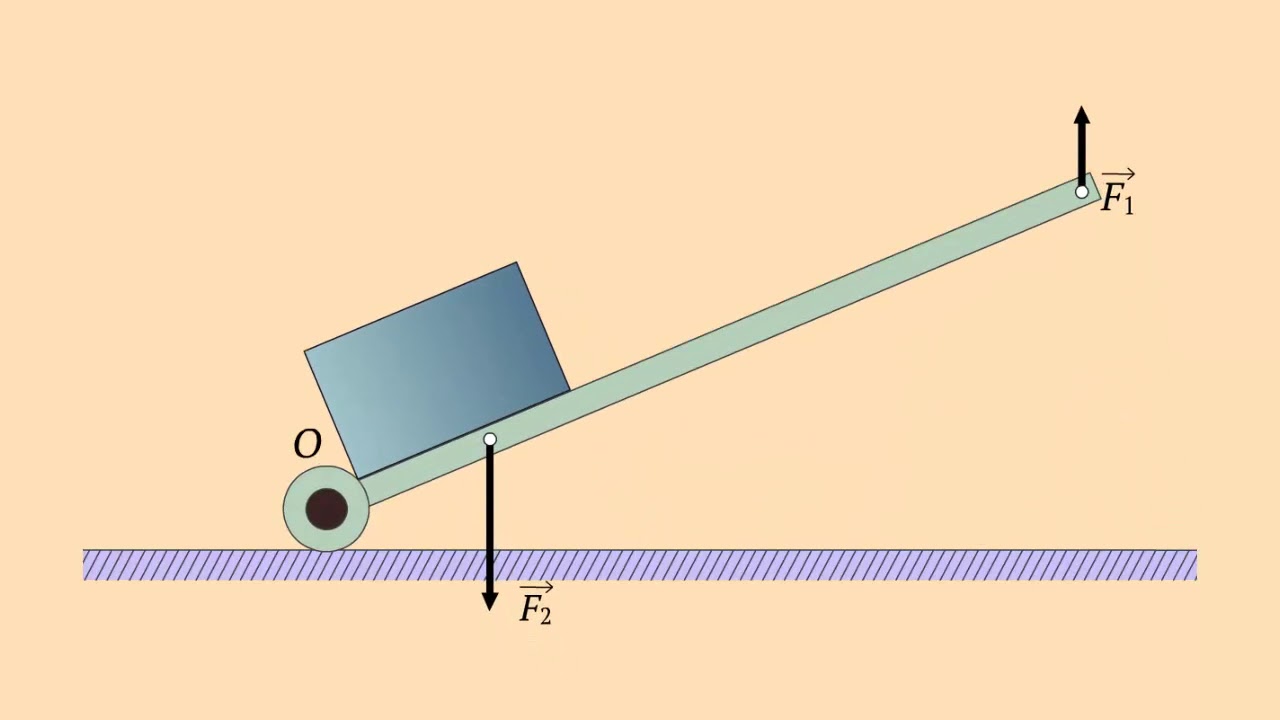 Вы можете видеть некоторых людей сзади с камерами в рамках экспериментальной пилотной программы, финансируемой Фондом Хьюлетта, и в какой-то момент они решат, что они будут делать с этими лекциями. Скорее всего, они разместят их где-нибудь, чтобы люди в других местах могли воспользоваться тем, что вы сидите в классе.Так что мне сказали, что с этого момента мы просто игнорируем камеру и работаем как обычно. Ничего не изменится. Я пытался договориться о треке смеха, чтобы, если шутки не сработают, мы могли наложить смех. Мне сказали «нет». Я просто должен иметь дело с этим, как это происходит. Так и будет — это похоже на одно из реалити-шоу, где все будет так, как есть, и, надеюсь, через некоторое время мы научимся действовать и вести себя нормально и не беспокоиться о его присутствии. Затем, переходя к остальным деталям курса.Кстати, на сайте, который я разместил, есть более подробная информация, которую мне дал университет, если вы хотите узнать больше о том, о чем все это.
Вы можете видеть некоторых людей сзади с камерами в рамках экспериментальной пилотной программы, финансируемой Фондом Хьюлетта, и в какой-то момент они решат, что они будут делать с этими лекциями. Скорее всего, они разместят их где-нибудь, чтобы люди в других местах могли воспользоваться тем, что вы сидите в классе.Так что мне сказали, что с этого момента мы просто игнорируем камеру и работаем как обычно. Ничего не изменится. Я пытался договориться о треке смеха, чтобы, если шутки не сработают, мы могли наложить смех. Мне сказали «нет». Я просто должен иметь дело с этим, как это происходит. Так и будет — это похоже на одно из реалити-шоу, где все будет так, как есть, и, надеюсь, через некоторое время мы научимся действовать и вести себя нормально и не беспокоиться о его присутствии. Затем, переходя к остальным деталям курса.Кстати, на сайте, который я разместил, есть более подробная информация, которую мне дал университет, если вы хотите узнать больше о том, о чем все это.
Организация курса довольно проста. Мы собираемся встречаться в понедельник и среду в этом зале с 11:30 до 12:45. В среду я дам вам несколько задач и размещу их на сайте. Вы, ребята, должны привыкнуть ходить на сайт класса. Я действительно, очень зависим от этого сейчас. Наконец-то я научился им пользоваться. Я буду использовать это для размещения информации, возможно, время от времени посылать электронные письма всему классу.Если вы хотите получать эти электронные письма, вы должны подписаться на курс, потому что я нажимаю кнопку, и он отправляется всем, кто там записался. Домашнее задание будет дано в среду, и оно должно быть выполнено перед уроком в следующую среду.
Мы собираемся встречаться в понедельник и среду в этом зале с 11:30 до 12:45. В среду я дам вам несколько задач и размещу их на сайте. Вы, ребята, должны привыкнуть ходить на сайт класса. Я действительно, очень зависим от этого сейчас. Наконец-то я научился им пользоваться. Я буду использовать это для размещения информации, возможно, время от времени посылать электронные письма всему классу.Если вы хотите получать эти электронные письма, вы должны подписаться на курс, потому что я нажимаю кнопку, и он отправляется всем, кто там записался. Домашнее задание будет дано в среду, и оно должно быть выполнено перед уроком в следующую среду.
Позвольте представить вам нашего руководителя TA, Мару Даниэль, которая недавно стала Марой Барабан. Таким образом, Мара будет человеком, который встретится с вами после урока, и она возьмет наборы задач, которые вы отправили до урока, и даст вам оцененные после урока.Хорошо? Это будет отсортировано, это будет там. Таким образом, вы должны бросить домашнюю работу до того, как придете в класс, а не яростно работать над ней во время урока, и решения будут опубликованы в тот же день. Так что нет особого смысла давать домашнюю работу с опозданием. Но время от времени, вы знаете, вы найдете причину, с которой я просто не могу спорить. Вы поженились, вам сделают трансплантацию, что бы это ни было. Это нормально. У тебя пересадка, я хочу увидеть старую часть тела. Ты вышла замуж, я хочу видеть твоего супруга.Если что-то случилось с бабушкой и дедушкой, я считаю. До четырех у меня нет подозрений. Давай пять, шесть, семь, восемь, мне придется заглянуть в генеалогическое древо. Но, знаете ли, любое разумное оправдание будет принято.
Так что нет особого смысла давать домашнюю работу с опозданием. Но время от времени, вы знаете, вы найдете причину, с которой я просто не могу спорить. Вы поженились, вам сделают трансплантацию, что бы это ни было. Это нормально. У тебя пересадка, я хочу увидеть старую часть тела. Ты вышла замуж, я хочу видеть твоего супруга.Если что-то случилось с бабушкой и дедушкой, я считаю. До четырех у меня нет подозрений. Давай пять, шесть, семь, восемь, мне придется заглянуть в генеалогическое древо. Но, знаете ли, любое разумное оправдание будет принято.
Относительная важность, придаваемая этим разным вещам: 20 % на домашнее задание, 30 % на среднесрочное задание, которое будет где-то в октябре, и 50 % на итоговое задание. Это будет средневзвешенное значение. Но у меня есть еще один план под названием «План амнистии», в котором я также сравниваю только вашу итоговую оценку, то, что вы сделали на выпускном экзамене, и то, что выше из двух, я возьму для определения вашей общей оценки за курс. Это то, о чем я обычно объявлял ближе к концу, но потом некоторые люди посчитали несправедливым не знать об этом с самого начала. Итак, я говорю вам с самого начала, но не мечтайте и не думайте, что Финал каким-то образом будет сильно отличаться от ваших обычных повседневных выступлений, а даст вам какую-то причину жить после Промежуточного экзамена. Итак, вы чувствуете, что есть надежда. Я могу изменить все за одну ночь; это случается. Я вставил это не просто так, потому что иногда некоторые из вас не прошли курс физики и не знают, как добиться хороших результатов в физике, и постепенно вы соображаете, и к выпускному экзамену вы взламываете код; вы умеете делать хорошо.Насколько я понимаю, это просто прекрасно. Если в конце семестра вы сдаете трехчасовой экзамен в закрытой среде и отвечаете на все вопросы, мне все равно, что вы делали дома или на контрольной. Это не актуально.
Это то, о чем я обычно объявлял ближе к концу, но потом некоторые люди посчитали несправедливым не знать об этом с самого начала. Итак, я говорю вам с самого начала, но не мечтайте и не думайте, что Финал каким-то образом будет сильно отличаться от ваших обычных повседневных выступлений, а даст вам какую-то причину жить после Промежуточного экзамена. Итак, вы чувствуете, что есть надежда. Я могу изменить все за одну ночь; это случается. Я вставил это не просто так, потому что иногда некоторые из вас не прошли курс физики и не знают, как добиться хороших результатов в физике, и постепенно вы соображаете, и к выпускному экзамену вы взламываете код; вы умеете делать хорошо.Насколько я понимаю, это просто прекрасно. Если в конце семестра вы сдаете трехчасовой экзамен в закрытой среде и отвечаете на все вопросы, мне все равно, что вы делали дома или на контрольной. Это не актуально.
Вот как будет проходить оценка. У нас есть группа ассистентов Мары. Она главный ассистент, и именно ей следует писать, когда у вас возникают проблемы. Тогда у нас также есть два преподавателя. Один из них — докторант Марк Каприо. Так что по вторникам с 13:00 до 14:00 у него будет дискуссионная секция в Sloane Lab.И Стив Фурланетто — я не знаю, Стив здесь или нет. Это Стив, наш новый доцент. У него будет своя секция во вторник вечером в Dunham Lab, в кабинете 220. Вечер вторника — это ночь, когда вы, ребята, понимаете, что домашняя работа должна быть сделана в среду. Итак, мы это знаем, поэтому он будет рядом, чтобы утешить вас и оказать любую помощь, в которой вы нуждаетесь. Хорошо. Мои собственные рабочие часы я еще не определил. Я должен буду узнать, когда это будет хорошо для вас. Вы знаете, я живу и работаю в лаборатории Слоан на холме, и было легко работать в офисе до или после уроков, но теперь вам нужно совершить особую поездку.Итак, просто дайте мне немного времени, чтобы узнать, может быть, запросив у вас ответы по электронной почте, какое время было бы подходящим для моего рабочего дня. Но если говорить о каких-то процедурных вещах, например, о том, что этот набор задач не был оценен должным образом и так далее, нет смысла писать мне по электронной почте, потому что я все равно отправлю его Маре.
Тогда у нас также есть два преподавателя. Один из них — докторант Марк Каприо. Так что по вторникам с 13:00 до 14:00 у него будет дискуссионная секция в Sloane Lab.И Стив Фурланетто — я не знаю, Стив здесь или нет. Это Стив, наш новый доцент. У него будет своя секция во вторник вечером в Dunham Lab, в кабинете 220. Вечер вторника — это ночь, когда вы, ребята, понимаете, что домашняя работа должна быть сделана в среду. Итак, мы это знаем, поэтому он будет рядом, чтобы утешить вас и оказать любую помощь, в которой вы нуждаетесь. Хорошо. Мои собственные рабочие часы я еще не определил. Я должен буду узнать, когда это будет хорошо для вас. Вы знаете, я живу и работаю в лаборатории Слоан на холме, и было легко работать в офисе до или после уроков, но теперь вам нужно совершить особую поездку.Итак, просто дайте мне немного времени, чтобы узнать, может быть, запросив у вас ответы по электронной почте, какое время было бы подходящим для моего рабочего дня. Но если говорить о каких-то процедурных вещах, например, о том, что этот набор задач не был оценен должным образом и так далее, нет смысла писать мне по электронной почте, потому что я все равно отправлю его Маре. Так что напрямую разбирайтесь с сильными мира сего.
Так что напрямую разбирайтесь с сильными мира сего.
Хорошо, наконец, я хочу дать вам несколько советов о том, как преуспеть в этом курсе и какой у вас должен быть настрой. Во-первых, я советую вам приходить на лекции.Это не корыстно; это не столько в мою пользу. Я думаю, что есть что-то полезное в том, чтобы услышать предмет, представленный один раз в устной форме. Во-вторых, книга, видите ли, у одного из вас была вот такая книга, в ней около 1100 страниц, а когда я учил физику, там было около 300 страниц. Теперь, я осматриваю эту комнату, я не вижу никого, чья голова в три раза больше моей, поэтому я знаю, что вы не можете переварить всего, что есть в книгах. Так что я должен убрать то, что я считаю действительно важной частью, и рассказать о ней в лекции.Итак, вы приходите на занятия, чтобы узнать, что входит, а что нет. Если вы этого не сделаете, есть опасность, что вы узнаете что-то, что вам не нужно, а мы этого не хотим. Хорошо, поэтому вы пришли на урок.
Во-вторых, самое главное для хорошей успеваемости по физике, это делать домашнюю работу.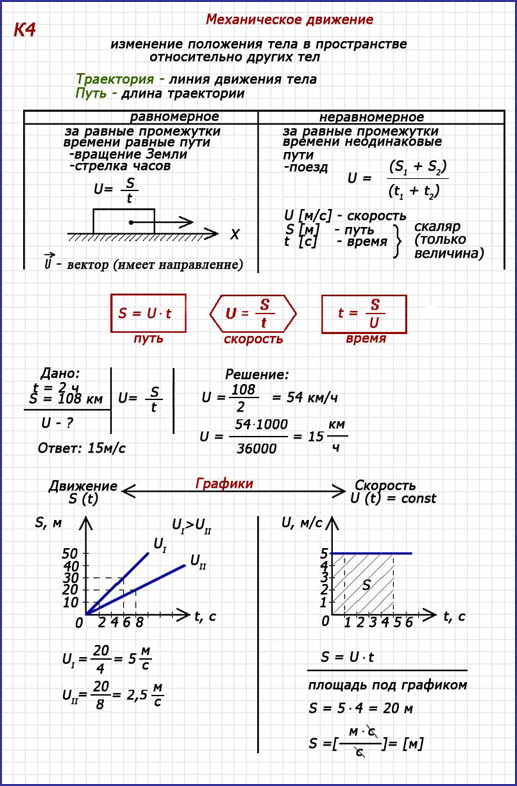 20%, отдаваемые домашнему заданию, не являются реальной мерой его важности. Домашнее задание — это когда вы действительно выясняете, сколько вы знаете и чего не знаете. Если вы посмотрите, как я делаю это на доске, это выглядит очень разумно.Похоже, вы можете это сделать, но единственный способ узнать об этом — когда вы действительно решите проблему. Это единственный раз, когда ты узнаешь. Итак, я прошу вас решать задачи по мере их публикации. Поэтому, если я опубликую его в среду, чтобы осветить материал на эту неделю, вам следует попробовать его как можно быстрее, потому что я предполагаю, что вы справились с задачами, когда придете на следующие несколько лекций. А при выполнении домашнего задания совершенно нормально работать в группах.Вам не нужно делать это самостоятельно. Так не делается в физике. Сейчас я пишу статью с двумя другими людьми. Это мои коллеги-экспериментаторы, которые пишут статьи вместе с 400, может быть, даже с 1000 человек. Когда они проводят большие эксперименты на коллайдерах в Женеве или в Фермилабе, количество совместных проектов может исчисляться сотнями.
20%, отдаваемые домашнему заданию, не являются реальной мерой его важности. Домашнее задание — это когда вы действительно выясняете, сколько вы знаете и чего не знаете. Если вы посмотрите, как я делаю это на доске, это выглядит очень разумно.Похоже, вы можете это сделать, но единственный способ узнать об этом — когда вы действительно решите проблему. Это единственный раз, когда ты узнаешь. Итак, я прошу вас решать задачи по мере их публикации. Поэтому, если я опубликую его в среду, чтобы осветить материал на эту неделю, вам следует попробовать его как можно быстрее, потому что я предполагаю, что вы справились с задачами, когда придете на следующие несколько лекций. А при выполнении домашнего задания совершенно нормально работать в группах.Вам не нужно делать это самостоятельно. Так не делается в физике. Сейчас я пишу статью с двумя другими людьми. Это мои коллеги-экспериментаторы, которые пишут статьи вместе с 400, может быть, даже с 1000 человек. Когда они проводят большие эксперименты на коллайдерах в Женеве или в Фермилабе, количество совместных проектов может исчисляться сотнями. Таким образом, совершенно нормально участвовать в сотрудничестве, но вы должны убедиться, что делаете все возможное. Вы должны быть уверены, что если вы объясните другим, как решить эту задачу, то кто-то еще внесет свой вклад во что-то еще, но вы знаете, какой вклад в итоге сделали все.Так что игра состоит не в том, чтобы так или иначе получить решение поставленной задачи, а в том, чтобы полностью понять, как это делается, и ТА вам в этом помогут.
Таким образом, совершенно нормально участвовать в сотрудничестве, но вы должны убедиться, что делаете все возможное. Вы должны быть уверены, что если вы объясните другим, как решить эту задачу, то кто-то еще внесет свой вклад во что-то еще, но вы знаете, какой вклад в итоге сделали все.Так что игра состоит не в том, чтобы так или иначе получить решение поставленной задачи, а в том, чтобы полностью понять, как это делается, и ТА вам в этом помогут.
Каждый день в холле для студентов будет ассистент. Я призываю вас использовать это. Это красивая новая гостиная, которую проректор разрешил нам построить для физиков и химиков, или для тех, кто находится в здании. Если вы пойдете туда, на третий этаж Слоана, вы можете столкнуться с такими же людьми, как и вы, которые пытаются работать над проблемами.Вы можете столкнуться со старшеклассниками, более продвинутыми учениками, вы столкнетесь со своей ТА. Значит хороший климат. Есть кофемашины, есть диваны для отдыха и все остальное. Там есть компьютеры, есть принтеры, так что это хорошая гостиная, и я думаю, что если вы ходите туда один день в неделю, чтобы решить свои задачи, чаще это хорошее место для встреч, я рекомендую это.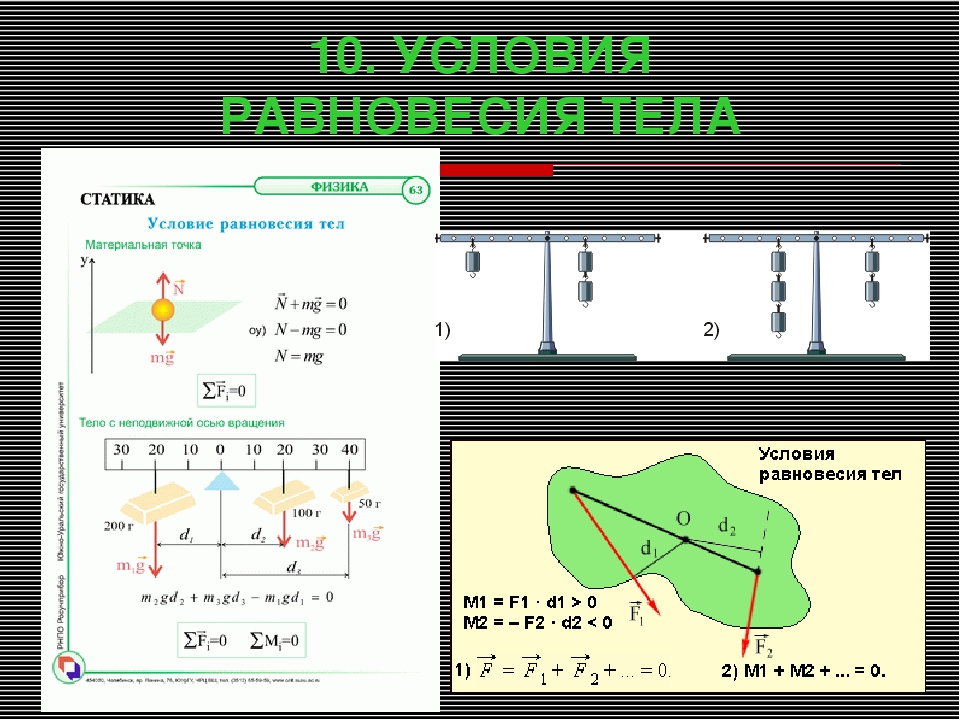
Последний совет, это очень важно, так что обратите на это внимание, а именно, я прошу вас не разговаривать с соседями во время лекции.Это выглядит очень безобидно, но вы обнаружите, что это единственное, что действительно меня поддерживает. Большую часть времени мне все равно. Я действительно либерал, но это меня беспокоит, потому что я смотрю на вас, я пытаюсь увидеть по вашей реакции, какую часть моей лекции вы слушаете, и потом это очень отвлекает, когда люди говорят. Поэтому, пожалуйста, не делайте этого. Если вы заговорите, я предполагаю, что вы говорите обо мне. Если вы будете смеяться, я буду считать, что вы смеетесь надо мной.Это не совсем то, что я думаю, но вот как это раздражает, когда люди говорят, и очень хорошие студенты, которые не осознают этого, часто нарушают ход моих мыслей. Поэтому я прошу вас свести это к минимуму. Время от времени вам придется поговорить с соседом и сказать: «Не могли бы вы передать мне мой упавший кардиостимулятор?» Это нормально. Затем вы возвращаетесь к своим делам. Но не делайте этого слишком много.
Но не делайте этого слишком много.
Наконец, есть древняя тема про сон на уроках. Теперь, на мой взгляд, все в порядке, хорошо.Я знаю, что вам, ребята, нужен отдых, и что интересно, лучшие спящие находятся в первых парах рядов. Я не встречал вас, ребята. Это не личное. Я обнаружил, что некоторым людям действительно приходится сидеть в первом и втором ряду, потому что они утверждают, что если они меня не слышат, то не могут заснуть. Это было правдой в Слоане, но я думаю, что у Люси очень хорошая акустика, так что вы можете растянуться сзади. Но мой единственный критерий — если вы разговариваете во сне, теперь это запрещено, потому что говорить нельзя.Далее, если вы собираетесь спать, я прошу вас сесть между двумя неспящими, потому что иногда, что случается, весь ряд опрокидывается. Нам не нужен эффект домино. Теперь это будет записано на пленку, и это очень плохо скажется на моей репутации, так что распространяйтесь среди других людей. Хорошо. Вот и все с точки зрения класса, вы знаете, логистики и всего остального.
Я собираюсь заняться собственно физикой. Я постараюсь заканчивать каждую лекцию вовремя, но иногда, если я нахожусь в середине предложения или в середине вывода, мне, возможно, придется пробежать пару минут; нет необходимости шаркать ногами и передвигать вещи.Я знаю, который час. Я тоже хочу уйти, как и вы, ребята, но позвольте мне закончить кое-что. В другие дни я могу закончить на несколько минут раньше времени. Это потому, что идеи физики не укладываются в 75-минутные отрезки и иногда немного растекаются. Кроме того, я привык преподавать этот курс три раза в неделю, а теперь это внезапно два раза в неделю, и поэтому вещи, которые укладывались в хорошие 50-минутные блоки, теперь обрезаются по-разному, так что это довольно сложно. Так что даже для меня кое-что из этого будет новым, и время может быть неподходящим.Прежде всего, я должен сказать вам, что на этом уроке запись не повлияет на вас, потому что камера будет находиться за вашей головой. Я упомянул вам на веб-сайте, что это не та большая возможность, которую вы искали, чтобы стать звездой. Будет виден только затылок. В некоторых случаях затылок может быть более выразительным, чем перед, и в этом случае это ваша возможность, и я желаю вам удачи. Но в остальном просто не беспокойтесь об этом, потому что вас только услышат.Вас могут даже не услышать. Итак, меня спросили, что, если вопрос не очень ясен, я должен повторить его, чтобы люди, слушающие его позже, знали, в чем был вопрос.
Будет виден только затылок. В некоторых случаях затылок может быть более выразительным, чем перед, и в этом случае это ваша возможность, и я желаю вам удачи. Но в остальном просто не беспокойтесь об этом, потому что вас только услышат.Вас могут даже не услышать. Итак, меня спросили, что, если вопрос не очень ясен, я должен повторить его, чтобы люди, слушающие его позже, знали, в чем был вопрос.
Позвольте мне прояснить одну вещь. То есть я не за то, чтобы вы разговаривали друг с другом, потому что вы отвлекаете. Если ты остановишь меня в любой момент, это нормально. Я приветствую это, потому что я видел эту тему бог знает сколько лет. Единственное, что меня отличает, это вопросы, которые у вас есть.Вы можете остановить меня в любое время, и вы не должны чувствовать, что каким-то образом останавливаете ход урока. Фиксированной программы нет. Мы можем перемещать вещи, и мне гораздо интереснее отвечать на ваши вопросы, чем вести монолог. Так что не беспокойтесь об этом. Так что останавливайте меня каждый раз, когда вы чего-то не понимаете, и не думайте, что вы чего-то не понимаете, потому что с вашим уровнем понимания что-то не так. Довольно часто вы, ребята, задаете вопросы, которые никогда не приходят мне в голову, так что это очень интересно.И вещи, которые мы повторяем год за годом, потому что они звучат так разумно, внезапно звучат неразумно, когда кто-то из вас указывает на какой-то аспект, которому вы не следовали. Таким образом, всем нам может быть очень интересно обсудить вопросы в классе, и довольно часто некоторые вопросы очень распространены, и ваши одноклассники будут вам благодарны за то, что вы подняли их. В противном случае, как вы знаете, ассистенты получают десять электронных писем с одним и тем же вопросом. Хорошо. Итак, я начну прямо сейчас. У кого-нибудь есть вопросы по классу? Формат? Среднесрочная? Экзамены? Хорошо.Да?
Довольно часто вы, ребята, задаете вопросы, которые никогда не приходят мне в голову, так что это очень интересно.И вещи, которые мы повторяем год за годом, потому что они звучат так разумно, внезапно звучат неразумно, когда кто-то из вас указывает на какой-то аспект, которому вы не следовали. Таким образом, всем нам может быть очень интересно обсудить вопросы в классе, и довольно часто некоторые вопросы очень распространены, и ваши одноклассники будут вам благодарны за то, что вы подняли их. В противном случае, как вы знаете, ассистенты получают десять электронных писем с одним и тем же вопросом. Хорошо. Итак, я начну прямо сейчас. У кого-нибудь есть вопросы по классу? Формат? Среднесрочная? Экзамены? Хорошо.Да?
Студент : Вы сказали, что будет объявлено два часа. Как нам ждать [неразборчиво]
Профессор Рамамурти Шанкар : О, вы имеете в виду мои рабочие часы?
Студент : Нет. Я думал, что [неразборчиво]
Профессор Рамамурти Шанкар : Нет, дискуссионные секции проводятся во вторник днем с 1:00 до 2:00 и во вторник вечером с 8:00 до 10:00, и на веб-сайте есть все подробности о том, когда и где. Да?
Да?
Студент : Таким образом, лабораторные часы все равно будут [неразборчиво]
Профессор Рамамурти Шанкар : Ага. Есть много, много лабораторных раз, и вы должны пойти на веб-сайт для лаборатории. И, кстати, мне это напомнило. У меня есть много листовок, которые дал мне директор лабораторий, в которых указано, какая лаборатория вам подходит, и они предлагаются много раз в неделю. Да?
Ученик : Что касается знания материала только из вашего класса, насколько важно сдавать лабораторные одновременно с этим классом?
Профессор Рамамурти Шанкар : Я думаю, что это хорошая идея пройти лабораторию, особенно в этом конкретном классе, потому что у меня нет никаких демонстраций.Они все в другом здании. Итак, это напомнит вам, что физика, в конце концов, экспериментальная наука, и вы сможете увидеть, откуда берутся все законы физики. Так что, если вы собираетесь принимать его, вы должны принимать его в одно и то же время. Да?
Да?
Студент : Не могли бы вы рассказать о том, когда вы ожидаете [неразборчиво]
Профессор Рамамурти Шанкар : А, очень хорошо. Это класс, основанный на исчислении, и я ожидаю, что все знакомы хотя бы с основами дифференциального исчисления.Что такое функция, что такое производная, что такое вторая производная, как брать производные от элементарных функций, как решать элементарные интегралы. Некоторое время спустя я буду иметь дело с функциями более чем одной переменной, о которых я кратко расскажу вам, потому что это может быть не обязательным условием, но, безусловно, тем, чему вы научитесь и сможете использовать время от времени. Но есть разные подходы к физике. Моя цель — снова и снова демонстрировать, как мало математики вам нужно, чтобы выполнить работу.Есть и другие, которым нравится показывать вам, как много математики вы могли бы каким-то образом внедрить в процесс, хорошо.
В эту игру можно играть по-разному, и некоторые из нас очень гордятся тем, что нашли самый простой способ что-то понять.![]() Это определенно моя торговая марка; именно так я провожу свое исследование. Так что, если вы чувствуете, что математики недостаточно, я гарантирую вам, что знаю достаточно, чтобы в конце концов завалить весь класс снегом, но не в этом дело. Я буду использовать его умеренно и использовать его с наилучшим возможным эффектом, а не использовать его только потому, что он есть.Хорошо. Так что я не знаю вашего математического образования, но в учебнике есть приложение, которое является разумным показателем того, сколько вы должны знать по математике. Вы должны знать свою тригонометрию, вы должны знать, что такое синус и что такое косинус. Вы не можете сказать: «Я посмотрю». Ваш день рождения и номер социального страхования — это то, что вы ищете. Тригонометрические функции, которые вы знаете все время. Хорошо. Я спрошу тебя, и ты сделаешь. Хорошо. И, конечно же, есть тригонометрические тождества, знакомые вам со школы.Страницы и страницы, так что никто не ожидает, что вы знаете все эти личности, но есть несколько популярных, которые мы будем использовать.
Это определенно моя торговая марка; именно так я провожу свое исследование. Так что, если вы чувствуете, что математики недостаточно, я гарантирую вам, что знаю достаточно, чтобы в конце концов завалить весь класс снегом, но не в этом дело. Я буду использовать его умеренно и использовать его с наилучшим возможным эффектом, а не использовать его только потому, что он есть.Хорошо. Так что я не знаю вашего математического образования, но в учебнике есть приложение, которое является разумным показателем того, сколько вы должны знать по математике. Вы должны знать свою тригонометрию, вы должны знать, что такое синус и что такое косинус. Вы не можете сказать: «Я посмотрю». Ваш день рождения и номер социального страхования — это то, что вы ищете. Тригонометрические функции, которые вы знаете все время. Хорошо. Я спрошу тебя, и ты сделаешь. Хорошо. И, конечно же, есть тригонометрические тождества, знакомые вам со школы.Страницы и страницы, так что никто не ожидает, что вы знаете все эти личности, но есть несколько популярных, которые мы будем использовать.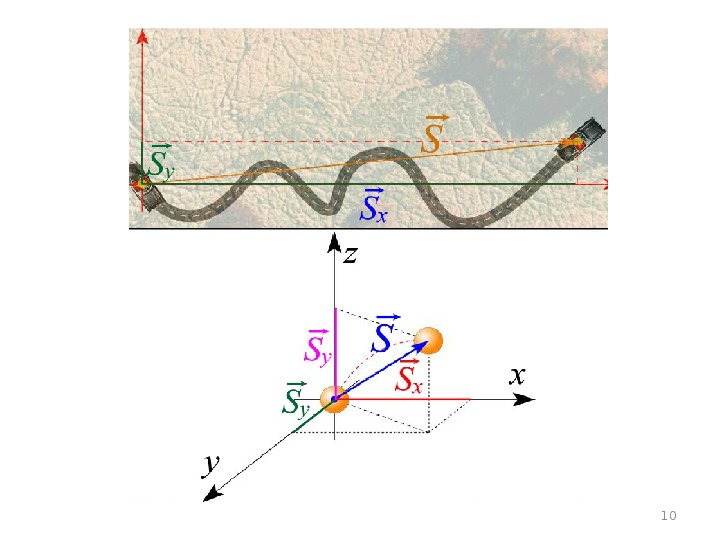 Хорошо. Что-нибудь еще? Да?
Хорошо. Что-нибудь еще? Да?
Студент : Может, и рановато, но когда у нас будет Промежуточный экзамен?
Профессор Рамамурти Шанкар : Ага. Промежуточный период будет где-то около 20 октября. Я должен узнать точное время. У нас есть 24 лекции для этого класса, и первые 12 примерно будут частью промежуточного семестра, но после 12-й лекции я могу подождать неделю, чтобы у вас было время решить задачи и получить решения.Тогда я дам вам Промежуточный экзамен. Да?
Студент : Если вам нужен один из двух лабораторных курсов, какой вы порекомендуете?
Профессор Рамамурти Шанкар : Да, это подробно. Этот флаер отвечает именно на это. Хорошо, был еще один вопрос от кого-то? Да?
Студент : Несколько человек, с которыми я разговаривал, рекомендовали начать сдавать лабораторные во втором семестре, а не в первом. Будет ли это целесообразно или мы должны принимать оба одновременно?
Профессор Рамамурти Шанкар : У меня нет твердой точки зрения. Я думаю, тебе стоит когда-нибудь сдать лабораторную, но я не знаю, сколько семестров тебе нужно сдать. Но я бы сказал, что советы ваших предшественников очень важны. Если они скажут вам, что это то, что работает, это лучше, чем то, что может сказать вам кто-то вроде меня. Также вам следует поговорить со Стивеном Айронсом, директором лабораторий. Он видел все возможные ситуации. Он даст вам хороший совет.
Я думаю, тебе стоит когда-нибудь сдать лабораторную, но я не знаю, сколько семестров тебе нужно сдать. Но я бы сказал, что советы ваших предшественников очень важны. Если они скажут вам, что это то, что работает, это лучше, чем то, что может сказать вам кто-то вроде меня. Также вам следует поговорить со Стивеном Айронсом, директором лабораторий. Он видел все возможные ситуации. Он даст вам хороший совет.
Глава 2. Ньютоновская механика: динамика и кинематика [00:21:25]
Начнем прямо сейчас.Хорошо. Итак, вначале мы будем изучать то, что называется ньютоновской механикой. Весьма примечательно, что все это сооружение строится всего одним человеком — Ньютоном — и он отправил нас на путь понимания всех природных явлений до 18-го с чем-то года, когда Максвелл изобрел законы электромагнетизма и записал их. знаменитые уравнения Максвелла. За исключением электромагнетизма, основы механики, а именно движение бильярдных шаров, грузовиков, шариков и многого другого, были заложены Ньютоном.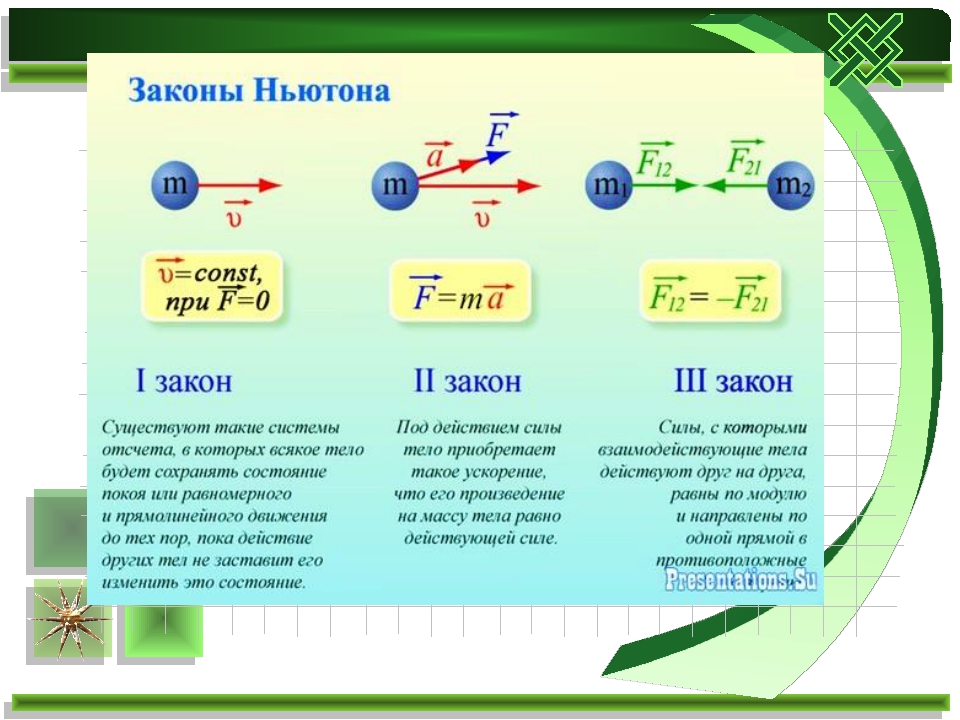 Вот на чем мы сосредоточимся, и вы обнаружите, что законы физики за весь семестр, безусловно, можно написать на одной из этих досок или даже на половине этих досок.
Вот на чем мы сосредоточимся, и вы обнаружите, что законы физики за весь семестр, безусловно, можно написать на одной из этих досок или даже на половине этих досок.
И цель этого курса состоит в том, чтобы снова и снова показывать вам, что, исходя из этих одного или двух законов, вы можете вывести все, и я призываю вас думать так же. На самом деле, я бы посоветовал вам думать так, как думают физики, даже если вы не планируете стать физиком, потому что это самый простой способ изучить этот предмет, а именно следовать рассуждениям, лежащим в основе всего, что я вам даю.И моя цель будет заключаться не в том, чтобы сказать что-то как постулат, а в том, чтобы показать вам, откуда все происходит, и для вас будет лучше всего, если вы попытаетесь следовать логике. Таким образом, вам не нужно хранить слишком много вещей в своей голове. В первые дни, когда есть четыре или пять формул, вы можете запомнить их все и попробовать каждую из них, пока что-то не сработает, но через пару недель у вас будет сотня формул, и вы не сможете их запомнить все.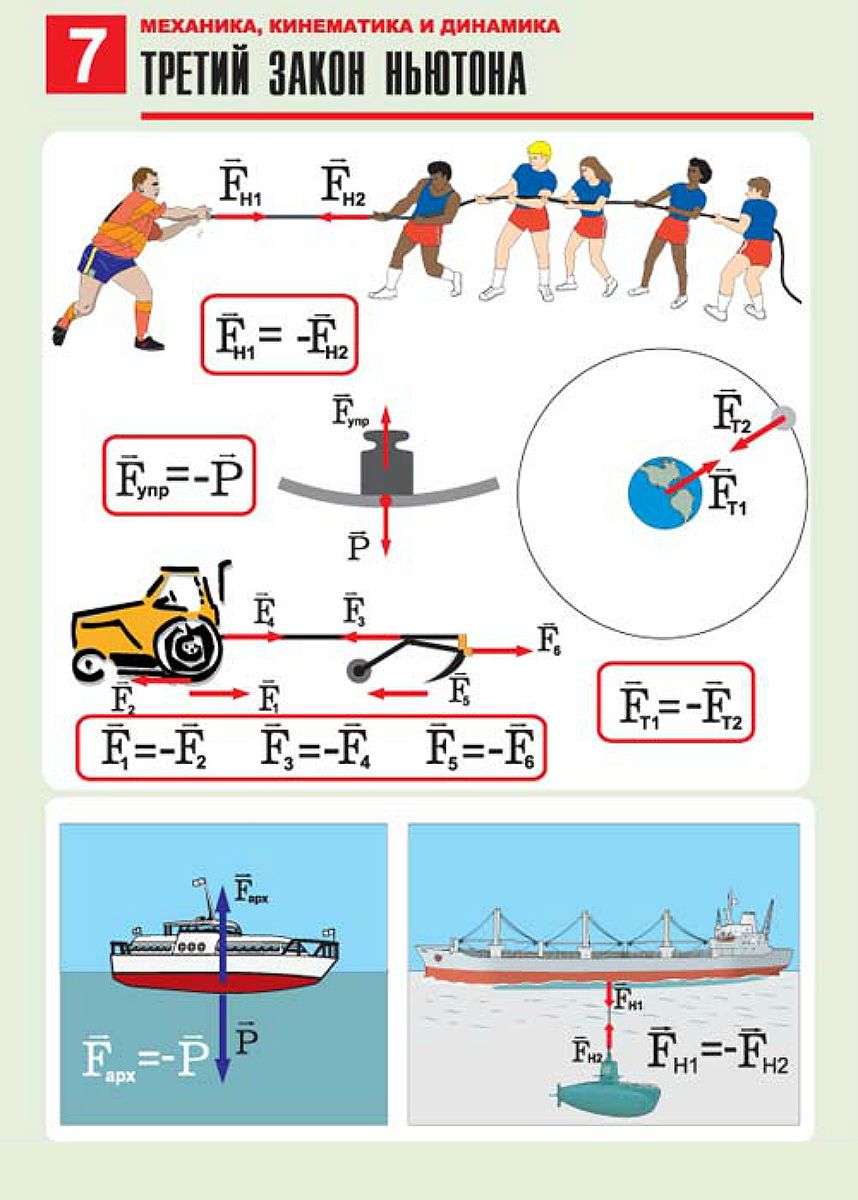 Нельзя прибегать к пробам и ошибкам.Так что надо знать логику. Таким образом, логический путь — это не только то, как это делают физики, это более простой способ. Если есть другой способ, который будет работать для нефизиков, я без колебаний научу вас этому, если он окажется лучшим. Так что старайтесь следовать логике во всем. Хорошо.
Нельзя прибегать к пробам и ошибкам.Так что надо знать логику. Таким образом, логический путь — это не только то, как это делают физики, это более простой способ. Если есть другой способ, который будет работать для нефизиков, я без колебаний научу вас этому, если он окажется лучшим. Так что старайтесь следовать логике во всем. Хорошо.
Итак, ньютоновская механика – наша первая тема. Итак, ньютоновская механика состоит из двух частей. Вся физика — это программа, состоящая из двух частей. План каждый раз состоит в том, чтобы предсказывать будущее, исходя из настоящего.Это то, что мы всегда делаем. Когда мы делаем это правильно, мы удовлетворены. Итак, вопрос: «Что вы подразумеваете под «предсказывать будущее»?» Что вы подразумеваете под будущим? Что вы имеете в виду под настоящим? Под «настоящим» мы подразумеваем, что мы выбираем какую-то часть Вселенной, которую хотим изучить, и спрашиваем: «Какую информацию мне нужно знать об этой системе в начальный момент времени, например, прямо сейчас, чтобы быть способен предсказывать будущее?» Так, например, если вы пытались изучить движение какого-то объекта, вот один пример.
[бросает конфету, чтобы кто-нибудь поймал]
Профессор Рамамурти Шанкар : Видите, это пример ньютоновской механики. Я дам вам еще одну демонстрацию. Посмотрим, кто сможет поймать этого.
[бросает еще одну фишку]
Профессор Рамамурти Шанкар : Хороший пример. Итак, это была ньютоновская механика в действии, потому что что я сделал? Я выпустил конфету, выбросил ее из руки, и начальные условия связаны с тем, куда я ее выпустил и с какой скоростью.Это то, что он видит своими глазами. Тогда это все, что вам действительно нужно знать. Затем он знает, что она пойдет вверх, она будет искривляться, следовать какой-то параболе, а затем его руки тянутся туда, чтобы принять ее. Это проверка предсказания. Он предсказывал, что конфета упадет сюда, а потом положил руку туда. Он также знал, куда приземлится конфета, но не мог вовремя добраться туда. Но мы всегда можем делать прогнозы. Но это хороший пример того, что вам нужно знать. Я утверждаю, что вы должны знать об этом брошенном объекте начальное местоположение объекта и начальную скорость.То, что она была синей или красной, значения не имеет, и если я бросил в него гориллу, то неважно, какого цвета горилла, в каком она настроении. Это вещи, с которыми мы не имеем дело в физике. .
Я утверждаю, что вы должны знать об этом брошенном объекте начальное местоположение объекта и начальную скорость.То, что она была синей или красной, значения не имеет, и если я бросил в него гориллу, то неважно, какого цвета горилла, в каком она настроении. Это вещи, с которыми мы не имеем дело в физике. .
Есть высотное здание, стандартная задача по физике. Объект падает с высокого здания. Объектом может быть человек. Так что мы не спрашиваем, почему этот парень покончил со всем этим сегодня? Мы не знаем, и мы не можем с этим смириться. Так что не на все отвечаем. Мы просто хотим знать, когда он ударится о тротуар и с какой скоростью.Поэтому мы задаем очень ограниченное количество вопросов, поэтому мы хвастаемся тем, насколько точно мы можем предсказывать будущее. Таким образом, мы ставим только ограниченные цели, и нам действительно удается их достичь. Итак, мы в основном имеем дело с неодушевленными предметами.
Таким образом, продукт ньютоновской механики предсказания будущего по настоящему состоит из двух частей, одна из которых называется кинематикой, а другая — динамикой. Итак, кинематика — это полное описание настоящего. Это список того, что вы должны знать о системе прямо сейчас.Например, если вы говорите о меле — если я брошу мел, вам нужно будет знать, где он находится и как быстро он движется. Затем динамика сообщает вам, почему объект поднимается, почему объект опускается, почему его тянет вниз и так далее. Это динамика. Причина, по которой он падает, в том, что гравитация притягивает его. В кинематике вы ничего не спрашиваете о причине. Вы просто хотите описать вещи такими, какие они есть, а затем динамика расскажет вам, как они изменились и почему они изменились.
Итак, кинематика — это полное описание настоящего. Это список того, что вы должны знать о системе прямо сейчас.Например, если вы говорите о меле — если я брошу мел, вам нужно будет знать, где он находится и как быстро он движется. Затем динамика сообщает вам, почему объект поднимается, почему объект опускается, почему его тянет вниз и так далее. Это динамика. Причина, по которой он падает, в том, что гравитация притягивает его. В кинематике вы ничего не спрашиваете о причине. Вы просто хотите описать вещи такими, какие они есть, а затем динамика расскажет вам, как они изменились и почему они изменились.
Итак, я собираюсь проиллюстрировать идею кинематики на самом простом примере.Именно так я и буду делать все в этом курсе. Я собираюсь начать с самого простого примера и постепенно добавлять навороты и свистки, делая его все более и более сложным. Итак, некоторые из вас могут сказать: «Ну, я уже видел это раньше», так что, возможно, здесь нет ничего нового. Это вполне может быть. Я не знаю, сколько вы видели, но довольно часто то, как вы изучали физику в старшей школе, вероятно, отличается от того, как об этом думают профессиональные физики. Наши ценности, вещи, которые нас волнуют, другие, и проблемы могут быть более сложными.Но я хочу начинать каждый пример, каждую ситуацию, которую я вам объясняю, с самого простого примера и постепенно добавлять новые вещи.
Я не знаю, сколько вы видели, но довольно часто то, как вы изучали физику в старшей школе, вероятно, отличается от того, как об этом думают профессиональные физики. Наши ценности, вещи, которые нас волнуют, другие, и проблемы могут быть более сложными.Но я хочу начинать каждый пример, каждую ситуацию, которую я вам объясняю, с самого простого примера и постепенно добавлять новые вещи.
Глава 3. Средняя и мгновенная скорость движения [00:28:20]
Итак, сейчас мы будем изучать неживой объект, и мы выберем его в качестве математической точки. Таким образом, объект является математической точкой. У него нет размера. Если покрутишь, то не узнаешь. Это не похоже на картошку. Берешь картошку, переворачиваешь, она выглядит иначе.Итак, недостаточно сказать, что картошка здесь. Вы должны сказать, в какую сторону указывает нос и так далее. Итак, мы не хотим иметь дело с этим сейчас. Это приходит позже, когда мы изучаем то, что мы называем «твердые тела». Прямо сейчас мы хотим изучить объект, который не имеет пространственной протяженности. Итак, просто точка, и точка может перемещаться по всему пространству. Так что мы собираемся упростить и это. Мы возьмем сущность, расположенную вдоль оси x .
Итак, просто точка, и точка может перемещаться по всему пространству. Так что мы собираемся упростить и это. Мы возьмем сущность, расположенную вдоль оси x .
[рисует линию с интегралами]
Он движется вдоль линии.Итак, вы можете представить бусину с проходящей через нее проволокой, и бусина может скользить только вперед и назад. Итак, речь идет о самом простом. Я не могу уменьшить количество измерений. Один из них является самым низким измерением. Я не могу сделать объект проще, чем просто математическая точка. Затем вы должны сказать: «Что я должен знать об этом объекте в начальный момент времени? Что составляет настоящее или что составляет максимальную информацию о настоящем?» Итак, что мы делаем, так это выбираем начало координат, называем его нулем, помещаем туда маркеры для измерения расстояния и говорим, что этот парень сидит на 1, 2, 3, 4, 5.Он сидит в точке x = 5. Теперь, конечно, у нас должны быть единицы измерения, а единицами длины будут метры. Единицей времени будет секунда, и время будет измеряться в секундах. Потом мы подойдем к другим подразделениям.
Потом мы подойдем к другим подразделениям.
Сейчас в кинематике это все, что вам нужно. Теперь в книге есть несколько сложных задач. Иногда они дают вам скорость в милях в час, километрах в год, фунтах на квадратный фут, что бы это ни было. Вы должны научиться преобразовывать их, но я не буду этого делать.Я думаю, что это довольно элементарные вещи. Но иногда я могу не записывать единицы, но я заслужил право делать это, а вы, ребята, нет, так что вам придется следить за своими единицами. Все должно быть в правильных единицах. Если у вас нет единиц, то если вы скажете, что ответ равен 19, то мы не знаем, что это значит. Хорошо.
Итак, вот объект. В данный момент у него есть местоположение. Итак, что мы хотели бы сделать, так это описать, что делает объект, нарисовав график зависимости времени от пространства, и график будет примерно таким.Вы должны научиться читать этот график. Я предполагаю, что все знают, как это читать.
[рисует график x против t ]
Это не означает, что объект качается вверх и вниз. Я надеюсь, вы понимаете это. Несмотря на то, что график движется вверх и вниз, объект движется слева направо. Так, например, когда он делает это, он пересекает начало координат и движется влево от начала координат. Теперь, слева от начала координат, оно разворачивается и начинает приближаться к началу координат и двигаться вправо.То есть х против т . Итак, на языке исчисления x — это функция времени, и это особая функция. У этой функции нет имени. Есть и другие функции, у которых есть имя. Например, это x = t , x = t 2 , у вас будет x = sin t и стоимость t и log t . Итак, некоторые функции имеют имя, некоторые функции не имеют имени. То, что пытается сделать частица, обычно является какой-то сумасшедшей вещью, у которой нет имени, но это функция x (t) .Поэтому вы должны знать, когда смотрите на такой график, что он делает.
Я надеюсь, вы понимаете это. Несмотря на то, что график движется вверх и вниз, объект движется слева направо. Так, например, когда он делает это, он пересекает начало координат и движется влево от начала координат. Теперь, слева от начала координат, оно разворачивается и начинает приближаться к началу координат и двигаться вправо.То есть х против т . Итак, на языке исчисления x — это функция времени, и это особая функция. У этой функции нет имени. Есть и другие функции, у которых есть имя. Например, это x = t , x = t 2 , у вас будет x = sin t и стоимость t и log t . Итак, некоторые функции имеют имя, некоторые функции не имеют имени. То, что пытается сделать частица, обычно является какой-то сумасшедшей вещью, у которой нет имени, но это функция x (t) .Поэтому вы должны знать, когда смотрите на такой график, что он делает.
Итак, две самые элементарные идеи, которые вы усвоите, это то, какова средняя скорость объекта, как это упорядочено символом v -бар.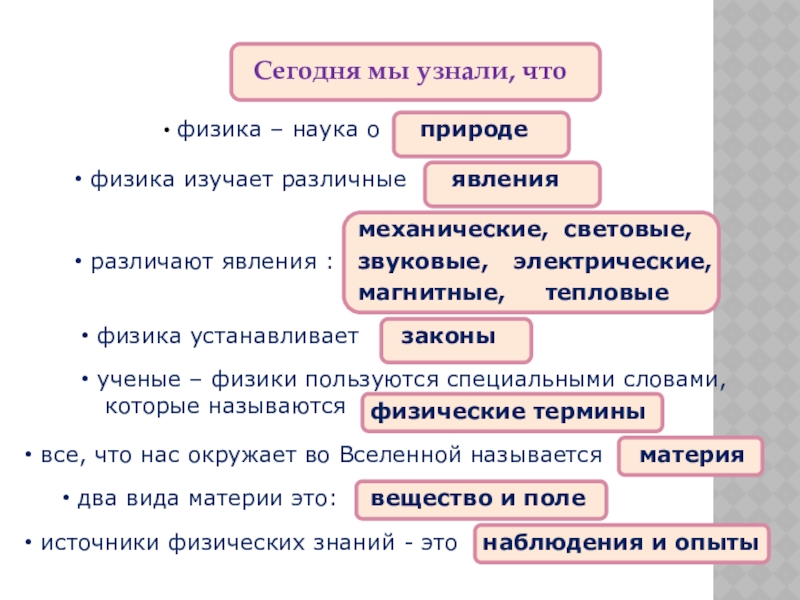 Итак, среднее значение находится путем взятия двух моментов времени, скажем, t 1 и позже t 2 , и вы узнаете, где оно было в t 2 минус где оно было в t 1 и разделить на время.Таким образом, средняя скорость может не рассказать вам всю историю. Например, если вы начали здесь, сделали все это и вернулись сюда, средняя скорость будет равна нулю, потому что вы начинаете и заканчиваете с одним и тем же значением x , вы что-то получаете; 0 со временем все равно будет 0. Таким образом, вы не можете сказать по среднему значению все, что произошло, потому что другой способ получить тот же 0 — просто не двигаться вообще. Так что среднее так оно и есть. Это среднее значение, оно не дает вам достаточно подробностей. Так что полезно иметь среднюю скорость.Полезно иметь среднее ускорение, которое можно найти, взяв аналогичные разности скоростей. Но прежде чем вы это сделаете, я хочу дать вам определение важного понятия, которое представляет собой скорость в данный момент времени v (t) .
Итак, среднее значение находится путем взятия двух моментов времени, скажем, t 1 и позже t 2 , и вы узнаете, где оно было в t 2 минус где оно было в t 1 и разделить на время.Таким образом, средняя скорость может не рассказать вам всю историю. Например, если вы начали здесь, сделали все это и вернулись сюда, средняя скорость будет равна нулю, потому что вы начинаете и заканчиваете с одним и тем же значением x , вы что-то получаете; 0 со временем все равно будет 0. Таким образом, вы не можете сказать по среднему значению все, что произошло, потому что другой способ получить тот же 0 — просто не двигаться вообще. Так что среднее так оно и есть. Это среднее значение, оно не дает вам достаточно подробностей. Так что полезно иметь среднюю скорость.Полезно иметь среднее ускорение, которое можно найти, взяв аналогичные разности скоростей. Но прежде чем вы это сделаете, я хочу дать вам определение важного понятия, которое представляет собой скорость в данный момент времени v (t) . Итак, это центральная идея исчисления, верно? Я надеюсь, что если вы изучили свое исчисление, вы узнали о производных и так далее, глядя на x против t .
Итак, это центральная идея исчисления, верно? Я надеюсь, что если вы изучили свое исчисление, вы узнали о производных и так далее, глядя на x против t .
Итак, еще раз напомню, что это не курс исчисления.Мне не нужно делать это в деталях. Я нарисую известную картину движения какой-то частицы, и она находится здесь в t с некоторым значением x . Чуть позже, что составляет t + Δt . Таким образом, Δt всегда будет обозначать небольшой конечный интеграл времени; бесконечно малый промежуток времени еще не 0 . Итак, за это время частица прошла отсюда туда, то есть x + Δx , а средняя скорость в этом интервале равна Δx/ Δt .Графически этот парень равен Δ x , а этот парень равен Δt , и Δx на Δt является отношением. Итак, в исчислении вам нужно получить понятие скорости прямо сейчас. У всех нас сейчас есть интуитивное представление о скорости. Когда вы едете в машине, стрелка показывает 60; это ваша скорость в данный момент.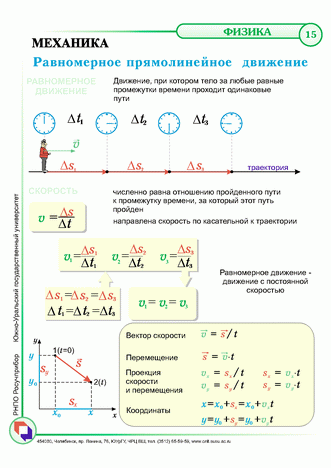 Это очень интересно, потому что кажется, что для определения скорости требуется два разных времени — начальное время и конечное время. И все же, вы хотите поговорить о скорости прямо сейчас.В этом весь триумф исчисления в том, чтобы знать, что, взглянув на положение сейчас, на положение чуть позже, взяв соотношение и приблизив позже как можно ближе к прямому моменту, мы определяем величину, которую мы можем назвать скоростью в этой точке. мгновенное.
Это очень интересно, потому что кажется, что для определения скорости требуется два разных времени — начальное время и конечное время. И все же, вы хотите поговорить о скорости прямо сейчас.В этом весь триумф исчисления в том, чтобы знать, что, взглянув на положение сейчас, на положение чуть позже, взяв соотношение и приблизив позже как можно ближе к прямому моменту, мы определяем величину, которую мы можем назвать скоростью в этой точке. мгновенное.
Таким образом, v из t, v(t) является пределом, Δt переходит в 0 из Δx поверх Δt , и мы используем символ dx/dt для скорости. Итак, технически, если вы спросите, что означает скорость, позвольте мне нарисовать общую ситуацию.Если частица движется отсюда сюда, Δx над Δt , я не знаю, насколько хорошо вы можете видеть это на этом рисунке здесь, это наклон прямой линии, соединяющей эти две точки, и как точки приходят ближе и ближе, прямая стала бы касательной к кривой. Таким образом, скорость в любой части кривой касается кривой в этой точке. Тангенс этого угла, этого θ, равен Δx над Δt.
Таким образом, скорость в любой части кривой касается кривой в этой точке. Тангенс этого угла, этого θ, равен Δx над Δt.
Итак, если вы можете взять одну производную, вы можете взять любое количество производных, и производная скорости называется ускорением, и мы запишем ее как вторую производную положения.Поэтому я надеюсь, что вы, ребята, не против взять одну, две или любое количество производных. Интересно, что у первых двух производных есть название. Первое — скорость, второе — ускорение. Третьей производной, к сожалению, так и не дали названия, и я не знаю почему. Я думаю, что основная причина в том, что не существует уравнений, в которых явно фигурирует третья производная. F = ма . и — вот этот парень, и ничему другому не дается независимое имя.Конечно, вы можете брать функцию и производные сколько угодно раз. Таким образом, вы должны знать, например, что если x(t) равно t n , вы должны знать, что dx/dt равно nt n-1 .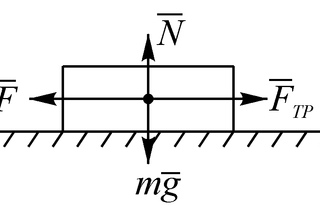 Затем вы должны знать производные простых функций, таких как синусы и косинусы. Так что если вы этого не знаете, то, конечно, вам придется работать больше, чем другим людям. Если вы это знаете, этого может хватить на некоторое время.
Затем вы должны знать производные простых функций, таких как синусы и косинусы. Так что если вы этого не знаете, то, конечно, вам придется работать больше, чем другим людям. Если вы это знаете, этого может хватить на некоторое время.
Глава 4. Движение с постоянным ускорением [00:37:56]
Итак, до сих пор я говорил, что частица, движущаяся во времени от точки к точке, может быть представлена графом, x против t .В любой точке графика вы можете взять производную, которая будет касаться кривой в каждой точке, и ее числовое значение будет тем, что вы можете назвать мгновенной скоростью этой точки, и вы можете взять производную по производной и назвать это ускорение. Итак, мы собираемся специализироваться на очень ограниченном классе задач в остальной части этого класса. Ограниченный класс задач — это задачи, в которых ускорение — просто константа. Это не самое общее, но я уверен, что вы, ребята, понимаете, почему мы в этом заинтересованы.Кто-нибудь знает, почему так много времени тратится на это? Да?
Студент : [неразборчиво]
Профессор Рамамурти Шанкар : Простите?
Студент : [неразборчиво]
Профессор Рамамурти Шанкар : Верно. Самый известный пример: когда предметы падают вблизи поверхности Земли, все они имеют одинаковое ускорение, а постоянное ускорение называется g , то есть 9,8 метра в секунду 2 .Так что это очень типичная проблема. Когда вы падаете на поверхность Земли, вы описываете проблему постоянного ускорения. Вот почему так много внимания уделяется заточке зубов, выполняя этот класс задач. Итак, вопрос, который мы собираемся задать, следующий: «Если я скажу вам, что частица имеет постоянное ускорение x , можете ли вы сказать мне, что такое положение x ?»
Самый известный пример: когда предметы падают вблизи поверхности Земли, все они имеют одинаковое ускорение, а постоянное ускорение называется g , то есть 9,8 метра в секунду 2 .Так что это очень типичная проблема. Когда вы падаете на поверхность Земли, вы описываете проблему постоянного ускорения. Вот почему так много внимания уделяется заточке зубов, выполняя этот класс задач. Итак, вопрос, который мы собираемся задать, следующий: «Если я скажу вам, что частица имеет постоянное ускорение x , можете ли вы сказать мне, что такое положение x ?»
Обычно я дам вам функцию и попрошу взять любое количество производных.Это очень легко. Это обратная проблема. Вам только дали, что частица имеет ускорение x , и вас попросили выяснить, что такое x ? Другими словами, ваша задача состоит в том, чтобы угадать функцию, вторая производная которой равна a , и это называется интегрированием, противоположным дифференцированию, а интегрирование — это просто угадывание. Интеграция — это не алгоритмический процесс, подобный дифференцированию. Если я дам вам функцию, вы знаете, как взять производную. Измените независимую переменную, найдите изменение функции, возьмите отношение и получите производную.Здесь спрашивают об обратном. Я рассказываю вам кое-что о второй производной функции и спрашиваю вас, что это за функция. Мы делаем это так: гадаем, а гадаем уже 300 лет, так что мы как бы знаем, как гадать.
Интеграция — это не алгоритмический процесс, подобный дифференцированию. Если я дам вам функцию, вы знаете, как взять производную. Измените независимую переменную, найдите изменение функции, возьмите отношение и получите производную.Здесь спрашивают об обратном. Я рассказываю вам кое-что о второй производной функции и спрашиваю вас, что это за функция. Мы делаем это так: гадаем, а гадаем уже 300 лет, так что мы как бы знаем, как гадать.
Итак, позвольте мне подумать вслух и спросить, как я буду догадываться в этой задаче. Я бы сказал, хорошо, этот парень хочет, чтобы я нашел функцию, которая сводится к числу a , когда я беру две производные, и я знаю где-то здесь этот результат, который говорит, что когда я беру производную, я теряю степень т .В конце концов никакие мощности т мне не нужны. Совершенно очевидно, что я должен начать с функции, которая выглядит как t 2 . Таким образом, когда я возьму две производные, не останется ни , ни . Ну, к сожалению, мы знаем, что это неправильный ответ, потому что если взять первую производную, то получится 2 t . Если я возьму вторую производную, я получу 2, но я хочу получить как , а не 2. Тогда очень ясно, как вы это исправляете, умножая на эту константу, и теперь все готово.Эта функция будет иметь правую вторую производную. Таким образом, это определенно описывает частицу, ускорение которой равно a . и не зависят от времени. Но вопрос в том, является ли это самым общим ответом, или это всего лишь один ответ, и я думаю, вы все знаете, что это не самый общий ответ. Это один ответ. Но я могу добавить к этому некоторое число, например 96, которое по-прежнему будет иметь то свойство, что если вы возьмете две производные, вы получите одинаковое ускорение. Итак, 96 теперь является типичной константой, поэтому я собираюсь дать этой константе имя c .
Ну, к сожалению, мы знаем, что это неправильный ответ, потому что если взять первую производную, то получится 2 t . Если я возьму вторую производную, я получу 2, но я хочу получить как , а не 2. Тогда очень ясно, как вы это исправляете, умножая на эту константу, и теперь все готово.Эта функция будет иметь правую вторую производную. Таким образом, это определенно описывает частицу, ускорение которой равно a . и не зависят от времени. Но вопрос в том, является ли это самым общим ответом, или это всего лишь один ответ, и я думаю, вы все знаете, что это не самый общий ответ. Это один ответ. Но я могу добавить к этому некоторое число, например 96, которое по-прежнему будет иметь то свойство, что если вы возьмете две производные, вы получите одинаковое ускорение. Итак, 96 теперь является типичной константой, поэтому я собираюсь дать этой константе имя c .
Из исчисления всем известно, что если вы пытаетесь найти функцию, о которой вы знаете только производную, вы всегда можете добавить константу к ответу одного человека, ничего не меняя. Но я думаю здесь, вы знаете, что можете сделать больше, не так ли? Вы можете добавить что-то еще к ответу, не аннулируя его, и это что-нибудь с одной степенью t в нем, потому что, если вы возьмете одну производную, она выживет, но если вы возьмете две производные, она будет уничтожена. . Теперь это не очевидно, но это правда, что вы больше не можете ничего добавить к этому.Основная идея решения этих уравнений и интегрирования заключается в том, что вы найдете один ответ, поэтому, когда вы возьмете достаточное количество производных, функция сделает то, что должна делать. Но затем, найдя один ответ, вы можете добавить к нему все, что убивает акт взятия производных. Если вы берете только одну производную, вы можете добавить константу. Если вы берете две производные, вы можете добавить константу и что-то линейное в t . Если бы вы знали только третью производную функции, вы могли бы получить что-то квадратное в t без изменения результата.
Но я думаю здесь, вы знаете, что можете сделать больше, не так ли? Вы можете добавить что-то еще к ответу, не аннулируя его, и это что-нибудь с одной степенью t в нем, потому что, если вы возьмете одну производную, она выживет, но если вы возьмете две производные, она будет уничтожена. . Теперь это не очевидно, но это правда, что вы больше не можете ничего добавить к этому.Основная идея решения этих уравнений и интегрирования заключается в том, что вы найдете один ответ, поэтому, когда вы возьмете достаточное количество производных, функция сделает то, что должна делать. Но затем, найдя один ответ, вы можете добавить к нему все, что убивает акт взятия производных. Если вы берете только одну производную, вы можете добавить константу. Если вы берете две производные, вы можете добавить константу и что-то линейное в t . Если бы вы знали только третью производную функции, вы могли бы получить что-то квадратное в t без изменения результата.
Итак, это наиболее общее положение для частицы с постоянным ускорением, а. Теперь вы должны помнить, что это описывает движение частицы из стороны в сторону. Я также могу описать движение частицы вверх и вниз. Если я сделаю так, я хотел бы назвать координату y , тогда я напишу то же самое. Вы должны понимать, что в исчислении символы, которые вы называете x и y , совершенно произвольны. Если вы знаете, что вторая производная от y равна a , то ответ выглядит так.Если бы вы знали вторую производную от x , ответ выглядел бы так. Теперь мы должны спросить, что это за числа, b, и c.
Теперь вы должны помнить, что это описывает движение частицы из стороны в сторону. Я также могу описать движение частицы вверх и вниз. Если я сделаю так, я хотел бы назвать координату y , тогда я напишу то же самое. Вы должны понимать, что в исчислении символы, которые вы называете x и y , совершенно произвольны. Если вы знаете, что вторая производная от y равна a , то ответ выглядит так.Если бы вы знали вторую производную от x , ответ выглядел бы так. Теперь мы должны спросить, что это за числа, b, и c.
Итак, позвольте мне теперь вернуться к этому выражению, x(t) = at 2 / 2 + c + bt . Это верно математически, вы можете сложить два числа, но вы должны спросить себя: «Что я делаю как физик, когда складываю эти два числа?» Что мне делать с и ? Я имею в виду, с b и c ? Какое значение выбрать? Ответ заключается в том, что просто знать, что частица имеет ускорение, недостаточно, чтобы сказать вам, где она будет находиться.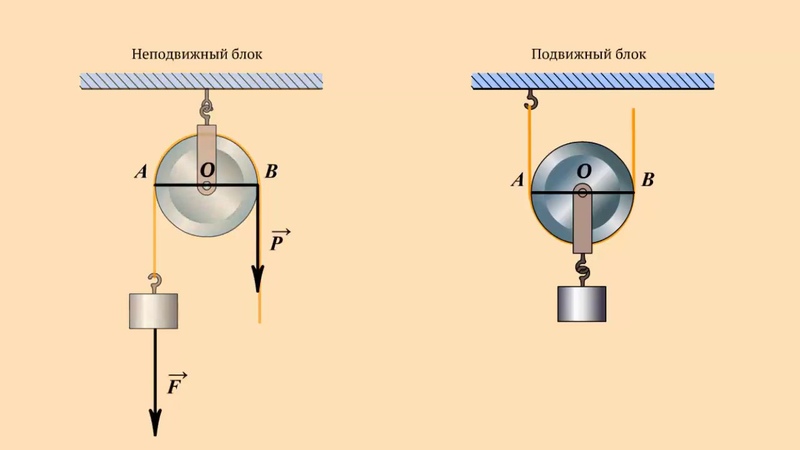 Например, возьмем случай, когда частица падает под действием силы тяжести. Тогда вы, ребята, знаете, вы только что сказали мне, ускорение -9,8, мой g -9,8. Мы называем это «минусом», потому что оно ускоряется вниз, а вверх считается положительным направлением. В этом случае y(t) будет -1/2 gt 2 + c + bt.
Например, возьмем случай, когда частица падает под действием силы тяжести. Тогда вы, ребята, знаете, вы только что сказали мне, ускорение -9,8, мой g -9,8. Мы называем это «минусом», потому что оно ускоряется вниз, а вверх считается положительным направлением. В этом случае y(t) будет -1/2 gt 2 + c + bt.
Итак, дело в том, что каждый объект, падающий под действием гравитации, задается одной и той же формулой, но есть много, много объектов, которые могут иметь много историй, все они падают под действием силы тяжести, и что отличается от одного объекта, а другой объект, когда Падал ли он, с какой высоты и с какой начальной скоростью.Вот о чем нам скажут эти цифры, и мы можем проверить это следующим образом. Если вы хотите узнать, что такое число c , вы говорите, давайте положим время t = 0 . На самом деле, позвольте мне вернуться к этому уравнению. Вы поместите время t = 0 , x( 0 ) не имеет этого члена, не имеет этого члена, и это c. Итак, я понимаю, что константа c является начальным местоположением объекта, и очень часто это обозначается как x 0 .
Итак, я понимаю, что константа c является начальным местоположением объекта, и очень часто это обозначается как x 0 .
Значит, константа c означает, где находился объект в начальный момент времени? Это могло быть где угодно. Простого знания ускорения недостаточно, чтобы сказать вам, где оно было в начальный момент времени. Вы можете выбрать, где это было в начальный момент времени. Затем, чтобы найти значение b , мы возьмем одну производную от этого, dx/dt , это скорость как функцию времени, и если вы возьмете производную этого парня, вы найдете как at + b . Это скорость объекта.Тогда вы сможете понять, что v( 0 ) — это то же самое, что b , которое мы записываем как v 0 . Итак, окончательный ответ таков: x(t) выглядит как x 0 + v 0 t + 1/2 в 2 . Хорошо. Итак, я хочу сказать, что мы специализируемся на ограниченном классе движений, когда частица имеет определенное ускорение, и .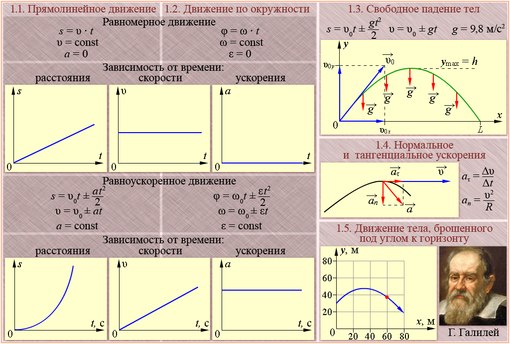 Тогда в каждой ситуации, когда тело имеет ускорение a , местоположение должно иметь следующую форму, где это число ( x 0 ) находится там, где оно было изначально, это ( v 0 ) было начальная скорость объекта.Итак, когда я подбросил эту штуку, и вы ее поймали, то, что вы делаете мысленно, сразу выясняло, где она началась и с какой скоростью. Это были ваши исходные данные. Затем в своем уме, сами того не осознавая, вы нашли траекторию всех будущих времен.
Тогда в каждой ситуации, когда тело имеет ускорение a , местоположение должно иметь следующую форму, где это число ( x 0 ) находится там, где оно было изначально, это ( v 0 ) было начальная скорость объекта.Итак, когда я подбросил эту штуку, и вы ее поймали, то, что вы делаете мысленно, сразу выясняло, где она началась и с какой скоростью. Это были ваши исходные данные. Затем в своем уме, сами того не осознавая, вы нашли траекторию всех будущих времен.
Есть еще одна знаменитая формула, связанная с этим. Я найду это, а потом приведу пример. Теперь я полностью осознаю, что это не самый яркий пример в физике, но сейчас меня это не беспокоит.Вы увидите достаточно вещей, которые вас смутят, но прямо сейчас я хочу продемонстрировать простую парадигму того, что значит знать настоящее и что значит сказать, что это то, каким будет поведение в будущем. Мы хотим сделать это в самом простом контексте, тогда мы можем делать пример все более и более сложным, но явление останется тем же. Итак, что мы выяснили на данный момент, я намеренно иду от x к y , потому что я хочу, чтобы вы знали, что неизвестная переменная может быть названа x или может быть названа y .Это не имеет значения, пока вторая производная равна a ; это ответ.
Итак, что мы выяснили на данный момент, я намеренно иду от x к y , потому что я хочу, чтобы вы знали, что неизвестная переменная может быть названа x или может быть названа y .Это не имеет значения, пока вторая производная равна a ; это ответ.
Отсюда вытекает вторая формула. Вы, ребята, наверное, тоже знаете это по своим дням в детском саду, но я хочу вывести формулу и представить ее, тогда мы посмотрим, как ее использовать. Вторая формула пытается связать конечную скорость некоторого времени, t , с начальной скоростью и пройденным расстоянием без привязки ко времени. Таким образом, хитрость заключается в том, чтобы исключить время из этого уравнения.
Итак, давайте посмотрим, как мы можем устранить время. Вы знаете, что если вы возьмете производную от этого, то обнаружите, что v(t) равно v 0 + at. Это означает, что если вы знаете скорость данного времени и вы знаете начальную скорость, вы знаете, который сейчас час. На самом деле время v — v 0 над a . Если я не покажу вам никаких аргументов для v , это означает, что v в момент времени t , а нижний индекс 0 означает, что t равно нулю.Это говорит о том, что вы можете измерять время, имея собственные часы. Часы говорят вам, который сейчас час, но вы также можете сказать, который сейчас час, видя, как быстро движется частица, потому что вы знаете, что она началась с некоторой скоростью. Он набирает скорость с некоторой скоростью в . Итак, если сейчас скорость была такой-то, то и время должно было быть таким. Таким образом, время может быть косвенно выведено из этих величин. Затем вы берете эту формулу здесь (t) и вставляете ее сюда, (y(t)) , чтобы увидеть a умножить на t , вы вставляете это выражение.Итак, что вы получите? Получим выражение, в котором нет t ; t был изгнан в пользу v. Итак, я не собираюсь тратить ваше время, спрашивая, что произойдет, если вы его вставите.
На самом деле время v — v 0 над a . Если я не покажу вам никаких аргументов для v , это означает, что v в момент времени t , а нижний индекс 0 означает, что t равно нулю.Это говорит о том, что вы можете измерять время, имея собственные часы. Часы говорят вам, который сейчас час, но вы также можете сказать, который сейчас час, видя, как быстро движется частица, потому что вы знаете, что она началась с некоторой скоростью. Он набирает скорость с некоторой скоростью в . Итак, если сейчас скорость была такой-то, то и время должно было быть таким. Таким образом, время может быть косвенно выведено из этих величин. Затем вы берете эту формулу здесь (t) и вставляете ее сюда, (y(t)) , чтобы увидеть a умножить на t , вы вставляете это выражение.Итак, что вы получите? Получим выражение, в котором нет t ; t был изгнан в пользу v. Итак, я не собираюсь тратить ваше время, спрашивая, что произойдет, если вы его вставите. Я просто скажу, что вы хотите, чтобы произошло. В результате вы обнаружите, что v 2 = v o 2 + 2a умножить на (y-y 0 ) . [Примечание: Профессор сказал x, когда имел в виду y] Сколько людей видели эту штуку раньше? Хорошо. Это много.Послушайте, я знаю, что вы видели это.
Я просто скажу, что вы хотите, чтобы произошло. В результате вы обнаружите, что v 2 = v o 2 + 2a умножить на (y-y 0 ) . [Примечание: Профессор сказал x, когда имел в виду y] Сколько людей видели эту штуку раньше? Хорошо. Это много.Послушайте, я знаю, что вы видели это.
На данный момент мне нужно пройтись по более стандартным материалам, прежде чем мы перейдем к более нестандартным материалам. Если эта часть очень проста для вас, я мало что могу сделать прямо сейчас. Итак, позвольте мне нарисовать коробку. Нарисовать коробку для вас, ребята, значит важно. Это две важные вещи. Помните, я хочу, чтобы вы поняли одну вещь. Сколько из этого вы должны запомнить? Предположим, вы никогда не видели этого в старшей школе. Сколько ты должен запомнить? Я бы сказал, сведите это к минимуму, потому что то, что говорит вам первая формула, должно быть настолько интуитивным, что вам не нужно зубрить это.Речь идет о частицах с постоянным ускорением. Это означает, что когда я беру две производные, я хочу получить a , тогда вы должны знать достаточно математических вычислений, чтобы знать, что это должно быть что-то вроде в 2 , и половина получается из двух производных. Два других, которые вы знаете, — это то, что вы можете добавить, и вы знаете, где вы их добавляете, потому что у частицы есть фора. У него есть начальное положение. Даже at = 0, и у него есть начальная скорость, поэтому даже без всякого ускорения он будет двигаться от y 0 до y 0 + vt .Ускорение дает вам дополнительный материал, квадратичный по времени. Как только вы это сделаете, одна производная даст вам скорость, а затем вы можете исключить из и подставить их в эту формулу. Но большинство людей в конечном итоге запоминают эти два, потому что вы используете их так много раз. Это в конечном итоге застревает в вас, но вы не должны пытаться запомнить все.
Это означает, что когда я беру две производные, я хочу получить a , тогда вы должны знать достаточно математических вычислений, чтобы знать, что это должно быть что-то вроде в 2 , и половина получается из двух производных. Два других, которые вы знаете, — это то, что вы можете добавить, и вы знаете, где вы их добавляете, потому что у частицы есть фора. У него есть начальное положение. Даже at = 0, и у него есть начальная скорость, поэтому даже без всякого ускорения он будет двигаться от y 0 до y 0 + vt .Ускорение дает вам дополнительный материал, квадратичный по времени. Как только вы это сделаете, одна производная даст вам скорость, а затем вы можете исключить из и подставить их в эту формулу. Но большинство людей в конечном итоге запоминают эти два, потому что вы используете их так много раз. Это в конечном итоге застревает в вас, но вы не должны пытаться запомнить все.
Глава 5. Пример задачи: физический смысл уравнений [00:52:37]
Итак, сейчас мы решим одну стандартную задачу, где убедим себя, что можем применить эти формулы и предсказать будущее, зная настоящее. Итак, проблема, которую я хочу решить: есть много вещей, которые вы могли бы сделать, но я выбрал только одну, и это та, где числа круглые, поэтому я могу сделать это без калькулятора. Вот в чем проблема. Вот это здание, и оно будет 15 метров в высоту, и я собираюсь что-то бросить, и оно будет подниматься и опускаться. То, что я подбрасываю, имеет начальную скорость 10 метров в секунду. Итак, мы должны спросить сейчас, теперь, когда я утверждаю, что вы можете задать мне любой вопрос об этой частице, который вы хотите, и я могу ответить вам.Вы можете спросить меня, где он будет через девять секунд, через восемь секунд, как быстро он будет двигаться. Я вообще могу ответить на что угодно. Но для решения этой задачи мне нужно было найти эти два неизвестных. Итак, вы должны привыкнуть к представлению о том, что будет дано в целом, а что сделано специально для случая. Итак, мы знаем, что в этом примере начальная высота должна быть 15 метров, а начальная скорость должна быть 10, а для ускорения я буду использовать — g и, чтобы не усложнять жизнь, я назову это — 10.
Итак, проблема, которую я хочу решить: есть много вещей, которые вы могли бы сделать, но я выбрал только одну, и это та, где числа круглые, поэтому я могу сделать это без калькулятора. Вот в чем проблема. Вот это здание, и оно будет 15 метров в высоту, и я собираюсь что-то бросить, и оно будет подниматься и опускаться. То, что я подбрасываю, имеет начальную скорость 10 метров в секунду. Итак, мы должны спросить сейчас, теперь, когда я утверждаю, что вы можете задать мне любой вопрос об этой частице, который вы хотите, и я могу ответить вам.Вы можете спросить меня, где он будет через девять секунд, через восемь секунд, как быстро он будет двигаться. Я вообще могу ответить на что угодно. Но для решения этой задачи мне нужно было найти эти два неизвестных. Итак, вы должны привыкнуть к представлению о том, что будет дано в целом, а что сделано специально для случая. Итак, мы знаем, что в этом примере начальная высота должна быть 15 метров, а начальная скорость должна быть 10, а для ускорения я буду использовать — g и, чтобы не усложнять жизнь, я назову это — 10. Как вы знаете, правильный ответ 9,8, но мы не хотим сейчас пользоваться калькулятором, поэтому назовем его -10. Следовательно, для этого объекта известно положение y , в любой момент времени t равное 15 + 10 t — 5 t 2 . Вот и вся история этого предмета. Конечно, вы должны быть немного осторожны, когда используете его. Например, положим t равным 10 000 лет. Что вы собираетесь получить? Когда х равно 10 000 лет или 10 000 секунд, вы обнаружите, что х — это какое-то огромное отрицательное число.Знаете, это неправильно, что не так с этим рассуждением?
Как вы знаете, правильный ответ 9,8, но мы не хотим сейчас пользоваться калькулятором, поэтому назовем его -10. Следовательно, для этого объекта известно положение y , в любой момент времени t равное 15 + 10 t — 5 t 2 . Вот и вся история этого предмета. Конечно, вы должны быть немного осторожны, когда используете его. Например, положим t равным 10 000 лет. Что вы собираетесь получить? Когда х равно 10 000 лет или 10 000 секунд, вы обнаружите, что х — это какое-то огромное отрицательное число.Знаете, это неправильно, что не так с этим рассуждением?
Студент : [неразборчиво]
Профессор Рамамурти Шанкар : Таким образом, вы не можете использовать формулу, как только она упадет на землю, потому что, как только она упадет на землю, фундаментальная предпосылка, что a было константой -9,8 или -10, неверна. Так что это еще одна вещь, которую нужно помнить. Как только вы получите формулу, вы всегда должны помнить термины, в соответствии с которыми формула была получена. Если вы будете использовать его вслепую за пределами его действия, вы получите результаты, которые не имеют никакого смысла.И наоборот, если вы получаете ответ, и он кажется бессмысленным, то вам нужно вернуться и спросить, не нарушаю ли я некоторые из предположений, и здесь вы найдете предположение, что частица имела это ускорение верно, пока оно свободно падает под действием силы тяжести, но не когда вы падаете на землю. Теперь, если вы выкопали яму здесь, пока там, и, конечно, это может работать, пока это не произойдет, ладно. Но они у вас есть каждый раз. Это так очевидно в этой задаче, но когда вы видите более сложную формулу, вы можете не знать всех предположений, которые использовались при выводе, и довольно часто вы будете использовать ее, когда не должны.Хорошо.
Как только вы получите формулу, вы всегда должны помнить термины, в соответствии с которыми формула была получена. Если вы будете использовать его вслепую за пределами его действия, вы получите результаты, которые не имеют никакого смысла.И наоборот, если вы получаете ответ, и он кажется бессмысленным, то вам нужно вернуться и спросить, не нарушаю ли я некоторые из предположений, и здесь вы найдете предположение, что частица имела это ускорение верно, пока оно свободно падает под действием силы тяжести, но не когда вы падаете на землю. Теперь, если вы выкопали яму здесь, пока там, и, конечно, это может работать, пока это не произойдет, ладно. Но они у вас есть каждый раз. Это так очевидно в этой задаче, но когда вы видите более сложную формулу, вы можете не знать всех предположений, которые использовались при выводе, и довольно часто вы будете использовать ее, когда не должны.Хорошо.
Видите ли, вы согласны, это полное решение этой миниатюрной, крохотной проблемы с Микки-Маусом. Вы дадите мне время, и я скажу вам, где это. Если вы хотите узнать, с какой скоростью он движется в данный момент времени, если вы хотите узнать скорость, я просто возьму производную от этого ответа, которая равна 10 — 10 t . Итак, позвольте мне выбрать пару тривиальных вопросов, которые можно задать. Можно задать следующий вопрос. Как высоко это идет? Насколько высоко он поднимется? На какую высоту он поднимется? Итак, мы знаем, что он пойдет вверх, развернется и упадет.Мы пытаемся увидеть, насколько это высоко. Итак, это сложная проблема для начала, потому что если вы возьмете эту формулу здесь, она скажет вам y , если вы знаете t , но нет, мы не говорим этого. Мы не знаем время и не знаем, как высоко оно поднимается, поэтому вы можете спросить: «Как мне решить эту проблему?» Затем вы вкладываете в свой разум кое-что еще, что вы знаете, а именно, что наивысшая точка — это точка, когда она не поднимается и не опускается. Если она растет, то это не самая высокая точка.
Вы дадите мне время, и я скажу вам, где это. Если вы хотите узнать, с какой скоростью он движется в данный момент времени, если вы хотите узнать скорость, я просто возьму производную от этого ответа, которая равна 10 — 10 t . Итак, позвольте мне выбрать пару тривиальных вопросов, которые можно задать. Можно задать следующий вопрос. Как высоко это идет? Насколько высоко он поднимется? На какую высоту он поднимется? Итак, мы знаем, что он пойдет вверх, развернется и упадет.Мы пытаемся увидеть, насколько это высоко. Итак, это сложная проблема для начала, потому что если вы возьмете эту формулу здесь, она скажет вам y , если вы знаете t , но нет, мы не говорим этого. Мы не знаем время и не знаем, как высоко оно поднимается, поэтому вы можете спросить: «Как мне решить эту проблему?» Затем вы вкладываете в свой разум кое-что еще, что вы знаете, а именно, что наивысшая точка — это точка, когда она не поднимается и не опускается. Если она растет, то это не самая высокая точка. Если она снижается, то это не самая высокая точка. Поэтому в самой высокой точке он не может ни подняться, ни опуститься. Это точка, где скорость равна 0. Если вы сделаете это, давайте назовем конкретное время t* , тогда 10 t* — 10 = 0, или t* равно 1 секунде. Итак, мы знаем, что он поднимется на одну секунду, затем развернется и вернется обратно.
Если она снижается, то это не самая высокая точка. Поэтому в самой высокой точке он не может ни подняться, ни опуститься. Это точка, где скорость равна 0. Если вы сделаете это, давайте назовем конкретное время t* , тогда 10 t* — 10 = 0, или t* равно 1 секунде. Итак, мы знаем, что он поднимется на одну секунду, затем развернется и вернется обратно.
Теперь мы закончили, потому что теперь мы можем спросить, как высоко это идет, и вы вернетесь к своему, и y (1) это 15 + 10 — 5, что это? Двадцать метров.Кстати, вы обнаружите, что я делаю довольно много ошибок на доске. Вы обнаружите, знаете ли, в один из этих лет, когда вы начнете преподавать, что, когда вы подходите очень близко к доске, вы просто не можете думать. Определенно существует некоторая обратная зависимость между уровнем вашего мышления и близостью к доске. Так что, если вы обнаружите, что я делаю ошибку, вы должны остановить меня. Почему ты останавливаешь меня? По двум причинам. Во-первых, мне очень приятно, когда это происходит, потому что я вполне уверен, что могу сделать это по принуждению, но не могу каждый раз делать это правильно.Но если мои ученики могут поймать меня на ошибке, значит, они следят за ней и не стесняются сказать мне. Во-вторых, по мере того, как мы переходим к более продвинутой части курса, мы возьмем результат с этой части доски, вставим во вторую часть и продолжим манипулировать, так что, если я облажался в начале, а вы, ребята, молчите , нам придется сделать все это снова.
Во-первых, мне очень приятно, когда это происходит, потому что я вполне уверен, что могу сделать это по принуждению, но не могу каждый раз делать это правильно.Но если мои ученики могут поймать меня на ошибке, значит, они следят за ней и не стесняются сказать мне. Во-вторых, по мере того, как мы переходим к более продвинутой части курса, мы возьмем результат с этой части доски, вставим во вторую часть и продолжим манипулировать, так что, если я облажался в начале, а вы, ребята, молчите , нам придется сделать все это снова.
Я бы попросил вас, когда вы будете следить за этим делом, делать это активно. Постарайся быть на шаг впереди меня. Например, если меня ударит молния, ты сможешь что-нибудь сделать? Можете ли вы догадаться, что я собираюсь сказать дальше? Ты хоть представляешь, куда это идет? У тебя должна быть подсказка.Если я умру, а ты остановишься, это плохой знак, ладно. Вы должны продолжать идти немного дальше, потому что вы должны следовать логике. Так, например, вы знаете, я собираюсь вычислить следующий, когда он упадет на землю.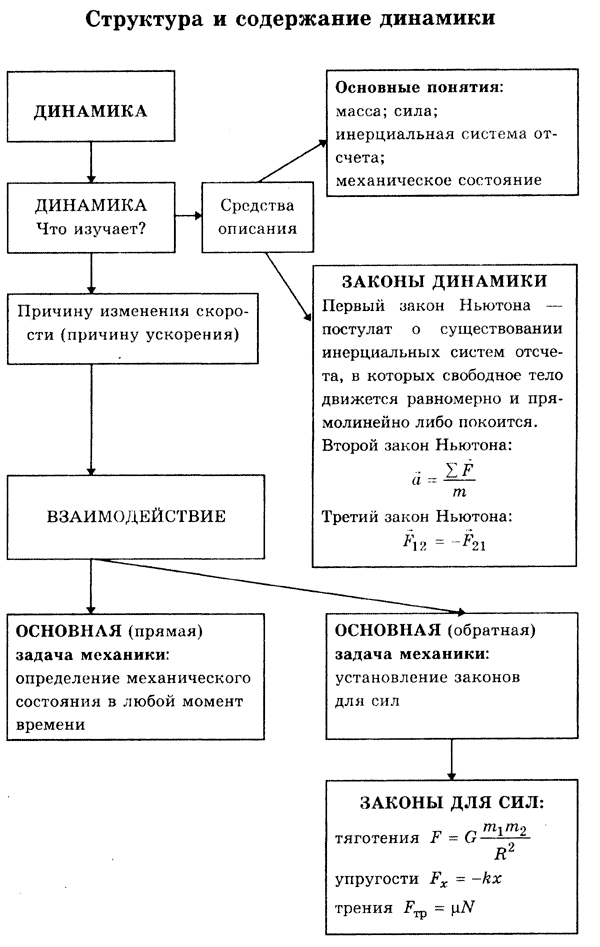 Вы должны иметь некоторое представление о том, как я это сделаю. Но это не зрелищный вид спорта. Если вы просто будете смотреть на меня, вы ничему не научитесь. Это как смотреть Открытый чемпионат США и думать, что ты какой-то игрок. Вам придется пролить слезы, и вы должны биться головой о стену и пройти через свою личную борьбу.Я не могу сделать это для вас. Я даже не могу сделать это сложным, потому что я запомнил эту проблему с детства, поэтому я никак не могу сделать это сложным. Это твоя работа.
Вы должны иметь некоторое представление о том, как я это сделаю. Но это не зрелищный вид спорта. Если вы просто будете смотреть на меня, вы ничему не научитесь. Это как смотреть Открытый чемпионат США и думать, что ты какой-то игрок. Вам придется пролить слезы, и вы должны биться головой о стену и пройти через свою личную борьбу.Я не могу сделать это для вас. Я даже не могу сделать это сложным, потому что я запомнил эту проблему с детства, поэтому я никак не могу сделать это сложным. Это твоя работа.
Хорошо. Итак, мы знаем, что эта точка в одну секунду составляет 20 метров, поэтому давайте просто зададим еще один вопрос и остановимся. Еще один вопрос может звучать так: «Когда он коснется земли и с какой скоростью?» — типичный вопрос физики. Так когда же он упадет на землю? Что ж, я думаю, теперь вы должны знать, как сформулировать этот вопрос.«Когда он упадет на землю» — это «Когда y = 0 » ? Кстати, я вам этого не говорил, но я думаю, вы знаете, что я выбрал свое происхождение, чтобы быть здесь, и измерил и положительно, чтобы они были вверху, и я назвал это 15 метрами. Вы можете назвать это своим происхождением. Если вы назовете это своим началом, ваши y 0 будут равны 0, а земля будет называться — 15. Итак, в конце концов, физика та же, но числа, описывающие ее, могут быть разными. Мы должны интерпретировать данные по-разному.Но стандартным началом для всех является подножие здания. Вы можете выбрать свое происхождение здесь, в каком-то сумасшедшем месте. Это не имеет значения. Но некоторые истоки более равны, чем другие, потому что там есть какая-то природная достопримечательность. Здесь подножие здания — это то, что я называю началом. Итак, в этих обозначениях я хочу спросить, когда y = 0? Я спрашиваю, когда y = 0, тогда я говорю 0 = 15 + 10 t — 5 t 2 . Или я везде отменяю 5 и меняю здесь знак, получаю t 2 — 2 t — 3 = 0.Это когда он падает на землю. Итак, давайте узнаем, который час. Таким образом, t равно 2 + или — или + 12 на 2, что равно 2 + или — 4 на 2, что равно -1 или 3.
Вы можете назвать это своим происхождением. Если вы назовете это своим началом, ваши y 0 будут равны 0, а земля будет называться — 15. Итак, в конце концов, физика та же, но числа, описывающие ее, могут быть разными. Мы должны интерпретировать данные по-разному.Но стандартным началом для всех является подножие здания. Вы можете выбрать свое происхождение здесь, в каком-то сумасшедшем месте. Это не имеет значения. Но некоторые истоки более равны, чем другие, потому что там есть какая-то природная достопримечательность. Здесь подножие здания — это то, что я называю началом. Итак, в этих обозначениях я хочу спросить, когда y = 0? Я спрашиваю, когда y = 0, тогда я говорю 0 = 15 + 10 t — 5 t 2 . Или я везде отменяю 5 и меняю здесь знак, получаю t 2 — 2 t — 3 = 0.Это когда он падает на землю. Итак, давайте узнаем, который час. Таким образом, t равно 2 + или — или + 12 на 2, что равно 2 + или — 4 на 2, что равно -1 или 3. Итак, вы получаете два ответа, когда он падает на землю. Итак, ясно, что мы должны выбрать 3. Но вы можете спросить: «Почему это дает мне второе решение?» Кто-нибудь знает, почему?
Итак, вы получаете два ответа, когда он падает на землю. Итак, ясно, что мы должны выбрать 3. Но вы можете спросить: «Почему это дает мне второе решение?» Кто-нибудь знает, почему?
Студент : Потому что была целая парабола [неразборчиво]
Профессор Рамамурти Шанкар : Верно.Так что ее ответ был таков: если бы это была полная парабола, то мы знаем, что она была бы у земли до того, как я установил часы на 0. Прежде всего, отрицательное время не должно никого беспокоить; t = 0 — это когда я устанавливал часы, я измерял время вперед, но вчера было бы t = -1 день, верно? Так что у нас нет проблем с негативными временами. Итак, дело в том, что это уравнение ничего не знает о здании. Не знает всей песни и танца о том, что вы подошли к зданию и бросили камень или что-то в этом роде.Что знает математика? Он знает, что эта частица имела высоту 15, время 0 и скорость 10, время 0, и она падает под действием силы тяжести с ускорением -10. Это все, что он знает. Если это все, что он знает, то в этом сценарии нет ни здания, ни чего-то еще; он продолжает траекторию как вперед во времени, так и назад во времени, и он говорит, что сколько бы секунд, за одну секунду до того, как вы установили свои часы на 0, он был бы на земле. Это означает, что если бы вы выпустили камень в этом месте за секунду до этого с определенной скоростью, которую мы можем рассчитать, он оказался бы здесь с точно такими же положением и скоростью, которые были в начале нашего эксперимента.
Это все, что он знает. Если это все, что он знает, то в этом сценарии нет ни здания, ни чего-то еще; он продолжает траекторию как вперед во времени, так и назад во времени, и он говорит, что сколько бы секунд, за одну секунду до того, как вы установили свои часы на 0, он был бы на земле. Это означает, что если бы вы выпустили камень в этом месте за секунду до этого с определенной скоростью, которую мы можем рассчитать, он оказался бы здесь с точно такими же положением и скоростью, которые были в начале нашего эксперимента.
Так что иногда дополнительное решение очень интересно, и вы всегда должны прислушиваться к математике, когда получаете дополнительные решения. На самом деле, когда очень известный физик Поль Дирак искал энергию частицы в релятивистской квантовой механике, он обнаружил, что энергия частицы связана с ее импульсом, это p и есть то, что мы называем импульсом, а его масса по этому соотношению. Это частица с массой 92 726 m 92 727 и импульсом 92 726 p 92 727 имеет эту энергию, так что если найти энергию, то получишь два ответа. Теперь у вас есть искушение оставить первый ответ, потому что вы знаете, что энергия не будет отрицательной. Частица движется, у нее есть энергия, и все. Но математики сказали Дираку: «Вы не можете игнорировать решение с отрицательной энергией, потому что оно говорит вам, что есть второе решение, и вы не можете его отбросить», и оказалось, что второе решение с отрицательной энергией было получено, когда теория говорит вам, эй, есть частицы и есть античастицы, и отрицательная энергия при правильной интерпретации будет описывать античастицы.Так что уравнения очень умные.
Теперь у вас есть искушение оставить первый ответ, потому что вы знаете, что энергия не будет отрицательной. Частица движется, у нее есть энергия, и все. Но математики сказали Дираку: «Вы не можете игнорировать решение с отрицательной энергией, потому что оно говорит вам, что есть второе решение, и вы не можете его отбросить», и оказалось, что второе решение с отрицательной энергией было получено, когда теория говорит вам, эй, есть частицы и есть античастицы, и отрицательная энергия при правильной интерпретации будет описывать античастицы.Так что уравнения очень умные.
Физика работает следующим образом: вы находите какие-то законы движения в математической форме, вводите начальные условия чего угодно, решаете уравнения и получаете ответ, у вас нет выбора. Вы должны принять ответ, но помимо того, который вы искали, есть новые ответы. Вы должны думать о том, что они означают, и это одна из лучших вещей в физике, потому что здесь есть человек, который не ищет античастиц. Он пытался описать электроны, но теория говорила, что у квадратного уравнения два корня, и второй корень математически так же интересен, как и первый.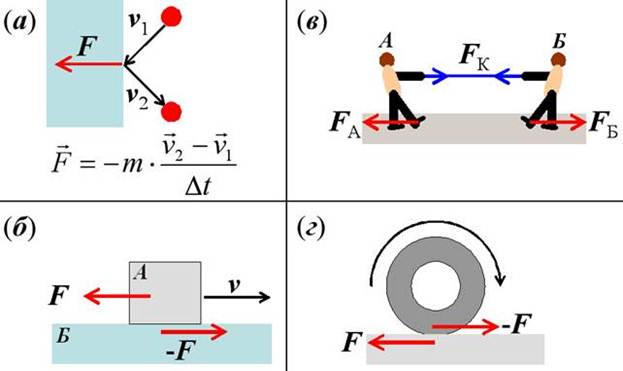 Это должно быть частью теории, а затем, пытаясь настроить ее так, чтобы ее можно было включить, вы обнаруживаете античастицы. Для нас всегда удивительно, как мы погружаемся в проблему, наш глаз или разум могут видеть один класс решений, но математика подскажет вам, что иногда есть новые решения, и вы должны уважать это, понимать и интерпретировать нежелательные решения, и это простой пример, где вы можете проследить, что означает второе решение. Это означает, что к проблеме, которую вы ставите, есть больше ответов, чем вы могли себе представить.Здесь имеется в виду частица, вышедшая из-под земли ранее. Там это означало нечто гораздо более интересное, в основном античастицы, сопровождающие частицы. Они обязательно будут сопровождать частицы, так как каждое квадратное уравнение имеет два решения.
Это должно быть частью теории, а затем, пытаясь настроить ее так, чтобы ее можно было включить, вы обнаруживаете античастицы. Для нас всегда удивительно, как мы погружаемся в проблему, наш глаз или разум могут видеть один класс решений, но математика подскажет вам, что иногда есть новые решения, и вы должны уважать это, понимать и интерпретировать нежелательные решения, и это простой пример, где вы можете проследить, что означает второе решение. Это означает, что к проблеме, которую вы ставите, есть больше ответов, чем вы могли себе представить.Здесь имеется в виду частица, вышедшая из-под земли ранее. Там это означало нечто гораздо более интересное, в основном античастицы, сопровождающие частицы. Они обязательно будут сопровождать частицы, так как каждое квадратное уравнение имеет два решения.
Хорошо, теперь в этой задаче мы можем сделать что-то немного другое, и давайте использовать здесь это выражение, и я сделаю это, а затем остановлюсь на сегодня. Если вы задавали вопросы, например, как высоко он поднимается, но не спрашивали, когда он достигает наивысшей точки, то вам не нужно проходить весь процесс поиска времени, в которое он развернулся.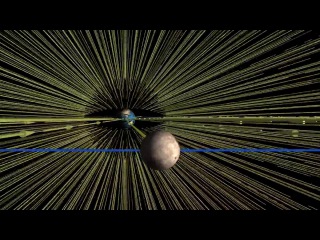 .Я не знаю, где то, что исчезло на доске, подставив затем в эту формулу время, равное 1 секунде. Если вопрос времени явно не поднимается, то следует знать, что пользоваться этой формулой придется. Итак, как мы получим его здесь? Ну, мы говорим, что в верхней части цикла, когда он поднимается и опускается, скорость равна 0. Следовательно, вы говорите, что 0 2 = начальная скорость 2 + 2 умножить на -g , это мой разгон, раз у — у 0 .Если вы решите это, вы найдете y — y 0 = v 0 2 на 2 g , и если вы подставите v 0 , то я вам дал, что и было 10? Это 100 на 20, то есть 5 метров. Итак, y = y 0 + 5 метров, и это была высота, на которую он поднимается. Я думаю, что мы получили это где-то еще. Мы обнаружили, что максимальная высота составляет 20 метров. Еще одна вещь, которую вы можете сделать, это найти скорость здесь.
.Я не знаю, где то, что исчезло на доске, подставив затем в эту формулу время, равное 1 секунде. Если вопрос времени явно не поднимается, то следует знать, что пользоваться этой формулой придется. Итак, как мы получим его здесь? Ну, мы говорим, что в верхней части цикла, когда он поднимается и опускается, скорость равна 0. Следовательно, вы говорите, что 0 2 = начальная скорость 2 + 2 умножить на -g , это мой разгон, раз у — у 0 .Если вы решите это, вы найдете y — y 0 = v 0 2 на 2 g , и если вы подставите v 0 , то я вам дал, что и было 10? Это 100 на 20, то есть 5 метров. Итак, y = y 0 + 5 метров, и это была высота, на которую он поднимается. Я думаю, что мы получили это где-то еще. Мы обнаружили, что максимальная высота составляет 20 метров. Еще одна вещь, которую вы можете сделать, это найти скорость здесь. Если вы хотите найти скорость там, вы подставляете уравнение v 2 = v 0 2 + 2 раза -g (y — y 0 ).Что такое у — у 0 ? Конечные y равны 0, начальные y равны 15 . Решите это уравнение и получите конечную скорость. Так что, если время не занято, можно сделать и так.
Если вы хотите найти скорость там, вы подставляете уравнение v 2 = v 0 2 + 2 раза -g (y — y 0 ).Что такое у — у 0 ? Конечные y равны 0, начальные y равны 15 . Решите это уравнение и получите конечную скорость. Так что, если время не занято, можно сделать и так.
Глава 6. Получение новых соотношений с использованием математических законов пределов [01:08:42]
Я хочу получить последний результат другим способом, затем я остановлюсь, и это довольно интересно, потому что это говорит вам об использовании и злоупотреблении исчислением. Поэтому я собираюсь найти для вас этот результат, используя исчисление другим способом.Итак, из исчисления мы знаем, что dv/dt = a . Теперь умножьте обе части на v . Теперь вы должны знать из элементарного исчисления, что v умножить на dv/dt на самом деле d на dt из v 2 на 2.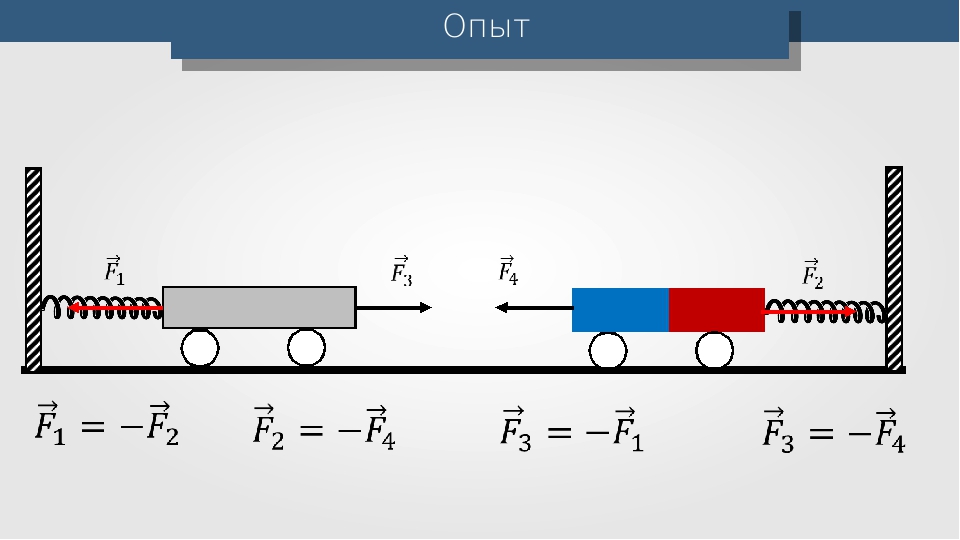 Теперь, я надеюсь, вы, ребята, знаете, что такое исчисление, что когда вы берете производную функции от функции, а именно v 2 над 2 является функцией v , а само v является функцией t , тогда первое правило взятия производной возьмите производную v этого объекта, затем возьмите d по dt из t , который является этим.С правой стороны я напишу как a dx/dt . Это стандартно.
Теперь, я надеюсь, вы, ребята, знаете, что такое исчисление, что когда вы берете производную функции от функции, а именно v 2 над 2 является функцией v , а само v является функцией t , тогда первое правило взятия производной возьмите производную v этого объекта, затем возьмите d по dt из t , который является этим.С правой стороны я напишу как a dx/dt . Это стандартно.
Я собираюсь сделать то, что почему-то нам говорят никогда не делать, а именно отменить dt s. Вы все знаете, что когда вы делаете dy/dx , вы не должны отменять d . Это действительно правильно. Вы же не хотите отменять д в производной. Но это оказывается совершенно законным, поэтому я собираюсь предположить, что это правда, и, может быть, уделю секунду и объясню, почему это законно.На самом деле это означает, что в заданное время Δt изменение этой величины в и раз превышает изменение этой величины. Следовательно, вы можете умножить обе части на Δt , но единственное, что вы должны понимать, это то, что Δ t, пока оно мало и конечно, приведет к некоторым небольшим бесконечным ошибкам в формуле, потому что формула действительно предел, в котором Δx и Δt оба обращаются к 0. Итак, что вам нужно сделать, это умножить обе части на Δt , но помните, что в конце концов оно должно быть исчезающе малым.Пока мы это понимаем, мы можем сделать это сокращение, и это говорит о том, что в левой части изменение количества v 2 на 2 равно a раз больше изменения количества x. Итак, сложите все изменения или то, что вы подразумеваете под интегралом. То же самое. Сложите все изменения. Изменение v 2 над 2 будет окончательным v 2 над 2 — начальным v 2 над 2, а другая сторона будет изменением в раз x ; х — х 0 и это формула, которую я написал для вас: v 2 это v 0 2 + 2 а (х — х
Следовательно, вы можете умножить обе части на Δt , но единственное, что вы должны понимать, это то, что Δ t, пока оно мало и конечно, приведет к некоторым небольшим бесконечным ошибкам в формуле, потому что формула действительно предел, в котором Δx и Δt оба обращаются к 0. Итак, что вам нужно сделать, это умножить обе части на Δt , но помните, что в конце концов оно должно быть исчезающе малым.Пока мы это понимаем, мы можем сделать это сокращение, и это говорит о том, что в левой части изменение количества v 2 на 2 равно a раз больше изменения количества x. Итак, сложите все изменения или то, что вы подразумеваете под интегралом. То же самое. Сложите все изменения. Изменение v 2 над 2 будет окончательным v 2 над 2 — начальным v 2 над 2, а другая сторона будет изменением в раз x ; х — х 0 и это формула, которую я написал для вас: v 2 это v 0 2 + 2 а (х — х

Итак, дело в том, что всякий раз, когда у вас есть производные с чем-то больше dt , не стесняйтесь отменять dt s и думать о них как Δv 2 больше 2 равно a умножить на 2 7 х. Это действительно так, пока обе величины исчезающе малы. Они будут становиться все более и более верными по мере того, как Δx и Δv 2 станут исчезающе малыми, в пределе, в котором они приближаются к 0, они будут фактически равны.Если x является конечной величиной, например 1 секундой, это будет неверно, потому что в исходном уравнении Δx и Δt и Δv 2 предполагались бесконечно малыми. Так что не стесняйтесь делать манипуляции такого типа, и я буду делать их довольно часто. Поэтому вы должны понимать, когда все в порядке, а когда нет. Это означает, что за время Δt эта величина изменяется на некоторую величину, и в то же время Δt эта величина изменяется на некоторую величину, тогда, сохраняя Δt равным некоторому числу, мы можем приравнять изменения двух величин при условии, что Δv 2 на 2 является изменением v 2 на 2 за то же время, за которое частица прошла расстояние Δx . Добавляя различия, мы исключаем время и получаем вот такой окончательный результат.
Добавляя различия, мы исключаем время и получаем вот такой окончательный результат.
Хорошо. Итак, если вы зайдете сегодня на свой веб-сайт, вы обнаружите, что я назначил некоторые задачи, и вы должны попытаться их решить. Они относятся к этой главе. Затем на следующей неделе мы будем решать более сложные задачи, связанные с движением в более высоких измерениях, как перейти к двухмерному или трехмерному.
[конец стенограммы]
НаверхУрок Видео: Механические работы | Нагва
Стенограмма видео
В этом видео мы говорим о
механическая работа.В нашей повседневной жизни, когда мы используем
этим словом «работа» мы могли бы говорить о многих вещах. Когда мы делаем домашнее задание или
скажем, дела по дому, мы говорим, что делаем работу. А потом, когда мама или папа уходят
за день и возвращается, мы говорим, что они были на работе. Однако в мире физики
этот термин имеет очень конкретное значение.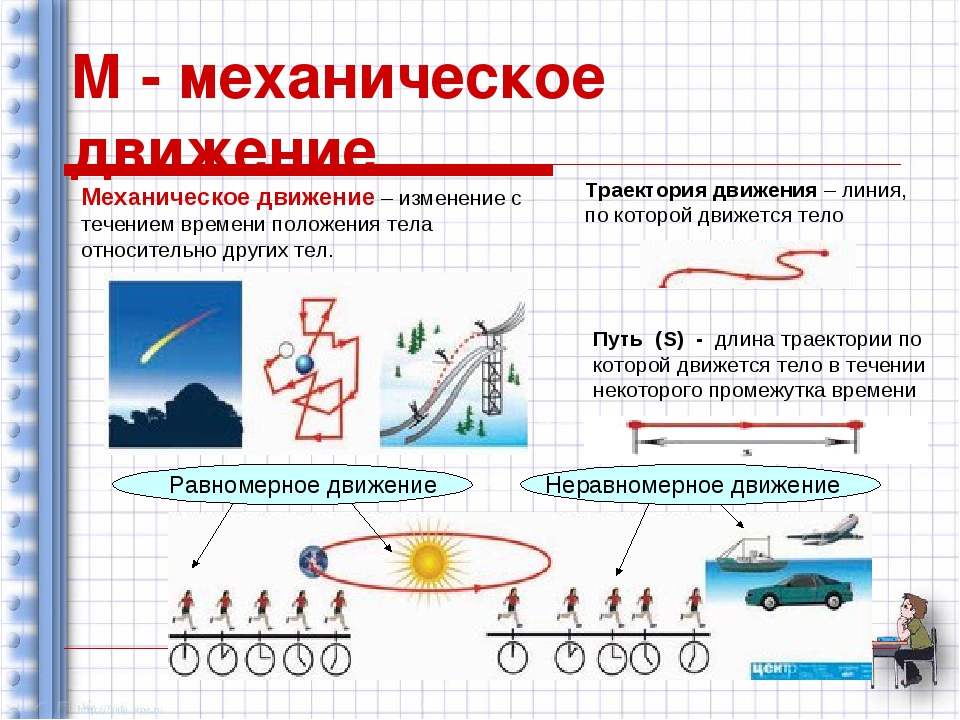
Вот определение работы, которая мы будем использовать. Это произведение силы применяется к объекту и смещению этого объекта.Другими словами, мы находим работу на объект путем умножения силы, приложенной к нему, на силу этого объекта. пройденное расстояние по прямой. На основании этого определения мы можем напишите уравнение для работы, где работа обычно обозначается заглавной 𝑊. Мы сказали, что работа — это продукт силы и перемещения, значит, мы можем написать, что работа равна силе 𝐹 умножается на смещение 𝑑.Вот пример работы на.
Допустим, у нас есть машина, путешествующая
по дороге. Автомобиль движется влево
правильно. Что здесь происходит, так это дорога
поверхность давит на шины автомобиля в таком направлении, что он двигает автомобиль
вперед. Можно сказать, что полная сила
дорога относится к этим автомобильным шинам 𝐹. И если — благодаря этой силе 𝐹 —
автомобиль движется вперед на расстояние, которое мы можем назвать 𝑑, тогда мы можем сказать, что работа выполнена
на этом автомобиле — назовем его 𝑊 sub 𝑐 — равна силе, приложенной дорогой
на автомобиль, умноженный на расстояние, пройденное автомобилем.
И если — благодаря этой силе 𝐹 —
автомобиль движется вперед на расстояние, которое мы можем назвать 𝑑, тогда мы можем сказать, что работа выполнена
на этом автомобиле — назовем его 𝑊 sub 𝑐 — равна силе, приложенной дорогой
на автомобиль, умноженный на расстояние, пройденное автомобилем.
Представьте, что у нас есть коробка. Можно сказать, что эта коробка имеет массу 𝑚
и он стоит на столе. Тогда скажем, мы подбираем это
коробка. И мы поднимаем эту коробку немного
расстояние — мы можем назвать это 𝑑 — выше этого уровня стола. Что мы сделали, так это применили
направленное вверх усилие на коробку. Это сила здесь, в нашем
уравнение для работы. И мы сделали это в течение определенного
расстояние 𝑑. Таким образом, поднимая эту коробку, мы
проделал работу над ним.Так что это были некоторые примеры
процессы, в которых происходит работа. Но чтобы лучше понять это
уравнения, давайте рассмотрим члены, входящие в него, один за другим.
Но чтобы лучше понять это
уравнения, давайте рассмотрим члены, входящие в него, один за другим.
Мы можем начать с силы
вовлеченный. Мы знаем, что основная единица СИ
сила — это ньютон, символизирующий заглавную букву 𝑁. И мы можем вспомнить, что один ньютон
сила, необходимая для ускорения тела массой в один килограмм с
ускорение один метр в секунду в квадрате.Другими словами, единица измерения ньютон
равен килограмму на метр в секунду в квадрате. И затем далее мы можем рассмотреть это
смещение 𝑑, также известное как расстояние по прямой, пройденное нашим
объект. Базовая единица СИ смещения или
расстояние метры. Исходя из задействованных тогда единиц
как для силы, так и для смещения, мы можем видеть, что, когда мы умножаем силу на
смещения, у нас будут ньютоны, умноженные на метры.Эти единицы показывают нам, что действительно
когда мы говорим о работе, мы говорим о силах на расстояниях.
Теперь, если мы умножим один ньютон силы на один метр перемещения, то произведение этих двух величин равно своя единица. Джоуль называется. Эта единица, сокращенно просто как заглавная 𝐽, это единица работы. Итак, как мы видели, единицей силы ньютон, единица перемещения метры.А если умножить ньютон на метр, мы получаем эту единицу, называемую джоулем, и это единица работы. Тогда мы могли бы сказать, что какой-то процесс может включать работу в 100 джоулей или что человек может выполнить работу в 250 джоулей поднимая коробку. Вот так мы говорим о работе Выполнено.
Итак, теперь, учитывая сценарий, в котором мы
есть сила в ньютонах и перемещение в метрах, мы можем вычислить работу
производится в единицах джоулей.Но есть пара вещей, чтобы
следить за при применении этого конкретного уравнения. Во-первых, уравнение предполагает
что сила, о которой мы говорим, является постоянной силой. Он не меняется со временем. Это означает, что он всегда имеет то же самое
величина или сила, и она также всегда указывает в одном и том же направлении. Еще одно предположение, которое мы делаем
Здесь сила и перемещение направлены в одном направлении. Например, если у нас есть некоторый объект
с действующей на него силой и сказать, что сила действует вправо, то это
Уравнение — записанное как есть — предполагает, что перемещение объекта также находится в
того же направления, что и сила, действующая на него.
Он не меняется со временем. Это означает, что он всегда имеет то же самое
величина или сила, и она также всегда указывает в одном и том же направлении. Еще одно предположение, которое мы делаем
Здесь сила и перемещение направлены в одном направлении. Например, если у нас есть некоторый объект
с действующей на него силой и сказать, что сила действует вправо, то это
Уравнение — записанное как есть — предполагает, что перемещение объекта также находится в
того же направления, что и сила, действующая на него.
Итак, это две вещи, на которые стоит обратить внимание
поскольку, когда мы применяем это уравнение для выполненной работы: приложенная сила постоянна
и что сила и перемещение объекта направлены в одном направлении. Теперь самый лучший способ получить некоторые
Опыт с этими отношениями заключается в том, чтобы применить их на практике. Давайте сделаем это сейчас через пару
примерных упражнений.
Какая из следующих формул правильно показывает связь между величиной силы и работой, совершаемой этой силы, и расстояние, пройденное в направлении приложенной силы объект, к которому приложена сила?
Прежде чем мы рассмотрим наш ответ
вариантов, давайте рассмотрим, что происходит в этой ситуации.У нас есть какой-то объект. Мы скажем, что это наше
объект. И мы воображаем, что какая-то сила
применяется к этому объекту. Мы можем назвать эту силу 𝐹. И что наряду с этим,
объект перемещается или перемещается на некоторое расстояние — мы можем назвать это 𝑑 — в одном и том же
направлении при приложении этой силы 𝐹. Исходя из этого, наш вопрос:
какой из этих пяти вариантов — A, B, C, D или E — дает нам правильную формулу,
показывая связь между этими двумя величинами — силой, расстоянием — и
третья величина работа, проделанная над нашим объектом. Другими словами, мы хотим знать, как
работа, сила и расстояние связаны друг с другом математически.
Другими словами, мы хотим знать, как
работа, сила и расстояние связаны друг с другом математически.
При этом давайте посмотрим на наш ответить кандидатам. А) Работа равна расстоянию разделить силой. Б) Работа равна силе, разделенной по расстоянию. в) работа равна расстоянию минус сила. Г) Работа равна силе, умноженной на время. расстояние. Е) Работа равна силе минус расстояние.
Первое, что мы можем сделать
чтобы начать сужать наши варианты ответов, нужно рассмотреть единицы, участвующие в
эти выражения. Каждое из этих выражений
включает в себя три термина. Есть работа, 𝑊, сила, 𝐹 и
расстояние, 𝑑. Теперь, если мы рассмотрим единицы
каждый из этих трех терминов, работы, силы и расстояния, затем, начиная сверху,
единицей работы является джоуль, сокращенно столица 𝐽.Базовая единица силы, которую мы знаем
быть Ньютоном, сокращенно заглавной 𝑁. И базовая единица для расстояния или
смещение — метр.
И базовая единица для расстояния или
смещение — метр.
Теперь давайте рассмотрим на мгновение что единицей работы является джоуль. Глядя на эти пять ответов варианты, мы видим, что работа появляется слева от каждого из них. А поскольку единицей работы является джоулей, это означает, что левая часть каждого из этих уравнений имеет единицы джоули.Теперь, если некоторое количество работы в единиц джоулей равно какой-либо другой величине, то есть величине на правая часть, то это означает, что правая часть правильной формулы должна также выражаться в конечном счете в этих же единицах, в единицах джоулей. Это означает, что если мы можем сказать для уверен, что единицы в правой части любого из этих выражений не могут быть джоулей, в таком случае эти варианты ответа не могут быть правильной формулой.
Имея это в виду, давайте
рассмотрите варианты ответов C и E.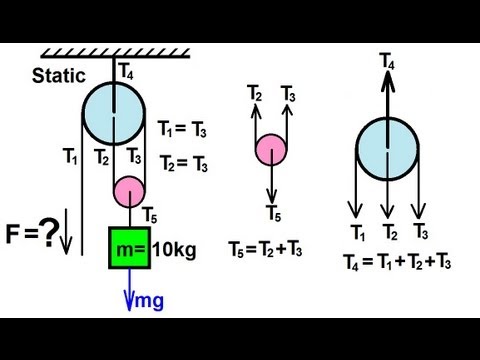 Вариант C утверждает, что работа равна
на расстояние минус сила, где вариант E утверждает, что работа равна силе минус
расстояние. Мы знаем, что единицы силы
ньютоны, а единицами расстояния являются метры. Но это значит, что мы не в состоянии
соединить таким образом единицы этих слагаемых и получить единицы джоулей,
что мы должны были бы сделать, если бы они согласились с левой частью.Например, для варианта ответа С
у нас было бы расстояние в метрах минус сила в ньютонах. Но вычитая некоторое количество
ньютонов с некоторого количества метров не дает нам какое-то количество джоулей. Единицы не работают. А это значит, что вариант ответа С
не может быть нашей правильной формулой.
Вариант C утверждает, что работа равна
на расстояние минус сила, где вариант E утверждает, что работа равна силе минус
расстояние. Мы знаем, что единицы силы
ньютоны, а единицами расстояния являются метры. Но это значит, что мы не в состоянии
соединить таким образом единицы этих слагаемых и получить единицы джоулей,
что мы должны были бы сделать, если бы они согласились с левой частью.Например, для варианта ответа С
у нас было бы расстояние в метрах минус сила в ньютонах. Но вычитая некоторое количество
ньютонов с некоторого количества метров не дает нам какое-то количество джоулей. Единицы не работают. А это значит, что вариант ответа С
не может быть нашей правильной формулой.
Вариант ответа E выпадает для
та же самая причина. Некоторое количество ньютонов минус некоторое
количество метров не может равняться какому-то количеству джоулей. Итак, мы подошли к варианту ответа А,
B и D. Теперь, в этот момент, мы можем вспомнить
что существует соотношение, которое связывает между собой единицы джоулей, ньютонов и
метров. Определение единицы джоуля
что один джоуль равен одному ньютону силы, умноженному на один метр
расстояние. Написано по-другому, мы можем сказать
что джоуль равен ньютон-метру. Это показывает нам, что независимо от нашего
правильный вариант ответа, у нас будут единицы ньютонов, умноженные на метры на
правая часть нашего выражения.
Итак, мы подошли к варианту ответа А,
B и D. Теперь, в этот момент, мы можем вспомнить
что существует соотношение, которое связывает между собой единицы джоулей, ньютонов и
метров. Определение единицы джоуля
что один джоуль равен одному ньютону силы, умноженному на один метр
расстояние. Написано по-другому, мы можем сказать
что джоуль равен ньютон-метру. Это показывает нам, что независимо от нашего
правильный вариант ответа, у нас будут единицы ньютонов, умноженные на метры на
правая часть нашего выражения.
Глядя на вариант А, мы видим, что
у этого кандидата единицы измерения метры, разделенные на ньютоны, поэтому не ньютоны, умноженные на метры,
тогда как вариант B имеет единицы справа от ньютонов, разделенных на метры. Тогда, наконец, вариант 𝑑 имеет единицы
в правой части ньютонов, умноженных на метры. Мы видим, что именно этот вариант
дает нам единицы в правой части, которые согласуются с единицами, эквивалентными
джоуль. Следовательно, вариант D имеет правильный
отношения между единицами в левой и правой части. И поэтому это наш выбор
за формулу, правильно представляющую связь между работой, силой и
расстояние. Работа равна произведению силы
по расстоянию.
Следовательно, вариант D имеет правильный
отношения между единицами в левой и правой части. И поэтому это наш выбор
за формулу, правильно представляющую связь между работой, силой и
расстояние. Работа равна произведению силы
по расстоянию.
Теперь давайте посмотрим на второй пример. связанных с механической работой.
Сила в 320 ньютонов равна постоянно применяется, чтобы протолкнуть тележку через парковку супермаркета.Если тележку толкают на расстояние 15 метров, какую работу совершила тележка?
Теперь первое, что мы можем здесь сказать
в том, что тележка в данном случае — это еще одно слово для корзины для покупок. Итак, у нас есть эта тележка, и мы
толкая его вокруг стоянки. Нам конкретно говорят, что, поскольку мы
толкаем тележку, мы прикладываем силу — мы можем назвать ее 𝐹 — в 320 ньютонов. И что благодаря этой силе
применительно к тележке, тележка проходит расстояние — мы можем назвать это расстояние 𝑑 —
дается как 15 метров.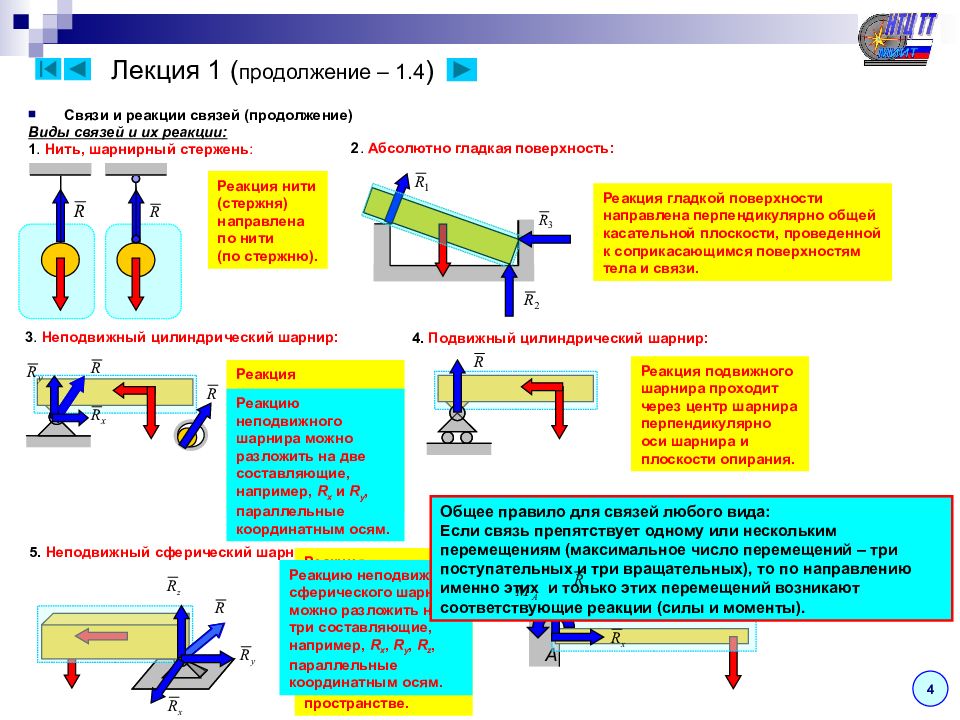 То, что мы хотим узнать, дано
при этой силе и при таком расстоянии какую работу совершила тележка? Чтобы разобраться в этом, давайте вспомним
отношения, связывающие работу с силой и расстоянием.
То, что мы хотим узнать, дано
при этой силе и при таком расстоянии какую работу совершила тележка? Чтобы разобраться в этом, давайте вспомним
отношения, связывающие работу с силой и расстоянием.
При двух условиях и получим к тому, что это всего за секунду. Работа, выполненная над объектом, 𝑊, равна равна силе, приложенной к объекту, умноженной на расстояние, на которое он движется. Теперь вот эти два условия мы упоминали.Для того чтобы это уравнение было действительно, сила 𝐹 должна быть постоянной силой. Он не может меняться, становясь меньше или больше. И второе условие состоит в том, что сила 𝐹 и расстояние 𝑑, которое проходит объект, должны быть одинаковыми. направление. Когда мы смотрим на наш сценарий, мы видим что оба эти условия соблюдены.
Имеем постоянную силу 320
ньютонов, и сила направлена в том же направлении, что и наша тележка. Это означает, что мы действительно можем решить для
работу, совершаемую над этой тележкой, путем умножения приложенной к ней силы на расстояние
что оно путешествует. То, что сделано на тележке — мы можем
назовем его 𝑊 sub 𝑐 — равно силе, действующей на тележку, 320 ньютонов, умноженной на
расстояние, которое он проходит, 15 метров. Поскольку и наша сила, и наша
расстояние уже в своих основных единицах СИ, ньютонах и метрах соответственно, мы
можно просто перемножить эти два значения вместе с их единицами, чтобы найти работу
в единицах джоулей.Когда мы это сделаем, мы обнаружим, что 𝑊 sub 𝑐
составляет 4800 джоулей. Вот сколько работы было выполнено
на этой тележке.
Это означает, что мы действительно можем решить для
работу, совершаемую над этой тележкой, путем умножения приложенной к ней силы на расстояние
что оно путешествует. То, что сделано на тележке — мы можем
назовем его 𝑊 sub 𝑐 — равно силе, действующей на тележку, 320 ньютонов, умноженной на
расстояние, которое он проходит, 15 метров. Поскольку и наша сила, и наша
расстояние уже в своих основных единицах СИ, ньютонах и метрах соответственно, мы
можно просто перемножить эти два значения вместе с их единицами, чтобы найти работу
в единицах джоулей.Когда мы это сделаем, мы обнаружим, что 𝑊 sub 𝑐
составляет 4800 джоулей. Вот сколько работы было выполнено
на этой тележке.
Давайте на минутку обобщить то, что мы узнали на этом уроке о механической работе.
Во-первых, мы увидели, что работа
равна силе, действующей на объект, умноженной на расстояние, на которое объект
путешествия. Записав уравнение, мы можем сказать
что работа 𝑊 равна силе 𝐹, умноженной на расстояние 𝑑.Мы узнали о задействованных подразделениях
в этом выражении, что основными единицами силы являются ньютоны, основная единица
расстояние — метры, а основная единица работы — джоули,
сокращенная заглавная 𝐽. И мы узнали, что джоуль
равно ньютону, умноженному на метр. Или, другими словами, джоуль
работа равна ньютону силы, действующей на расстояние в метр.
Записав уравнение, мы можем сказать
что работа 𝑊 равна силе 𝐹, умноженной на расстояние 𝑑.Мы узнали о задействованных подразделениях
в этом выражении, что основными единицами силы являются ньютоны, основная единица
расстояние — метры, а основная единица работы — джоули,
сокращенная заглавная 𝐽. И мы узнали, что джоуль
равно ньютону, умноженному на метр. Или, другими словами, джоуль
работа равна ньютону силы, действующей на расстояние в метр.
И, наконец, мы увидели, что это
уравнение, которое мы выучили для работы — что работа равна силе, умноженной на расстояние — имеет два
требования для того, чтобы быть действительным.Во-первых, есть требование,
прилагаемая сила должна быть постоянной. И второе условие состоит в том, что
приложенная сила и смещение или расстояние, пройденное объектом, должны
указывают в том же направлении. При выполнении этих условий мы
можно использовать это математическое соотношение для расчета работы, проделанной над объектом.
При выполнении этих условий мы
можно использовать это математическое соотношение для расчета работы, проделанной над объектом.
Видео-урок: Орбитальная механика | Нагва
Стенограмма видео
В этом видео наша тема орбитальная механика.Орбитальная механика посвящена тому, как движение объектов, которые движутся по орбитам, таких объектов, как планеты, луны или спутники, может быть описывается математически. Мы собираемся открыть, а также использовать два уравнения, описывающие это движение. Итак, давайте приступим к делу. Мы можем вспомнить из того, что мы уже знаем, что вообще существует два типа орбит. Один круговой, где объект на орбите находится на постоянном расстоянии от объекта, который вращается вокруг него.И есть также эллиптические орбиты, где что расстояние между двумя объектами постоянно меняется.
В этом уроке мы сосредоточимся на
именно на круговых орбитах. Это ситуации, когда орбитальная
радиус, мы можем назвать его 𝑟, является постоянной величиной по всей орбите. Вот что это значит для орбитального пути
быть круглым. Теперь, когда мы рассматриваем этот случай
по круговой орбите, мы можем видеть, что у нее есть ряд параметров.Мы уже видели, что есть
радиус орбиты, а затем, наряду с этим, мы знаем, что объект на орбите будет иметь некоторый орбитальный
скорость. Мы можем назвать эту скорость 𝑠.
Вот что это значит для орбитального пути
быть круглым. Теперь, когда мы рассматриваем этот случай
по круговой орбите, мы можем видеть, что у нее есть ряд параметров.Мы уже видели, что есть
радиус орбиты, а затем, наряду с этим, мы знаем, что объект на орбите будет иметь некоторый орбитальный
скорость. Мы можем назвать эту скорость 𝑠.
Итак, почему мы говорим, что этот объект движется по орбите, потому что он движется по пути, который повторяется снова и снова и снова. Как только объект закончил движение, все путь по кругу, затем он снова начинает движение по тому же пути. Мы видим, что расстояние до этого путь равен длине окружности со значением радиуса 𝑟.И это подводит нас к нашему первому математическое соотношение для описания орбитального движения.
Если мы хотим узнать длину окружности
круговая орбита, мы назовем это 𝑐, затем мы берем два и умножаем на 𝜋 и
умножьте это на радиус орбиты. Глядя на это уравнение, мы можем вспомнить
что это уравнение для длины окружности, происходит ли орбитальное движение
или нет. Полезная вещь об этом уравнении, для
наших целей, заключается в том, что он сообщает нам, какое расстояние проходит наш объект, проходя через один
оборот своей орбиты.
Глядя на это уравнение, мы можем вспомнить
что это уравнение для длины окружности, происходит ли орбитальное движение
или нет. Полезная вещь об этом уравнении, для
наших целей, заключается в том, что он сообщает нам, какое расстояние проходит наш объект, проходя через один
оборот своей орбиты.
Итак, мы сказали, что наш объект имеет некоторые постоянная скорость, мы назвали это 𝑠, поскольку он движется по этой орбите. И теперь мы знаем, что, когда это происходит за один оборот он проходит расстояние, которое мы можем назвать 𝑐. Итак, имеем постоянную скорость и расстояние, пройденное объектом, движущимся с этой скоростью. И это может напомнить нам уравнение который связывает скорость, расстояние и третью переменную, время. Мы можем вспомнить, что в целом средняя скорость тела равна расстоянию, которое проходит тело, деленному на время нужно пройти это расстояние.
В нашем случае скорость 𝑠. Это скорость нашего обращения
объект. И мы можем сказать, что расстояние, 𝑑,
который движется наш объект, равен длине окружности, по которой он движется. Итак, если бы мы переписали это уравнение
для средней скорости, применимой к случаю кругового орбитального движения, мы могли бы написать, что скорость
равно расстоянию, которое в два раза 𝜋 раз 𝑟 разделить на время. И когда приходит время в этом
уравнение, мы можем видеть, что это время показывает, сколько времени требуется объекту, чтобы двигаться
вокруг кругового пути один раз.Но для этого есть специальное название.
количество времени. Он называется орбитальным периодом. И это обычно представлено не с
строчная 𝑡, но с прописной 𝑇.
И мы можем сказать, что расстояние, 𝑑,
который движется наш объект, равен длине окружности, по которой он движется. Итак, если бы мы переписали это уравнение
для средней скорости, применимой к случаю кругового орбитального движения, мы могли бы написать, что скорость
равно расстоянию, которое в два раза 𝜋 раз 𝑟 разделить на время. И когда приходит время в этом
уравнение, мы можем видеть, что это время показывает, сколько времени требуется объекту, чтобы двигаться
вокруг кругового пути один раз.Но для этого есть специальное название.
количество времени. Он называется орбитальным периодом. И это обычно представлено не с
строчная 𝑡, но с прописной 𝑇.
Чтобы выяснить, каков орбитальный период
орбитальный объект, мы могли бы сделать что-то вроде этого. Учитывая определенное положение этого объекта
что мы можем назвать его исходной позицией, мы можем запустить секундомер. И затем, когда объект движется вокруг своей
круговой орбите, подождите, пока он не вернется в то место, где он начал. В этот момент мы останавливаем наш секундомер,
а полное прошедшее время — это период обращения объекта. Это означает, что теперь у нас есть математическое
отношения, которые связывают скорость, расстояние и время, но с точки зрения орбитального движения. Здесь 𝑇 — период обращения, удвоенный
𝜋 раз 𝑟 — длина пути орбиты, длина окружности, представляющая
это, а 𝑠, как мы видели, — это орбитальная скорость.
В этот момент мы останавливаем наш секундомер,
а полное прошедшее время — это период обращения объекта. Это означает, что теперь у нас есть математическое
отношения, которые связывают скорость, расстояние и время, но с точки зрения орбитального движения. Здесь 𝑇 — период обращения, удвоенный
𝜋 раз 𝑟 — длина пути орбиты, длина окружности, представляющая
это, а 𝑠, как мы видели, — это орбитальная скорость.
Одна из причин, по которой мы говорим об орбитальной скорости
а не орбитальная скорость заключается в том, что скорость может быть постоянной по мере того, как этот объект движется через свою
орбита.Это потому, что скорость, как мы помним,
количество скалера. Нет направления, связанного с ним
а только размер или величина. Это означает, что даже когда наша орбита
объект движется по круговой траектории, он будет иметь постоянную скорость. Он всегда будет двигаться одновременно
число, скажем, метров в секунду или километров в секунду. Но скорость, с другой стороны, будет
постоянно меняется для этого объекта. И это потому, что скорость как вектор
учитывает изменения направления.И мы видим, что направление этого
объект на орбите постоянно меняется.
Но скорость, с другой стороны, будет
постоянно меняется для этого объекта. И это потому, что скорость как вектор
учитывает изменения направления.И мы видим, что направление этого
объект на орбите постоянно меняется.
Итак, для такой круговой орбиты мы здесь скорость объекта на орбите постоянна, а скорость нет. И эта скорость равна удвоенной 𝜋 умноженный на радиус орбиты, деленный на период обращения, время, которое требуется объекту, чтобы пройти около одного полного оборота. Теперь, когда у нас есть эти математические описания того, как движутся объекты, движущиеся по круговым орбитам, давайте попрактиковаться в работе с этими уравнениями на примере.
Допустим, у нас есть такой сценарий.
Планета движется вокруг звезды в
круговая орбита. Радиус этой орбиты равен 6,0 умножить на 10
до седьмого километра, и время, которое требуется этой планете, чтобы полностью обернуться вокруг своей
орбита один раз составляет 210 дней.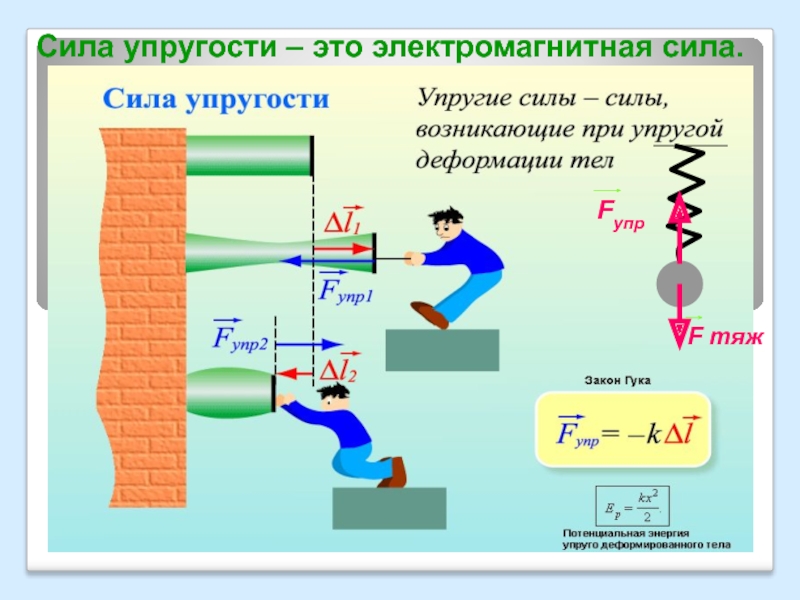 Это орбитальный период. Зная все это, допустим, что мы хотим
чтобы определить скорость этого объекта на орбите, мы можем назвать эту орбитальную скорость 𝑠.
Это орбитальный период. Зная все это, допустим, что мы хотим
чтобы определить скорость этого объекта на орбите, мы можем назвать эту орбитальную скорость 𝑠.
Чтобы начать вычисление 𝑠, мы можем вспомнить общее уравнение для тел, движущихся с постоянной скоростью.Это соотношение говорит о том, что скорость объект равен расстоянию, которое проходит объект, деленному на затраченное время. В нашем примере мы хотим рассчитать орбитальная скорость 𝑠. А для этого нужно знать расстояние, на которое перемещается объект, совершая один полный оборот, и время, затрачиваемое на это тот. Что ж, нам дали время. Это орбитальный период, капитал 𝑇. Но мы еще не знаем орбиту пройденное расстояние. Но взглянув еще раз на нашу орбиту, мы можем см., что это расстояние будет равно длине окружности с радиусом 𝑟.
Понимая это, мы помним, что
длина окружности 𝑐 круга равна удвоенному 𝜋 радиусу круга. И вот эта окружность
расстояние 𝑑, которое мы хотим использовать в нашем уравнении для орбитальной скорости. Итак, вот что мы можем написать. Орбитальная скорость нашего объекта, т.
то, что мы хотим решить, равно расстоянию, которое он проходит, то есть один раз вокруг
круговая орбита, два раза 𝜋 раз 𝑟, все делится на период обращения, заглавная 𝑇.И когда мы смотрим на известную информацию,
мы видим, что нам дано 𝑟 и нам дано заглавное 𝑇. Итак, теперь мы можем заменить эти два
значения в нашем уравнении для орбитальной скорости 𝑠.
Итак, вот что мы можем написать. Орбитальная скорость нашего объекта, т.
то, что мы хотим решить, равно расстоянию, которое он проходит, то есть один раз вокруг
круговая орбита, два раза 𝜋 раз 𝑟, все делится на период обращения, заглавная 𝑇.И когда мы смотрим на известную информацию,
мы видим, что нам дано 𝑟 и нам дано заглавное 𝑇. Итак, теперь мы можем заменить эти два
значения в нашем уравнении для орбитальной скорости 𝑠.
Сделав это, мы можем видеть, что если мы
вычислите эту дробь прямо сейчас, мы получим единицы километров в сутки. Это будут единицы, относительно которых
мы вычисляем нашу орбитальную скорость. Теперь, когда мы говорим об астрономии
таких тел, как эта планета, вращающихся вокруг звезды, нет ничего необычного в том, чтобы оставить расстояния в терминах
километров, потому что расстояния в астрономическом масштабе очень велики.Но редко оставляют время в единицах
дней. Итак, вместо того, чтобы выражать время таким образом,
давайте сделаем это с точки зрения базовой единицы времени СИ, секунды.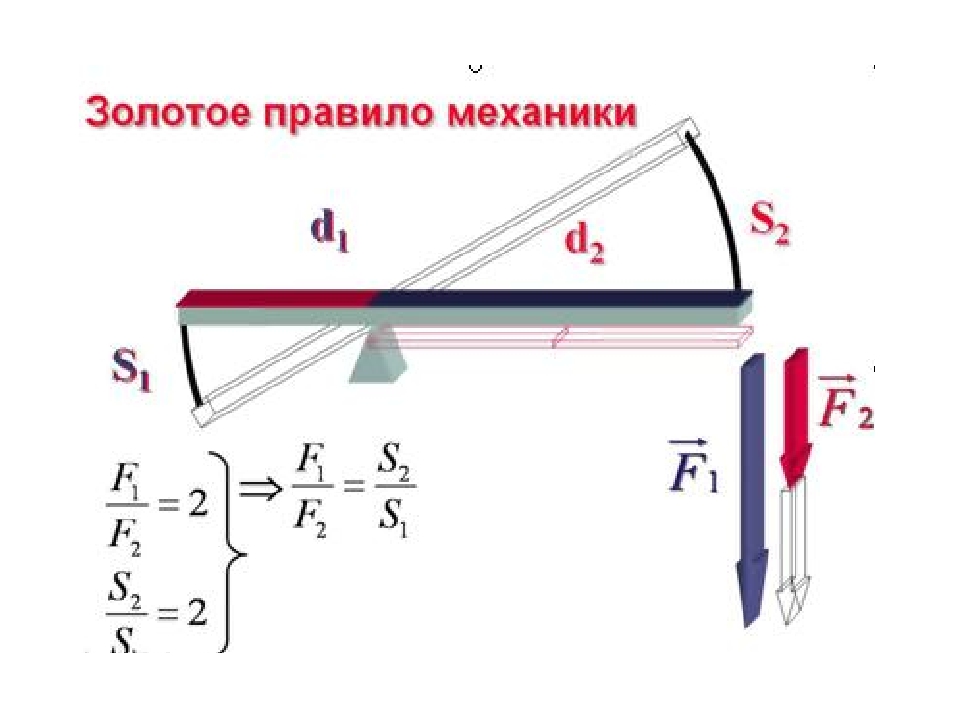
Для этого нам нужно преобразовать это единица времени. И вот что мы можем вспомнить, чтобы помочь нам с этим. Мы можем вспомнить, что один день равен 24 часов времени и один час равен 3600 секундам. И причина, по которой мы знаем, что один час 3600 секунд это один час это 60 минут и в каждой минуте 60 секунд.Итак, если мы умножим 60 минут на 60 секунд в минуту, мы получаем 3600 секунд. Теперь мы хотим повторно выразить 210 дней как некоторое количество секунд. Мы можем сделать это таким образом. Мы можем взять наше исходное значение времени, 210 дней и умножить на количество часов в сутках, а затем умножить на количество секунд в одном часе.
Обратите внимание, что эти две дроби, 24 часа
в сутках и 3600 секунд в часе, пришло из воспоминания о том, как конвертировать разные
единицы времени.И когда мы умножаем наше первоначальное время
значение 210 дней на эти две дроби, посмотрите, что происходит с единицами.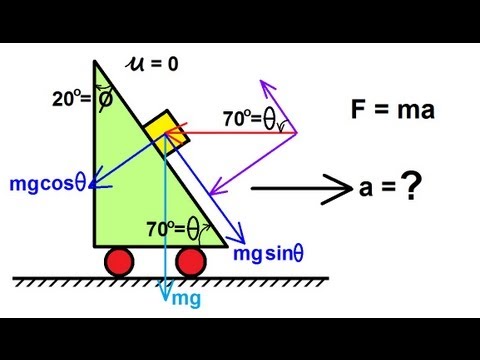 Во-первых, рассмотрим единицы дней. У нас есть эта единица в числителе и
теперь еще и в знаменателе, а это значит, что умножение на приводит к тому, что это отменяется. А также, у нас есть единицы часов в
числитель и знаменатель. Значит, эта единица времени тоже отменяется. Единица, с которой мы остались, когда все
пыль оседает, это просто единицы секунд, единица времени, которую мы хотели.
Во-первых, рассмотрим единицы дней. У нас есть эта единица в числителе и
теперь еще и в знаменателе, а это значит, что умножение на приводит к тому, что это отменяется. А также, у нас есть единицы часов в
числитель и знаменатель. Значит, эта единица времени тоже отменяется. Единица, с которой мы остались, когда все
пыль оседает, это просто единицы секунд, единица времени, которую мы хотели.
Итак, чтобы получить период обращения 210 дней, выраженных в секундах, нам нужно умножить 210 на 24 на 3600. Переписав наше выражение таким образом, мы можем теперь видим, что когда мы вычислим эту дробь, мы действительно получим скорость 𝑠 в единицах километров в секунду. И когда мы вводим все эти значения на нашем калькулятор, мы находим, что с точностью до двух значащих цифр орбитальная скорость этого орбитального планеты составляет 21 километр в секунду. Вот как быстро движется эта планета. движется по своей орбите.
Теперь рассмотрим второй пример. с участием орбитальной механики.
В этом случае спутник находится в круговом орбиту вокруг земли. Когда он проходит через один полный оборота спутник проходит расстояние 4,0 умножить на 10 на 10-м метрах. Каков радиус его орбиты?
Итак, в этом сценарии, если это здесь планету Земля, то нам говорят, что спутник находится на круговой орбите вокруг Земли. И это, когда он проходит через один полный оборот своей орбиты, то есть один полный оборот по этому кругу, он проходит всего расстояние указано как 4.0 раз по 10 до 10 метров. На основе этой информации мы хотим найдите радиус орбиты, который мы назвали 𝑟. Чтобы найти этот радиус, ключ осознание того, что существует математическая связь между окружностью круг и его радиус. Эти отношения говорят, что круг длина окружности, 𝑐, равна удвоенному 𝜋, умноженному на радиус окружности, 𝑟.
Теперь, поскольку наш спутник движется по круговая орбита, что означает, что это пройденное расстояние равно длине окружности круговой траектории, по которой он движется.И это означает, что мы можем использовать это отношение, чтобы решить для радиуса круга, 𝑟. Вот как мы можем это сделать. Начнем с перестановки этого уравнения так что 𝑟 является предметом уравнения. То есть это одна сторона уравнения все само собой. Для этого мы можем разделить обе части уравнение в два раза 𝜋. И когда мы делаем это, это означает, что два раз 𝜋 сокращается в правой части. У нас осталось уравнение, которое говорит что 𝑐 над двумя 𝜋, длина окружности, деленная на два 𝜋, равна радиус окружности.И это именно то, что мы хотим рассчитать.
Теперь, когда мы думаем о замене в на левую часть этого уравнения, чтобы мы могли вычислить 𝑟, мы можем вспомнить, что 𝜋 в знаменатель — константа. 𝜋 равно 3,1415…, и так далее и дальше. Итак, мы будем использовать приблизительное значение для 𝜋. Мы будем относиться к нему как к 3,14. Затем посмотрите на окружность круга дается нам в условии задачи. Это 4,0 умножить на 10 на 10-м метрах.Прежде чем мы продолжим и вычислим 𝑟, обратите внимание, что единицами измерения в этом выражении являются метры, единицы измерения расстояния. Тогда радиус, который мы рассчитываем, будет в единицах метров. Когда мы вычисляем эту дробь до двух значащие цифры, мы находим результат 6,4 умножить на 10 до девятого метра. Это радиус этого спутника орбита.
Теперь давайте обобщим то, что мы узнали об орбитальной механике. Начиная с того, что мы видели, что объекты в орбита может двигаться либо по кругу, как здесь, либо по эллипсу, как здесь.Для случая круговых орбит мы видели что если 𝑐 — это длина окружности этой круговой орбиты, расстояние до объекта, находящегося на орбите совершает один полный оборот своей орбиты, а 𝑟 — радиус орбиты, то 𝑐 — равно удвоенному 𝜋 умноженному на 𝑟.
А потом, когда мы подумали о объект, движущийся по орбите со скоростью, которую мы можем назвать 𝑠, мы увидели, что эта орбитальная скорость равна равна длине окружности орбиты, умноженной на два раза на 𝜋 ее радиуса, и все это делится на заглавная буква 𝑇, период обращения, то есть время, необходимое орбитальному объекту для перемещения через один полный оборот.



 Использовать измерительные инструменты для измерения расстояния, промежутка времени. Обосновывать результаты измерений и выявлять на этой основе зависимости пути от времени. Выражать результаты измерений в единицах СИ. Приводить примеры практического использования физических знаний о механических явлениях. Решать задачи на применение изученных физических законов в нестандартной ситуации. Использовать приобретенные знания и умения в повседневной жизни.
Использовать измерительные инструменты для измерения расстояния, промежутка времени. Обосновывать результаты измерений и выявлять на этой основе зависимости пути от времени. Выражать результаты измерений в единицах СИ. Приводить примеры практического использования физических знаний о механических явлениях. Решать задачи на применение изученных физических законов в нестандартной ситуации. Использовать приобретенные знания и умения в повседневной жизни.