Физика идеальный газ формулы: Формула идеального газа

Молекулярная физика — Физика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Основные положения МКТ

К оглавлению…

Молекулярно-кинетической теорией называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химического вещества. В основе молекулярно-кинетической теории лежат три основных положения:

• Все вещества – жидкие, твердые и газообразные – образованы из мельчайших частиц – молекул, которые сами состоят из атомов («элементарных молекул»). Молекулы химического вещества могут быть простыми и сложными и состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы (соответственно: катионы и анионы).
• Атомы и молекулы находятся в непрерывном хаотическом движении и взаимодействии, скорость которого зависит от температуры, а характер – от агрегатного состояния вещества.
• Частицы взаимодействуют друг с другом силами, имеющими электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.

Атом – наименьшая химически неделимая частица элемента (атом железа, гелия, кислорода). Молекула – наименьшая частица вещества, сохраняющая его химические свойства. Молекула состоит из одного и более атомов (вода – Н₂О – 1 атом кислорода и 2 атома водорода). Ион – атом или молекула, у которых один или несколько электронов лишние (или электронов не хватает).

Молекулы имеют чрезвычайно малые размеры. Простые одноатомные молекулы имеют размер порядка 10^–10 м. Сложные многоатомные молекулы могут иметь размеры в сотни и тысячи раз больше. 

Беспорядочное хаотическое движение молекул называется тепловым движением.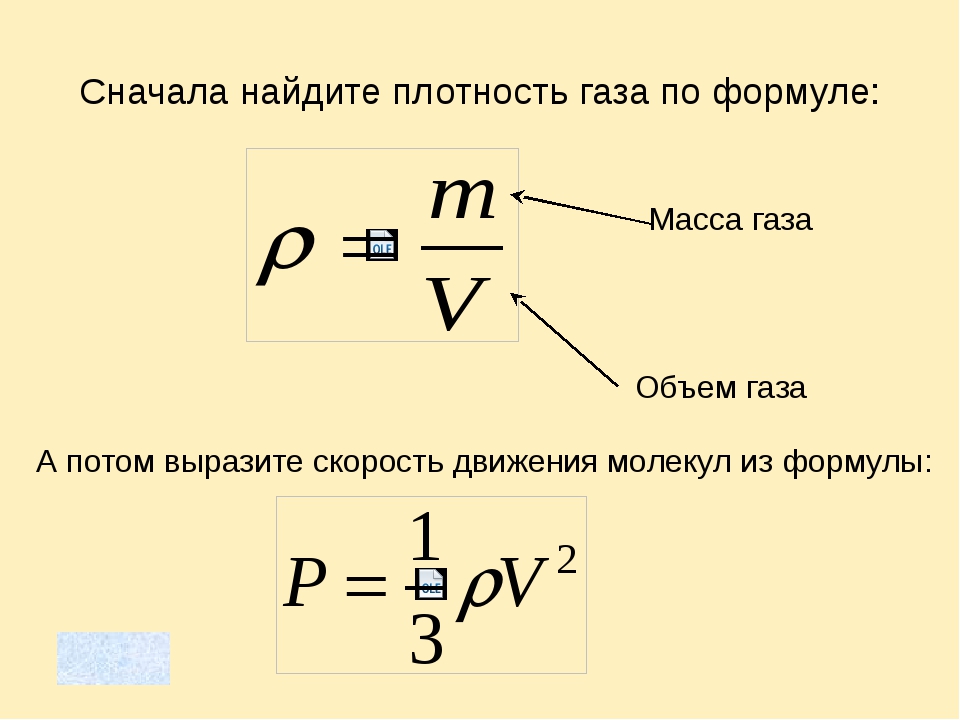

Кинетическая энергия теплового движения растет с возрастанием температуры. При низких температурах молекулы конденсируются в жидкое или твердое вещество. При повышении температуры средняя кинетическая энергия молекулы становится больше, молекулы разлетаются, и образуется газообразное вещество.

В твердых телах молекулы совершают беспорядочные колебания около фиксированных центров (положений равновесия). Эти центры могут быть расположены в пространстве нерегулярным образом (аморфные тела) или образовывать упорядоченные объемные структуры (кристаллические тела).

В жидкостях молекулы имеют значительно большую свободу для теплового движения. Они не привязаны к определенным центрам и могут перемещаться по всему объему жидкости. Этим объясняется текучесть жидкостей.

В газах расстояния между молекулами обычно значительно больше их размеров. Силы взаимодействия между молекулами на таких больших расстояниях малы, и каждая молекула движется вдоль прямой линии до очередного столкновения с другой молекулой или со стенкой сосуда.

Среднее расстояние между молекулами воздуха при нормальных условиях порядка 10^–8 м, то есть в сотни раз превышает размер молекул. Слабое взаимодействие между молекулами объясняет способность газов расширяться и заполнять весь объем сосуда. В пределе, когда взаимодействие стремится к нулю, мы приходим к представлению об идеальном газе.

Идеальный газ – это газ, молекулы которого не взаимодействуют друг с другом, за исключением процессов упругого столкновения и считаются материальными точками.

В молекулярно-кинетической теории количество вещества принято считать пропорциональным числу частиц. Единица количества вещества называется молем (моль).

Моль – это количество вещества, содержащее столько же частиц (молекул), сколько содержится атомов в 0,012 кг углерода ¹²C. Молекула углерода состоит из одного атома. Таким образом, в одном моле любого вещества содержится одно и то же число частиц (молекул). Это число называется постоянной Авогадро: N_А = 6,022·10²³ моль^–1.

Постоянная Авогадро – одна из важнейших постоянных в молекулярно-кинетической теории. Количество вещества определяется как отношение числа N частиц (молекул) вещества к постоянной Авогадро N_А, или как отношение массы к молярной массе:

Массу одного моля вещества принято называть молярной массой M. Молярная масса равна произведению массы m₀ одной молекулы данного вещества на постоянную Авогадро (то есть на количество частиц в одном моле). Молярная масса выражается в килограммах на моль (кг/моль). Для веществ, молекулы которых состоят из одного атома, часто используется термин атомная масса. В таблице Менделеева молярная масса указана в граммах на моль. Таким образом имеем еще одну формулу:

где: M – молярная масса, N_A – число Авогадро, m₀ – масса одной частицы вещества, N – число частиц вещества содержащихся в массе вещества m. Кроме этого понадобится понятие концентрации (количество частиц в единице объема):

Напомним также, что плотность, объем и масса тела связаны следующей формулой:

Если в задаче идет речь о смеси веществ, то говорят о средней молярной массе и средней плотности вещества. Как и при вычислении средней скорости неравномерного движения, эти величины определяются полными массами смеси:

Не забывайте, что полное количество вещества всегда равно сумме количеств веществ, входящих в смесь, а с объемом надо быть аккуратными. Объем смеси газов не равен сумме объемов газов, входящих в смесь. Так, в 1 кубометре воздуха содержится 1 кубометр кислорода, 1 кубометр азота, 1 кубометр углекислого газа и т.д. Для твердых тел и жидкостей (если иное не указано в условии) можно считать, что объем смеси равен сумме объемов ее частей.

 

Основное уравнение МКТ идеального газа

К оглавлению…

При своем движении молекулы газа непрерывно сталкиваются друг с другом. Из-за этого характеристики их движения меняются, поэтому, говоря об импульсах, скоростях, кинетических энергиях молекул, всегда имеют в виду средние значения этих величин.

Число столкновений молекул газа в нормальных условиях с другими молекулами измеряется миллионами раз в секунду. Если пренебречь размерами и взаимодействием молекул (как в модели идеального газа), то можно считать, что между последовательными столкновениями молекулы движутся равномерно и прямолинейно. Естественно, подлетая к стенке сосуда, в котором расположен газ, молекула испытывает столкновение и со стенкой. Все столкновения молекул друг с другом и со стенками сосуда считаются абсолютно упругими столкновениями шариков. При столкновении со стенкой импульс молекулы изменяется, значит на молекулу со стороны стенки действует сила (вспомните второй закон Ньютона). Но по третьему закону Ньютона с точно такой же силой, направленной в противоположную сторону, молекула действует на стенку, оказывая на нее давление. Совокупность всех ударов всех молекул о стенку сосуда и приводит к возникновению давления газа.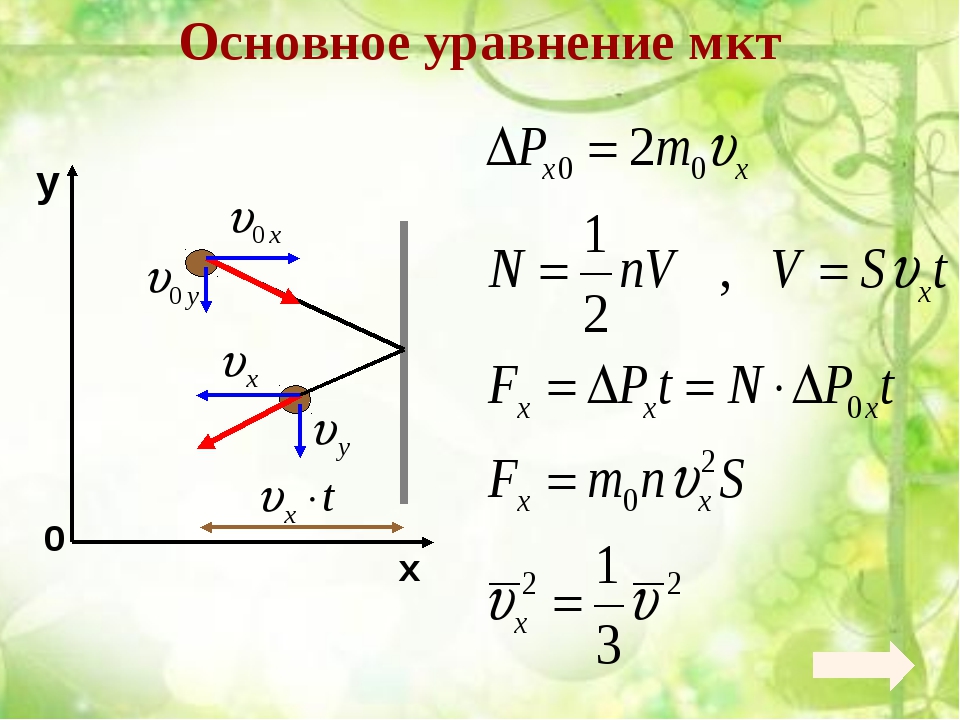

Давление газа – это результат столкновений молекул со стенками сосуда. Если нет стенки или любого другого препятствия для молекул, то само понятие давления теряет смысл. Например, совершенно антинаучно говорить о давлении в центре комнаты, ведь там молекулы не давят на стенку. Почему же тогда, поместив туда барометр, мы с удивлением обнаружим, что он показывает какое-то давление? Правильно! Потому, что сам по себе барометр является той самой стенкой, на которую и давят молекулы.

Поскольку давление есть следствие ударов молекул о стенку сосуда, очевидно, что его величина должна зависеть от характеристик отдельно взятых молекул (от средних характеристик, конечно, Вы ведь помните про то, что скорости всех молекул различны). Эта зависимость выражается основным уравнением молекулярно-кинетической теории идеального газа:

где: p — давление газа, n — концентрация его молекул, m₀ — масса одной молекулы, v_кв — средняя квадратичная скорость (обратите внимание, что в самом уравнении стоит квадрат средней квадратичной скорости).

Физический смысл этого уравнения состоит в том, что оно устанавливает связь между характеристиками всего газа целиком (давлением) и параметрами движения отдельных молекул, то есть связь между макро- и микромиром.

Следствия из основного уравнения МКТ

Как уже было отмечено в предыдущем параграфе, скорость теплового движения молекул определяется температурой вещества. Для идеального газа эта зависимость выражается простыми формулами для средней квадратичной скорости движения молекул газа:

где: k = 1,38∙10^–23 Дж/К – постоянная Больцмана, T – абсолютная температура. Сразу же оговоримся, что далее во всех задачах Вы должны, не задумываясь, переводить температуру в кельвины из градусов Цельсия (кроме задач на уравнение теплового баланса). Закон трех постоянных

:

где: R = 8,31 Дж/(моль∙К) – универсальная газовая постоянная. Следующей важной формулой является формула для средней кинетической энергии поступательного движения молекул газа:

Оказывается, что средняя кинетическая энергия поступательного движения молекул зависит только от температуры, одинакова при данной температуре для всех молекул. Ну и наконец, самыми главными и часто применяемыми следствиями из основного уравнения МКТ являются следующие формулы:

Измерение температуры

Понятие температуры тесно связано с понятием теплового равновесия. Тела, находящиеся в контакте друг с другом, могут обмениваться энергией. Энергия, передаваемая одним телом другому при тепловом контакте, называется количеством теплоты.

Тепловое равновесие – это такое состояние системы тел, находящихся в тепловом контакте, при котором не происходит теплопередачи от одного тела к другому, и все макроскопические параметры тел остаются неизменными.

Температура – это физический параметр, одинаковый для всех тел, находящихся в тепловом равновесии.

Для измерения температуры используются физические приборы – термометры, в которых о величине температуры судят по изменению какого-либо физического параметра. Для создания термометра необходимо выбрать термометрическое вещество (например, ртуть, спирт) и термометрическую величину, характеризующую свойство вещества (например, длина ртутного или спиртового столбика). В различных конструкциях термометров используются разнообразные физические свойства вещества (например, изменение линейных размеров твердых тел или изменение электрического сопротивления проводников при нагревании).

Термометры должны быть откалиброваны. Для этого их приводят в тепловой контакт с телами, температуры которых считаются заданными. Чаще всего используют простые природные системы, в которых температура остается неизменной, несмотря на теплообмен с окружающей средой – это смесь льда и воды и смесь воды и пара при кипении при нормальном атмосферном давлении. По температурной шкале Цельсия точке плавления льда приписывается температура 0°С, а точке кипения воды: 100°С. Изменение длины столба жидкости в капиллярах термометра на одну сотую длины между отметками 0°С и 100°С принимается равным 1°С.

Английский физик У.Кельвин (Томсон) в 1848 году предложил использовать точку нулевого давления газа для построения новой температурной шкалы (шкала Кельвина). В этой шкале единица измерения температуры такая же, как и в шкале Цельсия, но нулевая точка сдвинута:

При этом изменение температуры на 1ºС соответствует изменению температуры на 1 К.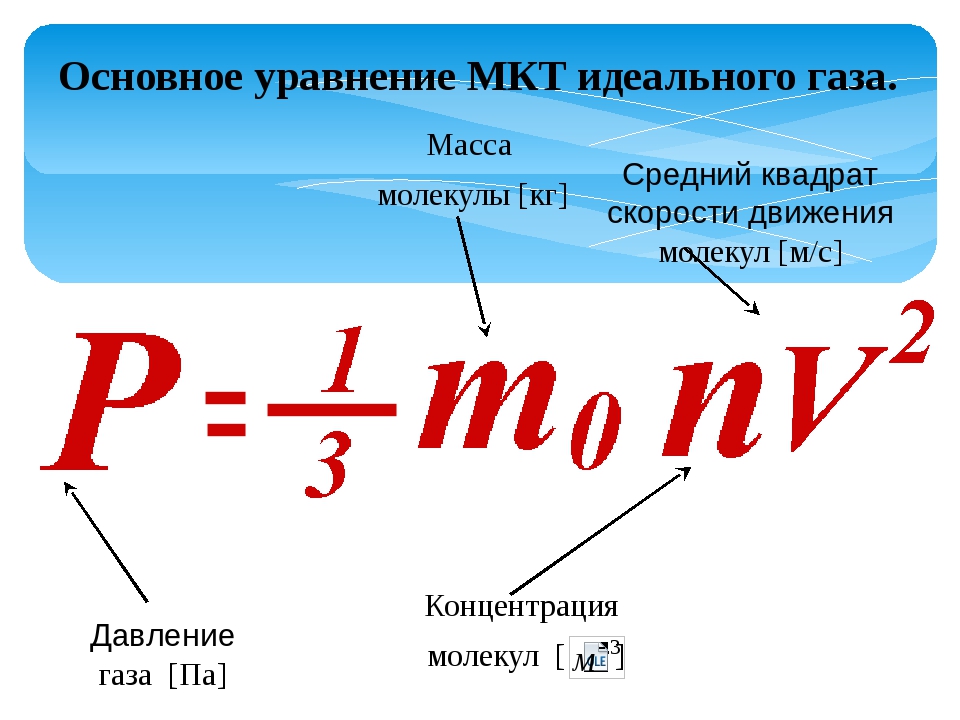 Изменения температуры по шкале Цельсия и Кельвина равны. В системе СИ принято единицу измерения температуры по шкале Кельвина называть кельвином и обозначать буквой К. Например, комнатная температура T_С = 20°С по шкале Кельвина равна T_К = 293 К. Температурная шкала Кельвина называется абсолютной шкалой температур. Она оказывается наиболее удобной при построении физических теорий.

 

Уравнение состояния идеального газа или уравнение Клапейрона-Менделеева

К оглавлению…

Уравнение состояние идеального газа является очередным следствие из основного уравнения МКТ и записывается в виде:

Данное уравнение устанавливает связь между основными параметрами состояния идеального газа: давлением, объемом, количеством вещества и температурой. Очень важно, что эти параметры взаимосвязаны, изменение любого из них неизбежно приведет к изменению еще хотя бы одного. Именно поэтому данное уравнение и называют уравнением состояния идеального газа.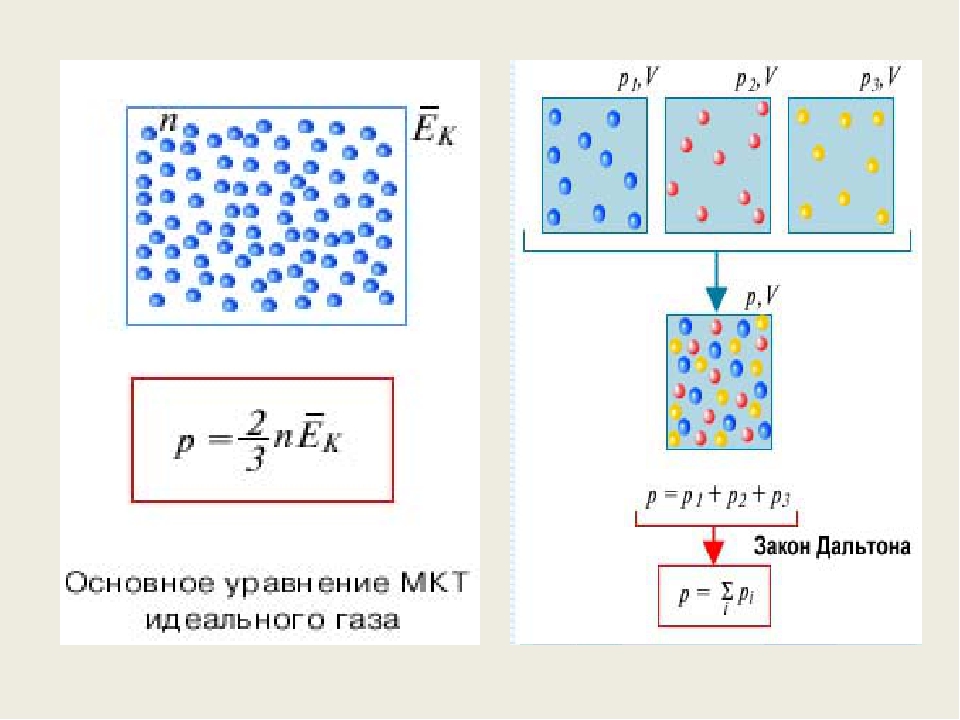 Оно было открыто сначала для одного моля газа Клапейроном, а впоследствии обобщено на случай большего количество молей Менделеевым.

Если температура газа равна T_н = 273 К (0°С), а давление p_н = 1 атм = 1·10⁵ Па, то говорят, что газ находится при нормальных условиях.

 

Газовые законы

К оглавлению…

Решение задач на расчет параметров газа значительно упрощается, если Вы знаете, какой закон и какую формулу применить. Итак, рассмотрим основные газовые законы.

1. Закон Авогадро. В одном моле любого вещества содержится одинаковое количество структурных элементов, равное числу Авогадро.

2. Закон Дальтона. Давление смеси газов равно сумме парциальных давлений газов, входящих в эту смесь:

Парциальным давлением газа называют то давление, которое он бы производил, если бы все остальные газ внезапно исчезли из смеси. Например, давление воздуха равно сумме парциальных давлений азота, кислорода, углекислого газа и прочих примесей. При этом каждый из газов в смеси занимает весь предоставленный ему объем, то есть объем каждого из газов равен объему смеси.

3. Закон Бойля-Мариотта. Если масса и температура газа остаются постоянными, то произведение давления газа на его объем не изменяется, следовательно:

Процесс, происходящий при постоянной температуре, называют изотермическим. Обратите внимание, что такая простая форма закона Бойля-Мариотта выполняется только при условии, что масса газа остается неизменной.

4. Закон Гей-Люссака. Сам закон Гей-Люссака не представляет особой ценности при подготовке к экзаменам, поэтому приведем лишь следствие из него. Если масса и давление газа остаются постоянными, то отношение объема газа к его абсолютной температуре не изменяется, следовательно:

Процесс, происходящий при постоянном давлении, называют изобарическим или изобарным. Обратите внимание, что такая простая форма закона Гей-Люссака выполняется только при условии, что масса газа остается неизменной. Не забывайте про перевод температуры из градусов Цельсия в кельвины.

5. Закон Шарля. Как и закон Гей-Люссака, закон Шарля в точной формулировке для нас не важен, поэтому приведем лишь следствие из него. Если масса и объем газа остаются постоянными, то отношение давления газа к его абсолютной температуре не изменяется, следовательно:

Процесс, происходящий при постоянном объеме, называют изохорическим или изохорным. Обратите внимание, что такая простая форма закона Шарля выполняется только при условии, что масса газа остается неизменной. Не забывайте про перевод температуры из градусов Цельсия в кельвины.

6. Универсальный газовый закон (Клапейрона). При постоянной массе газа отношение произведения его давления и объема к температуре не изменяется, следовательно:

Обратите внимание, что масса должна оставаться неизменной, и не забывайте про кельвины.

Итак, существует несколько газовых законов. Перечислим признаки того, что нужно применять один из них при решении задачи:

1. Закон Авогадро применяется во всех задачах где речь идет о количестве молекул.
2. Закон Дальтона применяется во всех задачах, в которых идет речь о смеси газов.
3. Закон Шарля применяют в задачах, когда объем газа остается неизменным. Обычно это или сказано явно, или в задаче присутствуют слова «газ в закрытом сосуде без поршня».
4. Закон Гей-Люссака применяют, если неизменным остается давление газа. Ищите в задачах слова «газ в сосуде, закрытом подвижным поршнем» или «газ в открытом сосуде». Иногда про сосуд ничего не сказано, но по условию понятно, что он сообщается с атмосферой. Тогда считается, что атмосферное давление всегда остается неизменным (если в условии не сказано иного).
5. Закон Бойля-Мариотта. Тут сложнее всего. Хорошо, если в задаче написано, что температура газа неизменна. Чуть хуже, если в условии присутствует слово «медленно». Например, газ медленно сжимают или медленно расширяют. Еще хуже, если сказано, что газ закрыт теплонепроводящим поршнем. Наконец, совсем плохо, если про температуру не сказано ничего, но из условия можно предположить, что она не изменяется. Обычно в этом случае ученики применяют закон Бойля-Мариотта от безысходности.
6. Универсальный газовый закон. Его используют, если масса газа постоянна (например, газ находится в закрытом сосуде), но по условию понятно, что все остальные параметры (давление, объем, температура) изменяются. Вообще, часто вместо универсального закона можно применять уравнение Клапейрона-Менделеева, вы получите правильный ответ, только в каждой формуле будете писать по две лишние буквы.

 

Графическое изображение изопроцессов

К оглавлению…

Во многих разделах физики зависимость величин друг от друга удобно изображать графически. Это упрощает понимание взаимосвязи параметров, происходящих в системе процессов. Такой подход очень часто применяется и в молекулярной физике. Основными параметрами, описывающими состояние идеального газа, являются давление, объем и температура. Графический метод решения задач и состоит в изображении взаимосвязи этих параметров в различных газовых координатах. Существует три основных типа газовых координат: (p; V), (p; T) и (V; T). Заметьте, что это только основные (наиболее часто встречающиеся типы координат). Фантазия составителей задач и тестов не ограничена, поэтому Вы можете встретить и любые другие координаты. Итак, изобразим основные газовые процессы в основных газовых координатах.

Изобарный процесс (p = const)

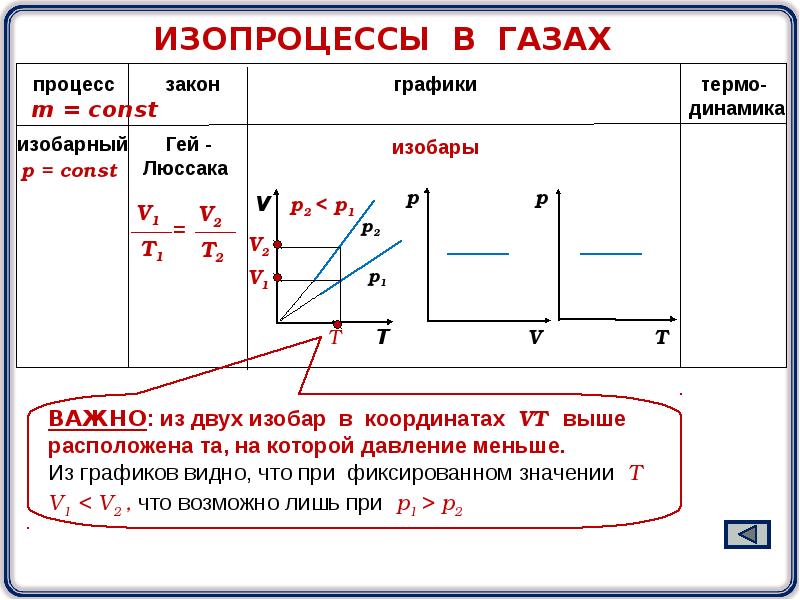
Изобарным процессом называют процесс, протекающий при неизменным давлении и массе газа. Как следует из уравнения состояния идеального газа, в этом случае объем изменяется прямо пропорционально температуре. Графики изобарического процесса в координатах р–V; V–Т и р–Т имеют следующий вид:

Обратите внимание на то, что продолжение графика в V–T координатах направлено точно в начало координат, однако этот график никогда не сможет начаться прямо из начала координат, так как при очень низких температурах газ превращается в жидкость и зависимость объема от температура меняется.

Изохорный процесс (V = const)

Изохорный процесс – это процесс нагревания или охлаждения газа при постоянном объеме и при условии, что количество вещества в сосуде остается неизменным. Как следует из уравнения состояния идеального газа, при этих условиях давление газа изменяется прямо пропорционально его абсолютной температуре. Графики изохорного процесса в координатах р–V; р–Т и V–Т имеют следующий вид:

Обратите внимание на то, что продолжение графика в p–T координатах направлено точно в начало координат, однако этот график никогда не сможет начаться прямо из начала координат, так как газ при очень низких температурах превращается в жидкость.

Изотермический процесс (T = const)

Изотермическим процессом называют процесс, протекающий при постоянной температуре. Из уравнения состояния идеального газа следует, что при постоянной температуре и неизменном количестве вещества в сосуде произведение давления газа на его объем должно оставаться постоянным. Графики изотермического процесса в координатах р–V; р–Т и V–Т имеют следующий вид:

Заметим, что при выполнении заданий на графики в молекулярной физике не требуется особой точности в откладывании координат по соответствующим осям (например, чтобы координаты p₁ и p₂ двух состояний газа в системе p(V) совпадали с координатами p₁ и p₂ этих состояний в системе p(T). Во–первых, это разные системы координат, в которых может быть выбран разный масштаб, а во–вторых, это лишняя математическая формальность, отвлекающая от главного – от анализа физической ситуации. Основное требование: чтобы качественный вид графиков был верным.

 

Неизопроцессы

К оглавлению…

В задачах этого типа изменяются все три основных параметра газа: давление, объем и температура. Постоянной остается только масса газа. Наиболее простой случай, если задача решается «в лоб» с помощью универсального газового закона. Чуть сложнее, если Вам надо отыскать уравнение процесса, описывающего изменение состояния газа, или проанализировать поведение параметров газа по данному уравнению. Тогда действовать надо так. Записать данное уравнение процесса и универсальный газовый закон (или уравнение Клапейрона-Менделеева, что Вам удобнее) и последовательно исключать ненужные величины из них.

 

Изменение количества или массы вещества

К оглавлению…

В сущности, ничего сложного в таких задачах нет. Надо только помнить, что газовые законы не выполняются, так как в формулировках любых из них записано «при постоянной массе». Поэтому действуем просто. Записываем уравнение Клапейрона-Менделеева для начального и конечного состояний газа и решаем задачу.

 

Перегородки или поршни

К оглавлению…

В задачах этого типа опять применяются газовые законы, при этом необходимо учесть следующие замечания:

• Во-первых, газ через перегородку не проходит, то есть масса газа в каждой части сосуда остается неизменной, и таким образом, для каждой части сосуда выполняются газовые законы.
• Во-вторых, если перегородка теплонепроводящая, то при нагревании или охлаждении газа в одной части сосуда температура газа во второй части останется неизменной.
• В-третьих, если перегородка подвижна, то давления по обе ее стороны равны в каждый конкретный момент времени (но это равное с обоих сторон давление может меняться со временем).
• А дальше пишем газовые законы для каждого газа по отдельности и решаем задачу.

 

Газовые законы и гидростатика

К оглавлению…

Специфика задач состоит в том, что в давлении надо будет учитывать «довески», связанные с давлением столба жидкости. Какие тут могут быть варианты:

• Сосуд с газом погружен под воду. Давление в сосуде будет равно: p = p_атм + ρgh, где: h – глубина погружения.
• Горизонтальная трубка закрыта от атмосферы столбиком ртути (или другой жидкости). Давление газа в трубке точно равно: p = p_атм атмосферному, так как горизонтальный столбик ртути не оказывает давления на газ.
• Вертикальная трубка с газом закрыта сверху столбиком ртути (или другой жидкости). Давление газа в трубке: p = p_атм + ρgh, где: h – высота столбика ртути.
• Вертикальная узкая трубка с газом повернута открытым концом вниз и заперта столбиком ртути (или другой жидкости). Давление газа в трубке: p = p_атм – ρgh, где: h – высота столбика ртути. Знак «–» ставится, так как ртуть не сжимает, а растягивает газ. Часто ученики спрашивают, почему ртуть не вытекает из трубки. Действительно, если бы трубка была широкой, ртуть бы стекла вниз по стенкам. А так, поскольку трубка очень узкая, поверхностное натяжение на дает ртути разорваться посередине и пропустить внутрь воздух, а давление газа внутри (меньшее, чем атмосферное) удерживает ртуть от вытекания.

Как только Вы сумели правильно записать давление газа в трубке, применяйте какой-либо из газовых законов (как правило, Бойля-Мариотта, так как большинство таких процессов изотермические, или универсальный газовый закон). Применяйте выбранный закон для газа (ни в коем случае не для жидкости) и решайте задачу.

 

Тепловое расширение тел

К оглавлению…

При повышении температуры возрастает интенсивность теплового движения частиц вещества. Это приводит к тому, что молекулы более «активно» отталкиваются друг от друга. Из-за этого большинство тел увеличивает свои размеры при нагревании. Не совершите типичную ошибку, сами атомы и молекулы не расширяются при нагревании. Увеличиваются лишь пустые промежутки между молекулами. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:

где: V₀ – объем жидкости при 0°С, V – при температуре t, γ – коэффициент объемного расширения жидкости. Обратите внимание, что все температуры в этой теме нужно брать в градусах Цельсия. Коэффициент объемного расширения зависит от рода жидкости (и от температуры, что не учитывается в большинстве задач). Обратите внимание, что численное значение коэффициента, выраженное в 1/°С или в 1/К, одинаково, так как нагреть тело на 1°С это то же самое, что нагреть его на 1 К (а не на 274 К).

Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:

где: l₀, S₀, V₀ – соответственно длина, площадь поверхности и объем тела при 0°С, α – коэффициент линейного расширения тела. Коэффициент линейного расширения зависит от рода тела (и от температуры, что не учитывается в большинстве задач) и измеряется в 1/°С или в 1/К.

Идеальный газ – Определение, свойства, условия

В жизни мы встречаем вещества в газообразном состоянии, когда чувствуем запахи. Запах очень легко распространяется, потому что газ не имеет ни формы, ни объема (занимает весь предоставленный объем) и состоит из хаотично движущихся молекул, расстояние между которыми больше, чем размеры молекул.

Агрегатных состояний точно три?

На самом деле есть еще четвертое — плазма. Звучит как что-то из научной фантастики, но это просто ионизированный газ — газ, в котором, помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.

Модель идеального газа

В физике есть такое понятие, как модель. Модель — это что-то идеализированное, она нужна в случаях, когда можно пренебречь некоторыми параметрами объекта или процесса.

Идеальный газ — это модель реального газа. Молекулы идеального газа представляют собой материальные точки, которые не взаимодействуют друг с другом на расстоянии, но взаимодействуют при столкновениях друг с другом или со стенками сосуда. При работе с идеальным газом можно пренебречь потенциальной энергией молекул (но не кинетической).

Важно знать

Модель идеального газа не может описать ситуацию, когда газ сжимают так сильно, что он конденсируется — переходит в жидкое состояние.

В повседневной жизни идеальный газ, конечно, не встречается. Но реальный газ может вести себя почти как идеальный. Такое случается, если среднее расстояние между молекулами во много раз больше их размеров, то есть если газ очень разреженный.

Свойства идеального газа

1. Расстояние между молекулами значительно больше размеров молекул.


2. Молекулы газа очень малы и представляют собой упругие шары.


3. Силы притяжения между молекулами пренебрежимо малы.


4. Молекулы взаимодействуют только при соударениях.


5. Молекулы движутся хаотично.


6. Молекулы движутся по законам Ньютона.

Среднеквадратичная скорость

Потенциальной энергией молекул газа пренебречь можно, а вот кинетической — никак нельзя. Потому что кинетическая энергия — это энергия движения, а мы не можем пренебрегать скоростью движения молекул.

На графике показано распределение Максвелла — то, как молекулы распределяются по скоростям. Судя по графику, большинство молекул движутся со средним значением скорости. Хотя есть и быстрые, и медленные молекулы, просто их значительно меньше.

Но наш газ идеальный, а в идеальном газе случаются чудеса. Одно из таких чудес — то, что все молекулы идеального газа двигаются с одинаковой скоростью. Эта скорость называется средней квадратичной.

Средняя квадратичная скорость v1, v2, vn — скорости разных молекул [м/с] N — количество молекул [-]

Давление идеального газа

Молекулы газа беспорядочно движутся. Во время движения они сталкиваются друг с другом, а также со стенками сосуда, в котором этот газ находится. Поскольку молекул много, ударов тоже много.

Например, в комнате, в которой вы сейчас находитесь, за одну секунду на каждый квадратный сантиметр молекулы воздуха наносят столько ударов, что их количество выражается двадцатитрехзначным числом.

Хотя сила удара отдельной молекулы мала, действие всех молекул на стенки сосуда приводит к значительному давлению. Представьте, что комар пытается толкать машину — она не сдвинется с места. Но если за работу возьмется пара сотен миллионов комаров, то машину получится сдвинуть.

Эксперимент

Чтобы смоделировать давление газа, возьмите песок и лист бумаги, зажатый между двумя книгами. Песчинки будут выступать в роли молекул газа, а лист — в роли сосуда, в котором этот газ находится. Когда вы начинаете сыпать песок на лист бумаги, бумага отклоняется под воздействием множества песчинок. Так же и молекулы газа оказывают давление на стенки сосуда, в котором находятся.

Зависимость давления от других величин

Зависимость давления от объема

В механике есть формула давления, которая показывает, что давление прямо пропорционально силе и обратно пропорционально площади, на которую эта сила оказывается.

Давление p = F/S F — сила [Н] S — площадь [м2]

То есть если наши двести миллионов комаров будут толкать легковую машину, они распределятся по меньшей площади, чем если бы толкали грузовой автомобиль, — просто потому, что легковушка меньше грузовика. Из формулы давления следует, что давление на легковой автомобиль будет больше из-за его меньшей площади.

Рассмотрим аналогичный пример с двумя сосудами разной площади.

Давление в левом сосуде будет больше, чем во втором, потому что его площадь меньше. А раз меньше площадь сосуда, то меньше и его объем. Значит, давление зависит от объема следующим образом: чем больше объем, тем меньше давление, и наоборот.

При этом зависимость будет не линейная, а примет вот такой вид (при условии, что температура постоянна):

Зависимость давления от объема называется законом Бойля-Мариотта. Она экспериментально проверяется с помощью такой установки:

Объем шприца увеличивают с помощью насоса, а манометр измеряет давление. Эксперимент показывает, что при увеличении объема давление действительно уменьшается.

Зависимость давления от температуры

Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Исследования в этой области впервые провел французский изобретатель Жак Шарль в XVIII веке.

В ходе эксперимента газ нагревали в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Незначительным увеличением объема колбы при нагревании можно пренебречь, как и столь же незначительным изменением объема при смещении ртути в узкой манометрической трубке. Таким образом, объем газа можно считать неизменным.

Подогревая воду в сосуде, окружающем колбу, ученый измерял температуру газа термометром, а давление — манометром.

Эксперимент показал, что давление газа увеличивается с увеличением температуры. Это связано с тем, что при нагревании молекулы газа движутся быстрее, из-за чего чаще ударяются о стенки сосуда.

С температурой все проще. Зависимость давления от температуры при постоянных объеме и массе будет линейной:

Эта зависимость называется законом Шарля в честь ученого, открывшего ее.

Основное уравнение МКТ

Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами: массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа или кратко — основным уравнением МКТ.

В основе молекулярно-кинетической теории лежат три положения.

1. Все вещества образованы из мельчайших частиц — молекул, которые состоят из атомов.

   Молекулы химического вещества могут быть простыми и сложными, то есть состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.



2. Атомы и молекулы находятся в непрерывном хаотическом движении.


3. Частицы взаимодействуют друг с другом силами, которые имеют электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.

Мы уже выяснили, что причина давления газа на стенки — это удары молекул. Давление напрямую зависит от количества молекул — чем их больше, тем больше ударов о стенки и тем больше давление. А количество молекул в единице объема — это концентрация. Значит, давление газа зависит от концентрации.

Также давление пропорционально квадрату скорости, так как чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории для идеального газа имеет следующий вид.

Основное уравнение МКТ p = nkT или p — давление газа [Па] n — концентрация [м-3] T — температура газа [К] m0 — масса одной молекулы [кг] v — средняя квадратичная скорость [м/с]

Коэффициент 1/3 обусловлен трехмерностью пространства: во время хаотического движения молекул все три направления равноправны.

Важный нюанс: средняя квадратичная скорость сама по себе не в квадрате! Ее формула указана выше, а в основном уравнении МКТ (да и не только в нем) она возведена в квадрат. Это значит, что формулу средней квадратичной скорости нужно подставлять не вместо v2, а вместо v— и потом уже возводить эту формулу в квадрат. Это часто провоцирует путаницу.

Мы знаем, что кинетическая энергия вычисляется по следующей формуле:

Кинетическая энергия Ек = mv2/2 Ек — кинетическая энергия [Дж] m — масса тела [кг] v — скорость [м/с]

Для молекулы газа формула примет вид:

Средняя кинетическая энергия поступательного движения молекулы Ек = m0v2/2 Ек — средняя кинетическая энергия поступательного движения молекулы [Дж] m0 — масса молекулы [кг] v — скорость молекулы [м/с]

Из этой формулы можно выразить m₀v² и подставить в основное уравнение МКТ. Подставим и получим, что давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

Основное уравнение МКТ p — давление газа [Па] n — концентрация [м-3] E — средняя кинетическая энергия поступательного движения молекулы [Дж]

Хранение и транспортировка газов

Если нужно перевезти значительное количество газа из одного места в другое или если газ необходимо длительно хранить, его помещают в специальные прочные металлические сосуды. Из-за того, что при уменьшении объема увеличивается давление, газ можно закачать в небольшой баллон, но он должен быть очень прочным.

Сосуды, предназначенные для транспортировки газов, выдерживают высокие давления. Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.

Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать. Например, держать под прямыми лучами солнца или пытаться сделать в них отверстие — даже после использования.

Идеальный газ, параметры состояния, давление, температура, средняя квадратичная скорость. Основное уравнение молекулярно-кинетической теории

Тестирование онлайн

Идеальный газ

Это несуществующая физическая модель газа, который состоит из большого числа молекул, размеры которых ничтожно малы по сравнению со средними расстояниями между ними. Молекулы такого газа можно считать материальными точками, это означает, что их вращательное и колебательное движения не принимаются во внимание. Движение молекул происходит без столкновений с другими молекулами, подчиняется законам Ньютона. Соударения молекул со стенками сосуда являются абсолютно упругими.

Параметры состояния газа

Давление, температура и объем — параметры состояния газа. Или их называют макропараметрами. Температура — внешняя характеристика скоростей частиц газа. Давление — внешняя характеристика соударений со стенками, например, сосуда. Объем — место, куда заключены частицы газа. Газ занимает весь предоставленный ему объем. Существуют еще внешние параметры, например тела или поля, действующие на газ из вне.

Микропараметры (маленькие, внутренние характеристики) газа — это параметры, которые мы не можем оценить без специальных экспериментов, например, скорость и направление движения каждой молекулы газа.

Состояние термодинамической системы, когда все ее параметры при неизменных внешних условиях не изменяются со временем, называют равновесным.

Основное уравнение молекулярно-кинетической теории

Уравнение связывает микропараметры и макропараметры (давление, объем и температуру) идеального газа.

Рассмотрим идеальный газ, который находится в кубическом сосуде. Каждая молекула упруго сталкивается со стенкой сосуда, при этом изменятся ее импульс. Столкновение всех молекул со стенкой на макроуровне ощущается как давление газа на сосуд. В формулах будут присутствовать средние значения, потому что какая-то молекула движется быстрее, какая-то помедленнее, для того, чтобы оценить примерную скорость, будем брать средние значения.

Основное уравнение мкт имеет вид

Средний квадрат скорости молекул

Средняя квадратичная скорость v_кв молекул это квадратный корень из среднего квадрата скорости

Средняя кинетическая энергия молекул

Можно вывести формулы

Температура

Это макропараметр, который характеризует способность тел к теплопередаче. Если два тела разной температуры контактируют, то произойдет переход энергии или передача теплоты от более горячего к холодному. Установится тепловое равновесие, все части будут одинаковой температуры.

Температура характеризует интенсивность движения частиц, поэтому связана со средней кинетической энергией частиц. Из опыта известно, что средняя кинетическая энергия молекул не зависит от вида газа и определяется температурой.

Связь между температурами по шкале Цельсия и по шкале Кельвина

Уравнение состояния идеального газа — материалы для подготовки к ЕГЭ по Физике

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: модель идеального газа, связь между давлением и средней кинетической энергией теплового движения молекул идеального газа, связь температуры газа со средней кинетической энергией его частиц, уравнение , уравнение Менделеева—Клапейрона.

Из трёх агрегатных состояний вещества наиболее простым для изучения является газообразное. В достаточно разреженных газах расстояния между молекулами намного больше размеров самих молекул (тогда как в жидкостях и твёрдых телах молекулы «упакованы» весьма плотно).Поэтому силы взаимодействия между молекулами таких газов очень малы.

Для описания разреженных газов в физике используется модель идеального газа. В рамках этой модели делаются следующие допущения.

1. Пренебрегаем размерами молекул. Иными словами, молекулы газа считаются материальными точками.
2. Пренебрегаем взаимодействием молекул на расстоянии.
3. Соударения молекул друг с другом и со стенками сосуда считаем абсолютно упругими.

Таким образом, идеальный газ — это газ, частицы которого являются не взаимодействующими на расстоянии материальными точками и испытывают абсолютно упругие соударения друг с другом и со стенками сосуда.

Средняя кинетическая энергия частиц газа

Оказывается, что ключевую роль в описании идеального газа играет средняя кинетическая энергия его частиц.

Частицы газа двигаются с разными скоростями. Пусть в газе содержится частиц, скорости которых равны . Масса каждой частицы равна . Кинетические энергии частиц:

Средняя кинетическая энергия частиц газа это среднее арифметическое их кинетических энергий:

Последний множитель — это средний квадрат скорости, обозначаемый просто :

Тогда формула для средней кинетической энергии приобретает привычный вид:

(1)

Корень из среднего квадрата скорости называется средней квадратической скоростью:

Основное уравнение МКТ идеального газа

Cвязь между давлением газа и средней кинетической энергией его частиц называется основным уравнением молекулярно-кинетической теории идеального газа. Эта связь выводится из законов механики и имеет вид:

(2)

где — концентрация газа (число частиц в единице объёма). С учётом (1) имеем также:

(3)

Что такое ? Произведение массы частицы на число частиц в единице объёма даёт массу единицы объёма, то есть плотность: . Получаем третью разновидность основного уравнения:

(4)

Энергия частиц и температура газа

Можно показать, что при установлении теплового равновесия между двумя газами выравниваются средние кинетические энергии их частиц. Но мы знаем, что при этом становятся равны и температуры газов. Следовательно, температура газа — это мера средней кинетической энергии его частиц.

Собственно, ничто не мешает попросту отождествить эти величины и сказать, что температура газа — это средняя кинетическая энергия его молекул. В продвинутых курсах теоретической физики так и поступают. Определённая таким образом температура измеряется в энергетических единицах — джоулях.

Но для практических задач удобнее иметь дело с привычными кельвинами. Связь средней кинетической энергии частиц и абсолютной температуры газа даётся формулой:

(5)

где Дж/К — постоянная Больцмана.

Молекулярная физика. Основные положения МКТ. Основные понятия и формулы. Свойства идеального газа. Основное уравнение МКТ. Температура. Уравнение состояния идеального газа. Уравнение Менделеева-Клайперона. Газовые законы — изотерма, изобара, изохора

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа.  / / Молекулярная физика. Основные положения МКТ. Основные понятия и формулы. Свойства идеального газа. Основное уравнение МКТ. Температура. Уравнение состояния идеального газа. Уравнение Менделеева-Клайперона. Газовые законы — изотерма, изобара, изохора Поделиться:    Молекулярная физика. Основные положения МКТ. Основные понятия и формулы. Свойства идеального газа. Основное уравнение МКТ. Температура. Уравнение состояния идеального газа. Уравнение Менделеева-Клайперона. Газовые законы — изотерма, изобара, изохора Поиск в инженерном справочнике DPVA. Введите свой запрос: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Уравнение состояния идеального газа • Джеймс Трефил, энциклопедия «Двести законов мироздания»

Термодинамические характеристики идеального газа описываются одним простым уравнением.

Математическая запись универсального газового закона проста:

    pV = nRT *

Она содержит основные характеристики поведения газов: p, V и T — соответственно давление, объем и абсолютная температура газа (в градусах Кельвина), R — универсальная газовая постоянная, общая для всех газов, а n — число, пропорциональное числу молекул или атомов газа (так называемое число молей газа — см. Закон Авогадро).

Чтобы понять, как работает этот закон, давайте представим, что температура газа постоянна. В этом случае в правой части уравнения получается константа. Значит, произведение давления и объема при неизменной температуре оказывается неизменным. Повышение давления сопровождается уменьшением объема, и наоборот. Это не что иное, как закон Бойля—Мариотта — одна из первых экспериментально полученных формул, описывающих поведение газов. С другой стороны, при постоянном давлении (например, внутри воздушного шарика, где давление газа равно атмосферному) повышение температуры сопровождается увеличением объема. А это — закон Шарля, другая экспериментальная формула поведения газов. Закон Авогадро и закон Дальтона также являются следствиями универсального газового закона.

Этот закон представляет собой то, что в физике принято называть уравнением состояния вещества, поскольку он описывает характер изменения свойств вещества при изменении внешних условий. Строго говоря, этот закон в точности выполняется только для идеального газа. Идеальный газ представляет собой упрощенную математическую модель реального газа: молекулы считаются движущимися хаотически, а соударения между молекулами и удары молекул о стенки сосуда — упругими, то есть не приводящими к потерям энергии в системе. Такая упрощенная модель очень удобна, поскольку позволяет обойти очень неприятную трудность — необходимость учитывать силы взаимодействия между молекулами газа. И это себя оправдывает, поскольку в природных условиях поведение большинства реальных газов практически не отличается от поведения идеального газа — отклонения в поведении практически всех природных газов, например атмосферного азота и кислорода, от поведения идеального газа не превышают 1%. Это позволяет ученым спокойно включать уравнение состояния идеального газа даже в весьма сложные теоретические расчеты. Например, астрономы при моделировании горячих звезд обычно считают вещество звезды идеальным газом и весьма точно прогнозируют давления и температуры внутри них. (Заметьте, что вещество внутри звезды ведет себя как идеальный газ, хотя его плотность несопоставимо выше плотности любого вещества в земных условиях. А дело в том, что вещество звезды состоит из полностью ионизированных ядер водорода и гелия — то есть из частиц значительно меньшего диаметра, чем диаметр атомов земных газов.) В будущем, по мере совершенствования теоретических методов, возможно, будут выведены более точные уравнения для описания состояния реальных газов с учетом их характеристик на молекулярном уровне.

---

* Эта формула была получена в 1874 году Д. И. Менделеевым путем объединения закона Авогадро и общего газового закона (pV/T = const), сформулированного в 1834 году Б. П. Э. Клапейроном. Поэтому этот закон (в Европе, по крайней мере) принято называть законом Менделеева—Клапейрона. По существу, этот закон позволил ввести все ранее сделанные эмпирические заключения о характере поведения газов в рамки новой молекулярно-кинетической теории. (Примечание переводчика)

См. также:

Глава 13. Газовые законы

Задачи на газовые законы часто предлагаются школьникам на едином государственном экзамене. Для решения этих задач вполне достаточно знать уравнение состояния идеального газа (закон Клапейрона-Менделеева) и уметь использовать его алгебраически и геометрически (для построения графиков зависимости одних параметров газа от других) в простейших ситуациях. Кроме того, нужно понимать, как описываются смеси идеальных газов (закон Дальтона).

Уравнение, связывающее параметры газа друг с другом, называется уравнением состояния. Для идеального газа, взаимодействие молекул которого мало, уравнение состояния имеет вид

(13.1)

где — давление газа, — концентрация молекул газа (число молекул в единице объема), — постоянная Больцмана, — абсолютная (в шкале Кельвина) температура. Учитывая, что , где — число молекул газа, — объем сосуда, в котором находится газ (часто говорят объем газа), получим из (13.1)

(13.2)

Число молекул можно связать с количеством вещества газа : , где — число Авогадро. Поэтому формулу (13.2) можно переписать в виде

(13.2)

где произведение постоянных Авогадро и Больцмана обозначено как . Постоянная = 8,31 Дж/(К•моль) называется универсальной газовой постоянной. Количество вещества газа можно также выразить через его массу и молярную массу этого газа

(13.3)

С учетом (13.3) закон (13.2) можно переписать и в таком виде

(13.4)

Уравнение состояния идеального газа (13.1)-(13.4), которое также называется уравнением (или законом) Клапейрона-Менделеева, позволяет связывать параметры идеального газа и проследить за их изменением в тех или иных процессах.

В школьном курсе физики рассматриваются три изопроцесса, в которых один из трех параметров газа (давление, температура и объем) не изменяется. В изобарическом процессе не изменяется давление газа, в изотермическом — температура, в изохорическом — объем. Изопроцессам отвечают следующие графики зависимости давления от объема, давления от температуры, объема от температуры.

Для изобарического процесса

Первые два графика очевидны. Последний получается так. Из закона Клапейрона-Менделеева следует, что зависимость объема от температуры при постоянном давлении имеет вид

(13.5)

где — постоянная. Графиком функции (13.5) является прямая, продолжение которой проходит через начало координат.

Для изохорического процесса

Второй график следует из соотношения

(13.6)

где — постоянная при постоянном объеме.

Для изотермического процесса

Первый график следует из закона Клапейрона-Менделеева, который при постоянной температуре газа можно привести к виду

(13.7)

где — постоянная. Отсюда следует, что графиком зависимости от в изотермическом процессе является гипербола.

Важнейшее свойство уравнения состояния идеального газа (13.1)-(13.4) заключается в том, что «индивидуальность» газа никак не проявляется в этих законах — единственный параметр собственно газа, входящий в уравнение состояния, — это число молекул. Например, 1 моль гелия и 1 моль азота, находящиеся в одинаковых объемах и имеющие одинаковые температуры, оказывают одинаковое давление. Отсюда следует, что и давление смеси идеальных газов определяется суммарным числом молекул всех компонент смеси:

(13.8)

где — число молекул первой, второй, третьей и т.д. компонент смеси, — постоянная Больцмана, — абсолютная температура смеси, — объем сосуда. Величины , имеющие смысл давления каждой компоненты смеси при условии, что она имела бы такую же температуру и занимала бы весь объем, называются парциальными давлениями компонент. Закон (13.8) называется законом Дальтона. Рассмотрим теперь в рамках этих законов предложенные выше задачи.

В задаче 13.1.1 из уравнения состояния в форме (13.1), получаем для давления в конце процесса :

т.е. давление газа увеличилось в 6 раз (ответ 1).

Применяя закон Клапейрона-Менделеева (13.2) к первому и второму газам (задача 13.1.2), получаем

где — искомый объем. Сравнивая первую и вторую формулы, заключаем, что (ответ 1).

Закон Клапейрона-Менделеева для газа в начальном и конечном состояниях (задача 13.1.3) дает

где — неизвестная температура. Из сравнения этих формул получаем , т.е. температуру газа в сосуде нужно повысить вдвое (ответ 2).

Из закона Клапейрона-Менделеева для начального и конечного состояний газа в задаче 13.1.4 имеем

Отсюда , т.е. количество вещества газа в сосуде увеличилось в 1,25 раза (ответ 3).

Первым, кто понял, почему жидкость поднимается вместе с трубкой (задача 13.1.5), и почему «природа боится пустоты» (Аристотель), но только до определенного предела, был знаменитый итальянский физик, современник Г. Галилея Э. Торричелли. Давайте рассмотрим рассуждения Торричелли подробно. Основная идея Торричелли заключалась в том, что атмосферный воздух оказывает давление на все поверхности, с которыми он контактирует. В равновесии жидкость занимает такое положение, чтобы все воздействия на каждый ее элемент компенсировались. Если бы трубка была открыта (см. левый рисунок), то жидкость не поднялась бы в трубке. Действительно, в этом случае на бесконечно малый элемент жидкости в трубке около поверхности (выделен на рисунке) действовали бы сила со стороны атмосферного воздуха в трубке, направленная вниз. С другой стороны, атмосферный воздух действует и на остальную поверхность жидкости, и это воздействие благодаря закону Паскаля передается выделенному элементу жидкости в трубке снизу. Таким образом, воздействие воздуха на поверхность жидкости в трубке и на свободную поверхность жидкости компенсируют друг друга, если уровень жидкости в трубке совпадает с уровнем жидкости в остальном сосуде. Если же мы поднимаем трубку, выпустив из нее воздух, на рассматриваемый элемент жидкости воздух сверху не действует (его нет в трубке), поэтому воздействие воздуха на свободную поверхность жидкости приведет к тому, что жидкость войдет в трубку и заполнит ее. При вытаскивании трубки жидкость будет подниматься вслед за ней. Однако при дальнейшем поднятии трубки наступит такой момент, когда воздействие воздуха на свободную поверхность и столба жидкости в трубке сравняются (в этот момент атмосферное давление будет равно гидростатическому давлению жидкости в трубке на уровне свободной поверхности). Дальнейший подъем трубки уже не приведет к поднятию жидкости — атмосферное давление не сможет «держать» столб жидкости большей высоты. Для воды этот столб составляет около 10 м, для ртути, с которой и экспериментировал Э. Торричелли, — 76 сантиметров. Таким образом, жидкость в трубке поднимается благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля (ответ 4).

Сравнивая графики процессов 1, 2, 3 и 4, данные в условии задачи 13.1.6, с графиками изопроцессов, приведенными во введении к настоящей главе, заключаем, что: процесс 1 — изотермический, 2 — изохорический, 3 — изобарический. В процесс 4 меняются и давление, и объем, и температура газа (ответ 4).

В изотермическом процессе давление зависит от объема как ; на диаграмме этот процесс изображается гиперболой. Поэтому изотермическими являются процессы 1 и 3 (задача 13.1.7), но в процессе 1 объем газа убывает. Следовательно, изотермическим расширением является процесс 3 (ответ 3).

Изохорическим охлаждением в задаче 13.1.8 является процесс 4 (см. рисунок) В двух последних задачах этого варианта нужно с помощью закона Клапейрона-Менделеева вычислить один из параметров газа, если даны остальные параметры. В задаче 13.1.9 из закона Клапейрона-Менделеева

получим

(ответ 1).

В задаче 13.1.10 при вычислениях следует не забыть перевести температуру газа в Кельвины. Из закона Клапейрона-Менделеева находим

(ответ 1).

Из уравнения состояния в форме (13.2) следует, что при одинаковых объемах и температурах давление идеального газа определяется только полным числом молекул. Поэтому отношение давления водорода и гелия в задаче 13.2.1 равно 2 (ответ 2).

Поскольку перегородка в задаче 13.2.2 подвижная и находится в равновесии, давления газа в отсеках сосуда слева и справа от перегородки равны. Применяя к ним при этом условии закон Клапейрона-Менделеева, получим

для гелия

для азота

где температуры и массы газов по условию одинаковы. Деля эти уравнения друг на друга, находим отношение объемов частей сосуда

(ответ 4).

Если бы точки, отвечающие состояниям 1 и 2 в задаче 13.2.3, лежали на одной прямой, продолжение которой проходит через начало координат, то эти состояния принадлежали бы одной и той же изохоре, и, следовательно, объем газа в этих состояниях был одинаковым (см. формулу (13.6)). Поэтому для сравнения объемов этих состояний построим изохоры, проходящие через точки 1 и 2, и сравним отвечающие им объемы (см. рисунок; изохоры, проходящие через точки 1 и 2, показаны пунктиром).

Из формулы (13.6) следует, что чем больше объем, тем меньше коэффициент перед в зависимости (13.6), и, следовательно, меньше наклон соответствующей изохоры к оси температур. Поэтому изохоре 1 отвечает больший объем, чем изохоре 2, и, следовательно, объем газа в процессе 1-2 уменьшается (ответ 2).

Аналогичные рассуждения в задаче 13.2.4 показывают, что наибольшему давлению отвечает изобара, проходящая через точку (поскольку соответствующая прямая имеет наименьший наклон к оси температур; см. рисунок ниже). Поэтому правильный ответ в этой задаче — 3.

В закон Клапейрона-Менделеева входит абсолютная температура газа, поэтому данные в задаче 13.2.5 значения нужно перевести в Кельвины. В результате для отношения давлений газа в конечном и начальном состояниях получаем

(ответ 4).

Как следует из опыта, при приведении тел в тепловой контакт выравниваются их температуры. Это же касается и частей одного тела или даже компонент смеси газов (задача 13.2.6). Поэтому температуры компонент смеси будут одинаковы (ответ 1). Что касается парциальных давлений, плотностей или концентрации компонент смеси, то их значения зависят от количества молекул каждой компоненты смеси и могут быть различны.

Парциальное давление компонент смеси – это давление, которое оказывают только молекулы каждой компоненты. Как следует из формулы (13.8) парциальное давление любой компоненты можно найти, применяя только к ней закон Клапейрона-Менделеева и считая, что она имеет такую же температуру, как и вся смесь, и занимает такай же объем, как и вся смесь газов. Поэтому отношение парциальных давлений отдельных компонент смеси равно отношению количеств вещества (или числа молекул) этих компонент. Поэтому для отношения парциальных давлений углекислого газа и гелия в сосуде в задаче 13.2.7 имеем (ответ 2).

Как следует из закона Дальтона, давление смеси газов определяется полным количеством молекул в ней. Поэтому для анализа изменения давления смеси газов при протекании в ней химической реакции (задача 13.2.8) необходимо исследовать изменение числа молекул. Гелий не участвует в химической реакции — один моль гелия был и в начальном, и в конечном состоянии смеси. С озоном происходила реакция

т.е. из двух молекул озона в результате реакции получились три молекулы кислорода. Поэтому два моля озона превратились в три моля кислорода, и общее количество вещества смеси стало равно четырем молям. Поэтому давление смеси увеличивается в 4/3 раза (ответ 2).

Поскольку объемы и температуры газов одинаковы (задача 13.2.9), для сравнения их давлений необходимо сравнить число молекул в них. По условию в одном сосуде находится один моль азота, в другом 1 г водорода (т.е. половина моля) и 3 • 10²³ молекул гелия (тоже половина моля). Поэтому и в одном и в другом сосуде находятся одинаковые количества молекул, и, следовательно, давление газов в них одинаково (ответ 3).

Плотность газа (задача 13.2.10) можно найти из следующей цепочки формул

(ответ 4). Здесь — масса газа, — масса одной молекулы газа.

Закон об идеальном газе | Физика

Цели обучения

К концу этого раздела вы сможете:

• Сформулируйте закон идеального газа, используя молекулы и моль.
• Используйте закон идеального газа для расчета изменения давления, температуры, объема или количества молекул или молей в заданном объеме.
• Используйте число Авогадро для преобразования числа молекул в число молей.

Рисунок 1.Воздух внутри этого воздушного шара, летящего над Путраджайей, Малайзия, горячее, чем окружающий воздух. В результате воздушный шар испытывает подъемную силу, толкающую его вверх. (Источник: Кевин По, Flickr)

В этом разделе мы продолжаем исследовать термическое поведение газов. В частности, мы исследуем характеристики атомов и молекул, из которых состоят газы. (Большинство газов, например азот, N ₂ , и кислород, O ₂ , состоят из двух или более атомов. Мы в первую очередь будем использовать термин «молекула» при обсуждении газа, потому что этот термин также может применяться к одноатомные газы, такие как гелий.)

Газы легко сжимаются. Мы можем увидеть доказательства этого в Таблице 1 в Термическом расширении твердых тел и жидкостей, где вы заметите, что газы имеют самых больших коэффициента объемного расширения . Большие коэффициенты означают, что газы расширяются и сжимаются очень быстро при изменении температуры. Кроме того, вы заметите, что большинство газов расширяются с той же скоростью или имеют ту же скорость β . Это поднимает вопрос о том, почему все газы должны действовать почти одинаково, когда жидкости и твердые тела имеют сильно различающиеся скорости расширения.

Ответ кроется в большом разделении атомов и молекул в газах по сравнению с их размерами, как показано на рисунке 2. Поскольку атомы и молекулы имеют большие расстояния между ними, силами между ними можно пренебречь, кроме случаев, когда они сталкиваются друг с другом во время столкновений. . Движение атомов и молекул (при температурах значительно выше температуры кипения) происходит быстро, так что газ занимает весь доступный объем, и газы расширяются быстро. Напротив, в жидкостях и твердых телах атомы и молекулы расположены ближе друг к другу и весьма чувствительны к силам между ними.

Рис. 2. Как показано, атомы и молекулы в газе обычно широко разделены. Поскольку силы между ними на этих расстояниях довольно слабы, свойства газа больше зависят от количества атомов в единице объема и от температуры, чем от типа атома.

Чтобы получить некоторое представление о том, как давление, температура и объем газа связаны друг с другом, рассмотрим, что происходит, когда вы закачиваете воздух в изначально спущенную шину. Сначала объем шины увеличивается прямо пропорционально количеству впрыскиваемого воздуха без значительного увеличения давления в шине.Когда шина расширилась почти до своего полного размера, стенки ограничивают объемное расширение. Если продолжать закачивать в него воздух, давление возрастает. Давление будет еще больше увеличиваться, когда автомобиль едет, а шины двигаются. Большинство производителей указывают оптимальное давление в шинах для холодных шин. (См. Рисунок 3.)

Рис. 3. (a) Когда воздух закачивается в спущенную шину, его объем сначала увеличивается без значительного увеличения давления. (b) Когда шина заполнена до определенной точки, стенки шины сопротивляются дальнейшему расширению, и давление увеличивается с увеличением количества воздуха.(c) Когда шина накачана, ее давление увеличивается с температурой.

При комнатной температуре столкновениями между атомами и молекулами можно пренебречь. В этом случае газ называется идеальным газом, и в этом случае соотношение между давлением, объемом и температурой задается уравнением состояния, называемым законом идеального газа.

Закон об идеальном газе

Закон идеального газа гласит, что PV = NkT , где P — абсолютное давление газа, V — объем, который он занимает, N — количество атомов и молекул в газе. газа, а T — его абсолютная температура.Константа k называется постоянной Больцмана в честь австрийского физика Людвига Больцмана (1844–1906) и имеет значение k = 1,38 × 10 ⁻²³ Дж / К.

Закон идеального газа может быть выведен из основных принципов, но первоначально он был выведен из экспериментальных измерений закона Чарльза (объем, занимаемый газом, пропорционален температуре при фиксированном давлении) и закона Бойля (для фиксированной температуры, произведение PV является константой).В модели идеального газа объем, занимаемый его атомами и молекулами, составляет ничтожную долю от V . Закон идеального газа описывает поведение реальных газов в большинстве условий. (Обратите внимание, например, что N — это общее количество атомов и молекул, независимо от типа газа.)

Давайте посмотрим, как закон идеального газа согласуется с поведением заполнения шины при медленной прокачке и постоянной температуре. Сначала давление P по существу равно атмосферному давлению, а объем V увеличивается прямо пропорционально количеству атомов и молекул N , введенных в шину.Как только объем шины остается постоянным, уравнение PV = NkT предсказывает, что давление должно увеличиваться пропорционально числу N атомов и молекул .

Пример 1. Расчет изменений давления из-за изменений температуры: давление в шинах

Предположим, шина вашего велосипеда полностью накачана, с абсолютным давлением 7,00 × 10 ⁵ Па (манометрическое давление чуть менее 90,0 фунтов / дюйм ² ) при температуре 18,0 ° C.Какое давление будет после повышения температуры до 35,0ºC? Предположим, что нет заметных утечек или изменений объема.

Стратегия

Давление в шине меняется только из-за изменения температуры. Сначала нам нужно определить, что мы знаем и что мы хотим знать, а затем определить уравнение, которое нужно решить для неизвестного.

Нам известно начальное давление P ₀ = 7,00 × 10 ⁵ Па, начальная температура T ₀ = 18.0ºC, а конечная температура T _f = 35,0ºC. Мы должны найти конечное давление P _f . Как мы можем использовать уравнение PV = NkT ? На первый взгляд может показаться, что информации недостаточно, потому что объем V и количество атомов N не указаны. Что мы можем сделать, так это использовать уравнение дважды: P ₀ V ₀ = NkT ₀ и P _f V _f = NkT _f .Если мы разделим P _f V _f на P ₀ V ₀ , мы сможем получить уравнение, которое позволяет нам решить для P _f .

[латекс] \ displaystyle \ frac {P _ {\ text {f}} V _ {\ text {f}}} {P_0V_0} = \ frac {N _ {\ text {f}} kT _ {\ text {f}}} {N_0kT_0} \\ [/ латекс]

Поскольку громкость постоянна, V _f и V ₀ одинаковы, и они компенсируются. То же самое верно для N _f и N ₀ и k , что является константой.Следовательно,

[латекс] \ displaystyle \ frac {P _ {\ text {f}}} {P_0} = \ frac {T _ {\ text {f}}} {T_0} \\ [/ latex]

Затем мы можем изменить это, чтобы решить для P _f : [latex] P _ {\ text {f}} = P_0 \ frac {T _ {\ text {f}}} {T_0} \\ [/ latex] , Где температура должна быть в единицах кельвина, потому что T ₀ и T _f являются абсолютными температурами.

Решение

Преобразование температуры из Цельсия в Кельвин:

Т ₀ = (18.5 \ text {Pa} \\ [/ latex]

Обсуждение

Конечная температура примерно на 6% выше исходной температуры, поэтому конечное давление также примерно на 6% больше. Обратите внимание, что в законе идеального газа необходимо использовать абсолютное давление и абсолютное давление .

Установление соединений: домашний эксперимент — охлаждение воздушного шара

Надуйте баллон при комнатной температуре. Оставьте надутый баллон в холодильнике на ночь.Что происходит с воздушным шаром и почему?

Пример 2. Расчет количества молекул в кубическом метре газа

Сколько молекул содержится в типичном объекте, таком как газ в шине или вода в напитке? Мы можем использовать закон идеального газа, чтобы дать нам представление о типичных размерах N .

Вычислите количество молекул в кубическом метре газа при стандартной температуре и давлении (STP), которое определяется равным 0ºC и атмосферному давлению.

Стратегия

Поскольку давление, объем и температура заданы, мы можем использовать закон идеального газа PV = NkT , чтобы найти N .{25} \ text {молекулы} \\ [/ latex]

Обсуждение

Это число, несомненно, большое, учитывая, что газ — это в основном пустое пространство. N огромен даже в небольших объемах. Например, 1 см ³ газа на STP содержит 2,68 × 10 ¹⁹ молекул. Еще раз отметим, что N одинаков для всех типов или смесей газов.

Родинки и число Авогадро

Иногда при измерении количества вещества удобно работать с единицей, отличной от молекул. моль (сокращенно моль) определяется как количество вещества, которое содержит столько атомов или молекул, сколько атомов содержится ровно в 12 граммах (0,012 кг) углерода-12. Фактическое количество атомов или молекул в одном моле называется числом Авогадро ( N _A ) по признанию итальянского ученого Амедео Авогадро (1776–1856). Он разработал концепцию мола, основываясь на гипотезе о том, что равные объемы газа при одинаковом давлении и температуре содержат равное количество молекул.То есть количество не зависит от типа газа. Эта гипотеза подтвердилась, и значение числа Авогадро составляет N _A = 6,02 × 10 ²³ моль ^-1 .

Число Авогадро

Один моль всегда содержит 6,02 × 10 ²³ частиц (атомов или молекул), независимо от элемента или вещества. Моль любого вещества имеет массу в граммах, равную его молекулярной массе, которую можно вычислить из атомных масс, указанных в периодической таблице элементов.

N _A = 6,02 × 10 ²³ моль ⁻¹

Рис. 4. Насколько велика родинка? На макроскопическом уровне один моль мячей для настольного тенниса покроет Землю на глубину около 40 км.

Проверьте свое понимание

Активным ингредиентом таблетки Тайленола является 325 мг ацетаминофена (C ₈ H ₉ NO ₂ ). Найдите количество активных молекул парацетамола в одной таблетке.

Решение

Сначала нам нужно вычислить молярную массу (массу одного моля) ацетаминофена.{-3} \ text {moles} \\ [/ latex]

Затем используйте число Авогадро, чтобы вычислить количество молекул.

N = (2,15 × 10 ⁻³ моль) (6,02 × 10 ²³ молекулы / моль) = 1,30 × 10 ²¹ молекулы

Пример 3. Расчет молей на кубический метр и литров на моль

Рассчитайте следующее:

1. Количество молей в 1,00 м ³ газа на СТП
2. Количество литров газа на моль.3} = 22,5 \ text {л / моль} \ [/ латекс]

Обсуждение

Это значение очень близко к принятому значению 22,4 л / моль. Небольшая разница связана с ошибками округления, вызванными использованием трехзначного ввода. Опять же, это число одинаково для всех газов. Другими словами, он не зависит от газа.

(Средняя) молярная масса воздуха (примерно 80% N ₂ и 20% O ₂ составляет M = 28,8 г. Таким образом, масса одного кубического метра воздуха равна 1,28 кг.Если гостиная имеет размеры 5 м × 5 м × 3 м, масса воздуха внутри комнаты составляет 96 кг, что является типичной массой человека.

Проверьте свое понимание

Плотность воздуха при стандартных условиях ( P, = 1 атм и T, = 20ºC) составляет 1,28 кг / м ³ . При каком давлении будет плотность 0,64 кг / м ³ , если температура и количество молекул остаются постоянными?

Решение

Лучший способ подойти к этому вопросу — подумать о том, что происходит.Если плотность упадет до половины от первоначального значения и никакие молекулы не потеряны, объем должен удвоиться. Если мы посмотрим на уравнение PV = NkT , мы увидим, что при постоянной температуре давление обратно пропорционально объему. Следовательно, если объем увеличится вдвое, давление должно упасть до половины своего первоначального значения, и P _f = 0,50 атм.

Закон об идеальном газе, переформулированный с использованием молей

Очень распространенное выражение закона идеального газа использует число молей, n , а не число атомов и молекул, N .Начнем с закона идеального газа, PV = NkT , умножим и разделим уравнение на число Авогадро N _A . Это дает [latex] PV = \ frac {N} {N _ {\ text {A}}} N _ {\ text {A}} kT \\ [/ latex].

Обратите внимание, что [латекс] n = \ frac {N} {N _ {\ text {A}}} \\ [/ latex] — это количество молей. Мы определяем универсальную газовую постоянную R = N _A k и получаем закон идеального газа в молях.

Закон идеального газа (в молях)

Закон идеального газа (в молях): PV = nRT .

Числовое значение R в единицах СИ: R = N _A k = (6,02 × 10 ²³ моль ⁻¹ ) (1,38 × 10 ⁻²³ Дж / К ) = 8,31 Дж / моль · К.

В других единицах,

R = 1,99 кал / моль · K

R = 0,0821 л · атм / моль · K

Вы можете использовать любое значение R , наиболее подходящее для конкретной задачи.

Пример 4. Расчет количества молей: газ в шине велосипеда

Сколько молей газа в шине велосипеда объемом 2.00 × 10 ⁻³ м ³ (2,00 л), давление 7,00 × 10 ⁵ Па (манометрическое давление чуть менее 90,0 фунтов / дюйм ² ) и при температуре 18,0 ° C?

Стратегия

Определите известные и неизвестные и выберите уравнение для решения неизвестного. В этом случае мы решаем закон идеального газа, PV = nRT , для числа молей n .

Решение

Определить известных:

[латекс] \ begin {array} {lll} P & = & 7.3 \ right)} {\ left (8.31 \ text {J / mol} \ cdot \ text {K} \ right) \ left (291 \ text {K} \ right)} \\\ text {} & = & 0. 579 \ text {mol} \ end {array} \\ [/ latex]

Обсуждение

Наиболее удобный выбор для R в этом случае — 8,31 Дж / моль · К, потому что наши известные количества выражены в единицах СИ. Давление и температура получены из начальных условий в Примере 1, но мы получили бы тот же ответ, если бы использовали окончательные значения.

Закон идеального газа можно рассматривать как еще одно проявление закона сохранения энергии (см. Сохранение энергии).Работа, выполняемая с газом, приводит к увеличению его энергии, увеличению давления и / или температуры или уменьшению объема. Эту повышенную энергию также можно рассматривать как увеличенную внутреннюю кинетическую энергию с учетом атомов и молекул газа.

Закон идеального газа и энергия

Давайте теперь исследуем роль энергии в поведении газов. Когда вы накачиваете велосипедную шину вручную, вы выполняете работу, многократно прилагая силу на расстоянии. Эта энергия идет на повышение давления воздуха внутри шины и повышение температуры насоса и воздуха.

Закон идеального газа тесно связан с энергией: единицы измерения с обеих сторон — джоули. Правая часть закона идеального газа в PV = NkT равна NkT . Этот термин примерно соответствует количеству поступательной кинетической энергии N атомов или молекул при абсолютной температуре T , как мы формально увидим в «Кинетической теории: атомное и молекулярное объяснение давления и температуры». Левая часть закона идеального газа — это PV , которое также имеет единицы измерения в джоулях.Из нашего исследования жидкостей мы знаем, что давление — это один из видов потенциальной энергии на единицу объема, поэтому давление, умноженное на объем, является энергией. Важным моментом является то, что в газе есть энергия, связанная как с его давлением, так и с его объемом. Энергия может изменяться, когда газ выполняет работу по мере расширения — это мы исследуем в разделе «Методы тепло- и теплопередачи» — аналогично тому, что происходит в бензиновых или паровых двигателях и турбинах.

Стратегия решения проблем: Закон об идеальном газе

Шаг 1. Изучите ситуацию, чтобы определить, что речь идет об идеальном газе. Большинство газов почти идеальны.

Шаг 2. Составьте список того, какие количества указаны или могут быть выведены из проблемы, как указано (определить известные количества). Преобразуйте известные значения в соответствующие единицы СИ (K для температуры, Па для давления, m ³ для объема, молекул для N и молей для n ).

Шаг 3. Определите, что именно необходимо определить в проблеме (определите неизвестные количества).Письменный список полезен.

Шаг 4. Определите, известно ли количество молекул или количество молей, чтобы решить, какую форму закона идеального газа использовать. Первая форма — PV = NkT и включает N , количество атомов или молекул. Вторая форма — PV, = nRT и включает n , количество молей.

Шаг 5. Решите закон идеального газа для количества, которое необходимо определить (неизвестное количество).Вам может потребоваться соотношение конечных состояний к начальным состояниям, чтобы исключить неизвестные количества, которые остаются фиксированными.

Шаг 6. Подставьте известные величины вместе с их единицами измерения в соответствующее уравнение и получите численные решения с указанием единиц. Обязательно используйте абсолютную температуру и абсолютное давление.

Шаг 7. Проверьте ответ, чтобы узнать, разумен ли он: имеет ли он смысл?

Проверьте свое понимание

Жидкости и твердые вещества имеют плотность примерно в 1000 раз больше, чем газы.Объясните, как это означает, что расстояния между атомами и молекулами в газах примерно в 10 раз больше, чем размер их атомов и молекул.

Решение

Атомы и молекулы в твердых телах и жидкостях расположены близко друг к другу. В газах они разделены пустым пространством. Таким образом, газы имеют меньшую плотность, чем жидкости и твердые тела. Плотность — это масса на единицу объема, а объем связан с размером тела (например, сферы) в кубе. Таким образом, если расстояние между атомами и молекулами увеличивается в 10 раз, то занимаемый объем увеличивается в 1000 раз, а плотность уменьшается в 1000 раз.

Сводка раздела

• Закон идеального газа связывает давление и объем газа с количеством молекул газа и температурой газа.
• Закон идеального газа можно записать через количество молекул газа: PV = NkT , где P — давление, V — объем, T — температура, N — число. молекул, k — постоянная Больцмана k = 1,38 × 10 ^–23 Дж / K.
• Моль — это количество атомов в образце углерода-12 массой 12 г.
• Число молекул в кроте называется числом Авогадро NA , NA = 6,02 × 10 ²³ моль ^-1 .
• Моль любого вещества имеет массу в граммах, равную его молекулярной массе, которая может быть определена из периодической таблицы элементов.
• Закон идеального газа также может быть записан и решен в терминах числа молей газа: PV = nRT , где n — число молей, а R — универсальная газовая постоянная, R = 8 .31 Дж / моль ⋅ К.
• Закон идеального газа обычно действует при температурах, значительно превышающих температуру кипения.

Концептуальные вопросы

Узнайте человеческое население Земли. Есть ли на Земле крот людей? Если средняя масса человека 60 кг, рассчитайте массу родинки людей. Как соотносится масса крота людей с массой Земли?

При каких обстоятельствах вы ожидаете, что газ будет вести себя значительно иначе, чем предсказывает закон идеального газа?

Газовый термометр постоянного объема содержит фиксированное количество газа.Какое свойство газа измеряется, чтобы указать его температуру?

Задачи и упражнения

1. Манометрическое давление в шинах вашего автомобиля составляет 2,50 × 10 ⁵ Н / м ² при температуре 35,0ºC, когда вы едете на пароме на Аляску. Какое у них манометрическое давление позже, когда их температура упадет до –40,0ºC?
2. Преобразование абсолютного давления 7,00 × 10 ⁵ Н / м ² в манометрическое давление в фунтах / дюйм ² .(Было заявлено, что это значение чуть меньше 90,0 фунтов / дюйм ² в Примере 4. Это так?)
3. Предположим, что газовая лампа накаливания изготовлена ​​так, что газ внутри колбы находится под атмосферным давлением, когда колба имеет температуру 20,0 ° C. (a) Найдите манометрическое давление внутри такой колбы, когда она горячая, при условии, что ее средняя температура составляет 60,0ºC (приблизительное значение), и пренебрегая любыми изменениями в объеме из-за теплового расширения или утечки газа. (b) Фактическое конечное давление для лампочки будет меньше, чем рассчитано в части (а), потому что стеклянная колба расширится.Каким будет фактическое конечное давление с учетом этого? Это незначительная разница?
4. Большие шары, наполненные гелием, используются для подъема научного оборудования на большие высоты. (а) Каково давление внутри такого воздушного шара, если он начинается на уровне моря с температурой 10,0ºC и поднимается на высоту, на которой его объем в двадцать раз превышает первоначальный объем, а его температура составляет –50,0ºC? б) Какое манометрическое давление? (Предположим, что атмосферное давление постоянно.)
5. Подтвердите, что единицы nRT являются единицами энергии для каждого значения R: (a) 8.31 Дж / моль K, (b) 1,99 кал / моль K, и (c) 0,0821 л атм / моль ⋅ K.
6. В тексте было показано, что N / V = 2,68 × 10 ²⁵ м ⁻³ для газа на СТП. (a) Покажите, что эта величина эквивалентна N / V = 2,68 × 10 ¹⁹ см ⁻³ , как указано. (b) Примерно сколько атомов содержится в одном мкм ³ (кубический микрометр) в STP? (c) Что ваш ответ на часть (b) подразумевает разделение атомов и молекул?
7. Посчитайте количество родинок в 2.00-литровый объем воздуха в легких обычного человека. Учтите, что температура воздуха 37,0 ° C (температура тела).
8. У пассажира самолета 100 см. ³ воздуха в желудке непосредственно перед вылетом из аэропорта на уровне моря. Какой объем будет в воздухе на крейсерской высоте, если давление в салоне упадет до 7,50 × 10 ⁴ Н / м ² ?
9. (a) Каков объем (в км ³ ) числа песчинок Авогадро, если каждое зерно представляет собой куб и имеет стороны равные 1.0 мм в длину? (b) Сколько километров протяженностью пляжей это покрыло бы, если бы ширина пляжа в среднем составляла 100 м, а глубина — 10,0 м? Пренебрегайте воздушными промежутками между зернами.
10. Дорогая вакуумная система может достичь давления всего 1,00 × 10 ^–7 Н / м ² при 20ºC. Сколько атомов в кубическом сантиметре при таком давлении и температуре?
11. Плотность атомов газа в определенном месте в космосе над нашей планетой составляет примерно 1,00 × 10 ¹¹ м ⁻³ , а давление равно 2.75 × 10 ^–10 Н / м ² в этом пространстве. Какая там температура?
12. Велосипедная шина имеет давление 7,00 × 10 ⁵ Н / м ² при температуре 18,0 ° C и содержит 2,00 л газа. Каким будет его давление, если вы выпустите воздух объемом 100 см3 при атмосферном давлении? Предположим, что температура и объем шины остаются постоянными.
13. Газовый баллон высокого давления содержит 50,0 л токсичного газа при давлении 1,40 × 10 ⁷ Н / м ² и температуре 25.0ºC. Его клапан протекает после падения баллона. Цилиндр охлаждается до температуры сухого льда (–78,5 ° C), чтобы снизить скорость утечки и давление, чтобы его можно было безопасно отремонтировать. (а) Каково конечное давление в резервуаре, если предположить, что утечка газа при охлаждении незначительна, и что фазового перехода нет? б) Какое будет конечное давление, если одна десятая часть газа улетучится? (c) До какой температуры необходимо охладить резервуар, чтобы снизить давление до 1,00 атм (при условии, что газ не меняет фазу и что во время охлаждения нет утечки)? (d) Является ли охлаждение резервуара практическим решением?
14. Найдите количество родинок в 2.00 л газа при 35,0ºC и давлении 7,41 × 10 ⁷ Н / м ² .
15. Вычислите глубину, на которую количество мячей Авогадро для настольного тенниса покроет Землю. Каждый шар имеет диаметр 3,75 см. Предположим, что пространство между шарами добавляет дополнительные 25,0% к их объему, и предположим, что они не раздавлены собственным весом.
16. (a) Каково манометрическое давление в автомобильной шине 25,0 ° C, содержащей 3,60 моль газа в объеме 30,0 л? (b) Каким будет его манометрическое давление, если вы добавите 1.00 л газа первоначально при атмосферном давлении и 25,0 ° C? Предположим, что температура возвращается к 25,0 ° C, а объем остается постоянным.
17. (a) В глубоком космосе между галактиками плотность атомов всего лишь 10 ⁶ атомов / м ³ , а температура — холодная 2,7 К. Что такое давление? б) Какой объем (в м ³ ) занимает 1 моль газа? (c) Если этот объем является кубом, какова длина его сторон в километрах?

Глоссарий

закон идеального газа: физический закон, который связывает давление и объем газа с числом молекул газа или числом молей газа и температурой газа

постоянная Больцмана: k , физическая постоянная, которая связывает энергию с температурой; к = 1.38 × 10 ^–23 Дж / К

Число Авогадро: NA , количество молекул или атомов в одном моль вещества; NA = 6,02 × 10 ²³ частиц / моль

моль: количество вещества, масса которого (в граммах) равна его молекулярной массе

Избранные решения проблем и упражнения

1. {2} \ right) \\ & = & \ text {N} \ cdot \ text {m} = \ text {J} \ конец {массив} \\ [/ латекс]

7.7,86 × 10 ⁻² моль

9. (а) 6.02 × 10 ⁵ км ³ ; (б) 6,02 × 10 ⁸ км

11. -73.9ºC

13. а) 9,14 × 10 ⁶ Н / м ² ; б) 8,23 × 10 ⁶ Н / м ² ; (в) 2,16 К; (d) Нет. Требуемая конечная температура слишком низкая, чтобы ее можно было легко достичь для большого объекта.

15. 41 км

17. (а) 3,7 × 10 ⁻¹⁷ Па; б) 6.0 × 10 ¹⁷ м ³ ; (в) 8.4 × 10 ² км

Калькулятор закона идеального газа

Этот калькулятор закона идеального газа поможет вам определить свойства идеального газа, подверженного изменениям давления, температуры или объема. Прочтите, чтобы узнать о характеристиках идеального газа, о том, как использовать уравнение закона идеального газа и об определении постоянной идеального газа.

Что такое идеальный газ

Идеальный газ — это особый случай любого газа, который удовлетворяет следующим условиям:

• Газ состоит из большого количества молекул, которые перемещаются беспорядочно.
• Все молекулы — точечные частицы (они не занимают места).
• Молекулы не взаимодействуют, кроме столкновения.
• Все столкновения между частицами газа совершенно упругие.
• Частицы подчиняются законам движения Ньютона.

Уравнение закона идеального газа

Все свойства идеального газа суммируются в одной формуле вида:

пВ = nRT

где:

• p — давление газа, измеренное в Па;
• V — объем газа, измеряемый в м³;
• n — количество вещества, измеренное в молях;
• R — идеальная газовая постоянная; и
• T — температура газа в градусах Кельвина.

Чтобы найти любое из этих значений, просто введите другие в калькулятор закона идеального газа.

Например, если вы хотите рассчитать объем 40 молей газа под давлением 1013 гПа и при температуре 250 K, результат будет равен:

V = nRT / p = 40 * 8,3144598 * 250/101300 = 0,82 м³ .

Постоянная идеального газа

Газовая постоянная (символ R) также называется молярной или универсальной постоянной. Он используется во многих фундаментальных уравнениях, таких как закон идеального газа.

Значение этой постоянной составляет 8,3144626 Дж / (моль · К) .

Газовая постоянная часто определяется как произведение постоянной Больцмана k (которая связывает кинетическую энергию и температуру газа) на число Авогадро (количество атомов в моль вещества):

R = N A k = (6,02214076 × 10 23 / моль) * (1,38064852 × 10 -23 Дж / К) = 8,3144626 Дж / (моль · К)

Этот калькулятор атмосферного давления на высоте может оказаться полезным и для вас.

12.4: Закон идеального газа — Physics LibreTexts

учебных целей

• Опишите, как был получен закон идеального газа.

Закон идеального газа — это уравнение состояния гипотетического идеального газа (иллюстрация приведена в). В идеальном газе нет взаимодействия молекулы с молекулой, и допускаются только упругие столкновения. Это хорошее приближение к поведению многих газов во многих условиях, хотя у него есть несколько ограничений.Впервые это было сформулировано Эмилем Клапейроном в 1834 году как сочетание закона Бойля и закона Чарльза.

Атомы и модули в газе : Атомы и молекулы в газе обычно широко разделены, как показано. Поскольку силы между ними на этих расстояниях довольно малы, они часто описываются законом идеального газа.

Эмпирический вывод

Закон Бойля гласит, что давление P и объем V данной массы ограниченного газа обратно пропорциональны:

\ [\ mathrm {P∝ \ dfrac {1} {V},} \]

, в то время как закон Чарльза гласит, что объем газа пропорционален абсолютной температуре T газа при постоянном давлении

\ [\ mathrm {V∝T.} \]

Объединив два закона, мы получим

\ [\ mathrm {\ dfrac {PV} {T} = C,} \]

, где C — постоянная величина, прямо пропорциональная количеству газа n (представляющая количество молей).

Коэффициент пропорциональности — это универсальная газовая постоянная R, то есть \ (\ mathrm {C = nR} \).

Отсюда и закон идеального газа

\ [\ mathrm {PV = nRT} \]

Эквивалентно его можно записать как \ (\ mathrm {PV = NkT} \),

где k — постоянная Больцмана, а N — количество молекул.

(Поскольку N = nN _A , вы можете видеть, что \ (\ mathrm {R = N_ {Ak}} \), где N _A — число Авогадро.)

Обратите внимание, что эмпирический вывод не учитывает микроскопические детали. Однако это уравнение может быть выведено из первых принципов классической термодинамики (что выходит за рамки этого атома).

Версия для микроскопа

Мы видели в Атоме в «Происхождении давления», что

\ [\ mathrm {P = \ dfrac {Нм \ bar {v ^ 2}} {3V},} \]

где P — давление, N — количество молекул, m — масса молекулы, v — скорость молекул, а V — объем газа.2}} \]

Изотермы

Изотермический процесс — это изменение системы, в которой температура остается постоянной: \ (\ mathrm {ΔT = 0} \).

учебных целей

• Укажите условия, при которых могут происходить изотермические процессы.

Изотермический процесс — это изменение системы, в которой температура остается постоянной: ΔT = 0. Обычно это происходит, когда система находится в контакте с внешним тепловым резервуаром (термостатом), и изменение происходит достаточно медленно, чтобы позволить системе для постоянной адаптации к температуре резервуара за счет теплообмена.Напротив, адиабатический процесс происходит, когда система не обменивается теплом с окружающей средой (Q = 0). Другими словами, в изотермическом процессе значение ΔT = 0, но Q ≠ 0, а в адиабатическом процессе ΔT ≠ 0, но Q = 0.

Для идеального газа произведение PV (P: давление, V: объем) является постоянным, если газ поддерживается в изотермических условиях (закон Бойля). Согласно закону идеального газа, значение постоянной равно NkT, где N — количество молекул газа, а k — постоянная Больцмана.

Это означает, что выполняется \ (\ mathrm {p = \ frac {NkT} {V} = \ frac {Constant} {V}} \).

Семейство кривых, генерируемых этим уравнением, показано на графике, представленном на. Каждая кривая называется изотермой. Такие графики называются индикаторными диаграммами — они впервые использовались Джеймсом Ваттом и другими для мониторинга эффективности двигателей. Температура, соответствующая каждой кривой на рисунке, увеличивается от левого нижнего угла к правому верхнему.

Изотермы идеального газа : Несколько изотерм идеального газа на фотоэлектрической диаграмме.{V_B} PdV.} \]

(Это уравнение получено в нашем Атоме для «Постоянного давления» в соответствии с кинетической теорией. Обратите внимание, что \ (\ mathrm {P = \ frac {F} {A}} \). Это определение согласуется с нашим определением работы как силы умножить на расстояние.)

Для изотермического обратимого процесса этот интеграл равен площади под соответствующей изотермой давление-объем и обозначен синим цветом in для идеального газа. Опять же, применяется \ (\ mathrm {P = \ frac {nRT} {V}} \), и если T является постоянным (поскольку это изотермический процесс), мы имеем:

Работа, выполненная газом во время расширения : Синяя область представляет «работу», совершаемую газом во время расширения для этого изотермического изменения.{V_B} \ dfrac {NkT} {V} dV} \\ & \ mathrm {= NkT \ ln \ dfrac {⁡V_B} {V_A}.} \ End {align} \]

По соглашению, работа определяется как работа, которую система выполняет в своей среде. Если, например, система расширяется поршнем, движущимся в направлении силы, приложенной внутренним давлением газа, то работа считается положительной. Поскольку эта работа выполняется за счет использования внутренней энергии системы, в результате внутренняя энергия уменьшается. И наоборот, если окружающая среда воздействует на систему так, что ее внутренняя энергия увеличивается, эта работа считается отрицательной (подробности о внутренней энергии см. В нашем Атоме «Внутренняя энергия идеального газа»).

Постоянное давление

Изобарический процесс — это термодинамический процесс, в котором давление остается постоянным (при постоянном давлении работа, выполняемая газом, равна \ (\ mathrm {PΔV} \)).

учебных целей

• Опишите поведение одноатомного газа во время изобарных процессов.

При определенных ограничениях (например, давлении) газы могут расширяться или сжиматься; в зависимости от типа ограничения конечное состояние газа может измениться. Например, идеальный газ, который расширяется при постоянной температуре (так называемый изотермический процесс), будет существовать в другом состоянии, чем газ, который расширяется при постоянном давлении (так называемый изобарический процесс).Этот Атом обращается к изобарическому процессу и коррелированным терминам. Мы обсудим изотермический процесс в следующем атоме.

Изобарический процесс

Изобарный процесс — это термодинамический процесс, в котором давление остается постоянным: \ (\ mathrm {ΔP = 0} \). Для идеального газа это означает, что объем газа пропорционален его температуре (исторически это называется законом Чарльза). Давайте рассмотрим случай, когда газ действительно воздействует на поршень при постоянном давлении P, ссылаясь на рис. 1 в качестве иллюстрации.Поскольку давление постоянно, прилагаемая сила постоянна, а выполненная работа выражается как W = Fd, где F (= PA) — это сила, прилагаемая к поршню со стороны давления, а d — смещение поршня. Следовательно, работа, совершаемая газом (Вт), равна:

\ [\ mathrm {W = PAd} \]

Поскольку изменение объема цилиндра равно его площади поперечного сечения A, умноженной на смещение d, мы видим, что Ad = ΔV, изменение объема. Таким образом,

\ [\ mathrm {W = PΔV} \]

(как видно на рис. 2 — изобарный процесс).Примечание: если ΔV положительно, тогда W положительно, что означает, что работа выполняется газом во внешнем мире. Используя закон идеального газа \ (\ mathrm {PV = NkT (P = const)} \),

Рис. 2 : График зависимости давления от объема для постоянного давления или изобарического процесса. Площадь под кривой равна работе, совершаемой газом, поскольку W = PΔV.

\ [\ mathrm {W = NkΔT} \]

(уравнение 1) для идеального газа, подвергающегося изобарическому процессу.

Одноатомный газ

Согласно первому закону термодинамики,

\ [\ mathrm {Q = ΔU + W} \]

(Ур.2), где W — работа, совершаемая системой, U — внутренняя энергия, Q — тепло. Закон гласит, что тепло, передаваемое системе, действительно работает, но также изменяет внутреннюю энергию системы. Так как,

\ (\ mathrm {U = \ frac {3} {2} NkT} \) для одноатомного газа, мы получаем \ (\ mathrm {ΔU = \ frac {3} {2} NkΔT} \)

(уравнение 3; подробности о внутренней энергии см. В нашем разделе «Внутренняя энергия идеального газа»). Используя уравнения 1 и 3, уравнение. 2 можно записать как:

\ (\ mathrm {Q = \ frac {5} {2} NkΔT} \) для одноатомного газа в изобарическом процессе.

Удельная теплоемкость

Удельная теплоемкость при постоянном давлении определяется следующим уравнением:

\ (\ mathrm {Q = ncPΔT} \)

Здесь n — количество частиц в газе, выраженное в молях. Отметив, что \ (\ mathrm {N = N_An} \) и \ (\ mathrm {R = kN_A} \) _{(N A : число Авогадро, R: универсальная газовая постоянная), мы получаем:}

\ (\ mathrm {c_P = \ frac {5} {2} kN_A = \ frac {5} {2} R} \) для одноатомного газа.

Решение проблем

С помощью закона идеального газа мы можем вычислить давление, объем или температуру, а также количество молей газа при идеальных термодинамических условиях.

учебных целей

• Укажите шаги, используемые для решения уравнения идеального газа.

Закон идеального газа — это уравнение состояния гипотетического идеального газа. Это хорошее приближение к поведению многих газов во многих условиях, хотя у него есть несколько ограничений. Он наиболее точен для одноатомных газов при высоких температурах и низких давлениях.

Закон идеального газа имеет вид:

\ [\ mathrm {PV = nRT,} \]

, где R — универсальная газовая постоянная, и с ее помощью мы можем найти значения давления P, объема V, температуры T или числа молей n при определенных идеальных термодинамических условиях . Обычно вам дают достаточно параметров, чтобы вычислить неизвестное. Вариации уравнения идеального газа могут помочь легко решить проблему. Вот несколько общих советов.

Закон идеального газа также может иметь форму:

\ [\ mathrm {PV = NkT,} \]

где N — количество частиц в газе, а k — постоянная Больцмана.

Для решения уравнения идеального газа:

1. Запишите всю информацию, которую вы знаете о газе.
2. При необходимости преобразуйте известные значения в единицы СИ.
3. Выберите соответствующее уравнение закона газа, которое позволит вам вычислить неизвестную переменную.
4. Подставьте известные значения в уравнение. Рассчитайте неизвестную переменную.

Помните, что общее уравнение газа применимо только в том случае, если молярное количество газа фиксировано. Например, если газ смешивается с другим газом, вам, возможно, придется применить уравнение отдельно для отдельных газов.

Пример

Представим, что в начале пути шина грузовика имеет объем 30 000 см ³ и внутреннее давление 170 кПа.Температура шины составляет 16 C. К концу поездки объем шины увеличился до 32 000 см ³ , а температура воздуха внутри шины составляет 40 ^∘ C. Что такое давление в шинах в конце пути?

Давление в шинах : Давление в шинах может значительно измениться во время эксплуатации автомобиля. В основном это связано с изменением температуры воздуха в шинах.

Решение:

Шаг 1.Запишите всю информацию, которую вы знаете о газе: P ₁ = 170 кПа и P ₂ неизвестно. V ₁ = 30 000 см ³ и V ₂ = 32 000 см ³ . T ₁ = 16 ^∘ C и T ₂ = 40 ^∘ C.

Шаг 2. Преобразуйте известные значения в единицы СИ, если необходимо: Здесь температуру необходимо перевести в Кельвины. Следовательно, T ₁ = 16 + 273 = 289 K, T ₂ = 40 + 273 = 313 K

Шаг 3.Выберите соответствующее уравнение закона газа, которое позволит вам вычислить неизвестную переменную: Мы можем использовать общее уравнение газа для решения этой проблемы: \ (\ mathrm {\ frac {P_1V_1} {T_1} = \ frac {P_2V_2} {T_2} } \).

Следовательно, \ (\ mathrm {P_2 = \ frac {P_1 \ times V_1 \ times T_2} {T_1 \ times V_2}} \).

Шаг 4. Подставьте известные значения в уравнение. Вычислить неизвестную переменную:

\ [\ mathrm {P_2 = \ dfrac {170 \ times 30 000 \ times 313} {289 \ times 32 000} = 173 \; кПа} \]

Давление в шине в конце пути 173 кПа.

Обратите внимание, что на шаге 2 мы не удосужились преобразовать значения объема в ³ м. На шаге 4 давление появляется как в числителе, так и в знаменателе. В этом случае преобразование не требовалось.

Число Авогадора

Число молекул в молье называется числом Авогадро (N _A ) и определяется как 6,02 x 10 ²³ моль ^-1 .

учебных целей

• Объясните связь между числом Авогадро и родинкой.

При измерении количества вещества иногда проще работать с единицей измерения, отличной от количества молекул. Моль (сокращенно моль) — основная единица Международной системы единиц (СИ). Он определяется как любое вещество, содержащее столько атомов или молекул, сколько ровно в 12 граммах (0,012 кг) углерода-12. Фактическое количество атомов или молекул в одном моль называется постоянной Авогадро (N _A ) по признанию итальянского ученого Амедео Авогадро.

Амадео Авогадро : Амедео Авогадро (1776–1856). Он установил, что соотношение между массами одного и того же объема разных газов (при одинаковых температуре и давлении) соответствует соотношению между их соответствующими молекулярными массами.

Число Авогадро (N) обозначает количество молекул в одной грамм-молекуле кислорода. Это указывает на количество вещества, а не на независимое измерение.В 1811 году Амедео Авогадро впервые предположил, что объем газа (при данном давлении и температуре) пропорционален количеству атомов или молекул, независимо от природы газа (т. Е. Это число универсально и не зависит от типа газа). газ). В 1926 году Жан Перрен получил Нобелевскую премию по физике, в основном за его работу по определению постоянной Авогадро (несколькими различными методами). Значение постоянной Авогадро, N _A , оказалось равным 6,02 × 10 ²³ моль ^-1 .{−1}.} \]

Измерение N

_A

Определение N _A имеет решающее значение для расчета массы атома, поскольку последняя получается делением массы моля газа на постоянную Авогадро. В своем исследовании броуновского движения в 1905 году Альберт Эйнштейн предположил, что эта постоянная может быть определена на основе величин, наблюдаемых в броуновском движении. Впоследствии идея Эйнштейна была проверена, что привело к первому определению N _A в 1908 году в результате экспериментальной работы Жана Батиста Перрена.

Абсолютная температура

Абсолютная температура — это наиболее часто используемая термодианмическая единица измерения температуры и стандартная единица измерения температуры.

учебных целей

• Опишите взаимосвязь между абсолютной температурой и кинетической энергией.

Термодинамическая температура — это абсолютная мера температуры. Это один из основных параметров термодинамики и кинетической теории газов. Термодинамическая температура — это «абсолютная» шкала, потому что это мера фундаментального свойства, лежащего в основе температуры: ее нулевая или нулевая точка («абсолютный ноль») — это температура, при которой частицы, составляющие материю, имеют минимальное движение и не могут стать холоднее.То есть, они имеют минимальное движение, сохраняя только квантово-механическое движение, как показано на схеме.

График зависимости давления от температуры : График зависимости давления от температуры для различных газов, поддерживаемых в постоянном объеме. Обратите внимание, что все графики экстраполированы на нулевое давление при одной и той же температуре

В самом простом случае, «температура» возникает из кинетической энергии случайных движений составляющих материальных частиц, таких как молекулы или атомы, как показано на.Поэтому разумно выбрать абсолютный ноль, при котором все классическое движение прекращается, в качестве точки отсчета (T = 0) нашей температурной системы. Используя шкалу абсолютных температур (система Кельвина), которая является наиболее часто используемой термодинамической температурой, мы показали, что средняя поступательная кинетическая энергия (KE) частицы в газе имеет простую связь с температурой:

Поступательное движение гелия : Реальные газы не всегда ведут себя в соответствии с идеальной моделью при определенных условиях, таких как высокое давление.Здесь размер атомов гелия относительно их расстояния показан в масштабе при давлении 1950 атмосфер.

\ [\ mathrm {\ bar {KE} = \ dfrac {3} {2} тыс. Т.} \]

Обратите внимание, что это уравнение не выглядело бы так элегантно, если бы вместо него использовалась шкала Фаренгейта.

Шкала Кельвина

Кельвин (или «абсолютная температура») — это стандартная термодианмическая единица измерения температуры. Это одна из семи основных единиц Международной системы единиц (СИ), которой присвоен символ единицы K.По международному соглашению единица измерения кельвина и ее шкала определяются двумя точками: абсолютным нулем и тройной точкой Венской стандартной средней океанской воды (вода с определенной смесью изотопов водорода и кислорода). Абсолютный ноль, минимально возможная температура, определяется как 0 K и −273,15 ° C. Тройная точка воды определяется точно как 273,16 K и 0,01 ° C.

Ключевые моменты

• Закон идеального газа был получен эмпирическим путем путем объединения закона Бойля и закона Чарльза.2}.} \)
• Изотермические процессы обычно происходят, когда система находится в контакте с внешним тепловым резервуаром (тепловой ванной), и изменение происходит достаточно медленно, чтобы позволить системе постоянно приспосабливаться к температуре резервуара посредством теплообмена.
• Для идеального газа согласно закону идеального газа \ (\ mathrm {PV = NkT, PV} \) остается постоянным в результате изотермического процесса. Кривая на диаграмме P-V, порожденная уравнением \ (\ mathrm {PV = const} \), называется изотермой.
• Для изотермического обратимого процесса работа, совершаемая газом, равна площади под соответствующей изотермой «давление-объем». Он задается как \ (\ mathrm {W_A \ rightarrow B = NkT \ ln \ frac {⁡V_B} {V_A}} \).
• Газы могут расширяться или сжиматься при определенных ограничениях. В зависимости от ограничения конечное состояние газа может измениться.
• Тепло, передаваемое системе, работает, но также изменяет внутреннюю энергию системы. В изобарическом процессе для одноатомного газа тепло и изменение температуры удовлетворяют следующему уравнению: \ (\ mathrm {Q = \ frac {5} {2} NkΔT} \).
• Для одноатомного идеального газа удельная теплоемкость при постоянном давлении равна \ (\ mathrm {\ frac {5} {2} R} \).
• Запишите всю информацию, которую вы знаете о газе, и при необходимости преобразуйте известные значения в единицы СИ.
• Выберите соответствующее уравнение закона газа, которое позволит вам вычислить неизвестную переменную, и подставьте известные значения в уравнение. Затем вычислите неизвестную переменную.
• Общее уравнение газа применимо только в том случае, если молярное количество газа фиксировано.
• Авогадро предположил, что равные объемы газа при одинаковом давлении и температуре содержат равное количество молекул, независимо от типа газа.
• Постоянная Авогадро — это коэффициент масштабирования между макроскопическими и микроскопическими (атомный масштаб) наблюдениями за природой. Он обеспечивает связь между другими физическими константами и свойствами.
• Альберт Эйнштейн предположил, что число Авогадро можно определить на основе величин, наблюдаемых в броуновском движении.Впервые числовая апертура была измерена Жаном Батистом Перреном в 1908 году.
• Температура возникает из кинетической энергии случайных движений компонентов материи, таких как молекулы или атомы. Поэтому разумно выбрать за точку отсчета абсолютный ноль, при котором все классическое движение прекращается.
• Согласно международному соглашению, единица измерения кельвина и ее шкала определяются двумя точками: абсолютным нулем и тройной точкой стандартизированной воды.
• При абсолютном нуле частицы, составляющие материю, имеют минимальное движение и не могут стать холоднее.Они сохраняют минимальное квантово-механическое движение.

Ключевые термины

• моль : В Международной системе единиц — основная единица количества вещества; количество вещества системы, которая содержит столько же элементарных объектов, сколько атомов в 12 г углерода-12. Символ: мол.
• идеальный газ : гипотетический газ, молекулы которого не взаимодействуют и подвергаются упругому столкновению друг с другом и со стенками контейнера.
• Число Авогадро : количество составляющих частиц (обычно атомов или молекул) в одном моль данного вещества. Он имеет размеры обратного моля и его значение равно 6.02214129 · 1023 моль-1
.
• адиабатический : Происходит без увеличения или уменьшения тепла.
• внутренняя энергия : сумма всей энергии, присутствующей в системе, включая кинетическую и потенциальную энергию; эквивалентно, энергия, необходимая для создания системы, за исключением энергии, необходимой для перемещения ее окружения.
• первый закон термодинамики : Вариант закона сохранения энергии: изменение внутренней энергии замкнутой системы равно количеству тепла, подаваемого в систему, за вычетом количества работы, выполняемой системой на его окрестности.
• удельная теплоемкость : Отношение количества тепла, необходимого для повышения температуры единицы массы вещества на единицу градуса, к количеству тепла, необходимому для повышения температуры той же массы воды на такое же количество.
• единиц СИ : Международная система единиц (сокращенно СИ от французского: Le Système international d’unités). Это современная форма метрической системы.
• газовая постоянная : Универсальная постоянная R, которая появляется в законе идеального газа (PV = nRT), полученная из двух фундаментальных констант, постоянной Больцмана и числа Авогадро (R = NAk).
• Постоянная Фарадея : Величина электрического заряда на моль электронов.
• Броуновское движение : Случайное движение взвешенных в жидкости частиц, возникающее в результате столкновения этих частиц с отдельными молекулами жидкости.
• абсолютный ноль : максимально низкая температура: ноль по шкале Кельвина и приблизительно -273,15 ° C и -459,67 ° F. Полное отсутствие тепла; температура, при которой движение всех молекул прекратится.
• Международная система единиц : (СИ): Стандартный набор основных единиц измерения, используемый в мировой научной литературе.
• Венский стандарт средней океанской воды : Стандарт, определяющий стандартизованный изотопный состав воды.

ЛИЦЕНЗИИ И АТРИБУЦИИ

CC ЛИЦЕНЗИОННЫЙ КОНТЕНТ, ПРЕДЫДУЩИЙ РАЗДЕЛ

CC ЛИЦЕНЗИОННОЕ СОДЕРЖАНИЕ, СПЕЦИАЛЬНЫЙ АТРИБУЦИЯ

• идеальный газ. Источник : Викисловарь. Адрес: : en.wiktionary.org/wiki/ideal_gas . Лицензия : CC BY-SA: Attribution-ShareAlike
• Закон об идеальном газе. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Ideal_gas_law%23Empirical . Лицензия : CC BY-SA: Attribution-ShareAlike
• Номер Авогадро. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Avogadro’s%20number . Лицензия : CC BY-SA: Attribution-ShareAlike
• моль. Источник : Викисловарь. Адрес: : en.wiktionary.org/wiki/mole . Лицензия : CC BY-SA: Attribution-ShareAlike
• Колледж OpenStax, Закон об идеальном газе. 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42216/latest/ . Лицензия : CC BY: Attribution
• идеальный газ. Источник : Викисловарь. Адрес: : en.wiktionary.org/wiki/ideal_gas . Лицензия : CC BY-SA: Attribution-ShareAlike
• Изотермический процесс. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY-SA: Attribution-ShareAlike
• Безграничный. Источник : Безграничное обучение. Адрес: : www.boundless.com//physics/definition/internal-energy . Лицензия : CC BY-SA: Attribution-ShareAlike
• адиабатический. Источник : Викисловарь. Адрес: : en.wiktionary.org/wiki/adiabatic . Лицензия : CC BY-SA: Attribution-ShareAlike
• Колледж OpenStax, Закон об идеальном газе.4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42216/latest/ . Лицензия : CC BY: Attribution
• Изотермический процесс. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
• Изотермический процесс. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
• Колледж OpenStax, Первый закон термодинамики и некоторые простые процессы. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42233/latest/ . Лицензия : CC BY: Attribution
• Изобарический процесс. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isobaric_process . Лицензия : CC BY-SA: Attribution-ShareAlike
• первый закон термодинамики. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/the%20first%20law%20of%20thermodynamics . Лицензия : CC BY-SA: Attribution-ShareAlike
• удельная теплоемкость. Источник : Викисловарь. Адрес: : en.wiktionary.org/wiki/specific_heat . Лицензия : CC BY-SA: Attribution-ShareAlike
• Колледж OpenStax, Закон об идеальном газе. 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42216/latest/ . Лицензия : CC BY: Attribution
• Изотермический процесс. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
• Изотермический процесс. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
• Колледж OpenStax, Первый закон термодинамики и некоторые простые процессы.5 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42233/latest/ . Лицензия : CC BY: Attribution
• идеальный газ. Источник : Викисловарь. Адрес: : en.wiktionary.org/wiki/ideal_gas . Лицензия : CC BY-SA: Attribution-ShareAlike
• Закон об идеальном газе. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Ideal_gas_law . Лицензия : CC BY-SA: Attribution-ShareAlike
• Бесплатный проект научных текстов для старших классов, Тепловые свойства и идеальные газы: закон идеального газа и общее уравнение газа. 17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m39086/latest/ . Лицензия : CC BY: Attribution
• Безграничный. Источник : Безграничное обучение. Адрес: : www.boundless.com//physics/definition/si-units . Лицензия : CC BY-SA: Attribution-ShareAlike
• Колледж OpenStax, Закон об идеальном газе. 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http: // cnx.org / content / m42216 / latest / . Лицензия : CC BY: Attribution
• Изотермический процесс. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
• Изотермический процесс. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
• Колледж OpenStax, Первый закон термодинамики и некоторые простые процессы. 5 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42233/latest/ . Лицензия : CC BY: Attribution
• Шина. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Tire . Лицензия : CC BY: Attribution
• Броуновское движение. Источник : Викисловарь. Адрес: : en.wiktionary.org/wiki/Brownian_motion . Лицензия : CC BY-SA: Attribution-ShareAlike
• Постоянная Авогадро. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Avogadro_constant%23Measurement . Лицензия : CC BY-SA: Attribution-ShareAlike
• Броуновское движение. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Brownian_motion . Лицензия : CC BY-SA: Attribution-ShareAlike
• Колледж OpenStax, Закон об идеальном газе.17 сентября 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42216/latest/ . Лицензия : CC BY: Attribution
• Постоянная Фарадея. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Faraday%20constant . Лицензия : CC BY-SA: Attribution-ShareAlike
• газовая постоянная. Источник : Викисловарь. Адрес: : en.wiktionary.org/wiki/gas_constant . Лицензия : CC BY-SA: Attribution-ShareAlike
• Колледж OpenStax, Закон об идеальном газе. 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42216/latest/ . Лицензия : CC BY: Attribution
• Изотермический процесс. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
• Изотермический процесс. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
• Колледж OpenStax, Первый закон термодинамики и некоторые простые процессы.5 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42233/latest/ . Лицензия : CC BY: Attribution
• Шина. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Tire . Лицензия : CC BY: Attribution
• Авогадро Амедео. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/File:Avogadro_Amedeo.jpg . Лицензия : CC BY-SA: Attribution-ShareAlike
• абсолютный ноль. Источник : Викисловарь. Адрес: : en.wiktionary.org/wiki/absolute_zero . Лицензия : CC BY-SA: Attribution-ShareAlike
• Термодинамическая температура. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Thermodynamic_temperature . Лицензия : CC BY-SA: Attribution-ShareAlike
• Международная система единиц. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/International%20System%20of%20Units . Лицензия : CC BY-SA: Attribution-ShareAlike
• Венский стандарт средней океанской воды. Источник : Викисловарь. Адрес: : en.wiktionary.org/wiki/Vienna_Standard_Mean_Ocean_Water . Лицензия : CC BY-SA: Attribution-ShareAlike
• Колледж OpenStax, Закон об идеальном газе. 4 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42216/latest/ . Лицензия : CC BY: Attribution
• Изотермический процесс. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
• Изотермический процесс. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Isothermal_process . Лицензия : CC BY: Attribution
• Колледж OpenStax, Первый закон термодинамики и некоторые простые процессы.5 февраля 2013 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42233/latest/ . Лицензия : CC BY: Attribution
• Шина. Источник : Википедия. Расположен по адресу : http://en.Wikipedia.org/wiki/Tire . Лицензия : CC BY: Attribution
• Авогадро Амедео. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/File:Avogadro_Amedeo.jpg . Лицензия : CC BY-SA: Attribution-ShareAlike
• OpenStax College, Температура. 28 апреля 2014 г. Предоставлено : OpenStax CNX. Расположен по адресу : http://cnx.org/content/m42214/latest/ . Лицензия : CC BY: Attribution
• Кинетическая теория. Источник : Википедия. Расположен по адресу : en.Wikipedia.org/wiki/Kinetic_theory . Лицензия : Общественное достояние: неизвестно Авторские права

6.1: Уравнение идеального газа

В 1660 году достопочтенный Роберт Бойль, отец химии, седьмой сын графа Корка и один из основателей Лондонского королевского общества, провел несколько экспериментов физико-механических, прикоснувшись к Весна воздуха .Он удерживал некоторое количество воздуха в закрытом рукаве J-образной стеклянной трубки с помощью столба ртути и измерял объем воздуха, когда он подвергался все большему и большему давлению. В результате этих экспериментов он установил то, что сейчас известно как Закон Бойля :

.

Давление фиксированной массы газа, выдерживаемого при постоянной температуре (т.е. в изотермическом процессе) , обратно пропорционально ее объему.

То есть

\ [PV = \ text {постоянная}.\]

Более поздние эксперименты показали, что объем фиксированной массы газа, находящейся под постоянным давлением, линейно увеличивается с температурой. В частности, у большинства газов примерно одинаковый объемный коэффициент расширения. При 0 ^o C это примерно 0,00366 C ^{o -1} или 1/273 C ^{o -1} .

Если экстраполировать объем фиксированной массы газа, находящейся под постоянным давлением, на все более низкие температуры, экстраполированный объем упадет до нуля при −273 ^o C.Это не является прямым основанием нашей веры в невозможность получения температуры ниже -273 ^o C. С одной стороны, настоящий газ сжижается задолго до того, как эта температура будет достигнута. Тем не менее, по причинам, которые будут обсуждаться в более поздней главе, мы действительно считаем, что это абсолютный ноль температуры. В любом случае:

Объем фиксированной массы газа, удерживаемый при постоянном давлении (т.е. в изобарическом процессе), прямо пропорционален его температуре Кельвина.

Наконец,

Давление фиксированной массы газа, удерживаемого в постоянном объеме (то есть в изохорном процессе), прямо пропорционально его температуре Кельвина.

Если разрешено изменять P, V и T , эти три закона становятся

\ [PV / T = \ text {constant} \]

Значение постоянной зависит от количества газа; в частности, он пропорционален количеству молей (следовательно, количеству молекул) газа.То есть

\ [PV / T = RN, \]

, где N — число молей, а R — константа пропорциональности, которая оказывается примерно одинаковой для большинства газов.

Конечно, реальные газы ведут себя примерно так, как описано, и только при условии, что эксперименты проводятся в умеренных диапазонах температуры, давления и объема, и при условии, что температура газа намного выше температуры, при которой он будет сжижаться. Тем не менее, при соблюдении этих условий, большинство газов вполне удовлетворяет уравнению 6.1.3 с примерно одинаковой константой пропорциональности для каждого.

Газ, подчиняющийся уравнению

\ [PV = NRT \]

называется идеальным газом , а уравнение 6.1.4 называется уравнением состояния для идеального газа . В этом уравнении V — общий объем газа, N — количество молей, а R — универсальная газовая постоянная. Уравнение также можно записать

\ [PV = RT. \]

В данном случае V — это молярный объем .Некоторые авторы используют разные символы (например, V , v и V _m ) для общего, удельного и молярного объема. Вероятно, это хорошая идея, и есть некоторый риск, что я не собираюсь этого делать, и я надеюсь, что контекст прояснит, о каком томе я говорю, когда использую простой символ V в любой конкретной ситуации. Обратите внимание, что в то время как общий объем составляет экстенсивного количества , удельный и молярный объемы составляют интенсивного .

При использовании уравнения 6.1.5 невозможно ошибиться в 10 раз. ³ . Если вы используете единицы измерения CGS, P будет выражено в динах на квадратный см, V — это объем моля (т. Е. Объем, занимаемый 6,0221 × 10 ²³ молекул), а значение универсального газа константа .8,3145 × 10 ⁷ эрг моль ⁻¹ K ⁻¹ . Если вы используете единицы СИ, P будет выражено в паскалях (Н · м ^-2 ), V будет объемом в киломоль (т. Е.е. объем, занимаемый 6,0221 × 10 ²⁶ молекулами), а значение универсальной газовой постоянной составляет 8,3145 × 10 ³ Дж киломоль ⁻¹ K ⁻¹ . Если желаете выразить давление в торр, атм. или батончики, и энергия в калориях, вы сами по себе.

Вы можете записать уравнение 6.1.4 (с V = общий объем) как \ (P = \ frac {NN_ {\ text {A}}} {V} \ frac {RT} {N_ {\ text {A}) }} \) где N _A — число Авогадро, которое составляет 6,0221 × 10 ²³ молекул на моль, или 6.02221 × 10 ²⁶ молекул на километр. Первый член справа — это общее количество молекул, деленное на объем; то есть это количество молекул в единице объема, n . Во втором члене R / N _A равно постоянная Больцмана , k = 1,3807 10 ⁻²³ × J K ⁻¹ . Следовательно, уравнение состояния идеального газа можно записать

\ [P = nkT. \]

Разделите обе части уравнения 6.1,5 на молярную массу («молекулярный вес») µ. Плотность ρ пробы газа равна молярной массе, деленной на молярный объем, и, следовательно, уравнение состояния идеального газа также может быть записано

\ [P = \ frac {\ rho RT} {\ mu}. \]

Таким образом, уравнения 6.1.4, 6.1.5, 6.1.6 и 6.1.7 являются общепринятыми эквивалентными формами уравнения состояния идеального газа.

С этого момента я буду использовать V для обозначения молярного объема , если не указано иное, так что я буду использовать уравнение 6.1.5, а не 6.1.4 для уравнения состояния идеального газа. Обратите внимание, что молярный объем (в отличие от общего объема) — это интенсивная переменная состояния .

В сентябре 2007 г. значения, указанные для вышеупомянутых физических констант на веб-сайте Национального института науки и технологий (http://physics.nist.gov/cuu/index.html), составляли:

Молярная газовая постоянная R = 8314,472 (15) Дж · кмоль ⁻¹ K ⁻¹ .

Константа Авогадро N _A = 6.022141 79 (30) × 1026 частиц кмоль ⁻¹ .

Постоянная Больцмана k = 1.380 6504 (24) × 10−23 Дж K ⁻¹ на частицу.

Число в скобках обозначает стандартную погрешность двух последних цифр.

[Существует предложение, которое, вероятно, станет официальным в 2015 году, дать определенные точные числовые значения постоянным Авогадро и Больцмана, а именно 6,022 14 x 10 ²³ моль частиц ⁻¹ и 1,380 6 x 10 ^–23 JK ⁻¹ на частицу.На первый взгляд это может показаться чем-то вроде определения числа π равным 3, но на самом деле это совсем не так. Все это является частью общего сдвига в определении многих единиц, используемых в физике, в терминах фундаментальных физических величин (таких как заряд электрона), а не в терминах стержней или цилиндров из платины, хранящихся в Париже.]

Закон об идеальном газе

При изучении поведения газов в замкнутых пространствах полезно ограничиться изучением идеальных газов.Идеальные газы — это теоретические модели реальных газов, в которых используется ряд основных предположений, упрощающих их изучение. Эти допущения включают рассмотрение газа как состоящего из множества частиц, которые беспорядочно перемещаются в контейнере. Частицы, в среднем, находятся далеко друг от друга, и они не оказывают друг на друга силы, если только они не вступают в контакт при упругом столкновении.

При нормальных условиях, таких как стандартная температура и давление, большинство газов ведут себя так же, как идеальный газ.Тяжелые газы, а также газы при очень низких температурах или очень высоких давлениях не так хорошо моделируются идеальным газом.

Закон об идеальном газе связывает давление, объем, количество частиц и температуру идеального газа в одном уравнении, и его можно записать разными способами.

В этом уравнении P — давление газа (в паскалях), V — объем газа (в кубических метрах), n — количество молей газа, N — количество молекул газа, R — универсальная газовая постоянная, равная 8.31 Дж / моль · К (что также составляет 0,08206 л · атм / моль · К), kB — постоянная Больцмана (1,38 × 10 ^-23 Дж / К), а T — температура в Кельвинах. Чтобы преобразовать молекулы в моль, вы можете использовать число Авогадро (N0 = 6,02 × 10 ^-23 молекулы / моль):

Обратите внимание, что Паскаль, умноженный на кубический метр, — это ньютон-метр или Джоуль. Кроме того, постоянная Больцмана — это постоянная закона идеального газа, деленная на число Авогадро.

Вопрос: Сколько молей идеального газа эквивалентно 3.01 × 10 ²⁴ молекулы?

Ответ:

Вопрос: Найдите количество молекул в 0,4 моля идеального газа.

Ответ:

Вопрос: Сколько молей газа содержится в 0,3 м баллоне с углекислым газом ³ , выдерживаемом при температуре 320 К и давлении 1 × 10 ⁶ Паскалей?

Ответ:

Вопрос: Кубический метр углекислого газа при комнатной температуре (300 К) и атмосферном давлении (101 325 Па) сжимается до объема 0.1 м ³ и выдерживали при температуре 260К. Какое давление сжатого углекислого газа?

Ответ: Поскольку количество молей газа постоянно, вы можете упростить уравнение идеального газа до закона комбинированного газа, установив соотношение начального давления, объема и температуры, равное конечному давлению, объему и температуре.

Поскольку вам известны все величины в этом уравнении, кроме конечного давления, вы можете напрямую вычислить конечное давление.

Вопрос: Один моль газообразного гелия помещается в воздушный шар. Каково давление внутри воздушного шара, когда воздушный шар поднимается до точки в атмосфере, где температура составляет -12 ° C, а объем воздушного шара составляет 0,25 кубических метра?

Ответ: Сначала вы должны перевести температуру из градусов Цельсия в Кельвины.

Затем вы можете использовать закон идеального газа для определения давления внутри воздушного шара.

Также довольно просто найти полную внутреннюю энергию идеального газа. Напомним, что средняя кинетическая энергия частиц идеального газа описывается формулой:

Полная внутренняя энергия идеального газа может быть найдена умножением средней кинетической энергии частиц газа на количество частиц (N) в газе. Следовательно, внутреннюю энергию газа можно рассчитать по формуле:

Вопрос: Найдите внутреннюю энергию 5 молей кислорода при температуре 300К.

Ответ:

Вопрос: Какова температура 20 молей аргона с полной внутренней энергией 100 кДж?

Ответ:

Идеальные газы и закон идеального газа: pV = nRT

Температура, Т

Температура должна быть в градусах Кельвина.Не забудьте добавить 273, если вам дана температура в градусах Цельсия.

Использование уравнения идеального газа

Расчеты с использованием уравнения идеального газа включены в мою книгу расчетов (см. Ссылку в самом низу страницы), и я не могу повторить их здесь. Однако есть пара расчетов, которые я не выполнил в книге, которые дают разумное представление о том, как работает уравнение идеального газа.

Молярный объем по стандарту

Если вы выполнили простые вычисления по уравнениям, вы, вероятно, использовали молярный объем газа.

1 моль любого газа занимает 22,4 дм. ³ при stp (стандартные температура и давление, принимаемые как 0 ° C и давление в 1 атмосферу). Вы также могли использовать значение 24,0 дм ³ при комнатной температуре и давлении (принятое примерно за 20 ° C и 1 атмосферу).

На самом деле эти цифры верны только для идеального газа, и мы посмотрим, откуда они берутся.

Мы можем использовать уравнение идеального газа для вычисления объема 1 моля идеального газа при 0 ° C и давлении 1 атмосфера.

Во-первых, мы должны правильно определить единицы.

0 ° C составляет 273 К. T = 273 К.

1 атмосфера = 101325 Па. P = 101325 Па

Мы знаем, что n = 1, потому что мы пытаемся вычислить объем 1 моля газа.

И, наконец, R = 8.31441 J K ^-1 моль ^-1 .

Вставка всего этого в уравнение идеального газа и последующее преобразование дает:

И, наконец, поскольку нас интересует объем в кубических дециметрах, вы должны не забыть умножить его на 1000, чтобы преобразовать кубические метры в кубические дециметры.

Таким образом, молярный объем идеального газа составляет 22,4 дм. ³ на стандартном давлении.

И, конечно, вы можете повторить этот расчет, чтобы найти объем 1 моля идеального газа при комнатной температуре и давлении — или при любой другой температуре и давлении.

Определение относительной формулы массы газа по его плотности

Это примерно так же сложно, как и при использовании уравнения идеального газа.

Плотность этана 1.264 г дм ^-3 при 20 ° C и 1 атмосфере. Рассчитайте относительную формульную массу этана.

Значение плотности означает, что 1 дм ³ этана весит 1,264 г.

Опять же, прежде чем мы сделаем что-нибудь еще, разберитесь с неудобными юнитами.

Давление в 1 атмосферу составляет 101325 Па.

Объем 1 дм. ³ нужно пересчитать в кубические метры, разделив на 1000. У нас объем 0,001 м. ³ .

Температура 293 К.

Теперь представьте все числа в форме уравнения идеального газа, которое позволяет вам работать с массами, и измените его так, чтобы вычислить массу 1 моля.

Масса 1 моля чего-либо — это просто относительная масса по формуле в граммах.

Таким образом, относительная формула массы этана равна 30,4, к 3 сигн.

Теперь, если вы сложите относительную формульную массу этана, C ₂ H ₆ , используя точные значения относительных атомных масс, вы получите ответ 30.07 до 4 значащих цифр. Что отличается от нашего ответа — так что не так?

Есть две возможности.

• Возможно, я использовал неверное значение плотности. Я снова подсчитал, используя немного другое значение, указанное при другой температуре из другого источника. На этот раз я получил ответ 30,3. Таким образом, значения плотности могут быть не совсем точными, но они оба дают примерно одинаковый ответ.

• Этан — не идеальный газ.Ну конечно не идеальный газ — такого не бывает! Однако, если предположить, что значения плотности близки к правильным, ошибка находится в пределах 1% от ожидаемого. Так что, хотя этан не совсем похож на идеальный газ, он не за горами.

Если вам нужно знать о настоящих газах, сейчас самое время прочитать о них.

Закон идеального газа — уравнение, формула, вывод и константа

Что такое закон идеального газа?

Закон идеального газа или Закон идеального газа представляет собой смешанную взаимосвязь между давлением, объемом и температурой газов для изучения физических свойств молекулы газа в физике или химии.Уравнение идеального газа, уравновешивающее эти переменные состояния в терминах универсальной газовой постоянной (R). Формулу закона идеального или идеального газа можно использовать для вычисления значения давления, объема, температуры, диффузии или излива, концентрации и количества молекул газа в единице объема или плотности. Закон Бойля 1662 года, закон Чарльза 1787 года и закон Авогадро дают общую формулу вывода уравнения идеального или совершенного газа, а кинетическая теория газа обеспечивает свойства идеальных газов.

Четыре термодинамические переменные в газовых законах для идеального или совершенного газа — это давление, объем, температура и число молей.Некоторые из них зависят от массы системы, а другие не зависят от массы.

• В термодинамике свойство, пропорциональное массе системы, называется интенсивным свойством.
• Свойство системы, не зависящее от массы системы, называется интенсивным свойством.

Согласно закону идеального газа, объем — это интенсивное свойство, а температура и давление — экстенсивные свойства при выводе термодинамики.

Вывод формулы закона идеального газа

Закон Бойлса V 1 / T, когда n и T постоянны.Закон Чарльза, V ∝ T, когда n и P постоянны. Закон Авогадро, V ∝ n, когда P и T постоянны. Когда все переменные газовых законов приняты во внимание, мы находим математическое выражение уравнения идеального газа, PV = nRT, где R = универсальная газовая постоянная.

Закон идеального газа определяет соотношение между давлением, объемом, температурой и составом газов. Но уравнение оказалось наиболее удовлетворительным при низком давлении или напряжении до нуля. При обычных температуре и давлении уравнение отклоняется примерно на 5%.Следовательно, реальный газ, или газ Ван-дер-Ваальса, подчиняется закону идеального газа только при низких давлениях и очень высоких температурах.

Значение универсальной газовой постоянной

Единицу измерения универсальной постоянной величины и размер можно рассчитать по закону идеального газа, PV = nRT. На НТП 1 моль газов при давлении 1 атмосфера занимали 22,4 литра объема. Из уравнения идеального газа R = PV / nT = (1 атм × 22,4 л) / (1 моль × 273 K) = 0,082 л атм моль ^-1 K ^-1 .

Значение универсальной газовой постоянной в СГС

В СГС давление = 1 атм = 76 × 13.6 × 981 дин см ^-2 и объем = 22,4 литра = 22,4 × 103 см ³ . Подставляя значения P, V, T и n в закон идеального газа, мы получаем универсальную газовую постоянную (R) = (7,6 × 13,6 × 981 × 22,4 × 10 ³ ) / (1 × 273) = 8,314 × 10 ⁷ дин см ² моль ^-1 K ^-1 = 8,314 × 10 ⁷ эрг моль ^-1 K ^-1 , где дин см ² = эрг.

Значение универсальной газовой постоянной в системе СИ

Значение универсальной постоянной (R) в системе CGS = 8.314 × 10 ⁷ эрг моль ^-1 K ^-1 . Но 1 Дж = 10 ⁷ эрг. Универсальная постоянная в единицах СИ = 8,314 Дж моль ^-1 K ^-1 . Исходя из отношения удельной теплоемкости, 4,18 Дж = 1 калория. Следовательно, универсальная газовая постоянная из уравнения закона идеального газа = (8,314 / 4,18) кал-моль ^-1 K ^-1 = 1,987 калорий в месяц ^л-1 K ^-1 ≃ 2 калорий моль ^-1 K ^-1 .

Важность закона об идеальном газе

Для n моль идеальных газов PV = nRT или R = PV / nT.Единица универсальной газовой постоянной = (единица давления × единица объема) / (количество молекулы газа × единица температуры). Здесь единица давления = длина силы ^-2 , а объем = длина ³ . Единица R = (сила × длина) / (количество молекулы газа × единица температуры), где сила × длина = работа или энергия.

Из общего определения уравнения закона идеального газа при изучении химии или физики, R = энергия на моль на кельвин или количество работы или энергии, которые могут быть получены от одного моля газа при повышении его температуры на один кельвин.

Расчет идеальной плотности газа

Закон идеального газа для n моль, PV = nRT = (г / м) × RT, где g = вес в граммах, M = молярная масса. Следовательно, P = dRT / M, где d = density = g / V. Формула закона идеального газа, используемая в науке для определения плотности газов по известной молярной массе смешанных газов.

Задача: Плотность аммиака при давлении 5 атмосфер и температуре 30 ° C 3,42 г лит ^-1 . Как мы можем рассчитать молярную массу аммиака из уравнения идеального газа?

Раствор: Молярная масса (M) = dRT / P.Молекулярная масса аммиака, M _Nh4 = (3,42 × 0,082 × 303) / 5 = 16,99 г моль-1≃ 17 г моль ^-1 .

Число молекул на единицу объема

PV = nRT = (N / N ₀ ) × RT
, где N = количество присутствующих молекул газа
N ₀ = число Авогадро = 6,023 × 10 ²³

∴ P = (N / V) × (R / N ₀ ) × T = N′KT
, где N ′ = количество молекул в единице объема.
k = постоянная Больцмана = R / N
= 1,38 × 10 ^-16 эрг-молекул ^-1 K ^-1

Задача: Оцените по уравнению идеального газа количество газообразных молекул, оставшихся в объем 1 мл, если его откачать, чтобы создать вакуум 7.6 × 10⁻³ мм рт. Ст. При 0 ° C.

Раствор: Объем (V) = 1 мл = 10 ^-6 дм ³ , Давление (P) = 7,6 × 10 ^-3 мм рт. Ст. = 1,01235 × 10 ^-3 кПа. Число молекул газа, N ’= (1,01235 × 10 ^-3 ) / (1,38 × 10 ^-9 × 273) = 2,68 × 10 ^-11 .

Общее давление газовой смеси

Предполагая идеальное поведение или подчиняясь закону идеального газа, чтобы определить смешанное давление, оказываемое 2 г органического соединения, такого как метан, и 3 г молекул углекислого газа в сосуде емкостью 5 литров при 50 ° C .

n _Ch5 = 2/16 = 0,125
n _CO2 = 3/44 = 0,0682
Всего молей (n ₁ + n ₂ ) = (0,125 + 0,0682)
= 0,1932
∴ P _всего = (0,1932 × 0,082 × 323) / 5 атм
= 5,30 атм

Общее давление молекул смешанного идеального газа может быть получено из закона идеального газа и используется для расчета смешанного давления для различных газов, таких как кислород, азот , углекислый газ, углеводород и др.