Глава 1. Путь, перемещение, скорость. Движение с постоянной скоростью. Относительность движения
В рамках этой темы необходимо знать ряд простых определений, понимать логику определения скорости и закона сложения скоростей.
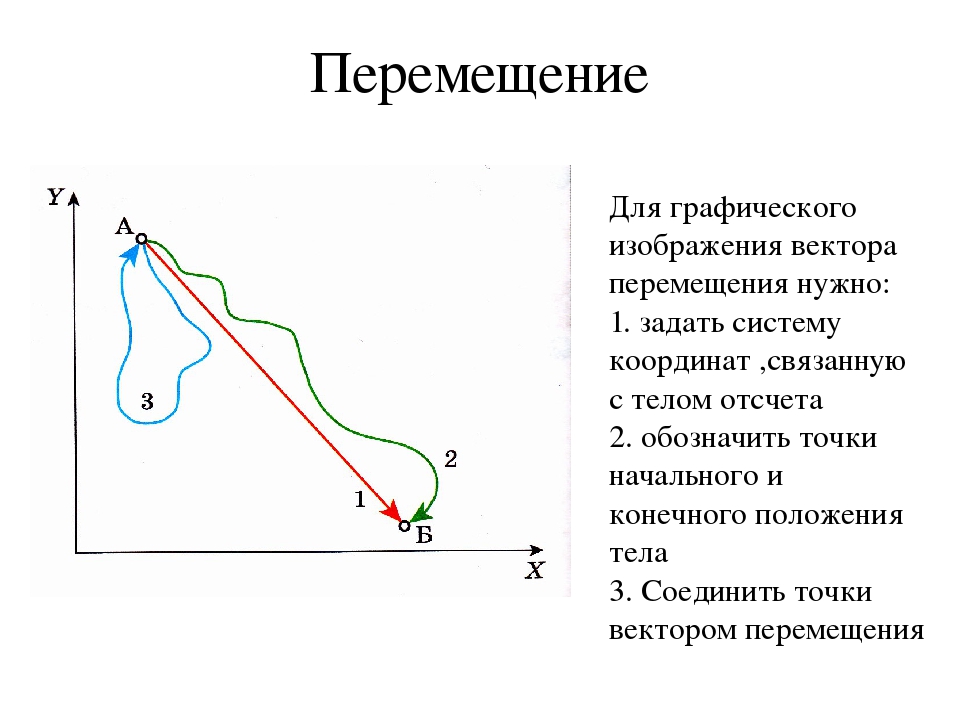
Перемещением тела называется вектор, связывающий начальное и конечное положение тела, а пройденным путем — длина траектории. Поэтому величина(или модуль) перемещения — это расстояние от конечной до начальной точки по прямой, а путь — расстояние траектории тела. В задаче 1.1.1 пройденный телом за четверть периода путь — длина четверти окружности , перемещение — (см. рисунок), правильный ответ — 3.
Скорость тела определяется как отношение перемещения тела ко времени , затраченному на это перемещение
| (1.1) |
Для прямолинейного движения в одном направлении для величины вектора скорости получаем из (1.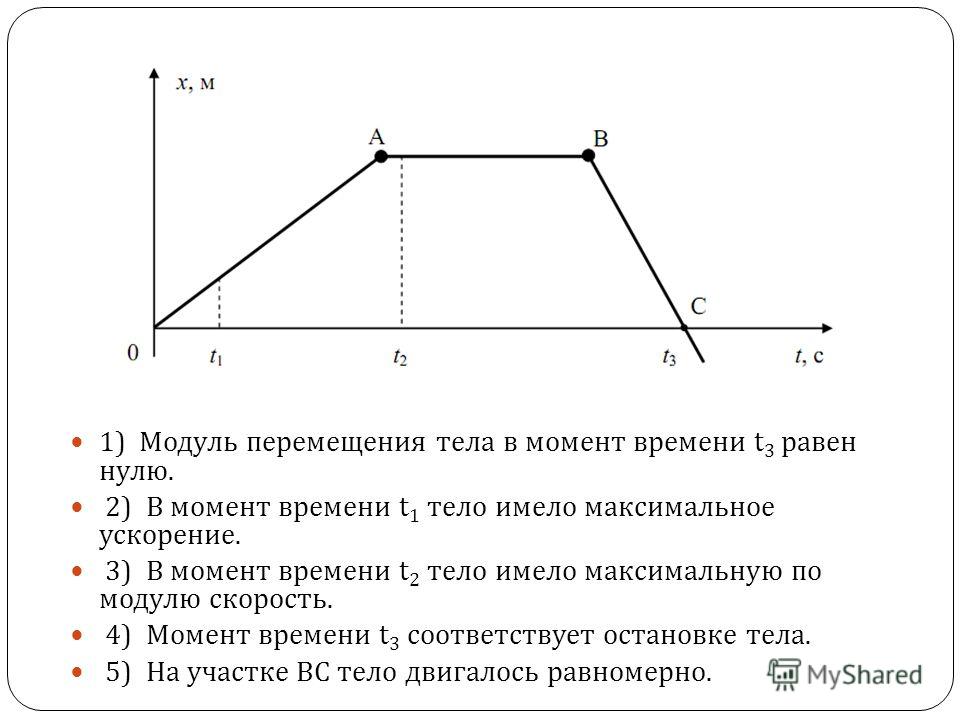 1)
1)
| (1.2) |
где — путь, пройденный за время . Если определение (1.1) приводит к одной и той же величине для любого интервала времени , то скорость тела есть величина постоянная, а такое движение называется равномерным (задача 1.1.2 — ответ 4). В этом случае согласно (1.1) и (1.2) перемещение и пройденный путь линейно зависят от времени и . По этой причине линейно зависят от времени и координаты тела в любой системе координат. Поэтому графиком зависимости координат тела от времени для равномерного движения является прямая (задача 1.1.3 — ответ 1). Как следует из (1.1), (1.2), наклон этой прямой определяется скоростью: чем больше скорость, тем «круче» наклонен график зависимости координаты тела от времени к оси времени. Поэтому в задаче 1.1.4 на каждом из интервалов времени — от 0 до 1 с, от 1 до 2 с, от 2 до 3 с и от 3 до 4 с движение тела будет равномерным, а самой большой скорость тела будет в интервале времени от 3 до 4 с, в котором наклон графика максимален (ответ
4).
В задаче 1.1.5 нужно по графику зависимости координаты тела от времени найти его скорость. Это можно сделать так. Перемещение тела внутри каждого из интервалов времени — 0–1, 1–2 и 2–3 с — разность координат тела вначале и в конце этого интервала. Поэтому из графика находим
Таким образом, скорость тела равна 2 м/с внутри интервала времени 1–2 с (ответ 2).
Задача 1.1.6 посвящена размерности скорости. Из определения заключаем, что размерность скорости есть
И, следовательно, размерностью скорости могут быть
(или любые другие отношения единиц расстояний и времени). Для пересчета скорости из одних единиц в другие нужно выразить расстояние и время в требуемых единицах. Например, в
(правильный ответ — 3).
При движении с постоянной скоростью определения (1. 1) или (1.2) могут быть применены к любым этапам движения. Например, в задаче 1.1.7 можно из данных о движении жука вдоль периметра прямоугольника найти его скорость (=14/7=2 см/с), а затем использовать ее для описания движения жука вдоль диагонали (длина которой составляет 5 см): 1=5/2=2,5 с (правильный ответ 2).
1) или (1.2) могут быть применены к любым этапам движения. Например, в задаче 1.1.7 можно из данных о движении жука вдоль периметра прямоугольника найти его скорость (=14/7=2 см/с), а затем использовать ее для описания движения жука вдоль диагонали (длина которой составляет 5 см): 1=5/2=2,5 с (правильный ответ 2).
Аналогичные соотношения используются в задаче 1.1.8. Рассматривая движение автомобиля на одной трети пути, получаем , где — расстояние между городами. А на оставшихся двух третях (с учетом трехкратного увеличения скорости) 1. Поэтому полное время движения равно (ответ 1).
В задаче 1.1.9 следует использовать следующее свойство графика зависимости проекции скорости тела на некоторую ось от времени: площадь под этим графиком есть проекция перемещения тела на рассматриваемую ось. Причем площадь под участками графика, лежащими выше оси времени, нужно считать положительной, ниже оси времени — отрицательной.
(ответ — 4).
Важным физическим законом, знание которого часто проверяется на едином государственном экзамене по физике, является закон сложения скоростей. Этот закон утверждает, что скорости одного и того же тела по отношению к разным системам отсчета связаны соотношением
(1.3) |
Здесь и — скорости тела относительно первой и второй системы отсчета, — скорость второй системы отсчета относительно первой. Закон сложения скоростей является векторным. Это означает, три вектора , и образуют треугольник векторного сложения, и соотношение между величинами скоростей , и — такое же, как и между длинами сторон треугольника. Углы этого треугольника равны углам между направлениями скоростей , и .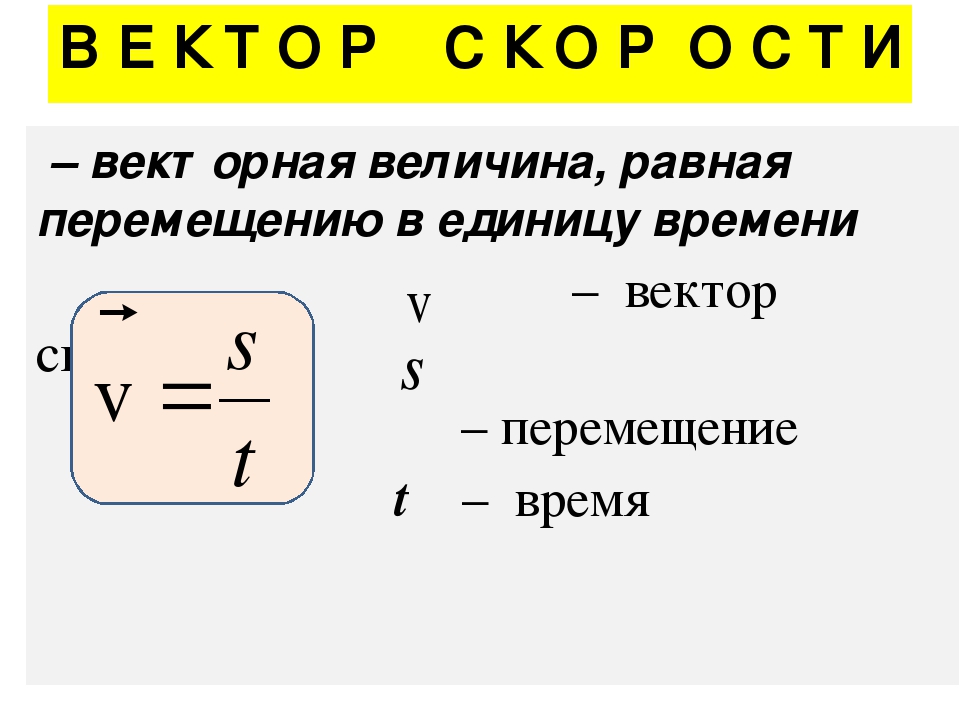
Примеры треугольников сложения скоростей приведены на рисунке, причем на среднем и правом рисунке приведены примеры «треугольников» скоростей в случаях, когда скорость тела в системе 2 и скорость системы 2 относительно системы 1 направлены одинаково (средний рисунок) и противоположно (правый рисунок). Из этих рисунков следует, что скалярное соотношение, аналогичное (1.3) для величин скоростей , справедливо только, если векторы и направлены одинаково (средний рисунок). Если же векторы и направлены противоположно, для значений скоростей справедливо соотношение (или наоборот , если — правый рисунок. Из этих рассуждений ясно, что поскольку в
задаче 1.1.10 векторы скорости пассажира относительно поезда и поезда относительно земли направлены одинаково, скорость пассажира относительно земли равна (правильный ответ — 2). В задаче 1.2.1 ситуация обратная — вектор скорости первой машины относительно земли и второй машины относительно земли направлены противоположно.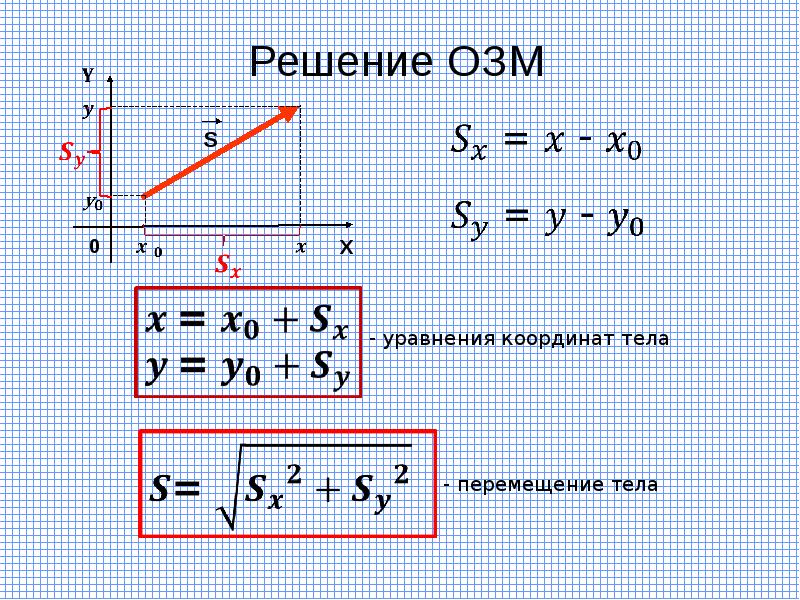 Поэтому , направлен вектор на север — правильный ответ 4.
Поэтому , направлен вектор на север — правильный ответ 4.
В задаче 1.2.2 эти идеи применяются к движению лодки по и против течения. Из закона сложения скоростей заключаем, что при движении лодки по течению ее скорость относительно земли равна , при движении против течения — ( — скорость лодки в стоячей воде, — скорость течения). Отсюда находим, что при движении лодки по течению, ее скорость относительно земли 15 км/ч, а при движении против течения — 5 км/ч. Поэтому время движения между городами и по течению втрое больше времени движения лодки между этими городами против течения (ответ —
Все следующие задачи этой главы являются более сложными, поскольку в них рассматривается движение не одного, а двух тел, а закон сложения скоростей используется в случаях, когда векторы скоростей не направлены вдоль одной прямой. В задаче 1.2.3 встреча тел происходит в такой точке, что расстояния, пройденные первым и вторым телом, отличаются втрое (так как в три раза отличаются скорости тел). Поэтому при выходе из точки тела встретятся в такой точке , что длины дуг отличаются в три раза. Следовательно, угол — прямой, и длина отрезка равна . (ответ 4).
Поэтому при выходе из точки тела встретятся в такой точке , что длины дуг отличаются в три раза. Следовательно, угол — прямой, и длина отрезка равна . (ответ 4).
Если два тела, начав движение одновременно, движутся навстречу друг другу (задача 1.2.4), то время встречи тел можно найти следующим образом. Так как тела двигались до встречи одинаковое время, они прошли расстояния и , сумма которых равна первоначальному расстоянию между телами . Поэтому (ответ 2). Отметим, что данные в условии задачи ответы 3 и 4 имеют неправильную размерность — 1/с и потому могут быть отброшены сразу. Задача 1.2.5 решается с помощью таких соображений: время движения первого пешехода между городами , второго — , встречи пешеходов (см. предыдущую задачу). Отсюда
Сокращая в этой формуле величину , получаем
или ч (правильный ответ — 1).
В задаче 1.2.6 начальное и конечное положения вагона и человека показаны на правой и левой частях рисунка.
Отсюда заключаем, что разность перемещений вагона и человека равна длине вагона . Поэтому время, через которое провожающий окажется около конца вагона, определяется из соотношения . Из этой формулы находится время, а затем и расстояние, пройденное провожающим (ответ
Задача 1.2.7 посвящена вычислению средней скорости движения на некотором пути, которая определяется как отношение этого пути к затраченному времени. Если расстояние между городами и равно , то полное время движения между городами складывается из времен, затраченных на первую и вторую половины пути
Отсюда находим км/ч (правильный ответ — 3).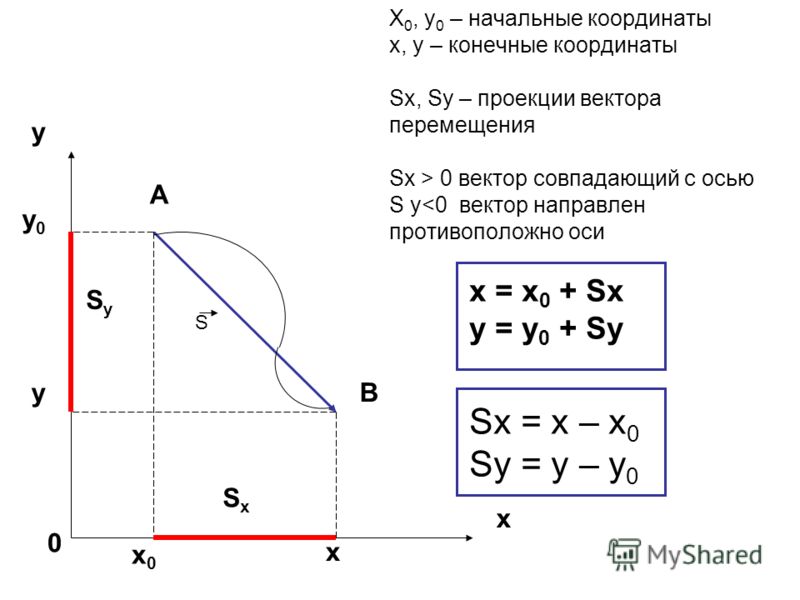
В задачах 1.2.8–1.2.9 закон сложения скоростей рассматривается в ситуациях, когда векторы , и направлены не вдоль одной прямой. В этом случае необходимо использовать закон сложения скоростей в векторной форме (1.3). Когда человек в поезде идет перпендикулярно направлению его движения (задача 1.2.8), треугольник сложения скоростей (1.3) имеет вид, показанный на рисунке.
Здесь — вектор скорости поезда относительно земли, — вектор скорости человека относительно поезда, который по условию направлен перпендикулярно вектору . Поэтому согласно закону сложения скоростей вектор скорости человека относительно земли представляет собой гипотенузу прямоугольного треугольника, катетами которого являются векторы и (см. рисунок). Следовательно, величину скорости человека относительно земли можно найти по теореме Пифагора (ответ 3).
Задачи 1.2.9. и 1.2.10 удобнее решать, переходя из той системы отсчета, в которой задача поставлена (в системе отсчета, связанной с землей) в некоторую другую систему, в которой рассматриваемое явление является более простым.
В задаче 1.2.10 рассматривается движение трех тел. В системе отсчета, связанной с землей ответ неочевиден. Быстрый катер дольше уплывет от лодки, но будет двигаться быстрее и при обратном движении, медленный — наоборот. Однако если перейти в систему отсчета, связанную с водой, решение очень несложно. В этой системе отсчета плот покоится, каждый катер при движении от плота и к плоту движется с одинаковой скоростью. Поэтому каждый катер вернется к плоту через то же самое время после разворота, в течение которого он двигался от плота. Следовательно, катера вернутся одновременно (ответ 3).
Быстрый катер дольше уплывет от лодки, но будет двигаться быстрее и при обратном движении, медленный — наоборот. Однако если перейти в систему отсчета, связанную с водой, решение очень несложно. В этой системе отсчета плот покоится, каждый катер при движении от плота и к плоту движется с одинаковой скоростью. Поэтому каждый катер вернется к плоту через то же самое время после разворота, в течение которого он двигался от плота. Следовательно, катера вернутся одновременно (ответ 3).
Путь и перемещение в физике
Содержание:
Путь и перемещение:
Вы знаете, что любой вид движения совершается по определенной траектории.
Траектория — это линия, которую описывает материальная точка при своем движении в данной системе отсчета. Эта линия может быть и невидима, например, траектория движения рыбы в воде, самолета в небе, пчелы в воздухе и др., которые можно только вообразить. По форме траектории механическое движение делится на прямолинейное и криволинейное.
Движение, траектория которого представляет собой прямую линию относительно данной системы отсчета, называется прямолинейным движением (b), а движение, траектория которого кривая линия, — криволинейным (с).
Длина траектории движения материальной точки, называется пройденным путем. Пройденный путь является положительной скалярной величиной, обозначается буквой
Для полного описания движения материальной точки необходимо определить изменение его положения в пространстве с течением времени, т.е. определить изменение координат материальной точки, или же изменение его радиус-вектора.
Изменение любой физической величины равно разности его конечного и начального значений и обозначается знаком (буква греч. алфавита) перед этой величиной.
Изменение координат материальной точки во время движенияИзменение координат материальной точки во время движения может быть, как положительным, так и отрицательным. Например, предположим, что муравей, двигаясь по показанной на рисунке траектории, попадает из точки М в точку N (d). Так как координата муравья по оси X увеличивается то изменение координаты по этой оси будет положительным: Координата же муравья по оси У уменьшается поэтому изменение его координаты по этой оси будет отрицательным:
Например, предположим, что муравей, двигаясь по показанной на рисунке траектории, попадает из точки М в точку N (d). Так как координата муравья по оси X увеличивается то изменение координаты по этой оси будет положительным: Координата же муравья по оси У уменьшается поэтому изменение его координаты по этой оси будет отрицательным:
На следующем рисунке представлены радиус-векторы и начального и конечного положения, материальной точки (муравья) соответственно (е). Вектор соединяющий концы этих радиус-векторов называют перемещением данной материальной точки за промежуток времени Согласно правилу сложения векторов: Из последнего выражения получается, или где — перемещение материальной точки.
Перемещение — это направленный отрезок прямой, соединяющий начальное положение движущейся материальной точки с ее конечным положением.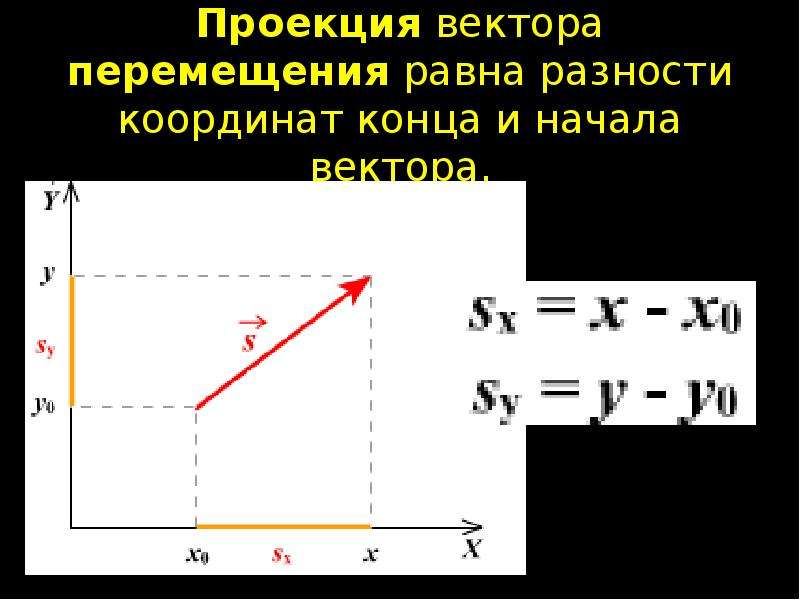 Перемещение — векторная величина.
Перемещение — векторная величина.
Векторная величина — это величина, определяемая, кроме числового значения (модуля), также и направлением.
К вектору перемещения, как векторной величине, можно применить известные действия над векторами — сложение и вычитание векторов, определение результирующего вектора методом треугольника и параллелограмма.
Единицей измерения перемещения, как и пути, в СИ является метр, однако, перемещение имеет отличающийся физический смысл: перемещение показывает, на какое расстояние и в каком направлении изменилось начальное положение материальной точки за данный промежуток времени.
Внимание! Только при прямолинейном движении без изменения направлении, модуль перемещения равен пройденному пути, во всех остальных случаях (при изменении направления прямолинейного движения, криволинейном движении) пройденный путь больше модуля перемещения (е).
Материальная точка прошла расстояние от точки М до точки N по прямой линии.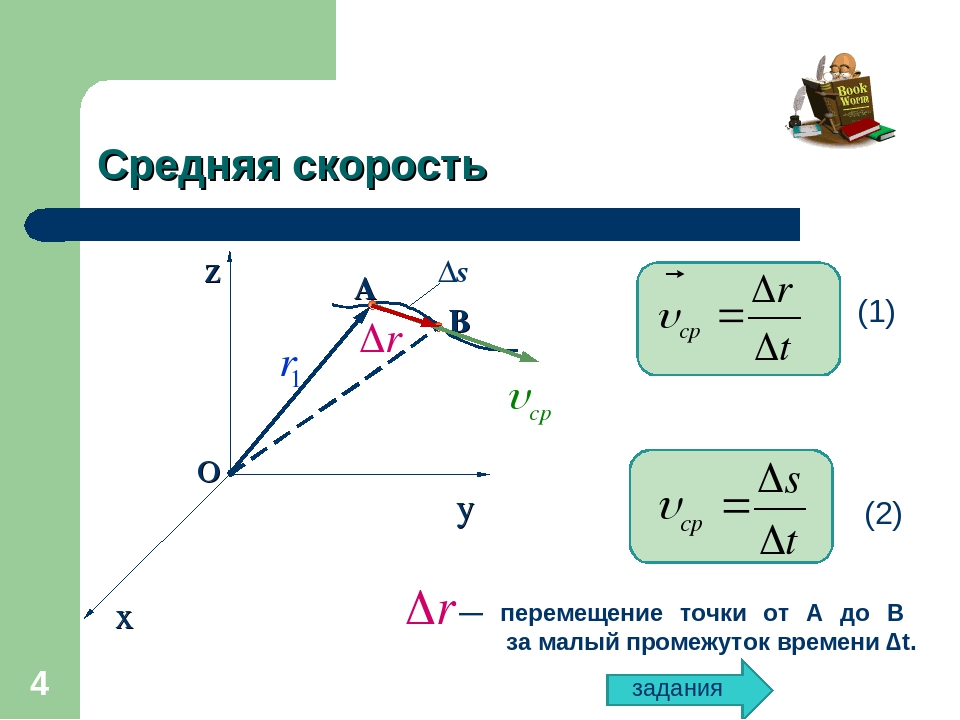 В этом случае пройденный путь равен модулю перемещения:
В этом случае пройденный путь равен модулю перемещения:
Материальная точка прошла расстояние от точки М до точки N по прямой линии, а затем по этой же линии вернулась назад в точку В этом случае материальная точка прошла путь, равный а модуль перемещения равен нулю:
Если при движении материальной точки на плоскости известны его начальные координаты и вектор перемещения, то можно определить координаты конечного положения точки. Например, предположим, что материальная точка совершила перемещение Опуская перпендикуляры на оси ОХ и OY из начала и конца этого вектора, получаем проекции перемещения и (h). Как видно из рисунка, эти проекции равны разности начальных и конечных координат материальной точки:
Одинаковы ли путь и перемещениеЗадача:
Велосипедист движется по круговому велотреку радиусом 80 м. Он стартует из точки А. Определите путь и перемещение велосипедиста при первом прохождении точки В (i).
Он стартует из точки А. Определите путь и перемещение велосипедиста при первом прохождении точки В (i).
Дано:
Решение:
Пройденный путь равен длине дуги:
Модуль перемещения же равен диаметру окружности:
Вычисление:
Что такое путь и перемещениеАвтобус отправился из Москвы в 9 часов утра. Можно ли определить, где находился автобус в 11 часов, если известно, что он проделал путь
Конечно, нет. Ясно лишь, что в 11 часов он находился в месте, удаленном от Минска не более чем на 100 км (т. е. внутри окружности, изображенной на рисунке 37). Не исключено, что к 11 часам автобус вернулся в Москву.
Значит, для определения конечного положения тела недостаточно знать его начальное положение и пройденный им путь.
Мы нашли бы местонахождение автобуса в 11 часов, если бы знали траекторию его движения (зеленая линия на рисунке 38). Отсчитав 100 км от начальной точки маршрута вдоль траектории, найдем, что в 11 часов автобус прибыл в Борисов.
А можно поступить иначе. Конечное положение автобуса можно определить, зная его начальное положение и всего одну векторную величину, называемую перемещением.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
Обозначим перемещение символом На рисунке 38 вектор — это перемещение автобуса из Минска в Мытищи, вектор — из Мытищь в Балашиху, а вектор — из Минска в Борисов.
Теперь, даже не зная траектории, по начальной точке и перемещению мы можем найти конечную точку для каждого из участков движения автобуса и для всего маршрута в целом.
Можно ли сравнивать путь S, пройденный телом, с его перемещением Нельзя, поскольку путь S — скаляр, а перемещение — вектор.
Сравнивать путь S можно с модулем перемещения который является скалярной величиной. Равен ли путь модулю перемещения?
В рассматриваемом примере путь, пройденный автобусом за два часа, Он равен длине траектории движения автобуса от Москвы через Мытищи до Балашихи (см.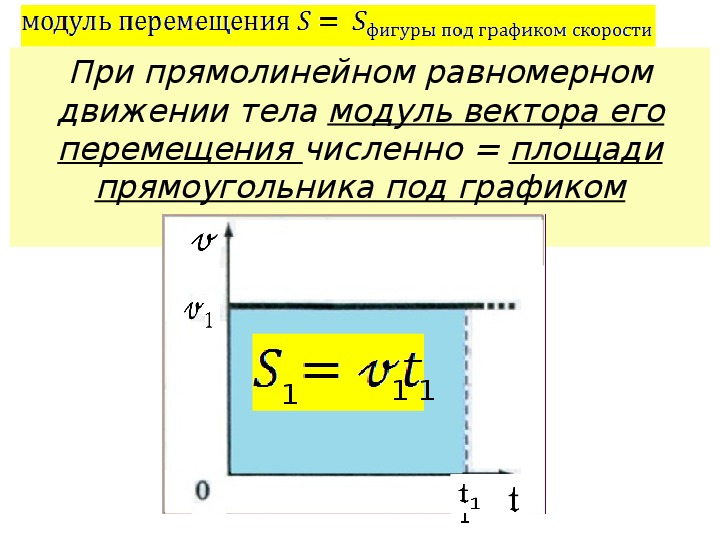 рис. 38). А модуль перемещения автобуса за это время равен расстоянию от Минска до Борисова: Путь автобуса больше модуля его перемещения:
рис. 38). А модуль перемещения автобуса за это время равен расстоянию от Минска до Борисова: Путь автобуса больше модуля его перемещения:
Пройденный путь был бы равен модулю перемещения, если бы автобус все время двигался по прямой, не изменяя направления движения.
Следовательно, путь всегда не меньше модуля перемещения:
Как складывают между собой пути и как — перемещения? Из рисунка 38 находим:
Пройденные пути складывают арифметически, а перемещения — по правилам сложения векторов.
Равен ли при этом модуль сумме модулей Ответьте самостоятельно.
Мы выяснили, что путь и траектория относительны. Покажите на примерах, что перемещение тоже относительно, т. е. зависит от выбора системы отсчета.
При решении задач важно уметь находить проекции перемещения. Построим вектор перемещения куска мела по школьной доске из точки А в точку С (рис. 39). Из рисунка видно, что проекции вектора на координатные оси Ох и Оу равны разности координат конца и начала этого вектора:
Главные выводы:
- Путь — это длина участка траектории, пройденного телом за данный промежуток времени.
 Путь — положительная скалярная величина.
Путь — положительная скалярная величина. - Перемещение тела — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
- Путь не меньше модуля перемещения тела за то же время.
- Пройденные пути складываются арифметически, а перемещения — по правилам сложения векторов.
Пример:
Конькобежец пересек прямоугольную ледовую площадку по диагонали АВ, а пешеход прошел из точки А в точку В по краю площадки (рис. 40). Размеры площадки 60 х 80 м. Определите модули перемещения конькобежца и пешехода и пути, пройденные ими.
Решение
Из рисунка 40 видно, что перемещения пешехода и конькобежца одинаковы. Модуль перемещения:
Путь конькобежца:
Путь пешехода:
Ответ:
Траектория движенияВозьмите лист бумаги и карандаш. Поставьте на листе точки А и В и соедините их кривой линией (рис.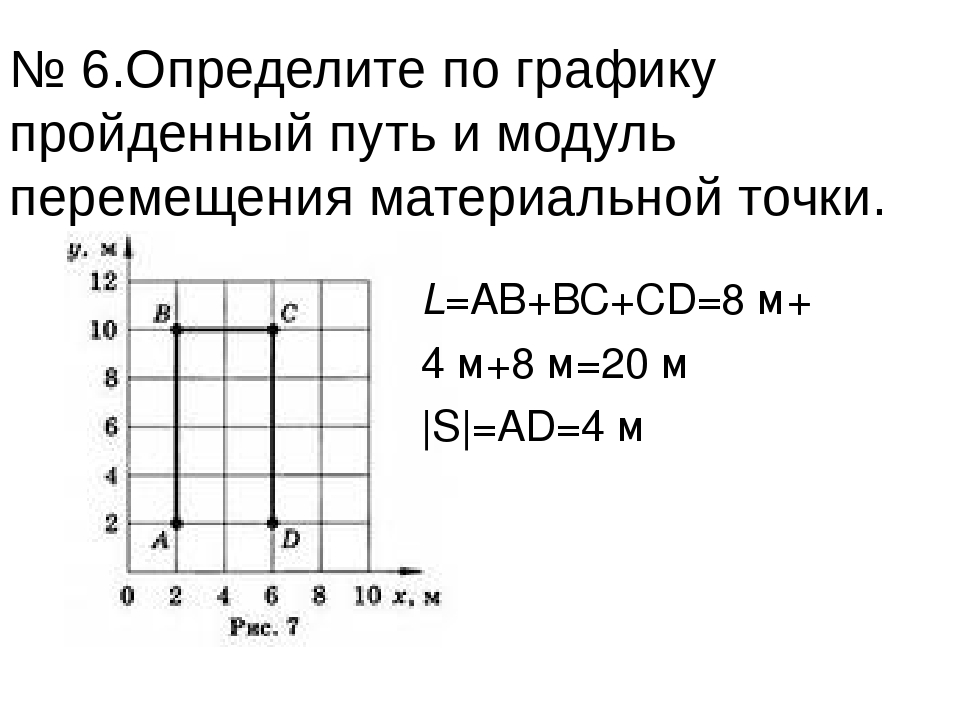 7.1). Эта линия совпадает с траекторией движения кончика карандаша, то есть линией, в каждой точке которой последовательно побывал кончик карандаша во время своего движения.
7.1). Эта линия совпадает с траекторией движения кончика карандаша, то есть линией, в каждой точке которой последовательно побывал кончик карандаша во время своего движения.
Траектория движения — это воображаемая линия, которую описывает в пространстве движущаяся точка. Обычно мы не видим траектории движения тел, но иногда бывают исключения.
Так, в безоблачную погоду высоко в небе можно увидеть белый след, который во время своего движения оставляет самолет*. По этому следу можно определить траекторию движения самолета. Траектории движения каких тел можно восстановить по следам, изображенным на рис. 7.2? В каких случаях траекторию движения «заготавливают» заранее? Форма траектории может быть разной: прямая, окружность, дуга, ломаная и т. д. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел (рис. 7.3).
Форма траектории движения тела зависит от того, относительно какой системы отсчета рассматривают движение. Приведем пример. У мальчика, едущего в автобусе, упало из рук яблоко (рис. 7.4). Для девочки, сидящей напротив, траектория движения яблока — короткий отрезок прямой. В этом случае система отсчета, относительно которой рассматривается движение яблока, связана с салоном автобуса. Но все время, пока яблоко падало, оно «ехало» вместе с автобусом, поэтому для человека, стоящего на обочине дороги, траектория движения яблока абсолютно другая. Система отсчета в таком случае связана с дорогой.
Приведем пример. У мальчика, едущего в автобусе, упало из рук яблоко (рис. 7.4). Для девочки, сидящей напротив, траектория движения яблока — короткий отрезок прямой. В этом случае система отсчета, относительно которой рассматривается движение яблока, связана с салоном автобуса. Но все время, пока яблоко падало, оно «ехало» вместе с автобусом, поэтому для человека, стоящего на обочине дороги, траектория движения яблока абсолютно другая. Система отсчета в таком случае связана с дорогой.
Вернемся к началу (см. рис. 7.1). Чтобы найти путь, который прошел конец карандаша, рисуя кривую линию, необходимо измерить длину этой линии, то есть найти длину траектории (рис. 7.5). Путь — это физическая величина, равная длине траектории. Путь обозначают символом l. Единица пути в СИ — метр: [l]= м. Используют также дольные и кратные единицы пути, например миллиметр (мм), сантиметр (см), километр (км):
Путь, пройденный телом, будет разным относительно разных систем отсчета. Вспомним яблоко в автобусе (см. рис. 7.4): для пассажиров яблоко прошло путь около полуметра, а для человека на обочине дороги — несколько метров. Вернемся к рис. 7.1. Соединив точки А и В отрезком прямой со стрелкой, получим направленный отрезок, который покажет, в каком направлении и на какое расстояние переместился конец карандаша (рис. 7.6).
Вспомним яблоко в автобусе (см. рис. 7.4): для пассажиров яблоко прошло путь около полуметра, а для человека на обочине дороги — несколько метров. Вернемся к рис. 7.1. Соединив точки А и В отрезком прямой со стрелкой, получим направленный отрезок, который покажет, в каком направлении и на какое расстояние переместился конец карандаша (рис. 7.6).
Направленный отрезок прямой, соединяющий начальное и конечное положения тела, называют перемещением. Перемещение обозначают символом . Стрелка над символом показывает, что перемещение — это векторная физическая величина*. Чтобы правильно задать перемещение, необходимо указать не только его значение (модуль), но и направление.
Модуль перемещения, то есть расстояние, на которое переместилось тело в определенном направлении, также обозначают символом s, но без стрелки. Единица перемещения в СИ такая же, как и единица пути, — метр: [s]= м. В общем случае перемещение не совпадает с траекторией движения тела (рис. 7.7, а, б), поэтому путь, пройденный телом, обычно больше модуля перемещения. Путь и модуль перемещения равны только в том случае, когда тело движется вдоль прямой в неизменном направлении (рис. 7.7, в).
7.7, а, б), поэтому путь, пройденный телом, обычно больше модуля перемещения. Путь и модуль перемещения равны только в том случае, когда тело движется вдоль прямой в неизменном направлении (рис. 7.7, в).
Итоги:
Воображаемая линия, которую описывает в пространстве движущаяся точка, называется траекторией. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел. Путь l — это физическая величина, равная длине траектории. Перемещение — это направленный отрезок прямой, соединяющий начальное и конечное положения тела. Единица пути и перемещения в СИ — метр (м).
Физические величины, имеющие значение и направление, называется векторными а имеющие только значение — скалярными.
Физика 9 кл. Перемещение при прямолинейном равномерном движении
Физика 9 кл. Перемещение при прямолинейном равномерном движении
- Подробности
- Просмотров: 236
1. Когда тело движется прямолинейно и равномерно?
Когда тело движется прямолинейно и равномерно?
Тело движется прямолинейно и равномерно, если оно движется по прямолинейной траектории и проходит за любые равные промежутки времени одинаковые пути.
2. Что называется скоростью равномерного прямолинейного движения?
Скорость равномерного прямолинейного движения — это постоянная векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка.
При прямолинейном равномерном движении векторы скорости и перемещения направлены в одну и ту же сторону.
Формула для перемещения при прямолинейном равномерном движении::
3. Как найти проекцию вектора перемещения тела, движущегося прямолинейно и равномерно, если известны проекция вектора скорости и время движения?
По знаку проекции можно судить о том, как направлен соответствующий ей вектор по отношению к выбранной оси.
4. При каком условии модуль вектора перемещения, совершённого телом за некоторый промежуток времени, равен пути, пройденному телом за тот же промежуток времени?
При движении в одном направлении модуль вектора перемещения, совершённого телом за некоторый промежуток времени, равен пути, пройденному этим телом за тот же промежуток времени.
Если при решении задачи на прямолинейное движение нас не интересует направление векторов перемещения и скорости, то можно воспользоваться формулой, в которую входят их модули:
Если направление движения тела меняется, то пройденный путь окажется больше модуля вектора перемещения.
5. Что представляет собой график скорости при прямолинейном равномерном движении?
При прямолинейном равномерном движении скорость не меняется.
Графиком скорости является горизонтальная прямая, параллельная координатной оси времени.
При прямолинейном равномерном движении тела модуль вектора его перемещения численно равен площади прямоугольника, заключённого между графиком скорости, осью Ot и перпендикулярами к этой оси, восставленными из точек, соответствующих моментам начала и конца наблюдения (в данном случае О и t1).
Часто эту площадь называют площадью под графиком скорости.
6. Докажите, что при равномерном движении модуль вектора перемещения численно равен площади под графиком скорости.
При прямолинейном равномерном движении тела модуль вектора перемещения s1, совершённого телом за промежуток времени t1 определяется по формуле:
s1 = v1t1
Одновременно произведение v1t1 численно равно площади закрашенного прямоугольника под графиком скорости, так как отрезки v1, и t1 являются смежными сторонами этого прямоугольника.
Значит, при прямолинейном равномерном движении тела модуль вектора его перемещения численно равен площади прямоугольника, заключенного под графиком скорости.
7. Какую информацию о движении двух тел можно получить по графикам, изображённым на рисунке?
График зависимости проекции вектора скорости от времени:
На графиках проекций отражены не только модули проекций, но и знаки.
График проекции вектора скорости 1-го тела проходит в области положительных значений оси скорости.
ax1 > 0
Значит тело 1 движется в направлении координатной оси Ot.
График проекции вектора скорости 2-го тела проходит в области отрицательных значений оси скорости.
ax2 < 0
Значит тело 2 движется в направлении противоположном координатной оси Ot.
То же самое можно сказать и про прямоугольники, площади которых численно равны проекциям векторов перемещений:
Проекция вектора перемещения 1-го тела : sx1 > 0.
Вектор перемещения 1-го тела направлен в направлении оси Ot.
Проекция вектора перемещения 2-го тела : sx2 < 0.
Вектор перемещения 2-го тела направлен противоположно оси Ot.
Направления векторов скорости и перемещения для каждого тела совпадают.
Следующая страница — смотреть
Назад в «Оглавление» — смотреть
Перемещение тела при равноускоренном движении
Прямолинейным равноускоренным движением называется движение, при котором скорость тела за любые равные
промежутки времени изменялась на одинаковую величину. И основной
характеристикой такого движения являлось ускорение — это физическая
векторная величина, характеризующая быстроту изменения скорости.
И основной
характеристикой такого движения являлось ускорение — это физическая
векторная величина, характеризующая быстроту изменения скорости.
Как определить координату тела, пройденный путь и перемещение при прямолинейном равноускоренном движении?
Это можно сделать, если рассмотреть прямолинейное равноускоренное движение как набор большого количества очень малых равномерных перемещений тела.
Первым решил задачу местоположения тела
в определённый момент времени при ускоренном движении итальянский учёный
Галилео Галилей. Галилей использовал
наклонную плоскость с гладкой канавкой посередине, по которой скатывались
латунные шары. По водным часам он засекал определённый интервал времени и
фиксировал расстояния, которые за это время преодолевали шары. Галилей выяснил,
что если время увеличить в два раза, то шары прокатятся в четыре раза дальше
(т.е. зависимость квадратичная). Это опровергало мнение Аристотеля, что
скорость шаров будет постоянной.
Получим формулу для определения перемещения при равноускоренном движении графическим методом.
Известно, что при равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с течением времени не остается постоянной, а меняется со временем согласно формуле
Т. е. скорость является линейной функцией, и поэтому графики скорости имеют вид прямой.
Прямая 1 соответствует движению с положительным ускорением (скорость увеличивается), прямая 2 — движению с отрицательным ускорением (скорость убывает).
График скорости разобьем на маленькие прямоугольные участки. Каждый участок будет соответствовать определённой постоянной скорости.
Необходимо определить пройденный путь за первый промежуток времени. Запишем формулу
Теперь посчитаем суммарную площадь всех имеющихся у нас фигур. А
сумма площадей при равномерном движении – это полный пройденный путь.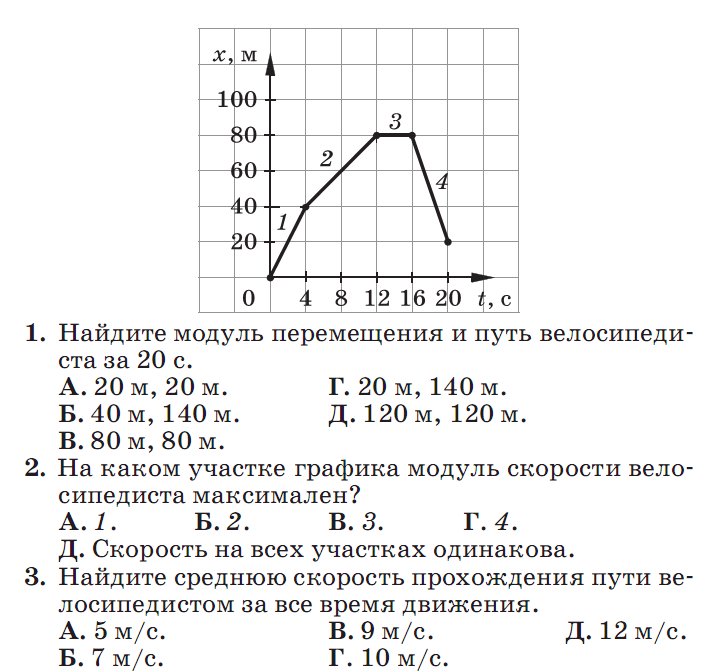
Обратите внимание, от точки к точке скорость будет изменяться, тем самым можно получить путь, пройденный телом именно при прямолинейном равноускоренном движении.
Заметим, что при прямолинейном равноускоренном движении тела, когда скорость и ускорение направлены в одну сторону, модуль перемещения равен пройденному пути, поэтому, когда определяется модуль перемещения, то определяется и пройденный путь.
В данном случае можно говорить, что модуль перемещения будет равен площади фигуры, ограниченной графиком скорости и осью времени.
Фигура, ограниченная графиком скорости и осью времени есть не что иное, как прямоугольная трапеция. Из математики известна формула для нахождения площади трапеции. Площадь трапеции равна произведению половины суммы её оснований на высоту.
Следовательно, перемещение за все время tчисленно
равно площади трапеции ОАВС. В
нашем случае длина одного из оснований численно равна υoх, длина другого
— υх.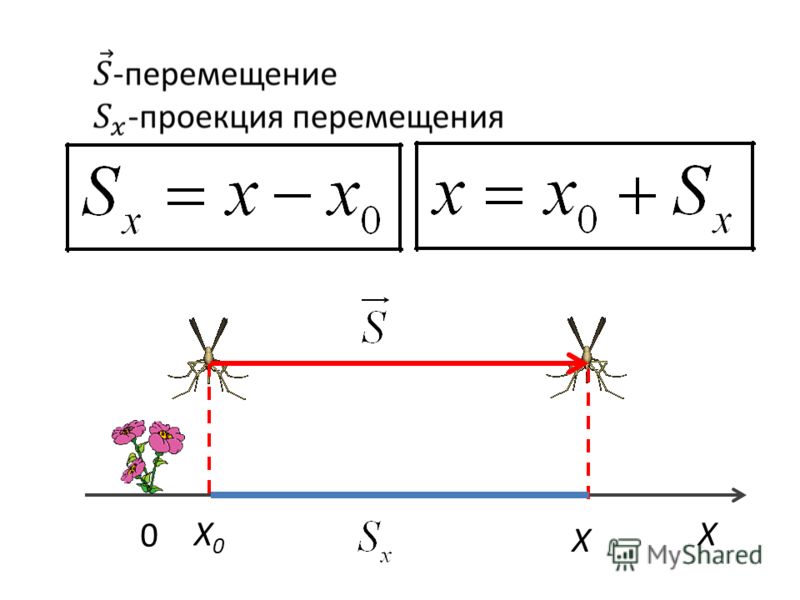 Высота же ее численно равна t. Отсюда следует, что перемещение равно:
Высота же ее численно равна t. Отсюда следует, что перемещение равно:
Подставим в эту формулу вместо υ равную ей величину υ0 + at.Тогда
Разделив почленно числитель на знаменатель, получим
Это есть уравнение перемещения в проекциях на ось координат.
При пользовании этой формулой нужно помнить, что s, υ0 и а могут быть как положительными, так и отрицательными — ведь это проекции векторов пути, начальной скорости и ускорения на ось X.
Теперь вспомним, что пройденный путь, равный в нашем случае модулю перемещения, выражается разностью: s = x – x0
Если в уравнение подставить полученное нами выражение для S, то запишем закон, по которому движется тело при прямолинейном равноускоренном движении:
Это уравнение называется основным кинематическим уравнением
равноускоренного движения.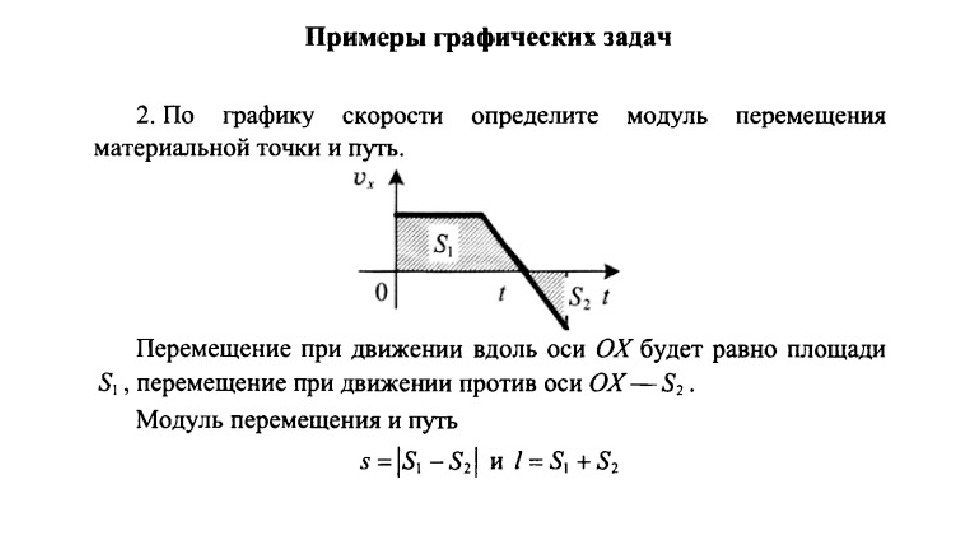
Если тело движется из состояния покоя, график проходит через начало координат, фигура под графиком – прямоугольный треугольник, площадь которого равна половине произведения катетов.
Тогда формула для определения перемещения принимает вид:
Это уравнение перемещения при равноускоренном движении без начальной скорости.
Тогда
x = x0 + at2/2
Это кинематическое уравнение равноускоренного движения , без начальной скорости.
Рассмотрим некоторые важные зависимости между величинами равноускоренного движения. Для равноускоренного движения без начальной скорости путь, пройденный телом, пропорционален квадрату времени. Значит, пути, пройденные телом за 1 с, 2 с, 3 с, 4 с будут относиться как квадраты последовательных натуральных чисел.
Для любого равноускоренного движения, пути, пройденные телом за
любые равные промежутки времени, будут относиться как последовательный ряд
нечетных чисел.
Основные выводы:
– Перемещение тела за все время t численно равно площади трапеции, ограниченной графиком скорости и осью времени.
— уравнениеперемещения
— кинематическое уравнение равноускоренного движения
– Для равноускоренного движения без начальной скорости путь, пройденный телом, пропорционален квадрату времени.
– Для любого равноускоренного движения, пути, пройденныетеломза любые равные промежутки времени, будутотноситьсякакпоследовательный ряд нечетных чисел.
Механическая работа — определение, формула, виды, свойства
Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.
Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.
Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.
Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.
|
Механическая работа А = FS A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] |
Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.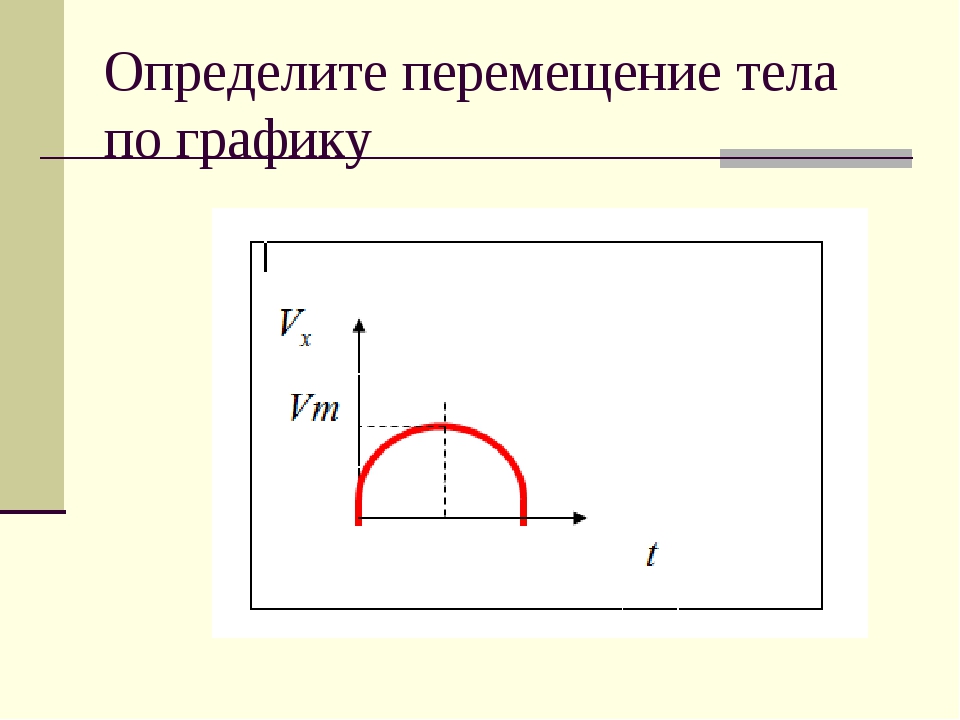
Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.
|
Механическая работа А = FScosα A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] α — угол между векторами силы и перемещения [] |
Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.
Для совершения работы необходимы два условия:
- чтобы на тело действовала сила,
- чтобы происходило перемещение тела.

Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.
Запомнить!
Работа равна нулю, если при приложенной силе перемещение отсутствует.
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Полезная и затраченная работа
Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».
Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.
Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.
|
Потенциальная энергия Еп = mgh m — масса тела [кг] g — ускорение свободного падения [м/с2] h — высота [м] На планете Земля g ≈ 9,8 м/с2 |
Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.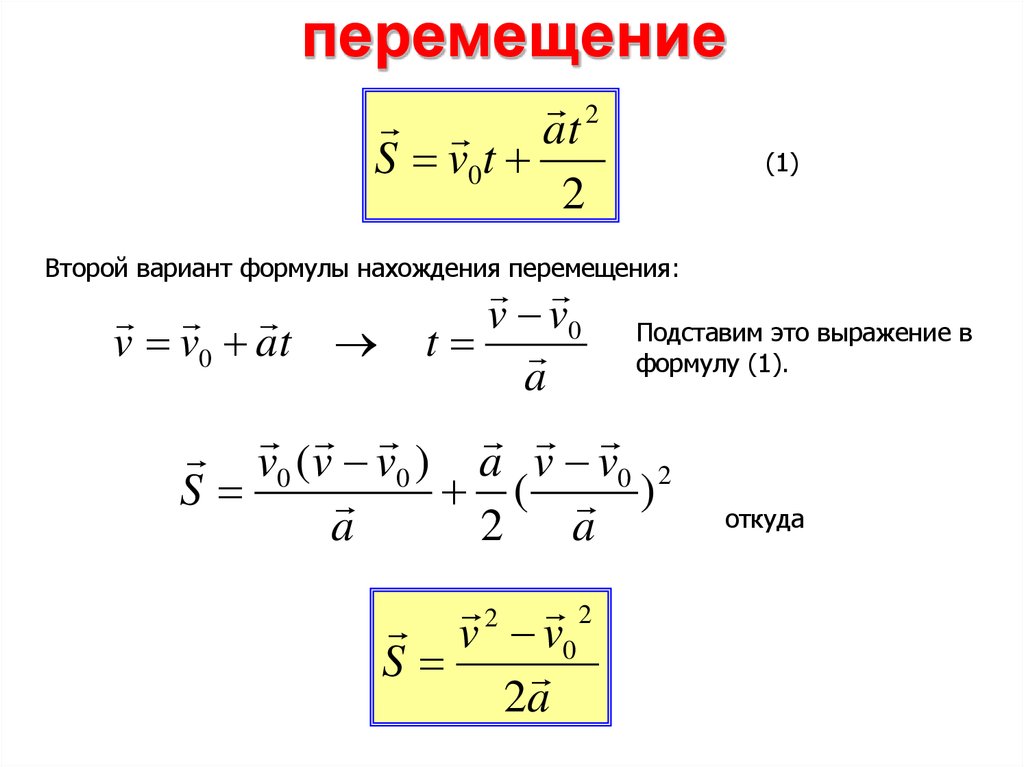
|
Механическая работа А = FS A — механическая работа [Дж] F — приложенная сила [Н] S — путь [м] |
И как же достоверно определить, какая работа полезная, а какая затраченная?
Все очень просто! Задаем два вопроса:
- За счет чего происходит процесс?
- Ради какого результата?
В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).
Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.
Мощность
На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.
Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.
Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.
|
Мощность N = A/t N — мощность [Вт] A — механическая работа [Дж] t — время [с] |
Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.
Также для мощности справедлива другая формула:
|
Мощность N = Fv N — мощность [Вт] F — приложенная сила [Н] v — скорость [м/с] |
Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.
Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:
|
Мощность N = Fvcosα N — мощность [Вт] F — приложенная сила [Н] v — скорость [м/с] α — угол между векторами силы и скорости [] |
Примеры решения задач
Задача 1
Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:
- Выталкивающая сила.
- Сила вязкого трения.

- Сила тяжести.
- Ни одна из перечисленных сил.
Решение
Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.
Ответ: 3.
Задача 2
Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?
Решение
Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:
Ответ: 3200 Дж.
Задача 3
Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?
Решение
В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.
Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:
A = Fl = 30 * 5 = 150 Дж
Ответ: 150 Дж.
Задача 4
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости vx тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?
Решение
На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.
Мощность можно найти по формуле N = Fv.
N = FV = 2×5 = 10 Вт
Ответ: 10 Вт.
Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!
Перемещение, путь, траектория при равномерном прямолинейном движении
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.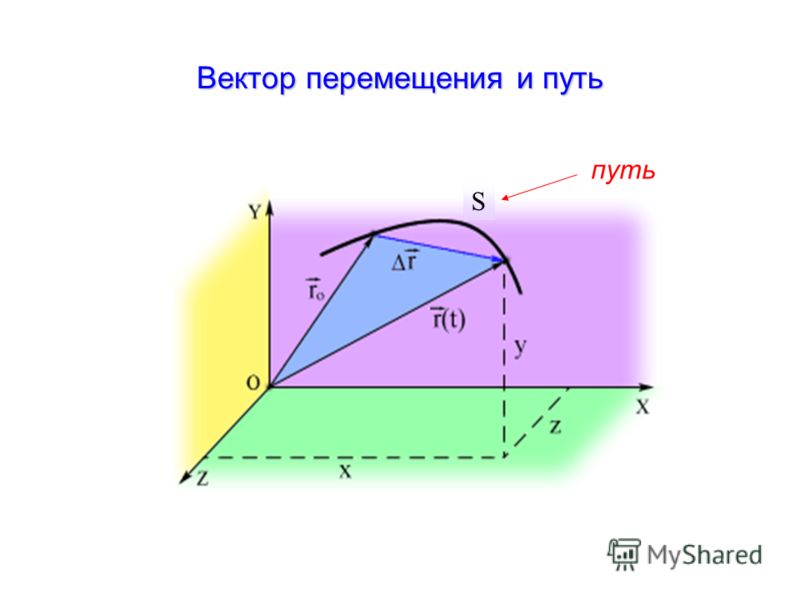
Линия, по которой движется точка тела, называется траекторией движения.
Длина траектории называется пройденным путем.
Обозначается l, измеряется в метрах. (траектория – след, путь – расстояние)
Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.
Вектор, соединяющий начальную и конечную точки траектории, называется перемещением.
Обозначается S, измеряется в метрах. (перемещение – вектор, модуль перемещения – скаляр).
Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций.
Проекция перемещения тела численно равна площади прямоугольника под графиком, так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.
Правило определения перемещения по графику v(t): при прямолинейном равномерном движении модуль вектора перемещения равен площади прямоугольника под графиком скорости.
Зависимость перемещения от времени. График s(t) — наклонная линия:
Из графика видно, что проекция скорости равна:
vх=S/t=tga
Рассмотрев эту формулу, мы можем сказать, чем больше угол a, тем быстрей движется тело и оно проходит больший путь за меньшее время.
Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.
Обозначения:
vх — скорость равномерного прямолинейного движения
S — перемещение тела (расстояние, на которое передвинулось тело)
t — промежуток времени перемещения (время)
a — угол наклона графика к оси времени
v(t) — изменение скорости со временем
S(t) — изменение перемещения (пути) со временем
«Перемещение.
 Траектория. Путь» (9-й класс)
Траектория. Путь» (9-й класс)
Цели урока:
- Образовательная:
– ввести понятия “перемещение”, “путь”, “траектория”. - Развивающая:
– развивать логическое мышление, правильную физическую речь, использовать соответствующую терминологию. - Воспитательная:
– достигать высокой активности класса, внимания, сосредоточенности учащихся.
Оборудование:
- пластмассовая бутылка вместимостью 0,33 л с водой и со шкалой;
- медицинский флакончик вместимостью 10 мл (или малая пробирка) со шкалой.
Демонстрации: Определение перемещения и пройденного пути.
Ход урока
1. Актуализация знаний.
– Здравствуйте, ребята! Садитесь! Сегодня мы с вами продолжим изучать тему
“Законы взаимодействия и движения тел” и на уроке познакомимся с тремя новыми
понятиями (терминами), касающихся этой темы.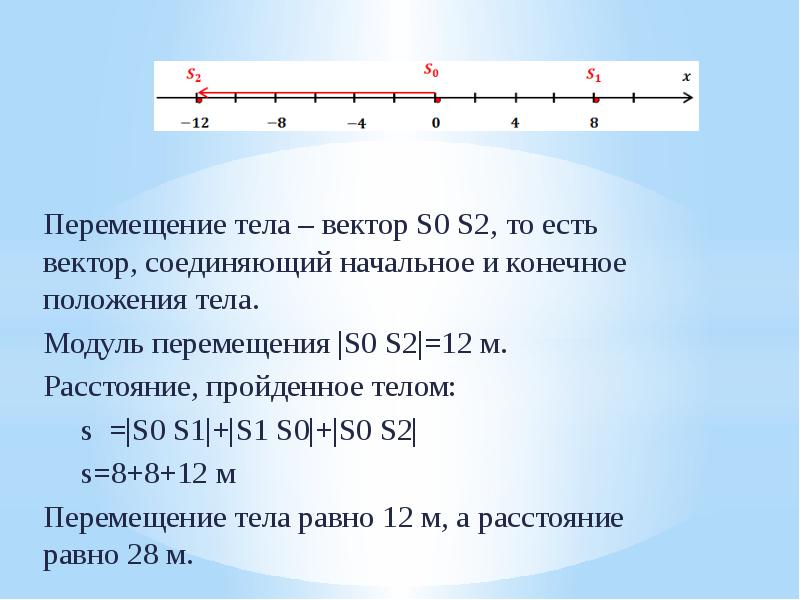 А пока проверим выполнение вами
домашнего задания у данному уроку.
А пока проверим выполнение вами
домашнего задания у данному уроку.
2. Проверка домашнего задания.
Перед уроком один учащийся выписывает на доске решение следующего домашнего задания:
Двум учащимся раздаются карточки с индивидуальными заданиями, которые выполняются во время устной проверки упр. 1 стр. 9 учебника. [1]
Карточка 1: (Приложение 1)
1. Какую систему координат(одномерную, двухмерную, трехмерную) следует выбрать для определения положения тел:
а) трактор в поле;
б) вертолет в небе;
в) поезд
г) шахматная фигура на доске.
2. Дано выражение: S = υ0 · t + (а · t2) / 2, выразите: а, υ0
Карточка 2: (Приложение 2)
1. Какую систему координат (одномерную, двухмерную, трехмерную) следует выбрать для определения положения таких тел:
а) люстра в комнате;
б) лифт;
в) подводная лодка;
г) самолет на взлетной полосе.
2. Дано выражение: S = (υ2 – υ02 ) / 2 · а, выразите: υ2 , υ02.
3. Изучение нового теоретического материала.
С изменениями координат тела связана величина, вводимая для описания движения, – ПЕРЕМЕЩЕНИЕ.
Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.
Перемещение принято обозначать буквой . В СИ перемещение измеряется в метрах (м).
[ ] – [ м ] – метр.
Перемещение – величина векторная, т.е. кроме числового значения имеет еще и направление. Векторную величину изображают в виде отрезка, который начинается в некоторой точке и заканчивается острием, указывающим направление. Такой отрезок-стрелка называется вектором.
– вектор, проведенный из точки М в М1Знать вектор перемещения – значит, знать его направление и модуль. Модуль
вектора – это скаляр, т.е. численное значение. Зная начальное положение и вектор
перемещения тела, можно определить, где находится тело.
Модуль
вектора – это скаляр, т.е. численное значение. Зная начальное положение и вектор
перемещения тела, можно определить, где находится тело.
В процессе движения материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом движущаяся точка “описывает” в пространстве какую-то линию. Иногда эта линия видна, – например, высоко летящий самолет может оставлять за собой след в небе. Более знакомый пример – след куска мела на доске.
Воображаемая линия в пространстве, по которой движется тело называется ТРАЕКТОРИЕЙ движения тела.
Траектория движения тела – это непрерывная линия, которую описывает движущееся тело (рассматриваемое как материальная точка) по отношению к выбранной системе отсчета.
Движение, при котором все точки тела движутся по
одинаковым траекториям, называется поступательным.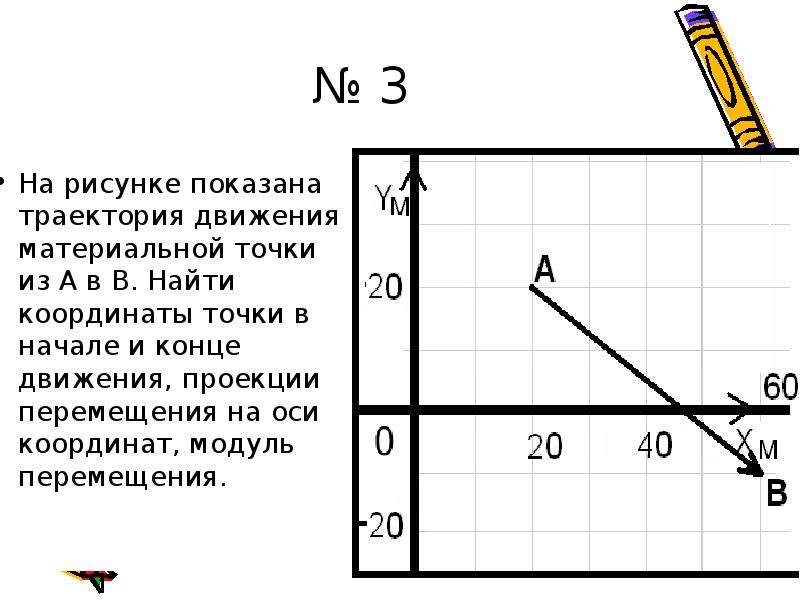
Очень часто траектория – невидимая линия. Траектория движущейся точки может быть прямой или кривой линией. Соответственно форме траектории движение бывает прямолинейным и криволинейным.
Длина траектории – это ПУТЬ. Путь является скалярной величиной и обозначается буквой l. Путь увеличивается, если тело движется. И остается неизменным, если тело покоится. Таким образом, путь не может уменьшаться с течением времени.
Модуль перемещения и путь могут совпадать по значению, только в том случае, если тело движется вдоль прямой в одном направлении.
Чем же отличается путь от перемещения? Эти два понятия часто смешивают, хотя на самом деле они очень сильно отличаются друг от друга. Рассмотрим эти отличия: (Приложение 3) (раздаются в виде карточек каждому ученику)
- Путь – скалярная величина и характеризуется только числовым значением.
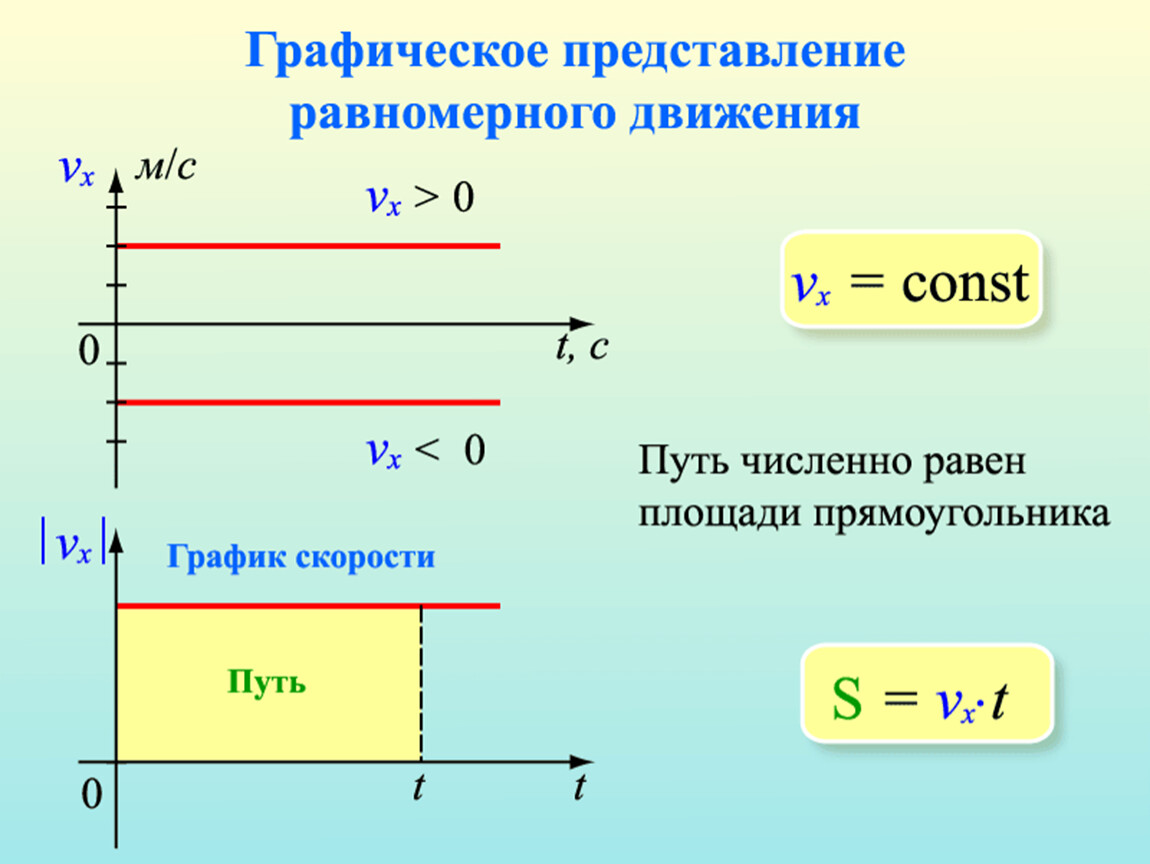
- Перемещение – векторная величина и характеризуется как числовым значением (модулем), так и направлением.
- При движении тела путь может только увеличиваться, а модуль перемещения может как увеличиваться, так и уменьшаться.
- Если тело вернулось в начальную точку, его перемещение равно нулю, а путь нулю не равен.
| Путь | Перемещение | |
| Определение | Длина траектории, описываемой телом за определенное время | Вектор, соединяющий начальное положение тела с его последующим положением |
| Обозначение | l [ м ] | S [м ] |
| Характер физических величин | Скалярная, т. е. определяется только
числовым значением е. определяется только
числовым значением |
Векторная, т.е. определяется числовым значением (модулем) и направлением |
| Необходимость введения | Зная начальное положение тела и путь l, пройденный за промежуток времени t, нельзя определить положение тела в заданный момент времени t | Зная начальное положение тела и S за промежуток времени t, однозначно определяется положение тела в заданный момент времени t |
| l = S в случае прямолинейного движения без возвратов | ||
4. Демонстрация опыта (учащиеся выполняют самостоятельно на своих местах за партами, учитель вместе с учащимися выполняет демонстрацию этого опыта)
- Заполните водой до горловины пластмассовую бутылку со шкалой.
- Флакончик со шкалой заполните водой на 1/5 его объема.

- Наклоните бутылку так, чтобы вода подошла к горловине, но не вытекала из бутылки.
- Быстро опустите флакончик с водой в бутылку (не закрывая его пробкой) так, чтобы горловина флакончика вошла в воду бутылки. Флакончик плавает на поверхности воды в бутылке. Часть воды при этом из бутылки выльется
- Завинтите крышку бутылки.
- Сжимая боковые стенки бутылки, опустите поплавок на дно бутылки.
- Ослабляя давление на стенки бутылки, добейтесь всплытия поплавка. Определите путь и перемещение поплавка:________________________________________________________
- Опустите поплавок на дно бутылки. Определите путь и перемещение поплавка:______________________________________________________________________________
- Заставьте поплавок всплыть и утонуть. Каков путь и перемещение поплавка в этом случае?_______________________________________________________________________________________
5. Упражнения и вопросы для повторения.
Упражнения и вопросы для повторения.
- Путь или перемещение мы оплачиваем при поездке в такси? (Путь)
- Мяч упал с высоты 3 м, отскочил от пола и был пойман на высоте 1 м. найти путь и перемещение мяча. (Путь – 4 м, перемещение – 2 м.)
6. Итог урока.
Повторение понятий урока:
– перемещение;
– траектория;
– путь.
7. Домашнее задание.
§ 2 учебника [1], вопросы после параграфа, упражнение 2 (стр.12) учебника [1], повторить выполнение опыта урока дома.
Список литературы
1. Перышкин А.В., Гутник Е.М. Физика. 9 кл.: учеб.для общеобразоват.учреждений – 9-е изд., стереотип. – М.: Дрофа, 2005.
3.1 Положение, смещение и средняя скорость — University Physics Volume 1
Learning Objectives
К концу этого раздела вы сможете:
- Определите положение, смещение и пройденное расстояние.
- Рассчитайте общее смещение для данного положения как функцию времени.
- Определите общее пройденное расстояние.
- Рассчитайте среднюю скорость с учетом смещения и затраченного времени.
Когда вы находитесь в движении, нужно задать следующие основные вопросы: где вы? Куда ты направляешься? Как быстро ты туда добираешься? Ответы на эти вопросы требуют, чтобы вы указали свое положение, смещение и среднюю скорость — термины, которые мы определяем в этом разделе.
Позиция
Чтобы описать движение объекта, вы должны сначала уметь описать его положение ( x ): , где он находится в любой конкретный момент времени . Точнее, нам нужно указать его положение относительно удобной системы отсчета. Система отсчета — это произвольный набор осей, по которым описывается положение и движение объекта. Земля часто используется в качестве системы отсчета, и мы часто описываем положение объекта по отношению к стационарным объектам на Земле. Например, запуск ракеты можно описать с точки зрения положения ракеты по отношению к Земле в целом, тогда как положение велосипедиста можно описать с точки зрения ее положения по отношению к зданиям, мимо которых он проезжает, рис. 3.2. В других случаях мы используем системы отсчета, которые не являются стационарными, но движутся относительно Земли. Например, чтобы описать положение человека в самолете, мы используем самолет, а не Землю в качестве системы отсчета. Чтобы описать положение объекта, совершающего одномерное движение, мы часто используем переменную x .Позже в этой главе, при обсуждении свободного падения, мы будем использовать переменную y .
Например, запуск ракеты можно описать с точки зрения положения ракеты по отношению к Земле в целом, тогда как положение велосипедиста можно описать с точки зрения ее положения по отношению к зданиям, мимо которых он проезжает, рис. 3.2. В других случаях мы используем системы отсчета, которые не являются стационарными, но движутся относительно Земли. Например, чтобы описать положение человека в самолете, мы используем самолет, а не Землю в качестве системы отсчета. Чтобы описать положение объекта, совершающего одномерное движение, мы часто используем переменную x .Позже в этой главе, при обсуждении свободного падения, мы будем использовать переменную y .
Фигура 3,2 Этих велосипедистов во Вьетнаме можно описать по их положению относительно зданий или канала. Их движение можно описать изменением положения или перемещением в системе отсчета. (кредит: модификация работы Сьюзан Блэк)
Рабочий объем
Если объект перемещается относительно системы координат — например, если профессор перемещается вправо относительно доски Рис.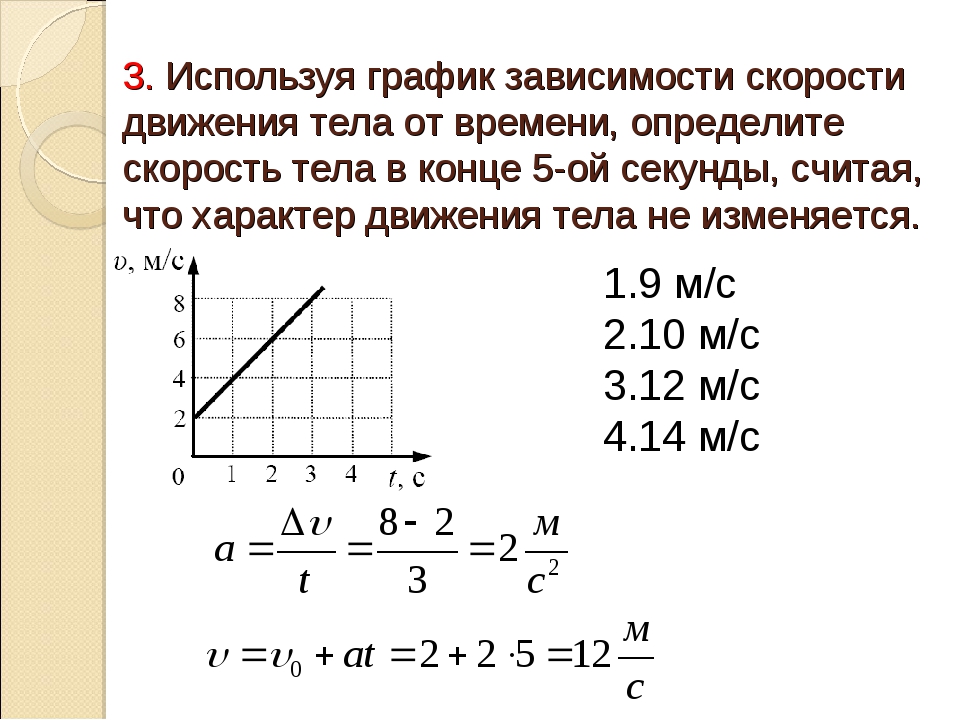 3.3 — затем положение объекта меняется. Это изменение положения называется смещением. Слово смещение подразумевает, что объект переместился или был перемещен. Хотя позиция — это числовое значение x вдоль прямой линии, где мог бы находиться объект, смещение дает изменение положения на вдоль этой линии. Поскольку смещение указывает направление, оно является вектором и может быть как положительным, так и отрицательным, в зависимости от выбора положительного направления.Кроме того, в анализ движения может быть встроено множество смещений. Если значение right положительно, и объект перемещается на 2 м вправо, затем на 4 м влево, отдельные смещения равны 2 м и −4−4 м соответственно.
3.3 — затем положение объекта меняется. Это изменение положения называется смещением. Слово смещение подразумевает, что объект переместился или был перемещен. Хотя позиция — это числовое значение x вдоль прямой линии, где мог бы находиться объект, смещение дает изменение положения на вдоль этой линии. Поскольку смещение указывает направление, оно является вектором и может быть как положительным, так и отрицательным, в зависимости от выбора положительного направления.Кроме того, в анализ движения может быть встроено множество смещений. Если значение right положительно, и объект перемещается на 2 м вправо, затем на 4 м влево, отдельные смещения равны 2 м и −4−4 м соответственно.
Фигура
3.3
Профессор ходит влево и вправо, читая лекцию. Ее положение относительно Земли составляет x . Смещение профессора на +2,0 м относительно Земли показано стрелкой, указывающей вправо.
Смещение
Смещение ΔxΔx — изменение положения объекта:
Δx = xf − x0, Δx = xf − x0,3.1
, где ΔxΔx — смещение, xfxf — конечное положение, а x0x0 — начальное положение.
Мы используем прописную греческую букву дельта (Δ) для обозначения «изменения» любой величины, следующей за ней; таким образом, ΔxΔx означает изменение положения (конечное положение минус исходное положение). Мы всегда вычисляем смещение, вычитая начальную позицию x0x0 из конечной позиции xfxf. Обратите внимание, что единицей СИ для смещения является метр, но иногда мы используем километры или другие единицы длины.Имейте в виду, что когда в задаче используются единицы, отличные от метров, вам может потребоваться преобразовать их в метры, чтобы завершить расчет (см. Приложение B).
Движущиеся объекты также могут иметь серию перемещений. В предыдущем примере с профессором кардиостимулятора отдельные смещения равны 2 м и −4−4 м, что дает общее смещение −2 м. Мы определяем полное смещение ΔxTotalΔxTotal как сумму отдельных смещений и выражаем это математически уравнением
Мы определяем полное смещение ΔxTotalΔxTotal как сумму отдельных смещений и выражаем это математически уравнением
3.2
где ΔxiΔxi — отдельные перемещения. В предыдущем примере
Δx1 = x1 − x0 = 2−0 = 2m. Δx1 = x1 − x0 = 2−0 = 2m.Аналогично
Δx2 = x2 − x1 = −2− (2) = — 4 м. Δx2 = x2 − x1 = −2− (2) = — 4 м.Таким образом,
ΔxTotal = Δx1 + Δx2 = 2−4 = −2m .ΔxTotal = Δx1 + Δx2 = 2−4 = −2m.Полное смещение составляет 2 — 4 = −2 м по оси x . Также полезно рассчитать величину смещения или его размер. Величина смещения всегда положительная. Это абсолютное значение смещения, потому что смещение является вектором и не может иметь отрицательного значения величины.В нашем примере величина полного смещения составляет 2 м, тогда как величина отдельных смещений составляет 2 м и 4 м.
Величину общего смещения не следует путать с пройденным расстоянием. Пройденное расстояние xTotalxTotal — это общая длина пути, пройденного между двумя позициями. В предыдущей задаче пройденное расстояние представляет собой сумму величин отдельных смещений:
Пройденное расстояние xTotalxTotal — это общая длина пути, пройденного между двумя позициями. В предыдущей задаче пройденное расстояние представляет собой сумму величин отдельных смещений:
Средняя скорость
Чтобы вычислить другие физические величины в кинематике, мы должны ввести переменную времени. Переменная времени позволяет нам не только указывать, где находится объект (его положение) во время его движения, но и насколько быстро он движется. Скорость движения объекта определяется скоростью изменения его положения со временем.
Для каждой позиции xixi мы назначаем определенное время titi. Если детали движения в каждый момент не важны, скорость обычно выражается как средняя скорость v – v–.Эта векторная величина представляет собой просто общее смещение между двумя точками, деленное на время, необходимое для путешествия между ними. Время, необходимое для путешествия между двумя точками, называется затраченным временем ΔtΔt.
Средняя скорость
Если x1x1 и x2x2 — позиции объекта в моменты времени t1t1 и t2t2, соответственно, то
Средняя скорость = v– = Смещение между двумя точками Затраченное время между двумя точками v– = ΔxΔt = x2 − x1t2 − t1. Средняя скорость = v– = Смещение между двумя точками Затраченное время между двумя точками v– = ΔxΔt = x2 − x1t2 − t1.3.3
Важно отметить, что средняя скорость является вектором и может быть отрицательной в зависимости от положений x1x1 и x2x2.
Пример 3.1
Доставка листовок
Джилл отправляется из своего дома, чтобы доставить листовки о распродаже во дворе, двигаясь на восток по своей улице, усеянной домами. На 0,50,5 км и через 9 минут у нее заканчиваются листовки, и ей приходится возвращаться домой, чтобы получить еще. Это займет еще 9 минут. Собрав еще листовки, она снова отправляется по тому же пути, продолжая с того места, на котором остановилась, и заканчивает 1. 0 км от ее дома. Этот третий этап ее путешествия занимает 1515 минут. В этот момент она поворачивает обратно к своему дому, направляясь на запад. Через 1,751,75 км и 2525 минут она останавливается на отдых.
0 км от ее дома. Этот третий этап ее путешествия занимает 1515 минут. В этот момент она поворачивает обратно к своему дому, направляясь на запад. Через 1,751,75 км и 2525 минут она останавливается на отдых.
- Каково полное перемещение Джилл до точки, в которой она останавливается, чтобы отдохнуть?
- Какова величина окончательного смещения?
- Какая средняя скорость во время всего путешествия?
- Какое общее расстояние пройдено?
- Постройте график зависимости положения от времени.
Набросок движений Джилл показан на рис. 3.4.
Фигура 3,4 Хронология перемещений Джилл.
Стратегия
Задача содержит данные о различных этапах путешествия Джилл, поэтому было бы полезно составить таблицу физических величин. Нам дается позиция и время в формулировке задачи, чтобы мы могли рассчитать смещения и затраченное время. Мы принимаем восток как положительное направление. Из этой информации мы можем найти полное смещение и среднюю скорость.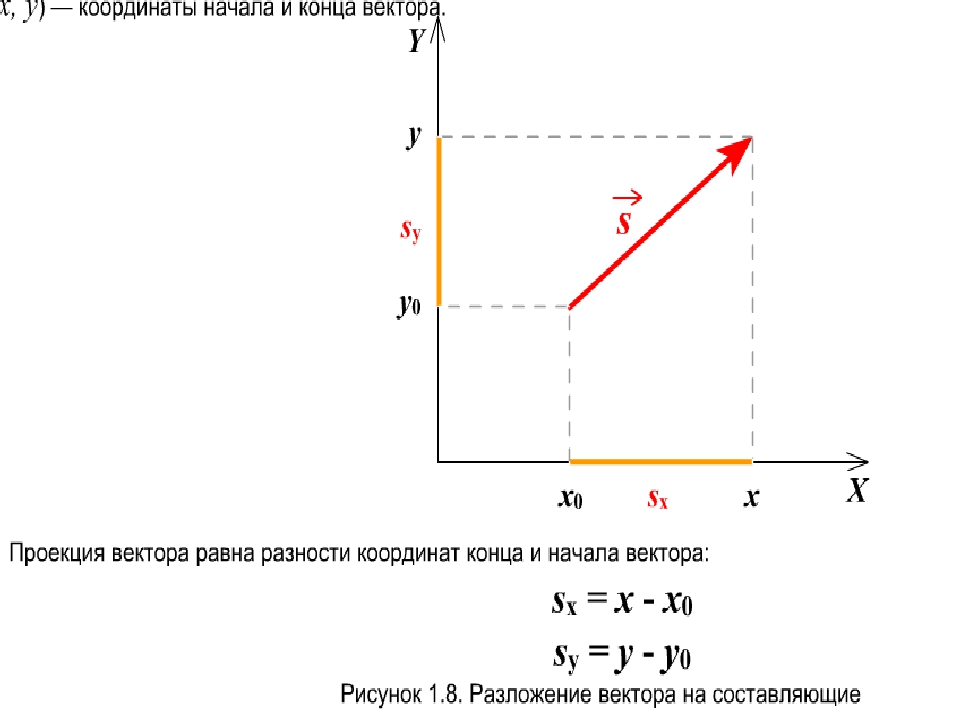 Дом Джилл — отправная точка x0x0. В следующей таблице указаны время и положение Джилл в первых двух столбцах, а смещения рассчитываются в третьем столбце.
Дом Джилл — отправная точка x0x0. В следующей таблице указаны время и положение Джилл в первых двух столбцах, а смещения рассчитываются в третьем столбце.
| Время т i (мин) | Позиция xixi (км) | Водоизмещение ΔxiΔxi (км) |
|---|---|---|
| t0 = 0t0 = 0 | х0 = 0х0 = 0 | Δx0 = 0Δx0 = 0 |
| t1 = 9t1 = 9 | x1 = 0,5×1 = 0,5 | Δx1 = x1 − x0 = 0.5Δx1 = x1 − x0 = 0,5 |
| t2 = 18 t2 = 18 | x2 = 0x2 = 0 | Δx2 = x2 − x1 = −0,5Δx2 = x2 − x1 = −0,5 |
| t3 = 33t3 = 33 | x3 = 1. 0x3 = 1.0 0x3 = 1.0 |
Δx3 = x3 − x2 = 1,0 Δx3 = x3 − x2 = 1,0 |
| t4 = 58 t4 = 58 | x4 = -0,75×4 = -0,75 | Δx4 = x4 − x3 = −1,75 Δx4 = x4 − x3 = −1,75 |
Решение
- Из приведенной выше таблицы полное смещение равно ∑Δxi = 0,5−0,5 + 1,0−1,75 км = −0,75 км. Δxi = 0,5−0,5 + 1.0−1,75 км = −0,75 км.
- Величина полного смещения составляет | -0,75 | км = 0,75 км | -0,75 | км = 0,75 км.
- Средняя скорость = Общее смещение Затраченное время = v — = — 0,75 км 58 мин = −0,013 км / мин Средняя скорость = Общее время затраченного смещения = v — = — 0,75 км 58 мин = −0,013 км / мин
- Общее пройденное расстояние (сумма величин отдельных смещений) равно xTotal = ∑ | Δxi | = 0,5 + 0,5 + 1,0 + 1,75 км = 3,75 км xTotal = ∑ | Δxi | = 0,5 + 0,5 + 1,0 + 1,75 км = 3,75 км.
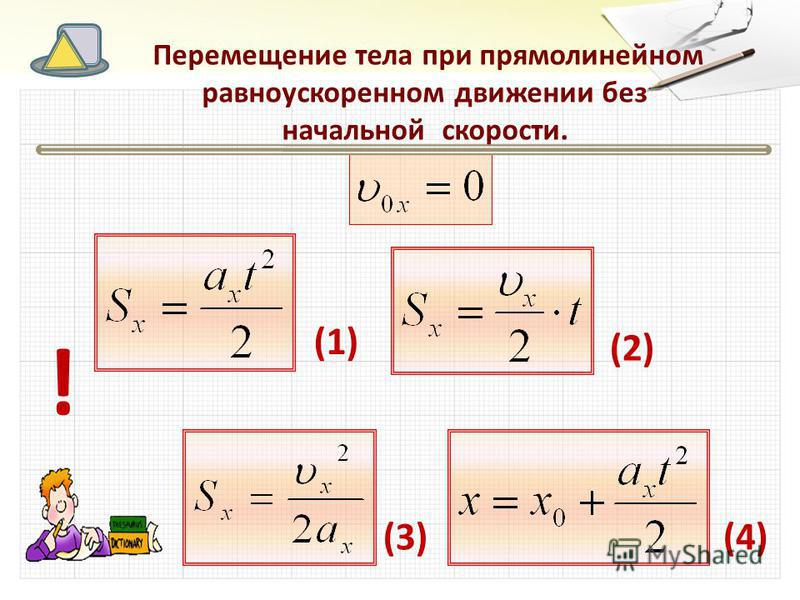
- Мы можем построить график положения Джилл в зависимости от времени, чтобы помочь увидеть движение; график показан на рисунке 3.5.
Фигура 3.5 На этом графике показано положение Джилл во времени. Средняя скорость — это наклон линии, соединяющей начальную и конечную точки.
Значение
Общее перемещение Джилл составляет -0,75 км, что означает, что в конце поездки она проходит 0,75 км0,75 км к западу от своего дома. Средняя скорость означает, что если кто-то будет идти строго на запад со скоростью 0,0130,013 км / мин, начиная с того же времени, когда Джилл вышла из дома, они оба прибудут в конечную точку остановки одновременно.Обратите внимание, что если бы Джилл завершила поездку в своем доме, ее полное смещение было бы равно нулю, как и ее средняя скорость. Общее расстояние, пройденное за 58 минут времени ее поездки, составляет 3,75 км.Проверьте свое понимание 3.1
Велосипедист едет на 3 км на запад, затем разворачивается и едет на 2 км на восток. а) Каково его смещение? б) Какое расстояние пройдено? в) Какова величина его перемещения?
а) Каково его смещение? б) Какое расстояние пройдено? в) Какова величина его перемещения?
2.1 Относительное движение, расстояние и смещение — Физика
Наше изучение физики начинается с кинематики — изучения движения без рассмотрения его причин.Куда бы вы ни посмотрели, объекты движутся. Все, от игры в теннис до полета космического зонда над планетой Нептун, связано с движением. Когда вы отдыхаете, ваше сердце перемещает кровь по венам. Даже в неодушевленных предметах атомы всегда движутся.
Как узнать, что что-то движется? Местоположение объекта в любой момент времени — это его положение. Точнее, нужно указать его положение относительно удобной системы отсчета. Земля часто используется в качестве системы отсчета, и мы часто описываем положение объекта по отношению к неподвижным объектам в этой системе отсчета.Например, запуск ракеты можно описать с точки зрения положения ракеты по отношению к Земле в целом, а положение профессора можно описать с точки зрения ее положения по отношению к соседней белой доске. В других случаях мы используем системы отсчета, которые не являются стационарными, но движутся относительно Земли. Например, чтобы описать положение человека в самолете, мы используем самолет, а не Землю в качестве системы отсчета. (См. Рис. 2.2.) Таким образом, вы можете знать только, насколько быстро и в каком направлении изменяется положение объекта на фоне чего-то еще, что либо не движется, либо движется с известной скоростью и направлением.Система отсчета — это система координат, в которой описывается положение объектов.
В других случаях мы используем системы отсчета, которые не являются стационарными, но движутся относительно Земли. Например, чтобы описать положение человека в самолете, мы используем самолет, а не Землю в качестве системы отсчета. (См. Рис. 2.2.) Таким образом, вы можете знать только, насколько быстро и в каком направлении изменяется положение объекта на фоне чего-то еще, что либо не движется, либо движется с известной скоростью и направлением.Система отсчета — это система координат, в которой описывается положение объектов.
Ваш класс можно использовать в качестве ориентира. В классе стены не двигаются. Ваше движение, когда вы идете к двери, можно измерить на неподвижном фоне стен классной комнаты. Вы также можете сказать, движутся ли другие предметы в классе, например, ваши одноклассники входят в класс или книга падает со стола. Вы также можете сказать, в каком направлении что-то движется в классе.Вы можете сказать: «Учитель идет к двери». Ваша система отсчета позволяет вам определять не только то, что что-то движется, но и направление движения.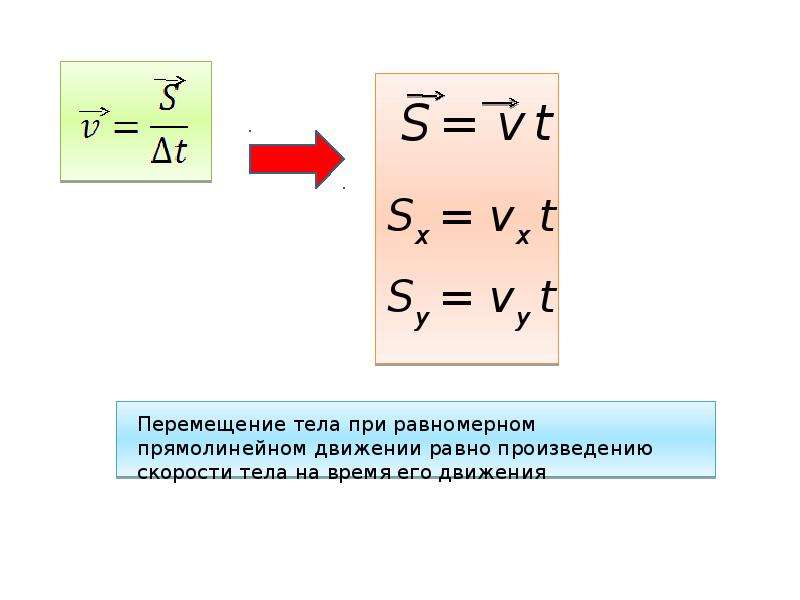
Вы также можете служить ориентиром для движения других. Если вы остались сидеть, когда ваши одноклассники выходили из комнаты, вы бы измерили их перемещение от вашего постоянного местоположения. Если вы и ваши одноклассники выйдете из комнаты вместе, ваше видение их движения изменится. Вы, как система отсчета, двигались бы в том же направлении, что и другие движущиеся одноклассники.Как вы узнаете из Snap Lab, ваше описание движения может сильно отличаться при просмотре с разных опорных кадров.
Расстояние от смещения
Изучая движение объектов, мы сначала должны уметь описать положение объекта. Прежде чем родители отвезут вас в школу, машина стоит на подъездной дорожке. Ваша подъездная дорожка — это стартовая позиция для автомобиля. Когда вы добираетесь до старшей школы, машина меняет положение. Его новая позиция — ваша школа.
Рис. 2.4 Общее изменение вашего положения измеряется от вашего дома до школы.
Физики используют переменные для представления терминов. Мы будем использовать d для обозначения положения автомобиля. Мы будем использовать нижний индекс, чтобы различать начальное положение, d 0 , и конечное положение, d f . Кроме того, векторы, которые мы обсудим позже, будут выделены жирным шрифтом или будут иметь стрелку над переменной.Скаляры будут выделены курсивом.
Советы для успеха
В некоторых книгах для описания положения используется x или s вместо d . В d 0 , указанном d ноль , нижний индекс 0 означает начальный . Когда мы начинаем говорить о двухмерном движении, иногда для описания горизонтального положения используются другие индексы, d x , или вертикальное положение, d y .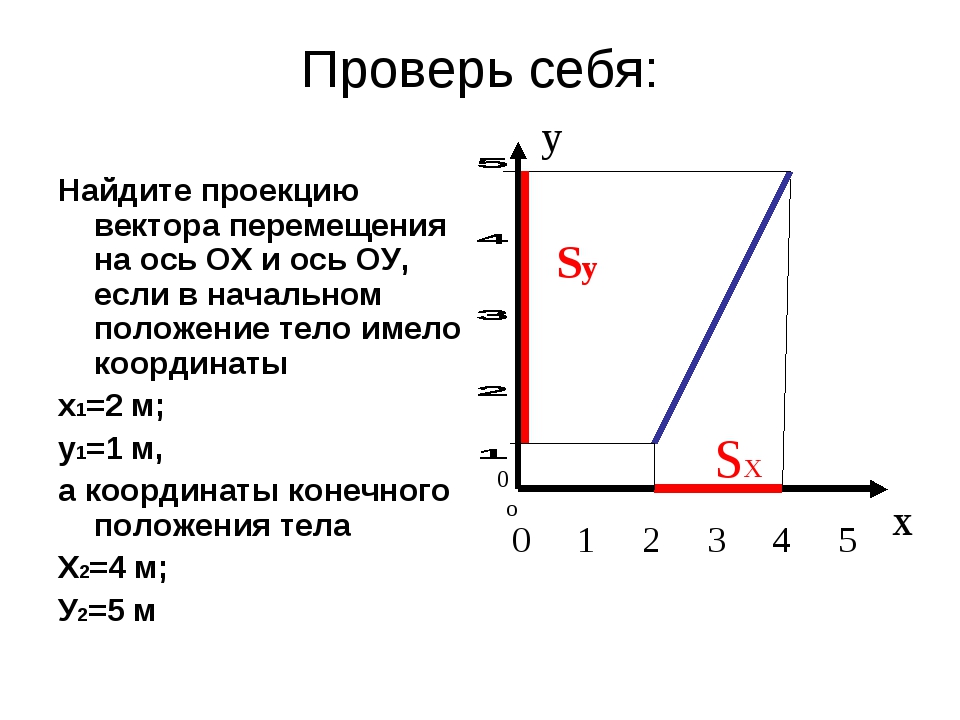 Итак, вы можете увидеть ссылки на d 0x и d fy .
Итак, вы можете увидеть ссылки на d 0x и d fy .
А теперь представьте, что вы едете от своего дома к дому друга, который находится в нескольких километрах от вас. Как далеко вы бы проехали? Расстояние, на которое перемещается объект, — это длина пути между его начальным положением и его конечным положением. Расстояние, которое вы проедете до дома друга, зависит от вашего пути. Как показано на рисунке 2.5, расстояние отличается от длины прямой линии между двумя точками.Расстояние, которое вы проезжаете до дома друга, вероятно, больше, чем прямая линия между двумя домами.
Рис. 2.5 Начальная и конечная точки этого движения разделяются короткой линией, но расстояние по траектории движения значительно больше.
Мы часто хотим быть более точными, когда говорим о позиции. Описание движения объекта часто включает больше, чем просто расстояние, на которое он перемещается.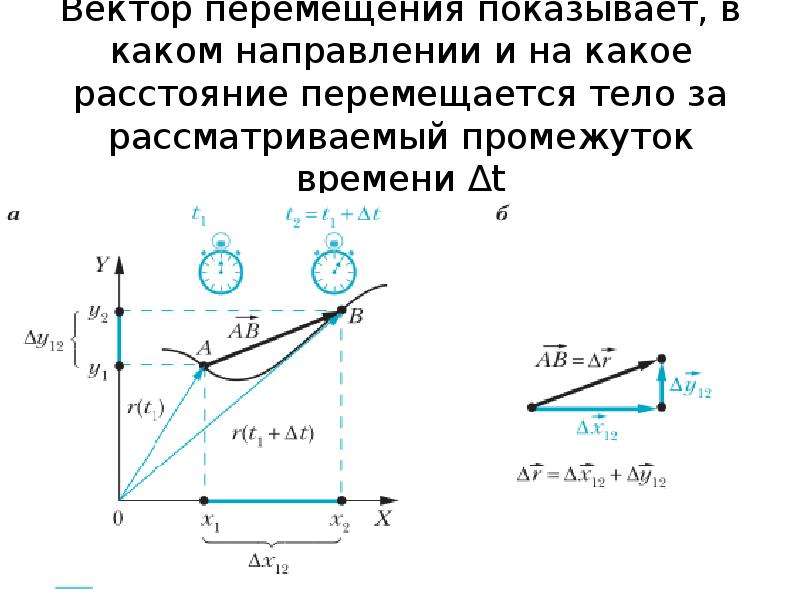 Например, если до школы ехать пять километров, то пройденное расстояние составляет 5 километров.После того, как вы отвезли вас в школу и поехали домой, ваш родитель проехал в общей сложности 10 километров. Автомобиль и ваш родитель окажутся в одной исходной позиции в космосе. Чистое изменение положения объекта — это его смещение, или Δd.Δd. Греческая буква дельта, ΔΔ, означает изменение в .
Например, если до школы ехать пять километров, то пройденное расстояние составляет 5 километров.После того, как вы отвезли вас в школу и поехали домой, ваш родитель проехал в общей сложности 10 километров. Автомобиль и ваш родитель окажутся в одной исходной позиции в космосе. Чистое изменение положения объекта — это его смещение, или Δd.Δd. Греческая буква дельта, ΔΔ, означает изменение в .
Рис. 2.6 Общее расстояние, которое ваша машина преодолевает, составляет 10 км, но полное перемещение равно 0.
Поддержка учителей
Поддержка учителей
Демонстрация учителей
Помогите ученикам узнать разницу между расстоянием и смещением, показывая примеры движения.
- Пока ученики смотрят, пройдите через комнату и попросите учеников оценить длину вашего пути.
- Затем в той же начальной точке пройдите по извилистой дороге к той же конечной точке.
- Опять же, попросите учащихся оценить длину вашего пути.
Спросите: какое движение показало смещение? Какой показывал расстояние? Обратите внимание на то, что первое движение показывает смещение, а второе — расстояние вдоль пути.В обоих случаях начальная и конечная точки были одинаковыми.
[OL] Будьте осторожны, чтобы ученики не предполагали, что начальная позиция всегда равна нулю. Подчеркните, что, хотя исходное положение часто равно нулю, движение может начаться из любого положения относительно начальной точки.
[Визуальный] Продемонстрируйте положительное и отрицательное смещение, поместив двухметровые палки на землю так, чтобы их нулевые метки встали встык. Пока ученики смотрят, поместите небольшую машину у нулевой отметки. Медленно переместите машину справа от студентов на небольшое расстояние и спросите студентов, каково ее смещение.Затем переместите машину слева от нулевой отметки. Обратите внимание на то, что у автомобиля теперь отрицательный рабочий объем.
Студенты узнают больше о векторах и скалярах позже, когда будут изучать двумерное движение. На данный момент достаточно ввести термины и сообщить учащимся, что вектор включает в себя информацию о направлении.
[BL] Спросите студентов, является ли каждая из следующих величин векторной или скалярной величиной: температура (скаляр), сила (вектор), масса (скаляр).
[OL] Попросите учащихся привести примеры векторных и скалярных величин.
[Кинестетика] Раздайте учащимся большие стрелки, вырезанные из плотной бумаги. Попросите их использовать стрелки, чтобы определить величину (количество или длину стрелок) и направление смещения. Подчеркните, что расстояние не может быть представлено стрелками, потому что расстояние не включает направление.
Snap Lab
Расстояние и смещение
В этом упражнении вы сравните расстояние и смещение.Какой термин более полезен при проведении измерений?
- 1 записанная песня доступна на портативном устройстве
- 1 рулетка
- 3 куска малярной ленты
- Комната (похожая на спортзал) со стеной, которая достаточно велика и чиста, чтобы все пары учеников могли ходить взад и вперед, не сталкиваясь друг с другом.

Процедура
- По одному ученику от каждой пары следует стоять спиной к самой длинной стене в классе.Студенты должны стоять на расстоянии не менее 0,5 метра друг от друга. Отметьте эту начальную точку куском малярной ленты.
- Второй ученик из каждой пары должен стоять лицом к партнеру на расстоянии примерно двух-трех метров. Отметьте эту точку вторым куском малярной ленты.
- Студенческие пары выстраиваются в линию у отправной точки вдоль стены.
- Учитель включает музыку. Каждая пара ходит взад и вперед от стены до второй отмеченной точки, пока музыка не перестанет играть.Подсчитайте, сколько раз вы ходите по полу.
- Когда музыка остановится, отметьте конечную позицию третьим куском малярной ленты.
- Измерьте расстояние от начальной начальной позиции до конечной конечной позиции.
- Измерьте длину вашего пути от начальной позиции до второй отмеченной позиции.
 Умножьте полученное значение на общее количество ходов по полу. Затем добавьте это число к своему измерению, полученному на шаге 6.
Умножьте полученное значение на общее количество ходов по полу. Затем добавьте это число к своему измерению, полученному на шаге 6. - Сравните два измерения из шагов 6 и 7.
Контроль захвата
- Какие измерения путешествовала ваше общее расстояние?
- Какое измерение является вашим перемещением?
- Когда вы можете использовать один над другим?
- Измерение общей длины вашего пути от исходного положения до конечного положения дает пройденное расстояние, а измерение от исходного положения до конечного положения является смещением.Используйте расстояние, чтобы описать общий путь между начальным и конечными точками, и использованием перемещением, чтобы описать кратчайший путь между начальным и конечными точками.
- Измерения общей длины вашего пути от исходного положения в конечное положение, это расстоянии, и измерение от вашего начального положения к конечному положению является смещением.
 Используйте расстояние, чтобы описать кратчайший путь между начальным и конечными точками, и использованием перемещением, чтобы описать общий путь между начальным и конечными точками.
Используйте расстояние, чтобы описать кратчайший путь между начальным и конечными точками, и использованием перемещением, чтобы описать общий путь между начальным и конечными точками. - Измерение от исходного положения до конечного положения — это пройденное расстояние, а измерение общей длины вашего пути от исходного положения до конечного положения — смещение. Используйте расстояние, чтобы описать общий путь между начальной и конечной точками, и используйте смещение, чтобы описать кратчайший путь между начальной и конечной точками.
- Измерение от исходного положения до конечного положения — это пройденное расстояние, а измерение общей длины вашего пути от исходного положения до конечного положения — смещение.Используйте расстояние, чтобы описать кратчайший путь между начальной и конечной точками, и используйте смещение, чтобы описать общий путь между начальной и конечной точками.
Поддержка учителя
Поддержка учителя
Выберите комнату, достаточно большую, чтобы все ученики могли беспрепятственно ходить. Убедитесь, что общий пройденный путь достаточно короткий, чтобы учащиеся могли пройти по нему несколько раз в течение песни. Попросите их измерить расстояние между двумя точками и прийти к единому мнению.Когда учащиеся измеряют свое смещение, убедитесь, что они измеряют вперед от направления, которое они отметили в качестве исходного положения. После того, как они завершили лабораторную работу, предложите им обсудить свои результаты.
Убедитесь, что общий пройденный путь достаточно короткий, чтобы учащиеся могли пройти по нему несколько раз в течение песни. Попросите их измерить расстояние между двумя точками и прийти к единому мнению.Когда учащиеся измеряют свое смещение, убедитесь, что они измеряют вперед от направления, которое они отметили в качестве исходного положения. После того, как они завершили лабораторную работу, предложите им обсудить свои результаты.
Если вы описываете только поездку в школу, то пройденное расстояние и перемещение одинаковы — 5 километров. Когда вы описываете весь путь туда и обратно, расстояние и смещение разные. Когда вы описываете расстояние, вы включаете только величину, размер или величину пройденного расстояния.Однако, когда вы описываете смещение, вы принимаете во внимание как величину изменения положения, так и направление движения.
В нашем предыдущем примере автомобиль проезжает в общей сложности 10 километров, но пять из них проезжает вперед, в сторону школы, и пять километров назад, в обратном направлении. Если мы приписываем прямому направлению положительное (+), а противоположное направление — отрицательное (-), то две величины будут уравновешивать друг друга при сложении.
Если мы приписываем прямому направлению положительное (+), а противоположное направление — отрицательное (-), то две величины будут уравновешивать друг друга при сложении.
Величина, такая как расстояние, которая имеет величину (т.е. насколько велика или сколько), но не учитывает направление, называется скаляром. Величина, такая как смещение, которая имеет как величину, так и направление, называется вектором.
Смотреть Physics
Векторы и скаляры
Это видео знакомит с различиями между векторами и скалярами. Он также вводит величины, с которыми мы будем работать во время изучения кинематики.
Проверка захвата
Как это видео помогает вам понять разницу между расстоянием и смещением? Опишите различия между векторами и скалярами на примерах физических величин.- Он объясняет, что расстояние — это вектор, и направление важно, тогда как смещение — это скаляр, и к нему не привязано направление.
- Он объясняет, что расстояние — это скаляр и направление важно, тогда как смещение — это вектор, и к нему не привязано направление.
- Он объясняет, что расстояние является скаляром и не имеет направления, в то время как смещение — это вектор, и направление важно.
- Он объясняет, что и расстояние, и смещение являются скалярными и к ним не привязаны направления.
Teacher Support
Teacher Support
Определите концепции векторов и скаляров перед просмотром видео.
[OL] [BL] Придумайте несколько примеров векторов и скаляров и попросите учащихся классифицировать их.
[AL] Обсудите, как концепция направления может быть важна для изучения движения.
Проблемы смещения
Надеюсь, теперь вы понимаете концептуальную разницу между расстоянием и смещением. Понимание концепций — это половина дела в физике. Другая половина — математика. Камнем преткновения для начинающих студентов-физиков является попытка пройти через математику физики, одновременно пытаясь понять связанные с ней концепции. Эта борьба может привести к неправильным представлениям и бессмысленным ответам. Как только концепция усвоена, математика становится гораздо менее запутанной.
Понимание концепций — это половина дела в физике. Другая половина — математика. Камнем преткновения для начинающих студентов-физиков является попытка пройти через математику физики, одновременно пытаясь понять связанные с ней концепции. Эта борьба может привести к неправильным представлениям и бессмысленным ответам. Как только концепция усвоена, математика становится гораздо менее запутанной.
Итак, давайте рассмотрим ситуацию и посмотрим, сможем ли мы понять смысл смещения в терминах чисел и уравнений. Вы можете рассчитать смещение объекта, вычтя его исходное положение, d 0 , из его конечного положения d f . В математических терминах это означает
Если конечная позиция совпадает с исходной, тогда Δd = 0Δd = 0.
Чтобы присвоить этим величинам числа и / или направление, нам нужно определить ось с положительным и отрицательным направлениями.Нам также необходимо определить происхождение, или O .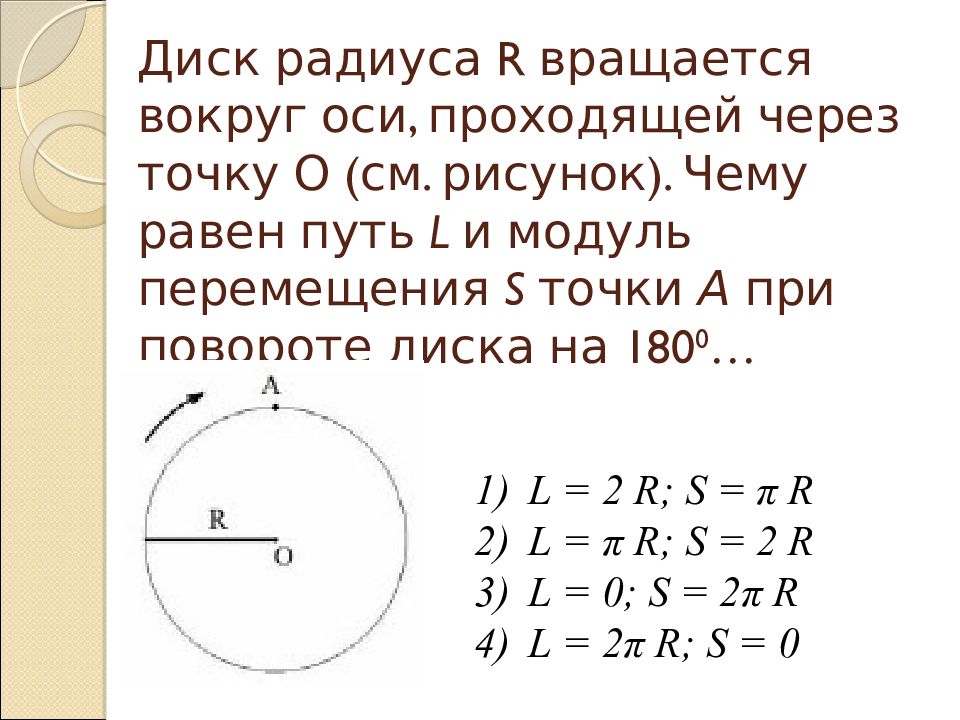 На рисунке 2.6 ось проходит по прямой линии с домом в нуле и школой в положительном направлении. Если бы мы вышли из дома и поехали из школы в обратном направлении, движение было бы в отрицательном направлении. Мы бы присвоили ему отрицательное значение. В круговом движении d f и d 0 оба были на нулевом километре. При поездке в школу в один конец d f находился на расстоянии 5 километров, а d 0 находился на нулевом километре.Итак, ΔdΔd было 5 километров.
На рисунке 2.6 ось проходит по прямой линии с домом в нуле и школой в положительном направлении. Если бы мы вышли из дома и поехали из школы в обратном направлении, движение было бы в отрицательном направлении. Мы бы присвоили ему отрицательное значение. В круговом движении d f и d 0 оба были на нулевом километре. При поездке в школу в один конец d f находился на расстоянии 5 километров, а d 0 находился на нулевом километре.Итак, ΔdΔd было 5 километров.
Советы для успеха
Вы можете разместить свое происхождение где угодно. Вы должны убедиться, что вы рассчитываете все расстояния последовательно от вашего нуля и определяете одно направление как положительное, а другое как отрицательное. Поэтому имеет смысл выбрать наиболее легкую ось, направление и ноль. В приведенном выше примере мы взяли нулевое значение, потому что это позволило нам избежать интерпретации решения с отрицательным знаком.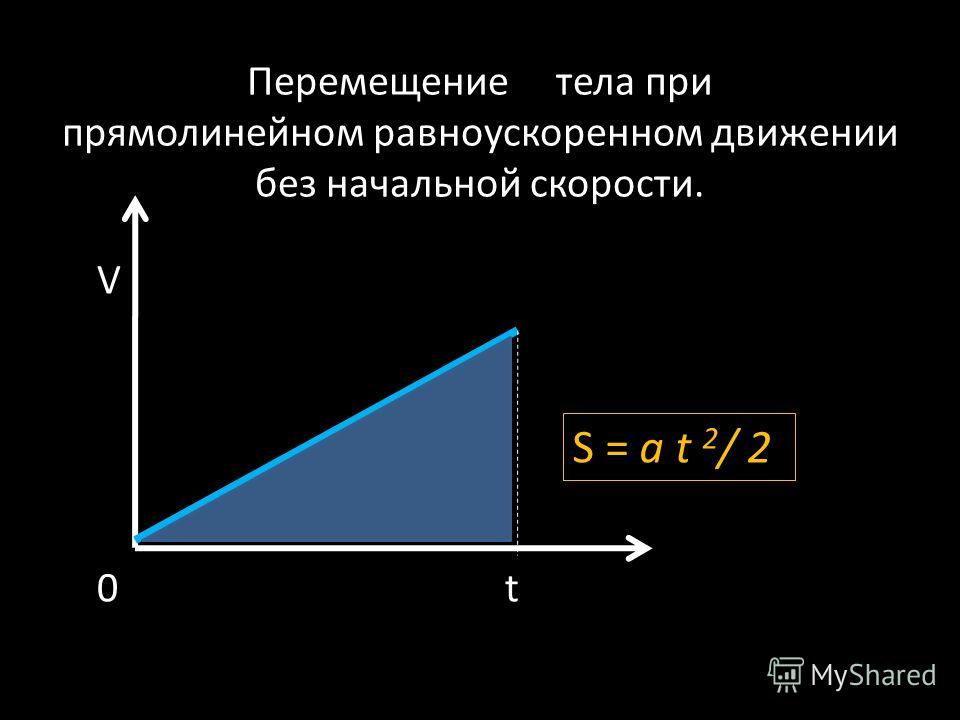
Рабочий пример
Расчет расстояния и смещения
Велосипедист едет на 3 км на запад, затем разворачивается и едет на 2 км на восток.а) Каково ее смещение? б) Какое расстояние она проезжает? в) Какова величина ее перемещения?
Стратегия
Чтобы решить эту проблему, нам нужно найти разницу между конечной позицией и начальной позицией, обращая внимание на направление на оси. Конечное положение — это сумма двух смещений, Δd1Δd1 и Δd2Δd2.
Решение
- Водоизмещение: Водоизмещение всадника составляет Δd = df − d0 = −1 км Δd = df − d0 = −1 км.
- Расстояние: Пройденное расстояние составляет 3 км + 2 км = 5 км.
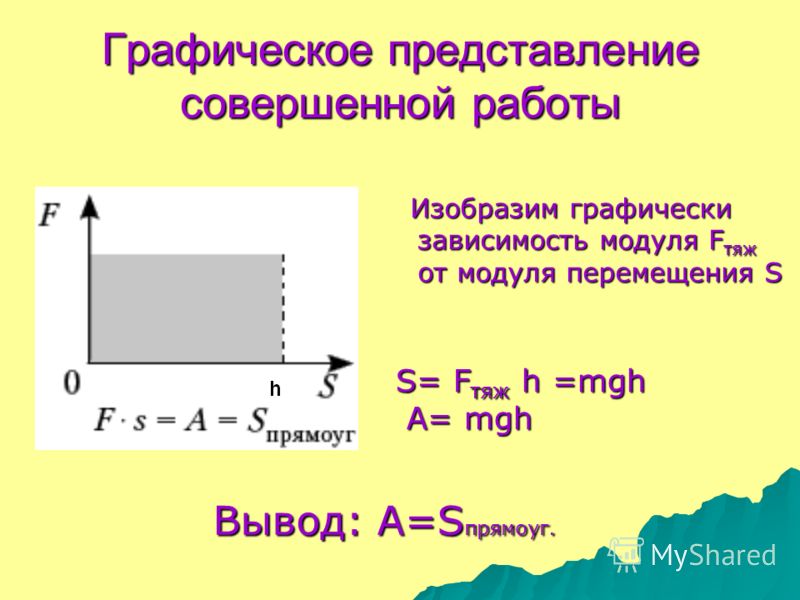
- Величина смещения 1 км.
Обсуждение
Смещение отрицательное, потому что мы выбрали восток как положительный, а запад как отрицательный. Мы также могли описать смещение как 1 км к западу. При расчете смещения имело значение направление, но при расчете расстояния направление не имело значения. Проблема будет работать так же, если проблема будет в направлении север-юг или y .
Советы для успеха
Физики любят использовать стандартные единицы, чтобы было легче сравнивать записи. Стандартные единицы для расчетов называются единиц СИ, единиц (Международная система единиц). Единицы СИ основаны на метрической системе. Единицей измерения смещения в системе СИ является метр (м), но иногда вы можете столкнуться с проблемой с километрами, милями, футами или другими единицами измерения длины.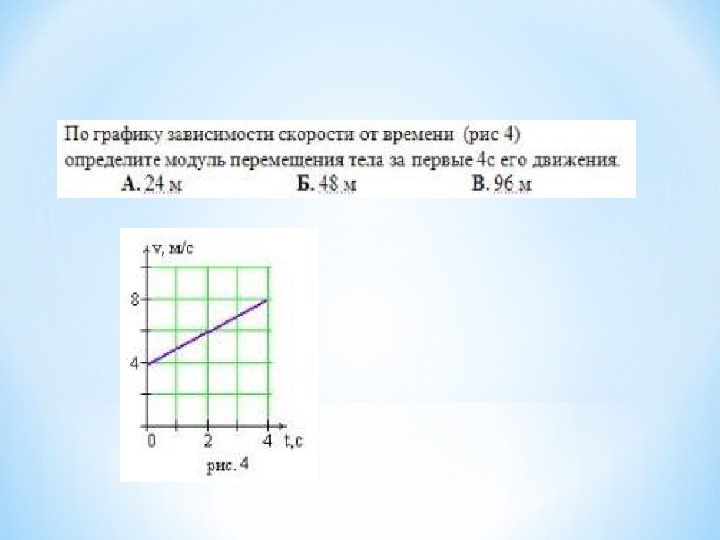 Если одна единица проблемы является единицей СИ, а другая — нет, вам нужно будет преобразовать все ваши количества в одну и ту же систему, прежде чем вы сможете выполнить расчет.2
Если одна единица проблемы является единицей СИ, а другая — нет, вам нужно будет преобразовать все ваши количества в одну и ту же систему, прежде чем вы сможете выполнить расчет.2
Использование калькулятора
Этот калькулятор смещения находит пройденное расстояние или смещение (я) объекта, используя его начальную скорость (u), ускорение (a) и время (t) пройденного пути. Используемое уравнение: s = ut + ½at 2 ; ниже, чтобы показать, как найти решение для каждой отдельной переменной. Калькулятор можно использовать для решения относительно s, u, a или t.
Уравнения смещения для этих расчетов:
Смещение (с) объекта равно скорости (u), умноженной на время (t), плюс 1/2 ускорения (a), умноженное на квадрат времени (t 2 ).2 \)
Где:
с = рабочий объем
u = начальная скорость
a = ускорение
t = время
Используйте стандартную гравитацию a = 9,80665 м / с 2 для уравнений, в которых гравитационная сила Земли используется как скорость ускорения объекта. 2 \)
2 \)
Где:
с = рабочий объем
v i = начальная скорость
a = ускорение
t = время
Расчет смещения, используемый в калькуляторе:
Решая различные переменные, мы можем использовать следующие формулы:
- Учитывая u, t и вычислить s
По заданной начальной скорости, времени и ускорению вычислите смещение.- s = ut + ½ при 2 : найти s
- Учитывая s, t и вычислить u
При заданном смещении, времени и ускорении вычисляется окончательная скорость.- u = s / t — ½at: решить относительно u
- Учитывая a, u и s, вычислить t
Время вычисляется с учетом ускорения, начальной скорости и смещения.
- ½at 2 + ut — s = 0: найти t, используя формулу корней квадратного уравнения
- По заданным s, t и u вычислить
При заданном смещении, времени и начальной скорости вычисляется ускорение.- a = 2s / t 2 — 2u / t: решить для
Задача вытеснения 1:
Автомобиль, движущийся со скоростью 25 м / с, начинает ускоряться со скоростью 3 м / с 2 в течение 4 секунд.Как далеко уезжает машина за 4 секунды разгона?
Три переменные, необходимые для определения расстояния, представлены как u (25 м / с), a (3 м / с 2 ) и t (4 секунды).
с = ut + ½ при 2
с = 25 м / с * 4 с + ½ * 3 м / с 2 * (4 с) 2 = 124 метра
Задача смещения 2:
Самолету с начальной скоростью 20 м / с требуется 8 секунд, чтобы достичь конца взлетно-посадочной полосы. Если самолет ускоряется со скоростью 10 м / с 2 , какова длина взлетно-посадочной полосы?
Если самолет ускоряется со скоростью 10 м / с 2 , какова длина взлетно-посадочной полосы?
с = ut + ½ при 2
с = 20 м / с * 8 с + ½ * 10 м / с 2 * (8 с) 2 =
600 метров
Размеры и единицы
Механическая система, испытывающая одномерные демпфированные колебания, может быть моделируется уравнением
, где \ (m \) — масса системы, \ (b \) — некоторый коэффициент демпфирования,
\ (k \) — жесткость пружины, а \ (u (t) \) — смещение
система.Это уравнение, выражающее баланс трех физических
эффекты: \ (mu » \) (масса, умноженная на ускорение), \ (bu ‘\) (демпфирующая сила) и
\ (ку \) (сила пружины). Различные физические величины, такие как \ (m \),
\ (u (t) \), \ (b \) и \ (k \), все имеют разные измерения , измеренные в
разные единицы , но \ (mu » \), \ (bu ‘\) и \ (ku \) должны иметь одинаковые
размерность, иначе добавлять их не было бы смысла.
Основные концепции
Базовые блоки и размеры
Базовые единицы обладают важным свойством, присущим всем остальным единицам. от них.В системе СИ таких базовых единиц семь и соответствующих физические величины: метр (м) на длину, килограмм (кг) для массы, секунды на время, кельвин (K) для температуры, ампер (А) для электрического тока, кандела (кд) для силы света, и моль (моль) для количества вещества.
Нам нужны подходящие математические обозначения для вычислений с такие измерения, как длина, масса, время и т. д. Размер длина записывается как [L], размерность массы как [M], размерность времени как [T], а размерность температуры как \ ([\ Theta] \) ( размеры остальных базовых блоков просто опущены, так как мы не производим много их использую в этом тексте).2 \)
Далее перечислены некоторые общие физические величины и их размеры. {- 2}] \)
{- 2}] \)
Префиксы для единиц
Единицы часто имеют префиксы.9 \) Па.
Теорема Букингема Пи
Почти все тексты по масштабированию имеют трактовку знаменитого Букингема. Теорема Пи, которую можно использовать для вывода физических законов на основе единицы измерения совместимость, а не лежащие в основе физические механизмы. Этот буклет сосредоточен на моделях, в которых физические механизмы уже выражены через дифференциальные уравнения. Тем не менее, Pi Теорема занимает заметное место в литературе по масштабированию, и поскольку мы время от времени будем на него ссылаться, теорема такова: кратко обсуждается ниже.
Сама теорема просто состоит из двух частей. Во-первых, если проблема
включает \ (n \) физические параметры, в которых \ (m \) независимые типы единиц
(например, длина, масса и т. д.), тогда параметры могут быть
в сочетании с ровно \ (n-m \) независимыми безразмерными числами, отнесенными
как Пи. Во-вторых, любое безединичное отношение между исходным \ (n \)
параметры могут быть преобразованы в отношение между \ (n-m \)
безразмерные числа. Такие отношения могут быть идентичностями или
неравенства, указывающие, например, на то, является ли данный эффект
незначительный.Более того, преобразование системы уравнений в
безразмерная форма соответствует выражающим коэффициентам, а также
как свободные и зависимые переменные в единицах числа Пи.
Такие отношения могут быть идентичностями или
неравенства, указывающие, например, на то, является ли данный эффект
незначительный.Более того, преобразование системы уравнений в
безразмерная форма соответствует выражающим коэффициентам, а также
как свободные и зависимые переменные в единицах числа Пи.
В качестве примера представьте тело, движущееся с постоянной скоростью \ (v \). Что расстояние \ (s \), пройденное за время \ (t \)? Теорема Пи приводит к одна безразмерная переменная \ (\ pi = vt / s \) и приводит к формуле \ (s = Cvt \), где \ (C \) — неопределенная константа. Результат очень близко к известной формуле \ (s = vt \), возникающей из дифференциала уравнение \ (s ‘= v \) в физике, но с дополнительной константой.
На первый взгляд теорема Пи может показаться граничащей с
тривиально. Тем не менее, это может привести к значительному прогрессу для избранных
проблемы, такие как турбулентные струи, ядерные взрывы или подобное
решения, без детальных знаний математических или физических
модели. Следовательно, новичку в масштабировании это может показаться чем-то особенным.
очень глубокий, если не волшебный. Во всяком случае, если перейти к более сложным
задач со многими параметрами, использование теоремы дает
сравнительно меньший выигрыш по мере увеличения числа Пи.Многие Пи также могут быть
рекомбинированы разными способами. Итак, хорошо
физическое понимание и / или информация, передаваемая через набор уравнений,
требуется для
выбрать полезные безразмерные числа или соответствующее масштабирование
упомянутый набор уравнений. Иногда изучение уравнений также
показывает, что некоторые числа Пи, полученные в результате применения теоремы, на самом деле
может быть снято с проблемы. Как следствие, когда
моделирование сложной физической задачи, реальная оценка масштабирования
и безразмерные числа так или иначе будут включены в
анализ основных уравнений вместо того, чтобы быть отдельной проблемой
с теоремой Пи.И в учебниках, и в статьях обсуждение
масштабирование в контексте уравнений слишком часто отсутствует или
представлен в нерешительности.
Следовательно, новичку в масштабировании это может показаться чем-то особенным.
очень глубокий, если не волшебный. Во всяком случае, если перейти к более сложным
задач со многими параметрами, использование теоремы дает
сравнительно меньший выигрыш по мере увеличения числа Пи.Многие Пи также могут быть
рекомбинированы разными способами. Итак, хорошо
физическое понимание и / или информация, передаваемая через набор уравнений,
требуется для
выбрать полезные безразмерные числа или соответствующее масштабирование
упомянутый набор уравнений. Иногда изучение уравнений также
показывает, что некоторые числа Пи, полученные в результате применения теоремы, на самом деле
может быть снято с проблемы. Как следствие, когда
моделирование сложной физической задачи, реальная оценка масштабирования
и безразмерные числа так или иначе будут включены в
анализ основных уравнений вместо того, чтобы быть отдельной проблемой
с теоремой Пи.И в учебниках, и в статьях обсуждение
масштабирование в контексте уравнений слишком часто отсутствует или
представлен в нерешительности.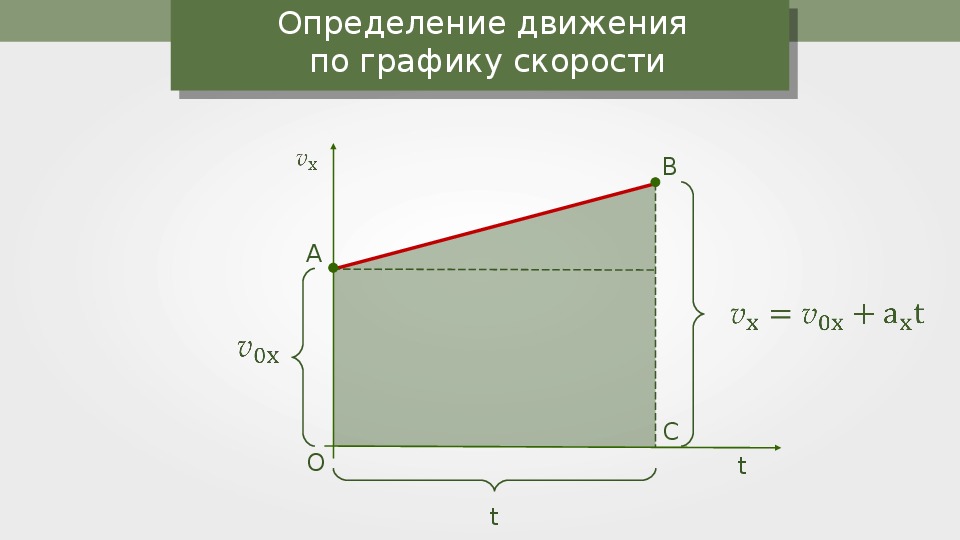 Следовательно, внимание авторов будет
об этом процессе, хотя мы не приводим много примеров
по теореме Пи. Мы не говорим, что теорема Пи мало
ценность. В ряде случаев, например, в экспериментах, он может
предоставить ценные и даже важные рекомендации, но в частности
В учебнике мы стремимся рассказать дополнительную историю о масштабировании.Кроме того, как будет показано в этом буклете, безразмерные числа в
проблема также возникает очень естественным образом из-за масштабирования
дифференциальные уравнения. Если есть модель, основанная на
дифференциальных уравнений, классические
размерный анализ.
Следовательно, внимание авторов будет
об этом процессе, хотя мы не приводим много примеров
по теореме Пи. Мы не говорим, что теорема Пи мало
ценность. В ряде случаев, например, в экспериментах, он может
предоставить ценные и даже важные рекомендации, но в частности
В учебнике мы стремимся рассказать дополнительную историю о масштабировании.Кроме того, как будет показано в этом буклете, безразмерные числа в
проблема также возникает очень естественным образом из-за масштабирования
дифференциальные уравнения. Если есть модель, основанная на
дифференциальных уравнений, классические
размерный анализ.
Абсолютные ошибки, относительные ошибки и единицы
Математически не имеет значения, какие единицы мы используем для физического количество. Однако когда мы имеем дело с приближениями и ошибками, единицы важны.{-3} \) независимо от того, измеряется ли длина в км или мм.
Тем не менее, вместо того, чтобы полагаться исключительно на относительные ошибки,
лучше масштабировать проблему так, чтобы количества, входящие в
вычисления имеют размер единицы (или, по крайней мере, умеренные), а не очень
большой или очень маленький. Техника этих заметок показывает, как это
осуществимо.
Техника этих заметок показывает, как это
осуществимо.
Агрегаты и ЭВМ
Традиционные числовые вычисления включают только числа и, следовательно, требует безразмерных математических выражений.Обычно неявный используется тривиальное масштабирование. Можно, например, просто масштабировать по всей длине величин на 1 м, всех временных величин на 1 с и всех массовых величин на 1 кг, чтобы получить необходимые для расчетов безразмерные числа. Это наиболее распространенный подход, хотя он очень редко используется в явном виде. заявил.
Пакеты символьных вычислений, такие как Mathematica и Maple, позволяют
вычисления с величинами, имеющими размерность. Это тоже возможно
в популярных компьютерных языках, используемых для численных вычислений (раздел PhysicalQuantity: инструмент для вычислений с помощью единиц предоставляет конкретный пример на Python).{-3} \)).
Хотя таблицы преобразования единиц измерения
часто встречаются в школе, ошибки при пересчете единиц измерения, вероятно, ранжируют
самый высокий среди всех ошибок, совершаемых учеными и инженерами (и
когда из-за ошибки преобразования единиц в самолете заканчивается топливо,
это серьезно!).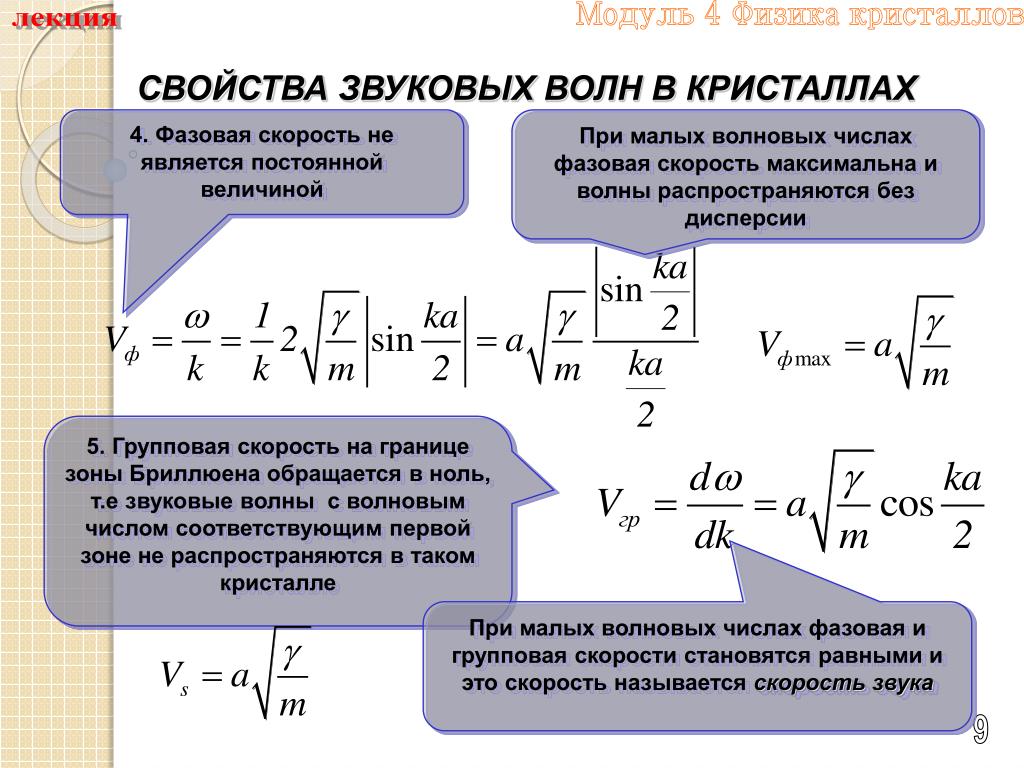 Наличие хороших программных инструментов для помощи в подразделении
поэтому конверсия имеет первостепенное значение, что мотивирует лечение этого
тема в разделах PhysicalQuantity: инструмент для вычислений с единицами измерения и Parampool: пользовательские интерфейсы с автоматическим преобразованием единиц измерения.Читатели, которые
в первую очередь заинтересованы в методе математического масштабирования.
смело пропустите этот материал и сразу переходите к разделу Задачи экспоненциального распада.
Наличие хороших программных инструментов для помощи в подразделении
поэтому конверсия имеет первостепенное значение, что мотивирует лечение этого
тема в разделах PhysicalQuantity: инструмент для вычислений с единицами измерения и Parampool: пользовательские интерфейсы с автоматическим преобразованием единиц измерения.Читатели, которые
в первую очередь заинтересованы в методе математического масштабирования.
смело пропустите этот материал и сразу переходите к разделу Задачи экспоненциального распада.
Пример проблем, связанных с системами единиц
Слегка доработанный пример масштабирования в реальном
научный / инженерный проект может стимулировать читателя
мотивация. В полном объеме изучено цунами и пролета.
геофизика, геология, история, гидродинамика, статистика, геодезия,
инженерия и гражданская защита.Эта сложность отражается в
разнообразие практик использования единиц, весов и
концепции. Если сузить рамки до моделирования цунами
распространения, аспект масштабирования, по крайней мере, может показаться простым, поскольку мы
в основном касается продолжительности и времени. Тем не менее, даже здесь
неоднородность физических единиц является препятствием.
Тем не менее, даже здесь
неоднородность физических единиц является препятствием.
Незначительной проблемой является случайное использование единиц, не относящихся к системе СИ, таких как дюймы или
в старых диаграммах, даже саженях. Более важна неоднородность
величина различных переменных и различия в
присущие, в частности, горизонтальные и вертикальные масштабы.Обычно
отметки поверхности указаны в метрах или меньше. Для дальнего поля на большой глубине
распространения, а также небольшие цунами (которые до сих пор остаются научными
интереса) отметки поверхности часто указываются в см или даже
мм. В глубоком океане характерная глубина порядка
величина больше этой, обычно \ (5000 \, \ hbox {m} \). Распространение
расстояния, с другой стороны, составляют сотни или тысячи
километров. Часто лучше всего описываются местоположения и вычислительные сети.
в географических координатах (долгота / широта), которые связаны с
Единицы СИ на 1 минуту широты составляют примерно одну морскую милю. (\ (1852 \, \ hbox {m} \)), и 1 минута долготы составляет это количество раз
косинус широты.Периоды волн цунами в основном колеблются от
от минут до часа, надеюсь, достаточно коротких, чтобы их можно было хорошо разделить
из полусуточного периода приливов. Время распространения
обычно часы или, может быть, лучшая часть дня, когда Тихий океан
Океан пройден.
(\ (1852 \, \ hbox {m} \)), и 1 минута долготы составляет это количество раз
косинус широты.Периоды волн цунами в основном колеблются от
от минут до часа, надеюсь, достаточно коротких, чтобы их можно было хорошо разделить
из полусуточного периода приливов. Время распространения
обычно часы или, может быть, лучшая часть дня, когда Тихий океан
Океан пройден.
Ученые, инженеры и бюрократы в сообществе цунами
имеют тенденцию быть конкретными и не соответствовать форматам и единицам измерения, поскольку
а также тип требуемых данных. Чтобы удовлетворить эти требования,
Разработчик моделирования цунами должен производить разнообразные данные, которые представлены в единицах измерения.
и форматы, которые нельзя использовать внутри ее моделей.На
с другой стороны, она также должна быть готова принять входные данные в
разнообразные формы. Некоторые наборы данных могут быть большими, что означает
ненужное дублирование с другими единицами измерения или масштабированием должно быть
избегали. Кроме того, модели цунами часто маркируются через
сравнение с экспериментальными данными. Лабораторный масштаб обычно
\ (\ hbox {cm} \) или \ (\ hbox {m} \), самое большее, что подразумевает, что измеренные данные
представлены в единицах, отличных от используемых в реальных событиях земного масштаба,
или даже в вольтах,
с информацией о преобразовании, полученной от измерительных приборов.
Кроме того, модели цунами часто маркируются через
сравнение с экспериментальными данными. Лабораторный масштаб обычно
\ (\ hbox {cm} \) или \ (\ hbox {m} \), самое большее, что подразумевает, что измеренные данные
представлены в единицах, отличных от используемых в реальных событиях земного масштаба,
или даже в вольтах,
с информацией о преобразовании, полученной от измерительных приборов.
Все подробности устройства в различных форматах файлов явно мешают и порождают ряд заблуждений и ошибок, которые могут вызвать потеря драгоценного времени или усилий. Чтобы уменьшить такие проблемы, разработчики вычислительных средств должны сочетать разумную гибкость относительно единиц ввода и вывода с четким и последовательным соглашение о масштабировании в инструментах. Фактически, это также относится к академические инструменты для внутреннего использования.
Приведенное выше обсуждение указывает на некоторые передовые методы, которые
продвигает.Во-первых, всегда выполняйте вычисления с помощью масштабированного дифференциального уравнения. модели. В этом буклете рассказывается, как это сделать. Во-вторых, пользователи программного обеспечения
часто хотят указать входные данные с измерением и получить выходные данные
с размером. Затем программное обеспечение должно применить такие инструменты, как
модели. В этом буклете рассказывается, как это сделать. Во-вторых, пользователи программного обеспечения
часто хотят указать входные данные с измерением и получить выходные данные
с размером. Затем программное обеспечение должно применить такие инструменты, как
PhysicalQuantity (раздел PhysicalQuantity: инструмент для вычислений с единицами)
или более сложный пакет Parampool (раздел Parampool: пользовательские интерфейсы с автоматическим преобразованием единиц измерения), чтобы разрешить ввод с явными размерами и
при необходимости преобразуйте размеры в нужные типы.Эти инструменты тривиально применять, если вычислительное программное обеспечение
написан на Python, но это просто, если программное обеспечение
написаны на скомпилированных языках, таких как Fortran, C или C ++. В последнем
случай, когда вы просто создаете модуль чтения ввода в Python, который захватывает данные из
пользовательский интерфейс и передает их в вычислительное программное обеспечение, либо
через файлы или вызовы функций (вызываемые соответствующие функции
должны быть завернуты в Python с такими инструментами, как
f2py,
Cython,
Ткать
SWIG,
Мгновенное,
или аналогичный, см. [Ref03] (Приложение C) для основных
примеры обертывания кода C и Fortran в f2py и Cython).
[Ref03] (Приложение C) для основных
примеры обертывания кода C и Fortran в f2py и Cython).
PhysicalQuantity: инструмент для вычислений с модулями
Эти заметки содержат довольно много компьютерного кода, чтобы проиллюстрировать, как теория подробно отображает работающее программное обеспечение. Python — это язык программирования используется, прежде всего потому, что это легко читаемый, мощный, полноценный язык, позволяющий использовать MATLAB-подобный код а также код на основе классов, обычно используемый в Java, C # и C ++. Экосистема Python для научных вычислений за последние годы выросла. быстро набирает популярность и заменяет более специализированные инструменты как MATLAB, R и IDL.Примеры кодирования в этом буклете требуют только знания основных процедурное программирование на Python.
Читатели без знания переменных Python, функций, тестов if,
и при импорте модулей следует обращаться, например, к краткому руководству по научным
Python,
конспект лекций по Python,
или полный учебник [Ref04] параллельно с чтением о
Код Python в настоящих заметках.
Эти примечания относятся к Python 2.7
Python существует в двух несовместимых версиях, пронумерованных 2 и 3.Различия можно сделать небольшими, и есть инструменты для написания код, работающий под обеими версиями.
Поскольку Python версии 2 все еще доминирует
в научных вычислениях мы придерживаемся этой версии, но
написать код версии 2.7, максимально приближенный к версии 3.4
и позже. В большинстве наших программ отличается только оператор print
между версиями 2 и 3.
Вычисления с модулями в Python хорошо поддерживаются
очень полезный инструмент PhysicalQuantity из пакета ScientificPython от Конрада
Хинсен.К сожалению, в ScientificPython на момент создания этого
писать, работать с NumPy версии 1.9 или новее, поэтому мы изолировали
PhysicalQuantity объект в модуле PhysicalQuantities и сделал его общедоступным
доступно на GitHub. Также существует альтернативный пакет Unum для вычислений с числами с
единиц, но здесь мы будем придерживаться первого модуля.
Продемонстрируем использование объекта PhysicalQuantity путем
вычисляя \ (s = vt \), где \ (v \) — скорость, указанная в единицах измерения ярдов на
минута , а \ (t \) — время в часах.Сначала нам нужно знать, что
единицы называются в PhysicalQuantities . Для этого запустите pydoc.
Физические количества или
Терминал> pydoc Scientific.Physics.PhysicalQuantities
, если у вас установлен весь пакет ScientificPython. В
итоговая документация показывает имена
единицы. Особенно,
ярды задаются ярдов , минуты мин , а часы
по ч . Теперь мы можем вычислить \ (s = vt \) следующим образом:
>>> # С ScientificPython:
>>> от Науч.Physics.PhysicalQuantities import \
... PhysicalQuantity как PQ
>>> # С PhysicalQuantities как отдельным / автономным модулем:
>>> из PhysicalQuantities импортировать PhysicalQuantity как PQ
>>>
>>> v = PQ ('120 ярдов / мин') # скорость
>>> t = PQ ('1 h') # время
>>> s = v * t # расстояние
>>> print s # s - строка
120,0 ч * ярд / мин
Нечетная единица ч * ярд / мин лучше преобразовать в стандартную единицу СИ, например
как метр:
>>> с.convertToUnit ('м') >>> print s 6583,68 м
Обратите внимание, что s — это объект PhysicalQuantity со значением и
Блок. Для математических вычислений нам нужно извлечь
value как объект с плавающей запятой. Мы также можем извлечь единицу в виде строки:
>>> print s.getValue () # float 6583,68 >>> print s.getUnitName () # строка м
Вот пример того, как преобразовать единицы нечетной скорости ярды на минута на что-то более стандартное:
>>> v.{-1} \)
где джоуль заменяет калорийность?
>>> c = PQ ('1 кал / (г * К)')
>>> c.convertToUnit ('Дж / (г * К)')
>>> печать c
4,184 Дж / К / г
Parampool: пользовательские интерфейсы с автоматическим преобразованием единиц
Пакет Parampool позволяет
создание пользовательских интерфейсов с поддержкой юнитов и юнитов
конверсия. Значения параметров можно задать в виде числа с
Блок. Параметры могут быть зарегистрированы заранее с предпочтительным
единица, и все, что предписывает пользователь, значение и единица измерения
преобразован таким образом, что единица становится зарегистрированной единицей. 2 \), \ (t \) быть
время измеряется в с, и, следовательно, \ (с \) будет расстоянием, измеренным в м.
2 \), \ (t \) быть
время измеряется в с, и, следовательно, \ (с \) будет расстоянием, измеренным в м.
Пул параметров
Во-первых, Parampool требует от нас определить пул всех входных данных.
параметры, которые здесь просто представлены списком словарей, где каждый
словарь содержит информацию об одном параметре. Возможно
организовать входные параметры в древовидной структуре с подпулами, которые
сами могут иметь
субпулы,
но для нашего простого приложения нам просто нужна плоская структура с
три входных параметра:
\ (v_0 \), \ (a \) и \ (t \).Эти параметры помещаются в подпул под названием
"Главный". Пул создается по коду
def define_input ():
бассейн = [
'Главный', [
dict (name = 'начальная скорость', по умолчанию = 1.0, unit = 'm / s'),
dict (name = 'ускорение', по умолчанию = 1.0, unit = 'm / s ** 2'),
dict (name = 'time', по умолчанию = 10.0, unit = 's')
]
]
из parampool. pool.UI import listtree2Pool
pool = listtree2Pool (pool) # преобразовать список в объект Pool
возвратный бассейн
pool.UI import listtree2Pool
pool = listtree2Pool (pool) # преобразовать список в объект Pool
возвратный бассейн
Для каждого параметра мы можем определить логическое имя, например начальная скорость ,
значение по умолчанию и единица измерения.Дополнительные свойства
также разрешены, см. документацию Parampool.
Совет: укажите значения чисел по умолчанию как объекты с плавающей запятой
Обратите внимание, что мы пишем не просто 1, а 1.0 по умолчанию.
Если бы использовалось 1, Parampool интерпретировал бы наш параметр как
целое число и поэтому преобразует ввод вроде 2,5 м / с в 2 м / с .
Чтобы гарантировать, что параметр с действительным знаком становится объектом с плавающей запятой внутри
пула, мы должны указать значение по умолчанию как действительное число: 1. или 1.0 .
(Тип входного параметра может быть также задан явно с помощью
свойство str2type , например, str2type = float .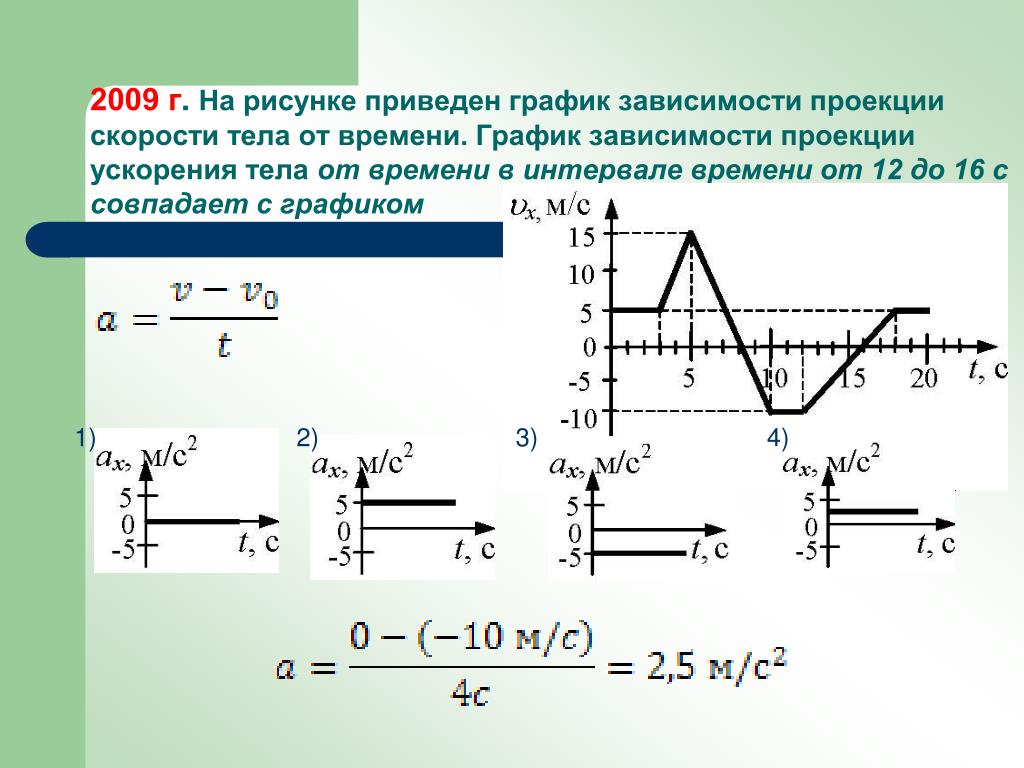 )
)
Получение данных пула для вычислений
Мы можем сделать небольшую функцию для получения значений из пула
и вычисление \ (s \):
def расстояние (бассейн):
v_0 = pool.get_value ('начальная скорость')
a = pool.get_value ('ускорение')
t = pool.get_value ('время')
s = v_0 * t + 0.5 * а * т ** 2
вернуть s
Функция pool.get_value возвращает числовое значение
названный параметр, после того, как единица была преобразована из того, что
Пользователь указал, что было зарегистрировано в пуле.
Например, если пользователь предоставляет аргумент командной строки
- время '2 ч' , Parampool преобразует это количество в секунды и
pool.get_value ('time') вернет 7200.
Чтение параметров командной строки
Для запуска вычислений мы определяем пул, загружаем значения из
командная строка и позвоните по номеру на расстояние :
пул = define_input ()
из Parampool. menu.UI import set_values_from_command_line
pool = set_values_from_command_line (пул)
s = расстояние (бассейн)
print 's =% g'% s
menu.UI import set_values_from_command_line
pool = set_values_from_command_line (пул)
s = расстояние (бассейн)
print 's =% g'% s
В именах параметров с пробелами должен использоваться символ подчеркивания вместо пробела.
в параметре командной строки, например, в --Initial_velocity .
Теперь мы можем запустить
Терминал> python distance.py --initial_velocity '10 km / h '\
- ускорение 0 - время '1 ч
s = 10000
Обратите внимание на ответ ( с ), что 10 км / ч преобразуется в м / с, а 1 ч - в с.
Также можно получить значения параметров как PhysicalQuantity
объекты из пула по телефону
v_0 = pool.get_value_unit ('Начальная скорость')
Следующий вариант функции Расстояние вычисляет с
значений и единиц:
def distance_unit (пул):
# Вычислить с помощью единиц
из parampool.PhysicalQuantities импортировать PhysicalQuantity как PQ
v_0 = pool. get_value_unit ('начальная скорость')
a = pool.get_value_unit ('ускорение')
t = бассейн.get_value_unit ('время')
s = v_0 * t + 0,5 * a * t ** 2
вернуть s.getValue (), s.getUnitName ()
get_value_unit ('начальная скорость')
a = pool.get_value_unit ('ускорение')
t = бассейн.get_value_unit ('время')
s = v_0 * t + 0,5 * a * t ** 2
вернуть s.getValue (), s.getUnitName ()
Тогда мы можем сделать
с, s_unit = Distance_unit (пул)
print 's =% g'% s, s_unit
и получите результат с нужным блоком.
Установка значений по умолчанию в файле
В больших приложениях с большим количеством входных параметров часто нравится
для определения (огромного) набора значений по умолчанию для конкретного случая, а затем
переопределите некоторые из них в командной строке.Такие наборы значений по умолчанию
может быть установлен в файле с использованием синтаксиса типа
subpool Главный
начальная скорость = 100! ярд / мин
ускорение = 0! м / с ** 2 # ускорение падения
конец
Аппарат можно отдать после ! Символ (и перед символом комментария # ).
Для чтения таких файлов нам нужно добавить строки
из parampool. pool.UI import set_defaults_from_file
pool = set_defaults_from_file (пул)
pool.UI import set_defaults_from_file
pool = set_defaults_from_file (пул)
перед звонком на set_defaults_from_command_line .
Если приведенные выше команды сохранены в файле distance.dat , мы даем
информация об этом файле в программу через
option --poolfile distance.dat . Запуск всего
Терминал> python distance.py --poolfile distance.dat
s = 15,25 м
сначала загружает скорость
100 ярдов / мин преобразовано в 1,524 м / с и нулевое ускорение
в систему пула и затем мы вызываем distance_unit , который
загружает эти значения из пула вместе со значением по умолчанию для
время, установленное на 10 с.Тогда расчет будет \ (s = 1,524 \ cdot 10 + 0 = 15,24 \).
с блоком м. Мы можем изменить время и / или два других
параметры в командной строке:
Терминал> python distance.py --poolfile distance.dat --time '2 h'
s = 10972,8 м
В результате вычислений будет \ (s = 1,524 \ cdot 7200 + 0 = 10972,8 \). Предлагаем вам поиграть с программой distance.py.
Предлагаем вам поиграть с программой distance.py.
Указание нескольких значений входных параметров
Parampool имеет интересную особенность: можно назначить несколько значений.
к входному параметру, тем самым облегчая приложению
пройти через все комбинации всех параметров.Мы можем продемонстрировать эту особенность, составив таблицу из \ (v_0 \), \ (a \), \ (t \) и
\ (s \) значения. В функции вычисления нам нужно вызвать pool.get_values
вместо pool.get_value , чтобы получить список всех значений, которые
были указаны для рассматриваемого параметра. Вложением петель поверх
все параметры, мы посещаем все комбинации всех параметров как
указано пользователем:
def Distance_table (бассейн):
"" "Получение нескольких значений параметров из пула." ""
таблица = []
для v_0 в пуле.get_values ('начальная скорость'):
для a в pool.get_values ('ускорение'):
для t в pool.get_values ('time'):
s = v_0 * t + 0,5 * a * t ** 2
table.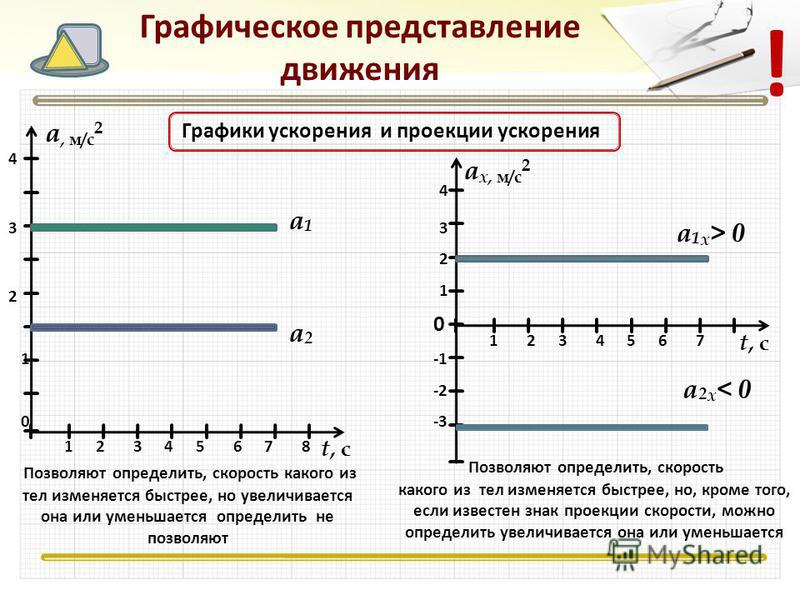 append ((v_0, a, t, s))
таблица возврата
append ((v_0, a, t, s))
таблица возврата
Если для параметра было указано только одно значение, pool.get_values
возвращает только это значение, и будет только один проход в связанном
петля.
После загрузки аргументов командной строки в объект пула мы можем вызвать
Distance_table вместо Distance или Distance_unit и
напишите красиво отформатированную таблицу результатов:
table = distance_table (бассейн)
print '| ----------------------------------------------- ------ | '
печать '| v_0 | а | т | с | '
print '| ----------------------------------------------- ------ | '
для v_0, a, t, s в таблице:
печать '|% 11.3f | % 10.3f | % 10.3f | % 12.3f | ' % (v_0, a, t, s)
print '| ----------------------------------------------- ------ | '
Вот пример выполнения,
Терминал> python distance.py --time '1 ч и 2 ч и 3 ч' \
- ускорение '0 м / с ** 2 и 1 м / с ** 2 и 1 ярд / с ** 2' \
--initial_velocity '1 и 5'
| ------------------------------------------------- ---- |
| v_0 | а | т | s |
| ------------------------------------------------- ---- |
| 1.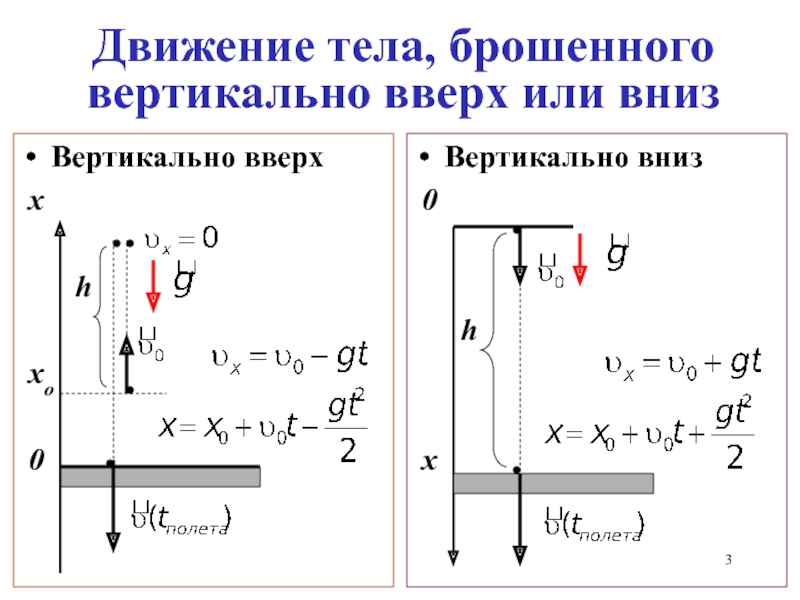 000 | 0,000 | 3600.000 | 3600.000 |
| 1.000 | 0,000 | 7200.000 | 7200.000 |
| 1.000 | 0,000 | 10800.000 | 10800.000 |
| 1.000 | 1.000 | 3600.000 | 6483600.000 |
| 1.000 | 1.000 | 7200.000 | 25927200.000 |
| 1.000 | 1.000 | 10800.000 | 58330800.000 |
| 1.000 | 0,914 | 3600.000 | 5928912.000 |
| 1.000 | 0,914 | 7200.000 | 23708448.000 |
| 1.000 | 0,914 | 10800.000 | 53338608.000 |
| 5.000 | 0,000 | 3600.000 | 18000.000 |
| 5.000 | 0,000 | 7200.000 | 36000.000 |
| 5.000 | 0,000 | 10800.000 | 54000.000 |
| 5.000 | 1.000 | 3600.000 | 6498000.000 |
| 5.000 | 1.000 | 7200.000 | 25956000.000 |
| 5.000 | 1.000 | 10800.000 | 58374000.000 |
| 5.000 | 0,914 | 3600.000 | 5943312.000 |
| 5.000 | 0,914 | 7200.000 | 23737248.000 |
| 5.000 | 0,914 | 10800.000 | 53381808.000 |
| ------------------------------------------------- ---- |
000 | 0,000 | 3600.000 | 3600.000 |
| 1.000 | 0,000 | 7200.000 | 7200.000 |
| 1.000 | 0,000 | 10800.000 | 10800.000 |
| 1.000 | 1.000 | 3600.000 | 6483600.000 |
| 1.000 | 1.000 | 7200.000 | 25927200.000 |
| 1.000 | 1.000 | 10800.000 | 58330800.000 |
| 1.000 | 0,914 | 3600.000 | 5928912.000 |
| 1.000 | 0,914 | 7200.000 | 23708448.000 |
| 1.000 | 0,914 | 10800.000 | 53338608.000 |
| 5.000 | 0,000 | 3600.000 | 18000.000 |
| 5.000 | 0,000 | 7200.000 | 36000.000 |
| 5.000 | 0,000 | 10800.000 | 54000.000 |
| 5.000 | 1.000 | 3600.000 | 6498000.000 |
| 5.000 | 1.000 | 7200.000 | 25956000.000 |
| 5.000 | 1.000 | 10800.000 | 58374000.000 |
| 5.000 | 0,914 | 3600.000 | 5943312.000 |
| 5.000 | 0,914 | 7200.000 | 23737248.000 |
| 5.000 | 0,914 | 10800.000 | 53381808.000 |
| ------------------------------------------------- ---- |
Обратите внимание, что некоторые из нескольких значений имеют разные размеры.
из зарегистрированного измерения для этого параметра, а таблица
показывает, что преобразование в правильное измерение имело место.
Создание графического пользовательского интерфейса
Для удовольствия мы можем легко создать графический пользовательский интерфейс.
через Parampool. Мы оборачиваем функцию distance_unit в функцию, которая
возвращает результат в красивом HTML-коде:
def distance_unit2 (пул):
# Перенести результат из distance_unit в HTML
s, s_unit = Distance_unit (пул)
return ' Distance: % .2f% s'% (s, s_unit)
Вдобавок надо сделать файл generate_distance_GUI.py с
простое содержание
из импорта parampool.generator.flask сгенерировать
с расстояния импорт distance_unit2, define_input
генерировать (Distance_unit2, pool_function = define_input, MathJax = True)
Запуск generate_distance_GUI.py создает веб-сайт на основе Flask.
интерфейс
для нашей функции distance_unit , см. Рисунок Web GUI, где параметры могут быть указаны с единицами измерения.
Текстовые поля в этом графическом интерфейсе позволяют указывать параметры с
числа и единицы, e. g., ускорение с единицей измерения ярдов в минуту в квадрате,
как показано на рисунке. Слегка наведя указатель мыши слева от
текстовое поле вызывает появление небольшого черного окошка с зарегистрированным устройством
этого параметра.
g., ускорение с единицей измерения ярдов в минуту в квадрате,
как показано на рисунке. Слегка наведя указатель мыши слева от
текстовое поле вызывает появление небольшого черного окошка с зарегистрированным устройством
этого параметра.
Веб-интерфейс, в котором параметры могут быть указаны в единицах измерения
С примерами, показанными выше, читатель должен уметь использовать
PhysicalQuantity объект и пакет Parampool в программах
и тем самым безопасно работать с юнитами. В следующем тексте, где мы обсуждаем
умение масштабировать подробно, мы просто будем работать в стандартных единицах СИ
и избегайте преобразования единиц измерения, чтобы больше не использовать
PhysicalQuantity и Parampool.
От ядерной физики до расчета повреждений смещения и распространения неопределенностей в CONRAD
https://doi.org/10.1016/j.rinp.2020.103023 Получить права и контент Основные моменты
- •
-
Модели ядерных реакций и модели радиационных повреждений являются соединены для вычисления поперечного сечения повреждения.
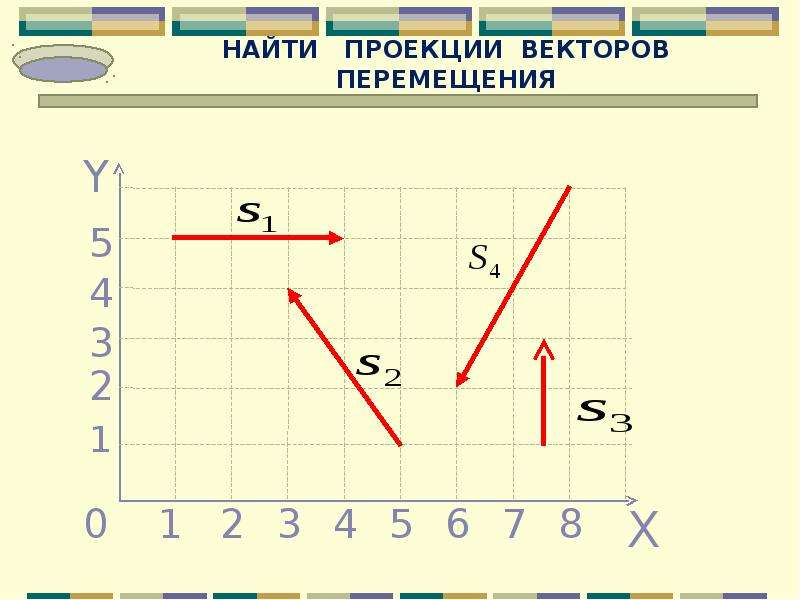
- •
-
Неопределенности ядерных моделей и моделей повреждений распространяются на неопределенность поперечного сечения повреждений.
- •
-
Рассчитаны чувствительности поперечного сечения повреждений к различным параметрам модели.
- •
-
Корреляция между различными параметрами очень важна для определения неопределенности и корреляции поперечного сечения повреждения.
Abstract
Ввиду важности радиационного повреждения материалов на ядерных установках представляет интерес точный расчет ущерба и соответствующей неопределенности. Код CONRAD разработан в CEA Cadarache для оценки ядерных данных и соответствующих неопределенностей с использованием различных методов.Различные модели смещения на атом (DPA) были недавно реализованы в CONRAD для выполнения расчетов, анализа чувствительности и распространения неопределенности поперечных сечений радиационного повреждения. Текущая версия CONRAD может рассчитывать поперечное сечение повреждений и соответствующую ковариационную матрицу на основе параметров ядерной модели и параметров модели DPA. В дополнение к чувствительности поперечного сечения повреждения 56 Fe к различным параметрам ядерной модели и параметрам модели DPA, настоящая работа иллюстрирует важность полной ковариационной матрицы между различными ядерными данными, в то время как эти корреляции обычно не приводятся в текущей версии. оцененные библиотеки ядерных данных.
В дополнение к чувствительности поперечного сечения повреждения 56 Fe к различным параметрам ядерной модели и параметрам модели DPA, настоящая работа иллюстрирует важность полной ковариационной матрицы между различными ядерными данными, в то время как эти корреляции обычно не приводятся в текущей версии. оцененные библиотеки ядерных данных.
Ключевые слова
Сечение повреждения
Смещение на атом
Модели ядерных реакций
Ядерные данные
Анализ чувствительности
Распространение неопределенности
CONRAD
Рекомендуемые статьи Цитирующие статьи (0)
Авторы. Опубликовано Elsevier B.V.Рекомендуемые статьи
Цитирующие статьи
Смещение волны: определение и формула - видео и стенограмма урока
Расстояние vs.Смещение
Прежде чем мы узнаем о волновом смещении, давайте поговорим немного о концепции смещения в целом. Вы помните разницу между смещением и расстоянием? Может показаться, что это так, но это не одно и то же. Расстояние - это расстояние, на которое прошел объект, а смещение - это измерение изменения исходного положения объекта.
Расстояние - это расстояние, на которое прошел объект, а смещение - это измерение изменения исходного положения объекта.
Лучший способ визуализировать разницу между ними - использовать пример поездки туда и обратно.Представим, что вы едете 10 миль на работу или в школу, а затем в конце дня возвращаетесь домой. В таком случае расстояние, которое вы проехали, составляет 20 миль, а ваше перемещение - 0 миль. Это потому, что вы начинаете и заканчиваете поездку в одном и том же месте - в своем доме. Итак, нет общего изменения позиции, с которой вы начали поездку.
Что такое смещение волны?
Теперь, когда мы знаем, что такое смещение, какое именно смещение вызывает волна? Давайте вернемся к нашему примеру со скакалкой, чтобы изучить двумерную поперечную волну.В двух измерениях единственные возможные направления смещения лежат на той же оси, что и направление волны, или перпендикулярно ей. Для упрощения мы назовем направление движения волны горизонтальным, а перпендикулярное направление - вертикальным. Затем они могут быть представлены визуально осью x и осью y .
Затем они могут быть представлены визуально осью x и осью y .
Для волны на нашей скакалке есть только вертикальное смещение. Смещаются частицы самой скакалки, а скакалка движется только вертикально вверх и вниз.Помните, что сама веревка не движется с волной горизонтально. Это означает, что поперечное смещение волны представляет собой изменение вертикального положения частицы от того места, где она находилась до того, как волна прошла через нее.
Формула смещения волны
Теперь, когда мы знаем, что нам нужно найти вертикальное смещение, вызванное волной, как нам это сделать? Мы хотим найти смещение в любой точке скакалки, и скакалка движется в форме гармонической синусоидальной волны.Итак, для описания нашего смещения имеет смысл использовать синусоидальную функцию.
Чтобы найти смещение гармонической волны, распространяющейся в положительном направлении x , мы используем следующую формулу:
Для волны, движущейся в отрицательном направлении x , вы просто меняете знак вычитания на знак сложения.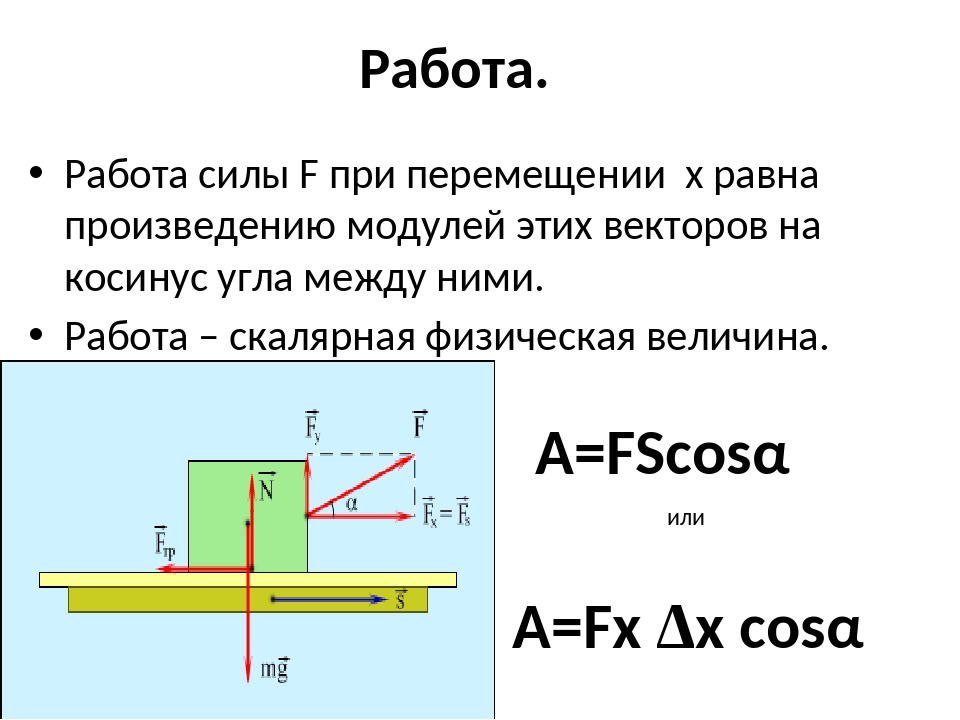
В этой формуле много чего, поэтому давайте разберем разные части.Смещение, y (x, t) является функцией горизонтального положения ( x ) в точке смещения и количества времени ( t ), в течение которого волна прошла. Переменная перед синусоидальной функцией, A , представляет собой амплитуду волны, которая представляет собой высоту гребней и впадин волны.
Последние две переменные немного сложнее. Символ омега - это угловая частота волны, а k - угловое волновое число.Частота волны - это количество волн, которые проходят через заданную точку за период времени. Каждый раз, когда вы настраиваетесь на радиостанцию, вы сортируете их по частоте излучаемых ими радиоволн. Волновое число - это количество длин волн в волне на заданном расстоянии.
Угловая частота и угловое волновое число отличаются от стандартной частоты ( f ) и волнового числа (или nu bar ) только на коэффициент 2 * pi. В этом можно убедиться, сравнив их формулы:
В обеих системах уравнений лямбда, - длина волны, а T - период.
Это, наконец, все, что вам нужно знать, чтобы найти смещение волны. Это намного больше, чем вы могли ожидать, но все это необходимо для гармонического движения волны.
Резюме урока
По мере того, как волна проходит через среду, она создает в ней смещение , которое представляет собой изменение положения этой среды по сравнению с ее начальным положением до того, как волна прошла через нее. Волновое смещение поперечной волны перпендикулярно направлению распространения волны, поскольку сам материал не движется вместе с волной.
Когда мы хотим найти смещение, которое создает гармоническая волна, движущаяся в положительном направлении x , мы используем следующую формулу:
Для волны, движущейся в отрицательном направлении x , мы меняем знак вычитания в уравнении на знак сложения.
В этой формуле y (x, t) - это смещение, x - это положение волны на той же оси, что и движение волны в точке смещения, а t - это время, в течение которого волна была путешествия.
Остальные три переменные; A , k и omega - это амплитуда волны, угловая частота и угловое волновое число соответственно. Амплитуда определяется как высота гребней и впадин волны. Частота - это количество волн, которые проходят через точку за определенный период времени. Наконец, волновое число - это количество длин волн, которые появляются в волне на заданном расстоянии.
Заметки по исчислению I, раздел 3-3
Заметки по исчислению I, раздел 3-3 Примечания, Урок 3.3Темпы изменений в естественных и социальных науках
Мы знаем, что производная - это мгновенная скорость изменения. У нас есть уже видел, насколько это полезно в физике при изучении расстояния, скорости, и ускорение в уроке 2-1, а в уроке 2-6, а также в типовых задачах урока 3-2, и в уроке 3-1. В этом уроке мы также см. приложения по химии, биологии, экономике, геологии, географии, метеорология и другие науки.
Пример физической задачи: Положение частицы
дается уравнением,. где t измеряется в секундах, а s - в метрах. (а) Найдите скорость
в момент времени t; (б) Какова скорость через 3 с? Через 4 с ?; (c) Когда частица
в состоянии покоя?
где t измеряется в секундах, а s - в метрах. (а) Найдите скорость
в момент времени t; (б) Какова скорость через 3 с? Через 4 с ?; (c) Когда частица
в состоянии покоя?
| Часть (а).
Наш первый шаг - найти производную функции положения.Это будет наша формула скорости. |
|
| Часть (б).
Теперь, когда у нас есть формула скорости, мы можем найти скорость при в любой момент. В этом случае нам нужно найти скорость в момент при t = 4. Ответ: 16 м / с. Нам также нужно найти скорость, когда т = 3. |
|
| Часть (с).
Чтобы найти, когда частица находится в состоянии покоя, мы берем скорость (1-я производная формулу), установите его равным нулю и решите относительно t . |
|
| Мы находим, что это произойдет дважды. |
Использование вашего Инструменты для обогащения исчисления CD (прилагаемый
вместе с книгой), загрузите и запустите Module 3. 3 / 3.4 / 3.5 .
Этот модуль позволит вам увидеть анимацию графика с расстоянием,
скорость и ускорение на одном графике. 3 / 3.4 / 3.5 .
Этот модуль позволит вам увидеть анимацию графика с расстоянием,
скорость и ускорение на одном графике. |
Пример экономической задачи: В экономике мгновенное
Скорость изменения стоимости по отношению к количеству произведенных единиц называется
предельные затраты экономистов. Предположим, компания подсчитала, что стоимость
(в долларах) производства предмета x составляет:.
Найдите мгновенную скорость изменения стоимости относительно числа
произведенных единиц (предельная стоимость).
| Данная функция стоимости. | |
| Мы различаем правило мощности двумя отдельными терминами. | |
| Подставляем значение x , указанное в задаче.
Следовательно, предельные затраты при x = 500 составляют 26 долларов за единицу. 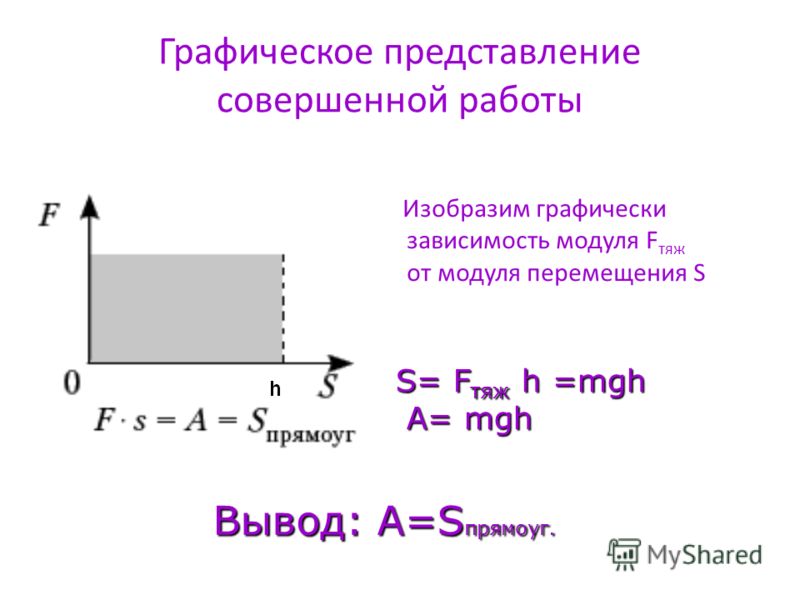 прогнозируемая стоимость 501-го элемента.
прогнозируемая стоимость 501-го элемента. |
Скорость изменений Обучающий видео
| Проверить концепции |
| № 1: Верно или неверно: в любой области науки или экономики, возможность рассчитать мгновенную скорость изменения ценна. |
Выбрать одно верно Неверно |
| # 2: Верно или неверно: предельная стоимость является производной от функция стоимости. |
Выбрать одно верно Неверно |
| # 3: Верно или неверно: Ускорение является производной скорости. |
Выберите один TrueIFalse |
# 4: __________________ - это то, что в биологии
можно было бы лучше изучить с помощью математического анализа.
|
