Электростатика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Электрический заряд и его свойства
К оглавлению…
Электрический заряд – это физическая величина, характеризующая способность частиц или тел вступать в электромагнитные взаимодействия. Электрический заряд обычно обозначается буквами q или Q. В системе СИ электрический заряд измеряется в Кулонах (Кл). Свободный заряд в 1 Кл – это гигантская величина заряда, практически не встречающаяся в природе. Как правило, Вам придется иметь дело с микрокулонами (1 мкКл = 10–6 Кл), нанокулонами (1 нКл = 10–9 Кл) и пикокулонами (1 пКл = 10–12 Кл). Электрический заряд обладает следующими свойствами:
1. Электрический заряд является видом материи.
2. Электрический заряд не зависит от движения частицы и от ее скорости.
3.
4. Существует два рода электрических зарядов, условно названных положительными и отрицательными.
5. Все заряды взаимодействуют друг с другом. При этом одноименные заряды отталкиваются, разноименные – притягиваются. Силы взаимодействия зарядов являются центральными, то есть лежат на прямой, соединяющей центры зарядов.
6. Существует минимально возможный (по модулю) электрический заряд, называемый элементарным зарядом. Его значение:
e = 1,602177·10–19 Кл ≈ 1,6·10–19 Кл.
Электрический заряд любого тела всегда кратен элементарному заряду:
где:
N – целое число. Обратите внимание, невозможно существование заряда, равного 0,5е; 1,7е; 22,7е и так далее. Физические величины, которые могут принимать только дискретный (не непрерывный) ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда.
Обратите внимание, невозможно существование заряда, равного 0,5е; 1,7е; 22,7е и так далее. Физические величины, которые могут принимать только дискретный (не непрерывный) ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда.
7. Закон сохранения электрического заряда. В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:
Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. Из закона сохранения заряда так же следует, если два тела одного размера и формы, обладающие зарядами q1 и q2 (совершенно не важно какого знака заряды), привести в соприкосновение, а затем обратно развести, то заряд каждого из тел станет равным:
С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному (то есть минимально возможному) заряду e.
Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному (то есть минимально возможному) заряду e.
В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером. Атом данного вещества может потерять один или несколько электронов, или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион. Обратите внимание, что положительные протоны входят в состав ядра атома, поэтому их число может изменяться только при ядерных реакциях. Очевидно, что при электризации тел ядерных реакций не происходит. Поэтому в любых электрических явлениях число протонов не меняется, изменяется только число электронов.
Иногда в задачах электрический заряд распределен по некоторому телу. Для описания этого распределения вводятся следующие величины:
1. Линейная плотность заряда. Используется для описания распределения заряда по нити:
где: L – длина нити. Измеряется в Кл/м.
2. Поверхностная плотность заряда. Используется для описания распределения заряда по поверхности тела:
где: S – площадь поверхности тела. Измеряется в Кл/м2.
3. Объемная плотность заряда. Используется для описания распределения заряда по объему тела:
где: V – объем тела. Измеряется в Кл/м3.
Обратите внимание на то, что масса электрона равна:
me = 9,11∙10–31 кг.
Закон Кулона
К оглавлению…
Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь. На основании многочисленных опытов Кулон установил следующий закон:
Силы взаимодействия неподвижных точечных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:
где: ε – диэлектрическая проницаемость среды – безразмерная физическая величина, показывающая, во сколько раз сила электростатического взаимодействия в данной среде будет меньше, чем в вакууме (то есть во сколько раз среда ослабляет взаимодействие). Здесь k – коэффициент в законе Кулона, величина, определяющая численное значение силы взаимодействия зарядов. В системе СИ его значение принимается равным:
k = 9∙109 м/Ф.
Силы взаимодействия точечных неподвижных зарядов подчиняются третьему закону Ньютона, и являются силами отталкивания друг от друга при одинаковых знаках зарядов и силами притяжения друг к другу при разных знаках. Взаимодействие неподвижных электрических зарядов называют электростатическим
Закон Кулона справедлив для точечных заряженных тел, равномерно заряженных сфер и шаров. В этом случае за расстояния r берут расстояние между центрами сфер или шаров. На практике закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними. Коэффициент k в системе СИ иногда записывают в виде:
где: ε0 = 8,85∙10–12 Ф/м – электрическая постоянная.
Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции: если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.
Запомните также два важных определения:
Проводники – вещества, содержащие свободные носители электрического заряда. Внутри проводника возможно свободное движение электронов – носителей заряда (по проводникам может протекать электрический ток). К проводникам относятся металлы, растворы и расплавы электролитов, ионизированные газы, плазма.
Диэлектрики (изоляторы) – вещества, в которых нет свободных носителей заряда. Свободное движение электронов внутри диэлектриков невозможно (по ним не может протекать электрический ток). Именно диэлектрики обладают некоторой не равной единице диэлектрической проницаемостью ε.
Для диэлектрической проницаемости вещества верно следующее (о том, что такое электрическое поле чуть ниже):
Электрическое поле и его напряженность
К оглавлению…
По современным представлениям, электрические заряды не действуют друг на друга непосредственно.
Электрическое поле, окружающее заряженное тело, можно исследовать с помощью так называемого пробного заряда – небольшого по величине точечного заряда, который не вносит заметного перераспределения исследуемых зарядов. Для количественного определения электрического поля вводится силовая характеристика — напряженность электрического поля E.
Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на пробный заряд, помещенный в данную точку поля, к величине этого заряда:
Напряженность электрического поля – векторная физическая величина. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.
Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.
Для наглядного представления электрического поля используют силовые линии. Эти линии проводятся так, чтобы направление вектора напряженности в каждой точке совпадало с направлением касательной к силовой линии. Силовые линии обладают следующими свойствами.
- Силовые линии электростатического поля никогда не пересекаются.
- Силовые линии электростатического поля всегда направлены от положительных зарядов к отрицательным.
- При изображении электрического поля с помощью силовых линий их густота должна быть пропорциональна модулю вектора напряженности поля.
- Силовые линии начинаются на положительном заряде или бесконечности, а заканчиваются на отрицательном или бесконечности. Густота линий тем больше, чем больше напряжённость.
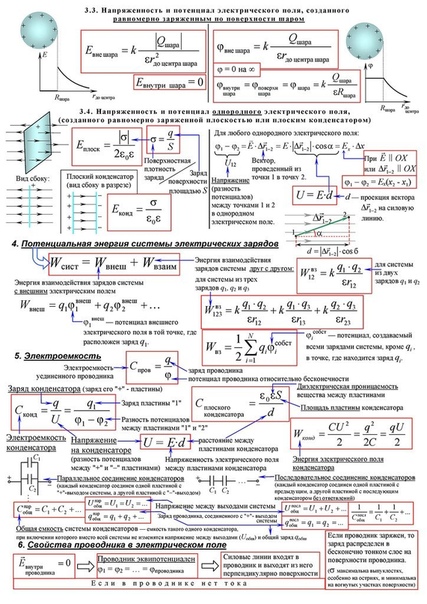
- В данной точке пространства может проходить только одна силовая линия, т.к. напряжённость электрического поля в данной точке пространства задаётся однозначно.
Электрическое поле называют однородным, если вектор напряжённости одинаков во всех точках поля. Например, однородное поле создаёт плоский конденсатор – две пластины, заряженные равным по величине и противоположным по знаку зарядом, разделённые слоем диэлектрика, причём расстояние между пластинами много меньше размеров пластин.
Во всех точках однородного поля на заряд q, внесённый в однородное поле с напряжённостью E, действует одинаковая по величине и направлению сила, равная F = Eq. Причём, если заряд q положительный, то направление силы совпадает с направлением вектора напряжённости, а если заряд отрицательный, то вектора силы и напряжённости противоположно направлены.
Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рисунке:
Принцип суперпозиции
К оглавлению. ..
..
Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряжённостей электрических полей, создаваемых в той же точке зарядами в отдельности:
Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции. В соответствии с законом Кулона, напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:
Это поле называется кулоновским. В кулоновском поле направление вектора напряженности зависит от знака заряда Q: если Q > 0, то вектор напряженности направлен от заряда, если Q < 0, то вектор напряженности направлен к заряду. Величина напряжённости зависит от величины заряда, среды, в которой находится заряд, и уменьшается с увеличением расстояния.
Величина напряжённости зависит от величины заряда, среды, в которой находится заряд, и уменьшается с увеличением расстояния.
Напряженность электрического поля, которую создает заряженная плоскость вблизи своей поверхности:
Итак, если в задаче требуется определить напряженность поля системы зарядов, то надо действовать по следующему алгоритму:
- Нарисовать рисунок.
- Изобразить напряженность поля каждого заряда по отдельности в нужной точке. Помните, что напряженность направлена к отрицательному заряду и от положительного заряда.
- Вычислить каждую из напряжённостей по соответствующей формуле.
- Сложить вектора напряжённостей геометрически (т.е. векторно).
Потенциальная энергия взаимодействия зарядов
К оглавлению…
Электрические заряды взаимодействуют друг с другом и с электрическим полем. Любое взаимодействие описывается потенциальной энергией. Потенциальная энергия взаимодействия двух точечных электрических зарядов рассчитывается по формуле:
Обратите внимание на отсутствие модулей у зарядов. Для разноименных зарядов энергия взаимодействия имеет отрицательное значение. Такая же формула справедлива и для энергии взаимодействия равномерно заряженных сфер и шаров. Как обычно, в этом случае расстояние r измеряется между центрами шаров или сфер. Если же зарядов не два, а больше, то энергию их взаимодействия следует считать так: разбить систему зарядов на все возможные пары, рассчитать энергию взаимодействия каждой пары и просуммировать все энергии для всех пар.
Для разноименных зарядов энергия взаимодействия имеет отрицательное значение. Такая же формула справедлива и для энергии взаимодействия равномерно заряженных сфер и шаров. Как обычно, в этом случае расстояние r измеряется между центрами шаров или сфер. Если же зарядов не два, а больше, то энергию их взаимодействия следует считать так: разбить систему зарядов на все возможные пары, рассчитать энергию взаимодействия каждой пары и просуммировать все энергии для всех пар.
Задачи по данной теме решаются, как и задачи на закон сохранения механической энергии: сначала находится начальная энергия взаимодействия, потом конечная. Если в задаче просят найти работу по перемещению зарядов, то она будет равна разнице между начальной и конечной суммарной энергией взаимодействия зарядов. Энергия взаимодействия так же может переходить в кинетическую энергию или в другие виды энергии. Если тела находятся на очень большом расстоянии, то энергия их взаимодействия полагается равной 0.
Обратите внимание: если в задаче требуется найти минимальное или максимальное расстояние между телами (частицами) при движении, то это условие выполнится в тот момент времени, когда частицы движутся в одну сторону с одинаковой скоростью.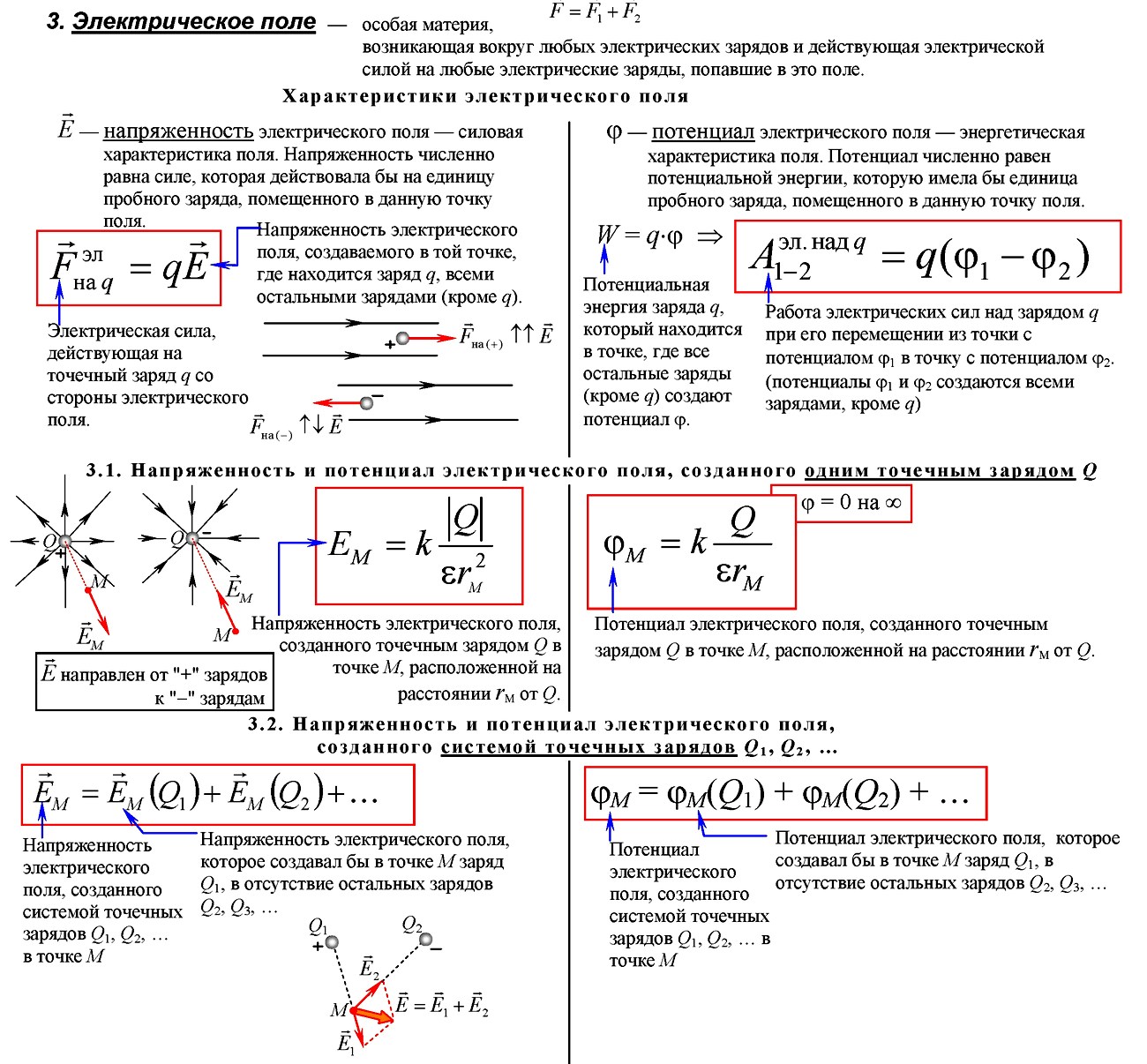 Поэтому решение надо начинать с записи закона сохранения импульса, из которого и находится эта одинаковая скорость. А далее следует писать закон сохранения энергии с учетом кинетической энергии частиц во втором случае.
Поэтому решение надо начинать с записи закона сохранения импульса, из которого и находится эта одинаковая скорость. А далее следует писать закон сохранения энергии с учетом кинетической энергии частиц во втором случае.
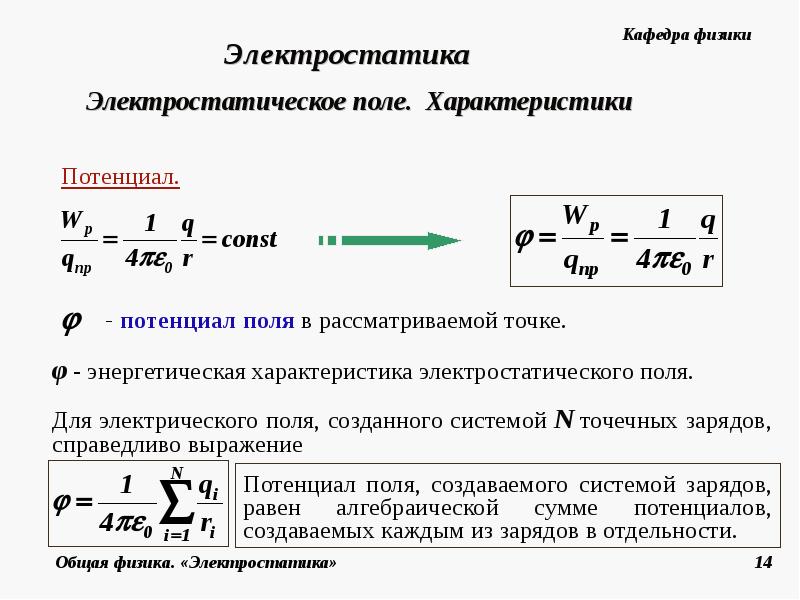
Потенциал. Разность потенциалов. Напряжение
К оглавлению…
Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.
Свойство потенциальности (независимости работы от формы траектории) электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. А физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
Потенциал φ является энергетической характеристикой электростатического поля. В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал — скалярная величина.
В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал — скалярная величина.
Во многих задачах электростатики при вычислении потенциалов за опорную точку, где значения потенциальной энергии и потенциала обращаются в ноль, удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом: потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Вспомнив формулу для потенциальной энергии взаимодействия двух точечных зарядов и разделив ее на величину одного из зарядов в соответствии с определением потенциала получим, что потенциал φ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
Потенциал рассчитанный по этой формуле может быть положительным и отрицательным в зависимости от знака заряда создавшего его. Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.
Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.
Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.
Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:
В однородном электрическом поле существует связь между напряженностью поля и напряжением:
Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:
Работа электрического поля в общем случае может быть вычислена также и по одной из формул:
В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:
В этих формулах:
- φ – потенциал электрического поля.

- ∆φ – разность потенциалов.
- W – потенциальная энергия заряда во внешнем электрическом поле.
- A – работа электрического поля по перемещению заряда (зарядов).
- q – заряд, который перемещают во внешнем электрическом поле.
- U – напряжение.
- E – напряженность электрического поля.
- d или ∆l – расстояние на которое перемещают заряд вдоль силовых линий.
Во всех предыдущих формулах речь шла именно о работе электростатического поля, но если в задаче говорится, что «работу надо совершить», или идет речь о «работе внешних сил», то эту работу следует считать так же, как и работу поля, но с противоположным знаком.
Принцип суперпозиции потенциала
Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов (при этом знак потенциала поля зависит от знака заряда, создавшего поле):
Обратите внимание, насколько легче применять принцип суперпозиции потенциала, чем напряженности. Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.
Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.
Электрическая емкость. Плоский конденсатор
К оглавлению…
При сообщении проводнику заряда всегда существует некоторый предел, более которого зарядить тело не удастся. Для характеристики способности тела накапливать электрический заряд вводят понятие электрической емкости. Емкостью уединенного проводника называют отношение его заряда к потенциалу:
В системе СИ емкость измеряется в Фарадах [Ф]. 1 Фарад – чрезвычайно большая емкость. Для сравнения, емкость всего земного шара значительно меньше одного фарада. Емкость проводника не зависит ни от его заряда, ни от потенциала тела. Аналогично, плотность не зависит ни от массы, ни от объема тела. Емкость зависит лишь от формы тела, его размеров и свойств окружающей его среды.
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
Величина электроемкости проводников зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.
Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.
Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами.
Каждая из заряженных пластин плоского конденсатора создает вблизи своей поверхности электрическое поле, модуль напряженности которого выражается соотношением уже приводившимся выше. Тогда модуль напряженности итогового поля внутри конденсатора, создаваемого двумя пластинами, равен:
За пределами конденсатора, электрические поля двух пластин направлены в разные стороны, и поэтому результирующее электростатическое поле E = 0.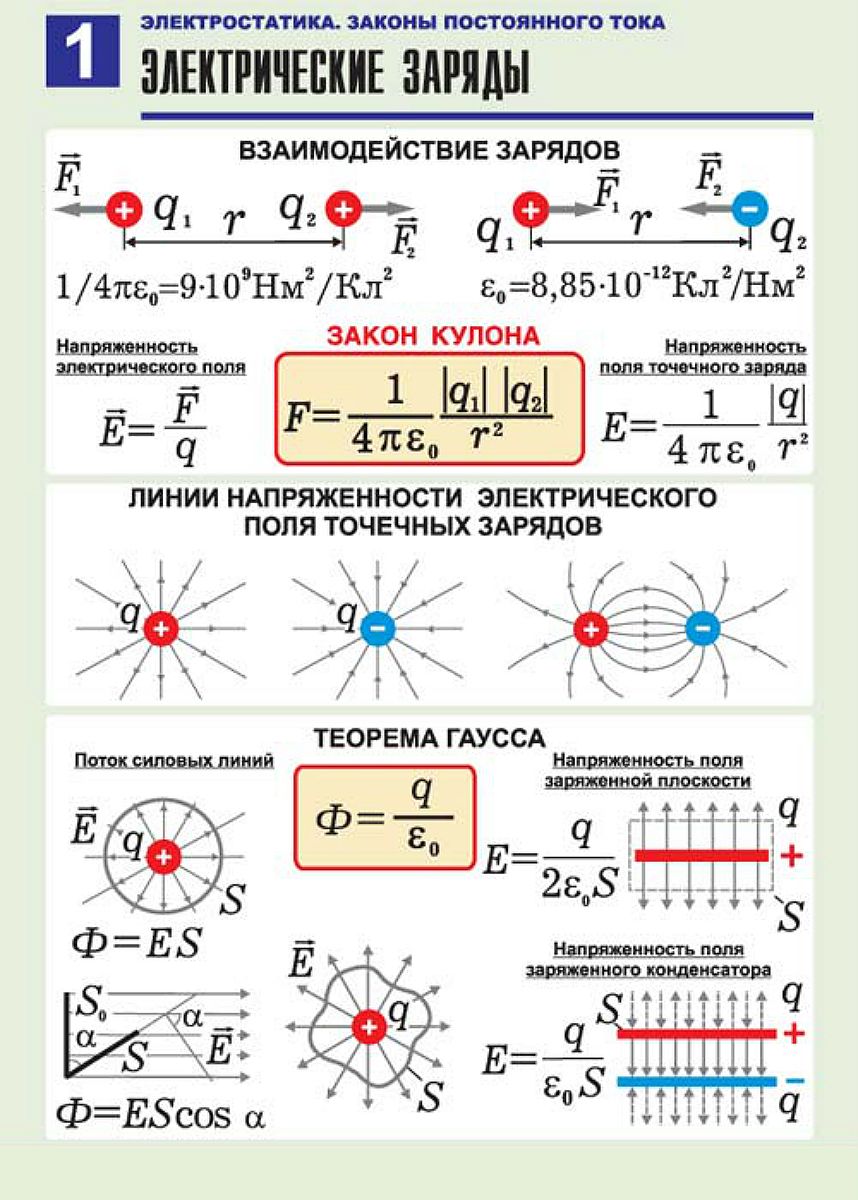 Электроёмкость плоского конденсатора может быть рассчитана по формуле:
Электроёмкость плоского конденсатора может быть рассчитана по формуле:
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз. Обратите внимание, что S в этой формуле есть площадь только одной обкладки конденсатора. Когда в задаче говорят о «площади обкладок», то имеют в виду именно эту величину. На 2 умножать или делить её не надо никогда.
Еще раз приведем формулу для заряда конденсатора. Под зарядом конденсатора понимают только заряд его положительной обкладки:
Сила притяжения пластин конденсатора. Сила, действующая на каждую обкладку, определяется не полным полем конденсатора, а полем, созданным противоположной обкладкой (сама на себя обкладка не действует). Напряженность этого поля равна половине напряженности полного поля, и сила взаимодействия пластин:
Энергия конденсатора. Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):
Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):
Особое внимание обращайте на фразу: «Конденсатор подключён к источнику». Это означает, что напряжение на конденсаторе не изменяется. А фраза «Конденсатор зарядили и отключили от источника» означает, что заряд конденсатора не изменится.
Энергия электрического поля
Электрическую энергию следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля.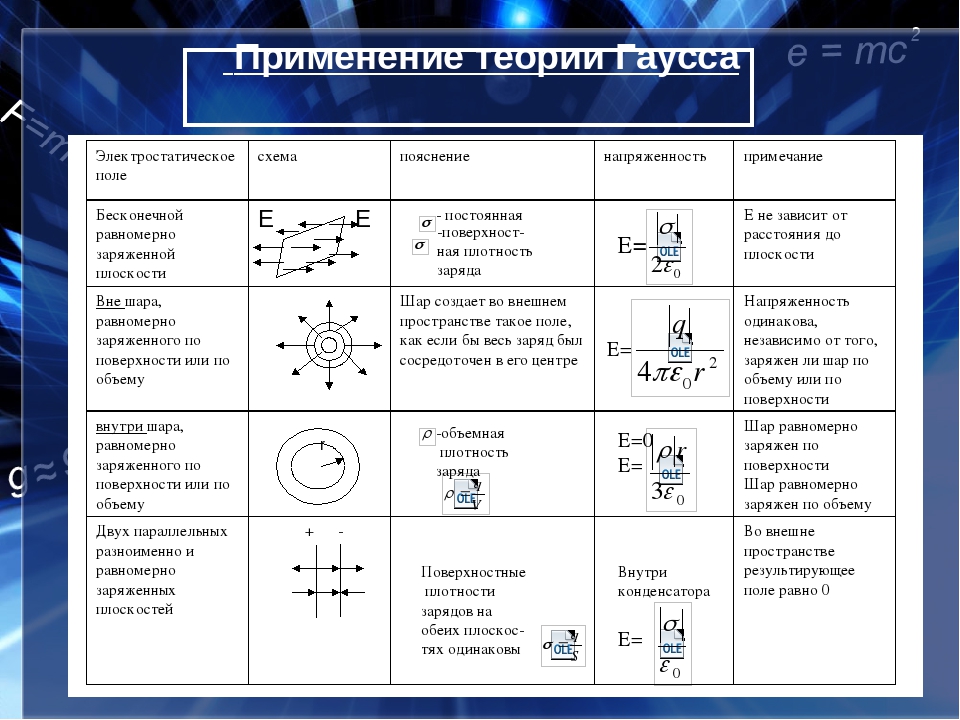 Энергия заряженных тел сосредоточена в пространстве, в котором есть электрическое поле, т.е. можно говорить об энергии электрического поля. Например, у конденсатора энергия сосредоточена в пространстве между его обкладками. Таким образом, имеет смысл ввести новую физическую характеристику – объёмную плотность энергии электрического поля. На примере плоского конденсатора, можно получить такую формулу для объёмной плотности энергии (или энергии единицы объёма электрического поля):
Энергия заряженных тел сосредоточена в пространстве, в котором есть электрическое поле, т.е. можно говорить об энергии электрического поля. Например, у конденсатора энергия сосредоточена в пространстве между его обкладками. Таким образом, имеет смысл ввести новую физическую характеристику – объёмную плотность энергии электрического поля. На примере плоского конденсатора, можно получить такую формулу для объёмной плотности энергии (или энергии единицы объёма электрического поля):
Соединения конденсаторов
К оглавлению…
Параллельное соединение конденсаторов – для увеличения ёмкости. Конденсаторы соединены одноименно заряженными обкладками, как бы увеличивая площадь одинаково заряженных пластин. Напряжение на всех конденсаторах одинаковое, общий заряд равен сумме зарядов каждого из конденсаторов, и общая ёмкость также равна сумме емкостей всех конденсаторов соединенных параллельно. Выпишем формулы для параллельного соединения конденсаторов:
При последовательном соединении конденсаторов общая ёмкость батареи конденсаторов всегда меньше, чем ёмкость наименьшего конденсатора, входящего в батарею. Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов. Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:
Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов. Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:
Из закона сохранения заряда следует, что заряды на соседних обкладках равны:
Напряжение равно сумме напряжений на отдельных конденсаторах.
Для двух последовательно соединённых конденсаторов формула выше даст нам следующее выражение для общей емкости:
Для N одинаковых последовательно соединённых конденсаторов:
Проводящая сфера
К оглавлению…
Напряженность поля внутри заряженного проводника равна нулю. В противном случае на свободные заряды внутри проводника действовала бы электрическая сила, которая вынуждала бы эти заряды двигаться внутри проводника. Это движение, в свою очередь, приводило бы к разогреванию заряженного проводника, чего на самом деле не происходит.
Факт того, что внутри проводника нет электрического поля можно понять и по-другому: если бы оно было то заряженные частицы опять таки двигались бы, причем они бы двигались именно так, чтобы свести это поле к нолю своим собственным полем, т.к. вообще-то двигаться им не хотелось бы, ведь всякая система стремится к равновесию. Рано или поздно все двигавшиеся заряды остановились бы именно в том месте, чтобы поле внутри проводника стало равно нолю.
На поверхности проводника напряжённость электрического поля максимальна. Величина напряжённости электрического поля заряженного шара за его пределами убывает по мере удаления от проводника и рассчитывается по формуле, аналогичной формулам для напряженности поля точечного заряда, в которой расстояния отсчитываются от центра шара.
Так как напряженность поля внутри заряженного проводника равна нулю, то потенциал во всех точках внутри и на поверхности проводника одинаков (только в этом случае разность потенциалов, а значит и напряжённость равна нулю).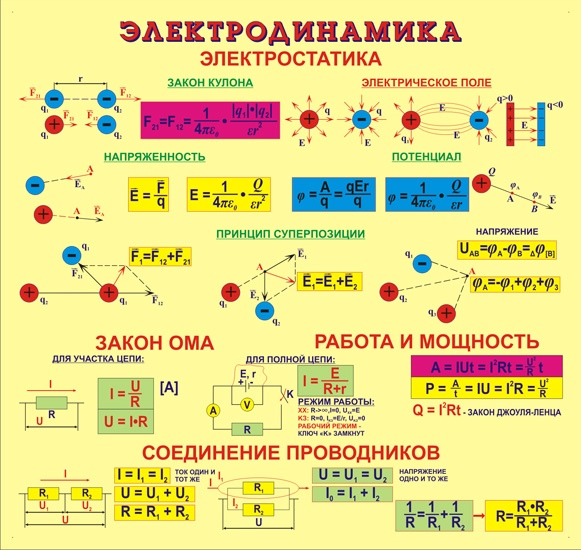 Потенциал внутри заряженного шара равен потенциалу на поверхности. Потенциал за пределами шара вычисляется по формуле, аналогичной формулам для потенциала точечного заряда, в которой расстояния отсчитываются от центра шара.
Потенциал внутри заряженного шара равен потенциалу на поверхности. Потенциал за пределами шара вычисляется по формуле, аналогичной формулам для потенциала точечного заряда, в которой расстояния отсчитываются от центра шара.
Электрическая емкость шара радиуса R:
Если шар окружен диэлектриком, то:
Свойства проводника в электрическом поле
К оглавлению…
- Внутри проводника напряженность поля всегда равна нулю.
- Потенциал внутри проводника во всех точках одинаков и равен потенциалу поверхности проводника. Когда в задаче говорят, что «проводник заряжен до потенциала … В», то имеют в виду именно потенциал поверхности.
- Снаружи от проводника вблизи от его поверхности напряженность поля всегда перпендикулярна поверхности.
- Если проводнику сообщить заряд, то он весь распределится по очень тонкому слою вблизи поверхности проводника (обычно говорят, что весь заряд проводника распределяется на его поверхности).
 Это легко объясняется: дело в том, что сообщая заряд телу, мы передаем ему носители заряда одного знака, т.е. одноименные заряды, которые отталкиваются. А значит они будут стремиться разбежаться друг от друга на максимальное расстояние из всех возможных, т.е. скопятся у самых краев проводника. Как следствие, если из проводника удалить сердцевину, то его электростатические свойства никак не изменятся.
Это легко объясняется: дело в том, что сообщая заряд телу, мы передаем ему носители заряда одного знака, т.е. одноименные заряды, которые отталкиваются. А значит они будут стремиться разбежаться друг от друга на максимальное расстояние из всех возможных, т.е. скопятся у самых краев проводника. Как следствие, если из проводника удалить сердцевину, то его электростатические свойства никак не изменятся. - Снаружи проводника напряженность поля тем больше, чем кривее поверхность проводника. Максимальное значение напряженности достигается вблизи остриев и резких изломов поверхности проводника.
Замечания к решению сложных задач
К оглавлению…
1. Заземление чего-либо означает соединение проводником данного объекта с Землей. При этом потенциалы Земли и имеющегося объекта выравниваются, а необходимые для этого заряды перебегают по проводнику с Земли на объект либо наоборот. При этом нужно учитывать несколько факторов, которые следуют из того, что Земля несоизмеримо больше любого объекта находящегося не ней:
- Общий заряд Земли условно равен нолю, поэтому ее потенциал также равен нолю, и он останется равным нолю после соединения объекта с Землей.
 Одним словом, заземлить – означает обнулить потенциал объекта.
Одним словом, заземлить – означает обнулить потенциал объекта. - Для обнуления потенциала (а значит и собственного заряда объекта, который мог быть до этого как положительным так и отрицательным), объекту придется либо принять либо отдать Земле некоторый (возможно даже очень большой) заряд, и Земля всегда сможет обеспечить такую возможность.
2. Еще раз повторимся: расстояние между отталкивающимися телами минимально в тот момент, когда их скорости становятся равны по величине и направлены в одну сторону (относительная скорость зарядов равна нулю). В этот момент потенциальная энергия взаимодействия зарядов максимальна. Расстояние между притягивающимися телами максимально, также в момент равенства скоростей, направленных в одну сторону.
3. Если в задаче имеется система, состоящая из большого количества зарядов, то необходимо рассматривать и расписывать силы, действующие на заряд, который не находится в центре симметрии.
Таблицы DPVA.ru — Инженерный Справочник |
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Электростатика. Основные понятия. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона. Принцип суперпозиции. Теория близкодействия. Потенциал электрического поля. Конденсатор.
Поделиться:
| |||||||||||||||||||||||||||||||||||||||||
|
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. |
||||||||||||||||||||||||||||||||||||||||||
|
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая |
Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||
Задачи и формулы по электростатике
Формулы электростатики
—Заряд электрона qe = -1,6*10-19 Кл
Масса электрона me = 9,1*10-31 кг
Протон – р+
Заряд протона qр = +1,6*10-19 Кл
Масса протона mp = 1,67*10-27 кг
Электрическая постоянная
Закон Кулона
где 𝑘 = 9
Напряженность точечного заряда E
измерение напряженности —
Напряженность заряженной пластины (плоскости)
где — поверхностная плотность заряда (заряд, приходящая на единицу площади пластины)
Напряженность плоского конденсатора
Напряженность заряженного шара
где r – расстояние от точки, в которой определяется напряженность, до центра шара.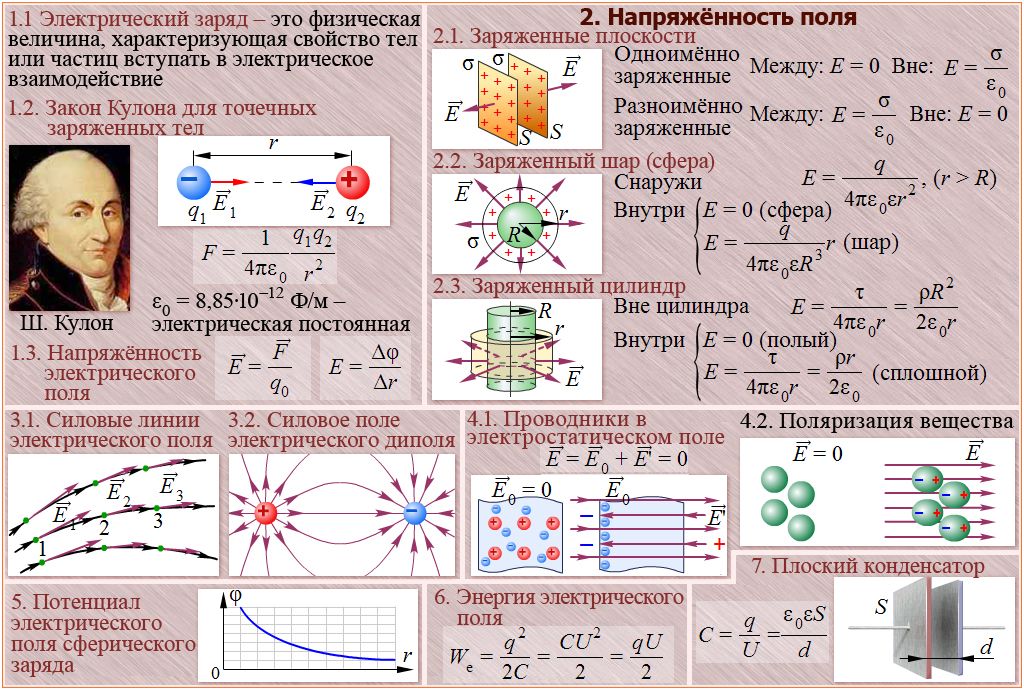
Напряженность заряженного цилиндра
где — линейная плотность заряда (заряд, приходящийся на единицу длины цилиндра)
r – расстояние от точки, в которой определяется напряженность, до оси цилиндра.
Работа электрического поля при перемещении заряда
А = qEd где q – заряд,
Е – напряженность электрического поля,
d – перемещение заряда вдоль (параллельно) силовых линий поля.
Потенциал электрического поля точечного заряда
Разность потенциалов
—
Электроемкость плоского конденсатора
или через параметры
где: — диэлектрическая проницаемость вещества
S – площадь пластин конденсатора
d – расстояние между пластинами
Энергия заряженного конденсатора
Общая емкость конденсаторов соединенных последовательно
Общая емкость конденсаторов соединенных параллельно
Cоб = С1+С2+…. +Сn
+Сn
нахождения величины заряда и количество заряда
Электрический заряд – это основа работы любого электронного прибора и та величина, без которой невозможно посчитать ни один важный показатель в электродинамике и электростатике. Подробная расшифровка термина, описание формулы нахождения электрического заряда и образец решения типовой задачи приведены в данной статье.
Что такое электрический заряд q
Электрический заряд, обозначаемый в международной системе единиц буквами q и Q, считается скалярной физической величиной, которая определяет свойство частицы или тела выступать в качестве источника электромагнитного поля и вступать в прямое взаимодействие с ним. В физике существует несколько видов электромагнитных заряженных частиц, и они называются положительными или отрицательными. Обе единицы измеряются в Кулонах, а найти их можно путём вычисления произведения одного Ампера с одной секундой.
Понятие из учебного пособияФормула нахождения заряда
Определить искомую величину можно из физико-математической формулы силы тока. -19 Кулон.
-19 Кулон.
Обратите внимание! Формула заряда является следствием прямой зависимости напряженности электромагнитного поля от потенциала его частицы, что является основным правилом нахождения емкости заряженного конденсатора и величины энергии, накопленной в нём. Кроме того, вычислить количество заряда можно через силу Лоренца.
Основные формулыКак вычислять с помощью законов
Поскольку q и Q являются скалярными единицами, вычислить их с помощью законов можно через точные формулы, выведенные известными учеными-физиками. К примеру, в соответствии с законом Кулона, можно найти величину и силовое направление взаимодействия заряженных частиц между несколькими неподвижными телами.
Закон сохранения
Все элементарные частицы подразделяются на нейтральные или заряженные. Они вступают во взаимодействие друг с другом внутри электромагнитного поля. Частицы, которые имеют одноименный электрон, отталкиваются, а разноименный – притягиваются. В первом случае наблюдается избыток электронов, а во втором – их недостаток. Оба типа частиц заряжаются посредством электризации. На практике, при возникновении данного явления, заряженные частицы равны по модулю, несмотря на противоположность знаков. Когда разные частицы притягиваются, то между ними происходит электризация и сохранение электрона. При этом, сумма всех изолированных системных частиц не изменяется, то есть, q + q + q…= const.
Оба типа частиц заряжаются посредством электризации. На практике, при возникновении данного явления, заряженные частицы равны по модулю, несмотря на противоположность знаков. Когда разные частицы притягиваются, то между ними происходит электризация и сохранение электрона. При этом, сумма всех изолированных системных частиц не изменяется, то есть, q + q + q…= const.
Закон Кулона
Выше было сказано, что электрические заряженные микрочастицы бывают как положительными, так и отрицательными, а их наличие подтверждается силовым взаимодействием, которое с помощью экспериментов на весах описал в 1785 году О. Кулон, создав свой физико-математический закон.
Закон Кулона представляет собой физическую закономерность, которая описывает взаимодействие наэлектризованных частиц между не электризованными, в зависимости от промежутка между ними. В соответствии с этой формулировкой, чем больше электронов имеет частица, тем ближе она расположена к другой элементарной единице заряда, и, соответственно, сила возрастает.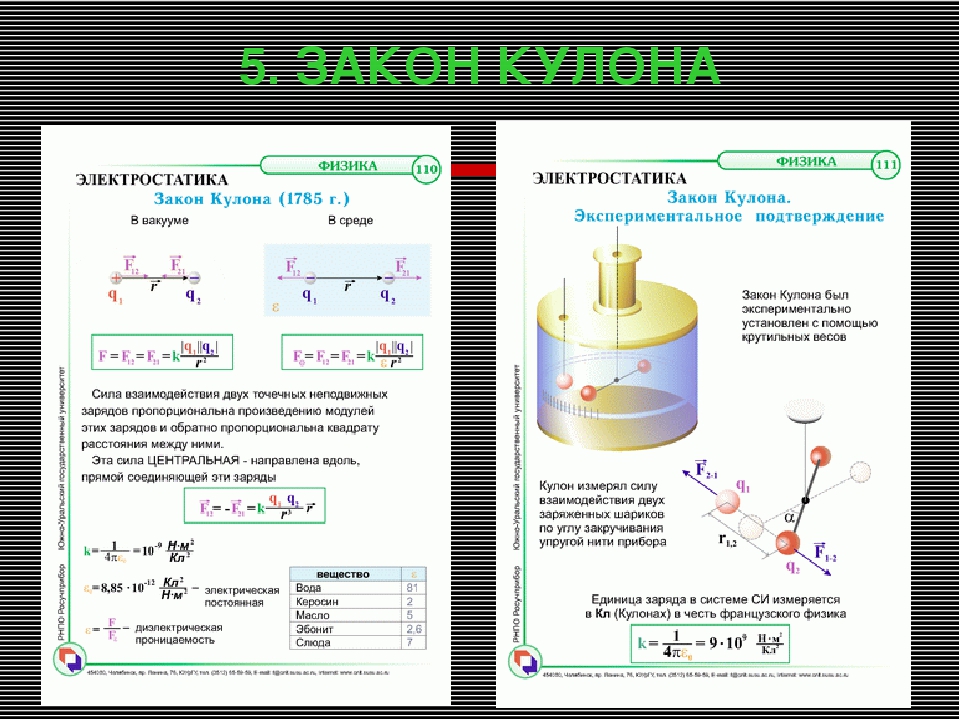
Обратите внимание! При увеличении расстояния между частицами, сал их взаимодействия неизменно убывает. В математической формуле это выглядит так: F1 = F2 = K*(q1*q2/r2), где q1 и q2 считаются модулями заряженных микрочастиц, k является коэффициентом пропорциональности, который зависит от системного выбора единицы, а r — расстоянием.
Закон КулонаОбразец решения задач по теме «Электрический заряд»
Ниже приведены образцы решения простых задач по электростатике, в частности, на закон Кулона.
Задача 1. Несколько одинаковых заряженных шаров имеют показатели q1 = 6 микрокулон и q2 = -18 микрокулон. Они располагаются друг от друга на 36 сантиметров (0,36 метров). Насколько будет меняться сила их взаимодействия при соприкосновении друг с другом и разведении в сторону?
Чтобы решить эту задачу, нужно воспользоваться эл заряд формулой F=K*(q1*q2/r2), подставив вместо букв известные величины. В результате, выйдет число 7,5.
Задача 2. Маленькие одинаковые шары находятся на промежутке в 0,15 метра и притягиваются с силой 1 микроньютон.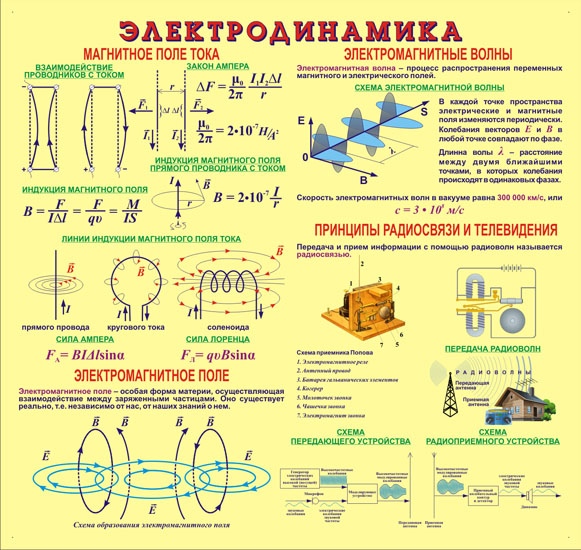 -7 или 10 микрокулон.
-7 или 10 микрокулон.
В целом, электрический заряд представляет собой физическую скалярную величину, которая определяет способность тел являться источником электромагнитного поля и участвовать во взаимодействии с ним. Отыскать величину, которая обозначается буквами q и Q, для решения задач или для выполнения другой работы, можно через закон сохранения, Кулона и представленные выше основные физические формулы.
Урок Электростатика — Физика 10 класс
ЭлектростатикаВзаимодействие электрических зарядов. Два вида заряда. Закон сохранения электрического заряда.
Электрический заряд , наряду с массой , является важнейшей характеристикой частицы.
Электрическим зарядом называется величина, определяющая интенсивность электромагнитного взаимодействия заряженных частиц. [q] =Кулон (Кл)
[q] =Кулон (Кл)
Электрические заряды могут быть положительными и отрицательными,
причем, одноименные заряды отталкиваются, разноименные – притягиваются.
Обычно носителем элементарного отрицательного заряда является
электрон, а положительного – протон. По модулю значение элементарного
заряда равно: Кл.
Любые заряды в целое число раз больше элементарного:
Из опыта следует закон сохранения заряда: в электрически замкнутой системе полный заряд сохраняется.
Экспериментально также установлен закон инвариантности электрического заряда: величина заряда не зависит от скорости, с которой он движется (т.е. инвариантна относительно инерциальных систем отсчета).
Электростатика изучает законы взаимодействия электрических неподвижных зарядов.
Точечный заряд – это заряженное тело, размерами которого можно пренебречь в условиях данной задачи.
Закон Кулона.
Сила взаимодействия двух неподвижных точечных зарядов определяется законом Кулона:
e — диэлектрическая проницаемость среды (табличное данное), — модули зарядов.
, Можно записать закон Кулона: .
Электрическое поле. Напряженность. Принцип суперпозиции.
Силовой характеристикой электростатического поля является напряженность :
F – сила, действующая на неподвижный точечный заряд q.
Модуль напряженности электростатического поля, созданного точечным зарядом q на расстоянии r от заряда вычислим по формуле:
. Если a — угол между векторами , то напряженность поля, созданного двумя зарядами, вычисляют по формуле:.
Графическое изображение поля
Для графического изображения электрического поля используют линии
напряженности (силовые линии). Линии напряженности начинаются на
положительных зарядах, заканчиваются на отрицательных или уходят в
бесконечность.
Вектор напряженности направлен по касательной к линии напряженности в каждой точке.
Густота линий пропорциональна модулю напряженности поля.
Примеры изображений электрических полей
Потенциал и разность потенциалов. Работа по перемещению заряда.
Энергетической характеристикой поля является потенциал.
W – потенциальная энергия точечного заряда q, помещенного в данную точку поля.
Потенциал – величина алгебраическая. Потенциал поля, создаваемого точечным зарядом q на расстоянии r от заряда, вычисляется по формуле:
, q > 0, j > 0, q Связь разности потенциалов с напряженностью
(j1 — j2) – разность потенциалов
Электрическое поле, в котором напряженность одинакова по модулю и направлению в любой точке пространства, называется однородным.
В однородном поле , d – расстояние между точками с потенциалами j1 и j2.
Работа электростатического поля при перемещении заряда
Работа, совершаемая силами поля по перемещению заряда из точки 1 вточку 2 вычисляется по формуле: .

Поверхность,
во всех точках которой потенциал электрического поля имеет одинаковое
значение, называется эквипотенциальной поверхностью. Эквипотенциальными
поверхностями точечного заряда являются сферы, в центре которых
расположен заряд.
Электрическая емкость. Конденсатор. Энергия электрического поля.
Для накопления значительных разноименных электрических зарядов применяются конденсаторы.
Конденсатор – это две проводящих поверхности, обычно плоской,
цилиндрической или сферической формы, расположенные на небольшом
расстоянии друг от друга. Проводники — обкладки конденсатора — заряжают
разноименными зарядами, равными по абсолютной величине — — разность потенциалов между обкладками.
Электроемкость конденсатора: , [C]=Фарада (Ф)
Электроемкость плоского конденсатора:
S – площадь обкладок,
d – расстояние между обкладками,
e — диэлектрическая проницаемость вещества, заполняющего пространство между обкладками,
eo — электрическая постоянная (eо=8,85 10-12 Ф/м).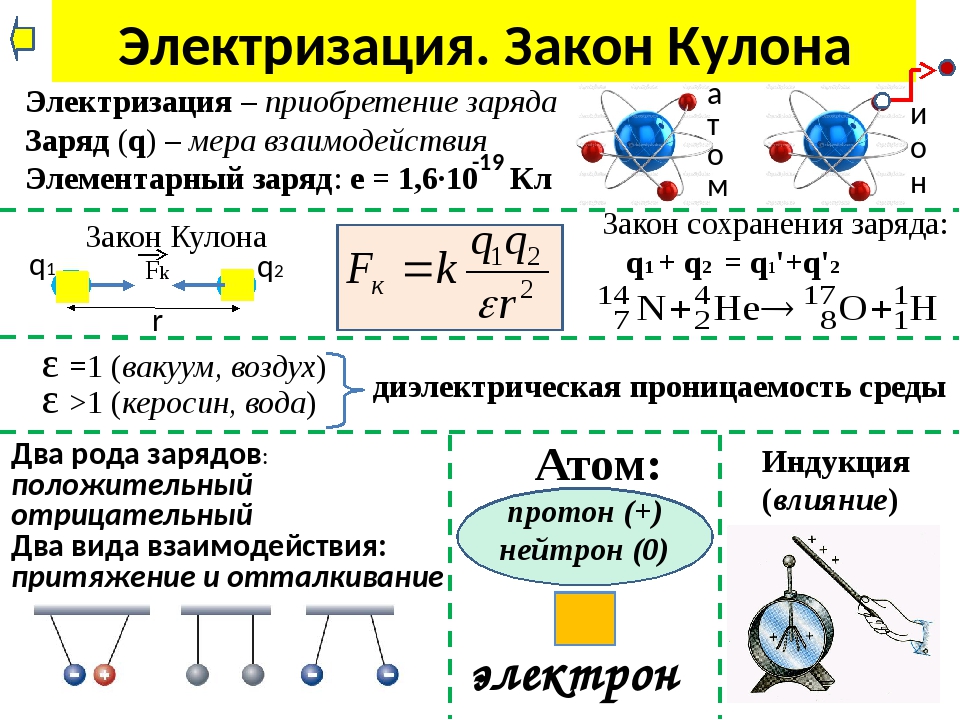
Энергия заряженного конденсатора
Энергия заряженного конденсатора любой формы вычисляется по формуле:
С – емкость конденсатора, — разность потенциалов между обкладками конденсатора,
q – заряд пластины конденсатора.
Энергия электрического поля плоского конденсатора:
ТЕСТОВЫЕ ЗАДАНИЯ
- Два одинаковых металлических шарика заряжены одноименно так, что величина зарядов на одном шарике в n раз больше, чем на другом. Шарики привели в соприкосновение и раздвинули на прежнее расстояние, много больше размеров шарика. Во сколько раз изменилась сила взаимодействия между шариками?
- Два шарика радиусом R1 и R2 заряжены до потенциалов j1 и j2 соответственно, находятся на большом расстоянии друг от друга. Шарики соединяют длинным тонким проводником. Какой общий потенциал устанавливается на шариках?
- При перемещении заряда в электрическом поле по любой замкнутой
траектории работа сил электрического поля оказалась равной нулю.
 Какое
это было поле?
Какое
это было поле? - Две параллельные металлические пластины находятся на расстоянии 5 см одна от другой. Между пластинами приложено напряжение 20 В. Какова напряженность электрического поля между пластинами?
- Как изменится электроемкость конденсатора при уменьшении расстояния между пластинами в 4 раза?
- Укажите направление и рассчитайте напряженность электрического поля в точке, лежащей посередине между зарядами q1=2 10-7 Кл и q2=-4 10-7 Кл . Расстояние между зарядами равно 10 см.
- Пластины плоского конденсаторы имеют электрические заряды +q и –q, площадь одной пластины S. Расстояние между пластинами d. Какую работу нужно совершить для того, чтобы раздвинуть пластины на небольшое расстояние Dd?
- Напряжение на обкладках конденсатора было 100 В. При полной разрядке конденсатора через резистор в цепи прошел электрический заряд 0,1 Кл. Какова электроемкость конденсатора и какое количество энергии выделилось на резисторе?
- К положительному заряду q1 с большого расстояния приближается на
расстояние R отрицательный заряд q2.
 Как изменятся напряженность и
потенциал электрического поля в точке на середине расстояния между
зарядами q1 и q2 ?
Как изменятся напряженность и
потенциал электрического поля в точке на середине расстояния между
зарядами q1 и q2 ? - На нейлоновой нити подвешен электрически нейтральный алюминиевый стержень. Имеется стеклянный стержень, обладающий отрицательным электрическим зарядом. Как сообщить алюминиевому стержню положительный заряд?
- Так как расстояние между шариками значительно больше их размеров, то силу взаимодействия заряженных шариков вычислим по закону Кулона. До соприкосновения: После соприкосновения заряды шариков станут одинаковыми. По закону сохранения заряда:, , ,
- Заряд
шариков до соединения проводником: q1=j1×c1, q2=j2×c2.
Электроемкость
уединенного проводника, шара радиусом R вычисляем по формуле: с=4peeoR. Тогда:. Если
шарики соединить, то будет происходить перераспределение зарядов между
шариками до тех пор, пока потенциалы шариков j не станут
равными.
 Заряд первого шара второго шара и .
Заряд первого шара второго шара и . - Работа перемещения заряда в электростатическом поле
Если контур замкнут, то , значит - .
- , т.к. d уменьшается в 4 раза, то С увеличивается в 4 раза.
- В/м В/м . Определим направление , выполним рисунок. Так как направлены в одну и ту же сторону, то: В/м.
- Работа равна изменению энергии заряженного конденсатора: .
- По определению: .
Энергия заряженного конденсатора выделится на резисторе при полном разряде? - Напряженность увеличится на величину .
Потенциал– величина
алгебраическая:
—
потенциал в точке в 1-ом случае.
 При приближении отрицательного
заряда потенциал
, значит потенциал уменьшится.
При приближении отрицательного
заряда потенциал
, значит потенциал уменьшится. - Нужно поднести стеклянный стержень к одному концу алюминиевого стержня без соприкосновения и в это же время коснуться рукой противоположного конца алюминиевого стержня.
Электродинамика, формулы. Основные формулы электродинамики Основные формулы электродинамики таблица
Шпаргалка с формулами по физике для ЕГЭ
Шпаргалка с формулами по физике для ЕГЭ
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
И не только (может понадобиться 7, 8, 9, 10 и 11 классам). Для начала картинка, которую можно распечатать в компактном виде.
Шпаргалка с формулами по физике для ЕГЭ и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
А потом вордовский файл , который содержит все формулы чтобы их распечатать, которые находятся внизу статьи.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 —υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ —υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей — Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля — Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 — Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 — Т 2)/ Т 1
Электростатика и электродинамика — формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
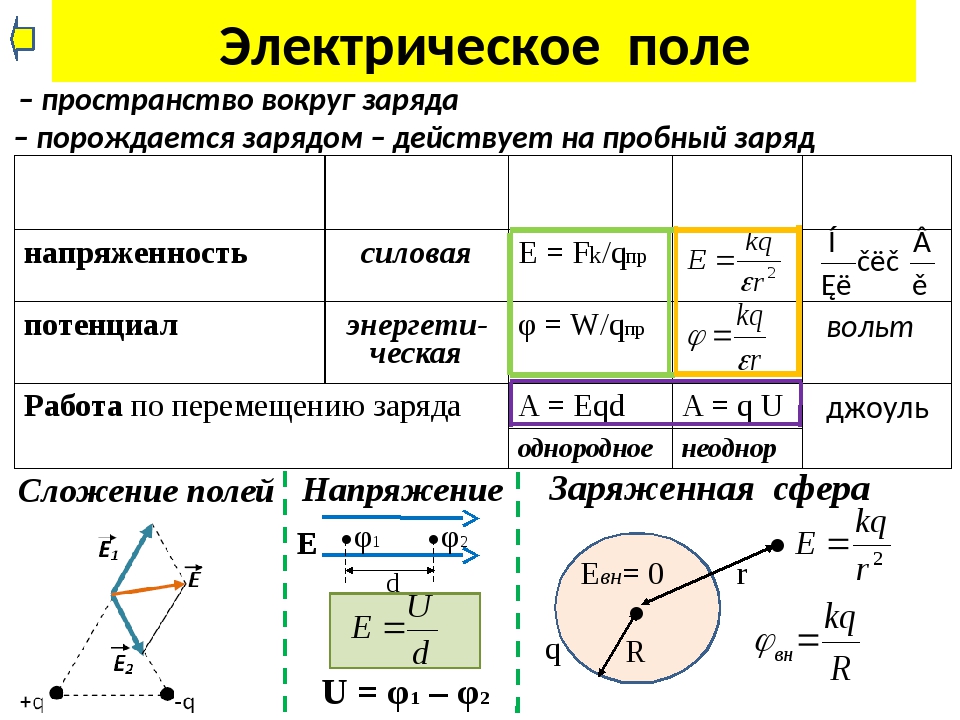 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
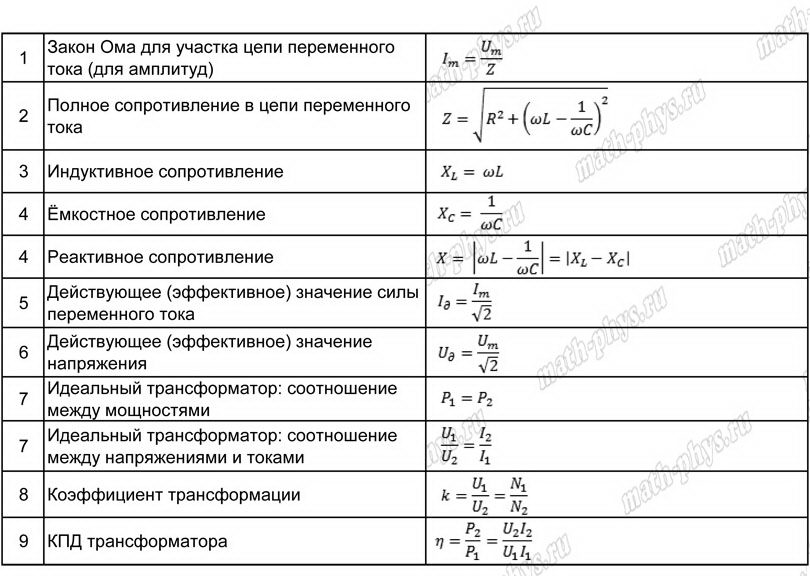
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
- Закон радиоактивного распада N=N 0 ∙2 — t / T
- Энергия связи атомных ядер
E CB =(Zm p +Nm n -Mя)∙c 2
СТО
- t=t 1 /√1-υ 2 /c 2
- ℓ=ℓ 0 ∙√1-υ 2 /c 2
- υ 2 =(υ 1 +υ)/1+ υ 1 ∙υ/c 2
- Е = mс 2
Формулы электричества и магнетизма. Изучение основ электродинамики традиционно начинается с электрического поля в вакууме. Для вычисления силы взаимодействия между двумя точными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона. Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип
Изучение основ электродинамики традиционно начинается с электрического поля в вакууме. Для вычисления силы взаимодействия между двумя точными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона. Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т.д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип
При изучении темы «Постоянный ток» необходимо рассмотреть во всех формах законы Ома и Джоуля-Ленца При изучении «Магнетизма» необходимо иметь в виду, что магнитное поле порождается движущимися зарядами и действует на движущиеся заряды. Здесь следует обратить внимание на закон Био-Савара-Лапласа. Особое внимание следует обратить на силу Лоренца и рассмотреть движение заряженной частицы в магнитном поле.
Электрические и магнитные явления связаны особой формой существования материи — электромагнитным полем. Основой теории электромагнитного поля является теория Максвелла.
Таблица основных формул электричества и магнетизма
|
Физические законы, формулы, переменные |
Формулы электричество и магнетизм |
||||||||
|
Закон Кулона:
|
|||||||||
|
Напряженность электрического поля: где Ḟ — сила, действующая на заряд q 0 , находящийся в данной точке поля. |
|||||||||
|
Напряженность поля на расстоянии r от источника поля: 1) точечного заряда 2) бесконечно длинной заряженной нити с линейной плотностью заряда τ: 3) равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ: 4) между двумя разноименно заряженными плоскостями |
|
||||||||
|
Потенциал электрического поля: где W — потенциальная энергия заряда
q
0 . |
|||||||||
|
Потенциал поля точечного заряда на расстоянии r от заряда: |
|||||||||
|
По принципу суперпозиции полей, напряженность: |
|||||||||
|
Потенциал: где Ē i и ϕ i — напряженность и потенциал в данной точке поля, создаваемый i-м зарядом. |
|||||||||
|
Работа сил электрического поля по перемещению заряда q из точки с потенциалом ϕ 1 в точку с потенциалом ϕ 2 : |
|||||||||
|
Связь между напряженностью и потенциалом 1) для неоднородного поля: 2) для однородного поля: |
|||||||||
|
Электроемкость уединенного проводника: |
|||||||||
|
Электроемкость конденсатора: |
|||||||||
|
Электроемкость плоского конденсатора: где S — площадь пластины (одной) конденсатора, d — расстояние между пластинами. |
|||||||||
|
Энергия заряженного конденсатора: |
|||||||||
|
Сила тока: |
|||||||||
|
Плотность тока: где S — площадь поперечного сечения проводника. |
|||||||||
|
Сопротивление проводника: l — длина проводника; S — площадь поперечного сечения. |
|||||||||
|
Закон Ома 1) для однородного участка цепи: 2) в дифференциальной форме: 3) для участка цепи, содержащего ЭДС: Где ε — ЭДС источника тока, R и r — внешнее и внутреннее сопротивления цепи; 4) для замкнутой цепи: |
|
||||||||
|
Закон Джоуля-Ленца 1) для однородного участка цепи постоянного тока: 2) для участка цепи с изменяющимся со временем током: |
|
||||||||
|
Мощность тока: |
|||||||||
|
Связь магнитной индукции и напряженности магнитного поля: где B — вектор магнитной индукции, |
|||||||||
|
Магнитная индукция
(индукция магнитного поля):
2) поля бесконечно длинного прямого тока 3) поля, созданного отрезком проводника с током |
Электродинамика — это раздел физики, изучающий теорию электромагнитного поля, а также взаимодействие между электрическими зарядами. Электродинамика стала еще одной ступенью бурного развития физики. Имеются формулы по электродинамике, а также шпоры и задачи по электродинамике.
Как наука зародилась в результате многочисленных открытий и экспериментов. Разделом электродинамики, изучающим взаимодействия и электрические поля покоящихся электрических зарядов, является электростатика.
Классическая электродинамика
Электродинамика развивалась бурными темпами, многие известные ученые внесли свой вклад в развитие электродинамики. В 1785 г. французским физиком Ш. Кулоном был экспериментально установлен закон взаимодействия двух неподвижных точечных зарядов. Кулон Шарль Огюстен В 1820 г. датский физик Х. Эрстед показал, что ток, текущий по проводам, создает вокруг себя магнитное поле. Эрстед Ханс Христиан В 1831 г. М.Фарадей открыл электромагнитную индукцию. Фарадей Майкл Электродинамика — наука, занимающаяся изучением электромагнитного поля. Это поле проявляет себя посредством силового взаимодействия с теми частицами вещества, которые имеют электрический заряд. привлекла английского ученого Дж. Максвелла. Основываясь на опытных данных, он предложил уравнения, достаточные для описания всех электромагнитных явлений.Учебник скачать бесплатно с сайта
Название: Электродинамика и распространение радиоволн
Закон Кулона:
где F – сила электростатического взаимодействия между двумя заряженными телами;
q 1 , q 2 – электрические заряды тел;
ε – относительная, диэлектрическая проницаемость среды;
ε 0 =8,85·10 -12 Ф/м – электрическая постоянная;
r
– расстояние между двумя заряженными телами.
Линейная плотность заряда:
где dq – элементарныйзаряд, приходящийся на участок длины dl.
Поверхностная плотность заряда:
где dq – элементарныйзаряд, приходящийся на поверхность ds.
Объемная плотность заряда:
где dq – элементарныйзаряд, в объеме dV.
Напряженность электрического поля:
где F – сила действующая на заряд q .
Теорема Гаусса:
где Е – напряженность электростатического поля;
dS – вектор, модуль которого равен площади пронизываемой поверхности, а направление совпадает с направлением нормали к площадке;
q – алгебраическая сумма заключенных внутри поверхности dS зарядов.
Теорема о циркуляции вектора напряженности:
Потенциал электростатического поля:
где W
p – потенциальная энергия точечного заряда q
.
Потенциал точечного заряда:
Напряженность поля точечного заряда:
.
Напряженность поля, создаваемого бесконечной прямой равномерно заряженной линией или бесконечно длинным цилиндром:
где τ – линейная плотность заряда;
r – расстояние от нити или оси цилиндра до точки, напряженность поля в которой определяется.
Напряженность поля, создаваемого бесконечной равномерной заряженной плоскостью:
где σ – поверхностная плотность заряда.
Связь потенциала с напряженностью в общем случае:
E= – gradφ= .
Связь потенциала с напряженностью в случае однородного поля:
E = ,
где d – расстояние между точками с потенциалами φ 1 и φ 2 .
Связь потенциала с напряженностью в случае поля, обладающего центральной или осевой симметрией:
Работа сил поля по перемещению заряда q из точки поля с потенциалом φ 1 в точку с потенциалом φ 2:
A=q(φ 1 – φ 2).
Электроемкость проводника:
где q – заряд проводника;
φ – потенциал проводника при условии, что в бесконечности потенциал проводника принимается равным нулю.
Электроемкость конденсатора:
где q – заряд конденсатора;
U – разность потенциалов между пластинами конденсатора.
Электроемкость плоского конденсатора:
где ε – диэлектрическая проницаемость диэлектрика, расположенного между пластинами;
d – расстояние между пластинами;
S – суммарная площадь пластин.
Электроемкость батареи конденсаторов:
б) при параллельном соединении:
Энергия заряженного конденсатора:
,
где q – заряд конденсатора;
U – разность потенциалов между пластинами;
C – электроемкость конденсатора.
Сила постоянного тока:
где dq
– заряд, протекший через поперечное сечение проводника за время dt
.
Плотность тока:
где I – сила тока в проводнике;
S – площадь проводника.
Закон Ома для участка цепи, не содержащего ЭДС:
где I – сила тока на участке;
U
R – сопротивление участка.
Закон Ома для участка цепи, содержащего ЭДС:
где I – сила тока на участке;
U – напряжение на концах участка;
R – полное сопротивление участка;
ε – ЭДС источника.
Закон Ома для замкнутой (полной) цепи:
где I – сила тока в цепи;
R – внешнее сопротивление цепи;
r – внутреннее сопротивление источника;
ε – ЭДС источника.
Законы Кирхгофа:
2. ,
где – алгебраическая сумма сил токов, сходящихся в узле;
– алгебраическая сумма падений напряжений в контуре;
– алгебраическая сумма ЭДС в контуре.
Сопротивление проводника:
где R – сопротивление проводника;
ρ – удельное сопротивление проводника;
l – длина проводника;
S
Проводимость проводника:
где G – проводимость проводника;
γ – удельная проводимость проводника;
l – длина проводника;
S
– площадь поперечного сечения проводника.
Сопротивление системы проводников:
а) при последовательном соединении:
а) при параллельном соединении:
Работа тока:
,
где A – работа тока;
U – напряжение;
I – сила тока;
R – сопротивление;
t – время.
Мощность тока:
.
Закон Джоуля – Ленца
где Q – количество выделившейся теплоты.
Закон Ома в дифференциальной форме:
j =γE ,
где j – плотность тока;
γ – удельная проводимость;
E – напряженность электрического поля.
Связь магнитной индукции с напряженность магнитного поля:
B =μμ 0 H ,
где B – вектор магнитной индукции;
μ– магнитная проницаемость;
H – напряженность магнитного поля.
Закон Био – Савара – Лапласа:
,
где dB – индукция магнитного поля, создаваемая проводником в некоторой точке;
μ – магнитная проницаемость;
μ 0 =4π·10 -7 Гн/м – магнитная постоянная;
I – сила тока в проводнике;
dl – элемент проводника;
r
– радиус-вектор, проведенный из элемента dl
проводника в точку, в которой определяется индукция магнитного поля.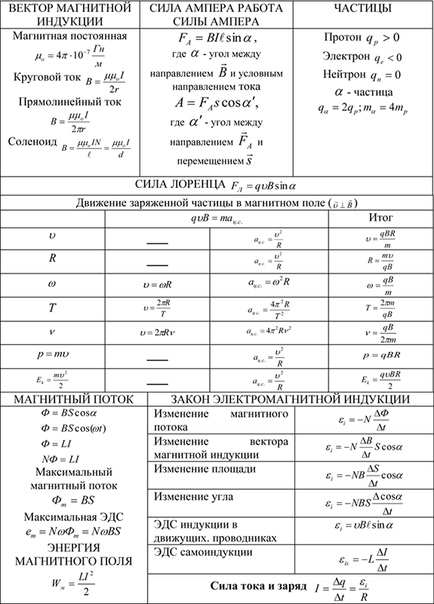
Закон полного тока для магнитного поля (теорема о циркуляции вектора B ):
,
где n – число проводников с токами, охватываемых контуром L произвольной формы.
Магнитная индукция в центре кругового тока:
где R – радиус кругового витка.
Магнитная индукция на оси кругового тока:
,
где h – расстояние от центра витка до точки, в которой определяется магнитная индукция.
Магнитная индукция поля прямого тока:
где r 0 – расстояние от оси провода до точки, в которой определяется магнитная индукция.
Магнитная индукция поля соленоида:
B= μμ 0 nI,
где n – отношение числа витков соленоида к его длине.
Сила Ампера:
dF =I,
где dF – сила Ампера;
I – сила тока в проводнике;
dl – длина проводника;
B
– индукция магнитного поля.
Сила Лоренца:
F =qE +q [v B ],
где F – сила Лоренца;
q – заряд частицы;
E – напряженность электрического поля;
v – скорость частицы;
B – индукция магнитного поля.
Магнитный поток:
а) в случае однородного магнитного поля и плоской поверхности:
Φ=B n S ,
где Φ –магнитный поток;
B n – проекция вектора магнитной индукции на вектор нормали;
S – площадь контура;
б) в случае неоднородного магнитного поля и произвольной проекции:
Потокосцепления (полный поток) для тороида и соленоида:
где Ψ – полный поток;
N – число витков;
Φ – магнитный поток, пронизывающий один виток.
Индуктивность контура:
Индуктивность соленоида:
L= μμ 0 n 2 V,
где L – индуктивность соленоида;
μ – магнитная проницаемость;
μ 0 – магнитная постоянная;
n – отношение числа витков к его длине;
V
– объем соленоида.
Закон электромагнитной индукции Фарадея:
где ε i – ЭДС индукции;
– изменение полного потока в единицу времени.
Работа по перемещению замкнутого контура в магнитном поле:
A=I ΔΦ,
где A – работа по перемещению контура;
I – сила тока в контуре;
ΔΦ – изменение магнитного потока, пронизывающего контур.
ЭДС самоиндукции:
Энергия магнитного поля:
Объемная плотность энергии магнитного поля:
,
где ω – объемная плотность энергии магнитного поля;
B – индукция магнитного поля;
H – напряженность магнитного поля;
μ – магнитная проницаемость;
μ 0 – магнитная постоянная.
3.2. Понятия и определения
? Перечислите свойства электрического заряда.
1. Существуют заряды двух типов – положительные и отрицательные.
2. Одноименные заряды отталкиваются, разноименные притягиваются.
3.Заряды обладают свойством дискретности – все кратны наименьшему элементарному.
4. Заряд инвариантен, его величина не зависит от системы отсчета.
5. Заряд аддитивен — заряд системы тел равен сумме зарядов всех тел системы.
6. Полный электрический заряд замкнутой системы есть величина постоянная
7. Неподвижный заряд – источник электрического поля, движущийся заряд – источник магнитного поля.
? Сформулируйте закон Кулона.
Сила взаимодействия двух точечных неподвижных зарядов пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния между ними. Направлена сила вдоль линии, соединяющей заряды.
? Что такое электрическое поле? Напряженность электрического поля? Сформулируйте принцип суперпозиции напряженности электрического поля.
Электрическое поле – вид материи, связанный с электрическими зарядами и передающий действие одних зарядов на другие. Напряженность – силовая характеристика поля, равная силе, действующий на единичный положительный заряд, помещенный в данную точку поля. Принцип суперпозиции – напряженность поля, создаваемая системой точечных зарядов, равна векторной сумме напряженностей поля каждого заряда.
Напряженность – силовая характеристика поля, равная силе, действующий на единичный положительный заряд, помещенный в данную точку поля. Принцип суперпозиции – напряженность поля, создаваемая системой точечных зарядов, равна векторной сумме напряженностей поля каждого заряда.
? Что называют силовыми линиями напряженности электростатического поля? Перечислите свойства силовых линий.
Линия, касательная в каждой точке которых совпадает с направлением вектора напряженности поля называется силовой. Свойства силовые линии – начинаются на положительных, заканчиваются на отрицательных зарядах, не прерываются, не пересекаются друг с другом.
? Дайте определение электрического диполя. Поле диполя.
Система из двух равных по модулю, противоположных по знаку точечных электрических зарядов, расстояние между которыми мало по сравнению с расстоянием до точек, где наблюдается действие этих зарядов.Вектор напряженности имеет направление, противоположное вектору электрического момента диполя (который, в свою очередь, направлен от отрицательного заряда к положительному).
? Что такое потенциал электростатического поля? Сформулируйте принцип суперпозиции потенциала.
Скалярная величина, численно равная отношению потенциальной энергии электрического заряда, помещенного в данную точку поля, к величине этого заряда. Принцип суперпозиции – потенциал системы точечных зарядов в некоторой точке пространства равен алгебраической сумме потенциалов, которые создали бы по отдельности эти заряды в этой же точке пространства.
? Какова связь между напряженностью и потенциалом?
E =- (E -напряженность поля в данной точке поля, j — потенциал в этой точке.)
? Определите понятие «поток вектора напряженности электрического поля». Сформулируйте электростатическую теорему Гаусса.
Для произвольной замкнутой поверхности поток вектора напряженности E электрического поля Ф Е = . Теорема Гаусса:
= (здесь Q i
– заряды, охваченные замкнутой поверхностью). Справедлива для замкнутой поверхности любой формы.
Справедлива для замкнутой поверхности любой формы.
? Какие вещества называют проводниками? Как распределены заряды и электростатическое поле в проводнике? Что такое электростатическая индукция?
Проводники -вещества, в которых под действием электрического поля могут двигаться упорядоченно свободные заряды. Под действием внешнего поля заряды перераспределяются, создавая собственное поле, равное по модулю внешнему и направленное противоположно. Поэтому результирующая напряженность внутри проводника равна 0.
Электростатическая индукция — вид электризации, при котором под действием внешнего электрического поля происходит перераспределение зарядов между частями данного тела.
? Что такое электроемкость уединенного проводника, конденсатора. Как определить емкость плоского кондесатора, батареи конденсаторов, соединенных последовательно, параллельно? Единица измерения электроемкости.
Уединенный проводник: где С
–емкость, q
— заряд, j — потенциал. Единица измерения – фарад [Ф ]. (1 Ф – емкость проводника, у которого потенциал возрастает на 1 В при сообщении проводнику заряда 1 Кл).
Единица измерения – фарад [Ф ]. (1 Ф – емкость проводника, у которого потенциал возрастает на 1 В при сообщении проводнику заряда 1 Кл).
Емкость плоского конденсатора . Последовательное соединение: . Параллельное соединение: С общ =С 1 +С 2 +…+С n
? Какие вещества называют диэлектриками? Какие типы диэлектриков вы знаете? Что такое поляризация диэлектриков?
Диэлектрики — вещества, в которых при обычных условиях нет свободных электрических зарядов. Существуют диэлектрики полярные, неполярные, сегнетоэлектрики. Поляризацией называется процесс ориентации диполей под воздействием внешнего электрического поля.
? Что такое вектор электрического смещения? Cформулируйте постулат Максвелла.
Вектор электрического смещения D
характеризует электростатическое поле, создаваемое свободными зарядами (т.е. в вакууме), но при таком распределении в пространстве, какое имеется при наличии диэлектрика. Постулат Максвелла: . Физический смысл – выражает закон создания электрических полей действием зарядов в произвольных средах.
Постулат Максвелла: . Физический смысл – выражает закон создания электрических полей действием зарядов в произвольных средах.
? Сформулируйте и поясните граничные условия для электростатического поля.
При переходе электрического поля через границу раздела двух диэлектрических сред вектор напряженности и смещения скачкообразно меняются по величине и направлению. Соотношения, характеризующие эти изменения, называются граничными условиями. Их 4:
(3), (4)
? Как определяется энергия электростатического поля? Плотность энергии?
Энергия W= (E- напряженность поля, e-диэлектрическая проницаемость, e 0 -электрическая постоянная, V — объем поля), плотность энергии
? Определите понятие «электрический ток». Виды токов. Характеристики электрического тока. Какое условие необходимо для его возникновения и существования?
Ток — упорядоченное движение заряженных частиц. Виды – ток проводимости, упорядоченное движение свободных зарядов в проводнике, конвекционный – возникает при перемещении в пространстве заряженного макроскопического тела. Для возникновения и существования тока необходимо наличие заряженных частиц, способных перемещаться упорядоченно, и наличие электрического поля, энергия которого восполняясь, расходовалась бы на это упорядоченное движение.
Виды – ток проводимости, упорядоченное движение свободных зарядов в проводнике, конвекционный – возникает при перемещении в пространстве заряженного макроскопического тела. Для возникновения и существования тока необходимо наличие заряженных частиц, способных перемещаться упорядоченно, и наличие электрического поля, энергия которого восполняясь, расходовалась бы на это упорядоченное движение.
? Приведите и поясните уравнение непрерывности. Сформулируйте условие стационарности тока в интегральной и дифференциальной формах.
Уравнение непрерывности . Выражает в дифференциальной форме закон сохранения заряда. Условие стационарности (постоянства) тока в интегральной форме: и дифференциальной — .
? Запишите закон Ома в интегральной и дифференциальной формах.
Интегральная форма – (I
–ток, U
— напряжение, R
-сопротивление). Дифференциальная форма — (j
-плотность тока, g- удельная электрическая проводимость, E
— напряженность поля в проводнике).
? Что такое сторонние силы? ЭДС?
Сторонние силы разделяют заряды на положительные и отрицательные. ЭДС- отношение работы по перемещению заряда вдоль всей замкнутой цепи к его величине
? Как определяется работа и мощность тока?
При перемещении заряда q по электрической цепи, на концах которой действует напряжение U , электрическим полем совершается работа , мощность тока (t-время)
? Сформулируйте правила Кирхгофа для разветвленных цепей. Какие законы сохранения заложены в правилах Кирхгофа? Сколько независимых уравнений надо составить на основе первого и второго законов Кирхгофа?
1. Алгебраическая сумма токов, сходящихся в узле, равна 0.
2. В любом произвольно выбранном замкнутом контуре алгебраическая сумма падений напряжений равна алгебраической сумме ЭДС, встречающихся в этом контуре. Первое правило Кирхгофа вытекает из закона сохранения электрического заряда. Число уравнений в сумме должно быть равно числу искомых величин (в систему уравнений должны входить все сопротивления и ЭДС).
Число уравнений в сумме должно быть равно числу искомых величин (в систему уравнений должны входить все сопротивления и ЭДС).
? Электрический ток в газе. Процессы ионизации и рекомбинации. Понятие о плазме.
Электрический ток в газах – направленное движение свободных электронов и ионов. При нормальных условиях газы – диэлектрики, проводниками становятся после ионизации. Ионизация – процесс образования ионов путем отделения электронов от молекул газа. Происходит вследствие воздействия внешнего ионизатора – сильного нагрева, рентгеновского или ультрафиолетового облучения, бомбардировки электронами. Рекомбинация – процесс, обратный ионизации. Плазма – представляет собой полностью или частично ионизированный газ, в котором концентрации положительных и отрицательных зарядов равны.
? Электрический ток в вакууме. Термоэлектронная эмиссия.
Носители тока в вакууме – электроны, вылетевшие вследствие эмиссии с поверхности электродов. Термоэлектронная эмиссия – испускание электронов нагретыми металлами.
Термоэлектронная эмиссия – испускание электронов нагретыми металлами.
? Что вы знаете о явлении сверхпроводимости?
Явление, при котором сопротивление некоторых чистых металлов (олово, свинец, алюминий) падает до нуля при температурах, близких к абсолютному нулю.
? Что вы знаете об электрическом сопротивлении проводников? Что такое удельное сопротивление, зависимость его от температуры, удельная электрическая проводимость? Что вы знаете о последовательном и параллельном соединении проводников. Что такое шунт, дополнительное сопротивление?
Сопротивление — величина, прямо пропорциональная длине проводника l
и обратно пропорциональная площади S
поперечного сечения проводника: (r-удельное сопротивление). Проводимость- величина, обратная сопротивлению. Удельное сопротивление (сопротивление проводника длиной 1 м сечением 1 м 2). Удельное сопротивление зависит от температуры , здесь a — температурный коэффициент, R
и R
0 , r и r 0 –сопротивления и удельные сопротивления при t
и 0 0 С.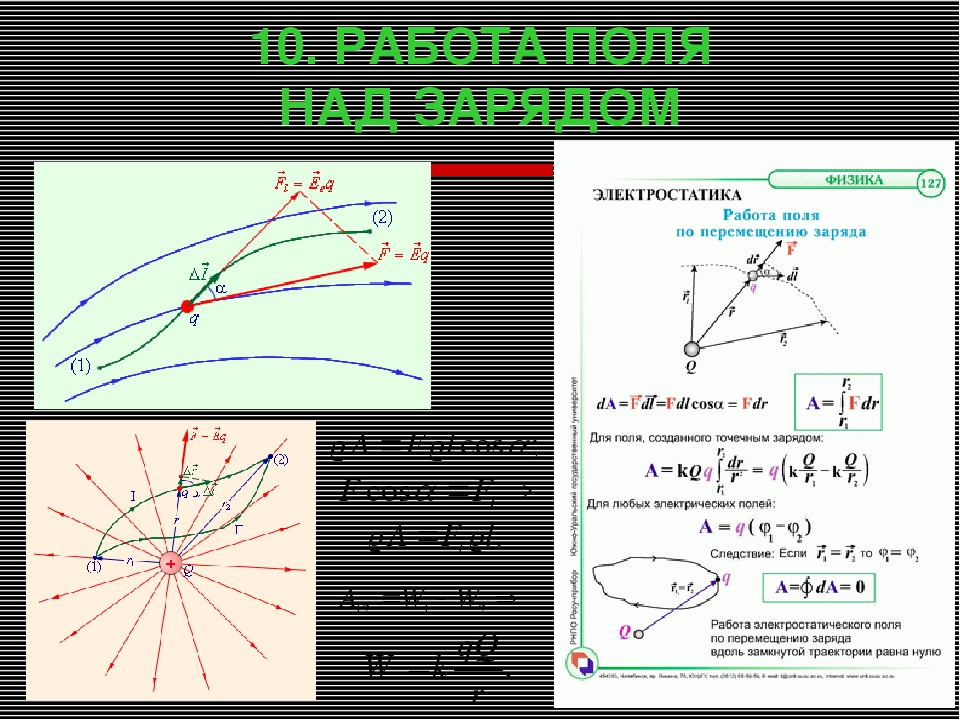 Параллельное — , последовательное R=R
1 +R
2 +…+R n
. Шунт- резистор, подключаемый параллельно электроизмерительному прибору, для отведения части электрического тока, чтобы расширить пределы измерений.
Параллельное — , последовательное R=R
1 +R
2 +…+R n
. Шунт- резистор, подключаемый параллельно электроизмерительному прибору, для отведения части электрического тока, чтобы расширить пределы измерений.
? Магнитное поле. Какие источники могут создавать магнитное поле?
Магнитное поле – особый вид материи, посредством которой взаимодействуют движущиеся электрические заряды. Причина существования постоянного магнитного поля неподвижный проводник с постоянным электрическим током, или постоянные магниты.
? Сформулируйте закон Ампера. Как взаимодействуют проводники, по которым ток течет в одном (противоположном) направлении?
На проводник с током действует сила Ампера, равная .
B — магнитная индукция, I-
ток в проводнике, Dl
–длина участка проводника, a-угол между магнитной индукцией и участком проводника. В одном направлении -притягиваются, в противоположном – отталкиваются.
? Дайте определение силы Ампера. Как определить ее направление?
Это сила, действующая на проводник с током, помещенный в магнитное поле. Направление определяем так: ладонь левой руки располагаем так, чтобы в нее входили линии магнитной индукции, а четыре вытянутых пальца были направлены по току в проводнике. Отогнутый большой палец покажет направление силы Ампера.
? Поясните движение заряженных частиц в магнитном поле. Что такое сила Лоренца? Как находится ее направление?
Движущаяся заряженная частица создает свое собственное магнитное поле. Если ее поместить во внешнее магнитное поле, то взаимодействие полей проявится в возникновении силы, действующей на частицу со стороны внешнего поля – силы Лоренца. Направление – по правилу левой руки. Для положительного заряда- вектор B
входит в ладонь левой руки, четыре пальца направлены по движению положительного заряда (вектору скорости), отогнутый большой палец показывает направление силы Лоренца.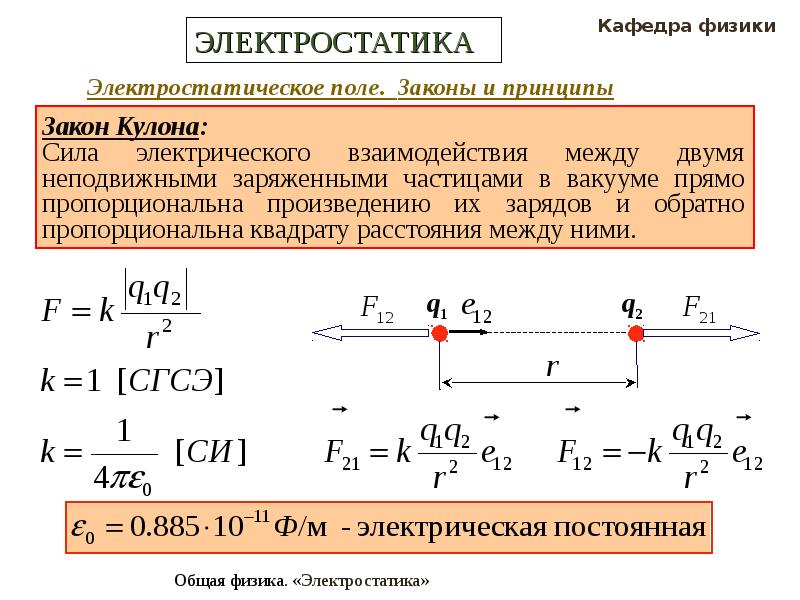 На отрицательный заряд та же сила действует в обратном направлении.
На отрицательный заряд та же сила действует в обратном направлении.
(q -заряд, v -скорость, B — индукция, a- угол между направлением скорости и магнитной индукции).
? Рамка с током в однородном магнитном поле. Как определяется магнитный момент?
Магнитное поле оказывает на рамку с током ориентирующее действие, поворачивая ее определенным образом. Вращающий момент определяется формулой: M =p m xB , где p m — вектор магнитного момента рамки с током, равный ISn (ток на площадь поверхности контура, на единичную нормаль к контуру), B -вектор магнитной индукции, количественная характеристика магнитного поля.
? Что такое вектор магнитной индукции? Как определить его направление? Как графически изображают магнитное поле?
Вектор магнитной индукции – это силовая характеристика магнитного поля.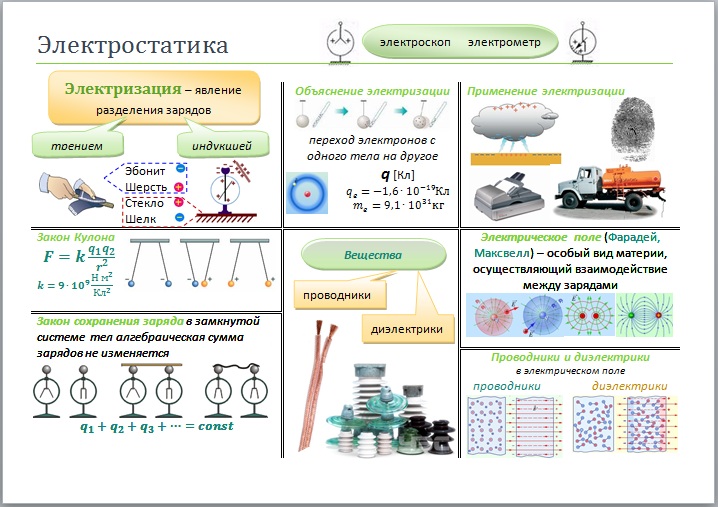 Магнитное поле наглядно изображают с помощью силовых линий. В каждой точке поля касательная к силовой линии совпадает с направлением вектора магнитной индукции.
Магнитное поле наглядно изображают с помощью силовых линий. В каждой точке поля касательная к силовой линии совпадает с направлением вектора магнитной индукции.
? Сформулируйте и поясните закон Био – Савара — Лапласа.
Закон Био – Савара — Лапласа позволяет рассчитать для проводника с током I магнитную индукцию поля dB , создаваемого в произвольной точке поля dl проводника: (здесь m 0 -магнитная постоянная, m-магнитная проницаемость среды). Направление вектора индукции определяется по правилу правого винта, если поступательное движение винта соответствует направлению тока в элементе.
? Сформулируйте принцип суперпозиции для магнитного поля.
Принцип суперпозиции — магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:
?
Поясните основные характеристики магнитного поля: магнитный поток, циркуляция магнитного поля, магнитная индукция.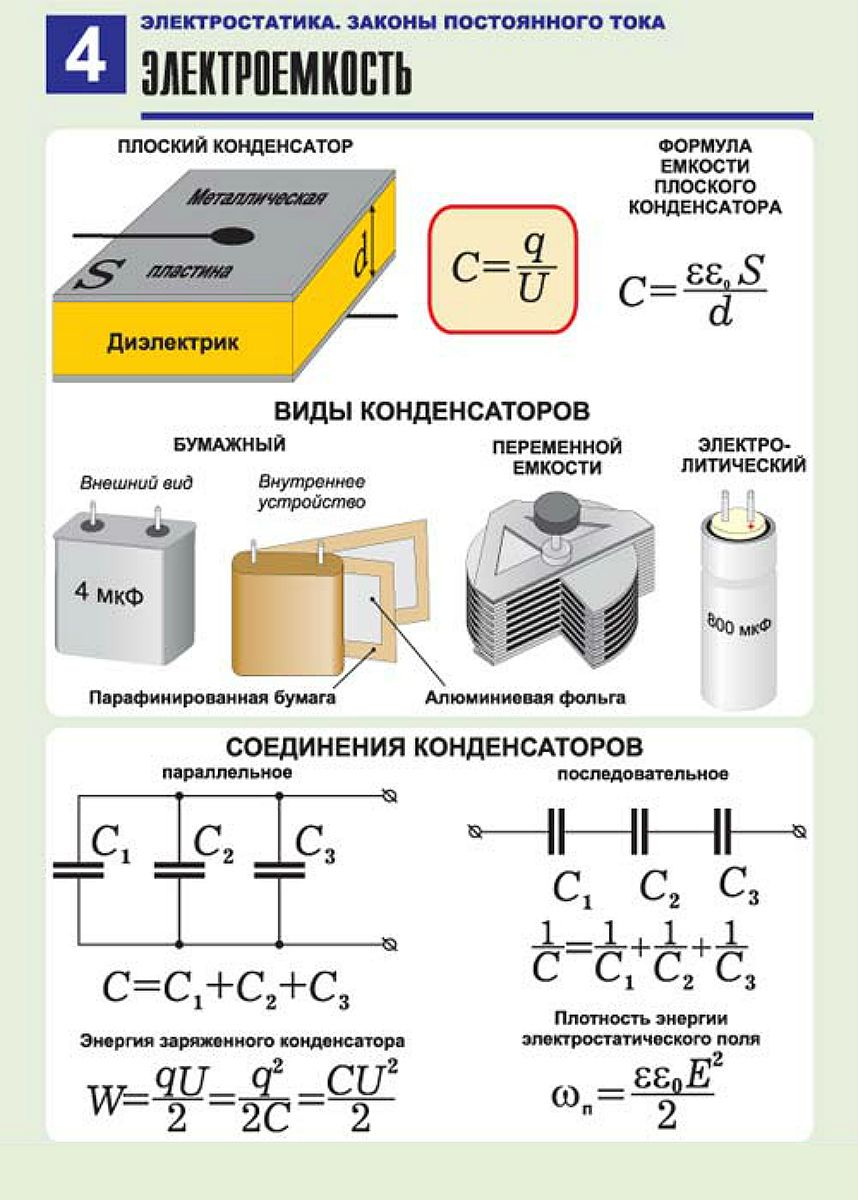
Магнитным потоком Ф через какую-либо поверхность S называют величину, равную произведению модуля вектора магнитной индукции на площадь S и косинус угла a между векторами B и n (внешней нормалью к поверхности). Циркуляцией вектора B по заданному замкнутому контуру называется интеграл вида , где dl — вектор элементарной длины контура. Теорема о циркуляции вектора B : циркуляция вектора B по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром. Вектор магнитной индукции – это силовая характеристика магнитного поля. Магнитное поле наглядно изображают с помощью силовых линий. В каждой точке поля касательная к силовой линии совпадает с направлением вектора магнитной индукции.
?
Запишите и прокомментируйте условие соленоидальности магнитного поля интегральной и дифференциальной формах.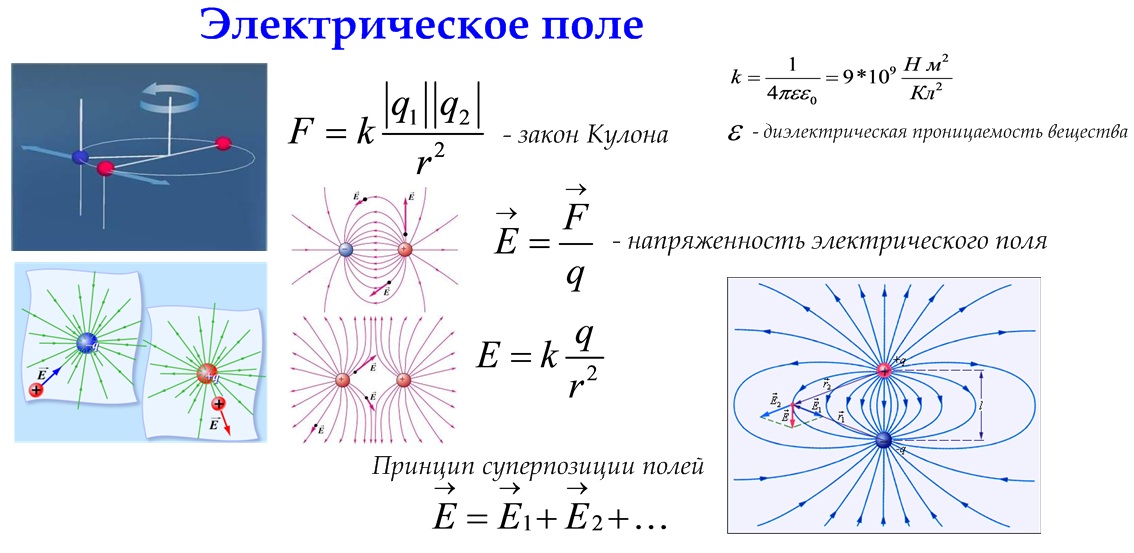
Векторные поля, в которых отсутствуют источники и стоки, называют соленоидальными. Условие соленоидальности магнитного поля в интегральной форме: и дифференциальной форме:
? Магнетики. Виды магнетиков. Феромагнетики и их свойства. Что такое гистерезис?
Вещество является магнетиком, если оно способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Вещества, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагнетиками.Намагничивающиеся во внешнем магнитном поле по направлению поля – парамагнетиками. Эти два класса называют слабомагнитными веществами. Сильномагнитные вещества, намагниченные даже при отсутствии внешнего магнитного поля, называют ферромагнетиками.
Магнитный гистерезис – различие в значениях намагниченности ферромагнетика при одной и той же напряженности Н намагничивающего поля в зависимости от значения предварительной намагниченности. Такая графическая зависимость называется петлей гистерезиса.
? Сформулируйте и поясните закон полного тока в интегральной и дифференциальной формах (основные ур-я магнитостатики в веществе).
? Что такое электромагнитная индукция? Сформулируйте и поясните основной закон электромагнитной индукции (закон Фарадея). Сформулируйте правило Ленца.
Явление возникновения электродвижущей силы (ЭДС индукции) в проводнике, находящемся в переменном магнитном поле или движущемся в постоянном в постоянном магнитном поле называют электромагнитной индукцией. Закон Фарадея: какова бы не была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре ЭДС
Знак минус определяется правилом Ленца – индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшего этот индукционный ток.
?
В чем заключается явление самоиндукции? Что такое индуктивность, единицы измерения? Токи при замыкании и размыкании электрической цепи.
Возникновение ЭДС индукции в проводящем контуре под действием собственного магнитного поля при его изменении, происходящем в результате изменения в проводнике силы тока. Индуктивность – коэффициент пропорциональности, зависящий от формы и размеров проводника или контура, [Гн]. В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи. Поэтому величина силы тока не может меняться мгновенно (механический аналог – инертность).
? Явление взаимной индукции. Коэффициент взаимной индукции.
Если два неподвижных контура расположены близко друг к другу, то при изменении силы тока в одном контуре, возникает ЭДС в другом контуре. Это явление называется взаимной индукцией. Коэффициенты пропорциональности L 21 и L 12 называют взаимной индуктивностью контуров, они равны.
?
Запишите уравнения Максвелла в интегральной форме. Поясните их физический смысл.
; ;
; .
Из теории Максвелла следует, что электрическое и магнитное поле нельзя рассматривать как независимые – изменение во времени одного приводит к изменению другого.
? Энергия магнитного поля. Плотность энергии магнитного поля.
Энергия , L –индуктивность, I – сила тока.
Плотность , В – магнитная индукция, Н – напряженность магнитного поля, V -объем.
? Принцип относительности в электродинамике
Общие закономерности электромагнитных полей описываются уравнениями Максвелла. В релятивистской электродинамике установлено, что релятивистская инвариантность этих уравнений имеет место только при условии относительности электрических и магнитных полей, т.е. при зависимости характеристик этих полей от выбора инерциальных систем отсчета. В подвижной системе электрическое поле такое же, как в неподвижной, но в подвижной системе имеется магнитное поле, которого в неподвижной системе нет.
Колебания и волны
Шпаргалка с формулами по физике для ЕГЭ
и не только (может понадобиться 7, 8, 9, 10 и 11 классам).
Для начала картинка, которую можно распечатать в компактном виде.
Механика
- Давление Р=F/S
- Плотность ρ=m/V
- Давление на глубине жидкости P=ρ∙g∙h
- Сила тяжести Fт=mg
- 5. Архимедова сила Fa=ρ ж ∙g∙Vт
- Уравнение движения при равноускоренном движении
X=X 0 +υ 0 ∙t+(a∙t 2)/2 S=(υ 2 —υ 0 2) /2а S=(υ +υ 0) ∙t /2
- Уравнение скорости при равноускоренном движении υ =υ 0 +a∙t
- Ускорение a=(υ —υ 0)/t
- Скорость при движении по окружности υ =2πR/Т
- Центростремительное ускорение a=υ 2 /R
- Связь периода с частотой ν=1/T=ω/2π
- II закон Ньютона F=ma
- Закон Гука Fy=-kx
- Закон Всемирного тяготения F=G∙M∙m/R 2
- Вес тела, движущегося с ускорением а Р=m(g+a)
- Вес тела, движущегося с ускорением а↓ Р=m(g-a)
- Сила трения Fтр=µN
- Импульс тела p=mυ
- Импульс силы Ft=∆p
- Момент силы M=F∙ℓ
- Потенциальная энергия тела, поднятого над землей Eп=mgh
- Потенциальная энергия упруго деформированного тела Eп=kx 2 /2
- Кинетическая энергия тела Ek=mυ 2 /2
- Работа A=F∙S∙cosα
- Мощность N=A/t=F∙υ
- Коэффициент полезного действия η=Aп/Аз
- Период колебаний математического маятника T=2π√ℓ/g
- Период колебаний пружинного маятника T=2 π √m/k
- Уравнение гармонических колебаний Х=Хmax∙cos ωt
- Связь длины волны, ее скорости и периода λ= υ Т
Молекулярная физика и термодинамика
- Количество вещества ν=N/ Na
- Молярная масса М=m/ν
- Cр.
 кин. энергия молекул одноатомного газа Ek=3/2∙kT
кин. энергия молекул одноатомного газа Ek=3/2∙kT - Основное уравнение МКТ P=nkT=1/3nm 0 υ 2
- Закон Гей – Люссака (изобарный процесс) V/T =const
- Закон Шарля (изохорный процесс) P/T =const
- Относительная влажность φ=P/P 0 ∙100%
- Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
- Работа газа A=P∙ΔV
- Закон Бойля – Мариотта (изотермический процесс) PV=const
- Количество теплоты при нагревании Q=Cm(T 2 -T 1)
- Количество теплоты при плавлении Q=λm
- Количество теплоты при парообразовании Q=Lm
- Количество теплоты при сгорании топлива Q=qm
- Уравнение состояния идеального газа PV=m/M∙RT
- Первый закон термодинамики ΔU=A+Q
- КПД тепловых двигателей η= (Q 1 — Q 2)/ Q 1
- КПД идеал. двигателей (цикл Карно) η= (Т 1 — Т 2)/ Т 1
Электростатика и электродинамика – формулы по физике
- Закон Кулона F=k∙q 1 ∙q 2 /R 2
- Напряженность электрического поля E=F/q
- Напряженность эл.
 поля точечного заряда E=k∙q/R 2
поля точечного заряда E=k∙q/R 2 - Поверхностная плотность зарядов σ = q/S
- Напряженность эл. поля бесконечной плоскости E=2πkσ
- Диэлектрическая проницаемость ε=E 0 /E
- Потенциальная энергия взаимод. зарядов W= k∙q 1 q 2 /R
- Потенциал φ=W/q
- Потенциал точечного заряда φ=k∙q/R
- Напряжение U=A/q
- Для однородного электрического поля U=E∙d
- Электроемкость C=q/U
- Электроемкость плоского конденсатора C=S∙ε ∙ε 0 /d
- Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
- Сила тока I=q/t
- Сопротивление проводника R=ρ∙ℓ/S
- Закон Ома для участка цепи I=U/R
- Законы послед. соединения I 1 =I 2 =I, U 1 +U 2 =U, R 1 +R 2 =R
- Законы паралл. соед. U 1 =U 2 =U, I 1 +I 2 =I, 1/R 1 +1/R 2 =1/R
- Мощность электрического тока P=I∙U
- Закон Джоуля-Ленца Q=I 2 Rt
- Закон Ома для полной цепи I=ε/(R+r)
- Ток короткого замыкания (R=0) I=ε/r
- Вектор магнитной индукции B=Fmax/ℓ∙I
- Сила Ампера Fa=IBℓsin α
- Сила Лоренца Fл=Bqυsin α
- Магнитный поток Ф=BSсos α Ф=LI
- Закон электромагнитной индукции Ei=ΔФ/Δt
- ЭДС индукции в движ проводнике Ei=Вℓυ sinα
- ЭДС самоиндукции Esi=-L∙ΔI/Δt
- Энергия магнитного поля катушки Wм=LI 2 /2
- Период колебаний кол.
 контура T=2π ∙√LC
контура T=2π ∙√LC - Индуктивное сопротивление X L =ωL=2πLν
- Емкостное сопротивление Xc=1/ωC
- Действующее значение силы тока Iд=Imax/√2,
- Действующее значение напряжения Uд=Umax/√2
- Полное сопротивление Z=√(Xc-X L) 2 +R 2
Оптика
- Закон преломления света n 21 =n 2 /n 1 = υ 1 / υ 2
- Показатель преломления n 21 =sin α/sin γ
- Формула тонкой линзы 1/F=1/d + 1/f
- Оптическая сила линзы D=1/F
- max интерференции: Δd=kλ,
- min интерференции: Δd=(2k+1)λ/2
- Диф.решетка d∙sin φ=k λ
Квантовая физика
- Ф-ла Эйнштейна для фотоэффекта hν=Aвых+Ek, Ek=U з е
- Красная граница фотоэффекта ν к = Aвых/h
- Импульс фотона P=mc=h/ λ=Е/с
Физика атомного ядра
Электрическая энергия 10 класс онлайн-подготовка на Ростелеком Лицей
Электрическая энергия
Электрический ток может быть использован для передачи энергии. Источник напряжения переводит какой-то другой тип энергии в энергию электрического тока, а в приборах энергия электрического тока вновь переходит в другой тип. Таким образом, электрическая энергия может быть переведена в другой тип энергии: механическую, тепловую, световую или химическую. Например, в работе утюга, чайника, лампочки, электродвигателя или аккумулятора.
Источник напряжения переводит какой-то другой тип энергии в энергию электрического тока, а в приборах энергия электрического тока вновь переходит в другой тип. Таким образом, электрическая энергия может быть переведена в другой тип энергии: механическую, тепловую, световую или химическую. Например, в работе утюга, чайника, лампочки, электродвигателя или аккумулятора.
Как вычислить энергию электрического тока?
Рассмотрим аккумулятор, подключенный к резистору. Вся энергия источника в этом случае переходит в тепловую. Тепло, которое выделяется на резисторе, может быть вычислено по формуле:
Q=IU △ t
Перепишем эту формулу в другом виде, используя закон Ома:
I = UR → U = IR
Q = IU△t = I2R△t
Q = I2R△t
Эта формула выражает закон Джоуля-Ленца: тепло, выделившееся на проводнике, равно произведению квадрата тока, протекающего через проводник, сопротивления проводника и времени, в течении которого течет ток.
Таким образом, мы имеем две формулы для энергии электрического поля:
W = A△t = IU – наиболее общая формула для мощности источника
W = Q△t = I2R — формула для тепловой мощности, выделяющейся на проводнике
В случае постоянного тока, когда вся энергия переходит в тепловую, эти формулы эквивалентны. Но в общем случае, при переменном токе, между ними есть существенная разница.
Например, рассмотрим, параллельное соединение двух проводников. Это могут быть две лампочки, подключенные в бытовую сеть. На каком проводнике выделится больше тепла, на большем или на меньшем?
Т.е. 100-ватная лампочка имеет меньшее сопротивление, чем 50-ватная. Рассмотрим теперь последовательное соединение двух сопротивлений. Например, этими сопротивлениями могут быть лампочка и подводящие провода.
Wr = I2r
WR = I2R
WrWR=rR
Более сложный пример: вы подсоединяете удлинитель в розетку, и подключаете к нему холодильник, стиральную машину, чайник и утюг. 2 R . Т.к. ток через подводящий провод в N раз больший, то мощность, выделяемая источником, равна INU, т.е. примерно в N раз больше. Т.е. чем больше утюгов вы подключите, тем больше источнику потребуется работать.
2 R . Т.к. ток через подводящий провод в N раз больший, то мощность, выделяемая источником, равна INU, т.е. примерно в N раз больше. Т.е. чем больше утюгов вы подключите, тем больше источнику потребуется работать.
2. При большом количестве утюгов тепло, выделяющееся на подводящем проводе, оказывается немалым. Допустим, сопротивление подводящего провода r. Тогда на нем выделится тепловая мощность (IN)2 Rr. Т.е. мощность будет пропорциональна N2.
3. Если сопротивление подводящих проводов слишком велико, то выделяющаяся теплота превысит некоторое пороговое значение.
При подключении большого числа электроприборов или мощных электроприборов стоит помнить о том, что подводящие провода должны быть достаточно толстыми, чтобы выдержать эту нагрузку.
Памятка по электростатике
Электростатика Памятка
Структура атома:
Положительно заряженные частицы
В этом типе частиц количество положительных ионов больше, чем количество отрицательных ионов.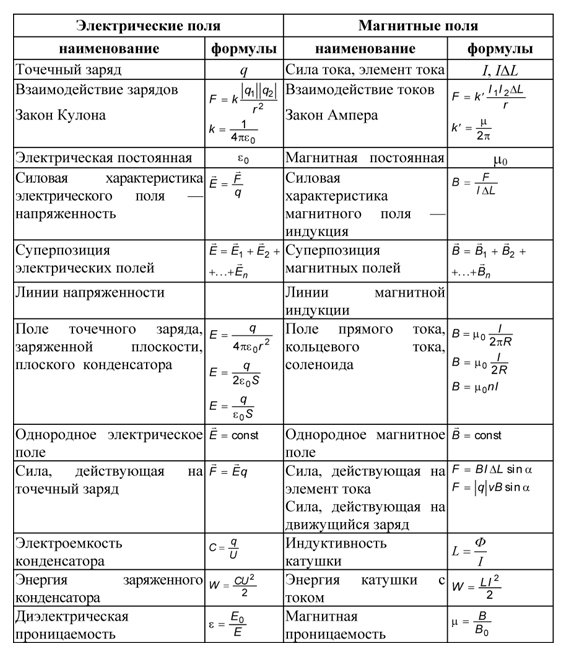 Другими словами, количество протонов больше, чем количество электронов.
Другими словами, количество протонов больше, чем количество электронов.
р + >е —
Отрицательно заряженные частицы
В этом типе частиц количество отрицательных ионов больше, чем количество положительных ионов.Другими словами, количество электронов больше, чем количество протонов.
е + >p —
Нейтральные частицы
Эти типы частиц включают равное количество протонов и электронов. Будьте осторожны, у них есть и протоны, и нейтроны, и электроны, однако количество «+» ионов равно количеству «-» ионов.
е + =p —
Атомы с одинаковым зарядом отталкиваются, а атомы с противоположными зарядами притягиваются.
Типы зарядки
Зарядка означает получение или потерю электрона. Материю можно заряжать тремя способами: зарядкой трением, зарядкой контактом и зарядкой индукцией.
Материю можно заряжать тремя способами: зарядкой трением, зарядкой контактом и зарядкой индукцией.
Зарядка трением
Когда вы трете один материал о другой, они заряжаются от трения. Материал, отдающий электрон, заряжен положительно, а материал, приобретающий электрон, заряжен отрицательно.Количество приобретенных и потерянных электронов равно друг другу.
Зарядка от контакта
В нейтральном веществе равное количество электронов и протонов. Если что-то изменит этот баланс, мы можем сказать, что он списан.
1. Когда заряженный объект касается нейтрального объекта, они оба имеют одинаковый заряд.
2. Когда два заряженных вещества касаются друг друга, общий заряд системы сохраняется, и они делят общий заряд в соответствии со своими емкостями.Если они имеют одинаковое количество разных зарядов, когда мы касаемся друг друга, они становятся нейтральными. Если количество зарядов разное, то после протекания заряда они оба заряжены отрицательно или положительно. Наличие противоположных зарядов после контакта невозможно.
Наличие противоположных зарядов после контакта невозможно.
Индукционная зарядка
Проводники A и B вначале нейтральны. Когда мы кладем рядом с ними положительно заряженную пластину, она притягивает электроны в проводниках.Электроны перемещаются в левую часть, а протоны остаются. Таким образом, когда мы разделяем пластины А и В, они заряжены индукцией, А заряжена отрицательно, а В заряжена отрицательно. Будьте осторожны, контакта нет; они заряжаются только индукцией.
Электроскоп
Это устройство, которое используется для определения того, заряжен объект или нет. Это также определяет тип заряда.
Электрические силы Закон Кулона
Кулон провел несколько экспериментов и нашел следующее уравнение электрических сил.
· Если объекты имеют одинаковый тип заряда, то сила отталкивающая, если они имеют противоположные заряды, то сила притяжения.
· Электрические силы отталкивания или притяжения равны по величине, но противоположны по направлению, не зависят от величины зарядов.
Ф 1 =-Ф 2
Электрическое поле
Заряженная частица воздействует на частицы вокруг себя.Воздействие этой силы на окружающую среду мы можем назвать электрическим полем.
Электрическое поле является векторной величиной. И уменьшается с увеличением расстояния. k =9,10 9 Н·м 2 /C 2
Сила, действующая на заряженную частицу внутри электрического поля
Э=Ф/к
F=E.q где; F — сила, действующая на заряд внутри электрического поля E. Используя это уравнение, мы можем сказать, что;
Если q положителен, то F=+E.q и направления силы и электрического поля совпадают
Если q отрицательно, то F=-E. q и направления Силы и Электрического Поля противоположны.
q и направления Силы и Электрического Поля противоположны.
Электрический потенциал и электрическая потенциальная энергия
Мы узнали, что в главе работы «Энергия энергии» объекты обладают потенциальной энергией из-за своего положения.В этом случае заряд в электрическом поле обладает еще и потенциальной энергией из-за своего положения.
Электрический потенциал
Электрический потенциал – электрическая потенциальная энергия на единицу заряда. В целом оно известно как напряжение, обозначается буквой V и имеет единицу измерения вольт (джоуль/Кл).
В=к.кв/д
В — скалярная величина.Если q отрицательное, то V становится отрицательным, или если q положительное, то V становится положительным.
Поверхности, имеющие равные потенциалы, называются эквипотенциальными поверхностями.
Емкость и конденсаторы
Емкость – это отношение накопленного заряда к потенциалу, полученному проводниками. Единицей емкости является кулон на вольт, и она называется фарад (Ф).
Емкость является скалярной величиной.
Конденсаторы
Конденсаторы – это устройства, предназначенные для накопления заряда. Они обычно используются в компьютерах или электронных системах.
Емкость пластин находится по следующей формуле;
Конденсаторы последовательно и параллельно
В этой схеме конденсаторы соединены параллельно.
Находим заряд каждого конденсатора как;
Q 1 =C 1 . В
В
Q 2 =C 2 .V
Q 3 =C 3 .V
C экв. =C 1 +C 2 +C 3
Теперь мы увидим конденсаторы последовательно.
Каждый конденсатор имеет одинаковый заряд с батареей.
С 1 .V 1 =Q
C 2 .V 2 =Q , V=V 1 +V 2 +V 3 и Q=C eq .V
6 6С 3 .V 3 =Q
Электростатические исследования и решения
| Конденсаторы последовательно и параллельно< Предыдущая |
|---|
Электростатика: резюме и формулы — Физика
РЕЗЮМЕ
· Одноименные заряды отталкиваются, а разноименные притягиваются
· Общий заряд во Вселенной сохраняется
·
Заряд квантуется. — единичный вектор вдоль соединения q 1 ,
q 2 )
— единичный вектор вдоль соединения q 1 ,
q 2 )
· Для непрерывных распределений заряда можно использовать методы интегрирования. использовал.
· Электростатическая сила подчиняется принципу суперпозиции.
· Электрическое поле на расстоянии r от точечного заряда:
· Линии электрического поля начинаются с положительного заряда и заканчиваются на отрицательный заряд или на бесконечности
· Электрическое поле из-за электрического диполя в точках на осевой линии :
· Электрическое поле из-за электрического диполя в точках на экваторе строка:
· Крутящий момент, испытываемый диполем в однородном электрическом поле:
· Электростатический потенциал на расстоянии r от точечного заряда:
· Электростатический потенциал из-за электрического диполя:
· Электростатический потенциал одинаков во всех точках эквипотенциальная поверхность.
· Связь между электрическим полем и электростатическим потенциалом:
·
Электростатическая потенциальная энергия системы зарядов равна
работа по размещению зарядов в заданной конфигурации.
· Электростатическая потенциальная энергия, запасенная в дипольной системе в однородное электрическое поле:
· Полный электрический поток через замкнутую поверхность: Φ E = Q/ε 0 где Q – суммарный заряд, заключенный в поверхности
.· Электрическое поле заряженной бесконечной проволоки:
· Электрическое поле из-за заряженной бесконечной плоскости:
· Электрическое поле внутри заряженной сферической оболочки равно нулю.За точек снаружи:
· Электрическое поле внутри проводника равно нулю. Электрическое поле на поверхность проводника нормальна к поверхности и имеет величину E = σ/ε 0 .
· Поверхность проводника имеет одинаковый потенциал во всех точках на поверхности.
· Проводник можно заряжать, используя процесс индукции.
·
Диэлектрик или изолятор не имеет свободных электронов.Когда электрический
поле приложено, диэлектрик поляризуется.
· Емкость определяется выражением C = Q/V.
· Емкость плоского конденсатора: C = εA / d
· Электростатическая энергия, накопленная в конденсаторе: U = 1/2 CV 2
· Эквивалентная емкость для параллельного соединения равна сумма отдельных емкостей конденсаторов.
· Для последовательной комбинации: обратная эквивалентная емкость равна равна сумме обратных величин емкостей отдельных конденсаторов.
· Распределение зарядов в проводниках зависит от формы проводника. Для более острого края плотность поверхностного заряда больше. Этот принцип используется в грозовом разряднике
· Чтобы создать большую разность потенциалов, генератор Ван де Граафа используется
Учебник по физике: Закон Кулона
Взаимодействие между заряженными объектами представляет собой бесконтактную силу, действующую на некотором расстоянии друг от друга.Заряд, заряд и расстояние. Каждое электрическое взаимодействие включает в себя силу, которая подчеркивает важность этих трех переменных. Будь то пластиковая трубка для гольфа, притягивающая кусочки бумаги, два одинаково заряженных шарика, отталкивающиеся, или заряженная пластина из пенополистирола, взаимодействующая с электронами в куске алюминия, всегда есть два заряда и расстояние между ними как три критические переменные, влияющие на прочность. взаимодействия. В этом разделе урока 3 мы рассмотрим важность этих трех переменных.
Каждое электрическое взаимодействие включает в себя силу, которая подчеркивает важность этих трех переменных. Будь то пластиковая трубка для гольфа, притягивающая кусочки бумаги, два одинаково заряженных шарика, отталкивающиеся, или заряженная пластина из пенополистирола, взаимодействующая с электронами в куске алюминия, всегда есть два заряда и расстояние между ними как три критические переменные, влияющие на прочность. взаимодействия. В этом разделе урока 3 мы рассмотрим важность этих трех переменных.
Сила как вектор Количество
Электрическая сила, как и все силы, обычно выражается в единицах Ньютон. Будучи силой, сила электрического взаимодействия является векторной величиной, имеющей как величину, так и направление. Направление электрической силы зависит от того, заряжены ли заряженные объекты одинаковым или противоположным зарядом, а также от их пространственной ориентации. Зная тип заряда на двух объектах, направление силы на любой из них можно определить с небольшими рассуждениями. На приведенной ниже диаграмме объекты A и B имеют одинаковый заряд, из-за чего они отталкиваются друг от друга. Таким образом, сила на объекте А направлена влево (от В), а сила на объекте В направлена вправо (от А). С другой стороны, объекты C и D имеют противоположный заряд, поэтому они притягиваются друг к другу. Таким образом, сила на объекте C направлена вправо (к объекту D), а сила на объекте D направлена влево (к объекту C). Когда дело доходит до вектора электрической силы, возможно, лучший способ определить его направление — это применить фундаментальные правила взаимодействия зарядов (противоположности притягиваются, а подобные отталкиваются), используя небольшие рассуждения.
На приведенной ниже диаграмме объекты A и B имеют одинаковый заряд, из-за чего они отталкиваются друг от друга. Таким образом, сила на объекте А направлена влево (от В), а сила на объекте В направлена вправо (от А). С другой стороны, объекты C и D имеют противоположный заряд, поэтому они притягиваются друг к другу. Таким образом, сила на объекте C направлена вправо (к объекту D), а сила на объекте D направлена влево (к объекту C). Когда дело доходит до вектора электрической силы, возможно, лучший способ определить его направление — это применить фундаментальные правила взаимодействия зарядов (противоположности притягиваются, а подобные отталкиваются), используя небольшие рассуждения.
Электрическая сила также имеет величину или силу. Как и для большинства типов сил, существует множество факторов, влияющих на величину электрической силы. Два шара с одинаковым зарядом будут отталкивать друг друга, и силу их отталкивания можно изменить, изменив три переменные. Во-первых, на силу отталкивания будет влиять количество заряда одного из шаров. Чем сильнее заряжен воздушный шар, тем больше сила отталкивания.Во-вторых, количество заряда второго шара будет влиять на силу отталкивания. Аккуратно потрите два шарика шерстью животных, и они немного оттолкнутся. Энергично потрите два шарика, чтобы придать им обоим больше заряда, и они сильно отталкиваются. Наконец, расстояние между двумя шарами будет иметь значительное и заметное влияние на силу отталкивания. Электрическая сила наиболее сильна, когда воздушные шары находятся ближе всего друг к другу. Уменьшение разделительного расстояния увеличивает силу.Говорят, что величина силы и расстояние между двумя шарами обратно пропорциональны .
Во-первых, на силу отталкивания будет влиять количество заряда одного из шаров. Чем сильнее заряжен воздушный шар, тем больше сила отталкивания.Во-вторых, количество заряда второго шара будет влиять на силу отталкивания. Аккуратно потрите два шарика шерстью животных, и они немного оттолкнутся. Энергично потрите два шарика, чтобы придать им обоим больше заряда, и они сильно отталкиваются. Наконец, расстояние между двумя шарами будет иметь значительное и заметное влияние на силу отталкивания. Электрическая сила наиболее сильна, когда воздушные шары находятся ближе всего друг к другу. Уменьшение разделительного расстояния увеличивает силу.Говорят, что величина силы и расстояние между двумя шарами обратно пропорциональны .
Уравнение закона Кулона
Количественное выражение влияния этих трех переменных на электрическую силу известно как закон Кулона. Закон Кулона гласит, что электрическая сила между двумя заряженными объектами прямо пропорциональна произведению количества заряда на объектах и обратно пропорциональна квадрату расстояния между двумя объектами.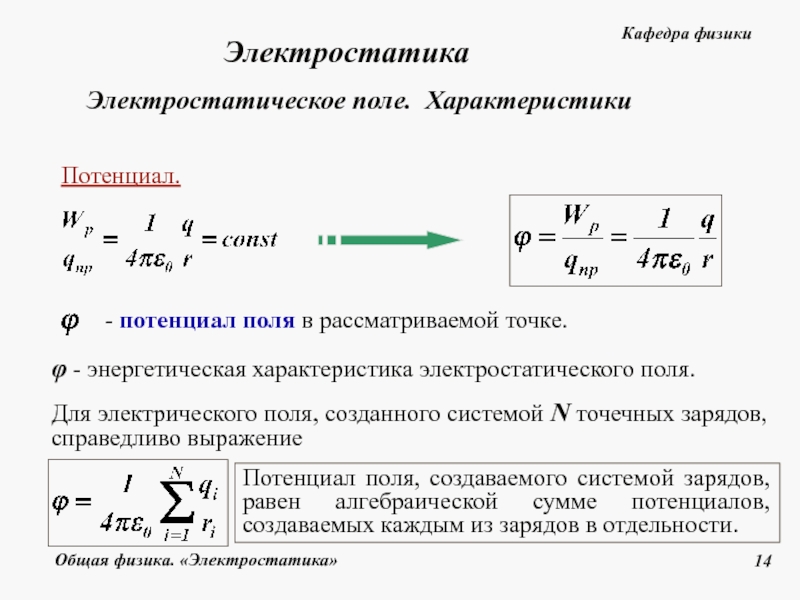 В форме уравнения закон Кулона можно сформулировать как
В форме уравнения закон Кулона можно сформулировать как
, где Q 1 представляет количество заряда на объекте 1 (в кулонах), Q 2 представляет количество заряда на объекте 2 (в кулонах), а d представляет собой расстояние между два объекта (в метрах). Символ k представляет собой константу пропорциональности, известную как константа закона Кулона. Значение этой константы зависит от среды, в которую погружены заряженные объекты.В случае воздуха значение составляет примерно 9,0 x 10 9 Н • м 2 / C 2 . Если заряженные объекты присутствуют в воде, значение k может быть уменьшено в 80 раз. Стоит отметить, что единицы измерения k таковы, что при подстановке в уравнение единиц на заряд (кулоны) и единицы расстояния (метры) будут отменены, оставив Ньютон в качестве единицы силы.
Уравнение закона Кулона обеспечивает точное описание силы между двумя объектами, когда объекты действуют как точечных зарядов . Заряженный проводящий шар взаимодействует с другими заряженными объектами так, как если бы весь его заряд был сосредоточен в его центре. Хотя заряд равномерно распределен по поверхности сферы, центр заряда можно считать центром сферы. Сфера действует как точечный заряд с избыточным зарядом, расположенным в ее центре. Поскольку закон Кулона применим к точечным зарядам, расстояние d в уравнении — это расстояние между центрами заряда обоих объектов (а не расстояние между их ближайшими поверхностями).
Заряженный проводящий шар взаимодействует с другими заряженными объектами так, как если бы весь его заряд был сосредоточен в его центре. Хотя заряд равномерно распределен по поверхности сферы, центр заряда можно считать центром сферы. Сфера действует как точечный заряд с избыточным зарядом, расположенным в ее центре. Поскольку закон Кулона применим к точечным зарядам, расстояние d в уравнении — это расстояние между центрами заряда обоих объектов (а не расстояние между их ближайшими поверхностями).
Символы Q 1 и Q 2 в уравнении закона Кулона представляют количество заряда на двух взаимодействующих объектах. Поскольку объект может быть заряжен положительно или отрицательно, эти величины часто выражаются как значения «+» или «-». Знак заряда просто показывает, имеет ли объект избыток электронов (отрицательно заряженный объект) или недостаток электронов (положительно заряженный объект).Может возникнуть соблазн использовать знаки «+» и «-» при расчете силы. Хотя эта практика не рекомендуется, в этом, безусловно, нет никакого вреда. При использовании знаков «+» и «-» при расчете силы результатом будет то, что значение «-» для силы является признаком силы притяжения, а значение «+» для силы означает силу отталкивания. Математически значение силы будет положительным, когда Q 1 и Q 2 имеют одинаковый заряд — либо оба «+», либо оба «-».И значение силы будет отрицательным, когда Q 1 и Q 2 имеют противоположный заряд — один «+», а другой «-». Это согласуется с концепцией о том, что противоположно заряженные объекты взаимодействуют притягивающе, а заряженные объекты отталкиваются. В конце концов, если вы мыслите концептуально (а не просто математически), вы вполне сможете определить природу силы — притягивающей или отталкивающей — без использования знаков «+» и «-» в уравнении.
Хотя эта практика не рекомендуется, в этом, безусловно, нет никакого вреда. При использовании знаков «+» и «-» при расчете силы результатом будет то, что значение «-» для силы является признаком силы притяжения, а значение «+» для силы означает силу отталкивания. Математически значение силы будет положительным, когда Q 1 и Q 2 имеют одинаковый заряд — либо оба «+», либо оба «-».И значение силы будет отрицательным, когда Q 1 и Q 2 имеют противоположный заряд — один «+», а другой «-». Это согласуется с концепцией о том, что противоположно заряженные объекты взаимодействуют притягивающе, а заряженные объекты отталкиваются. В конце концов, если вы мыслите концептуально (а не просто математически), вы вполне сможете определить природу силы — притягивающей или отталкивающей — без использования знаков «+» и «-» в уравнении.
Расчеты по закону Кулона
В курсах физики закон Кулона часто используется в качестве своего рода алгебраического рецепта для решения задач по физике. Здесь показаны три таких примера.
Здесь показаны три таких примера.
|
Пример А
Предположим, что два точечных заряда, каждый с зарядом +1,00 Кулона, находятся на расстоянии 1 друг от друга.00 метров. Определить величину электрической силы отталкивания между ними. |
Это не самая сложная математическая задача, которую можно было выбрать. Он определенно не был выбран из-за его математической строгости. Используемая здесь стратегия решения проблем может показаться ненужной, учитывая простоту данных значений. Тем не менее, эта стратегия будет использоваться, чтобы проиллюстрировать ее полезность для любой проблемы закона Кулона.
Первым шагом стратегии является идентификация и перечисление известной информации в переменной форме.Здесь мы знаем заряды двух объектов (Q 1 и Q 2 ) и расстояние между ними (d). Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме. В этом случае задача запрашивает информацию о силе. Таким образом, F Elect — это неизвестная величина. Результаты первых двух шагов представлены в таблице ниже.
В этом случае задача запрашивает информацию о силе. Таким образом, F Elect — это неизвестная величина. Результаты первых двух шагов представлены в таблице ниже.
|
Дано: Q 1 = 1.00 С |
Найти: F избранный = ??? |
Следующий и последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для поиска неизвестной информации. Этот шаг показан ниже.
F избранный = k • Q 1 • Q 2 / d 2F Elect = (9,0 x 10 9 Н•м 2 /C 2 ) • (1,00 C) • (1,00 C) / (1,00 м) 2
F избранный = 9,0 x 10 9 N
Сила отталкивания двух зарядов +1,00 Кулон, находящихся на расстоянии 1,00 м друг от друга, составляет 9 миллиардов ньютонов. Это невероятно большая сила, по величине сравнимая с весом более 2000 реактивных лайнеров.
Это невероятно большая сила, по величине сравнимая с весом более 2000 реактивных лайнеров.
Эта проблема была выбрана в первую очередь из-за ее концептуального сообщения. Объекты просто не приобретают зарядов порядка 1,00 кулона. На самом деле более вероятные значения Q порядка 10 -9 или, возможно, 10 -6 кулонов. По этой причине перед кулоновской единицей заряда часто используется греческий префикс. Заряд часто выражается в микрокулонах (мкКл) и нанокулонах (нКл). Если в задаче указан заряд в этих единицах, рекомендуется сначала преобразовать в кулоны перед подстановкой в уравнение закона Кулона.Следующие единицы эквивалентности помогут в таких преобразованиях.
1 Кулон = 10 6 микроКулон1 Кулон = 10 9 наноКулон
Стратегия решения проблем, использованная в примере А, включала три шага:
- Определите и перечислите известную информацию в переменной форме.
- Перечислите неизвестную (или желаемую) информацию в переменной форме.

- Подставьте известные значения в уравнение закона Кулона и, используя соответствующие алгебраические шаги, найдите неизвестную информацию.(В некоторых случаях и для некоторых учащихся может быть проще сначала выполнить алгебраические вычисления с использованием переменных, а затем выполнить подстановку в качестве последнего шага.)
Эта же стратегия решения проблем демонстрируется в Примере B ниже.
|
Пример В
Два баллона заряжены одинаковым количеством и типом заряда: -6,25 нКл. Их разделяют на расстоянии 61.7 см. Определить величину электрической силы отталкивания между ними. |
В задаче указано значение Q 1 и Q 2 . Поскольку эти значения выражены в единицах нанокулонов (нКл), необходимо выполнить преобразование в кулоны. В задаче также указывается разделительное расстояние (d). Поскольку расстояние указывается в сантиметрах (см), необходимо также выполнить преобразование в метры. Эти преобразования необходимы, поскольку единицами заряда и расстояния в постоянной Кулона являются кулоны и метры.Неизвестной величиной является электрическая сила (F). Результаты первых двух шагов представлены в таблице ниже.
Поскольку расстояние указывается в сантиметрах (см), необходимо также выполнить преобразование в метры. Эти преобразования необходимы, поскольку единицами заряда и расстояния в постоянной Кулона являются кулоны и метры.Неизвестной величиной является электрическая сила (F). Результаты первых двух шагов представлены в таблице ниже.
|
Дано: Ом 1 = -6,25 нКл = -6,25 х 10 -9 Кл |
Найти: F избранный = ??? |
Последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для поиска неизвестной информации.Эта замена и алгебра показаны ниже.
F Elect = (9,0 x 10 9 Н•м 2 /C 2 ) • (6,25 x 10 -9 C) • (6,25 x 10 -9 C) • (6,25 x 10 -9 C)1 м) 2
F избранный = 9,23 x 10 -7 N
Обратите внимание, что перед подстановкой в уравнение закона Кулона знак «-» был удален из значений Q 1 и Q 2 .Как упоминалось выше, использование знаков «+» и «-» в уравнении приведет к положительному значению силы, если Q 1 и Q 2 одинаково заряжены, и к отрицательному значению силы, если Q 1 и Q 2 заряжены противоположно. Полученные в результате знаки «+» и «-» на F означают, является ли сила притягательной (значение «-» F) или отталкивающей (значение «+» F).
|
Пример С
Два шара с зарядом +3. |
В задаче указано значение Q 1 и Q 2 . Поскольку эти значения выражены в микрокулонах (мкКл), будет выполнено преобразование в кулоны. В задаче также указывается электрическая сила (F). Неизвестной величиной является разделительное расстояние (d). Результаты первых двух шагов представлены в таблице ниже.
|
Дано: Ом 1 = +3,37 мкКл = +3,37 х 10 -6 Кл |
Найти: д = ??? |
Как упоминалось выше, использование знаков «+» и «-» необязательно. Однако, если они используются, то они должны использоваться последовательно для значений Q и значений F. Их использование в уравнении показано в этой задаче.
Однако, если они используются, то они должны использоваться последовательно для значений Q и значений F. Их использование в уравнении показано в этой задаче.
Последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для поиска неизвестной информации. В этом случае алгебра выполняется первой, а подстановка выполняется последней. Эта алгебра и замена показаны ниже.
F избранный = k • Q 1 • Q 2 / d 2d 2 • F избранный = k • Q 1 • Q 2
d 2 = k • Q 1 • Q 2 / F избранный
d = SQRT(k • Q 1 • Q 2 ) / F избранный
д = SQRT [(9.0 x 10 9 Н•м 2 /C 2 ) • (-8,21 x 10 -6 C) • (+3,37 x 10 -6 C) / (-0,0626 N)]
d = Кв. [ +3,98 м 2 ]
[ +3,98 м 2 ]
d = +1,99 м
Сравнение электрических и гравитационных сил
Электрическая сила и гравитационная сила — две бесконтактные силы, обсуждаемые в учебнике «Класс физики».Уравнение закона Кулона для электрической силы очень похоже на уравнение Ньютона для всемирного тяготения.
Эти два уравнения имеют очень похожую форму. Оба уравнения показывают обратную квадратичную зависимость между силой и разделяющим расстоянием. И оба уравнения показывают, что сила пропорциональна произведению величины, вызывающей силу, — заряда в случае электрической силы и массы в случае гравитационной силы. Тем не менее, между этими двумя силами есть некоторые поразительные различия.Во-первых, сравнение констант пропорциональности — k и G — показывает, что константа закона Кулона (k) значительно больше, чем ньютоновская постоянная всемирного тяготения (G). Следовательно, единица заряда будет притягивать единицу заряда со значительно большей силой, чем единица массы притягивает единицу массы. Во-вторых, гравитационные силы действуют только притягивающе; электрические силы могут быть как притягивающими, так и отталкивающими.
Во-вторых, гравитационные силы действуют только притягивающе; электрические силы могут быть как притягивающими, так и отталкивающими.
Зависимость обратного квадрата между силой и расстоянием, вплетенная в уравнение, является общей для обеих бесконтактных сил.Эта взаимосвязь подчеркивает важность разделяющего расстояния, когда речь идет об электрическом взаимодействии между заряженными объектами. Этому посвящен следующий раздел Урока 3.
Мы хотели бы предложить … Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного закона Кулона.Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный закон Кулона позволяет учащимся исследовать влияние заряда и разделяющего расстояния на величину электрической силы между двумя заряженными объектами.

Проверьте свое понимание
Используйте свое понимание, чтобы ответить на следующие вопросы. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.
1. Q в уравнении закона Кулона означает _____.
а. масса заряженного объекта
б. # избыточных электронов на объекте
в. ток заряженного объекта
д. расстояние между заряженными объектами
эл.заряд заряженного объекта
2. Символ d в уравнении закона Кулона обозначает расстояние от ___.
а.
от А до Б
б. от А до Д
в.от В до С
д. от В до Д
эл. С-D
ф. от А до G
г. от В до F
ч. от С до Е
3.Определить электрическую силу притяжения между двумя шарами с отдельными зарядами +3,5 х 10 -8 Кл и -2,9 х 10 -8 Кл при расстоянии 0,65 м друг от друга.
4. Определить электрическую силу притяжения между двумя шариками, заряженными противоположным типом заряда, но одинаковым количеством заряда. Заряд на воздушных шарах составляет 6,0 x 10 -7 Кл, и расстояние между ними равно 0.50 м.
5. Джоанна натерла шарик шерстью, чтобы придать ему заряд -1,0 x 10 -6 Кл. Затем она приобрела пластиковую трубку для гольфа с зарядом +4,0 x 10 -6 Кл, локализованным в заданной точке. должность. Она держит место заряда на пластиковой трубке для гольфа на расстоянии 50,0 см над баллоном. Определить электрическую силу притяжения между трубкой для гольфа и шариком.
Затем она приобрела пластиковую трубку для гольфа с зарядом +4,0 x 10 -6 Кл, локализованным в заданной точке. должность. Она держит место заряда на пластиковой трубке для гольфа на расстоянии 50,0 см над баллоном. Определить электрическую силу притяжения между трубкой для гольфа и шариком.
6. Баллон с зарядом 4,0 мкКл держат на расстоянии 0,70 м от второго баллона с таким же зарядом. Вычислите величину силы отталкивания.
7. На каком расстоянии друг от друга должны находиться два заряда в 1,00 мкК, чтобы сила отталкивания между ними была эквивалентна весу (на Земле) 1.00 кг массы?
Что такое электростатика – читайте заметки по физике, книги, формулы, уравнения
В детстве вы играли в пластиковый стул и полотенце? Если вы еще не играли, то давайте попробуем эту интересную игру. Для этой игры вам потребуется 2-3 человека, один пластиковый стул и полотенце. Прежде всего, один человек должен сесть на стул обеими ногами над землей (ни одна часть тела не должна соприкасаться с землей или какой-либо другой вещью, кроме стула), а затем один человек берет полотенце и ударяет по спинке стула в течение 30 секунд. секунды.Когда кто-то прикоснется к человеку, сидящему на стуле, он или она получит очень легкий удар электрическим током. Теперь, если вам интересно, как такое может происходить, то концепции электростатики помогут вам понять это явление. Электростатика состоит из двух слов: «Электро» означает электрон или заряд, а «Статика» означает в покое. Итак, в этой игре с пластиковым стулом и полотенцем из-за ударов полотенца генерируются заряды, и мы получаем удар током из-за этих статических зарядов. Аналогичное явление, когда мы расчесываем волосы в сухой день и подносим расческу близко к крошечным кусочкам бумаги, мы замечаем, что они быстро притягиваются к расческе.
Для этой игры вам потребуется 2-3 человека, один пластиковый стул и полотенце. Прежде всего, один человек должен сесть на стул обеими ногами над землей (ни одна часть тела не должна соприкасаться с землей или какой-либо другой вещью, кроме стула), а затем один человек берет полотенце и ударяет по спинке стула в течение 30 секунд. секунды.Когда кто-то прикоснется к человеку, сидящему на стуле, он или она получит очень легкий удар электрическим током. Теперь, если вам интересно, как такое может происходить, то концепции электростатики помогут вам понять это явление. Электростатика состоит из двух слов: «Электро» означает электрон или заряд, а «Статика» означает в покое. Итак, в этой игре с пластиковым стулом и полотенцем из-за ударов полотенца генерируются заряды, и мы получаем удар током из-за этих статических зарядов. Аналогичное явление, когда мы расчесываем волосы в сухой день и подносим расческу близко к крошечным кусочкам бумаги, мы замечаем, что они быстро притягиваются к расческе.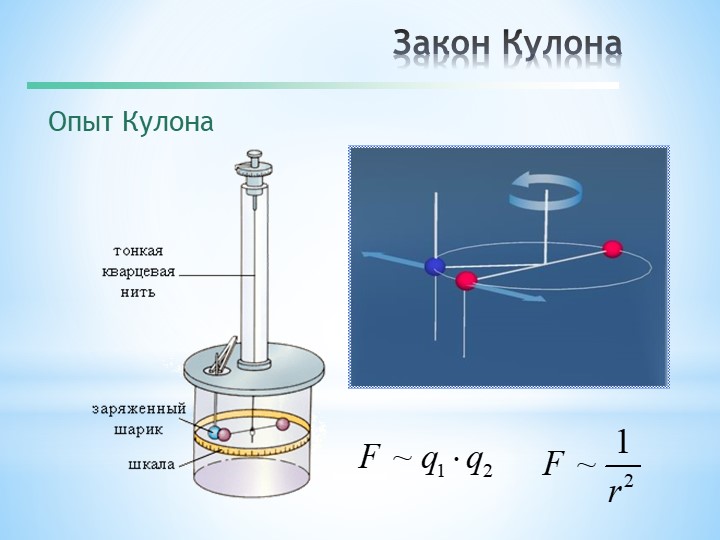
Электростатика — Темы
Электрический заряд, Проводник и изоляторы, Зарядка тела, Закон Кулона, Электрическое поле, Электрическая потенциальная энергия, Электрический потенциал, Связь между электрическим полем и потенциалом, Эквипотенциальные поверхности, Электрический диполь, Закон Гаусса, Свойства проводника, Электрическое поле и Потенциал из-за заряженной сферической оболочки или твердой проводящей поверхности, емкости, энергии, запасенной в заряженном конденсаторе, последовательного и параллельного соединения конденсаторов, двух законов емкости, плотности энергии, цепей CR
Обзор электростатики
В электростатике нас интересует только заряд, который находится в состоянии покоя, то есть заряд не движется, как электрический ток.В этой главе вы найдете много общего между электростатикой и гравитацией. Если у вас есть слабые представления о гравитации, сначала прочитайте эту главу. Как и в случае с гравитацией, у нас есть заряд (электроны) вместо массы, и отношение Электрической силы также аналогично, здесь Электрическая Сила, воздействующая одним точечным зарядом на другой, действует вдоль линии между зарядами. Оно изменяется обратно пропорционально квадрату расстояния, разделяющего заряды, и пропорционально произведению зарядов. Основное различие между гравитационной силой и электрической силой состоит в том, что первая притягивает только тогда, когда вторая притягивает только в том случае, если заряды имеют противоположную природу (положительную и отрицательную), а сила отталкивания действует, если заряды имеют одинаковую природу.Известно, что электроны имеют отрицательный заряд, а протоны — положительный. Когда вы продолжите, вы найдете другие понятия, похожие на гравитацию, такие как электрическое поле и электрический потенциал. А затем вы узнаете о законе Гаусса, который помогает легко рассчитать электрическое поле, и это очень важная концепция, потому что расчет электрического поля с использованием интегрирования иногда может привести к беспорядку.
Как и в случае с гравитацией, у нас есть заряд (электроны) вместо массы, и отношение Электрической силы также аналогично, здесь Электрическая Сила, воздействующая одним точечным зарядом на другой, действует вдоль линии между зарядами. Оно изменяется обратно пропорционально квадрату расстояния, разделяющего заряды, и пропорционально произведению зарядов. Основное различие между гравитационной силой и электрической силой состоит в том, что первая притягивает только тогда, когда вторая притягивает только в том случае, если заряды имеют противоположную природу (положительную и отрицательную), а сила отталкивания действует, если заряды имеют одинаковую природу.Известно, что электроны имеют отрицательный заряд, а протоны — положительный. Когда вы продолжите, вы найдете другие понятия, похожие на гравитацию, такие как электрическое поле и электрический потенциал. А затем вы узнаете о законе Гаусса, который помогает легко рассчитать электрическое поле, и это очень важная концепция, потому что расчет электрического поля с использованием интегрирования иногда может привести к беспорядку. Другим важным понятием в этой главе является электрический диполь (формируется, когда пара равных и противоположных точечных зарядов находится на фиксированном расстоянии друг от друга), который встречается в природе в различных ситуациях.Молекула фтористого водорода (HF) является типичным примером электрического диполя. Каждый электрический диполь характеризуется своим электрическим дипольным моментом, который представляет собой вектор «р», направленный от отрицательного заряда к положительному. В гравитации у нас нет диполей, можете подсказать почему?
Другим важным понятием в этой главе является электрический диполь (формируется, когда пара равных и противоположных точечных зарядов находится на фиксированном расстоянии друг от друга), который встречается в природе в различных ситуациях.Молекула фтористого водорода (HF) является типичным примером электрического диполя. Каждый электрический диполь характеризуется своим электрическим дипольным моментом, который представляет собой вектор «р», направленный от отрицательного заряда к положительному. В гравитации у нас нет диполей, можете подсказать почему?
Crack JEE 2021 с онлайн-программой подготовки к JEE/NEET
Начинай сейчасДа, вы правы, гравитационная сила всегда притягивает, поэтому диполя не образуется.
Далее в этой главе вы узнаете еще об одной важной концепции конденсаторов. Конденсатор — это устройство, которое может накапливать электрический заряд и потенциальную энергию. Конденсаторы имеют различные применения в реальной жизни, такие как фонарики в камерах, в двигателях вентиляторов и т. д.
д.
Формулы для электростатики
-
Электрическая сила, где q1 и q2 — точечные заряды
-
Электрическое поле,
-
Электрическая потенциальная энергия,
-
Электрический потенциал,
-
Дипольный момент, где 2а — расстояние между двумя зарядами
-
Емкость,
-
Эквивалентная емкость
-
Параллельное расположение,
-
Комплектация серии
,
-
Как подготовить электростатику?
Прежде чем решать вопросы электростатики, вы должны сначала освоиться с понятиями, которые вы прочитали в гравитации, из-за сходства для вас очень важно хорошо усвоить гравитационные понятия. В этой главе в большинстве задач вам будет предложено вычислить электрическое поле или электрический потенциал, поэтому попрактикуйтесь в этих концепциях. Кроме того, в некоторых задачах вы можете найти использование концепций механики, поэтому продолжайте пересматривать и механическую часть. Эта глава больше основана на концепции, чем на памяти, поэтому практика здесь является ключом.
В этой главе в большинстве задач вам будет предложено вычислить электрическое поле или электрический потенциал, поэтому попрактикуйтесь в этих концепциях. Кроме того, в некоторых задачах вы можете найти использование концепций механики, поэтому продолжайте пересматривать и механическую часть. Эта глава больше основана на концепции, чем на памяти, поэтому практика здесь является ключом.
Наконечники для электростатики
-
Не просто запоминайте формулы электрического поля и потенциала различных объектов, сначала докажите их самостоятельно с помощью выводов, а затем заучите.
-
Имейте в виду единицы измерения и размерные формулы различных сущностей, потому что иногда вопросы прямо задаются, чтобы преобразовать одну сущность в другую. Пример. Если дана электрическая сила, то каково электрическое поле в точке P.
-
Использование векторов очень необходимо, иногда прямо задаются вопросы о направлении электрического поля или силы и т.
 д.
д. -
Не запутайтесь в параллельном и последовательном соединении конденсаторов, всегда помните формулу для расчета эквивалентной емкости в обоих этих расположениях.
-
Проводите регулярные пробные онлайн-тесты по темам для получения концептуальных знаний.
-
Прежде чем решать вопрос, сначала посмотрите, какие величины даны, а затем придумайте стратегию решения вопроса.
Книги по Электростатика
Прежде всего, прочтите книгу NCERT, каждая концепция объясняется очень простым языком, а примеры, приведенные в книге, тоже хороши.После прочтения вы сможете решать вопросы из NCERT Exemplar. А если вы готовитесь к конкурсным экзаменам, таким как JEE или NEET, вы можете пройти курс «Понимание физики» DC Pandey.
Примечания по главам физики для технических и медицинских экзаменов
Потенциальная энергия: Формула электростатических точечных частиц
Потенциальная энергия — это энергия, запасенная в системе. Существует возможность или потенциал для ее преобразования в кинетическую энергию.Точечные частицы с зарядом действуют друг на друга с силой. Для противоположных зарядов сила притяжения. Для одинаковых зарядов сила отталкивающая. В обоих случаях существует потенциальная энергия, связанная с положением зарядов друг относительно друга. Единицей электрического заряда является кулон, Кл. Как и всякая работа и энергия, единицей потенциальной энергии является джоуль (Дж), где 1 Дж = 1 кг м 2 /с 2 .
Существует возможность или потенциал для ее преобразования в кинетическую энергию.Точечные частицы с зарядом действуют друг на друга с силой. Для противоположных зарядов сила притяжения. Для одинаковых зарядов сила отталкивающая. В обоих случаях существует потенциальная энергия, связанная с положением зарядов друг относительно друга. Единицей электрического заряда является кулон, Кл. Как и всякая работа и энергия, единицей потенциальной энергии является джоуль (Дж), где 1 Дж = 1 кг м 2 /с 2 .
U = потенциальная энергия электростатических точечных частиц
k = постоянная Кулона, k = 8.99 x 10 9 Н∙м 2 /C 2 . Можно записать = 1/(4πϵ 0 ).
ϵ 0 = диэлектрическая проницаемость свободного пространства, ϵ 0 = 8,854 x 10 -12 Кл 2 /(Н∙м 2
) )q 1 = заряд одной из точечных частиц
q 2 = заряд другой точечной частицы
r = расстояние между двумя точечными зарядами
Потенциальная энергия: Формула электростатических точечных частиц Вопросы:
1) Две заряженные частицы равны 1.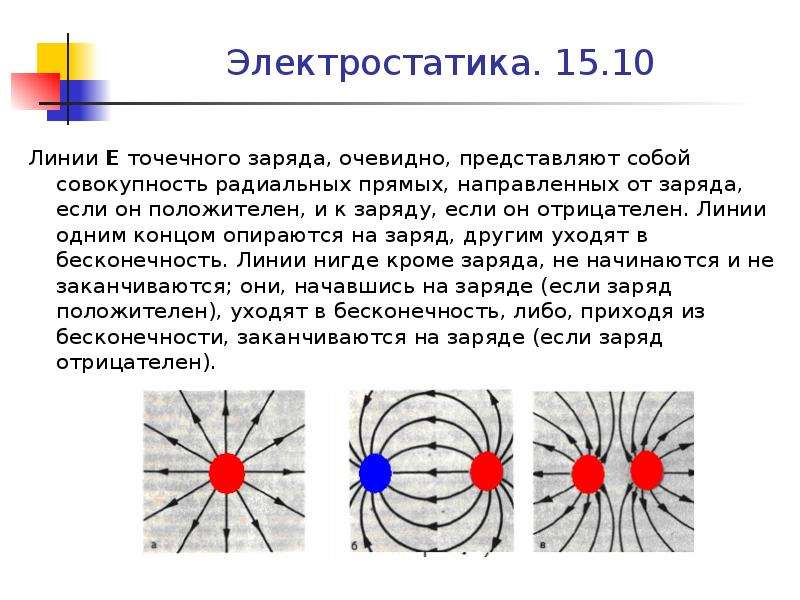 0 мм (0,0010 м) друг от друга. Один имеет заряд +3,0 мкКл (микрокулоны), а другой имеет заряд -8,0 мкКл. Какова потенциальная энергия в этой двухчастичной системе?
0 мм (0,0010 м) друг от друга. Один имеет заряд +3,0 мкКл (микрокулоны), а другой имеет заряд -8,0 мкКл. Какова потенциальная энергия в этой двухчастичной системе?
Ответ: Потенциальную энергию можно найти по формуле. Заряды даны в микрокулонах (мкКл): 1,0 мкКл = 1,0 x 10 -6 Кл. Перед решением уравнения заряды необходимо преобразовать в правильные единицы:
U = -215,8 Н∙м
У = -215.8 Дж
Потенциальная энергия этой конфигурации составляет -215,8 Дж. Потенциальная энергия всегда определяется по отношению к некоторому положению, где U = 0. Для этой формулы положение с U = 0 находится на бесконечном расстоянии, поэтому отрицательный знак означает, что эти заряды будут удаляться от бесконечности, если им позволить свободно двигаться и, следовательно, навстречу друг другу.
2) Две заряженные частицы находятся на расстоянии r друг от друга. Одна из этих частиц имеет заряд -5. 0 мкКл, а другой имеет заряд -1,80 мкКл. Если потенциальная энергия между ними U = +27,0 Дж, то каково расстояние между этими частицами?
0 мкКл, а другой имеет заряд -1,80 мкКл. Если потенциальная энергия между ними U = +27,0 Дж, то каково расстояние между этими частицами?
Ответ: Уравнение потенциальной энергии можно изменить так, чтобы найти решение для r:
Заряды даны в микрокулонах (мкКл): 1,0 мкКл = 1,0 x 10 -6 Кл. Перед решением уравнения заряды необходимо преобразовать в правильные единицы:
r = 0.0030 м
r = 3,0 мм
Расстояние между этими частицами 3,0 мм.
Электростатическая сила – формула – закон Кулона
Электростатическая сила – формула – закон Кулона
Силы между статическими электрически заряженными частицами подчиняются закону Кулона . Закон Кулона можно использовать для расчета силы между заряженными частицами (например, двумя протонами). Электростатическая сила прямо пропорциональна электрическим зарядам двух частиц и обратно пропорциональна квадрату расстояния между частицами. Закон Кулона формулируется в виде следующего уравнения.
Закон Кулона формулируется в виде следующего уравнения.
И закон Кулона, и закон магнитной силы суммируются в законе силы Лоренца. По сути, и магнитные, и электрические силы являются проявлениями обменной силы, включающей обмен фотонами.
Фотон, квант электромагнитного излучения , элементарная частица, являющаяся переносчиком электромагнитной силы. Фотоны — калибровочные бозоны , не имеющие ни электрического заряда, ни массы покоя и одну единицу спина.Общим для всех фотонов является скорость света , универсальная физическая константа. В пустом пространстве фотон движется со скоростью c ( скорость света – 299 792 458 метров в секунду ).
Электромагнитная сила играет важную роль в определении внутренних свойств большинства объектов, с которыми мы сталкиваемся в повседневной жизни. Химические свойства атомов и молекул определяются количеством протонов, фактически количеством и расположением электронов.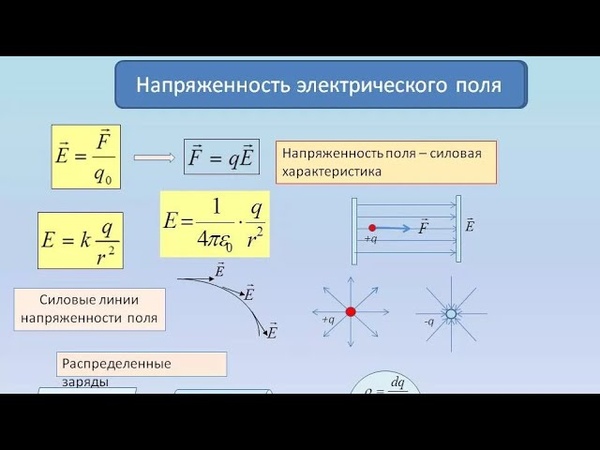 Конфигурация этих электронов следует из принципов квантовой механики.Количество электронов в электронных оболочках каждого элемента, особенно в самой внешней валентной оболочке, является основным фактором, определяющим поведение его химической связи. В периодической таблице элементы перечислены в порядке возрастания атомного номера Z. На самом деле силы электрического притяжения и отталкивания электрических зарядов настолько преобладают над тремя другими фундаментальными силами, что ими можно пренебречь как определяющими факторами. атомарное и молекулярное строение.
Конфигурация этих электронов следует из принципов квантовой механики.Количество электронов в электронных оболочках каждого элемента, особенно в самой внешней валентной оболочке, является основным фактором, определяющим поведение его химической связи. В периодической таблице элементы перечислены в порядке возрастания атомного номера Z. На самом деле силы электрического притяжения и отталкивания электрических зарядов настолько преобладают над тремя другими фундаментальными силами, что ими можно пренебречь как определяющими факторами. атомарное и молекулярное строение.
Примечания к редакции электростатического разряда | аскИИТианцы
Электростатическая сила и электростатическое поле:- |
F = K q 1 q 2 / r 2 5 Здесь K = 1/4π ε 0 = 9×10 9 Н·м 2 C 5 ( -2 в свободном пространстве)
Относительная диэлектрическая проницаемость ( ε r ) среды определяется как отношение диэлектрической проницаемости среды ( ε ) к диэлектрической проницаемости ( ε 0 ) свободного пространства. ε r = ε / ε 0 Если q 1 q 2 >0, RHS положительный. Если q 1 q 2 <0, отрицательный знак от q 1 q 2 изменится.Отношение снова будет истинным, так как в этом случае направления совпадают. CGS, q = ±1 стат-кулон SI, q = ±1 Кулон 1 кулон = 3×10 9 стат-кулон 1 кулон = (1/10) аб-кулон (эм.е.м. заряда) Итак, ε R = ε / ε 0 = F 1 / F 2 Здесь F 1 и F 2 — величины силы между ними в свободном пространстве и в среде соответственно. ? Линейный заряд, λ = q / л Поверхностный заряд, σ = q / A Объемный заряд, ρ = q / В E = [Ньютон/Кулон] или [Джоуль/(Кулон) (метр)] Свойства:- (а) Силовые линии направлены от положительно заряженного проводника и направлены к отрицательно заряженному проводнику. (b) Силовая линия начинается с положительного заряда и заканчивается на отрицательном заряде. Это означает, что силовая линия начинается с более высокого потенциала и заканчивается с более низким потенциалом. ? (a) В точке на своей оси. E = ( λ /4π ε 0 ) [1/ a – 1/ a + L ] Здесь λ — линейная плотность заряда. (b) В точке на линии, перпендикулярной одному концу. ? Здесь λ — заряд линии. в точке на оси, E = (1/4π ε 0 0 ) [ QX / ( A / ( A 2 + x 2 ) 3/2 ] Здесь σ — поверхностный заряд. (a) E вых = (1/4π ε 0 ) ( q / r 4 5 2 )
(б) E в = 0 (a) Внешняя точка:- E out = (1/4π ε 0 ) ( Q / r 90 39022 5 0 3 4 2)
(b) Внутренняя точка:- E в = (1/4π ε 0 ) ( Qr / R 3
(c) На поверхности:- E поверхность = (1/4π ε 0 ) ( Q / R 2
Здесь Q — это общий заряд (a) Вне цилиндра:- E = λ/2πε0r (b) Внутри цилиндра:- E = 0 (a) Снаружи цилиндра:- E = λ /2π ε 0 r (b) Внутри точки:- E = ρr /2 ε 0 (a) Электрическое поле в точках вне заряженных слоев:- E P = E R = 0 (b) Электрическое поле в точке между заряженными листами:- E Q = σ / ε 0 (a) В любой точке осевой линии: — Alt Tag: Электрическое поле из-за электрического диполя на осевой линии. (b) В точке на экваториальной линии (биссектрисе):- (c) В любой момент:- = pE sin θ Здесь p — дипольный момент, а θ — угол между направлением дипольного момента и электрическим полем E . E = λ /2π ε 0 r Направление электрического поля E радиально наружу для линии положительного заряда. (а) точка на улице ( R > R ): — E = (1/4π ε 0 ) ( Q / R 2 ), здесь Q это общий заряд. (б) точка внутри ( R < R ): — E = (1/4π ε 0 ) ( qr / R 3 ), здесь Q это общий заряд. E = σ /2 ε 0 Это означает, что электрическое поле вблизи заряженного листа не зависит от расстояния точки от листа, а зависит только от плотности его заряда и направлено нормально к листу. ? E = σ / ε 0 P elec = (½ ε 0 ) σ 2 (a) Электрический потенциал в любой точке определяется как отрицательный линейный интеграл электрического поля от бесконечности до этой точки вдоль любого пути. (b) V ( r ) = ккв / r (c) Разность потенциалов между любыми двумя точками в электрическом поле определяется как работа, совершаемая при переносе единичного положительного заряда из одной точки в другую против электрического поля. Вт AB = q [ В А — В В ] Итак, В = [ В А — В В ] = Вт / q Единицы:- вольт (С.I), стат-вольт (C.G.S) Размер:- [ V ] = [ML 2 T -3 A -1 ] Соотношение между вольт и стат-вольт:- 1 вольт = (1/300) стат-вольт E = — dV / dx = — dV / dr V = (1/4π ε 0 ) ( q / r ) V = (1/4π ε 0 ) [ Q 1 / R 1 + Q 2 / R 2 + Q 3 / р 3 ] = В 1 + В 2 + В 2 +…. (a) Снаружи, V out = (1/4π ε 0 ) ( q / r ) 3
(b) Внутри, В в = — (1/4π ε 0 ) ( q /R) (c) На поверхности, V поверхность = (1/4π ε 0 ) ( q / R ) (a) Снаружи, V out = (1/4π ε 0 ) ( q / r ) (б) внутри, V в = (1/4π ε 0 ) [ Q (3 R 2 — R 2 ) / 2 R 3 ] (c) На поверхности, V поверхность = (1/4π ε 0 ) ( q / R ) (d) В центре, V центре = (3/2) [(1/4π ε 0 ) ( q / R / R (а) общий потенциал, v = (1/4π ε 0 ) [( q 1 + q 2 ) / ( R 1 + г 2 )] (б) Q 1 1 = R 1 ( Q 1 + Q 2 ) / ( R 1 + R 2 ) = r 1 Q / r 1 + r 2 ; q 2 = r 2 Q / r 1 + r 8 0 9013 8 0 9013
(C) Q 1 Q / R R = R 1 / R 2 или Σ 1 / Σ 2 = R 1 / р 2 V ( R , θ , θ ) = θ COS θ / 4π ε / 4π ε 0 R 2 = P COS θ / 4π ε 0 р 2 (a) Точка, лежащая на осевой линии:- V = p /4π ε 0 r 2 (b) Точка, расположенная на экваториальных линиях:- V = 0 (a) R = n 1/3 r (b) Q = nq (c) В = n 2/3 В маленький (d) σ = n 1/3 σ маленький (e) E = n 1/3 E маленький w = u = (1/4π ε 0 ) ( Q 1 Q 2 / R 12 ) = Q 1 V 1 W = U = (1/4π ε 0 ) ( Q 1 Q 2 / R 12 + Q 1 Q 3 / r 13 + q 2 q 3 / r 23 (a) Если θ = 90º, то W = 0 (b) Если θ = 0º, то W = — pE (c) Если θ = 180°, то W = pE K. E = ½ мв 2 = эВ Проводники:- Проводники – это вещества, через которые легко происходит электрический заряд. Изоляторы:- Изоляторы (также называемые диэлектриками) представляют собой вещества, через которые электрический заряд не проходит легко. Емкость: — Емкость проводника определяется как отношение заряда проводника к его потенциалу C = Q / В Единицы:- С. CGS – стат-фарад (стат-кулон/стат-вольт) Размер C :- [M -1 L -2 T 4 A 2 ] C = 4π ε 0 r Конденсатор:- Конденсатор или конденсатор представляет собой устройство, которое обеспечивает большую емкость в меньшем пространстве. Емкость конденсатора с плоскими пластинами:- C воздух = ε 0 A / d C med = Kε 0 A / d Здесь A — общая площадь двух пластин, а d — расстояние между пластинами. C = ε 0 A /[ d — t +( t /K03)
Здесь d — расстояние между пластинами, t — толщина диэлектрической пластины, A — площадь и K — диэлектрическая проницаемость материала пластины. Если пространство полностью заполнено диэлектрической средой ( t = d ), то C = ε 0 КА / d (a) C воздух = 4π ε 0 R (b) C med = K (4π ε 0 R ) (a) Когда внешняя сфера заземлена: — C воздух = 4π ε 0 [ ab /( b — a )] C med = 4π ε 0 [K ab /( b — a )] (b) Когда внутренняя сфера заземлена:- C 1 = 4π ε 0 [ ab /( b — a )] C 2 = 4π ε 0 b ? Полезная емкость, C ‘=4π ε 0 [ b 2 / b — a ] Увеличение емкости, Δ C = 4π ε 0 б Это означает, что, соединяя внутреннюю сферу с землей и заряжая внешнюю, мы получаем дополнительную емкость, равную емкости внешней сферы. C C C Air = λl / [( λ / 2π ε 0 ) (log E B / A )] = [2π ε 0 l /(log e b / a ) ] C med = [2π Kε 0 l /(log e b / a ) ] W = ½ QV = ½ Q 2 / C = ½ CV 2 U = ½ ε 0 E 2 = ½ ( Σ 2 / ε 0 ) Это означает, что плотность энергии конденсатора не зависит от площади пластин и расстояния между ними до тех пор, пока значение E не изменится. ?(а) (i) Конденсаторы параллельно: — C = C = C 1 + C 2 + C 3 + …. + C N Результирующая емкость нескольких конденсаторов, соединенных параллельно, равна сумме их индивидуальных емкостей. (ii) В 1 = В 2 = В 3 = В (III) Q 1 1 = C 1 V , Q 2 = C 2 V , Q 3 = C 3 В (iv) Сохраненная энергия, U = U 1 + U 2 + U 3 (б) (i) Конденсаторы в серии:- 1/ C = 1/ C 1 + 1/ C 2 +……+ 1/ C 3 53 8 54
?Величина, обратная результирующей емкости ряда конденсаторов, соединенных последовательно, равна сумме обратных величин их индивидуальных емкостей. (ii) q 1 = q 2 = q 3 = q q
(III) V 1 (iv) Сохраненная энергия, U = U 1 + U 2 + U 3 (a) Энергия, накопленная в последовательной комбинации конденсаторов:- W = ½ ( Q 2 / C 1 Таким образом, чистая энергия, запасенная в комбинации, равна сумме энергий, запасенных в конденсаторах компонентов. (b) Энергия, накопленная в параллельной комбинации конденсаторов:- W = ½ C 1 V 2 + ½ C 2 V 2 + ½ C 3 V 2 = W 1 + Вт 2 + Вт 3 Чистая энергия, запасенная в комбинации, равна сумме энергий, запасенных в конденсаторах компонентов. (a) F = ½ ε 0 E 2 A (б) F = σ 2 A /2 ε 0 (в) F=Q 2 /2 ε 0 А F = ( Q 2 /2 C 2 ) ( DC / DX / DX ) = ½ V 2 ( DX / DX ) V = [ C 1 V 1 + C + C 2 V 2 ] / [ C 1 + C 2 ] = [ Q 1 + Q 2 ]/ [ C 1 + C 2 ] δ q = [ C 1 C 2 / C C 1 + C 2 ] [ V 1 — V 2 ] δ U = ½ [ C C C 2 / C 1 + C 2 ] [ V 1 — V 2 ] 2 (a) Q = Q 0 (1-e — t / RC ) (b) В = В 0 (1-e — t / RC ) (c) I = I 0 (1-e — t / RC ) (d) I 0 = V 0 / R (a) Q = Q 0 (e -t/RC ) (b) В = В 0 (e — t / RC ) (c) I = I 0 (e — t / RC ) Титул: Примечания к редакции электростатического разряда | аскИИТианцы Мета-описание: Примечания к редакции по электростатической силе, электростатическому полю, электростатическому потенциалу, электростатической энергии и емкости предоставлены askIITians.
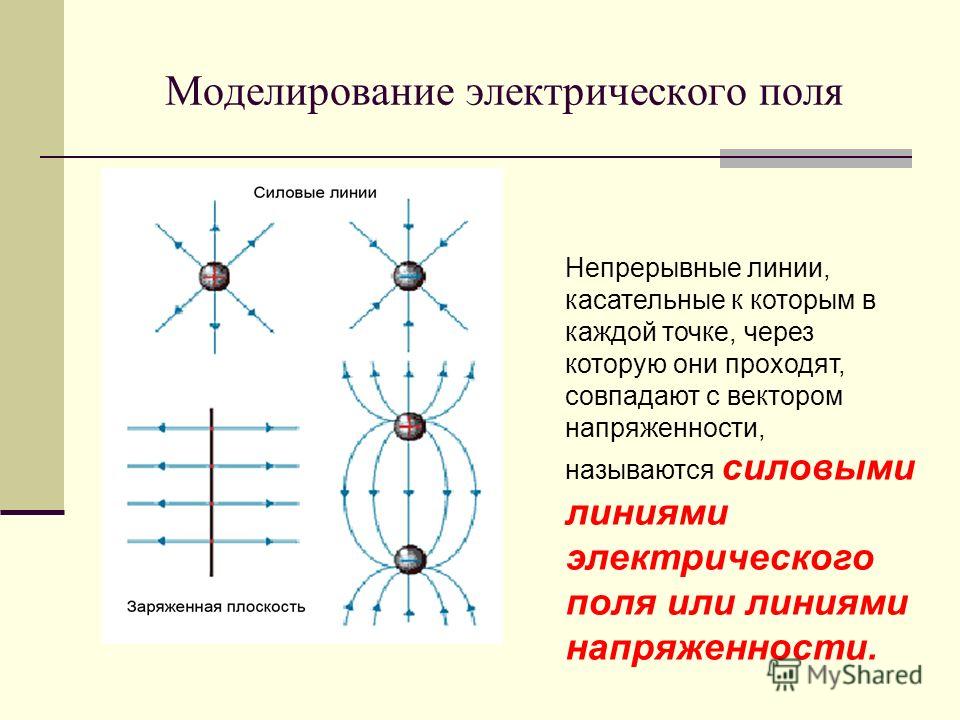

 Направление движения единичного положительного заряда дает направление силовой линии.
Направление движения единичного положительного заряда дает направление силовой линии.




Электростатический потенциал и емкость:-


 поле.
поле.
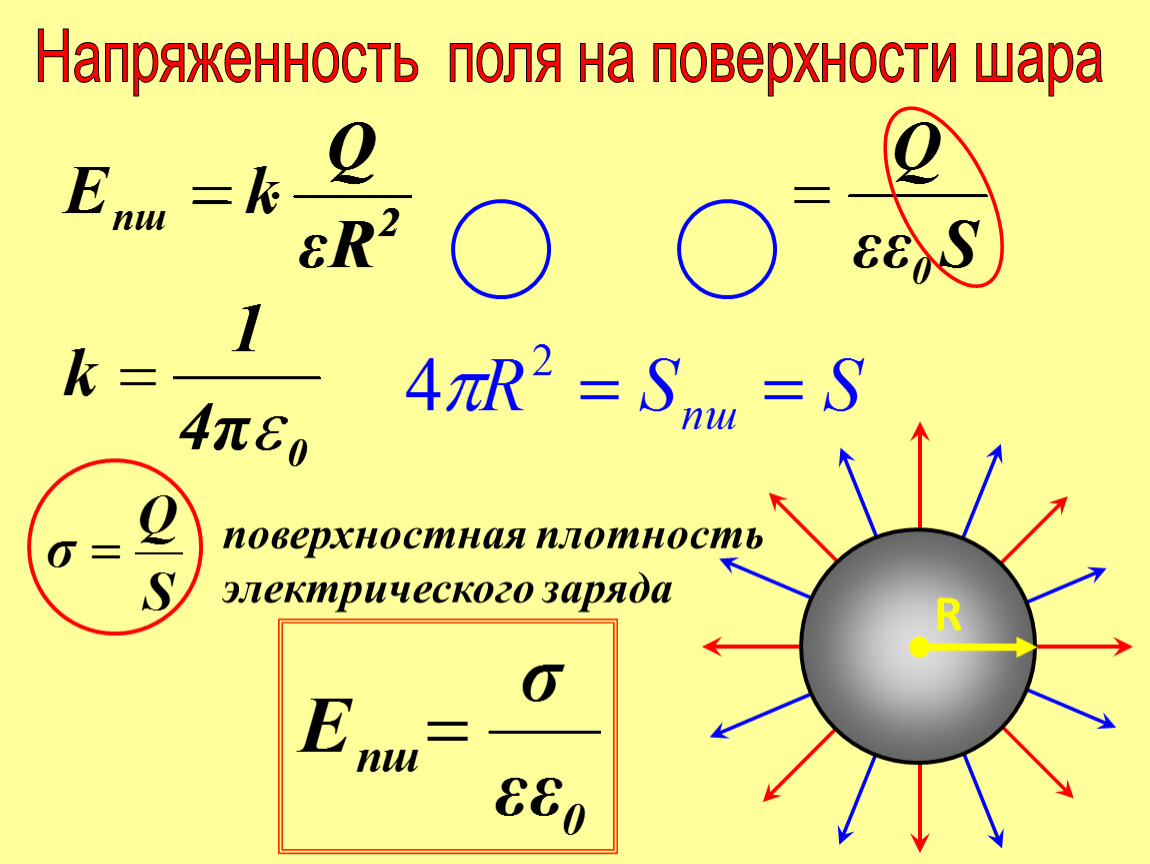 I – фарад (кулон/вольт)
I – фарад (кулон/вольт)



 Основные понятия. Электрический заряд. Закон сохранения электрического
Основные понятия. Электрический заряд. Закон сохранения электрического
 ….qn, равна геометрической сумме (= векторной сумме) сил F12+….F1n, действующих на данный заряд со стороны каждого из зарядов:
….qn, равна геометрической сумме (= векторной сумме) сил F12+….F1n, действующих на данный заряд со стороны каждого из зарядов:
 …En, то результирующая напряженность электрического поля в этой точке равна векторной сумме отдельных напряжённостей:
…En, то результирующая напряженность электрического поля в этой точке равна векторной сумме отдельных напряжённостей:
 Введите свой запрос:
Введите свой запрос:

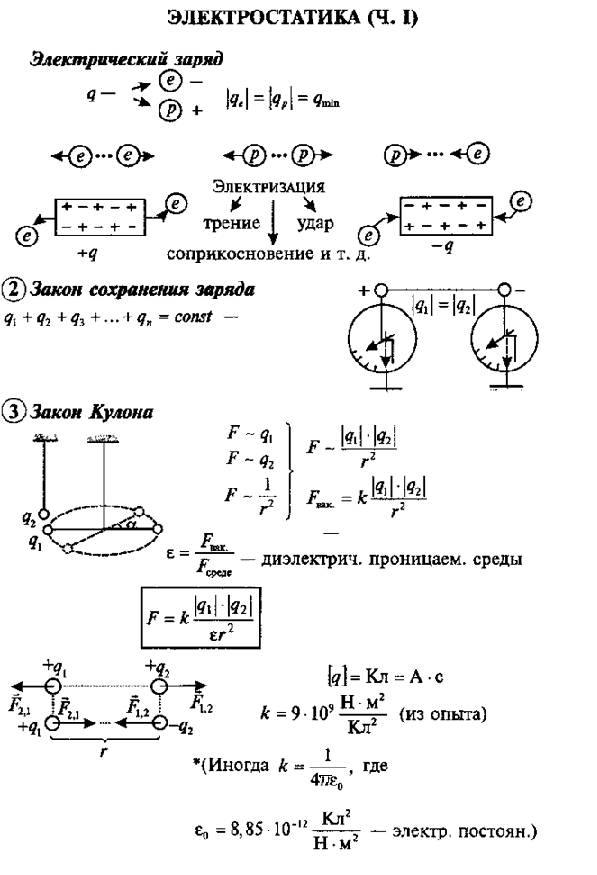
 37 мкКл и -8,21 мкКл притягиваются друг к другу с силой 0,0626 ньютона. Определите расстояние между двумя шарами.
37 мкКл и -8,21 мкКл притягиваются друг к другу с силой 0,0626 ньютона. Определите расстояние между двумя шарами.