Тригонометрические уравнения фипи – Тригонометрические уравнения и преобразования | ЕГЭ по математике (профильной)

ЕГЭ. Задача 13. Тригонометрические (и не только) уравнения

Подготовка к единому государственному экзамену по математике. Полезные материалы по тригонометрии, большие теоретические видеолекции, видеоразборы задач и подборка заданий прошлых лет.

Полезные материалы

Записи онлайн-занятий

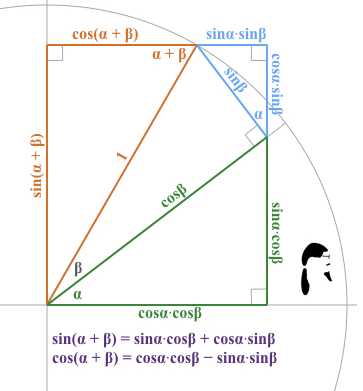
Тригонометрические формулы

Тригонометрические уравнения

1. Необходимая теория для решения задач.
2. а) Решите уравнение $7\cos^2 x — \cos x — 8 = 0$.
   б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -\dfrac{7\pi}{2}; -\dfrac{3\pi}{2} \right]$.
3. а) Решите уравнение $\dfrac{6}{\cos^2 x} — \dfrac{7}{\cos x} + 1 = 0$.
   б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -3\pi; -\pi \right]$.
4. Решите уравнение $\sin\sqrt{16 — x^2} = \dfrac12$.
5. а) Решите уравнение $2\cos 2x — 12\cos x + 7 = 0$.
   б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -\pi; -\dfrac{5\pi}{2} \right]$.
6. а) Решите уравнение $\dfrac{5}{\mathrm{tg}^2 x} — \dfrac{19}{\sin x} + 17 = 0$.
   б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -\dfrac{7\pi}{2}; -2\pi \right]$.
7. Решите уравнение $\dfrac{2\cos^3 x + 3 \cos^2 x + \cos x}{\sqrt{\mathrm{ctg}x}} = 0$.
8. Решите уравнение $\dfrac{\mathrm{tg}^3x — \mathrm{tg}x}{\sqrt{-\sin x}} = 0$.
9. а) Решите уравнение $\cos 2x = 1 — \cos\left(\dfrac{\pi}{2} — x\right)$.
   б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -\dfrac{5\pi}{2}; -\pi \right)$.
10. а) Решите уравнение $\cos 2x = \sin\left(\dfrac{3\pi}{2} — x\right)$.
    б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ \dfrac{3\pi}{2}; \dfrac{5\pi}{2} \right]$.
11. а) Решите уравнение $2\sin^2\left(\dfrac{3\pi}{2} + x\right) = \sqrt3\cos x$.
    б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -\dfrac{7\pi}{2}; -2\pi \right]$.

Видеоразборы задач

а) Решите уравнение $\cos^2 (\pi — x) — \sin \left( x — \dfrac{3\pi}{2} \right) = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\dfrac{5\pi}{2}; 4\pi \right]$.

 

а) Решите уравнение $8^x — 9 \cdot 2^{x + 1} + 2^{5 — x} = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\log_5 2; \log_5 20 \right]$.

 

а) Решите уравнение $8 \sin^2 x + 2\sqrt{3} \cos \left( \dfrac{3\pi}{2} — x\right) = 9$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[- \dfrac{5\pi}{2}; -\pi \right]$.

 

а) Решите уравнение $2\log_3^2 (2 \cos x) — 5\log_3 (2 \cos x) + 2 = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\pi; \dfrac{5\pi}{2} \right]$.

а) Решите уравнение $\left( \dfrac{1}{49} \right)^{\sin x} = 7^{2 \sin 2x}$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\dfrac{3\pi}{2}; 3\pi \right]$.

 

а) Решите уравнение $\sin x + \left(\cos \dfrac{x}{2} — \sin \dfrac{x}{2}\right)\left(\cos \dfrac{x}{2} + \sin \dfrac{x}{2}\right) = 0$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[\pi; \dfrac{5\pi}{2}\right]$.

 

а) Решите уравнение $\log_4 (\sin x + \sin 2x + 16) = 2$.
б) Найдите все корни этого уравнения, принадлежащие промежутку $\left[ -4\pi; -\dfrac{5\pi}{2} \right]$.

Подборка заданий прошлых лет

1. а) Решите уравнение $\cos 2x = 1 — \cos \left( \dfrac{\pi}{2} — x\right)$.
   б) Укажите корни этого уравнения, принадлежащие полуинтервалу $\left[ — \dfrac{5\pi}{2}; \ -\pi\right)$. (Демоверсия ЕГЭ-2018)
2. а) Решите уравнение $2x \cos x — 8\cos x + x — 4 = 0$.
   б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -\dfrac{\pi}{2};\ \pi \right]$. (ЕГЭ-2017, основная волна, резервный день)
3. а) Решите уравнение $\log_3 (x^2 — 2x) = 1$.
   б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \log_2 0{,}2;\ \log_2 5 \right]$. (ЕГЭ-2017, основная волна, резервный день)
4. а) Решите уравнение $\log_3 (x^2 — 24x) = 4$.
   б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \log_2 0{,}1;\ 12\sqrt{5} \right]$. (ЕГЭ-2017, основная волна, резервный день)
5. а) Решите уравнение $0{,}4^{\sin x} + 2{,}5^{\sin x} = 2$.
   б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ 2\pi;\ \dfrac{7\pi}{2} \right]$. (ЕГЭ-2017, основная волна)
6. а) Решите уравнение $\log_8 \left(7\sqrt{3} \sin x — \cos 2x — 10\right) = 0$.
   б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{3\pi}{2};\ 3\pi \right]$. (ЕГЭ-2017, основная волна)
7. а) Решите уравнение $\log_4 \left(2^{2x} — \sqrt{3} \cos x — 6\sin^2 x\right) = x$.
   б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{5\pi}{2};\ 4\pi \right]$. (ЕГЭ-2017, основная волна)
8. а) Решите уравнение $2\log_2^2 \left(\sin x\right) — 5 \log_2 \left(\sin x\right) — 3 = 0$.
   б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ — 3\pi;\ — \dfrac{3\pi}{2} \right]$. (ЕГЭ-2017, основная волна)
9. а) Решите уравнение $81^{\cos x} — 12\cdot 9^{\cos x} + 27 = 0$.
   б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ — 4\pi;\ — \dfrac{5\pi}{2} \right]$. (ЕГЭ-2017, основная волна)
10. а) Решите уравнение $8^x — 9 \cdot 2^{x + 1} + 2^{5 — x} = 0$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \log_5 2;\ \log_5 20 \right]$. (ЕГЭ-2017, досрочная волна)
11. а) Решите уравнение $2\log^2_9 x — 3 \log_9 x + 1 = 0$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \sqrt{10};\ \sqrt{99} \right]$. (ЕГЭ-2016, основная волна, резервный день)
12. а) Решите уравнение $6\log^2_8 x — 5 \log_8 x + 1 = 0$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ 2;\ 2{,}5 \right]$. (ЕГЭ-2016, основная волна, резервный день)
13. а) Решите уравнение $\sin 2x = 2\sin x + \sin \left( x + \dfrac{3\pi}{2} \right) + 1$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -4\pi;\ -\dfrac{5\pi}{2} \right]$. (ЕГЭ-2016, основная волна, резервный день)
14. а) Решите уравнение $2\cos^2 x + 1 = 2\sqrt{2} \cos \left( \dfrac{3\pi}{2} — x \right)$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{3\pi}{2};\ 3\pi \right]$. (ЕГЭ-2016, основная волна)
15. а) Решите уравнение $2\log^2_2 (2\cos x) — 9 \log_2 (2\cos x) + 4 = 0$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -2\pi;\ -\dfrac{\pi}{2} \right]$. (ЕГЭ-2016, основная волна)
16. а) Решите уравнение $8^x — 7 \cdot 4^x — 2^{x + 4} + 112 = 0$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \log_2 5;\ \log_2 11 \right]$. (ЕГЭ-2016, досрочная волна)
17. а) Решите уравнение $\cos 2x + \cos^2 \left( \dfrac{3\pi}{2} — x \right) = 0,25$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -4\pi;\ -\dfrac{5\pi}{2} \right]$. (ЕГЭ-2016, досрочная волна)
18. а) Решите уравнение $\dfrac{13\sin^2 x — 5\sin x}{13\cos x + 12} = 0$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -3\pi;\ -\dfrac{3\pi}{2} \right]$. (ЕГЭ-2016, досрочная волна)
19. а) Решите уравнение $\dfrac{\sin2x}{\sin\left( \dfrac{7\pi}{2} — x \right)} = \sqrt{2}$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[2\pi;\ \dfrac{7\pi}{2}\right]$. (ЕГЭ-2015, основная волна)
20. а) Решите уравнение $4 \sin^2 x = \mathrm{tg} x$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ — \pi;\ 0\right]$. (ЕГЭ-2015, основная волна)
21. а) Решите уравнение $3\cos 2x — 5\sin x + 1 = 0$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \pi;\ \dfrac{5\pi}{2}\right]$. (ЕГЭ-2015, основная волна)
22. а) Решите уравнение $\cos 2x — 5\sqrt{2}\cos x — 5 = 0$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -3\pi;\ -\dfrac{3\pi}{2}\right]$. (ЕГЭ-2015, основная волна)
23. а) Решите уравнение $\sin 2x + \sqrt{2} \sin x = 2\cos x + \sqrt{2}$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \pi;\ \dfrac{5\pi}{2}\right]$. (ЕГЭ-2015, досрочная волна)
24. а) Решите уравнение $2\cos^3 x — \cos^2 x + 2\cos x — 1 = 0$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ 2\pi;\ \dfrac{7\pi}{2}\right]$. (ЕГЭ-2015, досрочная волна)
25. а) Решите уравнение $\mathrm{tg}^2 x + (1 + \sqrt{3}) \mathrm{tg} x + \sqrt{3} = 0$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{5\pi}{2}; \ 4\pi\right]$. (ЕГЭ-2014, основная волна)
26. а) Решите уравнение $2\sqrt{3} \cos^2\left( \dfrac{3\pi}{2} + x\right) — \sin 2x = 0$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{3\pi}{2}; \ 3\pi\right]$. (ЕГЭ-2014, основная волна)
27. а) Решите уравнение $\cos 2x + \sqrt{2} \sin\left( \dfrac{\pi}{2} + x\right) + 1 = 0$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -3\pi; \ -\dfrac{3\pi}{2}\right]$. (ЕГЭ-2014, основная волна)
28. а) Решите уравнение $-\sqrt{2} \sin\left( -\dfrac{5\pi}{2} + x\right) \cdot \sin x = \cos x$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ \dfrac{9\pi}{2}; \ 6\pi\right]$. (ЕГЭ-2014, досрочная волна)
29. а) Решите уравнение $\sin 2x = \sin\left( \dfrac{\pi}{2} + x\right)$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -\dfrac{7\pi}{2}; \ -\dfrac{5\pi}{2}\right]$. (ЕГЭ-2013, основная волна)
30. а) Решите уравнение $6 \sin^2 x + 5\sin\left( \dfrac{\pi}{2} — x\right) — 2 = 0$.
    б) Укажите корни этого уравнения, принадлежащие отрезку $\left[ -5\pi; \ — \dfrac{7\pi}{2}\right]$. (ЕГЭ-2012, вторая волна)

trushinbv.ru

Задача 13: тригонометрические уравнения с ограничениями

Типичная задача №13 из ЕГЭ по математике 2016 содержит два пункта:

1. Решить несложное тригонометрическое уравнение (хотя иногда попадаются довольно сложные).
2. Среди полученных корней отобрать те, которые принадлежат заданному отрезку. Вот здесь большинство учеников «пасует».

Все видеоуроки по задачам №13, опубликованные на моем сайте, содержат оба пункта: и решение уравнения (со всеми тонкостями), и различные подходы к отбору корней.

Глава 1.

Тригонометрические уравнения

§ 1.

Задача C1: тригонометрические уравнения с ограничением

§ 2.

Задача C1: тригонометрические уравнения и формула двойного угла

§ 3.

Задача C1: тригонометрия и показательная функция — 1 вариант

§ 4.

Задача C1: тригонометрия и показательная функция — 2 вариант

Глава 2.

Показательные и логарифмические уравнения

§ 1.

Задача C1: показательные уравнения с ограничением

§ 2.

Задача C1: еще одно показательное уравнение

§ 3.

Логарифмические уравнения в задаче C1

§ 4.

Задача C1: логарифмы и тригонометрия в одном уравнении

§ 5.

Вебинар по задачам С1: тригонометрия

§ 6.

Формулы двойного угла в тригонометрических уравнениях из ЕГЭ

§ 7.

Отбор корней из некрасивых арктангенсов, арксинусов и т.д.

§ 8.

Нестандартные периоды и отбор корней в тригонометрическом уравнении

§ 11.

Задача из пробного ЕГЭ 2016 от 3 марта

§ 12.

Вебинар по заданию 13: предварительное задание

Логарифмические и показательные уравнения

1

2

3

4

5

6

7

8

9

10

11

Тригонометрические уравнения

12

www.berdov.com

Тригонометрические уравнения — задание 13 профильного ЕГЭ

1. Решить уравнение.

   

Решение: преобразуем косинус разности:

   

   

По формуле основного тригонометрического тождества:

   

   

Получили квадратное уравнение относительно . Его корни:

   

Либо

   

Первый корень – посторонний, поэтому

   

Либо

   

Тогда

   

   

Ответ: ,

 

2. Решить уравнение.

   

   

Справа – разность квадратов.

   

По формуле основного тригонометрического тождества:

   

   

   

Первый корень – ,

Приравниваем к нулю второй множитель:

   

   

   

Ищем корни этого квадратного уравнения, по Виету – посторонний корень, остается . Решение:

   

Ответ: ,

 

3. Решить уравнение.

   

Преобразуем косинус двойного аргумента:

   

   

   

Мы видим полный квадрат:

   

Или , ,

Ответ:

4. Решить уравнение.

   

   

Поскольку перед нами корень, то сразу определим ОДЗ:

   

   

   

   

   

ОДЗ:

   

   

   

   

При имеем:

   

   

   

   

Так как второй корень квадратного уравнения отрицателен, то к рассматриваемому промежутку он отношения не имеет.

При имеем:

   

   

   

Второй корень квадратного уравнения положителен, а мы рассматриваем случай, когда  – поэтому мы его отбросили.

   

или  

Оба полученных решения удовлетворяют ОДЗ.

Ответ: и

 

5. Решить уравнение.

   

   

   

   

   

   

   

Получили биквадратное уравнение относительно . Обозначаем :

   

Корни этого уравнения: и . Так как , то отрицательный корень является посторонним. Тогда , и .

Определяем :

   

 

6. Решить уравнение.

   

Представим как косинус двойного угла:

   

   

   

Уравнение распалось на два:

   

   

Первое решение:

   

   

Второе решение:

   

   

   

 

7. Решить уравнение.

   

Функцию синуса заменим косинусом:

   

Разность косинусов удобно заменить произведением синусов:

   

Уравнение распадается на два:

   

Или

   

Решение первого:

   

   

   

Решение второго:

   

   

   

Ответ: ,

easy-physic.ru

Задание С1. Тригонометрические уравнения | Подготовка к ЕГЭ по математике

 

В 2013 году задание С1 — это скорее всего тригонометрическое уравнение с явным или неявным отбором корней.

Из всех заданий вида С задание С1 является самым легким, с ним справляется около 20% всех выпускников, а примерно 40% получают за это задание 1 балл, т.е. выполняют часть задачи.

Так что не стоит его бояться. Тригонометрия на самом деле очень понятная и интересная наука, и ее может осилить средний ученик.

При серьезной подготовке надо научиться решать любые уравнения, а не только тригонометрические. Хотя бы потому, чтобы не ограничивать свои знания, чтобы подготовиться к успешному решению других задач, таких, как С3 и С5, и дальнейшему обучению в Вузе.

Но исходя из того, что предлагается на экзаменах последних лет и в типовых экзаменационных вариантах, опубликованных ФИПИ, следует ожидать на ЕГЭ-2013 в качестве задания С1 именно тригонометрическое уравнение с выбором корней. Кроме того, вид этих уравнений довольно однотипен. Так что следует обратить свое внимание именно на этот вид уравнений.

 

---

Что надо знать и уметь:

1. Понимать, уметь «читать» числовую окружность. При этом использовать не только градусную меру углов, но и радианную.

2. Знать определения синуса, косинуса, тангенса и котангенса.

3. Знать таблицу значений тригонометрических функций основных аргументов и аргументов первой четверти. Применяя числовую окружность, уметь находить значения тригонометрических функций аргументов других четвертей.

4. Используя числовую окружность, уметь читать и применять свойства тригонометрических функций (знаки, четность, периодичность, формулы симметричных точек).

5. Уметь решать простейшие тригонометрические уравнения по формулам и с использованием числовой окружности.

6. Уметь решать простейшие тригонометрические неравенства, используя числовую окружность.

7. Уметь выбирать корни согласно условию задачи или по виду уравнения, для чего уметь находить области определения различных функций, заданных формулой.

8. Знать основные тригонометрические формулы, формулы двойных аргументов.

9. Знать основные методы решения тригонометрических уравнений (замена, разложение на множители).

 

---

 

Работать над темой рекомендую в соответствии со следующим планом:

 

1. Числовая окружность.
2. Числовая окружность в координатной плоскости.
3. Градусная и радианная мера угла.
4. Определение, значения и свойства синуса, косинуса, тангенса и котангенса.
5. Обратные тригонометрические функции и их свойства.
6. Простейшие тригонометрические уравнения.
7. Простейшие тригонометрические неравенства.
8. Выбор корней при решении тригонометрических уравнений.
9. Методы решения тригонометрических уравнений.
10. Системы тригонометрических уравнений.
11. Примеры решения задания С1 из экзаменационных вариантов.

 

---

 

Примеры         задания С1.

Пример 1.

Решение:

Учтем, что подкоренное выражение, стоящее в знаменателе, может принимать только положительные значения:

Решим это неравенство:

 , где  (*)

Теперь приравняем к нулю числитель (необходимое условие равенства дроби нулю) и решим полученное тригонометрическое уравнение:

Из полученных решений выбираем только те, которые удовлетворяют условию (*):

Пример 2  (фоторешение).

Примерно так можно записать решение:

 

Пример 3  ( видеорешение) с объяснением учителя

 

 

Пример 4. Видео-решение, объяснение учителя с использованием презентации

 

 

 

Критерии оценки задания

 

Для самостоятельной подготовки можно использовать пособия:

 

Корянов А.Г. и Прокофьев А.А. Математика. ЕГЭ-2011

Корянов А.Г. и Прокофьев А.А. МАТЕМАТИКА ЕГЭ 2012/Тригонометрические уравнения: методы решений и отбор корней (типовые задания С1)

Корянов А.Г. и Прокофьев. 

Отбор корней в тригонометрических уравнениях (типовые задания С1)

 

 

Хотите больше?

Видео — курс по решению задач типа С1.

 

 

Записаться на консультацию — здесь.

 

Если у вас есть предложения и ли вопросы, обращайтесь по вкладке:

 

Комментарии, открытые для всех читателей сайта, пишите ниже:

 

www.xn--80aknic8a0b.xn--p1ai

Репетитор по математике, подготовка к ЕГЭ и ГИА. Видеоуроки

В Заданиях №5 ЕГЭ по математике проверяется умение решать простейшие
рациональные,
иррациональные,
показательные,
логарифмические,
тригонометрические уравнения.

Сейчас мы рассмотрим основные типы простейших тригонометрических уравнений

, которые могут встретиться на экзамене.

Вы можете пройти автотренинг по подготовке к ЕГЭ по математике «Тригонометрия».

Прежде настоятельно рекомендую освоить значения основных тригонометрических функций (по кругу) и посмотрите, как решать самые простые тригонометрические уравнения!

Задание 1.
Найдите корень уравнения: .

В ответе запишите наибольший отрицательный корень.

Решение: + показать

Задание 2.

Решите уравнение . В ответе напишите наименьший положительный корень.

Решение: + показать

Задание 3.

Решите уравнение   В ответе напишите наибольший отрицательный корень.

Решение: + показать

На оси тангенсов находим , «выходим на круг»:

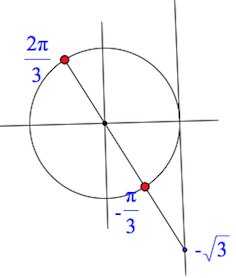И далее  – действия, аналогичные действиям в примерах 1 и 2:

Наибольший отрицательный корень – при :

Ответ: -0,5. 

 

Для вас – аналогичные задания с ответами.  Проверьте себя!

1) Решите уравнение . В ответе напишите наименьший положительный корень.

Ответ + показать

0,25

2) Решите уравнение  . В ответе напишите наибольший отрицательный корень.

Ответ + показать

-1

3) Решите уравнение  В ответе напишите наименьший положительный корень.

Ответ + показать

1

egemaximum.ru

Тригонометрические уравнения

   Тригонометрические уравнения. В составе экзамена по математике в первой части имеется задание связанное с решением уравнения — это простые уравнения, которые решаются за минуты, многие типы можно решить устно.  Включают в себя: линейные, квадратные, рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения.

В этой статье мы рассмотрим тригонометрические уравнения. Их решение отличается и по объёму вычисления и по сложности от остальных задач этой части. Не пугайтесь, под словом «сложность», имеется виду их относительную сложность по сравнению с другими заданиями.  

Кроме нахождения самих корней уравнения, необходимо определить наибольший отрицательный, либо наименьший положительный корень. Вероятность того, что вам на экзамене попадёт тригонометрическое уравнение, конечно же, мала.

Их в данной части ЕГЭ менее 7%. Но это не означает, что их нужно оставить без внимания. В части С тоже необходимо решить тригонометрическое уравнение, поэтому хорошо разобраться с методикой решения и понимать теорию просто необходимо.

Понимание раздела «Тригонометрия»  в математике во многом определяет ваш успех при решении многих задач. Напоминаю, что ответом является целое число или конечная десятичная дробь. После того, как получите корни уравнения, ОБЯЗАТЕЛЬНО сделайте проверку. Много времени это не займёт, а вас избавит от ошибки.

В будущем мы также рассмотрим и другие уравнения, не пропустите! Вспомним формулы корней тригонометрических уравнений, их необходимо знать:

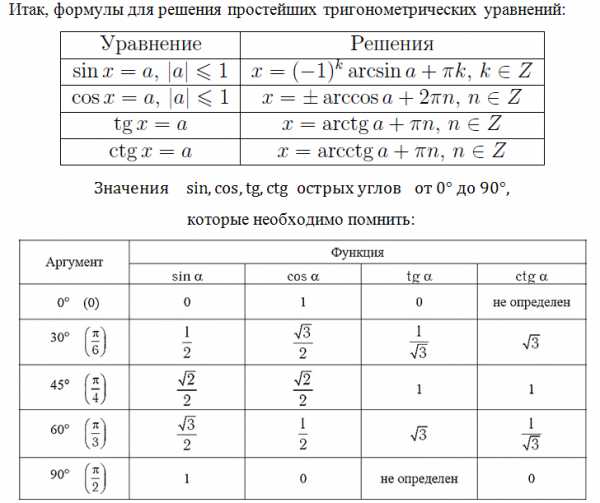
Знание этих значений необходимо, это «азбука», без которой  невозможно будет справиться с множеством заданий. Отлично, если память хорошая, вы легко выучили и запомнили эти значения. Что делать, если этого сделать не получается, в голове путаница, да  просто вы  именно при сдаче экзамена сбились. Обидно будет потерять бал из-за того, что вы запишите при расчётах неверное значение.

Алгоритм восстановления этих значений прост, он также приведён в теории,  полученной вами во втором письме после  подписки на рассылку. Если ещё не подписались, сделайте это! В будущем также рассмотрим, как эти значения можно определить по тригонометрической окружности. Не даром её называют «Золотое сердце тригонометрии».

Сразу поясню, во избежание путаницы, что в рассматриваемых ниже уравнениях даны определения арксинуса, арккосинуса, арктангенса с  использованием угла х для соответствующих  уравнений: cosx=a, sinx=a, tgx=a, где х может быть  и выражением. В примерах ниже у нас аргумент задан именно выражением.

Итак, рассмотрим следующие задачи:

Найдите корень уравнения:

В ответе запишите наибольший отрицательный корень.

Решением уравнения cos x = a  являются два корня:

Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.

Значит

Выразим x:

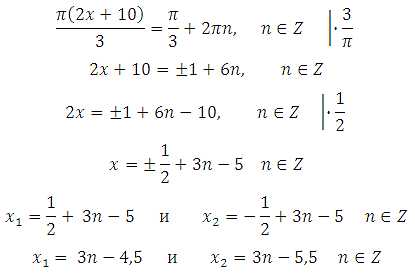
Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.

Общая рекомендация для всех подобных задач: для начала берите диапазон  n  от   – 2  до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x:  – 3 и 3,  – 4  и 4 и так далее.

Вычисляем:

При  n = – 2     х₁= 3 (– 2) – 4,5 = – 10,5      х₂= 3 (– 2) – 5,5 = – 11,5

При  n = – 1     х₁= 3 (– 1) – 4,5 = – 7,5        х₂= 3 (– 1) – 5,5 = – 8,5

При  n = 0        х₁= 3∙0 – 4,5 = – 4,5            х₂= 3∙0 – 5,5 = – 5,5

При  n = 1        х₁= 3∙1 – 4,5 = – 1,5            х₂= 3∙1 – 5,5 = – 2,5

При  n = 2        х₁= 3∙2 – 4,5 =  1,5              х₂= 3∙2 – 5,5 = 0,5

Получили, что наибольший отрицательный корень равен   –1,5

Ответ:  –1,5

Решите самостоятельно:

Посмотреть решение

Решите уравнение:

В ответе напишите наименьший положительный корень.

Решением уравнения sin x = a  являются два корня:

Либо (он объединяет оба указанные выше):

Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от   – 90^о до 90^о синус которого равен a.

Значит

Выразим x (умножим обе части уравнения на 4 и разделим на Пи):

Найдём наименьший положительный корень. Здесь сразу видно, что при подстановке отрицательных значений n мы получим отрицательные корни. Поэтому будем подставлять n =  0,1,2 …

При  n = 0     х = (– 1)⁰ + 4∙0 + 3 = 4

При  n = 1     х = (– 1)¹ + 4∙1 + 3 = 6

При  n = 2     х = (– 1)² + 4∙2 + 3 = 12

Проверим при   n = –1     х = (–1)^–1 + 4∙(–1) + 3 = –2

Значит наименьший положительный корень равен 4.

Ответ: 4

Решите самостоятельно:

Посмотреть решение

Решите уравнение:

В ответе напишите наименьший положительный корень.

Решением уравнения tg x = a  является корень:

Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90^о до 90^о,  тангенс которого равен a.

Значит

Выразим x (умножим обе части уравнения на 6 и разделим на  Пи):

Найдём наименьший положительный корень. Подставим значения  n = 1,2,3…    Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:

Таким образом, наименьший положительный корень равен 0,25.

Ответ: 0,25

Решите самостоятельно:

Посмотреть решение

Определение котангенса: Арккотангенсом числа a (a – любое число) называется угол x принадлежащий интервалу (0;П), котангенс которого равен a.

Здесь хочу добавить, что в уравнениях в правой части может стоять отрицательное число, то есть тригонометрическая функция от аргумента может иметь отрицательное значение. Если  в ходе решения вы не сможете определить угол, например, для

то данные формулы вам помогут:

 

Спасибо за внимание, учитесь с удовольствием!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Решение тригонометрических уравнений

В данной статье остановимся кратко на решении задач C1 из ЕГЭ по математике. Эти задания представляют собой уравнения, которые требуется, во-первых, решить (то есть найти их решения, причем все), во-вторых, осуществить отбор решений по тому или иному ограничению. В последние годы на ЕГЭ по математике в заданиях C1 школьникам предлагаются для решения тригонометрические уравнения, поэтому в данной статье разобраны только они. Примеры структурированы по методам решения уравнений, от самых элементарных, до достаточно сложных.

Прежде чем перейти к разбору конкретных тригонометрических уравнений, вспомним основные формулы тригонометрии. Приведем их здесь в справочном виде.

Основные тригонометрические формулы

Решение простейших тригонометрических уравнений

Решение простейших тригонометрических уравнений

Пример 1. Найдите корни уравнения

   

принадлежащие промежутку

Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем (на всякий случай, эта запись означает, что числа и принадлежат множеству целых чисел):

   

Другими словами, нам нужно подобрать такое число из промежутка косинус которого был бы равен Это число Используя это, получаем:

   

Вообще, значения тригонометрических функций от основных аргументов нужно знать. Их совсем чуть-чуть:

Таблица значений тригонометрических функций

Хотя на самом деле запоминать их вовсе не обязательно. Существует очень простой алгоритм, используя который, можно в уме легко вычислять значения тригонометрических функций всех основных аргументов. Просто у каждого он свой. Придумайте его и для себя. Просто посмотрите на эту таблицу. Числа в ней расположены не случайным образом, определенная закономерность есть, постарайтесь ее найти.

Итак, вернемся к нашему заданию. Из полученных серий выбираем только те ответы, которые принадлежат промежутку  Воспользуемся для этого методом двойных неравенств. Вы помните, что и — целые числа:

1)

2)

Задача для самостоятельного решения №1. Найдите корни уравнения принадлежащие промежутку

Показать ответОтвет:

Решение линейных тригонометрических уравнений

Пример 2. Найдите корни уравнения

   

принадлежащие промежутку

yourtutor.info