Разбор 2 задания ЕГЭ 2016 по информатике
Разбор 2 задания ЕГЭ 2016 года по информатике из демоверсии. Это задание на умение строить таблицы истинности и логические схемы (уметь строить модели объектов, систем и процессов в виде таблицы истинности для логического высказывания). Это задание базового уровня сложности. Примерное время выполнения задания 3 минуты.
Задание 2:
Логическая функция F задаётся выражением (¬z)/\x \/ x/\y. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
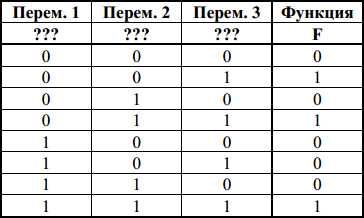
В ответе напишите буквы x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая 1-му столбцу; затем – буква, соответствующая 2-му столбцу; затем – буква, соответствующая 3-му столбцу). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и таблица истинности:
Тогда 1-му столбцу соответствует переменная y, а 2-му столбцу соответствует переменная x. В ответе нужно написать: yx.
Ответ: ________
Разбор 2 задания ЕГЭ 2016:
Для начала, преобразуем наше исходное выражение:
(¬z)/\x \/ x/\y = (¬z/\x) (\/ x/\y) = х /\ (¬z \/ y)
Конъюнкция истинна тогда и только тогда, когда истинны оба высказывания. Следовательно переменной х должен соответствовать тот столбец, в котором значение 1 стоит в тех же строках, что и в столбце F.
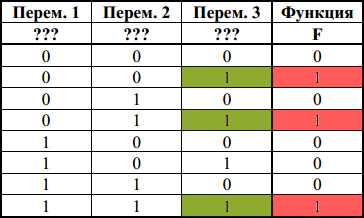
Таким образом переменной x соответствует 3 столбец.
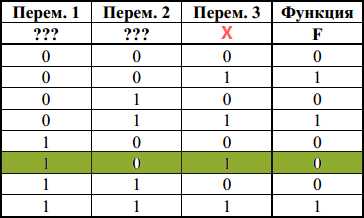
Дизъюнкция двух высказываний ложна тогда и только тогда, когда ложны оба высказывания.
Дизъюнкция ¬z \/ y в данной строке ложна. Следовательно у=0, z=1.
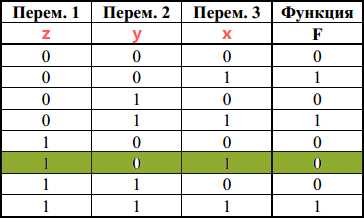
Ответ: zyx
infedu.ru
Разбор 2 задания и демоверсия егэ по информатике 2019
Задание 2. Таблицы истинности: Демоверсия егэ по информатике 2019; государственный выпускной экзамен 2019; тренировочные варианты ЕГЭ по информатике, тематические тестовые задания и задачи из тренажера по информатике 2019
*** КАНАЛ ЮТЬЮБ ***
ЕГЭ по информатике -> ЕГЭ 2019 -> ЕГЭ 2019
Разбор 2 задания. Демоверсия егэ по информатике 2019:
Миша заполнял таблицу истинности функции
(¬x ∧ ¬y) ∨ (y≡z) ∨ ¬w ,
но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Определите, какому столбцу таблицы соответствует каждая из переменных
📹 Видеоразбор демоверсии егэ 2019
✍ Решение:
1 способ:- Поскольку внешне операцией является дизъюнкция — логическое сложение — то результат 0 может быть только, когда все части выражения:
1 часть 2 часть 3 часть (¬x ∧ ¬y) ∨ (y≡z) ∨ ¬w = 0 (¬x ∧ ¬y) = 0 (y≡z) = 0 ¬w = 0
1. (¬x ∧ ¬y) = 0 x y F 0 0 1 0 1 0 1 0 0 1 1 0
2. (y≡z) = 0 y z F 0 0 1 0 1 0 1 0 0 1 1 1
3. ¬w = 0 w F 0 1 1 0
x y z w F 0 1 0 1 0 1 0 1 1 0 1 1 0 1 0
Так как w может принимать только значение 1, то в исходной таблице ей соответствует столбец № 4. Дозаполним столбец еще одной единицей:
x y z w F 0 1 0 1 0
x y z w F 0 1 0 1 0 1 0 1 1 0 11 0 1 0
2 способ смотрите на видео (см. выше).
Результат: zyxw
labs.org.ru
Информатика ЕГЭ 8 задание разбор
Разберем листинг программы:- Результатом программы является вывод значения s.
- В цикле s меняется, увеличиваясь на k, при начальном значении s = 3.
- Цикл зависит от k. Выполнение цикла завершится при k >= 25. Начальное значение k = 1.
- В цикле k постоянно увеличивается на 2 -> значит, можно найти количество итераций цикла.
- Количество итераций цикла равно:
n = 25 / 2 ~ 12
(т.к. k изначально равнялось 1, то в последнее, 12-е прохождение цикла, k = 25; условие цикла ложно)
s:=0; k:=1; while k
1 + 3 + 5 + 7 ... количество членов прогрессии - 12, т.к. 12 итераций цикла
s = ((2 * a1 + d * (n — 1)) / 2) * n
где a1 — первый член прогрессии,
d — разность,
n — количество членов прогрессии (в нашем случае — кол-во итераций цикла)
(2 * 1 + 2 * 11) / 2 * 12 = 144
144+3 = 147
labs.org.ru
Информатика ЕГЭ 23 задание разбор, метод отображения, побитовая маска
На уроке рассмотрено решение 23 задания ЕГЭ по информатике: дается подробное объяснение и разбор задания 2017 года
Объяснение задания 23 ЕГЭ по информатике
23-е задание характеризуется, как задание высокого уровня сложности, время выполнения – примерно 10 минут
Элементы алгебры логики: преобразования логических выражений
Для выполнения 23 задания ЕГЭ необходимо повторить следующие темы и понятия:
Разные типы заданий 23 и их решение от простого к сложному:
1. Одно уравнение с непересекающимися операндами внешней операции и одним вариантом решения:
2. Одно уравнение с непересекающимися операндами внешней операции и несколькими вариантами решения
3. Одно уравнение с пересекающимися операндами внешней операции
4 + 3 + 3 = 10
4. Несколько уравнений: метод отображения решений уравнения
Сколько существует различных наборов значений логических переменных?
Метод отображения можно использовать:
- Если структура всех уравнения аналогична, и меняются лишь неизвестные.
- Если какие-либо операнды внешней операции первого уравнения повторяются во втором, второго — в третьем, и т.д.
Пример решения
5. Несколько уравнений: использование битовых масок
Сколько существует различных наборов значений логических переменных?
Побитовая маска (битовая маска) — метод, который можно использовать:
- Если при рассмотрении одного из уравнений в нем не обнаружены пересекающиеся переменные внешней операции (случай когда одна из переменных первого операнда встречается во втором операнде уже не подходит).
- Если структура всех уравнения аналогична, и меняются лишь неизвестные.
- Если какие-либо операнды внешней операции первого уравнения повторяются во втором, второго — в третьем, и т.д.

Пример решения
Решение 23 заданий ЕГЭ по информатике
Разбор 23 задания ЕГЭ по информатике 2017 года ФИПИ вариант 1 (Крылов С.С., Чуркина Т.Е.):Сколько существует различных наборов значений логических переменных x1, x2, … x6, y1, y2, … y6, которые удовлетворяют всем перечисленным ниже условиям?
(¬(x1 ∨ y1)) ≡ (x2 ∨ y2)
(¬(x2 ∨ y2)) ≡ (x3 ∨ y3)
…
(¬(x5 ∨ y5)) ≡ (x6 ∨ y6)
✍ Решение с использованием метода побитовая маска:
- Поскольку в скобках одинаковые действия, и переменные повторяются, то введем обозначения:
¬a ≡ b ¬b ≡ c ¬c ≡ d ¬d ≡ e ¬e ≡ f
a ≠ b b ≠ c c ≠ d d ≠ e e ≠ f
| x1 | x2 | F |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
цеп.1 цеп.2 a 0 1 b 1 0 c 0 1 d 1 0 e 0 1 f 1 0
x1 ∨ y1 = 1 тогда, когда: либо 0 ∨ 1, либо 1 ∨ 0, либо 1 ∨ 1 x1 ∨ y1 = 0 тогда и только тогда, когда 0 ∨ 0
27 * 2 = 54
Результат: 54
Подробное объяснение данного задания смотрите на видео:
Разбор 23 задания ЕГЭ по информатике 2017 года ФИПИ вариант 3 (Крылов С.С., Чуркина Т.Е.):Сколько существует различных наборов значений логических переменных x1, x2, … x9, y1, y2, … y9, которые удовлетворяют всем перечисленным ниже условиям?
(¬(x1 ∧ y1)) ≡ (x2 ∧ y2)
(¬(x2 ∧ y2)) ≡ (x3 ∧ y3)
…
(¬(x8 ∧ y8)) ≡ (x9 ∧ y9)
В качестве ответа Вам нужно указать количество таких наборов.
✍ Решение (использование метода побитовая маска):
- Поскольку в скобках одинаковые действия, и переменные повторяются, то введем обозначения:
¬a ≡ b ¬b ≡ c ¬c ≡ d ¬d ≡ e ¬e ≡ f ¬f ≡ g ¬g ≡ h ¬h ≡ i
a ≠ b b ≠ c c ≠ d d ≠ e e ≠ f f ≠ g g ≠ h h ≠ i
| x1 | x2 | F |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
например a ≠ b = 0, если: a=0 и b=0 или a=1 и b=1
Это означает, что для одного условия не может быть такого случая, что a=0 и b=0 или a=1 и b=1.
цеп.1 цеп.2 цеп. цеп. a 0 1 0 1 b 1 0 0 1 не может быть! c 0 1 ... ... d 1 0 e 0 1 f 1 0 g 0 1 h 1 0 i 0 1
x1 ∧ y1 = 0 тогда, когда: либо 0 ∧ 1, либо 1 ∧ 0, либо 0 ∧ 0 x1 ∧ y1 = 1 тогда и только тогда, когда 1 ∧ 1
243 + 81 = 324
Результат: 324
Предлагаем посмотреть видео с решением данного 23 задания:
Разбор 23 задания ЕГЭ по информатике 2017 года ФИПИ вариант 5 (Крылов С.С., Чуркина Т.Е.):Сколько существует различных наборов значений логических переменных x1, x2, … x8, y1, y2, … y8, которые удовлетворяют всем перечисленным ниже условиям?
¬(((x1 ∧ y1) ≡ (x3 ∧ y3)) → (x2 ∧ y2))
¬(((x2 ∧ y2) ≡ (x4 ∧ y4)) → ¬(x3 ∧ y3))
¬(((x3 ∧ y3) ≡ (x5 ∧ y5)) → (x4 ∧ y4))
¬(((x4 ∧ y4) ≡ (x6 ∧ y6)) → ¬(x5 ∧ y5))
¬(((x5 ∧ y5) ≡ (x7 ∧ y7)) → (x6 ∧ y6))
¬(((x6 ∧ y6) ≡ (x8 ∧ y8)) → ¬(x7 ∧ y7))
В качестве ответа Вам нужно указать количество таких наборов.
✍ Решение с использованием метода побитовая маска:
- Поскольку в скобках одинаковые действия, и скобки повторяются в разных уравнениях, то введем обозначения. Обозначим латинскими буквами в алфавитном порядке скобки с переменными согласно их номерам:
1-a 2-b 3-c 4-d 5-e 6-f 7-g 8-h
¬((a ≡ c) → b) ¬((b ≡ d) → ¬c) ¬((c ≡ e) → d) ¬((d ≡ f) → ¬e) ¬((e ≡ g) → f) ¬((f ≡ h) → ¬g)
- Избавимся от импликации:
- По закону Де Моргана избавимся от отрицания над общей внешней скобкой:
было: ¬((a ≡ c) → b) стало: ¬(¬(a ≡ c) ∨ b)
было: ¬(¬(a ≡ c) ∨ b) стало: (a ≡ c) ∧ ¬b
(a ≡ c) ∧ ¬b (b ≡ d) ∧ c (c ≡ e) ∧ ¬d (d ≡ f) ∧ e (e ≡ g) ∧ ¬f (f ≡ h) ∧ g
например: (a ≡ c) ∧ ¬b возвратит истину, если: (a ≡ c) = 1 и ¬b = 1
Это означает, что все операнды, стоящие после знака конъюнкции, должны быть истинны.
цеп.1 a ? b 0 c 1 d 0 e 1 f 0 g 1 h ?
цеп.1 a 1 b 0 c 1 d 0 e 1 f 0 g 1 h 0
x1 ∧ y1 = 0 тогда, когда: либо 0 ∧ 1, либо 1 ∧ 0, либо 0 ∧ 0 x1 ∧ y1 = 1 тогда и только тогда, когда 1 ∧ 1
34 * 14 = 81 набор значений
Результат: 81
Для закрепления материала рекомендуем посмотреть видео с разбором данного 23 задания:
Разбор 23 задания ЕГЭ по информатике демоверсия 2018 года ФИПИ:
Сколько существует различных наборов значений логических переменных x1, x2, … x7, y1, y2, … y7, которые удовлетворяют всем перечисленным ниже условиям?
(¬x1 ∨ y1) → (¬x2 ∧ y2) = 1
(¬x2 ∨ y2) → (¬x3 ∧ y3) = 1
…
(¬x6 ∨ y6) → (¬x7 ∧ y7) = 1
В качестве ответа Вам нужно указать количество таких наборов.
✍ Решение, используется метод отображения:
- Внешняя операция в отдельно взятом уравнении — это импликация, результат которой должна быть истина. Импликация истинна если:
0 -> 0 0 -> 1 1 -> 1
т.е. ложна только, когда 1 -> 0
(¬x1 ∨ y1) = 0, то для скобки (¬x2 ∧ y2) возможны варианты 0 или 1.(¬x1 ∨ y1) = 1, то для скобки (¬x2 ∧ y2) возможен один вариант — 1.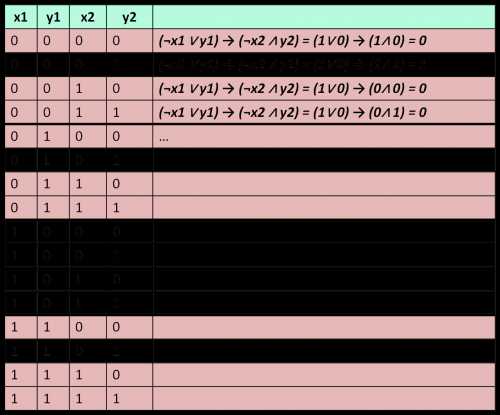
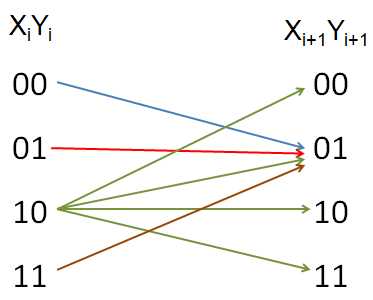
1 + 19 + 1 + 1 = 22
Результат: 22
Видеоразбор демоверсии 2018 23 задания смотрите здесь:
Решение 23 задания ЕГЭ по информатике 2018 (диагностический вариант, С.С. Крылов, Д.М. Ушаков, Тренажер ЕГЭ 2018 года):Сколько различных решений имеет уравнение:
(a → b) ∨ (c → ¬d) ∨ ¬(e ∨ a ∨ c) = 1
где a, b, c, d, e — логические переменные?
В качестве ответа указать количество таких наборов.
✍ Решение:
- Внешняя логическая операция — ∨ — дизъюнкция. Таблица истинности:
0 ∨ 0 = 0 0 ∨ 1 = 1 1 ∨ 0 = 1 1 ∨ 1 = 1
количество строк в ТаблИстин = 25 = 32
(a → b) ∨ (c → ¬d) ∨ ¬(e ∨ a ∨ c) = 0 0 0 0
1. (a → b) = 0, импликация ложна в одном случае (1 → 0) = 0 т.е. имеем a = 1, b = 0
2. (c → ¬d) = 0, импликация ложна в одном случае (1 → 0) = 0 т.е. имеем c = 1, d = 1
3. ¬(e ∨ a ∨ c) = 0
¬e ∧ ¬a ∧ ¬c = 0 Конъюнкция равна 0, когда хоть один операнд = 0.
¬0 ∧ ¬1 ∧ ¬1 = 0 ¬1 ∧ ¬1 ∧ ¬1 = 0
1. a = 1, b = 0, c = 1, d = 1, e = 0 2. a = 1, b = 0, c = 1, d = 1, e = 1
32 - 2 = 30
Результат: 30
Разбор 23 задания демоверсии егэ по информатике 2019:
Сколько существует различных наборов значений логических переменных x1, x2, … x7, y1, y2, … y7, которые удовлетворяют всем перечисленным ниже условиям?
(y1 → (y2 ∧ x1)) ∧ (x1 → x2) = 1 (y2 → (y3 ∧ x2)) ∧ (x2 → x3) = 1 … (y6 → (y7 ∧ x6)) ∧ (x6 → x7) = 1 y7 → x7 = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, … x7, y1, y2, … y7, при которых выполнена данная система равенств.
В качестве ответа Вам нужно указать количество таких наборов.
✍ Решение:
- Поскольку все равенства однотипны (кроме последнего), отличаются только сдвигом номеров переменных на единицу, то для решения будем использовать метод отображения: когда, найдя результат для первого равенства, необходимо применить тот же принцип с последующими равенствами, учитывая полученные результаты для каждого из них.
- Рассмотрим первое равенство. В нем внешняя операция — это конъюнкция, результат которой должна быть истина. Конъюнкция истинна если:
1 -> 1
т.е.:
(y1 → (y2 ∧ x1)) ∧ (x1 → x2) = 1
11
(y1 → (y2 ∧ x1)) ∧ (x1 → x2) = 0
1 -> 0 = 0 т.е. случаи: y1=1 → (y2=0 ∧ x1=1) y1=1 → (y2=1 ∧ x1=0) y1=1 → (y2=0 ∧ x1=0)
(x1=1 → x2=0)
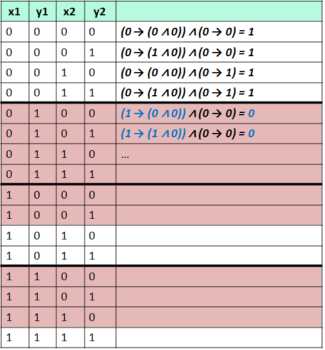
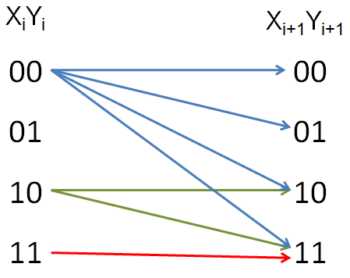
y7=1 → x7=0 = 0
1 + 7 + 28 = 36
Результат: 36
Видео решения 23 задания демоверсии егэ 2019:
labs.org.ru
