Задание №13 ЕГЭ по математике базовый уровень
Наглядная стереометрия
В 13 задании ЕГЭ базового уровня мы будем иметь дело с задачами по стереометрии, но не абстрактными, а наглядными примерами. Это могут быть задачи на уровень жидкости в сосудах, которую я разобрал ниже, или же задачи на модификации фигуры — например, у которой отрезали вершины. Нужно быть готовым к решению простых задач по стереометрии — они обычно сводятся сразу к задачам на плоскости, необходимо только правильно посмотреть на чертеж.
Разбор типовых вариантов заданий №13 ЕГЭ по математике базового уровня
Первый вариант задания (демонстрационный вариант 2018)
Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у данного? Ответ дайте в сантиметрах.
Алгоритм выполнения:
- Записать формулу объема цилиндра.
- Подставить значения для цилиндра с жидкостью в первом и во втором случае.
- Объем жидкости не изменялся, следовательно, можно приравнять объемы.
- Полученное уравнение решить относительно второй высоты h2.
- Подставить данные и вычислить искомую величину.
Решение:
Запишем формулу объема цилиндра.
Если вы забыли формулу объема цилиндра, то напомню, как ее можно легко вывести. Объем простых фигур, таких как куб и цилиндр, можно вычислить умножив площадь основания на высоту. Площадь основания в случае с цилиндром равна площади окружности, которую, вы, наверняка помните: π • r2.
Следовательно, объем цилиндра равен π • r2 • h
Подставим значения для цилиндра с жидкостью в первом и во втором случае.
V1 = π r12 h1
V2 = π r22 h2
Объем жидкости не изменялся, следовательно, можно приравнять объемы.
V1 = V2
Левые части равны, значит можно приравнять и правые.
π r12 h1 = π r22 h2
Полученное уравнение решим относительно второй высоты h2.
h2 – неизвестный множитель. Чтобы найти неизвестный множитель нужно произведение разделить на известный множитель.
h2 =( π r12 h1)/ π r22
По условию площадь основания стала в 4 раза больше, то есть r2 = 4 r1 .
Подставим r2 = 4 r1 в выражение для h1.
Получим: h2 =( π r12 h1)/ π (4 r1) 2
Полученную дробь сократим на π, получим h2 =( r12 h1)/ 16 r12
Полученную дробь сократим на r1, получим h2 = h1/ 16.
Подставим известные данные: h2 = 80/ 16 = 5 см.
Ответ: 5.
Второй вариант задания
Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в четыре с половиной раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
Алгоритм выполнения:
- Записать формулу, для вычисления объема правильной четырехугольной призмы.
- Записать в общем виде формулу для нахождения объема в первом и втором случае.
- Найти отношение объемов.
- Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
- Сократить получившуюся дробь.
Решение:
Запишем формулу, для вычисления объема правильной четырехугольной призмы.
V = a · b · c
Запишем в общем виде формулу для нахождения объема в первом и втором случае.
V1 = a1 · b1 · c1
V2 = a2 · b2 · c2
Найдем отношение объемов.
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2)
Преобразуем полученное выражение с учетом соотношения измерений первой и второй призмы.
По условию c1 = 4,5 c2 (первая коробка в четыре с половиной раза выше второй),
b2 = 3 b1 (вторая коробка втрое шире первой).
Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a2 = 3 a1
Подставим эти выражения в формулу отношения объемов:
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2) = (a1 · b1 · 4,5c2)/ ( 3a1 · 3b1 · c2) = (a1 · b1 · 4,5c2)/ ( 9a1 · b1 · c2)
Сократим получившуюся дробь на a1 · b1 · c2. Получим:
V1 / V2 = (a1 · b1 · 4,5c2)/ ( 9a1 · b1 · c2) = 4,5/9 = ½.
Объем первой коробочки в 2 раза меньше объема второй.
Ответ: 2.
Третий вариант задания
Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в полтора раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
Алгоритм выполнения:
- Записать формулу, для вычисления объема правильной четырехугольной призмы.
- Записать в общем виде формулу для нахождения объема в первом и втором случае.
- Найти отношение объемов.
- Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
- Сократить получившуюся дробь.
Решение:
Запишем формулу, для вычисления объема правильной четырехугольной призмы.
V = a · b · c
Запишем в общем виде формулу для нахождения объема в первом и втором случае.
V1 = a1 · b1 · c1
V2 = a2 · b2 · c2
Найдем отношение объемов.
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2)
Преобразуем полученное выражение с учетом соотношения измерений первой и второй призмы.
По условию c1 = 1,5 c2 (первая коробка в полтора раза выше второй), b2 = 3 b1 (вторая коробка втрое шире первой).
Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a2 = 3 a1
Подставим эти выражения в формулу отношения объемов:
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2) = (a1 · b1 · 1,5c2)/ ( 3a1 · 3b1 · c2) = (a1 · b1 · 1,5c2)/ ( 9a1 · b1 · c2)
Сократим получившуюся дробь на a1 · b1 · c2. Получим:
V1 / V2 = (a1 · b1 · 1,5c2)/ ( 9a1 · b1 · c2) = 1,5/9 = 15/(10 · 9) = 3/(2 · 9) = 1/ (2 · 3) = 1/6.
Объем первой коробочки в 6 раза меньше объема второй.
Ответ: 6.
Вариант тринадцатого задания 2017
От деревянного кубика отпилили все его вершины (см. рис.). Сколько граней у получившегося многогранника (невидимые ребра на рисунке не изображены)?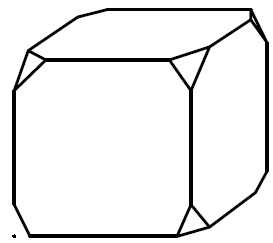
Сначала вспомним сколько всего граней и вершин у куба: шесть граней и восемь вершин. Теперь на месте каждой вершины образуется новая грань после отпила, значит у модифицированного в задании куба шесть родных граней и восемь новых (после отпила). Итого получаем: 6 + 8 = 14 граней.
Ответ: 14.
Если бы нас спросили, а сколько вершин у нового «куба». Очевидно, если вместо одной становится три, а их всего восемь, то получаем: 8 • 3 = 24
spadilo.ru
Задание №16 ЕГЭ по математике базового уровня
Стереометрия
В задании №16 базового уровня ЕГЭ по математике нам предстоит столкнуться со стереометрией. Как таковой «стереометрии» мы не встретим, обычно условие задания содержит объемную фигуру, в которой нам необходимо найти какое-либо расстояние. В данном задании необходимо правильно применить пространственное мышление и выбрать нужное сечение, остальные расчеты происходят в плоскости, причем по несложным формулам (теорема Пифагора и т.д.). Какой-либо конкретной теории я пока приводить не буду, а рассмотрю типовые варианты, на которых мы и рассмотрим алгоритмы решения задач данного типа.
Разбор типовых вариантов заданий №16 ЕГЭ по математике базового уровня
Первый вариант задания (демонстрационный вариант 2018)
Радиус основания цилиндра равен 13, а его образующая 18. Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12. Найдите площадь этого сечения.
Алгоритм выполнения:
- Определить тип фигуры, образующей сечение.
- Записать формулу для нахождения площади фигуры, образующей сечение.
- Вычислить недостающие данные.
- Вычислить искомую площадь сечения.
Решение:
Из рисунка видно, что сечение является прямоугольником, одна из сторон которого образующая цилиндра.
Площадь прямоугольника равна произведению длины на ширину.
Длина прямоугольника – 18, из условия. Осталось вычислить ширину. Сделаем дополнительный чертеж цилиндра сверху:
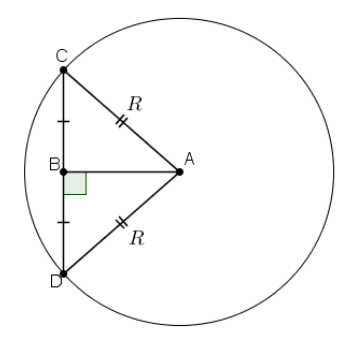
Ширина прямоугольника – CD.
По условию «Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12». Расстояние от точки до прямой – это длина перпендикуляра, проведенного из этой точки на прямую. То есть на чертеже АВ = 12.
СD = СВ + ВD. СВ = ВD
Рассмотрим треугольник ВСА. Треугольник ВСА – прямоугольный.
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
В данном случае СА2 = СВ2 + АВ2
СВ2 — неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
СВ2 = СА2 — АВ2
СВ = √(СА2 — АВ2)
СВ = √(132 — 122) = √(169 — 144) = √25 = 5
Для решения задачи необходимо знать СD = СВ + ВD = 5 + 5 = 10
Вычислим искомую площадь сечения.
10 · 18 = 180
Ответ: 180.
Второй вариант задания
Стороны основания правильной треугольной пирамиды равны 24, а боковые рёбра равны 37. Найдите площадь боковой поверхности этой пирамиды.
Алгоритм выполнения:
- Проанализировать какие данные необходимо вычислить для ответа на вопрос задачи.
- Найти площади треугольников.
- Найти площадь боковой поверхности пирамиды.
Решение:
Проанализируем, какие данные необходимо вычислить для ответа на вопрос задачи.
В основании правильной треугольной пирамиды лежит равносторонний треугольник. Боковые ребра пирамиды, равные 37, образуют три равнобедренных треугольника, которые составляют ее боковую поверхность.
Найдем площади треугольников.
Так как треугольник равнобедренный, то высота BH делит сторону AC пополам, то есть, AH=AC:2=24:2=12.
Рассмотрим треугольник АВН.
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
В данном случае АВ2 = ВН2 + АН2
ВН2 — неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
ВН2 = АВ2 — АН2
Следовательно, высота BH, равна:
Площадь треугольника равна половине произведения основания на высоту.
Тогда, площадь треугольника может быть вычислена как
Найдем площадь боковой поверхности пирамиды.
Боковая поверхность пирамиды состоит из трех треугольников. Найдем ее площадь:
Ответ: 1260.
Третий вариант задания
Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
Алгоритм выполнения:
- Проанализировать какие данные необходимо вычислить для ответа на вопрос задачи.
- Найти площади треугольников.
- Найти площадь боковой поверхности пирамиды.
Решение:
Проанализируем, какие данные необходимо вычислить для ответа на вопрос задачи.
В основании правильной треугольной пирамиды лежит равносторонний треугольник. Боковые ребра пирамиды, равные 17, образуют три равнобедренных треугольника, которые составляют ее боковую поверхность.
Найдем площади треугольников.
Так как треугольник равнобедренный, то высота BH делит сторону AC пополам, то есть, AH=AC:2=16:2=8.
Рассмотрим треугольник АВН.
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
В данном случае АВ2 = ВН2 + АН2
ВН2 — неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
ВН2 = АВ2 — АН2
Следовательно, высота BH, равна:
Площадь треугольника равна половине произведения основания на высоту.
Тогда, площадь треугольника может быть вычислена как
Найдем площадь боковой поверхности пирамиды.
Боковая поверхность пирамиды состоит из трех треугольников. Найдем ее площадь:
Ответ: 360.
Вариант шестнадцатого задания 2017
Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √17.
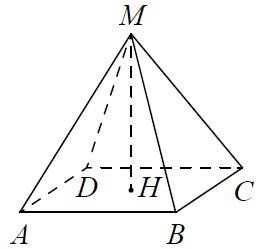
Вспомним формулу площади правильной пирамиды — одна треть от произведения площади основания и высоты.
Площадь основания рассчитываем по формуле площади квадрата — квадрат стороны:
После этого перейдем к нахождению высоты. Для этого нам необходимо рассмотреть прямоугольный (так как основание перпендикулярно высоте) треугольник AMH. AH — половина диагонали квадрата, которая равна √2 его стороны, то есть в нашем случае диагональ равна 4√2, ну а половина — AH = 2√2. Зная гипотенузу и один из катетов, найдем высоту:
После этого легко вычисляем объем:
V = 1/3 • 16 •3 = 16
Ответ: 16
spadilo.ru
Задание №4 ЕГЭ по математике базовый уровень
Преобразование выражений
В задании №4 ЕГЭ по математике базового уровня нам необходимо продемонстрировать умения работы с выражениями. В данных задачах необходимо выразить из заданного выражения нужную переменную и вычислить её, подставив значения.
Разбор типовых вариантов заданий №4 ЕГЭ по математике базового уровня
Первый вариант задания (демонстрационный вариант 2018)
Найдите v0 из равенства v = v0 + at, если v = 20, t = 2, a = 7.
Алгоритм выполнения:
- Подставить данные значения в выражение.
- Решить уравнение относительно неизвестной.
Решение:
Подставим все значения в данное выражение, получим:
20 = v0 + 7 · 2
Преобразуем:
20 = v0 + 14.
Найдем неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
v0 = 20 – 14
v0 = 6
Ответ: v0 = 6
Второй вариант задания (демонстрационный вариант 2018)
Скорость камня (в м/с), падающего с высоты h (в м), в момент удара о землю можно найти по формуле . Найдите скорость (в м/с), с которой ударится о землю камень, падающий с высоты 0,9 м. Считайте, что ускорение свободного падения g равно 9,8 м/с2.
Алгоритм выполнения:
- Подставить все значения в данную формулу.
- Произвести вычисления.
Решение:
По условию задания дана высота h=0,9 м и ускорение свободного падения g=9,8 м/с2. Подставим эти значения в формулу вычисления скорости v, получим:
Делаем умножение 1,8 на 9,8, имеем:
Примечание: При умножении в столбик десятичных дробей запятая записывается строго под запятой. В полученном результате справа отсчитывают столько знаков, сколько поле запятой в ОБЕИХ дробях ВМЕСТЕ.
и извлекаем из числа 17,64 квадратный корень:
м/с.
Ответ: 4,2 м/с.
Третий вариант задания
Энергия заряженного конденсатора W (в Дж) вычисляется по формуле , где C — ёмкость конденсатора (в Ф), a q — заряд на одной обкладке конденсатора (в Кл). Найдите энергию конденсатора (в Дж) ёмкостью Ф, если заряд на его обкладке равен 0,019 Кл.
Алгоритм выполнения задания:
- Подставить все известные значения в данную формулу.
- Провести вычисления.
Решение:
Подставим в формулу энергии конденсатора значения q=0,019 Кл и C = Ф, получим:
Пояснения:
Если степень стоит за скобкой, а внутри скобки произведение, то степень относится к каждому из множителей. То есть (19 · 10-3)2 = 192 · 10-3·2.
Чтобы найти вторую степень числа нужно умножить число само на себя.
192 = 19 · 19 = 361
Умножить на число в отрицательной степени, значит разделить на это число, но только в положительной степени.
361 · 10-3 = 361/1000 = 0,361
Ответ: 0,361.
Четвертый вариант задания
Энергия заряженного конденсатора W (в Дж) вычисляется по формуле , где C — ёмкость конденсатора (в Ф), a q — заряд на одной обкладке конденсатора (в Кл). Найдите энергию конденсатора (в Дж) ёмкостью Ф, если заряд на его обкладке равен 0,07 Кл.
Алгоритм выполнения:
- Подставить все известные значения в данную формулу.
- Провести вычисления.
Решение:
Подставим в формулу энергии конденсатора значения q=0,07 Кл и C = Ф, получим:
.
Пояснения:
Если степень стоит за скобкой, а внутри скобки произведение, то степень относится к каждому из множителей. То есть (7 · 10-2)2 = 72 · 10-2·2.
Чтобы найти вторую степень числа нужно умножить число само на себя.
72 = 7 · 7 = 49
Умножить на число в отрицательной степени, значит разделить на это число, но только в положительной степени.
49 · 10-1 = 49/10 = 4,9
Ответ: 4,9.
Пятый вариант задания (демонстрационный вариант 2018)
Найдите m из равенства F = ma, если F = 84 и a = 12.
Алгоритм выполнения:
- Подставить данные значения в выражение.
- Решить уравнение относительно неизвестной.
Решение:
Подставим все значения в данное выражение, получим:
84 = m ·12
2. Найдем неизвестный множитель. Чтобы найти неизвестный множитель нужно разделить произведение на известный множитель.
m = 84 : 12
m = 7
Ответ: 7 кг.
Вариант четвертого задания из ЕГЭ 2017 (1)
Найдите m из равенства F = ma , если F = 84 и a =12.
В начале выразим из формулы m, так как это множитель, то он равен произведению, деленному на второй множитель.
m=F/a
Теперь можем подставить числа из условия:
m=84/12=7
Ответ: 7
Вариант четвертого задания из ЕГЭ 2017 (2)
Найдите v0 из равенства v = v0 + at , если v = 20 , t = 2 и a = 7 .
Аналогично выразим v0, перенеся at в левую часть:
v — at = v0
Подставим значения:
20 — 7 • 2 = 6 = v0
Ответ: 6
Вариант четвертого задания из ЕГЭ 2017 (3)
Найдите S из равенства S = v0t + at2/2 , если v0 = 6 , t = 2 , a = −2.
В данном случае нам необходимо просто подставить числа и выполнить вычисления:
S = 6 • 2 + (-2) • 22/2 = 12 -4 = 8
Ответ: 8
spadilo.ru
