Задание 14 из ЕГЭ по математике 2016
В задании 14 ЕГЭ по математике выпускникам, сдающим экзамен, необходимо решить задачу по стереометрии. Именно поэтому научиться решать такие задачи должен каждый школьник, если он хочет получить положительную оценку на экзамене. В данной статье представлен разбор двух типов заданий 14 из ЕГЭ по математике 2016 года (профильный уровень) от репетитора по математике в Москве.
| В правильной четырехугольной пирамиде SABCD сторона основания АВ равна 16, а высота равна 4. На ребрах АВ, CD и AS отмечены точки M, N и К соответственно, причем AM = DN = 4 и АК = 3.
а) Докажите, что плоскости MNK и SBC параллельны. б) Найдите расстояние от точки К до плоскости SBC. |
Доступен видеоразбор данного задания:
Рисунок к заданию будет выглядеть следующим образом:
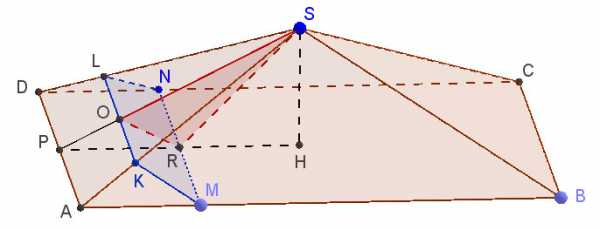
а) Поскольку прямая MN параллельна прямой DA, которая принадлежит плоскости DAS, то прямая MN параллельна плоскости DAS. Следовательно, линия пересечения плоскости DAS и сечения KMN будет параллельна прямой MN. Пусть это линия KL. Тогда KMNL — искомое сечение.
Докажем, что плоскость сечения параллельна плоскости SBC. Прямая BC параллельна прямой MN, так как четырехугольник MNCB является прямоугольником (докажите сами). Теперь докажем подобие треугольников AKM и ASB. AC — диагональ квадрата. По теореме Пифагора для треугольника ADC находим:
AH — половина диагонали квадрата, поэтому . Тогда из теоремы Пифагора для прямоугольного треугольника находим:
Тогда имеют место соотношения:
Получается, что стороны, образующие угол A в треугольниках AKM и ASB, пропорциональны. Следовательно, треугольники подобны. Из этого следует равенство углов, в частности, равенство углов AMK и ABS. Так как эти углы соответственные при прямых KM, SB и секущей MB, то KM параллельна SB.
Итак, мы получили, что две пересекающиеся прямые одной плоскости (KM и NM) соответственно параллельны двум пересекающимся прямым другой плоскости (SB и BC). Следовательно, плоскости MNK и SBC параллельны.
б) Поскольку плоскости параллельны, расстояние от точки K до плоскости SBC равно расстоянию от точки S до плоскости KMN. Ищем это расстояние. Из точки S опускаем перпендикуляр SP к прямой
Действительно, KL перпендикулярна плоскости OSR, так как она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости (OR и OS). Перпендикулярность OR и KL следует из теоремы о трёх перпендикулярах. Следовательно, KL перпендикулярна высоте треугольника ORS, проведенной к стороне OR. То есть эта высота перпендикулярна двум пересекающимся прямым, лежащим в плоскости KMN, а значит перпендикулярна этой плоскости.
Ищем стороны треугольника SOR. Сторону SR ищем по теореме Пифагора из прямоугольного треугольника RSH: . Длину SP находим по теореме Пифагора из прямоугольного треугольника PSH: . Треугольники SOK и SPA подобны (докажите это сами) с коэффициентом подобия . Тогда и
yourtutor.info
Задание №14 ЕГЭ по математике базовый уровень
Графики функций
В задании №13 ЕГЭ по математике базового уровня придется продемонстрировать умения и знания одного из понятий поведения функции: производных в точке или скоростей возрастания или убывания. Теория к этому заданию будет добавлена чуть позже, но это не помешает нам подробно разобрать несколько типовых вариантов.
Разбор типовых вариантов заданий №14 ЕГЭ по математике базового уровня
Первый вариант задания (демонстрационный вариант 2018)
На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя; на вертикальной оси – температура двигателя в градусах Цельсия.
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
ИНТЕРВАЛЫ ВРЕМЕНИ: А) 0 – 1 мин. Б) 1 – 3 мин. В) 3 – 6 мин. Г) 8 – 10 мин.
| ХАРАКТЕРИСТИКИ:
|
В таблице под каждой буквой укажите соответствующий номер.
Алгоритм выполнения:
- Выбрать интервал времени, на котором температура падала.
- Приложить линейку к 30°С и определить интервал времени, на котором температура была ниже 30°С.
- С помощью карандаша и линейки найдем на каком интервале времени температура находилась в пределах от 40°С до 80°С.
- Методом исключения выберем недостающий вариант ответа.
Решение:
Выберем интервал времени, на котором температура падала. Этот участок видно не вооруженным глазом, он начинается в 8 мин от момента запуска двигателя.
Г — 2
Приложим линейку к 30°С и определить интервал времени, на котором температура была ниже 30°С.
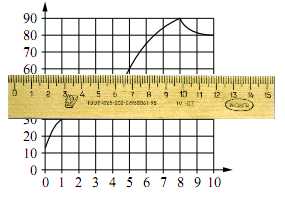
Ниже линейки окажется участок, соответствующий интервалу времени 0 – 1 мин.
А — 4
С помощью карандаша и линейки найдем на каком интервале времени температура находилась в пределах от 40°С до 80°С.
Опустим из точек, соответствующих 40°С и 80°С перпендикуляры на график, а из полученных точек опустим перпендикуляры на ось времени.

Видим, что этому температурному интервалу соответствует интервал времени 3 – 6,5 мин. То есть из приведенных в условии 3 – 6 мин.
В — 3
Методом исключения выберем недостающий вариант ответа.
Б – 1
Ответ:
А – 4
Б – 1
В – 3
Г — 2
Второй вариант задания
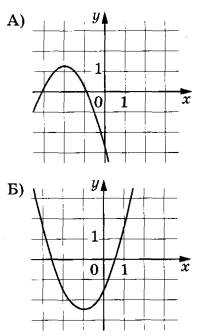
Установите соответствие между графиками функций и графиками их производных.
ГРАФИКИ ФУНКЦИЙ
| ГРАФИКИ ПРОИЗВОДНЫХ
|
Алгоритм выполнения для каждой из функций:
- Определить промежутки возрастания и убывания функций.
- Определить точки максимума и точки минимума функций.
- Сделать выводы, поставить в соответствие предложенные графики.
Решение:
Проанализируем график функции А. Если Функция возрастает, то производная положительна и наоборот. Производная функции равна нулю в точках экстремума.
Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.
Сначала функция А возрастает, т.е. производная положительна. Этому соответствуют графики производных 2 и 3. В точке максимума функции x=-2, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 3.
А — 3
Проанализируем график функции Б.
Сначала функция Б убывает, т.е. производная отрицательна. Этому соответствуют графики производных 1 и 4. Точка максимума функции x=-2, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 4.
Б — 4
Проанализируем график функции В.
Сначала функция В возрастает, т.е. производная положительна. Этому соответствуют графики производных 2 и 3. Точка максимума функции x = 1, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 2.
В — 2
Методом исключения можем определить, что графику функции Г соответствует график производной под номером 1.
Г – 1
А – 3
Б – 4
В – 2
Г — 1
Ответ: 3421.
Третий вариант задания
Установите соответствие между графиками функций и графиками их производных.
ГРАФИКИ ФУНКЦИЙ
| ГРАФИКИ ПРОИЗВОДНЫХ
|
Алгоритм выполнения для каждой из функций:
- Определить промежутки возрастания и убывания функций.
- Определить точки максимума и точки минимума функций.
- Сделать выводы, поставить в соответствие предложенные графики.
Решение:
Проанализируем график функции А.
Если функция возрастает, то производная положительна и наоборот. Производная функции равна нулю в точках экстремума.
Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.
Сначала функция А возрастает, т.е. производная положительна. Этому соответствуют графики производных 3 и 4. В точке максимума функции x=0, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 4.
А — 4
Проанализируем график функции Б.
Сначала функция Б убывает, т.е. производная отрицательна. Этому соответствуют графики производных 1 и 2. Точка минимума функции x=-1, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 2.
Б — 2
Проанализируем график функции В.
Сначала функция В убывает, т.е. производная отрицательна. Этому соответствуют графики производных 1 и 2. Точка минимума функции x = 0, то есть в данной точке производная должна быть равна нулю. Этому условию соответствует график под номером 1.
В — 1
Методом исключения можем определить, что графику функции Г соответствует график производной под номером 3.
Г – 3
А – 4
Б – 2
В – 1
Г – 3
Ответ: 4213.
Вариант четырнадцатого задания 2017
На рисунке изображен график функции и касательные, проведённые к нему в точках с абсциссами А, В, С и D. В правом столбце указаны значения производной в точках А, В, С и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
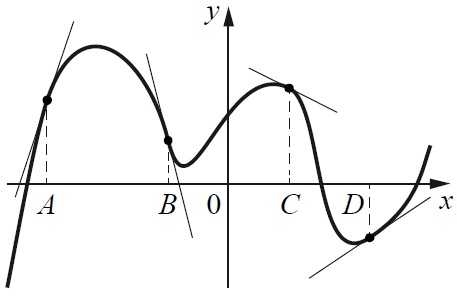
ТОЧКИ
А
В
С
D
ЗНАЧЕНИЯ ПРОИЗВОДНОЙ
1) –4
2) 3
3) 2/3
4) -1/2
Вспомним, что означает производная, а именно ее значение в точке — значение функции производной в точке равно тангенсу угла наклона (коэффициенту) касательной.
В ответах у нас есть два положительных, и два отрицательных варианта. Как мы помним, если коэффициент прямой (графика y = kx+ b) положительный — то прямая возрастает, если же он отрицательный — то прямая убывает.
Возрастающих прямых у нас две — в точке A и D. Теперь вспомним, что же означает значение коэффициента k?
Коэффициент k показывает, насколько быстро возрастает или убывает функция (на самом деле коэффициент k сам является производной функции y = kx+ b).
Поэтому k = 2/3 соответствует более пологой прямой — D, а k = 3 — A.
Аналогично и в случае с отрицательными значениями: точке B соответствует более крутая прямая с k = — 4, а точке С — -1/2.
spadilo.ru
Задание 14 (стереометрия) — Решения вариантов ЕГЭ по математике: 2017, 2018
В правильной треугольной пирамиде МАВС с основанием ABC стороны основания равны 6, а боковые рёбра равны 5. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре AM — точка L. Известно, что AD = Читать далее …
На рисунке изображён многогранник, все двугранные углы которого прямые. а) Постройте сечение многогранника плоскостью, проходящей через точки А, В и С1 б) Найдите площадь этого сечения. Решается аналогично как здесь

В правильной треугольной пирамиде SABC с основанием ABC все ребра равны 6. а) Постройте сечение пирамиды плоскостью, проходящей через вершину S и перпендикулярной отрезку, соединяющему середины ребер AB и BC. б) найдите расстояние от плоскости этого сечения до центра грани Читать далее …
Похоже на решение вариантов 22 и 29. Посмотрите решение в варианте 22.
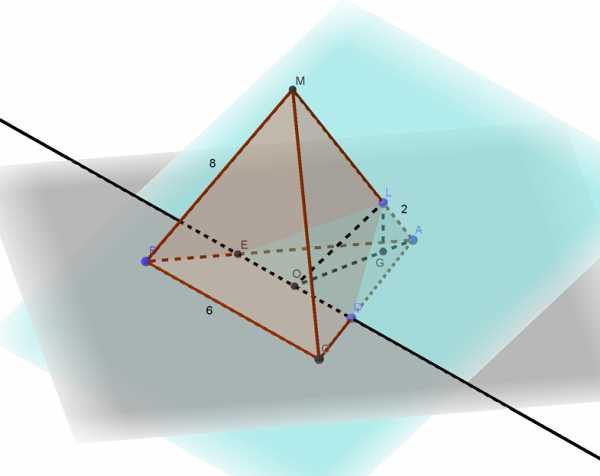
В правильной треугольной пирамиде МАВС с основанием ABC стороны основания равны 6, а боковые рёбра равны 8. На ребре АС находится точка D, на ребре АВ находится точка Е, а на ребре AM — точка L. Известно, что CD = Читать далее …
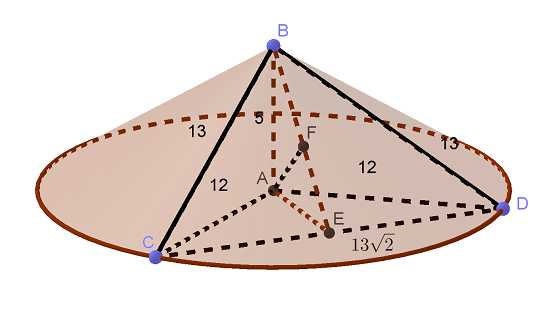
Радиус основания конуса равен 12, а высота конуса равна 5. а) Постройте сечение конуса плоскостью, проходящей через вершину конуса и взаимно перпендикулярные образующие. б) Найдите расстояние от плоскости сечения до центра основания конуса. Трехмерная картинка, которую можно крутить в 3D, Читать далее …
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 4 и ВС = 6. Длины боковых рёбер пирамиды SA = 3, SB = 5, SD = . а) Докажите, что SA — высота пирамиды. б) Найдите расстояние Читать далее …
Вокруг куба с ребром 3 описана сфера. На ребре взята точка М так, что плоскость, проходящая через точки А, В, и М, образует угол 15° с плоскостью ABC. а) Постройте линию пересечения сферы и плоскости, проходящей через точки А, В Читать далее …
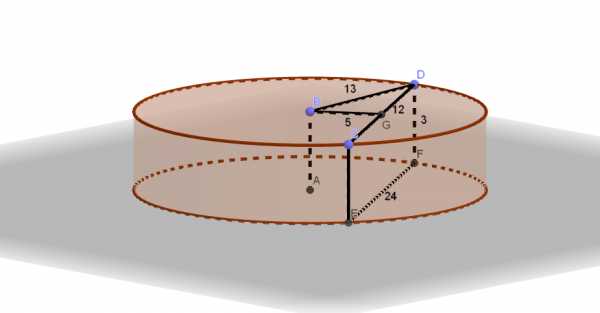
Высота цилиндра равна 3, а радиус основания равен 13. а) Постройте сечение цилиндра плоскостью, проходящей параллельно оси цилиндра, так, чтобы площадь этого сечения равнялась 72. б) Найдите расстояние от плоскости сечения до центра основания цилиндра. Трехмерная картинка, которую можно крутить Читать далее …
В кубе все рёбра равны 4. На его ребре отмечена точка K так, что KB=3. Через точки K и проведена плоскость α, параллельная прямой . а) Докажите, что , где Р — точка пересечения плоскости α с ребром . б) Читать далее …
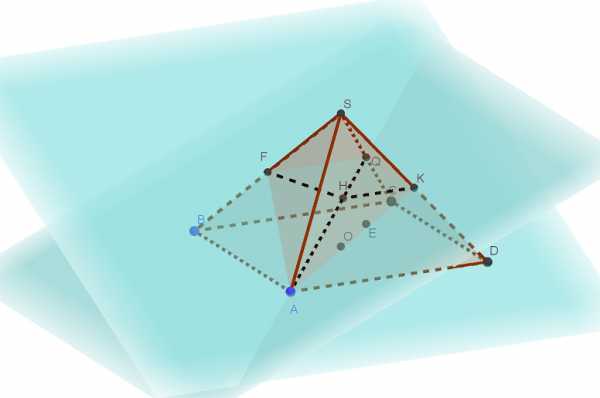
В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F — середина ребра SB, G — середина ребра SC. а) Постройте прямую пересечения плоскостей ABG и GDF. б) Найдите угол между плоскостями ABG и GDF. Трехмерная картинка, которую можно Читать далее …
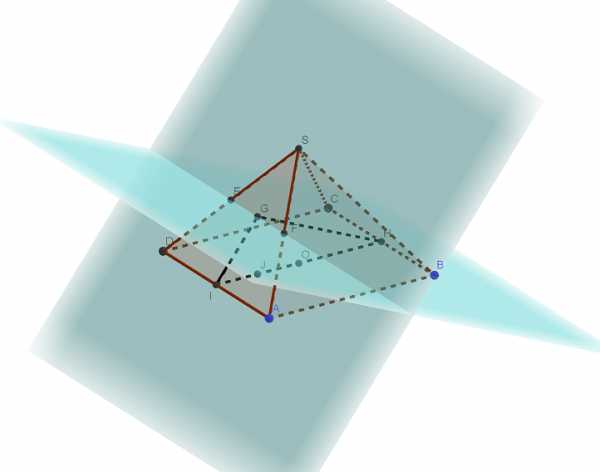
В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. Точка F — середина ребра AS. а) Постройте прямую пересечения плоскостей SAD и BCF. б) Найдите угол между плоскостями SAD и BCF. Трехмерная картинка, которую можно крутить в 3D, доступна по Читать далее …
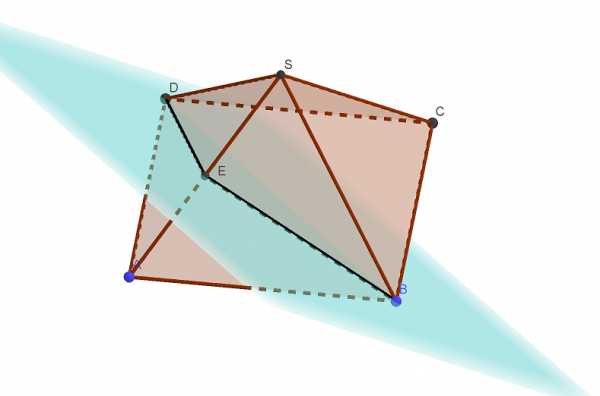
В правильной четырёхугольной пирамиде SABCD все рёбра равны 1. а) Постройте прямую пересечения плоскости SAD с плоскостью, проходящей через точку В перпендикулярно прямой AS. б) Найдите угол между плоскостью SAD и плоскостью, проходящей через точку В перпендикулярно прямой AS. Трехмерная Читать далее …
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 4 и ВС = 3. Длины боковых рёбер пирамиды SA = √11 , SB = 3√3, SD = 2√5. а) Докажите, что SA — высота пирамиды. б) Найдите Читать далее …
ege-resheniya.ru
Задание 14 (ЕГЭ профиль) — Мои решения
Posted by Репетитор & filed under Подготовка к ЕГЭ по математике Comments: 0
Метки: Задание 14 (ЕГЭ профиль), Задачи на построение сечений
В прямоугольном параллелепипеде ABCDAA1B1C1D1 известны ребра АВ = 5, AD = 3, AA1 = 8. Точка R принадлежит ребру АА1 и делит его в отношении 3 : 5, считая от вершины А. а) Постройте сечение параллелепипеда плоскостью, проходящей через точки B, R и D1. б) Найдите площадь этого се..
Read more
Posted by Репетитор & filed under Подготовка к ЕГЭ по математике Comments: 0
Метки: Задание 14 (ЕГЭ профиль), Задачи на построение сечений
В правильной шестиугольной призме A…F1 все ребра равны 1. а) Постройте сечение призмы плоскостью, проходящей через точки A1, B1 и C. б) Найдите расстояние от точки C до прямой A1B1. Решение: а) Пусть α плоскость образованная точками A1, B1 и C. Ребро А1В1 принадлежит α . Точки В1 и С принадлежат секущей плоскости α и грани ..
Read more
Posted by Репетитор & filed under Подготовка к ЕГЭ по математике Comments: 0
Метки: Задание 14 (ЕГЭ профиль), Задачи на построение сечений
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра АВ = 6, ВС = 6, СС1 = 4. а) Докажите, что плоскость BDD1 перпендикулярна отрезку АС. б) Найдите тангенс угла между плоскостями ACD1 ..
Read more
Posted by Репетитор & filed under Подготовка к ЕГЭ по математике Comments: 0
Метки: Задание 14 (ЕГЭ профиль), Задачи на построение сечений
Точка P является серединой ребра BB1 куба A…D1. Длина ребра куба равна 4. Плоскость α проходит через точку D1 параллельно прямой C1P так, что из трех следующих утверждений два истинны, а одно ложно: 1) α параллельна AB1; 2) α параллельна AC; 3) площадь сечения куба плоскостью α меньше 8. а) Постройте сечение этого куба плоскостью ..
Read more
Posted by Репетитор & filed under Подготовка к ЕГЭ по математике Comments: 2
Метки: Задание 14 (ЕГЭ профиль), Задачи на построение сечений
Прямые, содержащие ребра DA и BC треугольной пирамиды DABC, взаимно перпендикулярны, DA = 10, BC = 24. а) Постройте сечение пирамиды плоскостью, проходящей через середину ребра BD и параллельной прямым AD и BC. б) Найдите расстояние между серединами ребер..
Read more
Posted by Репетитор & filed under Подготовка к ЕГЭ по математике Comments: 0
Метки: Задание 14 (ЕГЭ профиль), Задачи на построение сечений
В правильной шестиугольной призме A…F1 все ребра равны 10. а) Постройте сечение призмы плоскостью, проходящей через точки E, B1 и C1. б) Найдите расстояние от точки E до прям..
Read more
Posted by Репетитор & filed under Подготовка к ЕГЭ по математике Comments: 0
Метки: Задание 14 (ЕГЭ профиль), Задачи на построение сечений
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. а) Постройте сечение призмы плоскостью, проходящей через точки F1, A и C. б) Найдите расстояние от точки F1 до прямой AC. Ре..
Read more
my-solutions.ru
Решение задачи №14 из банка заданий ЕГЭ по математике (профильный уровень)
Решение задачи №14 из банка заданий ЕГЭ по математике (профильный уровень)
В прямоугольном параллелепипеде стороны оснований и равны соответственно 8 и 5, а боковое ребро равно 4. На ребре отмечена точка , а на луче — точка , причём и . Плоскость пересекает ребро в точке .
а) Докажите, что .
б) Найдите площадь сечения параллелепипеда плоскостью .
Решение.
а) Построим сечение параллелепипеда плоскостью (см. рис. 1).
— точка пересечения ребра и отрезка .
В плоскости проведём лучи и , пересекает в точке . В плоскости проведём отрезок , пересекает в точке , а — в точке . Пятиугольник — искомое сечение.
, значит, — средняя линия , отсюда , а так как , то — средняя линия ,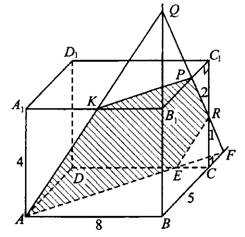
Рис.1
следовательно,
б) Прямоугольные треугольники и равны по двум катетам , отсюда
как площадь равностороннего треугольника со стороной .
по первому признаку подобия ( , — как вертикальные). Из подобия следует, . По доказанному в а), , тогда и . Так как — средняя линия , то
В равнобедренном прямоугольном треугольнике , тогда .
В , отсюда
— равносторонний.
Ответ:
Похожие публикации
math-helper.net