Уравнения с параметром. Задания ЕГЭ по математике (профильный уровень)
Уравнение x^3+3x^2-x\log_{3}(a+1)+5=0 имеет единственное решение на отрезке [0;2], если графики функций y=x^3+3x^2 и y=x\log_{3}(a+1)-5 имеют единственную точку пересечения на отрезке [0;2].
Построим графики этих функций.
1) y=x^3+3x^2.
Найдём стационарные точки: y’=3x^2+6x=3x(x+2). y’=0 при x=0, x=-2
y(-2)=-8+3(-2)^2=-8+12=4, y(0)=0. Отсюда получаем график y=x^3+3x^2.
2) y=x\log_{3}(a+1)-5. Графиком функции является прямая, угловой коэффициент которой k=\log_{3}(a+1). Прямая y=kx-5 проходит через точку (0;-5).
Найдём точку x_{0}, в которой прямая y=kx-5 является касательной к графику функции y=x^3+3x^2.
Уравнение касательной y=(x_{0}^3+3x_{0}^2)+(3x_{0}^2+6x_{0})(x-x_{0}) проходит через точку (0;-5), следовательно, -5=(x_{0}^3+3x_{0}^2)-x_{0}(3x_{0}^2+6x_{0}),
2x_{0}^3+3x_{0}^2-5=0. x_{0}=1 — точка касания.
2x_{0}^3+3x_{0}^2-5=(x_{0}-1)(2x_{0}^2+5x_{0}+5).

Других точек касания нет, так как уравнение 2x_{0}^2+5x_{0}+5=0 корней не имеет.
Если x=1, то y=4, тогда 4=k-5, откуда k=9.

Найдем значение k, при котором прямая y=kx-5 проходит через точку (2;20). 20=2k-5, k=12,5, y=12,5x-5.
Для k=9 и k > 12,5 графики функций y=x^3+3x^2 и y=kx-5 имеют на отрезке [0;2] единственную общую точку. Найдем значения параметра a.
\log_{3}(a+1)=9, a+1=3^9, a=3^9-1.
\log_{3}(a+1) > 12,5, a+1 > 3^{\tfrac{25}{2}}. a > 3^{12,5}-1.
Итак, если a=3^9-1 или a > 3^{12,5}-1, то уравнение x^3+3x^2-x\log_{3}(a+1)+5=0 имеет единственное решение на отрезке [0;2].
academyege.ru
Системы уравнений с параметром. Задания ЕГЭ по математике (профильный уровень)
Решим задачу графически. Построим графики первого и второго уравнения и определим, сколько точек пересечения они имеют при различных значениях параметра.
Первое уравнение \frac{xy^2-5xy-5y+25}{\sqrt {x+5}}=0 параметра не содержит и представляет собой равенство дроби нулю. Это выполняется, если числитель равен нулю, а знаменатель не равен нулю, при этом оба выражения имеют смысл.
Запишем уравнение в виде \frac{(y-5)(xy-5)}{\sqrt {x+5}}=0, разложив числитель на множители. При x \leqslant -5 левая часть не имеет смысла. При x>-5 уравнение задаёт прямую y=5 и гиперболу y=\frac5x.
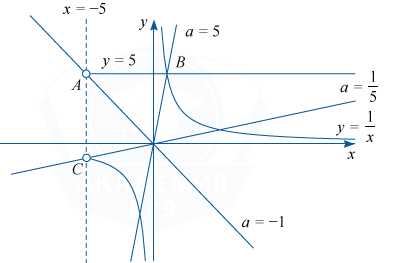
Найдём координаты точек A, B и C. B — точка пересечения прямой y=5 и гиперболы y=\frac5x , чтобы найти её координаты, нужно решить систему уравнений \begin{cases} y=5,\\y=\frac5x. \end{cases}
Получаем B(1; 5).
У точек A и C абсцисса равна -5, ординаты находим из уравнений прямой и гиперболы. A(-5;5) и C(-5;-1).
При каждом значении a уравнение y=ax задаёт прямую с угловым коэффициентом a, проходящую через начало координат. Чтобы найти значение a, при котором такая прямая проходит через точку с указанными координатами, нужно подставить координаты в уравнение прямой.
Например, для точки A(-5; 5) получаем x=-5, y=5, 5=a\cdot (-5), a=-1.
Аналогично для B(1;5),\, a=5 и для C(-5;-1), a=\frac15.
При x>-5 прямая y=ax пересекает прямую y=5 при a<-1 и a>0, пересекает правую ветвь гиперболы y=\frac5x при a>0, пересекает левую ветвь гиперболы y=\frac5x при a>\frac15. При этом прямая y=ax проходит через точку пересечения прямой y=5 и гиперболы y=\frac5x при a=5.
Число решений исходной системы равно числу точек пересечения прямой y=5 и гиперболы y=\frac5x с прямой y=ax при условии x>-5.
Таким образом, исходная система имеет ровно два решения при 0 < a \leqslant 0,2; a=5.
academyege.ru
ЗАДАЧИ С ПАРАМЕТРОМ – Репетитор по математике
Рассмотрим решение задачи с параметром с помощью метода инвариант.
Найдите все пары действительных чисел и , для каждой из которых имеет единственное решение система уравнений.
Этот метод обычно применяют в тех случаях, если нужно найти значения параметра, при которых уравнение или система уравнений имеют единственное решение.
Заметим, что если мы в системе заменим на , то система от этого не изменится. Это значит, что если пара чисел является решением системы, то пара чисел также будет решением этой системы. Поэтому, чтобы система имела единственное решение, эти пары чисел должны быть одинаковыми. А это будет только в том случае, если .
Пусть . (1)
Тогда получим систему:
(2)
Теперь в полученной системе если мы заменим на , то система не изменится. Это значит, что если некоторое значение является решением системы, то число также будет решением системы. Чтобы эта система имела единственное решение, нужно, чтобы выполнялось условие . А это возможно только если .
Тогда, с учетом (1) получим и .
Подставим эти значения в систему, получим
Из последнего уравнения получим или .
Рассмотрим оба варианта.
1) , тогда и .
2) , тогда и .
Теперь осталось установить, при какой паре значений и система имеет единственное решение.
Проверим каждую пару и .
1) Подставим и в систему (2).
Получим
Из первого уравнения выразим через
и подставим во второе уравнение.
Получим:
.
Это уравнение имеет два решения: . Проверим каждое.
При получим систему:
(3)
Из второго уравнения системы (3) выразим :
и подставим в третье уравнение системы:
Это уравнение имеет более одного корня, поэтому пара , нам не подходит.
2) Подставим и в систему (2).
Получим
(4)Из первого уравнения выразим через
и подставим во второе уравнение.
Получим:
ege-ok.ru
Подготовка к ЕГЭ. Уравнения с параметром
Подготовка к ЕГЭ. Уравнения с параметром
- Найдите все значения параметра , при каждом из которых уравнение имеет ровно 3 различных корня.
- Найдите все значения параметра , при которых уравнение имеет ровно 3 различных корня. Если количество значений более одного, то в ответе запишите сумму.
- Найдите все значения параметра , при которых уравнение имеет ровно 2 различных корня. Если количество значений более одного, то в ответе запишите их сумму.
- При каком наименьшем натуральном значении параметра уравнение имеет хотя бы одно решение?
- При каком наибольшем натуральном значении параметра уравнение имеет ровно 2 корня?
- Укажите все целые значения параметра , при которых хотя бы один из корней уравнения принадлежит промежутку [-2; -1]. Если значений более одного, то в ответе запишите их сумму.
- Укажите наименьшее целое значение параметра , при котором уравнение имеет ровно четыре корня.
- Укажите все значения параметра , при которых уравнение имеет ровно три корня. Если таких значений более одного, то в ответе запишите их сумму.
- Найдите все значения параметра , при которых уравнение имеет хотя бы одно решение.
- Найдите все значения параметра , при которых уравнение имеет единственное решение.
- Найдите все целые значения параметра , при которых уравнение имеет ровно два положительных корня
- Найдите наибольшее целое значение параметра , при котором уравнение не имеет корней
- Найдите наибольшее целое значение параметра , при котором уравнение имеет ровно два отрицательных корня
- Найдите наибольшее целое значение параметра , при котором корень уравнения принадлежит промежутку [-2; -1]
- Найдите все значения , при каждом из которых уравнение имеет хотя бы один корень.
- Найдите все целые значения , при каждом из которых корни уравнения принадлежат промежутку [3;4]
Ответы
- 0,25
- 1
- 12
- -4
- 19
- [-20; 30]
- -15; -14; -11; -10; -9
Метки ЕГЭ. Смотреть запись.
www.itmathrepetitor.ru
Уравнение с параметром
В этой задаче надо найти такие значения параметра, при которых уравнение будет иметь одно решение. А уравнение квадратное, но присутствует и дробь, поэтому может так случиться, что один из корней совпадет с корнем знаменателя и таким образом станет посторонним. Поэтому такой случай, кроме нулевого дискриминанта, надо обязательно предусмотреть.
Задача. При каких значениях параметра уравнение
имеет одно решение?
Приведем к общему знаменателю обе дроби и правую часть:
Дробь равна нулю, когда ее числитель равен нулю, а знаменатель – нет. Поэтому равносильна система:
Получили квадратное уравнение относительно , и оно будет иметь одно решение, если его дискриминант будет равен :
При полученных значениях параметра уравнение имеет одно решение. Определим его, чтобы убедиться, что оно не совпадает с и :
Выражение такое простое, так как это вершина параболы. Подставим :
Это значение не равно , и не равно , следовательно, параметр берем в ответ.
Но вдруг уравнение имеет два корня, но просто один из них либо равен , либо ? Проверим это предположение простой подстановкой:
Тогда:
Тогда , или .
Если , то второй (сумма корней равна ) .
Подставим найденные значения параметра: , или
Таким образом, при принятом получили полностью устраивающие нас и .
Теперь примем . Тогда:
Последнее значение уже мелькало и было нами проверено. Если , то второй (сумма корней равна ) .
При , что не равно .
Ответ:
easy-physic.ru
Параметрические уравнения, неравенства и системы, часть С | ЕГЭ по математике (профильной)
Параметрические уравнения
Уравнение, которое кроме неизвестной величины содержит также другую дополнительную величину, которая может принимать различные значения из некоторой области, называется параметрическим. Эта дополнительная величина в уравнении называется параметр. На самом деле с каждым параметрическим уравнением может быть написано множество уравнений.
Способ решения параметрических уравнений
- Находим область определения уравнения.
- Выражаем a как функцию от $х$.
- В системе координат $хОа$ строим график функции, $а=f(х)$ для тех значений $х$, которые входят в область определения данного уравнения.
- Находим точки пересечения прямой, $а=с$, где $с∈(-∞;+∞)$ с графиком функции $а=f(х)$. Если прямая, а=с пересекает график, $а=f(х)$, то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение вида, $а=f(х)$ относительно $х$.
- Записываем ответ.
Общий вид уравнения с одним параметром таков:
$F(x, a) = 0$
При различных значениях, а уравнение $F(x, a) = 0$ может иметь различные множества корней, задача состоит в том, чтобы изучить все случаи, выяснить, что будет при любом значении параметра. При решении уравнений с параметром обычно приходится рассматривать много различных вариантов. Своевременное обнаружение хотя бы части невозможных вариантов имеет большое значение, так как освобождает от лишней работы.
Поэтому при решении уравнения $F(x, a) = 0$ целесообразно под ОДЗ понимать область допустимых значений неизвестного и параметра, то есть множество всех пар чисел ($х, а$), при которых определена (имеет смысл) функция двух переменных $F(x, а)$. Отсюда естественная геометрическая иллюстрация ОДЗ в виде некоторой области плоскости $хОа$.
ОДЗ различных выражений (под выражением будем понимать буквенно — числовую запись):
1. Выражение, стоящее в знаменателе, не должно равняться нулю.
${f(x)}/{g(x)}; g(x)≠0$
2. Подкоренное выражение должно быть неотрицательным.
$√{g(x)}; g(x)≥0$.
3. Подкоренное выражение, стоящее в знаменателе, должно быть положительным.
${f(x)}/{√{g(x)}}; g(x) > 0$
4. У логарифма: подлогарифмическое выражение должно быть положительным; основание должно быть положительным; основание не может равняться единице.
$log_{f(x)}g(x) \{\table\g(x) > 0; \f(x) > 0; \f(x)≠1;$
Алгебраический способ решения квадратных уравнений с параметром $ax^2+bx+c=0$
Квадратное уравнение $ax^2+bx+c=0, а≠0$ не имеет решений, если $D < 0$;
Квадратное уравнение имеет два различных корня, когда $D > 0$;
Квадратное уравнение имеет один корень, если $D=0$
Тригонометрические тождества
1. $tgα={sinα}/{cosα}$
2. $ctgα={cosα}/{sinα}$
3. $sin^{2}α+cos^{2}α=1$ (Основное тригонометрическое тождество)
Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
$sinα=±√{1-cos^{2}α}$
$cosα=±√{1-sin^{2}α$
4. $tgα·ctgα=1$
5. $1+tg^{2}α={1}/{cos^{2}α}$
6. $1+ctg^{2}α={1}/{sin^{2}α}$
Формулы двойного угла
1. $sin2α=2sinα·cosα$
2. $cos2α=cos^{2}α-sin^{2}α=2cos^{2}α-1=1-2sin^{2}α$
3. $tg2α={2tgα}/{1-tg^{2}α}$
Формулы суммы и разности
$cosα+cosβ=2cos{α+β}/{2}·cos{α-β}/{2}$
$cosα-cosβ=2sin{α+β}/{2}·sin{β-α}/{2}$
$sinα+sinβ=2sin{α+β}/{2}·cos{α-β}/{2}$
$sinα-sinβ=2sin{α-β}/{2}·cos{α+β}/{2}$
Формулы произведения
$cosα·cosβ={cos{α-β}+cos{α+β}}/{2}$
$sinα·sinβ={cos{α-β}-cos{α+β}}/{2}$
$sinα·cosβ={sin{α+β}+sin{α-β}}/{2}$
Формулы сложения
$cos(α+β)=cosα·cosβ-sinα·sinβ$
$cos(α-β)=cosα·cosβ+sinα·sinβ$
$sin(α+β)=sinα·cosβ+cosα·sinβ$
$sin(α-β)=sinα·cosβ-cosα·sinβ$
Решение тригонометрического уравнения с параметром рассмотрим на примере.
Пример:
Найдите все значения параметра с, при каждом из которых уравнение $3cos2x-2sin2x=c$ имеет решение.
Решение:
Преобразуем данное уравнение к виду
$√{3^2+(-2)^2}(cos2xcosφ-sin2xsinφ)=c$
Воспользуемся тригонометрической формулой и свернем второй множитель как косинус суммы
$√{13}cos(2x+φ)=c$, где $φ=arccos{3}/{√{13}}$
Уравнение $√{13}cos(2x+φ)=c$ имеет решения тогда и только тогда, когда $-1≤ {c}/{√{13}} ≤ 1$, домножим полученное неравенство на $√{13}$ и получим
$-√{13} ≤ c ≤ √{13}$
Ответ: $-√{13} ≤ c ≤ √{13}$
Неравенства с параметром
Если имеется неравенство вида $F(a,x) ≤ G(a,x)$ то оно будет иметь одно решение, если $F'(a, x)=G'(a, x)$.
Системы уравнений:
Выделяют четыре основных метода решения систем уравнений:
- Метод подстановки: из какого-либо уравнения системы выражаем одно неизвестное через другое и подставляем во второе уравнение системы.
- Метод алгебраического сложения: путем сложения двух уравнений получить уравнение с одной переменной.
- Метод введения новых переменных: ищем в системе некоторые повторяющиеся выражения, которые обозначим новыми переменными, тем самым упрощая вид системы.
- Графический метод решения: из каждого уравнения выражается $«у»$, получаются функции, графики которых необходимо построить и посмотреть координаты точек пересечения.
Логарифмические уравнения и системы уравнений
Основное логарифмическое тождество:
$a^{log_{a}b}=b$
Это равенство справедливо при $b> 0, a> 0, a≠1$
Свойства логарифмов:
Все свойства логарифмов мы будем рассматривать для $a> 0, a≠ 1, b> 0, c> 0, m$ – любое действительное число.
1. Для любых действительных чисел $m$ и $n$ справедливы равенства:
$log_{а}b^m=mlog_{a}b$;
$log_{a^m}b={1}/{m}log_{a}b$.
$log_{a^n}b^m={m}/{n}log_{a}b$
2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.
$log_a(bc)=log_{a}b+log_{a}c$
3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию
$log_a{b}/{c}=log_{a}b-log_{a}c$
4. При умножении двух логарифмов можно поменять местами их основания
$log_{a}b·log_{c}d=log_{c}b·log_{a}d$, если $a, b, c, d >0, a≠1, b≠1$.
5. $c^{log_{a}b}=b^{log_{a}b}$, где $а, b, c > 0, a≠1$
6. Формула перехода к новому основанию
$log_{a}b={log_{c}b}/{log_{c}a}$
7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение
$log_{a}b={1}/{log_{b}a}$
При решении систем, содержащих логарифмические уравнения, часто удается, избавившись от логарифма, заменить одно или оба уравнения системы рациональными уравнениями. После этого надо выразить одну переменную через другую и после постановки получить уравнение с одной переменной. Кроме того, часто встречаются задачи на замену переменной в пределах одного или обоих уравнений системы и системы, требующие отбора решений.
Логарифмические неравенства:
1. Определить ОДЗ неравенства.
2. По свойствам логарифма преобразовать неравенство к простому виду, желательно получить с двух сторон логарифмы по одинаковому основанию.
3. Перейти к подлогарифмическим выражениям, при этом надо помнить, что:
а) если основание больше единицы, то при переходе к подлогарифмическим выражениям знак неравенства остается прежним;
b) если основание меньше единицы, то при переходе к подлогарифмическим выражениям знак неравенства меняется на противоположный;
с) если в основании находится переменная, надо рассмотреть оба варианта.
4. Решить неравенство.
5. Выбрать решения с учетом ОДЗ из п.1
При решении логарифмических неравенств с переменной в основании легче всего воспользоваться тождественными преобразованиями:
$log_{a}f > b ↔ \{\table\ (f-a^b)(a-1) > 0; \f > 0; \a > 0;$
$log_{a}f+log_{a}g > 0 ↔ \{\table\(fg-1)(a-1)> 0; \f > 0,g > 0; \a > 0;$
$log_{a}f+b > 0 ↔ \{\table\(fa^b-1)(a-1) > 0; \f > 0; \a > 0;$
Системы, содержащие показательные уравнения
Свойства степеней
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
$a^n·a^m=a^{n+m}$
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются
$a^n:a^m=a^{n-m}$
3. При возведении степени в степень основание остается прежним, а показатели перемножаются
$(a^n)^m=a^{n·m}$
4. При возведении в степень произведения в эту степень возводится каждый множитель
$(a·b)^n=a^n·b^n$
5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
$({a}/{b})^n={a^n}/{b^n}$
6. При возведении любого основания в нулевой показатель степени результат равен единице
$a^0=1$
Основные методы решения систем, содержащих показательные уравнения, ничем принципиально не отличаются от методов решения других систем: это метод алгебраического сложения, замена переменной в пределах одного уравнения или всей системы, подстановка. Единственная особенность – положительность выражения $a^{f(x)}$, которую полезно учитывать, вводя соответствующее ограничение при замене переменной.
Показательные неравенства, сводящиеся к виду $a^{f(x)} ≥ a^{g(x)}$:
1. Преобразовать показательное уравнение к виду $a^{f(x)} ≥ a^{g(x)}$
2. Перейти показателям степеней, при этом если основание степени меньше единицы, то знак неравенства меняется на противоположный, если основание больше единицы – знак неравенства остается прежним.
3. Решить полученное неравенство.
4. Записать результат.
Показательные неравенства, которые можно разложить на множители или сделать замену переменной.
1. Для данного метода во всем неравенстве по свойству степеней надо преобразовать степени к одному виду $a^{f(x)}$.
2. Сделать замену переменной $a^{f(x)}=t, t>0$.
3. Получаем рациональное неравенство, которое можно решить методом интервалов путем разложения на множители выражения.
4. Делаем обратную замену с учетом того, что $t>0$. Получаем простейшее показательное неравенство $a^{f(x)}=t$, решаем его и результат записываем в ответ.
Уравнения с многочленами
Многочлен может обозначаться записью $Р(х)$ — это означает, что многочлен зависит от «х», если записать $Р(х+1)$ — это означает, что в многочлене вместо «х» надо сделать замену на скобку $(х+1)$
Пример:
Найдите значение выражения: $4(p(2x)−2p(x+3))$, если $p(x)=x−6$
Решение:
В данном условии задан многочлен, зависящий от «х», как $p(x)=x−6$.
Чтобы было понятнее, назовем исходный многочлен основной формулой, тогда, чтобы записать $p(2x)$, в основной формуле заменим «х» на «2х».
$p(2x)=2х-6$
Аналогично $p(x+3)=(х+3)-6=х+3-6=х-3$
Соберем все выражение: $4(p(2x)−2p(x+3))=4((2х-6)-2(х-3))$
Далее осталось раскрыть скобки и привести подобные слагаемые
$4((2х-6)-2(х-3))=4(2х-6-2х+6)=4·0=0$
Ответ: $0$
Системы иррациональных уравнений
Основные методы решения систем, содержащих иррациональные уравнения, ничем принципиально не отличаются от методов решения других систем: это метод алгебраического сложения, замена переменной в пределах одного уравнения или всей системы, подстановка. Единственная особенность – надо расписать ОДЗ каждого уравнения, а в конце решения выбрать решение системы с учетом ОДЗ.
Чтобы решить иррациональное уравнение, необходимо:
1. Преобразовать заданное иррациональное уравнение к виду
$√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
2. Обе части уравнение возвести в квадрат
$√{f(x)}^2={g(x)}^2$ или $√{f(x)}^2=√{g(x)}^2$
3. Решить полученное рациональное уравнение.
4. Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)
examer.ru
Уравнение с параметром — «Шпаргалка ЕГЭ»
Найдите все значения , при которых уравнение имеет единственное решение.
.
Решение задачи
 Данный урок показывает, как правильно решить уравнение с параметром, если известно, что корень уравнения единственный. При данных исходных условиях необходимо всегда проверить возможность наличия противоположных корней уравнения, учитывая, что данное уравнение содержит степени и модули. В данном случае получается, что если существует положительный корень уравнения, то обязательно будет существовать такой же, но отрицательный корень. Это противоречит условию задачи, а значит, единственным корнем уравнения в таком случае может быть только нуль. Исходя из этого предположения, вместо неизвестной х переходим к уравнению с неизвестной величиной а. При этом получаем несколько значений параметра. Осталось проверить эти параметры, так как при наличии корней и модулей могут появится лишние корни. Так и получается – один из корней оказывается лишним (при подстановке количество корней исходного уравнения больше одного). Оставшиеся значения записываем в ответ.
Данный урок показывает, как правильно решить уравнение с параметром, если известно, что корень уравнения единственный. При данных исходных условиях необходимо всегда проверить возможность наличия противоположных корней уравнения, учитывая, что данное уравнение содержит степени и модули. В данном случае получается, что если существует положительный корень уравнения, то обязательно будет существовать такой же, но отрицательный корень. Это противоречит условию задачи, а значит, единственным корнем уравнения в таком случае может быть только нуль. Исходя из этого предположения, вместо неизвестной х переходим к уравнению с неизвестной величиной а. При этом получаем несколько значений параметра. Осталось проверить эти параметры, так как при наличии корней и модулей могут появится лишние корни. Так и получается – один из корней оказывается лишним (при подстановке количество корней исходного уравнения больше одного). Оставшиеся значения записываем в ответ.
Решение данной задачи рекомендовано для учащихся 11-х классов при изучении тесы «Уравнения и неравенства. Системы уравнений и неравенств» («Уравнения и неравенства с параметром, простейшие примеры», «Квадратичная функция в задачах с параметром»). При подготовке к ЕГЭ урок рекомендован при повторении темы «Уравнения и неравенства. Системы уравнений и неравенств».
shpargalkaege.ru
