Логарифмы егэ – Логарифмы в заданиях ЕГЭ скачать

Свойства логарифмов, формулы | Подготовка к ЕГЭ по математике

Категория: Справочные материалы

Елена Репина 2013-02-18 2013-07-07

Логарифм числа по основанию определяется как показатель степени, в которую нужно возвести основание , чтобы получить число .

Обозначение читается как логарифм по основанию .

Например, , так как  (2 – основание степени, 3 – показатель степени).

 

Логарифмы

Определение

Основное логарифмическое тождество

Свойства логарифмов

Чаще всего используют логарифмы с основаниями (натуральный логарифм, например, ), (десятичный, например, ) и (двоичный).

 

Автор: egeMax | комментариев 12 | Метки: Логарифмы, шпаргалки-таблицы

egemaximum.ru

Логарифмы. Единые государственные экзамены, ЕГЭ по математике: уроки, тесты, задания.

1.	Вычисление десятичного логарифма Сложность: лёгкое	1
2.	Вычисление логарифма Сложность: лёгкое	1
3.	Вычисление логарифма Сложность: лёгкое	1
4.	Применение свойств логарифмов Сложность: лёгкое	1
5.	Применение свойств логарифмов Сложность: лёгкое	3
6.	Формула перехода логарифма к новому основанию Сложность: лёгкое	1
7.	Использование основного тождества логарифмов Сложность: среднее	2
8.	Сравнение логарифмов Сложность: лёгкое	1
9.	Нахождение области определения логарифма Сложность: среднее	1
10.	Нахождение области определения логарифма Сложность: среднее	2
11.	Определение основания логарифма Сложность: среднее	2
12.	Логарифмическое уравнение,определение логарифма Сложность: лёгкое	1
13.	Логарифмическое уравнение,определение логарифма Сложность: лёгкое	3
14.	Логарифмическое уравнение(неизвестно основание) Сложность: среднее	4
15.	Логарифмическое уравнение(произведение равно 0) Сложность: среднее	2
16.	Логарифмическое уравнение (свойства логарифмов) Сложность: среднее	4
17.	Логарифмическое уравнение (свойства логарифмов) Сложность: среднее	3
18.	Логарифмическое уравнение (логарифм в квадрате) Сложность: среднее	3
19.	Логарифмическое уравнение (новая переменная) Сложность: среднее	4
20.	Логарифмическое уравнение (новая переменная) Сложность: среднее	5
21.	Логарифмическое уравнение (разлож. на множит.) Сложность: среднее	5
22.	Логарифмическое уравнение с тригонометрией Сложность: сложное	7
23.	Логарифмическое уравнение (графический способ) Сложность: сложное	3
24.	Логарифмическое неравенство(основание меньше 1) Сложность: лёгкое	1
25.	Логарифмическое неравенство (квадратичное) Сложность: среднее	2
26.	Логарифмическое неравенство (квадратичное) Сложность: среднее	2
27.	«Ц-Уровень» Логарифмическое неравенство Сложность: сложное	1

www.yaklass.ru

Логарифмические выражения

Логарифмические выражения, решение примеров. В этой статье мы рассмотрим задачи связанные с решением логарифмов. В заданиях ставится вопрос о нахождении значения выражения. Нужно отметить, что понятие логарифма используется во многих заданиях и понимать его смысл крайне важно. Что касается ЕГЭ, то логарифм используется при решении уравнений, в прикладных задачах, также в заданиях связанных с исследованием функций.

Приведём примеры для понимания самого смысла логарифма:

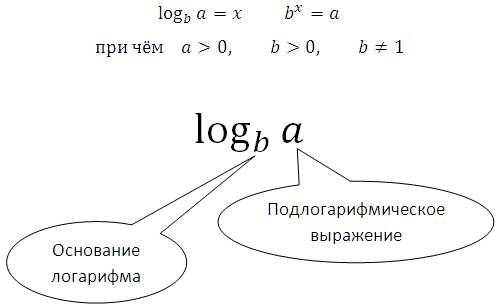
Основное логарифмическое тождество:

Свойства логарифмов, которые необходимо  всегда помнить:

*Логарифм произведения равен сумме логарифмов сомножителей.

* * *

*Логарифм частного (дроби) равен разности логарифмов сомножителей.

* * *

*Логарифм степени равен произведению показателя степени на логарифм ее основания.

* * *

*Переход к новому основанию

* * *

Ещё свойства:

* * *

Вычисление логарифмов тесно связано с использованием свойств показателей степени.

Перечислим некоторые из них:

Суть данного свойства заключается в том, что при переносе числителя в знаменатель и наоборот, знак показателя степени меняется на противоположный.  Например:

Следствие из данного свойства:

* * *

При возведении степени в степень основание остаётся прежним, а показатели перемножаются.

* * *

При возведении в степень произведения в эту же степень возводится каждый множитель.

Так же необходимо знать следующее свойство:

Рассмотрим примеры:

*Данный контент (более 20 подробно решённых примеров) доступен только для зарегистрированных пользователей! Вкладка регистрации (входа) находится в ГЛАВНОМ МЕНЮ сайта. После прохождения регистрации войдите на сайт и обновите данную страницу.

Как вы убедились само понятие логарифма несложное. Главное то, что необходима хорошая практика, которая даёт определённый навык. Разумеется знание формул обязательно. Если навык в преобразовании элементарных логарифмов не сформирован, то при решении  простых заданий можно легко допустить ошибку.

Практикуйтесь, решайте сначала простейшие примеры из курса математики, затем переходите к более сложным. В будущем обязательно покажу, как решаются «страшненькие» логарифмы, таких на ЕГЭ не будет, но они представляют интерес, не пропустите!

На этом всё! Успеха Вам!

С уважением, Александр Крутицких

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Логарифмы в ЕГЭ — Математика

Тема урока: Логарифмы в заданиях ЕГЭ.

Метод решения хорош, если с самого начала мы можем предвидеть – и в последствии подтвердить это, — 
что, следуя этому методу, мы достигнем цели.
Г.Лейбниц

ТИП УРОКА: Закрепление и совершенствование знаний.

ЦЕЛИ:

Дидактическая — Повторить и закрепить свойства логарифмов; логарифмические уравнения; закрепить методы решения наибольшего и наименьшего значения функции; совершенствовать применение полученных знаний при решении задач ЕГЭ С1 и С3;

Развивающая — Развитие логического мышления, памяти, познавательного интереса, продолжить формирование математической речи и графической культуры, вырабатывать умение анализировать;

Воспитательная — Формировать навыки общения, умения работать в коллективе.

Способствовать воспитанию познавательного интереса к математике 

Оборудование:

• Персональный компьютер у учителя.

• Мультимедийный проектор, экран.

• Презентация к уроку.

• Ноутбуки для учащихся с тестами самоконтроля.

• Раздаточный материал: сопроводительный лист с заданиями и оценочной таблицей, справочный материал.

 Формы работы: фронтальная, индивидуальная, коллективная.

Основные этапы урока:

1. Организационный момент.

2. Актуализация.

3. Формулирование темы урока, постановка целей и задач урока.

4. Закрепление знаний.

5. Физкультминутка.

6. Усвоение знаний.

7. Подведение итогов урока.

8. Инструктаж по домашнему заданию.

9. Рефлексия.

ХОД УРОКА

1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ

Наш урок я хочу начать со слов американского математика Айвена Нивена:

“Нельзя изучать математику, наблюдая за тем, как это делаем сосед…” (слайд 1)

Чтобы оценить свою работу на уроке у вас на сопроводительных листах есть оценочная таблица (слайд 2). Отмечайте, количество баллов, которое вы себе поставите после каждого этапа урока.

2. ПОСТАНОВКА ЦЕЛИ

Какова тема урока?

(Ответ: Свойства логарифмов. Подготовка в ЕГЭ)

Какова цель урока?

(Ответ: Подготовиться к ЕГЭ)

Какие задачи для этого нам нужно выполнить?

(Ответ: 1. Вспомнить свойства логарифмов, свойства степеней, решение простейших логарифмических уравнений

2. Научиться решать лог. уравнения повышенной сложности)

3. Развитие внимания, мышления, памяти.

4. Воспитание познавательного интереса к математике.

3. АКТУАЛИЗАЦИЯ ЗНАНИЙ

Проанализировать: в каких заданиях ЕГЭ встречаются логарифмы.

Базовый-5,7-преобразования лог.выражений, простейшие логарифмические уравнения

Профильный 3,5,10,12-преобразование логарифмических выражений, уравнения, задачи физического содержания, связанные с логарифмами, нахождение наибольшего и наименьшего значения функции.

С-1- тригонометрические уравнения, содержащие логарифм

С-3 – система неравенств, содержащая логарифмическое неравенство)

На данном этапе проводится устная работа, в ходе которой учащиеся не только вспоминают свойства логарифмов, но и выполняют простейшие задания ЕГЭ.

1. Начнем с того что дадим определение логарифма.

2. Какие вы знаете свойства логарифма? (и условия ?)

1. log_b b = 1
2. log_b 1 = 0, 3. log_c (ab) = log_c a + log_c b.
4. log_c (a:b) = log_c a – log_c b.
5.  log_c (b ^k ) = k * log_c 

6= 

7.   

3) Что такое десятичный логарифм? ()

4) Что такое натуральный логарифм? ()

5) Что такое число е?

6) Чему равна производная от ? ()

7) чему равна производная ln x ?

5. УСТНАЯ РАБОТА для всех обучающихся

Вычислить устно: (задания В-11)

=  =  = =

15 2 1 144 -1/2

6. Самостоятельная деятельность учащихся по решению заданий

Решение уравнений с последующей проверкой

Решите уравнения (первые два уравнения проговаривают устно, а остальные решает самостоятельно весь класс и записывает решение в тетрадь):

(Пока ученики работают на месте самостоятельно, к доске выходят 3 ученика и работают по индивидуальным карточкам)

После проверки с места 3-5 уравнений, ребятам предлагается доказать, что уравнение  не имеет решения (устно)

7. Решение В-10 — (задачи физического содержания, связанные с логарифмами)

Весь класс решает задачу (у доски 2 человека: 1-й решает вместе с классом, 2-й решает аналогичную задачу самостоятельно)  

На­хо­дя­щий­ся в воде во­до­лаз­ный ко­ло­кол, со­дер­жа­щий  моля воз­ду­ха при дав­ле­нии  ат­мо­сфе­ры, мед­лен­но опус­ка­ют на дно водоeма. При этом про­ис­хо­дит изо­тер­ми­че­ское сжа­тие воз­ду­ха. Ра­бо­та, со­вер­ша­е­мая водой при сжа­тии воз­ду­ха, опре­де­ля­ет­ся вы­ра­же­ни­ем  (Дж), где  – по­сто­ян­ная,  – тем­пе­ра­ту­ра воз­ду­ха,  (атм) – на­чаль­ное дав­ле­ние, а  (атм) – ко­неч­ное дав­ле­ние воз­ду­ха в ко­ло­ко­ле. До ка­ко­го наи­боль­ше­го дав­ле­ния  можно сжать воз­дух в ко­ло­ко­ле, если при сжа­тии воз­ду­ха со­вер­ша­ет­ся ра­бо­та не более чем 6900 Дж? Ответ при­ве­ди­те в ат­мо­сфе­рах.(6)

8. УСТНАЯ РАБОТА (вопросы)

Вспомнить алгоритм нахождения наибольшего и наименьшего значения функции на отрезке и на промежутке.

Работа на доске и в тетради.

(прототип В15 — ЕГЭ)

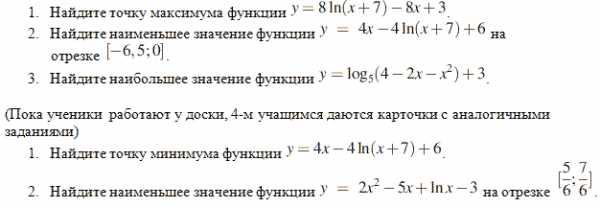
9 Блиц-опрос.

И напоследок проверим себя, насколько каждый владеет определением и свойствами логарифмов (слайд 16). В сопроводительных листах необходимо ответить только «да» или «нет».

Подлогарифмическое выражение всегда должно быть больше нуля.	да
Основание логарифма всегда строго больше нуля.	нет
Логарифм частного равен разности логарифмов.	да
Логарифм произведения равен произведению логарифмов.	нет
Если подлогарифмическое выражение записано в виде степени, то показатель можно вынести вперед и умножить на логарифм основания.	да

10.Мини-тест с самоконтролем на ноутбуках

Тест

№	1 вариант	2 вариант
1.
2.
3.
4.
5.
6.	Найдите наибольшее значение функции	Найдите наименьшее значение функции

Ключи к тесту

	№1	№2	№3	№4	№5	№6
Вариант №1	250	49	4	-8	3	8
Вариант №2	63	144	13	-22	7	3

Ребята меняются друг с другом работами и выступают в роли экспертов.

10. Решение заданий С1

Учащиеся выполняют задание, 1 человек работает у доски.

а) Решите уравнение  

б) найдите корни уравнения, принадлежащие промежутку (;3)

12. ДОМАШНЕЕ ЗАДАНИЕ

Учитель поясняет домашнее задание, обращая внимание на то, что аналогичные задания были рассмотрены на уроке. Учащиеся внимательно прослушав пояснения учителя, записывают домашнее задание.

ФИПИ (открытый банк заданий: раздел геометрия, 6-я страница)

uztest.ru (преобразование логарифмов)

С3 – задание второй части ЕГЭ

13. ПОДВЕДЕНИЕ ИТОГОВ

Сегодня на уроке мы повторили свойства логарифмов; логарифмические уравнения; закрепили методы нахождения наибольшего и наименьшего значения функции; рассмотрели задачи физического содержания, связанные с логарифмами; решали задачи С1 и С3, которые предлагаются на ЕГЭ по математике в прототипах В7, В11, В12, В15, С1 и С3.

Выставление оценок.

multiurok.ru

Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия

Предыдущую статью о показательных уравнениях мы начали с уравнения 2^x = 8. Там всё было ясно: x = 3.

А теперь рассмотрим уравнение 2^x = 7.

По графику функции y = 2^x мы видим, что это уравнение имеет корень, и притом единственный.

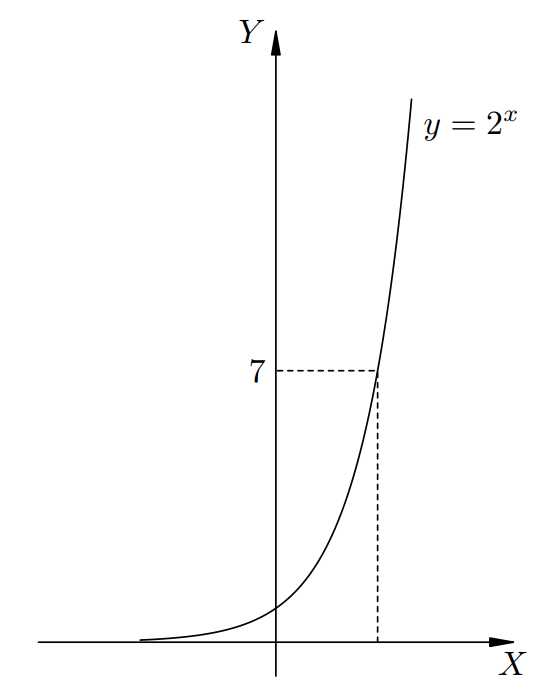
Ясно, что этот корень — не целое число (так как 2² = 4, 2³ = 8). Более того, оказывается, что он не является даже рациональным числом, т. е. не представляется в виде обыкновенной дроби. Интуитивно мы чувствуем лишь, что он меньше 3, но не намного.

Этот корень обозначается log₂7 (читается: «логарифм семи по основанию два». Он является иррациональным числом, т. е. бесконечной непериодической десятичной дробью. Калькулятор даёт: log₂7 = 2,807354922057604107…

Итак, наше число log₂7 — это показатель степени, в которую надо возвести 2, чтобы получить 7.

Теперь дадим общее определение логарифма. Пусть a > 0 и a ≠ 1 (условия те же, что и для основания показательной функции).

Определение. Логарифм положительного числа b по основанию a (обозначается log_ab) — это показатель степени, в которую надо возвести a, чтобы получить b.

Иными словами,

Например:

  так как  

, так как 

  так как  ;

, так как  .

Логарифм с основанием 10 называется десятичным и обозначается lg. Например, lg 100 = 2, lg 1000 = 3, lg 0,01 = −2.

Логарифм с основанием e</em > называется натуральным и обозначается ln.

Обратите внимание: логарифм определён только для положительных чисел. Причина заключается в том, что показательная функция может принимать лишь положительные значения. Например, число log₂(−4) не существует: в какую бы степень мы ни возводили 2, мы никогда не получим −4.

Не забывайте также про ограничения на основание логарифма: 0 < a < 1 или a > 1.

Основные формулы

По определению, log_ab — это показатель степени, в которую надо возвести число a, чтобы получить число b:

Формула (1) называется основным логарифмическим тождеством.
Вот ещё один вариант записи определения логарифма:

log_aa^x=x.

Перечислим свойства логарифмов. Они являются простыми следствиями правил действия со степенями. Все логарифмы ниже считаются определёнными.

Логарифм произведения — это сумма логарифмов:

loga(bc) = logab + logac.

(2)

Логарифм частного — это разность логарифмов:

(3)

Показатель степени логарифмируемого числа «спрыгивает» перед логарифмом:

(4)

Показатель степени основания логарифма тоже «спрыгивает», но в виде обратного числа:

(5)

Формулы (4) и (5) вместе дают:

(6)

В частности, если m = n, мы получаем формулу:

(7)

Например, .

Наконец, важнейшая формула перехода к новому основанию:

(8)

В частности, если c = b, то log_bb = 1, и тогда:

(9)

Задача 5

Приведём несколько примеров из банка заданий.
1. (применили формулу (2) суммы логарифмов).

2. (применили основное логарифмическое тождество(1))

3. (применили формулу (4).

4. (применили формулу (9), перейдя к новому основанию 0,8).

5. (применили формулу (3) разности логарифмов)

Немного истории

Теперь вы поняли, что такое логарифмы и как ими пользоваться. Но для чего они всё-таки нужны? Или это просто такая математическая игрушка с хитрой инструкцией по применению?

Понятие логарифма и логарифмические таблицы появились в 17 веке, и значение их было огромно.

Это в наши дни вычисления не представляют труда — у каждого есть калькулятор. А как считали в «докомпьютерные» времена?

Складывать и вычитать можно было на счётах, а вот умножать и делить приходилось «в столбик» — медленно и трудно.

В 15–17 веках, в эпоху великих географических открытий, стали бурно развиваться торговля, экономика и наука. Требования к математике росли: расчёты становились более сложными, а точность — например, для решения навигационных задач — нужна была всё более высокая.

Необходим был инструмент, позволяющий упростить и ускорить расчёты, и таким инструментом явились логарифмы.

Предположим, что b и c — большие числа, которые надо перемножить. Появление таблиц логарифмов (например, с основанием 10) существенно упростило эту задачу. Теперь вычислителю достаточно было найти по таблицам десятичные логарифмы чисел b и c, сложить их (на счётах) и получить логарифм произведения: lgb + lgc = lg(bc).

А затем по таблице логарифмов найти само произведение чисел b и c.

Недаром французский математик и астроном Лаплас сказал, что изобретение логарифмов удлинило жизнь вычислителей. Логарифмическая линейка (которой инженеры пользовались до 70-х годов двадцатого века) была не менее прогрессивным изобретением, чем современный калькулятор.

Но это еще не всё! Мы не занимались бы логарифмами, если бы они имели лишь историческую, «музейную» ценность. О неожиданных применениях логарифмов мы расскажем в следующей статье, посвящённой логарифмической функции.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Логарифмы. Логарифмические формулы. Свойства логарифмов

Факт 1.
\(\bullet\) Логарифм по основанию \(a\) от \(b\) – это число \(t\), которое показывает, в какую степень нужно возвести \(a\), чтобы получить \(b\).
Ограничения: числа \(a\) и \(b\) такие, что \(a>0,\ a\ne 1,\ b>0\).
\[\Large{{\color{blue}{\log_a{b}=t\quad\Leftrightarrow\quad a^t=b }}}\]
Т.к. мы имеем право возводить в любую степень, то \(t\in \mathbb{R}\).
Таким образом, верно основное логарифмическое тождество \[{\Large{a^{\log_ab}=b}}\]
\(\bullet\) Справедливы следующие формулы: \[{\large{\begin{array}{|ll|l|} \hline \qquad \qquad \qquad \qquad {\small{\text{Формулы}}} && \qquad \qquad{\small{\text{Ограничения}}}\\ &&\\ \hline \textbf{(1)} \log_a1=0&&a>0, a\ne 1\\ &&\\ \textbf{(2)} \log_aa=1 &&a>0, a\ne 1\\ &&\\ \textbf{(3)} \log_{a}{b^m}=m\log_a|b|&(m — {\small{\text{четн.}}})&a>0, a\ne 1, b\ne 0\\ &&\\ \textbf{(4)}\log_{a}{b^m}=m\log_ab& (m — {\small{\text{нечетн.}}})&a>0, a\ne 1, b>0\\ &&\\ \textbf{(5)} \log_{a^n}{b}=\frac 1n\log_{|a|}b&(n — {\small{\text{четн.}}})&a\ne 0, a\ne 1, b>0\\ &&\\ \textbf{(6)}\log_{a^n}b=\frac1n\log_ab&(n — {\small{\text{нечетн.}}})&a>0, a\ne 1, b>0\\ &&\\ \textbf{(7)} \log_a{bc}=\log_a|b|+\log_a|c|&&a>0, a\ne 1, bc\ne 0\\ &&\\ \textbf{(8)} \log_a{\dfrac bc}=\log_a|b|-\log_a|c|&&a>0, a\ne 1,bc\ne 0 \\ &&\\ \textbf{(9)} a^{\log_ab}=b &&a>0, a\ne 1, b>0\\ &&\\ \textbf{(10)}c^{\log_ab}=b^{\log_ac}&&a>0, a\ne 1, b>0, c>0\\ &&\\ \textbf{(11)} \log_ab\cdot \log_bc=\log_ac && a>0, a\ne 1,b>0, b\ne 1, c>0\\ &&\\ \textbf{(11′}) \log_bc=\dfrac{\log_ac}{\log_ab}&&a>0, a\ne 1,b>0, b\ne 1, c>0\\ &&\\ &&\\ {\small{\text{ЧАСТНЫЕ СЛУЧАИ:}}}&& \\ \textbf{(12)} \log_ab\cdot \log_ba=1 && a>0, a\ne 1, b>0, b\ne 1\\ &&\\ \textbf{(12′}) \log_ab=\dfrac1{\log_ba}&&a>0, a\ne 1, b>0, b\ne 1\\ &&\\ \hline \end{array}}}\]

Заметим, что при выполнении ограничений данные формулы верны в обе стороны!

 

shkolkovo.net