Как решать параметры егэ – Исследовательская работа «Приемы и способы решения заданий с параметром на ЕГЭ по математике»

Задачи с параметрами из ЕГЭ

Автор Сергей

Воскресенье, Март 11, 2012

Решение задач с параметрами требует наличия определенной математической культуры. С реше-нием задач с параметрами приходится сталкиваться не только в математике. Очень многие законы и закономерности из физики, эконо-мики и других областей описываются уравнениями и неравенствами с параметрами. Фактически, решая задачи по физике, химии, экономике и некоторым другим школьным дисциплинам, ученик имеет дело с параметрами. Решению задач с параметрами посвящено большое количество учебно-методической литературы. В данной статей приводятся лишь некоторые представления о том, как рассуждают при решении подобных заданий. С этой целью рассмотрены несколько примеров, большая часть которых взята из вариантов ЕГЭ по математике прошлых лет (задача C5).

Решение «типичных» задач с параметрами

Пример 1. При каких значениях корни уравнения положительны?

Решение.

1) Начнем с рассмотрения случая, когда . Тогда уравнение принимает вид , откуда получаем, что — положительный корень. Значит данное значение нам подходит. Запомнили.

2) Теперь рассматриваем случай, когда . Разделим обе части уравнения на . В результате получаем следующее квадратное уравнение:

   

Так как ветви соответствующей параболы направлены вверх, данное уравнение имеет два положительных корня в том случае, если эта парабола пересекает ось OY в точке, находящейся выше нуля (то есть значение соответствующей квадратичной функции при положительно), абсцисса вершины параболы положительна, а дискриминант квадратного уравнения неотрицателен. То есть имеет место следующая система:

   

Решая данную систему неравенств, получаем промежуточный ответ: .

3) Объединяем решения, полученные в предыдущих двух пунктах. В результате получаем окончательный ответ: .

Задача для самостоятельного решения №1. Для каждого значения

yourtutor.info

уравнения и неравенства с параметром

Существует ровно три генеральных метода решения задач 18:

• Метод перебора — классический перебор вариантов. Например, когда выражение под модулем больше нуля и когда меньше;
• Графический метод — привлечение чертежа. Во многих задачах 18 достаточно начертить графики функций — и решение становится очевидным;
• Метод следствий — нестандартный и, как правило, самый изощренный. Если в исходном условии удастся подметить что-нибудь полезное, в дальнейшем можно значительно упростить решение всей задачи.

Конечно, одну и ту же задачу зачастую можно решить разными способами. Но далеко не все они оптимальны: выбрав неправильный «путь», можно увязнуть в вычислениях, так и не дойдя до ответа.

Поэтому в данном разделе я рассмотрю все способы, а ваша задача — практиковаться и учиться правильно выбирать.:)

Глава 1.

Графический подход

§ 1.

Вебинар по задачам 18: модуль и окружности

§ 2.

Как решать задачу 18: графический подход

§ 3.

Задача 18: две окружности и модуль

§ 4.

Задача 18: пересечение графиков окружности и модуля

§ 5.

Новая задача 18 из пробного ЕГЭ — наглядный пример того, как эффективно работает графическое решение задач с параметром.

Глава 2.

Аналитический подход

§ 1.

Задачи 18: Аналитическое решение

§ 2.

Окружность и модуль: задачи 18 с двумя параметрами

§ 3.

Аналитическое решение задачи 18 с перебором различных вариантов

Глава 3.

Нестандартные приемы

§ 1.

Задача 18: метод симметричных корней

§ 2.

Как увидеть симметрию корней в задаче 18?

§ 3.

Метод мажорант в задаче 18

§ 4.

Графическое решение сложных задач 18 с модулем

§ 5.

Задание 18: Симметрия корней в системе уравнений

§ 6.

Анализ знаков квадратного трёхчлена в сложных задачах 18

§ 7.

Применение производной для отыскания точек пересечения графиков

§ 8.

Продвинутый метод симметричных корней

§ 9.

Новая задача 18 с графическим решением

Функции с параметром

1

2

3

4

5

6

7

8

9

10

11

12

Уравнения с параметром

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

56

57

58

59

60

61

62

63

64

65

66

67

68

69

70

71

72

73

74

75

76

77

78

79

80

81

82

83

84

85

86

87

88

89

90

91

92

93

94

95

96

97

98

99

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

Неравенства с параметром

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

Системы с параметром

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

www.berdov.com

Задачи с параметром. ЕГЭ по математике

Уравнение x^3+3x^2-x\log_{3}(a+1)+5=0 имеет единственное решение на отрезке [0;2], если графики функций y=x^3+3x^2 и y=x\log_{3}(a+1)-5 имеют единственную точку пересечения на отрезке [0;2].

Построим графики этих функций.

1) y=x^3+3x^2.

Найдём стационарные точки: y’=3x^2+6x=3x(x+2). y’=0 при x=0, x=-2

y(-2)=-8+3(-2)^2=-8+12=4, y(0)=0. Отсюда получаем график y=x^3+3x^2.

2) y=x\log_{3}(a+1)-5. Графиком функции является прямая, угловой коэффициент которой k=\log_{3}(a+1). Прямая y=kx-5 проходит через точку (0;-5).

Найдём точку x_{0}, в которой прямая y=kx-5 является касательной к графику функции y=x^3+3x^2.

Уравнение касательной y=(x_{0}^3+3x_{0}^2)+(3x_{0}^2+6x_{0})(x-x_{0}) проходит через точку (0;-5), следовательно, -5=(x_{0}^3+3x_{0}^2)-x_{0}(3x_{0}^2+6x_{0}),

2x_{0}^3+3x_{0}^2-5=0. x_{0}=1 — точка касания.

2x_{0}^3+3x_{0}^2-5=(x_{0}-1)(2x_{0}^2+5x_{0}+5).

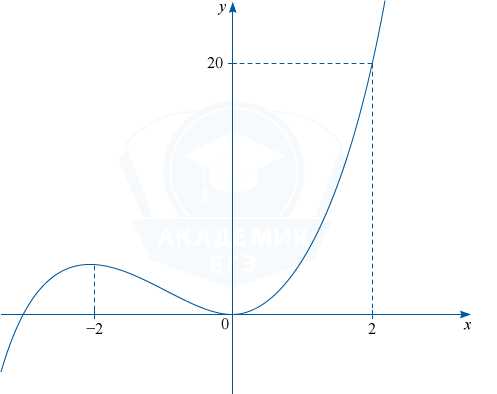
Других точек касания нет, так как уравнение 2x_{0}^2+5x_{0}+5=0 корней не имеет.

Если x=1, то y=4, тогда 4=k-5, откуда k=9.

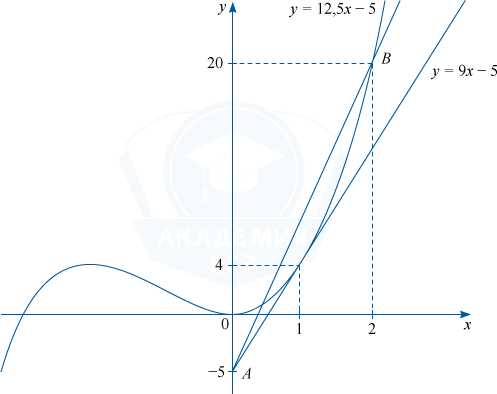
Найдем значение k, при котором прямая y=kx-5 проходит через точку (2;20). 20=2k-5, k=12,5, y=12,5x-5.

Для k=9 и k > 12,5 графики функций y=x^3+3x^2 и y=kx-5 имеют на отрезке [0;2] единственную общую точку. Найдем значения параметра a.

\log_{3}(a+1)=9, a+1=3^9, a=3^9-1.

\log_{3}(a+1) > 12,5, a+1 > 3^{\tfrac{25}{2}}. a > 3^{12,5}-1.

Итак, если a=3^9-1 или a > 3^{12,5}-1, то уравнение x^3+3x^2-x\log_{3}(a+1)+5=0 имеет единственное решение на отрезке [0;2].

academyege.ru

Урок по теме «Методы решения задач с параметрами»

Разделы: Математика

---

Цель данной работы – изучение различных способов решения задач с параметрами. Возможность и умение решать задачи с параметрами демонстрируют владение методами решения уравнений и неравенств, осмысленное понимание теоретических сведений, уровень логического мышления, стимулируют познавательную деятельность. Для развития этих навыков необходимы длительнее усилия, именно поэтому в профильных 10-11 классах с углубленным изучением точных наук введен курс: “Математический практикум”, частью которого является решение уравнений и неравенств с параметрами. Курс входит в число дисциплин, включенных в компонент учебного плана школы.

Успешному изучению методов решения задач с параметрами могут помочь элективный или факультативный курсы, или компонент за сеткой по теме: “Задачи с параметрами”.

Рассмотрим четыре больших класса задач с параметрами:

1. Уравнения, неравенства и их системы, которые необходимо решить для любого значения параметра, либо для значений параметра, принадлежащих определенному множеству.
2. Уравнения, неравенства и их системы, для которых требуется определить количество решений в зависимости от значения параметра.
3. Уравнения, неравенства и их системы, для которых требуется найти все те значения параметра, при которых указанные уравнения (системы, неравенства) имеют заданное число решений.
4. Уравнения, неравенства и их системы, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.

Методы решений задач с параметрами.

1. Аналитический метод.

Это способ прямого решения, повторяющий стандартные процедуры нахождения ответа в задачах без параметра.

Пример 1. Найдите все значения параметра a, при которых уравнение:

(2a – 1)x² + ax + (2a – 3) =0  имеет не более одного корня.

Решение:

При 2a – 1 = 0 данное уравнение квадратным не является, поэтому случай a =1/2 разбираем отдельно.

Если a = 1/2, то уравнение принимает вид 1/2x – 2 = 0, оно имеет один корень.

Если a ≠ 1/2, то уравнение является квадратным; чтобы оно имело не более одного корня необходимо и достаточно, чтобы дискриминант был неположителен:

D = a² – 4(2a – 1)(2a – 3) = -15a² + 32a  – 12;

Чтобы записать окончательный ответ, необходимо понять,

2. Графический метод.

В зависимости от задачи (с переменной x и параметром a) рассматриваются графики в координатной плоскости (x;y) или в плоскости (x;a).

Пример 2. Для каждого значения параметра a определите количество решений уравнения .

Решение:

Заметим, что количество решений уравнения   равно количеству точек пересечения графиков функций и y = a.

График функции показан на рис.1.

Рис.1

Рис. 2

Рис. 3

y = a – это горизонтальная прямая. По графику несложно установить количество точек пересечения в зависимости от a (например, при  a = 11 – две точки пересечения; при a = 2 – восемь точек пересечения).

Ответ: при a < 0 – решений нет; при a = 0 и a = 25/4  – четыре решения; при 0 < a < 6  – восемь решений; при a = 6 – семь решений; при

6 < a < 25/4 – шесть решений; при a > 25/4 – два решения.

3. Метод решения относительно параметра.

При решении этим способом переменные х и а принимаются равноправными, и выбирается та переменная, относительно которой аналитическое решение становится более простым. После упрощений нужно вернуться к исходному смыслу переменных х и а и закончить решение.

Пример 3. Найти все значения параметра а , при каждом из которых уравнение = —ax +3a +2  имеет единственное решение.

Решение:

Будем решать это уравнение заменой переменных. Пусть = t , t ≥ 0 , тогда x = t² + 8  и уравнение примет вид at² + t + 5a – 2 = 0  . Теперь задача состоит в том, чтобы найти все а, при которых уравнение at² + t + 5a – 2 = 0  имеет единственное неотрицательное решение. Это имеет место в следующих случаях.

1) Если а = 0, то уравнение имеет единственное решение t = 2.

Решение некоторых типов уравнений и неравенств с параметрами.

Задачи с параметрами помогают в формировании логического мышления, в приобретении навыков исследовательской деятельности.

Решение каждой задачи своеобразно и требует к себе индивидуального, нестандартного подхода, поскольку не существует единого способа решения таких задач.

Ⅰ

. Линейные уравнения.

Задача № 1. При каких значениях параметра b уравнение не имеет корней?

Ⅱ

. Степенные уравнения, неравенства и их системы.

Задача №2. Найти все значения параметра a, при которых множество решений неравенства:

содержит число 6, а также содержит два отрезка длиной 6, не имеющие общих точек.

Решение:

.

Преобразуем обе части неравенства.

 

Для того, чтобы множество решений неравенства содержало число 6, необходимо и достаточно выполнение условия:

Рис.4

При a > 6 множество решений неравенства: .

Интервал (0;5) не может содержать ни одного отрезка длины 6. Значит, два непересекающихся отрезка длины 6 должны содержаться в интервале (5; a).

Это

Ⅲ

. Показательные уравнения, неравенства и системы.

Задача № 3. В области определения функции взяли все целые положительные числа и сложили их. Найти все значения, при которых такая сумма будет больше 5, но меньше 10.

Решение:

1) Графиком дробно-линейной функции     является гипербола. По условию x > 0. При неограниченном возрастании х дробь монотонно убывает и приближается к нулю, а значения функции z возрастают и приближаются к 5. Кроме того, z(0) = 1.

Рис. 5

2) По определению степени область определения D(y) состоит из решений неравенства . При a = 1 получаем неравенство, у которого решений нет. Поэтому функция у нигде не определена.

3) При 0 < a < 1 показательная функция с основанием а убывает и неравенство   равносильно неравенству . Так как x > 0 , то z(x) > z(0) = 1 . Значит, каждое положительное значение х является решением неравенства . Поэтому для таких а указанную в условии сумму нельзя найти.

4) При a > 1 показательная функция с основанием а возрастает и неравенство   равносильно неравенству . Если a  ≥ 5, то любое положительное число является его решением, и указанную в условии сумму нельзя найти. Если 1 < a < 5, то множество положительных решений – это интервал (0;x₀) , где a = z(x₀) .

5) Целые числа расположены в этом интервале подряд, начиная с 1. Вычислим суммы последовательно идущих натуральных чисел, начиная с 1 : 1; 1+2 = 3; 1+2+3 = 6; 1+2+3+4 = 10;… Поэтому указанная сумма будет больше 5 и меньше 10, только если число 3 лежит в интервале (0;x₀), а число 4 не лежит в этом интервале. Значит, 3 < x₀ ≤ 4 . Так как   возрастает на , то z(3) < z(x₀) ≤ z(4) .

Решение иррациональных уравнений и неравенств, а также уравнений, неравенств и систем, содержащих модули рассмотрены в Приложении 1.

Задачи с параметрами являются сложными потому, что не существует единого алгоритма их решения. Спецификой подобных задач является то, что наряду с неизвестными величинами в них фигурируют параметры, численные значения которых не указаны конкретно, но считаются известными и заданными на некотором числовом множестве. При этом значения параметров существенно влияют на логический и технический ход решения задачи и форму ответа.

По статистике многие из выпускников не приступают к решению задач с параметрами на ЕГЭ. По данным ФИПИ всего 10% выпускников приступают к решению таких задач, и процент их верного решения невысок: 2–3%, поэтому приобретение навыков решения трудных, нестандартных заданий, в том числе задач с параметрами, учащимися школ по-прежнему остается актуальным.

xn--i1abbnckbmcl9fb.xn--p1ai

«Подготовка к ЕГЭ :Задачи с параметрами»

Доклад на ГМО учителя математики МБОУ СОШ №9

Молчановой Елены Владимировны

«Подготовка к ЕГЭ по математике: задачи с параметрами ».

Поскольку в школьных учебниках нет определения параметра, я предлагаю взять за основу следующий его простейший вариант.

Определение. Параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.

Что означает «решить задачу с параметром»?

Естественно, это зависит от вопроса в задаче. Если, например, требуется решить уравнение, неравенство, их систему или совокупность, то это означает предъявить обоснованный ответ либо для любого значения параметра, либо для значения параметра, принадлежащего заранее оговоренному множеству.

Если же требуется найти значения параметра, при которых множество решений уравнения, неравенства и т. д. удовлетворяет объявленному условию, то, очевидно, решение задачи и состоит в поиске указанных значений параметра.

Более прозрачное понимание того, что означает решить задачу с параметром, у читателя сформируется после ознакомления с примерами решения задач на последующих страницах.

 Какие основные типы задач с параметрами?

Тип 1. Уравнения, неравенства, их системы и совокупности, которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству.

Этот тип задач является базовым при овладении темой «Задачи с параметрами», поскольку вложенный труд предопределяет успех и при решении задач всех других основных типов.

Тип 2. Уравнения, неравенства, их системы и совокупности, для которых требуется определить количество решений в зависимости от значения параметра (параметров).

Обращаю внимание на то, что при решении задач данного типа нет необходимости ни решать заданные уравнения, неравенства, их системы и совокупности и т. д., ни приводить эти решения; такая лишняя в большинстве случаев работа является тактической ошибкой, приводящей к неоправданным затратам времени. Однако не стоит абсолютизировать сказанное, так как иногда прямое решение в соответствии с типом 1 является единственным разумным путем получения ответа при решении задачи типа 2.

Тип 3. Уравнения, неравенства, их системы и совокупности, для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы и совокупности имеют заданное число решений (в частности, не имеют или имеют бесконечное множество решений).

Легко увидеть, что задачи типа 3 в каком-то смысле обратны задачам типа 2.

Тип 4. Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.

Например, найти значения параметра, при которых:

1) уравнение выполняется для любого значения переменной из заданного промежутка;
2) множество решений первого уравнения является подмножеством множества решений второго уравнения и т. д.

Комментарий. Многообразие задач с параметром охватывает весь курс школьной математики (и алгебры, и геометрии), но подавляющая часть из них на выпускных и вступительных экзаменах относится к одному из четырех перечисленных типов, которые по этой причине названы основными.

Наиболее массовый класс задач с параметром — задачи с одной неизвестной и одним параметром. Следующий пункт указывает основные способы решения задач именно этого класса.

 Каковы основные способы (методы) решения задач с параметром?

Способ I (аналитический). Это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Иногда говорят, что это способ силового, в хорошем смысле «наглого» решения.

Комментарий.  Аналитический способ решения задач с параметром есть самый трудный способ, требующий высокой грамотности и наибольших усилий по овладению им.

Способ II (графический). В зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a).

Комментарий. Исключительная наглядность и красота графического способа решения задач с параметром настолько увлекает изучающих тему «Задачи с параметром», что они начинают игнорировать другие способы решения, забывая общеизвестный факт: для любого класса задач их авторы могут сформулировать такую, которая блестяще решается данным способом и с колоссальными трудностями остальными способами. Поэтому на начальной стадии изучения опасно начинать с графических приемов решения задач с параметром.

Способ III (решение относительно параметра). При решении этим способом переменные x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных x и a и заканчиваем решение.

Перейду теперь к демонстрации указанных способов решения задач с параметром, так как это мой любимый метод решения заданий данного типа.

Проанализировав все задания с параметрами, решаемыми графическим методом, я знакомство с параметрами начинаю с заданий ЕГЭ В7 2002 года :

При каком целом значении к уравнение 45х – 3х² – х³ + 3к = 0 имеет ровно два корня ?

Эти задания позволяют, во первых, вспомнить как строить графики с использованием производной, а во-вторых, объяснить смысл прямой у = к.

На последующих занятиях я пользуюсь подборкой легких и средних по уровню конкурсных задач с параметрами для подготовки к ЕГЭ, уравнений с модулем. Эти задания можно рекомендовать учителям по математике в качестве стартового комплекта упражнений для обучения работе с параметром, заключенным под знак модуля. Большинство номеров решаются графическим способом и предоставляют учителю готовый план урока (или двух уроков) с сильным учеником. Начальная подготовка к ЕГЭ по математике на упражнениях, близких по сложности к реальным номерам С5. Многие из предложенных заданий взяты из материалов для подготовки к ЕГЭ 2009 года, а некоторые – из интернета из опыта коллег.

1) Укажите все значения параметра p, при которых уравнение имеет 4 корня?
Ответ:

2) При каких значениях параметра а уравнение не имеет решений?
Ответ:

3) Найдите все значения а, при каждом из которых уравнение имеет ровно 3 корня?
Ответ: а=2

4) При каких значениях параметра b уравнение имеет единственное решение? Ответ:

5) Найдите все значения m, при которых уравнение не имеет решений.
Ответ:

6) Найдите все значения а, при которых уравнение имеет ровно 3 различных корня. (Если значений а более одного, то в ответе запишите их сумму.)

Ответ: 3

7) При каких значениях b уравнение имеет ровно 2 решения?
Ответ:

8) Укажите такие параметры k, при которых уравнение имеет не менее двух решений.
Ответ:

9) При каких значениях параметра p уравнение имеет только одно решение?
Ответ:

10) Найдите все значения а, при каждом из которых уравнение (х + 1) имеет ровно 2 корня? Если значений а окажется несколько, то в ответ запишите их сумму.

Ответ: — 3

11) Найдите все значения а, при которых уравнение имеет ровно 3 корня? (Если значений а более одного, то в ответ запишите их сумму).

Ответ: 4

12) При каком наменьшем натуральном значении параметра а уравнение – = 11 имеет только положительные корни?

Ответ: 19

13) Найдите все значения а, при каждом из которых уравнение = 1 имеет ровно 3 корня? (Если значений а более одного, то в ответе запишите их сумму).

Ответ:- 3

14) Укажите такие значения параметра t, при которых уравнение имеет 4 различных решения. Ответ:

15) Найдите такие параметры m, при которых уравнение имеет два различных решения. Ответ:

16) При каких значениях параметра p уравнение имеет ровно 3 экстремума? Ответ:

17) Укажите все возможные параметры n, при которых функция имеет ровно одну точку минимума. Ответ:

Опубликованный комплект регулярно используется мной для работы со способным, но не самым сильным учеником, претендующим, тем не менее, на высокий балл ЕГЭ за счет решения номера С5. Подготовку такого ученика учитель проводит в несколько этапов, выделяя для тренировки отдельных навыков, необходимых для поиска и реализации длинных решений, отдельные уроки. Эта подборка подходит для стадии формирования представлений о плавающих рисунках в зависимости от параметра. Номера 16 и 17 составлены по образцу реального уравнения с параметром на ЕГЭ 2011г. Задачи выстроены в порядок возрастания их сложности.

Задание C5 по математике ЕГЭ 2012

    Здесь мы имеем традиционную задачу с параметром, требующую умеренного владения материалом и применения нескольких свойств и теорем. Это задание является одним из самых сложных заданий Единого государственного экзамена по математике. Оно рассчитано, прежде всего, на тех, кто собирается продолжать образование в вузах с повышенными требованиями к математической подготовке абитуриентов. Для успешного решения задачи важно свободно оперировать изученными определениями, свойствами, теоремами, применять их в различных ситуациях, анализировать условие и находить возможные пути решения.

На сайте подготовки к ЕГЭ Александра Ларина с 11.05.2012 года были предложены тренировочные варианты №1 – 22 с заданиями уровня «С», С5 некоторых из них были аналогичны тем заданиям, которые были на реальном экзамене. Например, найдите все значения параметра а, при каждом из которых графики функций f(х) = и g(х) = а(х + 5) + 2 не имеют общих точек?

Разберем решение задания С5 из экзамена 2012 года.

Задание С5 из ЕГЭ-2012

При каких значениях параметра a уравнение имеет не менее двух корней.

Решим эту задачу графически. Построим график левой части уравнения:   и график правой части:   и сформулируем вопрос задачи так: при каких значениях параметра  a графики функций  и  имеют две или более общих точки.

В левой части исходного уравнения параметр отсутствует, поэтому мы можем построить график функции .

Будем строить это график с помощью линейных преобразований графика функции :

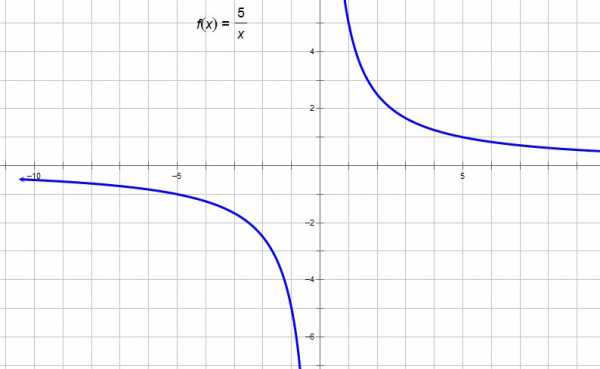
1. Сдвинем график функции  на 3 единицы вниз вдоль оси OY, получим график функции :

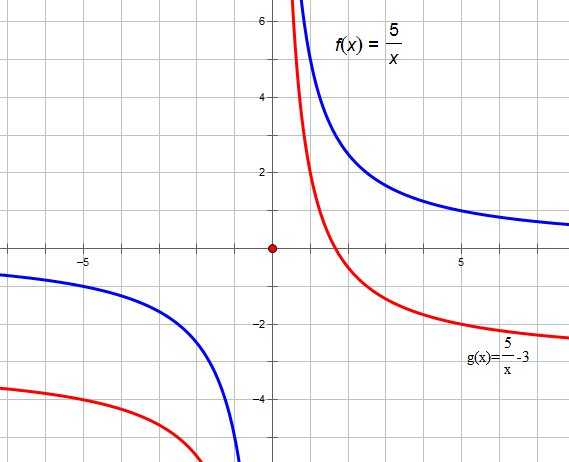
2. Построим график функции . Для этого часть графика функции , расположенную ниже оси ОХ, отобразим симметрично относительно этой оси:

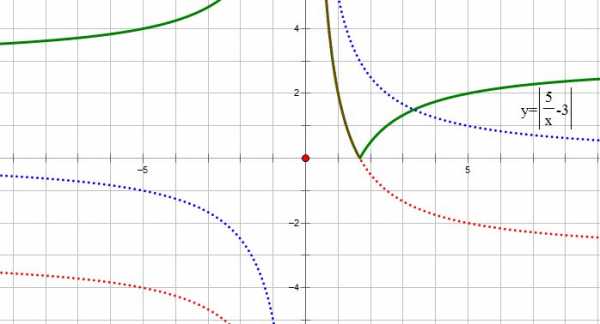
Итак, график функции  имеет вид:

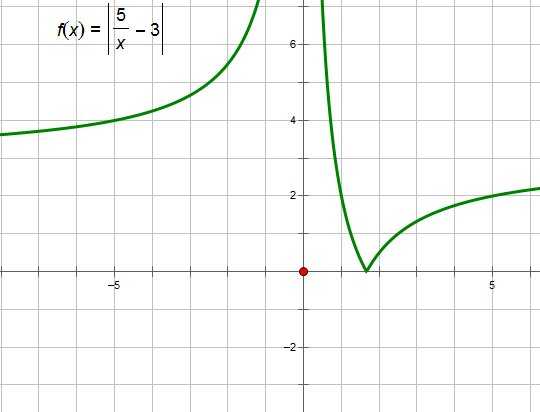
График функции  представляет собой семейство прямых с переменным коэффициентом наклона, равным а, сдвинутых на 1 единицу вниз вдоль оси OY. То есть точка с координатами (0;1) представляет собой центр вращения этого семейства прямых:

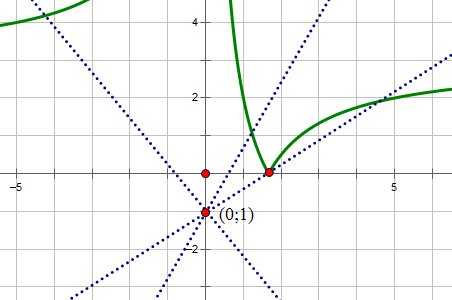
Рассмотрим положения прямой , в которых она имеет более одной точки пересечения с графиком функции :

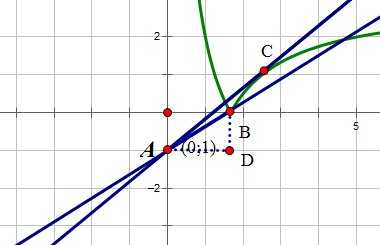
Прямые АВ и АС имеют две точки пересечения с графиком функции. Все прямые, расположенные между ними имеют 3 точки пересечения с графиком функции  .

Чтобы найти коэффициент наклона прямой АВ, найдем абсциссу  точки  В.

Точка В – это точка пересечения графика функции  с осью ОХ. В этой точке у=0. Получим уравнение: , отсюда . Коэффициент а наклона прямой АВ равен тангенсу угла BAD треугольника ABD и равен 

Найдем коэффициент наклона прямой АС. Точка С – это точка, в которой прямая  касается графика функции  (точка С принадлежит части графика функции , отображенной симметрично относительно оси ОХ). То есть это точка, в которой графики функции    и  имеют одну общую точку.

Теперь нам нужно найти значение параметра а, при котором уравнение   имеет одно решение.

Умножим обе части уравнения на х и перенесем все слагаемые влево. Получим квадратное уравнение  Это уравнение  имеет единственный корень, если дискриминант равен нулю.

, 

Таким образом,

уравнение  имеет два решения, если  или

Уравнение имеет три решения, если 

Несколько советов при обучении решению задач с параметрами (тезисы коллег):

1) Для обучения решению сложных задач на модули графическим образом желательно провести хотя бы один урок на подготовку к выполнению необходимых построений. Нужно разобрать темы «построение графика функции», «построение множества точек, заданных уравнением с двумя переменными».

2) Перед тем, как приступить к задачам С5 хорошенько подумайте, стоит ли тратить время и силы на задания, успех в выполнении которых зависит в первую очередь от количества решенного математического материала без параметра. Ученик должен иметь отличную подготовку по уравнениям с одной переменной и уметь представлять себе весь процесс их решения от начала до самого конца. Если таких навыков нет — не тратье лишнее время на профильную подготовку к ЕГЭ. Уделите лучше время простой математике, без параметров.

3) Никогда не задавайте ученику того, что не было разобрано на занятии и предостерегайте его от потерь случаев. Параметры — коварная тема! Очень легко запутаться в многообразии случаев и какой-нибудь из них упустить.

infourok.ru

Примеры решения задач с параметрами

«Примеры решения задач с параметрами (С5 ЕГЭ)»

Симакина Елена Анатольевна,

учитель математики МБОУ «Лицей»

Новомосковск

март 2014

Цели и задачи:

1) оказание практической помощи учителям математики в решении задач с параметрами;

2) создание банка методических материалов, которые могут быть использованы учителями в практической деятельности;

3) повышение педагогического и методического мастерства, развитие и поддержка новых технологий в организации образовательного процесса;

4) обмен педагогическим опытом.

Задачи с параметрами традиционно считаются наиболее трудными. Это связано с тем, что часто они являются исследовательскими, то есть при их решении надо не просто применить те или иные формулы, а найти те значения параметра, при которых выполнено некоторое условие для корней. При этом не всегда требуется искать сами корни, а бывает, что их и вовсе невозможно найти.

Единого «рецепта» решения задач с параметром не существует. Как это обычно бывает, задачи с параметром допускают весьма разнообразные способы решения. Наиболее распространенными из них являются:

— чисто алгебраический способ решения;

— способ решения, основанный на построении и исследовании геометрической модели данной задачи;

— функциональный способ, в котором могут быть и алгебраические, и геометрические моменты, но базовым является исследование некоторой функции.

Зачастую (но далеко не всегда) графический метод более ясно ведет к цели.

Далее рассмотрены некоторые способы решения заданий С5 , которые предлагались на ЕГЭ прошлых лет.

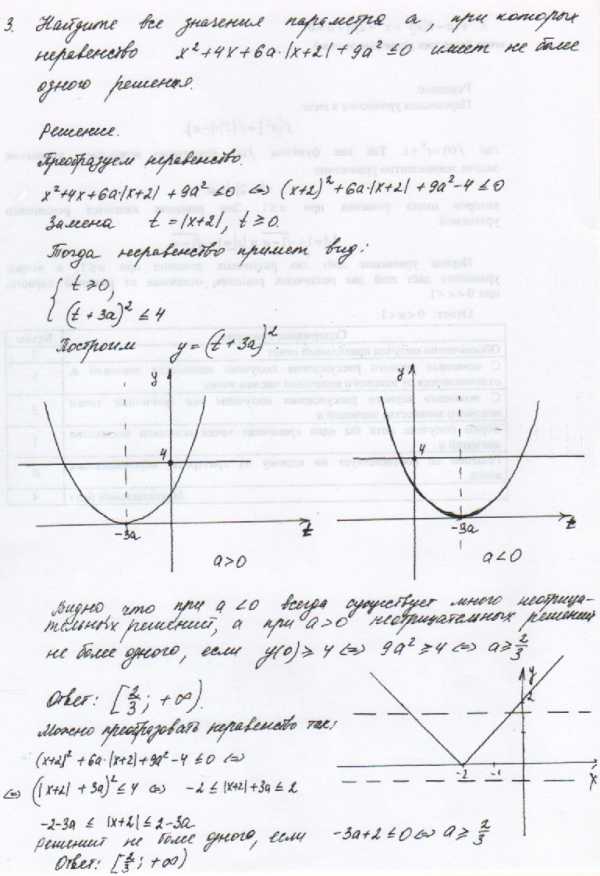
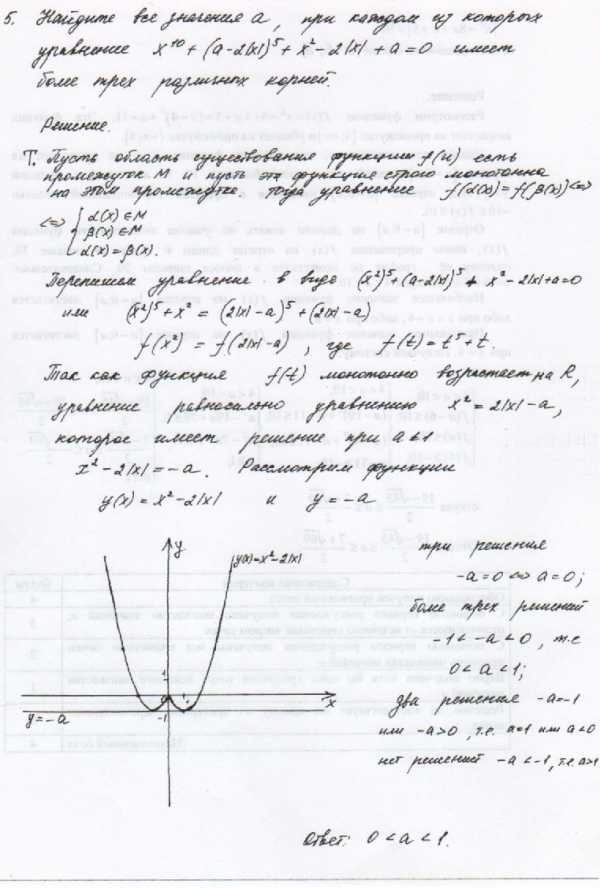
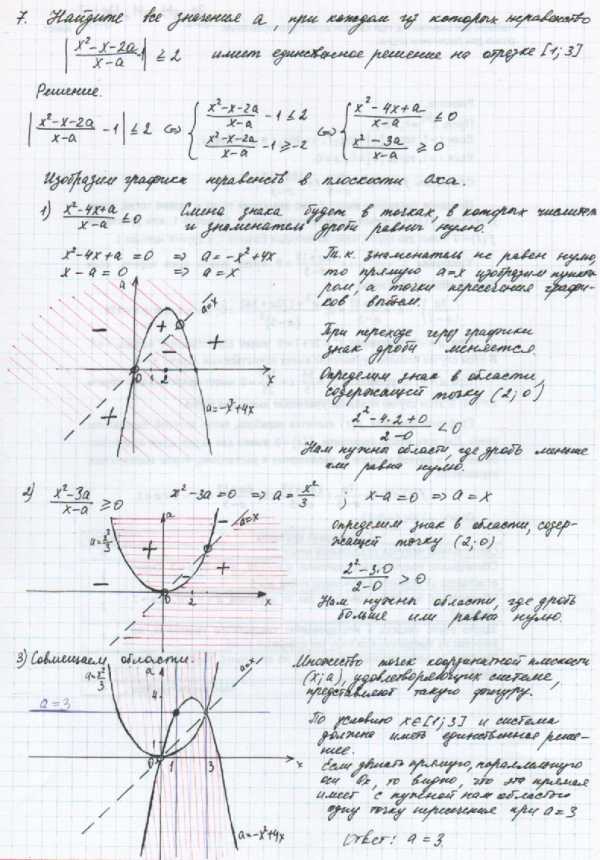
Заключение.

Выше разобранные задачи естественно не исчерпывают все возможные типы задач С5, которые могут быть предложены на экзамене. Показаны отдельные методические приемы решения задач данной направленности, которые могут быть использованы учителями математики при подготовке учащихся к успешной сдаче ЕГЭ.

Источники:

1. Задачи с параметром. ЕГЭ. Математика / С.И. Колесникова. – М.: ООО «Азбука – 2000», 2013. (Серия «МФТИ помогает готовиться к ЕГЭ», выпуск 8)

2. Математика – абитуриенту /В.В. Ткачук. – М.: МЦНМО, 2005.

3. Корянов А.Г., Прокофьев А.А. Различные подходы к решению задач С5 ЕГЭ // Математика. М.: Издательский Дом «Первое сентября», 2011, №5

4. Самое полное издание типовых ва- риантов реальных заданий ЕГЭ 2012: Математика / авт.-сост. И.Р. Высоцкий, Д.Д. Гущин, П.И. Захаров и др.; под ред. А.Л. Семенова, И.В. Ященко. – М.: АСТ: Астрель, 2011. – 93 с. – (Федеральный институт педагогических измерений).

5. www.mathege.ru – Математика ЕГЭ 2012 (открытый банк заданий)

6. www.alexlarin.net – сайт по оказанию информационной поддержки студентам и абитуриентам при подготовке к ЕГЭ, поступлению в ВУЗы и изучении различных разделов высшей математики

infourok.ru

Подготовка к заданиям 18 из ЕГЭ 2018

Приглашаю всех желающих на новый курс, посвящённый задачам 18.

Подробнее о курсе смотрите в видео

Что представляет собой этот курс? Комплект лекций, посвящённых решению задач с параметром из ЕГЭ по математике. После каждой лекции есть задачи, которые надо решить.

Первые лекции покажутся вам совсем простыми, а первые задачи — почти устными. Однако по мере изучения лекций задачи будут становиться всё сложнее, а методы их решения — более изощрёнными. В итоге мы разберём всё, что встречается в настоящем экзамене, и вы просто не сможете не решить задачу 18.

Но это ещё не всё. Начиная с 3-го урока домашняя работа становится обязательной. Вы не получите доступа к следующему уроку, пока не сдадите домашку предыдущего!

Зачем это нужно? Только так можно по-настоящему разобраться в материале. Только так вы научитесь решать действительно сложные задачи. И только так я смогу быть уверен, что вы сдадите настоящий ЕГЭ по математике.

Я не хочу, чтобы вы просто просмотрели очередной комплект уроков (пускай и очень полезных). Я хочу, чтобы вы получили реальные знания и применили их на практике. Чтобы получили дополнительные баллы там, где большинство учеников не будут даже пытаться. Именно для вас я и создаю эти курсы.

Ну что, готовы? Тогда приступаем!

§ 1.

Урок 1.0. На что вообще влияет параметр

§ 2.

Урок 1.1. Метод опорных линий и специфика его применения

§ 3.

Урок 2. Ключевые принципы графического решения задач с параметром

§ 4.

Урок 3. Монотонность функции и её применение для решения задач с параметром.

§ 5.

Урок 4: Развиваем аналитические методы и переходим к более сложным задачам

§ 6.

Урок 5: Модуль и комбинация функций в графическом решении

§ 8.

Урок 6. Доказательство в задачах с параметром

§ 9.

Урок 7. Анализ знаков функций

www.berdov.com