Как решать 2 задание егэ по информатике – Разбор задания 2 ЕГЭ. Построение таблиц истинности логических выражений. Часть 2. | Учи Урок информатики

Теория и практика решения задания 2 ЕГЭ по информатике

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа №101»

Теория и практика решения задания 2

ЕГЭ по информатике

Автор:

учитель информатики

Угулава Наталия Владимировна

Саратов, 2018

Типы задания 2

• Задания на отрезки
• Задания на множества
• Задания на поразрядную конъюнкцию
• Задания на условие делимости

Разбор 2 задания ЕГЭ 2018 по информатике и ИКТ из демоверсии.

Это задание базового уровня сложности.

Примерное время выполнения задания 3 минуты.

— умение строить таблицы истинности и логические схемы

— умение строить таблицы истинности и логические схемы

— умение строить таблицы истинности и логические схемы

Проверяемые элементы содержания:

— умение строить таблицы истинности и логические схемы.

Элементы содержания, проверяемые на ЕГЭ:

— высказывания, — логические операции, — кванторы, — истинность высказывания.

ТАБЛИЦЫ ИСТИННОСТИ И ПОРЯДОК

ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ

Для логических операций приняты следующие обозначения :

¬ A, A

не A (отрицание, инверсия)

A ∧ B, A ⋅ B

A и B (логическое умножение, конъюнкция)

A ∨ B, A + B

A или B (логическое сложение, дизъюнкция)

A → B

импликация (следование)

A ↔ B, A ≡ B, A ∼ B

эквиваленция (эквивалентность, равносильность)

A ⊕ B

сложение по модулю 2 (XOR)

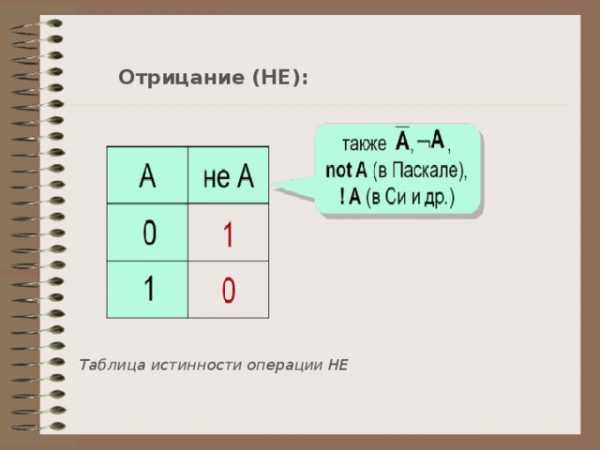
Отрицание (НЕ):

Таблица истинности операции НЕ

Конъюнкция (И):

Таблица истинности операции И (конъюнкция)

Дизъюнкция (ИЛИ):

Таблица истинности операции ИЛИ (дизъюнкция)

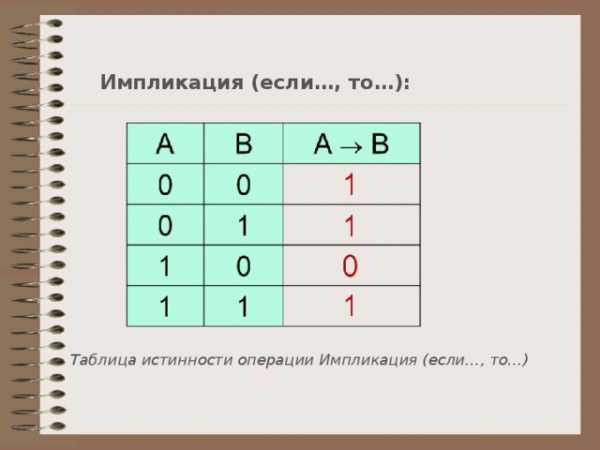
Импликация (если … , то … ):

Таблица истинности операции Импликация (если … , то … )

Задание 2

Логическая функция   F   задаётся выражением ¬ x   \/   y   \/ ( ¬ z   /\   w ). На рисунке приведён фрагмент таблицы истинности функции   F , содержащий   все   наборы аргументов, при которых функция   F   ложна. Определите, какому столбцу таблицы истинности функции   F   соответствует каждая из переменных   w, x, y, z.

Эквивалентность (тогда и только тогда, … ):

Таблица истинности операции Эквивалентность (тогда и только тогда, … )

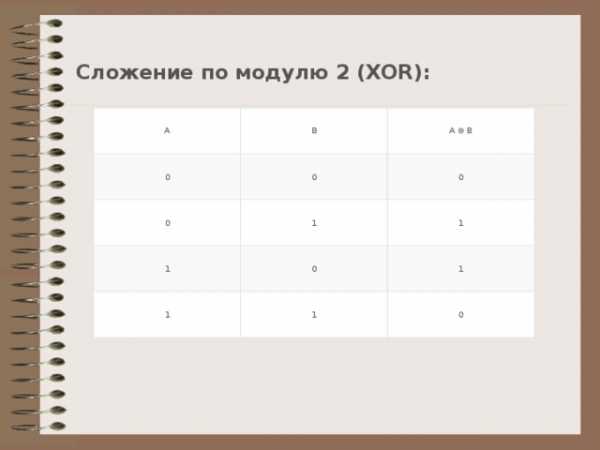
Сложение по модулю 2 (XOR):

A

B

0

A ⊕ B

0

0

1

0

1

1

0

1

1

1

0

Порядок выполнения операций:

• если в выражении нет скобок, сначала выполняются все операции « НЕ » , затем – « И » , затем – « ИЛИ » , импликация, равносильность

Решение заданий 2 ЕГЭ по информатике

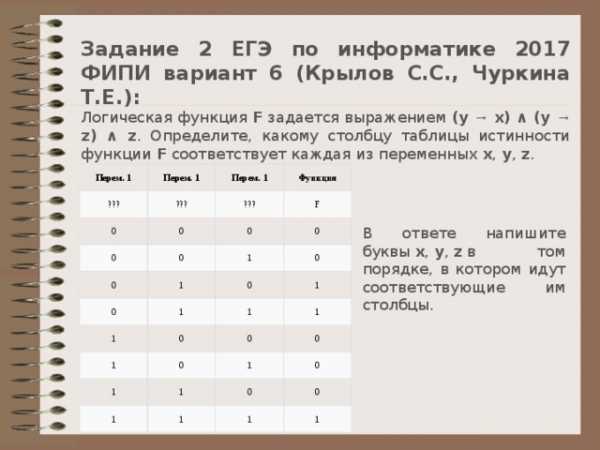
Задание 2 ЕГЭ по информатике 2017 ФИПИ вариант 6 (Крылов С.С., Чуркина Т.Е.):

Логическая функция   F   задается выражением   (y → x) ∧ (y → z) ∧ z . Определите, какому столбцу таблицы истинности функции   F   соответствует каждая из переменных   x ,   y ,   z .

Перем. 1

Перем. 1

???

???

Перем. 1

0

Функция

???

0

0

F

0

0

0

1

0

1

0

0

1

1

0

0

1

1

1

1

0

1

0

0

1

1

1

0

1

0

0

1

1

В ответе напишите буквы   x ,   y ,   z   в том порядке, в котором идут соответствующие им столбцы.

Решение:

• За основу необходимо взять логическую операцию, которую мы будем выполнять в последнюю очередь — это логическое   И   (конъюнкция) или   ∧
• Конъюнкцию легче рассматривать по тем строкам таблицы, там где функция F =   1
• Поскольку для конъюнкции функция истинна только тогда, когда все переменные истинны, то необходимо чтобы отдельно каждая скобка была истинна ((y → x) = 1 и (y → z)=1) и переменная 
  z   тоже была истинной (1)
• Поскольку со скобками сложней работать, определим сначала какому столбцу соответствует   z . Для этого выберем строку, где   F=1   и в остальных ячейках только одна единица, а остальные нули:

0

1

0

1

• Таким образом, из этой строки делаем вывод, что   z   находится во втором столбце (отсчет ведем слева):

???

z

???

F

• Рассмотрим скобку   (y → x)   и строку таблицы:

0

1

1

1

• Для этой строки только   y   может быть   0 , т.к. если   x = 0 , тогда   y=1 , и скобка в результате возвратит ложь ( 1
  → 0 = 0 ). Соответственно,   y   находится в первом столбце. А   x   значит в третьем:
• Для этой строки только   y   может быть   0 , т.к. если   x = 0 , тогда   y=1 , и скобка в результате возвратит ложь ( 1 → 0 = 0 ). Соответственно,   y   находится в первом столбце. А   x   значит в третьем:

y

z

x

F

Результат:   yzx

Задание 2 ЕГЭ по информатике 2017 ФИПИ вариант 11 (Крылов С.С., Чуркина Т.Е.): Каждое из логических выражений   F   и   G   содержит   5   переменных. В таблицах истинности выражений F и G есть ровно   5   одинаковых строк, причем ровно в   4 из них в столбце значений стоит   1 . Сколько строк таблицы истинности для выражения   F ∨ G   содержит   1

  в столбце значений?

Решение:

• Поскольку в каждом из выражений присутствует 5 переменных, то эти 5 переменных порождают таблицу истинности из   32   строк: т.к. каждая из переменных может принимать оно из двух значений (0 или 1), то различных вариантов с пятью переменными будет   2 5 =32 , т.е. 32 строки.
• Из этих 32 строк для каждого выражения (и F и G) мы знаем наверняка только о 5 строках: в 4 из них 1, а в одной — 0.
• В исходных таблицах для каждого выражения F и G мы знаем о существовании только одного 0, т.е. в остальных строках может быть 1. Т.о. для каждого выражения и F и G в   31 строке могут быть единицы   ( 32-1=31 ), а лишь в одной — ноль.
• Тогда для выражения   F ∨ G   только в одном случае будет 0, когда и F=0 и G = 0:
• Вопрос стоит о количестве строк = 1 для таблицы истинности выражения   F ∨ G . Данной выражение — дизъюнкция, которая   ложна только в одном случае  — если   F = 0   и одновременно   G = 0

№

1

F

0

G

2

0

0

…

0

…

32

1

…

1

…

1

…

1

Результат:   31

Решение задачи на отрезки

В ответе напишите буквы   w, x, y, z   в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

¬ x  \/  y  \/ (¬ z  /\  w )

Дизъюнкция (логическое сложение) истинна тогда и только тогда, когда истинно хотя бы одно высказывание.

Следовательно, для того чтобы вся функция была ложна, переменной   х   должен соответствовать тот столбец, в котором стоит значение   1   (так как, ¬ x   превращает 1 в 0) , а переменной   y   столбец со значениями   0 .

Таким образом: — переменной   x   соответствует столбец с   переменной 1 , — переменной   y   соответствует столбец с   переменной 4 .

Решение задачи на отрезки

Конъюнкция (логическое умножение) истинна тогда и только тогда, когда истинны все высказывания  (ложна — если ложно хотя бы одно высказывание).

Конъюнкция  ¬ z  /\  w  в нашем выражении будет истинна только если z=0, w=1.

Посмотрим на вторую строчку таблицы, где переменная 2 равна 1, а переменная 3 равна 0.

Решение задачи

Так как  ¬ z  /\  w  должна равняться 0, то  z  = 1 и  w  = 0 (в противном случае произведение будет равно 1)

Таким образом: — переменной   z   соответствует столбец с переменной 2 (2 столбец), — переменной   w   соответствует столбец с переменной 3 (3 столбец).

Ответ: xzwy

Спасибо за внимание!

multiurok.ru

Разбор 2 задания ЕГЭ 2017 по информатике из демоверсии

Разбор 2 задания ЕГЭ 2017 года по информатике из проекта демоверсии. Это задание базового уровня сложности. Примерное время выполнения задания 3 минуты.

Проверяемые элементы содержания: умение строить таблицы истинности и логические схемы. Элементы содержания, проверяемые на ЕГЭ: высказывания, логические операции, кванторы, истинность высказывания.

Задание 2:

Логическая функция F задаётся выражением x /\¬y /\ (¬z \/ w).
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.

В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Если бы функция была задана выражением ¬x \/ y, зависящим от двух переменных: x и y, и был приведён фрагмент её таблицы истинности, содержащий все наборы аргументов, при которых функция F истинна.

Тогда первому столбцу соответствовала бы переменная y, а второму столбцу – переменная x. В ответе следовало бы написать: yx.

Ответ: ________

Разбор 2 задания ЕГЭ 2017:

x /\¬y /\ (¬z \/ w)

Конъюнкция (логическое умножение) истинна тогда и только тогда, когда истинны все высказывания. Следовательно переменной х должен соответствовать тот столбец, в котором стоит значение 1.

Таким образом, переменной x соответствует столбец с переменной 3.

Переменной ¬y должен соответствовать тот столбец, в котором стоит значение 0.

Дизъюнкция (логическое сложение) двух высказываний истинна тогда и только тогда, когда истинно хотя бы одно высказывание.
Дизъюнкция ¬z \/ w в данной строке будет истинна только если z=0, w=1.

Таким образом, переменной ¬z соответствует столбец с переменной 1 (1 столбец), переменной w соответствует столбец с переменной 4 (4 столбец).

Ответ: zyxw

infedu.ru

как решать задание 2 егэ по информатике видео Видео

…

3 лет назад

Многие жаловались, что задачу сложно разобрал. Ну ловите, простой способ:) Больше разборов на моём сайте:…

…

3 меc назад

Таблицы истинности. Алгебра логики. Демо по всем предметам: http://fipi.ru/ege-i-gve-11/demoversii-specifikacii-kodifikatory — Видео…

…

1 лет назад

Все официальные демоверсии: http://fipi.ru/ege-i-gve-11/demoversii-specifikacii-kodifikatory Логические операции: https://youtu.be/IF7Blq2TT6s —…

…

6 меc назад

Основы алгебры логики. Досрочные по всем предметам: http://fipi.ru/content/kim-ege-2018-dosrochnyy-period Ссылка на видео про закорю…

…

5 лет назад

Мы дарим вам неделю бесплатного доступа на курс по информатике – https://foxford.ru/courses/589/landing?activate_certificate=1&code=FOXYOUTUBE…

…

2 лет назад

Простое задание на знание основ алгебры логики. Дополнительный урок по логике тут: https://youtu.be/IF7Blq2TT6s Репетит…

…

5 лет назад

http://vk.com/vasbka_ololoshkin.

…

5 лет назад

Записывайтесь на бесплатное вводное занятие — https://foxford.ru/I/NG На сайте школьники могут подготовиться к ЕГЭ,…

…

3 лет назад

Подготовка к ОГЭ по информатике. Разбор решения 2 задания. Логические операции. Сложные логические выражени…

…

1 лет назад

Все официальные демоверсии: http://fipi.ru/ege-i-gve-11/demoversii-specifikacii-kodifikatory — Репетиторство по скайпу: https://vk.com/inf_bu?w=page-8…

…

1 лет назад

Полуторачасовой разбор 12-ти систем логических уравнений. Вы систем хотите? Их есть у меня! Разбираем номера…

…

2 лет назад

Теория игр. Оформление 2 части тут: https://youtu.be/PSAzyxpM81s ———— Поддержать канал можно тут: http://yasobe.ru/na/infbu Или…

…

2 лет назад

Простое задание на знание основ логики.

…

3 меc назад

Графы. Информационные модели. Демо по всем предметам: http://fipi.ru/ege-i-gve-11/demoversii-specifikacii-kodifikatory — Другие разборы…

…

3 меc назад

Системы счисления. Демо по всем предметам: http://fipi.ru/ege-i-gve-11/demoversii-specifikacii-kodifikatory — Другие разборы задач №1:…

…

2 лет назад

Разбор заданий 1, 17, 18, 23 досрочного ЕГЭ−2016 по информатике (Дмитрий Гущин)

…

3 лет назад

В этом видео уроке показывается, как решать задание ГИА (ОГЭ) номер №2 — по информатике за 9 класс. Показано…

…

3 меc назад

Алгоритмы. Демо по всем предметам: http://fipi.ru/ege-i-gve-11/demoversii-specifikacii-kodifikatory — Другие разборы задач №6: https://youtu.be/q…

…

1 лет назад

Разбираем 18 задачу, а затем ваши. Из присланных разберем номера 22, 25 и 27. За мат, политоту, «ауе» в чате — перман…

…

4 лет назад

Практическое задание из ГИА по электронным таблицам. Задание: В столбце A записан продукт; в столбцеB…

4k-video.ru

Разбор 2 задания ЕГЭ 2018 по информатике и ИКТ из демонстрационного варианта

Разбор 2 задания ЕГЭ 2018 по информатике и ИКТ из демоверсии. Это задание базового уровня сложности. Примерное время выполнения задания 3 минуты.

Проверяемые элементы содержания:
— умение строить таблицы истинности и логические схемы.

Элементы содержания, проверяемые на ЕГЭ:
— высказывания,
— логические операции,
— кванторы,
— истинность высказывания.

Задание 2

Логическая функция F задаётся выражением ¬x \/ y \/ (¬z /\ w).
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна.
Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.

В ответе напишите буквы w, x, y, z в том порядке, в котором идут соответствующие им столбцы (сначала – буква, соответствующая первому столбцу; затем – буква, соответствующая второму столбцу, и т.д.) Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.

Пример. Если бы функция была задана выражением ¬x \/ y, зависящим от двух переменных: x и y, и был приведён фрагмент её таблицы истинности, содержащий все наборы аргументов, при которых функция F истинна.

Тогда первому столбцу соответствовала бы переменная y, а второму столбцу – переменная x. В ответе следовало бы написать: yx.

Ответ: ________

Разбор 2 задания ЕГЭ 2018 по информатике

¬x \/ y \/ (¬z /\ w)

Дизъюнкция (логическое сложение) истинна тогда и только тогда, когда истинно хотя бы одно высказывание.

Следовательно, для того чтобы вся функция была ложна, переменной х должен соответствовать тот столбец, в котором стоит значение 1 (так как, ¬x превращает 1 в 0), а переменной y столбец со значениями 0.

Таким образом:
— переменной x соответствует столбец с переменной 1,
— переменной y соответствует столбец с переменной 4.

Конъюнкция (логическое умножение) истинна тогда и только тогда, когда истинны все высказывания (ложна — если ложно хотя бы одно высказывание).
Конъюнкция ¬z /\ w в нашем выражении будет истинна только если z=0, w=1.

Посмотрим на вторую строчку таблицы, где переменная 2 равна 1, а переменная 3 равна 0.

Так как ¬z /\ w должна равняться 0, то z = 1 и w = 0 (в противном случае произведение будет равно 1)

Таким образом:
— переменной z соответствует столбец с переменной 2 (2 столбец),
— переменной w соответствует столбец с переменной 3 (3 столбец).

Ответ: xzwy

infedu.ru

Разбор задания 2 ЕГЭ. Построение таблиц истинности логических выражений. Часть 2. | Учи Урок информатики

Основано на: демонстрационных вариантах ЕГЭ по информатике за 2015 год, на учебнике Босовой Людмилы Леонидовны

В предыдущей части 1 мы разобрали с вами логические операции Дизъюнкция и Конъюнкция, нам с вами осталось разобрать инверсию и перейти к решению задания ЕГЭ.

Инверсия

Инверсия — логическая операция, которая каждому высказыванию ста­вит в соответствие новое высказывание, значение которого противопо­ложно исходному.

Для записи инверсии используются следующие знаки: НЕ, `¯` , `¬`

Инверсия определяется следующей таблицей истинности:

Инверсию иначе называют логическим отрицанием.

Любое сложное высказывание можно записать в виде логического выражения — выражения, содержащего логические переменные, знаки логических операций и скобки. Логические операции в логи­ческом выражении выполняются в следующей очерёдности: инвер­сия, конъюнкция, дизъюнкция. Изменить порядок выполнения опе­раций можно с помощью расстановки скобок.

Логические операции имеют следующий приоритет: инверсия, конъюнк­ция, дизъюнкция.

И так, перед нами задание №2 из ЕГЭ по информатике 2015 года

Задание: 

Александра заполняла таблицу истинности для выражения F. Она успела заполнить лишь небольшой фрагмент таблицы:

x1	x2	x3	x4	x5	x6	x7	x8	F
	0						1	0
1			0					1
			1				1	1

Каким выражением может быть F?
1) x1 /\ ¬x2 /\ x3 /\ ¬x4 /\ x5 /\ x6 /\ ¬x7 /\ ¬x8
2) x1 \/ x2 \/ x3 \/ ¬x4 \/ ¬x5 \/ ¬x6 \/ ¬x7 \/ ¬x8
3) ¬x1 /\ x2 /\ ¬x3 /\ x4 /\ x5 /\ ¬x6 /\ x7 /\ x8
4) x1 \/ ¬x2 \/ x3 \/ ¬x4 \/ ¬x5 \/ ¬x6 \/ ¬x7 \/ ¬x8

Значительно облегчает решение задания то, что в каждом варианте сложного выражения F только одна логическая операция: умножение или сложение. В случае умножения /\ если хотя бы одна переменная будет равна нулю, то значение всего выражения F так же должно быть равно нулю. А в случае со сложением V если хотя бы одна переменная будет равна единице, то значение всего выражения F должно быть равно 1.

Тех данных, которые есть в таблице по каждой из 8 переменных выражения F, нам вполне достаточно для решения.

Проверим выражение номер 1:

• по первой строчке таблицы x2=0, х8=1 мы с вами видим что F=0 (? /\ 1 /\ ? /\ ? /\ ? /\ ? /\ ? /\ 0)
• по второй строчке таблицы x1=1, х4=0 мы с вами видим что F возможно и может быть равным = 1, если все остальные переменные равны 1 (1 /\ ? /\ ? /\ 1 /\ ? /\ ? /\ ? /\ ?)
• по третьей строчке таблицы x4=1, х8=1 мы с вами видим что F=0 (? /\ ? /\ ? /\ 0 /\ ? /\ ? /\ ? /\ 0), а в таблице у нас F=1, и это значит, что выражение под номером один нам ТОЧНО НЕ ПОДХОДИТ.

Проверим выражение номер 2:

• по первой строчке таблицы x2=0, х8=1 мы с вами видим что F возможно и может быть равным = 0, если все остальные переменные равны 0 (? V 0 V ? V ? V ? V ? V ? V 0)
• по второй строчке таблицы x1=1, х4=0 мы с вами видим что F = 1 (1 V ? V ? V 1 V ? V ? V ? V ?)
• по третьей строчке таблицы x4=1, х8=1 мы с вами видим что F возможно и может быть равным = 1, если хотя бы одна из оставшихся переменных будет равна 1 (? V ? V ? V 0 V ? V ? V ? V 0)
  

Проверим выражение номер 3:

• по первой строчке таблицы x2=0, х8=1 мы с вами видим что F=0 (? /\ 0 /\ ? /\ ? /\ ? /\ ? /\ ? /\ 1)
• по второй строчке таблицы x1=1, х4=0 мы с вами видим что F =0 (0 /\ ? /\ ? /\ 0 /\ ? /\ ? /\ ? /\ ?), а в таблице у нас F=1, и это значит, что выражение под номером три нам ТОЧНО НЕ ПОДХОДИТ.

Проверим выражение номер 4:

• по первой строчке таблицы x2=0, х8=1 мы с вами видим что F=1 (? V 1 V ? V ? V ? V ? V ? V 0), а в таблице у нас F=0, и это значит, что выражение под номером четыре нам ТОЧНО НЕ ПОДХОДИТ.

В решении задания на едином государственном экзамене вам нужно поступать точно таким же образом: отбрасывать те варианты, которые точно не подходят по тем данным, которые есть в таблице. Оставшийся возможный вариант (как в нашем случае вариант номер 2) и будет правильным ответом.

Пожалуйста, оцените статью

4.18 из 5. (Всего голосов:307)

Все статьи раздела

www.uchiurok.ru

Информатика ЕГЭ 5 задание разбор и объяснение

Урок посвящен тому, как решать 5 задание ЕГЭ по информатике

Кодирование информации

5-я тема характеризуется, как задания базового уровня сложности, время выполнения – примерно 2 минуты

• Кодирование — это представление информации в форме, удобной для её хранения, передачи и обработки. Правило преобразования информации к такому представлению называется кодом.
• Кодирование бывает равномерным и неравномерным:
• при равномерном кодировании всем символам соответствуют коды одинаковой длины;
• при неравномерном кодировании разным символам соответствуют коды разной длины, это затрудняет декодирование.

Пример: Зашифруем буквы А, Б, В, Г при помощи двоичного кодирования равномерным кодом и посчитаем количество возможных сообщений:

Таким образом, мы получили равномерный код, т.к. длина каждого кодового слова одинакова для всех кодов (2).

Кодирование и расшифровка сообщений

Декодирование (расшифровка) — это восстановление сообщения из последовательности кодов.

Для решения задач с декодированием, необходимо знать условие Фано:

Условие Фано: ни одно кодовое слово не должно являться началом другого кодового слова (что обеспечивает однозначное декодирование сообщений с начала)

Префиксный код — это код, в котором ни одно кодовое слово не совпадает с началом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно.

• если сообщение декодируется с конца, то его можно однозначно декодировать, если выполняется обратное условие Фано:

Обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова

Постфиксный код — это код, в котором ни одно кодовое слово не совпадает с концом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно и только с конца.



• условие Фано – это достаточное, но не необходимое условие однозначного декодирования.

Однозначное декодирование обеспечивается:

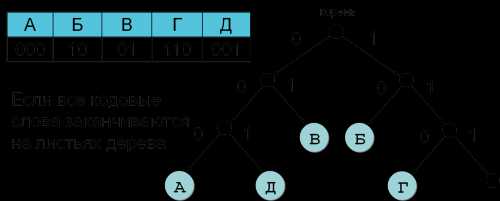
Однозначное декодирование

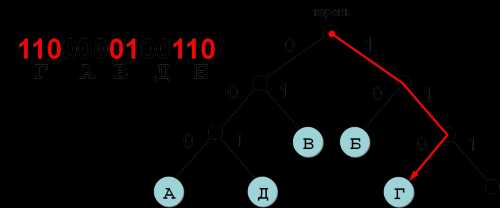
Декодирование

Егифка ©:

Решение 5 заданий ЕГЭ

ЕГЭ 5.1: Для кодирования букв О, В, Д, П, А решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления).

Закодируйте последовательность букв ВОДОПАД таким способом и результат запишите восьмеричным кодом.

✍ Решение:

• Переведем числа в двоичные коды и поставим их в соответствие нашим буквам:

О -> 0 -> 00
В -> 1 -> 01
Д -> 2 -> 10
П -> 3 -> 11
А -> 4 -> 100

Теперь закодируем последовательность букв из слова ВОДОПАД:

010010001110010

Разобьем результат на группы из трех символов справа налево, чтобы перевести их в восьмеричную систему счисления:

010 010 001 110 010
 ↓   ↓   ↓   ↓   ↓
 2   2   1   6   2

Результат: 22162

Решение ЕГЭ данного задания по информатике, видео:

Рассмотрим еще разбор 5 задания ЕГЭ:

ЕГЭ 5.2: Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:

a	b	c	d	e
000	110	01	001	10

Какой набор букв закодирован двоичной строкой 1100000100110?

✍ Решение:

110 000 01 001 10
 ↓   ↓   ↓  ↓  ↓
 b   a  c   d  e 

Результат: b a c d e.

✎ 2 вариант решения:

Этот вариант решения 5 задания ЕГЭ более сложен, но тоже верен.
• Сделаем дерево, согласно кодам в таблице:



• Сопоставим закодированное сообщение с кодами в дереве:

110 000 01 001 10

Результат: b a c d e.

Кроме того, вы можете посмотреть видео решения этого задания ЕГЭ по информатике:

Решим следующее 5 задание:

ЕГЭ 5.3:
Для передачи чисел по каналу с помехами используется код проверки четности. Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины 4, и к получившейся последовательности дописывается сумма её элементов по модулю 2 (например, если передаём 23, то получим последовательность 0010100110).

Определите, какое число пе­ре­да­ва­лось по ка­на­лу в виде 01100010100100100110.

✍ Решение:

• Рассмотрим пример из условия задачи:

Было 2310
Стало 00101001102

Где сами цифры исходного числа (выделим их красным цветом):

 0010100110  (0010 - 2, 0011 - 3)

Первая добавленная цифра 1 после двоичной двойки — это проверка четности (1 единица в 0010 — значит нечетное), 0 после двоичной тройки — это также проверка нечетности (2 единицы в 0011, значит — четное).

Исходя из разбора примера решаем нашу задачу так: поскольку «нужные» нам цифры образуются из групп по 4 числа в каждой плюс одно число на проверку четности, то разобьем закодированное сообщение на группы по 5, и отбросим из каждой группы последний символ:

разбиваем по 5:

01100 01010 01001 00110

отбрасываем из каждой группы последний символ:

0110 0101 0100 0011

Результат переводим в десятичную систему:

0110 0101 0100 0011
 ↓    ↓     ↓    ↓
 6    5     4    3

Ответ: 6 5 4 3

 

Вы можете посмотреть видео решения этого задания ЕГЭ по информатике:

ЕГЭ 5.4:
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К — кодовое слово 10.

Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?

✍ Решение: ✎ 1 вариант решения основан на логических умозаключениях:

• Найдём самые короткие возможные кодовые слова для всех букв.
• Кодовые слова 01 и 00 использовать нельзя, так как тогда нарушается условие Фано (начинаются с 0, а 0 — это Н).
• Начнем с двухразрядных кодовых слов. Возьмем для буквы Л кодовое слово 11. Тогда для четвёртой буквы нельзя подобрать кодовое слово, не нарушая условие Фано (если потом взять 110 или 111, то они начинаются с 11).
• Значит, надо использовать трёхзначные кодовые слова. Закодируем буквы Л и М кодовыми словами 110 и 111. Условие Фано соблюдается.
• Суммарная длина всех четырёх кодовых слов равна:

(Н)1 + (К)2 + (Л)3 + (М)3 = 9

✎ 2 вариант решения:

• Будем использовать дерево. Влево откладываем 0, вправо — 1:



• Теперь выпишем соответствие каждой буквы ее кодового слова согласно дереву:

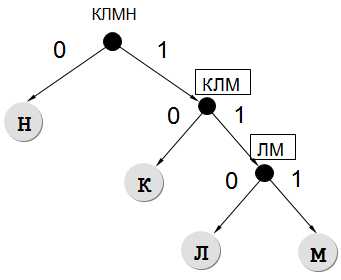
(Н) -> 0   -> 1 символ
(К) -> 10  -> 2 символа
(Л) -> 110 -> 3 символа
(М) -> 111 -> 3 символа

Суммарная длина всех четырёх кодовых слов равна:

(Н)1 + (К)2 + (Л)3 + (М)3 = 9

Ответ: 9

ЕГЭ по информатике 5 задание 2017 ФИПИ вариант 2 (под редакцией Крылова С.С., Чуркиной Т.Е.):

По каналу связи передаются сообщения, содержащие только 4 буквы: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются такие кодовые слова: А: 101010, Б: 011011, В: 01000.

Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

✍ Решение:

• Наименьшие коды могли бы выглядеть, как 0 и 1 (одноразрядные). Но это не удовлетворяло бы условию Фано (А начинается с единицы — 101010, Б начинается с нуля — 011011).
• Следующим наименьшим кодом было бы двухбуквенное слово 00. Так как оно не является префиксом ни одного из представленных кодовых слов, то Г = 00.

Результат: 00

ЕГЭ по информатике 5 задание 2017 ФИПИ вариант 16 (под редакцией Крылова С.С., Чуркиной Т.Е.):

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приемной стороне канала связи. Использовали код: А — 01, Б — 00, В — 11, Г — 100.

Укажите, каким кодовым словом должна быть закодирована буква Д. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования. Если таких кодов несколько, укажите код с наименьшим числовым значением.

✍ Решение:

• Так как необходимо найти кодовое слово наименьшей длины, воспользуемся деревом. Влево будем откладывать нули, а вправо — единицы:



• Поскольку у нас все ветви завершены листьями, т.е. буквами, кроме одной ветви, то остается единственный вариант, куда можно поставить букву Д:



• Перепишем сверху вниз получившееся кодовое слово для Д: 101

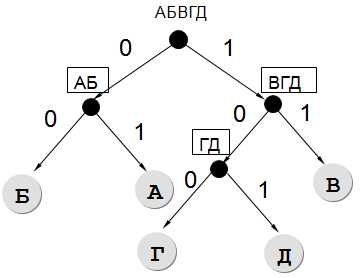
Результат: 101

Подробней разбор урока можно посмотреть на видео ЕГЭ по информатике 2017:

ЕГЭ по информатике 5 задание 2017 ФИПИ вариант 17 (Крылов С.С., Чуркина Т.Е.):

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д и Е, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приемной стороне канала связи. Использовали код: А — 0, Б — 111, В — 11001, Г — 11000, Д — 10.

Укажите, каким кодовым словом должна быть закодирована буква Е. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования. Если таких кодов несколько, укажите код с наименьшим числовым значением.

✍ Решение:

• Для того, чтобы выполнялось условие Фано, необходимо, чтобы код буквы Е не совпадал с началом кода любого кодового слова.
• Поскольку кодовые слова достаточно длинные, то использовать для решения дерево не совсем удобно. Воспользуемся таблицей:



• Теперь, начиная с однобитных кодов, и, двигаясь сверху вниз, подбираем такой код, который бы удовлетворял условию Фано. С 0 можно не начинать, так как уже есть код 0 для буквы А:

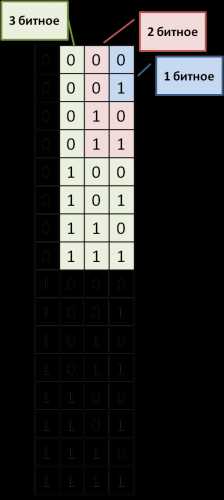
1   - не подходит (все буквы кроме А начинаются с 1)
10  - не подходит (соответствует коду Д)
11  - не подходит (начало кодов Б, В и Г)
100 - не подходит (код Д - 10 - является началом данного кода)
101 - не подходит (код Д - 10 - является началом данного кода)
110 - не подходит (начало кода В и Г)
111 - не подходит (соответствует коду Б)
1000 - не подходит (код Д - 10 - является началом данного кода)
1001 - не подходит (код Д - 10 - является началом данного кода)
1010 - не подходит (код Д - 10 - является началом данного кода)
1011 - не подходит (код Д - 10 - является началом данного кода)
1100 - не подходит (начало кода В и Г)
1101 - подходит

Результат: 1101

Более подробное решение данного задания представлено в видеоуроке:

5 задание. Демоверсия ЕГЭ 2018 информатика (ФИПИ):

По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У. Для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова.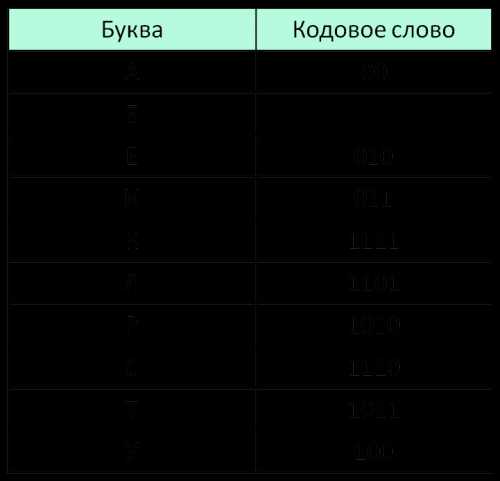

Укажите кратчайшее кодовое слово для буквы Б, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.

✍ Решение:

• Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.



• При рассмотрении дерева видим, что все ветви «закрыты» листьями, кроме одной ветви — 1100:

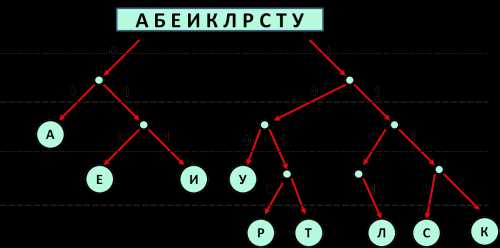
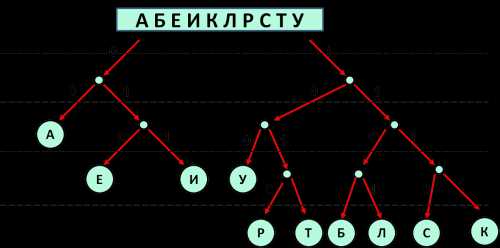
Результат: 1100

Подробное решение данного 5 задания из демоверсии ЕГЭ 2018 года смотрите на видео:

Задание 5_9. Типовые экзаменационные варианты 2017. Вариант 4 (Крылов С.С., Чуркина Т.Е.):

По каналу связи передаются шифрованные сообщения, содержащие только четыре букв: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются кодовые слова:

А: 00011 
Б: 111 
В: 1010

Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

✍ Решение:

• Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.
• Поскольку в задании явно не указано о том, что код должен удовлетворять условию Фано, то дерево нужно построить как с начала (по условию Фано), так и с конца (обратное условие Фано).

Дерево по условию Фано (однозначно декодируется с начала):


• Получившееся числовое значение кодового слова для буквы Г — 01.

Дерево по обратному условию Фано (однозначно декодируется с конца):


• Получившееся числовое значение кодового слова для буквы Г — 00.
• После сравнения двух кодовых слов (01 и 00), код с наименьшим числовым значением — это 00.

Результат: 00

Задание 5_10. Тренировочный вариант №3 от 01.10.2018 (ФИПИ):

По каналу связи передаются сообщения, содержащие только буквы: А, Е, Д, К, М, Р; для передачи используется двоичный код, удовлетворяющий условию Фано. Известно, что используются следующие коды:

Е – 000
Д – 10
К – 111

Укажите наименьшую возможную длину закодированного сообщения ДЕДМАКАР.
В ответе напишите число – количество бит.

✍ Решение:

• С помощью дерева отобразим известные коды для букв:



• В результирующем слове — ДЕДМАКАР — вде буквы А. Значит, для получения наименьшей длины необходимо для буквы А выбрать наименьший код в дереве. Учтем это и достроим дерево для остальных трех букв А, М и Р:



• Расположим буквы в порядке их следования в слове и подставим их кодовые слова:

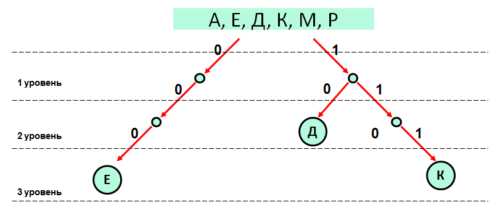
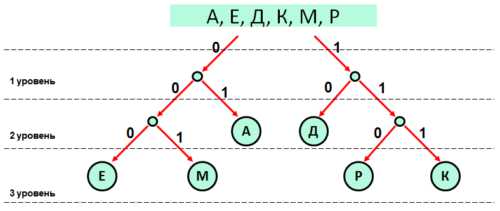
Д   Е   Д   М   А   К   А   Р
10 000 10  001 01  111 01  110

Посчитаем количество цифр в итоговом коде и получим 20.

Результат: 20

Смотрите виде решения задания:

labs.org.ru

Задание 3 ЕГЭ по информатике 2018 и 2017

Урок посвящен тому, как решать 3 задание ЕГЭ по информатике

Объяснение заданий 3 ЕГЭ по информатике

3-я тема характеризуется, как задания базового уровня сложности, время выполнения – примерно 3 минуты

* Некоторые изображения страницы взяты из материалов презентации К. Полякова

  

Структурирование информации и информационные модели

Рассмотрим кратко необходимые для решения 3 задания ЕГЭ понятия.

Структурирование информации — это установление главных элементов в информационных сообщениях и установление связей между ними.

Структурирование выполняется с целью облегчения восприятия и поиска информации.

Структурирование возможно при помощи следующих структур (информационных моделей):

множество:

перечисление элементов, собранных по характерному признаку;

Вася, Петя, Коля
1, 17, 22, 55

В множестве упорядочивание элементов не обязательно, т.е. порядок следования не важен.

линейный список

Важна упорядоченность следования элементов.

таблица

В таблицах выделяются объекты (отдельные записи таблиц) и свойства (названия столбцов или названия строк):

дерево или иерархия объектов

Уровни в дереве

Рассмотрим родственные отношения в дереве:

«Сыновья» А: B, C.

«Родитель» B: A.

«Потомки» А: B, C, D, E, F, G.

«Предки» F: A, C.

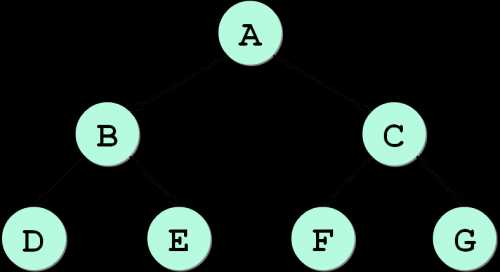
Корень – узел без предков (A).
Лист – узел без потомков (D, E, F, G).
Высота – наибольшее расстояние от корня до листа (количество уровней).

файловая система (иерархия)

Допустим, на жестком диске компьютера имеются следующие папки (каталоги) с файлами:

Получим дерево:

графы

Иногда очень трудно структурировать информацию описанными структурами из-за сложных «взаимоотношений» между объектами. Тогда можно использовать графы:

Граф – это набор вершин и связей между ними, называющихся рёбрами:

Граф, отображающий дороги между поселками

матрица и список смежности

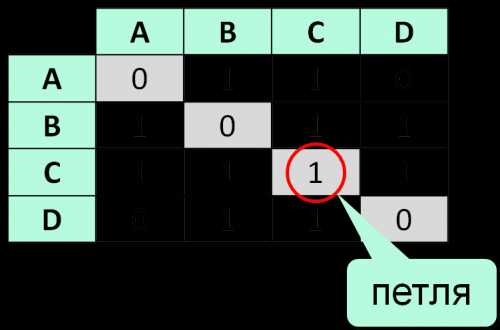
Связный граф – это граф, между любыми вершинами которого существует путь.

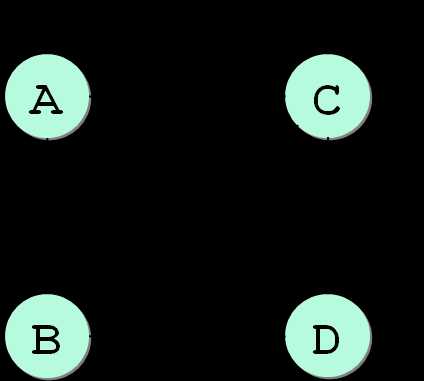
Связный граф

Дерево – это связный граф без циклов (замкнутых участков).

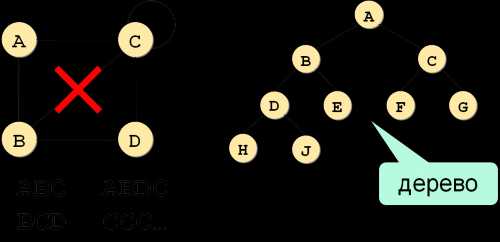
Дерево — связный граф без циклов

взвешенные графы и весовая матрица

У взвешенных графов указан «вес ребра»:

Из взвешенных графов получается весовая матрица, обратное преобразование тоже возможно.

Весовая матрица

 

Поиск кратчайшего пути (перебор)

Определение кратчайшего пути между пунктами A и D

• В заданиях ЕГЭ этой темы чаще всего используются две информационные модели — таблицы и схемы.
• Информация в таблице строится по следующим правилам: на пересечении строки и столбца находится информация, характеризующая комбинацию этой строки и столбца.
• На схеме информация строится по следующему правилу: если между объектами схемы имеется связь, то она отображается линией, соединяющей названия этих объектов на схеме.

Егифка ©:

Решение заданий 3 ЕГЭ по информатике

ЕГЭ по информатике 2017, задание из сборника Ушакова Д.М, 1 вариант:

На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о длинах этих дорог (в километрах).

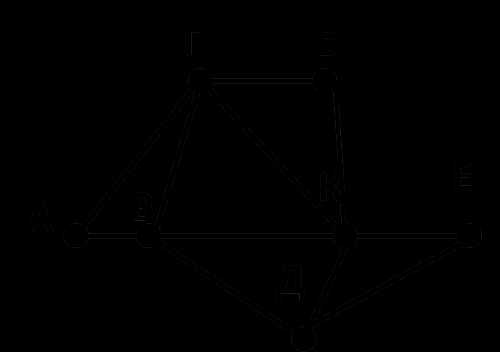Так как таблицу и схему рисовали независимо друг от друга, то нумерация населенных пунктов в таблице никак не связана с буквенными обозначениями на графе.
Определите, какова длина дороги из пункта Д в пункт К. В ответе запишите целое число — так, как оно указано в таблице.

✍ Решение:

• Рассмотрим граф и посчитаем количество ребер из каждой вершины:

А - > 2 ребра (Г, В)
В - > 4 ребра (А, Г, К, Д)
Г - > 4 ребра (А, В, К, Д)
Б - > 2 ребра (Г, К)
К - > 5 ребер (Б, Г, В, Д, Е)
Е - > 2 ребра (К, Д)
Д - > 3 ребра (В, К, Е)

Мы выделили вершины, с уникальным числом ребер: 3 ребра соответствует только вершине Д, а 5 ребер соответствует только вершине К.

Рассмотрим таблицу и найдем те строки или столбцы, в которых 5 значений и 3 значения: Это П2 и П4.

Получаем П2 соответствует Д, а П4 соответствует К. На пересечении находится цифра 20.

Результат: 20

Кроме того, Вы можете посмотреть видео решения этого задания ЕГЭ по информатике:

3 задание. Демоверсия ЕГЭ 2018 информатика (ФИПИ):

На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).

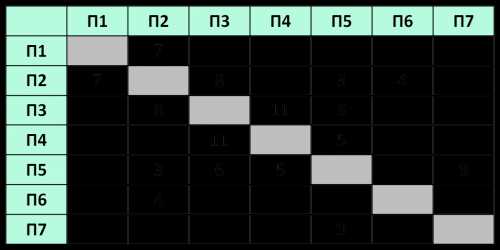Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова протяжённость дороги из пункта А в пункт Г. В ответе запишите целое число – так, как оно указано в таблице.

✍ Решение:

• Посчитаем сколько ребер у каждой вершины:

A -> 3 (В Г Д)
Б -> 1 (В)
В -> 4 (А Б Г Е)
Г -> 4 (А В Д К)
Д -> 2 (А Г)
Е -> 1 (В)
К -> 1 (Г)

Три ребра имеет только одна вершина — А, поэтому только А может соответствовать П3.

Уникальное значение количества ребер имеет также вершина Д, — два ребра. В таблице вершине Д будет соответствовать П4.

Вершины Г и В имеют по 4 ребра. Рассмотрим матрицу, в ней 4 числа соответствуют пунктам П2 и П5.

С пунктом Д пересекается только вершина Г (Г -> 4 (А В Д К)). В весовой матрице с вершиной Д пресекается П5. Значит вершина Г соответствует П5.

В П5 на пересечении с П3 находится число 6.

Результат: 6

Подробное решение данного 3 задания из демоверсии ЕГЭ 2018 года смотрите на видео:

Решение 3 задания ЕГЭ по информатике (контрольный вариант № 1 экзаменационной работы 2018 года, С.С. Крылов, Д.М. Ушаков):

Между населенными пунктами A, B, C, D, E, F построены дороги, протяженность которых приведена в таблице (если ячейка пуста — дороги нет).

	A	B	C	D	E	F
A		7	3
B	7		2	4	1
C	3	2		7	5	9
D		4	7		2	3
E		1	5	2		7
F			9	3	7

Определите длину кратчайшего пути между пунктами A и F.

✍ Решение:

• Для решения задачи используем построение дерева с подсчетом значений для каждой ветви (протяженности дорог).
• При движении от корня дерева (А) вниз будем иметь в виду, что:
• рассматривать вершины, которые уже есть в текущей «ветви», — не нужно,
• если получаемое число (суммарная протяженность дорог) превышает какое-либо из найденных вариантов от A до F, то дальше эту ветвь можно не рассматривать.
• В итоге получим дерево:



• Самый короткий путь: A -> C -> B -> E -> D -> F = 11

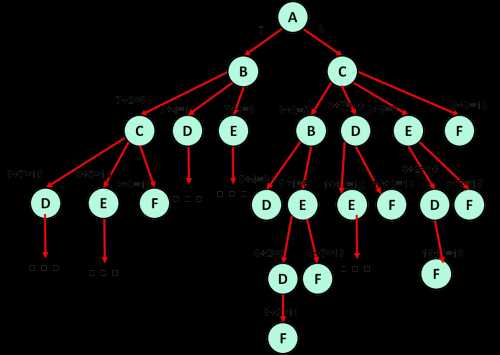
Результат: 11

Видеоразбор задания:

Решение 3 задания ЕГЭ по информатике (11 вариант ГВЭ по информатике 2018 года):

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.

	A	B	C	D	E	F
A		3	7		6
B	3			4	4
C	7			5		9
D		4	5			5
E	6	4				8
F			9	5	8

Определите длину кратчайшего пути между пунктами A и F при условии, что передвигаться можно только по указанным в таблице дорогам.

✍ Решение:

• Решим задание при помощи построения дерева, вершиной которого является отправной пункт — A. На ребрах дерева будем записывать числа — результат протяженности пути до конкретной вершины.



• Кратчайший путь: A -> B -> D -> F = 12

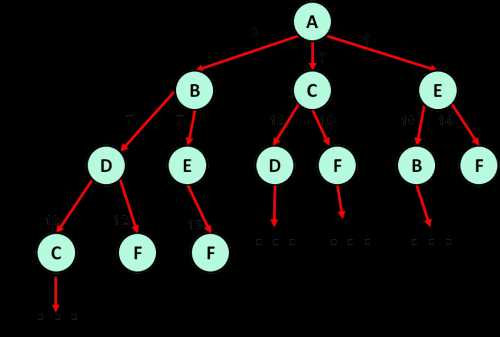
Результат: 12

Решение 2* задания ЕГЭ по информатике 2018, вариант 10 (ФИПИ, «ЕГЭ информатика и ИКТ, типовые экзаменационные варианты 2018», С.С. Крылов, Т.Е. Чуркина):

Между населенными пунктами A, B, C, D, E, F, Z построены дороги с односторонним движением. В таблице указана протяженность каждой дороги (отсутствие числа в таблице означает, что прямой дороги между пунктами нет).

	A	B	C	D	E	F	Z
A		3		5			14
B			2				8
C		2					7
D					1	4	4
E						1	5
F			12		1		9
Z

Сколько существует таких маршрутов из A в Z, которые проходят через пять и более населенных пунктов? Пункты A и Z при подсчете учитывайте. Два раза проходить через один пункт нельзя.

* в новых учебниках задания 2 и 3 поменяли местами: теперь 2 — Поиск кратчайшего пути, а 3 — Алгебра логики

✍ Решение:

• Для решения будем использовать дерево:



• Розовым отмечены неподходящие маршруты, а голубым — подходящие.
• Заметим, что после 4-го уровня сверху, все варианты будут подходить.

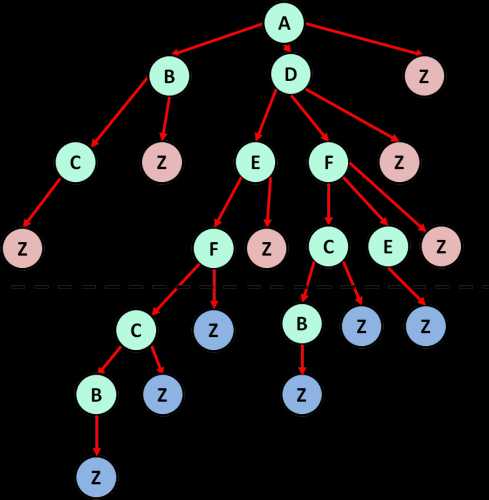
Результат: 6

labs.org.ru