Формулы по планиметрии для ЕГЭ 2019 / Блог :: Бингоскул
- Блог
- →
- Формулы по планиметрии для ЕГЭ 2019
Косинус α – это отношение прилежащего катета к гипотенузе \cosα = \frac{b}{c}
Синус α – это отношение противолежащего катета к гипотенузе \sinα = \frac{a}{c}
Тангенс α – это отношение противолежащего катета к прилежащему \tgα = \frac{a}{b}
Котангенс α – это отношение прилежащего катета к противолежащему \ctgα = \frac{b}{a}
Центральный угол – это угол с вершиной в центре окружности называется центральным углом. ∠AOB = ∪ AB
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. ∠ACB = \frac{1}{2} ∪ AB
Площади фигур
Параллелограмм
S=aha
S=ab sinγ
Треугольник
S=\frac{1}{2}ah_a
S=\frac{1}{2}ab \sin \gamma
Трапеция
S=\frac{a+b}{2}\cdot h
Ромб
d1,d2 — диагонали
S=\frac{1}{2} \cdot d_1d_2
Средняя линия треугольника и трапеции
BC ‖AD
MN — ср. линия
MN ‖AD
MN=\frac {BC+AD}{2}
MN— ср. линия
MN‖AC
MN=\frac {AC}{2}
Касательная к окружности – это прямая, имеющая с окружностью ровно одну общую точку.
Свойства касательных:
- касательная перпендикулярна радиусу окружности, проведенному к точке касания;
- через любую точку вне окружности можно провести ровно две касательные к окружности;
- отрезки касательных, проведенных к окружности из одной точки, от общей точки до точек касания равны друг другу.
Секущая – это прямая, пересекающая окружность в двух точках.
Хорда – это отрезок, соединяющий две точки окружности .
Основные свойства:
- самая длинная хорда окружности — это диаметр ;
- равные хорды стягивают дуги одинаковой градусной меры ;
- если хорда стягивает дугу с градусной мерой α, то ее длина l=2R sin \frac{a}{2}.
Вписанная окружность
Центр вписанной окружности – точка пересечения биссектрис.
Радиус вписанной окружности: r= \frac {S}{p}, где S — площадь треугольника p=\frac {(a+b+c)}{2}
Описанная окружность
Центр описанной окружности – точка пересечения серединных перпендикуляров.
Радиус описанной окружности: R=\frac {abc}{4S}, где S- площадь треугольника
Смотри также:
Решай с разбором и узнавай ответы:
bingoschool.ru
Подготовка школьников к ЕГЭ в учебном центре «Резольвента» (Справочник по математике — Стереометрия
Введем следующие обозначения:
Используя эти обозначения, составим таблицу с формулами для вычисления объемов, площадей боковой поверхности и площадей полной поверхности различных видов призм.
| Призма | Рисунок | Формулы для объема, площади боковой и полной поверхности |
| Куб | V = a3, Sбок = 4a2, Sполн = 6a2, где a – длина ребра куба. | |
| Прямоугольный параллелепипед | V = abc, Sбок = 2ac + 2bc, Sполн = 2ac + 2bc +2ab, где | |
| Прямой параллелепипед, в основании которого лежит параллелограмм со сторонами a, b и углом φ | Sосн = ab sin φ, V = Sоснh = abh sin φ, Sбок = 2ah + 2bh, Sполн = 2ab sin φ + 2ah +2bh, где | |
| Произвольный параллелепипед | Sосн = ab sin φ, V = Sоснh = abh sin φ, V = Sперпс, Sбок = Pперпс, Sполн = 2ab sin φ + Pперпс, где | |
| Прямая призма | V = Sоснh, Sбок = Pоснh, Sполн = 2Sосн + Sбок, где | |
| Правильная n – угольная призма | (см. раздел «правильные многоугольники»), V = Sоснh, Sбок = Pоснh = anh, Sполн = 2Sосн + Sбок, где | |
| Произвольная призма | V = Sоснh, V = Sперпl, Sбок = Pперпl, Sполн = 2Sосн + Sбок, где |
| Куб |
Формулы для объема, площади боковой и полной поверхности: V = a3, Sбок = 4a2, Sполн = 6a2, где a – длина ребра куба. |
| Прямоугольный параллелепипед |
Формулы для объема, площади боковой и полной поверхности: V = abc, Sбок = 2ac + 2bc, Sполн = 2ac + 2bc +2ab, где |
| Прямой параллелепипед, в основании которого лежит параллелограмм со сторонами a, b и углом φ |
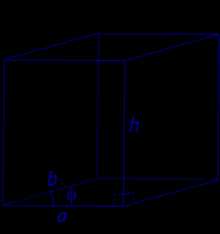 Формулы для объема, площади боковой и полной поверхности: Sосн = ab sin φ, V = Sоснh = abh sin φ, Sбок = 2ah + 2bh, Sполн = где |
| Произвольный параллелепипед |
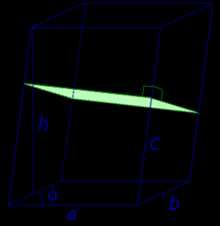 Формулы для объема, площади боковой и полной поверхности: Sосн = ab sin φ, V = Sоснh = abh sin φ, V = Sперпс, Sбок = Pперпс, Sполн = где |
| Прямая призма |
Формулы для объема, площади боковой и полной поверхности: V = Sоснh, Sбок = Pоснh, Sполн = 2Sосн + Sбок, где |
| Правильная n – угольная призма |
Формулы для объема, площади боковой и полной поверхности: (см. раздел «правильные многоугольники»), V = Sоснh, Sбок = Pоснh = anh, Sполн = 2Sосн + Sбок, где |
| Произвольная призма |
Формулы для объема, площади боковой и полной поверхности: V = Sоснh, V = Sперпl, Sбок = Pперпl, Sполн = 2Sосн + Sбок, где |
Замечание 1. С понятием призмы и различными видами призм можно ознакомиться в разделе «Призмы».
Замечание 2. С определением сечения призмы и способами построения сечений призмы можно ознакомиться в разделе «Сечения призмы. Перпендикулярные сечения призмы».
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Стереометрия на ЕГЭ по математике. Задание В10
Задачи по стереометрии в первой части Профильного ЕГЭ по математике
Часть 1: Просто применяем формулы
Стереометрия на ЕГЭ по математике — это целых три задачи. Для начала надо выучить формулы. Все они есть в наших таблицах:
Часто в задачах ЕГЭ, посвященных стереометрии, требуется посчитать объем тела или площадь его поверхности. Или как-то использовать эти данные. Поэтому заглянем в толковый словарь русского языка и уточним понятия.
Объем — величина чего-нибудь в длину, ширину и высоту, измеряемая в кубических единицах.
Другими словами, чем больше объем, тем больше места тело занимает в трехмерном пространстве.
Площадь — величина чего-нибудь в длину и ширину, измеряемая в квадратных единицах.
Представьте себе, что вам нужно оклеить всю поверхность объемного тела. Сколько квадратных сантиметров (или метров) вы бы обклеили? Это и есть его площадь поверхности.
Объемные тела — это многогранники (куб, параллелепипед, призма, пирамида) и тела вращения (цилиндр, конус, шар).
Чтобы найти площадь поверхности многогранника, сложите площади всех его граней.
Вам могут также встретиться понятия «прямая призма, правильная призма, правильная пирамида».
Прямой называется призма, боковые ребра которой перпендикулярны основанию.
Если призма — прямая и в ее основании лежит правильный многоугольник, призма будет называться правильной.
А правильная пирамида — такая, в основании которой лежит правильный многоугольник, а вершина проецируется в центр основания.
Ты нашел то, что искал? Поделись с друзьями!
Перейдем к практике.
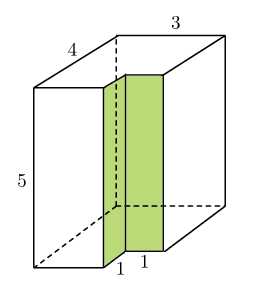
. Одна из распространенных задач в части 1 — такая, где надо посчитать объем или площадь поверхности многогранника, из которого какая-нибудь часть вырезана. Например, такого:
Что тут нарисовано? Очевидно, это большой параллелепипед, из которого вырезан «кирпичик», так что получилась «полочка». Если вы увидели на рисунке что-то другое — обратите внимание на сплошные и штриховые линии. Сплошные линии — видимы. Штриховыми линиями показываются те ребра, которые мы не видим, потому что они находятся сзади.
Объем найти просто. Из объема большого «кирпича» вычитаем объем маленького. Получаем:
А как быть с площадью поверхности? Почему-то многие школьники пытаются посчитать ее по аналогии с объемом, как разность площадей большого и малого «кирпичей». В ответ на такое «решение» я обычно предлагаю детскую задачу — если у четырехугольного стола отпилить один угол, сколько углов у него останется? 🙂
На самом деле нам нужно посчитать сумму площадей всех граней — верхней, нижней, передней, задней, правой, левой, а также сумму площадей трех маленьких прямоугольников, которые образуют «полочку». Можно сделать это «в лоб», напрямую. Но есть и способ попроще.
Прежде всего, если бы из большого параллелепипеда ничего не вырезали, его площадь поверхности была бы равна . А как повлияет на него вырезанная «полочка»?
Давайте посчитаем сначала площадь всех горизонтальных участков, то есть «дна», «крыши» и нижней поверхности «полочки». С дном — все понятно, оно прямоугольное, его площадь равна .
А вот сумма площадей «крыши» и горизонтальной грани «полочки» тоже равна ! Посмотрите на них сверху.
…В этот момент и наступает понимание. Кому-то проще нарисовать вид сверху. Кому-то — представить, что мы передвигаем дно и стенки полочки и получаем целый большой параллелепипед, площадь поверхности которого равна . Каким бы способом вы ни решали, результат один — площадь поверхности будет такой же, как и у целого параллелепипеда, из которого ничего не вырезали.
Ответ: .
Следующую задачу, попроще, вы теперь решите без труда. Здесь тоже надо найти площадь поверхности многогранника:
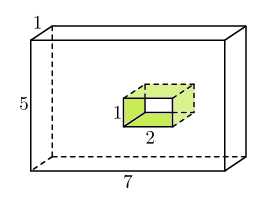А здесь нарисована прямоугольная плитка с «окошком». Задание то же самое — надо найти площадь поверхности.
Сначала посчитайте сумму площадей всех граней. Представьте, что вы дизайнер, а эта штучка — украшение. И вам надо оклеить эту штуку чем-то ценным, например, бриллиантами Сваровски. И вы их покупаете на свои деньги. (Я не знаю почему, но эта фраза мгновенно повышает вероятность правильного ответа!) Оклеивайте все грани плитки. Но только из площадей передней и задней граней вычтите площадь «окошка». А затем — само «окошко». Оклеивайте всю его «раму».
Правильный ответ: .
Следующий тип задач — когда одно объемное тело вписано в другое.
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны . Найдите объем параллелепипеда.
Прежде всего, заметим, что высота цилиндра равна высоте параллелепипеда. Нарисуйте вид сверху, то есть круг, вписанный в прямоугольник. Тут сразу и увидите, что этот прямоугольник — на самом деле квадрат, а сторона его в два раза больше, чем радиус вписанной в него окружности. Итак, площадь основания параллелепипеда равна , высота равна , объем равен .
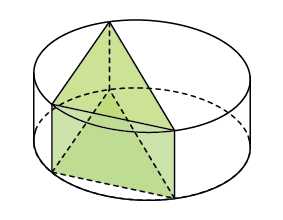. В основании прямой призмы лежит прямоугольный треугольник с катетами и . Боковые ребра равны . Найдите объем цилиндра, описанного около этой призмы. В ответ запишите .
Очевидно, высота цилиндра равна боковому ребру призмы, то есть . Осталось найти радиус его основания.
Рисуем вид сверху. Прямоугольный треугольник вписан в окружность. Где будет находиться радиус этой окружности? Правильно, посередине гипотенузы. Гипотенузу находим по теореме Пифагора, она равна . Тогда радиус основания цилиндра равен пяти. Находим объем цилиндра по формуле и записываем ответ: .
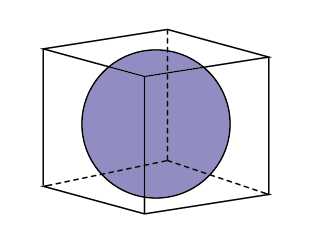
. В прямоугольный параллелепипед вписан шар радиуса . Найдите объем параллелепипеда.
Эта задача тоже проста. Нарисуйте вид сверху. Или сбоку. Или спереди. В любом случае вы увидите одно и то же — круг, вписанный в прямоугольник. Очевидно, этот прямоугольник будет квадратом. Можно даже ничего не рисовать, а просто представить себе шарик, который положили в коробочку так, что он касается всех стенок, дна и крышки. Ясно, что такая коробочка будет кубической формы. Длина, ширина и высота этого куба в два раза больше, чем радиус шара.
Ответ: .
Следующий тип задач — такие, в которых увеличили или уменьшили какой-либо линейный размер (или размеры) объемного тела. А узнать нужно, как изменится объем или площадь поверхности.
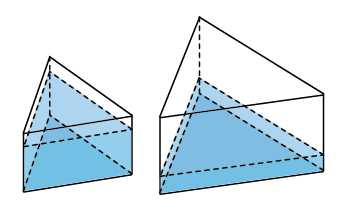
Слова «другой такой же сосуд» означают, что другой сосуд тоже имеет форму правильной треугольной призмы. То есть в его основании — правильный треугольник, у которого все стороны в два раза больше, чем у первого. Мы уже говорили о том, что площадь этого треугольника будет больше в раза. Объем воды остался неизменным. Следовательно, в раза уменьшится высота.
Ответ: .
. Одна цилиндрическая кружка вдвое выше второй, зато вторая в два раза шире. Найдите отношение объема второй кружки к объему первой.
Давайте вспомним, как мы решали стандартные задачи, на движение и работу. Мы рисовали таблицу, верно? И здесь тоже нарисуем таблицу. Мы помним, что объем цилиндра равен .
Считаем объем второй кружки. Он равен . Получается, что он в два раза больше, чем объем первой.
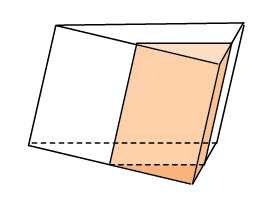. Следующая задача тоже решается сразу и без формул.
Через среднюю линию основания треугольной призмы, объем которой равен , проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Высота меньшей призмы высота такая же, как и у большой. А какой же будет ее площадь основания? Очевидно, в раза меньше. Вспомните свойство средней линии треугольника — она равна половине основания. Значит, объем отсеченной призмы равен .
И еще одна классическая задача. Никаких формул!
. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в раза?
Только не надо обмирать от ужаса при слове «октаэдр». Тем более — он здесь нарисован и представляет собой две сложенные вместе четырехугольные пирамиды. А мы уже говорили — если все ребра многогранника увеличить в три раза, площадь поверхности увеличится в раз, поскольку .
Следующий тип задач — такие, в которых надо найти объем части конуса, или части пирамиды. Они тоже решаются элементарно.
. Найдите объем части цилиндра, изображенной на рисунке. Радиус цилиндра равен 15, высота равна 5. В ответе укажите .
Изображен не целый цилиндр, а его часть. Из него, как из круглого сыра, вырезали кусок. Надо найти объем оставшегося «сыра».
Какая же часть цилиндра изображена? Вырезан кусок с углом градусов, а — это одна шестая часть полного круга. Значит, от всего объема цилиндра осталось пять шестых. Находим объем всего цилиндра, умножаем на пять шестых, делим на , записываем ответ: .
Продолжение: другие типы задач по стереометрии. Удачи вам в подготовке к ЕГЭ!
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Задачи по стереометрии
Задачи по стереометрии. Друзья! В предыдущей статье были представлены основные формулы, которые необходимы для решения задач по стереометрии на экзамене по математике, и не только. Эти формулы знать НЕОБХОДИМО! Если вас интересует какая либо задача — вы можете ввести начало условия в строку ПОИСКА на карте блога или пройтись по рубрикам «СТЕРЕОМЕРИЯ». В этой публикации некоторые теоретические факты.
По ходу учебного процесса, при систематическом решении задач, все они запоминаются и откладываются в памяти крепко и надолго. Учите их, практикуйтесь в решении задач, они запомнятся, ни куда не денутся ;). К домашнему заданию добавляйте ещё пару задач самостоятельно. Понимаю, что никому не хочется создавать себе дополнительную работу, но ваш результат на будущем ЕГЭ целиком зависит только от вас.
В этой статье хочу напомнить вам некоторые моменты, которые необходимы для решения ряда задач по стереометрии. В этих примерах речь идёт о площади поверхности тел и объёме (относится к призме, параллелепипедам и другим телам). Данные факты используются во многих типах заданий. Уверен, представленная ниже информация вам известна, но всё же…
Не буду их здесь делить на теоремы, свойства, следствия и объяснять что из чего исходит. Предлагаю вам освежить их в памяти и запомнить именно как факты.
Немало задач, где при решении необходимо помнить, что:
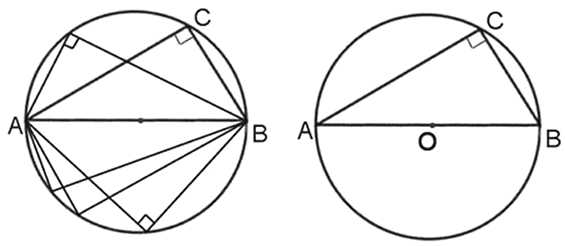
1. У прямоугольного треугольника вписанного в окружность гипотенуза совпадает с диаметром. Центр этой окружности совпадает с серединой гипотенузы.
Если в окружность вписан треугольник и одна его сторона совпадает с диаметром этой окружности, то треугольник является прямоугольным.
То есть, если мы на диаметре окружности построим треугольник, вершина которого будет лежать на любой точке окружности, то такой треугольник будет являться прямоугольным.
2. Во многих типах задач часто говорится об отрезке, который соединяет середины двух соседних сторон треугольника. Понятно, что речь идёт о средней линии треугольника. Что мы о ней знаем?
Средняя линия треугольника – это отрезок, концы которого лежат на серединах двух соседних сторон данного треугольника, она параллельна третьей стороне и равна её половине
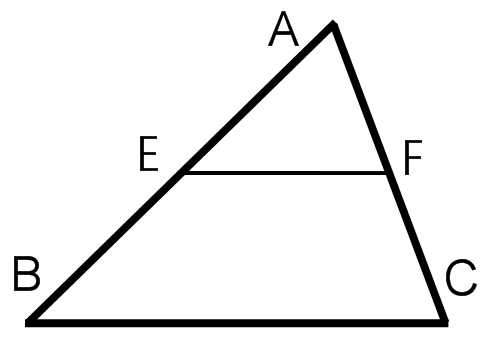
Что нам это даёт?
— Она отсекает от исходного треугольника подобный ему.
— Коэффициент подобия равен k = 0,5. Так как стороны отсечённого треугольника равны половине сторон исходного.
— Все линейные элементы отсечённого треугольника равны половине соответствующих им элементам исходного (стороны, высоты, медианы, биссектрисы, а также периметр треугольника).
— Площадь отсечённого треугольника равна одной четвёртой площади исходного треугольника. Это подтверждается формулой взаимосвязи площадей подобных фигур:
*А также равенством треугольников, посмотрите рисунок:
AD = DB, BE = EC, AF = FC, DE = AF, EF = AD, DF= EC
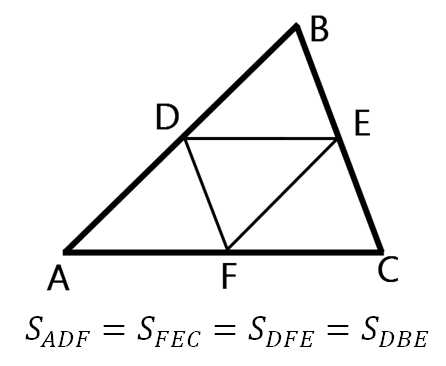
Треугольники равны по третьему признаку (по трём сторонам). Хотя и остальные признаки равенства треугольников также применимы.
4. Есть не мало задач, где речь идёт об изменения объёма (пирамиды, куба, параллелепипеда, шара), путём увеличения или уменьшения рёбер (радиуса) в определённое количество раз. То есть речь идёт о подобных телах. Помните о том, что есть формула, которая связывает объёмы подобных тел:
Пример подобных тел:
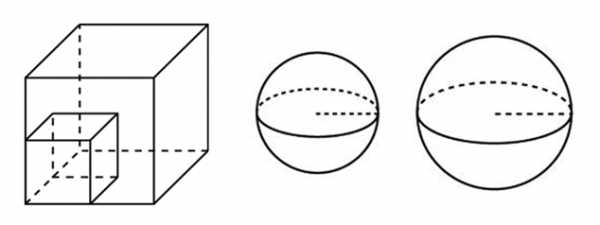
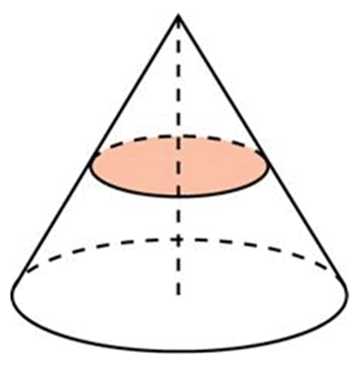
*Ещё пример: плоскость параллельная основанию конуса и проходящая перпендикулярно его высоте отсекает конус подобный исходному
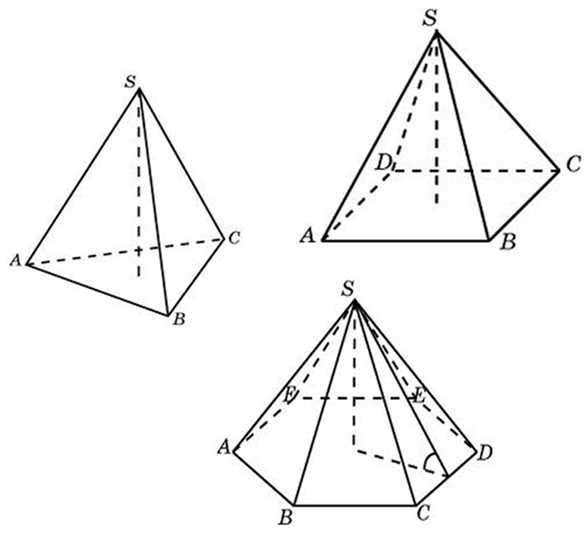
5. Кроме того, есть много задач, в которых фигурируют правильные пирамиды. Напомню, что это пирамиды в основании которых лежит правильный многоугольник (в наших задачах – правильный треугольник, квадрат, правильный шестиугольник). Что необходимо запомнить здесь?
Высота опущенная из вершины к основанию пирамиды проходит через середину этого основания
или
Отрезок соединяющий вершину правильной пирамиды и середину её основания является высотой пирамиды
6. Есть группа задач, где речь идёт о правильной шестиугольной призме (в основании лежит правильный шестиугольник). Условия и вопросы различные, но знание следующих фактов о правильном шестиугольнике считаю необходимым:
1. Стороны правильного шестиугольника равны.
2. Углы при вершинах равны 120 градусам.
3. Около правильного шестиугольника можно описать окружность.
4. Радиус окружности описанной около правильного шестиугольника равен сторонам этого шестиугольника.
5. Расстояние между двумя диаметрально противоположными вершинами (это диаметр описанной окружности) равно двум сторонам этого шестиугольника.
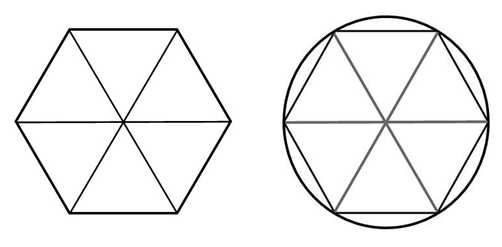
*Правильный шестиугольник как бы состоит из шести сложенных друг с другом равносторонних треугольников.
Ещё стоит отметить некоторые моменты. Их нетрудно вывести, но предлагаю запомнить их и положить в копилку ваших математических навыков. Простыми словами можно сказать так:
Отрезок соединяющий две вершины правильного шестиугольника (при чём этот отрезок не проходит через центр), отсекает треугольник площадь которого равна одной шестой площади данного шестиугольника
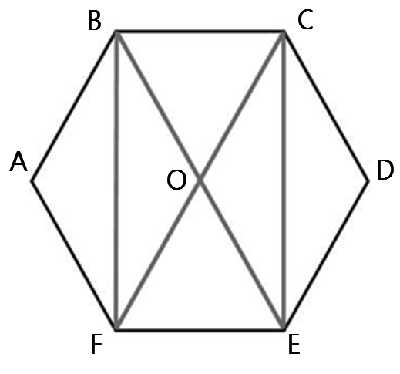
Нетрудно сделать и следующие выводы:
Я не говорю о том, что если вы не запомните представленную информацию, то задачи вам этой группы не решить. Нет! При наличии хорошей математической базы, и владения навыками решения стереометрических и планиметрических задач проблем при решении не будет никаких. Вы с лёгкостью вспомните теорию и быстро сделаете необходимые выводы. Но помня указанные выше моменты, вы сэкономите время и проведёте решение в два раза быстрее.
Отмечу, что для решения ряда задач, связанных с увеличением (уменьшением) ребра в параллелепипеде, пирамиде, кубе, либо радиуса конуса или шара, и стоит вопрос об изменении объёма, существует более рациональный метод, чем тот который используется при обучении в школьной программе. Мы с вами его изучим. Вы удивитесь простоте подхода, задачи решаются практически в одну строчку, не пропустите!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Стереометрия на ЕГЭ по математике
Автор Сергей
Среда, Май 23, 2012
Стереометрии в экзаменационных вариантах ЕГЭ по математике посвящены задачи B9 и C2, первые попроще, вторые посложнее. О некоторых методах решения задач C2 можно почитать в статье «Как решать задачи C2 ЕГЭ по математике — советы репетитора». В данной статье мы подробно остановимся на решении задач B9. Причем как репетитор по физике и математике постараюсь построить изложение таким образом, что через решение простых заданий B9 мы будем переходить к решению более сложных задач C2 по
Задачи по стереометрии из ЕГЭ, связанные с параллелепипедом
Пример 1. Найдите диагональ прямоугольного параллеле-пипеда, если она наклонена к его грани под углом а стороны этой грани равны и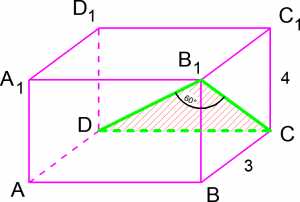
Чертеж к заданию
Решение. Так как — параллелепипед, то а значит и любой прямой, лежащей в этой плоскости, в том числе и То есть треугольник — прямоугольный, гипотенузой в нем будет являться искомая диагональ
Из прямоугольного треугольника находим гипотенузу Для прямоугольного треугольника имеем то есть
Ответ: 10.
Задача для самостоятельного решения №1. Диагональ прямоугольного параллелепипеда равна и наклонена к плоскости его грани под углом Найдите ребро параллелепипеда, перпендикулярное плоскости этой грани.
Показать ответОтвет:yourtutor.info
Геометрия на ЕГЭ по математике. Что нужно знать?
Геометрия на профильном ЕГЭ по математике — одна из сложных тем для абитуриентов. Дело в том, что когда-то экзамен по геометрии в школе был обязательным, а сейчас — нет. В результате у большинства абитуриентов знания по геометрии близки к нулю.
Геометрия на профильном ЕГЭ — это три в части 1 (сюда входит и планиметрия, и стереометрия), а также задача 14 (стереометрия) и для многих недосягаемая 16 (геометрия) из второй части. Как же научиться их решать?
Начнем с планиметрии. Прежде всего, выучите основные формулы геометрии.
На нашем сайте вы найдете курс геометрии с нуля — основные определения, формулы и теоремы, а также разбор множества экзаменационных задач по геометрии из части 1.
Для решения задач по геометрии из части 2 нужна более серьезная подготовка.
Первый этап — теория. Необходимый материал есть в учебнике по геометрии за 7-9 класс (автор — А. В. Погорелов или Л. С. Атанасян). Выпишите в тетрадь определения и формулировки теорем. Сделайте чертежи. Доказывать теоремы старайтесь самостоятельно.
Программа по геометрии.
1. Треугольники. Элементы треугольника. Вершины и стороны. Высоты, медианы, биссектрисы (определения).
2. Построение треугольника: практические задания.
а) Три стороны треугольника равны и сантиметров соответственно. Постройте треугольник с помощью циркуля и линейки.
б) В треугольнике угол равен градусов, сторона равна двум, равна . Постройте треугольник .
в) В треугольнике сторона равна , угол равен , угол равен . Постройте треугольник .
3. Три признака равенства треугольников. Неравенство треугольника.
4. Постройте с помощью циркуля и линейки:
а) серединный перпендикуляр к отрезку;
б) биссектрису угла.
5. Углы при параллельных прямых и секущей. Вертикальные, смежные, соответственные, односторонние и накрест лежащие углы. Их определение и свойства.
6. Теорема о сумме углов треугольника.
7. Внешний угол треугольника.
8. Постройте в одном и том же треугольнике
а) три высоты. Рассмотрите также случаи тупоугольного и прямоугольного треугольника.
б) три биссектрисы.
в) три медианы.
9. Равнобедренный треугольник. Определение и свойства. Высота в равнобедренном треугольнике.
10. Средняя линия треугольника и ее свойства.
11. Прямоугольный треугольник. Теорема Пифагора.
12. Определения синуса, косинуса и тангенса
— для острого угла прямоугольного треугольника
— для произвольного угла.
13. Четырехугольники. Сумма углов четырехугольника.
14. Параллелограмм. Определение и свойства. Площадь параллелограмма.
15. Виды параллелограммов и их свойства. (ромб, прямоугольник, квадрат).
16. Трапеция. Средняя линия трапеции. Площадь трапеции.
17. Подобные треугольники. Три признака подобия треугольников.
18. Площадь треугольника. Формулы и .
19. Теоремы синусов и косинусов.
20. Чему равно отношение площадей подобных фигур.
21. Свойство медианы (в каком отношении делятся медианы в точке пересечения?)
22. Свойство биссектрисы (в каком отношении биссектриса делит противоположную сторону?)
23. Окружность и круг. Длина окружности. Площадь круга. Длина дуги и площадь сектора.
24. Теорема о радиусе, проведенном в точку касания.
25. Центральный и вписанный углы. Связь между ними.
26. Теоремы о вписанных углах.
27. Теорема о пересекающихся хордах.
28. Теорема об отрезках длин касательных, проведенных из одной точки.
29. Теорема о секущей и касательной.
30. Дан треугольник . Постройте
а) окружность, вписанную в данный треугольник
б) окружность, описанную вокруг данного треугольника.
Где находятся центры этих окружностей?
31. Еще три формулы площади треугольника (через радиус вписанной окружности, через радиус описанной окружности и формула Герона).
32. Когда можно вписать окружность в четырехугольник? Когда — описать вокруг четырехугольника?
Программа по стереометрии
Отдельно — тема «Векторы». Напомним, что на ЕГЭ по математике векторы встречаются в задаче 4. Они также пригодятся вам в решении задачи С2 (14).
Освоив теорию, можно приступать к решению сложных задач по геометрии, входящих в часть ЕГЭ. Мы рекомендуем вам сборники:
Р. К. Гордин «ЕГЭ. Математика. Задача 16. Геометрия. Планиметрия» и
А. Шень. «Геометрия в задачах».
А. Г. Корянов и А. А. Прокофьев «Пособие по решению заданий типа ».
Разбирая и решая задания ЕГЭ по геометрии, вы заметите очень интересную вещь. Простые задачи из части 1, разобранные на нашем сайте, часто оказываются базовыми схемами, на которых строятся сложные задачи из части 2 профильного ЕГЭ.
Решая на ЕГЭ задачи по геометрии, обращайте особое внимание на оформление. Помните совет, который дал абитуриентам автор бестселлера «Математика — абитуриенту» В. В. Ткачук. Вот он, этот ценнейший совет:
«Подробность решения должна быть такова, чтобы его мог понять человек в 10 (десять) раз глупее вас».
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
