Задание 9 егэ по математике: Задание 9 из ЕГЭ по математике

Алгоритм решения:

1. Анализируем выражение.
2. Преобразовываем и вычисляем выражение.
3. Записываем ответ.

Решение:

1. Данное выражение представляет собой произведение множителей, которые можно по формулам сокращенного умножения записать в виде разности квадратов:

2. Имеем:

Ответ: -5.

Найдите значение выражения — задание из ЕГЭ по математике профильный уровень

Автор Ольга Викторовна На чтение 6 мин. Просмотров 1. 2k. Опубликовано 08.03.2020

Итак, давайте разберем, задание №9 в ЕГЭ по математике профильного уровня. Все эти задания требуют — найдите значение выражения. То есть, наша задача вычислить — найти значение выражения и записать в ответ число.

Задания ЕГЭ профильного уровня по математике

Какие бывают задания с требованием найти значение выражения. Эти задания бывают разными и относящимися к разным темам. Например, выражения в задании 9 ЕГЭ по математике профильного уровня бывают:

• степенные
• логарифмические
• тригонометрические
• числовые
• иррациональные (с корнями)
• с переменными заданными величинами

Давайте рассмотрим общий принцип и необходимые теоретические сведения для решения каждого типа выражения.

Степенные выражения

Для того, чтобы найти значение выражения со степенями, вам понадобятся формулы для вычисления степеней. Приведем самые распространенные из них, на которые обычно дается задание нахождения значения выражения со степенями. Вы должны четко понимать, что если число находится в какой то степени, то оно не свободное, оно в отношении степени. И нельзя сократить два числа в дроби, если у них одно основание и разные показатели степени. Или если разные основания и разные показатели степени.

Найдите значение выражения . Мы не можем сократить 3 и 9, потому что они находятся в отношении степени. И нам нужно сначала возвести в степень. Только потом мы можем разделить числитель на знаменатель.

Итак, найдем значение этого выражения: .

Здесь мы использовали свойство степени при делении степеней с одинаковыми основаниями. Приведем все необходимые для решения данных заданий свойства степеней:

Давайте рассмотрим еще несколько заданий.

Найдите значение выражения

Задание 1.

Найдите значение выражения .

Очевидно, что перед нами формула сокращенного умножения в развернутом виде: . Применяя эту формулу к нашему выражению, увидим, что , а . Получим: .

Ответ: -10.

Задание 2.

Найдите значение выражения .

При возведении произведения в степень, в нее возводится каждый множитель, то есть получим: .

Ответ: 7,5.

Ничего сложного, если вы знаете формулы сокращенного умножения и свойства степеней.

А для того, чтобы найти значение выражения, в котором есть логарифмы, нужно знать свойства логарифмов.

Задание 3.

Найдите значение выражения .

Здесь для нахождения значения выражения мы будем использовать следующие свойства логарифмов:

переход к новому основанию .

сложение логарифмов с одинаковыми основаниями: .

Итак, получим: 

Ответ: 1.

Задание 4.

Найдите значение выражения .

Помните: при возведении в степень произведения, в нее возводится каждый множитель:

Преобразуем выражение в числителе дроби:

Разложим 6 на множители 2 и 3, получим:

Далее используем свойства степеней:

.

Сокращая числитель и знаменатель на , получим: .

Ответ: 9.

Задание 5

Найдите значение выражения: .

Решим данное выражение, учитывая, что , а . Получим: . При возведении степени в степень, показатели степени перемножаются, имеем: .

Ответ: 27.

Задание 6

Найдите значение выражения .

Для того чтобы найти значение этого выражения надо применить  следующее свойство логарифмов: .

Получим: .

Ответ: 2.

Задание 7

Найдите значение выражения .

Действуем также, как и в предыдущем задании, используя свойство разности логарифмов:

.

Ответ: 2.

Задание 8

Найдите , если .

Для того, чтобы найти значение данного выражения нам понадобятся две тригонометрические формулы:

1. Основное тригонометрическое тождество: .
2. Косинус двойного аргумента: .

Итак, по формуле (2) распишем наше выражение в следующем виде: . Однако, нам известен только косинус, для того чтобы из синуса сделать косинус, используем основное тригонометрическое тождество: .

Тогда наше выражение примет вид:

.

Подставляем значение косинуса, получим:

.

Ответ: -0,56.

Задание 9

Найдите значение выражения .

Решим. Вынесем за скобки. Получим: .

В скобках видим формулу косинуса двойного аргумента: . Применяя ее, имеем:

Мы знаем, что . Но мы не знаем, чему равен , давайте рассуждать в это 3 и еще .

То есть, . Применяя формулы или правило приведения, получим: . Подставляя это значение в наше выражение , вычислим: 

Ответ: -3.

ЕГЭ по информатике 2021 — Задание 9 (Таблица Excel)

Девятое задание из ЕГЭ по информатике нового формата 2021 основывается на работе с таблицами Excel.

Это задание выполняется на компьютере в новом формате ЕГЭ 2021 года. Будет выдан файл Excel, по которому нужно получить правильный ответ и записать его в бланк заданий.

Если Вам урок удобнее смотреть в видеоформате, то можете перейти на ролик по 9 заданию из ЕГЭ по информатике 2021 на Youtube. Подписывайтесь на канал!

Здесь имеется столбец «Продукт». Другие столбцы: «Жиры», «Белки», «Углеводы», «Калорийность» – это характеристики этих продуктов.

В Excel можно каждой ячейке задавать какие-нибудь формулы. Например, пусть в ячейке F2 будет писаться СУММА из ячеек B2 (Жиры) и С2 (Белки).

Кликаем по ячейке F2, а затем на значок «вставить функцию».

Появится окно «Вставка функции«. Здесь все функции разбиты на категории: Финансовые, математические, логические и т. д. По умолчанию стоит категория «10 недавно используемых функций». В этой категории уже есть нужная нам функция СУММ. Выбираем её и кликаем «ОК». (Основная категория для функции СУММ является «математические»)

Появляется окно для функции СУММ.

Если мы напишем в поле Число1: «B2:E2» ,– то у нас суммируются три ячейки: B2, C2, E2. Таким образом, мы задали интервал.

Можно суммировать и вниз, т.е. ячейки одного столбца (B2:B1001).

Чтобы просуммировать отдельные ячейки, без интервала – необходимо уже использовать поле Число2.

Нам нужно просуммировать два числа: значение ячейки B2 и значение С2. Значит, пишем в поле Число1 — B2, а в поле Число2 — C2.

Нажимаем «Ок». Теперь у нас в ячейке F2 сумма значений ячеек B2 и С2.

Примечание 1: Мы могли сделать данную операцию с помощью интервала. Для этого нужно было написать в поле Число1: B2:C2.

Примечание 2: Так же мы могли суммировать и без вставки функции. Для этого нужно кликнуть по ячейке F2 и затем в поле, на которое показывает стрелка на рисунке, вписать формулу: «=B2+C2«. И нажать «Enter».

Необходимо подвести мышку к нижнему правому углу ячейки с формулой, чтобы появился чётный крестик:

И нажав левую кнопку мыши, тянем вниз. Таким образом, у нас формула распространится на весь столбец.

При изменении данных в ячейках столбцов В и С – значения в ячейках столбца F меняется автоматически.

Примерные задачи 9 задания ЕГЭ по информатике 2021

Задача (Среднее значение с условием)

Откройте файл электронной таблицы, содержащей результаты тестирования обучающихся по математике и информатике. Каков средний балл по информатике среди участников тестирования, получивших зачётные баллы по этому предмету (т.е. не менее 44 баллов)? В ответе округлить число до двух знаков после запятой.

Для решения этой задачи будем использовать функцию =СРЗНАЧЕСЛИ().

Кликнем в свободную ближайшую ячейку E2. Здесь мы хотим получить ответ на задачу. Нажмём на кнопку «Вставить функцию«, выберем категорию «статистические«, а затем выберем функцию СРЗНАЧЕСЛИ.

В диапазоне нужно указать все ячейки с числами столбца «Информатика» (Столбец D). Значит, напишем: D2:D273 (Чтобы понять сколько строчек в таблице, нужно прокрутить всю таблицу до самого конца вниз.). В условии напишем: >=44 (Т.к. мы должны считать среднее значение для тех ячеек, где число не меньше 44).

Нажимаем «ОК» и получаем в ячейке E2 число 68,60851064. Нам его нужно округлить до 2 знаков после запятой. Воспользуемся инструментом в программе Excel для округления.

Найдём кнопки «Уменьшить разрядность» и «Увеличить разрядность«. Их можно применять к выделенной ячейке.

Уменьшим разрядность до 2 знаков. Получается число 68,61. Это и будет ответ!

Примечание 1: Если мы хотим найти среднее значение без условия, есть функция СРЗНАЧ.

Примечание 2: СРЗНАЧЕСЛИ (СРЗНАЧ)- это и есть среднее арифметическое значение.

Посмотрим ещё один важный пример 9 задания ЕГЭ по информатике нового формата 2021.

Откройте файл электронной таблицы, содержащей данные о сотрудниках одного из предприятий города Москвы. Сколько человек в таблице имеют возраст меньше 30 лет, и их вес превышает 100 кг? В ответе напишите одно целое число.

Сначала поставим 1 в столбце F в тех строчках, которые удовлетворяют нашему условию: человек имеет возраст меньше 30 лет, и его вес превышает 100 кг. Если строчка не удовлетворяет условию, значит, в ячейке столбца F поставим 0.

Сначала настроим формулу для одной строчки, а затем формулу распространим на весь столбец.

Кликаем по ячейке F2. Нажимаем на кнопку «Вставить функцию«. Выбираем функцию ЕСЛИ из категории «Логические«.

В поле «Лог_выражение» задаём условие : И(C2>100; E2. Т.к. сначала мы задаём формулу для второй строки, то пишем ячейки C2 и E2. Мы написали условие нашей задачи для второй строки. Столбец C — отвечает за Вес, а столбец E — за возраст.

В условии ставим вначале союз «И«, т.к. одновременно два условия должны выполняться. Если бы в задаче говорилось, что мы должны подсчитать количество строчек, где хотя бы одно условие сработало, тогда бы поставили союз «ИЛИ«.

В поле «Значение_если_истина» ставим 1. В поле «Значение_если_ложь» ставим 0. Нажимаем «ОК».

Получилось, что в ячейке F2 высветился ноль. Значит, первый сотрудник не удовлетворяет условию задачи.

Теперь распространим формулу на весь столбец F. Подводим мышку к ячейке F2 к правому нижнему углу. Когда появился чёрный крестик, нажимаем левую кнопку мыши и тянем вниз, распространяя формулу на весь столбец.

Где-то будут получатся нули, а где-то единицы. Всё зависит от характеристик сотрудника.

После того, как формула будет распространена на весь столбец F, нам нужно посчитать количество единиц в столбце F. Это количество и покажет число сотрудников, которые подходят под условие задачи.

Воспользуемся функцией СУММ. Кликнем по ячейке G2. Именно здесь получим ответ. Затем нажмём на кнопку «Вставить функцию» и выберем СУММ из категории «Математические«.

В поле Число1 зададим интервал F2:F301 (Ведь всего у нас 301 строчка в таблице).

Нажимаем «ОК» и получаем в ячейке G2 ответ на нашу задачу. В ответе напишем 14.

Примечание: Для подчёта количества с условием можно использовать функцию СЧЁТЕСЛИ. Попробуйте решить с помощью неё самостоятельно.

Продолжаем тренироваться решать 9 задания из ЕГЭ по информатике нового формата 2021.

Откройте файл электронной таблицы, содержащей результаты тестирования обучающихся по математике, информатике и физике. Чему равна наименьшая сумма баллов по математике и информатике среди школьников, получивших более 50 баллов по математике или информатике?

В ответе запишете целое число.

В начале нужно выписать отдельно сумму баллов по математике и информатике для тех школьников, которые подходят под условие.

Выпишем сумму двух предметов, для удовлетворяющих условию строчек, в столбец F, с помощью функции ЕСЛИ.

В начале нужно задать формулу для одной ячейки F2. Кликаем по ячейке F2, нажимаем на кнопку «Вставить функцию«, выбираем функцию ЕСЛИ.

В поле «Лог_выражение» пишем: ИЛИ(C2>50; D2>50). В поле «Значение_если_истина«: C2+D2. В поле «Значение_если_ложь«: «» (Пустые двойные кавычки).

Важно: Здесь мы в поле «Значение_если_ложь» должны поставить пустые двойные кавычки, ведь, если поставить ноль, тогда, при поиске минимального значения будем находить всегда этот ноль. Мы ноль ставим в это поле только тогда, когда ищем количество строчек, ведь, тогда мы суммируем единицы, а ноль при суммировании не влияет на результат.

Нажимаем «ОК», и в ячейке F2 получается число 160. Это говорит о том, что первая строчка удовлетворяет условию задачи. И теперь в ячейке F2 лежит сумма баллов по математике и информатике для первого учащегося.

Распространим данную формулу на весь столбец F.

В основном получатся числа, но где-то ячейки останутся пустыми. Это значит, что эти строчки не подошли под условие задачи.

Теперь нужно с помощью функции МИН найти минимальное значение в столбце F.

Кликаем по ячейке G2, нажимаем «Вставить функцию«, выбираем функцию МИН из категории «Статистические«.

В поле Число1 пишем диапазон столбца F: F2:F273.

Получаем ответ 75.

Продолжаем оттачивать навыки работы с электронными таблицами в 9 задании из ЕГЭ по информатике нового формата 2021.

Откройте файл электронной таблицы, содержащей результаты тестирования обучающихся по математике, информатике и физике. Каков средний балл по математике обучающихся, набравших не менее 60 баллов по информатике?

В ответе запишите только целую часть получившегося числа.

Эту задачу решим двумя способами.

1 Способ

В этом способе решения будем снова использовать функцию СРЗНАЧЕСЛИ.

Кликаем по ячейке F2 и вставляем функцию СРЗНАЧЕСЛИ из категории «Статистические«.

Т.к. столбец, по которому мы будем проверять условие, отличается от того, по которому нужно искать среднее значение, то мы напишем следующие параметры:

В поле «Диапазон» пишем: D2:D273 (Это диапазон, который участвует в условии).

В поле «Условие«: >=60 (Это само условие, которое работает в диапазоне, написанный выше).

В поле «Диапазон_усреднения«: C2:C273 (Это диапазон, для которого будет найдено среднее арифметическое значение. Будут участвовать только те строчки, которые прошли условие).

Если последнее поле остаётся пустым, то среднее значение ищется по первому полю.

Нажимаем «ОК», и получаем число 60,0301205. Округлим это число до целых, получим число 60.

2 Способ

Этот способ подходит и для более запутанных ситуаций.

Для строчек, где выполняется условие задачи, перенесём значения столбца С в столбец F.

Кликаем в ячейку F2, нажимаем кнопку «Вставить функцию«, выбираем функцию Если.

Сначала нужно записать формулу для одной строки.

В поле «Лог_выражение» пишем: D2>=60 (Условие того, что человек набрал не менее 60 баллов по информатике)

В поле «Значение_если_истина» пишем: C2 (Переносим само значение столбца математики. Именно впоследствии мы должны найти среднее значение баллов по математике).

В поле «Значение_если_ложь» пишем: «» (Пустые кавычки. Нельзя писать ноль, иначе мы сильно занизим реальное среднее значение).

Нажимаем «ОК». Получается число 81 в ячейке F2.Оно перенеслось из ячейки C2, ведь значение по информатике больше 60 для этой строчки.

Распространяем формулу на весь столбец.

В строках, которые не удовлетворяют условию задачи, будут пустые ячейки.

Когда столбец готов, легко найти среднее значение для столбца F.

Кликаем в ячейку G2 и вставляем функцию СРЗНАЧ. В этой функции указываем диапазон F2:F273.

Получается число 60,0301205. Округляем его до целых, получается число 60.

Не редкий гость в примерных задачах 9 задания из ЕГЭ по информатике 2021.

Откройте файл электронной таблицы, содержащей данные о количестве белков, жиров и углеводов для различных продуктов. Сколько процентов от общего числа составили продукты, у которых более 10 г белка?

В ответе напишите одно целое число.

Задачи на проценты обычно сводятся к нахождению количества.

Найдём сколько продуктов, у которых белка более 10 г.

Кликаем по полю E2. Применим функцию СЧЕТЕСЛИ из категории «Статестические«.

Диапазон указываем: C2:C1001 (Столбец белка).

В поле критерий пишем: >10.

Нажимаем кнопку «ОК». В поле E2 получается число 373.

Чтобы найти проценты, нужно это количество, которое мы нашли, разделить на всё количество продуктов и умножить на сто.

Кликаем по верхнему полю («строка формул»):

Дописываем: =СЧЁТЕСЛИ(C2:C1001;»>10″)/1000 * 100

Всего у нас 1000 наименований продуктов. Строчек 1001, но начинаются продукты со второй строчки. Поэтому делим на 1000 (1001 — 1). Умножаем на 100, чтобы найти проценты.

Нажимаем Enter. Получается число 37,3. Округлим до целого числа, ответом будет 37.

В следующей примерной задаче 9 задания ЕГЭ по информатике 2021 будем комбинировать уже изученные приёмы.

Откройте файл электронной таблицы, содержащей вещественные числа – ведомость продуктового магазина. Наценкой товара считается разность между закупочной ценой и ценой реализации. Прибыль – количество проданных товаров, умноженное на значение наценки. Найдите товар с наценкой выше среднего значения, который принесет максимальную прибыль после его полной продажи. В качестве ответа укажите одно число – полученную после продажи найденного товара прибыль. Ответ округлите до целых чисел.

Сначала нужно найти среднее значение наценки. Запишем наценку в столбце E.

Запишем формулу сначала для одной ячейки E2. Кликаем по ячейки E2, затем кликаем по верхнему полю («строка формул») и пишем: =C2-B2.

Примечание: Формула начинается со знака «равно»!

Нажимаем Enter. Получается число 9,42.

Подводим курсор мышки к правому нижнему углу. После появления чёрного крестика, нажимаем левую кнопку мышку и тянем вниз. Тем самым распространим формулу на весь столбец.

Найдём среднее значение наценки, которая находится в столбце E.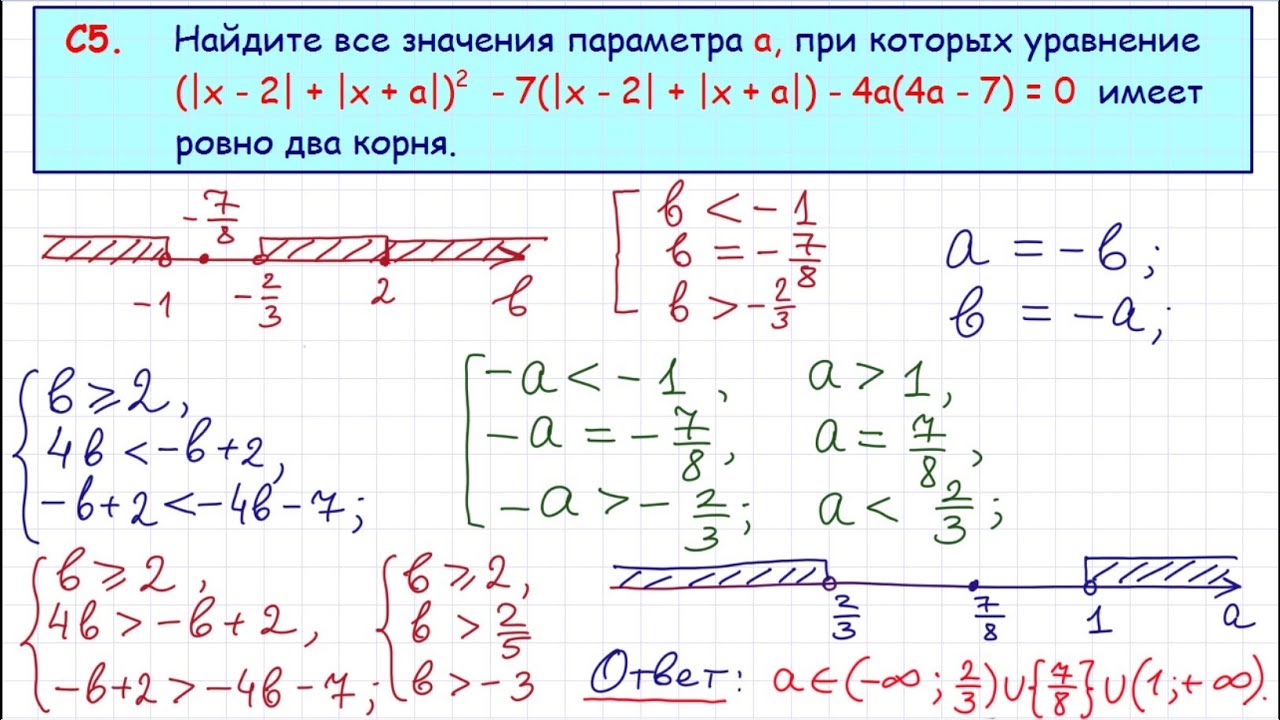

Кликаем по ячейке F2, затем на кнопку «Вставить функцию«, выбираем СРЗНАЧ. Диапазон указываем: E2:E100. Нажимаем «ОК» и получаем число 58,25. Это и есть среднее значение для наценки.

Теперь напишем в столбец G прибыль, но только для тех товаров, у которых наценка выше среднего значения.

Сначала запишем формулу для одной строчки. Кликаем по ячейки G2, нажимаем «Вставить функцию«, выбираем ЕСЛИ.

В поле «Лог_выражение» пишем: E2>58,25. Если наценка выше среднего, то будем считать прибыль.

Т.к. в столбце E все числа имеют не более двух знаков после запятой и число 58,25 тоже имеет два знака после запятой, то мы не получим ошибок из-за округления среднего значения.

В поле «Значение_если_истина» : E2 * D2 (Умножаем наценку на количество проданных товаров. Получаем прибыль).

В поле «Значение_если_ложь«: «» (Пустые кавычки. Ведь мы потом будем искать максимальное значение для прибыли, для товаров, у которых наценка выше среднего значения).

Нажимаем «ОК». Получается в G2 пустое окошко. Значит, для этого товара наценка не выше среднего значения.

Распространим формулу на весь столбец G. Где-то окажутся числа, а где-то пустые ячейки.

Кликнем по ячейке h3 и найдём с помощью функции МАКС (категория «Статистические») максимальную прибыль, в диапазоне указав: G2:G100. Округлив до целых, в ячейке h3 получается ответ 10185.

Примечание: Мы могли при составлении условия E2>58,25 использовать название ячейки F2 вместо числа 58,25. Но тогда нужно её «зацементировать» т.е. E2>$F$2 (Использовать абсолютную адресацию). Если мы всё-таки решили написать число, то нужно следить, чтобы точность была одинаковая у среднего значения, и у тех ячеек, которые мы сравниваем с этим средним значением.

Последнее. Если в задаче говорится о значении по абсолютной величине, т.е. о значении по модулю, то нужно использовать конструкцию ABS(). Например, разница по абсолютной величине двух ячеек A2 и B2 равна ABS(A2-B2). Это можно использовать при составлении формул.

Так же при подготовке к 9 заданию может быть полезна статья, которая была написана под старый формат ЕГЭ по информатике.

На этом всё. Комбинируйте приёмы, которые мы рассмотрели в этом уроке при подготовке к 9 заданию из ЕГЭ по информатике нового формата 2021. Удачи!

Единый государственный экзамен: уроки, тесты, задания.

1. 1. Главная информация в текстах разных жанров.

      Задание 1

   2. Подбор средства связи предложений в тексте. Задание 2

   3. Определение лексического значения слова. Задание 3

   4. Нормы ударения. Задание 4

   5. Различение паронимов.

      Задание 5

   6. Поиск лексической ошибки. Задание 6

   7. Формы слова. Задание 7

   8. Грамматические ошибки в предложениях. Задание 8

   9. Безударная гласная в разных типах корней.

      Задание 9

   10. Орфограммы в приставках. Задание 10

   11. Суффиксы разных частей речи. Задание 11

   12. Правописание суффиксов и окончаний глагольных форм. Задание 12

   13. Правописание частицы НЕ.

       Задание 13

   14. Написание слов слитно, раздельно, через дефис. Задание 14

   15. Суффиксы разных частей речи с Н/НН. Задание 15

   16. Знаки препинания при однородных членах и в сложносочинённых предложениях. Задание 16

   17. Знаки препинания при обособленных членах.

       Задание 17

   18. Знаки препинания при вводных словах и обращениях. Задание 18

   19. Знаки препинания в сложноподчинённых предложениях. Задание 19

   20. Знаки препинания в сложных предложениях с разными видами связи и на стыке союзов. Задание 20

   21. Анализ постановки знаков препинания в тексте.

       Задание 21

   22. Содержание текста. Задание 22

   23. Типы текстов. Задание 23

   24. Поиск слова по значению и употреблению. Задание 24

   25. Поиск предложения по средству связи с предыдущим предложением.

       Задание 25

   26. Средства художественной выразительности. Задание 26

   27. Сочинение-рассуждение. Задание 27

2. 1. Русский язык. Тренировочный вариант 1

   2. Русский язык.

      Тренировочный вариант 2

   3. Русский язык. Тренировочный вариант 3

   4. Русский язык. Тренировочный вариант 4

1. 1. Полезная информация для выпускников

   2. Задача из повседневной жизни.

      Задание 1

   3. Математика в повседневной жизни. Задача 1

   4. Проценты в быту. Задача 1

   5. Вопрос по графику, диаграмме. Задание 2

   6. Вычисления по графикам и диаграммам.

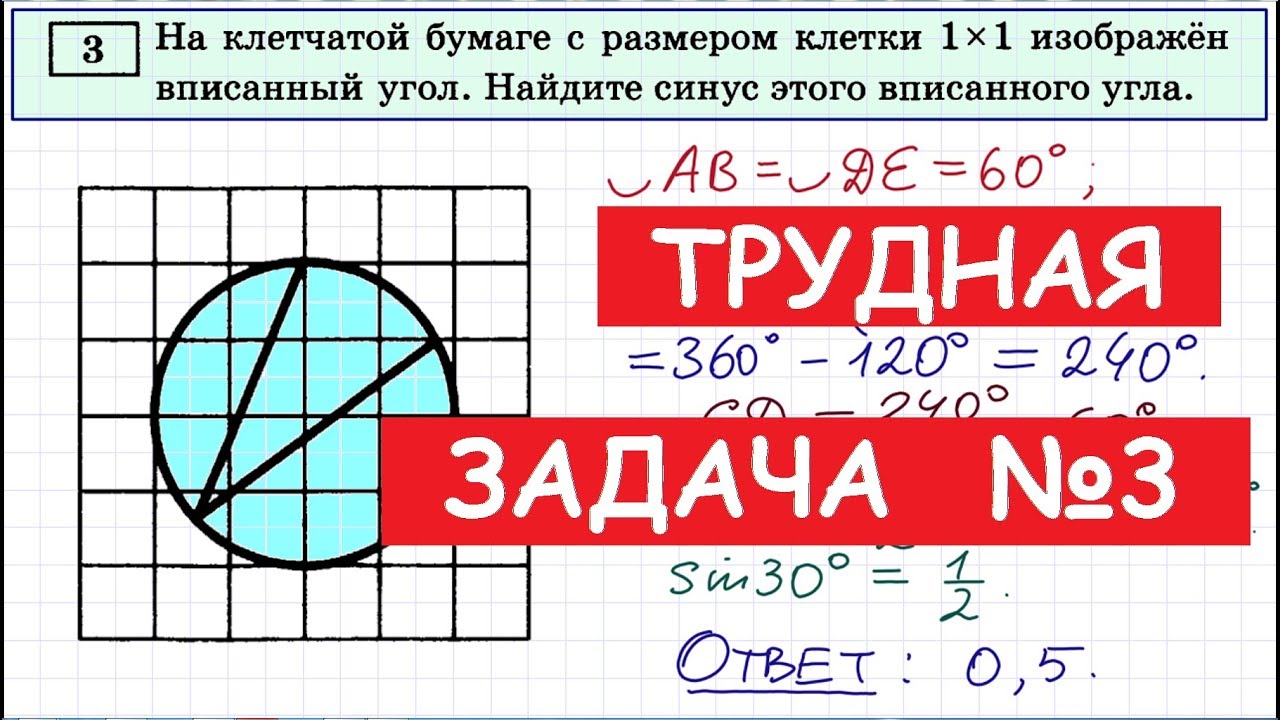      Задача 2

   7. Геометрическая задача по клеткам, координатам. Задание 3

   8. Вычисление площадей многоугольников по клеткам. Задача 3

   9. Вычисление элементов круга по клеткам. Задача 3

   10. Вычисление длин и углов по клеткам.

       Задача 3

   11. Нахождение вероятности события. Задание 4

   12. Вероятность случайного события. Задача 4

   13. Простейшее уравнение. Задание 5

   14. Целые рациональные уравнения.

       Задача 5

   15. Дробно-рациональные уравнения. Задача 5

   16. Иррациональные уравнения. Задача 5

   17. Показательные уравнения. Задача 5

   18. Логарифмические уравнения.

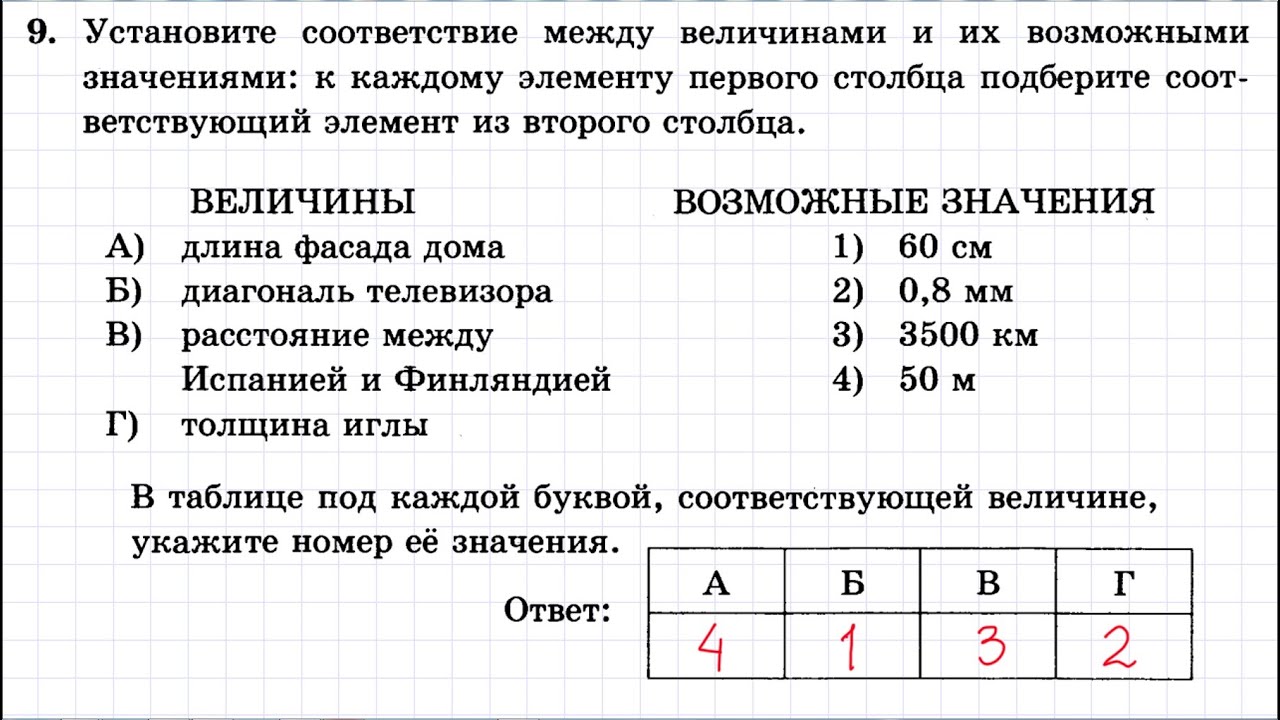       Задача 5

   19. Тригонометрические уравнения. Задача 5

   20. Геометрия треугольника, четырёхугольника, окружности. Задание 6

   21. Геометрия треугольника. Задача 6

   22. Геометрия четырёхугольника.

       Задача 6

   23. Геометрия окружности. Задача 6

   24. Геометрический и физический смысл производной. Задача 7

   25. Анализ функций с помощью производной. Задача 7

   26. Призма, пирамида, цилиндр, конус, шар.

       Задание 8

   27. Параллелепипеды. Задача 8

   28. Призмы. Задача 8

   29. Пирамиды. Задача 8

   30. Тела вращения.

       Задача 8

   31. Комбинации многогранников и тел вращения. Задача 8

   32. Рациональные выражения. Задача 9

   33. Степени с целыми и дробно-рациональными показателями. Задача 9

   34. Выражения с корнями.

       Задача 9

   35. Выражения с логарифмами. Задача 9

   36. Тригонометрия. Задача 9

   37. Расчёты по формулам. Задача 10

   38. Классические задачи на движение.

       Задача 11

   39. Работа и производительность труда. Задача 11

   40. Проценты. Смеси и сплавы. Задача 11

   41. Исследование поведения функции на промежутке. Задача 12

   42. Иррациональные уравнения с ограничениями. Задача 13

   43. Показательные и логарифмические уравнения с ограничениями. Задача 13

   44. Тригонометрические уравнения с ограничениями. Задача 13

   45. Уравнения смешанных типов с ограничениями. Задача 13

   46. Параллельность и перпендикулярность в пространстве. Задача 14

   47. Объёмы и сечения. Задача 14

   48. Углы и расстояния в пространстве. Задача 14

   49. Рациональные и иррациональные неравенства. Задача 15

   50. Показательные неравенства. Задача 15

   51. Логарифмические неравенства. Задача 15

   52. Отдельные геометрические факты. Задача 16

   53. Геометрия многоугольников. Задача 16

   54. Геометрия окружности. Задача 16

   55. Проценты. Вклады и кредиты. Задача 17

   56. Задачи на оптимизацию. Задача 17

   57. Аналитические и алгебраические методы решения уравнений с параметром. Задача 18

   58. Графические методы и исследование функций. Задача 18

   59. Делимость и сравнение по модулю. Примеры решения задач. Задача 19

   60. Задачи на оценку или пример. Задача 19

   61. Комбинаторные свойства последовательностей и прогрессий. Задача 19

2. 1. Математика. Базовый уровень. Тренировочные варианты

   2. Математика. Профильный уровень. Тренировочные варианты

1. 1. Русский язык. Тренировочный вариант 1

2. 1. Математика. Тренировочный вариант 1

1. 1. Тренировочный вариант 1. Версия 2019 года

   2. Тренировочный вариант 2. Версия 2019 года

   3. Тренировочный вариант 3. Версия 2019 года

   4. Тренировочный вариант 4. Версия 2019 года

   5. Тренировочный вариант 5. Версия 2019 года

   6. Тренировочный вариант 6. Версия 2019 года

   7. Тренировочный вариант 7. Версия 2019 года

   8. Тренировочный вариант 8. Версия 2019 года

   9. Тренировочный вариант 9. Версия 2018 года

   10. Тренировочный вариант 10 (без генераций). Версия 2017 года

2. 1. Тренировочный вариант 1. Базовый уровень. Версия 2019 года

   2. Тренировочный вариант 2. Базовый уровень. Версия 2019 года

   3. Тренировочный вариант 3. Базовый уровень. Версия 2019 года

   4. Тренировочный вариант 4. Базовый уровень. Версия 2019 года

   5. Тренировочный вариант 5. Базовый уровень. Версия 2018 года

   6. Тренировочный вариант 6. Профильный уровень. Версия 2018 года

   7. Тренировочный вариант 7 (без генераций). Версия 2017 года

3. 1. Тренировочный вариант 1. Версия 2018 года

   2. Тренировочный вариант 2 (без генераций). Версия 2017 года

4. 1. Тренировочный вариант 1. Версия 2018 года

   2. Тренировочный вариант 2 (без генераций). Версия 2017 года

Онлайн-подготовка к ЕГЭ по математике

Приближается пора экзаменов, и самое время начать активную подготовку. На этой странице вы найдете подборки материалов и видеоуроки от ведущих педагогов.

Для успешных результатов очень важно заниматься систематически, но при этом соблюдать баланс. Не тратьте много времени на прорешивание вариантов, потому что занятия должны быть тематическими. И не стоит забывать про задачи, которые даются вам легко – их решение позволит избежать случайных ошибок и придаст вам уверенности на экзамене.

Эксперты советуют уделять 15 минут в день простым заданиям, а остальное время потратить на выполнение домашних заданий к урокам.

Используйте для подготовки проверенные материалы ФИПИ, привычные учебники, рекомендации учителей и другие авторитетные источники. И помните, что даже 15 минут тренировки в день в итоге окажутся полезными на экзаменах.

Каждый урок включает: видеозапись, теоретические материалы и задачи.

ЕГЭ по математике. Базовый уровень.

Арифметика. Задание 1.
Видео Текстовый урок Тест

Преобразование показательных выражений. Задание 2.
Видео Текстовый урок Тест

Задачи на доли, проценты, отношения. Задание 3.
Видео Текстовый урок Тест

Вычисления по формуле. Задание 4.
Видео Текстовый урок Тест

Преобразование выражений. Задание 5.
Видео Текстовый урок Тест

Арифметические задачи. Задание 6.
Видео Текстовый урок Тест

Уравнения. Задание 7.
Видео Текстовый урок Тест

Наглядная планиметрия. Задание 8.
Видео Текстовый урок Тест

Сравнение величин. Задание 9.
Видео Текстовый урок Тест

Теория вероятностей. Задание 10.
Видео Текстовый урок Тест

Графики, диаграммы и таблицы. Задание 11.
Видео Текстовый урок Тест

Наилучший выбор. Задание 12.
Видео Текстовый урок Тест

Наглядная стереометрия. Задание 13.
Видео Текстовый урок Тест

Функции и их графики. Задание 14.
Видео Текстовый урок Тест

Планиметрия. Задание 15.
Видео Текстовый урок Тест

Стереометрия. Задание 16.
Видео Текстовый урок Тест

Числовая ось и неравенства. Задание 17.
Видео Текстовый урок Тест

Логика. Задание 18.
Видео Текстовый урок Тест

Свойства чисел. Задание 19.
Видео Текстовый урок Тест

Алгебра и арифметика. Задание 20.   
Видео Текстовый урок Тест

ЕГЭ по математике. Профильный уровень.

Арифметические задачи. Задание 1
Видео Текстовый урок Тест

Графики и диаграммы. Задание 2
Видео Текстовый урок Тест

Задачи на клетчатой бумаге. Задание 3
Видео Текстовый урок Тест

Теория вероятностей. Задание 4
Видео Текстовый урок Тест

Простейшие уравнения. Задание 5
Видео Текстовый урок Тест

Планиметрия. Задание 6
Видео Текстовый урок Тест

Планиметрия. Задание 16. Урок 1
Видео Текстовый урок Тест

Планиметрия. Задание 16. Урок 2
Видео Текстовый урок Тест

Задачи прикладного содержания. Задание 10
Видео Текстовый урок Тест

Тригонометрические уравнения. Задание 13. Урок 1
Видео Текстовый урок Тест

Тригонометрические уравнения. Задание 13. Урок 2
Видео Текстовый урок Тест

Преобразование выражений. Задание 9
Видео Текстовый урок Тест

Неравенства. Задание 15. Урок 1
Видео Текстовый урок Тест

Неравенства. Задание 15. Урок 2
Видео Текстовый урок Тест

Текстовые задачи. Задание 11
Видео Текстовый урок Тест

Задачи с экономическим содержанием. Задание 17. Урок 1
Видео Текстовый урок Тест

Задачи с экономическим содержанием. Задание 17. Урок 2
Видео Текстовый урок Тест

Стереометрия. Задание 8
Видео Текстовый урок Тест

Стереометрия. Задание 14. Урок 1
Видео Текстовый урок Тест

Стереометрия. Задание 14. Урок 2
Видео Текстовый урок Тест

Функции, заданные графиками, и их производные. Задание 7
Видео Текстовый урок Тест

Задачи с параметром. Задание 18. Урок 1
Видео Текстовый урок Тест

Задачи с параметром. Задание 18. Урок 2
Видео Текстовый урок Тест

Исследование функций. Задание 12
Видео Текстовый урок Тест

Авторы и методисты

Иван Валериевич Ященко, научный руководитель ЦПМ, руководитель федеральной группы разработчиков ЕГЭ по математике.

Андрей Викторович Семенов, член федеральной группы разработчиков ЕГЭ по математике, ведущий методист ЦПМ.

Иван Ростиславович Высоцкий, член федеральной группы разработчиков ЕГЭ по математике, начальник отдела ЦПМ.

Андрей Сергеевич Трепалин, член федеральной группы разработчиков ЕГЭ по математике, научный сотрудник Математического института им. В.А.Стеклова.

Екатерина Александровна Кукса, член федеральной группы разработчиков ЕГЭ по математике, разработчик контента образовательных продуктов МЦНМО и Яндекса.

Павел Иванович Самсонов, президент ассоциации учителей математики Москвы, член федеральной группы разработчиков ЕГЭ по математике.

Максим Яковлевич Пратусевич, член федеральной группы разработчиков ЕГЭ по математике, директор Президентского лицея 239.

Первая часть ЕГЭ по математике

Здесь могут быть задачи на движение или движение по реке, совместную работу, проценты, сплавы и растворы, оптимальный выбор и на числа. Нужно уметь по тексту задачи составлять уравнения и решать их. Как правило, это рациональные и линейные уравнения.

В задачах на движение необходимо знать формулу расстояния через скорость и время S=V*t. И иметь представление, как влияет течение на скорость движения: если плот, то скорость его движения равна скорости течения; если лодка плывет против течения, то из собственной скорости лодки нужно вычесть скорость течения; если плывет по течению, то скорость течения прибавляется.

Задачи на работу. Здесь нужно знать, что такое производительность труда. Поясним на примере. Пусть Денис делает домашнее задание за 5 часов, при этом каждый час он решает одно и тоже количество задач. Тогда получается, что за один час он решит пятую всех задач, за два часа две пятых. Обозначим все домашнее задание за 1, тогда за час Денис делает 1/5 домашнего задания – это есть его производительность. Таким образом, в задачах на работу часто всю работу обозначают за 1. В общем виде формула для производительности выглядит так: P=A/t, где A – полная, работа которую нужно выполнить, а t- время.

Задачи на проценты. Нужно хорошо понимать, что такое процент. Пусть у нас есть какая-то величина, поделим ее на 100 одинаковых частей, тогда одна часть из этих ста будет называться одним процентом (1%), соответственно пять частей – 5%. Обычно такие задачи решаются через пропорции.

Задачи на сплавы и растворы. При решении задач на растворы или сплавы, нужно понимать, что если у вас есть A литров некоего вещества и B литров воды, то общий объем раствора этого вещества в воде будет А+В литров. А в одном литре раствора будет содержаться A/(A+B) литров некоего вещества. Это отношение также называют концентрацией.

Задачи на числа. Эти задачи встречаются крайне редко. Но тут полезно помнить, что любое число можно разложить на слагаемые. Например, трехзначное число abc можно представить в виде 100a+10b+c.

6 Оценка аттестата по математике | Измерение того, что имеет значение: концептуальное руководство для оценки по математике

Три предложенных здесь принципа — содержание, обучение и справедливость — функционируют как гироскоп для реформы математического оценивания, который поможет продолжить реформу математики и привести к новым оценкам, которые отражают важную математику, поддерживают хорошее обучение и способствуют развитию возможностей каждого учащегося. учить.

Система наведения этого гироскопа является мощным инструментом на пути к реформе системы оценивания. Однако это всего лишь инструмент, сам по себе недостаточный для решения поставленной задачи. Не менее важны пригодность судна для рейса, экипаж, способный внести необходимые корректировки в середине курса, а также подробная навигационная карта, показывающая желаемый порт.

Сосудом реформы является общенациональный акцент на системных изменениях: скоординированный ответ всех основных компонентов образовательной системы (учебная программа, преподавание, оценка, управление, педагогическое образование, школьная организация и т. Д.)). По математике судно особенно крепкое и хорошо спущено на воду. Уже доступны описания задачи (Важен каждый), цели того, что студенты должны изучать (Учебный план и стандарты оценки), а также методы обучения, необходимые для поддержки этого обучения (Профессиональные стандарты преподавания математики). NCTM сейчас разрабатывает третий из серии томов стандартов, на этот раз по оценке. В этом томе, который планируется выпустить весной 1995 года, будут изложены стандарты оценивания, которые служат целому ряду целей — от обучения в классе до политики, оценки программ, планирования и распределения студентов.Три компонента стандартов — учебная программа, педагогика и оценка — обеспечивают основу для обновления педагогического образования, переосмысления школьной организации, повышения эффективности реформ и содействия диалогу о системных изменениях между многими заинтересованными сторонами в математическом образовании.

Резервы на рейс обеспечиваются материальными ресурсами, что стимулирует широкое участие в реформе оценивания. Эти ресурсы предоставляют богатый набор примеров высококачественного оценивания, созвучного видению математики и математического образования, выраженному в Стандартах .Некоторые предоставляют конкретные примеры, иллюстрирующие всеобъемлющие идеи (например, Mathematics Assess —

4 Оценивание для поддержки изучения математики | Измерение того, что имеет значение: концептуальное руководство для оценки по математике

, как правило, путем подсчета количества вопросов, на которые даны правильные ответы, и сравнения баллов одного человека с баллами другого на основании их относительного процентильного ранга. Так называемые оценки с привязкой к норме уже много лет беспокоят педагогов.Хотя высказывались различные критические замечания по поводу ссылок на нормы, основная проблема образования заключается в том, что такая информация недостаточно полезна для улучшения обучения и обучения и может, фактически, иметь контрпродуктивные образовательные последствия. В классе учителя и ученики должны знать, что ученики понимают хорошо, что они понимают хуже, и какими должны быть следующие шаги обучения. Относительные рейтинги протестированных студентов могут быть использованы вне контекста класса, но в этом контексте необходимы формы результатов, полезные для процесса преподавания и обучения.

Например, чтобы спланировать свое обучение, учителя должны знать о текущем понимании каждым учеником того, чему будут учить. Таким образом, программы оценки должны информировать учителей и учеников о том, что ученики узнали, как они учатся и как они думают о математике.Чтобы эта информация была полезной для учителей, она должна включать анализ конкретных сильных и слабых сторон понимания учащимся, а не только оценок вне контекста.

Чтобы обучение было эффективным, результаты оценки должны быть своевременными. ³⁵ Учебе учащихся не способствуют компьютерные распечатки, отправляемые учителям после того, как классы закончились в течение года и ученики ушли, ни учителя, которые уделяют слишком много времени оценке оценок.В частности, необходимо найти новые способы дать учителям и ученикам более непосредственные знания об успеваемости учеников по оценкам, предписанным внешними властями, чтобы эти оценки, а также собственные оценки учителя могли использоваться для улучшения обучения. Даже если основной целью оценки является определение достижений школы, штата или страны, оценка должна предоставлять учащимся и учителям отчеты об их успеваемости. Школьное время дорого.Когда учащимся не сообщают об их ошибках и заблуждениях, не говоря уже о том, чтобы помочь их исправить, оценка может усилить недопонимание и потратить драгоценное учебное время впустую.

Когда форма оценивания незнакома, учителя несут особую ответственность перед своими учениками, чтобы сообщить им заранее

сложных математических задач

Содержание страницы

Введение

Богатые математические задачи помогают учащимся осмыслить их через более глубокое обучение, которое требует высокого уровня мышления, рассуждений и решения проблем. Комитет VDOE Rich Mathematical Task Committee, состоящий из руководителей учителей математики со всего Содружества, создал математически насыщенные задачи, соответствующие стандартам обучения по математике 2016 года .Комитет создал шаблоны реализации задач до того, как приступить к их администрированию в классах. Для многих задач комитет оценивал задачи индивидуально, откалибровал их оценку с командой, предоставил обоснование выставления оценок и отобрал студенческие работы, которые будут служить в качестве якорных документов. Департамент образования Вирджинии хотел бы выразить особую благодарность Целевому комитету Rich Mathematical Task Committee, а также их коллегам, которые поддержали эту работу в своих подразделениях.

Планирование удаленного выполнения сложных математических задач

Эти ресурсы вместе с руководством по планированию удаленного выполнения сложных математических задач предназначены для поддержки учителей во внедрении в их классах «Стандартов обучения по математике » на 2016 год.Учителям рекомендуется не только использовать эти задания со своими учениками, но и стремиться к их точному выполнению, используя подробную информацию, представленную в шаблонах выполнения заданий.

Вебинары для поддержки удаленного выполнения сложных математических задач

Выполнение сложных математических задач в классах K-2

Выполнение сложных математических задач в классе 3–5 классов

Выполнение сложных математических задач в 6-8 классах

Выполнение сложных математических задач в 9–12 классах

Детский сад

Building Towers Task

Задача по сбору яблок

Задача «Совместное использование файлов cookie»

Загадки формы Task

Задача смешанных блоков

Утреннее рутинное задание

Наверх

1 класс

Сравнение точек Задача

Игрушечные машинки Task

Задача «Прогулка на природе»

Задание на парную игру

Игра с паттернами, задание

Как они могут быть равными? Задача

Наверх

2 класс

Mystery Number Task

Набор наклеек Task

Браслет Task

Сковороды для брауни Task

Talking Sticks Task

Монеты в кармане Задание

Задача «Сколько таблиц»

Количество учеников Задача

Наверх

3 класс

Задание для упаковки карандашей

Задание на вечеринку с пиццей

Карнавальные призы Задание

Корзины яблок Task

Деньги в копилке Задача

Многоугольные пазлы Задача

Наверх

4 класс

Специальное задание по доставке

Тако вторник, задание

Транспортное задание поездки

Задание по заливке красок

Обед у Леонардо.

Комбинации кемпинга Задача

Исследование четырехугольников, задание

Задача о возможностях равенства

Наверх

5 класс

Сохранение для велосипедного задания

Комната для обуви Task

Задача времени смешивания трассы

Bus A или Bus B Task

Задание на проектирование углов

Задача проектирования Windows

Наверх

6 класс

Задание на победу в игре

Задача пополнения печенья

Задача умного покупателя

Задача по отслеживанию акул

Задание на проектирование парка для собак

Задание по доставке пиццы

Задача экранного времени

Наверх

7 класс

Какой микроскоп Task

Задача по сбору средств для продажи выпечки

Задание на транспортировочную коробку

Задание «Прогулка по парку»

Задача отжима, отжима, отжима

Летнее задание

Задача по садоводству

Наверх

8 класс

Задача «Дилемма директора»

Задача преобразования монстров

Задача самого длинного пути

Задача «Ваш счастливый день»

Арахисовое масло Задание

Сколько камней мне понадобится Задача

Наверх

Алгебра I

Задача перевода покупок

Цветочные сады, задание

Забавное задание на качелях

Задача на полную парковку

Radical Rocks Task

Вечеринка на батутеTask

Задача сбережения велосипедов

Задача соревнований по футболу

Мы играем в баскетбол, задание

Наверх

Геометрия

Задача логических драйверов

Линии и тигры и медведи, о боже! Задача

Задача авиашоу

Задача игры «Выведи меня на мяч»

Sea Cities Task

Задача встряхивания, дребезжания и перекатывания

Наверх

Алгебра II

Задача лучшего друга дрона

Функция задания на поездку

Задача Animate It

Задача по лесным пожарам

Задача атаки водорослей

Наверх

Шаблон пустого задания