Шпоры для подготовки к егэ по профильной математике
© 2020 Андрей Павликов. MathStudy.online ЕГЭ профиль. Шпаргалка по первой части Задача 1. Процент — это сотая часть числа. 1% = 1 100 = 0,01. Чтобы найти 𝑝% от числа 𝑥 , необходимо умножить число 𝑥 на 𝑝 сотых. Получим 𝑝 100 ∙ 𝑥. Чтобы увеличить число 𝑥 на 𝑝 %, нужно число 𝑥 умножить на величину (1 + 𝑝 100 ), получим (1 + 𝑝 100 ) ∙ 𝑥. Чтобы уменьшить число 𝑥 на 𝑝%, нужно число 𝑥 умножить на величину (1 − 𝑝 100 ), получим (1 − 𝑝 100 ) ∙ 𝑥. Правило округления: если число округляют до какого-нибудь разряда, то все следующие за этим разрядом цифры заменяют нулями, а если они стоят после запятой, то их отбрасывают. При этом если первая отброшенная или замененная нулем цифра равна 5, 6, 7, 8 или 9, то стоящую перед ней цифру увеличивают на 1; а если первая отброшенная или замененная нулем цифра равна 0, 1, 2, 3 или 4, то стоящую перед ней цифру оставляют без изменения. Правило округления с избытком и недостатком. Округление с избытком или недостатком до ближайшего целого осуществляется по здравому смыслу: если мы спасаем людей, то количество спасательных лодок округляем с избытком; если покупаем товар на имеющиеся деньги, то количество единиц товара, которое можем купить, округляем с недостатком.
Задача 2. Задача на внимательность! Аккуратно читаем условие и вопрос задачи. Задача 4. Элементарный исход – простейшее событие, которым может окончиться случайный эксперимент. © 2020 Андрей Павликов. MathStudy.online Вероятность случайного события 𝐴 равна отношению числа 𝑚 благоприятных исходов к общему числу 𝑛 исходов, то есть 𝑝(𝐴) = 𝑚 𝑛 . Противоположное событию 𝐴 событие ?̅? состоит только из тех исходов, которые являются неблагоприятными для события 𝐴. При этом вероятность наступления события ?̅? находится по формуле 𝒑(?̅?) = 𝟏 − 𝒑(𝑨). Несовместные события 𝐴 и 𝐵 – события, которые не наступают одновременно. Формула сложения вероятностей для несовместных событий: вероятность наступления какого-либо из двух несовместных событий равна сумме вероятностей наступления этих событий (по отдельности), то есть 𝒑(𝑨 или 𝑩) = 𝒑(𝑨) + 𝒑(𝑩). Независимые события 𝐴 и 𝐵 – такие события, вероятность наступления каждого из которых не зависит от наступления другого. Формула умножения вероятностей для независимых событий: вероятность наступления двух независимых событий одновременно равна произведению вероятностей наступления этих событий (по отдельности), то есть 𝒑(𝑨 и 𝑩) = 𝒑(𝑨) ∙ 𝒑(𝑩).
Задачи 5/9/10. Алгебра Действия с дробями. Сложение дробей с одинаковыми знаменателями: 𝑎 𝑐 + 𝑏 𝑐 = 𝑎+𝑏 𝑐 . Вычитание дробей с одинаковыми знаменателями: 𝑎 𝑐 − 𝑏 𝑐 = 𝑎−𝑏 𝑐 . Чтобы сложить или вычесть две дроби с разными знаменателями, необходимо сначала привести дроби к общему знаменателю. Умножение дробей: 𝑎 𝑐 ∙ 𝑏 𝑑 = 𝑎∙𝑏 𝑐∙𝑑 . Чтобы разделить дробь на дробь, надо умножить первую дробь на дробь, обратную второй: 𝑎 𝑐 : 𝑏 𝑑 = 𝑎 𝑐 ∙ 𝑑 𝑏 . Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель, и разделить степень числителя на степень знаменателя. © 2020 Андрей Павликов. MathStudy.online Для решения квадратного уравнения необходимо привести его к виду 𝑎𝑥2 + 𝑏𝑥 + 𝑐 = 0 и вычислить дискриминант 𝐷 = 𝑏2 − 4𝑎𝑐. При этом, если 𝐷 > 0, то уравнение имеет два корня 𝑥1,2 = −𝑏±√𝐷 2𝑎 . если 𝐷 = 0, то уравнение имеет один корень 𝑥 = −𝑏 2𝑎 . если 𝐷 < 0, то уравнение корней не имеет. Неполное квадратное уравнение вида 𝑎𝑥2 + 𝑏𝑥 = 0 можно решить разложением на множители 𝑥 ∙ (𝑎𝑥 + 𝑏) = 0.
Тогда корни 𝑥1 = 0 и 𝑥2 = − 𝑏 𝑎 . Неполное квадратное уравнение вида 𝑥2 = 𝑞 при 𝑞 > 0 имеет два корня 𝑥 = ±√𝑞, при 𝑞 = 0 один корень 𝑥 = 0 и не имеет корней при 𝑞 < 0. Рациональные уравнения приводятся к целым путем умножения обеих частей уравнения на общее кратное знаменателей всех дробей. Степенные уравнения вида 𝑥𝑛 = 𝑎 решаются извлечением корня 𝑛-й степени из обеих частей. При этом, если 𝑛 – нечетное число, то 𝑥 = √𝑎 𝑛 ; если 𝑛 – четное число и 𝑎 > 0, то 𝑥 = ± √𝑎 𝑛 ; если 𝑛 – четное число и 𝑎 = 0, то 𝑥 = 0; если 𝑛 – четное число и 𝑎 < 0, то уравнение корней не имеет. Иррациональные уравнения решаются возведением обеих частей в степень. После решения получившегося уравнения необходимо сделать проверку: входят ли найденные корни в область допустимых значений исходного уравнения. Для решения показательного уравнения при 𝑎 ≠ 1 необходимо привести его к виду 𝑎𝑓(𝑥) = 𝑎𝑔(𝑥) , тогда 𝑓(𝑥) = 𝑔(𝑥). Или привести уравнение к виду 𝑎𝑓(𝑥) = 𝑏, тогда 𝑓(𝑥) = log𝑎 𝑏. Для решения логарифмического уравнения необходимо привести его к виду log𝑎 𝑓(𝑥) = log𝑎 𝑔(𝑥), тогда 𝑓(𝑥) = 𝑔(𝑥).
Или привести уравнение к виду log𝑎 𝑓(𝑥) = 𝑏, тогда 𝑓(𝑥) = 𝑎 𝑏. © 2020 Андрей Павликов. MathStudy.online Задача 11. Задачи на движение. Основная формула для решения задач: 𝑺 = 𝒗𝒕 , где 𝑆 — расстояние, 𝑣 — скорость, 𝑡 — время. В задачах на движение по воде скорость течения считается постоянной. При движении по течению скорость течения прибавляется к скорости плывущего тела, при движении против течения – вычитается из скорости тела. Скорость плота считается равной скорости течения. Средняя скорость вычисляется по формуле 𝑣ср = 𝑆общ 𝑡общ , где 𝑆общ – путь, пройденный телом, а 𝑡общ – время, за которое этот путь пройден. Если путь состоит из нескольких участков, то следует вычислить всю длину пути и все время движения. В задачах на движение протяженных поезд проходит мимо столба расстояние, равное длине поезда, при движении вдоль протяженной платформы – расстояние, равное сумме длин поезда и платформы. Задачи на работу. Основная формула для решения задач: 𝑨 = 𝒘𝒕, где 𝐴 — объем работы, 𝑤 — производительность, 𝑡 — время.
Задачи на раздельную работу являются аналогом задач на движение, где скоростью является производительность, а расстоянием – объем выполненной работы. В задачах на совместную работу общая производительность равна сумме производительностей. Задачи на концентрацию. Концентрация вещества с массой 𝑚 в растворе массы 𝑀 находится по формуле 𝝂 = 𝒎 𝑴 . Задачи 3/6/9/10. Тригонометрия Тригонометрия прямоугольного треугольника. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. © 2020 Андрей Павликов. MathStudy.online Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету. Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету. Основное тригонометрическое тождество. Для произвольного угла 𝛼 выполняется соотношение sin2𝛼 + cos2𝛼 = 1.
Таблица значений функций основных углов радианы 0 𝜋 6 𝜋 4 𝜋 3 𝜋 2 2𝜋 3 3𝜋 4 5𝜋 6 𝜋 градусы 0 30 45 60 90 120 135 150 180 sin 𝑥 0 1 2 √2 2 √3 2 1 √3 2 √2 2 1 2 0 cos 𝑥 1 √3 2 √2 2 1 2 0 − 1 2 − √2 2 − √3 2 −1 tg 𝑥 0 √3 3 1 √3 нет −√3 −1 − √3 3 0 ctg 𝑥 нет √3 1 √3 3 0 − √3 3 −1 −√3 нет Таблица знаков тригонометрических функций четверть I II III IV sin 𝑥 + + – – cos 𝑥 + – – + tg 𝑥 + – + – ctg 𝑥 + – + – Свойства тригонометрических функций Функции синус, тангенс и котангенс являются нечетными; косинус — четной, то есть: sin(−𝑥) = − sin 𝑥 cos(−𝑥) = cos 𝑥 tg(−𝑥) = − tg 𝑥 ctg(−𝑥) = − ctg 𝑥 © 2020 Андрей Павликов. MathStudy.online Треугольник называется равнобедренным, если две его стороны равны. Равные стороны называются боковыми, третья сторона — основанием равнобедренного треугольника. Теорема. В равнобедренном треугольнике углы при основании равны. Теорема. В равнобедренном треугольнике медиана, биссектриса и высота, проведенные из вершины к основанию, совпадают между собой. В прямоугольном треугольнике сторона, лежащая напротив прямого угла, называется гипотенузой прямоугольного треугольника, две другие стороны — катетами.
Теорема. Катет прямоугольного треугольника, лежащий напротив угла в 30°, равен половине гипотенузы. Теорема. Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°. Теорема. Медиана, проведенная из вершины прямого угла прямоугольного треугольника, равна половине гипотенузы. Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов, то есть 𝑐2 = 𝑎2 + 𝑏2, где 𝑐 — гипотенуза, 𝑎 и 𝑏 — катеты. Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. Теорема. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны. Теорема. Противоположные стороны параллелограмма равны. Теорема. Противоположные углы параллелограмма равны. Теорема. Диагонали параллелограмма точкой пересечения делятся пополам. Теорема. Диагонали параллелограмма делят его на два равных треугольника.
Прямоугольником называется параллелограмм, у которого все углы прямые. Теорема. Диагонали прямоугольника равны. © 2020 Андрей Павликов. MathStudy.online Ромбом называется параллелограмм, у которого все стороны равны. Теорема. Диагонали ромба взаимно перпендикулярны и делят его углы пополам. Квадратом называется параллелограмм, у которого все стороны равны и все углы равны. Теорема. Диагонали квадрата взаимно перпендикулярны, равны и делят его углы пополам. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны. Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами. Трапеция называется равнобедренной, если ее боковые стороны равны. Трапеция называется прямоугольной, если один из ее углов прямой. Средней линией трапеции называется отрезок, соединяющий середины боковых сторон. Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме. Формулы площади. Треугольник: 𝑆 = 1 2 𝑎ℎ𝑎 = 1 2 𝑏ℎ𝑏 = 𝑐ℎ𝑐, где ℎ𝑎, ℎ𝑏 , ℎ𝑐 — высоты, опущенные соответственно на стороны 𝑎, 𝑏, 𝑐.
𝑆 = 1 2 𝑎𝑏 sin 𝛾, где угол 𝛾 — угол между сторонами 𝑎 и 𝑏. 𝑆 = 𝑝𝑟 , где 𝑝 — полупериметр, 𝑟 — радиус вписанной в треугольник окружности. 𝑆 = 𝑎𝑏𝑐 4𝑅 , где 𝑅 — радиус окружности, описанной около треугольника. 𝑆 = √𝑝(𝑝 − 𝑎)(𝑝 − 𝑏)(𝑝 − 𝑐), где 𝑝 — полупериметр. Прямоугольный треугольник: 𝑆 = 1 2 𝑎𝑏, где 𝑎 и 𝑏 — катеты. Квадрат: 𝑆 = 𝑎2, где 𝑎 — сторона квадрата. © 2020 Андрей Павликов. MathStudy.online Прямоугольник 𝑆 = 𝑎𝑏, где 𝑎 и 𝑏 — стороны прямоугольника. Параллелограмм 𝑆 = 𝑎ℎ𝑎 = 𝑏ℎ𝑏, где ℎ𝑎, ℎ𝑏 — высоты, опущенные соответственно на стороны 𝑎, 𝑏. 𝑆 = 𝑎𝑏 sin 𝛾, где угол 𝛾 — угол между сторонами 𝑎 и 𝑏. 𝑆 = 1 2 𝑑1𝑑2 sin 𝛼 , где 𝑑1, 𝑑2 — диагонали параллелограмма, 𝛼 — угол между ними. Ромб 𝑆 = 𝑎ℎ, где 𝑎 — сторона ромба, ℎ — высота ромба. 𝑆 = 𝑎2 sin 𝛾, где 𝑎 — сторона ромба, 𝛾 — угол ромба. 𝑆 = 1 2 𝑑1𝑑2, где 𝑑1, 𝑑2 — диагонали ромба. Трапеция 𝑆 = 𝑎+𝑏 2 ℎ, где 𝑎 и 𝑏 — стороны трапеции, ℎ — высота. Треугольники называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Отношение сходственных сторон называется коэффициентом подобия. Теорема. Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности. Отрезок, соединяющий центр окружности с какой-либо точкой, лежащей на окружности, называется радиусом. Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется ее диаметром. Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. © 2020 Андрей Павликов. MathStudy.online Объем куба 𝑉 = 𝑎3. Площадь поверхности куба 𝑆 = 6𝑎2. Диагональ куба 𝑑 = 𝑎√3. Прямоугольный параллелепипед – многогранник, каждая грань которого является прямоугольником. Объем параллелепипеда 𝑉 = 𝑎𝑏𝑐. Площадь поверхности параллелепипеда 𝑉 = 2(𝑎𝑏 + 𝑎𝑐 + 𝑏𝑐). Диагональ параллелепипеда 𝑑 = √𝑎2 + 𝑏2 + 𝑐2.
𝒏-угольной призмой называется многогранник, две грани которого – равные 𝑛-угольники, лежащие в параллельных плоскостях, а остальные 𝑛 граней – параллелограммы. 𝑛 -угольники называются основаниями призмы, остальные грани – боковыми гранями призмы. Правильной призмой называется прямая призма, основания которой – правильные многоугольники. Высота правильной призмы равна ее боковому ребру, а все боковые грани прямой призмы – равные прямоугольники. Объем призмы 𝑉 = 𝑆осн ∙ ℎ. Площадь боковой поверхности прямой призмы 𝑆бок = 𝑃осн ∙ ℎ. Площадь полной поверхности призмы 𝑆полн = 𝑆бок + 2𝑆осн Пирамидой называется многогранник, который состоит из плоского многоугольника – основания пирамиды, точки, не лежащей в плоскости основания, – вершины пирамиды, и всех отрезков, соединяющих вершину пирамиды с точками основания. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами пирамиды. Поверхность пирамиды состоит из основания и боковых граней. Каждая боковая грань – треугольник.
Высотой пирамиды называется перпендикуляр, опущенный из вершины пирамиды на плоскость основания. Высота боковой грани пирамиды, проведенная к стороне основания, называется апофемой. Пирамида называется правильной, если ее основание – правильный многоугольник, а основание ее высоты – центр этого многоугольника. Треугольная пирамида называется также тетраэдром. Частным случаем правильной треугольной пирамиды является правильный тетраэдр, все грани которого представляют собой равные правильные треугольники. © 2020 Андрей Павликов. MathStudy.online Объем пирамиды 𝑉 = 1 3 𝑆осн ∙ ℎ. Площадь боковой поверхности правильной пирамиды 𝑆бок = 1 2 𝑃осн ∙ ℎбок . Площадь полной поверхности пирамиды 𝑆полн = 𝑆бок + 𝑆осн Цилиндром (круговым) называется фигура, полученная при вращении прямоугольника вокруг оси, содержащей его сторону. У цилиндра два основания – два круга, лежащие в параллельных плоскостях. Отрезки, соединяющие соответствующие точки окружностей оснований, называются образующими цилиндра.
Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Все образующие цилиндра параллельны и равны между собой. Ось цилиндра параллельна образующим. Осевым сечением цилиндра называется сечение, проходящее через ось цилиндра. Объем цилиндра 𝑉 = 𝑆осн ∙ ℎ = 𝜋𝑅 2ℎ . Площадь боковой поверхности цилиндра 𝑆бок = 𝑃осн ∙ ℎ = 2𝜋𝑅ℎ. Площадь полной поверхности цилиндра 𝑆полн = 𝑆бок + 2𝑆осн = 2𝜋𝑅ℎ + 2𝜋𝑅 2. Конусом (круговым) называется фигура, полученная при вращении прямоугольного треугольника вокруг оси, содержащей его катет. У конуса основание – круг. Вершина конуса – вершина треугольника, не лежащая в основании конуса. Отрезки, соединяющие точки окружности основания с вершиной конуса, называются образующими конуса. Радиусом конуса называется радиус его основания. Высотой конуса называется расстояние от вершины конуса до плоскости его основания. Осью конуса называется прямая, проходящая через вершину конуса и центр его основания.
Все образующие конуса равны между собой. Осевым сечением конуса называется сечение, проходящее через ось конуса. Объем конуса 𝑉 = 1 3 𝑆осн ∙ ℎ = 1 3 𝜋𝑅2ℎ. Площадь боковой поверхности конуса 𝑆бок = 1 2 𝐶осн ∙ 𝑙 = 𝜋𝑅𝑙. Площадь полной поверхности конуса 𝑆полн = 𝑆бок + 𝑆осн = 𝜋𝑅𝑙 + 𝜋𝑅 2. © 2020 Андрей Павликов. MathStudy.online Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не больше данного, от фиксированной точки. Эта точка называется центром шара, а расстояние – радиусом шара. Сферой называется поверхность шара. Любое сечение шара является кругом. Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом. Объем шара 𝑉 = 4 3 𝜋𝑅3. Площадь поверхности сферы 𝑆 = 4𝜋𝑅2. Задачи 7/12. Начала анализа Пусть функция 𝑓(𝑥) определена в некоторой окрестности точки 𝑥0. Предел отношения приращения ∆𝑦 функции в этой точке (если он существует) к приращению ∆𝑥 аргумента при условии приращению ∆𝑥 → 0, называется производной функции 𝑓(𝑥) в точке 𝑥0.
Обозначение 𝑓 ′(𝑥0). 𝑓′(𝑥0) = lim ∆𝑥→0 ∆𝑦 ∆𝑥 = lim ∆𝑥→0 𝑓(𝑥0 + ∆𝑥) − 𝑓(𝑥0) ∆𝑥 Физический смысл производной. Производная показывает (мгновенную) скорость изменения функции. Геометрический смысл производной. Если к графику функции 𝑓(𝑥) в точке с абсциссой 𝑥0 можно провести касательную 𝑦 = 𝑘𝑥 + 𝑚 , то производная функции 𝑓(𝑥) в точке 𝑥0 равна угловому коэффициенту касательной, то есть 𝑓′(𝑥0) = 𝑘 = tg 𝛼, где 𝛼 — угол между положительным направлением оси 𝑂𝑥 и касательной. Если к графику функции 𝑓(𝑥) в точке с абсциссой 𝑥0 можно провести касательную 𝑦(𝑥), то выполняются условия: { 𝑓(𝑥0) = 𝑦(𝑥0) 𝑓′(𝑥0) = 𝑦 ′(𝑥0) Применение к производной к исследованию функции. Если 𝑓′(𝑥) > 0 в каждой точке интервала 𝑀, то функция 𝑓(𝑥) возрастает на интервале 𝑀. Если 𝑓′(𝑥) < 0 в каждой точке интервала 𝑀, то функция 𝑓(𝑥) убывает на интервале 𝑀.
ЕГЭ по математике: материалы для подготовки
Алгебра
• Графики числовых функций1-3. Преобразование графиков
4. Чтение графиков
• Неравенства (1)
1.
Числовые неравенства и их свойства 2. Графическое решение неравенств
3. Двойное неравенство
4. Числовые промежутки
5. Линейные неравенства
6. Системы линейных неравенств
7. Квадратные неравенства
8. Дробно — рациональные неравенства
• Неравенства (2)
1. Метод интервалов
2. Показательные неравенства
3. Логарифмические неравенства
4. Тригонометрические неравенства
5. Графическое решение неравенств
6. Неравенства с двумя переменными
• Производные
1. Производные основных функций
2. Вычисление производной
3. Исследование функции с помощью производной
4. Касательная к графику функции
5. Наибольшее и наименьшее значения функций
6. График производной функции
7. Вторая производная функции. Выпуклость функции, точки экстремумов и перегиба
• Решение уравнений (1)
1. Линейные уравнение с одной переменной
2-3. Системы уравнений с двумя переменными
4.
Неполные квадратные уравнения 5. Квадратные уравнения
6. Теорема Виета
7. Дробные уравнения
8. Уравнения с двумя переменными и их графики
9. Графическое решение уравнений
10. Графическое решение систем линейных уравнений
11. Графическое решение систем НЕлинейных уравнений
12. Выражения. Тождества. Уравнения
• Решение уравнений (2)
1. Методы решения уравнений
2-3. Иррациональные уравнение
4. Показательные уравнения
5. Логарифмические уравнения
6. Тригонометрические уравнения
7-8. Решение тригонометрических уравнений
9. Графическое решение уравнений
• Тригонометрия и логарифмы
1-3. Формулы тригонометрии
4-6. Логарифм и его свойства
• Формулы и преобразование выражений
1-2. Формулы сокращенного умножения
3. Степени с натуральным и целым показателями
4. Степень с рациональным показателем
5. Квадратный корень и его свойства
6. Действия с квадратными корнями
7.
Корни натуральной степени 8. Одночлены и многочлены
9. Действия с многочленами
10. Разложение многочлена на множители
• Функции (1)
1. Прямая пропорциональность
2. Обратная пропорциональность
3. Линейная функция
4. Функции y=x2 и y=x3
5. Функции с корнем
6-7. Квадратичная функция
8. Функции и их графики
• Функции (2)
1. Тригонометрическая окружность. Синус и косинус угла
2. Тригонометрическая окружность. Тангенс и котангенс угла
3. Тригонометрические функции — синус и косинус
4. Тригонометрические функции — тангенс и котангенс
5. Обратные тригонометрические функции — арксинус и арккосинус
6. Обратные тригонометрические функции — арктангенс и арккотангенс
7. Степенная функция
8. Показательная функция
9. Логарифмическая функция
10. Графики функций
11. Взаимно-обратные функции
12. Свойства функций
13. Асимптоты графиков функций
• Числа, последовательности, проценты
1.
Числовые множества 2. Числовые последовательности
3. Арифметическая прогрессия
4-5. Геометрическая прогрессия
6. Сложные проценты
Геометрия (планиметрия)
• Многоугольник1. Свойства параллелограммов
2. Трапеция
3. Признаки параллелограмма и его видов
4. Свойства многоугольников
5. Теорема Фалеса
6. Правильные треугольник и четырехугольник
7. Правильные шестиугольник и восьмиугольник
8-9. Площадь многоугольника
• Окружность
1. Окружность. Хорды и касательные
2. Окружность, описанная около треугольника
3. Окружность, вписанная в треугольник
4. Центральные и вписанные углы
5. Свойства хорд и секущих
6. Вписанные и описанные четырехугольники
7. Длина окружности и площадь круга
• Треугольник
1. Виды треугольников. Равные треугольники
2. Признаки равенства треугольников
3. Основные линии в треугольнике
4. Равнобедренный треугольник
5.
Отношения отрезков в треугольнике 6. Прямоугольный треугольник
7. Теорема Пифагора
8. Синус, косинус, тангенс прямоугольного треугольника
9. Подобие треугольников
10. Теорема косинусов
11. Теорема синусов
12-13. Площадь треугольника
• Углы
1. Измерение отрезков и углов
2. Смежные и вертикальные углы
3. Биссектриса угла. Перпендикулярные прямые
4. Признаки параллельности прямых
5. Свойства параллельных прямых
6. Сумма углов треугольника. Внешний угол
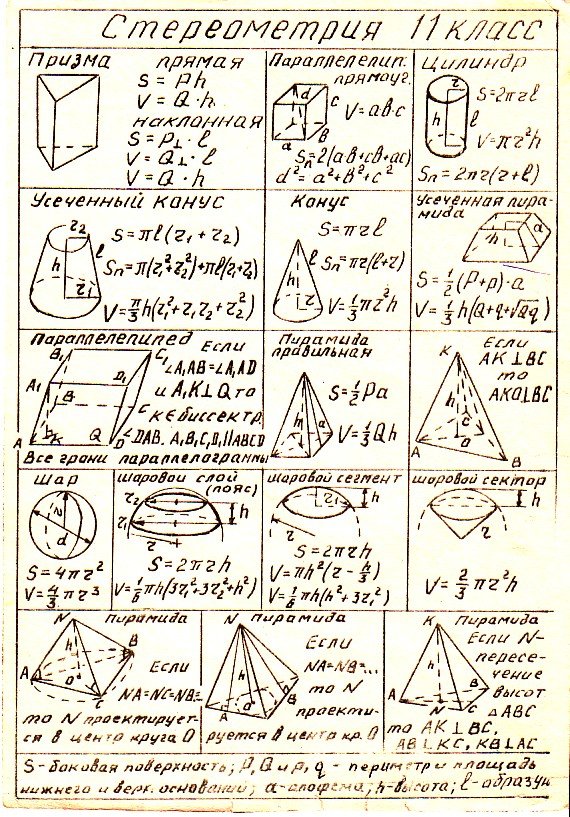
Геометрия (стереометрия)
• Вычисление расстояний и углов1. Расстояние между двумя точками
2. Расстояние от точки до прямой
3. Расстояние от точки до плоскости
4. Расстояние между скрещивающимися прямыми
5. Угол между скрещивающимися прямыми
6. Угол между прямой и плоскостью
7. Двугранные углы
8. Угол между двумя плоскостями
• Круглые тела
1. Цилиндр
2. Конус
3. Шар.
Сфера 4-5. Комбинации шара и пирамиды
6. Комбинации конуса и пирамиды
7. Комбинации цилиндра и призмы
8. Комбинации шара и призмы
9. Площади поверхностей круглых тел (S)
10. Объёмы круглых тел и их частей (V)
• Многогранники
1. Призма
2. Параллелепипед
3. Пирамида
4. Виды пирамид
5. Правильная пирамида
6. Усеченная пирамида
7. Площади поверхностей и объемы
вбросы в Сеть и погоревшие на шпаргалках
Накануне, 3 июня, в России прошел второй обязательный (после экзамена по русскому языку) ЕГЭ по математике. Несмотря на то, что ранее показательно были наказаны ученики, попавшиеся на шпаргалках и размещении в Интернете вариантов ответов, сообщения о попытках списать вновь приходят из разных регионов России.
Так, например, в Санкт-Петербурге ЕГЭ по математике сдавали 23 тысячи школьников. Из них (только по сообщениям на данный момент) с экзамена за шпаргалки были выгнаны 13 выпускников.
Об этом «РГ» сообщили в Региональном центре оценки качества образования и информационных технологий.
Судьбу нарушителей предстоит решить государственной экзаменационной комиссии, однако, по всей видимости, ЕГЭ им придется пересдавать через год. Как сообщает Федеральная служба по надзору в сфере образования и науки, «результаты экзаменационных работ нарушителей ЕГЭ должны аннулироваться без права пересдачи в текущем году».
В Пермском крае, как передает ГТРК «Пермь», в этом году ЕГЭ по математике сдавали 15 тысяч выпускников. Из этого региона официальных сообщений о нарушителях пока не приходило, однако представители государственной экзаменационной комиссии говорят, что нередко находят в туалетах много шпаргалок. Но поскольку их принадлежность конкретным ученикам доказать невозможно, то не было и никаких последствий.
Ольга Мясникова, помощник руководителя пункта проведения экзамена №514, отметила: «Организаторы вне аудиторий после того, как ребенок выходит, заходят и проверяют кабинки.
Если обнаруживают там шпаргалки, они приносят их в пункт проведения экзамена. Поскольку ребенок за руку не пойман, то карательных мер мы принять не можем».
Как сообщает пресс-служба правительства Новосибирской области, в этом регионе из пунктов проведения экзамена были удалены три выпускника. «Один участник ЕГЭ в Ленинском районе покинул аудиторию из-за наличия сотового телефона, два участника — за использование неразрешенных материалов. Это произошло в пунктах проведения экзамена в Калининском и Ленинском районах», — говорится в сообщении.
Всего в этом регионе в экзамене по математике приняли участие 14 676 выпускников, явка составила 96,3%. Процедуру проведения этого ЕГЭ контролировали 92 уполномоченных ГЭК и 392 общественных наблюдателя. Замечаний к организаторам от них не поступало. Апелляций по процедуре проведения со стороны участников нет, передает «Интерфакс».
Несмотря на обещанное ужесточение правил сдачи ЕГЭ после скандалов с ответами на КИМы по русскому языку, просочившимися в Интернет, аналогичная ситуация повторилась и с вариантами по математике.
Правда, накануне эксперты уверяли, что это – ложные ответы. Однако телеведущая Тина Канделаки в своем блоге еще накануне вечером сообщила о том, что нашла две шпаргалки.
«Одна представляла из себя 8 вариантов с комплектами вопросов, вторая – от руки написанные решения с другими заданиями. Мы предполагали, что именно первая шпаргалка совпадет с реальными вопросами, ведь именно так было во время ЕГЭ по русскому и истории. Тогда мы заранее имели в таком же хорошем качестве вопросы в 6 вариантах, и оба раза они в Москве сошлись на 100%. Логично было предположить, что и по математике вопросы из старого источника сойдутся. Однако, как сообщают нам школьники, на этот раз все оказалось иначе. Полностью совпала именно вторая шпаргалка, где от руки были написаны решения», — пишет Тина Канделаки и публикует фото этой шпаргалки.
Комментируя это сообщение, один из интернет-пользователей пишет, что на некоторых сайтах папку, где варианты были «заботливо разложены по регионам», разместили еще за несколько дней до проведения ЕГЭ по математике.
«До меня эта папка дошла вчера утром, т.е. за день до экзамена. 100% совпадение, включая разбивку по регионам, — признается блогер под ником molch64. — Я уже 5 приемных кампаний мониторю, но такой масштабный слив вижу впервые».
Ранее сообщалось, что условия сдачи ЕГЭ по математике были ужесточены из-за нарушений, зафиксированных во время экзамена по русскому языку, который проходил неделю назад. Тогда с ЕГЭ выгнали 13 учеников (12 — за мобильные телефоны, еще одного — за шпаргалку).
|
pdf 
1
1
1
1
1
, 20:07
docx 
pdf 
1Памятка для родителей по новой математике (бесплатно для печати)
Поднимите руку, если вы когда-либо были разочарованы, пытаясь помочь своему ребенку с математикой.
Домашнее задание по математике сегодня выглядит совсем иначе, чем когда мы учились в школе, и это касается не только общего Основной.
Нет, это не твое воображение. Математика сегодня сложнее. Это побуждает детей взглянуть на одну и ту же проблему с много разных точек зрения, вместо того, чтобы получить ответ и покончить с этим. И иногда, да, это сложнее, чем наша домашняя работа была!
Сегодня дети в детском саду уже знакомятся с понятиями на уровне колледжа, такие как алгебра и математическое моделирование, на упрощенном уровне.
Почему?
Большая часть различий связана с подготовкой учащихся к их будущему, а не к нашему настоящему.
Развитие сильных навыков критического мышления для постоянно меняющегося мира
В наши дни математическое образование сосредоточено на правилах, таких как 5 x 5 = 25, которые никогда не меняются.
Сегодня мы знаем, что наш мир постоянно меняется. А математическое образование учит детей смотреть вперед — изучите не только статические правила, но и гибкое мышление и модели, которые они могут использовать, изменять и улучшать для решения проблемы реального мира.
В будущем наши дети будут пользоваться электронными таблицами, телефонами и новыми технологиями, о которых мы даже не догадывались. когда им нужно сделать расчеты. Они не будут использовать каменные дощечки, счеты или логарифмическую линейку. Даже калькуляторы устаревают. (Когда вы в последний раз пользовались настоящим калькулятором вместо телефона?)
Карьера наших детей в будущем тоже будет выглядеть совсем по-другому.
«65% детей, поступающих сегодня в начальную школу, в конечном итоге
работая на совершенно новых видах работ, которых еще не существует»,
по данным Всемирного экономического форума.
Сегодняшнее математическое образование призвано помочь учащимся мыслить творчески, гибко и логично, и стать уверенными и успешными новаторами, решающими проблемы и лидерами.
Нужна дополнительная помощь по математике?
Репетиторы по математике Sylvan спешат на помощь!Если у вашего ребенка проблемы с математикой, и ему может понадобиться математическая помощь, вы не одиноки: Sylvan дает результаты. Наши ученики обычно видят до 2-кратного роста результатов по математике, чем их сверстники.
С нашим персонализированным репетиторством по математике ваш сын или дочь овладеют навыками, чтобы вернуться на правильный путь и развить уверенность и чувство собственного достоинства. И все это приводит к большим успехам в учебе, во время выполнения домашних заданий и в жизни.
Индивидуальные занятия по математике предлагаются во всех наших центрах Sylvan, а наши почасовые расценки очень конкурентоспособны по сравнению с местными репетиторами.
Так что да, вы можете получить лучшую математическую помощь для вашей семьи!
Шпаргалка по математике для медсестер
ОА
- O = заказанная доза
- A = Доступная доза
О×ВА
- O = заказанная доза
- V = Доступный объем дозы
- A = Доступная доза
ВХ
В×60 минМ
Сначала переведите микрограммы в минуту ( мкг/мин ) в миллиграммы в час (мг/ч).
Д×60 мин1000 мкг
Затем используйте формулу дозировки для расчета нормы.
О×ВА
- O = заказанная доза
- V = Доступный объем дозы
- A = Доступная доза
Сначала переведите микрограммы на килограмм в минуту ( мкг/кг/мин ) в миллиграммы в час (мг/ч).
Д×Ш×60 мин1000 мкг
- D = доза (мкг)
- Вт = Вес (кг)
Затем используйте формулу дозировки для расчета нормы.
О×ВА
- O = заказанная доза
- V = Доступный объем дозы
- A = Доступная доза
Используйте базовую формулу времени с внутривенной помпой для расчета часов.
ВР
Капли в минуту (gtt/min) должны быть переведены в часы при использовании калиброванной трубки без насоса.
В×К(Г×60 мин)
- В = Объем
- C = калибровка внутривенных трубок
- Г = гтт/мин
Р×АВ
- R = Ставка
- A = Доступная доза
- V = Доступный объем дозы
Сначала определите дозировку в миллиграммах/час (мг/час).
Р×АВ
- R = Ставка
- A = Доступная доза
- V = Доступный объем дозы
Затем переведите дозировку из мг/ч в микрограмм/минуту (мкг/мин).
D×1000 мг60 мин
Сначала определите дозировку в миллиграммах/час (мг/час).
Р×АВ
- R = Ставка
- A = Доступная доза
- V = Доступный объем дозы
Затем переведите дозировку из мг/ч в микрограмм/килограмм/минуту (мкг/кг/мин).
Д×1000 мг(60 мин×В)
- D = Доза (мг)
- Вт = Вес в килограммах (кг)
Шпаргалки по общей базовой математике — Бет Келли
Вы устали листать десятки страниц, чтобы понять, что такое тот или иной стандарт Common Core?! Я знаю, что был.
В этой халяве есть шпаргалки Common Core Math для классов K-5!!
Я решил сделать эту 1-страничную «шпаргалку», в которой есть все математические стандарты Common Core на 1 странице.Я храню его в конце папки с планами уроков математики. Это было чрезвычайно полезно. Я ловлю себя на том, что постоянно смотрю на него, когда мне нужно знать, что такое определенный стандарт.
Я также использовал эти шпаргалки для составления тестов по общей базовой математике для каждого класса. Взгляните на ссылки на продукты ниже. 🙂
Общие оценки математики CORE для 1-го класса
Общие основные математические оценки для 2-го класса
Оценка общего ядра для 3-го класса
Общие основные оценки математики для 4 класса
Общие основные математические оценки для 5 класс
2
2
2
2
2
2
2
Существует одна «шпаргалка» для каждого из следующих классов:
• Детский сад
• 1 класс (1 класс)
• 2 класс (2 класс)
• 3 класс (3 класс)
• 4 класс ( 4-й класс
• 5-й класс (5-й класс)
Каждая 1-страничная шпаргалка включает все стандарты в следующих разделах математики:
• Операции и алгебраическое мышление
• Числа и операции с основанием 10
• Геометрия
• Измерение и Data
Вас также могут заинтересовать мои осенние и зимние распечатки NO PREP для 1-3 классов.
Нажмите на ссылки ниже, чтобы просмотреть каждый продукт:
NO PREP Зимний математический пакет для 1-го класса
NO PREP Зимний математический пакет для 2-го класса
NO PREP Зимний математический пакет для 3-го класса
NO PREP Осенние распечатки Common Core Math и ELA
БЕЗ ПОДГОТОВКИ Осенние распечатки – 2-й класс Common Core Math и ELA
БЕЗ ПОДГОТОВКИ Осенние распечатки – 3-й класс Common Core Math и ELA
Наслаждайтесь!
Большое спасибо компании Glitter Meets Glue за дизайн обложки, Graphics From the Pond и Creative Clips за обрамление и KG Fonts за шрифты заголовков.🙂
Адрес электронной почты:
- Твитнуть
| $\{ \}$ | комплект | используется для определения набора | $S = \{ 1, 2, 3, 4, … \}$ |
| $\in$ | в, элемент | используется для обозначения того, что элемент является частью набора | $1 \in {1, 2, 3}$ |
| $\не\в$ | не входит, не является элементом | используется для обозначения того, что элемент не является частью набора | 4$\не\в {1, 2, 3}$ |
| $\mid S \mid$ | мощность | используется для описания размера набора (относится к количеству уникальных элементов, если набор конечен) | $S = \{1, 2, 2, 2, 3, 4, 5, 5 \}$ $\mid S \mid = 5$ |
| $:$, $\mid$ | такое, что | используется для обозначения состояния, обычно в нотации конструктора наборов или в математическом определении | $\{x^2 : x + 3 \text{ простое}\}$ |
| $\subseteq$ | подмножество | множество $A$ является подмножеством множества $B$, когда каждый элемент в $A$ также является элементом в $B$ | $A = \{ 1, 2 \}$ $B = \{ 2, 1, 4, 3, 5 \}$ $A \subseteq B$ |
| $\подмножество$ | правильное подмножество | Множество$A$ является правильным подмножеством множества $B$, когда каждый элемент в $A$ также является элементом в $B$ и $A \neq B$ | $A = \{ 1, 2, 3, 4, 5 \}$ $B = \{ 2, 1, 4, 3, 5 \}$ $A \subseteq B$ верно, но $A \subset B$ не соответствует действительности |
| $\supseteq$ | надмножество | множество $A$ является надмножеством множества $B$, когда $B$ является подмножеством $A$ | $A = \{ 2, 4, 6, 7, 8 \}$ $B = \{ 2, 4, 8 \}$ $A \supseteq B$ |
| $\чашка$ | союз | набор с элементами набора $A$ или набора $B$ | $A = \{1, 2\}$ $B = \{2, 3, 5\}$ $A \cup B = \{1, 2, 3, 5\}$ |
| $\cap$ | перекресток | набор с элементами набора $A$ и набора $B$ | $A = \{1, 2\}$ $B = \{2, 3, 5\}$ $A \cap B = \{2\}$ |
| $\emptyset$ | пустой набор | набор без элементов | $\{1, 2, 3\} \cap \{4, 5, 6\} = \emptyset$ |
| $-$, $\обратная косая черта$ | установить разницу | элемента в множестве $A$, которых нет в $B$ | $A = \{1, 2, 3, 4\}$ $B = \{2, 3, 5, 8\}$ $A — B = \{1, 4\}$ $B — А = \{5, 8\}$ |
| $\раз$ | Декартово произведение | набор, содержащий все возможные комбинации одного элемента из $A$ и одного элемента из $B$ | $A = \{1, 2\}$ $B = \{3, 4\}$ $A \times B = \{(1, 3), (2, 3), (1, 4) , (2, 4)\}$ $B \times A = \{(3, 1), (3, 2), (4, 1), (4, 2)\}$ |
| $A^c$ | дополнение | набор, содержащий элементы вселенной $U$, не входящие в набор $A$ | $U = \{1, 2, 3, 4, 5\}, A = \{2, 4\} \ подразумевает A^c=\{1, 3, 5\}$ |
| $f : A \стрелка вправо B$ | функция | функция $f$ отображает элементы множества $A$ в элементы множества $B$; $A$ — это домен, а $B$ — кодовый домен | .|
| $\mathbb{N}$ | множество натуральных чисел | набор натуральных чисел, начиная с $1$ | $\mathbb{N} = \{1, 2, 3, …\}$ |
| $\mathbb{N}_0$ | набор целых чисел | набор целых чисел, начиная с $0$ | $\mathbb{N}_0 = \{0, 1, 2, 3, …\}$ |
| $\mathbb{Z}$ | набор целых чисел | объединение целых чисел с их отрицательными значениями | $\mathbb{Z} = \{…, -3, -2, -1, 0, 1, 2, 3, …\}$ |
| $\mathbb{Q}$ | множество рациональных чисел | множество всех возможных комбинаций деления одного целого числа на другое, причем последнее целое число не равно нулю, т.е.е., $\mathbb{Q} = \{ \frac{p}{q} : p, q \in \mathbb{Z}, q \neq 0\}$ | $\{\frac{1}{2}, \frac{5}{14}, \frac{-17}{3}\} \subset \mathbb{Q}$ |
| $\клин $ | соединение/и | $P \wedge Q$ истинно, если оба $P$ и $Q$ истинны | если $P = (2 \text{ простое число}), Q = (8 \text{ идеальный куб})$, то $P \wedge Q$ истинно |
| $\vee$ | дизъюнкция/или | $P \vee Q$ истинно, если либо $P$ , либо $Q$ истинно | если $P = (2 \text{ простое}), Q = (4 \text{ идеальный квадрат})$, то $P \vee Q$ верно |
| $\отриц$ | отрицание | $\neg P$ истинно, если $P$ ложно, и наоборот | если $P = (\text{35 простое число})$, то $\neg P$ истинно |
| $\подразумевается$ | следствие | $P \имплицитно Q$ означает, что $Q$ истинно всякий раз, когда $P$ истинно (но , а не ничего не говорит о том, что происходит, когда $P$ ложно) | если $P = (x \text{ делится на 4})$, $Q = (x \text{ четно})$, то $P \подразумевает Q$ (но обратите внимание, что $P \nrightarrow Q$) |
| $\iff$ | тогда и только тогда, когда (iff) | $P \подразумевается Q$ и $Q\подразумевается P$ | , если $P = (\text{сейчас новый год})$ и $Q = (\text{сейчас 1 января})$, то $P \iff Q$ |
| $\forall$ | для всех | относится ко всем элементам в наборе | .
2+5$
