Ларин А.А. ЕГЭ (профильного уровня) по математике — Архив файлов
Оценивание
| № задания | 1-12 | 13-15 | 16-17 | 18-19 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 32 |
Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 cодержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий высокого уровня сложности с развёрнутым ответом.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–12 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой. Разрешается использовать только линейку
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 cодержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий высокого уровня сложности с развёрнутым ответом.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут
(235 минут).Ответы к заданиям 1–12 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой. Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
yagubov.ru
253 вариант Алекса Ларина. Разбор ЕГЭ математика 2019
Дано натуральное четырехзначное число n, в записи которого нет нулей. Для этого числа составим дробь $$f(n)$$ , в числителе которой само число n , а в знаменателе – произведение всех цифр числа n.
А) Приведите пример такого числа , для которого $$f(n)=\frac{643}{160}$$
Б) Существует ли такое n, что $$f(n)=\frac{343}{160}$$ ?
В) Какое наименьшее значение может принимать дробь $$f(n)$$, если она равна несократимой дроби со знаменателем 160?
Пусть число $$M=10^{3}a+10^{2}b+10c+d$$, $$0<a,b,c,d<9 \in N$$
A) $$\frac{643}{160}=\frac{643*k}{160*k}$$. $$M=643k$$ ; $$abcd=160k$$
Разложим 160: $$160=2^{5}*5$$. С учетом , что $$a,b,c,d \in N$$ и $$a,b,c,d \in [1;9]$$, то среди чисел точно есть 5. Рассмотрим умножение 643 на натуральное $$k\geq 2$$.
$$643*2=1286$$ — нет 5
$$643*3=1929$$ — нет 5
$$643*4=2572$$. При этом 2*5*7*2=140 не кратно 160.
$$643*5=3215\Rightarrow$$ $$3*2*1*5=30$$ — не подходит.
$$643*6=3858\Rightarrow$$ $$3*8*5*8=960=160*6$$ — подходит
Т.е. пример числа: 3858
B) Рассмотрим сначала наименьшее возможное f(n) . С учетом , что $$160=2^{5}*5$$ и $$a,b,c,d$$ – натуральные, меньшие 10, то возможные a,b,c и d : $$1,4,8,5$$; $$2,2,8,5$$; $$2,4,4,5$$ . При этом $$\frac{M}{abcd}\rightarrow min$$, при $$abcd\rightarrow max$$. Пусть k-множитель, который бы сокращался . $$k_{max}=18=2*3^{2}$$ т.к. тогда бы $$1\rightarrow 9$$; $$4\rightarrow 8$$ и M состояло бы из цифр $$9,8,8,5$$ (очевидно, что наибольшее k именно для множителей $$1,4,8,5$$) . При k>18 получим, что одна из цифр станет больше 9. При этом k — число составное.
Рассмотрим их. $$k=18\Rightarrow$$ $$a,b,c,d: 9,8,8,5$$. Но $$9+8+8+5=30$$, число 30 не делится нацело на 9, значит при сокращении на k мы не получим знаменатель 160.
$$k=16$$; $$a,b,c,d\Rightarrow$$ $$8,8,8,5$$. Комбинации с этими цифрами:
$$\frac{5888}{160*16}=\frac{368}{160}$$ — сократима дальше
$$\frac{8588}{160*16}=\frac{2147}{640}$$ — нет знаменателя 160
$$\frac{8858}{160*16}=\frac{4429}{1280}$$
$$\frac{8885}{160*16}$$ — не делится на 16
$$k=14$$: $$a,b,c,d: 7,8,8,5$$. Аналогично предыдущему нет чисел.
$$k=12$$: $$a,b,c,d :6,8,8,5$$. При использовании данных чисел наименьшее $$f(n)=\frac{5868}{160*12}=\frac{489}{160}$$
mathlesson.ru
250 вариант Алекса Ларина. Разбор ЕГЭ математика 2019
Найдите все значения параметра a при которых уравнение $$\sqrt[3]{\frac{1}{2}x^{3}+x+1}+\sqrt[3]{-\frac{1}{2}x^{3}+x-1}=\sqrt[3]{ax}$$ имеет ровно четыре корня
Вынесем $$\sqrt[3]{x}:$$ $$\sqrt[3]{x}(\sqrt[3]{1+\frac{1}{x}+\frac{x^{2}}{2}}+\sqrt[3]{1-\frac{1}{x}-\frac{x^{2}}{2}})=\sqrt[3]{x}*\sqrt[3]{a}$$
Следовательно, $$\sqrt[3]{x}=0\Leftrightarrow x=0$$ является корнем, значит надо еще три отличных от 0 корня.
Введем замену : $$\frac{x^{2}}{2}+\frac{1}{x}=t$$. Тогда: $$\sqrt[3]{1+t}+\sqrt[3]{1-t}=\sqrt[3]{a}$$
Рассмотрим замену: пусть $$f(x)=\frac{x^{2}}{2}+\frac{1}{x}$$ и g(x)=t. g(x)=t – прямая, параллельная Ox. При этом f(x)-совмещенный график параболы и обратной пропорциональности. Исследуем график:
$$f(x)=0\Leftrightarrow$$ $$\frac{x^{2}+2}{2x}=0\Leftrightarrow$$ $$x=-\sqrt[3]{2}$$
$$f'(x)=0\Leftrightarrow$$ $$x-\frac{1}{x^{2}}=0\Leftrightarrow$$ $$\frac{x^{3}-1}{x^{2}}=0$$
$$x=1$$ –точка минимума. При x=1: $$f(1)=\frac{1}{2}+1=1,5$$.
$$lim_{x\rightarrow -\infty} (\frac{x^{2}}{2}+\frac{1}{x})=+\infty$$; $$lim_{x\rightarrow +\infty} (\frac{x^{2}}{2}+\frac{1}{x})=+\infty$$
$$lim_{x\rightarrow -0} (\frac{x^{2}}{2}+\frac{1}{x})=-\infty$$; $$lim_{x\rightarrow +0} (\frac{x^{2}}{2}+\frac{1}{x})=+\infty$$.
При x=1: $$f(1)=\frac{1}{2}+1=1,5$$. Построим эскиз :
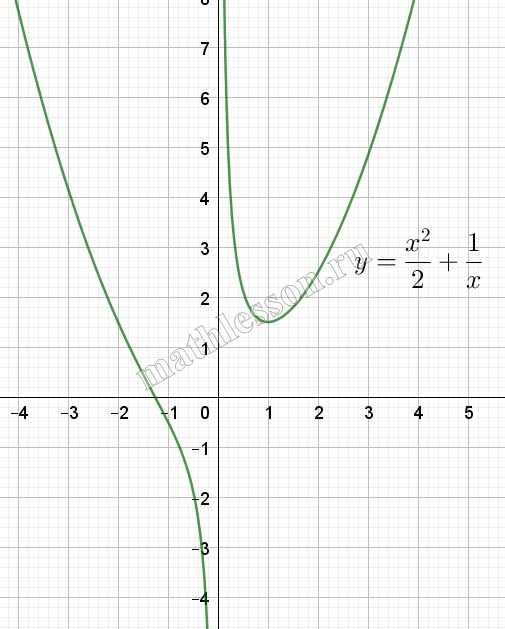
Видим что при t<1,5-одно решение, при t=1,5-два решения , при t>1,5 – три решения.
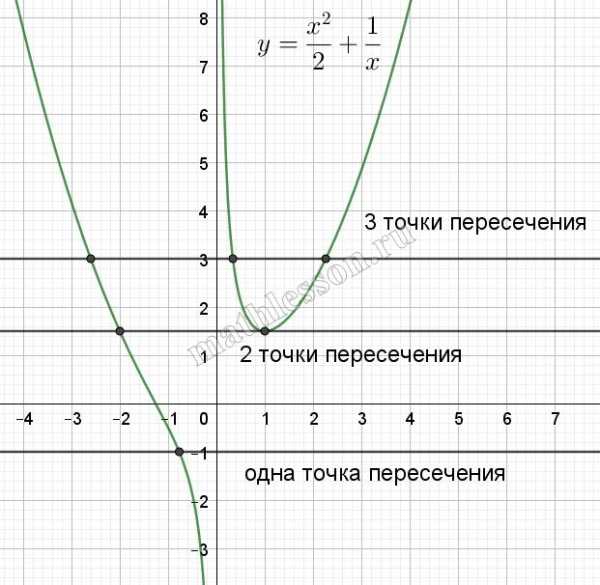
Рассмотрим уравнение: $$\sqrt[3]{t+1}+\sqrt[3]{1-t}=\sqrt[3]{a}$$. Пусть $$f(t)=\sqrt[3]{1+t}+\sqrt[3]{1-t}; g(t)=\sqrt[3]{a}$$
Построим график :
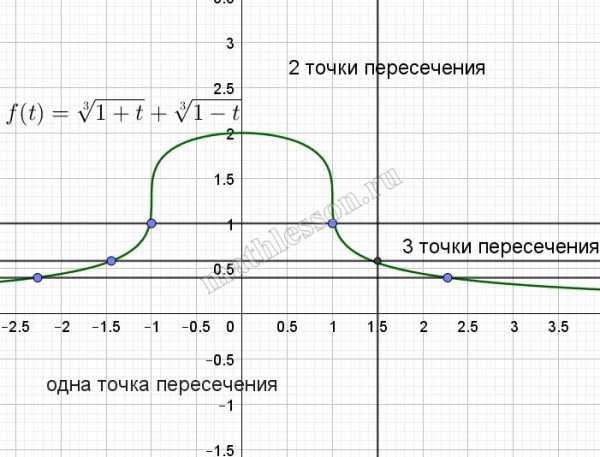
Каждое пересечение при t<1,5 , дает одно решение, при t>1,5 даёт три решения и т.е. есть всегда 1(при t<0) , то нас не устраивает .
При t=1,5 будет 2 решения, да еще одно ( область t<0)-следовательно, в общем получим 3, что и нужно .
Найдем a : $$\sqrt[3]{1+\frac{3}{2}}+\sqrt[3]{1-\frac{3}{2}}=\sqrt[3]{a}$$
$$\sqrt[3]{\frac{5}{2}}-\sqrt[3]{\frac{1}{2}}=\sqrt[3]{a}\Leftrightarrow$$ $$\frac{\sqrt[3]{5}-1}{\sqrt[3]{2}} =\sqrt[3]{a}\Leftrightarrow$$ $$a=\frac{(\sqrt[3]{5}-1)^{3}}{2}$$
mathlesson.ru
252 вариант Алекса Ларина. Разбор ЕГЭ математика 2019
Точки M,N и P лежат на боковых ребрах правильной треугольной призмы ABCA1B1C1 и делят их в отношении $$AM:MA_{1}=1:2$$, $$BN:NB_{1}=1:3$$, $$CP:PC_{1}=2:3$$
А) В каком отношении делит объем призмы плоскость, проходящая через точки M,N и P ?
Б) Докажите, что MNP ‐ прямоугольный треугольник, если сторона основания призмы равна $$2\sqrt{10}$$ , а боковое ребро равно 60 .
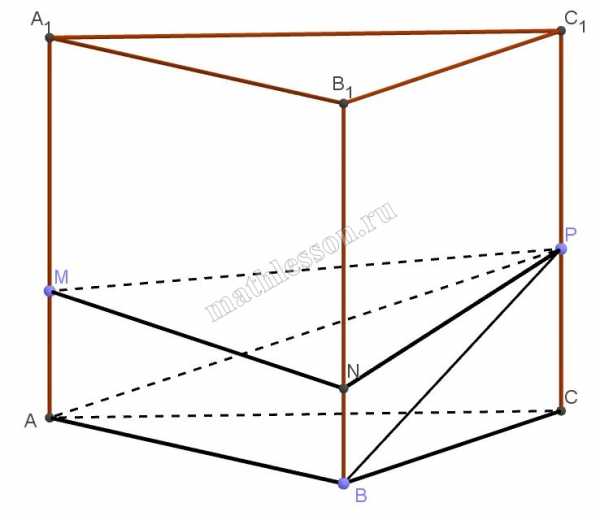
A) 1) Пусть a — ребро основания, b — боковое ребро. Тогда: $$AM=\frac{1}{3}b$$, $$NB=\frac{1}{4}b$$, $$CP=\frac{2}{5}b$$
2) Разобъем многогранник ABCMNP на пирамиды : PABNM и PABC
3) Пусть $$CH\perp AB$$ и h — перпендикуляр из P. Тогда $$CH=h\Rightarrow$$ $$V_{PABNM}=\frac{1}{3}S_{ABNM}*CH$$. Из $$\Delta ABC$$: $$CH=AB *\sin 60=\frac{\sqrt{3}a}{2}$$
$$S_{ABNM}=\frac{AM+NB}{2}*AB=$$$$\frac{\frac{1}{3}b+\frac{1}{4}b}{2}*a=\frac{7ab}{24}$$
$$V_{PABNM}=\frac{1}{3}*\frac{7ab}{24}*\frac{\sqrt{3}a}{2}=$$$$\frac{7a^{2}b\sqrt{3}}{144}$$
4) $$V_{PABC}=\frac{1}{3}S_{ABC}*CP$$
$$S_{ABC}=\frac{1}{2}*AB*BC*\sin 60=$$$$\frac{\sqrt{3}a^{2}}{4}$$
$$V_{PABC}=\frac{1}{3}*\frac{\sqrt{3}a^{2}}{4}*\frac{2}{5}b=$$$$\frac{2\sqrt{3}a^{2}b}{60}$$
Тогда $$V_{ABCMNP}=\frac{7a^{2}b\sqrt{3}}{144}=$$$$\frac{2\sqrt{3}a^{2}b}{60}=$$$$\frac{(35+24)\sqrt{3}a^{2}b}{720}=\frac{59\sqrt{3}a^{2}b}{720}$$
5) $$V_{ABCA_{1}B_{1}C_{1}}=S_{ABC}*CC_{1}=$$$$\frac{\sqrt{3}a^{2}}{4}*b=\frac{\sqrt{3}a^{2}b}{4}$$
6) $$V_{A_{1}B_{1}C_{1}MNP}=$$$$\frac{\sqrt{3}a^{2}b}{4}-\frac{59\sqrt{3}a^{2}b}{720}=$$$$\frac{121\sqrt{3}a^{2}b}{720}$$
Тогда: $$\frac{V_{ABCMNP}}{V_{A_{1}B_{1}C_{1}MNP}}=\frac{59}{121}$$
Б) 1) $$MN=AM-NB=5$$. $$NM_{1}\perp AM\Rightarrow$$ $$NM_{1}=AB=2\sqrt{10}$$
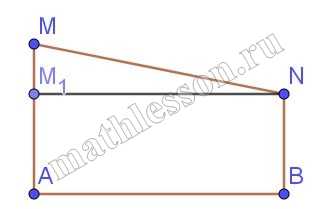
2) $$\Delta MNM_{1} MN=\sqrt{5^{2}+(2\sqrt{10}^{2})}=\sqrt{25+40}=\sqrt{65}$$
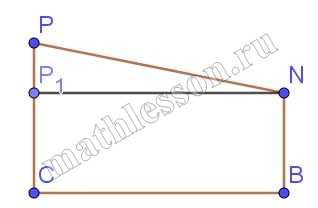
3) Аналогично $$PP_{1}=PC-NB=9$$. $$PN=\sqrt{81+40}=\sqrt{121}$$
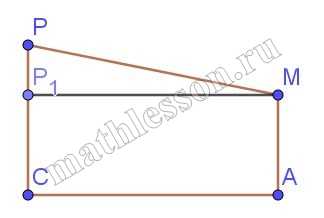
4) Аналогично : $$PM_{1}=24-20=4$$. $$MP=\sqrt{16+40}=\sqrt{56}$$
5) $$MN^{2}+MP^{2}=65+56=121=PN$$ — выполнилась теорема Пифагора
mathlesson.ru
Тренировочный вариант ЕГЭ (профильного уровня) № 161 по математике от Ларина 2017 года
Просмотр
ответы 60 3 6,5 0,15625 -1,3 20 2 16,4 -0,5 33 11 0,25
Ответы
Ответы к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
Решения
Решения к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
Статистика и загрузка
Скачать
Если загрузка не началась автоматически, повторите попытку или нажмите сюда!| Просмотров | 24037 | 4445 | Загрузок |
|---|---|---|---|
| Добавил | Samsung | 03.09.2016 | Дата |
| День | Суббота | 14:37 | Время |
Статья 1274: Свободное использование произведения в информационных, научных, учебных или культурных целях.
Все материалы сайта представлены исключительно в ознакомительных целях.
Источник/автор материала: Александр Александрович Ларин
Если вы скопируете данный файл, Вы должны незамедлительно удалить его сразу после ознакомления с содержанием. Копируя и сохраняя его, Вы принимаете на себя всю ответственность, согласно действующему международному законодательству. Все авторские права на данный файл сохраняются за правообладателем.
Любое коммерческое и иное использование, кроме предварительного ознакомления запрещено. Публикация данного документа не преследует никакой коммерческой выгоды. Но такие документы способствуют быстрейшему профессиональному и духовному росту читателей и являются рекламой бумажных и других различных видов изданий таких документов.
Если данный материал нарушает чьи-либо авторские права, то обратитесь на почту [email protected]
Оценивание
| № задания | 1-12 | 13-15 | 16-17 | 18-19 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 32 |
Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 cодержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий высокого уровня сложности с развёрнутым ответом.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–12 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой. Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
Справочные материалы
Загрузка формул…
Загрузка тестирования…
Обсуждения
Комментарии к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
yagubov.ru
Реальный вариант ЕГЭ (профильного уровня) № ЛАРИН А.А. по математике от Ларина 2017 года
Просмотр
Образцы заданий ПОЛУЧЕНЫ ИЗ ОТКРЫТЫХ ИСТОЧНИКОВ в Интернете и
ПУБЛИКУЮТСЯ ПОСЛЕ окончания ЭКЗАМЕНА в ознакомительных целях!
Ответы
Ответы к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
Решения
Решения к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
Статистика и загрузка
Скачать
Если загрузка не началась автоматически, повторите попытку или нажмите сюда!| Просмотров | 4507 | 686 | Загрузок |
|---|---|---|---|
| Добавил | Yagubov | 10.06.2017 | Дата |
| День | Суббота | 15:13 | Время |
Статья 1274: Свободное использование произведения в информационных, научных, учебных или культурных целях.
Все материалы сайта представлены исключительно в ознакомительных целях.
Источник/автор материала: Александр Александрович Ларин
Если вы скопируете данный файл, Вы должны незамедлительно удалить его сразу после ознакомления с содержанием. Копируя и сохраняя его, Вы принимаете на себя всю ответственность, согласно действующему международному законодательству. Все авторские права на данный файл сохраняются за правообладателем.
Любое коммерческое и иное использование, кроме предварительного ознакомления запрещено. Публикация данного документа не преследует никакой коммерческой выгоды. Но такие документы способствуют быстрейшему профессиональному и духовному росту читателей и являются рекламой бумажных и других различных видов изданий таких документов.
Если данный материал нарушает чьи-либо авторские права, то обратитесь на почту [email protected]
Оценивание
| № задания | 1-12 | 13-15 | 16-17 | 18-19 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 32 |
Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 cодержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий высокого уровня сложности с развёрнутым ответом.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–12 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой. Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
Справочные материалы
Загрузка формул…
Загрузка тестирования…
Обсуждения
Комментарии к заданиям доступны
для бесплатного просмотра
только зарегистрированным
пользователям проекта!
yagubov.ru
ЕГЭ (профильного уровня) по математике — Архив файлов
Оценивание
| № задания | 1-12 | 13-15 | 16-17 | 18-19 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 32 |
Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 cодержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий высокого уровня сложности с развёрнутым ответом.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–12 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой. Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
Экзаменационная работа состоит из двух частей, включающих в себя 19 заданий. Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 cодержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий высокого уровня сложности с развёрнутым ответом.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–12 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой. Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
yagubov.ru
