Задание №1 ЕГЭ по физике
Кинематика
В задании №1 ЕГЭ по физике необходимо решить простую задачу по кинематике. Это может быть нахождение пути, скорости, ускорения тела или объекта по графику из условия.
Теория к заданию №1 по физике
Упрощенные определения
Путь — линия перемещения тела в пространстве, имеет длину, измеряется в метрах, сантиметрах и т.д.
Скорость — количественное изменение положение тела за единицу времени, измеряется в м/с, км/час.
Ускорение — изменение скорости за единицу времени, измеряется в м/с2.
Если тело движется равномерно, его путь меняется по формуле
S=v∙t
В декартовой системе координат имеем:
S=x –x0, x – x0 =vt, x=x0+vt.
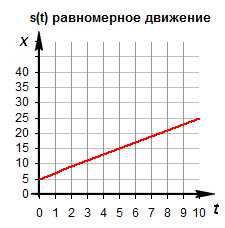
Графиком равномерного движения является прямая. Например, тело начало путь из точки с координатой хо=5, скорость тела равна v=2 м/с. Тогда зависимость изменения координаты примет вид: х=5+2t. И график движения имеет вид:
Если в прямоугольной системе построен график зависимости скорости тела от времени, причем тело движется равноускоренно или равномерно, путь можно найти, определив площадь треугольника:

или трапеции: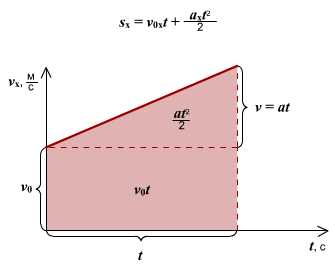
Перейдем к разборам заданий.
Разбор типовых вариантов заданий №1 ЕГЭ по физике
Демонстрационный вариант 2018
На рисунке показан график зависимости от времени для проекции Vx скорости тела. Какова проекция ах ускорения этого тела в интервале времени от 4 до 8 с?
Алгоритм решения:
- Рассматриваем по рисунку, как изменилась скорость тела за указанный отрезок времени.
- Определяем ускорение, как отношение изменения скорости ко времени.
- Записываем ответ.
Решение:
1. За отрезок времени от 4 с до 8 с скорость тела изменилась с 12 м/с до 4 /с. Уменьшаясь равномерно.
2. Поскольку ускорение равно отношению изменения скорости к отрезку времени, за который изменение происходило, имеем:
(4-12) / (8-4) = -8/4 = -2
Знак «–» поставлен по той причине, что движение было замедленным, а для такого движения ускорение имеет отрицательное значение.
Ответ: – 2 м/с2
Первый вариант задания (Демидова, №1)
На рисунке представлен график зависимости модуля скорости v автобуса от времени t. Определите по графику путь, пройденный автобусом в интервале времени от t1=0 с до t2 = 50 с.
Алгоритм решения:
- Рассматриваем по рисунку, как двигался автобус за указанный промежуток времени.
- Определяем пройденный путь, как площадь фигуры.
- Записываем ответ.
Решение:
1. По графику зависимости скорости v от времени t видим, что автобус в начальный момент времени стоял. Первые 20 секунд, он набирал скорость до 15 м/с. А потом двигался равномерно еще 30 секунд. На графике зависимость скорости от времени представляет собой трапецию.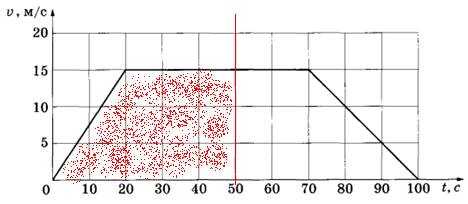
2. Пройденный путь S определяем как площадь трапеции.
Основания этой трапеции равны промежуткам времени: a = 50 с и b = 50-20=30 с, а высота представляет собой изменение скорости и равна h = 15 м/с.
Тогда пройденный путь равен:
(50 + 30) • 15 / 2 = 600
Ответ: 600 м
Второй вариант задания (Демидова, № 22)
На рисунке представлен график движения автобуса из пункта А в пункт Б и обратно. Пункт А находится в точке x = 0, а пункт Б — в точке х = 30 км. Чему равна скорость автобуса на пути из А в Б?
Алгоритм решения:
- Рассматриваем график зависимости пути от времени. Устанавливаем изменение скорость за указанный временной промежуток.
- Определяем скорость.
- Записываем ответ.
Решение:
Участок пути из А в Б это первый отрезок. На этом промежутке координата x увеличивается равномерно с нуля до 30 км за 0,5 ч. Тогда можно найти скорость по формуле:
(S-S0) / t = (30 — 0) км / 0,5 ч = 60 км/ч.
Ответ: 60.
Третий вариант задания (Демидова, №30)
Автомобиль движется по прямой улице. На графике представлена зависимость его скорости от времени. Определите модуль ускорения автомобиля на интервале времени от 30 с до 40 с.
Алгоритм решения:
- Рассматриваем по рисунку, как изменилась скорость тела за указанный отрезок времени.
- Определяем ускорение, как отношение изменения скорости ко времени.
- Записываем ответ.
Решение:
На отрезке времени от 30 с до 40 с скорость тела возрастала равномерно с 10 до 15 м/с. промежуток времени, в течение которого произошло изменение скорости равен:
40 с – 30 с=10 с. А сам промежуток времени равен 15 – 10 = 5м/с. Автомобиль на указанном промежутке двигался с постоянным ускорением. Тогда оно равно:
м/с2
Ответ: 0,5
spadilo.ru
Задание 1 ЕГЭ по физике 2019: разбор теории и практики
Задание 1
Это задание проверяет знания учащихся в области кинематики, к основным понятиям которой относятся понятия ускорение, скорости и перемещения. Так как это векторные величины, то в подавляющем большинстве учебников приведены формулы в векторном виде и подавляющее большинство моих коллег, с которыми мне доводилось общаться, также заставляют своих учеников учить формулы в векторном виде, что совершенно избыточно, на мой взгляд, и чаще мешает решать задания ЕГЭ, чем помогает. Конечно, важно знать, что скорость, ускорение и перемещение — это векторные величины, как и импульс, и сила. Но гораздо важнее, чтобы они понимали, что вычисляем мы, в конечном итоге, не вектора, а их проекции и модули. И вот с этим-то учащиеся часто путаются. К примеру, необходимо по графику скорости определить модуль или проекцию ускорения. Сколько формул для этого нужно учить — три, две или одну? Конечно же одну, для проекции ускорения. А модуль ускорения
С перемещением ситуация ещё интереснее. Часто мне приходится сталкиваться с ситуацией, когда ученики из других школ, с которыми я занимаюсь подготовкой к экзамену по физике в центре подготовки к ЕГЭ в городе Ногинске, не понимают почему проекцию перемещения нужно находить по той или иной формуле. Они просто не могут понять откуда взялись те или иные формулы перемещения. Но зато они легко могут написать эти формулы в векторном виде, от которого, как правило, мало толку. Да, есть проблема — когда изучается кинематика, в 10 классе, дети ещё не знакомы с элементами математического анализа и не знают ни понятия производной, ни понятия интеграла. Но это и не обязательно. Достаточно показать на простом примере равномерного движения, что проекция перемещения может быть определена как площадь фигуры под графиком скорости и затем применить эту идею к равноускоренному движению. Это, в принципе, показано и в учебнике Пёрышкина для 9 класс, в разделе Кинематика, и в учебнике для 10 класса углублённого уровня Мякишева. Но тем не менее, почему-то многие ученики затрудняются с вычислением пройденного пути по графику скорости, который есть ни что иное как модуль перемещения при прямолинейном движении. Особенно, если график представляет собой ломаную линию.
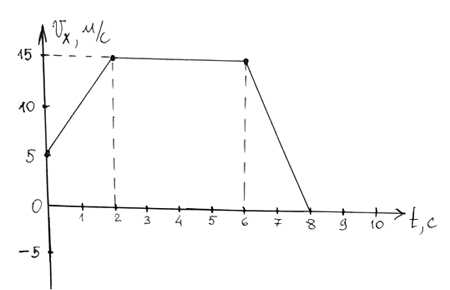
- Найти ax в промежутке времени от 0 до 2 с.
- Найти модуль ускорения в промежутке от 6 до 7 с.
- Найти пройденный путь за первые 5 с движения
Вот несколько примеров.

1)
2) На промежутке от 6 до 7 с ускорение такое же как и на промежутке от 6 до 8 с, а он удобнее, поэтому
a = │ax│ = 7,5 м/с2
3) На графике площадь заштрихованной области и есть
ЕГЭ-2020. Физика. Решение задач
В книге содержатся материалы для успешной сдачи ЕГЭ: краткие теоретические сведения по всем темам, задания разных типов и уровней сложности, решение задач повышенного уровня сложности, ответы и критерии оценивания. Учащимся не придется искать дополнительную информацию в интернете и покупать другие пособия. В данной книге они найдут все необходимое для самостоятельной и эффективной подготовки к экзамену.
Купить
rosuchebnik.ru
Задание №12 ЕГЭ по физике
Молекулярно-кинетическая теория
Задание №12 в ЕГЭ по физике — последнее тестовое задание на тему термодинамики.
Теория к заданию №12 ЕГЭ по физике
Тепловые машины преобразуют получаемую от сгорающего топлива энергию в механическую. К ним, например, относятся, которые устанавливаются в автомобилях. Автором теории таких машин является С. Карно.
Подобные двигатели характеризуются КПД, который определяется по формуле:
η=(Тн — Тх)/Тх, где Тн – температура нагревателя, Тх – холодильника
КПД можно определять как отношение теплоты, которую машина получает от нагревателя Qн к реально выполняемой работе А т.е η= Qн/А.
Адиабатный (адиабатический) процесс связан с первым термодинамическим законом. При нем изменение теплоты в системе равно сумме изменений тепловой энергии и выполненной работы, которую выполняет газ. Он протекает без передачи газу теплоты. Не происходит и передача теплоты газом внешней среде. Адиабатический процесс графически изображается так: 
Теория к заданию №11 ЕГЭ по физике
Демонстрационный вариант 2018
Тепловая машина работает по циклу Карно. Температуру холодильника тепловой машины повысили, оставив температуру нагревателя прежней. Количество теплоты, полученное газом от нагревателя за цикл, не изменилось. Как изменились при этом КПД тепловой машины и работа газа за цикл?
Для каждой величины определите соответствующий характер изменения:
- увеличилась,
- уменьшилась,
- не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| КПД тепловой машины | Работа газа за цикл |
Алгоритм решения:
- Записываем формулу расчета КПД.
- Анализируем, что произойдет, если температуру Qx увеличить.
- Анализируем, как изменится работа.
- Записываем ответ.
Решение:
1. Для любого двигателя показатель КПД определяется формулой:
,
где Тн – температурный показатель нагревателя, Тх – температурный показатель холодильника.
2. Легко видно, что увеличение температурного показателя холодильника приведет к уменьшению полезного коэффициента.
3. КПД определяется также как отношение тепла, которое получено от нагревателя Q, к реальной работе А. Тогда работа равняется А= ηQн. И если уменьшится КПД, работа тоже уменьшится.
4. Записываем ответ:
| КПД тепловой машины | Работа газа за цикл |
| 2 | 2 |
Ответ: 2 2
Первый вариант задания (Демидова,№3)
На рисунках приведены графики А и Б двух процессов, 1-2 и 3-4, происходящих с 1 моль гелия. Графики построены в координатах V-T и p-V, где р — давление, V — объём, Т — абсолютная температура газа. Установите соответствие между графиками и утверждениями, характеризующими изображённые на графиках процессы. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ГРАФИКИ | УТВЕРЖДЕНИЯ 1) Над газом совершают работу, при этом его внутренняя энергия увеличивается. 2) Над газом совершают работу, при этом газ отдаёт положительное количество теплоты. 3) Газ получает положительное количество теплоты и совершает работу. 4) Газ получает положительное количество теплоты, при этом его внутренняя энергия увеличивается. |
Алгоритм решения:
- Рассматриваем первый график таблицы. Ищем правильное предложение в графе справа.
- Проводим анализ второго графика в левой графе таблицы. Определяем правильный ответ в графе справа.
- Записываем ответ.
Решение:
1. На графике А) температура повышается, но объем не изменяется. Если объем, в данном случае постоянен, газ работы не выполняет. Но тепловая энергия увеличивается. Справедливо четвертое предложение.
2. Вариант Б) показывает: уменьшаются показатели объема газа и давления. Тогда из равенства общего состояния следует, что при этом должна снижаться и температура , газ отдает тепло. Это соответствует предложению 2.
Правильными будут варианты четвертого и второго ответов.
Ответ: 4 2
Второй вариант задания (Демидова, №20)
Установите соответствие между процессами в идеальном газе и формулами, которыми они описываются (N — число частиц, р — давление, V — объём, Т — абсолютная температура, Q — количество теплоты.) К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
| ПРОЦЕССЫ А) изохорный процесс при N = const Б) адиабатный процесс при N = const | ФОРМУЛЫ |
Алгоритм решения:
- Анализируем, что происходит при изохорном типе процесса.
- Определяем, какой вариант равенств соответствует такому процессу.
- Анализируем, каким образом происходит адиабатический процесс.
- Устанавливаем, какое равенство соответствует данному процессу.
- Записываем ответ.
Решение:
1. Справа вариантом А) записано, что происходит изохорный процесс. Он совершается при постоянном показателе объема.
2. В этом случае будет справедливым равенство: р/Т= const. Такое равенство стоит под первым номером.
3. При адиабатическом процессе Б) не происходит теплового обмена со средой, то есть выполняется равенство: Q=0.
4. Значит, правильные предложения 1 и 4.
Ответ: 1 4
spadilo.ru
Задание №11 ЕГЭ по физике
Молекулярно-кинетическая теория
Задание №11 ЕГЭ по физике продолжает тему термодинамики и молекулярно кинетической теории. Рассмотрим типовые варианты данных заданий и немного теории!
Теория к заданию №11 ЕГЭ по физике
На рисунках изображены графики зависимости V газа от значений температуры при разных процессах: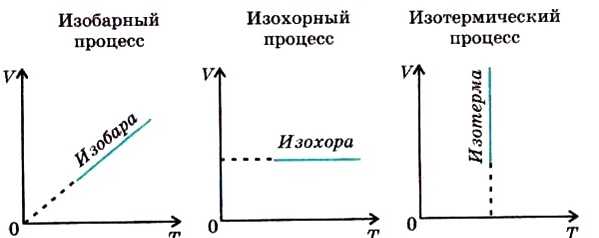
Уравнение состояния газа через концентрацию молекул имеет вид:
Зависимость давления от объема при разных процессах:
Среднее значение квадратичной скорости молекул определяется формулой
Разбор типовых вариантов заданий №11 ЕГЭ по физике
Демонстрационный вариант 2018
На рисунке показан график циклического процесса, проведённого с одноатомным идеальным газом, в координатах р–Т, где р – давление газа, Т – абсолютная температура газа. Количество вещества газа постоянно.
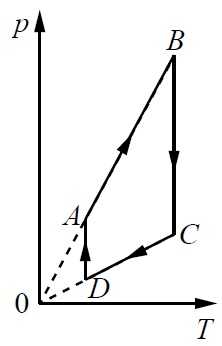
Из приведённого ниже списка выберите два правильных утверждения, характеризующих процессы на графике, и укажите их номера.
- Газ за цикл совершает положительную работу;
- В процессе АВ газ получает положительное количество теплоты;
- В процессе ВС внутренняя энергия газа уменьшается;
- В процессе CD над газом совершают работу внешние силы;
- В процессе DA газ изотермически расширяется.
Алгоритм решения:
- Рассматриваем рисунок, данный в задании.
- Анализируем газовые процессы, и проверяем правильность первого утверждения.
- Проверяем, истинно ли второе утверждение.
- Анализируем третье утверждение
- Проверяем, верно ли четвертое утверждение.
- Проверяем, какой происходит процесс на промежутке DA.
- Записываем результат.
Решение:
1. На приведенном в задании рисунке изображен процесс циклического характера, причем на участках цикла AB и CD объем не изменяется. Этот процесс изохорного типа.
На участках BC и DA график указывает на процесс изотермического типа. Причем, на первом из участков происходит расширение, а на втором сжатие. Расширяясь, газ выполняет положительную работу. При сжатии работу выполняет поршень. И она отрицательная. В результате поршень возвращается в начальное положение. Это означает, что разница объёмов в конце цикла нулевая. Работа имеет большее значение на том промежутке, где температурный показатель выше. Это происходит при расширении, на участке ВС. Тогда положительная работа больше по модулю, чем отрицательная. Следовательно, газ выполнил в результате положительную работу, и предложение 1 истинно.
2. На промежутке AB процесс относится к изохорному типу. При нем объем постоянный. Это видно при сравнении газовых процессов на графиках вверху. Работа не выполняется. Температура на промежутке АВ и энергия внутреннего теплового движения возрастают. Поскольку повышается температурный показатель, растет внутреннее давление при неизменном объеме. Следовательно и значение внутренней энергии возрастает. И второе предложение является правильным.
3. На промежутке ВС температурный показатель и энергия газа не меняются, потому как этот процесс является изотермическим. Следовательно, третье предложение ложное.
4. На промежутке СD газ не выполняет никакой работы, поскольку процесс здесь изохорного типа. Тогда четвертое предложение ложно.
5. На промежутке DA газ сжимают изотермическим способом, поскольку повышается показатель давления. Тогда и пятое утверждение ложно.
Ответ: 1 2
Второй вариант задания (Демидова, № 2)
При переводе одноатомного идеального газа из состояния 1 в состояние 2 давление p пропорциональна концентрации его молекул n (см. рисунок). Масса газа в процессе остаётся постоянной.
Из приведённого ниже списка выберите два правильных утверждения, характеризующих процесс 1-2.
- Абсолютная температура газа остаётся неизменной.
- Происходит изотермическое сжатие газа.
- Среднеквадратическая скорость теплового движения молекул газа увеличивается.
- Плотность газа уменьшается.
- Средняя кинетическая энергия теплового движения молекул газа уменьшается.
Алгоритм решения:
- Анализируем изображенный график.
- Выписываем формулу, позволяющую определить концентрацию молекул.
- Записываем уравнение газа через концентрацию.
- Анализируем процесс, происходящий в газе. Ищем ответ на вопрос 2.
- Определяем истинность утверждений 3 и 5.
- Устанавливаем, истинно ли 4 предложение.
- Записываем ответ.
Решение:
1. На графике изображена зависимость давления от показателя концентрации молекул.
2. Показатель концентрации определяется согласно равенству n=N/V. Здесь буквой N обозначено число молекул в объеме V. Тогда зависимость объема от концентрации выражена равенством: V=N/n. Если рассмотреть зависимость n от давления, то легко установить, прямая, которая содержит данный промежуток, проходит через точку (0;0). Следовательно, показатель n прямо пропорционален давлению. Положим коэффициент пропорциональности равным α,тогда n= αp. Отсюда получается V=N/(αp), и равенство Менделеева – Клапейрона примет вид
,
что означает: температура газа является величиной постоянной. Первое предложение верно.
3. В данном процессе температура не меняется. Это означает, что процесс изотермический. Предложение 2 истинно.
4. Из формулы αp=N/V легко видно, что объем данного количества газа, и показатель давления обратно пропорциональны. Поскольку в момент 2 на графике давление p растет, V уменьшается. Предложение 2 истинно.
5. Температура данного газа не изменилась, следовательно, не изменилось в процессе и значение среднеквадратической скорости. Предложение 3 ложное. Неверно и предложение 5.
6. Плотность данного газа n возрастает. Значит, предложение 4 ложное.
Ответ: 1 2
Третий вариант задания (Демидова, № 7)
Идеальный газ перевели из состояния 1 в состояние 3 так, как показано на графике зависимости давления р газа от объёма V. Количество вещества газа при этом не менялось.
Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике.
Абсолютная температура газа максимальна в состоянии 3.
- В процессе 1—2 абсолютная температура газа увеличилась в 2 раза.
- В процессе 2-3 абсолютная температура газа уменьшилась в 1,5 раза.
- Плотность газа минимальна в состоянии 1.
- В ходе процесса 1-2-3 среднеквадратичная скорость теплового движения молекул газа увеличилась в 3 раза.
Алгоритм решения:
- Рассматриваем типы процессов на графике.
- Выпишем равенство Менделеева – Клапейрона. Выведем зависимость объема от показателя температуры на первом участке, и зависимости показателя давления от уровня температуры на втором. Делаем вывод относительно абсолютной температуры.
- Устанавливаем истинность предложений 2 и 3.
- Определяем истинность четвертого предложения.
- Выясняем, истинно ли пятое предложение.
- Записываем ответ.
Решение:
1. На промежутке от состояния 1 до состояния 2 уровень давление постоянный. Следовательно, из уравнения состояния получаем, что V/T= const, поскольку p есть величина постоянная.
2. Показатель объема здесь возрастал, тогда и показатель T должен был расти. А на участке от состояния 2 к состоянию 3 постоянным является показатель температуры. Тогда и p/Т= const. На чертеже видно, что на участке от 1 к 2 давление росло, значит, и температура возросла пропорционально давлению. Значит, в момент 3 температура была наибольшей. Первое предложение справедливо.
3. В промежутке от 1 к 2, как установлено уже V/T= const. Поскольку объем увеличился в два раза, температура возросла также. Предложение 3 ложно.
4. На промежутке от 2-й к 3-й точке температура возрастала, так как, росло давление. Предложение 3 неверно.
5. В момент 1 задаваемого процесса объем, который занимал газ, был наименьшим. Масса данного газа – величина в данном случае постоянная. Значит, плотность, которая равна отношению массы на объем, была максимальной, а не минимальной. Предложение 4 ложно.
6. Уровень среднеквадратической скорости молекул прямо пропорционально зависит от корня показателя температуры. Поскольку масса и число молекул постоянны для данного газа. На промежутке от состояния 1 к 2 уровень температуры возрос в вдвое, а на промежутке от 2 к 3 – в полтора раза. Имеем: 2∙1,5 = 3. Тогда искомая скорость возросла в раз. Последнее предложение ложное.
Ответ: 1 2
spadilo.ru
Задание №7 ЕГЭ по физике
Установление соответствий
В задании №7 ЕГЭ по физике необходимо выбрать соответствия либо графикам и их процессам, либо формулам и условиям их применения. Теория к заданию схожа с теорией к заданию №2 (Теория к заданию №2 ЕГЭ по физике) Мы приведем еще раз некоторые пункты.
Теория к заданию №7 ЕГЭ по физике
Движение тела, брошенного под углом к горизонту
Если мяч бросить вертикально вверх, сила притяжения замедлит движение его по мере набора высоты. А вниз мяч полетит ускоренно.
Если мяч бросить строго горизонтально в пространстве, где нет действия силы притяжения, то он так и будет лететь горизонтально с постоянной скоростью (так гласит первый закон Ньютона). Но на земле так мяч лететь не будет.
Если мяч брошен под углом к горизонту, скорость и движение можно разложить на две составляющие. Относительно оси ОY мяч летит, как бы вертикально вверх. А относительно ОХ мяч летит прямолинейно с постоянной скоростью. Каждое мгновение эти составляющие складываются. результате траектория полета получается в виде параболы.

Импульс тела определяется формулой: p=mv.
Кинетическая энергия тела пропорциональна квадрату скорости: Ek=mv2/2, а потенциальная энергия не зависит от скорости. Она пропорциональна высоте поднятия мяча.
Гармонические колебания пружинного маятника
Если тело под действием пружины совершает гармонические колебания, его скорость изменяется по закону
Жесткость пружины связана с массой и угловой скоростью формулой: k=mω2
Разбор типовых заданий №7 ЕГЭ по физике
Демонстрационный вариант 2018
В момент t = 0 мячик бросают с начальной скоростью V0 под углом α к горизонту с балкона высотой h .
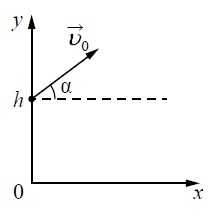
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y = 0.)

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Алгоритм решения:
- Размышляем о движении мяча.
- Анализируем, какая из величин, указанных в столбце справа, может вести себя так, как указано на графике Б слева.
- Записываем ответ в таблицу.
Решение:
1 Анализируем график А и варианты ответа. На нем величина с течением времени не изменяется. Какая это может быть величина?
2. Первый вариант ответа: проекция импульса мячика на ОY? Импульс, является вектором, направление которого совпадает с вектором скорости. А она меняется со временем. Значит, этот график – не проекция импульса.
Кинетическая энергия мячика определяется скоростью движения тела. При таком движении, скорость не является величиной постоянной, следовательно, энергия тоже не может быть величиной постоянной.
Во время полёта на мячик действует только сила тяжести, а она постоянная. Согласно второму закону Ньютона, сила тяжести равна произведению массы мяча на его ускорение. А поскольку сила и масса – величины постоянные, ускорение тоже постоянно. Значит график А) отвечает варианту ответа 3) – ускорение.
Рассматриваем график Б).
Уже было указано, что скорость при полете мяча не вляетс величиной постоянной. Но, импульс равен произведению массы на скорость, а следовательно прямо пропорционален ей. Но на графике изображена не прямая пропорциональность. Там парабола, следовательно. Там зависимость величины от квадрата скорости. Это кинетическая энергия. Она определяется формулой Ek=mv2/2.
Заполняем таблицу
Ответ 3,2
Первый вариант задания (Демидова, №7)
Один конец лёгкой пружины жёсткостью k прикреплён к бруску, а другой закреплён неподвижно. Брусок скользит по горизонтальной направляющей так, что его координата изменяется со временем по закону .
Установите соответствие между физическими величинами и формулами, выражающими их зависимость от времени.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ А) кинетическая энергия бруска Б) проекция ax(t) ускорения бруска ось x
| ФОРМУЛЫ |
Алгоритм решения:
- Определяем выражение кинетической энергии.
- Находим формулу для определения проекции ускорения.
- Записываем ответ.
Решение:
1. Кинетическая энергия тела зависит от времени через скорость. Она выражается формулой:
Здесь
Из равенства k=mω2 имеем:
Соединив эти равенства, получим выражение для определения кинетической энергии:
2. Проекцию ускорения ах(t) бруска определим как производную скорости по времени:
Ответ: 2,3
spadilo.ru
Задание №2 ЕГЭ по физике
Законы Ньютона и силы в природе
Во втором задании ЕГЭ по физике необходимо решить задачу на законы ньютона или связанную с действием сил. Ниже мы приводим теорию с формулами, которые необходимы для успешного решения задач по этой тематике.
Теория к заданию №2 ЕГЭ по физике
Второй закон Ньютона
Формула второго закона Ньютона F=ma. Здесь F и a – величины векторные. Величина a – это ускорение движения тела под действием указанной силы. Оно прямо пропорционально силе, действующей на данное тело и направлено в сторону действия силы.
Равнодействующая
Равнодействующая сила – это сила, действие которой заменяет действие всех сил, приложенных к телу. Или, другими словами, равнодействующая всех сил, приложенных к телу, равна векторной сумме этих сил.
Сила трения
Сила трения связана с силой нормального давления формулой Fтр=μN, где μ – коэффициент трения. Отсюда, зная величину силы трения и нормального к поверхности давления можно определить μ,которое является величиной постоянной для данного случая. Зная силу трения и силу нормального давления (эту силу называют еще силой реакции опоры), можно вычислить коэффициент трения.
Сила тяжести
Вертикальная составляющая движения зависит от сил, действующих на тело. Необходимо знание формулы силы тяжести F=mg, поскольку, как правило, действует на тело, брошенное под углом к горизонту, только она.
Сила упругости
Сила упругости — сила, возникающая в теле в результате его деформации и стремящаяся вернуть его в исходное (начальное) состояние. Для силы упругости используется закон Гука: F = k•δl, где k — коэффициент упругости (жесткость тела), δl — величина деформации.
Закон всемирного тяготения
Сила F гравитационного притяжения между двумя материальными точками массы m1 и m2, разделёнными расстоянием r, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними:
Разбор типовых вариантов заданий №2 ЕГЭ по физике
Демонстрационный вариант 2018
На графике приведена зависимость модуля силы трения скольжения от модуля силы нормального давления. Каков коэффициент трения?
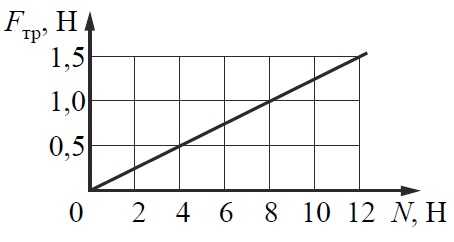
Алгоритм решения:
- Записываем формулу, связывающую эти силы. Выражаем коэффициент трения.
- Рассматриваем график, устанавливаем пару соответствующих значений сил нормального давления N и трения.
- Вычисляем коэффициент, исходя из значений сил, взятых из графика.
- Записываем ответ.
Решение:
- Сила трения связана с силой нормального давления формулой Fтр=μN, где μ – коэффициент трения. Отсюда, зная величину силы трения и нормального к поверхности давления можно определить μ,которое является величиной постоянной для данного случая. Зная силу трения и силу нормального давления (эту силу называют еще силой реакции опоры), можно вычислить коэффициент трения. Из приведенной формулы следует, что: μ = Fтр : N
- Рассматриваем график зависимости. Возьмем любую точку графика, например, когда N = 12 (Н), а Fтр = 1,5 (Н).
- Возьмём выбранные значения сил и вычислим значение коэффициента μ: μ=1,5/12 = 0,125
Ответ: 0,125
Первый вариант задания (Демидова, №3)
Сила F сообщает телу массой m ускорение a в инерциальной системе отсчёта. Определите ускорение тела массой 2m под действием силы 0,5F в этой системе отсчета.
1) ; 2) ; 3) ; 4)
Алгоритм решения:
- Записываем второй закон Ньютона. Выражаем ускорение из формулы.
- Подставляем в полученное выражение измененные значения массы и силы и находим новое значение ускорения, выраженное через первоначальное его значение.
- Выбираем правильный ответ.
Решение:
1. Согласно второму закону Ньютона F=m•a, сила F, которая действует на тело массой m, сообщает телу ускорение а. Имеем:
2. По условию m2=2m, F2=0,5 F.
Тогда измененное ускорение будет равно:
В векторной форме запись аналогична.
Ответ: 2)
Второй вариант задания (Демидова, №9)
Камень массой 200 г брошен под углом 60° к горизонту с начальной скоростью v = 20 м/с. Определите модуль силы тяжести, действующей на камень в верхней точке траектории.
Если тело брошено под углом к горизонту и силой сопротивления можно пренебречь, равнодействующая всех сил постоянна. Вертикальная составляющая движения зависит от сил, действующих на тело. Необходимо знание формулы силы тяжести F=mg,поскольку, как правило, действует на тело, брошенное под углом к горизонту, только она.
Алгоритм решения:
- Переводим в СИ значение массы.
- Определяем, какие силы действуют на камень.
- Записываем формулу силы тяжести. Вычисляем величину силы.
- Записываем ответ.
Решение:
- Масса камня m=200 г=0,2 кг.
- На брошенный камень действует сила тяжести Fт=mg. Поскольку в условии не оговорено обратное, то сопротивлением воздуха можно пренебречь.
- Сила тяжести одинакова в любой точке траектории камня. Это значит, данные в условии (нач. скорость v и угол к горизонту, под которым брошено тело) избыточны. Отсюда получаем: Fт=0,2∙10 =2 Н.
Ответ: 2
Третий вариант задания (Демидова, №27)
К системе из кубика массой 1 кг и двух пружин приложена постоянная горизонтальная сила величиной F = 9 Н (см. рисунок). Система покоится. Между кубиком и опорой трения нет. Левый край первой пружины прикреплён к стенке. Жёсткость первой пружины k1 = 300 Н/м. Жёсткость второй пружины k2 = 600 Н/м. Чему равно удлинение второй пружины?
Алгоритм решения:
- Записываем закон Гука для 2-й пружины. Находим ее связь с данной в условии силой F.
- Из полученного уравнения выражаем удлинение, вычисляем его.
- Записываем ответ.
Решение:
- По закону Гука удлинение пружины связано с жесткостью k пружины и приложенной к ней силе F выражением F =k∆l. На вторую пружину действует растягивающая ее сила F2=k2∆l. 1-я пружина растягивается силой F. По условию F=9 H. Поскольку пружины составляют единую систему, сила F растягивает и 2-ю пружину, т.е. F2=F.
- Удлинение Δl определяется так:
А это равно 1,5 см.
Ответ: 1,5
spadilo.ru
