Презентация по информатике на тему » Основы логики» (9 класс)
Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:
*
2 слайд Описание слайда:
Описание слайда:
ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ. ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ И ЛОГИЧЕСКИЕ ОПЕРАЦИИ. LOGO
3 слайд Описание слайда:
Описание слайда:
* В основе современной логики лежат учения, созданные еще древнегреческими мыслителями, хотя первые учения о формах и способах мышления возникли в Древнем Китае и Индии. Основоположником формальной логики является Аристотель, который впервые отделил логические формы мышления от его содержания. Согласно формальной логике основным элементом рассуждения человека является высказывание – утверждение, которое может быть либо истинным, либо ложным. Аристотель сформулировал ряд законов формальной логики. LOGO
 Описание слайда:
Описание слайда:
* Аристотель родился в Стагире (384г. до н.э.), греческой колонии, расположенной на северо-западном побережье Эгейского моря. Его отец Никомах, принадлежавший к роду врачей Асклепиадов, был придворным врачом Аминты III — македонского царя. LOGO
5 слайд Описание слайда:
Описание слайда:
Термин логика происходит от греческого «логос», что значит «рассуждение», «речь». Логика, как раздел математики – алгебра логики, возникла в XIX веке. Основателем этой науки был английский математик Джорж Буль. Джордж Буль впервые применил алгебраические методы для решения традиционных логических задач, которые до этого решались методами рассуждений, согласно формальной логике Аристотеля. Первоначально развитие математической логики носило исключительно теоретический характер. LOGO
6 слайд Описание слайда:
Описание слайда:
* Алгебра — это раздел математики, предназначенный для описания действий над переменными величинами, которые принято обозначать строчными латинскими буквами. Что изучает алгебра? Числа, числовые величины, числовые выражения, а так же правила выполнения действий над ними. Что изучает логика? Логика – (от древнегреч. – слово, мысль, понятие, высказывание, умозаключение) это наука о формах и способах мышления. Это учение о способах рассуждений и доказательств. Алгебра логики изучает общие операции над высказываниями. Основы данной алгебры были положены англ. математиком Джорджем Булем в 19 веке, так же её называют булевой алгеброй. LOGO
 Описание слайда:
Описание слайда:
* Высказывание (суждение) – это формулировка своего понимания окружающего мира. Это повествовательное предложение, в котором что – либо утверждается или отрицается. По поводу любого высказывания можно сказать истинно оно или ложно. Пример Истинное высказывание: «Буква «ю» — гласная». Ложное высказывание: «Компьютер был изобретен в середине XIX века». LOGO
8 слайд Описание слайда:
Описание слайда:
Определите какие из следующих выражений являются высказываниями: — Число 6 – четное. — Здравствуйте! — Все роботы являются машинами. — Кто отсутствует? — Выразите 1 ч 15 мин в секундах. — А – первая буква в алфавите. LOGO
9 слайд Описание слайда:
Описание слайда:
* Какие из предложений являются высказываниями? Определите их истинность. Какой длины эта лента? Прослушайте информацию. Делайте утреннюю зарядку! Назовите устройства вывода информации. Кто сегодня отсутствует? Париж- столица Канады. Число 11 является составным. 4+5=9 Сложите числа 2 и 5. Некоторые медведи живут на севере. Все медведи белые. Чему равно расстояние от Москвы до Ленинграда. LOGO
 Описание слайда:
Описание слайда:
* Основные понятия логики. Логические операции – логические действия. Базовые логические операции – конъюнкция, дизъюнкция, и отрицание. Дополнительные – импликация и эквивалентность. В алгебре логики высказывания обозначаются именами логических переменных (А, В, С), которые могут принимать значения истина (1) или ложь (о). Истина и ложь – логические константы. Логическое выражение – простое или сложное высказывание. Сложное высказывание строится из простых с помощью связок «И», «ИЛИ», «НЕ», которые в алгебре логики заменяются на логические операции. LOGO
11 слайд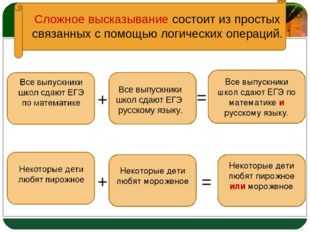 Описание слайда:
Описание слайда:
Сложное высказывание состоит из простых связанных с помощью логических операций. Все выпускники школ сдают ЕГЭ по математике и русскому языку. + = Некоторые дети любят мороженое Некоторые дети любят пирожное или мороженое + = LOGO
12 слайд Описание слайда:
Описание слайда:
Распределите высказывания по типам (простое, сложное) 1. Сегодня или завтра, или через месяц он напишет письмо. 2. В школе уроки начнутся в 9 утра. 3. Кончилось лето, и наступили прохладные дни. 4. У меня есть старший брат. 5. Круг – это не квадрат. Укажите связующие слова или союзы 1. Некоторые дети не любят конфеты. 2. Он позвонит или пришлет сообщение. 3. Мне должны подарить лыжи и самокат. LOGO
 Описание слайда:
Описание слайда:
* Конъюнкция Дизъюнкция Инверсия Импликация Эквивалент-ность Название Обозначение Союз в естественном языке LOGO
14 слайд Описание слайда:
Описание слайда:
Конъюнкция (логическое умножение) Это соединение двух простых логических выражений (высказываний) с помощью союза И. А – сегодня светит солнце, В – сегодня идет дождь А и В – сегодня светит солнце и идет дождь Вывод: результат будет истинным тогда и только тогда, когда оба исходных высказывания истинны, и ложным во всех остальных случаях. * А В А^В 0 0 0 0 1 0 1 0 0 1 1 1 LOGO
15 слайд Описание слайда:
Описание слайда:
Дизъюнкция (логическое сложение) Это соединение двух простых логических высказываний с помощью союза ИЛИ. А или В – сегодня светит солнце или идет дождь Вывод: результат будет ложным тогда и только тогда, когда оба исходных высказывания ложны, и истинным в остальных случаях. * А В АvВ 0 0 0 0 1 1 1 0 1 1 1 1 LOGO
16 слайд Описание слайда:
Описание слайда:
Инверсия (логическое отрицание) Это отрицание простого высказывания. Образуется с помощью частицы Не. (можно использовать словосочетание Неверно, что) * Вывод: если исходное выражение истинно, то результат его отрицания будет ложным, и наоборот, если исходное выражение ложно, то оно будет истинным. А А 0 1 1 0 LOGO
17 слайд Описание слайда:
Описание слайда:
Импликация (логическое следование) Эта операция связывает два простых логических выражения, из которых первое является условием, а второе — следствием из этого условия. Содержит конструкцию ЕСЛИ — ТО * Вывод: результат ложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно. А В А→В 0 0 1 0 1 1 1 0 0 1 1 1 LOGO
18 слайд Описание слайда:
Описание слайда:
Эквивалентность (логическое равенство) Логическое выражение содержит конструкцию «А ТОГДА И ТОЛЬКО ТОГДА, КОГДА В» Вывод: результат будет истинным тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны. * А В А≡ В 0 0 1 0 1 0 1 0 0 1 1 1 LOGO
19 слайд Описание слайда:
Описание слайда:
* Конъюнкция Дизъюнкция Инверсия Импликация Эквивалент-ность Название Логическое умножение Логическое сложение Отрицание Логическое следование Логическое равенство Обозначение А&В или А^В Аv В ¬ А или Ā А→В А(условие)В(следствие) А≡В или А↔В Союз в естественном языке А и В А или В Не А, Неверно, что А Если А, то В; когда А, тогда В; коль скоро А то В А тогда и только тогда, когда В LOGO
20 слайд Описание слайда:
Описание слайда:
Последовательность выполнения операций Инверсия. Конъюнкция. Дизъюнкция. Импликация. Эквивалентность. Для изменения указанного порядка выполнения операций применяют скобки. LOGO
21 слайд Описание слайда:
Описание слайда:
№ 1. Из двух простых высказываний постройте сложное высказывание, используя логические связки и установите истинность исходных высказываний и полученного высказывания: А : «Число 10 –четное» В : «Число 10 – отрицательное» * LOGO
22 слайд Описание слайда:
Описание слайда:
А : «Число 10 –четное» (1) В: «Число 10 – отрицательное» (0) Конъюнкция: A ^ B : «Число 10 – четное и отрицательное» — ложь (по таблице истинности) Дизъюнкция: А V B : «Число 10 – четное или отрицательное» — истина (по таблице истинности) * LOGO
23 слайд Описание слайда:
Описание слайда:
А : «Число 10 –четное» (1) В: «Число 10 – отрицательное» (0) Инверсия: А :«Число 10 – нечетное»- ложь (Неверно, что число 10 — четное) В : «Число 10- неотрицательное»- истина (Неверно, что число 10 — отрицательное) * LOGO
24 слайд Описание слайда:
Описание слайда:
А – «Число 10 –четное» (1) В- «Число 10 – отрицательное» (0) Импликация: А → В : «Если число 10- чётное, то оно отрицательное» — ложь Эквивалентность: А ↔ В : «Число 10- чётное тогда и только тогда, когда оно отрицательное» — ложь * LOGO
25 слайд Описание слайда:
Описание слайда:
Домашнее задание Выучить конспект урока Из двух простых высказываний постройте сложные высказывания, используя логические связки и установите истинность исходных высказываний и полученных высказываний: «Число 10 — составное», «Число 13 делится на 3». LOGO
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсемирная историяВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеДругоеДругойЕстествознаниеИЗО, МХКИзобразительное искусствоИностранные языкиИнформатикаИскусствоИспанский языкИсторияИстория РоссииИстория Средних вековИтальянский языкКлассному руководителюКультурологияЛитератураЛитературное чтениеЛогопедияМатематикаМировая художественная культураМузыкаМХКНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирОсновы безопасности жизнедеятельностиПриродоведениеРелигиоведениеРисованиеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФинский языкФранцузский языкХимияЧерчениеЧтениеШкольному психологуЭкология
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Общая информация
Номер материала: ДБ-1006157
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарийinfourok.ru
Урок по информатике для 9 класса «Основы логики»
Открытый урок по информатике в 9 классе
«Основы логики»
«Память становится мыслящей»
Д.Б. Эльконин
Цели:
Образовательные:
сформировать у учащихся понятие форм мышления;
сформировать понятия: логическое высказывание, логические величины, логические операции.
Развивающие:
Способствовать развитию логического мышления
Способствовать развитию памяти, внимания.
Научить правильно рассуждать, уметь давать ответы на поставленные вопросы.
Воспитательные:
Способствовать развитию воспитанию аккуратности, терпению.
Способствовать культурному и интеллектуальному развитию учеников.
Тип урока: изучение нового материала.
Требования к знаниям и умениям:
Учащиеся должны знать:
— формы мышления, значение понятий: логическое высказывание, логические величины, логические операции.
Учащиеся должны уметь:
— приводить примеры логических высказываний;
— называть логические величины, логические операции.
Ход урока
Постановка целей урока.
Сообщение ученика об Аристотеле.
Определение содержания и объёма понятий в игровой форме.
Релаксирующая пауза.
Введение понятия кругов Эйлера-Венна.
Тренировочные упражнения по определению истинности или ложности высказываний.
Электронный тест для закрепления усвоенных знаний.
Подведение итогов урока, оценивание, рефлексия.
1. Постановка целей урока
1. Как человек мыслит?
Что в нашей обыденной речи является высказыванием, а что — нет?
Предложение «Кто последний?» — это высказывание или нет?
Формы мышления:
Познание истины – одна из важнейших потребностей человека.
В Древней Греции, древней Индии, Древнем Риме законы и формы правильного мышления изучались в рамках ораторского искусства. Применение логических приемов рассуждения позволяло ораторам более убедительно доносить до аудитории
их точку зрения, склонять на свою сторону.
Мыслить логично – значит мыслить точно и последовательно,
не допускать противоречий в своих рассуждениях, уметь
вскрывать логические ошибки.
Сократ много размышлял и не боялся высказывать то,
о чём он думал.
Однажды он воскликнул: «Я знаю, что ничего не знаю!»
Законы развития есть у природы, общества, любой сложной системы и, конечно же, у самого мышления.
Существует даже мнение, что всякое движение нашей мысли, постигающей истину, добро и красоту, опирается на логические законы. Мы можем не осознавать их, но вынуждены всегда следовать этим законам, чтобы жить в обществе, общаться с людьми, понимать их и быть понятыми.
2. Сообщение ученика об Аристотеле. (презентация)
Логика – одна из древнейших наук.
В основе современной логики лежат учения, созданные еще древнегреческими мыслителями, хотя первые учения о формах и способах мышления возникли в Древнем Китае и Индии. Основоположником формальной логики является величайший древнегреческий философ Аристотель (IV в. до н.э.). Именно он впервые отделил логические формы мышления (речи) от его содержания, подробно разработал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления.
Логика (от греч. «logos», означающего слово, смысл, понятие, рассуждение, разум) –
наука о законах, формах и операциях правильного мышления.
Логика — это наука о формах и способах мышления. Это учение о способах рассуждений и доказательств.
Законы мира, сущность предметов, общее в них мы познаем посредством абстрактного мышления.
Логика позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны.
Основные формы абстрактного мышления:
Понятие — это форма мышления, которая выделяет существенные признаки отдельного предмета или класса предметов, позволяющие отличать их от других. Всякое понятие имеет содержание и объём.
Пример : Понятие «Черное море» — отражает единичный предмет
Понятие « компьютер» объединяет множество электронных устройств, которые предназначены для обработки информации и обладают монитором и клавиатурой.
Содержание понятия – совокупность существенных признаков множества, отраженных в этом понятии. Примеры:
Содержание понятия «ромб» является совокупность двух существенных признаков: быть параллелограммом и иметь равные стороны.
Содержание понятия «ученик» включает в себя признаки: познавать новое и иметь учителя.
Содержанием понятия «хороший ученик» включает в себя признаки: познавать новое, иметь учителя, иметь интерес к учебе, быть исполнительным, быть обязательным, быть воспитанным, помогать отстающим. К этой категории может относится и не отличник.
Объём понятия – множество предметов, которые мыслятся в понятии.
Примеры:Под объёмом понятия «тигр» подразумевается множество всех тигров, которые существовали, существуют и будут существовать.
Объём понятия ученик «ученик» включает в себя людей, которые когда-либо учились (в частности, «чему-нибудь и как-нибудь»), учатся сейчас или будут учиться когда-нибудь.
ИГРА: цель игры – определить содержание и объём понятий, заданных в виде изображений.
Развернуть монитор так, чтобы ученикам не был виден экран, вызвать одного ученика к этому монитору, открыть папку с картинками. Ученик, рассмотрев картинку, должен её описать, стараясь называть только самые существенные признаки, по одному. Класс должен угадать (желательно, чтобы характеристик было как можно меньше и самое главное).
Например: Фото котёнка – его существенным признаком – домашнее животное, пушистое, ласковое, любит молоко, игривое….
Изображение стрекозы, собачки …..
Итог: не всегда ученики могут выделить признаки предмета, а это главное при изучении чего-то нового, определить суть – понятие.
Релаксирующая пауза
(упражнения для снятия мышечной усталости и напряжения глаз)
Наглядная геометрическая иллюстрация объёмов понятий отношений между ними была предложена математиком, физиком и астрономом Леонардом Эйлером (1707 — 1781) и носит название кругов Эйлера.
Рассмотрим пример:
К — множество учеников вашего 10 класса.
С – множество спортсменов.
Л – множество учеников, увлекающихся литературой.
Х — множество учеников, которые хорошо учатся и отдыхают летом на море.
Предположим, что среди учеников, составляющих множество Х, нет ни одного, занимающегося спортом, т.е. множества Х и С не имеют общих элементов.
И – множество учеников, которые знают три иностранных языка. Это множество будет пустым, т. К. полиглотов в вашем классе нет.
В конце XIX века англ. ученый Джордж Венн усовершенствовал круги Эйлера, добавив к изображению объёма рассматриваемого понятия А изображение объёма логически противоположного ему понятия НЕ А ( А ).
Высказывание является повествовательным предложением, в котором что-либо утверждается или отрицается.
По поводу высказывания можно сказать, истинно оно или ложно.
Истинным будет высказывание, в котором связь понятий правильно отражает свойства и отношения реальных вещей.
Ложным высказывание будет в том случае, когда оно противоречит реальной действительности.
Пример : Истинное высказывание: «Буква «е» — гласная».
Ложное высказывание: «Компьютер был изобретен в середине XIX века».
Разумеется, не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения «ученик десятого класса» и «информатика — интересный предмет»!
Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределенное понятие «интересный предмет».
Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла.
Предложения типа «в городе А более миллиона жителей», «у него голубые глаза» не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения, о каком конкретно городе или человеке идет речь.
ВЫСКАЗЫВАНИЯОбщие
Частные
Единичные
Начинаются со слов:
все, всякий, каждый,
ни один, любой…
Начинаются со слов:
некоторые, большинство, многие…
Например:
А – первая буква алфавита
Тренировочные упражнения по определению истинности или ложности высказываний.
Упражнение 1 (устно): Какие из предложений являются высказываниями?
Москва – столица РФ. — высказывание
Алуштинский дворец (Ласточкино гнездо) находится в Крыму.
5-9+8
5-9+8 = 4 — высказывание
На юге Африки живут пингвины. — высказывание
Упражнение 2 (устно): Какие из предложений являются высказываниями, а какие нет?
Какие из высказываний истинные, а какие ложные?
Учить второй иностранный язык легче, чем первый.
Обязательно займись каким-либо видом спорта. – не являются
Переводчик должен знать хотя бы два языка.
Ты играешь в хоккей? — не являются
Вычти из неизвестного 5 – получишь 2. — не являются
К концу 11 класса хорошо выучу русский язык.
Упражнение 3 (устно): Какие из предложений являются высказываниями? Определите их истинность.
Какой длины эта лента?
Прослушайте сообщение.
Делайте утреннюю зарядку!
Назовите устройство ввода информации.
Кто отсутствует?
Париж — столица Англии.
Число 11 является простым.
8. 4+5= 10.
9. Без труда не вытащишь и рыбку из пруда.
Сложите числа 2 и 5.
Некоторые медведи живут на севере.
Все медведи — бурые.
Чему равно расстояние от Москвы до Ленинграда.
Умозаключение позволяет на основе известных фактов, выраженных в форме суждений (высказываний), получать новое знание.
Умозаключение — это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение (знание или вывод).
Умозаключения бывают:
Все ученики ходят в школу. Витя – ученик. Витя ходит в школу.
Банан и персик – сладкие. Значит, все фрукты сладкие на вкус.
Аналогия: Наши коровы едят траву и дают молоко. В Австралии есть поля, коровы едят эту траву. Следовательно, австралийские коровы тоже дают молоко.
Еще в древности было известно рассуждение, ставшее классическим образцом верного логического умозаключения:
Все люди смертны.
Сократ — человек.
————————-
Сократ смертен.
Пример : Дано высказывание: «Все углы равнобедренного треугольника равны».
Получить высказывание «Этот треугольник равносторонний» путем умозаключений.
В качестве закрепления умозаключения: Сделайте вывод из пары посылок:
Все антилопы стройные.
Стройные животные радуют глаз.
Все _____________ радуют глаз.
Электронный тест для закрепления усвоенных знаний. (с выставлением оценки)
Электронное пособие по теме «Основы логики» используется для обучения и тестирования в образовательных учреждениях или в качестве самоучителя.
Включает 3 программы: основная Logika_2.4.5_C – предназначена для обучения, самопроверки и контроля,
две дополнительные TaskEditor_C – редактор заданий;
TestEditor_C – редактор тестов, можно применить для создания или изменения обучающих заданий и контрольных тестов к программе Logika_2.4.5_C.
Подведение итогов урока, оценивание, рефлексия.
На столах ребят лежат карточки самооценки, в которых они надо проставят крестик в нужной строке.
-
Ничего не понял.
Многое не понял.
Понял, но не всё.
Всё понял, другим объяснить не могу.
Всё понял, могу объяснить другим.
infourok.ru
| Высказывание | Лев | Лиса | Зебра | Кролик | |
| A | Зверь полосатый | ||||
| B | Зверь хищный | ||||
|
| |||||
|
| |||||
| А В | |||||
| А В | ФИО обучающегося | «5» | «4» | «3» | «2» |
| 1. | |||||
| 2. | |||||
| 3. | |||||
| 4. |
doc4web.ru
9 класс: Формы и законы мышления
В мышлении жизни сила,
Дыхание и свет.
Без мысли – мрак могилы,
И жизни нет. (В.Блейк)
Логика – наука, изучающая формы и законы мышления. (греч. «logos» — мысль, разум).
Историческая справка. Этапы развития логики.
 1 этап — формальная логика. Основатель – Аристотель (384-322 гг.до н.э.), ввел основные формы абстрактного мышления.
1 этап — формальная логика. Основатель – Аристотель (384-322 гг.до н.э.), ввел основные формы абстрактного мышления.
2 этап – математическая логика. Основатель – немецкий ученый и философ Лейбниц (1642-1716), предпринял попытку логических вычислений.
3 этап – математическая логика (булева алгебра). Основатель – английский математик Джордж Буль (1815-1864), ввел алфавит, орфографию и грамматику для математической логики.До 20-х годов ХХ века логика развивалась в направлении формализации и каталогизации правильных способов рассуждений.
Классическая (двузначная) логика – это первая ступень развития формальной логики.
Вторая ступень – символическая (математическая) систематизирует формы мышления, применяя математические методы и специальный аппарат символов. Исследует содержательное мышление с помощью исчислений.Алгебра логики (булева алгебра, алгебра высказываний)– это математический аппарат, с помощью которого записывают (кодируют), упрощают, вычисляют и преобразовывают логические высказывания.
Математическая логика — система обозначений и правил, применимая ко всевозможным объектам, от чисел до предложений, и позволяющая закодировать высказывания с помощью символов своего языка, а затем манипулировать ими.
Что такое познание? Познание как процесс отражения объективного мира сознанием человека представляет собой единство чувственного и рационального познания.
Формы чувственного познания: ощущение, восприятие, представление. Таким образом, чувственное восприятие мира происходит через органы чувств – приемников информации. Чувственное познание дает нам знание об отдельных предметах, их внешних свойствах. Мы познаем явление, но не сущность.
Рациональное познание – познание с помощью разума, мышления.
Законы мира, сущность предметов и явлений, общее в них мы познаем посредством абстрактного мышления – более сложной формы познания. Абстрактное или рациональное мышление отражает мир и его процессы глубже и полнее, чем чувственное познание. Переход от чувственного познания к абстрактному мышлению – скачок в процессе познания, скачок от познания фактов к познанию законов.
Формы мышления: понятия, высказывания, умозаключения. Понятие – это форма мышления, отражающая существенные признаки объекта или класса объектов.
Существенные признаки – основные, самые важные, самые известные признаки объекта, по которым предмет можно отличить от других предметов. Остальные признаки являются второстепенными. Высказывание — это форма мышления, выраженная повествовательным предложением, в которой что-либо утверждается или отрицается об объектах, их свойствах или отношениях. Высказывание может принимать только одно из двух логических значений – истинно (1) или ложь (0). Истина – есть адекватное отражение действительности.Умозаключение — форма мышления, посредством которой из одного или нескольких суждений (посылок) по определенным правилам вывода получается новее суждение (заключение).
Для информационных процессов характерны определенные общие закономерности, связанные с сутью накопления, обработки и передачи различных видов информации. Суть единства этих процессов состоит в том, что информация в любых ее формах и проявлениях – это некоторое отражение действительности в форме знаков или сигналов. И накопление, обработка и передача информации с помощью компьютеров должны подчиняться тем же законам, которым подчиняются эти процессы в общении и деятельности людей.
Законы логики:Объективны, универсальны, имеют общечеловеческий характер.
Взаимопонимание в общении человека с человеком и человека с компьютером основывается на соблюдении закона тождества. Предмет обсуждения должен быть строго определен и не должен меняться до конца обсуждения.При несоблюдении закона тождества возникают разночтения и, как следствие, несогласованность в действиях людей из-за различного толкования цели совместной деятельности или предмета обсуждения. Расплывчатые формулировки, неточности, неопределенности или двусмысленности в утверждениях приводят к противоречиям, которые могут стать непреодолимым препятствием в совместной работе и мешать достижению взаимопонимания.
Проблемы взаимопонимания возникнут при создании экспертных систем, которые должны строится на базе определенных информационно-логических моделей. Различия же в определениях понятий, в выборе формализованных представлений могут послужить причиной рассогласования данных между различными экспертными системами и пользователями этих систем. В сфере производственной деятельности закон тождества преломляется в требования точности и однозначности любой технической информации – чертежей, документации, технических заданий. Эти же проблемы характерны и для разработки программ для компьютеров. По отношению к компьютерам однозначность и точность формулировок, требований, понятий должны становиться, по существу, математическими, т.е. не допускающими двойных толкований.Недопустимость двойных, противоречивых толкований в суждениях выражается законом противоречия.
Не могут быть одновременно истинны утверждение и его отрицание. Противоречия в формальных построениях, чертежах, проектах делают невозможной их реализацию. Для успешного осуществления необходимо привести их в соответствие с законами природы, техническими или иными требованиями. (Экспертные системы)Сложную логическую проблему: что же истинно – суждение или его отрицание разрешает закон исключенного третьего. Истинно либо суждение, либо его отрицание.
Применение данного закона является движущей силой в экспертных системах, т.к. эти системы пытаются на самом деле доказать, что для заданных вопросов нет соответствующих фактических данных. В ходе этой попытки опровержения осмысленности вопросов экспертные системы находят или выводят требуемое. Принцип категоричности. Всякое рассуждение необходимо доводить до определенного утверждения или его отрицания. Этот принцип выражает требование к логической завершенности рассуждений и построений. В программировании нарушениями этого принципа является разработка программ без технических заданий и описаний, по отношению к которым программы должны проверяться. Требуется наличие строгих и точных спецификаций программ, постановок задач, технических описаний проектируемых автоматизированных систем.Закон достаточного основания. Утверждения необходимо обосновывать исходя из суждений, истинность которых доказана.
Принцип доказательности. Всякое построение (предложение) должно иметь строгое обоснование, опирающееся на точно установленные факты или положения.
Любое утверждение должно предполагать наличие аргументов и фактов, достаточных для его обоснования. Достоверность информации, получаемой от компьютера, будет зависеть в соответствии с законом от правильности данных, накапливаемых в его памяти, и от правильности программ, организующих обработку этих данных.
В программировании – это необходимость строгого обоснования правильности и надежности разрабатываемых алгоритмов и программ. Правильность алгоритмов и качество получаемых программ не должны приниматься на веру, а должны доказываться с помощью законов логики, методов представления и обработки информации, а также знания технических возможностей вычислительных машин.Делаем вывод. Из всего перечисленного можно сделать вывод, что главными вопросами в информатике являются достоверность получаемой информации и правильность используемых алгоритмов обработки информации. Понимание и соблюдение перечисленных законов логики и информатики необходимы сегодня для успешной организации совместной деятельности людей, а также для эффективного предоставления информации с помощью вычислительных машин.
irdomracheva9kl.blogspot.com
Презентация к уроку законы логики
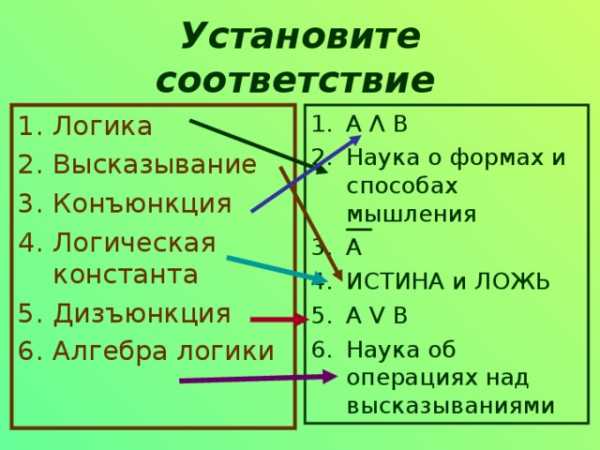
Установите соответствие
- Логика
- Высказывание
- Конъюнкция
- Логическая константа
- Дизъюнкция
- Алгебра логики
- А Λ В
- Наука о формах и способах мышления
- А
- ИСТИНА и ЛОЖЬ
- А V В
- Наука об операциях над высказываниями

Растение, знающее практически каждого.
Хрен
Под каким деревом сидит заяц, когда идет дождь?
Под мокрым
Когда человек бывает в комнате без головы?
Когда высовывает ее из окна на улицу
Сколько месяцев в году имеют 28 дней?
Все месяцы



Переместительный
Дизъюнкция:
X Y ≡ Y X
Конъюнкция:
X Y ≡ Y X

Основные законы алгебры высказываний
Сочетательный
Дизъюнкция:
X (Y Z) ≡ (X Y) Z
Конъюнкция:
X (Y Z) ≡ (X Y) Z

Распределительный
Дизъюнкция:
X (Y Z) ≡ X Y X Z
Конъюнкция:
X (Y Z) ≡ (X Y) (X Z)

Основные законы алгебры высказываний
Правила де Моргана
Дизъюнкция:
¬ (X Y) ≡ ¬ X ¬ Y
Конъюнкция:
¬ (X Y) ≡ ¬X ¬ Y

Основные законы алгебры высказываний
Идемпотенции
Дизъюнкция:
X X ≡ X
Конъюнкция:
X X ≡ X

Основные законы алгебры высказываний
Поглощения
Дизъюнкция:
X (X Y) ≡ X
Конъюнкция:
X (X Y) ≡ X
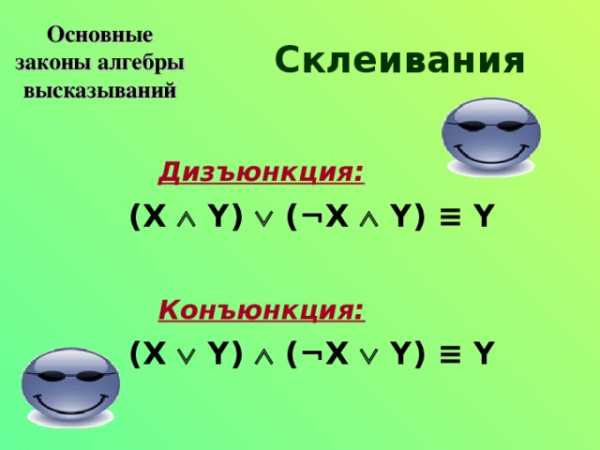
Основные законы алгебры высказываний
Склеивания
Дизъюнкция:
(X Y) ( ¬ X Y) ≡ Y
Конъюнкция:
(X Y) ( ¬ X Y) ≡ Y

Основные законы алгебры высказываний
Переменная со своей инверсией
Дизъюнкция:
X ¬ X ≡ 1
Конъюнкция:
X ¬ X ≡ 0

Основные законы алгебры высказываний
Операция с константами
Дизъюнкция:
X 0 ≡ X, X 1 ≡ 1
Конъюнкция:
X 0 ≡ 0, X 1 ≡ X

Основные законы алгебры высказываний
Двойного отрицания
¬(¬ X) ≡ X
Х = Х

Закон контрапозиции (правило перевертывания)
┐ (А→В) = А&┐В
┐ А&(АÚВ)= ┐А&В
АÚ┐А&В=АÚВ

Порядок действий
- Действия в скобках
- Отрицание
- Конъюнкция
- Дизъюнкция
- Импликация
- Эквивалентность


Выполни гимнастику для глаз по схеме:





УПРОСТИТЬ ВЫРАЖЕНИЕ
- ДАНО ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕ
Х ^ У ^ (Х ^ У)=
= Х ^ Х ^ У ^ У=
0 ^ У = 0
ЗАКОН де МОРГАНА
Переменная * на переменную = сама переменная
Переменная со своей инверсией = 0
ИСПОЛЬЗУЯ ПЕРЕМЕСТИТЕЛЬНЫЙ ЗАКОН, ПОЛУЧИМ
Учитывая это, получим

УПРОСТИТЬ ВЫРАЖЕНИЕ
Х ^ У v Х ^ У v Х=
распределительный
ЗАКОН де МОРГАНА
= Х ^ (У v У) v Х=
Х v Х=1
1
Х
 (B ∙A) «
(B ∙A) «
УПРОСТИТЬ
1. ¬ (А ∙В ∙С)+ ¬ ¬ ( А +В +¬С) 2. ¬ (А + В) = (B ∙A)
videouroki.net
9 класс Контрольная работа по теме «Законы алгебры логики»
Проверочная работа по теме «Логика»
1 вариант
1. Дана логическая функция F (a, b) = (a v ¬b) (b a).
а) Составьте таблицу истинности для данной логической функции.
б) Постройте схему для логической функции и упростите ее.
2. Дана логическая схема. Составьте логическую функцию, которая ей соответствует.
а
3. Постройте схему для логической функции F (a, b, c) = (¬a v b) &¬c v ¬(a & c).
Проверочная работа по теме «Логика»
2 вариант
1. Дана логическая функция F (a, b) = (¬a b) v ¬ (a v b).
а) Составьте таблицу истинности для данной логической функции.
б) Постройте схему для логической функции и упростите ее.
2. Дана логическая схема. Составьте логическую функцию, которая ей соответствует.
а
3. Постройте схему для логической функции F (a, b, c) = (¬a & ¬b) &(c v ¬a) & c.
Проверочная работа по теме «Логика»
3 вариант
1. Дана логическая функция F (a, b) = ¬ (a b) (a v ¬b).
а) Составьте таблицу истинности для данной логической функции.
б) Постройте схему для логической функции и упростите ее.
2. Дана логическая схема. Составьте логическую функцию, которая ей соответствует.
3. Постройте схему для логической функции F (a, b, c) = ¬ (a v b) & (c v ¬a) & b v c.
infourok.ru
Логика 8-9 класс (Законы булевой алгебры и упрощение логических выражений)
Тема: «Законы булевой алгебры и упрощение логических выражений»
Цели урока:
Образовательные: познакомить учащихся с законами логики; совершенствовать, развивать и углублять знания и умения по теме «Логические основы построения компьютера»; проконтролировать степень усвоения учебного материала. сформулировать правила преобразования логических выражений; научить учащихся приводить логическое выражение к нормальной форме; продолжить работу по подготовке к ЕГЭ, способствовать развитию у учащихся логического мышления.
Развивающие: развивать внимание, память, речь, мыслительную деятельность учащихся, умения анализировать, обобщать и наблюдать, сравнивать, выделять главное, делать выводы.
Воспитательные: стимулировать познавательную деятельность учащихся, привить интерес к предмету.
Задачи учителя:
сформировать у учащихся умение определять в сложной формуле действие различных законов; сформировать у учащихся умение применять законы булевой алгебры для упрощения логических выражений.
Требования к знаниям и умениям:
Учащиеся должны знать:
-правила преобразования логических выражений и законов логики.
Учащиеся должны уметь:
— упрощать логические выражения ;
— уметь решать логические задачи, сформулированные на обычном языке.
Тип урока: комбинированный урок.
Ход урока:
Организация начала занятия.
Проверка домашнего задания.
Разминка. Подготовка учащихся к восприятию материала на основном этапе занятия. Постановка проблемы.
Изложение материала
Закрепление изученного.
Подведение итогов урока.
Рефлексия деятельности и поведения.
Информация о домашнем задании.
Организационный этап.
Приветствие учителем учащихся, выявление отсутствующих, проверка подготовленности к уроку, организация внимания.
Этап проверки домашнего задания.
Фронтально проверяется задание, записанное в тетради:
Построить таблицу истинности функции F:
F=(
Решение:
| A | B | C |
|
|
|
|
|
| F |
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
Разминка. Подготовка учащихся к восприятию материала на основном этапе занятия.
Учитель:
Давайте в качестве разминки решим несколько задач по мат. логике из демо-версий ЕГЭ прошлых годов.
Для какого числа X истинно высказывание
A9. ((X3) \/(X (X
Учитель: Проверим все 4 возможных варианта значения Х и выберем из них тот вариант, когда значением выражения будет истина. Вызывает ученика к доске.
Решение:
Х=1
Выражение будет иметь вид: ((13) \/(1 (1 0 , откуда 1 – 0=0
Х=2
Выражение будет иметь вид: ((23) \/(2 (2 0 , откуда 1 – 0=0
Х=3
Выражение будет иметь вид: ((33) \/(3 (3 0 , откуда 0 – 0= 1
Х=4
Выражение будет иметь вид: ((43) \/(4 (4 0 , откуда 1 – 0=0
Ответ: верный ответ № 3.
A11. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
| X | Y | Z | F |
| 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
Какое выражение соответствует F?
| 1) | ¬X \/ Y \/ ¬Z |
| 2) | X /\ Y /\ ¬Z |
| 3) | ¬X /\ ¬Y /\ Z |
| 4) | X \/ ¬Y \/ Z |
Учитель: Составим таблицы истинности для каждого высказывания, и сравним результат с F.
| X | Y | Z | ¬X | ¬Y | ¬Z | ¬X \/ Y \/ ¬Z | X /\ Y /\ ¬Z | ¬X /\ ¬Y /\ Z | X \/ ¬Y \/ Z | F |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
Ответ: верный ответ 2
В2. Каково наибольшее целое число X, при котором истинно высказывание
(90X·X) – (X X -1)) ?
Вспомним таблицу истинности импликации. Импликация истинна в трёх случаях:
0→0;
0→1;
1→1;
Рассуждаем, т.к. вторая часть выражения X X -1) всегда ложна, остается только первый случай. (0→0) ; Т.о наибольшее целое число X, при котором 90X·X ложно равно 9
A10. Какое логическое выражение равносильно выражению ¬ (A /\ B) /\ ¬C?
| 1) | ¬A \/ B \/ ¬C |
| 2) | (¬A \/ ¬B) /\ ¬C |
| 3) | (¬A \/ ¬B) /\ C |
| 4) | ¬A /\ ¬B /\ ¬C |
Решение: (способ1).
Учитель: Каким способом мы можем решить эту задачу?
Ученики: Построим таблицы истинности для каждого из выражений, и сравним результаты
По заданию:
| А | В | С | A /\ B | ¬ (A /\ B) | ¬C | ¬ (A /\ B) /\ ¬C |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
.
Вариант1
| А | В | С | ¬A | ¬C | ¬A \/ B | ¬A \/ B \/ ¬C |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
Вариант2
| А | В | С | ¬A | ¬B | ¬C | ¬A \/ ¬B | (¬A \/ ¬B) /\ ¬C |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
Вариант3
| А | В | С | ¬A | ¬B | ¬C | ¬A \/ ¬B | (¬A \/ ¬B) /\ C |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
Вариант4
| А | В | С | ¬A | ¬B | ¬C | ¬A /\ ¬B | ¬A /\ ¬B /\ ¬C |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
Вывод: сравнивая таблицы мы пришли к выводу, что верный вариант 2
Учитель: А как вы думаете ребята, не показалось ли вам решение этой задачи слишком громоздким? Я, например, сразу могу сказать вам ответ этой задачи, не строя таблицы истинности. Как вы думаете, каким образом?
Правильно, существуют специальные законы преобразования выражений и сегодня мы с вами рассмотрим их.
IV. Изложение нового материала:
Важно подвести ребят к самостоятельному выводу о необходимости преобразований и упрощений выражений. Если логическое выражение содержит большое число операций, то составлять для него таблицу истинности сложно, в таких случаях формулы приводят к нормальной форме, т.е. в формуле отсутствуют знаки эквивалентности, импликации, двойного отрицания. Для приведения формулы к нормальной форме используют законы логики и правила логических преобразований. Законы записаны на слайде, вывести на экран (распечатать по одному экземпляру на парту), и по мере записи на доске, ученики пишут в тетрадь.
Логические законы:
1. Независимость от перестановки мест (коммутативность)
A v B = B v A
A ^ B = B ^ A
2. Независимость от порядка выполнения однотипных действий (ассоциативность)
(A v B) v С = A v (B v С)
(A ^ B) ^ С= A ^ (B ^ С)
3. Распределительный закон относительно логического умножения и сложения (дистрибутивность)
Распределение относительно логического умножения:
(А v В) ^ C = (A ^ C) v (В ^ C). Вспомним правила раскрытия скобок в алгебре, ведь недаром операции конъюнкции и дизъюнкции называют логическим умножением и сложением. И наоборот:
(A & B) v (В & C) = В & (А v C). Похоже на вынесение общего множителя за скобки в алгебре. Распределительный закон относительно логического умножения полностью повторяет аналогичный закон алгебры.
Далее мы рассмотрим группу законов, у которых нет аналогов в алгебре, но они легко воспринимаются учащимися из-за своей наглядности.
4. Отсутствие степеней и коэффициентов (идемпотентность)
А v А = А
А ^ А = А
Если высказывание А ложно (0), то результат 0 v 0, а также 0 ^ 0 – ложь; если высказывание А истинно (1), то результат 1 v 1, а также 1 ^ 1 — истина
5. Двойное отрицание (инволюция)
¬ (¬ А) = А
Ученикам предлагается заполнить таблицу истинности и сравнить 1 и 3 столбцы
6. Действия с абсолютно-истинными и абсолютно-ложными высказываниями. Абсолютно-истинное высказывание – высказывание, которое имеет значение ИСТИНА при любых значениях входящих в него простых высказываний. Такие высказывания обозначаются константой «истина» или 1. (пример: теорема Пифагора) Абсолютно-ложное высказывание – высказывание, которое имеет значение ЛОЖЬ при любых значениях входящих в него простых высказываний. Такие высказывания обозначаются константой «ложь» или 0.
А v 1 =1 (всегда истина)
А ^1 = А
А v 0 = А
А ^ 0 = 0 (всегда ложь)
7. Закон исключенного третьего
А v ¬ А = 1 (всегда истина)
В этом выражении что-то одно всегда истина, поэтому результат логического сложения – истина (открыть учебник на странице 353 и прочитать 1 правило — подсказки )
8. Закон противоречия
А ^ ¬ А = 0 (всегда ложь)
В этом выражении что-то одно (либо А, либо ¬ А) ложно, поэтому результат логического умножения – ложь.
Далее рассмотрим группу законов, которые необходимо проверить. Проверку произведем путем построения таблиц истинности для правой и левой части законов и последующего их сравнения. для построения таблиц истинности к доске вызвать ученика.
9. Законы де Моргана
¬ (А ^ В) = ¬ А v ¬ В
¬ (А v В) = ¬ А ^ ¬ В
10. Поглощение
А v А ^ В = А
А ^ (А v В) = А
11. Поглощение отрицания
А v ( ¬ А ^ В) = А v В
А ^ ( ¬ А v В) = А ^ В
Доказать свойства поглощения и поглощения отрицания можно путем упрощения на основе свойств дистрибутивности. (Доказательство оставить для домашней работы)
Импликации и эквивалентности иногда нет среди логических операций, а при решении задач они требуются. Существуют формулы замены данных операций с использованием только операций отрицания, дизъюнкции и конъюнкции. Так, вместо операции импликации можно использовать следующее тождественное выражение:
A → B = не A V B
Для замены операции эквивалентности существует два выражения:
A равносильно B = (A * B) V (не A * не B)
A равносильно B = (A V не B) * (не A V B)
V. Закрепление изученного: упрощение логических выражений
В этой части урока учитель показывает, на примере как упрощаются выражения: и объясняет, что для успешного упрощения нужна практика. Чем больше примеров будет решено, тем вероятнее, что ученик увидит возможные варианты упрощения в конкретном выражении.
Задания:
1). Упростить логическое выражение. (Демонстрируется слайд).
_______________
_____
F = (A v B) → (B v C)
Решение (используются законы де Моргана, закон двойного отрицания, распределительный закон):
_______________ _____
_____ _____
F = (A v B) → (B v C) = A v B & (B v C) = (A v B) & (B v C) = B v (A & C)
2) Выполнение аналогичных заданий по карточкам.
Учитель: А теперь попробуем применить изученные законы для решения задач.
3) Решим задачу:
Учитель. Представим такую ситуацию: по телевизору синоптик объявляет прогноз погоды на завтра и утверждает следующее:
Если не будет ветра, то будет пасмурная погода без дождя.
Если будет дождь, то будет пасмурно и без ветра.
Если будет пасмурная погода, то будет дождь и не будет ветра.
Так какая же погода будет завтра? (Ответы учеников)
Решим эту задачу средствами алгебры логики.
Решение:
а) Выделим простые высказывания и запишем их через переменные:
A – «Ветра нет»
B – «Пасмурно»
С – «Дождь»
б) Запишем логические функции (сложные высказывания) через введенные переменные:
1. Если не будет ветра, то будет пасмурная погода без дождя:
__
A → B & C
2. Если будет дождь, то будет пасмурно и без ветра:
С → B & A
3. Если будет пасмурная погода, то будет дождь и не будет ветра
B → C & A
в) Запишем произведение указанных функций:
_
F=(A→ B & C) & (C→B & A) & (B→ C & A)
г) Упростим формулу (используются законы де Моргана, переместительный закон, закон противоречия):
_
F=(A→ B & C) & (C→B & A) & (B→ C & A)
_ _ _ _
= (A v B & C) & (C v B&A) & (B v C&A) =
_ _ _ _
= (A v B & C) & (B v C&A) & (C v B&A) =
_ _ _ _ _ _
= (A & B v B&C&B v A&C&A v B&C&C&A) & (C v B&A)=
_ _ _ _ _ _ _
= A & B &(C v B&A) =A&B&C v A&B&B&A =
_ _ _
= A&B&C
д) Приравняем результат единице, т.е. наше выражение должно быть истинным:
_ _ _
F = A & B & C = 1
е) Проанализируем результат:
Логическое произведение равно 1, если каждый множитель равен 1.
Поэтому:
_ _ _
A = 1; B = 1; C = 1;
Значит: A = 0; B = 0; C = 0;
Ответ: погода будет ясная, без дождя, но ветреная.
Учитель: Ну а теперь вернёмся к задаче:
A10. Какое логическое выражение равносильно выражению ¬ (A /\ B) /\ ¬C?
| 1) | ¬A \/ B \/ ¬C |
| 2) | (¬A \/ ¬B) /\ ¬C |
| 3) | (¬A \/ ¬B) /\ C |
| 4) | ¬A /\ ¬B /\ ¬C |
Способ 2: Применим закон де Моргана. ¬ (A /\ B) = ¬A \/ ¬B
Раскрывая скобки получаем (¬A \/ ¬B) /\ ¬C = (¬A \/ ¬B) /\ ¬C
Ответ: верный ответ №2
Этап подведения итогов учебного занятия.
Учитель задает вопрос: Так какой же способ решения легче?: (Учащиеся должны ответить, что в некоторых заданиях не нужно чертить таблиц, решение с помощью Законов алгебры логики существенно экономит время).
VII. Рефлексия
Что было легко, а что трудно?
Что было интересно, а что не затронуло?
Что нового для себя вы узнали, чему научились?
Какие компетенции Вы приобрели?
VI
www.videouroki.by







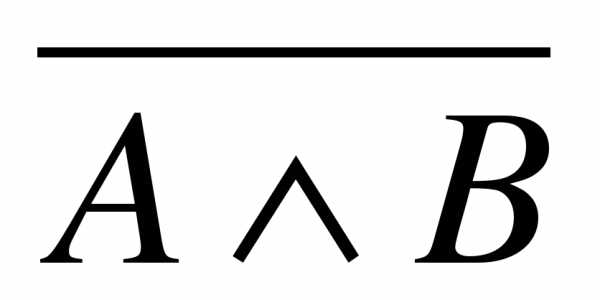
 C
C