Задания по геометрии – () - Управленческое образование - ЕГЭ, ОГЭ, общеобразовательные предметы

Содержание

Геометрия. Урок 7. Практические задачи по геометрии

Содержание страницы:

Два треугольника называются подобными, если углы одного треугольника соответственно равны углам другого треугольника, а стороны одного треугольника соответственно пропорциональны сторонам другого треугольника.

Подобие треугольников обозначается значком «∼». Запишем подобие двух треугольников:

△ABC∼△A1B1C1

Соответственные стороны двух подобных треугольников – это стороны, которые лежат напротив равных углов.

Пары равных углов:

∠A и ∠A1

∠B и ∠B1

∠C и ∠C1

Пары соответственных сторон:

BC и B1C1

AC и A1C1

AB и A1B1

Представьте себе, что на смартфоне или планшете вы открыли изображение треугольника. Вы захотели получше его рассмотреть и увеличили изображение. Сам треугольник увеличился, но его пропорции сохранились (он не сплюснулся, не вытянулся, просто стал больше). Вот такие два треугольника: исходный и увеличенный будут подобными. Масштаб увеличенной картинки изменился в k. Это число k будет являться коэффициентом подобия этих треугольников.

Коэффициент подобия k это число, равное отношению соответственных сторон подобных треугольников.

k=A1B1AB=A1C1AC=B1C1BC

Если стороны большего треугольника относить к сторонам меньшего треугольника, то коэффициент подобия k>1.

Если стороны меньшего треугольника относить к сторонам большего треугольника, то коэффициент подобия k<1.

Отношение периметров подобных треугольников равно коэффициенту подобия.

P△A1B1C1P△ABC=k

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

S△A1B1C1S△ABC=k2

Первый признак подобия треугольников (по двум углам)

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

∠A=∠A1∠B=∠B1|⇒△ABC∼△A1B1C1

Второй признак подобия треугольников (по двум сторонам и углу между ними)

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

∠A=∠A1A1B1AB=A1C1AC=k|⇒△ABC∼△A1B1C1

Третий признак подобия треугольников (по трём сторонам)

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

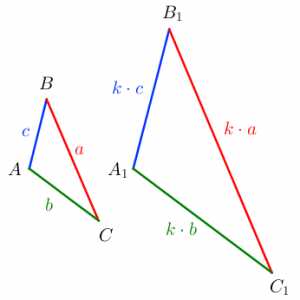
A1B1AB=A1C1AC=B1C1BC=k⇒△ABC∼△A1B1C1

В задании 17 ОГЭ встречаются задачи, в которых необходимо найти угол между часовой и минутной стрелкой. Давайте разберёмся, как их решать.

Часовой циферблат – это окружность.

Градусная мера всей окружности равна 360°.

Стрелки – стороны центральных углов.

На окружности 60 маленьких делений и 12 больших.

Каждое маленькое деление отсекает от окружности дугу, градусная мера которой равна 360°60=6°.

Каждое большое деление отсекает от окружности дугу, градусная мера которой равна 360°12=30°.

Можно рассуждать, что одна большая дуга содержит пять маленьких, то есть её градусная мера равна 6°⋅5=30°.

В задании 17 ОГЭ встречаются задачи, в которых дано колесо со спицами и требуется определить либо угол между соседними спицами (если дано количество спиц), либо количество спиц (если дан угол между соседними спицами). Будем разбираться, как такие задачи решать.

Пусть у нас есть колесо, в котором n спиц. Тогда эти спицы образуют n равных центральных углов α.

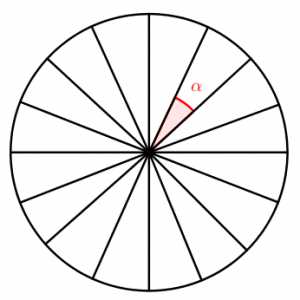
Формула, которая связывает количество спиц и угол между двумя соседними:

α⋅n=360°

В задаче данного типа дана лестница, состоящая из n ступенек. Каждая ступенька характеризуется своей высотой (вертикальный отрезок) и длиной (горизонтальный отрезок). Сама лестница характеризуется своей длиной (отрезок AC), высотой (отрезок BC) и отрезком AB.

Высота всей лестницы – количество ступенек, умноженное на высоту одной ступеньки. Длина всей лестницы – количество ступенек, умноженное на длину одной ступеньки. Для нахождения длины лестницы необходимо применить теорему Пифагора.

Теоретический и практический материал по нахождению площадей треугольников и четырехугольников можно найти в уроках 3 и 4 модуля геометрия.

Перейти по ссылкам:

epmat.ru

Примеры по геометрии 7 класс. | Геометрия

Примеры по геометрии 7 класс. | Геометрия — просто!

Добрый день!
Сегодня мы с вами разберём несколько примеров по геометрии 7 класса, которые даются в ОГЭ-2015.
Ведь действительно, Основной Государственный Экзамен — ОГЭ, рассчитан не только на знания 9 класса, но и на те знания, которые ученики получают в 7 и 8 классах по геометрии, и, начиная с 5 класса, по математике и алгебре.
Поэтому, в модуле «Геометрия» есть задачи из курса 7 класса.

Задача 1. В треугольнике АВС точка D на стороне АВ выбрана так, что АС=AD. Угол А треугольника АВС равен 16°, а угол АСВ равен 134°. Найти угол DCB.
Решение: Из треугольника ADC видно, что он равнобедренный, поскольку 2 боковые стороны его равны.
А в равнобедренном треугольнике углы при основании равны.
Значит, угол ADC равен углу АСВ.
Но сумма внутренних углов треугольника равна 180°.
Отсюда, сумма двух углов при основании равна 180-16=164°.
Углы, как мы уже сказали, равны. Поэтому, каждый из них равен 164:2 = 82°.
Угол АСВ по условию равен 134°.
А если внутри угла провести луч, то он разделит угол на 2 угла, сумма градусных мер которых будет равна градусной мере первоначального угла.
Т.е. Угол АСВ равен сумме углов АCD и DCB.
Отсюда, угол DCB равен 134 — 82 = 52°.
Ответ: угол DCB равен 52°.

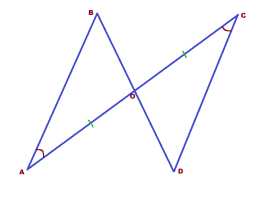Задача 2. Два отрезка АС и BD пересекают в точке О. Причём, АО=СО и ∠А=∠С. Доказать, что треугольники АОВ и OC равны.
Доказательство: В искомых треугольниках есть по одной равной стороне и одному равному углу. Значит, согласно признакам равенства треугольников, нам необходимо ещё либо по одной равной стороне, либо по одному равному углу.
Стороны как-то не проглядываются, а вот по равному углу можно ещё найти.
Углы АОВ и DOC — вертикальные.
А вертикальные углы, как мы знаем, равны.
В каждом из треугольников мы имеем по равной стороне и двум равным углам, прилежащим к ней.
Треугольники равны по 2 признаку.

Задача 3. В треугольнике АВС проведена биссектриса АК. Угол АКС равен 94°, а угол АВС равен 62°. Найти угол С треугольника АВС.
Решение: Угол АКС является внешним для треугольника АВК и равным сумме двух внутренних углов, не смежных с ним, т.е. сумме углов В и ВАК.
Отсюда мы можем найти угол ВАК.
Он равен 94 — 62 = 32°.
Поскольку АК — биссектриса угла А, то угол КАС тоже равен 32°.
А теперь, рассматривая треугольник АКС и зная в нём 2 угла, можно найти третий.
∠С = 180 — 32 — 94 = 54°.
Ответ: угол С равен 54°.

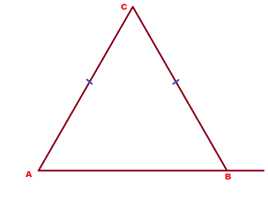Задача 4. В треугольнике АВС боковые стороны АС и АВ равны между собой. Внешний угол при вершине В равен 110°. Найти угол С.
Решение: Внешний угол В равен 110°, значит, смежный с ним внутренний угол в треугольнике равен
180-10 = 70°.
Но внутренний угол В равен углу А, как углы при основании равнобедренного треугольника. Значит, угол А равен 70°.
А сумма внутренних углов треугольника равна 180°.
И если 2 из них равны по 70, то на долю третьего угла С приходится 180 — 70 — 70 = 40°.
Ответ: угол с равен 40°.

Задача 5. В треугольнике АВС проведены высоты, которые пересекаются в точке О. Угол СОВ равен 119°. Найти угол А.
Решение: Угол ВОМ смежный углу СОМ и равен 180-119 = 61°.
Угол СМА внешний в треугольнике СМВ и равен сумме двух внутренних, не смежных с ним.
Отсюда, угол ОВМ равен 90-61 = 29°.
А из прямоугольного треугольника ВКА можно найти угол А, т.к. сумма острых углов в прямоугольном треугольнике равна 90°.
Значит, угол А равен 90 — 29 = 61°.
Ответ: угол А равен 61°.

На сегодня всё. В следующий раз мы продолжим решение геометрических задач для подготовки к ОГЭ.

Вам так же будет интересно:

Оставить комментарий

geometriyaprosto.ru

Решаем задачи по геометрии

В данном курсе приведены условия и решение задач по геометрии. Есть также некоторое количество задач из курса алгебры, если их содержание предполагало знания по геометрии.

Задачи структурированы по темам: Планиметрия, Треугольники, Четырехугольники, Многоугольники, Стереометрия и т.д. Все задачи по геометрии — с решением.

Если Вы не нашли решение задачи по геометрии интересующего Вас типа, напишите об этом в форуме — практически наверняка курс будет дополнен Вашей задачей.

Обратите внимание на то, что задача (тип задачи) решение которой Вас интересует, может находиться несколько в ином разделе, чем Вы рассчитываете. Например, в разделе «теорема синусов», если ее решение предполагает использование данной теоремы. Для решающего это не всегда очевидно.

Для ознакомления со справочной информацией, которая часто необходима для решения, например, относительно формул площади треугольника, площади параллелограмма, признаков подобия треугольников и т.д. перейдите к соответствующему разделу. Как правило, каждая глава содержит необходимую справочную информацию.

Идея курса — решение конкретных задач на примерах для получения навыков в их решении.

У даному курсі приведені умови і рішення задач з геометрії. Є також деяка кількість завдань з курсу алгебри, якщо їх вміст передбачав знання по геометрії.

Завдання структуровані по темах: Планіметрія, Трикутники, Чотирикутники, Багатокутники, Стереометрія і так далі. Всі завдання по геометрії — з рішенням.

Якщо Ви не знайшли рішення задачі по геометрії того типу, що цікавить Вас, напишіть про це на форумі — курс буде доповнений Вашим завданням.

Звернiть увагу на те, що завдання (тип завдання) вирішення якого Вас цікавить, може знаходитися декілька в іншому розділі, чим Ви розраховуєте. Наприклад, в розділі «теорема синусів», якщо її рішення передбачає використання даної теореми. Для учня це не завжди очевидно.

Для ознайомлення з довідковою інформацією, яка часто необхідна для вирішення, наприклад, відносно формул площі трикутника, площі паралелограма, ознак подібності трикутників і так далі — перейдіть до відповідного розділу. Як правило, кожна глава містить необхідну довідкову інформацію.

Ідея курсу — вирішення конкретних завдань на прикладах для здобуття навиків в їх рішенні.

profmeter.com.ua

Как решать задачи по геометрии: практические советы и рекомендации

Как решать задачи по геометрии? Многие учащиеся задаются этим вопросом на протяжении многих лет. Иногда даже сам предмет вызывает страх и отвращение из-за непонимания отдельных тем. Потом бывает очень сложно преодолеть неприязнь к геометрии и снова с заинтересованностью посещать уроки.

В чем причина

Во многом все зависит от того, как преподаватель объясняет свой предмет. Если учитель сможет заинтересовать учеников, дальше дело пойдет по накатанной, и каждый урок будет захватывающим. Дети даже будут оставаться на переменке, чтобы успеть решить как можно больше задач.

Если вам плохо объясняли этот предмет или есть еще какие-то причины, по которым у вас совершенно не получается вникнуть в тему, эта статья поможет разобраться.

Как научиться решать задачи по геометрии?

Для начала нужно понять, что за один день вы вряд ли далеко продвинетесь в своих знаниях, так что настраивайтесь на длительный процесс обучения.

Также нужно определиться с целью. Если вам нужно просто решить задачу по геометрии, чтобы не получить плохую оценку за контрольную работу, достаточно лишь выучить определенную тему и потренироваться в практических аспектах.

Что делать?

Возьмите учебник и пролистайте последние несколько параграфов, которые вы изучили. Постарайтесь вникнуть в информацию, поймите, что от этого зависит то, как будут оценены ваши знания. Теперь можете взять листочек и изучить несколько задач, обязательно смотрите в текст учебника и пытайтесь понять алгоритм решения.

Если что-то не получается, обратитесь к решебнику, который выпущен специально под ваш учебник. Только не списывайте абсолютно все, старайтесь понять, как решать задачи по геометрии.

Вспомните, о чем говорил преподаватель на занятиях, возможно, какая-то информация окажется полезной.

Не стоит пренебрегать и человеческим фактором. Хорошо знающие предмет школьники или студенты не откажут вам в помощи. Некоторые из них могут объяснить гораздо доходчивее преподавателей.

А тем, кто решил не просто разобраться в отдельных темах, а научиться решать задачи и как орешки их щелкать, нужно основательно потрудиться.

Во-первых, главное – это мотивировать себя на дальнейшие занятия. Бывает так, что вопрос о том, как научиться решать задачи по геометрии, встает лишь один раз, а потом начинается просто списывание примеров из интернета. Так делать крайне нежелательно.

Развивайте усидчивость. Посмотреть в решебник намного проще, разумеется, но подумайте, какое наслаждение вы испытаете, когда самостоятельно решите сложную задачку. Поэтому лучше лишние полчаса посидеть за учебником, чем стараться списать побыстрее чье-то решение.

Может быть, геометрия вам понадобится для будущей профессии. Тогда тем более не стоит откладывать дело в долгий ящик, нужно приниматься за задачи прямо сейчас.

Во-вторых, практика, и только она, поможет вам стать на шаг ближе к своей цели!

Заведите привычку узнавать что-то новое каждый день. Просто старайтесь с утра решать одну задачу, а потом проверяйте по ключам ее правильность. Позже заметите, что с каждым днем процесс идет все быстрее и качественнее.

Самое главное здесь – не сдаваться и не обращать внимания на мелкие трудности. Если вы включите в распорядок дня этот совет, то вопрос о том, как решать задачи по геометрии, отпадет сам собой.

В-третьих, обращайтесь за помощью к знакомым.

Не бойтесь в школе лишний раз поднять руку и выйти к доске, чтобы решить сложный пример, который никто не отважился постичь. Даже если что-то пойдет не так, и вам не удастся сделать задание, ничего страшного в этом нет. Преподаватель объяснит решение примера и даже похвалит вас за смелость. Также это неплохой способ показать свои знания одноклассникам.

Ребята могут помочь с выполнением заданий, когда узнают, что вы настроены серьезно в изучении предмета.

Не вешаем нос!

Не отчаивайтесь, если никто не откликнулся на вашу просьбу. Всегда можно обратиться за помощью к репетитору, который точно объяснит, как решить задачу по геометрии. Даже при ограничении в денежных средствах хорошим выходом станут занятия по скайпу, которые ничем не хуже уроков, проходящих при личной встрече.

Вот и все советы. Будем надеяться, что вы все-таки поняли, как решать задачи по геометрии. В любом случае старайтесь применять эти методы на практике, и вы осуществите задуманное!

fb.ru

Задачи по геометрии

Дата: марта 14, 2018 Автор: balu

На сколько частей делит пространство лента Мёбиуса бесконечной ширины?

Дата: декабря 5, 2017 Автор: balu

С помощью циркуля и линейки построить окружность, касающуюся двух данных окружностей, причем одной из них в данной точке.

Дата: апреля 21, 2017 Автор: balu

Город имеет форму круга радиуса R. По всей площади города магазины торговой сети расположены равномерно. Расстояние от центра города до распределительного центра сети равно r. Найти среднее расстояние от распределительного центра до магазина сети.

Дата: апреля 15, 2017 Автор: balu

Квадрат ABCD и правильный пятиугольник BEFGC имеют общую сторону BC. Вершины квадрата A и D лежат вне пятиугольника. Найти угол между отрезками AG и FD.

_{http://blog.kknop.com/2017/03/blog-post.html}

Дата: марта 5, 2017 Автор: balu

Метеорит падает на сферическую Землю радиусом R под углом ѳ к отвесу со скоростью V и упруго (без потери энергии) отскакивает. В каком случае (при каком соотношении параметров) метеорит, попрыгав. вернётся в точку падения? (Допустим, g не меняется с высотой).

_{Е.Скляревский}

Дата: февраля 26, 2017 Автор: balu

Проведем прямую AQ. С центром в точке O на ней построим окружность диаметром 3 так, что |AO|=1,5 (красная окружность). Отметим на прямой точку K так, что |AK|=1. Проведем через точку K под произвольным углом прямую, пересекающую окружность в точках G и E. Очевидно, в любом случае |GK|*|GE|=2. Построим с центром на прямой AQ окружность диаметром 17, касающуюся первой окружности в точке A (фиолетовая окружность). Пусть прямая GE пересекает вторую окружность в точках B и C. Очевидно, в любом случае |BK|*|CK|=16. Вращая прямую GE вокруг точки K можно найти такое ее положение, что |KE|=2^(1/3), а |GK|=2^(2/3), т.е. |GK|=|EK|^2. Вращая прямую BC вокруг точки K можно найти такое ее положение, что |KC|=2*2^(1/3), а |GE|=4*2^(2/3). С помощью гомотетии с коэффициентом 2 и центром в точке K построим синюю окружность. Точка C пересечения синей и фиолетовой окружности будет обладать замечательным свойством |KE|=|CK|=2^(1/3). Проверим наше построение с помощью окружности, полученной с помощью гомотетии с центром в точке K и коэффициентом 4 (зеленая окружность). На её пересечении с фиолетовой окружностью находится точка B такая, что |BK|=4*|GK|=4*2^(2/3), т.е. |BK|=|CK|^2. Легко убедиться, что точки B, K и E лежат на одной прямой.

Однако, почему не ликуют древние греки? Ведь мы построили отрезок, равный кубическому корню из 2, решив таким образом задачу об удвоении куба! Возможно, в наше построение вкралась ошибка? Найдите её.

Дата: февраля 6, 2017 Автор: balu

Дана окружность с отмеченной на ней точкой А и точка В вне окружности. Найти параболу (построив ее директрису) с фокусом в точке В, касающуюся окружности в точке А.

Дата: ноября 9, 2016 Автор: balu

В просторном зале, стоя на полу, вы видите на полу отражение светильника, подвешенного под потолком. Пусть ваш рост h, высота потолка H, расстояние между вами и точкой на полу под светильником S. Вы двигаетесь в направлении светильника со скоростью V. С какой скоростью вы догоняете отражение светильника? С какой скоростью отражение светильника движется к точке под светильником?

Дата: июня 30, 2016 Автор: balu

На плоскости построены два отрезка длинами a и b. С помощью циркуля и двух прямых углов (например, в виде школьных угольников) построить отрезки длинами c и d — два средних пропорциональных отрезка к данным a и b, т.е. чтобы выполнялось соотношение a:c = c:d = d:b.

Дата: июня 26, 2016 Автор: balu

Из точки, где плоскость, наклоненная под углом α к горизонту, сопрягается с горизонтальной плоскостью, выстрелили шариком под углом β к горизонту. Каким должен быть угол β, чтобы шарик, отскочив от наклонной плоскости, вернулся в точку выстрела?

_{Е. Скляревский}

Дата: июня 23, 2016 Автор: balu

Две окружности равного радиуса с центрами в точках О и О1 имеют общую хорду АВ. Из точки О проведен в произвольном направлении отрезок, пересекающий хорду AB, затем пересекающий окружность O в точке С и окружность О1 в точке D. Пусть М – середина отрезка CD. Доказать (или опровергнуть), что геометрическим местом точек M является дуга окружности.

Дата: июня 18, 2016 Автор: balu

Дана окружность и в ней центральный острый угол альфа. Построить угол, равный третьей части альфа, используя циркуль и линейку, на которой можно делать засечки, так, чтобы все построения не выходили за пределы окружности.

Дата: января 2, 2016 Автор: balu

В горизонтальной плите имеются два параллельных желоба полукруглого сечения радиуса R. Центры полукружий находятся в плоскости поверхности плиты на расстоянии L

Дата: января 2, 2016 Автор: balu

На наклонной плоскости два ткача придерживают два совершенно одинаковых рулона ткани. Одновременно отпускают. Один рулон скатывается со склона как цельный цилиндр, а второй во время спуска разматывается. Скольжение отсутствует. Какой рулон скатится быстрее?

Дата: января 1, 2016 Автор: balu

В горизонтальной металлической плите имеется лунка в форме полусферы радиусом R. Стержень длиной L лежит одним концом в лунке, второй конец торчит. Трение между стержнем и лункой отсутствует. Найти угол стержня к горизонту.

_{форум www.dxdy.ru}

geom.uz

Пять по геометрии

Хорошо ли вы помните школьную математику? А как с логикой и пространственным мышлением? Предлагаем вам попробовать свои силы и решить пять не самых очевидных задач по геометрии, которые подобрали для нас специалисты Московского центра непрерывного математического образования. Если вам понравится, вы можете продолжить — на сайте центра в открытом доступе выложены 10 тысяч геометрических задач.

1. По неподвижной окружности, касаясь ее изнутри, катится без скольжения окружность вдвое меньшего радиуса. Траектория фиксированной точки подвижной окружности лежит на:

Окружности
Прямой
Ломаной линии
Эллипсе
Кривой четвертого порядка

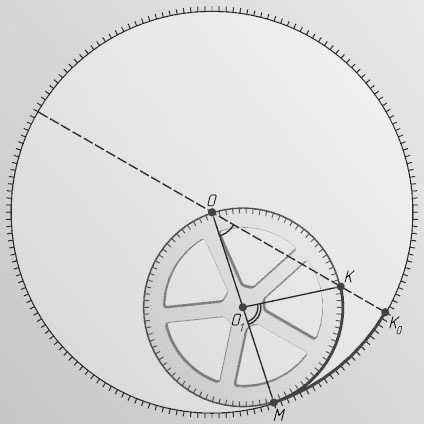
Правильно!

Это прямая. Решается задача так: пусть O —‍ центр неподвижной окружности, K‍₀ —‍ первоначальная точка касания окружностей, O‍₁ —‍ новый центр катящейся окружности, M —‍ новая точка касания, K —‍ движущаяся точка. Тогда дуга MK‍₀ = дуге MK.‍ Поэтому угол MO_‍1K = двойному углу MOK_‍0.‍ Следовательно, точка K‍ лежит на прямой OK‍₀.‍

Неправильно!

2. По стороне правильного треугольника катается окружность радиуса, равного высоте треугольника, причем противоположная этой стороне вершина треугольника все время находится внутри окружности. Как при этом меняется величина дуги, высекаемой на окружности сторонами треугольника?

3. На столе лежат двое плоских часов. И те, и другие идут точно, но не обязательно показывают одинаковое время. По какой линии движется середина M отрезка, соединяющего концы их минутных стрелок?

Эллипс
Ромб
Окружность
Отрезок

Правильно!

Это окружность. Пусть O_‍1‍ и O_‍2 —‍ центры часов, P‍₁‍ и P_‍2‍ соответственно — концы минутных стрелок, O‍ и M —‍ середины отрезков O_‍1O_‍2‍ и P_‍1P‍₂‍ соответственно. Рассмотрим параллелограммы P_‍1O‍₁OA‍ и P_‍2O‍₂OB.‍ Из равенства треугольников MP_‍2B‍ и MP_‍1A‍ (по двум сторонам и углу между ними) следует равенство углов BMP_‍2‍ и AMP_‍1,‍ поэтому точки A,‍ M‍ и B‍ лежат на одной прямой, причем M —‍ середина отрезка AB.‍ Стороны OA‍ и OB‍ треугольника AOB‍ соответственно равны и параллельны отрезкам O_‍1P_‍1‍ и O_‍2P‍₂.‍ Эти отрезки с одинаковой угловой скоростью (1 оборот в час) вращаются вокруг точек O_‍1‍ и O_‍2,‍ значит, медиана OM‍ треугольника AOB‍ вращается с той же угловой скоростью вокруг точки O.‍ Следовательно, точка M‍ движется по фиксированной окружности с центром O‍ и радиусом, равным медиане OM.‍

Неправильно!

4. Прямоугольный лист бумаги ABCD согнули так, что его вершина C совпала с серединой C_‍1 стороны AD, как показано на рисунке. Чему равно отношение CK : KD?

Однозначного ответа нет, он зависит от отношения сторон исходного прямоугольника
‍√3
2
2,25
√5

Правильно!

Отрезок СК вдвое длиннее. Из условия следует, что треугольники BC_‍1K‍ и BCK‍ равны, значит, BC_‍1 = BC,‍ C_‍1K = CK.‍ В прямоугольном треугольнике ABC‍₁‍ катет AC‍₁‍ равен половине гипотенузы BC_‍1,‍ значит, ∠ABC‍₁ = 30‍∘.‍ Тогда ∠AC‍₁B = 60‍∘, ∠DC_‍1K = 180‍∘ − ∠AC_‍1B − ∠BC_‍1K = 180‍∘ − 60‍∘ − 90‍∘ = 30‍∘.‍ В прямоугольном треугольнике KDC‍₁‍ катет, лежащий против угла в 30‍∘‍, равен половине гипотенузы, то есть DK = ‍1/2 KC_‍1 = ‍1/2 CK.‍

Неправильно!

5. Чему равна сумма углов при вершинах произвольной пятиконечной звезды? [Пятиконечная звезда — замкнутая пятизвенная ломаная, у которой каждое звено пересекает оба звена, не имеющих с ним общих вершин.]

Поздравляем, ваш результат: из

Одномерный геометр

Двумерное пространство для вас пока слишком сложно, попробуйте попрактиковаться в одномерном.

Поделиться результатами

Поздравляем, ваш результат: из

Двумерный геометр

На плоскости вы уже почти освоились, нужно еще немного потренироваться.

Поделиться результатами

Поздравляем, ваш результат: из

Готов выйти в трехмерное пространство

С планиметрией вы уже разобрались, теперь можно переходить к стереометрии!

Поделиться результатами

nplus1.ru

Задачи по геометрии. DjVu

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аргумент комплексного числа 344 Аффикс точки 345
Базис векторов в пространстве 308
на плоскости 308
ортонормальный 308
Базисы взаимные 9, 312, 314 Бимедиана тетраэдра 69 Брокардианы 66
Вектор 306
— направляющий 322
— ненулевой 306
— нормальный к плоскости 331 —, прямой 323
— нулевой 306
— плоскости главный 331
— прямой главный 323
— свободный 4
— скользящий 315
— аф 312
Векторы в пространстве 10
— коллинеарные 307
— компланарные 307
— линейно зависимые 308 независимые 308
— на плоскости 7
— симметричные 307
Геометрия Маскерони 279—283 Гомотетия 251
Деление комплексных чисел 344 — направленного отрезка в данном отношении 317, 318 Диагональ главная восьмиугольника 243
Длина отрезка 317 Долгота 282
Дополнение алгебраическое 305
Задача Аполлония 262
Извлечение корней из комплексных чисел 345 Инверсия 5, 249
— плоскости 249
— пространства 283 Инверсор 5
— Гарта 277, 278
— Поселье 277
Кардиоида 272
Квадрат вектора скалярный 310 Клин 23
Коллинеарность векторов 308, 309
— прямой и вектора 322
— точек 318
Комбинация векторов линейная 308 Компланарность вектора и плоскости 331
— векторов 307, 309
— прямой и плоскости 307
— прямых в пространстве 338
— точек 318
Координата полярная вторая 317 первая 317
— точки на прямой 324 Координаты барицентрические в пространстве 321
— — на плоскости 320
— вектора 308
ковариантные 313, 315
контравариантные 312, 315
— точки 316
общие декартовы 316
Коэффициент искажения отрезка 47
— угловой 323, 324 комплексный 347
Медиана тетраэдра 69 Медиатриса отрезка 26 Меридианы 289
Метапараллельность треугольников 247 Минор 306 Модуль вектора 307 — комплексного числа 344
Начало координат 316 Неравенство Йенсена 293
Объем ориентированного тетраэдра 320, 321
Окружность Аполлония 44
— девяти точек 25, 73
— единичная 347.
— инверсии 250
— ортоцентроидальная 160
— Эйлера 25, 73 Определитель 304
— Грама 311, 314
Ориентация тетраэдра 320
левая (отрицательная) 320
правая (положительная) 320
— треугольника 319 Ортологичность треугольников 248 Ортополюс прямой относительно треугольника 83, 130
Ортоцентр 25, 73 Оси координат 316 Ось абсцисс 316
— ординат 316
— пучка 334
— радикальная двух окружностей 41 Отложение вектора от точки 307 Отношение колли неарйых векторов 308
— ориентированных тетраэдров 321
— — треугольников 319 Отображение областей при инверсии
266—277
Пара векторов, имеющих отрицательную ориентацию 311
— положительную ориентацию 310
левая 311
правая 310
Параллели 282
Плоскость евклидова конформная 249
— конформная 249
— ориентированная 310
Площадь ориентированного треугольника 319, 329, 330, 345, 351
— треугольника 322, 351
Поворот вектора на угол я2 3, 312 Подобие 253
Полуплоскость отрицательная 323, 351
— положительная 323, 351
Полупространство отрицательное 331
— положительное 330 Полюс инверсии 249 Построения Маскерони 280—283 Преобразование изогональное относительно треугольника 199
— изометрическое второго рода 5 первого рода 5
— инволюционное 249
— круговое 5
— плоскостиаффинное 247
— подобия 5
— — второго рода 346 первого рода 346
— Чирнгауза 247
Приведение общего уравнения прямой (в пространстве) к каноническому 340 Проекция параллельная 47
— стереографическая 285 Произведение векторов векторное 314 псевдоскалярное 3, 311
скалярное 309
смешанное (в пространстве) 3,313
———(на плоскости) 3, 311
— комплексных чисел 343, 344
— числа на вектор 307 Пространство ориентированное — 313 Прямая Дроза — Фарни 172
— Симеона 77
Прямые, антипараллельные относительно угла 265 Псевдоквадрат 242 Пучок окружностей гиперболический 45, 298
эллиптический 45, 297
— плоскостей 334
несобственный 334
собственный 334
— прямых 325
несобственный 325
собственный 325
Равенство векторов 4, 307, 309
— комплексных чисел 343, 344 Радиус-вектор 316
Разность векторов 307 Расстояниемежду неколлинеарными прямыми кратчайшее 339
— от точкидо плоскости 335, 336
————-прямой 328, 329
—————в пространстве 338, 339
—————на плоскости комплексного переменного 350
Свойства векгорного произведения 314 — действий с комплексными числами 343 ч —
Свойства инверсии плоскости 251—253 — пространства 284
— определителей 304—306
— произведения числа на вектор 308
— псевдоскалярного (смешанного) произведения двух векторов 311
— скалярного произведения векторов 310
— смешанного произведения трех векторов 313
— сопряженности 345
— суммы векторов 307 f Связка плоскостей 334, 335
несобственная 335
собственная 334, 335
Симедиана треугольника 62,235 Система координат общая декартова 316 полярная 317
прямоугольная декартова 316
Соотношение Морлея 201 Степень инверсии 249
— комплексного числа 344
— точки относительно окружности 41, 342
сферы 343
Сумма векторов 307
— комплексных чисел 343 Суппорт 106
— скользящего вектора 315 Сфера Аполлония 57
Тензор фундаментальный 310 Теорема Брианшона 36
— Гамильтона 230
— Дезарга 37
— Дроза — Фарни Л72
— Карно 68 — Менелая 36 — Паскаля 246
— Пилатти 228
— Птолемея 254
— синусов длятрехгранного угла 10
— Чевы 39
— Шаля 140
— Шлёмильха 21 Тетраэдр 320
— вырожденный 320
— невырожденный 320
— ориентированный 320
— ортоцентрический 32 Тождества 315
Точка бесконечно удаленная 249
— Бутена 76
— единичная 76
— Лемуана 62, 204
— Монжа 32
— несобственная 249
— Понселе 44 45
— предельная 44,
Точки базисные эллиптического пучка окружностей 298 изогонально сопряженные относительно треугольника 199
— Понселе 298
— предельные гиперболического пучка окружностей 298
— Файербаха 180, 181, 263
— Эйлера 73
Трансверсаль треугольника 37
Транспонирование определителя 304
Треугольник 319
— вырожденный 319
— невырожденный 319
— ориентированный 319
— ортоцентрический для данного треугольника 83
— тангенциальный 244
Тройка векторов, имеющая отрицательную ориентацию 313
— положительную ориентацию 313
левая 313
правая 313
Угол между двумя плоскостями 336, 337
прямой и плоскостью 340, 341
прямыми 326, 327, 349
— от вектора а до вектора Ь 311
— трехгранника взаимный
Улитка Паскаля 273, 274 Умножение определителей 305 Уравнение антивозвратное 214
— нулевой окружности 342
сферы 342
— окружности 344
— плоскости в отрезках 333 нормальное 335
— — общее 330
— — проходящей через две точки и компланарной вектору 332
точку и компланарной
двум не коллинеарным векторам, — перпендикулярно вектору 331
— — три не коллинеарные
точки 332
— прямой автосопряженное 350 в отрезках 324
пространстве, проходящей через две точки 337, 338
— — нормальное 328 общее 322
———-в комплексной форме 349
параметрическое 324
проходящей через две точки 324
— — точки (гх) и (г2) 346
Уравнение прямой, проходящей через точку в заданном направлении 323
перпендикулярно вектору 325
с угловом коэффициентом 323,324
— сферы 342
Уравнения плоскости параметрические 332, 333
— прямой в пространстве канонические 338
————общие 339
————параметрические 337, 338
Условие коллинеарности вектора и прямой 322
векторов 309
прямых 327, 347
трех точек 318, 345
— компланарности вектора и,плоскости 331
двух прямых 338
точек 318
— параллельности плоскостей 333 прямых 325
— пересечения плоскостей 333 прямой и плоскости 340
— прямых 325
трех плоскостей в одной точке 334
— перпендикулярности прямой и плоскости 341
прямых 327, 328, 348
— подобия и одинаковой ориентированности треугольников 346
————противоположной ориентированности треугольников 346
Условие принадлежности трех прямых одному пучку 326
— совпадения плоскостей 334
прямых 325
Условия параллельности прямой и плоскости 340
— принадлежности прямой плоскости 340
Форма комплексного числа тригонометрическая 344 Формулы Гиббса 312, 315
— Муавра 345
— Эйлера 82
Центр пучка 325
— связки 335
— тяжести тетраэдра 69
треугольника 25, 73
Циссоида Диоклеса 276
Четверка точек гармоническая 44 Числа комплексные сопряженные 345
Широта 282
Элементы определителя 304

sheba.spb.ru

Задания по геометрии – ()

Геометрия. Урок 7. Практические задачи по геометрии