Входное тестирование по алгебре 9 класс
Входное тестирование по алгебре
9 класс
Пояснительная записка
1. Назначение работы — выяснить, насколько знания и умения учащихся 9-х классов на начало учебного года соответствуют основным программным требованиям по математике.
2. Характеристика структуры и содержания работы
Работа по математике состоит из 2-х частей и включает в себя 11 заданий, различающихся формой и уровнем сложности (таблица 1):
Часть 1 содержит 9 заданий: с выбором ответа-4( к каждому заданию приводится четыре варианта ответа, из которых верен только один) и 5 заданий, к которым требуется дать краткий ответ.
Часть 2 содержит 2 задания, к которым требуется дать развернутое решение.
Таблица 1. Распределение заданий по частям работы
Части работы
Число заданий
Максимальный балл
Тип заданий
1
Часть 1
9
9
Задания с выбором ответа или с кратким ответом
2
Часть 2
2
4
Задания с развернутым решением
Итого
11
13
3. Распределение заданий работы по уровням сложности
В работе представлены задания различных уровней сложности: базового, повышенного.
Задания базового уровня включены в первую часть работы. Это простые задания, проверяющие усвоение наиболее важных математических понятий.
Задания повышенного уровня включены во вторую часть работы. Эти задания направлены на проверку умения использовать понятия и законы для решения различных задач.4. Время выполнения работы — 45 минут (с учётом времени, отведённого на инструктаж обучающихся).
5. Дополнительные материалы и оборудование: при выполнении заданий разрешается пользоваться таблицей квадратов.
6. Система оценивания отдельных заданий и работы в целом
Задание с выбором ответа считается выполненным, если выбранный номер ответа совпадает с верным ответом. Каждое из заданий оценивается 1 баллом.
Задание с кратким ответом считается выполненным, если ответ совпадает с верным ответом. Каждое из заданий оценивается 1 баллом, если верно указаны все элементы ответа.
Задание с развернутым решением считается выполненным, если ответ совпадает с верным ответом. Каждое из заданий оценивается в 2 балла, если решение является полным, дан развернутый ответ.
Максимальное количество баллов – 13 балла.
Критерии оценки тестов
11
13
5
От 6 до 8
От 9 до 11
12 или 13
Вариант 1
ЧАСТЬ А
А1. Найдите значение алгебраической дроби 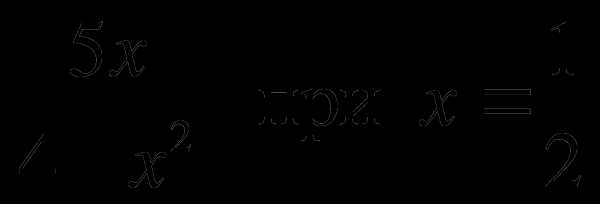 .
.
1)  2)
2)  3)
3)  4)
4) 
А2. Вычислить 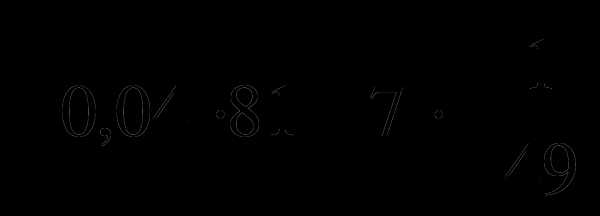
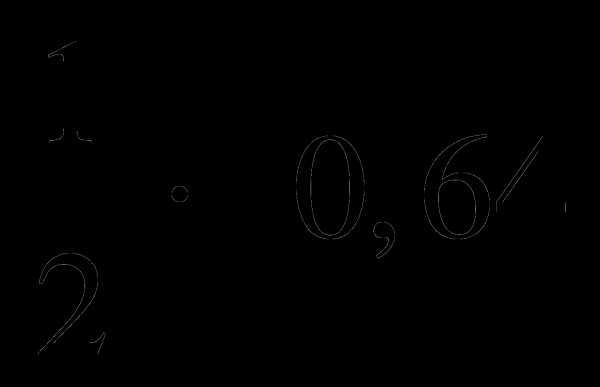 .
.
1) 17 2) 0,8 3) 17 6/7 4) 4
А3. Найдите сумму корней уравнения: .
1) -4 2) 4 3) -2 4) 2
А4. Запишите число 2 180 000 в стандартном виде.
Ответ:_______________________________
А5. Решите неравенство 3(х-2)-5(х+3)>x.
Ответ:__________________________________
А6. Выразите из формулы а2=1/2 (в+с) переменную с.
Ответ:__________________________________________
А7. Пусть 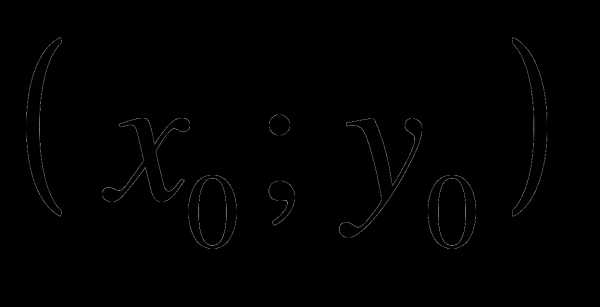 — решение системы линейных уравнений
— решение системы линейных уравнений 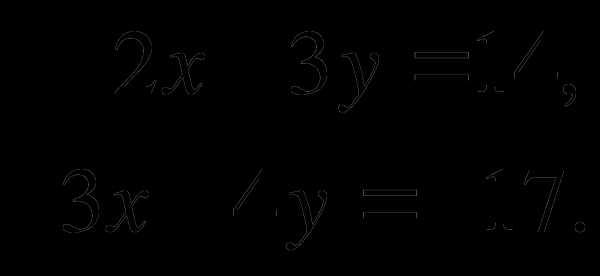
Найдите 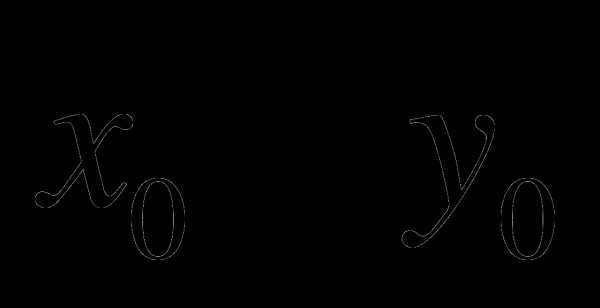
1)
 2)
2) 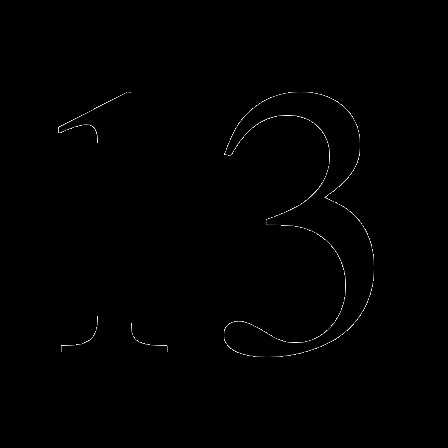 3)
3) 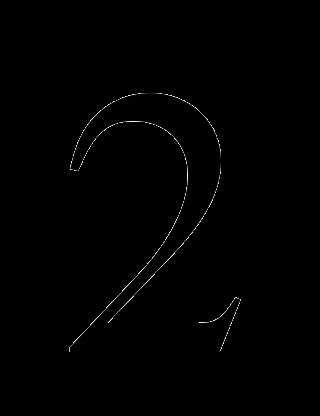 4)
4) 
А8. Выполните умножение 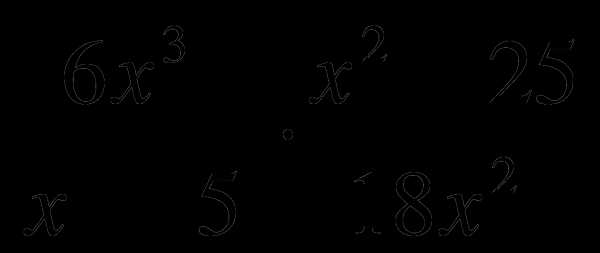 .
.
Ответ:____________________
А9. Найдите сумму наименьшего и наибольшего целых чисел из области определения функции
Ответ:____________________________________
ЧАСТЬ В
(решение заданий записать полностью)
В1. Решите уравнение 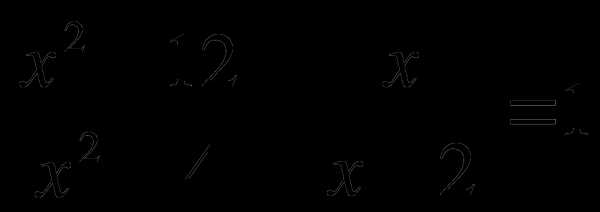

В2. Бассейн наполняется двумя трубами за 3ч. Первая труба, действуя одна, может заполнить бассейн на 8 ч. медленнее, чем вторая. За сколько часов наполнит бассейн одна вторая труба?
Вариант 2
ЧАСТЬ А
А1. Найдите значение алгебраической дроби 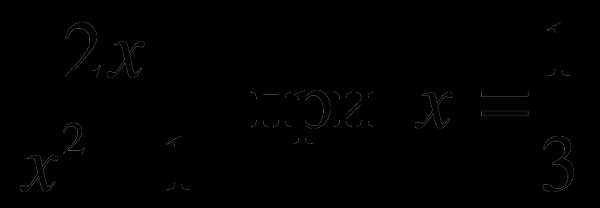 .
.
1)  2)
2)  3)
3)  4)
4) 
А2. Вычислить .
1) 1 2) 1,6 3) -0,06 4) -0,8
А3. Найдите произведение корней уравнения:
1) 70 2) -4 3) -70 4) -35
А4. Запишите число 0,000035 в стандартном виде.
Ответ:______________________________________
А5. Решите неравенство : 5(х+2)-х>6(х-2).
Ответ:____________________________________________________________________
А6. Выразите переменную V из формулы 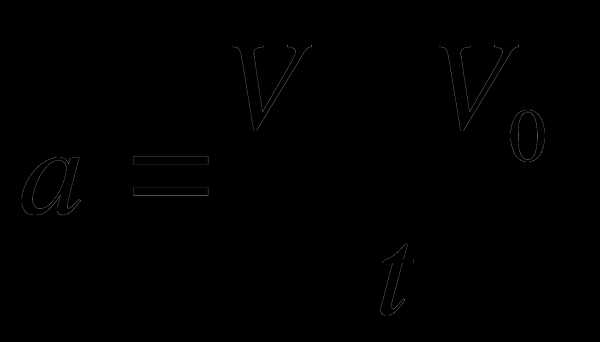 .
.
Ответ_________________________-
А7. Пусть 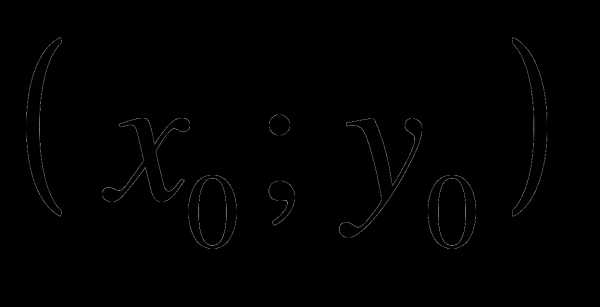 — решение системы линейных уравнений
— решение системы линейных уравнений 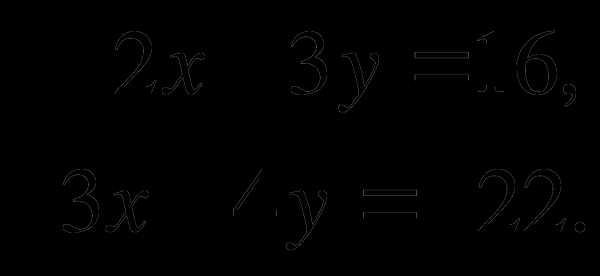
Найдите 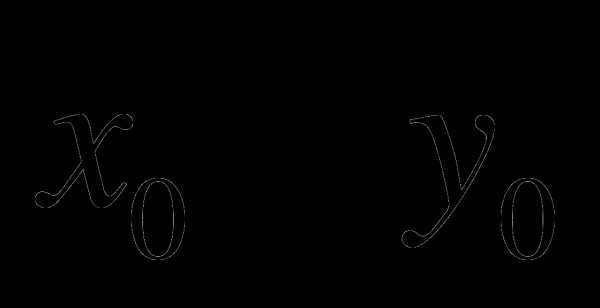 .
.
1)  2)
2) 
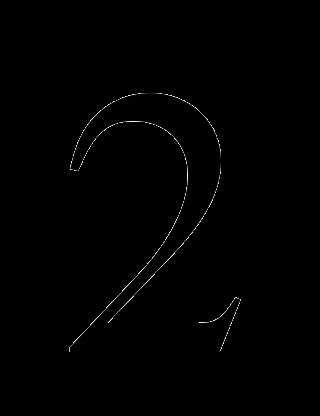 4)
4) 
А8. Выполните деление: 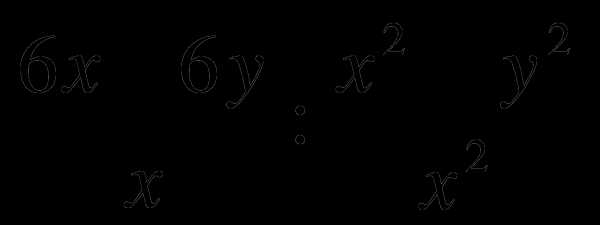 .
.
Ответ:___________________________
А9. Найдите сумму наименьшего и наибольшего целых чисел из области определения функции . Ответ:____________________________
ЧАСТЬ В
(решение заданий записать полностью)
В1. Решите уравнение 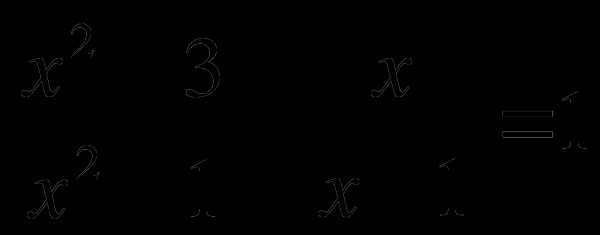
 .
.
В2. Две бригады, работая вместе, могут выполнить заказ за 2ч. Первой бригаде, если она будет работать одна, потребуется на выполнение заказа на 3ч больше, чем второй. За сколько часов может выполнить заказ одна вторая бригада?
Ответы:
Используемая литература:
Математика 9 класс. ОГЭ 2017 /Под ред. Д.А.Мальцева.-Ростов н/Д: Издатель Мальцев Д.А.; Народное образование,2017.
Контрольно-измерительные материалы. Алгебра.7класс, 8класс/Сост.Л.И.Мартышова-М:ВАКО,2015.
infourok.ru
Входной тест по математике (9 класс)
Входной тест по математике 9 класс
Входной тест по математике 9 класс (2014) Вариант 1
Часть А
Упростите выражение .
1) 2) 3) 6 4)
После сокращения дроби получится
1) 2) 3) 4)
Катер прошел по течению реки 8 км и вернулся обратно, потратив на весь путь 5 часов. Скорость течения реки – 3 км/ч. Какова собственная скорость катера?
Обозначьте собственную скорость катера буквой и составьте уравнение по условию задачи.
1) 2)
3) 4)
Вершина параболы находится в точке , если равно
1) 2 2) 1 3) -1 4) -2 5) 3
Если в равнобедренном треугольнике основание равно , а боковая сторона равна 12, то площадь треугольника равна
1) 128 2) 3) 4)
Прямая касается окружности с центром в точке . Если , то длина наибольшей хорды окружности равна
1) 16 2) 20 3) 6 4) 36 5) 12
Часть В
Найдите больший корень уравнения .
Найдите ординату общей точки графиков функций и .
Решите уравнение .
Основание трапеции равно 23 м, а каждая из трех других сторон равна 13 м. Найдите площадь трапеции.
Входной тест по математике 9 класс (2014) Вариант 2
Часть А
Упростите выражение .
1) 2) 5 3) 4)
После сокращения дроби получится
1) 2) 3) 4)
Лодка за одно и то же время может проплыть 30 км по течению реки или 18 км против течения. Найдите собственную скорость лодки, если скорость течения реки равна 2 км/ч.
Обозначьте собственную скорость лодки буквой и составьте уравнение по условию задачи.
1) 2)
3) 4)
Вершина параболы находится в точке , если равно
1) -1 2) -2 3) 2 4) -3 5) 3
Если в равнобедренном треугольнике с боковой стороной 4 см высота, опущенная на его основание, равна см, то площадь треугольника равна
1) см2 2) см2 3) см2 4) см2
Прямая касается окружности с центром в точке . Если , то длина наибольшей хорды окружности равна
1) 30 2) 64 3) 8 4) 16 5) 32
Часть В
Найдите меньший корень уравнения .
Найдите ординату общей точки графиков функций и .
Решите уравнение .
Основания равнобедренной трапеции равны 6 м и 18 м, а боковая сторона равна 10 м. Найдите площадь трапеции.
Входной тест по математике 9 класс (2014) Вариант 3
Часть А
Упростите выражение .
1) 2) 3) 4) 20
После сокращения дроби получится
1) 2) 3) 4)
Теплоход прошел вверх по реке 48 км и вернулся обратно, потратив на весь путь 7 часов. Собственная скорость теплохода – 12 км/ч. Найдите скорость течения реки.
Обозначьте скорость течения реки буквой и составьте уравнение по условию задачи.
1) 2)
3) 4)
Вершина параболы находится в точке , если равно
1) -2 2) -3 3) 3 4) 2 5) 1
Площадь треугольника со сторонами 5 см, 5 см, 6 см равна
1) 24 см2 2) 16 см2 3) 12 см2 4) 48 см2
Прямая касается окружности с центром в точке . Если , то длина наибольшей хорды окружности равна
1) 14 2) 49 3) 7 4) 50 5) 48
Часть В
Найдите больший корень уравнения .
Найдите ординату общей точки графиков функций и .
Решите уравнение .
Основание трапеции равно 22 м, а каждая из трех других сторон равна 10 м. Найдите площадь трапеции.
Входной тест по математике 9 класс (2014) Вариант 4
Часть А
Упростите выражение .
1) 2) 3) 4)
После сокращения дроби получится
1) 2) 3) 4)
Моторная лодка прошла по течению реки 16 км и вернулась обратно, потратив на весь путь 10 часов. Скорость течения реки – 3 км/ч. Найдите собственную скорость лодки.
Обозначьте собственную скорость лодки буквой и составьте уравнение по условию задачи.
1) 2)
3) 4)
Вершина параболы находится в точке , если равно
1) 1 2) 2 3) -2 4) -3 5) -1
Если в треугольнике высота равна см, см, то площадь треугольника равна
1) см2 2) см2 3) см2 4) см2
Прямая касается окружности с центром в точке . Если , то длина наибольшей хорды окружности равна
1) 9 2) 80 3) 82 4) 18 5) 81
Часть В
Найдите меньший корень уравнения .
Найдите ординату общей точки графиков функций и .
Решите уравнение .
Основание трапеции равно 11 м, а каждая из трех других сторон равна 5 м. Найдите площадь трапеции.
Ответы на входной тест по математике 9 класс (2014)
-
Структура входного теста по математике 9 класс (2014)
Часть А
Действия с квадратными корнями (умножение, деление, внесение под корень, вынесение из-под корня).
Сокращение алгебраической дроби (вынесение общего множителя за скобку, разложение квадратного трехчлена на множители).
Текстовая задача на движение (составление уравнения по условию задачи).
Квадратичная функция (умение использовать формулы нахождения координат вершины параболы).
Задача на нахождение площади равнобедренного треугольника (свойства равнобедренного треугольника, теорема Пифагора).
Задача на касательную к окружности (свойство касательной к окружности, теорема Пифагора, определение диаметра окружности).
Часть В
Распадающееся уравнение (умение решать линейные уравнения).
Нахождение общих точек графиков двух функций (умение решать квадратное уравнение, находить ординату общей точки).
Дробно-рациональное уравнение (приведение дробей к наименьшему общему знаменателю, формулы сокращенного умножения, отбор корней уравнения).
Задача на нахождение площади трапеции (определение и свойства равнобедренной трапеции, теорема Пифагора).
Учитель математики МБОУ «Ульяновский городской лицей при УлГТУ» Карягина Татьяна Владимировна
infourok.ru
Входной тест по математике (9 класс)
Входной тест по математике (9 класс)
Вариант 1
Часть А
А1 Решите уравнение: 3x2 + x – 4 = 0.
; 2 2) — ; 1 3) -1; 4) 4; -3
А2 Сократите дробь: .
-2b 2) 3) 4)
А3 Представьте в виде дроби: .
— 2) — 3) 4)
А4 Вычислите без калькулятора, используя свойства арифметического квадратного корня .
10 2) 25 3) 0,25 4) 5
А5 На каком чертеже изображен график функции y = ?
2) 3) 4)
А6 Запишите в стандартном виде число 30400 .
30,4 103 2) 3,04 104 3) 304 102 4) 0,304 105
А7 Сколько натуральных чисел в промежутке ( — 3,5; 2 ) ?
одно 2) два 3) три 4) пять
А8 Решите систему неравенств: .
( -3; 2) 3) ( -3; 4) ( -;
А9 При каких значениях переменной имеет смысл выражение ?
( -; ) 2) 3) ( -; 4) ( -; —
А10 У фигуры, изображенной на рисунке, стороны KM и KN равны, а также равны углы PKM и PKN.
Какой признак равенства треугольников позволяет доказать равенство треугольников KMQ и KNQ?
первый признак
второй признак
третий признак
ни один признак неприменим
А11 В четырехугольнике АВСD диагонали равны и точкой пересечения делятся
пополам, АВВС. Определите вид четырехугольника АВСD.
параллелограмм, отличный от прямоугольника
прямоугольник
ромб
квадрат
Часть В
В1 Вычислите: .
В2 Упростите выражение: ( — )2 + .
Входной тест по математике (9 класс)
Вариант 2
Часть А
А1 Решите уравнение: 2x2 + x – 3 = 0.
1) ; -1 2) 3 ; -2 3) ; 4) 1; —
А2 Сократите дробь: .
2) 3) 4)
А3 Представьте в виде дроби: .
1) 2) 3) — 4)
А4 Вычислите без калькулятора, используя свойства арифметического квадратного корня .
1) 2) 2 3) 8 4) 4
А5 На каком чертеже изображен график функции y = ?
1) 2) 3) 4)
А6 Запишите в стандартном виде число 548 10-5. .
5,48 10—7 2) 0,548 10—2 3) 5,48 10—4 4) 5,48 10—3
А7 Сколько целых чисел в промежутке ( — 2,1; ?
1)шесть 2) пять 3) три 4) четыре
А8 Решите систему неравенств: .
2) 3) ( -; 2) 4) ( 2;
А9 При каких значениях переменной имеет смысл выражение ?
1) 2) 3) 4)
А10 У фигуры, изображенной на рисунке, известно, что BD = CD,
1 = 2. Какой признак равенства треугольников позволяет доказать равенство треугольников ABD и ACD?
1) первый признак 2) второй признак
3) третий признак 4) ни один признак неприменим
А11 В четырехугольнике KMNP диагонали взаимно перпендикулярны и точкой пересечения делятся пополам, KN. Определите вид четырехугольника KMNP.
1) параллелограмм, отличный от ромба
2) прямоугольник
3) ромб
4) квадрат
Часть В
В1 Вычислите: .
В1 Упростите выражение: ( + )2 — .
infourok.ru
Входной контрольный срез по математике, для 9 класса, по материалам открытого банка заданий ОГЭ ,с ответами (5вариантов)
Вариант 1-9-вход
1. Найдите значение выражения
2. На координатной прямой отмечено число
Расположите в порядке убывания числа
В ответе укажите номер правильного варианта.
1) 2)
3) 4)
3. Значение какого из данных выражений является наименьшим?
В ответе укажите номер правильного варианта.
1) 2) 3) 4)
4.. Найдите корни уравнения .
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
5. На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются. Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.

УТВЕРЖДЕНИЯ
ПРОМЕЖУТКИ
А) функция возрастает на промежутке
Б) функция убывает на промежутке
1) [1;2]
2) [0;2]
3) [-1;0]
4) [-2;3]
6. Найдите значение выражения при и
7. Решение какого из данных неравенств изображено на рисунке?
В ответе укажите номер правильного варианта.
1) 2) 3) 4)
8. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 8.
9. Найдите площадь параллелограмма, изображённого на рисунке.
10. После уценки телевизора его новая цена составила 0,52 старой. На сколько процентов уменьшилась цена телевизора в результате уценки?
11. Площадь четырёхугольника можно вычислить по формуле где d1 и d2 — длины диагоналей четырёхугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если а
С1 . Решите систему уравнений
С2. Постройте график функции
и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Вариант 2-9-вход
1. Вычислите:
2. На координатной прямой отмечены числа x, y и z.
Какая из разностей z − x, x − y, z − y положительна?
В ответе укажите номер правильного варианта.
1) z – x 2) x – y 3) z – y 4) ни одна из них
3. Какое из выражений равно степени
1) 2) 3) 4)
4. Найдите наибольшее значение , удовлетворяющее системе неравенств
5. Найдите значение по графику функции , изображенному на рисунке.
1)
2)
3)
4)
6. Упростите выражение и найдите его значение при . В ответ запишите полученное число.
7. На каком рисунке изображено множество решений неравенства ?
В ответе укажите номер правильного варианта.
1) 1 2) 2 3) 3 4) 4
8.К окружности с центром в точке Опроведены касательная AB и секущая AO. Найдите радиус окружности, если AB = 14 см, AO = 50 см.
9. Основания трапеции равны 18 и 12, одна из боковых сторон равна 6, а тангенс угла между ней и одним из оснований равен . Найдите площадь трапеции.
10. Стоимость проезда в пригородном электропоезде составляет 198 рублей. Школьникам предоставляется скидка 50%. Сколько рублей стоит проезд группы из 4 взрослых и 12 школьников?
11. Закон всемирного тяготения можно записать в виде где — сила притяжения между телами (в ньютонах), и — массы тел (в килограммах), — расстояние между центрами масс (в метрах), а — гравитационная постоянная, равная 6.67 · 10−11 H·м2/кг2. Пользуясь формулой, найдите массу тела (в килограммах), если Н, кг, а м.
С1. Решите систему уравнений
С2. Постройте график функции и найдите все значения при которых он имеет ровно три общие точки с прямой
Вариант 3-9-вход
1. Найдите значение выражения
2. Между какими числами заключено число
В ответе укажите номер правильного варианта.
1) 2 и 3 2) 5 и 6 3) 33 и 35 4) 12 и 14
3. Сравните числа и 12.
В ответе укажите номер правильного варианта.
1) 2)
3)
4. Найдите корни уравнения
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
5. На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
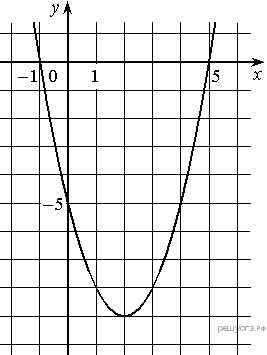
1) f(x)<0 при −1<x<5.
2) Функция возрастает на промежутке [2; +∞).
3) Наименьшее значение функции равно −5.
6. Найдите значение выражения при ,
7. При каких значениях a выражение 9a + 4 принимает положительные значения?
В ответе укажите номер правильного варианта.
1) 2) 3) 4)
8. В окружности с центром O AC и BD — диаметры. Угол ACB равен 26°. Найдите угол AOD. Ответ дайте в градусах.
9. Основания трапеции равны 1 и 11. Найдите бóльший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
10. Набор полотенец, который стоил 200 рублей, продаётся с 3%-й скидкой. При покупке этого набора покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить?
11. фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле , где — число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 11 колец.
С1. Решите систему уравнений
С2. Постройте график функции
и определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Вариант 4-9-вход
1. Укажите выражения, значения которых равны 0,25.
Номера запишите в порядке возрастания без пробелов, запятых и других дополнительных символов.
1)2)
3)
4)
2. На координатной прямой отмечены числа x и y.
Какое из приведенных утверждений неверно?
1) 2) 3) 4)
3. Какое из следующих чисел является наименьшим?
В ответе укажите номер правильного варианта.
1) 1,7·10−3 2) 2,3·10−4 3) 4,5·10−3 4) 8,9·10−4
4. Найдите наибольшее значение , удовлетворяющее системе неравенств
5. Найдите значение по графику функции изображенному на рисунке.
6.. Найдите значение выражения при
7. Решите неравенство .
В ответе укажите номер правильного варианта.
1) 2) 3) 4)
8.. 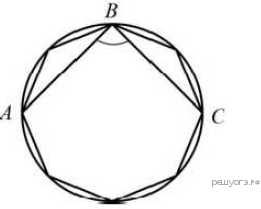 В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.
В окружность вписан равносторонний восьмиугольник. Найдите величину угла ABC.
9. Найдите площадь трапеции, изображённой на рисунке.
10.. Автомобиль проехал 17 километров за 15 минут. Сколько километров он проедет за 18 минут, если будет ехать с той же скоростью?
11. Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 158° по шкале Фаренгейта?
С1. Решите неравенство
С2. Постройте график функции найдите все значения , при которых прямая имеет с графиком данной функции ровно одну общую точку.
Вариант 5-9-вход
1. Найдите значение выражения
2. Числа x и y отмечены точками на координатной прямой. Расположите в порядке возрастания числа и 1.
В ответе укажите номер правильного варианта.
1) 1 2) 1; 3) 1 4) 1;
3. Сравните числа и 16.
В ответе укажите номер правильного варианта.
1) 2)
3)
4. Решите уравнение
5. На рисунке изображён график функции Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
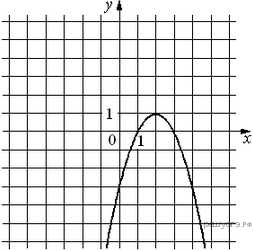
УТВЕРЖДЕНИЯ
ПРОМЕЖУТКИ
А) Функция возрастает на промежутке
Б) Функция убывает на промежутке
1) [0; 3] 2) [− 1; 1]
3) [2; 4] 4) [1; 4]
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
АБ
6. Упростите выражение и найдите его значение при . В ответе запишите найденное значение.
7. Решите неравенство
В ответе укажите номер правильного варианта.
1) (−∞; 9,5] 2) [−8,5; +∞) 3) [9,5; +∞) 4) (−∞; −8,5]
8. Найдите площадь квадрата, описанного вокруг окружности радиуса 7.
9.
. 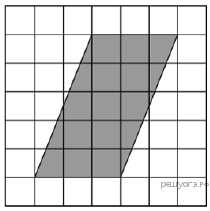 На клетчатой бумаге с размером клетки 1см × 1см изображён параллелограмм. Найдите длину его большей высоты. Ответ дайте в сантиметрах.
На клетчатой бумаге с размером клетки 1см × 1см изображён параллелограмм. Найдите длину его большей высоты. Ответ дайте в сантиметрах.
10. На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 120 человек. Голоса между кандидатами распределились в отношении 3:5. Сколько голосов получил победитель?
11. Автомобиль проехал 200 километров и израсходовал при этом a литров бензина. Сколько литров бензина потребуется, чтобы проехать 37 километров при таких же условиях езды? Запишите соответствующее выражение.
С1.Решите систему неравенств
С2. Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки.
ОТВЕТЫ
Вариант1
2
3
4
5
6
7
8
9
10
11
С1
С2
1
-2,68
1
4
0;5
31
14
4
4
75
48
11
(0;0) ; (0,125;0,125)
-1,5; 0
2
5,45
2
3
-4
3
-16
2
48
30
1980
4000
(2;1,5)
0; 1
3
1,75
2
1
-9;2
3
11
4
128
5,5
306
50500
(-3,5;1)
0; 1
4
13
1
2
-3
-1
0,5
2
90
24
20,4
70
(- ∞;-8];[8; + ∞)
К (-∞ ; -2) [0; +∞)
5
-3
1
1
-16
23
5,2
1
196
5
75
0,185а
[-3;5]
-4 ; 0
infourok.ru
