Всероссийская проверочная работа 6 класс по математике – Материал по математике (6 класс) на тему: Всероссийская проверочная работа по математике. 6кл. 2018г. | скачать бесплатно - Управленческое образование

Содержание

ВПР по математике 6 класс 2018 год

ВПР по математике 6 класс 2018 год — варианты с ответами

18 апреля впервые проведена всероссийская проверочная работа (ВПР) по математике для обучающихся 6 классов. ВПР в 6 классах в 2018 году проводится по решению школы.

Варианты ВПР 2018 по математике 6 класс с ответами

На выполнение работы по математике даётся 60 минут.

Работа содержит 13 заданий. При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. При необходимости участники могут использовать черновик.

Участники ВПР должны продемонстрировать владение понятиями отрицательные числа и обыкновенная дробь, умение находить часть числа и число по его части. В заданиях проверяется владение понятием десятичная дробь, умение оценивать размеры реальных объектов окружающего мира, извлекать информацию, представленную в таблицах и диаграммах.

Также участники должны продемонстрировать умение оперировать понятием модуль числа, сравнивать обыкновенные дроби, десятичные дроби и смешанные числа, умение находить значение арифметического выражения с обыкновенными дробями и смешанными числами, содержащего скобки.

Задания ВПР по математике в 6 классах направлены на проверку умения решать несложные логические задачи, а также на проверку умения находить пересечение, объединение, подмножество в простейших ситуациях, умения решать текстовые задачи на проценты, задачи практического содержания, применять геометрические представления при решении практических задач, а также на проверку навыков геометрических построений.

Максимальный первичный балл – 16.

Рекомендации по переводу первичных баллов ВПР по математике в отметки по пятибалльной шкале

Таблица 2

Отметка по пятибалльной шкале	2	3	4	5
Первичные баллы	0–5	6-9	10-13	14-16

Смотрите также:

ucthat-v-skole.ru

ВПР по математике 6 класс варианты с ответами 2018 год

Категория: 6 класс

Опубликовано: 18 Апрель 2018

18 апреля впервые проведена всероссийская проверочная работа (ВПР) по математике для 6 классов. ВПР в 6 классах в 2018 году проводится по решению школы.

Для подготовки к ВПР 2019 подойдут варианты 2018 года.

ВПР по математике 6 класс варианты с ответами 2018 год

На выполнение работы по математике даётся 60 минут.

Дополнительные материалы и оборудование не требуются.

Специальная подготовка к проверочной работе не требуется.

Структура варианта проверочной работы

Работа содержит 13 заданий.

В заданиях 1–8, 10 необходимо записать только ответ.

В задании 12 нужно изобразить рисунок или требуемые элементы рисунка.

В заданиях 9, 11, 13 требуется записать решение и ответ.

Успешное выполнение обучающимися заданий 12 и 13 в совокупности с высокими результатами по остальным заданиям говорит о целесообразности построения для них индивидуальных образовательных траекторий в целях развития их математических способностей.

Максимальный первичный балл – 16.

Шкала перевода первичных баллов ВПР по математике в отметки по пятибалльной шкале

Таблица 2

Отметка по пятибалльной шкале	2	3	4	5
Первичные баллы	0–5	6-9	10-13	14-16

Смотрите также:

vpr-ege.ru

Проверочная работа в форме ВПР по математике 6 класс

Региональная проверочная работа по математике дата _____.

ФИО ______________________________________________________________________________

______________________________________________________________________ класс 6 «_____»

Вариант 1

ЧАСТЬ 1

Задание 1.

Найдите значение выражения (214 – 34):18+144 : 12

Ответ _________________________________________________

Задание 2.

Запишите в виде обыкновенной дроби числа:

а) одна целая пять восьмых______________________________________________________

б) двенадцать целых восемьдесят три девяностых___________________________________

Задание 3.

Выберите верные утверждения. В ответ запишите номера верных ответов без пробелов, запятых и других символов

1	Дробь называется правильной если знаменатель больше числителя
2	Если числитель дроби увеличить в 7 раз и знаменатель увеличить в 7 раз, то дробь не изменится.
3	Сократить дробь -это сложить числитель со знаменателем
4	Знаменатель дроби показывает на сколько частей разделили

Ответ ________________________________________________________________________

Задание 4.

Представьте смешанное число в виде неправильной дроби

а) = ___________________

Выделите целую часть

б) =____________________

Задание 5.

Расположите числа в порядке

а) возрастания: , , ,.

б) убывания: ,, ,

Задание 6.

Вычислите:

а)

Ответ _____________________________________________

б)

Ответ ____________________________________________

Региональная проверочная работа по математике дата _____.

ФИО ______________________________________________________________________________

______________________________________________________________________ класс 6 «_____»

ЧАСТЬ 2

Задание 7.

Решите уравнение 1

Решение

Задание 8.

Решите задачу

Велосипедист ехал 2 ч со скоростью 12км/ч и 4 ч со скоростью10 км/ч. Сколько километров проехал велосипедист за все это время.

Решение

Ответ ___________________________________

Задание 9.

Решите задачу

В треугольнике АВС сторона АВ больше стороны ВС на 2 см и меньше стороны АС на 2 см. Найдите периметр треугольника АВС, если известно, что АС = 8 см.

Решение

Ответ __________________________________________________________________________

Задание 10.

Разрежьте фигуру на четыре равные части.

Для работы проверяющего

Часть

Основная часть

Дополнительная часть

Задание

Количество баллов

Региональная проверочная работа по математике дата _____.

ФИО ______________________________________________________________________________

______________________________________________________________________ класс 6 «_____»

Вариант 2

ЧАСТЬ 1

Задание 1.

Найдите значение выражения (314 – 34) :7+169 : 13

Ответ _________________________________________________

Задание 2.

Запишите в виде обыкновенной дроби числа:

а) пять целых семь девятых______________________________________________________

б) тринадцать целых пятьдесят три семидесятых ___________________________________

Задание 3.

Выберите верные утверждения. В ответ запишите номера верных ответов без пробелов, запятых и других символов

1	Дробь называется неправильной если числитель больше знаменателя
2	Если числитель дроби уменьшить в 6, а знаменатель увеличить в 6, то дробь уменьшится.
3	Число над чертой дроби называют числителем
4	Числитель дроби показывает сколько частей взято

Ответ ________________________________________________________________________

Задание 4.

Представьте смешанное число в виде неправильной дроби

а) = ___________________

Выделите целую часть

б)

=____________________

Задание 5.

Расположите числа в порядке

а) возрастания: , , ,.

б) убывания: ,, ,

Задание 6.

Вычислите:

а)

Ответ _____________________________________________

б)

Ответ ____________________________________________

Региональная проверочная работа по математике дата _____.

ФИО ______________________________________________________________________________

______________________________________________________________________ класс 6 «_____»

ЧАСТЬ 2

Задание 7.

Решите уравнение 1

Решение

Задание 8.

Решите задачу

Велосипедист ехал 4 ч со скоростью 8 км/ч и 4 ч со скоростью 5 км/ч. Сколько километров проехал велосипедист за все это время.

Решение

Ответ ___________________________________

Задание 9.

Решите задачу

В треугольнике АВС сторона АВ больше стороны ВС на 4 см и меньше стороны АС на 4 см. Найдите периметр треугольника АВС, если известно, что АС = 16 см.

Решение

Ответ __________________________________________________________________________

Задание 10.

Разрежьте фигуру на четыре равные части.

Для работы проверяющего

Часть	Основная часть						Дополнительная часть
Задание	1	2	3	4	5	6	7	8	9	10
Количество баллов

multiurok.ru

ВПР 6 класс математика 2018. Вариант 2 с ответами

ВПР по математике за 6 класс 2018 года В. И. Ахременкова — Вариант №2

При написании данной работы «ВПР по математике 6 класс — 2018. Вариант 2» было использовано пособие «Всероссийская Проверочная Работа. 6 класс. Математика. Практикум по выполнению типовых заданий. ФГОС. В. И. Ахременкова, Издательство «Экзамен», 2018 год».

Задание №1

Какое число надо подставить вместо *, чтобы равенство

стало верным?

Решение

Для того, чтобы определить неизвестное число второй дроби, для начала приведем обе дроби к одному знаменателю — это число 42:

Таким образом определяем, что числителем второй дроби было число, которое при умножение на 3 дало число 12 — это число 4

Или

Ответ:

Задание №2

Расположите в порядке убывания величины:

А) 3,002 км ; Б) 3 км 200 м; В) 3020 м

Запишите в ответ буквы в нужной последовательности.

Решение:

Для того, чтобы решить эту задачу, достаточно перевести все величины к единой форме отображения, например:

3,002 км = 3 км 2 м

3 км 200 м

3020 м = 3 км 20 м

Теперь с лёгкостью выстраиваем величины в порядке убывания — Б, В, А

Ответ:

БВА

Задание №3

Вычислите: 2,6 + 39 : 1,3

Решение:

Вспоминаем правило выполнения арифметических действий в примерах: сначала выполняются по порядку вычисления на умножение и деление, а затем на сложение и вычитание:

2,6 + 39 : 1,3

39 : 1,3 = 30

2,6 + 30 = 32,6

Ответ:

32,6

Задание №4

Шестиклассники соревновались в беге на лыжах на 2 км. В таблице представлены результаты пяти участников. Использую данные таблицы, вычислите, на сколько минут быстрее пробежал дистанцию Олег, чем Алексей.

Имя	Игорь	Никита	Олег	Юрий	Алексей
Результат, мин	15,2	14,7	13,1	13,7	14,9

Решение:

Из таблицы находим результаты бега Олега и Алексея:

Олег — 13,1 мин

Алексей — 14,9 мин

Получаем:

14,9 — 13,1 = 1,8

Ответ:

Олег пробежал дистанцию на 1,8 минут быстрее, чем Алексей

Задание №5

В продажу поступило 1200 билетов на концерт. За первую неделю было продано 68% билетов. Сколько билетов было продано за первую неделю?

Решение:

Чтобы найти процент от какого-либо числа, необходимо это число разделить на 100% и умножить на значение искомого процента:

1200 : 100% * 68 % = 816 (б)

Ответ:

816

Задание №6

Расположите в порядке возрастания дроби: 5,72; 5,8; 5,072

Решение:

В данном задании нужно внимательно посмотреть на величину каждой цифры после запятой (десятые, сотые и тысячные)

Получим: 5,072; 5,72; 5,8

Ответ:

5,072; 5,72; 5,8

Задание №7

Найдите значение выражения: 16,48 : 1,6 + 0,8 * 9,1 — 5,8 * 0,1

Решение:

Вспоминаем правило выполнения арифмитических действий в примерах: сначала выполняются по порядку вычисления на умножение и деление, а затем на сложение и вычитание:

16,48 : 1,6 + 0,8 * 9,1 — 5,8 * 0,1

16,48 : 1,6 = 10,3 (проще выполнять в столбик)

0,8 * 9,1 = 7,28 (проще выполнять в столбик)

5,8 * 0,1 = 0,58

10,3 + 7,28 — 0,58 = 17

Ответ:

Задание №8

Решите уравнение: 46,5 : (2x) = 7,5

Решение:

46,5 : (2x) = 7,5

2x = 46,5 : 7,5

2x = 6,2

x = 6,2 : 2

x = 3,1

проверяем:

46,5 : (2 * 3,1) = 7,5

46,5 : 6,2 = 7,5

7,5 = 7,5

Ответ:

3,1

Задание №9

Найдите наименьшее трёхзначное число, которое делится и на 6, и на 4

Решение:

Ближайшее трёхзначное число которое делится на 6 — это 102 (6 * 17 = 102), но оно не делится на 4.

Следующее число, которое делится на 6 — это 108 (102 + 6)

Число 108 делится на 4:

108 : 4 = 27

Ответ:

108

Задание №10

На диаграмме представлены данные о высоте вулканов над уровнем моря.

Пользуясь диаграммой, ответьте на вопросы:

Какой из представленных вулканов занимает четвертое место по высоте над уровнем моря?
Какой из представленных вулканов примерно в три раза ниже, чем Фудзияма?

Решение:

Для удобства, при решении этой задачи, можно пользоваться линейкой, ну или выполнять работу «на глаз»

Первым на диаграмме выделяется вулкан Охос-дельсальдо, затем Ключевская сопка, далее идет Фудзияма и только потом вулкан Этна (на четвертом месте).

Высота Фудзиямы на диаграмме составляет чуть меньше 4000 м — скажем около 3700 — 3800 м

В три раза меньше это 3800 : 3 ~ 1200 м. На диаграмме очень близок к этой высоте вулкан Везувий.

Ответ:

Этна
Визувий

Задание №11

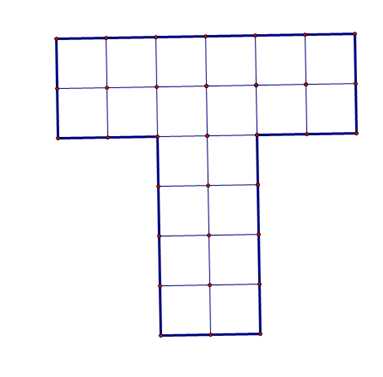
На рисунке изображена фигура, составленная из квадратов. Нарисуй фигуру с таким же периметром, но с меньшей площадью.

Решение:

Посчитав все клетки со всех сторон мы получаем:

P = 4 + 1 + 1 + 1 + 1 + 1 + 4 + 1 + 1 + 1 + 1 + 1 = 18

При этом площадь данной фигуры равна количеству клеток = 10

Теперь нарисуем с вами фигуру с тем же периметром, например:

Периметр которого равен:

P = 5 + 2 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 2 = 18

Но при этом его площадь равна — 8

Задание №12

Нарисуй, как с помощью двух прямых разделить квадрат на треугольник и три четырёхугольника.

Решение:

Приводим пример деления:

Задание №13

В магазин завезли морковь. В первый день продали 2/7 привезённой моркови и ещё 80 кг. После этого в магазине осталось 3/7 привезённой моркови. Сколько килограммов моркови привезли в магазин?

Решение:

Итак всего привезли моркови = 7/7, тогда получаем

Получаем, что в первый день было продано 4/7 от всей привезённой моркови. Тогда, будет верным равенство:

Итак, 80 кг — это две доли от всей привезенной моркови, т.е. 2/7.

Теперь узнаем сколько моркови привезли в магазин. Если 80 кг — это две доли от привезенной моркови, то одна доля будет равна

80 : 2 = 40 (кг)

В таком случае 7 долей будут равны:

40 * 7 = 280 (кг) — всего моркови привезли в магазин

Ответ:

280

Задание №14

Среди 80 опрошенных учащихся у 38 живёт дома собака, у 35 — кошка, а у 14 нет ни кошки, ни собаки. Сколько человек, принявших участие в опросе, содержат дома и кошку, и собаку?

Решение:

Для начала узнаем сколько человек имеют либо кошку, либо собаку.

38 + 35 = 73 (ч)

Теперь от общей суммы учащихся отнимем учеников, которые не имеют ни кошку, ни собаку:

80 — 14 = 66 (ч)

Теперь найдем количество учеников, которые содержат дома и кошку, и собаку:

73 — 66 = 7 (ч)

Ответ:

7 человек

Навигация по записям

gdzotl.ru

ВПР по математике 6 класс 2018 год — варианты с ответами

Варианты ВПР 2018 по математике 6 класс с ответами

ВПР по математике 6 класс 2018 год — демонстрационный вариант с ответами.

На выполнение работы по математике даётся 60 минут.

Максимальный первичный балл – 16.

Рекомендации по переводу первичных баллов ВПР по математике в отметки по пятибалльной шкале

Таблица 2

Отметка по пятибалльной шкале	2	3	4	5
Первичные баллы	0–5	6-9	10-13	14-16

Смотрите также:

vprklass.ru

ВПР 6 класс математика 2018. Вариант 1 с ответами

ВПР по математике за 6 класс 2018 года В. И. Ахременкова — Вариант №1

При написании данной работы «ВПР по математике 6 класс — 2018. Вариант 1» было использовано пособие «Всероссийская Проверочная Работа. 6 класс. Математика. Практикум по выполнению типовых заданий. ФГОС. В. И. Ахременкова, Издательство «Экзамен», 2018 год».

Задание №1

Какое число надо подставить вместо *, чтобы равенство

стало верным?

Решение

Для того, чтобы определить неизвестное число второй дроби, для начала приведем обе дроби к одному знаменателю — это число 70:

Таким образом определяем, что числитель второй дроби было число, которое при умножение на 5 дало число 15 — это число 3

Или

Ответ:

Задание №2

Расположите в порядке возрастания величины:

А) 5 кг 70 г ; Б) 5,007 кг; В) 5700 г

Запишите в ответ буквы в нужной последовательности.

Решение:

Для того, чтобы решить эту задачу, достаточно перевести все величины к единой форме отображения веса, например:

5 кг 70 г

5,007 кг = 5 кг 7 г

5700 г = 5 кг 700 г

Теперь с лёгкостью выстраиваем величины в порядке возрастания — Б, А, В

Ответ:

БАВ

Задание №3

Вычислите: 15 — 4,8 : 12

Решение:

15 — 4,8 : 12

4,8 : 12 = 0,4

15 — 0,4 = 14,6

Ответ:

14,6

Задание №4

Шестиклассники соревновались в беге на 30 м. В таблице представлены результаты пяти участников. Использую данные таблицы, вычислите, на сколько секунд быстрее пробежал дистанцию Илья, чем Максим.

Имя	Сергей	Илья	Олег	Иван	Максим
Результат, с	6,0	5,8	6,2	5,9	6,1

Решение:

Из таблицы находим результаты бега Ильи и Максима:

Илья — 5,8 с

Максим — 6,1 с

Получаем:

6,1 — 5,8 = 0,3

Ответ:

Илья пробежал дистанцию на 0,3 с быстрее, чем Максим

Задание №5

От посёлка до города по шоссе 48 км. Отремонтировали 35% дороги.Сколько километров дороги отремонтировали?

Решение:

48 : 100% * 35 % = 16,8 (км)

Ответ:

16,8

Задание №6

Расположите в порядке убывания дроби: 1,208; 1,03; 1,28

Решение:

Получим: 1,28; 1,208; 1,03

Ответ:

1,28; 1,208; 1,03

Задание №7

Найдите значение выражения: 15,75 : 1,5 — 6,2 * 0,4 + 98 : 100

Решение:

15,75 : 1,5 — 6,2 * 0,4 + 98 : 100

15,75 : 1,5 = 10,5 (проще выполнять в столбик)

6,2 * 0,4 = 2,48 (проще выполнять в столбик)

98 : 100 = 0,98

10,5 — 2,48 + 0,98 = 8,02 + 0,98 = 9

Ответ:

Задание №8

Решите уравнение: 2x : 1,8 = 2,5

Решение:

2x : 1,8 = 2,5

2x = 2,5 * 1,8

2x = 4,5

x = 4,5 : 2

x = 2,25

проверяем:

2 * 2,25 : 1,8 = 2,5

4,5 : 1,8 = 2,5

2,5 = 2,5

Ответ:

2,25

Задание №9

Найдите наименьшее трёхзначное число, которое делится и на 6, и на 15

Решение:

Ближайшее трёхзначное число которое делится на 15 — это 105 (15 * 7 = 105), но оно не делится на 6.

Следующее число, которое делится на 15 — это 120 (105 + 15)

Число 120 делится на 6:

120 : 6 = 20

Ответ:

120

Задание №10

На диаграмме представлены данные о массе некоторых динозавров.

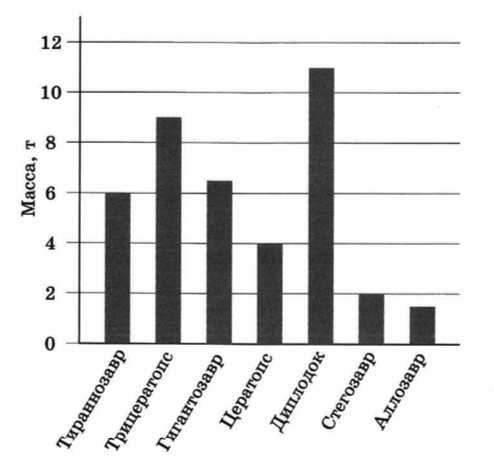
Пользуясь диаграммой, ответьте на вопросы:

Какой динозавр занимает третье место по массе среди представленных на диаграмме?
Масса каких динозавров отличается в три раза?

Решение:

Для удобства, при решении этой задачи, можно пользоваться линейкой или «на глаз»

Первым на диаграмме выделяется Диплодок, затем Трицератопс и уже потом Гигантозавр (на третьем месте).

На диаграмме четко показаны значения для трёх динозавров: Тиранозавр — 6 т, Цератопс — 4 т и Стегозавр — 2 т.

В три раза отличается масса Тиранозавра и Стегозавра

Ответ:

Гигантозавр
Тиранозавр и Стегозавр

Задание №11

На рисунке изображена фигура, составленная из квадратов. Нарисуй фигуру с таким же периметром, но с большей площадью.

Решение:

Посчитав все клетки со всех сторон мы получаем:

4 + 3 + 1 + 2 + 1 + 2 + 2 + 3 = 18

При этом площадь данной фигуры равна количеству клеток = 10

Теперь нарисуем с вами фигуру с тем же периметром, например:

Периметр которого равен:

4 + 5 + 1 +1 + 3 + 4 = 18

Но при этом его площадь равна — 17

Задание №12

Нарисуй, как с помощью трёх прямых разделить круг на пять частей.

Решение:

Приводим пример деления круга на 5 частей:

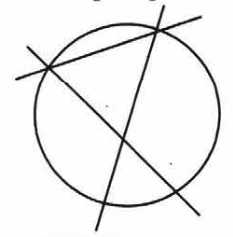
Задание №13

Маша взяла в библиотеке книгу. В первый день она прочитала 2/9 книги и ещё 60 страниц. После этого Маше осталось прочитать 4/9 книги. Сколько страниц в книге?

Решение:

Итак размер книги = 9/9, тогда получаем

Получаем, что в первый день Маша прочитала 5/9 книги. Тогда, будет верным равенство:

Мы можем найти для начала чему равна 1/9 книги, а затем умножить полученное значение на 9 и получить объем книги в страницах.

Однако, нам проще 60 умножить на три, поскольку 3/9 — это третья часть от 9/9

60 * 3 = 180

Ответ:

180

Задание №14

Из 30 учащихся классов 15 человек посещают спортивные секции, 17 человек — кружки, 4 учащихся не посещают ни спортивные секции, ни кружки. Сколько человек посещают и кружки и секции?

Решение:

Для начала узнаем сколько человек посещают либо кружки, либо спортивные секции.

15 + 17 = 32 (ч)

Теперь от общей суммы учащихся отнимем учеников, которые не посещают ни кружки, ни секции:

30 — 4 = 26 (ч)

Теперь найдем количество учеников, которые посещают и спортивные секции и кружки:

32 — 26 = 6 (ч)

Ответ:

6 человек

Навигация по записям

gdzotl.ru

ВПР 6 класс математика 2018. Вариант 5 с ответами

ВПР по математике за 6 класс 2018 года В. И. Ахременкова — Вариант №5

При написании данной работы «ВПР по математике 6 класс — 2018. Вариант 5» было использовано пособие «Всероссийская Проверочная Работа. 6 класс. Математика. Практикум по выполнению типовых заданий. ФГОС. В. И. Ахременкова, Издательство «Экзамен», 2018 год».

Задание №1

Какое число надо подставить вместо *, чтобы равенство

стало верным?

Решение

Для того, чтобы определить неизвестное число второй дроби, для начала приведем обе дроби к одному знаменателю — это число 66:

Таким образом определяем, что числителем второй дроби было число, которое при умножение на 3 дало число 21 — это число 7

Или

Ответ:

Задание №2

Расположите в порядке возрастания величины:

А) 2 мин 40 с; Б) 2,4 мин; В) 200 с

Запишите в ответ буквы в нужной последовательности.

Решение:

Для того, чтобы решить эту задачу, достаточно перевести все величины к единой форме отображения, например:

2 мин 40 с

2,4 мин = 2 мин 24 с

200 с = 3 мин 20 с

Теперь с лёгкостью выстраиваем величины в порядке возрастания — Б, А, В

Ответ:

БАВ

Задание №3

Вычислите: 45 — 7,2 : 18

Решение:

7,2 : 18 = 0,4

45 — 0,4 = 44,6

Ответ:

44,6

Задание №4

Шестиклассники соревновались в прыжках в длину с разбега. В таблице представлены результаты пяти участников. Использую данные таблицы, вычислите, на сколько метров дальше Андрея прыгнул Никита.

Имя	Иван	Андрей	Артём	Никита	Юрий
Результат, м	2,6	2,2	3,3	3,1	2,8

Решение:

Из таблицы находим результаты прыжков Андрея и Никиты:

Андрей — 2,2 м

Никита — 3,1

Получаем:

3,1 — 2,2 = 0,9

Ответ:

Никита прыгнул на 0,9 м дальше Андрея

Задание №5

От посёлка до города 35 км. Грунтовая дорога составляет 24% этого расстояния. Сколько километров длина грунтовой дороги?

Решение:

35 : 100% * 24 % = 8,4 (км)

Ответ:

8,4

Задание №6

Расположите в порядке убывания дроби: 6,305; 6,5; 6,35

Решение:

Получим: 6,5; 6,35; 6,305

Ответ:

6,5; 6,35; 6,305

Задание №7

Найдите значение выражения: 24,72 : 1,2 + 0,7 * 5,3 — 0,031 :0,1

Решение:

24,72 : 1,2 + 0,7 * 5,3 — 0,031 :0,1

24,72 : 1,2 = 20,6 (проще выполнять в столбик)

0,7 * 5,3 = 3,71 (проще выполнять в столбик)

0,031 :0,1 = 0,31

20,6 + 3,71 — 0,31 = 24

Ответ:

Задание №8

Решите уравнение: 3x : 2,4 = 2,8

Решение:

3x : 2,4 = 2,8

3x = 2,8 * 2,4

3x = 6,72

x = 6,72 : 3

x = 2,24

проверяем:

3x : 2,4 = 2,8

3 * 2,24 : 2,4 = 2,8

6,72 : 2,4 = 2,8

2,8 = 2,8

Ответ:

2,24

Задание №9

Найдите наибольшее двузначное число, которое делится и на 6, и на 9

Решение:

Наибольшее двузначное число которое делится на 6 — это 96 (16 * 6 = 96), но оно не делится на 9.

Зато, следущее число — 90 делится и на 6 ина 9

90 : 6 = 15

90 : 9 = 10

Ответ:

Задание №10

На диаграмме представлены данные о площади некоторых городов России.

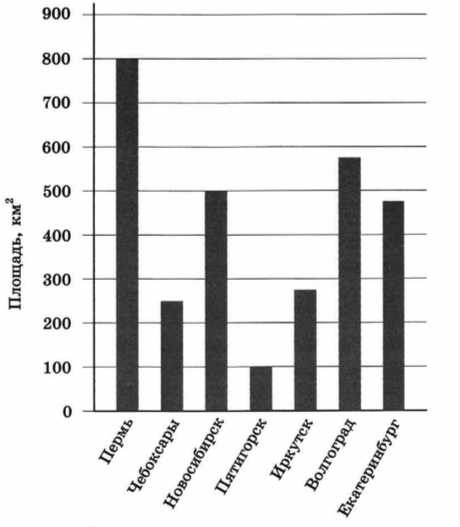
Пользуясь диаграммой, ответьте на вопросы:

Какое место по площади среди представленных городов занимает Иркутск?
На сколько больше площадь Екатеринбурга, чем площадь Иркутска?

Решение:

Находим на диаграмме город Иркутск и смотрим сколько Городов имею большую площадь — это четыре города: Екатеринбург, Волгоград, Новосибирск и иПермь. Значит город Иркутск занимает пятое место по площади среди представленных.

Площадь Иркутска согласно диаграмме составляет около 280 кв. км., тогда как площадь Екатеринбурга — около 480 гектар. Значит разница между ними:

480 — 280 = 200 (кв. км.) — на 200 (приблизительно) кв. км. площадь Екатеринбурга больше, чем площадь Иркутска

Примечание: Очень странно, но в авторы утверждают, что здесь разница в 190 кв. км. (спорить с ними не буду)

Ответ:

Задание №11

На рисунке изображена фигура, составленная из квадратов. Нарисуй фигуру с таким же периметром, но большей площадью.

Решение:

Посчитав все клетки со всех сторон мы получаем:

P = 3 + 2 + 1 + 1 + 1 + 2 + 3 + 5 = 18

При этом площадь данной фигуры равна количеству клеток = 14

Теперь нарисуем с вами фигуру с тем же периметром, например:

Периметр которой равен:

P = 3 + 2 + 1 + 1 + 1 + 2 + 3 + 5 = 18

Но при этом его площадь равна — 16

Задание №12

Нарисуй, как с помощью трёх прямых разделить круг на четыре части.

Решение:

Приводим пример деления:

Задание №13

Толе дали задание выучить английские слова. Сначала он выучил 5/9 всех слов и ещё 6 слов. После этого ему осталось выучить 2/9 всех слов. Сколько слов задали выучить Толе.

Решение:

Итак всего нужно было выучить = 9/9 слов, тогда получаем

Получаем, что в первый день Толя выучил 7/9 всех слов. Тогда, будет верным равенство:

Итак 6 слов составляют 2/9 от всех слов — т.е. две доли из 9. Найдем чему равна одна доля:

6 : 2 = 3 — одна доля из 9

3 * 9 = 27 — всего нужно было выучить слов

Ответ:

27 слов

Задание №14

Из 80 опрошенных 48 человек знают английский язык, 36 немецкий, а 11 не владеют иностранными языками. Сколько человек среди опрошенных знают и немецкий, и английский языки?

Решение:

Для начала узнаем сколько человек знают либо немецкий, либо английский языки:

48 + 36 = 84 (ч)

Теперь от общей суммы опрошенных отнимем тех, кто не владеет иностранными языками:

80 — 11 = 69 (ч)

Теперь найдем количество опрошенных, кто владеет обоими языками :

84 — 69 = 15 (ч)

Ответ:

15 человек

Навигация по записям

gdzotl.ru