Олимпиада по математике 8 класс школьный тур
Олимпиада по математике для 8 класса общеобразовательной школы. Составлена в соответствии с рекомендациями Министерства образования Нижегородской области. Олимпиада разработана для проведения школьного этапа. Работа состоит из 7 заданий различного уровня сложности, наивысший балл за работу 49 баллов.
Просмотр содержимого документа
«олимпиада по математике 8 класс школьный тур »
| Предмет | математика |
| Класс | 8 |
| Время выполнения | 2 часа |
| Количество баллов за каждое задание | 1, 2 задание – 5 баллов 3 задание – 7 баллов 4 задание -8 баллов 5 задание 10 баллов |
| Максимальный балл за работу | 35 |
| Учитель | Зуева Н.В. |
| Задания олимпиады | |
| Ключи и критерии оценивания |
Задания школьного этапа всероссийской олимпиады школьников
Для учащихся 8 класс по предмету математика.
Задание 1 (5 баллов)
Средний возраст одиннадцати футболистов – 22 года. Во время игры один из игроков получил травму и ушел с поля. Средний возраст оставшихся игроков стал 21 год. Каков возраст футболиста, ушедшего с поля?
Задание 2 (5 баллов)
В треугольнике АВС проведены биссектрисы углов А и В, угол между которыми составил 125°. Найдите угол С.
Задание 3 ( 7 баллов)
Постройте график функции
У = +
Пояснение: знаменатель первой дроби равен х2 — 25
Задание 4 (8 баллов)
Запишите уравнение прямой, проходящей через точки А и В. Точки А и В – это точки, симметричные относительно осей абсцисс и ординат точке С. Точка С принадлежит прямой у = 0,5х – 1 и имеет ординату -1.
Задание 5 (10 баллов)
При каких натуральных значениях п выражение (п2 + 5п — 8)/(п + 3) является целым числом?
Максимальный балл – 35 баллов.
Ответы и указания к решению.
Задание 1
Возраст игрока – 32 года.
Задание 2
Угол С равен 70°
Задание 3
У = 2, х ≠ ± 5
Задание 4
Точка лежащая на прямой у = = 0,5х – 1 с ординатой -1 имеет координаты (4 ; 1). Точки симметричные ей А(- 4; 1) и В (4; -1). Уравнение прямой, проходящей через эти точки, имеет вид У = — 0,25х.
Задание 5
Преобразуем дробь к виду (п + 3)(п + 2) — 14
(п + 3)
В итоге получим выражение п + 2 — , п – натуральное число. Если дробь будет являться целым числом, то и все выражение будет целым числом. Это возможно при п = 3 и п = 11.
Критерии оценивания
Максимальное количество баллов выставляется, если ученик верно решил задание, и привел ход решения или пояснил ответ.
kopilkaurokov.ru
Олимпиада по математике 8 класс с ответами 2017-2018 муниципальный этап
Олимпиадные задания по математике 8 класс
Задача 1.
Какой цифрой оканчивается сумма 92007 + 92006 ?
Ответ:
92007 + 92006 = 92006( 9 + 1) = 92006* 10.
Нулем.
Задача 2.
В оранжерее было срезано 360 гвоздик. Причем красных на 80 больше, чем белых, а розовых на 160 штук меньше, чем красных.
Какое наибольшее число одинаковых букетов можно составить из этого количества цветов ?
Сколько и каких цветов было в каждом букете?
Ответ:
Решая уравнение, получаем 40 розовых гвоздик,120 белых гвоздик, 200 красных гвоздик. НОД (40, 120,200) равен 40, следовательно из 360 гвоздик можно составить 40 букетов, причем каждый букет будет состоять из 1 розовой, 3 белых и 5 красных гвоздик.
Задача 3.
Существует ли такой круг, чтобы его площадь и длина окружности выражались одним и тем же числом ?
Ответ:
Да, при радиусе равном 2.
Задача 4.
После семи стирок измерения куска хозяйственного мыла, имеющего форму прямоугольного параллелепипеда, уменьшились в двое.
На сколько еще стирок хватит оставшегося куска мыла ?
Ответ:
Мыла хватит еще на одну стирку, т.к. объем оставшегося мыла составил 1/8 часть первоначального, израсходовано мыла: 1 — 1/8 = 7/8 куска,
значит на каждую стирку расходовалось 1/8 часть куска, именно столько осталось.
Задача 5.
Какими двумя цифрами заканчивается число 13! ?
Ответ:
В произведении 1*2*3…*13 есть множители 2, 5 и 10, значит число 13!
Заканчивается двумя нулями.
Задача 6.
Из 38 учащихся 28 посещают хор и 17 лыжную секцию.
Сколько лыжников посещает хор, если в классе нет учащихся, которые не посещают хор или лыжную секцию ?
Ответ:
7 человек. Хор не посещают 10 человек, все они лыжники.
Лыжников всего 17человек, значит 7 человек надо «взять» из хора.
Задача 7.
Окружность касается квадрата извне и «катится» по нему без скольжения.
Те же вопросы, если окружность «катится» по сторонам равностороннего треугольника.
Ответ:
В случае квадрата каждая точка окружности сделает 4 оборота около своего центра.
Центр окружности сделает четверть оборота около каждой вершины квадрата.
За один обход центр окружности совершает путь, равный 5*2Па см.
В случае треугольника — соответственно 3 оборота и 8П а см
Задача 8.
Во время похода палатки расположились в т. А,В, и С.
В каком месте удобно выбрать площадку для проведения общего костра,
чтобы расстояние от него до палаток было одинаковым ?
Ответ:
Точка осей симметрии точек А и В и точек В и С будет искомой.
Задача 9.
Найдите произведение всех целых чисел от (-99) до 99.
Ответ:
0
Задача 10.
Две семьи выехали каждая на машине «Жигули» на прогулку одновременно из одного места.
Обе семьи проехали на машинах одинаковые расстояния и вернулись домой в одно и то же время.
В пути они отдыхали.
Первая семья была в пути в двое больше времени, чем вторая.
Вторая была в пути втрое больше времени. Чем отдыхала первая.
Какая из этих семей двигалась на машине быстрее ?
Ответ:
1-я семья: 2х часов — время на езду, у часов — время на отдых.
2-я семья: 3у часов — время на езду, х часов — время на отдых 2х + у = 3у + х; х = 2у.
Вторая семья отдыхала в два раза больше, чем первая следовательно, она ехала быстрее первой.
Задача 11.
Сосуд имеет форму прямоугольного параллелепипеда.
Как, не делая никаких измерений и не имея других емкостей, наполнить водой ровно половину объема этого сосуда ?
Ответ:
Наклонить параллелепипед так, чтобы уровень воды находился по диагональному сечению параллелепипеда.
Задача № 1 :
В трех кучках лежат соответственно 12, 24 и 19 спичек. За ход можно переложить спичку из одной кучки в другую. За какое наименьшее число ходов можно получить три кучки с 8, 21 и 26 спичками?
Ответ : 4.
Решение :
Менее чем 4 ходами не обойтись: чтобы получить кучку из 8 спичек, придется из любой первоначальной кучки убрать как минимум 4 спички. Четырех ходов достаточно: перекладываем из кучки с 12 спичками по 2 спички в кучки с 19 и 24 спичками.
Задача № 2 :
Сколько всего есть четырехзначных чисел, которые делятся на 19 и оканчиваются на 19?
Ответ : 5 .
Решение :
Пусть — такое число. Тогда N – 19 тоже кратно 19. Но Поскольку 100 и 19 взаимно просты, то двузначное число делится на 19. А таких всего пять: 19, 38, 57, 76 и 95. Легко убедиться, что все числа 1919, 3819, 5719, 7619 и 9519 нам подходят.
Задача № 3 :
У даты 12.04.1961 (то есть 12 апреля 1961 года) сумма цифр равна 24. Найдите ближайшую дату после 01.01.2008, у которой сумма цифр равна: а) 35; б) 7.
Ответ : а) 29.09.2049; б) 03.01.2010.
Решение :
а) Наибольшая сумма цифр числа равна 11 для 29-го числа. Наибольшая сумма цифр месяца равна 9 для сентября, то есть для 09. Значит, наибольшая сумма цифр в текущем году будет у даты 29.09.2008. Она равна 30, что меньше 35. Следовательно, надо менять и год. Последняя цифра года не более 9, и если мы сохраняем первые две цифры, то придется цифру десятилетий увеличить до 4.
б) Для 2008 года сумма цифр года уже больше 27, поэтому год придется изменить. Ближайший год в будущем с меньшей суммой цифр — 2010-й. Соответственно, ближайшая подходящая дата 03.01.2010.
Задача № 4 :
Среди целых чисел от 8 до 17 включительно зачеркните как можно меньше чисел так, чтобы произведение оставшихся было точным квадратом. В ответе укажите сумму всех вычеркнутых чисел.
Ответ : 55.
Решение :
Чтобы произведение было точным квадратом, нужно, чтобы каждый простой множитель входил в него в четной степени. В произведение 8 · 9·…· 17 в нечетной степени входят 2, 7, 11, 13 и 17. Значит, мы обязаны вычеркнуть сомножители 11, 13 и 17. А вот чтобы «убить» лишние простые множители 2 и 7, хватит одного вычеркнутого сомножителя 14. Итого сумма вычеркнутых чисел равна 11 + 13 + 14 + 17 = 55.
Задача № 5 :
На гранях кубика расставлены 6 различных чисел от 6 до 11. Кубик бросили два раза. В первый раз сумма чисел на четырех боковых гранях оказалась равна 36, во второй — 33. Какое число написано на грани, противоположной той, где написана цифра 10?
Ответ : 8.
Решение :
Cумма чисел на всех гранях равна 6 + 7 + 8 + 9 + 10 + 11 = 51. При первом броске сумма на верхней и нижней гранях равна 51 – 36 = 15, при втором — 51 – 33 = 18. Значит, на третьей паре противоположных граней сумма равна 51 – 15 – 18 = 18. Сумму 18 можно получить двумя способами: 11 + 7 или 10 + 8. Значит, на парах граней с суммой 18 напротив 11 находится 7, а напротив 10 — 8.
Задача № 6 :
В конкурсе участвовали 5 человек. На каждый вопрос один из них дал неправильный ответ, остальные — правильный. Число правильных ответов у Пети равно 10 — меньше, чем у любого другого. Число правильных ответов у Васи равно 13 — больше, чем у любого другого. Сколько всего вопросов было в конкурсе?
Ответ : 14 .
Решение :
Так как на каждый вопрос были даны 4 правильных ответа, общее число правильных ответов делится на 4. Поскольку Петя дал 10 верных ответов, Вася — 13, а остальные трое — от 11 до 12, то общее число правильных ответов не меньше, чем 10 + 13 + 3·11 = 56, и не больше, чем 10 + 13 + 3·12 = 59. Из чисел в этих пределах только 56 кратно 4, поэтому число вопросов равно
Задача № 7 :
Команда из Пети, Васи и одноместного самоката участвует в гонке. Дистанция разделена на участки одинаковой длины, их количество равно 42, в начале каждого — контрольный пункт. Петя пробегает участок за 9 мин, Вася — за 11 мин, а на самокате любой из них проезжает участок за 3 мин. Стартуют они одновременно, а на финише учитывается время того, кто пришел последним. Ребята договорились, что один проезжает первую часть пути на самокате, остаток бегом, а другой — наоборот (самокат можно оставить на любом контрольном пункте). Сколько участков Петя должен проехать на самокате, чтобы команда показала наилучшее время?
Ответ : 18
Решение :
Если Петя проедет 18 участков и пробежит оставшиеся 42 – 18 = 24, он затратит 18·3 + 24·9 = 270 мин. При этом Васе, наоборот, достанется проехать 24 участка, а пробежать 18, на что уйдет 24·3 + 18·11 = 270 мин — то же самое время. Если же Петя проедет меньшее число участков, то его время (и, соответственно, время команды) увеличится. Если Петя проедет большее количество участков, то увеличится время Васи (и время команды).
Достаточно обозначить число проезжаемых Петей участков через x и решить уравнение
x·3 + (42 – x)·9 = (42 – x)·3 + 11x.
Задача № 1 :
Нарисуйте на плоскости пять различных прямых так, чтобы они пересекались ровно в семи различных точках.
Решение :
Три возможных ответа изображены на рисунке 1. Можно показать, что других конфигураций из пяти прямых, пересекающихся ровно в семи различных точках, нет.
Задача № 2 :
Мальчик пошел с отцом в тир. Отец купил ему 10 пулек. В дальнейшем отец за каждый промах отбирал у сына одну пульку, а за каждое попадание давал одну дополнительную пульку. Сын выстрелил 55 раз, после чего пульки у него кончились. Сколько раз он попал?
Ответ: 50.
Решение :
Каждый раз, когда мальчик попадал в цель, число имеющихся у него пулек оставалось прежним (одну использовал и одну получил от отца). Каждый раз, когда мальчик промахивался, число имеющихся у него пулек уменьшалось на 2 (одну использовал и одну отобрал отец). Это значит, что сын за 55 выстрелов промахнулся 10 : 2 = 5 раз, стало быть, попал 55 – 5 = 50 раз.
Задача № 3 :
Две биссектрисы треугольника пересекаются под углом 60°. Докажите, что один из углов этого треугольника равен 60°.
Решение :
Пусть биссектрисы AA1 и CC1 треугольника ABC пересекаются в точке I (рис.2). Допустим, что AIC1 = 60°. По теореме о внешнем угле треугольника
откуда
BAC + BCA = 120°
и
ABC = 180°– BAC – BCA = 60°.
Но это еще не все решение: ведь может случиться, что AIC = 60°. Однако тогда
IAC + ICA = 120°,
откуда
BAC + BCA = 240°,
что невозможно.
Задача № 4 :
Когда Винни-Пух пришел в гости к Кролику, он съел 3 тарелки меда, 4 тарелки сгущенки и 2 тарелки варенья, а после этого не смог выйти наружу из-за того, что сильно растолстел от такой еды. Но известно, что если бы он съел 2 тарелки меда, 3 тарелки сгущенки и 4 тарелки варенья или 4 тарелки меда, 2 тарелки сгущенки и 3 тарелки варенья, то спокойно смог бы покинуть нору гостеприимного Кролика. От чего больше толстеют: от варенья или от сгущенки?
Ответ : от сгущенки.
Решение :
По условию
3м + 4с + 2в > 2м + 3с + 4в,
откуда
м + с > 2в. (*)
По условию же
3м + 4с + 2в > 4м + 2с + 3в,
откуда
2с > м + в.
Складывая последнее неравенство с неравенством (*), получаем м + 3с > м + 3в, откуда с > в.
Задача № 5 :
В каждой клетке клетчатой доски размером 50 ? 50 записано по числу. Известно, что каждое число в 3 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по стороне, и в 2 раза меньше суммы всех чисел, записанных в клетках, соседних с ним по диагонали. Докажите, что каждую клетку доски можно покрасить в красный или синий цвет так, что сумма всех чисел, записанных в красных клетках, равна сумме всех чисел, записанных в синих клетках.
Решение :
Покажем, что подойдет раскраска клеток доски в шахматном порядке. Заметим, что сумма данного числа и его соседей по диагоналям равна сумме соседей этого числа по сторонам: обе суммы втрое больше данного числа. Поэтому в квадрате 2 ? 2, находящемся в углу доски, суммы чисел в красных и синих клетках совпадают: обе они втрое больше числа, стоящего в угловой клетке доски. Также совпадают суммы чисел в красных и синих клетках любого прямоугольника 3 ? 2, примыкающего длинной стороной к краю доски: обе они втрое больше числа, стоящего в средней клетке стороны, примыкающей к краю доски. Наконец, совпадают суммы чисел в красных и синих клетках любого квадрата 3 ? 3: обе они втрое больше числа, стоящего в центре квадрата.
Разобьем доску 50 ? 50 на квадрат 48 ? 48, квадрат 2 ? 2 и два прямоугольника 2 ? 48, как показано на рисунке 3. Квадрат 48 ? 48 разобьем на квадраты 3 ? 3, а прямоугольники 2 ? 48 — на прямоугольники 3 ? 2, примыкающие длинной стороной к краю доски. В каждом из этих квадратов и прямоугольников суммы чисел, стоящих в красных и синих клетках, равны. Значит, они равны и на всей доске.
konspekt-v-gruppe.ru
Школьная олимпиада 8 класс
Всероссийская олимпиада школьников по математике (школьный этап)
2015-2016 учебный год
8 класс
Задание 1
Какой цифрой оканчивается сумма ?
Ответ: Нулём.
Решение: .
Задание 2
Три математика ехали в разных вагонах одного поезда. Когда поезд подъезжал к станции, математики насчитали на перроне 7, 12 и 15 скамеек. Когда поезд отъезжал, каждый из них насчитал еще несколько скамеек, причем один из них насчитал в три раза больше, чем другой. А сколько насчитал третий?
Ответ: 7 скамеек.
Решение: Очевидно, что тот, кто до остановки проехал большую часть перрона, насчитал большее число скамеечек. Пусть первый насчитал 15 скамеек, второй 12, третий 7. Так как первый насчитал на 3 скамейки больше, чем второй, то, когда поезд будет отъезжать, второй увидит эти 3 скамейки, т.е. насчитает на 3 скамейки больше, чем первый. Аналогично третий насчитает на 8 скамеек больше, чем первый, и на 5 скамеек больше, чем второй. Раз кто-то насчитал в 3 раза больше, чем другой, то разница между насчитанными ими скамейками – четное
число (3x-x=2x). В нашем случае разность насчитанных скамеек четна только между первым и третьим и она равна 8. Значит, первый насчитал 8:2=4 скамейки, тогда второй 4+3=7 скамеек.
Замечание: Можно было обойтись и без четности. Пусть первый насчитал x скамеек. Тогда второй x+3, а третий x+8. А дальше составить всевозможные пары и решить получившиеся три уравнения (один насчитал в три раза больше, чем другой в паре): 3x=x+3, 3x=x+8, 3(x+5)=x+8. Только одно из них имеет целое решение.
Задание 3
Найдите 3 числа, обладающие следующими свойствами: они целые, положительные и сумма обратных величин этих чисел равна 1.
Ответ: (2; 4; 4), (2; 3; 6), (3; 3; 3)
Задание 4
Фирма изготавливает лимонный напиток, разбавляя лимонный сок водой. Сначала фирма производила напиток, содержащий 15% лимонного сока. Через некоторое время генеральный директор отдал указание снизить содержание лимонного сока до 10%. На сколько процентов увеличится количество производимого лимонного напитка при тех же объёмах поставок лимонов?
Ответ: На 50%.
Решение: 1 способ. Содержание лимонного сока в напитке после указания генерального директора снизилось в полтора раза. Значит, из тех же лимонов можно приготовить в полтора раза больше лимонного напитка. Иными словами, количество производимого лимонного напитка увеличится в полтора раза или на 50%.
2 способ. Пусть х – количество производимого напитка до указания генерального директора. Тогда количество лимонного сока в этом напитке – 0,15·х. Пусть теперь у – количество производимого напитка после указания генерального директора. Тогда количество лимонного сока в этом напитке – 0,1·у. Так как подразумевается, что количество лимонного сока не изменилось, получаем равенство 0,15·х = 0,1·у. Умножив обе части этого равенства на 10, получим: у = 1,5·х; или: у = х + 0,5·х. Значит, количество производимого напитка увеличилось на 50%.
Задание 5
Один из углов треугольника на 120° больше другого. Докажите, что биссектриса треугольника, проведённая из вершины третьего угла, вдвое длиннее, чем высота, проведенная из той же вершины.
Доказательство:
Пусть ABC — данный треугольник, B = α, A = 120° + α . Тогда C = 60° — 2α . Если CL — биссектриса данного треугольника, то CLA = LCB + LBC = (30° — α) + α = 30°. Пусть CH — высота треугольника АВС, тогда в треугольнике CLH катет CH, лежащий против угла в 30°, в два раза меньше, чем гипотенуза CL.
Примерные критерии оценивания заданий по математике
2015– 2016 учебный год
8 класс
В соответствии с регламентом проведения математических олимпиад школьников каждая задача оценивается из 7 баллов.
Соответствие правильности решения и выставляемых баллов приведено в таблице.
Баллы
Правильность (ошибочность) решения
7
Полное верное решение.
6 -7
Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.
5 — 6
Решение в целом верное. Однако оно содержит ряд ошибок, либо не рассмотрение отдельных случаев, но может стать правильным после небольших исправлений или дополнений.
4
Верно рассмотрен один из двух (более сложный) существенных случаев, или в задаче типа «оценка + пример» верно получена оценка.
2 — 3
Доказаны вспомогательные утверждения, помогающие в решении задачи.
1
Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).
0
Решение неверное, продвижения отсутствуют. Решение отсутствует.
8 класс
Задание 1
Какой цифрой оканчивается сумма ?
Задание 2
Три математика ехали в разных вагонах одного поезда. Когда поезд подъезжал к станции, математики насчитали на перроне 7, 12 и 15 скамеек. Когда поезд отъезжал, каждый из них насчитал еще несколько скамеек, причем один из них насчитал в три раза больше, чем другой. А сколько насчитал третий?
Задание 3
Найдите 3 числа, обладающие следующими свойствами: они целые, положительные и сумма обратных величин этих чисел равна 1.
Задание 4
Фирма изготавливает лимонный напиток, разбавляя лимонный сок водой. Сначала фирма производила напиток, содержащий 15% лимонного сока. Через некоторое время генеральный директор отдал указание снизить содержание лимонного сока до 10%. На сколько процентов увеличится количество производимого лимонного напитка при тех же объёмах поставок лимонов?
Задание 5
Один из углов треугольника на 120° больше другого. Докажите, что биссектриса треугольника, проведённая из вершины третьего угла, вдвое длиннее, чем высота, проведенная из той же вершины.
infourok.ru
Задания школьного этапа олимпиады школьников по математике 8 класс
Олимпиада по математике
Первый (школьный) этап Всероссийской олимпиады школьников.
Задания школьного этапа олимпиады школьников
по математике
8 класс
8.1 Решите уравнение: . (3б)
8.2 Число 56 разложите на два слагаемых так, чтобы первого
слагаемого была равна второго. (5б)
- Вычислите. (7б)
- Решите уравнение. (7б)
- Зная, что =, найдите значение выражения. (5б)
- Сколькими нулями оканчивается произведение всех целых чисел
от 1 до 100 включительно. (7б)
8.7 Постройте график функции (7б)
8. 9 Какой треугольник надо взять, чтобы после проведения в нем одного отрезка получить все известные виды треугольников: равносторонний, равнобедренный, прямоугольный, разносторонний, остроугольный, тупоугольный? (7б)
Ответы
к заданиям по олимпиаде для 8-го класса
1.
2. 24 и 32.
3.
4. или.
5. 1
6.В произведении всех чисел от 1 до 100 содержится 24 «пятерки»; по одной в числах 10, 20, 30, 40, 50, 60, 70, 80, 90, 5, 15, 25, 35, 45, 55, 65, 75, 85, 95 и по две в числах 25, 50, 75, 100. Так как произведение цифры «5» на любое четное число оканчивается нулем, то произведение чисел от 1 до100 оканчивается 24 нулями.
7. Упрощая правую часть, имеем:, где. Таким образом, графиком указанной функции является прямая, заданная формулой, без двух точек: и.
8. Треугольник с углами 600, 300, 900. На гипотенузе взять точку так, чтобы угол был равен 600. Тогда — прямоугольный, — остроугольный, — тупоугольный, — равносторонний, — равнобедренный, — разносторонний.
Просмотр содержимого документа
«Задания школьного этапа олимпиады школьников по математике 8 класс»
Олимпиада по математике
Первый (школьный) этап Всероссийской олимпиады школьников.
Задания школьного этапа олимпиады школьников по математике 8 класс8.1 Решите уравнение: . (3б)
8.2 Число 56 разложите на два слагаемых так, чтобы  первого
первого
слагаемого была равна 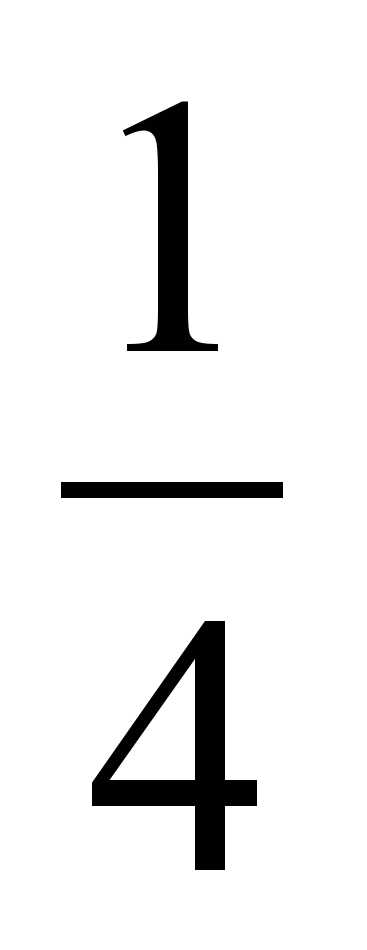 второго. (5б)
второго. (5б)
Вычислите
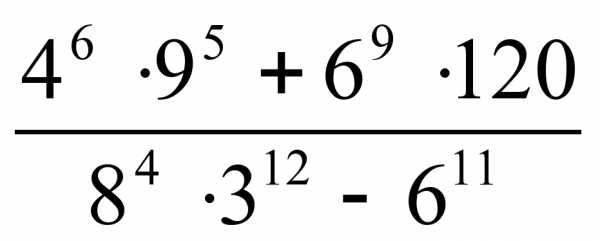 . (7б)
. (7б)
Решите уравнение
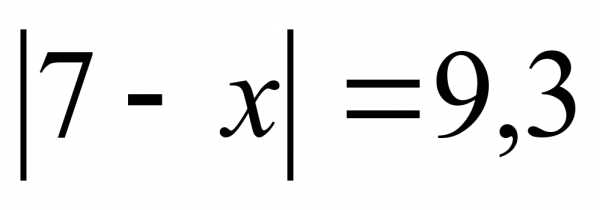 . (7б)
. (7б)
Зная, что
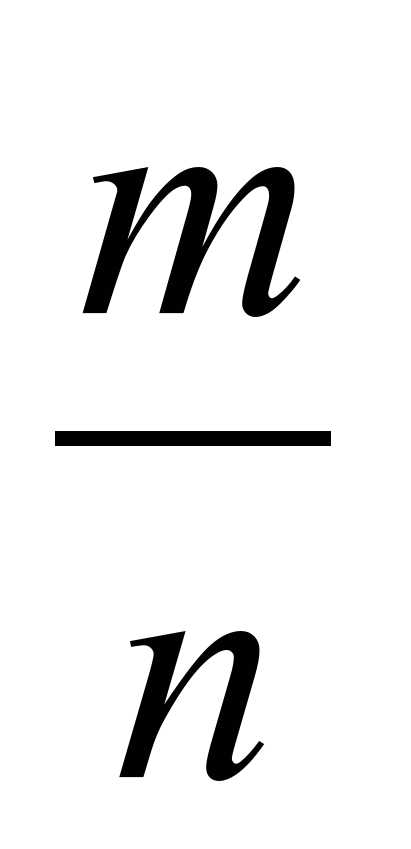 =
=  , найдите значение выражения
, найдите значение выражения  . (5б)
. (5б)
Сколькими нулями оканчивается произведение всех целых чисел
от 1 до 100 включительно. (7б)
8.7 Постройте график функции 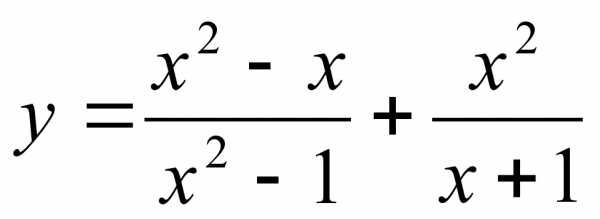 (7б)
(7б)
8. 9 Какой треугольник надо взять, чтобы после проведения в нем одного отрезка получить все известные виды треугольников: равносторонний, равнобедренный, прямоугольный, разносторонний, остроугольный, тупоугольный? (7б)
Ответы
к заданиям по олимпиаде для 8-го класса
1. 
2. 24 и 32.
3..
4. 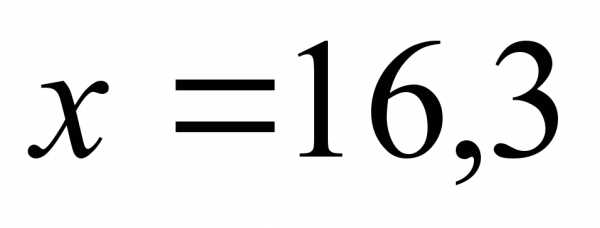 или
или 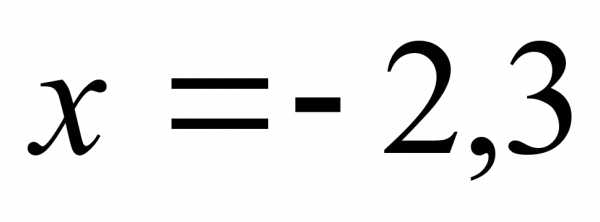 .
.
5. 1
6.В произведении всех чисел от 1 до 100 содержится 24 «пятерки»; по одной в числах 10, 20, 30, 40, 50, 60, 70, 80, 90, 5, 15, 25, 35, 45, 55, 65, 75, 85, 95 и по две в числах 25, 50, 75, 100. Так как произведение цифры «5» на любое четное число оканчивается нулем, то произведение чисел от 1 до100 оканчивается 24 нулями.
7. Упрощая правую часть, имеем: 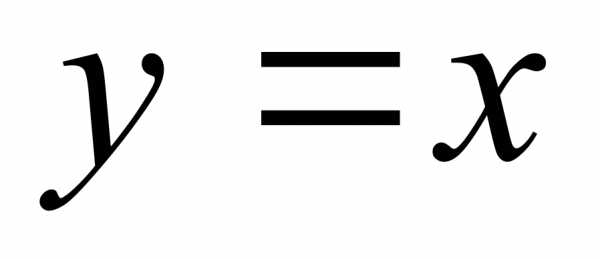 , где
, где 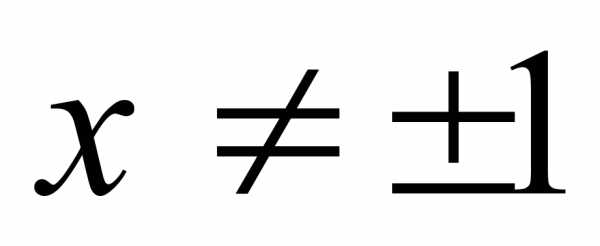 . Таким образом, графиком указанной функции является прямая, заданная формулой
. Таким образом, графиком указанной функции является прямая, заданная формулой 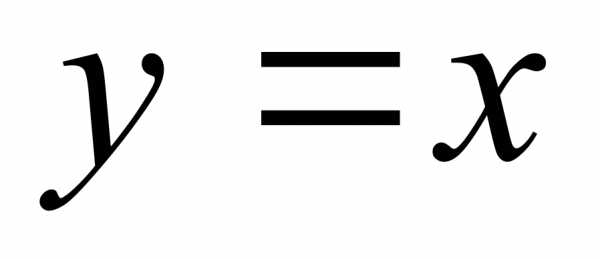 , без двух точек:
, без двух точек: 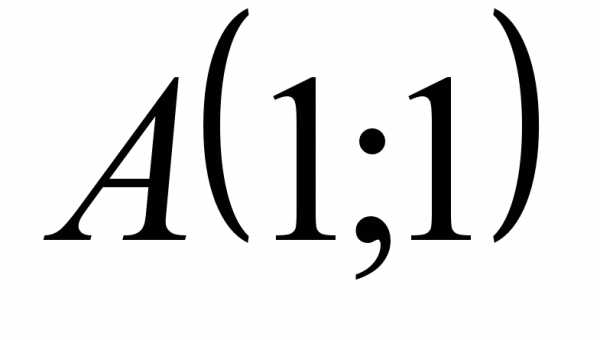 и
и 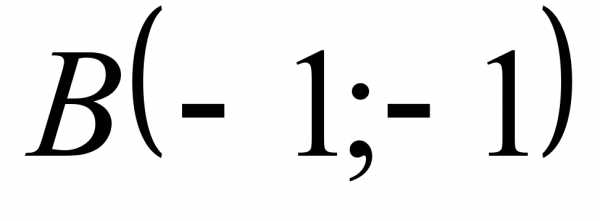 .
.
8. Треугольник с углами 600, 300, 900. На гипотенузе  взять точку
взять точку  так, чтобы угол
так, чтобы угол 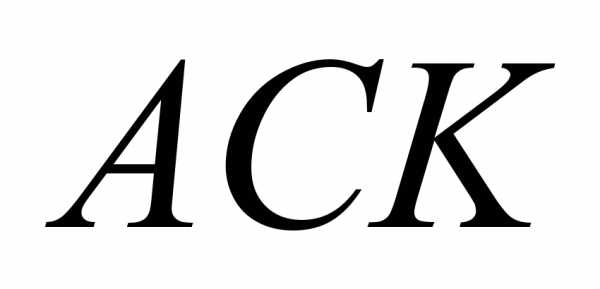 был равен 600. Тогда
был равен 600. Тогда  — прямоугольный,
— прямоугольный, 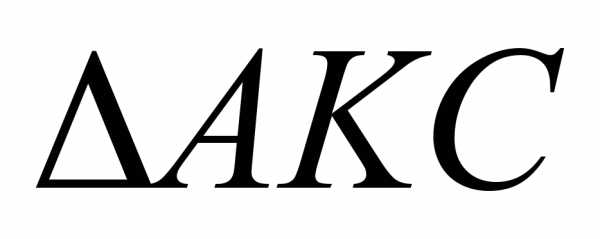 — остроугольный,
— остроугольный,  — тупоугольный,
— тупоугольный, 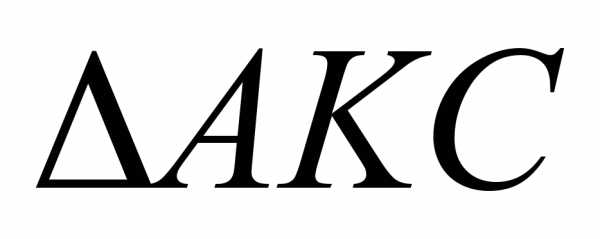 — равносторонний,
— равносторонний, 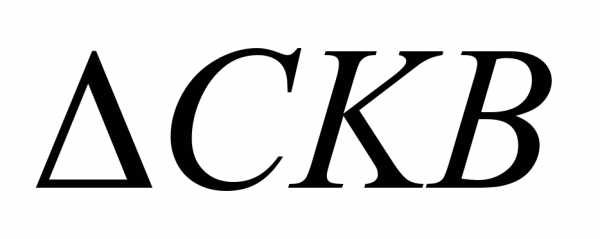 — равнобедренный,
— равнобедренный, 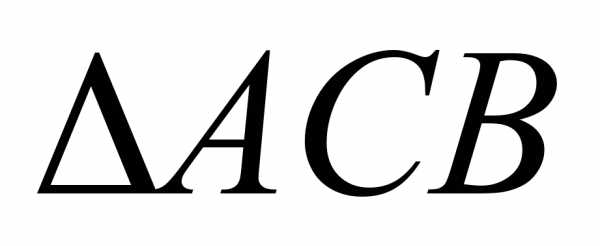 — разносторонний.
— разносторонний.
2
kopilkaurokov.ru
Олимпиада по математике. Муниципальный этап. 8 класс
- Подробности
- Родительская категория: Олимпиадные задания
- Категория: Олимпиадные задания по математике 8 класс
Олимпиада по математике. Решение олимпиадных задач по математике. 8 класс
№ 1. Две машины едут по трассе скоростью 80 км/ч и с интервалом 10 м. У знака ограничения скорости машины мгновенно снижают скорость до 60 км/ч. С каким интервалом они будут двигаться после знака ограничения? Решение
№ 2. В шестизначном числе зачеркнули одну цифру и получили пятизначное. Из исходного числа вычли это пятизначное число и получили 654321. Найдите исходное число. Решение
№ 3. Дан треугольник ABC. Точка M лежит на стороне BC. Известно, что AB= BM и
AM= MC, угол Bравен 100°. Найдите остальные углы треугольника ABC. Решение
№ 4. Какое наибольшее число ладей можно разместить на шахматной доске так, чтобы для каждой ладьи либо её горизонталь, либо её вертикаль (либо и та, и другая) были свободны от других ладей? Решение
№ 5. а) Даны натуральные числа a и b. Обязательно ли они имеют одинаковые остатки при делении на 10, если известно, что числа и имеют одинаковые остатки при делении на 10 ?
б) Даны натуральные числа a, b и с. Известно, что у чисел 2a+b, 2b+c и 2c+ a остатки при делении на 10 одинаковые. Докажите, что у чисел a, b и с остатки при делении на 10 тоже одинаковые. Решение
Городской этап.
metodtest.ru
Математика 8 класс, муниципальный этап (2 этап), г. Москва, 2016 год
Задание 1
Последняя цифра в записи натурального числа в 2016 раз меньше самого числа. Найдите все такие числа.
Ответ: 4032, 8064, 12096, 16128.
Решение. Пусть x – последняя цифра числа. Далее можно рассуждать по-разному.
Первый способ. Число 2016x должно оканчиваться на цифру х. Следовательно, x – четная цифра, причем x ≠ 0. Проверкой убеждаемся, что значения x, равные 2, 4, 6 и 8 удовлетворяют условию.
Можно также провести полный перебор всех возможных значений x: проверить все цифры от 0 до 9.
Второй способ. Пусть искомые числа имеют вид ax = 10a ≠x, где a – некоторое натуральное число.
Тогда x a 10a+x = 2016x ⇔ 2a = 403x. Так как 2 и 403 взаимно простые числа, то a делится на 403, а x делится на 2. Подставляя, например, в полученное равенство значения x, равные 2, 4, 6 и 8, находим соответствующие значения a и получаем ответ.
Критерии проверки
- “+” – приведено полное обоснованное решение (любым из способов, независимо от его рациональности)
- “±” – приведен только полностью верный ответ
- “ ” – приведено верное рассуждение, но в ответе пропущено какое-то одно из чисел
- “–” – в ответе верно приведено не более двух чисел
- “–” – задача не решена или решена неверно
Задание 2
Расставьте в левой части равенства
Равенство для задания 2
знаки арифметических операций и скобки так, чтобы равенство стало верным для всех а, отличных от нуля.
Ответ: например, так:
Ответ для задания 2
Существуют и другие примеры.
Критерии проверки
- “+” – приведена любая верная расстановка знаков и скобок
- “–” – задача не решена или решена неверно
Задание 3
Точки пересечения графиков четырех функций, заданных формулами y = kx + b, y = kx – b, y = mx + b и y = mx – b, являются вершинами четырехугольника. Найдите координаты точки пересечения его диагоналей.
Ответ: (0; 0).
Решение
Графики данных линейных функций – это две пары параллельных прямых, так как равны угловые коэффициенты у первой и второй прямой и угловые коэффициенты у третьей и четвертой прямой.
Значит, точки пересечения графиков являются вершинами параллелограмма. Две противоположные вершины этого параллелограмма – это М(0; b) и N(0; –b). Так как диагонали параллелограмма, пересекаясь, делятся точкой пересечения пополам, то искомая точка – середина отрезка MN, то есть точка (0; 0).
Критерии проверки
- “+” – приведено полное обоснованное решение
- “±” – приведено верное в целом рассуждение, содержащее незначительные пробелы или неточности
- “ ” – приведен только верный ответ
- “–” – задача не решена или решена неверно
Задание 4
В классе учатся 30 человек: отличники, троечники и двоечники. Отличники на все вопросы отвечают правильно, двоечники всегда ошибаются, а троечники на заданные им вопросы строго по очереди то отвечают верно, то ошибаются. Всем ученикам было задано по три вопроса: “Ты отличник?”, “Ты троечник?”,
“Ты двоечник?”. Ответили “Да” на первый вопрос – 19 учащихся, на второй – 12, на третий – 9. Сколько троечников учится в этом классе?
Ответ: 20 троечников
Решение. Пусть a – количество отличников, b – количество двоечников, c – количество троечников, которые ошиблись в ответе на первый вопрос, правильно ответили на второй и ошиблись в ответе на третий (назовем таких троечников троечниками первого типа), а d – количество троечников, которые правильно ответили на первый вопрос, ошиблись в ответе на второй и правильно ответили на третий (назовем таких троечников троечниками второго типа).
На первый вопрос ответили “Да” отличники, двоечники и троечники первого типа, следовательно, a + b + c = 19. На второй вопрос “Да” ответили двоечники и троечники первого типа, то есть b + c = 12. На третий вопрос “Да” ответили только троечники первого типа, то есть c = 9. Тогда из второго уравнения получим, что b = 3, а из первого уравнения: a = 7. В классе – 30 учащихся, значит d = 30 – 19 = 11, поэтому всего троечников: 9 + 11 = 20.
Критерии проверки
- “+” – приведено полное обоснованное решение
- “±” – приведено верное в целом рассуждение, содержащее незначительные пробелы или неточности
- “ ” – в приведенных рассуждениях указано, что троечники бывают двух типов, но дальнейших продвижений нет или допущена вычислительная ошибка.
- “–” – задача не решена или решена неверно
Задание 5
В прямоугольнике ABCD на диагонали AC отмечена точка K так, что CK = BC. На стороне ВС отмечена точка М так, что КМ = СМ. Докажите, что АK + ВМ = СМ.
Решение
На продолжении стороны BC за точку В отметим такую точку Е, что BЕ = AK, тогда CЕ = СB + BЕ = СK + KА = СА (см. рис. 8.5).
Рисунок 8.5
В треугольниках ЕKC и ABC: CЕ = CA, CK = CB, угол ECA – общий, значит, эти треугольники равны. Следовательно, ∠ЕKC = ∠ABC = 90°.
Пусть ∠KCM = ∠MKC = α, тогда ∠MKE = 90° – α = ∠MEK, значит, МЕ = MK = МС.
Таким образом, АK + ВМ = ВЕ + ВМ = МЕ = СМ, что и требовалось.
Сделав такое же дополнительное построение, можно вместо равенства треугольников EKC и АВС доказывать равенство треугольников KBE и BKA, используя равнобедренность треугольника BCK.
Существуют и другие способы решения.
Критерии проверки
- “+” – приведено полное обоснованное решение
- “±” – приведено верное в целом рассуждение, содержащее незначительные пробелы или неточности
- “–” – задача не решена или решена неверно
Задание 6
Какое наибольшее количество натуральных чисел, не превосходящих 2016, можно отметить так, чтобы произведение любых двух отмеченных чисел было бы точным квадратом?
Ответ: 44.
Решение
Найдем количество натуральных чисел, квадраты которых не больше, чем 2016. Таких чисел – 44, так как 442 = 1936 < 2016, а 452 = 2025 > 2016. Так как произведение двух точных квадратов является точным квадратом, то числа 1 = 12, 4 = 22, …, 1936 = 442 могут быть отмечены.
Докажем, что большее количество чисел отметить невозможно. Действительно, рассмотрим искомый набор чисел и разделим каждое из чисел этого набора на наибольший точный квадрат, на который оно делится. Получим новый набор чисел, причем в разложение каждого из получившихся чисел на простые множители эти множители могут входить только в первой степени. Заметим, что каждый простой множитель (если он есть) должен присутствовать во всех разложениях, так как при перемножении любых двух чисел полученного набора он должен оказаться в четной степени. Это означает, что после деления каждого числа искомого набора на наибольшие квадраты должно получиться одно и то же число q. Если q = 1, то получим набор из 44 чисел, которые сами являются точными квадратами (см. выше), а если q > 1, то получим набор из меньшего количества чисел, поскольку 1936q > 2016.
Критерии проверки
- “+” – приведено полное обоснованное решение
- “±” – приведено верное в целом рассуждение, содержащее незначительные пробелы или неточности
- “ ” – приведены только верный ответ и верный пример
- “–” – приведен только ответ
- “–” – задача не решена или решена неверно
olimpiadnye-zadanija.ru
Школьный тур олимпиады по математике «Олимпиада 8 класс»
Школьный тур Олимпиады по математике 8 класс
1. В равенстве (ayb)c=-64y6 замените a , b и c целыми числами, отличными от 1 , так, чтобы получилось тождество.
2. Петя тратит 1/3 своего времени на игру в футбол, 1/5 — на учебу в школе, 1/6 — на просмотр кинофильмов, 1/7 — на решение олимпиадных задач, и 1/3 — на сон. Можно ли так жить?
3. У колхозника было несколько одинакового веса поросят и несколько ягнят также одинакового веса. Пионер спросил колхозника, сколько весит один поросенок и один ягненок. Колхозник ответил, что 3 поросенка и 2 ягненка весят 22 кг, а 2 поросенка и 3 ягненка весят 23 кг. Как узнать, сколько весит один поросенок и сколько весит один ягненок?
4. Один из углов треугольника на 120° больше другого. Докажите, что биссектриса треугольника, проведённая из вершины третьего угла, вдвое длиннее, чем высота, проведенная из той же вершины.
5. У подводного царя служат осьминоги с шестью, семью или восемью ногами. Те, у кого 7 ног, всегда лгут, а у кого 6 или 8 ног, всегда говорят правду. Встретились четыре осьминога. Синий сказал: «Вместе у нас 28 ног», зеленый: «Вместе у нас 27 ног», желтый: «Вместе у нас 26 ног», красный: «Вместе у нас 25 ног». У кого сколько ног?
Решение школьного тура Олимпиады по математике 8 класс
1. В равенстве (ayb)c=-64y6 замените a , b и c целыми числами, отличными от 1 , так, чтобы получилось тождество.
Ответ: существует единственное решение: (—4 y2)3=-64y6 .
2. Петя тратит 1/3 своего времени на игру в футбол, 1/5 — на учебу в школе, 1/6 — на просмотр кинофильмов, 1/7 — на решение олимпиадных задач, и 1/3 — на сон. Можно ли так жить?
Решение Поскольку 1/5 + 1/6 > 1/3, то сумма данных дробей 1/3 + 1/5 + 1/6 + 1/7 + 1/3 > 1, что противоречит здравому смыслу. Нет, так жить нельзя.
3. У колхозника было несколько одинакового веса поросят и несколько ягнят также одинакового веса. Пионер спросил колхозника, сколько весит один поросенок и один ягненок. Колхозник ответил, что 3 поросенка и 2 ягненка весят 22 кг, а 2 поросенка и 3 ягненка весят 23 кг. Как узнать, сколько весит один поросенок и сколько весит один ягненок?
Решение. Если сложить вес трех поросят и двух ягнят с весом двух поросят и трех ягнят, то получим вес пяти поросят и пяти ягнят, равный 45 кг. Значит, один поросенок и один ягненок весят 9 кг, а два поросенка и два ягненка весят 18 кг. Вычтя это из первого данного веса, получим вес поросенка, равный 4 кг. Тогда ягненок весит 5 кг.
4. Один из углов треугольника на 120° больше другого. Докажите, что биссектриса треугольника, проведённая из вершины третьего угла, вдвое длиннее, чем высота, проведенная из той же вершины.
Решение Пусть ABC — данный треугольник, B = a, A = 120° + a. Тогда C = 60° — 2a. Если CL — биссектриса данного треугольника, то CLA = LCB + LBC = (30° — a) + a = 30°. Пусть CH — высота треугольника АВС, тогда в треугольнике CLH катет CH, лежащий против угла в 30°, в два раза меньше, чем гипотенуза CL.
5. У подводного царя служат осьминоги с шестью, семью или восемью ногами. Те, у кого 7 ног, всегда лгут, а у кого 6 или 8 ног, всегда говорят правду. Встретились четыре осьминога. Синий сказал: «Вместе у нас 28 ног», зеленый: «Вместе у нас 27 ног», желтый: «Вместе у нас 26 ног», красный: «Вместе у нас 25 ног». У кого сколько ног?
Решение Так как осьминоги противоречат друг другу, то возможны два случая: либо все осьминоги лгут, либо ровно один из них говорит правду. Если все осьминоги лгут, то у каждого из них по 7 ног. Значит, вместе у них 28 ног. Но тогда синий осьминог сказал правду — противоречие.
Если же три осьминога солгали, а четвёртый сказал правду, то у солгавших осьминогов должно быть по 7 ног, а у сказавшего правду — либо 6, либо 8. Поэтому вместе у них либо 27, либо 29 ног, то есть правду сказал зелёный осьминог. Таким образом, у зелёного осьминога 6 ног, а у остальных по 7 ног.
Критерии оценки.
Задание1. Максимальный балл 1
Задача оценивается, если имеется развёрнутое решение.
Задача2. Максимальный балл 2
Задача оценивается, максимально, если имеется развёрнутое, безошибочное решение. Каждая вычислительная ошибка снижает балл на 0,5.
Задача3. Максимальный балл 3
Задача оценивается, максимально, если имеется развёрнутое, безошибочное решение. Каждая вычислительная ошибка снижает балл на 0,5; каждая ошибка в рассуждениях снижает балл на 0,5.
Задача4. Максимальный балл 4
Задача оценивается, максимально, если имеется развёрнутое, безошибочное решение. Каждая вычислительная ошибка снижает балл на 0,5; каждая ошибка в рассуждениях снижает балл на 0,5.
Задача5. Максимальный балл 5
Задача оценивается, максимально, если имеется развёрнутое, безошибочное решение. Каждая вычислительная ошибка снижает балл на 0,5; каждая ошибка в рассуждениях снижает балл на 0,5.
infourok.ru
