Всероссийская олимпиада по математике 5 класс с ответами 2018 2018 – Олимпиадные задания по математике (5, 6, 7, 8, 9, 10, 11 класс) на тему: Школьный этап Всероссийской олимпиады школьников по математике | скачать бесплатно

Олимпиада по математике 5 класс с ответами 2017-2018 муниципальный этап

1. Напишите наименьшее десятичное число, у которого все цифры различны.

                                                                                                                              (2 балла)

2. В четырехэтажном доме Ваня живет выше Пети, но ниже Сени, а Коля живет ниже Пети. Кто на каком этаже живет?                                                        (3 балла)                                                                                                                                                        
3.  Переложите 4 спички таким образом, чтобы образовались три квадрата:

                                                                                                                           (4 балла)

4. Катя и Юра купили лотерейные билеты с номерами 625517 и 322324 и обнаружили, что в каждом из номеров можно расставить знаки арифметических действий и скобки так, что в каждом случае результат будет равняться 100. Как это можно сделать?                                                                                           (4 балла)                                                                                                          
5. В корзине лежат яблоки, груши и персики – всего 37 плодов. Яблок в корзине в два раза больше, чем персиков, и на 3 штуки больше, чем груш. Сколько в корзине яблок, груш и персиков?                                                                  (5 баллов)                                                                                    

Решение и ответы:

1. Ответ: 1023456789.
2. Ответ:

4 этаж	Сеня
3 этаж	Ваня
2 этаж	Петя
1 этаж	Коля

3. Ответ: 

4. Ответ: например, 62+55-17 и (3+22)*(3-2)*4
5. По условию задачи всего 37 плодов, составим уравнение  х+2х+2х-3=37,

5х-3=37, 5х=40,

х=8 – персиков

2*8=16 – яблок

16-3=13 – груш

Ответ: 8 персиков, 16 яблок, 13 груш.

Решение считается неполным, если оно:

1.  Содержит основные идеи, но не доведено до конечного результата;

2.   Опирается  на  недоказанные  утверждения,  которые  нельзя  считать известными или очевидными.

konspekt-v-gruppe.ru

Олимпиада по математике 5 класс с ответами 2017-2018 школьный этап

Задания для 5 класса.

Каждая задача оценивается в 5 баллов.

1. Найдите цифры, вместо которых стоят звездочки:

          * 8 *

          4 * 2

         ——-

          7 * 0

        * * *

    * * * *

    —————

  * * * * 2 *

2. На одной чаше весов лежат шесть одинаковых пачек чая и гиря массой 50г., а на другой – одна пачка чая и две гири массой 100 и 200 г. Весы находятся в равновесии. Определите, сколько граммов весит одна пачка чая?
   
3. В  олимпийской команде по конному спорту  пять  голов  и  четырнадцать  ног.  Сколько  из  них  людей, а сколько лошадей?
4. Разрежьте циферблат часов на три части так, чтобы сумма цифр
   в каждой части была одинаковой.

5. Талисманы олимпийских игр в Сочив 2014 году — Зайка, Белый Мишка и Леопард – после изнурительных тренировок сели пить чай. Белый Мишка и Зайка выпили вдвоём 11 чашек, Леопард и Белый Мишка — 15, а Зайка и Леопард — 14. Сколько чашек чая выпили все Зайка, Белый Мишка и Леопард вместе?

Решение.

1. Указание: Усмотреть, что последняя цифра в первом числе – это 0 или 5, а первая цифра – 3, а затем перебрать несколько вариантов.
   Ответ: 385·412=158620.
2. Решение: 1)100+200=300 грамм на одних весах.
   2)300-50=250 грамм чая
   3)250:(6-1)=50
   Ответ: 50 г.
3. Ответ. 3 человека и 2 лошади.

     Решение.  Предположим  сначала,  что  все  пятеро – люди. Это 5 голов и 10 ног.  Замена одного  человека  на лошадь дает +2 ноги. У нас пока что недостает 4 ноги. Значит, нужно 2 человека заменить лошадьми.

4. Решение:    Сумма всех цифр на циферблате равна 1+2+3+…+9+1+0+1+1+1+2=51. Значит, на каждой из частей сумма цифр должна быть равна 51:3=17.

5. Ответ: 20 чашек

Решение:

Зайка + Белый Мишка =11 — по условию задачи      

Леопард + Белый Мишка =15 — по условию задачи      

Зайка + Леопард + 2 Белый Мишка =26,

Зайка + Леопард =14- по условию задачи

14+2Белый Мишка =26

2Белый Мишка =12

Белый Мишка =6

Зайка =5

Леопард =9

Белый Мишка + Зайка + Леопард =20

konspekt-v-gruppe.ru

Олимпиадные задания по математике 5

Олимпиадные задания

по математике для проведения школьного этапа Всероссийской олимпиады школьников в 2017 — 2018 уч. году.

( 5-7 кл)

1. класс

1.  Замените знаки * цифрами:

1. Дедка вдвое сильнее Бабки, Бабка втрое сильнее Внучки, Внучка вчетверо сильнее Жучки, Жучка впятеро сильнее Кошки, Кошка вшестеро сильнее Мышки. Без Мышки все остальные не могут вытащить репку, а вместе с Мышкой – могут. Сколько мышек надо собрать вместе, чтобы эти мышки смогли вытащить репку сами?

2. Сумма всех чисел, изображенных на циферблате часов, равна 78. Раздели циферблат двумя прямыми линиями на три части так, чтобы сумма чисел в каждой части была одинаковой.

3. На одной чаше весов лежат шесть одинаковых пачек чая и гиря массой 50г., а на другой – одна пачка чая и две гири массой 100 и 200 г. Весы находятся в равновесии. Определите, сколько граммов весит одна пачка чая?

4. В семье четверо детей. Им 5, 8, 13, 15 лет. Детей зовут Аня, Боря, Вера, Галя. Сколько лет каждому ребёнку, если одна девочка ходит в детский сад, Аня старше Бори, и сумма лет Ани и Веры делится на 3.

1. класс

1. Одной черепахе 300 лет, а другой 15 лет. Через сколько лет первая черепаха будет вдвое старше второй?

2. Какие цифры скрываются за буквами:

–	МУХА		ХА
	ХА		УХА
	–	КХ
		АР
	–	УХА
		УХА
	0

1. На некотором острове каждый житель либо всегда лжет, либо всегда говорит правду. Трое островитян А, Б, В сказали следующее:

А: «Б – лжец»;

Б: «ровно один из А и В лжец»;

В: «у меня есть крокодил».

Есть ли у В крокодил?

1. Надя испекла пирожки с малиной, черникой и клубникой. Пирожков с малиной получилась половина от общего количества пирожков; пирожков с черникой – на 14 меньше, чем пирожков с малиной. А пирожков с клубникой получилось в два раза меньше, чем пирожков с малиной и черникой вместе. Сколько пирожков каждого вида испекла Надя?

2. Проведите 3 прямые так, чтобы тетрадный лист разделился на наибольшее число частей. Сколько получится частей? Проведите 4 прямые с тем же условием. Сколько теперь получилось частей?

1. класс

1. Вася может получить число 100, используя десять семерок, скобки и знаки арифметических действий:

100 = (77:7 – 7:7) · (77:7 – 7:7). Улучшите его результат: используя меньшее число семерок и получите число 100 (достаточно привести один пример).

1. Огород квадратной формы 5 м  5 м нужно разделить несколькими кусками ячеистой сетки на 5 равных по площади «клетчатых» участков. Это легко сделать, используя 20 м сетки, как показано на рисунке.

Хватит для этой цели 16 м сетки? Выполните рисунок.

1. В одной комнате сидят 9 человек, и их средний возраст – 25 лет. В другой комнате сидят 11 человек, и их средний возраст – 45 лет. Каков средний возраст всех 20 человек? (ответ обосновать).

2. Сколько прямоугольных пластин 20х45 см можно вырезать из фанерного листа 120х240 см? (ответ обосновать).

3. Дедушка решил подарить внукам по новогоднему подарку, состоящему из конфеты, яблока, апельсина, шоколадки и книги. На те же деньги он мог купить одни конфеты и их оказалось бы 224, яблоки– их было бы 112, апельсины – 56, шоколадки – 32, а книг – 16. Сколько внуков у дедушки?

Общие положения о проверке работ

Приведённые ниже решения задач не являются единственно возможными. Участники, вероятно, найдут и другие верные решения. При проверке и оценке решения учитывается только его верность и полнота. Приведённые ниже критерии по проверке задач также носят рекомендательный характер и могут быть уточнены и дополнены школьным жюри олимпиады в соответствии с особенностями решений школьников данной школы. Каждая задача оценивается целым числом баллов от 0 до 7. Итог подводится по сумме баллов, набранных участником.

Основные принципы оценивания задач :

7баллов — Полное верное решение.

6-7баллов Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение

5-6баллов Решение в целом верное. Однако оно содержит ряд ошибок, либо не рассмотрение отдельных случаев, но может стать правильным после небольших исправлений или дополнений.

4балла Верно рассмотрен один из двух (более сложный) существенных случаев.

2-3балла Доказаны вспомогательные утверждения, помогающие в решении задачи.

1балл Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).

0баллов Решение неверное, продвижения отсутствуют.

0 баллов Решение отсутствует.

Олимпиадная работа не является контрольной работой участника, поэтому любые исправления в работе, в том числе зачеркивание ранее написанного текста, не являются основанием для снятия баллов; недопустимо снятие баллов в работе за неаккуратность записи решений при ее выполнении. Баллы не выставляются «за старание участника», в том числе за запись в работе большого по объему текста, но не содержащего продвижений в решении задачи. Победителем в параллели считается участник, набравший наибольший суммарный балл и решивший не менее половины задач (не менее трех задач). Победителей в параллели может быть несколько. Призерами рекомендуется считать участников, решивших не менее половины задач, но набравших меньше баллов, чем победитель. Если ни один участник в данной параллели не решил более двух задач, жюри может принять решение считать призерами участников, решивших две задачи, однако победителей в этом случае не будет.

5 класс

№1 Замените знаки * цифрами:

Решение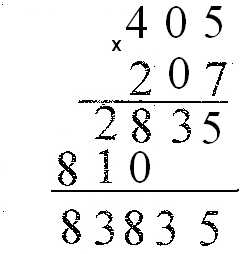

№2

Дедка вдвое сильнее Бабки, Бабка втрое сильнее Внучки, Внучка вчетверо сильнее Жучки, Жучка впятеро сильнее Кошки, Кошка вшестеро сильнее Мышки. Без Мышки все остальные не могут вытащить репку, а вместе с Мышкой – могут. Сколько мышек надо собрать вместе, чтобы эти мышки смогли вытащить репку сами?

Решение.

Кошка = 6 мышек;  жучка = 5 кошек = 30 мышек;  внучка = 4 жучки = 120 мышек; бабка = 3 внучки = 360 мышек; дедка = 2 бабки = 720 мышек. Все вместе дедка+бабка+внучка+жучка+кошка+мышка= 720+360+120+30+6+1=1237 мышек.

№3

Сумма всех чисел, изображенных на циферблате часов, равна 78. Раздели циферблат двумя прямыми линиями на три части так, чтобы сумма чисел в каждой части была одинаковой.

Решение задачи:

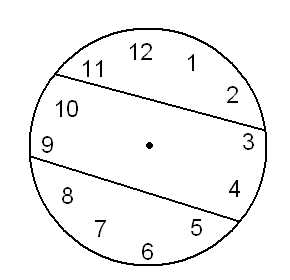
№4

На одной чаше весов лежат шесть одинаковых пачек чая и гиря массой 50г., а на другой – одна пачка чая и две гири массой 100 и 200 г. Весы находятся в равновесии. Определите, сколько граммов весит одна пачка чая?

Решение:

1. 6 пач.+50 г.=1 пач. +100 г.+200 г.

2 )6 пач.+50 г.=1 пач. +300 г.

3) 6 пач.=1 пач. +250 г.

4) 5 пач.=250 г.

5) 1 пач.=250:5=50 (г.)

Ответ: 50 (г.)

№5

В семье четверо детей. Им 5, 8, 13, 15 лет. Детей зовут Аня, Боря, Вера, Галя. Сколько лет каждому ребёнку, если одна девочка ходит в детский сад, Аня старше Бори, и сумма лет Ани и Веры делится на 3.

Решение.

5 лет — возраст ребёнка детского сада. Самый младший ребёнок — девочка в возрасте 5 лет.

Зная, что Аня старше Бори, получаем, что Ане либо 13, либо 15 лет.

Так как сумма лет Ани и Веры делится на 3, то получаем три случая:

1. Ане 15 лет, Вере 5 лет. 15+5=20, не делится на 3.

2. Ане 15 лет, Вере 8 лет. 15+8=23, не делится на 3.

3. Ане 13 лет, Вере 5 лет. 13+5=18, делится на 3.

Значит, Боре-8 лет, Гале-15 лет.

Ответ: Вере-5 лет, Боре-8 лет, Ане-13 лет, Гале-15 лет.

6 класс

1. Одной черепахе 300 лет, а другой 15 лет. Через сколько лет первая черепаха будет вдвое старше второй?

Решение. Разница между черепахами всегда 300-15=285 лет. Одна будет вдвое старше другой, когда второй будет столько лет, какова разница, т.е. 285. А 285 лет второй черепахе исполнится через 285-15=270 лет.

1. Какие цифры скрываются за буквами:

–	МУХА		ХА
	ХА		УХА
	–	КХ
		АР
	–	УХА
		УХА
	0

Ответ: 3125 : 25 = 125.

1. На некотором острове каждый житель либо всегда лжет, либо всегда говорит правду. Трое островитян А, Б, В сказали следующее:

А: «Б – лжец»;

Б: «ровно один из А и В лжец»;

В: «у меня есть крокодил».

Есть ли у В крокодил?

Решение: Первый способ. 1) Пусть А говорит правду. Тогда Б – лжец.

Тогда А и В оба лжецы или оба «правдивцы», но т.к. А –

«правдивец», то и В «правдивец», т.е. крокодил у него есть.

2) Пусть А – лжец. Тогда Б – «правдивец». Тогда ровно один из А

и В лжец, но т.к. А лжец, то В – «правдивец». Т.е. крокодил у него есть.

Таким образом, в обоих случаях получаем, что у В есть крокодил.

Второй способ. 1) Пусть Б «правдивец». Тогда ровно один из А и В лжец, но т.к. А говорит, что Б лжец, то А – лжец = В «правдивец» = крокодил у него есть.

2) Пусть Б лжец. Тогда оба А и В «правдивцы», или оба лжецы. Но А говорит, что Б лжец, т.е. говорят правду = они оба (А и В) «правдивцы», т.е. у В есть крокодил.

Ответ. Да, есть.

1. Надя испекла пирожки с малиной, черникой и клубникой. Пирожков с малиной получилась половина от общего количества пирожков; пирожков с черникой – на 14 меньше, чем пирожков с малиной. А пирожков с клубникой получилось в два раза меньше, чем пирожков с малиной и черникой вместе. Сколько пирожков каждого вида испекла Надя?

Решение.

Так как пирожков с малиной половина от общего количества, то пирожков с черникой и клубникой вместе столько же, сколько пирожков с малиной . При этом, пирожков с черникой на 14 меньше, чем пирожков с малиной, следовательно, эти 14 пирожков – с клубникой. Тогда пирожков с малиной и черникой: 14·2 = 28, значит, всего испечено 28 +14 = 42 пирожка. Таким образом, пирожков с малиной 42 : 2 = 21, с черникой – 7, а с клубникой – 14.

Ответ : 21 пирожок с малиной, 7 пирожков с черникой и 14 пирожков с клубникой.

1. Проведите 3 прямые так, чтобы тетрадный лист разделился на наибольшее число частей. Сколько получится частей? Проведите 4 прямые с тем же условием. Сколько теперь получилось частей?

1. класс

1. Вася может получить число 100, используя десять семерок, скобки и знаки арифметических действий:

100 = (77:7 – 7:7) · (77:7 – 7:7). Улучшите его результат: используя меньшее число семерок и получите число 100 (достаточно привести один пример).

Решение: 100 = (7 ·7 + 7 : 7)·(7:7+7:7), 100 = 777:7 – 77:7 могут быть и другие варианты

1. Огород квадратной формы 5 м  5 м нужно разделить несколькими кусками ячеистой сетки на 5 равных по площади «клетчатых» участков. Это легко сделать, используя 20 м сетки, как показано на рисунке.

Хватит для этой цели 16 м сетки? Выполните рисунок.

Решение: Ответ: хватит.

Одно из возможных решений показано на рисунке.

1. В одной комнате сидят 9 человек, и их средний возраст – 25 лет. В другой комнате сидят 11 человек, и их средний возраст – 45 лет. Каков средний возраст всех 20 человек? (ответ обосновать).

Решение: 1) 25·9 = 225(л) – общий возраст 9 человек

2) 45·11 = 495(л) – общий возраст 11человек

3) 225 + 495 = 720(л) – общий возраст 20 человек

4) 720 : 20 = 36(л) средний возраст 20 человек

Ответ: 36 лет. могут быть и другие варианты решения

1. Сколько прямоугольных пластин 20х45 см можно вырезать из фанерного листа 120х240 см? (ответ обосновать).

Решение: 1) 120·240 = 28800(см²) – площадь фанерного листа

2) 20·45 = 900(см²) – площадь пластины

3) 28800:900 = 32

Ответ: 32 пластины

1. Дедушка решил подарить внукам по новогоднему подарку, состоящему из конфеты, яблока, апельсина, шоколадки и книги. На те же деньги он мог купить одни конфеты и их оказалось бы 224, яблоки– их было бы 112, апельсины – 56, шоколадки – 32, а книг – 16. Сколько внуков у дедушки?

Ответ: 8 внуков.

Решение. Замечаем, что яблоко «стоит» 2 конфеты, апельсин – 4 конфеты, шоколадка – 7 конфет, книга – 14 конфет. Значит, «цена» подарка равна 1+2+4+7+14=28 (конфет). Следовательно, внуков у дедушки 224:28=8.

multiurok.ru

Олимпиада по математике 5 класс. Школьный этап.

ВСЕРОССИЙСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ

ПО МАТЕМАТИКЕ.

Школьный этап. 2016-2017 гг.

5. КЛАСС

1. Найдите значение выражения:

2012 ‒ 2011 + 2010 ‒ 2009 + 2008 ‒ … + 2 – 1.

2. Как разложить 9 гирь массой 1, 2, 3, 4, 5, 6, 7, 8, 9 граммов на 3 части, равных по массе?

3.  В семье четверо детей. Им 5, 8, 13, 15 лет. Детей зовут Аня, Боря, Вера, Галя. Сколько лет каждому ребёнку, если одна девочка ходит в детский сад, Аня старше Бори, и сумма лет Ани и Веры делится на 3.

4. Король хочет построить 6 крепостей и соединить каждые две из них дорогой. Начертите такую схему расположения крепостей и дорог, чтобы на ней было только три перекрестка, и на каждом из них пересекались только две дороги.

5. Дедка вдвое сильнее Бабки, Бабка втрое сильнее Внучки, Внучка вчетверо сильнее Жучки, Жучка впятеро сильнее Кошки, Кошка вшестеро сильнее Мышки. Без Мышки все остальные не могут вытащить репку, а вместе с Мышкой – могут. Сколько мышек надо собрать вместе, чтобы эти мышки смогли вытащить репку сами?

Критерии оценивания

Задания математических олимпиад являются творческими, допускают несколько различных вариантов решений. Кроме того, необходимо оценивать частичные продвижения в задачах (например, разбор важного случая, доказательство леммы, нахождение примера и т.п.). Наконец, возможны логические и арифметические ошибки в решениях. Окончательные баллы по задаче должны учитывать все вышеперечисленное.

В соответствии с регламентом проведения математических олимпиад школьников каждая задача оценивается из 7 баллов.

Соответствие правильности решения и выставляемых баллов приведено в таблице.

Баллы

Правильность (ошибочность) решения

7

Полное верное решение

6-7

Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.

5-6

Решение в целом верное. Однако решение содержит влияющие существенные ошибки либо пропущены случаи, не на логику рассуждений.

4

Верно рассмотрен один из двух (более сложный) существенных случаев + пример), или в задаче типа «оценка верно получена оценка.

2-3

Доказаны вспомогательные утверждения, помогающие в решении задачи.

0-1

Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).

0

Решение неверное, продвижения отсутствуют.

0

Решение отсутствует.

Важно отметить, что любое правильное решение оценивается в 7 баллов. Недопустимо снимать баллы за то, что решение слишком длинное, или за то, что решение школьника отличается от приведенного в методических разработках или от других решений, известных жюри.

В то же время любой сколь угодно длинный текст решения, не содержащий полезных продвижений, должен быть оценен в 0 баллов.

Ответы и указания к решению

5 класс.

1. Найдите значение выражения:

2012 ‒ 2011 + 2010 ‒ 2009 + 2008 ‒ … + 2 ‒ 1.

Решение.

Заметим, что разность чисел 2012 и 2011 равна 1, аналогично разность чисел 2010 и 2009 равна 1 и т. д. Всего таких разностей будет 2012:2=1006. В результате получается, что значение выражения равно 1006.

2. Как разложить 9 гирь массой 1, 2, 3, 4, 5, 6, 7, 8, 9 граммов на 3 части, равных по массе?

Решение.

1. 1+2+3+4+5+6+7+8+9=45 (г) общая масса гирь.

2. 45:3=15 (г) – в одной части.

Гири разложили так:(2+9+4) г; (1+8+6) г; (3+5+7) г.

3. В семье четверо детей. Им 5, 8, 13, 15 лет. Детей зовут Аня, Боря, Вера, Галя. Сколько лет каждому ребёнку, если одна девочка ходит в детский сад, Аня старше Бори, и сумма лет Ани и Веры делится на 3.

Решение.

5 лет — возраст ребёнка детского сада. Самый младший ребёнок — девочка в возрасте 5 лет.

Зная, что Аня старше Бори, получаем, что Ане либо 13, либо 15 лет.

Так как сумма лет Ани и Веры делится на 3, то получаем три случая:

1. Ане 15 лет, Вере 5 лет. 15+5=20, не делится на 3.

2. Ане 15 лет, Вере 8 лет. 15+8=23, не делится на 3.

3. Ане 13 лет, Вере 5 лет. 13+5=18, делится на 3.

Значит, Боре-8 лет, Гале-15 лет.

Ответ: Вере-5 лет, Боре-8 лет, Ане-13 лет, Гале-15 лет.

4. Король хочет построить 6 крепостей и соединить каждые две из них дорогой. Начертите такую схему расположения крепостей и дорог, чтобы на ней было только три перекрестка, и на каждом из них пересекались только две дороги.

Решение 1.

Рисуем 6 крепостей (на каждой надписываем цифру 1,2,3,4 и т.д.) От крепости номер 1 проводим дорогу к номеру 3, от 2 к 4, от 3 крепости проводим дорогу к 5 и от четвертой к шестой. При таком соединении образуется 3 перекреста и на каждом из них пересекутся 2 дороги.

Решение 2.

0-крепость
— -дорога
0—0
0—0
0—0

5. Дедка вдвое сильнее Бабки, Бабка втрое сильнее Внучки, Внучка вчетверо сильнее Жучки, Жучка впятеро сильнее Кошки, Кошка вшестеро сильнее Мышки. Без Мышки все остальные не могут вытащить репку, а вместе с Мышкой – могут. Сколько мышек надо собрать вместе, чтобы эти мышки смогли вытащить репку сами?

Решение.

Кошка = 6 мышек;  жучка = 5 кошек = 30 мышек;  внучка = 4 жучки = 120 мышек; бабка = 3 внучки = 360 мышек; дедка = 2 бабки = 720 мышек. Все вместе дедка+бабка+внучка+жучка+кошка+мышка= 720+360+120+30+6+1=1237 мышек.

Есть идея все выражать в мышках, но не доведено до конца или неправильно доведено (например, посчитано, что дедка —  это 720 мышек и в ответ записано 720 ) – 2 балла. Вычислительная ошибка – минус 1 балл (если вычислительных ошибок несколько, соответственно вычитается больше).

infourok.ru

Олимпиада по математике 5-11 классы школьный этап

Задания
для проведения школьного этапа
Всероссийской олимпиады школьников
по математике в 5 – 11 классах

2017

Школьный этап Всероссийской олимпиады школьников по математике

2017-2018 учебный год

Каждая задача оценивается целым числом баллов от 0 до 7

Максимальное количество набранных баллов — 35

Время проведения — 2 часа

5 класс

1. В записи 1 ☼ 2 ☼ 3 ☼ 4 ☼ 5 = 100 замените «☼» знаками действия и расставьте скобки так, чтобы получилось верное равенство.

2. На какое максимальное число кусков можно разделить круглый блинчик при помощи трех прямолинейных разрезов? Сделайте соответствующий рисунок.

3. Как отмерить 8 л воды, находясь около реки и имея два ведра вместимостью 10 л и 6 л? (8 л воды должно получиться в одном ведре).

4. Поросята Ниф-Ниф и Нуф-Нуф бежали от Волка к домику Наф-Нафа. Если бы поросята не убегали, а стояли на месте, Волк добежал бы до них за 4 минуты. Поросятам бежать до домика Наф-Нафа 6 минут. Волк бежит в 2 раза быстрее поросят. Успеют ли поросята добежать до домика Наф-Нафа?

5. Мачеха, уезжая на бал, дала Золушке мешок, в котором были перемешаны мак и просо, и велела перебрать их. Когда Золушка уезжала на бал, она оставила три мешка: в одном было просо, в другом — мак, а в третьем — ещё не разобранная смесь. Чтобы не перепутать мешки, Золушка к каждому из них прикрепила по табличке: «Мак», «Просо» и «Смесь». Мачеха вернулась с бала первой и нарочно поменяла местами все таблички так, чтобы на каждом мешке оказалась неправильная надпись. Ученик Феи успел предупредить Золушку, что теперь ни одна надпись на мешках не соответствует действительности. Тогда Золушка достала только одно-единственное зёрнышко из одного мешка и, посмотрев на него, сразу догадалась, где что лежит. Как она это сделала?

Ответы (5 кл.)

1. Ответ: 1 · ( 2 + 3 ) · 4 · 5 = 100.

Критерии проверки.

2. Ответ:7

   Решение

Критерии проверки.

• Верное решение – 7 баллов.

• 5-6 кусков — 4 балла

• 4 куска — 2 балла.

3. Решение. Запишем в виде таблицы последовательность наполнения ведер:

Ведро

10 л

вместимостью

Ведро

6 л

вместимостью

Комментарий

Сначала

0 л

0 л

1 шаг

10 л

0 л

Первое ведро наполнили из реки

2 шаг

4 л

6 л

Перелили из первого ведра во второе до его наполнения

3 шаг

4 л

0 л

Вылили из второго в

реку

4 шаг

0 л

4 л

Перелили из ведра во второе

первого

5 шаг

10 л

4 л

Первое ведро наполнили из реки

6 шаг

8 л

6 л

Перелили из первого

ведра во второе до его наполнения

Критерии проверки.

Правильный алгоритм – 7 баллов. Разумные продвижения, например, отмерено 4 л – до 3 баллов.

4. Ответ. Успеют.

Решение. От места расположения поросят до их дома волку бежать 6:2=3 минуты, т.е. всего ему бежать 4+3=7 минут.

5. Решение. Надо взять зёрнышко из того мешка, на котором написано «Смесь». В нём не может оказаться смесь, значит, в нём лежат именно те зёрна, которые мы оттуда достанем. Пусть для определённости в этом мешке лежит мак. Это значит, что в мешке с надписью «Мак» может лежать только просо (если бы там лежала смесь, то в мешке с надписью «Просо» лежало бы просо, что невозможно). Отсюда сразу следует, что в мешке с надписью «Просо» лежит смесь.

Школьный этап Всероссийской олимпиады школьников по математике

2017-2018 учебный год

Каждая задача оценивается целым числом баллов от 0 до 7

Максимальное количество набранных баллов — 35

Время проведения — 2 часа

6 класс

1. Замените звёздочки цифрами так, чтобы равенство стало верным и все девять цифр были различными: *** + ** = 1056.

2. Разрежьте фигуру на 2 равные фигуры.

3. Три лисы: Алиса, Лариса и Инесса разговаривали на полянке. Лариса: «Алиса не самая хитрая». Алиса: «Я хитрее Ларисы». Инесса: «Алиса хитрее меня». Известно, что самая хитрая лиса солгала, остальные сказали правду.

а) Может ли самой хитрой лисой быть Алиса? Почему?
б) Какая лиса самая хитрая? Дайте ответ и объясните, почему другие варианты не подходят.

4. Мышь, мышонок и сыр вместе весят 180г. Мышь весит на 100г больше, чем мышонок и сыр вместе взятые. Сыр весит в три раза меньше, чем мышонок. Сколько весит каждый из них? Ответ нужно подтвердить вычислениями.

5. В коробке лежат 26 бриллиантов, из которых один природного происхождения, остальные — его копии, изготовленные в лаборатории. Массы искусственных бриллиантов одинаковы, масса природного немного меньше. Придумайте план действий для нахождения природного бриллианта за три взвешивания на чашечных весах без гирь.

Ответы (6 кл.)

1. Возможные ответы: 984 + 72 = 1056

982 + 74 = 1056

974 + 82 = 1056

972 + 84 = 1056

Дополнительных объяснений не требуется.

Критерии проверки.

• Приведён любой из возможных ответов — 7 баллов.

• Приведён ответ, в котором какие-то две цифры совпадают, — 2 балла.

2. Решение.

3. Ответ. а) Не может, б) Инесса.

Решение.

а) Алиса не может быть самой хитрой, т.к. если она сама хитрая, то она хитрее Ларисы, т.е. Алиса сказала правду. Но самая хитрая лиса должна была солгать.

б) Самая хитрая лиса Инесса. Докажем это. Мы уже получили в пункте а), что Алиса не может быть самой хитрой лисой. Лариса тоже не может быть самой хитрой, т.к. она сказала правду про Алису, а самая хитрая лиса должна была солгать. Поэтому остался только один вариант: самая хитрая – Инесса.

Критерии проверки.

• Верное решение пункта а) – 3 балла, пункта б) – 4 балла.

• Только верные ответы на каждый из пунктов – 0 баллов.

4. Ответ. Мышь – 140г, сыр – 10г, мышонок – 30г.
   Решение. Из условия следует, что удвоенный вес мыши равен 180 + 100 = 280г. Поэтому вес мыши равен 140г. Тогда мышонок и сыр вместе весят 180 – 140 = 40г. А вес сыра, согласно условию, равен четверти этого веса.

5. Решение. Положим на чаши весов по 9 бриллиантов. В зависимости от результатов взвешивания определяем более легкую группу бриллиантов: 9, 9 или 8. Более легкую группу разложим на кучки 3+3+3 (или 3+3+2). Сравним вес двух кучек по 3 бриллианта. Если они одинаковы, то настоящий бриллиант в оставшейся кучке, в противном случае — в более легкой. Еще одно взвешивание требуется для определения более легкого (настоящего) бриллианта из 2-х или
   3-х.

Школьный этап Всероссийской олимпиады школьников по математике

2017-2018 учебный год

Каждая задача оценивается целым числом баллов от 0 до 7

Максимальное количество набранных баллов — 35

Время проведения — 3 часа

7 класс

1. Расставьте скобки, чтобы равенство стало верным: 0,5+0,5:0,5+0,5:0,5=5.

2. На часах половина девятого. Чему равен угол между часовой и минутной стрелками?

3. Разрежьте фигуру на 4 равные части. (Резать можно только по сторонам и диагоналям клеточек.
   

4. Вдоль забора растут 10 кустов смородины. Число ягод на соседних кустах отличается на 1. Может ли на всех кустах вместе быть 1000 ягод

5. Рядовой Петров взял ведро нечищеной картошки и за 1 час её почистил. При этом 25% картошки ушло в очистки. За какое время у него набралось полведра очищенной картошки?

Ответы (7 кл.)

1. Ответ: ((0,5+0,5):0,5+0,5):0,5=5.

Критерии проверки. • Верный ответ – 7 баллов.

2. Ответ. 75⁰.

Решение. В момент, когда часы показывают половину девятого, минутная стрелка указывает на цифру 6, а часовая на середину дуги между цифрами 8 и 9 (см. рисунок). Если из центра часов провести два луча к соседним цифрам циферблата, то между ними будет угол 3600:12=300. Угол между стрелками часов, когда они показывают половину девятого, в два с половиной раза больше. Следовательно, он равен 75⁰.

Критерии проверки.

• Верное решение – 7 баллов.

• Верный ответ с недостаточно полными обоснованиями – 5 баллов.

• Неверный из-за арифметической ошибки ответ, кратный 15⁰, при верном в целом решении – 3 балла.

• Только ответ – 1 балл.

3. Решение.
   

Критерии проверки.

• Приведён любой из возможных ответов — 7 баллов.

4. Ответ. Не может.
   Решение. Число ягод на двух соседних кустах отличается на 1, поэтому на двух соседних кустах вместе нечетное число ягод. Тогда количество ягод на десяти кустах равно сумме пяти нечетных чисел, т. е. числу нечетному. Значит, на всех кустах вместе не может быть 1000 ягод.
   Критерии проверки.

• Верное решение – 7 баллов.

• Верные соображения – до 3 баллов.

• Только ответ – 1 балл.

5. Ответ. За 40 минут. Решение. Так как четверть картошки ушло в очистки, то Петров получил за 1 час три четверти ведра почищенной картошки. Значит, четверть ведра почищенной картошки Петров получил за 20 минут, а половину ведра – за 40 минут.

Критерии проверки.

• Верное решение – 7 баллов.

• Верный ход решения, но арифметическая ошибка в конце решения (при этом ответ должен получиться разумным, не 1 час и не 10 минут) – 5 баллов.

• Верные соображения – до 2 баллов.

• Только ответ – 1 балл.

Школьный этап Всероссийской олимпиады школьников по математике

2017-2018 учебный год

Каждая задача оценивается целым числом баллов от 0 до 7

Максимальное количество набранных баллов — 35

Время проведения — 3 часа

9 класс

1. В равенстве 1 – 2 – 4 – 8 – 16 = 19 поставьте несколько знаков модуля так, чтобы оно стало верным.

2. Дима начертил графики четырёх линейных функций на координатной плоскости, но забыл отметить единичные отрезки. Когда он переписывал задание в тетрадь, то отвлекся и не дописал уравнения, задающие функции под номерами 3 и 4. Найдите эти уравнения. Ответ обоснуйте.

3. Произведение трех натуральных чисел оканчивается на 2222. Докажите, что их сумма не может равняться 9999.

4. В подземном царстве живут гномы, предпочитающие носить либо зелёные, либо синие, либо красные кафтаны. Некоторые из них всегда лгут, а остальные всегда говорят правду. Однажды каждому из них задали четыре вопроса. 1. «Ты предпочитаешь носить зелёный кафтан?» 2. «Ты предпочитаешь носить синий кафтан?» 3. «Ты предпочитаешь носить красный кафтан?» 4. «На предыдущие вопросы ты отвечал честно?» На первый вопрос «да» ответили 40 гномов, на второй — 50, на третий — 70, а на четвёртый — 100. Сколько честных гномов в подземном царстве?

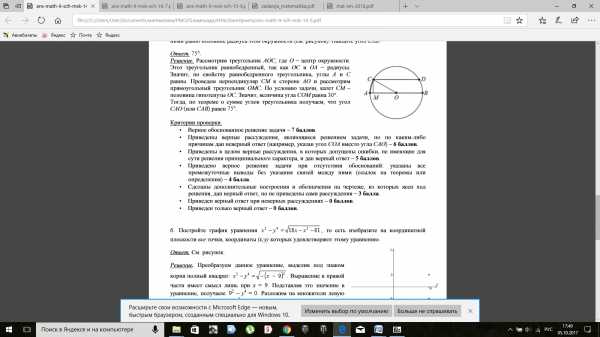
5. В окружности провели диаметр AB и параллельную ему хорду CD так, что расстояние между ними равно половине радиуса этой окружности (см. рисунок). Найдите угол CAB

Ответы (9 кл.)

1. Ответ. ||1− 2|−|4 −8|−16| = 19. Существуют и другие примеры.

Комментарий. Достаточно привести один пример. Пояснять, как он получен, не требуется.

Критерии проверки. • Любой верный пример — 7 баллов

2. Ответ. 3) y = –3x + 12; 4) y = – x – 12.

Решение. Из четырёх прямых только прямая а имеет положительный угловой коэффициент, следовательно, она задаётся уравнением 2 и пересекает оси координат в точках (0; 12) и (–12; 0).

Так как уравнение 1 Дима записал полностью, его графиком является прямая, проходящая через начало координат, то есть прямая с.

У прямой b модуль углового коэффициента больше, чем у прямой с, значит, начало уравнения прямой b Дима записал под номером 3. Так как эта прямая проходит через точку (0;12), она задаётся уравнением y = –3x + 12.

Прямая d проходит через точку (–12;0) и через точку (12; –24) – точку пересечения прямых b и с, координаты которой легко находятся как решение системы линейных уравнений: y = –3x + 12 и y = –2x.

Найдём уравнение прямой d. Для этого рассмотрим систему двух уравнений:

0 = –12k4 + b4; –24 = 12k4 + b4. Сложив эти уравнения, получим b4 = –12.

Подставив в первое уравнение, получим k4 = –1.

Критерии проверки.

Любое полное верное решение — 7 баллов.

В целом верное решение, в котором допущены арифметические ошибки, — 5 баллов.

Обоснованно найдены уравнения трёх прямых — 4 балла.

Если в решении указано, какие из изображённых прямых задаются уравнениями 1 и 2, но более не найдено ничего — 2 балла.

Приведён только верный ответ — 1 балл.

3. Решение. Если сумма трех целых чисел равна 9999, то либо они все нечетны (и тогда их произведение оканчивается на нечетную цифру), либо два из них четны, а одно нечетно (тогда их произведение делится на 4, а число, оканчивающееся на 22, на 4 не делится).

Критерии проверки соответствуют основным принципам оценивания работы.

4. Ответ: 40 честных гномов.

Решение. На 4-й вопрос и честный, и лгун ответят «да», поэтому в подземном царстве всего 100 гномов. Честный гном на один из трёх первых вопросов ответит «да», а на два — «нет». А лгун, наоборот, на два из первых трёх вопросов ответит «да», а на один — «нет». Далее ответ можно получить или уравнением, или рассуждением.

Способ 1. Пусть всего x честных гномов. Тогда всего на первые три вопроса будет x + 2 · (100 – x) = 200 – x ответов «да», т. е. 200 – x = 40 + 50 + 70 = 160, откуда x = 40.

Способ 2. В сумме на первые три вопроса было дано 40 + 50 + 70 = 160 ответов «да». Если бы все гномы говорили правду, то на первые три вопроса было бы 100 ответов «да». Так как каждый лжец даёт на один ответ «да» больше, всего отвечали 160 – 100 = 60 лжецов. Значит, честных гномов 40.

Критерии проверки.

• Верное решение — 7 баллов.

• Рассуждением найдено, сколько лжецов, а сколько честных гномов, не найдено — 5 баллов.

• Верный ответ без обоснования — 2 балла.

5. Ответ. 75°.

Решение. Рассмотрим треугольник АОС, где О – центр окружности. Этот треугольник равнобедренный, так как ОС и ОА – радиусы. Значит, по свойству равнобедренного треугольника, углы А и С равны. Проведем перпендикуляр СМ к стороне АО и рассмотрим прямоугольный треугольник ОМС. По условию задачи, катет СМ – половина гипотенузы ОС. Значит, величина угла СОМ равна 30°. Тогда, по теореме о сумме углов треугольника получаем, что угол САО (или САВ) равен 75°.

Критерии проверки. • Верное обоснованное решение задачи – 7 баллов. • Приведены верные рассуждения, являющиеся решением задачи, но по каким-либо причинам дан неверный ответ (например, указан угол СОА вместо угла САО) – 6 баллов. • Приведены в целом верные рассуждения, в которых допущены ошибки, не имеющие для сути решения принципиального характера, и дан верный ответ – 5 баллов. • Приведено верное решение задачи при отсутствии обоснований: указаны все промежуточные выводы без указания связей между ними (ссылок на теоремы или определения) – 4 балла. • Сделаны дополнительные построения и обозначения на чертеже, из которых ясен ход решения, дан верный ответ, но не приведены сами рассуждения – 3 балла. • Приведен верный ответ при неверных рассуждениях – 0 баллов. • Приведен только верный ответ – 0 баллов.

Школьный этап Всероссийской олимпиады школьников по математике

2017-2018 учебный год

Каждая задача оценивается целым числом баллов от 0 до 7

Максимальное количество набранных баллов — 35

Время проведения — 4 часа

10 класс

1. Делится ли 13²⁰¹⁵ + 13²⁰¹⁶ + 13²⁰¹⁷ на 61?

2. Лестница, стоящая на гладком полу у вертикальной стены соскальзывает вниз (всё время касаясь стены). По какой линии движется котёнок, сидящий на середине лестницы?

3. Постройте график функции

4. Каждый из 10 гномов либо всегда говорит правду, либо всегда лжет. Известно, что каждый из них любит ровно один сорт мороженого: сливочное, шоколадное или фруктовое. Сначала Белоснежка попросила поднять руки тех, кто любит сливочное мороженое, и все подняли руки, потом тех, кто любит шоколадное мороженое – и половина гномов подняли руки, потом тех, кто любит фруктовое мороженое – и руку поднял только один гном. Сколько среди гномов правдивых?

5. Числа образуют арифметическую прогрессию.

Верно ли, что числа a² , b² , c² также образуют арифметическую прогрессию?

Ответы (10 кл.)

1. Ответ. Да, делится.

Решение. Преобразуем данную сумму:

13²⁰¹⁵ + 13²⁰¹⁶ + 13²⁰¹⁷ =13²⁰¹⁵ ⋅ (1 + 13 + 13²) = 183 ⋅ 13²⁰¹⁵ = 61 ⋅ 3 ⋅ 13²⁰¹⁵.

Значит, данная сумма делится на 61.

Критерии проверки.

• Верное решение — 7 баллов.

• Вынесено за скобки число 13²⁰¹⁵, но число в скобках посчитано с ошибкой и поэтому утверждается, что выражение не делится на 61, — 3 балла.

• Приведён только ответ «да» — 1 балл.

2. Ответ: по дуге окружности.

Решение. В каждый момент расстояние от середины лестницы до вершины угла будет одно и то же (см. рис.): DC=0,5AB (свойство медианы прямоугольного треугольника). Таким образом, точка В будет описывать дугу окружности с центром в точке С и радиусом 0,5AB.

3. Ответ. См. рисунок.

Решение. Т.к. х²=|х|², то у=|х|, причем х ≠ 0. Можно также, используя определение модуля, получить, что

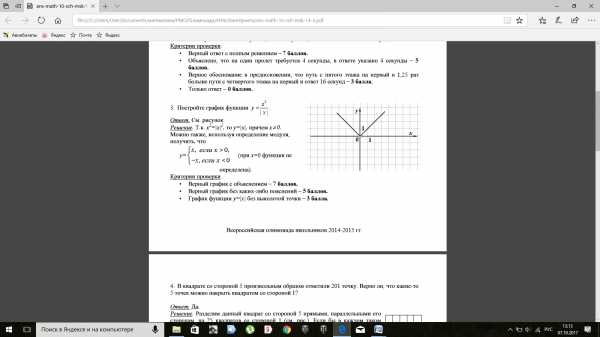
Критерии проверки.

• Верный график с объяснением – 7 баллов.

• Верный график без каких-либо пояснений – 5 баллов.

• График функции у=|x| без выколотой точки – 3 балла.

4. Ответ. 4.

Решение. Гномы, которые всегда говорят правду, подняли руку один раз, а гномы, которые всегда лгут, – два раза. Всего было поднято 16 рук (10+5+1). Если бы все гномы сказали правду, то было бы поднято 10 рук. Если одного правдивого гнома заменить на одного лгуна, то число поднятых рук увеличится на 1. Так как было поднято 6 «лишних» рук, то 6 гномов солгали, а 4 сказали правду.

Критерии проверки.

Полное решение – 7 баллов. Верный ответ, полученный на конкретном примере – 2 балла.

6. Ответ. Да.

Решение. Так как указанные три числа образуют арифметическую прогрессию, то верно равенство:

Тогда, приводя к общему знаменателю, получаем:

. Отсюда: (b+c)(b—c)=(a—b)(a+b) или b²—c²=a²—b², что в соответствии с

определением и означает, что числа а², b² и с² образуют арифметическую прогрессию. Можно также использовать характеристическое свойство арифметической прогрессии: числа х, у, z образуют арифметическую прогрессию тогда и только тогда, когда х+z=2у.

Критерии проверки.

• Полное доказательство – 7 баллов.

• Только ответ – 0 баллов.

infourok.ru

Всероссийская олимпиада Математика (5 класс) 2016-2017 г

1. Школьные олимпиады
2. Математика
3. 5 класс

Всероссийская олимпиада проходила в мае 2016 года, в ней приняло участие 1366 школьников с разных уголков нашей страны и ближнего зарубежья, и 126 из них стали финалистами.

Данные материалы предлагаются учителям математики и родителям учащихся. Они могут быть использованы на уроках по математике для 5 класса и во внеурочной деятельности.

Вопросы помогают проверить не только знания планового материала, но и усвоить знания и повысить познавательный интерес к предмету. Работа содержит правильные ответы и критерии оценивания.

1. Площадь прямоугольника равна 23,232 дм², а его длина равна 5,28 дм. Найдите ширину прямоугольника.

• А) 12,672 дм
• Б) 6,336 дм
• В) 4,4 дм
• Г) 4,44 дм

2. Сравните числа .

• А)
  
• Б)
  
• В)
  
• Г) сравнить нельзя

3. Решите уравнение .

• А) 0
• Б)
• В) 4
• Г)

4. Найдите корень уравнения: y+0,83−2,2=1,1.

• А) 4,13
• Б) 1,27
• В) 2,47
• Г) 2,57

5. Выполните умножение 80,002_*800.

• А) 64001,6
• Б) 64,0016
• В) 640016
• Г) 640,016

6. В равенстве 830=327*2+176 делителем является

• А) 327
• Б) 2
• В) 176
• Г) 830

7. Найдите площадь прямоугольника со сторонами 3,8 см и 2,25 см.

• А) 855 см²
• Б) 8,45 см^2
  
• В) 8,55 см^2
  
• Г) 85,5 см^2
  

8. Все цифры, которые можно подставить вместо звездочки, чтобы неравенство 57*3>5732 было верным, указаны в варианте: 

• А) 3;4;5;6;7;8;9   
• Б) 4;5;6;7;8;9
• В) 2;3;4;5;6;7;8;9   
• Г) 3;4;5;6;7;8

9. Целая часть смешанного числа  равна

• А) 2
• Б) 7
• В) 5
• Г)

10. Какое число разложили по разрядам 7 000 000+500 000+20 000+300+7?

• А) 7523007
• Б) 70520307
• В) 7520307
• Г) 75203070

11. В деревне 24 деревянных дома, а кирпичных домов – 3 / 4 от числа деревянных. Сколько всего домов в деревне?

• А) 40
• Б) 56
• В) 30
• Г) 42

12. Найдите значение выражения: 42⋅(28,6−18,1).

• А) 44,25
• Б) 441   
• В) 446,25
• Г) 425

13. Сад имеет форму прямоугольника со сторонами 40 м и 80 м. Три восьмые части сада заняты яблонями. Сколько квадратных метров занимают яблони?

• А) 2400
• Б) 1400
• В) 1800
• Г) 1200

14. Число 513 в выражении 714-513 является:

• А) уменьшаемым
• Б) вычитаемым
• В) разностью
• Г) слагаемым

15. Какое значение выражения 6⋅а – 15 будет при а = 7.

• А) 17
• Б) 18
• В) 11
• Г) 27

16. Выполните деление 0,0945:0,27.

• А) 0,35
• Б) 0,00035
• В) 35
• Г) 3,5

17. В магазине было 800 книг. В первый день продали 251 книгу, а во второй – 173 книги. Сколько книг осталось в магазине? Какое выражение соответствует решению задачи.

• А) 800-(251+173)
• Б) 800-(251-173)
• В) 800+251+173
• Г) 800-251+173

18. От проволоки длиной 8 м отрезали кусок длиной 5 дм. Сколько проволоки осталось?

• А) 3 м
• Б) 3 дм
• В) 7 м 5 дм
• Г) 795 дм

19. Выразите в метрах 0,003 км.

• А) 30 м
  
• Б) 300 м
• В) 0,3 м
  
• Г) 3 м
  

Всероссийская олимпиада по математике (5 класс) — ответы

Номер задания	Правильный ответ
1	В
2	А
3	Б
4	В
5	А
6	А
7	В
8	А
9	В
10	В
11	Г
12	Б
13	Г
14	Б
15	Г
16	А
17	А
18	В
19	Г

Поделись с коллегами:

dudoc.ru

Всероссийская олимпиада по математике 5 класс школьный этап 2016-2017 год

Здесь представлены задания всероссийской олимпиады по математике для 5 класса с верными ответами к ним.

Представленные задания можно использовать на занятии в 5 классе, тем самым дав ученикам способ обновить в памяти и усвоить ранее изученный материал, а также определить, насколько хорошо ученики подготовлены к олимпиадным заданиям.

1. Найдите значение буквенного выражения 5⋅х – 15, если х = 7.

• А) 20
• Б) 40
• В) 35
• Г) 15

2. Найдите периметр прямоугольника, площадь которого равна 48 см², а одна из его сторон — 4 см.

• А) 64 см
• Б) 32 см
• В) 24 см
• Г) 52 см

3. Масса одного мешка картошки 3 кг, а масса другого мешка на 520 г меньше. Найдите массу второго мешка картошки.

• А) 517 г
• Б) 2480 г
• В) 523 г
• Г) 1560 г

4. Решите уравнение .

• А) 0
• Б)
• В) 4
• Г)

5. Сколько сантиметров в 1 метре?

• А) 100 см
• Б) 10 см
• В) 1000 см
• Г) 10 000 см

6. Указать число единиц в разряде сотых дроби 635,421789.

7. В равенстве 49=21*2+7 неполным частным является:

• А) 21
• Б) 2
• В) 7
• Г) 49

8. Точка А лежит на окружности, радиус которой равен 5 см. Чему равен отрезок ОА, если О – центр окружности.

• А) 5 см
• Б) 3 см
• В) 10 см
• Г) 6 см

9. Найдите среднее арифметическое следующих чисел: 3,26; 3,05; 2,87; 2,76; 3; 3,15.

• А) 3,15
• Б) 3,015
• В) 2,87
• Г) 18,09

10. Какое наименьшее двузначное число при делении на 12 даст остаток 2?

• А) 14
• Б) 24
• В) 10
• Г) нельзя определить такое число

11. Составьте выражение по условию задачи: Катя собрала 8 белых грибов, а подосиновиков в m раз больше. Сколько всего грибов собрала Катя?

• А) 8+m
• Б) 8m
• В) 8+8m
• Г) 1+8m

12. Какое число является корнем уравнения х:6=18?

• А) 3
• Б) 108
• В) 128
• Г) 12

13. В одном пакете 5 кг конфет, а в другом – 12 кг тех же конфет. Второй пакет стоит на 700 р. дороже. Сколько стоит каждый пакет?

• А) 250 р. и 950
• Б) 500 р. и 1200 р
• В) 700 р. и 1400 р. 
• Г) 1000 р. и 1700 р  

14. Решите уравнение х:7,083=100

• А) 70,83
• Б) 708,3
• В) 7,083
• Г) 0,07083

15. Саша задумал число. Если из этого числа вычесть 5, а к полученному результату прибавить 17, то получиться 31. Выберите правильно составленное уравнение для этой задачи.

• А) (х+17)-5=31
• Б) (х+5)+17=31
• В) (х-5)+17=31
• Г) (х-5)-17=31

Ответы к всероссийской олимпиаде по математике 5 класс

В этой таблице представленны ответы на задания по математике к школьному этапу всеройссийской олимпиады

Номер задания	Правильный ответ
1	А
2	Б
3	Б
4	Б
5	А
6	А
7	Б
8	А
9	Б
10	А
11	В
12	Б
13	Б
14	Б
15	В

disinst.ru