Формулы тригонометрии
Формулы тригонометрии (тригонометрические формулы) для решения математических задач. Основные тригонометрические тождества, формулы понижения степени, сложения, вычитания и умножения, а также другие формулы. Дополнительно приведены значения тригонометрических функций для наиболее распространённых углов.
Основные тождества
… Подготовка формул …
Формулы двойного угла
… Подготовка формул …
Формулы тройного угла
… Подготовка формул …
Формулы понижения степени
… Подготовка формул …
Формулы понижения степени
… Подготовка формул …Формулы понижения степени
… Подготовка формул …
Формулы половинного аргумента
Формулы понижения степени
половинного аргумента
… Подготовка формул …
Формулы сложения
… Подготовка формул …
Формулы вычитания
… Подготовка формул …
Формулы преобразования суммы
в формулы произведения
… Подготовка формул …
Формулы преобразования разности
в формулы произведения
… Подготовка формул …
Формулы преобразования суммы
… Подготовка формул …Формулы преобразования произведения
в формулы суммы и разности
… Подготовка формул …
Формулы преобразования произведения
функций в степени
… Подготовка формул …
Формулы понижения степени
… Подготовка формул …
Универсальная
тригонометрическая подстановка
… Подготовка формул …
Значения тригонометрических функций
| α | 0 | ||||||||||||||||
| α° | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
| sin α | 0 | 1 | 0 | −1 | 0 | ||||||||||||
| cos α | 1 | 0 | −1 | 0 | 1 | ||||||||||||
| tg α | 0 | 1 | − | −1 | 0 | 1 | − | −1 | 0 | ||||||||
| ctg α | − | 1 | 0 | − | 1 | 0 | −1 | − |
Теория
Тригонометрия – раздел математики, изучающий зависимости углов и сторон треугольников, которые выражены функциями, называемыми тригонометрическими.
Функция – это правило, описывающее зависимость одной величины от другой.
Тождество – это равенство, справедливое при любых значениях, входящих в него переменных
Тригонометрические тождества (равенства) описывают зависимости между синусом, косинусом, тангенсом и котангенсом.
Скачать тригонометрические формулы
Вы можете скачать тригонометрические формулы в виде картинки:








doza.pro
Тригонометрические формулы. Основные тригонометрические тождества. Тригонометрические тождества
Основные тригонометрические тождества
- sin² α + cos² α = 1
- tg α · ctg α = 1
- tg α = sin α ÷ cos α
- ctg α = cos α ÷ sin α
- 1 + tg² α = 1 ÷ cos² α
- 1 + ctg² α = 1 ÷ sin² α
Формулы сложения
- sin (α + β) = sin α · cos β + sin β · cos α
- sin (α — β) = sin α · cos β — sin β · cos α
- cos (α + β) = cos α · cos β — sin α · sin β
- cos (α — β) = cos α · cos β + sin α · sin β
- tg (α + β) = (tg α + tg β) ÷ (1 — tg α · tg β)
- tg (α — β) = (tg α — tg β) ÷ (1 + tg α · tg β)
- ctg (α + β) = (ctg α · ctg β — 1) ÷ (ctg β + ctg α)
- ctg (α — β) = (ctg α · ctg β + 1) ÷ (ctg β — ctg α)
Формулы двойного угла
- cos 2α = cos² α — sin² α
- cos 2α = 2cos² α — 1
- cos 2α = 1 — 2sin² α
- sin 2α = 2sin α · cos α
- tg 2α = (2tg α) ÷ (1 — tg² α)
- ctg 2α = (ctg² α — 1) ÷ (2ctg α)
Формулы тройного угла
- sin 3α = 3sin α — 4sin³ α
- cos 3α = 4cos³ α — 3cos α
- tg 3α = (3tg α — tg³ α) ÷ (1 — 3tg² α)
- ctg 3α = (3ctg α — ctg³ α) ÷ (1 — 3ctg² α)
Формулы понижения степени
- sin² α = (1 — cos 2α) ÷ 2
- sin³ α = (3sin α — sin 3α) ÷ 4
- cos² α = (1 + cos 2α) ÷ 2
- cos³ α = (3cos α + cos 3α) ÷ 4
- sin² α · cos² α = (1 — cos 4α) ÷ 8
- sin³ α · cos³ α = (3sin 2α — sin 6α) ÷ 32
Переход от произведения к сумме
- sin α · cos β = ½ (sin (α + β) + sin (α — β))
- sin α · sin β = ½ (cos (α — β) — cos (α + β))
- cos α · cos β = ½ (cos (α — β) + cos (α + β))
Переход от суммы к произведению
Другие заметки по алгебре и геометрии
edu.glavsprav.ru
73 формулы тригонометрии
На странице вы найдете все формулы тригонометрии в удобном для использования оформлении. Формулы структурированы в блоки по количеству аргументов, степеням, арифметическим операциям над ними.
Все формулы тригонометрии
Основные тригонометрические тождества
{\tg \alpha = \dfrac {\sin \alpha}{ \cos \alpha} = \dfrac{1}{\ctg \alpha}}
{\ctg \alpha = \dfrac {\cos \alpha}{ \sin \alpha} = \dfrac{1}{\tg \alpha}}
{\sin ^2 \alpha + \cos ^2 \alpha = 1}
{1+\tg^2\alpha=\dfrac{1}{\cos^2\alpha}}
{1+\ctg^2\alpha=\dfrac{1}{\sin^2\alpha}}
{\tg\alpha \cdot \ctg\alpha=1}
Формулы двойного угла (аргумента)
{\sin(2\alpha)=2 \cdot \cos \alpha \cdot \sin \alpha}
{\sin(2\alpha)=\dfrac{2 \cdot \tg \alpha}{1+\tg ^2 \alpha}=\dfrac{2 \cdot \ctg \alpha}{1+\ctg ^2 \alpha}=\dfrac{2}{\tg \alpha + \ctg \alpha}}
{\cos(2\alpha)=\cos ^2 \alpha- \sin ^2 \alpha = 2 \cdot \cos ^2 \alpha- 1 = 1- 2 \cdot \sin ^2 \alpha}
{\cos(2\alpha)=\dfrac{1 -\tg ^2 \alpha}{1+\tg ^2 \alpha}=\dfrac{\ctg ^2 \alpha- 1}{\ctg ^2 \alpha +1}=\dfrac{\ctg \alpha-\tg \alpha}{\ctg \alpha + \tg \alpha}}
{\tg(2\alpha) = \dfrac{2 \cdot \tg \alpha}{1-\tg ^2 \alpha}=\dfrac{2 \cdot \ctg \alpha}{\ctg ^2 \alpha- 1}=\dfrac{2}{\ctg \alpha- \tg \alpha}}
{\ctg(2\alpha) = \dfrac{\ctg ^2 \alpha-1}{2 \cdot \ctg \alpha}=\dfrac{\ctg \alpha- \tg \alpha}{2}}
Формулы тройного угла (аргумента)
{\sin(3\alpha)=3 \cdot \sin \alpha- 4 \cdot \sin ^3 \alpha}
{\cos(3\alpha)= 4 \cdot \cos ^3 \alpha- 3 \cdot \cos \alpha}
{\tg(3\alpha)= \dfrac{3 \cdot \tg \alpha- \tg ^3 \alpha}{1-3 \cdot \tg ^2 \alpha}}
{\ctg(3\alpha)= \dfrac{\ctg ^3 \alpha- 3 \cdot \ctg \alpha}{3 \cdot \ctg ^2 \alpha -1}}
Формулы понижения степени тригонометрических функций
Вторая степень
{\sin ^2 \alpha = \dfrac{1-\cos(2\alpha)}{2}}{\cos ^2 \alpha = \dfrac{1+\cos(2\alpha)}{2}}
{\tg ^2 \alpha = \dfrac{1-\cos(2\alpha)}{1+\cos(2\alpha)}}
{\ctg ^2 \alpha = \dfrac{1+\cos(2\alpha)}{1-\cos(2\alpha)}}
{(\sin \alpha- \cos \alpha)^2=1-\sin(2 \alpha)}
{(\sin \alpha+ \cos \alpha)^2=1+\sin(2 \alpha)}
Третья степень
{\sin ^3 \alpha = \dfrac{3 \cdot \sin(\alpha)-\sin(3 \alpha)}{4}}{\cos ^3 \alpha = \dfrac{3 \cdot \cos(\alpha)+\cos(3 \alpha)}{4}}
{\tg ^3 \alpha = \dfrac{3 \cdot \sin (\alpha)-\sin(3 \alpha)}{3 \cdot \cos (\alpha)+\cos(3 \alpha)}}
{\ctg ^3 \alpha = \dfrac{3 \cdot \cos (\alpha)+\cos(3 \alpha)}{3 \cdot \sin (\alpha)-\sin(3 \alpha)}}
Четвёртая степень
{\sin ^4 \alpha = \dfrac{3-4 \cdot \cos(2 \alpha)+\cos(4 \alpha)}{8}}{\cos ^4 \alpha = \dfrac{3+4 \cdot \cos(2 \alpha)+\cos(4 \alpha)}{8}}
Пятая степень
{\sin ^5 \alpha = \dfrac{10 \cdot \sin(\alpha)-5 \cdot \sin(3 \alpha)+\sin(5 \alpha)}{16}}{\cos ^5 \alpha = \dfrac{10 \cdot \cos(\alpha)+5 \cdot \cos(3 \alpha)+\cos(5 \alpha)}{16}}
Формулы половинного угла (аргумента)
{\sin \Big( \dfrac{\alpha}{2} \Big)=\pm \sqrt{\dfrac{1-\cos \alpha}{2}}}
{\cos \Big( \dfrac{\alpha}{2} \Big)=\pm \sqrt{\dfrac{1+\cos \alpha}{2}}}
{\tg \Big( \dfrac{\alpha}{2} \Big)= \dfrac{1-\cos \alpha}{\sin \alpha}= \dfrac{\sin \alpha}{1+\cos \alpha}}
{\ctg \Big( \dfrac{\alpha}{2} \Big)= \dfrac{1+\cos \alpha}{\sin \alpha}= \dfrac{\sin \alpha}{1-\cos \alpha}}
Формулы понижения степени половинного угла (аргумента)
{\sin ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1-\cos \alpha}{2}}
{\cos ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1+\cos \alpha}{2}}
{\tg ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1-\cos \alpha}{1+\cos \alpha}}
{\ctg ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1+\cos \alpha}{1-\cos \alpha}}
Формулы сложения аргументов
{\sin(\alpha + \beta)=\sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta}
{\cos(\alpha + \beta)=\cos \alpha \cdot \cos \beta- \sin \alpha \cdot \sin \beta}
{\tg(\alpha + \beta)= \dfrac{\tg \alpha + \tg \beta}{1-\tg \alpha \cdot \tg \beta}}
{\ctg(\alpha + \beta)= \dfrac{\ctg \alpha \cdot \ctg \beta-1}{\ctg \alpha + \ctg \beta}}
Формулы вычитания аргументов
{\sin(\alpha- \beta)=\sin \alpha \cdot \cos \beta- \cos \alpha \cdot \sin \beta}
{\cos(\alpha- \beta)=\cos \alpha \cdot \cos \beta+ \sin \alpha \cdot \sin \beta}
{\tg(\alpha- \beta)= \dfrac{\tg \alpha- \tg \beta}{1+\tg \alpha \cdot \tg \beta}}
{\ctg(\alpha- \beta)= \dfrac{\ctg \alpha \cdot \ctg \beta+1}{\ctg \alpha- \ctg \beta}}
Формулы суммы тригонометрических функций
{\sin \alpha+ \sin \beta=2 \cdot \sin \big( \dfrac{\alpha + \beta}{2} \big) \cdot \cos \big( \dfrac{\alpha- \beta}{2} \big)}
{\cos \alpha+ \cos \beta=2 \cdot \cos \big( \dfrac{\alpha + \beta}{2} \big) \cdot \cos \big( \dfrac{\alpha- \beta}{2} \big)}
{\tg \alpha + \tg \beta = \dfrac{\sin(\alpha + \beta)}{\cos \alpha \cdot \cos \beta}}
{\ctg \alpha + \ctg \beta = \dfrac{\sin(\alpha + \beta)}{\cos \alpha \cdot \cos \beta}}
{\sin (\alpha)+\cos(\alpha)=\sqrt{2} \cdot \sin \Big( \alpha+ \dfrac{\pi}{4} \Big)}
Формулы разности тригонометрических функций
{\sin \alpha- \sin \beta=2 \cdot \sin \big( \dfrac{\alpha- \beta}{2} \big) \cdot \cos \big( \dfrac{\alpha+ \beta}{2} \big)}
{\cos \alpha- \cos \beta=-2 \cdot \sin \big( \dfrac{\alpha + \beta}{2} \big) \cdot \sin \big( \dfrac{\alpha- \beta}{2} \big)}
{\tg \alpha- \tg \beta = \dfrac{\sin(\alpha- \beta)}{\cos \alpha \cdot \cos \beta}}
{\ctg \alpha- \ctg \beta = \dfrac{\sin(\alpha + \beta)}{\sin \alpha \cdot \sin \beta}}
{\sin (\alpha)-\cos(\alpha)=\sqrt{2} \cdot \sin \Big( \alpha- \dfrac{\pi}{4} \Big)}
Формулы произведения тригонометрических функций
{\sin \alpha \cdot \sin \beta = \dfrac{\cos (\alpha- \beta)-\cos(\alpha + \beta)}{2}}
{\sin \alpha \cdot \cos \beta = \dfrac{\sin (\alpha- \beta)+\sin(\alpha + \beta)}{2}}
{\cos \alpha \cdot \cos \beta = \dfrac{\cos (\alpha- \beta)+\cos(\alpha + \beta)}{2}}
{\tg \alpha \cdot \tg \beta = \dfrac{\cos(\alpha- \beta)- \cos(\alpha+\beta)}{\cos(\alpha- \beta)+ \cos(\alpha+\beta)}=\dfrac{\tg \alpha + \tg \beta}{\ctg \alpha + \ctg \beta}}
{\ctg \alpha \cdot \ctg \beta = \dfrac{\cos(\alpha- \beta)+ \cos(\alpha+\beta)}{\cos(\alpha- \beta)- \cos(\alpha+\beta)}=\dfrac{\ctg \alpha + \ctg \beta}{\tg \alpha + \tg \beta}}
{\tg \alpha \cdot \ctg \beta = \dfrac{\sin(\alpha- \beta)+ \sin(\alpha+\beta)}{\sin(\alpha+ \beta)- \sin(\alpha-\beta)}}
Формулы произведения тригонометрических функций в степени
{\sin ^2 (\alpha) \cdot \cos ^2 (\alpha) = \dfrac{1-\cos(4 \alpha)}{8}}
{\sin ^3 (\alpha) \cdot \cos ^3 (\alpha) = \dfrac{3 \cdot \sin(2 \alpha)- \sin(6 \alpha)}{32}}
{\sin ^4 (\alpha) \cdot \cos ^4 (\alpha) = \dfrac{3-4 \cdot \cos(4 \alpha)+ \cos(8 \alpha)}{128}}
{\sin ^5 (\alpha) \cdot \cos ^5 (\alpha) = \dfrac{10 \cdot \sin (2 \alpha)-5 \cdot \sin(6 \alpha)+\sin (10 \alpha)}{512}}
Все формулы тригонометрии на одном листе
На этой картинке собраны все формулы тригонометрии для печати. Листо можно распечатать и использовать при решении задач ЕГЭ или вырезать таблицы и использовать как шпаргалку. Распечатанный лист можно применять как справочный материал при решении задач по тригонометрии в 10 и 11 классе.

Все формулы тригонометрии на одном листе
Ваша оценка
[Оценок: 8 Средняя: 5]Просмотров страницы: 451
mnogoformul.ru
Все формулы (уравнения) тригонометрии : sin(x) cos(x) tg(x) ctg(x)
Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.
Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)
sin(2α)- через sin и cos:
sin(2α)- через tg и ctg:
cos(2α)- через sin и cos:
cos(2α)- через tg и ctg:
tg(2α) и сtg(2α):
Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):
Тригонометрические формулы преобразования разности аргументов
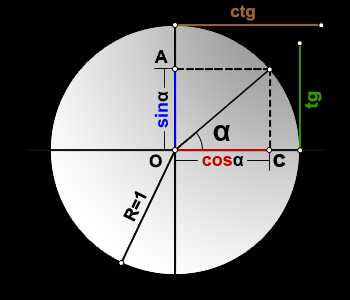
sin(α)=OA
cos(α)=OC
tg(α)=DE
ctg(α)=MK
R=OB=1
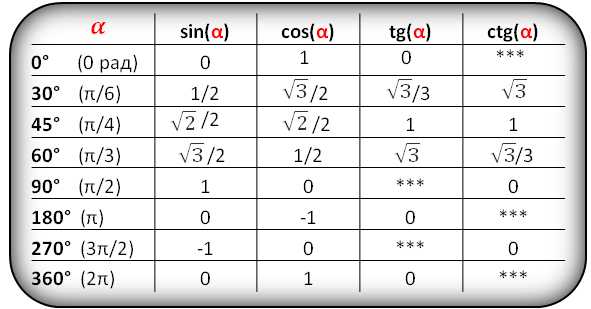
Значения функций для некоторых углов, α
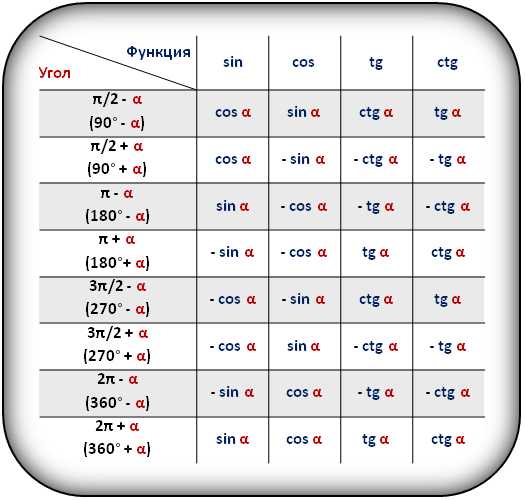
В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).
www-formula.ru
| 01) | Основные тригонометрические тождества |
|
| 01.1) | Основное тригонометрическое тождество |
формула основного тригонометрического тождества |
| 01.2) | Основное тождество через тангенс и косинус |
формула основного тождества через тангенс и косинус |
| 01.3) | Основное тождество через котангенс и синус |
формула основного тождества через котангенс и синус |
| 01.4) | Соотношение между тангенсом и котангенсом |
формула соотношения между тангенсом и котангенсом |
| 02) | Формулы двойного аргумента (угла) |
|
| 02.1) | Синус двойного угла |
формула синуса двойного угла |
| 02.2) | формула синуса двойного угла | |
| 02.3) | Косинус двойного угла |
формула синуса двойного угла |
| 02.4) | формула синуса двойного угла | |
| 02.5) | Тангенс двойного угла |
формула синуса двойного угла |
| 02.6) | Котангенс двойного угла |
формула синуса двойного угла |
| 03) | Формулы тройного аргумента (угла) |
|
| 03.1) | Синус тройного угла |
формула синуса тройного угла |
| 03.2) | Косинус тройного угла |
формула косинуса тройного угла |
| 03.3) | Тангенс тройного угла |
формула тангенса тройного угла |
| 03.4) | Котангенс тройного угла |
формула котангенса тройного угла |
| 04) | Формулы половинного аргумента (угла) |
|
| 04.1) | Синус половинного угла |
формула синуса половинного угла |
| 04.2) | Косинус половинного угла |
формула косинуса половинного угла |
| 04.3) | Тангенс половинного угла |
формула тангенса половинного угла |
| 04.4) | Котангенс половинного угла |
формула котангенса половинного угла |
| 04.5) | Тангенс половинного угла |
формула тангенса половинного угла |
| 04.6) | Котангенс половинного угла |
формула котангенса половинного угла |
| 05) | Формулы квадратов тригонометрических функций |
|
| 05.1) | Квадрат синуса |
формула квадрата синуса |
| 05.2) | Квадрат косинуса |
формула квадрата косинуса |
| 05.3) | Квадрат тангенса |
формула квадрата тангенса |
| 05.4) | Квадрат котангенса |
формула квадрата котангенса |
| 05.5) | Квадрат синуса половинного угла |
формула квадрата синуса половинного угла |
| 05.6) | Квадрат косинуса половинного угла |
формула квадрата косинуса половинного угла |
| 05.7) | Квадрат тангенса половинного угла |
формула квадрата тангенса половинного угла |
| 05.8) | Формулы кубов тригонометрических функций |
формула квадрата котангенса половинного угла |
| 06) | Формулы кубов тригонометрических функций |
|
| 06.1) | Куб синуса |
формула куба синуса |
| 06.2) | Куб косинуса |
формула куба косинуса |
| 06.3) | Куб тангенса |
формула куба тангенса |
| 06.4) | Куб котангенса |
формула куба котангенса |
| 07) | Формулы тригонометрических функций в четвертой степени |
|
| 07.1) | Четвертая степень синуса |
формула четвертой степени синуса |
| 07.2) | Четвертая степень косинуса |
формула четвертой степени косинуса |
| 08) | Формулы сложения и вычитания аргументов |
|
| 08.1) | Сложение аргументов синуса |
формула сложения аргументов синуса |
| 08.2) | Сложение аргументов косинуса |
формула сложения аргументов косинуса |
| 08.3) | Сложение аргументов тангенса |
формула сложения аргументов тангенса |
| 08.4) | Сложение аргументов котангенса |
формула сложения аргументов котангенса |
| 08.5) | Вычитание аргументов синуса |
формула вычитания аргументов синуса |
| 08.6) | Вычитание аргументов косинуса |
формула вычитания аргументов косинуса |
| 08.7) | Вычитание аргументов тангенса |
формула вычитания аргументов тангенса |
| 08.8) | Вычитание аргументов котангенса |
формула вычитания аргументов котангенса |
| 09) | Формулы суммы тригонометрических функций |
|
| 09.1) | Сумма синусов |
формула суммы синусов |
| 09.2) | Сумма косинусов |
формула суммы косинусов |
| 09.3) | Сумма тангенсов |
формула суммы тангенсов |
| 09.4) | Сумма котангенсов |
формула суммы котангенсов |
| 09.5) | Сумма синуса и косинуса |
формула суммы синуса и косинуса |
| 10) | Формулы разности тригонометрических функций |
|
| 10.1) | Разность синусов |
формула разности суммы синусов |
| 10.2) | Разность косинусов |
формула разности суммы косинусов |
| 10.3) | Разность тангенсов |
формула разности суммы тангенсов |
| 10.4) | Разность котангенсов |
формула разности котангенсов |
| 10.5) | Разность синуса и косинуса |
формула разности синуса и косинуса |
| 11) | Формулы произведения тригонометрических функций |
|
| 11.1) | Произведение синусов |
формула произведения синусов |
| 11.2) | Произведение косинусов |
формула произведения косинусов |
| 11.3) | Произведение синуса и косинуса |
формула произведения синуса и косинуса |
| 11.4) | Произведение тангенсов |
формула произведения тангенсов |
| 11.5) | Произведение котангенсов |
формула произведения котангенсов |
| 11.6) | Произведение тангенса и котангенса |
формула произведения тангенса и котангенса |
| 12) | Формулы понижения степени |
|
| 12.1) | Понижение степени синуса |
формула понижения степени синуса |
| 12.2) | Понижение степени косинуса |
формула понижение степени косинуса |
| 13) | Формулы суммы и разности разных тригонометрических функций |
|
| 13.1) | Сумма синуса и косинуса |
формула суммы синуса и косинуса |
| 13.2) | Разность синуса и косинуса |
формула разности синуса и косинуса |
| 13.3) | Сумма синуса и косинуса с коэффициентами |
формула суммы синуса и косинуса с коэффициентами |
| 13.4) | Разность синуса и косинуса с коэффициентами |
формула разности синуса и косинуса с коэффициентами |
| 14) | Формулы общего вида |
|
| 14.1) | Формула понижения nй четной степени синуса |
формула формулы формулы понижения n четной степени синуса |
| 14.2) | Формула понижения nй четной степени косинуса |
формула формулы понижения nй четной степени косинуса |
| 14.3) | Формула понижения nй нечетной степени синуса |
формула формулы понижения nй нечетной степени синуса |
| 14.4) | Формула понижения nй нечетной степени косинуса |
формула формулы понижения nй нечетной степени косинуса |
cae-cube.ru
Формулы для решения простейших тригонометрических уравнений
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Содержание статьи:
Простейшие тригонометрические уравнения
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
1. Уравнение `sin x=a`.
При `|a|>1` не имеет решений.
При `|a| \leq 1` имеет бесконечное число решений.
Формула корней: `x=(-1)^n arcsin a + \pi n, n \in Z`
Таблица арксинусов
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Таблица арккосинусов
Частные случаи для синуса и косинуса в графиках.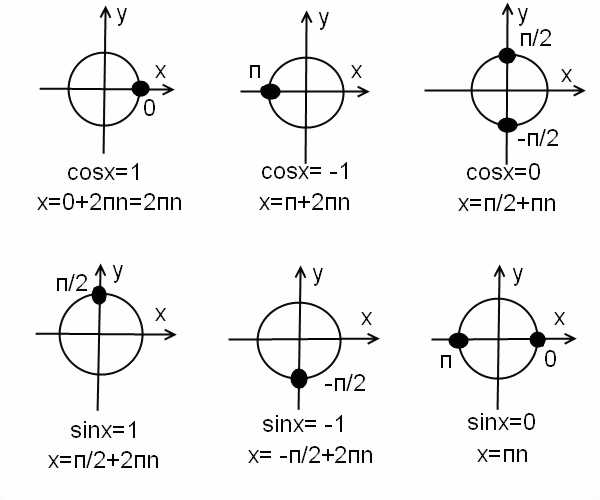
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
Таблица арктангенсов
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Таблица арккотангенсов
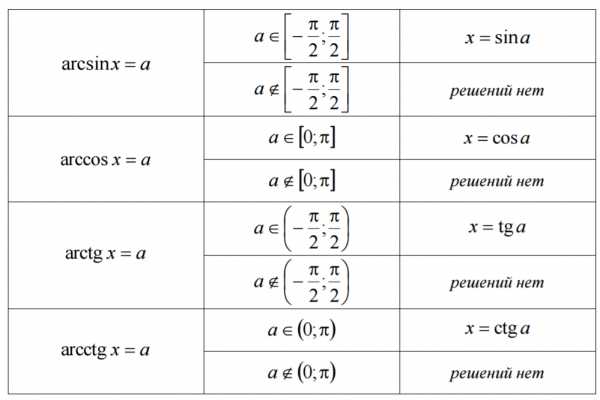
Формулы корней тригонометрических уравнений в таблице
Для синуса: Для косинуса:
Для косинуса: Для тангенса и котангенса:Формулы решения уравнений, содержащих обратные тригонометрические функции:
Для тангенса и котангенса:Формулы решения уравнений, содержащих обратные тригонометрические функции:
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью тригонометрических формул преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
Рассмотрим на примерах основные методы решения.
Алгебраический метод.
В этом методе делается замена переменной и ее подстановка в равенство.
Пример. Решить уравнение: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 — x)+1=0`
Решение. Используя формулы приведения, имеем:
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
делаем замену: `cos(x+\frac \pi 6)=y`, тогда `2y^2-3y+1=0`,
находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Ответ: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Разложение на множители.
Пример. Решить уравнение: `sin x+cos x=1`.
Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:
`sin x — 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n`, `x_2=\pi/2+ 2\pi n`.
Ответ: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Приведение к однородному уравнению
Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:
`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).
Потом разделить обе части на `cos x \ne 0` — для первого случая, и на `cos^2 x \ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.
Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.
Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x \ne 0`, получим:
`\frac {sin^2 x}{cos^2 x}+\frac{sin x cos x}{cos^2 x} — \frac{2 cos^2 x}{cos^2 x}=0`
`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:
- `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
- `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.
Ответ. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.
Переход к половинному углу
Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.
Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Применив описанный выше алгебраический метод, получим:
- `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Ответ. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Введение вспомогательного угла
В тригонометрическом уравнении `a sin x + b cos x =c`, где a,b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt {a^2+b^2}`:
`\frac a{sqrt {a^2+b^2}} sin x +` `\frac b{sqrt {a^2+b^2}} cos x =` `\frac c{sqrt {a^2+b^2}}`.
Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `\frac a{sqrt {a^2+b^2}}=cos \varphi`, ` \frac b{sqrt {a^2+b^2}} =sin \varphi`, `\frac c{sqrt {a^2+b^2}}=C`, тогда:
`cos \varphi sin x + sin \varphi cos x =C`.
Подробнее рассмотрим на следующем примере:
Пример. Решить уравнение: `3 sin x+4 cos x=2`.
Решение. Разделим обе части равенства на `sqrt {3^2+4^2}`, получим:
`\frac {3 sin x} {sqrt {3^2+4^2}}+` `\frac{4 cos x}{sqrt {3^2+4^2}}=` `\frac 2{sqrt {3^2+4^2}}`
`3/5 sin x+4/5 cos x=2/5`.
Обозначим `3/5 = cos \varphi` , `4/5=sin \varphi`. Так как `sin \varphi>0`, `cos \varphi>0`, то в качестве вспомогательного угла возьмем `\varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:
`cos \varphi sin x+sin \varphi cos x=2/5`
Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:
`sin (x+\varphi)=2/5`,
`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Дробно-рациональные тригонометрические уравнения
Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.
Пример. Решить уравнение. `\frac {sin x}{1+cos x}=1-cos x`.
Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:
`\frac {sin x}{1+cos x}=` `\frac {(1-cos x)(1+cos x)}{1+cos x}`
`\frac {sin x}{1+cos x}=` `\frac {1-cos^2 x}{1+cos x}`
`\frac {sin x}{1+cos x}=` `\frac {sin^2 x}{1+cos x}`
`\frac {sin x}{1+cos x}-` `\frac {sin^2 x}{1+cos x}=0`
`\frac {sin x-sin^2 x}{1+cos x}=0`
Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.
Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Материалы по теме:
Поделиться с друзьями:
Загрузка…matemonline.com
Тригонометрические формулы функций, более 100 шт
Тригонометрия в буквальном переводе означает измерение треугольников. Но это надо понимать как решение треугольников, то есть определения их сторон, углов или других элементов. Возникновение тригонометрии связано с землеизмерением, астрономией и строительством.
Основные тригонометрические формулы
Основное тригонометрическое тождество
Эти тождества используются для преобразования тригонометрических выражений; позволяют по значению одной из тригонометрических функций найти значения всех остальных.
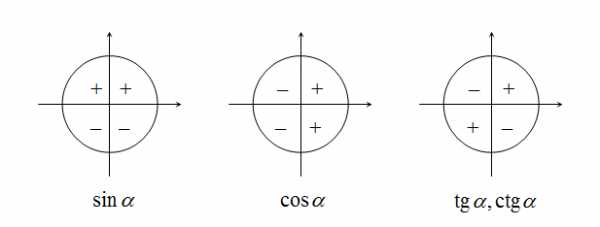
Знаки тригонометрических функций
Отсюда можем сделать вывод, что значения синусов углов лежащих в первой и второй четверти положительны (так как ординаты точек в этих четвертях больше нуля), а лежащих в третьей и четвёртой четверти – отрицательны.
Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент.
Формулы, выражающие тригонометрические функции через другие тригонометрические функции
Данные формулы позволяют находить одну тригонометрическую функцию угла если известная какая-нибудь иная функция этого угла. Используются при упрощениях и вычислениях:
Формулы, выражающие тригонометрические функции через тангенс половинного аргумента
Эти формулы находят свое широкое применение в интегральном исчислении.
Формулы двойных и тройных аргументов
Данные формулы довольно легко получить при помощи формул сложения аргументов тригонометрических функций, заменой на Используются при тригонометрических упрощениях и преобразованиях.
Синус двойного угла:
Косинус двойного угла:
Формулы половинного аргумента
Названные формулы выражают функции половинного аргумента через тригонометрические функции аргумента При меняются в тригонометрических преобразованиях.
Формулы сложения и вычитания аргументов
Тригонометрические формулы сложения и вычитания углов представляют собой тригонометрические уравнения, в которых в качестве аргумента тригонометрической функции выступает сумма или разность двух углов и Данные формулы позволяют по известным тригонометрическим функциям аргументов и определять значения этих функций для сумм или разностей указанных аргументов.
Формулы преобразования суммы тригонометрических функций в произведение
Сумма (и разность) тригонометрических функций преобразуется в произведение функций от других аргументов по следующим формулам, которые выводятся из теорем сложения, а также определений тангенса и котангенса:
Формулы для разложения тригонометрических выражений на множители.
Формулы преобразования произведения тригонометрических функций в сумму
Эти формулы получаются из сложения/вычитания соответствующих формул сложения и вычитания аргументов и дальнейшего упрощения:
Используются при тригонометрических преобразованиях.
Формулы понижения степени тригонометрических функций
Данные формулы используются при различных тригонометрических преобразованиях:
Другие формулы
ru.solverbook.com
