Posted in Советы по обучению

Тригонометрия алгебра формулы – Основные тригонометрические тождества, формулы приведения, сложения, двойного угла, суммы и разности, половинного аргумента, тангенс половинного аргумента. Тест

Содержание

Тригонометрические формулы

Наиболее часто встречающиеся тригонометрические формулы:

 

\(\blacktriangleright\) Основные тождества: \[\begin{array}{|l|l|} \hline \sin^2 \alpha+\cos^2 \alpha =1& \mathrm{tg}\, \alpha \cdot \mathrm{ctg}\, \alpha =1 \\ &(\sin\alpha\ne 0, \cos\alpha\ne 0)\\[0.5ex] \hline &\\ \mathrm{tg}\, \alpha=\dfrac{\sin \alpha}{\cos \alpha} &\mathrm{ctg}\, \alpha =\dfrac{\cos \alpha}{\sin \alpha} \\&\\ 1+\mathrm{tg}^2\, \alpha =\dfrac1{\cos^2 \alpha} & 1+\mathrm{ctg}^2\, \alpha=\dfrac1{\sin^2 \alpha}\\&\\ (\cos\alpha\ne 0)& (\sin\alpha\ne 0) \\ \hline \end{array}\]

\(\blacktriangleright\) Формулы сложения углов: \[\begin{array}{|l|r|} \hline &\\ \sin{(\alpha\pm \beta)}=\sin\alpha\cdot \cos\beta\pm \sin\beta\cdot \cos\alpha & \cos{(\alpha\pm \beta)}=\cos\alpha\cdot \cos\beta \mp \sin\alpha\cdot \sin\beta\\ &\\ \hline &\\ \mathrm{tg}\, (\alpha\pm \beta)=\dfrac{\mathrm{tg}\, \alpha\pm \mathrm{tg}\, \beta}{1 \mp \mathrm{tg}\, \alpha\cdot \mathrm{tg}\, \beta} & \mathrm{ctg}\, (\alpha\pm\beta)=-\dfrac{1\mp \mathrm{ctg}\, \alpha\cdot \mathrm{ctg}\, \beta}{\mathrm{ctg}\, \alpha\pm \mathrm{ctg}\, \beta}\\&\\ \cos\alpha\cos\beta\ne 0&\sin\alpha\sin\beta\ne 0\\ \hline \end{array}\]

\(\blacktriangleright\) Формулы двойного и тройного углов: \[\begin{array}{|lc|cr|} \hline \sin {2\alpha}=2\sin \alpha\cos \alpha & \qquad &\qquad & \cos{2\alpha}=\cos^2\alpha -\sin^2\alpha\\ \sin \alpha\cos \alpha =\dfrac12\sin {2\alpha} && & \cos{2\alpha}=2\cos^2\alpha -1\\ & & & \cos{2\alpha}=1-2\sin^2 \alpha\\ \hline &&&\\ \mathrm{tg}\, 2\alpha = \dfrac{2\mathrm{tg}\, \alpha}{1-\mathrm{tg}^2\, \alpha} && & \mathrm{ctg}\, 2\alpha = \dfrac{\mathrm{ctg}^2\, \alpha-1}{2\mathrm{ctg}\, \alpha}\\&&&\\ \cos\alpha\ne 0, \ \cos2\alpha\ne 0 &&& \sin\alpha\ne 0, \ \sin2\alpha\ne 0\\ \hline &&&\\ \sin {3\alpha}=3\sin \alpha -4\sin^3\alpha && & \cos{3\alpha}=4\cos^3\alpha -3\cos \alpha\\&&&\\ \hline \end{array}\]

\(\blacktriangleright\) Формулы понижения степени: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin^2\alpha=\dfrac{1-\cos{2\alpha}}2 &&& \cos^2\alpha=\dfrac{1+\cos{2\alpha}}2\\&&&\\ \hline \end{array}\]

\(\blacktriangleright\) Формулы произведения функций: \[\begin{array}{|c|} \hline \\ \sin\alpha\sin\beta=\dfrac12\bigg(\cos{(\alpha-\beta)}-\cos{(\alpha+\beta)}\bigg)\\\\ \cos\alpha\cos\beta=\dfrac12\bigg(\cos{(\alpha-\beta)}+\cos{(\alpha+\beta)}\bigg)\\\\ \sin\alpha\cos\beta=\dfrac12\bigg(\sin{(\alpha-\beta)}+\sin{(\alpha+\beta)}\bigg)\\\\ \hline \end{array}\]

\(\blacktriangleright\) Формулы суммы/разности функций: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin\alpha+\sin\beta=2\sin{\dfrac{\alpha+\beta}2}\cos{\dfrac{\alpha-\beta}2} &&& \sin\alpha-\sin\beta=2\sin{\dfrac{\alpha-\beta}2}\cos{\dfrac{\alpha+\beta}2}\\&&&\\ \cos\alpha+\cos\beta=2\cos{\dfrac{\alpha+\beta}2}\cos{\dfrac{\alpha-\beta}2} &&& \cos\alpha -\cos\beta=-2\sin{\dfrac{\alpha-\beta}2}\sin{\dfrac{\alpha+\beta}2}\\&&&\\ \mathrm{tg}\, \alpha \pm \mathrm{tg}\, \beta=\dfrac{\sin{(\alpha\pm\beta)}}{\cos\alpha\cos\beta} &&& \mathrm{ctg}\, \alpha\pm \mathrm{ctg}\, \beta= — \dfrac{\sin{(\alpha\pm \beta)}}{\sin\alpha\sin\beta}\\&&&\\ \hline \end{array}\]

\(\blacktriangleright\) Выражение синуса и косинуса через тангенс половинного угла: \[\begin{array}{|l|r|} \hline &\\ \sin{2\alpha}=\dfrac{2\mathrm{tg}\, \alpha}{1+\mathrm{tg}^2\, \alpha} & \cos{2\alpha}=\dfrac{1-\mathrm{tg}^2\, \alpha}{1+\mathrm{tg}^2\, \alpha}\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end{array}\]

\(\blacktriangleright\) Формула вспомогательного аргумента: \[\begin{array}{|c|} \hline \text{Частный случай}\\ \hline \\ \sin\alpha\pm \cos\alpha=\sqrt2\cdot \sin{\left(\alpha\pm \dfrac{\pi}4\right)}\\\\ \sqrt3\sin\alpha\pm \cos\alpha=2\sin{\left(\alpha\pm \dfrac{\pi}6\right)}\\\\ \sin\alpha\pm \sqrt3\cos\alpha=2\sin{\left(x\pm \dfrac{\pi}3\right)}\\\\ \hline \text{Общий случай}\\ \hline\\ a\sin\alpha\pm b\cos\alpha=\sqrt{a^2+b^2}\cdot \sin{(\alpha\pm \phi)}, \ \ \cos\phi=\dfrac a{\sqrt{a^2+b^2}}, \ \sin\phi=\dfrac b{\sqrt{a^2+b^2}}\\\\ \hline \end{array}\]

Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.

 

Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.

 

\(\blacktriangleright\) Вывод формулы косинуса разности углов \(\cos{(\alpha -\beta)}=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)

 

Рассмотрим тригонометрическую окружность и на ней углы \(\alpha\) и \(\beta\). Пусть этим углам соответствуют точки \(A\) и \(B\) соответственно. Тогда координаты этих точек: \(A(\cos\alpha;\sin\alpha), \ B(\cos\beta;\sin\beta)\).


 

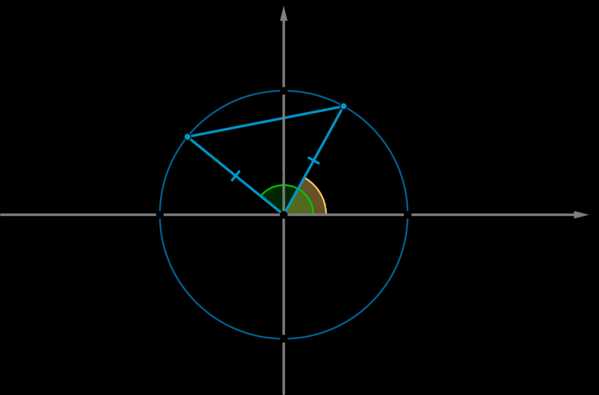
Рассмотрим \(\triangle AOB: \ \angle AOB=\alpha-\beta\). По теореме косинусов:

 

\(AB^2=AO^2+BO^2-2AO\cdot BO\cdot \cos(\alpha-\beta)=1+1-2\cos(\alpha-\beta) \ (1)\)  (т.к. \(AO=BO=R\) – радиус окружности)

 

По формуле расстояния между двумя точками на плоскости:

 

\(AB^2=(\cos\alpha-\cos\beta)^2+(\sin\alpha-\sin\beta)^2=\cos^2\alpha-2\cos\alpha\cos\beta+\cos^2\beta+\)

\(+\sin^2\alpha-2\sin\alpha\sin\beta+\sin^2\beta=\big(\cos^2\alpha+\sin^2\alpha\big)+\big(\cos^2\beta+\sin^2\beta\big)-2\big(\cos\alpha\cos\beta+\sin\alpha\sin\beta\big)=\)

\(=1+1-2\big(\cos\alpha\cos\beta+\sin\alpha\sin\beta\big) \ (2)\)

 

Таким образом, сравнивая равенства \((1)\) и \((2)\):

\(1+1-2\big(\cos\alpha\cos\beta+\sin\alpha\sin\beta\big)=1+1-2\cos(\alpha-\beta)\)

 

Отсюда и получается наша формула.

 

\(\blacktriangleright\) Вывод остальных формул суммы/разности углов:

 

Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения \(\sin x=\cos(90^\circ-x)\) и \(\cos x=\sin (90^\circ-x)\):

 

1) \(\cos(\alpha+\beta)=\cos(\alpha-(-\beta))=\cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)

 

2) \(\sin(\alpha+\beta)=\cos(90^\circ-(\alpha+\beta))=\cos((90^\circ-\alpha)-\beta)=\)

\(+\cos(90^\circ-\alpha)\cos\beta+\sin(90^\circ-\alpha)\sin\beta=\sin\alpha\cos\beta+\cos\alpha\sin\beta\)

 

3) \(\sin(\alpha-\beta)=\sin(\alpha+(-\beta))=\sin\alpha\cos(-\beta)+\sin(-\beta)\cos\alpha=\sin\alpha\cos\beta-\sin\beta\cos\alpha\)

 

4) \(\mathrm{tg}\,(\alpha\pm\beta)=\dfrac{\sin (\alpha\pm\beta)}{\cos (\alpha\pm\beta)}=\dfrac{\sin\alpha\cos\beta\pm\sin\beta\cos\alpha}{\cos\alpha\cos\beta\mp\sin\alpha\sin\beta}=\)

 

разделим числитель и знаменатель дроби на \(\cos\alpha\cos\beta\ne 0\)
(при \(\cos\alpha=0 \Rightarrow \mathrm{tg}\,(\alpha\pm\beta)=\mp \mathrm{ctg}\,\beta\), при \(\cos\beta=0 \Rightarrow \mathrm{tg}\,(\alpha\pm\beta)=\pm \mathrm{ctg}\,\alpha\)):

 

\(=\dfrac{\mathrm{tg}\,\alpha\pm\mathrm{tg}\,\beta}{1\mp\mathrm{tg}\,\alpha\cdot \mathrm{tg}\,\beta}\)

 

Таким образом, данная формула верна только при \(\cos\alpha\cos\beta\ne 0\).

 

5) Аналогично, только делением на \(\sin\alpha\sin\beta\ne 0\), выводится формула котангенса суммы/разности двух углов.

 

\(\blacktriangleright\) Вывод формул двойного и тройного углов:

 

Данные формулы выводятся с помощью предыдущих формул:

 

1) \(\sin 2\alpha=\sin(\alpha+\alpha)=\sin\alpha\cos\alpha+\sin\alpha\cos\alpha=2\sin\alpha\cos\alpha\)

 

2) \(\cos2\alpha=\cos(\alpha+\alpha)=\cos\alpha\cos\alpha-\sin\alpha\sin\alpha=\cos^2\alpha-\sin^2\alpha\)

 

Используя основное тригонометрическое тождество \(\sin^2\alpha+\cos^2\alpha=1\), получим еще две формулы для косинуса двойного угла:

 

2.1) \(\cos2\alpha=\cos^2\alpha-\sin^2\alpha=\cos^2\alpha-(1-\cos^2\alpha)=2\cos^2\alpha-1\)

 

2.2) \(\cos2\alpha=\cos^2\alpha-\sin^2\alpha=(1-\sin^2\alpha)-\sin^2\alpha=1-2\sin^2\alpha\)

 

3) \(\mathrm{tg}\,2\alpha=\dfrac{\sin2\alpha}{\cos2\alpha}=\dfrac{2\sin\alpha\cos\alpha}{\cos^2\alpha-\sin^2\alpha}=\)

 

разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0 \Rightarrow \mathrm{tg}\,2\alpha=0\)):

 

\(=\mathrm{tg}\,2\alpha=\dfrac{2\mathrm{tg}\,\alpha}{1-\mathrm{tg}^2\,\alpha}\)

 

Таким образом, эта формула верна только при \(\cos\alpha\ne 0\), а также при \(\cos2\alpha\ne 0\) (чтобы существовал сам \(\mathrm{tg}\,2\alpha\)).

 

4) \(\mathrm{ctg}\,2\alpha=\dfrac{\cos^2\alpha-\sin^2\alpha}{2\sin\alpha\cos\alpha}=\dfrac{\mathrm{ctg}^2\,\alpha-1}{2\mathrm{ctg}\,\alpha}\)

 

По тем же причинам при \(\sin\alpha\ne 0, \sin2\alpha\ne 0\).

 

5) \(\sin3\alpha=\sin(\alpha+2\alpha)=\sin\alpha\cos2\alpha+\cos\alpha\sin2\alpha=\sin\alpha(1-2\sin^2\alpha)+\cos\alpha\cdot 2\sin\alpha\cos\alpha=\)

\(=\sin\alpha-2\sin^3\alpha+2\sin\alpha(1-\sin^2\alpha)=3\sin\alpha-4\sin^3\alpha\)

 

6) Аналогично выводится, что \(\cos3\alpha=\cos(\alpha+2\alpha)=4\cos^3\alpha-3\cos\alpha\)

 

\(\blacktriangleright\) Вывод формул понижения степени:

 

Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:

 

1) \(\cos2\alpha=2\cos^2\alpha-1 \Rightarrow \cos^2\alpha=\dfrac{1+\cos2\alpha}2\)

 

2) \(\cos2\alpha=1-2\sin^2\alpha \Rightarrow \sin^2\alpha=\dfrac{1-\cos2\alpha}2\)

 

Заметим, что в данных формулах степень синуса/косинуса равна \(2\) в левой части, а в правой части степень косинуса равна \(1\).

 

\(\blacktriangleright\) Вывод формул произведения функций:

 

1) Сложим формулы косинуса суммы и косинуса разности двух углов:

 

\(\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)

 

\(\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)

 

Получим: \(\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)\)

 

2) Если вычесть из формулы косинуса суммы косинус разности, то получим:

 

\(\sin\alpha\sin\beta=\dfrac12\Big(\cos(\alpha-\beta)-\cos(\alpha+\beta)\Big)\)

 

3) Сложим формулы синуса суммы и синуса разности двух углов:

 

\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\sin\beta\cos\alpha\)

 

\(\sin(\alpha-\beta)=\sin\alpha\cos\beta-\sin\beta\cos\alpha\)

 

Получим: \(\sin\alpha\cos\beta=\dfrac12\Big(\sin(\alpha-\beta)+\sin(\alpha+\beta)\Big)\)

 

\(\blacktriangleright\) Вывод формул суммы/разности функций:

 

Обозначим \(\alpha+\beta=x, \alpha-\beta=y\). Тогда: \(\alpha=\dfrac{x+y}2, \ \beta=\dfrac{x-y}2\). Подставим эти значения в предыдущие три формулы:

 

1) \(2\cos{\dfrac{x+y}2}\cos{\dfrac{x-y}2}=\cos x+\cos y\)

 

Получили формулу суммы косинусов.

 

2) \(2\sin {\dfrac{x+y}2}\sin {\dfrac{x-y}2}=\cos y-\cos x\)

 

Получили формулу разности косинусов.

 

3) \(2\sin {\dfrac{x+y}2}\cos {\dfrac{x-y}2}=\sin y+\sin x\)

 

Получили формулу суммы синусов.

 

4) Формулу разности синусов можно вывести из формулы суммы синусов:

 

\(\sin x-\sin y=\sin x+\sin(-y)=2\sin {\dfrac{x-y}2}\cos {\dfrac{x+y}2}\)

 

5) \(\mathrm{tg}\,\alpha\pm\mathrm{tg}\,\beta=\dfrac{\sin\alpha}{\cos\alpha}\pm\dfrac{\sin\beta}{\cos\beta}=\dfrac{\sin\alpha\cos\beta\pm\sin\beta\cos\alpha}{\cos\alpha\cos\beta}=\dfrac{\sin(\alpha\pm\beta)}{\cos\alpha\cos\beta}\)

 

Аналогично выводится формула суммы котангенсов.

 

\(\blacktriangleright\) Вывод формул выражения синуса и косинуса через тангенс половинного угла:

 

1) \(\sin2\alpha=\dfrac{\sin2\alpha}1=\dfrac{2\sin\alpha\cos\alpha}{\sin^2\alpha+\cos^2\alpha}=\)

 

(разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0\) и \(\sin2\alpha=0\)):)

 

\(=\dfrac{2\mathrm{tg}\,\alpha}{1+\mathrm{tg}^2\,\alpha}\)

 

2) Так же, только делением на \(\sin^2\alpha\), выводится формула для косинуса.

 

\(\blacktriangleright\) Вывод формул вспомогательного угла:

 

Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.

 

Рассмотрим выражение \(a\sin x+b\cos x\). Домножим и разделим это выражение на \(\sqrt{a^2+b^2}\,\):

 

\(a\sin x+b\cos x=\sqrt{a^2+b^2}\left(\dfrac a{\sqrt{a^2+b^2}}\sin x+ \dfrac b{\sqrt{a^2+b^2}}\cos x \right)=\sqrt{a^2+b^2}\big(a_1\sin x+b_1\cos x\big)\)

 

Заметим, что таким образом мы добились того, что \(a_1^2+b_1^2=1\),   т.к. \(\left(\dfrac a{\sqrt{a^2+b^2}}\right)^2+\left(\dfrac b{\sqrt{a^2+b^2}}\right)^2=\dfrac{a^2+b^2}{a^2+b^2}=1\)

 

Таким образом, можно утверждать, что существует такой угол \(\phi\), для которого, например, \(\cos \phi=a_1, \ \sin \phi=b_1\). Тогда наше выражение примет вид:

 

\(\sqrt{a^2+b^2}\,\big(\cos \phi \sin x+\sin \phi\cos x\big)=\sqrt{a^2+b^2}\,\sin (x+\phi)\) (по формуле синуса суммы двух углов)

 

Значит, формула выглядит следующим образом: \[{\large{a\sin x+b\cos x=\sqrt{a^2+b^2}\,\sin (x+\phi),}} \quad \text{где } \cos \phi=\dfrac a{\sqrt{a^2+b^2}}\] Заметим, что мы могли бы, например, принять за \(\cos \phi=b_1, \ \sin \phi=a_1\) и тогда формула выглядела бы как \[a\sin x+b\cos x=\sqrt{a^2+b^2}\,\cos (x-\phi)\]

 

\(\blacktriangleright\) Рассмотрим некоторые частные случаи формул вспомогательного угла:

 

\(a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1{\sqrt2}\sin x\pm\dfrac1{\sqrt2}\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac{\pi}4\right)\)

 

\(b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac{\sqrt3}2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac{\pi}6\right)\)

 

\(c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac{\sqrt3}2\cos x\right)=2\,\sin\left(x\pm\dfrac{\pi}3\right)\)

 

shkolkovo.net

Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Тригонометрия

Справочник по математикеТригонометрия
Связи между тригонометрическими функциями одного угла
Тригонометрические функции суммы и разности двух углов
Тригонометрические функции двойного угла
Формулы понижения степени для квадратов тригонометрических функций
Формулы понижения степени для кубов синуса и косинуса
Выражение тангенса угла через синус и косинус двойного угла
Преобразование суммы тригонометрических функций в произведение
Преобразование произведения тригонометрических функций в сумму
Выражение тригонометрических функций через тангенс половинного угла
Тригонометрические функции тройного угла

Связи между тригонометрическими функциями одного угла

sin2α + cos2α = 1

Тригонометрические функции суммы и разности двух углов

ФормулаНазвание формулы
sin (α + β) = sin α cos β + cos α sin βСинус суммы
sin (α – β) = sin α cos β – cos α sin βСинус разности
cos (α + β) = cos α cos β – sin α sin βКосинус суммы
cos (α – β) = cos α cos β + sin α sin βКосинус разности
Тангенс суммы
Тангенс разности
Синус суммы
sin (α + β) = sin α cos β +
+ cos α sin β
Синус разности
sin (α – β) = sin α cos β –
– cos α sin β
Косинус суммы
cos (α + β) = cos α cos β –
– sin α sin β
Косинус разности
cos (α – β) = cos α cos β +
+ sin α sin β
Тангенс суммы
Тангенс разности

Тригонометрические функции двойного угла

ФормулаНазвание формулы
sin 2α = 2 sin α cos αСинус двойного угла

cos 2α = cos 2α – sin2α

cos 2α = 2cos 2α – 1

cos 2α = 1 – 2sin 2α

Косинус двойного угла
Тангенс двойного угла
Синус двойного угла
sin 2α = 2 sin α cos α
Косинус двойного угла

cos 2α = cos 2α – sin2α

cos 2α = 2cos 2α – 1

cos 2α = 1 – 2sin 2α

Тангенс двойного угла

Формулы понижения степени для квадратов тригонометрических функций

ФормулаНазвание формулы
Выражение квадрата синуса
через косинус двойного угла
Выражение квадрата косинуса
через косинус двойного угла
Выражение квадрата тангенса
через косинус двойного угла
Выражение квадрата синуса через косинус двойного угла
Выражение квадрата косинуса через косинус двойного угла
Выражение квадрата тангенса через косинус двойного угла

Формулы понижения степени для кубов синуса и косинуса

ФормулаНазвание формулы
Выражение куба синуса через
синус угла и синус тройного угла
Выражение куба косинуса через
косинус угла и косинус тройного угла
Выражение куба синуса через
синус угла и синус тройного угла
Выражение куба косинуса через
косинус угла и косинус тройного угла

Выражение тангенса через синус и косинус двойного угла

Преобразование суммы тригонометрических функций в произведение

ФормулаНазвание формулы
Сумма синусов
Разность синусов
Сумма косинусов
Разность косинусов
Сумма тангенсов
Разность тангенсов
Сумма синусов
Разность синусов
Сумма косинусов
Разность косинусов
Сумма тангенсов
Разность тангенсов

Преобразование произведения тригонометрических функций в сумму

ФормулаНазвание формулы
Произведение синусов
Произведение косинусов
Произведение синуса и косинуса
Произведение синусов
Произведение косинусов
Произведение синуса и косинуса

Выражение тригонометрических функций через тангенс половинного угла

ФормулаНазвание формулы
Выражение синуса угла через
тангенс половинного угла
Выражение косинуса угла через
тангенс половинного угла
Выражение тангенса угла через
тангенс половинного угла
Выражение синуса угла через тангенс половинного угла
Выражение косинуса угла через тангенс половинного угла
Выражение тангенса угла через тангенс половинного угла

Тригонометрические функции тройного угла

ФормулаНазвание формулы
sin 3α = 3sin α – 4sin3αСинус тройного угла
cos 3α = 4cos3α –3cos αКосинус тройного угла
Тангенс тройного угла
Синус тройного угла
sin 3α = 3sin α – 4sin3α
Косинус тройного угла
cos 3α = 4cos3α –3cos α
Тангенс тройного угла

      На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.

    Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными».

Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

подготовительные курсы для школьников 10 и 11 классов

      У нас также для школьников организованы

индивидуальные занятия с репетиторами по математике и русскому языку

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru

Все формулы тригонометрии

В таблице приведены формулы приведения для тригонометрических функций (sin, cos, tg, ctg).

 

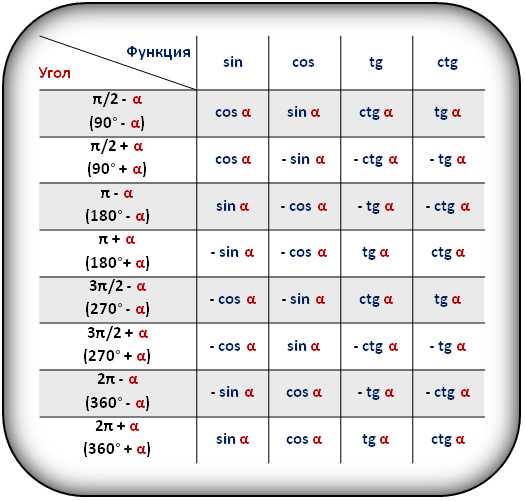
Тригонометрические формулы преобразования разности аргументов

 

 

 

 

 

 

Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)

 

sin(2α)- через sin и cos:

 

sin(2α)- через tg и ctg:

 

cos(2α)- через sin и cos:

 

cos(2α)- через tg и ctg:

 

 

tg(2α) и сtg(2α):

 

 

 

Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):

 

 

 

 

 

Уравнения разложения тригонометрических функций:

квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.

 

 

 

 

 

 

 

 

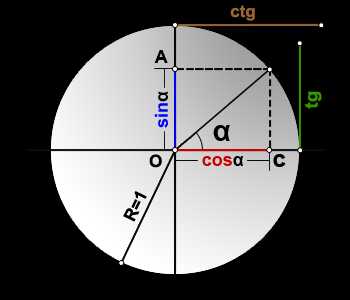
sin(α)=OA

cos(α)=OC

tg(α)=DE

ctg(α)=MK

R=OB=1

 

 

 

 

 

 

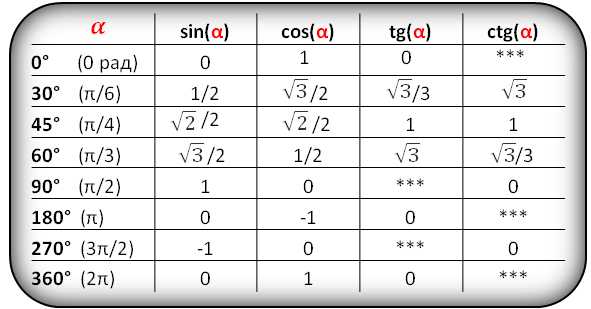
Значения функций для некоторых углов, α

 

 

 

zdesformula.ru

Тригонометрические формулы | Формулы с примерами

Формулы
Тригонометрические тождества:

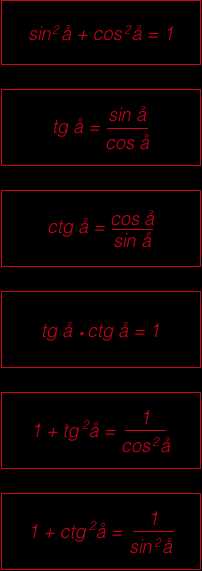
Формулы приведения:

Тригонометрические формулы сложения:

Формулы кратных углов:

Формулы половинного угла:

Формулы суммы и разности тригонометрических функций:

Формулы произведения тригонометрических функций:

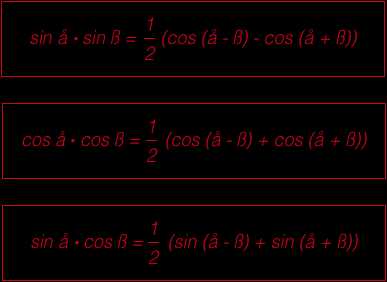
Формулы понижения степени:

1.  Формула понижения степени синуса:

2.  Формула понижения степени косинуса:

3.  Формула понижения степени тангенса:

4.  Формула понижения степени котангенса:

Формулы степеней функции:

Формулы универсальной тригонометрической подстановки

formula-xyz.ru

Основные тригонометрические тождества, формулы приведения, сложения, двойного угла, суммы и разности, половинного аргумента, тангенс половинного аргумента. Тест

Тестирование онлайн

Основные тригонометрические тождества

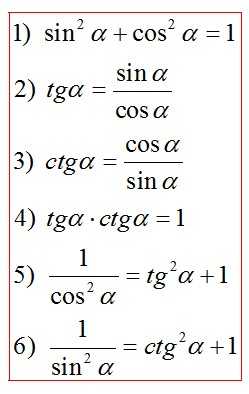
Четность, нечетность тригонометрических функций

Косинус является четной функцией; синус, тангенс, котангенс — нечетные.

Формулы приведения

Это соотношения, с помощью которых значения тригонометрических функций аргументов и др., выражаются через значения .

Правила преобразования:
1) Если аргумент содержит , где n — нечетное натуральное число , то функция меняется на «конфункцию», т.е. синус на косинус, тангенс на котангенс и наоборот. Если n — четное натуральное число , то название функции не изменяется.

2) Определяем знак («+» или «-«) значения первоначальной функции. Преобразованное выражение сохраняет знак своего родителя.

Формулы сложения и вычитания

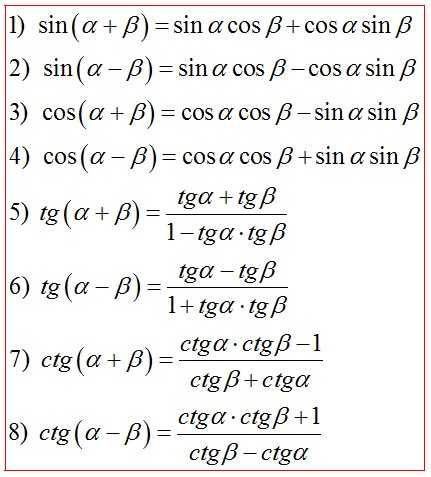
Формулы двойного угла

Формулы преобразования суммы и разности в произведение

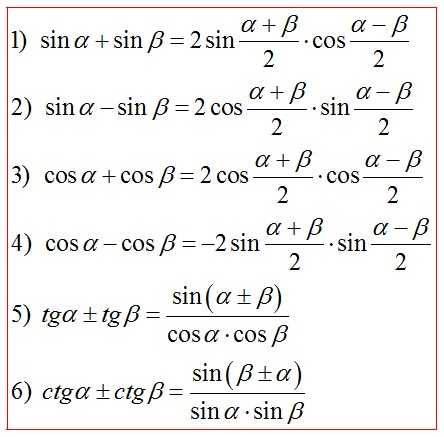
Формулы половинного аргумента

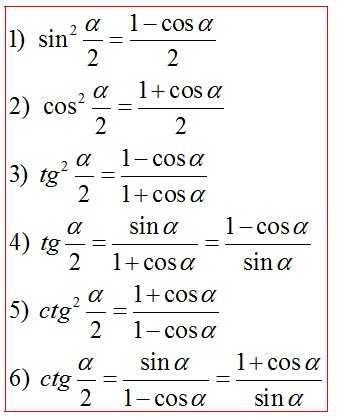
Формулы тройного угла*

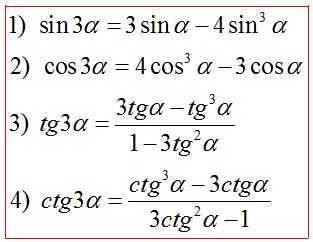
Формулы преобразования произведения в сумму (разность)*

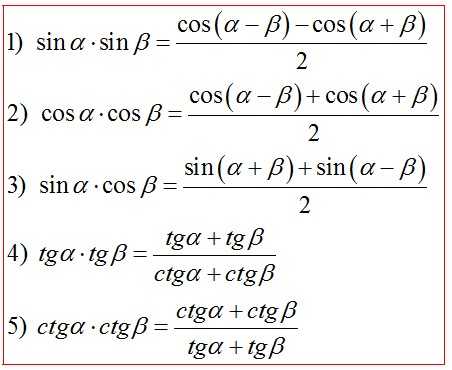
Универсальная подстановка через тангенс половинного аргумента*

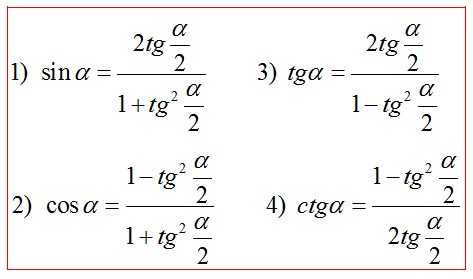
fizmat.by

Формулы тригонометрии

Взаимосвязь основных тригонометрических функций, каких как косинус и синус, тангенс и котангенс — называется формулы тригонометрии

. Из-за того что взаимосвязей очень большое количество, соответственно и формул не меньше. Часть формул объединяет тригонометрические функции в зависимости от угла, который может быть либо кратным, либо одинаковым. Так же может выражаться от тангенса половинного угла. Так же через понижение степени.
Мы разберем самые основные из тригонометрических формул. С помощью которых можно решить большинство тригонометрических заданий. Для большего удобства объединим их по значению, по таблицам.

Начнем с тригонометрических тождеств.


Основы в тригонометрических тождествах определяют взаимосвязь косинуса и синуса, тангенса и котангенса в одном угле. И выходят из их определения и единичной окружности. Дают возможность выделить через любую функцию другую.

Далее рассмотрим тригонометрические формулы приведения.

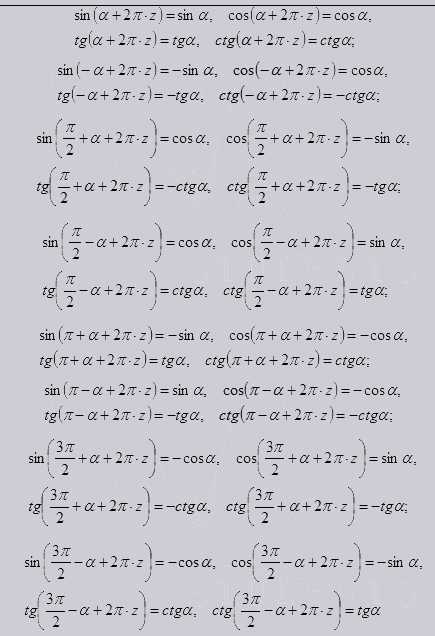
Они вытекают из свойств синусов, косинусов, котангенсов и тангенсов. Тем самым выражают такие свойства функции как: периодичность, симметричность и сдвиг к рассматриваемому углу. так же дают возможность работать с углами в радиусе до 90 градусов и произвольные углы.

Формулы на сложение.

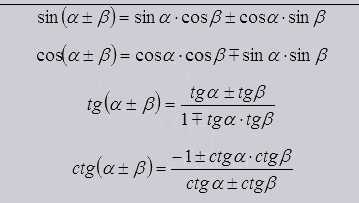
Из данных формул видно что функции на сумму или разность от 2 углов выводятся из их же тригонометрических функций. Так же являются основой для формул двойных, тройных и других углов.

Формула для двойных, тройных и других углов.

Из них видно что тригонометрическая функция двойного, тройного или какого то ни было угла выводится из т.ф. одинарных углов.

Так же как и одинарные, двойные, тройные и т.д. существуют и половинные углы


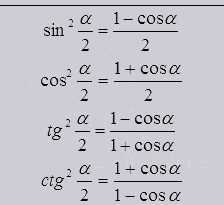
Из формул половинного угла видно, что он выходит из косинуса угла целого.

Так же существуют методы понижения степени выглядят они как:



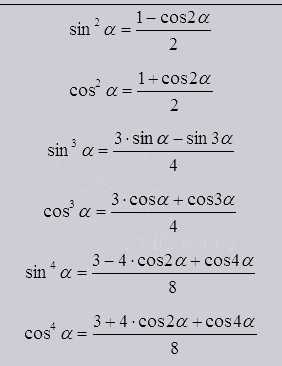
С помощью их использования возможно понизить функцию до первой степени. Взаимодействуя с натуральными степенями функций переводить до синусов и косинусов только кратных углов, в первую степень.

Сумма и разность в тригонометрической функции.

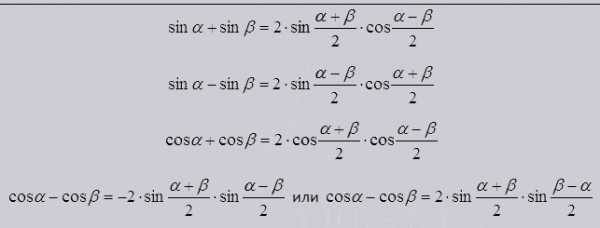
Помогают упростить тригонометрическое выражение, и разложить на множители синусы и косинусы.

Произведение синуса, косинуса, и одно на другое.



Метод универсальной тригонометрической подстановки.

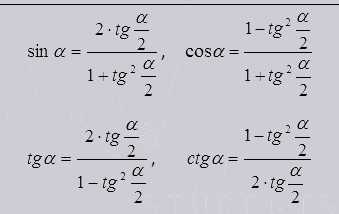
Такая подстановка удобна тем, что функции получаются без корней.

Заметка: Актуальные предложения, участие в тендерах на строительство бесплатное! Перейдите по ссылке строительно монтажные тендеры (http://www.b2bsearch.ru/tenders/stroy) узнайте подробнее.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

reshit.ru

Все формулы по тригонометрии

Все формулы по тригонометрии

Основные тригонометрические тождества

sin2x + cos2x = 1

tgx ctgx = 1

tg2x + 1

  =  

1

cos2x

ctg2x + 1

  =  

1

sin2x

Формулы двойного аргумента

sin2x = 2sinx cosx

sin2x

  =  

2tgx

  = 

2ctgx

  = 

2

1 + tg2x

1 + ctg2x

tgx + ctgx

cos2x = cos2 — sin2x = 2cos2x — 1 = 1 — 2sin2x

cos2x

  =  

1 — tg2x

  = 

ctg2x — 1

  = 

ctgx — tgx

1 + tg2x

ctg2x + 1

ctgx + tgx

tg2x

  =  

2tgx

  = 

2ctgx

  = 

2

1 — tg2x

ctg2x — 1

ctgx — tgx

ctg2x

  =  

ctg2x — 1

  = 

ctgx — tgx

2ctgx

2

Формулы тройного аргумента

sin3x = 3sinx — 4sin3x cos3x = 4cos3x — 3cosx

tg3x

  =  

3tgx — tg3x

1 — 3tg2x

ctg3x

  =  

ctg3x — 3ctgx

3ctg2x — 1

Формулы половинного аргумента

sin2

x

  =  

1 — cosx

2

2

cos2

x

  =  

1 + cosx

2

2

tg2

x

  =  

1 — cosx

2

1 + cosx

ctg2

x

  =  

1 + cosx

2

1 — cosx

tg

x

  =  

1 — cosx

  =  

sinx

2

sinx

1 + cosx

ctg

x

  =  

1 + cosx

  =  

sinx

2

sinx

1 — cosx

Формулы квадратов тригонометрических функций

sin2x

  =  

1 — cos2x

2

cos2x

  =  

1 + cos2x

2

tg2x

  =  

1 — cos2x

1 + cos2x

ctg2x

  =  

1 + cos2x

1 — cos2x

sin2

x

  =  

1 — cosx

2

2

cos2

x

  =  

1 + cosx

2

2

tg2

x

  =  

1 — cosx

2

1 + cosx

ctg2

x

  =  

1 + cosx

2

1 — cosx

Формулы кубов тригонометрических функций

sin3x

  =  

3sinx — sin3x

4

cos3x

  =  

3cosx + cos3x

4

tg3x

  =  

3sinx — sin3x

3cosx + cos3x

ctg3x

  =  

3cosx + cos3x

3sinx — sin3x

Формулы тригонометрических функций в четвертой степени

sin4x

  =  

3 — 4cos2x + cos4x

8

cos4x

  =  

3 + 4cos2x + cos4x

8

Формулы сложения аргументов

sin(α + β) = sinα cosβ + cosα sinβ cos(α + β) = cosα cosβ — sinα sinβ

tg(α + β)

  =  

tgα + tgβ

1 — tgα tgβ

ctg(α + β)

  =  

ctgα ctgβ — 1

ctgα + ctgβ

sin(α — β) = sinα cosβ — cosα sinβ cos(α — β) = cosα cosβ + sinα sinβ

tg(α — β)

  =  

tgα — tgβ

1 + tgα tgβ

ctg(α — β)

  =  

ctgα ctgβ + 1

ctgα — ctgβ

Формулы суммы тригонометрических функций

sinα + sinβ

  =  2sin

α + β

 ∙ cos

α — β

2

2

cosα + cosβ

  =  2cos

α + β

 ∙ cos

α — β

2

2

(sinα + cosα)2 = 1 + sin2α

tgα + tgβ

  =  

sin(α + β)

cosα cosβ

ctgα + ctgβ

  =  

sin(α + β)

sinα sinβ

Формулы разности тригонометрических функций

sinα — sinβ

  =  2sin

α — β

 ∙ cos

α + β

2

2

cosα — cosβ

  =  -2sin

α + β

 ∙ sin

α — β

2

2

(sinα — cosα)2 = 1 — sin2α

tgα — tgβ

  =  

sin(α — β)

cosα cosβ

ctgα — ctgβ

  =  – 

sin(α — β)

sinα sinβ

Формулы произведения тригонометрических функций

sinα ∙ sinβ

  =  

cos(α — β) — cos(α + β)

2

sinα ∙ cosβ

  =  

sin(α — β) + sin(α + β)

2

cosα ∙ cosβ

  =  

cos(α — β) + cos(α + β)

2

tgα ∙ tgβ

  =  

cos(α — β) — cos(α + β)

  =  

tgα + tgβ

cos(α — β) + cos(α + β)

ctgα + ctgβ

ctgα ∙ ctgβ

  =  

cos(α — β) + cos(α + β)

  =  

ctgα + ctgβ

cos(α — β) — cos(α + β)

tgα + tgβ

tgα ∙ ctgβ

  =  

sin(α — β) + sin(α + β)

sin(α + β) — sin(α — β)

studfiles.net

Author: alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *