Тренировочная работа по физике, 11 класс, 14 февраля 2018 г.
Пока выкладываю первую часть, завтра, надеюсь, последует вторая. Много времени ушло на оформление и рисунки)))
Задача 1. Велосипедист едет по кольцевому велотреку диаметром 200 м с постоянной по модулю скоростью. За минуту он проезжает путь, равный трём диаметрам трека. Чему равен модуль ускорения велосипедиста?
Итак, его скорость равна
Определяем нормальное (центростремительное) ускорение:
Ответ: 1 м/с.
Задача 2. Тело массой 2 кг лежит на гладкой горизонтальной плоскости. В момент времени к этому телу прикладывают две взаимно перпендикулярные силы и , направленные горизонтально, модули которых изменяются со временем по законам и , а направления не меняются. Определите модуль ускорения тела в момент времени с.
Определим равнодействующую:
Тогда через 4 с сила равна Н, а модуль ускорения тела
Ответ: 10 м/с.
Задача
Тогда
Ответ: 5 м/с.
Задача 4. К горизонтальной лёгкой рейке, лежащей на двух опорах А и В, в точке О прикреплён груз массой 10 кг. Длина отрезка ОА равна 4 м, длина отрезка ОВ равна 1 м. Определите модуль силы, с которой действует на рейку опора В.
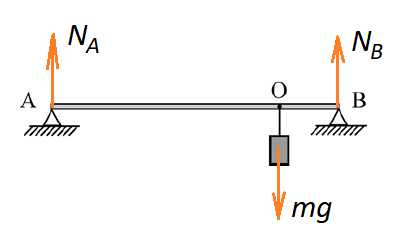
К задаче 4
Обозначим силы. Рейка легкая – у нее силы тяжести нет. Так как нас интересует , то уравнение моментов составим относительно точки , чтобы эта неизвестная реакция опоры исчезла из уравнения.
Ответ: 80 Н.
Задача 5. На рисунке приведён график зависимости модуля средней скорости материальной точки от времени при прямолинейном движении. Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
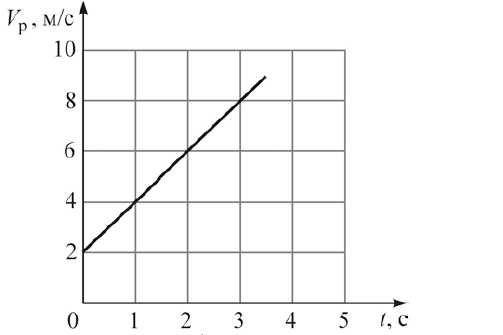
К задаче 5
1) Модуль ускорения точки равен 2 м/с.
2) Модуль ускорения точки равен 4 м/с.
3) За первые 3 с движения материальная точка проходит путь 8 м.
4) За первые 2 с движения материальная точка проходит путь 12 м.
5) Модуль начальной скорости материальной точки равен 1 м/с.
Сложное задание. Надо все время помнить, что есть средняя скорость, тогда будет несложно его решить. По графику видно, что начальная скорость равна 2 м/с. Так как при равноускоренном движении средняя скорость – это всегда полусумма конечной и начальной, то для запишем
Следовательно, тело за 1 с увеличило свою скорость на 4 м/с, что говорит о том, что его ускорение 4 м/c.
Далее, если помнить, что по определению средняя скорость – это весь путь, деленный на все время, нетрудно вычислить:
Ответ: 24
Задача 6. С края обрыва высотой 20 м бросают точечное тело с начальной скоростью 20 м/с под углом к горизонту. Определите, как изменятся через 2,5 с после начала полёта следующие величины: потенциальная энергия взаимодействия тела с Землёй и модуль проекции импульса тела на вертикальную плоскость.
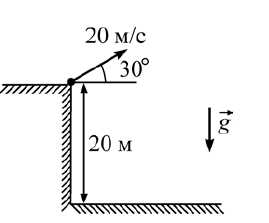
К задаче 6
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Определим время подъема тела на максимальную высоту:
Тогда через 2 с тело вернется на уровень, с которого его бросили и далее будет падать ниже этого уровня. Поэтому его потенциальная энергия к моменту 2,5 с уменьшится.
Через 2 с модуль вертикальной проекции скорости точно такой же, как при броске. А через 2,5 с он уже больше, следовательно, проекция импульса на вертикальную плоскость также больше, чем при броске.
Ответ: 21
Задача 7. Небольшое тело массой m, лежащее на краю гладкой полусферической лунки радиусом R, соскальзывает в неё, не имея начальной скорости. Установите соответствие между физическими величинами и формулами, при помощи которых их можно рассчитать.
К задаче 7
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
На краю лунки тело имеет потенциальную энергию . Эта энергия станет кинетической внизу лунки: . Поэтому скорость равна . Ну а ускорение .
Ответ: А-4, Б – 1
Задача 8. Идеальный газ находится в закрытом сосуде при нормальном атмосферном давлении. При неизменной концентрации молекул средняя кинетическая энергия хаотического теплового движения молекул уменьшается на 2 %. Определите конечное давление газа.
Давление газа определяется формулой . Если изменилась кинетическая энергия – следовательно, температура уменьшилась.
Таким образом, если кинетическая энергия снизилась на 2%, то и температура, а значит, и давление уменьшились тоже на 2%. Нормальное давление – 100 кПа, значит, стало 98 кПа.
Ответ: 98 кПа.
Задача 9. В гладкой горизонтальной трубе с площадью поперечного сечения 25 см расположен поршень. Слева от поршня всё время поддерживается постоянное давление 200 кПа, а справа от него всё время поддерживается постоянное давление 400 кПа. В исходном состоянии к поршню прикладывают некоторую силу, удерживая его в равновесии. Какую работу нужно совершить для того, чтобы очень медленно переместить поршень на 10 см вправо?
Работать будет сила, которая уравновешивает давления.
Ее работа
Ответ: 50 Дж.
Задача 10. Относительная влажность воздуха при температуре 100 °С равна 50 %. Определите массу водяного пара в одном литре такого влажного воздуха. Ответ приведите в граммах, округлив до десятых долей.
При температуре кипения давление насыщенного пара равно атмосферному. То есть
Тогда
Ответ: 0,3 г.
Задача 11. На pV-диаграмме представлен цикл идеальной тепловой машины (цикл Карно), совершаемый с постоянным количеством идеального газа.
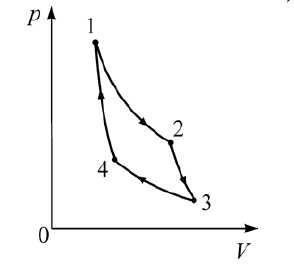
К задаче 11
Из приведённого ниже списка выберите два правильных утверждения.
1) Процессы 2–3 и 4–1 являются изотермическими.
2) Процессы 2–3 и 4–1 являются адиабатическими.
3) В процессе 3–4 газ не совершает работы.
4) В процессе 2–3 газ отдает некоторое количество теплоты.
5) В процессе 1–2 газ получает некоторое количество теплоты.
Утверждение 2 верно и опровергает 1. Так как 1-2 – изотермическое расширение, то работа газом совершается, значит, ему передают тепло извне, поскольку его внутренняя энергия неизменна.
Ответ: 25
Задача 12. На рисунке показаны pT-диаграммы двух циклических процессов, совершаемых с одним и тем же постоянным количеством идеального газа. Некоторая тепловая машина сначала осуществляет цикл 1− 2 − 3− 4 −1, а затем – цикл 5 − 6 − 7 −8 − 5 . Используя рисунок, определите, как изменятся указанные в таблице физические величины при переходе тепловой машины от функционирования по циклу 1− 2 − 3− 4 −1 к функционированию по циклу 5 − 6 − 7 −8 − 5 .
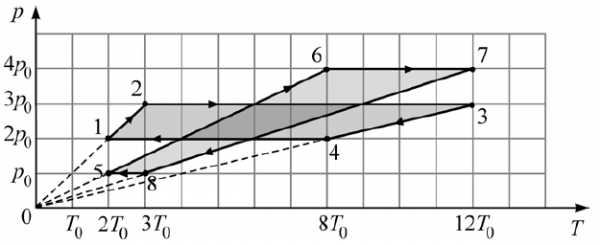
К задаче 12
Для каждой величины определите соответствующий характер изменения:
1) увеличится;
2) уменьшится;
3) не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины.
Перерисуем график в оси .
К задаче 12
Сразу видно, что работа за цикл – а она равна его площади – не изменилась, а вот в процессе изобарного сжатия она для этих циклов отличается. Это процессы 1-4 и 5-8, и работа в процессе 5-8 меньше, чем в процессе 1-4.
Ответ: 32
Задача 13. Положительный электрический заряд Q равномерно распределён по тонкому прямому отрезку. На продолжении этого отрезка находится точечный положительный заряд q (см. рисунок). Куда направлена относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) сила, действующая на заряд q со стороны заряда Q? Ответ запишите словом (словами).
К задаче 13
Так как заряды положительны, они будут отталкиваться. Сила направлена всегда вдоль прямой, на которой расположены точечные заряды. В данном случае распределенный заряд можно считать точечным с точки зрения заряда . Следовательно, сила направлена вправо.
Ответ: вправо.
Задача 14. Четыре конденсатора одинаковой электроёмкости C = 25 пФ соединены так, как показано на схеме. Определите электроёмкость полученной батареи конденсаторов.
К задаче 14
Два, включенных параллельно, сложатся, осталось посчитать последовательное соединение:
Ответ: 10 пФ.
Задача 15. Поток вектора магнитной индукции через некоторый проводящий контур изменяется от 10 мкВб до 30 мкВб. Сопротивление контура 5 Ом. Найдите модуль электрического заряда, который при этом протекает через контур.
Ответ: 4 мкКл.
Задача 16. Электрон влетает в пространство между пластинами плоского конденсатора со скоростью м/с (на рисунке показан вид сверху) на расстоянии от пластин. Расстояние между пластинами мм, длина пластин см, напряжение между ними 10 В.
К задаче 16
Выберите два верных утверждения.
1) Модуль напряжённости электрического поля в конденсаторе равен 2,5 кВ/м.
2) На электрон внутри конденсатора со стороны электрического поля будет действовать сила, всегда направленная вдоль отрицательного направления оси 0y .
3) В процессе движения электрона внутри конденсатора действующая на него со стороны поля электрическая сила не будет изменяться.
4) Траектория движения электрона в конденсаторе представляет собой прямую линию, направленную под углом к оси 0x .
5) Время, которое потребуется электрону для того, чтобы вылететь из конденсатора, равно 0,15 мкс.
Первое утверждение легко проверить:
Первое – верно.
Второе тоже неверно, так как электрон – отрицательно заряженная частица, и его будет притягивать положительно заряженная верхняя пластина.
Третье верно.
Осталось проверить пятое.
Неверно.
Ответ: 13
Задача 17. Плоский конденсатор заполнен непроводящим веществом с диэлектрической проницаемостью, равной 3, и подключён к источнику постоянного напряжения. Это вещество удаляют из конденсатора и взамен помещают между пластинами другой изолирующий материал с диэлектрической проницаемостью, равной 5. Как меняются в результате замены диэлектрика электрическая ёмкость конденсатора и заряд на его пластинах?
Для каждой величины определите соответствующий характер её изменения:
1) увеличивается;
2) уменьшается;
3) не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины.
Цифры в ответе могут повторяться.
Емкость конденсатора прямо зависит от качества диэлектрика.
Поэтому она увеличится при его замене. Так как емкость увеличилась при том же напряжении, конденсатор теперь способен держать больший заряд.
Ответ: 11
Задача 18. На рисунке изображена схема электрической цепи, содержащей резистор сопротивлением Ом, два резистора сопротивлением , незаряженный конденсатор ёмкостью 25 мкФ, ключ и источник постоянного напряжения с ЭДС 5 В и пренебрежимо малым внутренним сопротивлением. Ключ замыкают. Установите соответствие между физическими величинами и их значениями через достаточно большое время после замыкания ключа.
К задаче 18
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Когда ключ замкнут, конденсатор начнет заряжаться и зарядится до . Тогда ток в емкости прекратится. А напряжение будет, на каждой ветви – . Так как оба резистора в нижней ветке обладают одинаковым сопротивлением, то падать на них будет по В. Ток в неразветвленной части цепи будет
Ток поделится между ветвями как 4:1, сообразно сопротивлениям, поэтому в ветви с потечет А, а в ветви с сопротивлением – А – то есть 0,625 А.
Ответ: 23
Задача 19. В ноябре 2016 г. в периодическую таблицу Менделеева был официально внесён новый химический элемент с порядковым номером 115 – он получил название «московий» (обозначается Mc). Атомная масса наиболее стабильного изотопа этого элемента (из ныне известных) равна 289. Сколько протонов и сколько нейтронов содержится в атомном ядре этого изотопа московия?
Протонов – 115, как и электронов, нейтронов тогда 289-115=174
Ответ: 115, 174 (возможно, в бланк записывается без запятой!)
Задача 20. Период полураспада элемента 1 в три раза больше периода полураспада элемента 2. За некоторое время число атомов элемента 1 уменьшилось в 8 раз. Во сколько раз за это же время уменьшилось число атомов элемента 2?
Раз число атомов уменьшилось втрое, значит, прошло три периода полураспада. Тогда для второго элемента – 9, и распалось в раз больше.
Ответ: в 512 раз(-а).
Задача 21. Установите соответствие между описанием ядерной реакции и видом радиоактивного распада, происходящего в ходе этой реакции. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Ответ: 13
Задача 22. Мультиметр – это современный комбинированный электроизмерительный прибор, объединяющий в себе несколько функций. В минимальном наборе он включает функции вольтметра, амперметра и омметра.
К задаче 22
Пользуясь фотографией, определите напряжение, измеряемое с помощью мультиметра, если погрешность прямого измерения напряжения равна цене деления шкалы вольтметра.
Ответ: ( ) B.
Задача 23. Необходимо собрать экспериментальную установку, с помощью которой можно измерить сопротивление резистора. Для этого школьник взял исследуемый резистор, набор электрических проводов и вольтметр. Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента?
1) амперметр
2) резистор с известным сопротивлением
3) второй вольтметр
4) конденсатор
5) источник напряжения
Очевидно, потребуется источник. И еще амперметр – измерить ток.
Ответ: 15
Задача 24. Как известно, Эдвин Хаббл установил, что Вселенная расширяется. Выберите два утверждения, которые правильно описывают это явление.
1) Образовавшееся во время Большого взрыва жёсткое гамма-излучение регистрируется орбитальными телескопами в виде гамма-вспышек.
2) Причиной расширения Вселенной является большое количество антиматерии в галактиках.
3) Расширение Вселенной происходит с ускорением.
4) Все звёзды в нашей Галактике удаляются от Солнца.
5) Расстояние между достаточно удалёнными друг от друга объектами Вселенной со временем увеличивается.
Что называется, без комментариев:
Ответ: 35
easy-physic.ru
Диагностические и тренировочные работы – Репетитор по математике
Диагностические и тренировочные работы СтатГрад.
Математика. ЕГЭ 2016. Демонстрационный вариант (проект) — Базовый [/urlspan](pdf) ; [urlspan]Профильный (pdf) ; Скачать (zip) ; Изменения КИМ ЕГЭ-2016
ЕГЭ-2015. Математика. Досрочный экзамен, реальный вариант (базовый уровень) с решениями и ответами.
ЕГЭ-2015. Математика. Досрочный экзамен, реальный вариант (профильный уровень).
ЕГЭ-2014. Математика. Диагностическая работа № 1 (вар. 101-116) 24.09.2013г. (с ответами)
ЕГЭ-2014. Математика. Тренировочная работа № 1 (вар. 201-204) 14.11.2013г. (с ответами)
ЕГЭ-2014. Математика. Диагностическая работа № 2 (вар.301-316) 12.12.2013г. (с ответами)
ЕГЭ-2014. Математика. Тренировочная работа № 2 (вар. 401-404) 28.01.2014г. (с ответами)
ЕГЭ-2014. Математика. Диагностическая работа № 3 (вар.501-508) 13.03.2014г. (с критериями; отв. 501, 502, 505, 508)
ЕГЭ-2014. Математика. Тренировочная работа № 3 (вар. 601-604) 22.04.2014г. (с ответами)
ЕГЭ-2014. Математика. Тренировочная работа № 4 (вар. 703-704) 19.05.2014г. (с ответами)
Пробные, репетиционные, диагностические варианты.
11 класс. Математика. Диагностическая контрольная работа. Школьный этап. Свердловск. (вар.1-2) 12.11.2013г. (с ответами)
11 класс. Математика. Диагностическая контрольная работа. Муниципальный этап. Свердловск. (вар. 4)
ЕГЭ-2014. Математика. ФЦТ ФИПИ. (варианты 4-7)
11 класс. Математика. Краевая диагностическая работа. Краснодар (Вар. 1-15) 27.11.2013 (с ответами)
11 класс. Математика. Краевая диагностическая работа. ВСОШ. Краснодар (Вар. 1-15) 27.11.2013 (с ответами)
11 класс. Математика. Челябинск. Пробные варианты 1-4. Ноябрь 2013г.
11 класс. Математика. Челябинск. Пробные варианты 1-4. декабрь 2013г.
ЕГЭ-2014. Математика. Пробный экзамен. Иркутск. (вар. 1-4) декабрь 2013г. (с ответами)
ЕГЭ-2014. Математика. Агентство Лидер. Пробные варианты 261-272.
11 класс. Математика. Краевая диагностическая работа. Краснодар (Вар. 1-15) 29.01.2014 (с ответами)
ЕГЭ-2014. Математика. Самара. Пробный экзамен. (вар. 1-4) март 2014г.
ЕГЭ-2014. Математика. Краснодар. Пробный экзамен. (вар. 1-6) апрель 2014г. (с ответами)
ЕГЭ-2014. Математика. Краснодар. Репетиционный экзамен. (вар. 1-10) апрель 2014г. (с ответами)
ЕГЭ-2014. Математика. Репетиционный экзамен. Санкт-Петербург. (вар. 1-2) 14.04.2014г. (с ответами)
11 класс. Математика. Краевая диагностическая работа. Краснодар (Вар. 1-15) 23.04.2014г.
ЕГЭ-2014. Математика. Пробный экзамен. Брянск. (вар. 1-2) 23.04.2014г.
Различные реальные варианты ЕГЭ.
ЕГЭ-2014. Математика. Досрочный этап. 4 варианта КИМ (с сайта ФЦТ)
ЕГЭ-2014. Математика. Досрочный этап. 4 варианта КИМ (вариант 1 с ответами) 28.04.2014г.
10 класс.
10 класс. Диагностическая работа по алгебре и началам анализа (вар. 0101-0108) 27.11.2013г (с ответами)
10 класс. Математика. Краевая диагностическая работа. Краснодар (Вар. 1-15) 27.11.2013 (с ответами)
10 класс. Математика. Краевая диагностическая работа. ВСОШ. Краснодар (Вар. 1-15) 27.11.2013 (с ответами)
10 класс. Математика. Тренировочная работа (вар. 201-204) 26.02.2014г. (ответы к 201-202)
10 класс. Математика. Итоговая диагностическая работа. Базовый уровень (вар. 301-304) 16.05.2014г. (с ответами)
10 класс. Математика. Итоговая диагностическая работа. Углубленный уровень (вар. 401-402) 16.05.2014г. (с критериями)
10 класс. Математика. Диагностическая работа в формате перспективной модели ЕГЭ. Базовый уровень (вар. 501-504) 16.05.2014г.
10 класс. Математика. Диагностическая работа в формате перспективной модели ЕГЭ. Профильный уровень (вар. 601-604) 16.05.2014г. (с критериями)
ege-ok.ru
Тренировочная работа по химии 19 октября 2018 года
Доступны для скачивания варианты тренировочной работы по химии 19.10.2018.
Скачать бесплатно тренировочную работу МИОО (Статград) от 19 октября 2018 года можно здесь.
Критерии тренировочной работы можно скачать здесь.
Рассмотрим несколько любопытных заданий из тренировочной работы:
Задание 4, вариант ХИ10101.
Более подробно про химические связи можно прочитать здесь. А я напомню, что длина связи зависит, как правило, от двух факторов: кратности связи и радиусов атомов, образующих химическую связь. А именно:
При увеличении радиусов атомов, образующих связь, длина связи увеличится.
При увеличении кратности связи между атомами (атомные радиусы которых не отличаются, либо отличаются незначительно) длина связи уменьшится.
Поэтому правильный ответ: 14.
Как всегда, очень интересное задание 26, на практичсекую химию.
Учитывая, что вода прямо или косвенно используется почти во всех областях жизни)
Видимо, авторы имели в виду воду, которая используется для питания живых существ в сельском хозяйстве.
В случае хлора, видимо, нам необходимо вспомнить распространенный полимер — поливинилхлорид (ПВХ). А азотная кислота используется для производства нитратов — удобрений.
Правильный ответ: 132.
chemege.ru
Тренировочная работа МИОО по математике 18.12.2015 г
Тренировочная работа МИОО
18 декабря 2015 г
Условия задач, ответы и решения
(в процессе…)
Инструкция по выполнению работы
На выполнение работы по математике отводится 3 часа 55 минут (235 минут). Работа состоит из двух частей, включающих в себя 19 заданий.
Часть 1 содержит 8 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 4 задания повышенного уровня сложности с кратким ответом и 7 заданий повышенного и высокого уровней сложности с развёрнутым ответом.
Ответы к заданиям 1–12 записываются в виде целого числа или конечной десятичной дроби.
При выполнении заданий 13–19 требуется записать полное решение на отдельном листе бумаги.
При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.
Баллы, полученные Вами за выполненные задания, суммируются.
Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.
Желаем успеха!
9. Найдите значение выражения Решение
10. При движении ракеты её видимая для неподвижного наблюдателя длина, измеряемая в метрах, вычисляется по закону , где м — длина покоящейся ракеты, км/с — скорость света, а — скорость ракеты (в км/с). Какова должна быть скорость ракеты, чтобы её наблюдаемая длина стала равна 57 м? Ответ выразите в км/с. Решение
11. Двум гонщикам предстоит проехать 85 кругов по кольцевой трассе протяжённостью 8 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 17 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 48 минут? Ответ дайте в км/ч. Решение
12. Найдите наименьшее значение функции . Решение
13. а) Решите уравнение ; Решение
б) Найдите все корни этого уравнения, принадлежащие отрезку Решение
14. Все ребра правильной треугольной пирамиды с вершиной равны 9. Основание высоты этой пирамиды является серединой отрезка , — середина ребра , точка лежит на ребре так, что .
а) Докажите, что сечение пирамиды плоскостью — равнобокая трапеция.
б) Вычислите длину средней линии этой трапеции.
15 Решите неравенство Решение
16. В треугольник ABC вписана окружность радиуса R, касающаяся стороны AC в точке M , причём AM = 2R и CM = 3R.
а) Докажите, что треугольник ABC прямоугольный. Доказательство
б) Найдите расстояние между центрами его вписанной и описанной окружностей, если известно, что R = 2
17. По вкладу «А» банк в течение трёх лет в конце каждого года увеличивает на 10 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивает на 11 % в течение каждого из первых двух лет. Найдите наименьшее целое число процентов за третий год по вкладу «Б», при котором за все три года этот вклад всё ещё останется выгоднее вклада «А».
18. Найдите все значения параметра , при каждом из которых система имеет единственное решение.
19. Будем называть четырёхзначное число очень счастливым, если все цифры в его десятичной записи различны, а сумма первых двух из этих цифр равна сумме последних двух из них. Например, очень счастливым является число 3140.
а) Существуют ли десять последовательных четырёхзначных чисел, среди которых есть два очень счастливых?
б) Может ли разность двух очень счастливых четырёхзначных чисел равняться 2015?
в) Найдите наименьшее натуральное число, для которого не существует кратного ему очень счастливого четырёхзначного числа.
@СтатГрад
смотрите еще Демонстрационный вариант КИМ для проведения в 2016 году ЕГЭ по математике 11 класс Профильный уровень
Ответы
- 5
- 240000
- 150 км/ч
- 256
- а) б)
- б) 5.75
- {3/5}
- 9
- а) да б) нет в) 11
www.itmathrepetitor.ru
Тренировочная работа в формате ЕГЭ от 28 января 2014 года
Разбор заданий части В Т/Р по математике от 28.01.14
В1. В доме, в котором живет Женя, один подъезд. На каждом этаже по восемь квартир. Женя живет в квартире 87. На каком этаже живет Женя?
Решение:+ показать
Женя живет на 11 этаже, так как .
Ответ: 11.
В2. Для приготовления вишневого варенья на 1 кг вишни нужно 1,5 кг сахара. Сколько килограммовых упаковок сахара нужно купить, чтобы сварить варенье из 16 кг вишни?
Решение: + показать
При приготовлении варенья на 16 кг вишни расходуется кг сахара. Следовательно, требуется купить 24 упаковки (килограммовых) сахара.
Ответ: 24.
В3. На диаграмме показано распределение выплавки меди в 11 странах мира (в тысячах тонн) за 2006 год. Среди представленных стран первое место занимала Папуа – Новая Гвинея, одиннадцатое место – Индия. Какое место занимал Узбекистан?
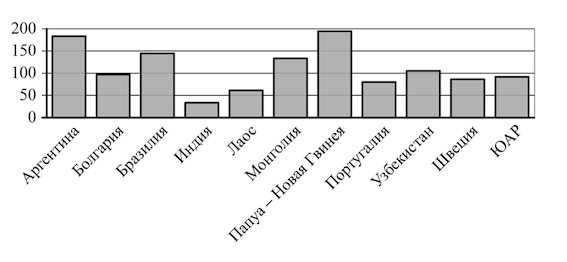
Решение: + показать
Ответ: 5.
В4. В трёх салонах сотовой связи один и тот же телефон продаётся в кредит на разных условиях. Условия даны в таблице.
Определите, в каком из салонов покупка обойдётся дороже всего (с учётом переплаты), и в ответ напишите эту наибольшую сумму в рублях.
Решение: + показать
В5. Точки , , – середины сторон треугольника . Периметр треугольника равен 5. Найдите периметр треугольника .
Решение: + показать
В6. В сборнике билетов по математике всего 20 билетов, в 5 из них встречается вопрос по теории вероятностей. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теории вероятностей.
Решение: + показать
Вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теории вероятностей есть
Ответ: 0,25.
В7. Найдите корень уравнения
Решение: + показать
В8. Два угла вписанного в окружность четырёхугольника равны 125° и 47°. Найдите меньший из оставшихся углов. Ответ дайте в градусах.
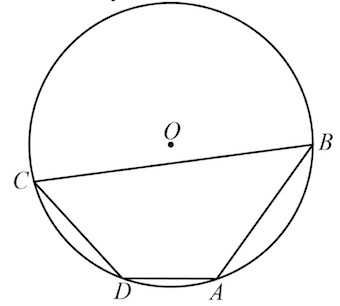
Решение: + показать
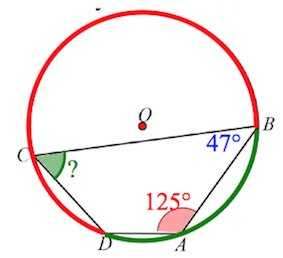Пусть, например*, и
Вписанный угол опирается на дугу , а угол – на дугу . Эти две дуги образуют собой окружность, то есть сумма градусных мер указанных дуг – 360˚. Тогда сумма вписанных углов и , опирающихся на эти дуги, будет равна 180˚, ведь вписанный угол измеряется половиной градусной меры дуги, на которую опирается.
Тогда
Аналогично
Меньший из найденных углов – угол , градусная мера которого 55˚.
* Заметим, данные два угла не могут быть противоположными (по вышесказанному), иначе их сумма должна была бы равняться 180°.
Ответ: 55.
В9. На рисунке изображён график производной y = f ′(x) функции f (x), определённой на интервале (−4; 8). В какой точке отрезка [−3; 1] функция f (x) принимает наименьшее значение?
Решение: + показать
В10. Найдите объём многогранника, изображённого на рисунке (все двугранные углы многогранника прямые).
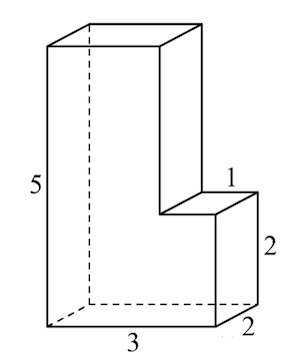
Решение: + показать
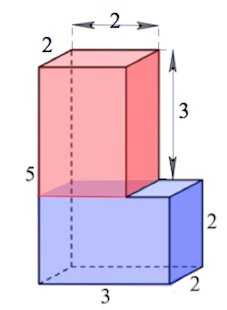
Многогранник, изображенный на рисунке, можно разбить, например, на 2 прямоугольных параллелепипеда так, как это показано на рисунке.
Причем, объемы у этих прямоугольных параллелепипедов равны: (Объем прямоугольного параллелепипеда есть произведение трех его измерений (длины, ширины и высоты)).
Тогда искомый объем есть
Ответ: 24.
В11. Найдите значение выражения
Решение: + показать
В12. Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объём и давление связаны соотношением , где (атм) — давление в газе, — объём газа в литрах. Изначально объём газа равен 24 л, а его давление равно одной атмосфере. До какого объёма нужно сжать газ, чтобы давление в сосуде поднялось до 128 атмосфер? Ответ выразите в литрах.
Решение: + показать
Так как изначально объём газа равен 24 л, а его давление равно одной атмосфере, то
Тогда
При давление в сосуде в 128 атмосфер имеем:
Тогда
Возведем обе части равенства в 5-ю степень:
Ответ: 0,75.
В13. В правильной четырехугольной пирамиде точка – центр основания, – вершина, Найдите длину отрезка
Решение: + показать
Уточним, раз пирамида правильная, то в основании лежит квадрат и вершина проецируется в центр этого квадрата, то есть в точку пересечения диагоналей.
В частности, у правильной пирамиды все боковые ребра равны между собой ().
Рассмотрим, например, треугольник . Он прямоугольный, так как , а значит перпендикулярна любой прямой плоскости , в частности, прямой .
В нем и (так как диагонали в квадрате равны и точкой пересечения делятся пополам).
По т. Пифагора
Ответ: 6.
В14. Первый и второй насосы наполняют бассейн за 10 минут, второй и третий – за 15 минут, а первый и третий – за 24 минуты. За сколько минут эти три насоса заполнят бассейн, работая вместе?
Решение: + показать
Как именно заполнялась таблица?
Принимаем работу (она состоит в наполнении бассейна) за 1.
I и II трубы наполняют бассейн за 10 минут, значит их совместная скорость заполнения бассейна часть бассейна в минуту.
Аналогично II и III трубы заполняют бассейн со скоростью часть бассейна в минуту.
И скорость заполнения бассейна I и III трубами –
Складывая совместные скорости труб I, II; I, III и II, III, мы получаем удвоенную совместную скорость работы труб I, II и III.
Поэтому совместная скорость заполнения трубами I, II и III бассейна есть
Тогда время заполнения бассейна тремя трубами есть (мин).
Ответ: 9,6.
В15. Найдите точку максимума функции
Решение: + показать
———————————————————————————————————
Смотрите также задания C1, С2, С3, С4 Тренировочной работы от 28 января 2014 года.
Здесь найдете все варианты работы (с ответами, критериями).
egemaximum.ru
