§ 8 Уравнение Теория — Документ
§ 8 Уравнение
Теория
Развитие теории уравнений как одной из основных содержательных линий курса математики надо вести, на наш взгляд, очень осторожно, накапливая практический опыт решения уравнений и разумно сочетая его с теоретическим осмыслением производимых действий.
К концу седьмого класса, к которому относится обсуждаемый нами текст, ученики имеют определенный опыт составления уравнений, решения линейных уравнений, знакомы с понятием «корень уравнения». Основное назначение темы, включенной нами в учебник 7 класса, состоит в следующем:
расширить запас уравнений, решаемых сведением их к линейным с помощью разложения на множители и замены неизвестного;
познакомить с рациональными уравнениями, преобразования которых к линейным уравнениям может привести к появлению «посторонних корней», научив при этом алгоритму отсеивания этих корней;
систематизировать способы решения линейных систем с двумя неизвестными;
начать знакомство с геометрической интерпретацией линейных систем и их исследованием на геометрическом языке.
Как вы видите, мы не вводим понятия равносильности и считаем пока преждевременным обсуждение логики решения уравнений и систем. Мы говорим, что стараемся привести уравнение к линейному цепочкой преобразований, но не уточняем, какой список (или тип) преобразований мы разрешаем, ни того, что происходит с множеством корней при совершаемых преобразованиях.
Для важнейшего нового преобразования – освобождение рационального уравнения от знаменателей и переход к многочленам – мы предлагаем традиционную технику: нахождение корней всех знаменателей, запись области допустимых значений (ОДЗ) уравнения, проверка попадания найденных корней многочленного уравнения в ОДЗ.
Мы рекомендуем внимательно разобрать удачное, на наш взгляд, вступление к решению уравнений, помещенное в задачник (возможно этот текст следовало бы перенести в учебник). В этом вступлении одновременно разбираются четыре похожих рациональных уравнения, коэффициенты которых отличаются внешне совсем незначительно. Разбор этого примера заменяет формальное исследование линейного уравнения и показывает все четыре возможных случая, которые возникают при сведении рационального уравнения к линейному: равносильность при наличии единственного корня, появление лишнего корня, не входящего в ОДЗ уравнения, наличие у линейного уравнения бесконечного множества корней, из которого надо исключить те, которые не входят в ОДЗ, и, наконец, отсутствие корней у линейного уравнения (это тоже случай равносильности, но такой, когда нет корней ни у исходного, ни у полученного уравнения).
Заметим, что ни одно из применяемых преобразований не может привести к «потере корней», поэтому такой случай мы откладываем на будущее, лишь делая предупреждение о недопустимости сокращения обеих частей уравнения на общий множитель.
Мы хотим предостеречь учителя от сосредоточения всего внимания на вопросах ОДЗ и лишних корнях. Все же главное содержание темы – нахождение новых способов решения уравнений. Поэтому задачи, в которых применяется разложение на множители и замена неизвестного, мы считаем центральными.
Особенно обратим внимание учителя на полезность решения квадратных уравнений методом разложения на множители. К восьмому классу, где будет обсуждаться общая формула для нахождения корней квадратного уравнения, ученик должен придти с твердыми навыками решения уравнений типа x2 = 4, (x – 1)2 = 9 и уравнений с маленькими коэффициентами и хорошими корнями (типа x2 – 5x + 6 = 0).
Мы рекомендуем не жалеть времени на обсуждение возможных замен неизвестного (зачастую даже не решая уравнений, а только находя способ его упрощения за счет подходящей замены).
При обсуждении решения линейной системы мы вводим математические термины несовместной и неопределенной системы. Запомнить эти термины нетрудно, так как они содержат понятные по смыслу корни из русского языка, на что полезно обратить внимание учеников.
Мы расширили запас решаемых систем за счет введения систем, приводящихся к линейной подходящей заменой неизвестных. В этом можно видеть одну из наших главных установок – учить в алгебре структуризации, анализу математического текста.
Учитывая нашу общую позицию – отложить до 8-9 класса функциональный подход и тем самым в меньшей степени использовать графики – мы мало занимаемся графическим исследованием линейных систем. Лишь последний параграф знакомит с уравнением прямой, а беседа – с графическим решением систем.
Комбинаторная линий впервые не представлена теорией в тексте учебника, а перенесена в задачи (диофантовы уравнения).
Решение заданий
1. Алгоритмические задания.
Перечислим те конкретные типы линейных уравнений, с которыми должен познакомиться ученик.
Линейные уравнения, решаемые устно .
Линейные уравнения с числовыми коэффициентами .
Линейные уравнения с буквенными коэффициентами .
Многочленные уравнения, приводящиеся к линейным после приведения многочленов к стандартному виду .
Рациональные уравнения, приводящиеся к линейным после выполнения действий над дробями .
Уравнения, решаемые разложением на линейные множители .
Стандартные замены неизвестного .
При решении линейных систем необходимо отработать стандартные методы (подстановка, сложение). Разумно познакомить с общим методом Гаусса (последовательного исключения неизвестных) на примере систем третьего порядка. В тексте задачника большое место уделено системам, приводящимся к линейным при соответствующих заменах неизвестных.
Обращаем внимание на важную задачу интерполяции – построение линейного двучлена по заданным двум направлениям.
2. Задания на соответствия
В этот раздел включены тесты на распознавание различных свойств корней линейного уравнения. Обратите внимание на то, что в тренажере и серии не требуется решать уравнения и системы, а только указать необходимые замены.
Геометрическая теория линейных уравнений (почти отсутствующая в тексте учебника) перенесена в задачи .
3. Прикладные задачи
В этот раздел естественно включены текстовые задачи (которые частично вошли и в алгоритмический раздел). Кроме них, полезно порешать задачи на выражение из формул одних величин через другие .
4. Задачи на доказательство
Мы включили задачи на исследование уравнений и систем с параметром, в которых явно выделен элемент доказательства.
5. Диофантовы задачи
Мы отказались от включения в этот параграф чисто комбинаторных задач, отдав предпочтение другой идее дискретной математики – решению уравнений в целых числах (так называемых
refdb.ru
Решение матричных уравнений: теория и примеры
Матричным уравнением называется уравнение вида
A ⋅ X = B
или
X ⋅ A = B,
где A и B — известные матрицы, X — неизвестная матрица, которую требуется найти.
Как решить матричное уравнение в первом случае? Для того, чтобы решить матричное уравнение вида A ⋅ X = B, обе его части следует умножить на обратную к A матрицу слева:
.
По определению обратной матрицы, произведение обратной матрицы на данную исходную матрицу равно единичной матрице: , поэтому
.
Так как E — единичная матрица, то E ⋅ X = X. В результате получим, что неизвестная матрица X равна произведению матрицы, обратной к матрице A, слева, на матрицу B:
.
Как решить матричное уравнение во втором случае? Если дано уравнение
X ⋅ A = B,
то есть такое, в котором в произведении неизвестной матрицы X и известной матрицы A матрица A находится справа, то нужно действовать аналогично, но меняя направление умножения на матрицу, обратную матрице A, и умножать матрицу B на неё справа:
,
.
Как видим, очень важно, с какой стороны умножать на обратную матрицу, так как . Обратная к A матрица умножается на матрицу B с той стороны, с которой матрица A умножается на неизвестную матрицу X. То есть с той стороны, где в произведении с неизвестной матрицей находится матрица A.
Как решить матричное уравнение в третьем случае? Встречаются случаи, когда в левой части уравнения неизвестная матрица X находится в середине произведения трёх матриц. Тогда известную матрицу из правой части уравнения следует умножить слева на матрицу, обратную той, которая в упомянутом выше произведении трёх матриц была слева, и справа на матрицу, обратную той матрице, которая располагалась справа. Таким образом, решением матричного уравнения
A ⋅ X ⋅ B = C,
является
.
Пример 1. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей
.
Теперь у нас есть всё, чтобы найти матрицу, обратную матрице A:
.
Наконец, находим неизвестную матрицу:
Решить матричное уравнение самостоятельно, а затем посмотреть решение
Пример 3. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Находим матрицу, обратную матрице A:
.
Находим неизвестную матрицу:
До сих пор мы решали уравнения с матрицами второго порядка, а теперь настала очередь матриц третьего порядка.
Пример 4. Решить матричное уравнение
.
Решение. Это уравнение первого вида: A ⋅ X = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится слева. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A слева. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:

Составим матрицу алгебраических дополнений:
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Находим матрицу, обратную матрице A, и делаем это легко, так как определитель матрицы A равен единице:
.
Находим неизвестную матрицу:

Пример 5. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид X ⋅ A = B, то есть в произведении матрицы A и неизвестной матрицы X матрица A находится справа. Поэтому решение следует искать в виде , то есть неизвестная матрица равна произведению матрицы B на матрицу, обратную матрице A справа. Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:

Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Находим матрицу, обратную матрице A:
.
Находим неизвестную матрицу:

Пример 6. Решить матричное уравнение
.
Решение. Данное уравнение имеет вид A ⋅ X ⋅ B = C, то есть неизвестная матрица X находится в середине произведения трёх матриц. Поэтому решение следует искать в виде . Найдём матрицу, обратную матрице A.
Сначала найдём определитель матрицы A:
.
Найдём алгебраические дополнения матрицы A:
.
Составим матрицу алгебраических дополнений:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей A:
.
Находим матрицу, обратную матрице A:
.
Найдём матрицу, обратную матрице B.
Сначала найдём определитель матрицы B:
.
Найдём алгебраические дополнения матрицы B:
Составим матрицу алгебраических дополнений матрицы B:
.
Транспонируя матрицу алгебраических дополнений, находим матрицу, союзную с матрицей B:
.
Находим матрицу, обратную матрице B:
.
Находим неизвестную матрицу:

Поделиться с друзьями
Начало темы «Матрицы»
Продолжение темы «Матрицы»
Другие темы линейной алгебры
function-x.ru
Теория о линейных уравнениях
ТЕОРИЯ ОБ УРАВНЕНИЯХ
Линейное уравнение с одной переменной
Линейное уравнение с двумя
переменными
Опр.
Уравнение вида ах = в называется линейным с одной переменной, где а, в – некоторые числа, х — переменная
Уравнение вида ах + ву = с называется линейным с двумя переменными, где а, в , с – некоторые числа, х, у — переменные
Решение
Это значение переменной х , при котором линейное уравнение превращается в верное равенство
Это любая пара чисел ( х ; у ), которая превращает любое уравнение в верное тождество
Например
3х = — 99
Если х = — 33 , значит
3 * ( — 33 )= — 99- верное равенство
3х + 2у = 7
Если х =1, у = 2 или ( 1 ; 2) , значит
3*1 + 2 * 2= 7 — верное тождество
Решить
уравнения
Значит найти все его корни или доказать , что их нет
0 * х = -8 ( корней нет ) 0 * х + у * 0 = -8,9 ( корней нет)
Опр.
Равносильные уравнения — это те уравнения, которые имеют одни и те же корни или их нет.
Св.ва
Свойства линейных уравнений с одной или двумя переменными
Если в уравнении перенести любой член из одной части в другую, изменив знак на противоположный, то получится уравнение равносильное данному.
Если обе части уравнения умножить или поделить на одно и то же число , не равное нулю, то получится уравнение равносильное данному.
График
Графиком линейной функции с одной переменной ( с двумя переменными) — это прямая, проходящая через две точки
ТЕОРИЯ ОБ УРАВНЕНИЯХ
Линейное уравнение с одной переменной
Линейное уравнение с двумя
переменными
Опр.
Уравнение вида ах = в называется линейным с одной переменной, где а, в – некоторые числа, х — переменная
Уравнение вида ах + ву = с называется линейным с двумя переменными, где а, в , с – некоторые числа, х, у — переменные
Решение
Это значение переменной х , при котором линейное уравнение превращается в верное равенство
Это любая пара чисел ( х ; у ), которая превращает любое уравнение в верное тождество
Например
3х = — 99
Если х = — 33 , значит
3 * ( — 33 )= — 99- верное равенство
3х + 2у = 7
Если х =1, у = 2 или ( 1 ; 2) , значит
3*1 + 2 * 2= 7 — верное тождество
Решить
уравнения
Значит найти все его корни или доказать , что их нет
0 * х = -8 ( корней нет ) 0 * х + у * 0 = -8,9 ( корней нет)
Опр.
Равносильные уравнения — это те уравнения, которые имеют одни и те же корни или их нет.
Св.ва
Свойства линейных уравнений с одной или двумя переменными
Если в уравнении перенести любой член из одной части в другую, изменив знак на противоположный, то получится уравнение равносильное данному.
Если обе части уравнения умножить или поделить на одно и то же число , не равное нулю, то получится уравнение равносильное данному.
График
Графиком линейной функции с одной переменной ( с двумя переменными) — это прямая, проходящая через две точки
ТЕОРИЯ ОБ УРАВНЕНИЯХ
Линейное уравнение с одной переменной
Линейное уравнение с двумя
переменными
Опр.
Уравнение вида ах = в называется линейным с одной переменной, где а, в – некоторые числа, х — переменная
Уравнение вида ах + ву = с называется линейным с двумя переменными, где а, в , с – некоторые числа, х, у — переменные
Решение
Это значение переменной х , при котором линейное уравнение превращается в верное равенство
Это любая пара чисел ( х ; у ), которая превращает любое уравнение в верное тождество
Например
3х = — 99
Если х = — 33 , значит
3 * ( — 33 )= — 99- верное равенство
3х + 2у = 7
Если х =1, у = 2 или ( 1 ; 2) , значит
3*1 + 2 * 2= 7 — верное тождество
Решить
уравнения
Значит найти все его корни или доказать , что их нет
0 * х = -8 ( корней нет ) 0 * х + у * 0 = -8,9 ( корней нет)
Опр.
Равносильные уравнения — это те уравнения, которые имеют одни и те же корни или их нет.
Св.ва
Свойства линейных уравнений с одной или двумя переменными
Если в уравнении перенести любой член из одной части в другую, изменив знак на противоположный, то получится уравнение равносильное данному.
Если обе части уравнения умножить или поделить на одно и то же число , не равное нулю, то получится уравнение равносильное данному.
График
Графиком линейной функции с одной переменной ( с двумя переменными) — это прямая, проходящая через две точки
infourok.ru
1. Равносильность уравнений. Теоремы о равносильности уравнений
Определение 1.
Два уравнения с одной переменной f(x)=g(x) и p(x)=h(x) называют равносильными, если множества их корней совпадают.
Иными словами,
два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.
Определение 2.Если каждый корень уравнения f(x)=g(x) \((1)\)
является в то же время корнем уравнения p(x)=h(x), \((2)\)
то уравнение \((2)\) называют следствием уравнения \((1)\).
Пример:
Уравнение x−22=9 является следствием уравнения x−2=3.
В самом деле, решив каждое уравнение, получим:
x−22=9x−2=3;x−2=−3×1=5;x2=−1 и x−2=3x=5
Корень второго уравнения является одним из корней первого уравнения, поэтому первое уравнение — следствие второго уравнения.
Очевидно следующее утверждение:
Два уравнения равносильны тогда и только тогда, когда каждое из них является следствием другого.
Решение уравнения, как правило, осуществляется в три этапа:
Первый этап — технический.
На этом этапе осуществляют преобразования по схеме (1)→(2)→(3)→(4)→… и находят корни последнего (самого простого) уравнения указанной цепочки.
Второй этап — анализ решения.
На этом этапе анализируем, все ли проведённые преобразования были равносильными.
Третий этап — проверка.
Если анализируя преобразования на втором этапе, делаем вывод, что получили уравнение-следствие, то обязательна проверка всех найденных корней их подстановкой в исходное уравнение.
Обрати внимание!
Решение уравнений, встречающихся в школьном курсе, основано на шести теоремах о равносильности.
Теорема 1.Если какой-либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному.
Теорема 2.Если обе части уравнения возвести в одну и ту же нечётную степень, то получится уравнение, равносильное данному.
Теорема 3.Показательное уравнение af(x)=ag(x), где \(a>0\), a≠1 равносильно
уравнению f(x)=g(x).
Определение 3.
Областью определения уравнения f(x)=g(x) или областью допустимых значений переменной (ОДЗ) называют множество тех значений переменной \(x\), при которых одновременно имеют смысл выражения \(f(x)\) и \(g(x)\).
Теорема 4.Если обе части уравнения f(x)=g(x) умножить на одно и то же выражение \(h(x)\), которое:
a) имеет смысл всюду в области определения (в области допустимых значений) уравнения f(x)=g(x);
б) нигде в этой области не обращается в \(0\),
то получится уравнение f(x)⋅h(x)=g(x)⋅h(x), равносильное данному.
Следствие теоремы 4.
Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Теорема 5.Если обе части уравнения f(x)=g(x) неотрицательны в области определения уравнения, то после возведения обеих его частей в одну и ту же чётную степень \(n\) получится уравнение, равносильное данному:f(x)n=g(x)n
Теорема 6.Если f(x)>0 и g(x)>0, то логарифмическое уравнение logaf(x)=logag(x), где \(a>0\), a≠1, равносильно уравнению f(x)=g(x)
www.yaklass.ru
Методы решения уравнений
Автор Сергей
Понедельник, Июль 9, 2012
 Статья о методах решения уравнений. Задач, которые связаны с решением уравнений, довольно много в вариантах ЕГЭ и ГИА по математике. Поэтому как репетитор по математике рекомендую освежить с памяти связанный с этим вопросом материал. К каждому разобранному в статье примеру прилагается аналогичное задание для самопроверки. Все свои вопросы вы можете смело задавать в комментариях. Ни один вопрос без ответа не останется. В статье также имеется видеоразбор одного из заданий.
Статья о методах решения уравнений. Задач, которые связаны с решением уравнений, довольно много в вариантах ЕГЭ и ГИА по математике. Поэтому как репетитор по математике рекомендую освежить с памяти связанный с этим вопросом материал. К каждому разобранному в статье примеру прилагается аналогичное задание для самопроверки. Все свои вопросы вы можете смело задавать в комментариях. Ни один вопрос без ответа не останется. В статье также имеется видеоразбор одного из заданий.
Основные методы решения уравнений
Решить уравнение значит найти все его корни или доказать, что их не существует. Стандартных методов решения уравнений много, нестандартных — еще больше. Последние подходят для решения небольшого количества (часто вообще одного) типа уравнений. При решении уравнений почти всегда приходится прибегать к тождественным преобразованиях алгебраических выражений. Поэтому целесообразно разобраться сперва с этим материалом, прежде чем переходить к решению уравнений. В данной статье разобраны в основном стандартные методы решения уравнений. Некоторые нестандартные методы кратко охарактеризованы в завершающей части статьи. Также на сайте есть отдельные статьи о решении тригонометрических, логарифмических и показательных уравнений, с которыми я также рекомендую читателю ознакомиться.
Метод разложения на множители
Суть данного метода в том, чтобы путем равносильных преобразований представить левую часть исходного уравнения, содержащую неизвестную величину в какой-либо степени, в виде произведения двух выражений, содержащих неизвестную величину в меньшей степени. При этом справа от знака равенства должен оказаться ноль. Проще всего уяснить эту идею на конкретном примере.
Пример 1. Решите уравнение методом разложения на множители:Решение. Осуществим разложение на множители (представим исходное выражение в виде произведения). Для этого вынесем переменную за скобки:
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Следовательно, или Из последнего уравнения получаем: или
Ответ: и
Задача для самостоятельного решения №1. Решите уравнение методом разложения на множители:
Показать ответ
Ответ: 0 или Пример 2. Решите уравнение методом разложения на множители:Решение. Для разложения на множители используем прием деления многочленов столбиком (или, как еще иногда говорят, уголком). Несложно догадаться, что — корень многочлена Следовательно, по теореме Безу он без остатка делится на Осуществим это деление (см. подробнее в видеоуроке):
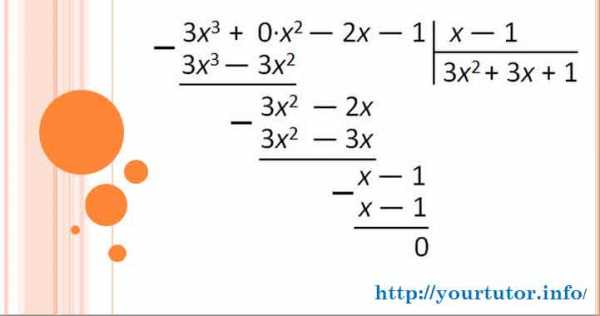
Деление многочленов уголком (столбиком)
Таким образом То есть исходное уравнение принимает вид:
Дискриминант первого квадратичного уравнения — отрицателен, поэтому корней у него нет. Из второго уравнения получается уже известный нам результат, что корень Это единственный корень уравнения.
Ответ: .
Задача для самостоятельного решения №2. Решите уравнение методом разложения на множители:
Показать ответ
Ответ: 2 и -1.
Метод замены переменной
Цель данного метода в том, чтобы удачным образом заменить сложное выражение, содержащее неизвестную величину, новой переменной, в результате чего уравнение принимает более простой вид. Далее полученное уравнение решается относительно новой переменной, после чего происходит возврат к исходной переменной. Все эти идеи проще осознать на конкретном примере.
Пример 3. Решите уравнение методом замены переменной:Решение. Такие уравнения называются биквадратными. Перепишем его в виде: Введем новую переменную Тогда исходное уравнение примет следующий простой вид: Решая полученное квадратичное уравнение, получаем, что или
Возвращаемся теперь к старой переменной (обратная замена): или Решений у первого уравнения нет, поскольку не существует такого действительного числа, квадрат которого был бы отрицателен. Второе уравнение имеет два корня
Ответ:
Задача для самостоятельного решения №3. Решите уравнение методом замены переменной:
Показать ответ
Ответ: или Пример 4. Решите уравнение методом замены переменной:
Решение. Обращаем внимание на то, что не является корнем данного уравнения. Следовательно, без потери или приобретения лишних корней можно разделить числитель и знаменатель обеих дробей на Тогда уравнение принимает вид:
Введем новую переменную:
yourtutor.info
РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ — алгоритмы и примеры
Квадратным уравнением называется уравнение вида
где a, b, c — коэффициенты, причем a ≠ 0, а x – неизвестное, которое нужно найти.
Квадратное уравнение можно свести к приведенному виду – это вид, при котором коэффициент a = 1.
Решение квадратного уравнения через дискриминант
Решение квадратного уравнения через дискриминант выполняется по строго определенному алгоритму:
1. Вычислить дискриминант по формуле
2. Если D < 0 — уравнение не имеет корней
3. Если D > 0 — уравнение имеет 2 корня, которые вычисляются по формулам:
4. Если D = 0 — уравнение имеет ровно 1 корень, который вычисляется по формуле:
Теорема Виета для решения квадратного уравнения
Квадратное уравнение можно решить и с помощью теоремы Виета.
Теорема: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а их произведение – свободному члену этого уравнения.
То есть, чтобы решить квадратное уравнение с помощью теоремы Виета, достаточно подобрать такие x1 и x2, чтобы выполнялось:
Пример решения квадратного уравнения
Решим квадратное уравнение 2x² — 16x + 30 = 0 двумя способами.
Решение через дискриминант:
a = 2, b = -16, c = 30
D = (-16)² — 4 ⋅ 2 ⋅ 30 = 256 — 240 = 16
D > 0 => имеется 2 различных корня
x1 = (-(-16) + √16) / (2 ⋅ 2) = (16 + 4) / 4 = 5
x2 = (-(-16) — √16) / (2 ⋅ 2) = (16 — 4) / 4 = 3
Ответ: 3 и 5
Решение через теорему Виета:
a = 2, b = -16, c = 30
x1 + x2 = -(-16) / 2 = 8
x1 ⋅ x2 = 30 / 2 = 15
Разложим 15 на возможные пары множителей:
15 = 1 ⋅ 15 = (-1) ⋅ (-15) = 3 ⋅ 5 = (-3) ⋅ (-5)
И проверим, какие из них подойдут в качестве решения:
1 + 15 = 16 ≠ 8
-1 — 15 = -16 ≠ 8
3 + 5 = 8
-3 — 5 = -8 ≠ 8
Таким образом, в качестве корней подойдут только 3 и 5.
Ответ: 3 и 5
После решения любого уравнения рекомендуется подставить полученные корни в начальное уравнение, чтобы проверить правильность решения.
Для проверки результатов можно воспользоваться онлайн-калькулятором для решения квадратных уравнений.
worksbase.ru
УРАВНЕНИЯ | Энциклопедия Кругосвет
Содержание статьиУРАВНЕНИЯ. Уравнением называется математическое соотношение, выражающее равенство двух алгебраических выражений. Если равенство справедливо для любых допустимых значений входящих в него неизвестных, то оно называется тождеством; например, соотношение вида (x – 1)2 = (x – 1)(x – 1) выполняется при всех значениях переменной x. Для обозначения тождества часто вместо обычного знака равенства = пишут знак є, который читается «тождественно равно». Тождества используются в алгебре при записи разложения многочленов на множители (как в приведенном выше примере). Встречаются они и в тригонометрии в таких соотношениях, как sin2x + cos2x = 1, а в общем случае выражают формальное отношение между двумя на первый взгляд различными математическими выражениями.
Если уравнение, содержащее переменную x, выполняется только при определенных, а не при всех значениях x, как в случае тождества, то может оказаться полезным определить те значения x, при которых это уравнение справедливо. Такие значения x называются корнями или решениями уравнения. Например, число 5 является корнем уравнения 2x + 7= 17.
Уравнения служат мощным средством решения практических задач. Точный язык математики позволяет просто выразить факты и соотношения, которые, будучи изложенными обычным языком, могут показаться запутанными и сложными. Неизвестные величины, обозначаемые в задаче символами, например x, можно найти, сформулировав задачу на математическом языке в виде уравнений. Методы решения уравнений составляют в основном предмет того раздела математики, который называется теорией уравнений.
ТИПЫ УРАВНЕНИЙ
Алгебраические уравнения.
Уравнения вида fn = 0, где fn – многочлен от одной или нескольких переменных, называются алгебраическими уравнениями. Многочленом называется выражение вида
fn = a0 xiyj … vk + a1 xlym … vn + ј + asxpyq … vr,
где x, y,…, v – переменные, а i, j,…, r – показатели степеней (целые неотрицательные числа). Многочлен от одной переменной записывается так:
f(x) = a0xn + a1xn – 1 +… + an – 1x + an
или, в частном случае, 3x4 – x3 + 2x2 + 4x – 1. Алгебраическим уравнением с одним неизвестным называется любое уравнение вида f(x) = 0. Если a0 № 0, то n называется степенью уравнения. Например, 2x + 3 = 0 – уравнение первой степени; уравнения первой степени называются линейными, так как график функции y = ax + b имеет вид прямой. Уравнения второй степени называются квадратными, а уравнения третьей степени – кубическими. Аналогичные названия имеют и уравнения более высоких степеней.
Трансцендентные уравнения.
Уравнения, содержащие трансцендентные функции, такие, как логарифмическая, показательная или тригонометрическая функция, называются трансцендентными. Примером могут служить следующие уравнения:
где lg – логарифм по основанию 10.
Дифференциальные уравнения.
Так называются уравнения, содержащие одну или несколько функций и их производные или дифференциалы. Дифференциальные уравнения оказались исключительно ценным средством точной формулировки законов природы. См. также ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Интегральные уравнения.
Уравнения, содержащие неизвестную функцию под знаком интеграла, например, f (s) = тK (s, t) f (t) dt, где f (s) и K(s,t) заданы, а f (t) требуется найти.
Диофантовы уравнения.
Диофантовым уравнением называется алгебраическое уравнение с двумя или более неизвестными с целыми коэффициентами, решение которого ищется в целых или рациональных числах. Например, уравнение 3x – 5y = 1 имеет решение x = 7, y = 4; вообще же его решениями служат целые числа вида x = 7 + 5n, y = 4 + 3n.
РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Для всех перечисленных выше типов уравнений общих методов решения не существует. И все же во многих случаях, особенно для алгебраических уравнений определенного типа, имеется достаточно полная теория их решения.
Линейные уравнения.
Эти простые уравнения решаются путем их сведения к эквивалентному уравнению, из которого непосредственно видно значение неизвестного. Например, уравнение x + 2 = 7 можно свести к эквивалентному уравнению x = 5 вычитанием числа 2 из правой и левой частей. Шаги, совершаемые при сведении простого уравнения, например, x + 2 = 7, к эквивалентному, основаны на использовании четырех аксиом.
1. Если равные величины увеличить на одно и то же число, то результаты будут равны.
2. Если из равных величин вычесть одно и то же число, то результаты будут равны.
3. Если равные величины умножить на одно и то же число, то результаты будут равны.
4. Если равные величины разделить на одно и то же число, то результаты будут равны.
Например, чтобы решить уравнение 2x + 5 = 15, мы воспользуемся аксиомой 2 и вычтем число 5 из правой и левой частей, в результате чего получим эквивалентное уравнение 2x = 10. Затем мы воспользуемся аксиомой 4 и разделим обе части полученного уравнения на 2, в результате чего исходное уравнение сведется к виду x = 5, что и является искомым решением.
Квадратные уравнения.
Решения общего квадратного уравнения ax2 + bx + c = 0 можно получить с помощью формулы
Таким образом, существуют два решения, которые в частном случае могут совпадать.
Другие алгебраические уравнения.
Явные формулы, аналогичные формуле для решения квадратного уравнения, можно выписать только для уравнений третьей и четвертой степеней. Но и эти формулы сложны и далеко не всегда помогают легко находит корни. Что же касается уравнений пятой степени или выше, то для них, как доказал Н.Абель в 1824, нельзя указать общую формулу, которая выражала бы корни уравнения через его коэффициенты при помощи радикалов. В отдельных частных случаях уравнения высших степеней удается легко решить, факторизуя их левую часть, т.е. разлагая ее на множители.
Например, уравнение x3 + 1 = 0 можно записать в факторизованном виде (x + 1)(x2 – x + 1) = 0. Решения мы находим, полагая каждый из множителей равным нулю:
Таким образом, корни равны x = –1, , т.е. всего 3 корня.
Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твердая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней.
Системы линейных уравнений.
Два линейных уравнения с двумя неизвестными можно записать в виде
Решение такой системы находится с помощью определителей
Оно имеет смысл, если Если же D = 0, то возможны два случая. (1) По крайней мере один из определителей и отличен от нуля. В этом случае решения уравнений не существует; уравнения несовместны. Численный пример такой ситуации – система
(2) Оба определителя равны нулю. В этом случае второе уравнение просто кратно первому и существует бесконечное число решений.
Общая теория рассматривает m линейных уравнений с n переменными:
Если m = n и матрица (aij) невырожденна, то решение единственно и может быть найдено по правилу Крамера:
где Aji – алгебраическое дополнение элемента aijв матрице (aij). В более общем плане существуют следующие теоремы. Пусть r – ранг матрицы (aij), s – ранг окаймленной матрицы (aij; bi), которая получается из aij присоединением столбца из чисел bi. Тогда: (1) если r = s, то существует n – r линейно независимых решений; (2) если r , то уравнения несовместны и решений не существует.
www.krugosvet.ru
