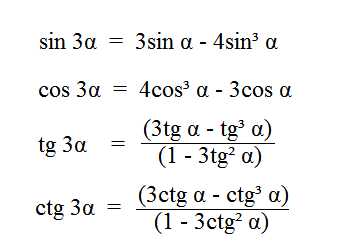Тригонометрические функции
|
Величины углов (аргументы функций): α, x |
Радиус круга: r |
1. Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол. С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
2. К тригонометрическим функциям относятся следующие 6 функций: синус, косинус, тангенс
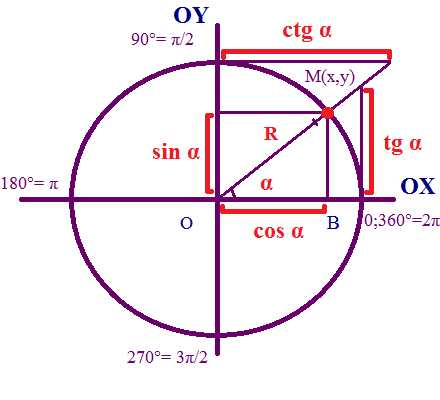
3. Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга. На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.
4. Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r:
sinα=y/r.
Поскольку r=1, то синус равен ординате точки M(x,y).
5. Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r:
cosα=x/r
6. Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x:
tanα=y/x,x≠0
7. Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
cotα=x/y,y≠0
secα=r/x=1/x,x≠0
9. Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y):
cscα=r/y=1/y,y≠0
10. В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
Синусом угла α называется отношение противолежащего катета к гипотенузе.
Косинусом угла α называется отношение прилежащего катета к гипотенузе.
Тангенсом угла α называется противолежащего катета к прилежащему.
Котангенсом угла α называется прилежащего катета к противолежащему.
Секанс угла α представляет собой отношение гипотенузы к прилежащему катету.
Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету.
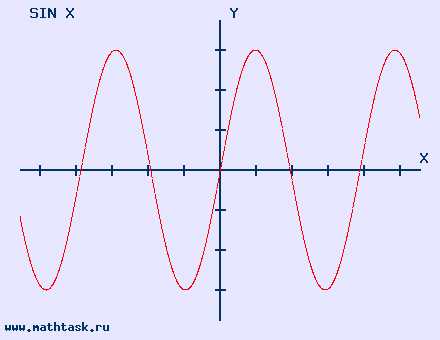
11. График функции синус
y=sinx, область определения: x∈R, область значений: −1≤sinx≤1
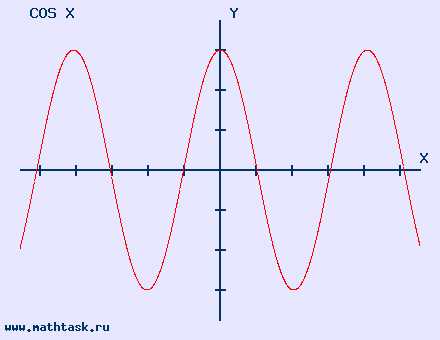
12. График функции косинус
y=cosx, область определения: x∈R, область значений: −1≤cosx≤1
13. График функции тангенс
y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞<tanx<∞
14. График функции котангенс
y=cotx, область определения: x∈R,x≠kπ, область значений: −∞<cotx<∞
15. График функции секанс
y=secx, область определения: x∈R,x≠(2k+1)π/2, область значений:secx∈(−∞,−1]∪[1,∞)
16. График функции косеканс
y=cscx, область определения: x∈R,x≠kπ, область значений: cscx∈(−∞,−1]∪[1,∞)
Где применяется тригонометрия
Тригонометрические вычисления применяются практически во всех сферах жизнедеятельности людей. Следует отметить применение в таких областях как: астрономия, физика, природа, биология, музыка, медицина и многие другие.
Тригонометрия в астрономии:
Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.
Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.
Составленные Гиппархом таблицы положений Солнца и Луны позволили предвычислять моменты наступления затмений (с ошибкой 1—2 ч). Гиппарх впервые стал использовать в астрономии методы сферической тригонометрии. Он повысил точность наблюдений, применив для наведения на светило крест нитей в угломерных инструментах — секстантах и квадрантах. Ученый составил огромный по тем временам каталог положений 850 звезд, разделив их по блеску на 6 степеней (звездных величин). Гиппарх ввел географические координаты — широту и долготу, и его можно считать основателем математической географии. (ок. 190 до н. э. — ок. 120 до н. э.)
Достижения Виета в тригонометрии
Полное решение задачи об определении всех элементов плоского или сферического треугольников по трем данным элементам, важные разложения sin пх и cos пх по степеням cos х и sinx. Знание формулы синусов и косинусов кратных дуг дало возможность Виету решить уравнение 45-й степени, предложенное математиком А. Рооменом; Виет показал, что решение этого уравнения сводится к разделению угла на 45 равных частей и что существуют 23 положительных корня этого уравнения. Виет решил задачу Аполлония с помощью линейки и циркуля.
Решение сферических треугольников- одна из задач астрономии Вычислять стороны и углы любого сферического треугольника по трем подходящим образом заданным сторонам или углам позволяют следующие теоремы: (теорема синусов) (теорема косинусов для углов) (теорема косинусов для сторон).
Тригонометрия в физике:
В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений.
Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:
Где х — значение изменяющейся величины, t — время, А — амплитуда колебаний, ω — циклическая частота колебаний, — полная фаза колебаний, r — начальная фаза колебаний.
Механические колебания . Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени. Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени. Примерами простых механических колебательных систем могут служить груз на пружине или математический маятник.
Тригонометрия в природе.
Мы часто задаем вопрос «Почему мы иногда видим то, чего нет на самом деле?». Для исследования предложены следующие вопросы: «Как возникает радуга? Северное сияние?», «Что такое оптические иллюзии?» ,«Как тригонометрия может помочь найти ответы на эти вопросы?».
Впервые теория радуги была дана в 1637 году Рене Декартом. Он объяснил радугу, как явление, связанное с отражением и преломлением света в дождевых каплях.
Северное сияние Проникновение в верхние слои атмосферы планет заряженных частиц солнечного ветра определяется взаимодействием магнитного поля планеты с солнечным ветром.
Сила, действующая на движущуюся в магнитном поле заряженную частицу называется силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости движения частицы.
Многофункциональная тригонометрия
· Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения.
· К тому же в биологии используется такое понятие как синус сонный, синус каротидный и венозный или пещеристый синус.
· Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца — комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.
Тригонометрия и тригонометрические функции в медицине и биологии.
· Одно из фундаментальных свойств живой природы — это цикличность большинства происходящих в ней процессов.
· Биологические ритмы, биоритмы – это более или менее регулярные изменения характера и интенсивности биологических процессов.
· Основной земной ритм – суточный.
· Модель биоритмов можно построить с помощью тригонометрических функций.
Тригонометрия в биологии
Какие биологические процессы связаны с тригонометрией?
· Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца — комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.
· Биологические ритмы, биоритмы связаны с тригонометрией
Связь биоритмов с тригонометрией
· Модель биоритмов можно построить с помощью графиков тригонометрических функций. Для этого необходимо ввести дату рождения человека ( день, месяц, год ) и длительность прогноза
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения.
При полёте птицы траектория взмаха крыльев образует синусоиду.
Возникновение музыкальной гармонии
· Согласно дошедшим из древности преданиям, первыми, кто попытался сделать это, были Пифагор и его ученики.
· Частоты, соответствующие одной и той же ноте в первой, второй и т.д. октавах, относятся, как 1:2:4:8…
· диатоническая гамма 2:3:5
Тригонометрия в архитектуре
· Детская школа Гауди в Барселоне
· Страховая корпорация Swiss Re в Лондоне
· Феликс Кандела Ресторан в Лос-Манантиалесе
Значения тригонометрических функций
Ключевые слова: радиан, радианная мера угла, тригонометрическая окружность, знаки тригонометрических функций
В геометрии угол определяется как часть плоскости, ограниченная двумя лучами.
При таком определении получаются углы от 0° до 180°. Однако угол можно рассматривать и как меру поворота.
Возьмем на координатной плоскости окружность радиуса R с центром O в начале координат.
Пусть одна сторона угла с вершиной в начале координат O идет по оси абсцисс, а сам угол положительный, то есть, по определению, отложен по направлению против часовой стрелки от положительного направления оси абсцисс.
Из геометрии известно, что отношение длины дуги l , на которую опирается этот угол, к радиусу R этой окружности не зависит от самого радиуса. Поэтому это отношение может быть выбрано характеристикой и мерой данного угла: =lR.
Такая мера называется радианной мерой угла и используется наравне с угловой.
Говорят, что угол равен определенному числу радиан.
Ясно, что угол в один радиан опирается на длину дуги окружности, равную её радиусу.
В самом деле: =RR=1 радиан. Обозначение радиана – «рад».
Так как длина всей окружности радиуса R равна 2R , то всей окружности соответствует угол =R2R=2 радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует 2360=180 градусов:
1рад=1805717. И наоборот, 1=180рад.
Значит, можно написать следующие формулы перехода от градусного измерения к радианному:
=180рад
и от радианного измерения к градусному:
=180 .
Обозначение «рад» при записи часто опускают и вместо, например, 180° = рад пишут просто 180° = .
Пользуясь этими формулами, легко получить следующую таблицу перевода некоторых наиболее часто встречающихся углов из градусной меры в радианную и обратно.
|
Угол, градусы |
0° |
30° |
45° |
60° |
90° |
180° |
270° |
360° |
|
Угол, радианы |
0 |
6 |
4 |
3 |
2 |
23 |
2 |
Так как, синус по определению равен ординате точки на единочной окружности, а косинус — абсциссе, то знаки тригонометрических функций по четвертям будут такими:
|
I |
II |
III |
IV |
|
|
sin |
+ |
+ |
— |
— |
|
cos |
+ |
— |
— |
+ |
|
tg |
+ |
— |
+ |
— |
|
ctg |
+ |
— |
+ |
— |
Вычисление тригонометрических функций некоторых углов.
Тригонометрические функции числового и углового аргументов
Тригонометрические функции числового аргумента.
Тригонометрические функции числового аргумента t – это функции вида y = cos t,
y = sin t, y = tg t, y = ctg t.
С помощью этих формул через известное значение одной тригонометрической функции можно найти неизвестные значения других тригонометрических функций.
Пояснения.
1) Возьмем формулу cos2 t + sin2 t = 1 и выведем с ее помощью новую формулу.
Для этого разделим обе части формулы на cos2 t (при t ≠ 0, то есть t ≠ π/2 + πk). Итак:
cos2 t sin2 t 1
——— + ——— = ———
cos2 t cos2 t cos2 t
Первое слагаемое равно 1. Мы знаем, что отношение синуса к конисусу – это тангенс, значит, второе слагаемое равно tg2 t. В результате мы получаем новую (и уже известную вам) формулу:
|
1 π |
2) Теперь разделим cos2 t + sin2 t = 1 на sin2 t (при t ≠ πk):
cos2 t sin2 t 1
——— + ——— = ———, где t ≠ πk + πk, k – целое число
sin2 t sin2 t sin2 t
Отношение косинуса к синусу – это котангенс. Значит:
|
1 |
Зная элементарные основы математики и выучив основные формулы тригонометрии, вы легко сможете самостоятельно выводить большинство остальных тригонометрических тождеств. И это даже лучше, чем просто зазубривать их: выученное наизусть быстро забывается, а понятое запоминается надолго, если не навсегда. К примеру, необязательно зазубривать, чему равна сумма единицы и квадрата тангенса. Забыли – можно легко вспомнить, если вы знаете самую простую вещь: тангенс – это отношение синуса к косинусу. Примените вдобавок простое правило сложения дробей с разными знаменателями – и получите результат:
sin2 t 1 sin2 t cos2 t + sin2 t 1
1 + tg2 t = 1 + ——— = — + ——— = —————— = ———
cos2 t 1 cos2 t cos2 t cos2 t
Точно так же легко можно найти сумму единицы и квадрата котангенса, как и многие другие тождества.
Тригонометрические функции углового аргумента.
В функциях у = cos t, у = sin t, у = tg t, у = ctg t переменная t может быть не только числовым аргументом. Ее можно считать и мерой угла – то есть угловым аргументом.
С помощью числовой окружности и системы координат можно легко найти синус, косинус, тангенс, котангенс любого угла. Для этого должны быть соблюдены два важных условия:
1) вершиной угла должен быть центр окружности, который одновременно является центром оси координат;
2) одной из сторон угла должен быть положительный луч оси x.
В этом случае ордината точки, в которой пересекаются окружность и вторая сторона угла, является синусом этого угла, а абсцисса этой точки – косинусом данного угла.
Пояснение. Нарисуем угол, одна сторона которого – положительный луч оси x, а вторая сторона выходит из начала оси координат (и из центра окружности) под углом 30º (см.рисунок). Тогда точка пересечения второй стороны с окружностью соответствует π/6. Нам известны ордината и абсцисса этой точки. Они же являются косинусом и синусом нашего угла:
√3 1
——; ——
2 2
А зная синус и косинус угла, вы уже легко сможете найти его тангенс и котангенс.
Таким образом, числовая окружность, расположенная в системе координат, является удобным способом найти синус, косинус, тангенс или котангенс угла.
Но есть более простой способ. Можно и не рисовать окружность и систему координат. Можно воспользоваться простыми и удобными формулами:
|
πα |
πα |
Пример: найти синус и косинус угла, равного 60º.
Решение:
π · 60 π √3
sin 60º = sin ——— = sin —— = ——
180 3 2
π 1
cos 60º = cos —— = —
3 2
ya-znau.ru
| Главная > Учебные материалы > Математика: Тригонометрия | |||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
1.Тригонометрия. 2.Тригонометрические функции.
|
|||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 9 | |||||||||||||||||||||||||
1. Тригонометрия – раздел математики, изучающий зависимости между углами и сторонами в треугольниках и тригонометрические функции. Основная задача тригонометрии — вычисление неизвестных величин треугольника, если известны значения других его величин. В тригонометрии также решают задачу о вычислении углов треугольника, если известны его стороны, задачу о вычислении сторон треугольника и т.д. |
|||||||||||||||||||||||||
Для измерения углов между сторонами треугольника используется такая единица измерения, как градус. Вся окружность с центром в точке О составляет 360°. Помимо градусной меры углов, также используется радианная мера. 1 рад ≈ 57,295779513° ≈ 57°17′44,806″ ≈ 206265″. Радианная и градусная меры связаны зависимостью 180°=π радиан. Угол в n° равен πn/ 180 радиан. Для того, чтобы рассчитать длину дуги угла α, используется следующая формула: l= αr Площадь S сектора круга радиуса r, дуга которого содержит α радиан, рассчитывается так: S = αr² / 2 |
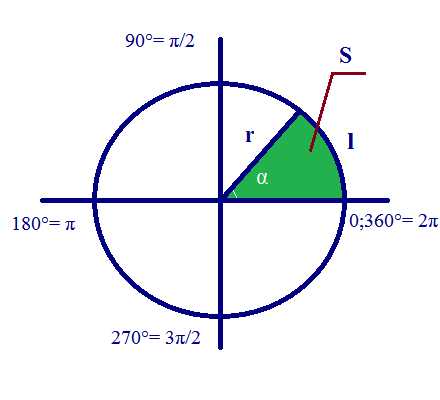 Площадь сектора круга. |
||||||||||||||||||||||||
2. Тригонометрические функции. Тригонометрические функции — математические функции от величины угла. Они используются при изучении геометрии, а также при исследовании переодических процессов в разных областях науки. Тригонометрические функции определяют отношения сторон прямоугольного треугольника в единичной окружности. Пусть на плоскости задана прямоугольная система координат с началом в точке O и с осями OX и OY . Возьмем в этой системе координат окружность с центром в точке O и радиусом, равным единице. Пусть отрезок OМ поворачивается на произвольный угол α вокруг центра O. Так как треугольник ОМВ прямоугольный, то тригонометрические функции угла α определяется из соотношений в прямоугольном треугольнике. Тогда: |
|||||||||||||||||||||||||
| Синусом угла α называется отношение противолежащего катета к гипотенузе или отношение координаты y точки М к длине отрезка OМ=R, где R — радиус окружности. Синус угла α обозначают sinα. Так как длина отрезка OМ=1, следовательно sinα = y. Косинусом угла α называется отношение прилежащего катета к гипотенузе или отношение координаты х точки М к длине отрезка OМ. Косинус угла α обозначают cosα. Так как ОМ=1, то cosα = х. Тангенсом угла α называется отношение противолежащего катета к прилежащему или координаты y точки М к x. Тангенс угла α обозначают tgα. Так как y = sin α и x = cos α, то tgα= sin α / cos α. Котангенсом угла α называется отношение прилежащего катета к противолежащему или отношение координаты х точки М к y. Котангенс угла α обозначают ctgα. Так как y = sin α и x = cos α, то ctgα= cosα / sinα. Из последних двух соотношений следует: ctg α= 1 / tg α |
sin, cos, tg, ctg на тригонометрическом круге. |
||||||||||||||||||||||||
y = sin x
|
График функции sin. |
||||||||||||||||||||||||
y = cos x
|
График функции cos. |
||||||||||||||||||||||||
y = tg x
|
 График функции tg. |
||||||||||||||||||||||||
y = ctg x
|
График функции сtg. |
||||||||||||||||||||||||
Значения синуса и косинуса для некоторых углов. |
|||||||||||||||||||||||||
 |
|||||||||||||||||||||||||
 |
|||||||||||||||||||||||||
| Значения тангенса и котангенса для углов 30, 45 и 60 находятся аналогично. | |||||||||||||||||||||||||
Пример 1 |
|||||||||||||||||||||||||
 |
|||||||||||||||||||||||||
| Пример 2 | |||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 9 | |||||||||||||||||||||||||
www.mathtask.ru
Тригонометрия — Циклопедия
Титульная страница «Тригонометрии» (переиздание 1612) В. Питиска, давшая название одноименному разделу математики Основы тригонометрии // KhanAcademyRussian (CC) [9:25] Основы тригонометрии Часть 2 // KhanAcademyRussian [12:22]Тригонометрия — раздел классической математики, лежащий на пересечении алгебры и геометрии: система законов-функций, по которым на евклидовой плоскости соотносятся стороны и углы треугольников.
Тригонометрия основывается на соотношении подобия. Треугольники с двумя равными углами подобны, поэтому подобны прямоугольные треугольники, в которых равен один острый угол. Отношение длин сторон у подобных треугольников одинаковое, поэтому отношение сторон прямоугольных треугольников зависит только от одного параметра — величины острого угла. Это обстоятельство позволяет обозначить тригонометрические функции: синус, косинус, тангенс, котангенс, секанс и косеканс, через отношение различных сторон прямоугольного треугольника.
[править] Исторические сведения
Некоторые сведения о науке, позже получившей название «тригонометрия», были еще у древних египтян. В папирусе Ахмеса есть пять задач, касающихся измерения пирамид, в которых упоминается какая-то функция угла — «сект». Есть мнение, что «сект» обозначает котангенс угла. Применение этой функции носило сугубо практическую причину: египетские архитекторы строили пирамиды, строго придерживаясь одного и того же значения угла наклона боковой грани к основанию (52°) и угла между ребром и диагональю основания (42°). А для этого надо было знать соответствующие отношения между линейными элементами четырехугольной пирамиды.
Вавилоняне так же имели некоторые знания об этой области математики: они ввели разделение круга на 360° и разделение градуса на 60 частей, что соответствовало принятой в древней Месопотамии шестидесятеричной системе счисления. Для измерения углов вавилоняне пользовались примитивной астролябией.
Древние греки умели решать многие тригонометрические задачи, но они применяли геометрические, а не алгебраические методы.
Тригонометрическую функцию синус впервые ввели древние индийцы в трактате «Сурья-сиддханта». Свойства этой функции исследовал индийский математик 5 века Ариабхата[1]. Дальнейший вклад в развитие тригонометрии сделали арабские математики. До 10 века они апеллировали всеми тригонометрическими функциями и протабулировали их. В Европу понятие тригонометрических функций пришло с переводами трудов ал-Баттани и Ат-Туси. Одной из первых работ европейской математики, посвященных тригонометрии была книга «De Triangulis» немецкого математика 15 века Региомонтана. Однако, еще в 16 веке тригонометрия была мало известна. Коперник вынужден был посвятить ее описанию 2 отдельных раздела в своей работе «Об обращении небесных сфер» (лат. «De revolutionibus orbium coelestium»).
Быстрое дальнейшее развитие тригонометрии было обусловлено требованиями навигации и картографии[2]. Сам термин тригонометрия ввел, опубликовав в 1595 книгу под таким же названием, немецкий математик Варфоломей Питиск (нем. Bartholomäus Pitiscus, 1561—1613)[3]. Гемма Фризий описал метод триангуляции.
Со становлением математического анализа тригонометрия получила новые методы. Благодаря трудам Брука Тейлора и Колина Маклорена тригонометрические функции получили представление в виде рядов[4]. Формула Муавра установила связь между тригонометрическими функциями и экспонентой. Леонард Эйлер расширил определение тригонометрических функций на комплексную плоскость.
- Синус — отношение противолежащего катета к гипотенузе.
- Косинус — отношение прилежащего катета к гипотенузе.
- Тангенс — отношение противолежащего катета к прилежащему.
- Котангенс — отношение прилежащего катета к противолежащему.
- Секанс — отношение гипотенузы к прилежащему катету.
- Косеканс — отношение гипотенузы к противолежащему катету.
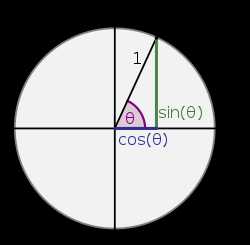
Данные определения позволяют вычислить значения функций для острых углов, то есть от 0° до 90° (от 0 до [math]\pi \over 2[/math] радиан). В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось. Рассмотрим в прямоугольной системе координат окружность единичного радиуса (см. рисунок) и отложим от горизонтальной оси угол [math]\theta[/math] (если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим A. Тогда:
Для острых углов новые определения совпадают с прежними.
[править] Свойства функции синус
Синус- Область определения функции — множество всех действительных чисел: [math]D(y) = R[/math].
- Множество значений — промежуток [−1; 1]: [math]E(y)[/math] = [−1;1].
- Функция [math] y = \sin \left( \alpha \right) [/math] является нечётной: [math] \sin \left( — \alpha \right) = — \sin \alpha[/math].
- Функция периодическая, наименьший положительный период равен [math]2\pi[/math]: [math] \sin \left( \alpha + 2 \pi \right) = \sin \left( \alpha \right) [/math].
- График функции пересекает ось Ох при [math] \alpha = \pi n \,, n \in Z[/math].
- Промежутки знакопостоянства: [math]y \gt 0[/math] при [math] \left( 2\pi n + 0; \pi + 2\pi n \right) \,, n \in Z [/math] и [math] y \lt 0 [/math] при [math]\left( \pi + 2\pi n; 2\pi + 2\pi n \right) \,, n \in Z [/math].
- Функция непрерывна и имеет производную при любом значении аргумента: [math]( \sin \alpha )’ = \cos \alpha[/math]
- Функция [math] y = \sin \alpha [/math] возрастает при [math] \alpha \in \left( — \frac{\pi}{2} + 2\pi n; \frac{\pi}{2} + 2\pi n \right) \,, n \in Z [/math], и убывает при [math] \alpha \in \left( \frac{\pi}{2} + 2\pi n; 3\frac{\pi}{2} + 2\pi n \right) \,, n \in Z [/math].
- Функция имеет минимум при [math] \alpha = -\frac{\pi}{2} + 2\pi n \,, n \in Z [/math] и максимум при [math] \alpha = \frac{\pi}{2} + 2\pi n \,, n \in Z [/math].
[править] Свойства функции косинус
Косинус- Область определения функции — множество всех действительных чисел: [math]D(y) = R[/math].
- Множество значений — промежуток [−1; 1]: [math]E(y)[/math] = [−1;1].
- Функция [math] y = \cos \left( \alpha \right) [/math] является чётной: [math] \cos \left( — \alpha \right) = \cos \alpha[/math].
- Функция периодическая, наименьший положительный период равен [math]2\pi[/math]: [math] \cos \left( \alpha + 2 \pi \right) = \cos \left( \alpha \right) [/math].
- График функции пересекает ось Ох при [math] \alpha = \frac{\pi}{2} + \pi n \,, n \in Z[/math].
- Промежутки знакопостоянства: [math]y \gt 0[/math] при [math] \left( -\frac{\pi}{2} + 2\pi n; \frac{\pi}{2} + 2\pi n \right) \,, n \in Z [/math] и [math] y \lt 0 [/math] при [math]\left( \frac{\pi}{2} + 2\pi n; 3\frac{\pi}{2} + 2\pi n \right) \,, n \in Z .[/math]
- Функция непрерывна и имеет производную при любом значении аргумента: [math]( \cos \alpha )’ = -\sin \alpha[/math]
- Функция [math] y = \cos \alpha [/math] возрастает при [math] \alpha \in \left( -\pi + 2\pi n; 2\pi n \right) \,, n \in Z ,[/math] и убывает при [math] \alpha \in \left( 2\pi n; \pi + 2\pi n \right) \,, n \in Z .[/math]
- Функция имеет минимум при [math] \alpha = \pi + 2\pi n \,, n \in Z [/math] и максимум при [math] \alpha = 2\pi n \,, n \in Z .[/math]
[править] Свойства функции тангенс
Тангенс- Область определения функции — множество всех действительных чисел: [math]D(y) = R[/math], кроме чисел [math] \alpha = \frac{\pi}{2} + \pi n . [/math]
- Множество значений — множество всех действительных чисел: [math] E(y) = R . [/math]
- Функция [math] y = \mathrm{tg} \left( \alpha \right) [/math] является нечётной: [math] \mathrm{tg} \left( — \alpha \right) = — \mathrm{tg}\ \alpha[/math].
- Функция периодическая, наименьший положительный период равен [math]\pi[/math]: [math] \mathrm{tg} \left( \alpha + \pi \right) = \mathrm{tg} \left( \alpha \right) [/math].
- График функции пересекает ось Ох при [math] \alpha = \pi n \,, n \in Z[/math].
- Промежутки знакопостоянства: [math] y \gt 0 [/math] при [math] \left( \pi n; \frac{\pi}{2} + \pi n \right) \,, n \in Z [/math] и [math] y \lt 0 [/math] при [math]\left( -\frac{\pi}{2} + \pi n; \pi n \right) \,, n \in Z [/math].
- Функция непрерывна и имеет производную при любом значении аргумента из области определения: [math]( \mathop{\operatorname{tg}}\, x )’ = \frac{1}{\cos ^2 x}.[/math]
- Функция [math] y = \mathrm{tg}\ \alpha [/math] возрастает при [math] \alpha \in \left( -\frac{\pi}{2} + \pi n; \frac{\pi}{2} + \pi n \right) \,, n \in Z [/math].
[править] Свойства функции котангенс
Котангенс- Область определения функции — множество всех действительных чисел: [math]D(y) = R,[/math] кроме чисел [math] \alpha = \pi n .[/math]
- Множество значений — множество всех действительных чисел: [math] E(y) = R .[/math]
- Функция [math] y = \mathop{\operatorname{ctg}} \left( \alpha \right) [/math] является нечётной: [math] \mathop{\operatorname{ctg}} \left( — \alpha \right) = — \mathop{\operatorname{ctg}}\ \alpha \,.[/math]
- Функция периодическая, наименьший положительный период равен [math]\pi[/math]: [math] \mathop{\operatorname{ctg}} \left( \alpha + \pi \right) = \mathop{\operatorname{ctg}} \left( \alpha \right) .[/math]
- График функции пересекает ось Ох при [math] \alpha = \frac{\pi}{2} + \pi n \,, n \in Z \,.[/math]
- Промежутки знакопостоянства: [math] y \gt 0 [/math] при [math] \left( \pi n; \frac{\pi}{2} + \pi n \right) \,, n \in Z [/math] и [math] y \lt 0 [/math] при [math]\left( \frac{\pi}{2} + \pi n; \pi \left( n + 1 \right) \right) \,, n \in Z .[/math]
- Функция непрерывна и имеет производную при любом значении аргумента из области определения: [math]( \mathop{\operatorname{ctg}}\, x )’ = -\frac{1}{\sin ^2 x}.[/math]
- Функция [math] y = \mathop{\operatorname{ctg}}\ \alpha [/math] убывает при [math] \alpha \in \left( \pi n; \pi \left( n + 1 \right) \right) \,, n \in Z .[/math]
[править] Основные теоремы тригонометрии
Определенные для прямоугольного треугольника тригонометрические функции позволяют решать произвольные треугольники с использованием основных теорем: теоремы синусов, теоремы косинусов и теоремы тангенсов.
[править] Теорема синусов
Теорема синусов утверждает, что отношение синуса угла к длине противоположной стороны треугольника одинакова для всех углов треугольника. Для плоского треугольника со сторонами [math]a, b, c[/math] и соответствующими противоположными них углами [math]A, B, C[/math] можно записать:
- [math]\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R,[/math]
где [math]R[/math] — радиус описанной окружности вокруг треугольника.
- [math]R = \frac{abc}{\sqrt{(a+b+c)(a-b+c)(a+b-c)(b+c-a)}}.[/math]
[править] Теорема косинусов
По теореме косинусов, квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. Для плоского треугольника со сторонами [math]a, b, c[/math] и углом [math]C[/math], между сторонами [math]a, b[/math]:
- [math]c^2=a^2+b^2-2ab\cos C ,\,[/math]
или:
- [math]\cos C=\frac{a^2+b^2-c^2}{2ab}.\,[/math]
Теорема косинусов позволяет определить длину третьей стороны треугольника, если известны длины двух сторон и значение угла между ними.
[править] Теорема тангенсов
Теорема тангенсов — теорема о соотношении между двумя сторонами произвольного треугольника и тангенса полусуммы и полуразности противоположных к ним углов, которая записывается уравнением (формула Региомонтана):
- [math]\frac{a-b}{a+b}=\frac{\mathop{\operatorname{tg}}\left[\tfrac{1}{2}(A-B)\right]}{\mathop{\operatorname{tg}}\left[\tfrac{1}{2}(A+B)\right]}[/math]
[править] Площадь треугольника
Площадь треугольника тоже может быть определена через тригонометрические функции: она равна половине произведения прилегающих сторон на синус угла между ними:
- [math]A = \frac{1}{2}ab\sin C .\,[/math]
[править] Простейшие тригонометрические уравнения
Уравнения, в которых фигурируют тригонометрические функции, называют тригонометрическими. Самые простые из них имеют аналитические решения, благодаря существованию обратных тригонометрических функций. Поскольку тригонометрические функции периодические, такие решения не единственные, а определяются с точностью до периода.
- [math]\begin{matrix} \sin x=a & (|a|\le1) & x=(-1)^n \arcsin a + \pi n \\ \cos x=a & (|a|\le1)& x=\pm \arccos a + 2 \pi n \\ \text{tg}\, x=a & & x=\text{arctg}\, a + \pi n \\ \text{ctg}\, x=a & & x=\text{arcctg}\, a + \pi n \\ \end{matrix}[/math]
[править] Формулы преобразования тригонометрических выражений
Синус и косинус суммы/разности:
- [math]\sin(x+y)=\sin x \cos y + \cos x \sin y \![/math]
- [math]\sin(x-y)=\sin x \cos y — \cos x \sin y \![/math]
- [math]\cos(x+y)=\cos x \cos y — \sin x \sin y \![/math]
- [math]\cos(x-y)=\cos x \cos y + \sin x \sin y \![/math]
Сумма/разность синусов и косинусов:
- [math]\sin x + \sin y = 2 \sin{\frac{x+y}{2}} \cos{\frac{x-y}{2}} \![/math]
- [math]\sin x — \sin y = 2 \sin{\frac{x-y}{2}} \cos{\frac{x+y}{2}} \![/math]
- [math]\cos x + \cos y = 2 \cos{\frac{x+y}{2}} \cos{\frac{x-y}{2}} \![/math]
- [math]\cos x — \cos y =-2 \sin{\frac{x+y}{2}} \sin{\frac{x-y}{2}} \![/math]
Сферическая тригонометрия — раздел сферической геометрии, главными объектами которого являются многоугольники (особенно треугольники) на сфере и соотношение между сторонами и углами. Возникновение сферической геометрии связано с задачами сферической астрономии.
Основными элементами сферической геометрии являются точки и большие круги сферы. Большие круги являются геодезическими линиями сферы, поэтому они в сферической геометрии играют роль, аналогичную роли прямых в планиметрии. Расстояние между двумя точками в сферической геометрии измеряется углом между радиусами сферы, проведенными в эти точки. Угол между двумя «прямыми» равен двугранному углу между плоскостями больших кругов, которые определяют эти «прямые». Две любые «прямые» в сферической геометрии пересекаются в двух точках и разбивают поверхность сферы на 4 двуугольника. Три «прямые», пересекаясь попарно, образуют 8 сферических треугольников. Эти треугольники имеют много необычных свойств, которые отличают их от плоских треугольников. Например, сумма углов сферического треугольника всегда больше 180° и меньше 540°.
Стороны и углы сферического треугольника связаны зависимостями:
- [math]\frac{\sin\frac{a}{R}}{\sin A}=\frac{\sin\frac{b}{R}}{\sin B}=\frac{\sin\frac{c}{R}}{\sin C};[/math]
- [math]\cos\frac{c}{R}=\cos\frac{a}{R}\cos\frac{b}{R}+\sin\frac{a}{R}\sin\frac{b}{R}\cos C;[/math]
- [math]\cos\frac{a}{R}=\frac{\cos A + \cos B\cos C}{\sin B\sin C}.[/math]
где [math]a, b, c[/math] — стороны сферического треугольника; [math]A, B, C[/math] — углы, противоположные этим сторонам; [math]R[/math] — радиус сферы.
Сферическая тригонометрия очень важна в астрономических вычислениях (небесной механике), а также в орбитальной, космической навигации и навигации на поверхности Земли.
- Андронов И. К., Окунев А. К. Курс тригонометрии, развиваемый на основе реальных задач. — М.: Просвещение, 1967. — 648 с.
- Волынский Б. А. Сферическая тригонометрия. — М.: Наука, 1977. — 136 с.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1984. — 830 c.
cyclowiki.org
Основные формулы по тригонометрии — Математика — Теория, тесты, формулы и задачи
Знание формул по тригонометрии является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по тригонометрии, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении тригонометрических задач. На этой странице сайта представлены основные формулы по школьной тригонометрии.
Изучать основные формулы по школьной тригонометрии онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (адрес электронной почты и ссылки в социальных сетях здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
educon.by
Тригонометрия — математика и искусство
Область применения тригонометрии охватывает самые разные сферы математики, некоторые разделы естествознания и техники.
Тригонометрия имеет несколько разновидностей:
Сферическая тригонометрия занимается изучением сферических треугольников.
Прямолинейная или плоская тригонометрия изучает обычнее треугольники.
Значительно развили тригонометрию древнегреческие и эллинистические ученые. Однако в работах Евклида и Архимеда тригонометрия представлена в геометрическом виде. Теоремы о длине хорд применяются в законах синусов. А теорема Архимеда для деления хорд соответствует формулам для синусов суммы и разности углов.
В настоящее время математики используют новую запись известных теорем, например, sin α/ sin β < α/β < tan α/ tan β, где 0° < β < α < 90°, тем самым, компенсируют недостатки таблиц хорд, времен Аристарха Самосского.
Предположительно первые тригонометрические таблицы были составлены Гиппархом Никейским, которого по праву считают «отцом тригонометрии». Ему принадлежит заслуга в создании сводной таблицы величин дуг и хорд для серии углов. Более того именно Гиппарх Никейский впервые стал использовать 360° окружности.
Клавдий Птолемей значительно развил и расширил учение Гиппарха. Теорема Птолемея гласит: сумма произведений противоположных сторон циклического четырехугольника равна произведению диагоналей. Следствием теоремы Птолемея стало понимание эквивалентности четырех формул суммы и разности для синуса и косинуса. Кроме того, Птолемей вывел формулу половинного угла. Все свои результаты Птолемей использовал при составлении тригонометрических таблиц. К сожалению, ни одной подлинной тригонометрической таблицы Гиппарха и Птолемея не сохранилось до наших дней.
Тригонометрические вычисления нашли свое применение почти во всех областях геометрии, физики и инженерного дела.
С помощью тригонометрии (техника триангуляции) можно измерять расстояния между звездами, между ориентирами в географии, производить контроль над системами навигации спутников.
Тригонометрия успешно применяется в технике навигации, теории музыки, акустике, оптике, при анализе финансовых рынков, электронике, теории вероятности, статистике, биологии и медицине, химии и теории чисел (криптографии), сейсмологии, метеорологии, океанологии, картографии, топографии и геодезии, архитектуре и фонетике, машиностроении и компьютерной графике.
matematikaiskusstvo.ru
| Главная > Учебные материалы > Математика: Тригонометрические формулы | |||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
1.Знаки тригонометрических функций.
|
|||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 | |||||||||||||||||||||||||
Знаки тригонометрических функций по четвертям в тригонометрическом круге |
|||||||||||||||||||||||||
Значения тригонометрических функций для некоторых углов |
|||||||||||||||||||||||||
Основные тригонометрические тождества |
Формулы приведения |
||||||||||||||||||||||||
 |
 |
||||||||||||||||||||||||
Формулы преобразования суммы |
Формулы сложения |
||||||||||||||||||||||||
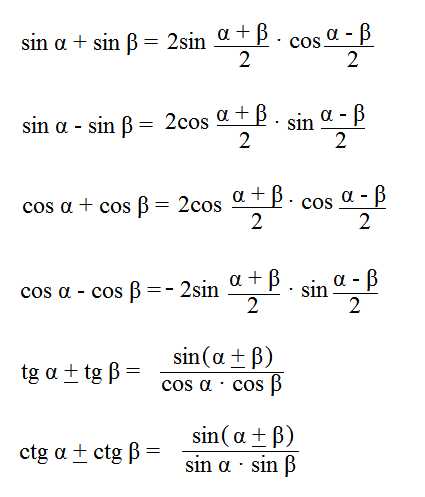 |
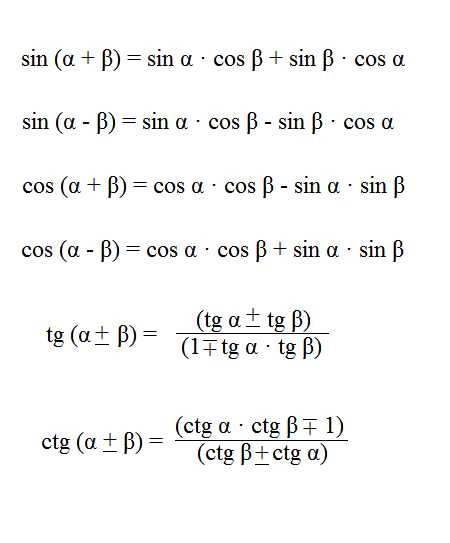 |
||||||||||||||||||||||||
Формулы половинного аргумента |
Формулы понижения степени |
||||||||||||||||||||||||
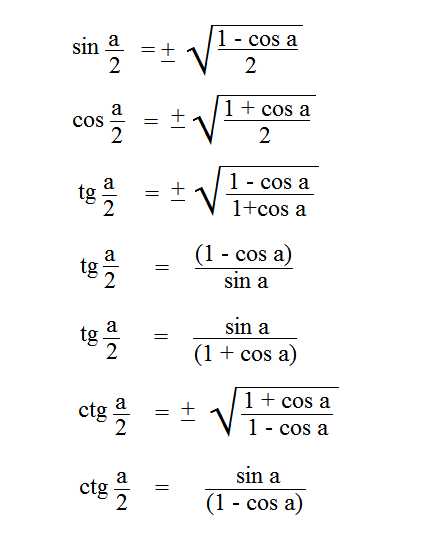 |
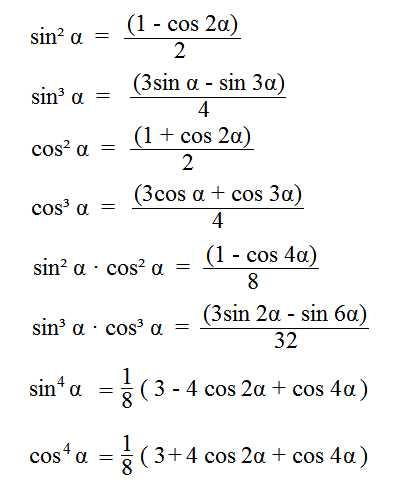 |
||||||||||||||||||||||||
Формулы двойного угла |
Переход от произведения к сумме |
||||||||||||||||||||||||
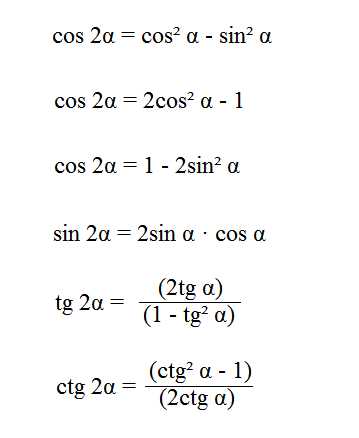 |
Формулы тройного угла
|
||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 | |||||||||||||||||||||||||
www.mathtask.ru
Тригонометрия Википедия
| Ссылки на статьи о тригонометрии |
| Тригонометрия |
 |
|
| Справочник |
|
| Законы и теоремы |
|
| Математический анализ |
|
Тригономе́трия (от др.-греч. τρίγωνον «треугольник» и μετρέω «измеряю», то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии[1]. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса (1561—1613), а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, архитектуре и геодезии (науке, исследующей размеры и форму Земли).
Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролирова
ru-wiki.ru