Таблицы истинности составление – «Составление таблиц истинности по логической формуле Приоритет логических операций ИНВЕРСИЯ КОНЪЮНКЦИЯ ДИЗЪЮНКЦИЯ Порядок действий можно указать с помощью.». Скачать бесплатно и без регистрации.

Составление таблиц истинности – ИКТ

Вопросы для повторения:

1.Установите, какие из этих предложения являются логическими высказываниями, а какие нет (объяснить):

2. Установите, какие из логических высказываний истинны, а какие ложны, а какие относятся к числу тех, истинность которых трудно или невозможно установить

а) «Солнце есть спутник Земли»

б) «2 + 3 = 4»

в) «Сегодня отличная погода»

г) «Музыка Баха слишком сложна»

д) «Скорость первой космической ракеты = 7,8 км/с»

е) «Если один угол в треугольнике прямой, то треугольник будет тупоугольным»

ж) «Санкт-Петербург расположен на Неве»

з)  «Идите убирать снег!»

и) «Если сумма квадратов двух сторон  треугольника равна квадрату третьей, то он прямоугольный»

к) «Химия – легкая наука»

 

2. Приведите примеры истинных и ложных логических высказываний из

а) физики                  б) математики            в) информатики

г) жизни                    д) биологии                 е) литературы

3. Как определить истинность простого высказывания?

Порядок выполнения логических операций в сложном логическом выражении

1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;

 

Логические выражения

Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.

Для записи составного высказывания в виде логического выражения на формальном языке (языке алгебры логики) в составном высказывании нужно выделить простые высказывания и логические связи между ними.

Решение логических выражений принято записывать в виде таблиц истинности – таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных.

При составлении таблиц истинности необходимо: 1. Выяснить количество строк в таблице  (=2n, где n – количество переменных). 2. Выяснить количество столбцов (= количество переменных + количество операций). 3. Установить последовательность  выполнения логических операций. 4. Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных. 5. Заполнить таблицу истинности по столбцам.

 

 

Задание 1. Построим таблицу истинности для выражения: F = (A v B) & (¬ A v ¬ B)

1. Определим количество строк  =2n = 22+1 =5
2. Определим количество столбцов = 2 переменные +  5 операций = 7
3. Расставим порядок выполнения операций: 1 3 5 4 2
4. Заполним  таблицу по столбцам:

А	В	A v B	¬ A	¬ B	¬  A v ¬ B	(A v B) & (¬ A v ¬ B)
0	0	0	1	1	1	0
0	1	1	1	0	1	1
1	0	1	0	1	1	1
1	1	1	0	0	0	0

 

Задание 2. Построить таблицу истинности логического выражения   F = (A & Ø B) ˅ (Ø A & B)

 

Задание 3. Построить таблицу истинности логического выражения F = X  v Y &  ¬ Z

 

X	Y	Z	¬ Z	Y & ¬ Z	F  = X v Y & ¬ Z
0	0	0	1	0	0
0	0	1	0	0	0
0	1	0	1	1	1
0	1	1	0	0	0
1	0	0	1	0	1
1	0	1	0	0	1
1	1	0	1	1	1
1	1	1	0	0	1

 

 

Задание 4. Построить таблицу истинности логического выражения   F = (Ø X ˅ Y) & (Ø Y ˅ Z)

 

Домашнее задание – выучить определения и построить таблицы истинности:

i-k-t.ru

Составление таблицы истинности

Чтобы проверить сложное суждение с помощью таблицы истинности, необходимо грамотно её составить.

Например, нужно проверить суждение: «Если пойдёт дождь, то дорога будет мокрая».

1. Определим все простые суждения, составляющие данное сложное высказывание и узнаем количество переменных n:

а– пойдёт дождь;b– дорога будет мокрая

Получилось две переменных (а, b), соединённых союзом «если, то»

2. Количество строк (k) в таблице определяется по формуле:k = 2ⁿ, гдеn– количество переменных (то есть количество простых суждений, составляющих сложное).

В данном примере k = 2² = 4 Значит будет четыре строчки в таблице.

3. Количество столбцов в таблице будет зависеть от количества операций (логических связок) в сложном суждении.

Сначала в первых столбцах распределяются все возможные значения истины и лжи для переменных.

В данном примере две переменные, следовательно, четыре строки.

В самом правом столбце (b) чередуют «и» и «л» по одному, начиная всегда с «истины»

Во втором справа столбце (а) чередуют подряд два значения «и» и два значения «л», начиная всегда с «истины».

а	b
и	и
и	л
л	и
л	л

Затем направо выписывают логические формы всех сложных суждений, входящих в рассматриваемое суждение. В данном примере указана одна логическая связка «если, то» – импликация.

а	b	a → b
и	и
и	л
л	и
л	л

Осталось определить значения истинности для импликации. Сложное суждение, соединённое импликацией, ложно только в одном случае: если основание (первое суждение) истинно, а следствие (второе суждение) ложно.

а	b	a → b
и	и	и
и	л	л
л	и	и
л	л	и

1. Дождь пошёл, дорога мокрая. а– истина;b– истина. Следовательно, если а, тоb(a → b)– истина

2. Дождь пошёл, но дорога не стала мокрая.

а– истина;b– ложь. Следовательно, если а, тоb(a → b)– ложно. Невозможно, чтобы причина была, а следствие не наступило.

3. Дождь не пошёл, но дорога мокрая а– ложь;b– истина. Следовательно,a → b – истина. Дорога может быть мокрой и по другой причине.

4. Дождь не пошёл и дорога не намокла. а– ложь;b– ложь. Следовательно,a → b – истина.

Если сложное суждение составлено из трёх простых, то есть состоит из трёх переменных (а,b,c), то таблица истинности, включающая все возможные комбинации истинности или ложности её переменных, будет состоять из 2³ = 8 строк.

Алгоритм распределения значений «и» и «л» для трёх переменных таков:

а	b	с		Начинаем распределять значения с крайнего правого столбца (с) и распределяем значения «и» и «л» попеременно, начиная с «истины». Затем распределяем значения во втором столбце справа (b), распределяем значения «и» и «л», чередуя подряд по два значения «и», затем по два значения «л»; затем опять два значения «и» и два значения «л». В крайнем левом столбце (а) чередуем «и» и «л», чередуя подряд сначала четыре значения «и» и затем четыре значения «л»
и	и	и
и	и	л
и	л	и
и	л	л
л	и	и
л	и	л
л	л	и
л	л	л

Упражнения:

1. Запишите высказывание в виде логической формы, используя логические связки: «Если ты сможешь доказать мне свои добрые намерения, то я поверю тебе или же мне придётся вызвать полицию и обвинить тебя в лжесвидетельстве» (Г. Каттнер. Источник миров).

Выпишем все простые суждения, входящие в состав сложного высказывания:

а–ты сможешь доказать мне свои добрые намерения

b–я поверю тебе

с–мне придётся вызвать полицию

d–(мне придётся) обвинить тебя в лжесвидетельствовании.

Определим связки между элементами: если а, то b или с и d

(a → b) ˅ (c ˄ d)

studfiles.net

Построить таблицу истинности следующих логических выражений

Проблема определения истинности выражения встаёт перед многими науками. Любая доказательная дисциплина должна опираться на некоторые критерии истинности доказательств. Наука, изучающая эти критерии, называется алгеброй логики. Основной постулат алгебры логики заключается в том, что любое самое витиеватое утверждение может быть представлено в виде алгебраического выражения из более простых утверждений, истинность или ложность которых легко определить.

Для любого «алгебраического» действия над утверждением задаётся правило определения истинности или ложности измененного утверждения, исходя из истинности или ложности исходного утверждения. Эти правила записываются через таблицы истинности выражения. Прежде, чем составлять таблицы истинности, надо поближе познакомиться с алгеброй логики.

Алгебраические преобразования логических выражений

Любое логическое выражение, как и его переменные (утверждения), принимают два значения: ложь или истина. Ложь обозначается нулём, а истина — единицей. Разобравшись с областью определения и областью допустимых значений, мы можем рассмотреть действия алгебры логики.

Отрицание

Отрицание и инверсия — самое простое логическое преобразование. Ему соответствует частица «не.» Это преобразование просто меняет утверждение на противоположное. Соответственно, значение утверждения тоже меняется на противоположное. Если утверждение А истинно, то «не А» — ложно. Например, утверждение «прямой угол — это угол, равный девяносто градусов» — истина. Тогда его отрицание «прямой угол не равен девяноста градусам» — ложь.

Таблица истинности для отрицания будет такова:

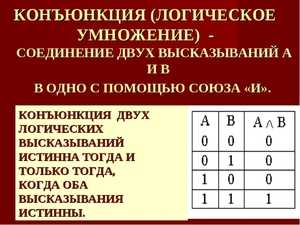
Конъюнкция

Конъюнкция аналогична умножению и соответствует союзу «и». Такое выражение будет верно, только если верны все утверждения, объединённые конъюнкцией. То есть, утверждение «А и Б» будет истинным, только если А — истина и Б — истина. Во всех остальных случаях выражение «А и Б» ложно. Например, высказывание «Земля круглая и плоская» будет ложно, так как первая часть истина, а вторая — ложь.

Таблица истинности конъюнкции

А	Б	А и Б
Л	Л	Л
Л	И	Л
И	Л	Л
И	И	И

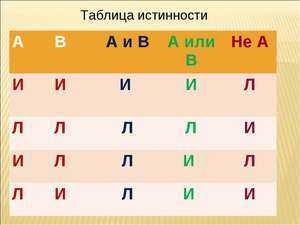
Дизъюнкция

Эта операция может быть обычной или строгой, их результаты будут различаться.

Обычная дизъюнкция или логическое сложение соответствует союзу «или». Она будет истинной если хотя бы одно из утверждений, входящих в неё — истина. Например, выражение «Земля круглая или стоит на трёх китах» будет истинным, так как первое утверждение — истинно, хоть второе и ложно.В таблице это будет выглядеть так:

А	Б	А или Б
Л	Л	Л
Л	И	И
И	Л	И
И	И	И

Строгую дизъюнкцию или сложение по модулю также называют «исключающим или». Эта операция может принимать вид грамматической конструкции «одно из двух: либо …, либо …». Здесь значение логического выражения будет ложным, если все утверждения, входящие в него, имеют одинаковую истинность. То есть, оба утверждения либо вместе истинны, либо вместе ложны.

Таблица значений исключающего или

А	Б	либо А, либо Б
Л	Л	Л
Л	И	И
И	Л	И
И	И	Л

Импликация и эквивалентность

Импликация представляет собой следствие и грамматически может быть выражена как «из А следует Б». Здесь утверждение А будет называться предпосылкой, а Б — следствием. Импликация может быть ложной, только в одном случае: если предпосылка истинна, а следствие ложно. То есть, ложь не может следовать из истины. Во всех остальных случаях импликация истинна. Варианты, когда оба утверждения имеют одинаковую истинность, вопросов не вызывают. Но почему верное следствие из неверной предпосылки — истина? Дело в том, что из ложной предпосылки может следовать что угодно. Это и отличает импликацию от эквивалентности.

В математике (и других доказательных дисциплинах) импликация используется для указания необходимого условия. Например, утверждение А — «точка О — экстремум непрерывной функции», утверждение Б — «производная непрерывной функции в точке О обращается в ноль». Если О, действительно, точка экстремума непрерывной функции, то производная в этой точке будет, и вправду, равна нулю. Если же О не является точкой экстремума, то производная в этой точке может быть нулевой, а может не быть. То есть Б необходимо для А, но не достаточно.

Таблица истинности для импликации выглядит следующим образом:

А	Б	из А следует Б
Л	Л	И
Л	И	И
И	Л	Л
И	И	И

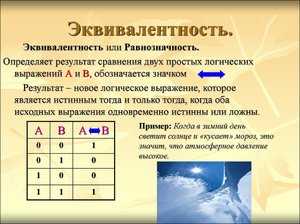
Логическая операция эквивалентность, по сути, является взаимной импликацией. «А эквивалентно Б» означает, что «из А следует Б» и «из Б следует А» одновременно. Эквивалентность верна, когда оба утверждения либо одновременно верные, либо одновременно неверные.

А	Б	А эквивалентно Б
Л	Л	И
Л	И	Л
И	Л	Л
И	И	И

В математике эквивалентность используется для определения необходимого и достаточного условия. Например, утверждение А — «Точка О является точкой экстремума непрерывной функции», утверждение Б — «В точке О производная функции обращается в ноль и меняет знак». Эти два утверждения эквивалентны. Б содержит необходимое и достаточное условие для А. Обратите внимание, что в данном примере утверждений Б на самом деле является конъюнкцией двух других: «производная в точке О обращается в ноль» и «производная в точке О меняет знак».

Прочие логические функции

Выше были рассмотрены основные логические операции, которые часто используются. Есть и другие функции, которые используются:

• Штрих Шеффера или несовместимость представляет собой отрицание конъюнкции А и Б
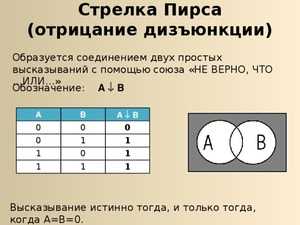
• Стрелка Пирса представляет сбой отрицание дизъюнкции.

Построение таблиц истинности

Чтобы построить таблицу истинности для какого-либо логического выражения, надо действовать в соответствии с алгоритмом:

1. Разбить выражение на простые утверждения и обозначить каждое из них как переменную.
2. Определить логические преобразования.
3. Выявить порядок действий этих преобразований.
4. Сосчитать строки в будущей таблице. Их количество равно два в степени N, где N — число переменных, плюс одна строка для шапки таблицы.
5. Определить число столбцов. Оно равно сумме количества переменных и количества действий. Можно представлять результат каждого действия в виде новой переменной, если так будет понятней.
6. Шапка заполняется последовательно, сначала все переменные, потом результаты действий в порядке их выполнения.
7. Заполнение таблицы надо начать с первой переменной. Для неё количество строк делится пополам. Одна половина заполняется нулями, вторая — единицами.
8. Для каждой следующей переменной нули и единицы чередуются вдвое чаще.
9. Таким образом заполняются все столбцы с переменными и для последней переменной значение меняется в каждой строке.
10. Потом последовательно заполняются результаты всех действий.

В итоге последний столбец отобразит значение всего выражения в зависимости от значения переменных.

Отдельно следует сказать о порядке логических действий. Как его определить? Здесь, как и в алгебре, есть правила, задающие последовательность действий. Они выполняются в следующем порядке:

1. выражения в скобках;
2. отрицание или инверсия;
3. конъюнкция;
4. строгая и обычная дизъюнкция;
5. импликация;
6. эквивалентность.

Примеры

Для закрепления материала можно попробовать составить таблицу истинности для ранее упомянутых логических выражений. Рассмотрим три примера:

• Штрих Шеффера.
• Стрелка Пирса.
• Определение эквивалентности.

Штрих Шеффера

Штрих Шеффера — это логическое выражение, которое можно записать в виде «не (А и Б)». Здесь две переменные, и два действия. Конъюнкция в скобках, значит, она выполняется первой. В таблице будет шапка и четыре строки со значениями переменных, а также четыре столбца. Заполним таблицу:

А	Б	А и Б	не (А и Б)
Л	Л	Л	И
Л	И	Л	И
И	Л	Л	И
И	И	И	Л

Отрицание конъюнкции выглядит как дизъюнкция отрицаний. Это можно проверить, если составить таблицу истинности для выражения «не А или не Б». Проделайте это самостоятельно и обратите внимание, что здесь будет уже три операции.

Стрелка Пирса

Рассматривая Стрелку Пирса, которая представляет собой отрицание дизъюнкции «не (А или Б)», сравним её с конъюнкцией отрицаний «не А и не Б». Заполним две таблицы:

А	Б	А или Б	не (А или Б)
Л	Л	Л	И
Л	И	И	Л
И	Л	И	И
И	И	И	Л

А	Б	не А	не Б	не А и не Б
Л	Л	И	И	И
Л	И	И	Л	Л
И	Л	Л	И	И
И	И	Л	Л	Л

Значения выражений совпали. Изучив два эти примера, можно прийти к выводу, как раскрывать скобки после отрицания: отрицание применяется ко всем переменным в скобках, конъюнкция меняется на дизъюнкцию, а дизъюнкция — на конъюнкцию.

Определение эквивалентности

Про утверждения А и Б можно сказать, что они эквивалентны, тогда и только тогда, когда из А следует Б и из Б следует А. Запишем это как логическое выражение и построим для него таблицу истинности. «(А эквивалентно Б) эквивалентно (из А следует Б) и (из Б следует А)».

Здесь две переменных и пять действий. Строим таблицу:

А	Б	В = (из А следует Б)	Г = (из Б следует А)	Д = А эквивалентно Б	Е = В и Г	Д эквивалентно Е
Л	Л	И	И	И	И	И
Л	И	И	Л	Л	Л	И
И	Л	Л	И	Л	Л	И
И	И	И	И	И	И	И

В последнем столбце все значения истинные. Это значит, что приведенное определение эквивалентности верно при любых значениях А и Б. Значит, оно всегда истинно. Именно так с помощью таблицы истинности можно проверить корректность любых определений и логических построений.

liveposts.ru

СОСТАВЛЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ — МегаЛекции

СЛОЖНЫЕ СУЖДЕНИЯ

Сложные суждения – это суждения, образованные из простых с помощью логических связок.

Связь между элементами сложного суждения осуществляется с помощью логических союзов (логических связок).

 

Логические связки:

 

Главная их особенность в том, что логические союзы однозначны, тогда как грамматические союзы имеют множество смыслов и оттенков.

 

1. КОНЪЮНКЦИЯ (от лат. сonjunctio – союз, связь).

Знак: ˄ или &

В русском языке конъюнкции соответствуют союзы: «и», «а», «но», «да», «хотя», «который», «зато», «однако», «при этом» и т.п.

 

Суждение «Она любит яблочный сок и зелёный чай» является конъюнкцией (связью) двух простых суждений: «она любит яблочный сок» и «она любит зелёный чай».

Запись этого суждения с помощью логических связок будет выглядеть: а ˄ bилиа & b

2. ДИЗЪЮНКЦИЯ (от лат. disjunctio – разобщение).

Знак: ˅

В русском языке конъюнкции соответствуют союзы: «или», «либо», «то ли… то ли».

 

Суждение «Мы пойдём в кино или в парк» является дизъюнкцией двух простых суждений: «мы пойдём в кино» или «мы пойдём в парк». Данная связка не является строгой, то есть не предполагает только один выбор, так как мы можем пойти и в кино, и погулять в парке.

Запись этого суждения с помощью логических связок будет выглядеть: а ˅ b

 

СТРОГАЯ ДИЗЪЮНКЦИЯ

Знак: .

Союз «или» может употребляться в строгом смысле – когда члены дизъюнкции исключают друг друга.

 

Суждение «Автор «Войны и мира» то ли Толстой, то ли Достоевский» является строгой дизъюнкцией

Запись этого суждения с помощью логических связок будет выглядеть:

 

4. ИМПЛИКАЦИЯ (от лат. implico – тесно связываю)

Знак: → .

В языке аналоги этой связки союзы: «если…, то»; «когда…, тогда»; «коль скоро…, то» и т.п.

Обычно с помощью импликации выражаются причинно-следственные отношения типа: «Если выглянет Солнце, то станет тепло». a → b.Первый элемент импликации называется основанием (антецедентом), второй – следствием (консеквентом).

 

5. ЭКВИВАЛЕНЦИЯ (от позднелат. aequivalens – равнозначный; равноценный)

Знак: ↔ или ≡ .

В языке аналоги этой связки союзы: «если и только если»; «тогда и только тогда, когда…»; «лишь при условии, что…, то».

 

Суждение: «Только тогда ребёнок получит конфету, когда доест весь суп» является эквиваленцией.

Запись этого суждения с помощью логической связки будет выглядеть: a ↔ bилиa ≡ b

 

6. ОТРИЦАНИЕ

Знак: ~ или . ставятся перед суждением ~а или а ; или черта, которая ставится над суждением

В языке отрицание выражается союзами и словами: «не», «неверно» и т.п.

Суждение: «Не заводится машина» записывается как ~а

Суждение: «Любит или не любит» содержит строгую дизъюнкцию и отрицание.

Упражнения: Запишите суждения в виде логической формы с помощью логических связок.

 

1. Он в кафе закажет чай или мороженое.	a ˅ b
2. Преступление может быть умышленным или совершённым по неосторожности.	a b
3. Если число делится на два без остатка, то оно чётное.	a → b
4. Простое число больше единицы и имеет только два натуральных делителя.	а ˄ b
5. «Пять» больше единицы, но не простое число.	а ˄ ~b

 

Самопроверка:Запишите суждения в виде логической формы с помощью логических связок

Для самопроверки выделите столбец «формула» и измените цвет шрифта

Суждение	Формула
1. Когда придёт весна, то станет тепло и растает весь снег.	a → (b ˄ с)
2. Если число больше единицы и имеет только два натуральных делителя, то оно является простым.	(а ˄ b) → c
3. студент получит зачёт-автомат по логике, только если он будет посещать занятия и правильно выполнит все задания.	a ↔ (b ˄ с)
4. Если болезнь запущена, то её трудно излечить. Однако, если болезнь не запущена, то её трудно распознать, но её не трудно излечить.	(а → b) ˄ ~a → (c ˄ ~b)

ТАБЛИЦЫ ИСТИННОСТИ

 

Значение истинности сложных суждений определяется с помощью таблиц истинности, где буквы a, b, c– переменные, обозначающие простые суждения; буква «и» обозначает истину, а «л» — ложь.

 

а	b	а ˄ b	а ˅ b	а b	a → b	a ↔ b	~а	~b
и	и	и	и	л	и	и	л	л
и	л	л	и	и	л	л	л	и
л	и	л	и	и	и	л	и	л
л	л	л	л	л	и	и	и	и

 

Также возможно обозначать истину нулём «1», а ложь единицей «0».

 

а	b	а ˄ b	а ˅ b	а b	a → b	a ↔ b	~а	~b

 

1. КОНЪЮНКЦИЯ а ˄ bилиа & b

 

Конъюнкция будет истинна в том и только в том случае, если суждения а и b оба истинны.

2. ДИЗЪЮНКЦИЯ а ˅ b

 

Сложное суждение истинно, если истинно хотя бы одно из составляющих его простых суждений, и ложно, если оба простых суждения ложны.

СТРОГАЯ ДИЗЪЮНКЦИЯ

 

Сложное суждение истинно, если истинно лишь одно из составляющих его простых суждений, так как элементы сложной дизъюнкции исключают друг друга.

 

4. ИМПЛИКАЦИЯ a → b

 

Сложное суждение, соединённое импликацией, ложно только в одном случае: если основание (первое суждение) истинно, а следствие (второе суждение) ложно.

 

5. ЭКВИВАЛЕНЦИЯ a ↔ bилиa ≡ b

Сложное суждение, соединённое эквиваленцией, истинно только в тех случаях, когда составляющие его простыt суждения, либо оба истинны, либо оба ложны.

6. ОТРИЦАНИЕ ~аили аили ~b; b;

Если а истинно, то его отрицание ложно. Если а ложно, то не-а (~а) – истинно.

Если b истинно, то его отрицание ложно. Если b ложно, то не-b (~b) – истинно.

 

Если отрицание стоит внутри суждения перед связкой «есть», то мы имеем дело с простым отрицательным суждением типа «Черепахи не летают». Если же отрицание присоединяется к суждению снаружи – «Неверно, что черепахи летают», то мы имеем дело с логической связкой, преобразующей простое суждение в сложное.

Если знак отрицания стоит непосредственно перед а или b, то есть ~а; ~b,то отрицание применяется только к одному суждению.

Если знак отрицания стоит перед скобкой ~(a → b), то отрицанию будет подвержена операция, указанная в скобках. В данном примере, ̶ это отрицание импликации. Сначала выполняется импликация, затем результат подвергается отрицанию.

Выполнимата формула, которая может принимать по крайней мере одно значение «истина».

Тождественно-истинная формулата, которая при любых комбинациях значений для входящих в неё переменных принимают значение «истина» (иначе она называется законом логики).

Тождественно-ложная формула та, которая принимает только значение «ложь» (иначе ‒ противоречие).

!!! Следует помнить, что логику интересует не содержание, а исключительно форма мысли!

Устанавливать истинность сложных суждений в логике, опираясь на здравый смысл или жизненный опыт, или обращение к действительности, ̶ неправильно!

Формально-логические связки не в состоянии учитывать многих смысловых оттенков естественного языка. Значения истинности некоторых сложных суждений достаточно близки к здравому смыслу, но другие могут показаться странными. Поэтому то, то с точки зрения содержания может выглядеть непривычно, с точки зрения формы будет являться правильным.

СОСТАВЛЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ

 

Чтобы проверить сложное суждение с помощью таблицы истинности, необходимо грамотно её составить.

Например, нужно проверить суждение: «Если пойдёт дождь, то дорога будет мокрая».

 

1. Определим все простые суждения, составляющие данное сложное высказывание и узнаем количество переменных n :

а – пойдёт дождь; b – дорога будет мокрая

 

Получилось две переменных (а, b), соединённых союзом «если, то»

 

2. Количество строк (k) в таблице определяется по формуле: k = 2ⁿ , где n – количество переменных (то есть количество простых суждений, составляющих сложное).

 

В данном примере k = 2² = 4 Значит будет четыре строчки в таблице.

 

3. Количество столбцов в таблице будет зависеть от количества операций (логических связок) в сложном суждении.

Сначала в первых столбцах распределяются все возможные значения истины и лжи для переменных.

а	b

 

В данном примере две переменные, следовательно, четыре строки.

 

 

а	b
	и
	л
	и
	л

В самом правом столбце (b) чередуют «и» и «л» по одному, начиная всегда с «истины»

 

Во втором справа столбце (а) чередуют подряд два значения «и» и два значения «л», начиная всегда с «истины».

а	b
и	и
и	л
л	и
л	л

 

Затем направо выписывают логические формы всех сложных суждений, входящих в рассматриваемое суждение. В данном примере указана одна логическая связка «если, то» – импликация.

 

а	b	a → b
и	и
и	л
л	и
л	л

 

Осталось определить значения истинности для импликации. Сложное суждение, соединённое импликацией, ложно только в одном случае: если основание (первое суждение) истинно, а следствие (второе суждение) ложно.

а	b	a → b
и	и	и
и	л	л
л	и	и
л	л	и

 

 

1. Дождь пошёл, дорога мокрая. а – истина; b – истина. Следовательно, если а, то b (a → b) – истина

2. Дождь пошёл, но дорога не стала мокрая. а – истина; b – ложь. Следовательно, если а, то b (a → b) – ложно. Невозможно, чтобы причина была, а следствие не наступило.

3. Дождь не пошёл, но дорога мокрая а – ложь; b – истина. Следовательно, a → b–истина. Дорога может быть мокрой и по другой причине.

4. Дождь не пошёл и дорога не намокла. а – ложь; b – ложь. Следовательно, a → b– истина.

Если сложное суждение составлено из трёх простых, то есть состоит из трёх переменных (а, b, c), то таблица истинности, включающая все возможные комбинации истинности или ложности её переменных, будет состоять из 2³ = 8 строк.

Алгоритм распределения значений «и» и «л» для трёх переменных таков:

 

а	b	с		Начинаем распределять значения с крайнего правого столбца (с) и распределяем значения «и» и «л» попеременно, начиная с «истины».   Затем распределяем значения во втором столбце справа (b), распределяем значения «и» и «л», чередуя подряд по два значения «и», затем по два значения «л»; затем опять два значения «и» и два значения «л».   В крайнем левом столбце (а) чередуем «и» и «л», чередуя подряд сначала четыре значения «и» и затем четыре значения «л»
и	и	и
и	и	л
и	л	и
и	л	л
л	и	и
л	и	л
л	л	и
л	л	л

Упражнения:

1. Запишите высказывание в виде логической формы, используя логические связки: «Если ты сможешь доказать мне свои добрые намерения, то я поверю тебе или же мне придётся вызвать полицию и обвинить тебя в лжесвидетельстве» (Г. Каттнер. Источник миров).

 

Выпишем все простые суждения, входящие в состав сложного высказывания:

а – ты сможешь доказать мне свои добрые намерения

b – я поверю тебе

с – мне придётся вызвать полицию

d – (мне придётся) обвинить тебя в лжесвидетельствовании.

Определим связки между элементами: если а, то b или с и d

 

(a → b) ˅ (c ˄ d)

---

Рекомендуемые страницы:

Воспользуйтесь поиском по сайту:

megalektsii.ru

1.3 Построение таблицы истинности для логического выражения

При составлении таблицы истинности для логического выражения необходимо:

1. Выяснить количество строк в таблице (вычисляется как 2ⁿ, где n – количество переменных).

2. Выяснить количество столбцов (определяется как количество переменных + количество логических операций).

3. Установить последовательность выполнения логических операций.

4. Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных.

5. Заполнить таблицу истинности по столбцам.

Контрольный пример. Построить таблицу истинности для выражения F = (A V B) & (¬A V ¬B).

Количество строк в таблице определяется как 2² (2 переменных) + 1 (заголовок таблицы) = 5.

Количество столбцов – как 2 логические переменные (A, B) + 5 логических операций (&, V, ¬, →, ↔).

Расставим порядок выполнения операций:

(A V B) & (¬A V ¬B).

Построим таблицу истинности для данного логического выражения (таблица 5).

Таблица 5 – Таблица истинности для логического выражения

A	B	A V B	¬A	¬B	(¬A V ¬B	(A V B) & (¬A V ¬B)
0	0	0	1	1	1	0
0	1	1	1	0	1	1
1	0	1	0	1	1	1
1	1	1	0	0	0	0

Контрольный пример. Построить таблицу истинности для логического выражения X V Y & ¬Z.

Количество строк = 2³+ 1 = 9.

Количество столбцов = 3 логические переменные + 3 логических операций = 6.

Укажем порядок действий:

3 2 1

X V Y & ¬Z.

Нарисуем и заполним таблицу 6:

Таблица 6 – Таблица истинности для логического выражения

X	Y	Z	¬Z	Y & ¬Z	X V Y & ¬Z
0	0	0	1	0	0
0	0	1	0	0	0
0	1	0	1	1	1
0	1	1	0	0	0
1	0	0	1	0	1
1	0	1	0	0	1
1	1	0	1	1	1
1	1	1	0	0	1

1.4 Построение логических схем

С точки зрения логики электрический ток либо течет, либо не течет; электрический импульс есть или нет; электрическое напряжение есть или нет. Рассмотрим электрические контактные схемы, реализующие логические операции (схемы 1 – 3). На схемах 1 – 3 контакты обозначены латинскими буквами A и B.

A

A

A

B

B

  

Схема 1 – Конъюнкция Схема 2 – Дизъюнкция Схема 3 – Инверсия

(автоматический ключ)

Схема 4 – Конъюнктор Схема 5 – Дизъюнктор Схема 6 – Инвертор

Цепь на схеме 1 с последовательным соединением контактов соответствует логической операции «И» и представляется конъюнктором (схема 4). Цепь на схеме 2 с параллельным соединением контактов соответствует логической операции «ИЛИ» и представляется дизъюнктором (схема 5). Цепь на схеме 3 (электромагнитное реле) соответствует логической операции «НЕ» и представляется инвертором (схема 6).

Именно такие электронные схемы нашли свое применение в качестве элементной базы ЭВМ. Элементы, реализующие базовые логические операции, назвали базовыми логическими элементами или вентилями и характеризуются они не состоянием контактов, а наличием сигналов на входе и выходе элемента. Их названия и условные обозначения являются стандартными и используются при составлении и описании логических схем компьютера.

Логические схемы необходимо строить из минимально возможного количества элементов, что, в свою очередь, обеспечивает большую скорость работы и увеличивает надежность устройства.

Правило построения логических схем:

1. Определить число логических переменных.

2. Определить количество базовых логических операций и их порядок.

3. Изобразить для каждой логической операции соответствующий ей вентиль.

4. Соединить вентили в порядке выполнения логических операций.

Контрольный пример. Пусть X = Истина (1), Y = Ложь (0). Составьте логическую схему для следующего логического выражения: F = X V Y & X.

1

2

1

) Две переменные –X и Y.

2) Две логические операции: X V Y & X.

3) Строим схему (рисунок 3).

4) Ответ: 1 V 0 & 1 = 1.

X

Y

Рисунок 3 – Логическая схема для логического выражения F = X V Y & X

studfiles.net

Логические выражения и таблица истинности в примерах решения задач

Примеры решения задач “Логические выражения и таблица истинности”

 №1.

Докажите, что А <=> В равносильно (A\/ ¬B) /\ (¬A\/ B)

 Для доказательства равносильности двух высказываний достаточно построить таблицу истинности для высказывания (A\/ ) /\ (\/ B) и сравнить ее с таблицей истинности эквивалентности:

А	В	¬B	A\/¬B	¬A	¬AVB	(A\/¬B) /\ (¬A \/B)
0	0	1	1	1	1	1
0	1	0	0	1	1	0
1	0	1	1	0	0	0
1	1	0	1	0	1	1

Последние столбцы этих функций совпадают, значит, они равносильны. ЧТД.

 

№2.

Укажите, какое логическое выражение равносильно выражению 

A /\ ¬ (¬B \/ C)

   1) ¬A \/ ¬B \/ ¬C

   2) A /\ ¬B /\ ¬C  

   3) A /\ B /\ ¬C 

   4) A /\ ¬B /\ C

Ответ:  3

№3.

Постройте таблицу истинности для логического выражения:

1)A=>B<=> ¬А \/  B 

Ответ:

А	В	A=>B	¬А	A → B<=> ¬А	A → B<=> ¬А \/  B
0	0	1	1	1	1
0	1	1	0	0	1
1	0	0	0	1	1
1	1	1	0	0	1

2)F=A<=>B<=>(¬А \/  B) /\ (¬B\/  А)

Ответ:

 

 

 

 

 

№4.

Определите истинность следующего высказывания: «За окном светит солнце, и нет дождя».

Решение:

Нам дано сложное составное высказывание. Выделим из него простые высказывания:

А = «За окном светит солнце»

В = «За окном дождь»

 Составим логическую функцию, соответствующую данному высказыванию.

F(A, B) = A /\ ¬B

построим таблицу истинности для данной логической функции.

A	B	¬B	A /\ ¬B
0	0	1	0
0	1	0	0
1	0	1	1
1	1	0	0

 Ответ: логическое выражение принимает значение истина только при наборе F(1,0)=1.Следовательно, данное нам высказывание истинно только тогда, когда первое простое высказывание истинно, а второе ложно.

 

№5.

Определите истинность следующего высказывания: «Гости смеялись, шутили и не расходились по домам».

Решение:

Выделим из данного сложного высказывания простые высказывания:

А = «Гости смеялись»

В = «Гости шутили»

С = «Гости расходились по домам»

Составим логическую функцию, соответствующую данному высказыванию.

F(A, B, С) = A/\ B /\¬C

Построим таблицу истинности для данной логической функции.

 

A	B	C	¬C	A /\ B/\¬C
0	0	0	1	0
0	0	1	0	0
0	1	0	1	0
0	1	1	0	0
1	0	0	1	0
1	0	1	0	0
1	1	0	1	1
1	1	1	0	0

Ответ: логическое выражение принимает значение истина только при наборе F(1,1,0)=1.Следовательно, данное нам высказывание истинно только тогда, когда первое и второе простые высказывания истинны, а второе ложно.

 

№6.

На языке алгебры логики составьте истинное тождество, соответствующее заданному условию задачи:

Школьника, Миша, остававшийся в классе на перемене, был вызван к директору по поводу разбитого в это время окна в кабинете. На вопрос директора о том, кто это сделал, мальчик ответили следующее: «Я не бил окно, и Коля тоже…»

Известно, что он либо сказал чистую правду, либо в одной части заявления соврал, а другое его высказывание истинно, либо оба факта исказил.

Решение:

Пусть

А = «Окно разбил Миша»

В = «Окно разбил Коля»

Если Миша сказал чистую правду, то¬А /\ ¬В = 1.

Если в одной части заявления Миша соврал, а другое его высказывание истинно, то (¬А /\ В) \/ (А /\¬В) = 1

Если Миша оба факта исказил, то А /\ В = 1.

Ответ:

Истинное тождество, соответствующее условию задачи будет выглядеть так: ¬А /\ ¬В  \/¬А /\ В \/А /\ ¬ В \/ А /\ В = 1.

mir-logiki.ru

Построение таблицы истинности online | Полезная информация

Что такое таблица истинности?

Таблица, описывающая логическую функцию, называется таблицей истинности.

В таблице истинности перечислены все возможные наборы входных переменных.

В последнем столбце таблицы истинности выводится число, соответствующее значению функции, по которой строилась данная таблица истинности.

 

Рассмотрим пример:

Допустим, у нас есть две булевых переменных x₁ и x₂. От этих переменных зависит логическая функция f(x₁,x₂)

Для примера возьмем f(x₁,x₂)=x₁∧x₂∨x₁.

Так как x₁, x₂ булевы, то они принимают значния 0 или 1 (Истина или Ложь, True или False, сокращенно можно писать T или F).

Все возможные варианты входных переменных x₁ и x₂ можно представить в таблице:

x1	x2	f(x1,x2)
0	0
0	1
1	0
1	1

 

Подставим значения переменных x₁ и x₂ в каждой строчке в функцию f(x₁,x₂).

f(0,0)= 0∧0∨0=0

f(0,1)= 0∧1∨0=0

f(1,0)= 1∧0∨1=1

f(1,1)= 1∧1∨1=1

 

Получившиеся значения запишем в последний столбец нашей таблицы:

x1	x2	f(x1,x2)
0	0	0
0	1	0
1	0	1
1	1	1

 

Мы получили таблицу истинности функции f(x₁,x₂)=x₁∧x₂∨x₁.

 

На нашем сайте вы можете построить таблицу истинности online.

Для этого вам всего лишь нужно ввести функцию в поле и нажать вычислить.

 

---

 

Таблицы истинности основных булевых функций:

 

Унарные функции:

Бинарные функции

spisok-literaturi.ru