Разработка урока по теме «Тригонометрические функции. Формулы тригонометрии». 10-й класс
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (2,6 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
- Проверка знания свойств тригонометрических функций, умения применять их при выполнении упражнений.
- Проверка знания тригонометрических формул, умения применять их при преобразовании тригонометрических выражений.
- Проверка знания формул приведения, уровня владения этими формулами.
- Развитие логического мышления, внимания, познавательного интереса, интуиции, способности к творчеству.
- Воспитания серьезного отношения к учебному труду.
Формы работы: фронтальная, индивидуальная.
Оснащение урока:
- Мультимедийный проектор;
- Экран;
- Маркерная доска;
- Индивидуальные карточки с заданиями для каждого ученика с заданиями повышенного уровня сложности.
Продолжительность урока: 2 урока
Предварительная подготовка к уроку:
- Создание презентации
- Изготовление индивидуальных карточек с заданиями повышенного уровня сложности.
Ход урока
Ребята, сегодня у нас итоговый, зачетный урок по теме “Тригонометрические функции и их свойства. Основные тригонометрические формулы”. Мы с вами хорошо поработали над данной темой, изучили много нового и интересного. Я уверена, что сегодня покажите хорошие и отличные знания. (Слайд 1)
Цели урока: (Слайд 2)
- Закрепление материала по теме “Тригонометрические функции. Формулы тригонометрии”.
- Проверка знаний в форме смотра знаний.
Девиз урока: (Слайд 3)
“Не бойтесь формул!
Учитесь владеть этим инструментом
Человеческого гения!
В формулах заключено величие
и могущество
Человеческого разума….”
Марков А.А
Слово “тригонометрия” известно с давних времен, оно было известно еще до нашей эры. (Слайд 4)
Зарождение тригонометрии относится к глубокой древности. Само название “тригонометрия” греческого происхождения, обозначающее “измерение треугольников”.
Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх (Hipparchos) (около 180—190 до н. э., Никея, — 125 до н. э., Родос), древнегреческий учёный
Гиппарх является автором первых тригонометрических таблиц и одним из основоположников астрономии.
Наш урок состоит из двух частей. В первой части нашей работы вы покажите знания основного, обязательного уровня сложности. Вам будут предложены устные упражнения и 8 индивидуальных заданий. Во второй части урока вам будут предложены задания повышенного уровня сложности.
Учет ваших устных ответов будут вести мои помощники- консультанты: учащиеся 11 класса. В конце урока мы оценим устную работу каждого ученика. Этот результат повлияет на общий итог работы каждого ученика.
Итак, начинаем. Я желаю вам успеха и удачи.
Первая часть урока
1.
- Дайте определение синуса
- Определение косинуса
- Какая функция называется тангенсом?
- Определение котангенса
- Какой угол поворота называют положительным?
- Какой угол поворота называют отрицательным?
Значения синуса и косинуса
Значения тангенса и котангенса
Значения тригонометрических функций. (Слайд 4)
Какой четверти принадлежит угол: (Слайд 5)
Найти ошибки: (Слайд 6)
Определите четверть, если: (Слайд 7)
Индивидуальное задание №1. Определите знак выражения. На выполнение задания отводится 3 минуты. За каждое верно выполненное задание вы можете получить 1 балл. (Слайд 8)
2.
Еще с 8 класса вы знаете значения синуса, косинуса, тангенса углов 30°, 45° и 60°. Сейчас ваши знания значительно расширились. Как таблицу умножения, вы должны знать значения тригонометрических функций углов: 0°, 30°, 45°, 60°, 90°, 180°, 270° и 360°. Сейчас мы и проверим знание тригонометрической таблицы.
Знание табличных значений: (Слайд 9)
Индивидуальное задание №2. Найдите значение выражения. (Слайд 10). На выполнение задания 3 минуты. За каждое верно выполненное задание – 1 балл.
Учитель проверяет выполнения задания№1. Все решено заранее. Результаты проверки выносятся на маркерную доску. Учащиеся сразу узнают свои результаты.
3.
- Какие тригонометрические функции являются четными?
- Какие тригонометрические функции являются нечетными?
Четность функций. (Слайд 11)
- Что называется радианом?
- Чему равен один радиан?
- Как радианы перевести в градусы?
- Как градусы перевести в радианы?
Индивидуальное задание №3. Перевести градусы в радианы, а радианы в градусы.
(Слайд 12).
На выполнения задания отводится 3 минуты. За каждое верно выполненное задание – 0,5 балла.
Учитель проверяет задание №2. Результаты – на маркерной доске.
4.
- Я вам называю углы в градусах, вы их переводите в радианы: 90°, 180°, 30°, 270°,45°, 360°, 60°.
- А сейчас обратная работа: надо перевести углы в градусы: /2, , /4, 2, /6, 3/2, /3
Индивидуальное задание № 4. Вычислите. (Слайд 13)
Учитель проверяет выполнения задания №3, выставляет результаты на маркерной доске.
5.
- Ребята, назовите основные тригонометрические формулы.
- Назовите основное тригонометрическое тождество.
- Как вы считаете, почему это тождество называется основным? Убедите меня в этом!
Индивидуальное задание №5. Основные тригонометрические формулы.(Слайд 14)
На выполнение задания отводится 5 минут. За каждое верно выполненное задание вы можете заработать 2 балла.
Учитель проверяет выполнение предыдущего задания. Результаты выполнения заносятся в таблицу на маркерной доске.
6.
Тригонометрические тождества позволяют нам легко и быстро упрощать тригонометрические выражения. Предлагаю вам следующее устное задание:
- Упростите выражение: (Слайд 15)
Индивидуальное задание №6. Упростите выражения: (Слайд 16)
Учитель проверяет выполнения задания №5. Результаты- на маркерной доске.
7.
- Какие формулы позволяют нам переходить от больших углом к острым углам первой четверти?
- Для каких углов название исходной функции не изменяется?
- Для каких углов название исходной функции изменяется?
- По какой функции мы определяем знак функции в правой части равенства?
- Замените функцией угла ?. (Слайд 17)
Индивидуальное задание №7. Формулы приведения. (Слайд 18). На выполнение задания отводится 4 минуты. За каждое верно выполненное задание вы получите 1 балл.
На маркерной доске выставляются результаты выполнения предыдущего задания.
К доске приглашаю двоих учеников: записать формулы двойного угла, другой формулы сложения.
Пока ребята записывают формулы, остальные отвечают на мои вопросы: Вычислите, использую формулы тригонометрии. (Слайд 19)
Индивидуальное задание №8: В виде тестов. На листе указано, сколько получите баллов за каждое задание. В вашем распоряжении 5 минут.
Вторая часть урока
Учащимся предлагаются задания повышенного уровня сложности. Каждый ученик получает карточку, на которой задания трех уровней сложности: на 3, 4 и 5 баллов. Какие задания выполнять и в каком порядке решает каждый индивидуально. Ученики стремятся набрать как можно больше баллов.
Учитель сразу проверяет выполнение заданий, которые решены заранее. Все баллы заносятся в таблицу на маркерной доске. Одновременно заносятся результаты выполнения индивидуального задания №8.
Консультанты подводят итоги подсчета устных ответов учащихся. Результаты заносятся в специальную графу в таблице учета работы каждого ученика.
Таблица учета работы каждого ученика
| Фамилия, имя | Устные ответы | № 1 | № 2 | № 3 | № 4 | № 5 | №6 | №7 | Задания повышенного уровня сложности. | Итог |
Содержание карточки с заданиями повышенного уровня сложности:
- Докажите тождество: ctg2a — cos2a = ctg2acos2a (3 балла)
- sina + cos?a= Найти: sinacosa (4 балла)
- sinacosa = Найти: sina + cosa (4 балла)
- sina = — , ctga>0 Найти: (5 баллов)
- cosa = — , ctga<0 Найти: (5 баллов)
- tga = Найти: (4 балла)
- сtga = Найти: (4 балла)
- Вычислите: tg1°tg3°tg5°……..tg85°tg87°tg89° (5 баллов)
- Вычислите: ctg2°ctg4°ctg6°…….ctg84°ctg86°ctg88° (5 баллов)
- ctga = Найти: sina, cosa (3 балла)
- Упростите: + tga (3 балла)
- Вычислите: ctgsintgcos(3 балла)
Учитель подводит результаты работы на уроке каждого ученика, анализирует, делает выводы.
Спасибо за урок! (Слайд 20)
xn--i1abbnckbmcl9fb.xn--p1ai
Урок по теме «Тригонометрические формулы». 10-й класс
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (1,2 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока. (Cлайд 1-3)
Дидактические:
- обобщить и систематизировать знания учащихся по теме;
- продолжить формирование умений и навыков по применению тригонометрических формул;
- проконтролировать степень усвоения знаний, умений и навыков по теме.
Развивающие:
Воспитательные:
- продолжить формирование навыков эстетического оформления записей в тетради;
- приучать к умению общаться и выслушивать других;
- воспитание сознательной дисциплины;
- развитие творческой самостоятельности и инициативы;
- стимулировать мотивацию и интерес к изучению тригонометрии.
Задачи урока:
- повторить определение синуса, косинуса, тангенса, котангенса числа ;
- повторить формулы приведения, формулы двойного угла, формулы сложения;
- повторить основное тригонометрическое тождество и формулы, выражающие связь между тангенсом и косинусом, между котангенсом и синусом.
- научить применять полученные знания при решении задач.
Тип урока: урок обобщения и систематизации знаний.
Оборудование: учебники, компьютер, мультимедийный проектор.
Ход урока: (слайд 4)
- Организационный момент, вступительная беседа.
- Блиц-опрос.
- Закрепление знаний и умений.
- Самостоятельная работа (тест) .
- Проверка самостоятельной работы.
- Это интересно.
- Подведение итогов урока.
- Домашнее задание.
1. Организационный момент.
Для успешного решения задач по тригонометрии необходимо уверенное владение многочисленными формулами. Тригонометрические формулы надо помнить. Но это не значит, что их надо заучивать все наизусть, главное запоминать не сами формулы, а алгоритмы их вывода. Любую тригонометрическую формулу можно довольно быстро получить, если твердо знать определения и основные свойства функций sin, cos, tg, ctg,соотношение sin2+ cos2=1 и формулы сложения. Каждый раз выводить нужную формулу, например, для преобразования тригонометрического уравнения время уйдет достаточно много. Поэтому круг формул, которые необходимо знать, должен быть достаточно широким.
Разучивание тригонометрических формул в школе не для того чтобы вы всю оставшуюся жизнь вычисляли синусы и косинусы, а для того чтобы ваш мозг приобрел способность работать. “Дороги не те знания, которые отлагаются в мозгу, как жир; дороги те, которые превращаются в умственные мышцы” писал Г. Спесер, английский философ и социолог.
Так вот, давайте сегодня на уроке работать активно, внимательно, будем поглощать знания с большим желанием, ведь они вам пригодятся.
Тема нашего урока: “Тригонометрические формулы”- последний урок по данной теме, следующий – контрольная работа.
2. Блиц-опрос (по формулам в форме математического диктанта). (Слайд 5-7)
Проверка проводится на уроке с выставлением оценок. (Приложение 1)
“5” — 12; “4” — 10 – 11; “3” — 7 – 9; “2” — 0 – 6
3. Закрепление знаний и умений. (Слайд 8-10)
4. Самостоятельная работа обучающего характера в форме теста, с последующей проверкой на уроке. (Слайд 11)
5. Проверка самостоятельной работы (проверка теста проводится на уроке, оценки выставляются выборочно). (Слайд 12)
6. Это интересно. (Слайд 13-17)
Зарождение тригонометрии относится к глубокой древности. Еще задолго до новой эры вавилонские ученые умели предсказывать солнечные и лунные затмения. Это позволяет сделать вывод о том, что им были известны простейшие сведения из тригонометрии. Само название “тригонометрия” греческого происхождения, обозначающее “измерение треугольников”. Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх является автором первых тригонометрических таблиц. [5]
Тригонометрия в ладони
Значения синусов и косинусов углов “находятся” на вашей ладони. Протяните руку и разведите как можно сильнее пальцы, так как показано на слайде. Сейчас мы измерим углы между вашими пальцами. (Возьмем два прямоугольных треугольника с углами 30°и 45° и приложим вершину нужного угла к бугру Луны на ладони. Бугор Луны находится на пересечении продолжений мизинца и большого пальца. Одну сторону угла совмещаем с мизинцем, а другую сторону — с одним из остальных пальцев)
Смотрите, я прикладываю угол в 30°; оказывается, это угол
— между мизинцем и безымянным пальцем;
— между мизинцем и средним пальцем — 45°;
— между мизинцем и указательным пальцем — 60°;
— между мизинцем и большим пальцем — 90°;
И это у всех людей без исключения.
Если пальцы считать лучами, исходящими из бугра Луны на ладони, то, если совместить (сжать) пальцы с мизинцем, угол между лучами будет равен 0°, то есть можно считать, что направление мизинца соответствует началу отсчета углов, то есть 0°, а поэтому введем нумерацию пальцев:
№0 — Мизинец
№1 — Безымянный
№2 — Средний
№3 -Указательный
№4 — Большой
| №0 Мизинец 0° №1 Безымянный 30° №2 Средний 45° №3 Указательный 60° №4 Большой 90° n — номер пальца |
Значения синуса и косинуса угла по “ладони” приведено в таблице.
Примечание. Для определения косинуса угла отсчет пальцев происходит от большого пальца руки. [6]
Значения синуса
Значения косинуса
7. Итоги урока.
8. Домашнее задание. (Cлайд 18)
“Проверь себя”, стр. 166
Спасибо, урок окончен! (Cлайд 19)
Используемая литература
- Алимов Ш.А., Колягин Ю.М. и др. Алгебра и начала анализа: учеб. Для общеобразовательных учреждений. – 16-е изд. – М.: Просвещение, 2010.
- Макеева А.В. Карточки по тригонометрии. 10-11 классы: Дидактический материал для учителя — ОАО “Издательство “Лицей”, Саратов, 2002.
- Изучение алгебры и начал анализа 10-11: Методические рекомендации к учеб.; кн. для учителя / Н.Е.Федорова, М.В. Ткачева. – М.: Просвещение, 2007.
- Дидактические материалы по алгебре и началам анализа для 10 класс/М.И. Шабунин, М.В. Ткачева и др. -2-е изд. — М.: Просвещение, 2007.
- Решетников Н.Н. Материалы курса “Тригонометрия в школе” лекции 1-8. – М.: Педагогический университет “Первое сентября”, 2006
- Газета “Первое сентября. Математика”. — №6, 2004.
- Сборники заданий к ЕГЭ 2002, 2011.
Электронная поддержка урока:
- Авторская презентация “Тригонометрические формулы”.
- Авторский тест “Тригонометрические формулы”.
Приложение
xn--i1abbnckbmcl9fb.xn--p1ai
Формулы по тригонометрии от репетитора по математике — Колпаков Александр Николаевич
Справочные материалы по тригонометрии. Формулы. Определения и свойства.
Комплект предназначен для слабых и средних по уровню учащихся, для репетиторов по математике и школьных преподавателей. Он специально адаптирован мной для слабых и средних по уровню учеников. В материалах применяются, на мой взгляд, лучшие приемы уменьшения нагрузки на память и упрощения работы с большими объемами информации. Их содержание дает репетитору по математике возможность преподнести тригонометрию в удобной для работы и для запоминания форме. В помощь репетитору по математике, работающему со слабыми учащимися, я специально исключил из списка формул те, которые не входят в основную программу, а также сложные формулы и различные формулы-следствия.
Определение тригонометрических функций: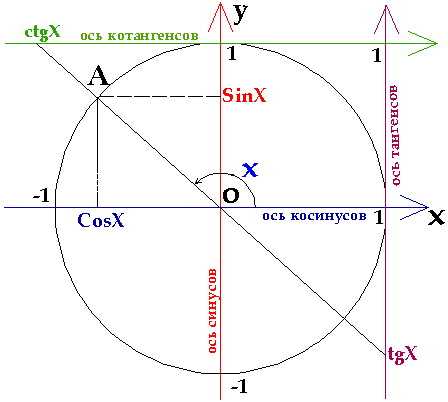
Определение: синусом угла поворота на называется ордината точки, изображающей данный угол.
Определение: косинусом угла поворота называется абсцисса точки, изображающей данный угол.
Определение: тангенсом угла поворота называется отношение ординаты точки, изображающей угол, к ее абсциссе.
Определение: котангенсом угла поворота называется отношение абсциссы точки, изображающей данный угол к ее ординате.
Основные тригонометрические свойства:
(основное тригонометрическое тождество)
Четность и нечетность тригонометрических функций:
нечетная
четная
нечетная
нечетная
примечание репетитора по математике:
функция незывается нечетной, если противоположным значениям аргумента соответствуют противоположные значения функции.
Функция называется четной, если противоположным значениям аргумента соответствуют равные значения функции.
Знаки тригонометрических функций
Таблица значений тригонометрических функций
Щелкните на таблице для ее увеличения.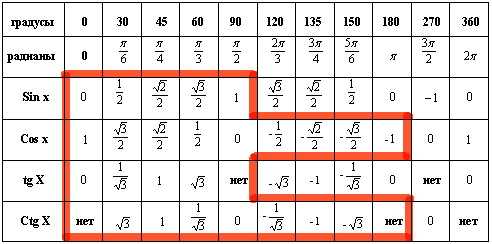
Прочтите о том, как репетитору по математике заучить с учеником таблицу значений.
Формулы приведения:
Чтобы написать правую часть формул приведения нужно:
1) найти четверть в которой лежит угол в скобках, считая X острым углом.
2) поставить знак данной функции в данной четверти.
3) сменить или сохранить функцию.
При или функция меняется (, )
При или функция не меняется.
Формулы сложения углов:
Формулы двойного угла:
Формулы сложения тригонометрических функций:
Простейшие тригонометрические уравнения:
1) Уравнения вида
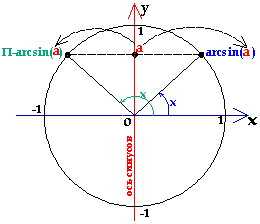 Уравнения вида ,
Уравнения вида ,
Частные формулы:
где
Общая формула:
,
где
Удобные случаи
2) Уравнения вида
 Уравнения вида ,
Уравнения вида ,
Частные формулы:
где
Общая формула:
,
где
Удобные случаи
1) Уравнения вида
 Уравнения вида
Уравнения вида
,
Частные формулы:
где
Общая формула:
,
где
Решение на круге.
1) Уравнения вида
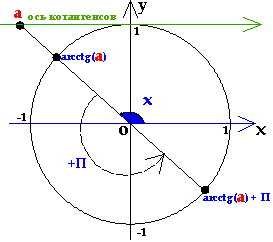 Уравнения вида
Уравнения вида
,
Частные формулы:
где
Общая формула:
,
где
Решение на круге.
Предлагаю репетиторам по математике использовать на своих занятиях материалы сайта в реальном времени. Часто во время занатия дети не выключают компьютер. Загрузите страничку с формулами и начинайте урок.
Вместо распечатывания формул на листочке дайте ученику ссылку на страницу или попросите сделать ее стартовой при входе в интернет. Это увеличит частоту появления формул перед глазами ученика и они быстрее запомнятся.
С уважением, Колпаков Александр Николаевич.
Репетитор по математике Москва.
Метки: Алгебра, Ученикам
ankolpakov.ru
| Функция | |||||||
| sin | cos | tg | ctg | ||||
| 15 | | | | | |||
| 18 | | | | | |||
| 36 | | | | | |||
| 54 | | | | | |||
| 72 | | | | | |||
| 75 | | | | | 0 | | |
| sin | 0 | | | 1 | 0 | –1 | |
| cos | 1 | | | 0 | –1 | 0 | |
| tg | 0 | | 1 | | — | 0 | — |
| ctg | — | | 1 | | 0 | — | 0 | Выражение искомой функции через |
| sin | cos | tg | сtg | ||||
| sin = | sin |
| | | |||
| cos = | | cos | | | |||
| tg = | | | tg | | |||
| сtg = | | | | сtg | Область значений | Знаки по четвертям | Четность – нечетность |
| | |||||||
| |sin t| 1 | sin(–t) = –sin t | Область значений | Знаки по четвертям | Четность – нечетность | |||
| | |||||||
| |cos t| 1 | cos(–t) = cos t | ||||||
| D(sin) = R | D(cos) = R | ||||||
| Область значений | |||||||
| E(sin) = [–1; 1] | E(cos) = [–1; 1] | ||||||
| Четность – нечетность | |||||||
| нечетная функция | четная функция | ||||||
| Периодичность | |||||||
| sin(x 2) = sin x | cos(x 2) = cos x | Область значений | Знаки по четвертям | Четность – нечетность | |||
| | |||||||
| tg t (–; +) | tg(–t) = –tg t | Область значений | Знаки по четвертям | Четность – нечетность | |||
| | | | | ||||
| ctg t (–; +) | ctg(–t) = –ctg t | ||||||
| Область значений | |||||||
| E(tg) = (–; +) | E(ctg) = (–; +) | ||||||
| Четность – нечетность | |||||||
| нечетная функция | нечетная функция | ||||||
| Периодичность | |||||||
| tg(x ) = tg x | ctg(x ) = ctg x | ||||||
doc4web.ru
Тригонометрия в таблицах
Разделы: Математика
Таблицы по тригонометрии
Основные тригонометрические тождества:
Тригонометрические функции суммы и разности двух аргументов:
Представление суммы одноименных тригонометрических функций в виде произведения:
Преобразование произведения тригонометрических функций в сумму:
Формулы двойных аргументов:
Выражение тригонометрических функций через тангенс половинного аргумента:
Формулы приведения («формулы лошади»): a - острый угол!!!
Вопросы лошадке:
1) функция меняется?
2) какой был знак и какой поставить в ответ?
Решение тригонометрических уравнений:
cos x=1 <=>
cos x=0 <=>
cos x= — 1 <=>
Формулы тройных аргументов:
Кроме того, необходимо знать:
Соотношения между тригонометрическими функциями одного и того же аргумента:
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Урок-игра «Тригонометрическая рулетка» в 10-м классе по теме «Основы тригонометрии»
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (2,3 МБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
- обобщение и систематизация знаний об основных тригонометрических понятиях;
- развитие логического мышления, алгоритмической культуры, развитие коммуникативных навыков;
- развитие познавательного интереса обучающихся, развитие навыков использования информационных технологий;
- воспитание самостоятельности и ответственности обучающихся.
Ход урока
1. Организационный момент.
Объяснение правил игры. (Слайд 1,2)
2. Актуализация опорных знаний.
Фронтальный опрос по основным понятиям.
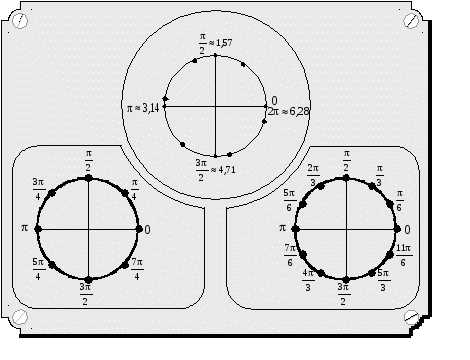
– Определение синуса, косинуса, тангенса и котангенса через координаты точки, полученной поворотом точки Р(1;0) на угол . (Слайд 3)
– Определение синуса, косинуса, тангенса и котангенса через соотношения между сторонами и углами прямоугольного треугольника. (Слайд 4)
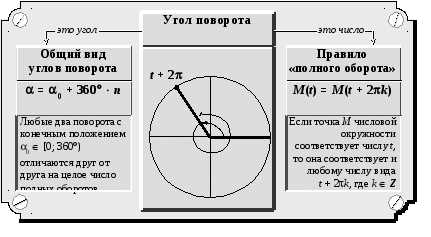
– Градусная и радианная мера углов. (Слайд 5)
– Таблица значений синуса, косинуса, тангенса и котангенса углов 30°, 45° и 60°. (Слайд №6)
– Знаки тригонометрических функций по четвертям. (Слайд №7)
– Зависимость между синусом, косинусом, тангенсом и котангенсом одного и того же аргумента (Слайд №8)
3. Устная работа на применение изученного материала.
– Выразить в радианной и градусной мере величины углов. (Слайд №9, 10)
1200, 1350, 2250, 3000, 72000.
-/2, -3, /18, -5/6, /36.
– Найдите координаты точек, полученных поворотом точки с координатами (1,0) на заданный угол. (Слайд №11)
Р90, Р180, Р270, Р-90, Р-180, Р-270.
– Сравните углы, выраженные в радианах. (Слайд №12)
=2 и =6,4; =3/2 и =4,7.
– Определите знак значения выражения. (Слайд №13)
sin1000 cos1000
cos1500 sin2500
tg1750 ctg2000
cos2500 sin3300
tg3500 ctg2100
tg1150 ctg2300
– Определите четверть в которой находится точка. (Слайд №14)
-, +, /2+, /2-, -, +, -/2, 3/2-.
– Найдите значение выражения. (Слайд №15)
3tg00+2cos900+3sin2700-3cos1800
sin1800+sin2700-ctg900+tg1800-cos900
tg-sin3/2+cos/2+sin
sin/2-cos3/2+cos-tg0
4sin cos25tg
– Может ли косинус и синус быть равным. (Слайд №16)
0,75; 5/3; -0,75; /2; р/3; -2.
4. Выполнение заданий на применение изученного материала.
– Решите уравнение. (Слайд №17)
1) cos0,5x=0 2) sin( х+7п)= 0 3) сos(5x+4п)=1 4) sin(+х)=-1
– Решение заданий типа В4 предлагаемых на ЕГЭ. (Слайд 18,19)
1. В равнобедренном треугольнике ABC с основанием AC боковая сторона AB равна 8, а cosA=/4. Найдите высоту, проведенную к основанию.
2. В треугольнике ABC угол C равен 90°, AB = 10, AB = 4. Найдите sinA.
– Решение заданий типа В8 предлагаемых на ЕГЭ (нахождение тангенса угла наклона). (Слайд №20,21)
Найдите тангенс угла наклона между прямой и положительным направлением оси Ох.
– Решение заданий типа В7 предлагаемых на ЕГЭ (нахождение значения тригонометрического выражения).
(Слайд №22)
- Найдите , если tg = -2,5.
- Найдите tg, если .
- Найдите 3 cos , если и
– Решение задач типа В10 предлагаемых на ЕГЭ прикладного содержания (нахождение наименьшего/наибольшего угла). (Слайд № 23,24,25)
1) Трактор тащит cани c cилой F=32кН, направленной под оcтрым углом к горизонту. Мощноcть (в киловаттах) трактора при cкороcти v=5м/c вычиcляетcя по формуле: N=Fvcos . При каком макcимальном угле (в градуcах) эта мощноcть будет не менее 80 кВт?
2) Мячик броcают под оcтрым углом к плоcкой горизонтальной поверхноcти земли. Раccтояние, которое пролетает мячик, вычиcляетcя по формуле L=V02/g sin2(м), где V0=11 м/c — начальная cкороcть мяча, а g — уcкорение cвободного падения (cчитайте g=10 м/c). При каком наименьшем значении угла (в градуcах) мяч перелетит реку шириной 6,05 м?
3) Катер должен переcечь реку шириной L=70 м и cо cкороcтью течения u=0,5 м/c так, чтобы причалить точно напротив меcта отправления. Он может двигатьcя c разными cкороcтями, при этом время в пути, измеряемое в cекундах, определяетcя выражением t=L/u ctg , где — оcтрый угол, задающий направление его движения (отcчитываетcя от берега). Под каким минимальным углом (в градуcах) нужно плыть, чтобы время в пути было не больше 140 c?
5. Тестовая работа. Учащиеся выполняют работу за компьютером.
– Проверка тестовой работы. Учащиеся меняются таблицами ответов и проверяют тестовую работу. (Слайд №27)
– Те, кто справился с работой быстрее, выполняют задания на карточках. Карточки даны в электронном варианте.
6. Поведение итогов.
Оборудование:
– ПК учителя;
– проектор;
– экран;
– компьютеры для учащихся:
– набор фишек красного, желтого и зеленого цветов.
xn--i1abbnckbmcl9fb.xn--p1ai
| Почему учителям и воспитателям следует проходить курсы повышения квалификации и профессиональной переподготовки в учебном центре «Инфоурок» ?• Огромный каталог: 677 курсов профессиональной переподготовки и повышения квалификации;• Очень низкая цена, при этом доступна оплата обучения в рассрочку – первый взнос всего 10%, оставшуюся часть необходимо оплатить до конца обучения; • Курсы проходят полностью в дистанционном режиме (форма обучения в документах не указывается); • Возможность оплаты курса за счёт Вашей организации. • Дипломы и Удостоверения от проекта «Инфоурок» соответствуют всем установленным законодательству РФ требованиям. (Согласно ФЗ «Об образовании в Российской Федерации» от 2012 года). |
infourok.ru

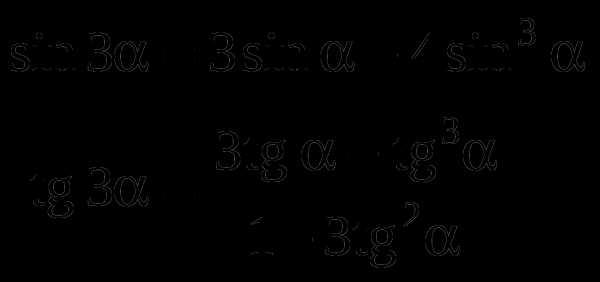
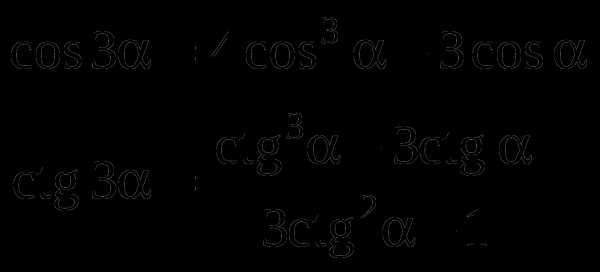


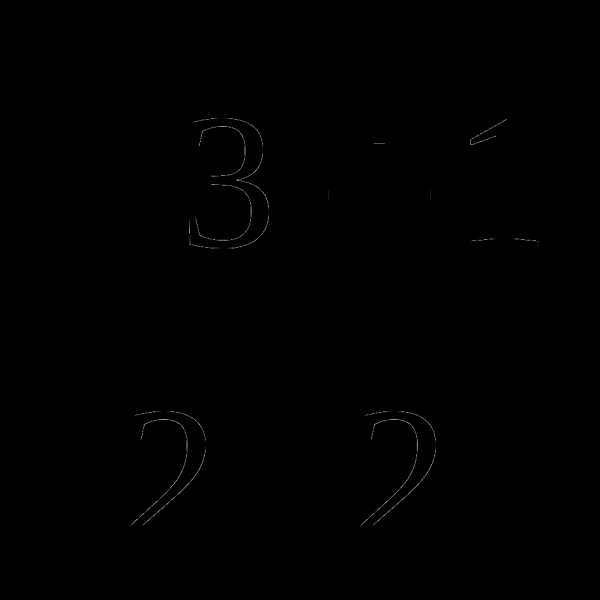








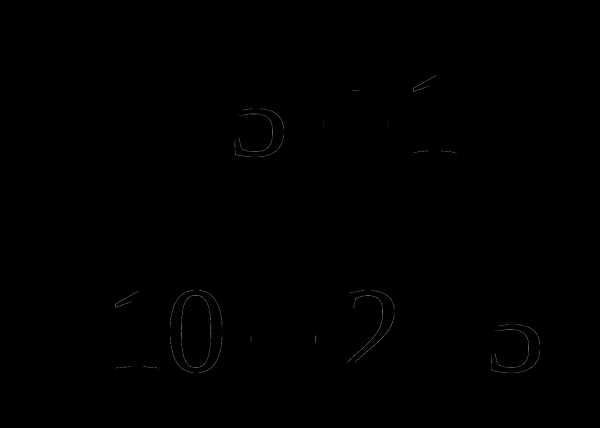
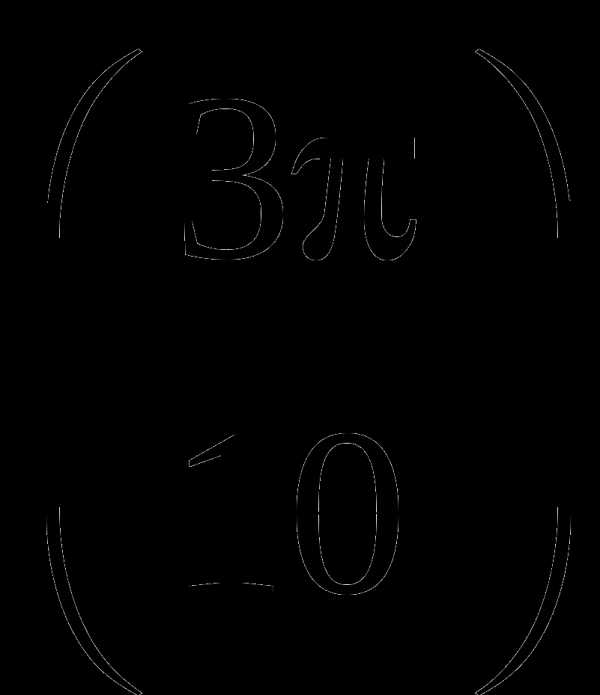



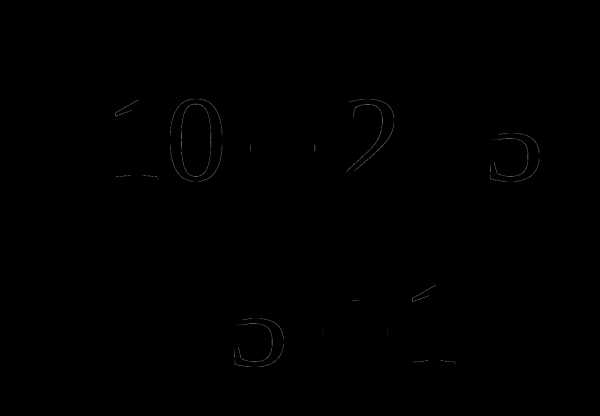




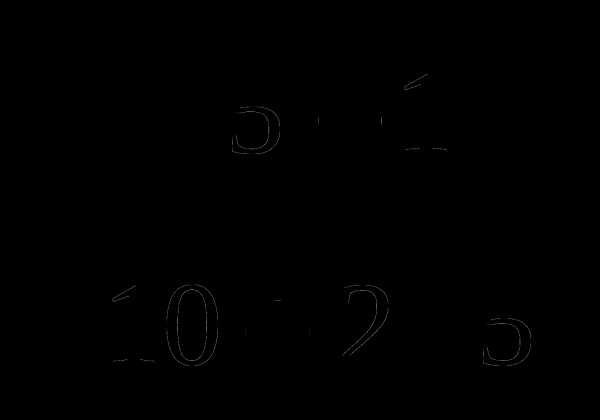
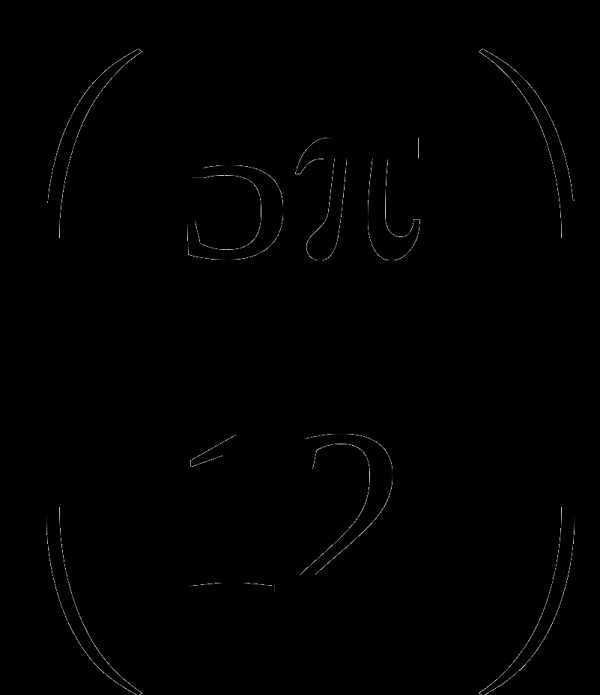
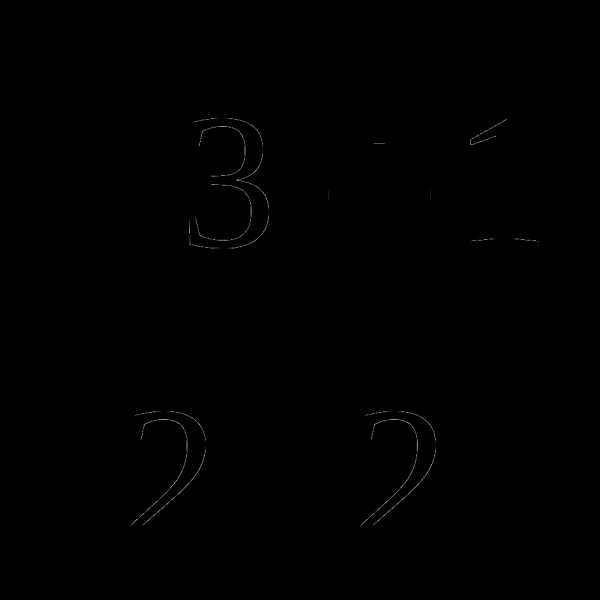




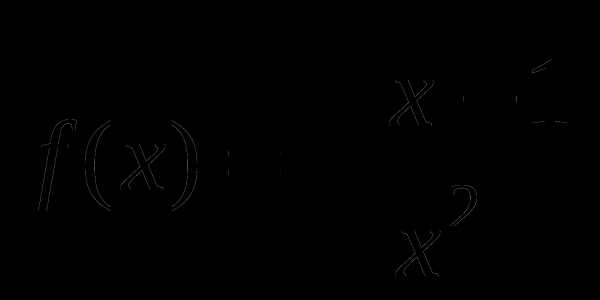

 .
.
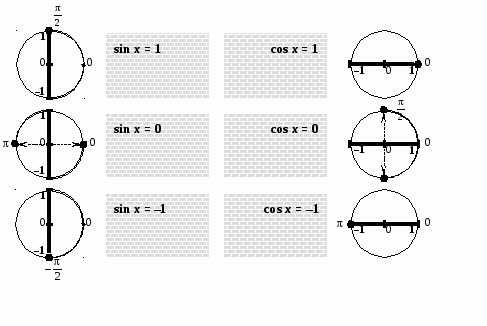

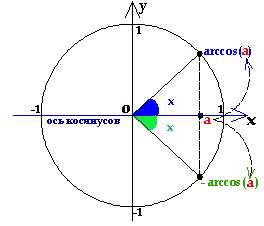
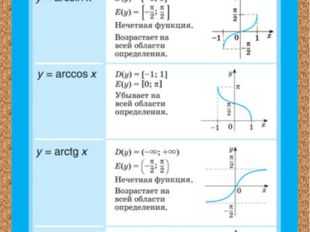
 , синус которого равен а.
, синус которого равен а. , тангенс которого равен а.
, тангенс которого равен а.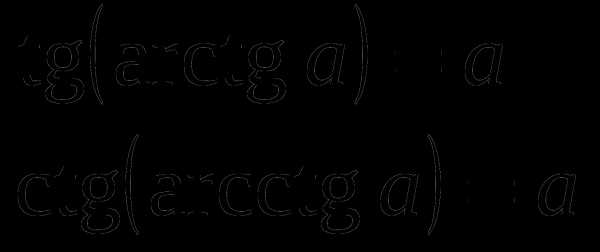
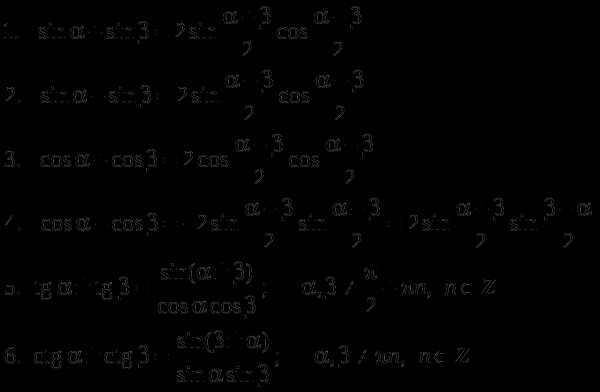
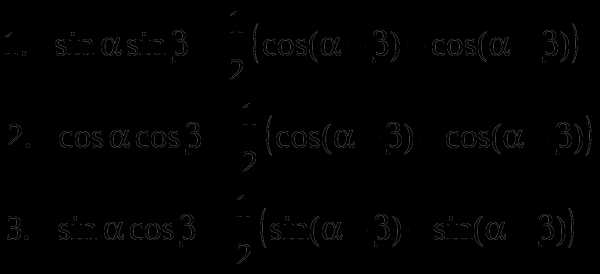
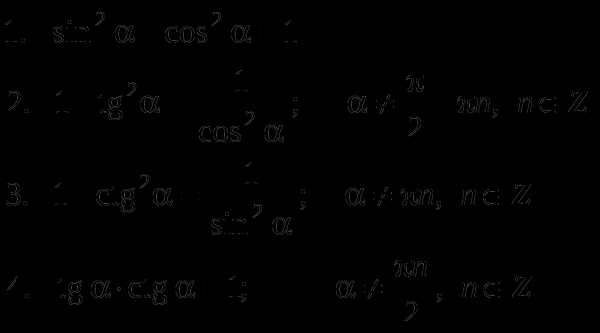
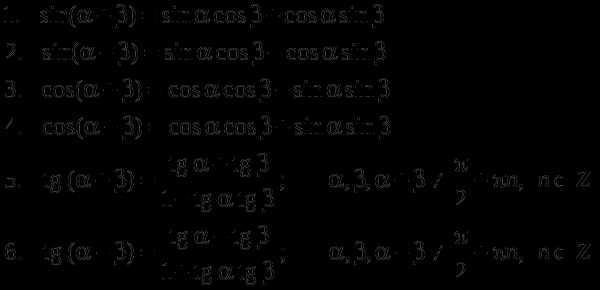


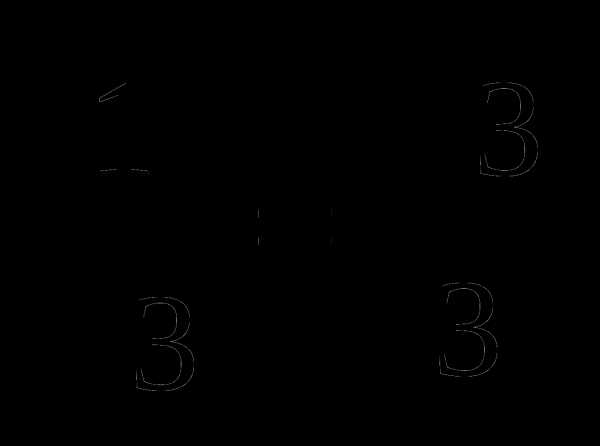
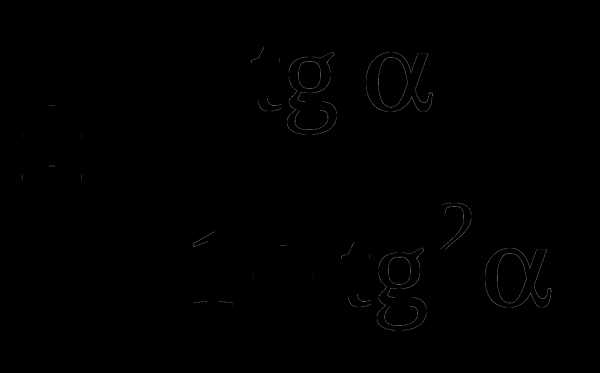
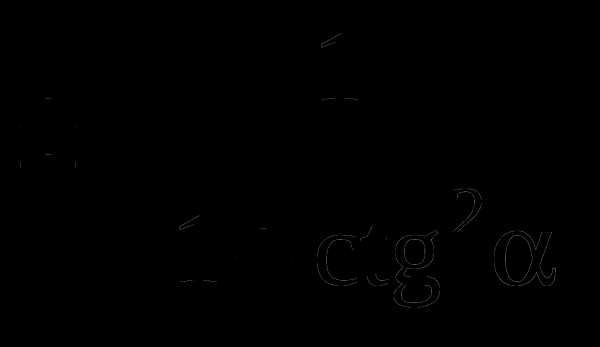


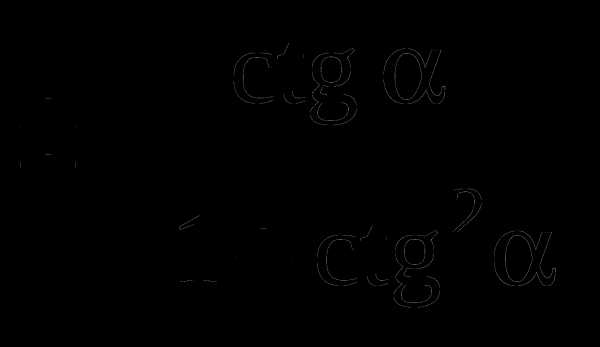
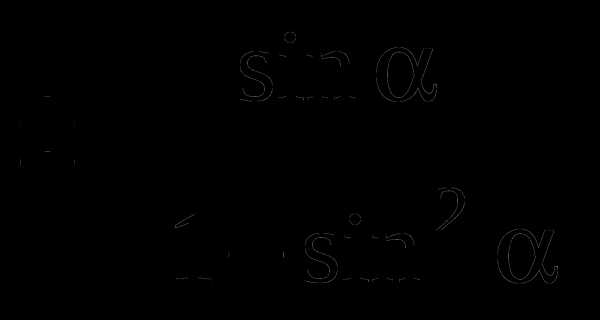

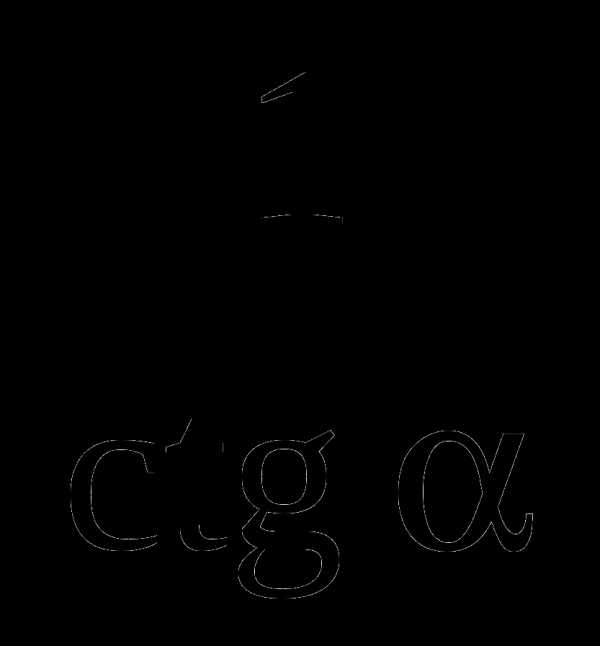
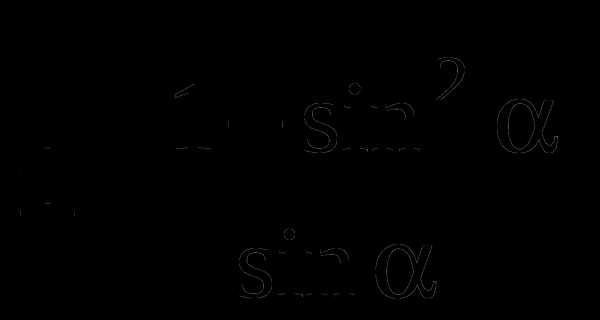



 Описание слайда:
Описание слайда:
 Описание слайда:
3 слайд
Описание слайда:
3 слайд
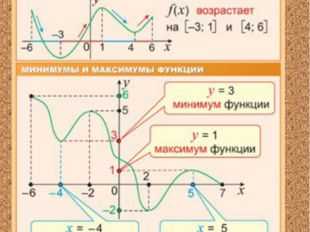 Описание слайда:
4 слайд
Описание слайда:
4 слайд
 Описание слайда:
5 слайд
Описание слайда:
5 слайд
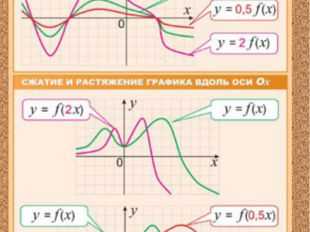 Описание слайда:
6 слайд
Описание слайда:
6 слайд
 Описание слайда:
7 слайд
Описание слайда:
7 слайд
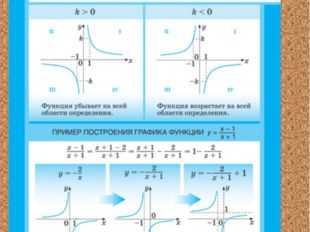 Описание слайда:
8 слайд
Описание слайда:
8 слайд
 Описание слайда:
9 слайд
Описание слайда:
9 слайд
 Описание слайда:
10 слайд
Описание слайда:
10 слайд
 Описание слайда:
11 слайд
Описание слайда:
11 слайд
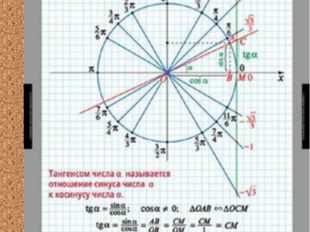 Описание слайда:
12 слайд
Описание слайда:
12 слайд
 Описание слайда:
13 слайд
Описание слайда:
13 слайд
 Описание слайда:
14 слайд
Описание слайда:
14 слайд
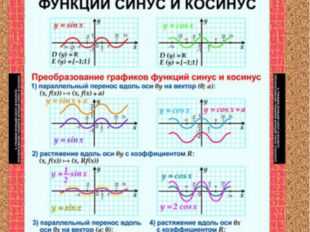 Описание слайда:
15 слайд
Описание слайда:
15 слайд
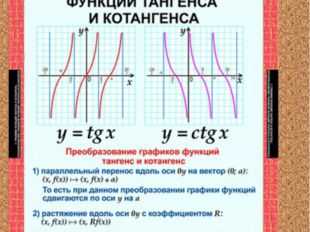 Описание слайда:
16 слайд
Описание слайда:
16 слайд
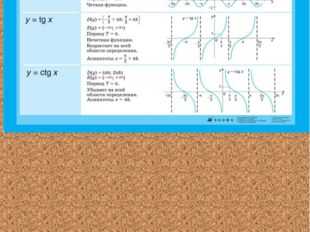 Описание слайда:
17 слайд
Описание слайда:
17 слайд
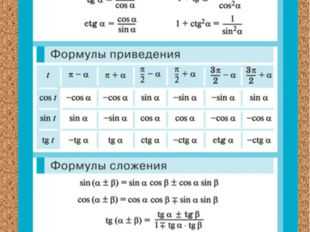 Описание слайда:
18 слайд
Описание слайда:
18 слайд
 Описание слайда:
19 слайд
Описание слайда:
19 слайд
 Описание слайда:
20 слайд
Описание слайда:
20 слайд
 Описание слайда:
21 слайд
Описание слайда:
21 слайд
 Описание слайда:
22 слайд
Описание слайда:
22 слайд
 Описание слайда:
23 слайд
Описание слайда:
23 слайд
 Описание слайда:
24 слайд
Описание слайда:
24 слайд
 Описание слайда:
25 слайд
Описание слайда:
25 слайд
 Описание слайда:
26 слайд
Описание слайда:
26 слайд
 Описание слайда:
27 слайд
Описание слайда:
27 слайд
 Описание слайда:
28 слайд
Описание слайда:
28 слайд
 Описание слайда:
29 слайд
Описание слайда:
29 слайд
 Описание слайда:
30 слайд
Описание слайда:
30 слайд
 Описание слайда:
31 слайд
Описание слайда:
31 слайд
 Описание слайда:
Описание слайда: