Таблица истинности а в с – Таблицы истинности определение таблица истинности – это таблица показывающая истинность сложного высказывания при всех возможных значениях входящих переменных

Таблицы истинности, с формулами и примерами

Они могут принимать значения «истина» или «ложь» (1 или 0). Для функции, содержащей две переменные, наборов значений переменных всего четыре:

   

Значения логических функций определяются с помощью таблица истинности.

Таблицы истинности для основных двоичных логических функций

1. Конъюнкция (логическое умножение) – сложное логическое выражение, которое является истинным только в том случае, когда истинны оба входящих в него простых выражения.

Обозначение:

2. Дизъюнкция (логическое сложение) – это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно, если оба простых логических выражения ложны.

Обозначение:

3. Импликация (логическое следствие) – это сложное логическое выражение, которое является ложным тогда и только тогда, когда условие истинно, а следствие ложно.

Обозначение:

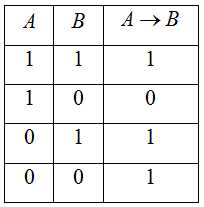
4. Эквиваленция – это сложное логическое высказывание, которое является истинным только при одинаковых значениях истинности простых выражений, входящих в него.

Обозначение:

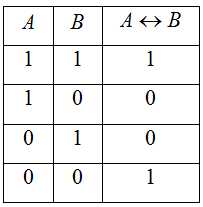
5. Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным.

Обозначение:

6. Штрих Шеффера – операция, отрицающая конъюнкцию, т.е. значение ложно тогда и только тогда, когда оба простых выражения истинны.

Обозначение:

7. Стрелка Пирса – операция, отрицающая конъюнкцию, т.е. значение истинно тогда и только тогда, когда оба простых выражения ложны.

Обозначение:

Порядок выполнения логических операций

При построении таблицы истинности необходимо учитывать порядок выполнения логических операций:

1. Инверсия
2. Конъюнкция
3. Дизъюнкция
4. Импликация
5. Эквиваленция
6. Штрих Шеффера
7. Стрелка Пирса

Для последних двух операций приоритет не определен.

Замечание. Если необходимо изменить указанный порядок выполнения логических операций используются скобки.

Примеры решения задач

ru.solverbook.com

Таблица истинности онлайн с примерами

Таблица истинности — это таблица, которая описывает логическую функцию. Логическая функция здесь — это функция, у которой значения переменных и значение самой функции выражают истинность. Например, они принимают значения «истина» либо «ложь» (true либо false, 1 либо 0).

Таблицы истинности применяются для определения значения какого-либо высказывания для всех возможных случаев значений истинности высказываний, которые его составляют. Количество всех существующих комбинаций в таблице находится по формуле N=2*n; где N — общее количество возможных комбинаций, n — число входных переменных. Таблицы истинности нередко используются в цифровой технике и булевой алгебре, чтобы описать работу логических схем.

Таблицы истинности для основных функций

Примеры: конъюнкция — 1&0=0, импликация — 1→0=0.

Порядок выполнения логических операций

Инверсия; Конъюнкция; Дизъюнкция; Импликация; Эквиваленция; Штрих Шеффера; Стрелка Пирса.

Последовательность построения (составления) таблицы истинности:

https://uchim.org/matematika/tablica-istinnosti — uchim.org

1. Определить количество N используемых переменных в логическом выражении.
2. Вычислить количество всевозможных наборов значений переменных M = 2^N , равное количеству строк в таблице.
3. Подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество логических операций.
4. Озаглавить столбцы таблицы названиями переменных и названиями логических операций.
5. Заполнить столбцы логических переменных наборами значений, например, от 0000 до 1111 с шагом 0001 в случае для четырех переменных.
6. Заполнить таблицу истинности по столбцам со значениями промежуточных операций слева направо.
7. Заполнить окончательный столбец значений для функции F.

Таким образом, можно составить (построить) таблицу истинности самостоятельно.

Составить таблицу истинности онлайн

Заполните поле ввода и нажмите OK. T — истина, F — ложь. Рекомендуем добавить страницу в закладки или сохранить в социальной сети.

Обозначения

1. Множества или выражения большими буквами латинского алфавита: A, B, C, D…
2. A’ — штрих — дополнения множеств
3. && — конъюнкция («и»)
4. || — дизъюнкция («или»)
5. ! — отрицание (например, !A)
6. \cap — пересечение множеств \cap
7. \cup — объединение множеств (сложение) \cup
8. A&!B — разность множеств A∖B=A-B
9. A=>B — импликация «Если …, то»
10. AB — эквивалентность

Всё для учебы » Математика в школе » Таблица истинности онлайн с примерами — логика

Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):

uchim.org

Логические выражения и логическая таблица истинности. Правила построения

Логические выражения и таблица истинности

 Таблица истинности – таблица, показывающая,  какие значения принимает составное высказывание при  всех сочетаниях (наборах)  значений  входящих в него простых высказываний.

Логическое выражение – составные высказывания в виде формулы.

Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «

=».

Алгоритм построения  таблицы  истинности:

1.    подсчитать количество переменных n в логическом выражении;

2.   определить число строк в таблице по формуле m=2ⁿ, где n – количество переменных;

3.   подсчитать количество логических операций в формуле;

4.   установить последовательность выполнения логических операций с учетом скобок и приоритетов;

5.   определить количество столбцов: число переменных + число операций;

6.   выписать наборы входных переменных;

7.   провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.

Заполнение таблицы:

1.      разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;

2.      разделить колонку  значений  второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;

3.      продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.

 

Пример 1. Для формулы  A/\ (B \/ ¬B /\¬C) постройте  таблицу истинности.

 Количество логических переменных 3, следовательно, количество строк – 2³ = 8.

Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов – 3 + 5 = 8.

 

 

 

 

 

 

Пример 2

. Определите истинность  логического выражения  F(А, В) = (А\/ В)/\(¬А\/¬В) .

1. В выражении две переменные А и В (n=2).

2.  m_строк=2ⁿ, m=2²=4 строки.

3. В формуле 5 логических операций.

4. Расставляем порядок действий

1) А\/ В;  2) ¬А;  3) ¬В;  4) ¬А\/¬В;  5) (А\/ В)/\(¬А\/¬В).

5. К_{столбцов}=n+5=2+5=7 столбцов.

 

А	В	А\/ В	¬А	¬В	¬А\/¬В	F
0	0	0	1	1	1	0
0	1	1	1	0	1	1
1	0	1	0	1	1	1
1	1	1	0	0	0	0

 Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.

 

Пример 3. Построёте таблицу истинности для логического выражения

F = (A\/ B) /\ ¬С

1. В данной функции три логические переменные – А, В, С
2. количество строк таблицы = 2³ =8
3. В формуле 3 логические операции.
4. Расставляем порядок действий

1) А\/ В;  2) ¬С; 3) (AVB) /\ ¬С  .

5. количество столбцов таблицы = 3 + 3 = 6

А	В	С	A\/B	¬С	(A\/B) /\ ¬С
0	0	0	0	1	0
0	0	1	0	0	0
0	1	0	1	1	1
0	1	1	1	0	0
1	0	0	1	1	1
1	0	1	1	0	0
1	1	0	1	1	1
1	1	1	1	0	0

 

Пример 4.  Определите истинность формулы: F = ((С \/В) =>  В) /\ (А /\ В) => В.

Построим таблицу истинности этой формулы.

 

 

 

 

 

 

Ответ: формула является тождественно истинной.

Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.

Дан фрагмент таблицы истинности выражения F:

 

X	Y	Z	F
0	0	0	1
0	0	1	0
0	1	0	1

 

Какое выражение соответствует F?

 1) ¬X/\¬Y/\Z                      2) ¬X\/¬Y\/Z                  3) X\/Y\/¬Z              4) X\/Y\/Z

 Решение (вариант 1, через таблицы истинности):

Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:

X	Y	Z	F	¬X	¬Y	¬Z	¬X/\¬Y/\Z	¬X\/¬Y\/Z	X\/Y\/¬Z	X\/Y\/Z
0	0	0	1	1	1	1	0	1	1	0
0	0	1	0	1	1	0	1	1	0	1
0	1	0	1	1	0	1	0	1	1	1

 Очевидно, что значения заданной функции F совпадают со значениями выражения X\/Y\/¬Z. Следовательно, правильный ответ – 3.

Ответ: 3

 Решение (Вариант 2):

Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y  и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.

 Рассмотрим данный конкретный пример:

1)      первое заданное выражение  ¬X/\¬Y/\Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;

2)      второе заданное выражение ¬X\/¬Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует  второй строке таблицы;

3)      третье выражение   X\/Y\/¬Z    соответствует F при всех предложенных комбинациях X,Y и Z;

4)      четвертое выражение X\/Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.

Ответ: 3

mir-logiki.ru

Таблица истинности. Базовые логические элементы.

Так же, как и стандартные Булевы выражения, информация на входах и выходах различных логических элементов или логических схем может быть собрана в единую таблицу – таблицу истинности.

Таблица истинности дает наглядное представление о системе логических функций. В таблице истинности отображаются сигналы на выходах логических элементов при всех возможных комбинациях сигналов на их входах.

В качестве примера, рассмотрим логическую схему с двумя входами и одним выходом. Входные сигналы отметим как «А» и «В», а выход «Q». Есть четыре (2²) возможных комбинаций входных сигналов, которые можно подать на эти два входа («ON — наличие сигнала» и «OFF — отсутствие сигнала»).

Однако, когда речь идет о логических выражениях и, особенно о таблице истинности логических элементов, вместо общего понятия «наличие сигнала» и «отсутствие сигнала» используют битные значения, которые представляют собой логический уровень «1» и логический уровень «0» соответственно.

Тогда четыре возможные комбинации «А» и «В» для 2-входного логического элемента можно представить в следующем виде:

1. «OFF» — «OFF» или (0, 0)
2. «OFF» — «ON» или (0, 1)
3. «ON» — «OFF» или (1, 0)
4. «ON» — «ON» или (1, 1) 

Следовательно, у логической схемы имеющей три входа будет восемь возможных комбинаций (2³)  и так далее. Для обеспечения легкого понимания сути таблицы истинности, мы будем изучать ее только на простых логических элементах с числом входов не превышающим двух. Но, несмотря на это, принцип получения логических результатов для многовходных элементов схемы остается таким же.

Практически, таблица истинности состоит из одного столбца для каждой из входных переменных (например, А и В), и один последний столбец для всех возможных результатов логической операции (Q). Следовательно, каждая строка таблицы истинности содержит один из возможных вариантов входных переменных (например, A = 1, B = 0), и результат операции с этими значениям.

Таблица истинности

Элемент «И»

Для логического элемента «И» выход Q будет содержать лог.1, только если на оба входа («А» и «В») будет подан сигнал лог.1

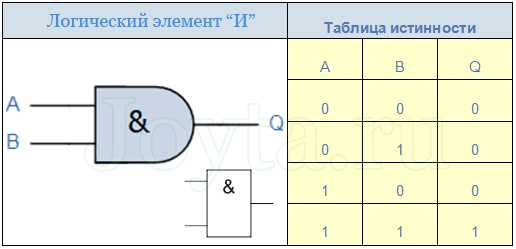
Микросхемы, содержащие логический элемент «И»:

• К155ЛИ1, аналог SN7408N
• К155ЛИ5 с открытым коллектором, аналог SN74451N
• К555ЛИ1, аналог SN74LS08N
• К555ЛИ2 с открытым коллектором, аналог SN74LS09N

Элемент «ИЛИ»

Выход Q, элемента «ИЛИ», будет иметь лог.1, если на любой из двух входов или же на оба входа сразу подать лог.1

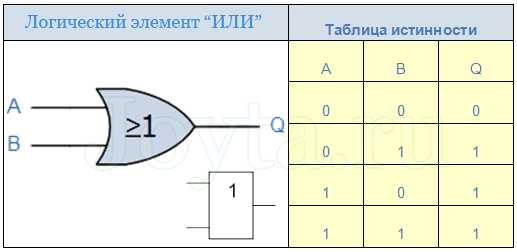
Микросхемы, содержащие логический элемент «ИЛИ»:

• К155ЛЛ1, аналог SN7432N
• К155ЛЛ2 с открытым коллектором, аналог SN75453N
• К555ЛЛ1, аналог SN74LS32N

Элемент «НЕ»

В данном случае выход Q, логического элемента «НЕ», будет иметь сигнал противоположный входному сигналу.

 

Микросхемы, содержащие логический элемент «НЕ»:

• К155ЛН1, аналог SN7404N
• К155ЛН2 с открытым коллектором, аналог SN7405N
• К155ЛН3, аналог SN7406N
• К155ЛН5 с открытым коллектором, аналог SN7416N
• К155ЛН6, аналог SN7466N

Элемент «И-НЕ»

На выходе Q элемента «И-НЕ» будет лог.1 если на обоих входах одновременно  отсутствует сигнал лог.1

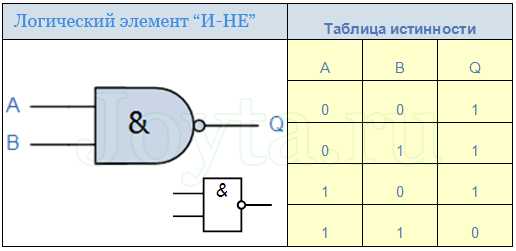
Микросхемы, содержащие логический элемент «И-НЕ»:

• К155ЛА3, аналог SN7400N
• К155ЛА8, аналог SN7401N
• К155ЛА9 с открытым коллектором, аналог SN7403N
• К155ЛА11 с открытым коллектором, аналог SN7426N
• К155ЛА12 с открытым коллектором, аналог SN7437N
• К155ЛА13 с открытым коллектором, аналог SN7438N
• К155ЛА18 с открытым коллектором, аналог SN75452N

Элемент «ИЛИ-НЕ»

Только если на оба входа логического элемента «ИЛИ-НЕ» подать лог.0 мы получим на его выходе Q сигнал соответствующий лог.1

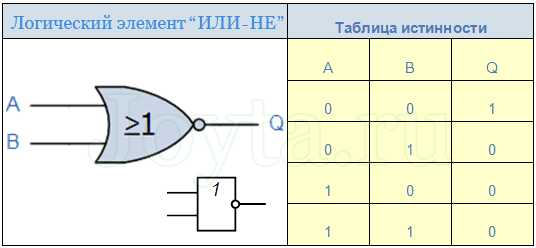
Микросхемы, содержащие логический элемент «ИЛИ-НЕ»:

• К155ЛЕ1, аналог SN7402N
• К155ЛЕ5, аналог SN7428N
• К155ЛЕ6, аналог SN74128N

Элемент «Исключающее ИЛИ»

В данном случае выход Q будет содержать лог.1, если на вход элемента «Исключающее ИЛИ» поданы два противоположных друг другу сигнала.

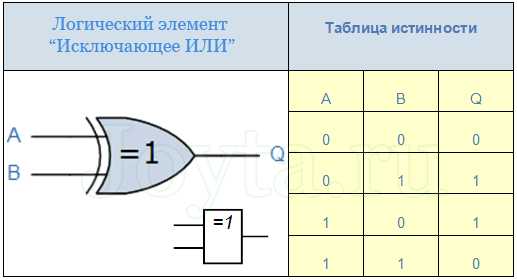
Микросхемы, содержащие логический элемент «Исключающее ИЛИ»:

• К155ЛП5, аналог SN7486N

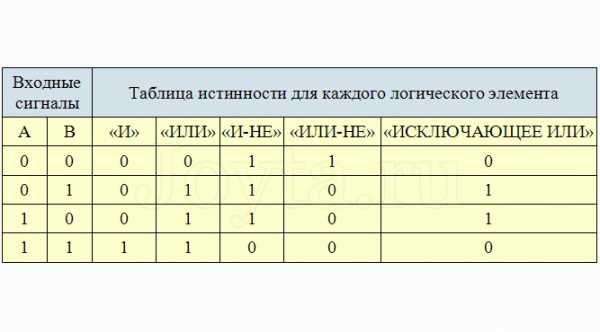
Подведем итог, собрав все полученные ранее результаты работы логических элементов в единую таблицу истинности:

www.joyta.ru

Логические схемы и таблицы истинности

В цифровой схемотехнике цифровой сигнал — это сигнал, который может принимать два значения, рассматриваемые как логическая «1» и логический «0».

Логические схемы реализуются на логических элементах: «НЕ», «И», «ИЛИ», «И-НЕ», «ИЛИ-НЕ», «Исключающее ИЛИ» и «Эквивалентность». Первые три логических элемента позволяют реализовать любую, сколь угодно сложную логическую функцию в булевом базисе. Мы будем решать задачи на логические схемы, реализованные именно в булевом базисе.

Для обозначения логических элементов используется несколько стандартов. Наиболее распространёнными являются американский (ANSI), европейский (DIN), международный (IEC) и российский (ГОСТ). На рисунке ниже приведены обозначения логических элементов в этих стандартах (для увеличения можно нажать на рисунок левой кнопкой мыши).

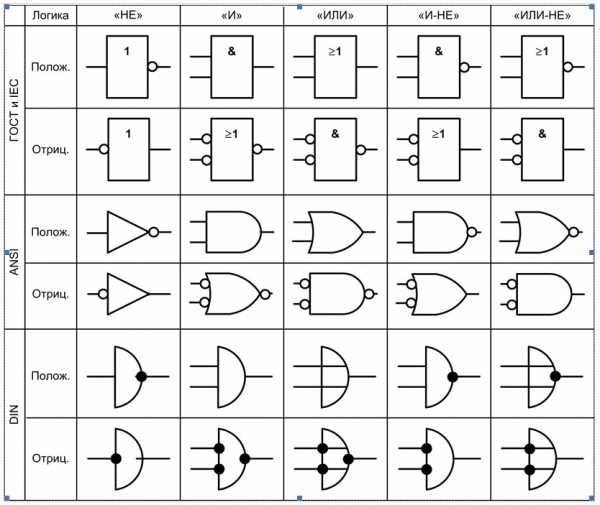
На этом уроке будем решать задачи на логические схемы, на которых логические элементы обозначены в стандарте ГОСТ.

Задачи на логические схемы бывают двух видов: задача синтеза логических схемы и задачи анализа логических схем. Мы начнём с задачи второго типа, так как в таком порядке удаётся быстрее научиться читать логические схемы.

Задача анализа заключается в определении функции f, реализуемой заданной логической схемой. При решении такой задачи удобно придерживаться следующей последовательности действий.

1. Логическая схема разбивается на ярусы. Ярусам присваиваются последовательные номера.
2. Выводы каждого логического элемента обозначаются названием искомой функции, снабжённым цифровым индексом, где первая цифра — номер яруса, а остальные цифры — порядковый номер элемента в ярусе.
3. Для каждого элемента записывается аналитическое выражение, связывающее его выходную функцию с входными переменными. Выражение определяется логической функцией, реализуемой данным логическим элементом.
4. Производится подстановка одних выходных функций через другие, пока не получится булева функция, выраженная через входные переменные.

Пример 1. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

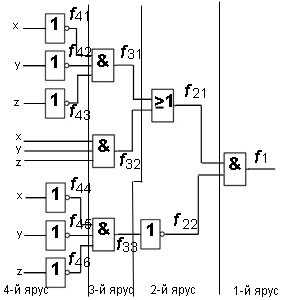
Решение. Разбиваем логическую схему на ярусы, что уже показано на рисунке. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z:

В итоге получим функцию, которую реализует на выходе логическая схема:

.

Таблица истинности для данной логической схемы:

x	y	z					f
1	1	1	0	1	1	1	1
1	1	0	0	0	0	1	0
1	0	1	0	0	0	1	0
1	0	0	0	0	0	1	0
0	1	1	0	0	0	1	0
0	1	0	0	0	0	1	0
0	0	1	0	0	0	1	0
0	0	0	1	0	1	0	0

Пример 4. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Решение. Разбиваем логическую схему на ярусы. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z:

В итоге получим функцию, которую реализует на выходе логическая схема:

.

Таблица истинности для данной логической схемы:

x	y	z			f
1	1	1	0	1	1
1	1	0	0	1	1
1	0	1	1	0	1
1	0	0	0	0	0
0	1	1	0	1	1
0	1	0	0	1	1
0	0	1	0	1	1
0	0	0	0	1	1

---

Пример 5. Найдите булеву функцию логической схемы и составьте таблицу истинности для логической схемы.

Решение. Разбиваем логическую схему на ярусы. Структура данной логической схемы, в отличие от предыдущих примеров, имеет 5 ярусов, а не 4. Но одна входная переменная — самая нижняя — пробегает все ярусы и напрямую входит в логический элемент в первом ярусе. Запишем все функции, начиная с 1-го яруса:

Теперь запишем все функции, подставляя входные переменные x, y, z:

В итоге получим функцию, которую реализует на выходе логическая схема:

.

Таблица истинности для данной логической схемы:

x	y	z			f
1	1	1	1	1	1
1	1	0	1	1	1
1	0	1	1	0	1
1	0	0	1	0	1
0	1	1	1	1	1
0	1	0	1	1	1
0	0	1	1	0	1
0	0	0	1	0	1

Разработка логической схемы по её аналитическому описанию имеет название задачи синтеза логической схемы.

Каждой дизъюнкции (логической сумме) соответствует элемент «ИЛИ», число входов которого определяется количеством переменных в дизъюнкции. Каждой конъюнкции (логическому произведению) соответствует элемент «И», число входов которого определяется количеством переменных в конъюнкции. Каждому отрицанию (инверсии) соответствует элемент «НЕ».

Часто разработка логической схемы начинается с определения логической функции, которую должна реализовать логическая схемы. В этом случае дана только таблица истинности логической схемы. Мы разберём именно такой пример, то есть, решим задачу, полностью обратную рассмотренной выше задаче анализа логических схем.

Пример 6. Построить логическую схему, реализующую функцию с данной таблицей истинности:

Решение. Разбираем таблицу истинности для логической схемы. Определяем функцию, которая получится на выходе схемы и промежуточные функции, которые на входе принимают аргументы x и y. В первой строке результатом реализации выходной функции при том, что значения входных переменных равны единицам, должен быть логический «0», во второй строке — при разных значениях входных переменных на выходе тоже должен быть логический «0». Поэтому нужно, чтобы выходная функция была конъюнкцией (логическим произведением).

Теперь подбираем промежуточные функции. Получаем следующую таблицу для промежуточных функций и выходной функции — конъюнкции промежуточных функций:

Для построения логической схемы необходимо элементы, реализующие логические операции, указанные в выходной функции, располагать в порядке, заданной этой функцией. Из выражения видно, что понадобятся 3 схемы «НЕ», две двухвходовых схемы «И» и одна двухвходовая схема «ИЛИ». В соответствии с выходной функцией получаем следующую логическую схему:

function-x.ru

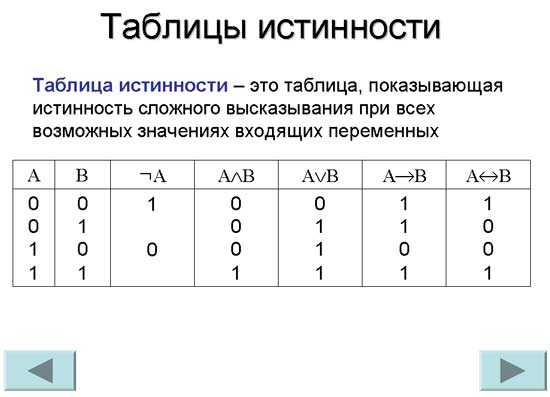
Таблицы истинности определение таблица истинности – это таблица показывающая истинность сложного высказывания при всех возможных значениях входящих переменных

ТАБЛИЦЫ ИСТИННОСТИ.

Определение. Таблица истинности – это таблица, показывающая истинность сложного высказывания при всех возможных значениях входящих переменных.

Разберем подробнее каждую логическую операцию в соответствии с ее определением:

1. Инверсия (отрицание) – это логическая о

перация, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

Таблица истинности схемы НЕ

x
0	1
1	0

2. Конъюнкция (умножение)– это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Таблица истинности схемы И

3. Дизъюнкция (сложение) – это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.

Таблица истинности схемы ИЛИ

4. Импликация (следование) – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие истинное, а следствие ложно.

5. Эквиваленция (равносильность) – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или ложны.

Разберем алгоритм составления таблицы истинности для сложного высказывания:

• Определить, сколько переменных входит в формулу.

• Определить количество комбинаций всевозможных значений переменных по формуле .

• Определить приоритет действий.

• Составить таблицу истинности.

Рассмотрим пример составления таблицы истинности для сложного высказывания:

Пример. Построить таблицу истинности для формулы: А V В → ¬А V С.

Решение:

Из примера видно, что таблицей истинности является не все решение, а только последнее действие (столбец, выделенный красным цветом).

textarchive.ru

Таблица истинности Википедия

Таблица истинности — это таблица, описывающая логическую функцию.

Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» (true{\displaystyle true} либо false{\displaystyle false}, 1{\displaystyle 1} либо 0{\displaystyle 0}).

Табличное задание функций встречается не только в логике, но для логических функций таблицы оказались особенно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики.

Таблицы истинности для основных двоичных логических функций

В программировании:

• Конъюнкция = AND = И = ∧{\displaystyle \land } = &
• Дизъюнкция = OR = ИЛИ = ∨{\displaystyle \lor } = |
• Сложение по модулю 2 = XOR = ИСКЛЮЧАЮЩЕЕ ИЛИ = ⊕{\displaystyle \oplus } = ~
• Отрицание = NOT = НЕ = ¬{\displaystyle \neg } = !

Таблицы истинности для некоторых троичных логических функций

x	2	1	0	2	1	0	2	1	0
y	2	2	2	1	1	1	0	0	0
min(x,y)	2	1	0	1	1	0	0	0	0

x	2	1	0	2	1	0	2	1	0
y	2	2	2	1	1	1	0	0	0
max(x,y)	2	2	2	2	1	1	2	1	0

x	2	1	0	2	1	0	2	1	0
y	2	2	2	1	1	1	0	0	0
F2TN22310	0	0	0	0	2	2	0	2	1

См. также

Примечания

Литература

• Яблонский С. В., Гаврилов Г. П., Кудрявцев В. Б. Функции алгебры логики и классы Поста. — М.: Наука, 1966. — (Математическая логика и основания математики).

Ссылки

wikiredia.ru