Свойства логических операций — урок. Информатика, 8 класс.
Рассмотрим основные свойства логических операций, называемых также законами алгебры логики.
Переместительный (коммутативный) закон:
- для логического умножения: A&B=B&A;
- для логического сложения: A∨B=B∨A.
Сочетательный (ассоциативный) закон:
- для логического умножения: A&B&C=A&B&C;
- для логического сложения: A∨B∨C=A∨B∨C.
Обрати внимание!
При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.
Распределительный (дистрибутивный) закон:
- для логического умножения: A&B∨C=A&B∨A&C;
- для логического сложения: A∨B&C=A∨B&A∨C.
Закон двойного отрицания:
A¯¯=A.
Обрати внимание!
Двойное отрицание исключает отрицание.
Закон исключённого третьего:
- для логического умножения: A&A¯=0;
- для логического сложения: A∨A¯=1.
Обрати внимание!
Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
Закон повторения:
- для логического умножения: A&A=A;
- для логического сложения: A∨A=A.
Законы операций с \(0\) и \(1\):
- для логического умножения: A&0=0; A&1=A;
- для логического сложения: A∨0=A; A∨1=1.
Законы общей инверсии:
- для логического умножения: A&B¯=A¯∨B¯;
- для логического сложения: A∨B¯=A¯&B¯.
Законы алгебры логики могут быть доказаны с помощью таблиц истинности. Докажем распределительный закон для логического сложения:
A∨B&C=A∨B&A∨C.
\(A\) | \(B\) | \(C\) | B&C | A∨B&C | A∨B | A∨C | A∨B&A∨C |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Совпадение значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
Источники:
Босова Л. Л., Босова А. Ю., Информатика: учебник для 8 класса. М. : БИНОМ. Лаборатория знаний, 30 с.
www.yaklass.ru
2.2. Высказывания. Логические операции и их основные свойства
Определение 1. Суждением называется форма мышления, в которой что-либо утверждается или отрицается о существовании предмета, связях между предметом и его свойствами или об отношениях между предметами.
Определение 2. Высказыванием называется повествовательное предложение, о котором в данной ситуации можно сказать, что оно истинно или ложно, но не то и другое одновременно.
Например, «Москва – столица России», «число 2 больше 5» – высказывания. Первое высказывание является истинным, а второе – ложным.
Будем обозначать высказывания латинскими буквами:
Логическое значение высказывания «истина» обозначается цифрой «1», «ложь» – «0».
Предложения: «Который час?», «ответьте на вопрос», «добро пожаловать!» – не являются высказываниями.
Предложение «Была метель» также не является высказыванием, поскольку нет достаточной информации, чтобы установить истинно оно или ложно (где и когда?).
Определение 3. Формализацией высказываний называют операцию замены высказывания естественного языка формулой математического языка, включающего высказывательные переменные и символы тех логических операций, которые соответствуют структуре самого высказывания.
Определение 4. Если суждение об истинности высказывания можно вынести из самого высказывания, то такое высказывание называют простым. В противном случае мы имеем сложное (составное) высказывание.
Значение истинности составного высказывания определяется значениями истинности его компонент.
Из простых высказываний можно образовать новые составные высказывания с помощью союзов «и», «или», «либо», «если…, то», «тогда и только тогда, когда», «неверно, что». Эти союзы называются логическими связками. Построение из данных высказываний нового составного высказывания называется логической операцией над высказываниями.
Основные логические операции: отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность (табл. 1).
Таблица 1
Логические операции
|
Название |
Прочтение |
Обозначение |
|
Отрицание |
Не; неверно, что |
() |
|
Конъюнкция |
И; а |
() |
|
Дизъюнкция |
Или | |
|
Импликация |
Если … то | |
|
Эквивалентность |
Тогда и только тогда, когда |
(~) |
Логическое значение сложного высказывания можно описать с помощью таблицы, называемой таблицей истинности (верхняя строка содержит обозначения высказываний, последующие строки – логическое значение высказываний).
Пусть даны два произвольных высказывания и.
Определение 5. Отрицанием высказывания называется высказывание(«не», «неверно, что»), которое истинно, когдаложно, и ложно, когдаистинно.
Таблица истинности для отрицания:
|
0 |
1 |
|
1 |
0 |
Определение 6. Конъюнкцией (логическим умножением) двух высказываний ,называется высказывание(«и»), которое истинно только в том случае, когдаиоба истинны.
Таблица истинности для конъюнкций:
Определение 7. Дизъюнкцией (логическим сложением) двух высказываний ,называется высказывание(«или»), которое истинно, когда хотя бы одно из них истинно.
Таблица истинности для дизъюнкций:
Определение 8. Импликацией двух высказываний ,называется высказывание («если, то», «влечёт», «изследует», «имплицирует»), которое ложно тогда и только тогда, когдаистинно, аложно.
Таблица истинности для импликаций:
Определение 9. Эквивалентностью высказываний ,называется высказывание(«эквивалентно», «тогда и только тогда, когда», «для того, чтобы, необходимо и достаточно, чтобы»), которое истинно тогда и только тогда, когдаи оба истинны или ложны.
Таблица истинности для эквивалентности:
Для образования составных высказываний наряду с единичным использованием каждой основной связки можно пользоваться основными связками многократно, получая более сложные составные высказывания, – аналогично тому, как с помощью основных арифметических операций образуются сложные алгебраические выражения.
Например, составными будут высказывания: ;;.
Замечание 1. Скобки указывают порядок выполнения действий. Если скобок нет, то операции надо выполнять в следующем порядке: конъюнкция, дизъюнкция, импликация, эквивалентность. Если отрицание относится ко всему высказыванию, например, , то оно выполняется последним. Если отрицание относится только к одному высказыванию, например,, тогда оно выполняется первым.
Каждое составное высказывание имеет свою таблицу истинности, которая может быть построена стандартным образом.
Определение 10. Формулой алгебры логики высказываний называется всякое простое высказывание, обозначаемое буквой, а также всякое составное высказывание, которое получается комбинированием простых высказываний с помощью конечного числа указанных выше основных операций (;;;;). Для любых формул можно построитьтаблицу истинности.
Определение 11. Таблицей истинности формулы называется сводная таблица всех значений входящих в нее высказываний и соответствующих значений самой формулы. Если формула содержит элементарных высказываний, то таблица содержитстрок.
Пример 1. Составьте таблицу истинности .
Решение
Составим таблицу истинности, последовательно выполняя логические операции, входящие в формулу:
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
0 |
|
1 |
1 |
0 |
1 |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
0 |
1 |
1 |
Пример 2. Пусть ,иобозначают соответственно высказывания: «Тимофей любит шахматы», «Тимофей любит футбол», «Тимофей любит баскетбол». Требуется записать высказывание: «Тимофей любит шахматы и неверно, что он любит футбол или баскетбол» в символической форме и указать соответствующую таблицу истинности.
Решение
Высказывание «Тимофей любит футбол или баскетбол» в символической форме записывается как . Высказывание «Неверно, что Тимофей любит футбол или баскетбол» символически записывается как, поскольку отрицание применяется ко всему высказыванию.
Итак, исходное высказывание символически изображается .
Таблица истинности этого высказывания:
|
1 1 1 1 0 0 0 0 |
1 1 0 0 1 1 0 0 |
1 0 1 0 1 0 1 0 |
1 1 1 0 1 1 1 0 |
0 0 0 1 0 0 0 1 |
0 0 0 1 0 0 0 0 |
Пример 3. Запишите высказывание «Если число 72 делится на 6, а число 6 делится на 2, то число 72 делится на 2» в символической форме.
Решение
Выделим простые высказывания «число 72 делится на 6», «число 6 делится на 2», «число 72 делится на 2» и заменим их логическими переменными ,исоответственно.
Тогда исходное высказывание символически изображается .
Особый интерес представляют сложные высказывания, имеющие различное строение, но принимающие одинаковые логические значения при любом наборе значений входящих в формулы элементарных высказываний. Такие высказывания называются логически эквивалентными (равносильными). Эквивалентность двух высказываний легко установить посредством сравнения их таблиц истинности.
Определение 12. Две формулы алгебры логики иназываютсяравносильными, если они принимают одинаковые логические значения (0 или 1) при одинаковых наборах значений входящих в них высказываний (пишут ).
Например, ,– равносильные формулы:
, так как илибо одновременно ложны, либо одновременно истинны при любом наборе значений высказываний, входящих в эти формулы, что и показано в таблице истинности:
|
0 0 1 1 |
0 1 0 1 |
1 1 0 1 |
1 1 0 0 |
1 1 0 1 |
Определение 13. Формула называется тавтологией или тождественно истинной, если она принимает значение «истина» при всех значениях входящих в неё переменных.
Формулы иравносильны тогда и только тогда, когда их эквивалентностьтождественно истинна. Записьозначает, что формулаявляется тождественно истинной.
Теорема. тогда и только тогда, когда.
Каждое высказывание вида – тавтология.
Определение 14. Логическая формула называетсятождественно ложной, или противоречием (записывается ), если для всех наборов значений входящих в нее переменных (высказываний) она принимает значение 0 («ложь»), т. е. если высказывание ложно в каждом случае.
Таблица истинности для противоречия содержит только значения 0 в итоговом столбце.
Заметим, что отрицание любой тавтологии есть противоречие: .
Определение 15. Формулы, не являющиеся ни тавтологией, ни противоречием, называются выполнимыми (разрешимыми). Таблица истинности таких формул содержит как 1, так и 0.
Равносильность формул можно доказывать либо с помощью таблиц истинности, либо методом равносильных (эквивалентных) преобразований, используя основные равносильности алгебры логики высказываний. Основные равносильности называют законами логики, они также применяются для упрощения формул, для приведения формул к заданному виду.
Основные равносильности алгебры высказываний:
–ассоциативность операций и;
–коммутативность операций и;
–закон идемпотентности;
–законы дистрибутивности;
–законы поглощения;
–законы склеивания;
–законы Порецкого;
–законы де Моргана;
;
;
;
–закон двойного отрицания;
–закон исключения третьего;
–закон противоречия;
–закон контрапозиции.
Пример 4. Докажите равносильность с помощью формул алгебры высказываний:
а) ;
б) .
Решение:
a) используя формулу, запишем:, тогда по закону де Моргана и по закону двойного отрицания получим, что и требовалось доказать;
б) преобразуем левую и правую части к одному и тому же виду. Согласно законам де Моргана и двойного отрицания получим следующие выражения.
Левая часть: .
Правая часть:
После равносильных преобразований получили одинаковые формулы. Равносильность доказана.
Вопросы и задачи для самостоятельного решения
1. Определите, какие из следующих предложений являются высказываниями:
а) «ученики школы»;
б) «7 + 5 = 12»;
в) «сегодня плохая погода»;
г) «если , то»;
д) «у каждого человека есть домашнее животное»;
е) «для всех действительных чисел иверно равенство»;
ж) «треугольник равен треугольнику»;
и) «берегись автомобиля!».
2. Составьте таблицы истинности для логических формул:
а) ; г);
б) ; д).
в) .
3. Запишите следующие высказывания в символической форме и укажите соответствующую таблицу истинности:
а) «неверно, что ни Евгений, ни Николай не умеют играть на гитаре»;
б) «если числовая последовательность монотонна и ограничена, то она имеет предел»;
в) «неверно, что если белый кубик больше зеленого, а зеленый – больше синего, то синий кубик больше белого».
4. Проверьте с помощью таблицы истинности, будут ли эквивалентны следующие логические формулы:
а) ;
б) ;
в) .
5. Используя основные законы логических операций, докажите равносильность формул и, когда:
Дополнительные логические операции. Кроме указанных ранее логических операций (отрицание, конъюнкция, дизъюнкция, импликация, эквивалентность), существуют и другие. Например, операция, через которую могут быть выражены все ранее указанные логические операции – штрих Шеффера. Эта операция обозначается символом .
Таблица истинности штриха Шеффера:
Очевидно, что ,. Из этих двух равносильностей следует, что всякая формула алгебры логики может быть заменена равносильной формулой, содержащей только штрих Шеффера. Операцию «штрих Шеффера» обычно определяют следующим образом.
Штрих Шеффера , или антиконъюнкция, по определению (читается «несовместимо с»).
В дополнение к ранее указанным пяти основным операциям перечислим новые логические операции (табл. 2).
Таблица 2
studfiles.net
Свойства Логики — Диалектическая логика в Живом Журнале
Особенность данного разговора, в отличие от разговора с, например, А.В. Болдыревым, в том, что Ваш собеседник, Михаил Петрович, имеет совершенно другой фон знаний, жизненного опыта и мотивации, чем у Ваших коллег.Причём, что интересно, скорее всего мы с Вами прочитали один и тот же набор текстов, там классиков философии, лингвистики, психологии, религии, всяких разных околофилософских и околонаучных вещей. Это следствие советского воспитания.
А вот связи между идеями и понятиями, заключенных в этих текстах у нас с Вами совершенно разные.
Это потому что жизнь по-разному сложилась.
Таким образом, ссылаясь на одни и те же тексты, мы, всё ж таки, имеем в виду разное.
Причём разное настолько, что я совершенно не согласен с Вашей фразой «Общеизвестным свойством формальной логики является её принудительная сила».
Логика как наука есть попытка описания правил построения высказываний и доказательств.
Грамматика есть попытка описания «правильного» построения предложений.
В результате: да, мы пользуемся понятиями «логика» и «грамматика», чтобы улучшить построение текста, сделать его более эффективным, правильным.
Но практика речи и общения постоянно ломает эти правила: мы их не соблюдаем.
Отсюда появление новых слов в языке, кащенитов, и более 30 различных логик, имеющих многочисленных приверженцев.
Я уже как-то писал в ДЛ, что по-моему, человек – совершенно НЕ логическое существо.
И это моё очень фундаментальное убеждение.
Поэтому ни у формальной, ни у какой другой логики или грамматики нет принудительной силы.
Тем не менее, совершенно нет грамотных людей, НЕ знакомых со словом – и понятием, идеей! – «грамматика» или «логика». То есть мы все как-то пользуемся этими понятиями по жизни.
Что принуждает нам прочитывать написанный текст и проверять правильность написанного?
«Грамматика» сама по себе?
Чистая Логика?
Это — отдельный большой вопрос.
У Вас есть желание его обсудить?
dia-logic.livejournal.com
Общая характеристика науки логики. Понятие логической формы и логического закона.
Вопросы к экзамену по логике
1. Общая характеристика науки логики. Понятие логической формы и логического закона.
2. Основные законы формальной логики: закон тождества, закон недопущения противоречия закон исключенного третьего, закон достаточного основания.
3. Понятие. Объем и содержание понятия. Закон обратного соотношения объема и содержания понятия.
4. Виды понятий: пустые, логически пустые, фактически пустые, непустые, общие, единичные, абстрактные, конкретные, собирательные, несобирательные, положительные, отрицательные.
5. Отношения между понятиями. Сравнимые и несравнимые понятия. Совместимые и несовместимые понятия. Равнообъемность, пересечение, подчинение; соподчинение, противоположность, противоречие.
6. Обобщение и ограничение понятий.
7. Деление понятий. Структура и виды деления.
8. Правила и ошибки деления.
9. Определение. Виды определений.
10. Правила и ошибки определения.
11. Суждение. Логическое значение как характеристика суждения. Структура простого атрибутивного суждения.
12. Количество и качество простого атрибутивного суждения.
13. Распределенность терминов простого атрибутивного суждения.
14. Отношения между простыми атрибутивными суждениями по истинности (контрарность, контрадикторность, субконтрарность, подчинение). Умозаключения по «логическому квадрату».
15. Сложные суждения. Понятие логического союза. Конъюнкция, дизъюнкция, строгая дизъюнкция, импликация, тождество (эквиваленция), отрицание (инверсия).
16. Табличное определение логических союзов.
17. Умозаключение. Структура и виды умозаключений.
18. Непосредственные умозаключения из простых атрибутивных суждений: обращение.
19. Непосредственные умозаключения из простых атрибутивных суждений: превращение.
20. Опосредованные умозаключения из простых атрибутивных суждений: простой категорический силлогизм (ПКС). Термины и посылки ПКС. Понятие фигуры и модуса ПКС.
21. Правила простого категорического силлогизма.
22. Метод опровержения неправильных модусов ПКС с помощью круговых схем.
23. Умозаключения из сложных суждений: условно-категорический силлогизм, разделительно-категорический силлогизм.
24. Умозаключения из сложных суждений: разделительно-категорический силлогизм.
25. Общая характеристика недедуктивных умозаключений.
26. Энумеративная индукция. Полная индукция и математическая индукция как виды демонстративных умозаключений.
27. Элиминативная индукция. Понятие причинной зависимости. Методы элиминативной индукции: единственного сходства, единственного различия, сопутствующих изменений, остатков.
28. Умозаключения по аналогии: виды аналогий, методы повышения достоверности вывода по аналогии.
29. Структура доказательства. Прямые и косвенные доказательства.
30. Правила доказательства. Ошибки и уловки в доказательствах.
Общая характеристика науки логики. Понятие логической формы и логического закона.
Логика-наука о формах и законах мышления.
Мышление – специфический предмет логики, цель которого наделить содержание формой.
Главный вопрос мышления –каким свойством должен обладать предмет для того ,чтобы удовлетворять определенным требованиям логики как науки.
—->Логику интересует объективный результат различных субъективных процессов—à
—-àРезультат мыслительного процесса- знание .
———àзнание является объективным исходом мыслительного процесса.
Знание
Состоит из 2 существенных разнородных компонентов
| |
| |
Содержание -это форма представления знания- Совокупность разнородных сведений, отвечает за системную связь истины
Значение которых отлично друг от друга
Источник появления знания — опыт
Понятие логической формы
Одна из задач логики заключается в выявлении и систематизации логических форм.
Логическая форма отражает объективный мир в его общих структурных связях, которые воплощаются и в структуре наших мыслей.
Мышление- источник появления логической формы.
Логической формой конкретной мысли является строение этой мысли, т.е. способ связи ее составных частей.
Понятия, суждения, умозаключения имеют свои специфические формы (структуры).
1. “если А, то В”- разные по содержанию высказывания эмфиморфны.
2. “А- это В”
3. “A R B”-форма отношения
4.
ТАКИМ ОБРАЗОМ ,ЗАДАЧА ЛОГИКИ-ВЫЯВИТЬ И СИСТЕМАТИЗИРОВАТЬ ЛОГИЧЕСКИЕ ЗАКОНЫ,А ТАК ЖЕ ПРИМЕНЯТЬ ИХ И УПРАВЛЯТЬ ИМИ
И наоборот
чем больше у понятия содержание, те м меньше у него объем
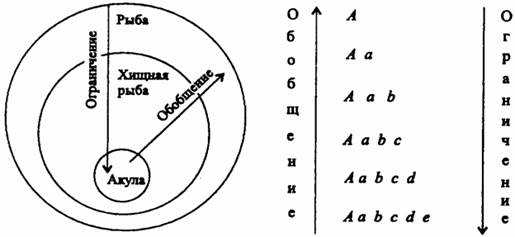
Ограничение — логическая операция перехода от родового понятия к видовому (например, “поэт”, “великий поэт”, “великий английский поэт”, “великий английский поэт Джордж Ноэл Гордон Байрон”). При ограничении мы переходим от понятия с большим объемом к понятию с меньшим объемом. Пределом ограничения является единичное понятие (в данном примере это “великий английский поэт Джордж Ноэл Гордон Байрон”).
Обобщение — логическая операция, обратная ограничению, когда осуществляется переход от видового понятия к родовому путем отбрасывания от первого его видообразующего признака или признаков. Пример обобщения: “Опера П. И. Чайковского “Евгений Онегин”, “опера П. И. Чайковского”, “опера русского композитора XIX в.”, “опера русского композитора”, “опера”, “произведение музыкального искусства”, “произведение искусства”. При обобщении мы переходим от понятия с меньшим объемом к понятию с большим объемом. Обобщение применяется во всех определениях понятий, которые даются через род и видовое отличие. Пределом обобщения являются категории (философские, общенаучные, категории конкретных наук)а
| Ограничение | Обобщение |
| 1. Река в Африке | 1. Большой пресный проточный водоем |
| 2. Река в Африке, впадающая в Средиземное море | 2. Пресный проточный водоем |
| 3. Большая река в Африке, впадающая в Средиземное море | 3. Пресный водоем |
| 4. Большая река в Египте | 4. Водоем |
| 5. Река Нил |
Правила и ошибки деления
.
Правило первое. Деление должно быть соразмерным. Это означает, что общий объем членов деления должен равняться объему делимого родового понятия, т.е. В+С=А. Например, в утверждении «звуки делятся на согласные и гласные» это правило учтено.
Данное правило гарантирует от двух ошибок:
а) неполного (с остатком) деления. Так, деление понятия «право» на государственное, административное, гражданское, уголовное будет неполным, с остатком;
б) обширного (с избытком) деления. Например, утверждение «По значению имена существительные делятся на собственные, нарицательные и одушевленные» будет широким, с избытком. В этом предложении понятие «одушевленные» явно лишнее.
Правило второе. Деление должно производиться по одному основанию. Хотя объем одного и того же понятия можно разделить по-разному в зависимости от избранного основания, однако при однократном делении нельзя наряду с видами, соответствующими основанию деления, называть виды, ему не соответствующие.
Ошибка, возникающая при нарушении этого правила, носит название «подмена основания»Ошибочно, например, любимое обращение деда Щукаря из романа «Поднятая целина» М. Шолохова к односельчанам: «Уважаемые граждане и старушки!» Здесь смешаны два основания — обращение к людям, являющимся гражданами страны, и обращение к женщинам пожилого возраста.
Правило третье. Деление должно быть последовательным. Это означает, что делимое понятие должно представлять ближайший род для членов деления, а члены деления должны быть непосредственными видами делимого понятия. Нельзя переходить к подвидам, минуя непосредственно видовые понятия.
Нарушение этого правила ведет к логической ошибке «скачок в делении«. Такую ошибку совершают, когда говорят: «Средства массовой информации делятся на государственные, коммерческие, местные, независимые и военные». Это неверно, так как средства массовой информации делятся на государственные и коммерческие, а те, в свою очередь, подразделяются на ряд подвидов.
Правило четвертое. Члены деления должны взаимно исключать друг друга. Согласно этому правилу, члены деления должны быть соподчиненными понятиями, их объемы не должны перекрещиваться.
Нарушение этого правила связано с потерей основания деления. Например, при осуществлении классификации войн говорят: «Войны бывают справедливые, несправедливые, захватнические». Здесь допущена логическая ошибка. Захватнические войны относятся к числу несправедливых войн, и поэтому члены деления «несправедливые войны» и «захватнические войны» не исключают друг друга.
Субъект, предикат и связку.
Субъектсуждения (S) — то, о чем говорится в суждении, т.е. это понятие о предмете суждения.
Предикатсуждения (P) — то, что говорится о субъекте суждения, т.е. это понятие о признаке предмета.
Связкасуждения — то, что связывает субъект и предикат в единое суждение; она обычно выражается словами «есть» или «не есть». Если субъект суждения обозначить буквой S, предикат — буквой P, то структуру атрибутивного суждения можно выразить так:
S –есть/не есть– Р
Структура умозаключений.
- посылки- исходные суждения
- следствие- суждение,вытекающее из посылок
- форма связи посылок и заключений
Виды умозаключений:
по характеру связи между знанием различной степени общности, выраженному в посылках и заключении:
1. дедуктивные- от общего знания к частному- умозаключение, в котором переход от общего знания к частному является логически необходимым.
В зависимости от количества посылок дедуктивные умазаключения делятся на:
1. непосредственные — умозаключения, вытекающие из одной посылки
2. апосредственные – умозаключения, вытекающие более чем из одной посылки
2.индуктивные- от частного знания кобщему
3. абдуктивные —умозаключения по аналогии-от частного знания к частному.
В зависимости от строгости правил вывода различают:
1. демонстративные (необходимые) — логическое следование в такого рода выводах представляет собой логический закон
2. недемонстративные (правдоподобные) — правила вывода обеспечивают лишь вероятностное следование заключения из посылок.
Вопросы к экзамену по логике
1. Общая характеристика науки логики. Понятие логической формы и логического закона.
2. Основные законы формальной логики: закон тождества, закон недопущения противоречия закон исключенного третьего, закон достаточного основания.
3. Понятие. Объем и содержание понятия. Закон обратного соотношения объема и содержания понятия.
4. Виды понятий: пустые, логически пустые, фактически пустые, непустые, общие, единичные, абстрактные, конкретные, собирательные, несобирательные, положительные, отрицательные.
5. Отношения между понятиями. Сравнимые и несравнимые понятия. Совместимые и несовместимые понятия. Равнообъемность, пересечение, подчинение; соподчинение, противоположность, противоречие.
6. Обобщение и ограничение понятий.
7. Деление понятий. Структура и виды деления.
8. Правила и ошибки деления.
9. Определение. Виды определений.
10. Правила и ошибки определения.
11. Суждение. Логическое значение как характеристика суждения. Структура простого атрибутивного суждения.
12. Количество и качество простого атрибутивного суждения.
13. Распределенность терминов простого атрибутивного суждения.
14. Отношения между простыми атрибутивными суждениями по истинности (контрарность, контрадикторность, субконтрарность, подчинение). Умозаключения по «логическому квадрату».
15. Сложные суждения. Понятие логического союза. Конъюнкция, дизъюнкция, строгая дизъюнкция, импликация, тождество (эквиваленция), отрицание (инверсия).
16. Табличное определение логических союзов.
17. Умозаключение. Структура и виды умозаключений.
18. Непосредственные умозаключения из простых атрибутивных суждений: обращение.
19. Непосредственные умозаключения из простых атрибутивных суждений: превращение.
20. Опосредованные умозаключения из простых атрибутивных суждений: простой категорический силлогизм (ПКС). Термины и посылки ПКС. Понятие фигуры и модуса ПКС.
21. Правила простого категорического силлогизма.
22. Метод опровержения неправильных модусов ПКС с помощью круговых схем.
23. Умозаключения из сложных суждений: условно-категорический силлогизм, разделительно-категорический силлогизм.
24. Умозаключения из сложных суждений: разделительно-категорический силлогизм.
25. Общая характеристика недедуктивных умозаключений.
26. Энумеративная индукция. Полная индукция и математическая индукция как виды демонстративных умозаключений.
27. Элиминативная индукция. Понятие причинной зависимости. Методы элиминативной индукции: единственного сходства, единственного различия, сопутствующих изменений, остатков.
28. Умозаключения по аналогии: виды аналогий, методы повышения достоверности вывода по аналогии.
29. Структура доказательства. Прямые и косвенные доказательства.
30. Правила доказательства. Ошибки и уловки в доказательствах.
Общая характеристика науки логики. Понятие логической формы и логического закона.
Логика-наука о формах и законах мышления.
Мышление – специфический предмет логики, цель которого наделить содержание формой.
Главный вопрос мышления –каким свойством должен обладать предмет для того ,чтобы удовлетворять определенным требованиям логики как науки.
—->Логику интересует объективный результат различных субъективных процессов—à
—-àРезультат мыслительного процесса- знание .
———àзнание является объективным исходом мыслительного процесса.
Знание
Состоит из 2 существенных разнородных компонентов
| |
| |
Содержание -это форма представления знания- Совокупность разнородных сведений, отвечает за системную связь истины
Значение которых отлично друг от друга
Источник появления знания — опыт
Понятие логической формы
Одна из задач логики заключается в выявлении и систематизации логических форм.
Логическая форма отражает объективный мир в его общих структурных связях, которые воплощаются и в структуре наших мыслей.
Мышление- источник появления логической формы.
Логической формой конкретной мысли является строение этой мысли, т.е. способ связи ее составных частей.
Понятия, суждения, умозаключения имеют свои специфические формы (структуры).
1. “если А, то В”- разные по содержанию высказывания эмфиморфны.
2. “А- это В”
3. “A R B”-форма отношения
4.
ТАКИМ ОБРАЗОМ ,ЗАДАЧА ЛОГИКИ-ВЫЯВИТЬ И СИСТЕМАТИЗИРОВАТЬ ЛОГИЧЕСКИЕ ЗАКОНЫ,А ТАК ЖЕ ПРИМЕНЯТЬ ИХ И УПРАВЛЯТЬ ИМИ
cyberpedia.su
Что такое логика: определение и законы
Логика – многообразное понятие, плотно вошедшее в нашу жизнь и культуру речи. В этой статье мы с вами рассмотрим с научной точки зрения, что такое логика. Определение, виды, законы логики и историческая справка нам в этом помогут.
Общая характеристика
Итак, что такое логика? Определение логики очень многогранно. В переводе с греческого она означает «мысль», «разум», «слово» и «закономерность». В современной интерпретации данное понятие используется в трех случаях:
- Обозначение взаимосвязей и закономерностей, объединяющих поступки людей или события в объективном мире. В этом смысле часто используют такие понятия, как «логическая цепочка», «логика фактов», «логика вещей» и так далее.
- Обозначение строгой последовательности и закономерности процесса мышления. В таком случае употребляются выражения типа: «логика рассуждения», «логика мышления», «логика речи» и так далее.
- Обозначение особой науки, изучающей логические формы и операции, а также связанные с ними законы мышления.

Задачи логики
Как можно заметить, в каждой конкретной ситуации может быть как минимум один из нескольких ответов на вопрос: «Что такое логика?» Определение задач логики менее объемно. Главная задача – прийти к выводу на основе предпосылок и получить знание о предмете рассуждения, чтобы глубже проникнуться его соотношениями с другими аспектами рассматриваемого явления. В любой науке одним из главных инструментов является логика. Она не только является важным подразделом философии, но и затрагивает некоторые математические учения. «Алгебра логики» – определение, известное в математических кругах. Иногда его путают с булевой алгеброй, которая является основой информатики, но это не совсем верно.
Неформальная логика
Главным образом логику классифицируют на:
- Неформальную.
- Формальную.
- Символическую.
- Диалектическую.
Неформальная логика – это исследование аргументации в первоначальном языке. Данный термин наиболее распространен в англоязычной литературе. Таким образом, главная задача неформальной логики – изучение логических ошибок в речи. Вывод, который сделан на естественном языке, может обладать чисто формальным содержанием, в случае если можно проиллюстрировать, что он является не иначе как частным применением универсального правила.

Формальная и символическая логика
Анализ вывода, раскрывающий то самое формальное содержание, и называется формальной логикой. Что же касается символической логики, то она исследует символические абстракции, фиксирующие формальный состав логического вывода.
Диалектическая логика
Диалектической логикой называют науку о мышлении, дающую знание об образе рассуждения, который расширяет возможности формального вывода. В этом случае понятие логики может быть использовано как в собственном логическом смысле, так и в виде некой метафоры.
Диалектическое рассуждение частично опирается на формальные законы логики. Вместе с тем, анализируя динамику перехода понятий в их противоположность, оно допускает совпадение противоположностей, а значит, ориентируется на диалектические законы.
Объект логики
Определение логики как науки подразумевает, что ее объектом является человеческое мышление. Мышление является сложным, многосторонним процессом, предполагающим обобщенное отражение человеком вещей и отношений окружающего мира. Данный процесс изучается разными науками: философией, психологией, генетикой, языкознанием, и кибернетикой. Философия рассматривает происхождение и суть мышления, а также его отождествление с материальным миром и познанием. Психология контролирует условия нормальной работы мышления и его развития, а также влияния на него окружающей среды. Генетика стремится к изучению механизма наследования способностей к размышлению. Языкознание ищет связи между мышлением речью. Ну а кибернетики пытаются построить технические модели человеческого мозга и мышления. Сама же логика смотрит на процесс мышления с точки зрения структуры мыслей, а также верности или неверности рассуждений, отвлекаясь при этом от содержания и развития мыслей.

Предмет логики
Предметом данной области знаний является логическая форма, связанные с ней операции и законы мышления. Лучше всего рассматривать предмет изучения логики, через процесс познания окружающего мира человеком. Познанием называют процесс, во время которого индивид получает знания о мире. Есть два способа получения знаний:
- Чувственное познание. Осуществляется с помощью органов чувств или приборов.
- Рациональное познание. Осуществляется с помощью абстрактного мышления.
Материалистическая теория познания основывается на теории отражения. Согласно этой теории, суждения, вещи и явления объективного мира могут воздействовать на органы чувств человека и активизировать работу системы передачи информации в мозг, а также активизировать сам мозг, в результате чего в мышлении человека создаются образ этих самых вещей и явлений.
Чувственное познание
Чувственными образом называют знание о внешних свойствах тех или иных вещей и явлений. Чувственное познание может протекать в трех формах:
- Ощущение. Отражает отдельные свойства предмета.
- Восприятие. Отражает предмет в целом, представляет собой его целостный образ.
- Представление. Это образ предмета, сохранившийся в памяти.
На стадии чувственного познания, человеку не всегда доступна сущность вещей и процессов, их внутренние свойства. Маленький принц из одноименного рассказа Экзюпери говорил: «Самого главного глазами не увидишь». Разум или абстрактное мышление приходят на помощь органам чувств в таких случаях.

Рациональное познание
Абстрактное мышление отражает действительность с точки зрения основных свойств и отношений. Познание мира через абстрактное мышление происходит опосредовано, а не явно. Оно не предполагает обращение к наблюдениям и практике, а строится на основе более глубоких рассуждений о свойствах и взаимоотношениях предметов и явлений. К примеру, по следам преступника можно воссоздать картину происшествия, по термометру можно узнать, какая погода на улице, и так далее.
Важной особенностью абстрактного мышления является его тесная связь с языком. Каждая мысль оформляется с помощью слов и словосочетаний, проговариваясь посредством внутренней или внешней речи. Мышление не только помогает человеку описать окружающий мир, но и позволяет сформулировать новые идеи, абстракции, прогнозы и предвидения, то есть решает многочисленные логические задачи. Определения «логика» и «мышление» в этой связи тесно связаны друг с другом. Мышление, независимости от того, абстрактное оно или рациональное, может протекать в трех главных формах: понятие, суждение и умозаключение. Рассмотрим их отдельно.
Понятие
Представляет собой форму мышления, с помощью которой человек создает мысленные образы о предметах, их характеристиках и взаимоотношениях. Понятие невозможно без определения. Но правила определений в логике мы рассмотрим немного ниже. В процессе формирования понятий индивид занимается анализом интересующего его предмета, сравнением его с другими предметами, выделением его основных отличительных черт, абстрагированием от несущественных черт и обобщением разных предметов на основе этих признаков. В результате создаются мысленные образы предметов, их свойств и отношений.
Понятия играют важную роль в познавательной деятельности человека. Благодаря им можно обобщать то, что в реальности существует по отдельности. В объективном мире нет таких понятий, как студент, ученик, клерк, спортсмен и т. д., все они представляют собой обобщенные образы, которые могут существовать только в идеальном мире, то есть в голове человека.

Образований понятий открывает возможность получения знаний о предметах и явлениях на основе основных свойств класса подобных предметов или явлений. О том, каким был бы мир, если люди не оперировали понятиями в общении друг с другом, повествует Джонатан Свифт в своем рассказе о путешествиях Гулливера. Согласно рассказу, однажды мудрец посоветовал людям в разговоре использовать не понятия о предметах, а непосредственно предметы. Многие последовали его рекомендации, но для того чтобы нормально поговорить с собеседником, им приходилось носить на плечах мешки с разными вещами. Разумеется, такая беседа с демонстрацией предметов даже у владельцев самых больших мешков была очень скудна.
Понятие не может существовать без определения. В разных науках определение может трактоваться с некоторыми отличиями. Определение понятий в логике – это процесс закрепления конкретного смысла за неким языковым термином. По своей сути понятие бесконечно, так как оно вырабатывается универсальным разумом. Определение конечно, так как оно представляет собой итог рассудочной (логической) деятельности. Согласно Гегелю, определение не соответствует Абсолюту и соотносится с представлением. Задача философии состоит в том, чтобы перевести понятия в представления, избавившись от конечных определений.
В понятии заключается смысл. А определение понятий в логике представляет собой действие, нацеленное на выявление этого смысла. Таким образом, понятием можно назвать слово, которое через логические умозаключения получило определение. Следовательно, без определения слово не является понятием, даже если оно имеет распространение. Дать определение понятию – значит описать его значение, уточнив все основные нюансы. Причем если сделать это за пределами рамок определенной системы знаний, то могут возникнуть ошибки в определениях. Логика у каждого своя, ровно как и понимание того или иного слова. Поэтому, говоря на философские темы, важно определять понятия.
Виды определений в логике представлены весьма широко. Определение бывает: интенсиональным, реальным, аксиоматическим, номинальным, явным, неявным, генетическим, контекстуальным, индуктивным и остенсивным.

Суждение
На основе понятий о предметах человек может высказывать относительно них суждения и делать умозаключения. Суждением называют форму мышления, в рамках которой в адрес предмета мысли что-то утверждается или отрицается. Из одного суждения можно получать другое. К примеру, на основе факта, что все люди смертны, можно сделать вывод, что тот, кто умер – человек. Во время построения понятий, суждений и умозаключений каждый может допустить ошибки как сознательные, так и бессознательные. Чтобы их избежать, нужно знать основы правильного мышления.
Правильным называют мышление, в рамках которого из истинных знаний получаются новые истинные знания. Результатом неправильного мышления могут стать также ложные знания. К примеру, есть два суждения: «Если Иван совершил грабеж – он преступник» и «Иван не совершал грабеж». Суждение «Иван не преступник», полученное на основе этой информации, может быть ложным, так как факт того, что он не совершал грабеж, не свидетельствует о том, что он не совершал других преступлений.
Умозаключения
Говоря о правильности умозаключений, ученые подразумевают соблюдение правил их построения и взаимосвязи. Именно на этом базируется определение законов логики как науки о мышлении. Формальная логика абстрагируется от конкретного содержания и развития мыслей. Вместе с тем она делает акцент на истинности и ложности этих мыслей. Часто правильное мышление называют логичным, делая акцент на названии науки, изучающей определенную сторону мышления.
Вопрос истинности или ложности суждений и умозаключений – это вопрос о соответствии или несоответствии того что в них говорится, объективному миру. В истинном суждении объективно отражается положение вещей в объективной реальности. Ложное суждение, наоборот, не соответствует действительности. Вопросом о том, что такое истина и как чувственное познание соотносится с абстрактным мышлением, занимается уже не логика, а философия.

Заключение
Сегодня мы с вами узнали, что такое логика. Определение этого понятия весьма емкое и многогранное, оно затрагивают широкую область знаний. Такое многообразие проявлений логики иллюстрирует ее взаимосвязь с другими науками, некоторые из которых вполне материалистичны. Также в статье были рассмотрены основные аспекты человеческого мышления: умозаключения, суждения, понятия и определения (в логике). Примеры из жизни помогли нам легче усвоить этот материал.
fb.ru
Свойство (логика) Википедия
Необходимое условие и достаточное условие — виды условий, логически связанных с некоторым суждением. Различие этих условий используется в логике и математике для обозначения видов связи суждений.
Необходимое условие
Если импликация A⇒B{\displaystyle A\Rightarrow B} является абсолютно истинным высказыванием, то истинность высказывания B{\displaystyle B} является необходимым условием для истинности высказывания A{\displaystyle A}[1][2].
Необходимыми условиями истинности утверждения А называются условия, без соблюдения которых А не может быть истинным.
Суждение P является необходимым условием суждения X, когда из (истинности) X следует (истинность) P. То есть, если P ложно, то заведомо ложно и X.
Для суждений X типа «объект принадлежит классу M» такое суждение P называется свойством (элементов) M.
Достаточное условие
Если импликация A⇒B{\displaystyle A\Rightarrow B} является абсолютно истинным высказыванием, то истинность высказывания A{\displaystyle A} является достаточным условием для истинности высказывания B{\displaystyle B}[1][2].
Достаточными называются такие условия, при наличии (выполнении, соблюдении) которых утверждение А является истинным.
Суждение P является достаточным условием суждения X, когда из (истинности) P следует (истинность) X, то есть в случае истинности P проверять X уже не требуется.
Для суждений X типа «объект принадлежит классу M» такое суждение P называется признаком принадлежности классу M.
Необходимое и достаточное условие
Суждение K является необходимым и достаточным условием суждения X, когда K является как необходимым условием X, так и достаточным. В этом случае говорят ещё что K и X равносильны, или эквивалентны, и обозначают K⇔X{\displaystyle K\Leftrightarrow X} или K↔X{\displaystyle K\leftrightarrow X}.
Это следует из тождественно истинной формулы, связывающей импликацию и операцию эквиваленции[3]:
(X↔Y)↔(X⇒Y)∧(Y⇒X){\displaystyle (X\leftrightarrow Y)\leftrightarrow (X\Rightarrow Y)\land (Y\Rightarrow X)}
Для суждений X типа «объект принадлежит классу M» такое суждение K называется критерием принадлежности классу M.
Пример
Суждение X: «Вася получает стипендию».
Необходимое условие P: «Вася — учащийся».
Достаточное условие Q: «Вася учится в вузе без троек».
Из того, что Вася — учащийся, ещё не следует, что он получает стипендию. Но это условие необходимо, то есть если Вася не учащийся, то он заведомо не получает стипендии.
Если же Вася учится в вузе без троек, то он заведомо получает стипендию. Тем не менее, студент Вася может получать стипендию (в виде пособия), если он учится с тройками, но, например, имеет хроническое заболевание.
В импликации A → B
A — это достаточное условие для B
B — это необходимое условие для A
См. также
Ссылки
- Видео о необходимом и достаточном условиях
Примечания
Литература
- Эдельман С.Л. Математическая логика. — М.: Высшая школа, 1975. — 176 с.
- Гиндикин С.Г. Алгебра логики в задачах. — М.: Наука, 1972. — 288 с.
wikiredia.ru
Свойство (логика) Википедия
Необходимое условие и достаточное условие — виды условий, логически связанных с некоторым суждением. Различие этих условий используется в логике и математике для обозначения видов связи суждений.
Необходимое условие[ | ]
Если импликация A⇒B{\displaystyle A\Rightarrow B} является абсолютно истинным высказыванием, то истинность высказывания B{\displaystyle B} является необходимым условием для истинности высказывания A{\displaystyle A}[1][2].
Необходимыми условиями истинности утверждения А называются условия, без соблюдения которых А не может быть истинным.
Суждение P является необходимым условием суждения X, когда из (истинности) X следует (истинность) P. То есть, если P ложно, то заведомо ложно и X.
Для суждений X типа «объект принадлежит классу M» такое суждение P называется свойством (элементов) M.
Достаточное условие[ | ]
Если импликация A⇒B{\displaystyle A\Rightarrow B} является абсолютно истинным высказыванием, то истинность высказывания A{\displaystyle A} является достаточным условием для истинности высказывания B{\displaystyle B}[1][2].
Достаточными называются такие условия, при наличии (выполнении, соблюдении) которых утверждение А является истинным.
Суждение P является достаточным условием суждения X, когда из (истинности) P следует (истинность) X, то есть в случае истинности P проверять X уже не требуется.
Для суждений X типа «объект принадлежит классу M» такое суждение P называется признаком принадлежности классу M.
Необходимое и достаточное условие[ | ]
Суждение K является необходимым и достаточным условием суждения X, когда K является как необходимым условием X, так и достаточным. В этом случае говорят ещё что K и X равносильны, или эквивалентны, и обозначают
ru-wiki.ru
