Сила ампера действующая на проводник с током i в магнитном поле индукцией в – ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ПРЯМОЛИНЕЙНЫЙ ПРОВОДНИК С ТОКОМ. ЗАКОН АМПЕРА. РАБОТА ПО ПЕРЕМЕЩЕНИЮ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ.

43. Сила Ампера. Сила Лоренца

Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.

Сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником:

F=B^.I^.ℓ^.sin α — закон Ампера.

Сила, действующая на заряженную движущуюся частицу в магнитном поле, называется силой Лоренца:

Если вектор vчастицы перпендикуляренвектору В,то частица описывает траекторию в виде окружности:

Роль центростремительной силы играет сила Лоренца: 

При этом радиус окружности: ,

Если вектор скорости и частицы не перпендикулярен В, то частица описывает траекторию в виде винтовой линии (спирали).

44. Теорема о циркуляции вектора магнитной индукции. Применение теоремы о циркуляции вектора магнитной индукции для расчета поля прямого тока. Циркуляция вектора магнитной индукции через замкнутый контур=произведению магнитной постоянной на алгебраическую сумму токов, охватываемых контуром.

∫BdL=μ₀I; I=ΣI_i

I2

I1>0 I2<0

Теорема говорит о том, что магнитное поле не является потенциальным, а является вихревым.

Применение в тетради

45. Закон электромагнитной индукции. Правило Ленца

Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции ε_инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:

Эта формула носит название закона Фарадея.

Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца.

Правило Ленца отражает тот экспериментальный факт, что ε_индивсегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

ε_i=-N, гдеN- кол-во витков

Способ возникновения ЭДС:

1.рамка неподвижна, но изменяется магнитный поток за счёт движения ккатушки или за счет изменения силы тока в ней.

2.рамка перемещается в поле непожвижной катушки.

46. Явление самоиндукции.

Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока называется явлением самоиндукции.

Магнитный поток, обусловленный собственным током контура (сцепленный с контуром), пропорционален магнитной индукции, которая, в свою очередь, по закону Био-Савара-Лапласа, пропорциональна току.

, где L –коэффициент самоиндукции или индуктивность, «геометрическая» характеристика проводника, так как зависит от его формы и размеров, а также от магнитных свойств среды.

47. Уравнения Максвелла в интегральной форме. Свойства уравнений Максвелла.

Закон Гаусса Поток электрической индукции через замкнутую поверхность s пропорционален величине свободного заряда, находящегося в объёме v, который окружает поверхность s.

Закон Гаусса для магнитного поля Поток магнитной индукции через замкнутую поверхность равен нулю (магнитные заряды не существуют).

Закон индукции Фарадея Изменение потока магнитной индукции, проходящего через незамкнутую поверхность, взятое с обратным знаком, пропорционально циркуляции электрического поля на замкнутом контуре, который является границей поверхности.

Теорема о циркуляции магнитного поля

Полный электрический ток свободных зарядов и изменение потока электрической индукции через незамкнутую поверхность , пропорциональны циркуляции магнитного поля на замкнутом контуре, который является границей поверхности.

Свойства уравнений Максвелла.

            А. Уравнения Максвелла линейны. Они содержат только первые производные полейEиBпо времени и пространственным координатам, а так же первые степени плотности электрических зарядов ρ и токов γ. Свойство линейности уравнений непосредственно связано с принципом суперпозиции.

            Б. Уравнения Максвелла содержат уравнение непрерывности, выражающее закон сохранения электрического заряда:

                                               ∫pdv=const

            В. Уравнения Максвелла выполняются во всех инерциальных системах отсчёта. Они являются релятивистски-инвариантными, что подтверждается опытными данными.

            Г. О симметрииуравнений Максвелла.

            Уравнения не симметричны относительно электрического и магнитного полей. Это обусловлено тем, что в природе существуют электрические заряды, но нет магнитных зарядов. Вместе с тем в нейтральной однородной среде, где ρ = 0 и j=0 ,уравнения Максвелла приобретают симметричный вид, т.е.Eтак связано с(dB/dt) , какBсdE/dt.

                                               

Различие только в знаках перед производными(dB/dt)  и(dD/dt)  показывает, что линии вихревого электрического поля, индуцированного уменьшением поляB, образуют с вектором(dB/dt)   левовинтовую систему, в то время как линии магнитного поля, индуцируемого изменениемD, образуют с вектором (dD/dt)   правовинтовую систему.

           

Д. Об электромагнитных волнах.

            Из уравнений Максвелла следует важный вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать самостоятельно без электрических зарядов и токов. При этом изменение его состояния обязательно имеет волновой характер. Всякое изменение во времени магнитного поля возбуждает поле электрическое, изменение электрического поля, в свою очередь, возбуждает магнитное поле. За счёт непрерывного взаимопревращения они и должны сохранятся. Поля такого рода называются электромагнитными волнами. Выяснилось также, что ток смещения(dD/dt)   играет в этом явлении первостепенную роль.

studfiles.net

Сила, действующая на проводник с током в магнитном поле

План решения задач

1. При расчете силы Ампера, действующей на проводник с током в магнитном поле, решение следует начать с рисунка, на котором нужно отразить форму проводника и направление вектора магнитной индукции поля, в котором находится проводник.

2. Необходимо иметь в виду, что формула силы Ампера справедлива только для прямого проводника с током длиной , который находится в однородном магнитном поле с индукцией . В случае неоднородного МП, а также для проводника криволинейной формы, проводник следует разделить на элементы тока и показать на рисунке векторы сил , действующих на элементы тока. Для этого необходимо выбрать два элемента тока, расположенных симметрично. Направление векторов определяем по правилу векторного произведения или

по правилу левой руки: располагаем руку так, чтобы линии магнитной индукции входили в ладонь, четыре пальца направляем вдоль тока , тогда отогнутый большой палец покажет направление силы Сила, действующая на весь проводник, определяется как сумма векторов элементарных сил по всей длине проводника :

.

3. Свободный замкнутый контур с током (рамка или виток) устанавливается в магнитном поле так, чтобы его магнитный момент был сонаправлен с вектором магнитной индукции . При этом механический (вращающий) момент , а силы Ампера , действующие на элементы тока контура, растягивают его. Такое положение ( контура с током в однородном магнитном поле является состоянием устойчивого равновесия контура.

Задача 32. По трем параллельным прямым проводникам, находящимся на одинаковом расстоянии друг от друга (рис. 63 а) текут одинаковые токи В двух проводниках направления токов совпадают. Вычислите для каждого проводника силу, действующую на единицу длины проводника.

Дано Решение

Сначала рассмотрим взаимодействие двух проводников – первого и второго (рис. 63 б). На второй проводник с током действует магнитное поле с индукцией , созданное током в первом проводе (соответственно, и на первый проводник действует магнитное поле , созданное вторым проводом). Выберем на втором проводнике элемент тока , проведем линию магнитной индукции (это окружность радиусом ) и по касательной к ней направим вектор . Сила Ампера, действующая на выбранный элемент тока второго проводника со стороны МП первого тока

(1)

Модуль этой силы

, (2)

где угол между векторами и (линия магнитного поля расположена в плоскости, перпендикулярной проводу). Согласно формуле (2), сила, действующая со стороны первого провода на единицу длины второго провода:

(3)

В формуле (3) индукция МП, созданная прямым длинным проводом с током в точках на расстоянии от провода, определяется следующим выражением:

(4)

Направление силы определяем по правилу левой руки, располагая ладонь в плоскости рисунка: элемент тока притягивается к первому проводнику. По третьему закону Ньютона, на элемент тока первого проводника будет действовать сила , т. е. равная по модулю (см. формулу (3)) и противоположно направленная (см. рис. 63 б). Таким образом, параллельные токи одинакового направления притягиваются друг к другу. Изменим мысленно на рис. 63 б направление второго тока на противоположное (как ток ) и правило левой руки покажет, что сила, действующая на элемент тока , направлена вправо, т. е. параллельные токи противоположных направлений взаимно отталкиваются.

На каждый из проводников действуют магнитные поля двух других токов. Величину каждой силы парного взаимодействия -того и -того проводов запишем, подставляя индукцию магнитного поля, определяемую формулой (4) (в данной задаче ), в формулу (3):

. (5)

В соответствии с полученным выражением (5), величина силы парного взаимодействия на единицу длины одинакова для каждого проводника.

Результирующую силу, действующую на каждый проводник, находим с помощью принципа суперпозиции сил:

(6)

Покажем эти силы магнитного взаимодействия токов на рис. 63 в, учитывая, во-первых, взаимное направление токов, и во-вторых, равенство модулей всех сил парного взаимодействия . На рисунке заменим элементарную силу силой, действующей на весь i-тый провод со стороны -того тока, так как эти силы сонаправлены: .

Согласно формулам (6), сложим по два вектора сил, действующих на каждый проводник, геометрически: по правилу параллелограмма (треугольника) (см. рис. 63 в). Так как треугольники, имеющие сторонами векторы сил , равносторонние, то модули этих сил

(7)

Модуль силы найдем по теореме косинусов:

(8)

Силы, действующие на единицу длины провода, с учетом формулы (5), представятся выражениями, соответствующими формулам (7) и (8):

; (9)

(10)

Вычисляем силы: а) на единицу длины первого и второго провода:

.

б) на единицу длины третьего провода:

.

Задача 33. Квадратная проволочная рамка со стороной расположена в одной плоскости с длинным прямым поводом (рис. 64 а). Расстояние от провода до ближайшей стороны рамки . Ток в проводе , в рамке . Определите силы , действующие на каждую сторону рамки, и силу, действующую на всю рамку.

Дано Решение

Индукция магнитного поля, создаваемого длинным прямым проводом с током в точке, находящейся на расстоянии от провода, определяется следующей формулой:

. (1)

Величина уменьшается по мере увеличения расстояния , следовательно, это магнитное поле неоднородное. Направление вектора определяем по такому вращению буравчика, чтобы винт перемещался бы вдоль тока . В области, где находится рамка, вектор направлен перпендикулярно плоскости рамки «от нас» (рис. 64 б).

Найдем силу , действующую на сторону , суммируя бесконечно малые силы , действующие на элементы тока :

; (2)

(3)

По правилу левой руки определяем, что все векторы , перпендикулярные вектору магнитной индукции , лежат в плоскости рамки, а в этой плоскости они перпендикулярны стороне . Силы являются сонаправленными, причем, сторона притягивается к проводу, так как ток в ней одинакового направления с током в проводе (см. рис. 64 б). Модуль силы :

(4)

Здесь величина (в соответствии с формулой (1), в которой для стороны ) одинакова во всех точках МП, где находится сторона рамки . Тогда действующая на нее сила

(5)

Аналогичный расчет будет и для силы , действующей на сторону рамки , так как вдоль этой стороны величина также одинакова, но меньше, чем для стороны , так как расстояние от провода больше: . Соответственно и модуль силы :

(6)

Вектор также перпендикулярен стороне рамки ( ), но он направлен от провода с током : токи в проводе и в стороне противоположных направлений, поэтому они отталкиваются (см. рис. 64 б).

Силы , действующие на стороны и рамки с током, также перпендикулярны элементам тока и вектору магнитной индукции , в соответствии с векторным произведением в формуле (2), и направления их определяем также по правилу левой руки (см. рис. 64 б). Стороны рамки и расположены одинаково по отношению к проводу с током , магнитное поле которого действует на ток в рамке. Следовательно, модули этих сил одинаковы: .

Рассчитаем, например, силу , суммируя элементарные силы по длине стороны :

. (7)

Здесь величина не одинакова вдоль стороны , но уменьшается по мере удаления элемента тока от провода, согласно формуле (1). В подинтегральном выражении (7) заменим (см. рис. 64 б), чтобы перейти к одной переменной – расстоянию элемента тока от провода; пределы по этой переменной: , – соответствуют начальному и конечному элементам тока на стороне . Продолжим расчет силы

(8)

Вычислим модули сил, действующих на стороны рамки, по формулам (5), (6) и (8):

.

.

.

Найдем результирующую силу, действующую на рамку в целом, складывая векторы сил, действующих на стороны рамки:

(9)

Здесь , так как и вектор (см. рис. 64 б). Так как сила , то модуль результирующей силы

Направление вектора результирующей силы совпадает с направлением большего из векторов сил – с вектором .

Таким образом, в неоднородном магнитном поле на данную рамку с током действует сила в направлении градиента индукции МП: , который направлен в область более сильного МП. Силы растягивают рамку с током, что соответствует данному случаю , где – магнитный момент рамки с током.

Задача 34.На оси контура с током, магнитный момент которого , находится другой такой же контур. Магнитный момент второго контура перпендикулярен оси первого контура. Расстояние межу контурами , причем, размеры контуров малы по сравнению с расстоянием Определите механический момент , действующий на второй контур.

Дано Решение

Магнитный момент контура с током – это вектор , направленный по нормали к плоскости контура так, что направление вектора связано с направлением тока в контуре правилом буравчика (правого винта). Первый контур с током создает магнитное поле с индукцией . Величина в точках на оси кругового контура рассчитана в решении задачи 27:

, (1)

где – расстояние от точек контура до точки в МП, в которой определяется величина . Так как по условию задачи расстояние велико по сравнению с радиусом контура, то величина .

На второй контур с током в магнитном поле с индукцией действует механический (вращающий) момент , величина которого определяется следующей формулой:

. (2)

Так как размеры второго контура тоже малы, то величина несущественно изменяется вдоль плоскости второго контура. Поэтому примем ее равной , определяемой формулой (1), в которой . Согласно векторному произведению в формуле (2), вектор перпендикулярен плоскости, в которой лежат векторы и , т. е. он перпендикулярен плоскости рисунка (см. рис. 65). Этот механический момент будет стремиться повернуть второй контур до положения, в котором вектор (при этом величина обратится в нуль).

Модуль вращающего момента, согласно формуле (2),

, (3)

где – угол между векторами магнитного момента контура и индукцией магнитного поля . По условию задачи вектор , а последний создает магнитное поле , следовательно, вектор (см. рис. 65) и .

Подставляя величину магнитной индукции по формуле (1) в выражение (3), получаем следующую расчетную формулу:

. (4)

Вычисляем по формуле (4) механический момент, действующий на второй контур с током в магнитном поле, созданном первым контуром с током:

.

Задача 35.Два прямолинейных длинных параллельных проводника находятся на расстоянии друг от друга. По проводникам в одном направлении текут токи и . Какую работу (на единицу длины проводника) нужно совершить, чтобы раздвинуть эти проводники до расстояния ?

Дано Решение

Параллельные токи одинакового направления притягиваются друг к другу, т. е. второй проводник с током притягивается к первому силой Ампера . Чтобы его отодвинуть от первого проводника, нужно приложить внешнюю силу , незначительно превышающую силу притяжения проводников: . Работа этой внешней силы

(1)

Найдем силу Ампера – силу магнитного взаимодействия проводников с током, как силу, с которой магнитное поле первого проводника действует на ток во втором проводнике:

(2)

В уравнении (2) суммируются элементарные силы , действующие на элементы тока , расположенные по всей длине второго проводника с током. Направление сил определяем по правилу левой руки, размещая ладонь в плоскости рисунка (рис. 66), так как вектор магнитной индукции перпендикулярен плоскости рисунка (он направлен «к нам»). Силы , действующие на элементы тока , сонаправлены, поэтому можем складывать их модули:

(3)

Здесь , так как вектор ; – магнитная индукция поля, созданного прямым током , она определяется формулой

, (4)

где – расстояние от проводника с током до точки, в которой определяется индукция магнитного поля.

Подставим величину в подинтегральное выражение (3) и выполним интегрирование, отметив, что расстояние всех элементов тока второго проводника от первого одинаково, так как проводники параллельные:

(5)

Сила Ампера, действующая на единицу длины проводника, в соответствии с формулой (5), представится следующим выражением:

(6)

Согласно полученной формуле, эта сила уменьшается с увеличением расстояния между проводниками, т. е. имеем дело с работой переменной силы, которая определяется, как сумма элементарных работ, интегралом (1). Работу на единицу длины проводника найдем, подставляя силу по формуле (6) в подинтегральное выражение (1):

(7)

Вычислим работу, которую совершает внешняя сила при удалении от первого проводника с током второго проводника с током на единицу его длины, принимая, что магнитная проницаемость воздуха :

.

Задача 36.Тонкий проводник в виде полукольца радиусом находится в однородном магнитном поле с индукцией . Плоскость полукольца перпендикулярна линиям магнитной индукции, а подводящие провода расположены вдоль линий . По проводнику протекает ток . Определите силу , действующую на проводник.

Дано Решение

Выделим на полукольце элемент тока и определим направление действующей на него силы Ампера

(1)

Для этого используем правило левой руки, располагая ладонь в плоскости рисунка (рис. 67). Так как элементы тока кольцевого проводника имеют различную ориентацию, то векторы , перпендикулярные элементам тока , образуют «веер векторов» в плоскости полукольца. Для сложения таких векторов каждый элементарный вектор силы разложим на составляющие по осям :

(2)

Силу, действующую на весь проводник длины , находим, суммируя по всей длине полукольца векторы сил, действующих на элементы тока:

(3)



infopedia.su

Referat. Сила Ампера — PhysBook

Сила Ампера

Сила, с которой магнитное поле действует на помещенный в него проводник с током, называется силой Ампера.

Величина этой силы, действующей на элемент Δl проводника с током I в магнитном поле с индукцией \(~\vec B\) , определяется законом Ампера:

\(~\Delta F = B \cdot I \cdot \Delta l \cdot \sin \alpha\) , (1)

где α – угол между направлениями тока и вектора индукции.

Направление силы Ампера можно найти с помощью правила левой руки (рис. 1):

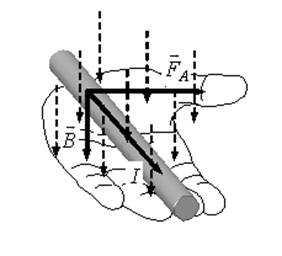
Рис. 1

если левую руку расположить так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца совпадали по направлению с направлением тока, то отогнутый на 90° большой палец укажет направление силы, действующей на элемент проводника.

Использование этого правила затруднительно лишь в том случае, когда угол α мал. Поскольку, однако, величина B∙sin α представляет собой модуль перпендикулярной проводнику с током компоненты вектора индукции \(~\vec B_{\perp}\) (рис. 2), то ориентацию ладони можно определять именно этой компонентой – она должна входить в открытую ладонь левой руки.

Рис. 2

Из (1) следует, что сила Ампера равна нулю, если проводник с током расположен вдоль линий магнитной индукции, и максимальна, если проводник перпендикулярен этим линиям.

Закон Ампера выполняется для любого магнитного поля. Предположим, что это поле создается длинным линейным проводником с током I₂, параллельным первому проводнику c током I₁ и находящимся на расстоянии r от него. Тогда индукцию магнитного поля в точках расположения первого проводника можно определить (с учетом замены I → I₂) по формуле:

\(~B = \frac{\mu_0 \cdot I}{2 \pi \cdot r} = \frac{\mu_0 \cdot I_2}{2 \pi \cdot r}\) .

Подставляя это выражение в (1) и замечая, что в рассматриваемом случае параллельных проводников α = 90°, находим силу, действующую на линейный элемент Δl первого проводника,

\(~\Delta F = \frac{\mu_0 \cdot I_2}{2 \pi \cdot r} \cdot I_1 \cdot \Delta l = \mu_0 \cdot \frac{I_2 \cdot I_1 \cdot \Delta l}{2 \pi \cdot r} \) . (2)

Совершенно ясно, что точно такое же выражение можно записать для силы, действующей на второй проводник. Используя правило буравчика (для определения магнитной индукции проводника с током) и правило левой руки (для определения силы, действующей на проводник с током), можно убедиться в том, что если токи в проводниках текут в одинаковых направлениях, то эти проводники притягиваются (рис. 3 а, б), а если в разных – отталкиваются (рис. 4, а, б), что и подтверждается опытом.

• а

• б

Рис. 3

• а

• б

Рис. 4

Выражение (2) было положено в основу принципа определения единицы силы тока. Если в (2) считать I₁ = I₂ = 1 А, r = 1 м, Δl = 1 м, то получим F = 2∙10^-7 Н/м. Другими словами,

если по двум параллельным, бесконечно длинным линейным проводникам, расположенным на расстоянии 1 м друг от друга, текут одинаковые токи в 1 А, то эти токи взаимодействуют с силой 2∙10^-7 Н на каждый метр длины проводников.

Заметим, что единица силы тока – ампер – в СИ принадлежит, наряду с секундой, метром, килограммом, кельвином, молем и канделой, к числу основных единиц измерения физических величин.

Момент сил, действующий на прямоугольную рамку с током

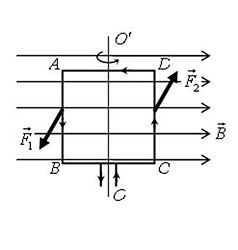
Поместим в однородном магнитном поле с индукцией \(~\vec B\) прямоугольную рамку с током ABCD (рис. 5 а – вид сбоку; рис. 5 б – вид сверху), где обозначим AB = a, AD = b, β – угол между перпендикуляром к рамке и вектором магнитной индукции.

• 

  а

• 

  б

Рис. 5

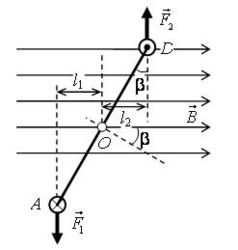
На участки AD и BC магнитное поле действуют с силами, которые меняются от нуля до максимального значения (в зависимости от угла поворота рамки β) и стремятся растянуть рамку (на рис. 5 эти силы не указаны). На участки AB и CD магнитное поле действуют с постоянными силами \(~\vec F_1\) и \(~\vec F_2\), которые направлены в противоположные стороны (на рис. 5 а силы направлены перпендикулярно плоскости рисунка) и стремятся повернуть рамку вокруг оси OO´. Таким образом, эти силы \(~\vec F_1\) и \(~\vec F_2\) создают вращающий момент \(~M = F_1 \cdot l_1 + F_2 \cdot l_2\) , где \(~F_1 = F_2 = I \cdot B \cdot l\) (угол α = 90°), \(~l_1 = l_2 = \frac{AD}{2} \sin \beta = \frac{b}{2} \sin \beta\) , \(~l = AB = CD = a\) . Тогда

\(~M = 2 F_1 \cdot l_1 = 2I \cdot B \cdot a \cdot \frac{b}{2} \cdot \sin \beta = I \cdot B \cdot a \cdot b \cdot \sin \beta = I \cdot B \cdot S \cdot \sin \beta\) ,

где \(~S = a \cdot b\) – площадь рамки.

Момент сил будет максимальным при β = 90° (рамка расположена вдоль линий индукции)

\(~M_{max} = I \cdot B \cdot S\) . (3)

Отметим, что формула (3) справедлива не только для квадратной рамки, но и для плоской рамки другой формы.

Применение силы Ампера в технике

Электрический двигатель постоянного тока

В электрических двигателях для преобразования электрической энергии в механическую используется действие силы Ампера.

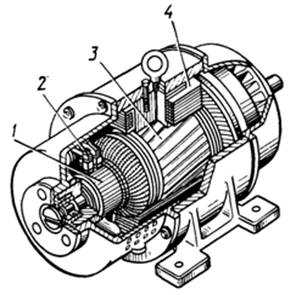
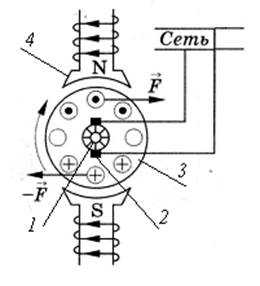
Основными частями электродвигателя постоянного тока (рис. 6) являются индуктор 4, с помощью которого создается постоянное магнитное поле, якорь 3, через обмотки которого пропускается ток, и коллектор 1 с электрическими щетками 2, с помощью которых осуществляется соединение обмоток якоря с источником тока.

• 

  а

• 

  б

Рис. 6

В простейшей машине постоянного тока индуктор – это постоянный магнит или электромагнит со стальным сердечником. Обмотки электромагнита индуктора называются обмотками возбуждения. Магнит индуктора имеет полюсные наконечники такой формы, что между ними образуется отверстие цилиндрической формы. Между полюсными наконечниками индуктора помещается якорь. Якорь состоит из сердечника – стального цилиндра с пазами, параллельными оси цилиндра, и обмоток, вложенных в пазы сердечника (рис. 7). Выводы каждой обмотки соединены с медными контактами коллектора.

Рис. 7

Якорь насажен на ось, концы которой установлены в подшипниках, и может свободно вращаться вокруг этой оси.

Для постоянного вращения рамки с током в магнитном поле необходимо устройство, меняющее направление тока. Такое устройство – коллектор – было изобретено в XIX веке. В простейшем случае он представляет собой два металлических полукольца 1, насаженных на общую с рамкой ось 2, и к которым припаяны провода обмотки 4 (рис. 8). К коллектору с двух противоположных сторон прижимаются щетки 3 из графита или меди; щетки подключаются проводами 5 к источнику постоянного напряжения.

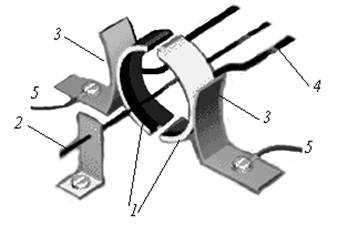
Рис. 8

При включении ток проходит через щетки, полукольца и обмотку, в результате чего под действием пары сил Ампера обмотка начинает поворачиваться и поворачивает полукольца коллектора. Когда плоскость обмотки окажется перпендикулярной линиям магнитной индукции, вращающий момент обратится в ноль. Однако это положение обмотка проскакивает по инерции, и с этого момента каждое из полуколец, повернувшись вместе с рамкой, станет прикасаться уже к другой щетке. В результате направление тока в обмотке изменится на противоположное, а возникший после такой смены направления тока вращающий момент будет вынуждать обмотку вращаться в прежнем направлении до тех пор, пока ее плоскость снова не станет перпендикулярной вектору индукции. После этого направление тока в обмотке снова изменится, и она продолжит вращение, и т.д.

Скорость вращения якоря электродвигателя можно регулировать, изменяя силу тока в его обмотках; направление вращения можно изменять, изменяя направление тока в обмотке якоря или индуктора.

Электродвигатель постоянного тока может приводить в движение колеса электровоза, троллейбуса, трамвая, приводить в действие электробритву, магнитофон и другие бытовые электроприборы.

Электроизмерительные приборы

В электроизмерительных приборах магнитоэлектрической системы используется действие магнитного поля на проводник с током (рис. 9).

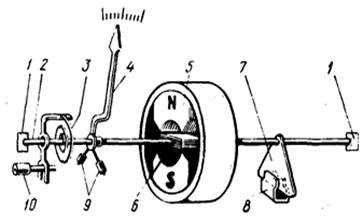
Рис. 9

Измеряемый электрический ток пропускается через рамку 6, помещенную в магнитное поле постоянного магнита 5. Рамка укреплена на оси 2. Измеряемый ток подводится к рамке 6 через спиральную пружину 3. На участки проводников, расположенные перпендикулярно линиям индукции магнитного поля, действует сила Ампера. Если бы подвижная часть измерительного механизма не имела пружину 3, противодействующую ее повороту, то при пропускании тока через рамку происходил бы поворот ее на 180° независимо от силы тока. Но силы упругости, возникающие при закручивании пружины, препятствуют повороту рамки. Сила упругости прямо пропорциональна углу закручивания пружины, поэтому угол поворота, при котором наступает равенство моментов сил Ампера и сил упругости, пропорционален силе тока в рамке. Шкала магнитоэлектрического прибора равномерная.

При изменениях силы тока равновесие моментов сил упругости и сил Ампера нарушается, в результате подвижная система начинает совершать колебания относительно нового положения равновесия. Вместе с ней колеблется и стрелка прибора. Для устранения этих колебаний в приборах применяются специальные успокоители. В них для торможения подвижной системы используется тонкая алюминиевая пластина 7, помещенная между полюсами постоянного магнита 8 и закрепленная на оси вращения подвижной системы. При повороте подвижной системы алюминиевая пластина успокоителя движется в поле постоянного магнита. Наводимые в ней при этом индукционные токи тормозят движение пластины и вместе с тем вращение всей подвижной системы электроизмерительного прибора.

Для того чтобы при любом положении указательной стрелки 4 подвижная часть была уравновешена в поле тяжести, имеются противовесы 9. Установка на нулевое деление шкалы производится с помощью корректора 10.

Прибор можно проградуировать так, чтобы угол поворота определял силу тока в амперах или других единицах. Согласно закону Ома сила тока в приборе \(~I = \frac{U}{R}\) . Поэтому прибор можно проградуировать и так, чтобы определенному углу отклонения стрелки соответствовало напряжение U на зажимах прибора в вольтах или других единицах.

Таким образом, прибор может служить как амперметром, так и вольтметром. В последнем случае для увеличения сопротивления прибора нужно последовательно с катушкой включить резистор с большим сопротивлением.

Литература

1. Буров Л.И., Стрельченя В.М. Физика от А до Я: учащимся, абитуриентам, репетиторам. – Мн.: Парадокс, 2000. – 560 с.
2. Мякишев, Г.Я. Физика : Электродинамика. 10-11 кл. : учеб. для углубленного изучения физики / Г.Я. Мякишев, А.3. Синяков, В.А. Слободсков. – М.: Дрофа, 2005. – 476 с.
3. Физика: Учеб. пособие для 10 кл. шк. и классов с углубл. изуч. физики/ О. Ф. Кабардин, В. А. Орлов, Э. Е. Эвенчик и др.; Под ред. А. А. Пинского. – 2-е изд. – М.: Просвещение, 1995. – 415 с.

www.physbook.ru

На проводник с током, находящийся в магнитном поле, действует сила, равная

F = I·L·B·sina

I — сила тока в проводнике;
B — модуль вектора индукции магнитного поля;
L — длина проводника, находящегося в магнитном поле;
a — угол между вектором магнитного поля инаправлением тока в проводнике.

Силу, действующую на проводник с током в магнитном поле, называют силой Ампера.

Максимальная сила Ампера равна:

F = I·L·B

Ей соответствует a = 90⁰.

Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая вектора магнитной индукции В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 градусов большой палец покажет направление силы, …
действующей на отрезок проводника с током, то есть силы Ампера.

 

25) Закон Био-Савара-Лапласа. Принцип суперпозиции. Пример

Опыт, как уже отмечалось, свидетельствует о том, что источником магнитного поля является электрический ток. Но каким образом можно вычислить вектор магнитной индукции поля, зная этот ток?

Для магнитного поля, также как и для электрического, справедлив принцип суперпозиции электрических полей. Справедливость этого принципа нельзя доказать теоретически. Он подтверждается только экспериментально.

Суть этого принципа состоит в следующих двух положениях.

1) Если ток I₁ создаёт в некоторой точке пространства магнитное поле , то этот вектор магнитной индукции не изменится при появлении других токов: I₂, I₃, …, I_n. Это означает, что появление новых токов и новых полей не искажает индукции магнитного поля исходного тока I₁.

2) Если магнитное поле создаётся несколькими токами, то индукция такого поля равна векторной сумме магнитных индукций складываемых полей:

(8.4)

Эти положения многократно подтверждены экспериментально.

Теперь применим принцип суперпозиции для расчёта магнитного поля электрического тока: вектор магнитной индукции поля, созданного электрическим током, равен векторной сумме магнитных индукций от отдельных элементов этого тока:

.

Для окончательного решения этой задачи нужно только знать, какое поле создаёт элемент тока .

В решении этой проблемы добились успеха французские учёные: физики экспериментаторы Био и Савар и математик Лаплас. Они установили, что вектор магнитной индукции поля, созданного элементом тока , равен:

(закон Био-Савара-Лапласа, 1820 г.), (8.5)

здесь: — элемент тока;

— радиус-вектор, проведённый от элемента тока в точку, где вычисляется магнитное поле (рис. 8.5.)

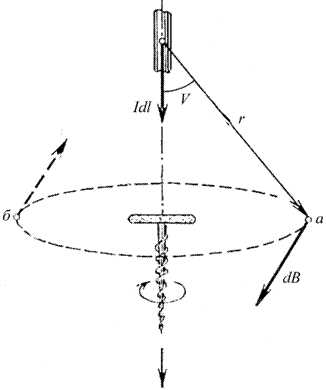
Рис. 8.5.

Таким образом, был найден «элементарный кирпичик» магнитного поля. Зная поле элемента тока (8.5), можно теперь, опираясь на принцип суперпозиции магнитных полей, рассчитать поле любого тока.

Прежде, чем перейти к примерам расчёта магнитных полей, напомним, что точно тот же самый метод мы использовали и при рассмотрении электростатических полей. Что являлось «элементарным кирпичиком» электростатического поля? Поле точечного заряда. А далее, используя принцип суперпозиции электрических полей, мы получали возможность рассчитать поле любого заряда, разделяя его на составляющие точечные заряды.

1. Магнитное поле прямолинейного тока

Ток I течёт по бесконечному прямолинейному проводнику. Вычислим индукцию магнитного поля этого тока на расстоянии lот проводника (рис. 8.6.).

 

Рис. 8.6.

Элемент тока создаёт в рассматриваемой точке магнитное поле:

.

Вектор направлен перпендикулярно плоскости рисунка от нас (правило буравчика).

В скалярной форме это уравнение можно записать так:

. (8.6)

Для отыскания полного поля в точке А нужно просуммировать вклады всех элементов данного тока, то есть, рассмотреть интеграл:

.

Как следует из рисунка:

, .

Используя эти данные в (8.6), получим:

.

Теперь при сложении этих вкладов, то есть, при интегрировании, будет меняться только угол a в пределах от 0 до p:

. (8.7)

Вектор магнитной индукции поля прямолинейного тока пропорционален величине тока I и обратно пропорционален расстоянию b от проводника до рассматриваемой точки.

Магнитное поле, также как и электростатическое, принято представлять графически магнитными силовыми линиями. Как и прежде, это, в общем случае, кривая, касательные к любой точке которой совпадают по направлению с векторами магнитной индукции в данных точках (рис. 8.7.).

 

Рис. 8.7.

Густота магнитных силовых линий равна значению индукции в данной области пространства.

«Густота» — это число силовых линий, проходящих через единичную поверхность, ориентированную перпендикулярно магнитному полю.

Поле прямолинейного тока обладает цилиндрической симметрией. Его силовые линии — окружности с центром на оси тока (рис. 8.8.).

 

26) Магнитная индукция от прямого проводника с током. Взаимодействие проводников с токами.

загрузка…

Магнитная индукция движущегося заряда. Взаимодействие движущихся зарядов.

 

Магнитные явления были известны еще в древнем мире. Компас был изобретен более 4500 лет тому назад. В Европе он появился приблизительно в XII веке новой эры. Однако только в XIX веке была обнаружена связь между электричеством и магнетизмом и возникло представление о магнитном поле.

Первыми экспериментами (проведены в 1820 г.), показавшими, что между электрическими и магнитными явлениями имеется глубокая связь, были опыты датского физика Х. Эрстеда. Эти опыты показали, что на магнитную стрелку, расположенную вблизи проводника с током, действуют силы, которые стремятся ее повернуть. В том же году французский физик А. Ампер наблюдал силовое взаимодействие двух проводников с токами и установил закон взаимодействия токов.

По современным представлениям, проводники с током оказывают силовое действие друг на друга не непосредственно, а через окружающие их магнитные поля.

Источниками магнитного поля являются движущиеся электрические заряды (токи). Магнитное поле возникает в пространстве, окружающем проводники с током, подобно тому, как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле. Магнитное поле постоянных магнитов также создается электрическими микротоками, циркулирующими внутри молекул вещества (гипотеза Ампера).

Ученые XIX века пытались создать теорию магнитного поля по аналогии с электростатикой, вводя в рассмотрение так называемые магнитные заряды двух знаков (например, северный N и южный S полюса магнитной стрелки). Однако опыт показывает, что изолированных магнитных зарядов не существует.

Магнитное поле токов принципиально отличается от электрического поля. Магнитное поле, в отличие от электрического, оказывает силовое действие только на движущиеся заряды (токи).

Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности электрического поля. Такой характеристикой является вектор магнитной индукции который определяет силы, действующие на токи или движущиеся заряды в магнитном поле.

За положительное направление вектора принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно ориентирующийся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора Такое исследование позволяет наглядно представить пространственную структуру магнитного поля. Аналогично силовым линиям в электростатике можно построить линии магнитной индукции, в каждой точке которых вектор направлен по касательной. Пример линий магнитной индукции полей постоянного магнита и катушки с током приведен на рис. 1.16.1.

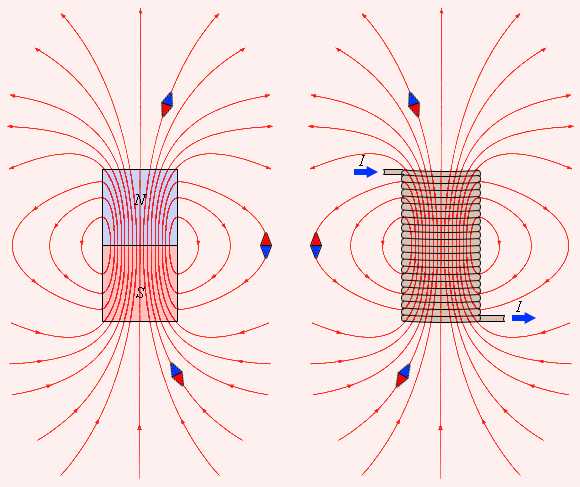Рисунок 1.16.1. Линии магнитной индукции полей постоянного магнита и катушки с током. Индикаторные магнитные стрелки ориентируются по направлению касательных к линиям индукции

Обратите внимание на аналогию магнитных полей постоянного магнита и катушки с током. Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми. Картину магнитной индукции можно наблюдать с помощью мелких железных опилок, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль линий индукции.

Для того, чтобы количественно описать магнитное поле, нужно указать способ определения не только направления вектора но и его модуля. Проще всего это сделать, внося в исследуемое магнитное поле проводник с током и измеряя силу, действующую на отдельный прямолинейный участок этого проводника. Этот участок проводника должен иметь длину Δl, достаточно малую по сравнению с размерами областей неоднородности магнитного поля. Как показали опыты Ампера, сила, действующая на участок проводника, пропорциональна силе тока I, длине Δl этого участка и синусу угла α между направлениями тока и вектора магнитной индукции:

Эта сила называется силой Ампера. Она достигает максимального по модулю значения F_max, когда проводник с током ориентирован перпендикулярно линиям магнитной индукции. Модуль вектора определяется следующим образом:

Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока I в проводнике и его длине Δl:

В общем случае сила Ампера выражается соотношением:

Это соотношение принято называть законом Ампера.

В системе единиц СИ за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (Тл).

Тесла – очень крупная единица. Магнитное поле Земли приблизительно равно 0,5·10^–4 Тл. Большой лабораторный электромагнит может создать поле не более 5 Тл.

Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику. Для определения направления силы Ампера обычно используют правило левой руки: если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы, действующей на проводник (рис. 1.16.2).

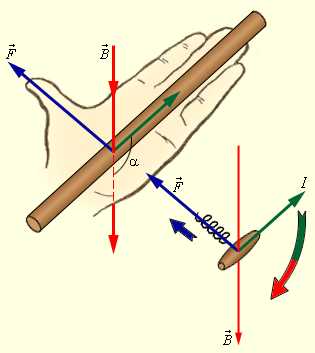Рисунок 1.16.2. Правило левой руки и правило буравчика

Если угол α между направлениями вектора и тока в проводнике отличен от 90°, то для определения направления силы Ампера более удобно пользоваться правилом буравчика: воображаемый буравчик располагается перпендикулярно плоскости, содержащей вектор и проводник с током, затем его рукоятка поворачивается от направления тока к направлению вектора Поступательное перемещение буравчика будет показывать направление силы Ампера (рис. 1.16.2). Правило буравчика часто называют правилом правого винта.

Одним из важных примеров магнитного взаимодействия является взаимодействие параллельных токов. Закономерности этого явления были экспериментально установлены Ампером. Если по двум параллельным проводникам электрические токи текут в одну и ту же сторону, то наблюдается взаимное притяжение проводников. В случае, когда токи текут в противоположных направлениях, проводники отталкиваются.

---

refac.ru

30. Действие магнитного поля на проводник с током. Закон Ампера. Единицы измерения магнитной индукции.

Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, ис­пытываемый рамкой, есть результат дейст­вия сил на отдельные ее элементы. Обоб­щая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находяще­гося в магнитном поле, прямо пропорцио­нальна силе тока I в проводнике и век­торному произведению элемента дли-

ной dl проводника на магнитную индук­цию В:

dF = I[dl, В]. (111.1)

Направление вектора dF может быть найдено, согласно (111.1), по общим пра­вилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.

Модуль силы Ампера (см. (111.1)) вычисляется по формуле

dF = IBdlsin, (111.2)

где a — угол между векторами dl и В.

Закон Ампера применяется для опре­деления силы взаимодействия двух токов. Рассмотрим два бесконечных прямолиней­ных параллельных тока I₁ и I₂ (направле­ния токов указаны на рис. 167), расстоя­ние между которыми равно R. Каждый из проводников создает магнитное поле, ко­торое действует по закону Ампера на дру­гой проводник с током. Рассмотрим, с ка­кой силой действует магнитное поле тока I₁ на элемент dl второго проводника с то­ком I₂. Ток I₁ создает вокруг себя магнит­ное поле, линии магнитной индукции кото­рого представляют собой концентрические окружности. Направление вектора b₁ за­дается правилом правого винта, его мо­дуль по формуле (110.5) равен

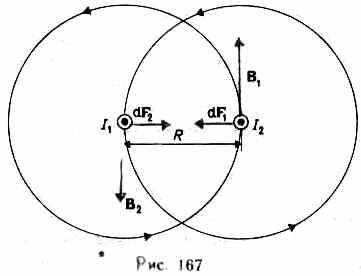
Направление силы dF₁, с которой поле B₁ действует на участок dl второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, со­гласно (111.2), с учетом того, что угол  между элементами тока I₂ и вектором B₁ прямой, равен

dF₁=I₂B₁dl, или, подставляя значение для В₁, получим

Рассуждая аналогично, можно пока­зать, что сила dF₂, с которой магнитное поле тока I₂ действует на элемент dl пер­вого проводника с током I₁, направлена в противоположную сторону и по модулю равна

Сравнение выражений (111.3) и (111.4) показывает, что

dF₁=dF₂,

т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой

Если токи имеют противоположные на­правления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяе­мая формулой (111.5).

Закон Ампера позволяет определить единицу магнитной индукции В. Предпо­ложим, что элемент проводника dl с током I перпендикулярен направлению магнит­ного поля. Тогда закон Ампера (см. (111.2)) запишется в виде

dF=IBdl,

откуда

Единица магнитной индукции — тесла (Тл): 1 Тл—магнитная индукция такого однородного магнитного поля, которое действует с силой в 1 Н на каждый метр длины прямолинейного проводника, распо­ложенного перпендикулярно направлению поля, если по этому проводнику проходит ток в 1 А:

1Тл=1Н/(А•м).

Так как ₀= 4•10^-7 Н/А², а в случае вакуума (=1), согласно (1.09.3), В =₀H, то для данного случая

H=В/₀.

Единица напряженности магнитного поля — ампер на метр (А/м): 1 А/м — напряженность такого поля, магнитная индукция которого в вакууме равна 4•10^-7 Тл.

studfiles.net

Репетитор-онлайн — подготовка к ЦТ

Пример 5. Два параллельных изолированных проводника длиной по 50 см расположены перпендикулярно силовым линиям магнитного поля с индукцией 0,10 Тл. В проводниках токи 8,0 и 6,0 А текут навстречу друг другу. Проводники скреплены между собой стержнем из непроводящего материала и находятся в непроводящей среде. Считая, что проводники не взаимодействуют друг с другом, определить модуль силы, действующей на стержень.

Решение. По условию задачи проводники не взаимодействуют между собой, но каждый из них взаимодействует с магнитным полем.

Со стороны магнитного поля на каждый из проводников действует сила Ампера:

• на первый проводник

F _1A = I ₁Bl,

где I ₁ — сила тока в первом проводнике, I ₁ = 8,0 А; B — модуль индукции магнитного поля, B = 0,10 Тл; l — длина первого проводника, l = 50 см;

• второй проводник

F _2A = I ₂Bl,

где I ₂ — сила тока во втором проводнике, I ₂ = 6,0 А; l — длина второго проводника, l = 50 см.

На рисунке показаны проводники с токами, направление индукции магнитного поля и силы Ампера, действующие на каждый из проводников с током со стороны магнитного поля.

Согласно правилу левой руки, сила Ампера, действующая на первый проводник, направлена влево, а сила Ампера, действующая на второй проводник, — вправо.

На стержень действуют следующие силы:

• со стороны первого проводника —

F→1=F→1A;

• со стороны второго проводника —

F→2=F→2A.

Направления сил, действующих на стержень, совпадают с направлением соответствующих сил Ампера.

Равнодействующая сил, действующих на стержень, равна векторной сумме:

F→=F→1+F→2,

проекция ее на координатную ось Ox:

F _x = −F ₁ + F ₂.

С учетом F ₁ = I ₁Bl и F ₂ = I ₂Bl проекция равнодействующей на указанную ось:

F _x = −I ₁Bl + I ₂Bl = Bl(I ₂ − I ₁).

Вычислим:

Fx=0,10⋅50⋅10−2(6,0−8,0)=−10⋅10−2 Н=−0,10 Н.

Модуль равнодействующей силы:

F=|Fx|=|−0,10| Н=0,10 Н.

vedy.by

Сила, действующая на проводник с током в магнитном поле (Сила Ампера)

Поиск Лекций

---

Если считать, что магнетизм обусловлен северными и южными магнитными массами (представления, господствовавшие до 20-ых годов 19 века), то характер взаимодействия этих масс в точности повторяет закон взаимодействия точечных зарядов в электростатике (сила взаимодействия электрических и магнитных зарядов направлена по полю). Однако, ситуация изменяется кардинальным образом, если считать, что магнитное поле создается проводниками с током: если поместить проводник с током в магнитное поле, то сила, действующая на проводник направлена не по полю, а перпендикулярно ему.

Для определения величины силы, действующей на проводник с током со стороны магнитного поля, следует поместить прямоугольный контур с током в однородное магнитное поле, откуда

 

 

Направление силы Ампера определяется по правилу буравчика: силовые линии поля входят в ладонь, четыре пальца показывают направление тока. Тогда отогнутый большой палец укажет направление силы.

 

Выражение для силы Ампера в дифференциальной форме

 

 

 

Закон Био-Савара-Лапласа.Лаплас, анализируя результаты экспериментов Био и Савара, предложил способ отыскания величины индукции магнитного поля, создаваемого отрезками проводников с током произвольной конфигурации: для определения величины В необходимо разбить проводник на малые, элементарные участки d и затем найти векторную сумму элементарных индукций d , создаваемых всеми участками проводника.

 

Id

d

Индукция магнитного поля в

центре кругового тока

Индукция магнитного поля,

создаваемая прямым

Проводником с током

Магнитное взаимодействие параллельных токов.

Один ток – источник магнитного поля, второй – объект его воздействия.

 

F- сила, действующая на единицу длины одного проводника, со стороны магнитного поля, создаваемого всем другим проводником.

.

Из этого выражения следует определение единицы измерения силы тока:

Один ампер — это сила постоянного тока, текущего по каждому из двух параллельных, бесконечно длинных проводников бесконечно малого кругового сечения в вакууме на расстоянии 1 метр, и создающая силу взаимодействия между ними 2×10⁻⁷ Н на каждый метр длины проводника.

Теорема о циркуляции вектора В.

Циркуляция вектора В магнитного поля, создаваемого прямым проводником с током I, по окружности радиуса R

 

 

Оказывается, что этот результат справедлив и для случая проводника с током и замкнутого контура интегрирования произвольных форм.

Используя принцип суперпозиции:Циркуляция вектора магнитной индукции равна алгебраической сумме токов, охватываемых контуром интегрирования, умноженной на μ₀.

 

 

Поле бесконечно длинного

Соленоида

где n- число витков, приходящееся

на единицу длины соленоида

Поле тороида

где N- общее число витков

Магнитное поле, создаваемое движущимся зарядом.Следуя историческому развитию теории магнетизма, найдем выражение для индукции магнитного поля, создаваемого движущимся зарядом, опираясь на закон Био-Савара-Лапласа – выражение для индукции магнитного поля, создаваемого элементом тока Id

 

poisk-ru.ru