Самостоятельная работа производная сложной функции 11 класс – Самостоятельная работа «Применение производной при исследовании свойств функции» 10 класс — Алгебра/ геометрия 10-11 класс — Математика — Методическая копилка — Международное сообщество педагогов «Я

Самостоятельная работа, 11 класс, алгебра и начала математического анализа

Самостоятельная работа по алгебре 11 класс по теме «Дифференцирование показательной и логарифмической функции». Вариант 1. 1.Найдите производную функции: а) у = ех + х2,5 ; б) у = ln(x2 + 1) – 4x ; в) у = 2ех + cos3x ; г) у = е2х-5 ∙ х3 ; д) у = 3-2х + . 2.Составьте уравнение касательной к графику функции у = 5х – 3 + ех-1 в точке с абсциссой, равной 1.

Самостоятельная работа по алгебре 11 класс по теме «Дифференцирование показательной и логарифмической функции». Вариант 2. 1.Найдите производную функции: а) у = х1,2 — ех б) у = ln(8-3х) – 8x ; в) у = 3ех — sin2x ; г) у = е2-x ∙ ; д) у = 25x + . 2.Составьте уравнение касательной к графику функции у = 2х + 5 — ех+3 в точке с абсциссой, равной — 3.

Самостоятельная работа по алгебре 11 класс по теме «Дифференцирование показательной и логарифмической функции». Вариант 3. 1.Найдите производную функции: а) у = е-х – tq2x ; б) у = — ln(x2 + 1) – 4x ; в) у = 2ех + cos3x + 3x5 ; г) у = ех-5 ∙ х2 ; д) у = 4-2х + . 2.Касательная к графику функции у = 5х – 4е2х параллельна прямой у = — 3х + 4. Найдите абсциссу точки касания.

Самостоятельная работа по алгебре 11 класс по теме «Дифференцирование показательной и логарифмической функции». Вариант 4. 1.Найдите производную функции: а) у = -е—x + ctq; б) у = ln(x + 1) + 4x3; в) у = 2ех + cos2x ; г) у = е2х-5 ∙ х4 ; д) у = 6-2х + . 2. Касательная к графику функции у = 4е3х – 7х параллельна прямой у = 5х — 1. Найдите абсциссу точки касания.

videouroki.net

Конспект урока алгебры 11 класса по теме «Производная сложной функции»

11 класс

Тема: Производная сложной функции.

Тип урока: – урок изучения нового материала.

Форма урока: применение информационных технологий.

Место урока в системе уроков по данному разделу: первый урок.

Цели:

• научить распознавать сложные функции, уметь применять правила вычисления производных; совершенствовать предметные, в том числе вычислительные, умения и навыки;

• развивать логическое и математическое мышление

• воспитывать самостоятельность.

Ход урока.

I. Организационный момент (1 мин.).

II. Постановка целей. Мотивация учащихся (1 мин.).

III. Актуализация опорных знаний (5 мин.).

1. Дать определение производной функции.

2. Назовите правила вычисления производной.

3. Устная работа.

Найдите производные функций.

а) y = 2x² + x ;

б) f(x) = 3x² – 7x + 5;

в) f(x) = ;

г) f(x) = 1/2x²;

д) f(x) = (2x – 5)(x + 3).

4. Правила вычисления производных.

Повторение формул по компьютеру со звуковым сопровождением.

IV. Программированный контроль (5 мин.).

Обменяйтесь тетрадями. Отметьте в диагностических картах верно выполненные задания знаком +, а неверно выполненные задания знаком “–”.

V. Изучение нового материала (5 мин.).

Сложная функция.

Рассмотрим функцию, заданную формулой f(x) = 

Для того, чтобы найти производную данной функции, надо сначала вычислить производную внутренней функции u= v(x) = xІ + 7x + 5, а затем вычисляют производную функции g(u) =  .

Говорят, что функция f(x) – есть сложная функция, составленная из функций g и v, и пишут:

f(x) = g(v(x)).

Область определения сложной функции – множество всех тех х из области определения функции v , для которыхv(x) входит в область определения функции g.

ТЕОРЕМА.

Пусть сложная функция у = f(x) = g(v(x)) такова, что функция у = v(x) определена на промежутке U , а функция u = v(x) определена на промежутке Х и множество всех её значений входит в промежуток U. Пусть функция u = v(x) имеет производную в каждой точке внутри промежутка Х , а функция y = g(u) имеет производную в каждой точке внутри промежутка U. Тогда функция y = f(x) имеет производную в каждой точке внутри промежутка Х , вычисляемую по формуле

y’_x = y’_u • u’_x.

Формулу читают так: производная y по x равна производной y по u

infourok.ru

Самостоятельная работа по теме «Производная» (11 класс)

Производная сложной функции.

2 вариант.

А1. . Найдите

.

А2. . Решите уравнение .

А3. . Найдите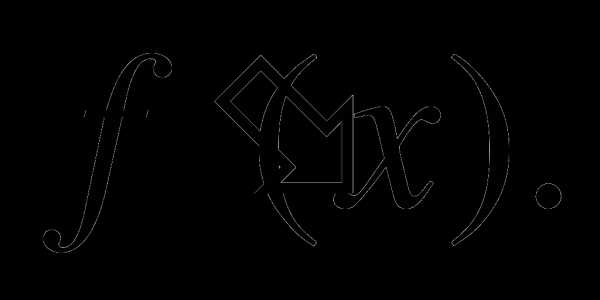

А4. . Вычислите .

В. Найти производную функции: а) ;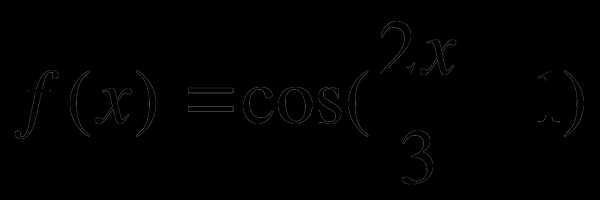

б) ; в) .

С. Решите уравнение , где .

Производная сложной функции.

1 вариант.

А1. . Найдите .

А2. . Решите уравнение .

А3. . Найдите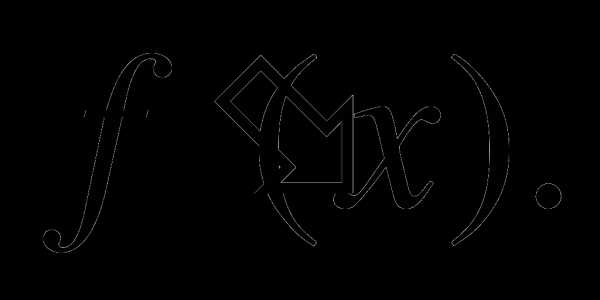

А4. . Вычислите .

В. Найти производную функции: а) ;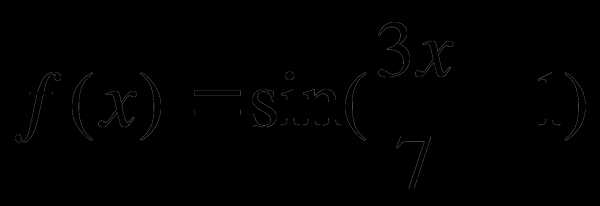

б) ; в) .

С. Решите уравнение , где .

Производная сложной функции.

2 вариант.

А1. . Найдите .

А2. . Решите уравнение .

А3. . Найдите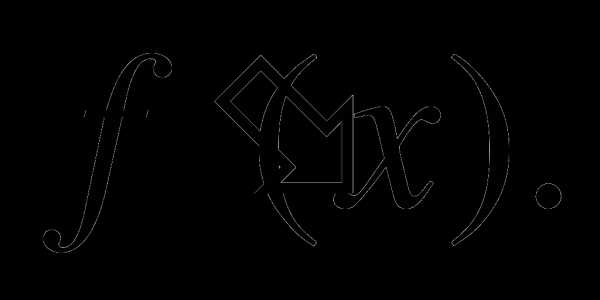

А4. . Вычислите

.

В. Найти производную функции: а) ;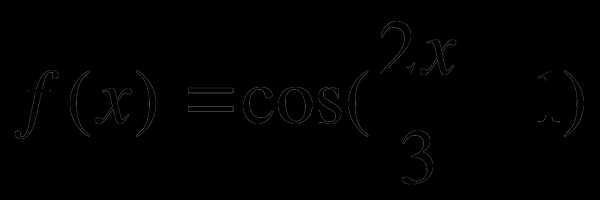

б) ; в) .

С. Решите уравнение , где .

Производная сложной функции.

1 вариант.

А1. . Найдите .

А2. . Решите уравнение .

А3. . Найдите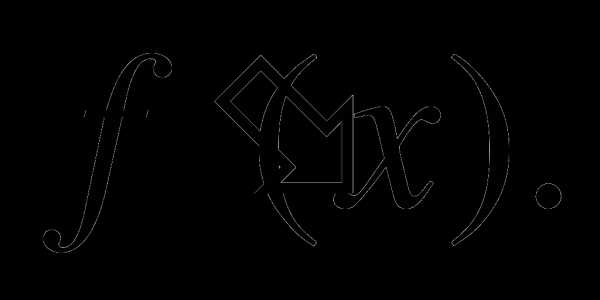

А4. . Вычислите .

В. Найти производную функции: а)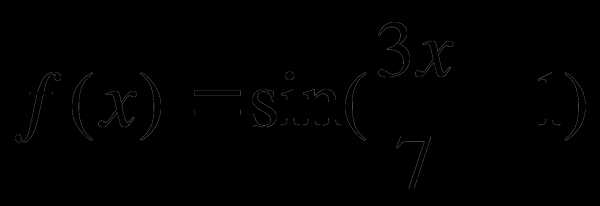

;

б) ; в) .

С. Решите уравнение , где .

infourok.ru

Урок по алгебре и началам анализа 11 класс по теме » Производная степенной функции.»

29.10.2015 г.Тема: Производная степенной функции. Класс 11.

Вид урока: объяснение нового материала. Открытый урок.

Цели урока: повторить степенную функцию, ее свойства; получить формулу для вычисления производной .

Задачи урока:

Развивающие:

• развитие навыка самостоятельного отношения поиска решения,

• привитие любви к математике, расширение кругозора;

 Воспитательные:

• повышение мотивации к обучению,

• формирование познавательного интереса,

 Дидактические:

Оборудование:  мультимедийный проектор, доска, мел, учебник

Ход урока

1. Сообщение темы и целей урока,мотивация.(слайд)

Тот кто ночами, забыл про кровать

Усердно роется в книжной груде

Чтобы ещё кое-что узнать

Из того что знают другие люди.

( П.Хейне- американский экономист) О ком идёт речь? ( учёный)

II. Повторение и закрепление пройденного материала

1. Проверка домашнего задания.

Контроль усвоения ранее пройденного материала (самостоятельная работа у доски)

III. Изучение нового материала

1. Теоретический материал

Степенная функция и ее производная.
Вы уже знаете, что для любого действительного числа α и каждого положительного х определено число х^α. Зафиксируем число α на промежутке (0; ∞).

Определение.

Функция, заданная формулой f (x)=x^α, называется степенной (с показателем степени α).

Если α >0, то степенная функция определена и при х = 0, поскольку 0^α = 0. При целых α формулой f(x)=x^α степенная функция f определена и для x<0. При четных α эта функция четная, а при нечетных α — нечетная. Поэтому исследование степенной функции достаточно провести только на промежутке (0; ∞).В предыдущих разделах курса были получены формулы для производной функции у=х^α лишь при целых показателях степени, а также α =1/2. Теперь нам остается вывести формулу при произвольном α. Докажем, что для любого х из области определения производная степенной функции находится так:

(x^α)` = α x ^α-1.

Действительно, так как х = е^{1п х} , то х^α = е ^{α ln x}. Отсюда по правилу вычисления производной сложной функции получаем:

Формула (1) доказана.

При α <0 степенная функция убывает на промежутке (0; ∞), поскольку (х

α )` = α x^{α -1}<0 при α>0. При α>0 имеем (х^α)’ =αх^α-1>0, поэтому степенная функция возрастает при x>0. Кроме того, надо учесть, что при х=0 степенная функция равна 0 и х^α→0 при х и x>0. Поэтому точка 0 присоединяется к промежутку возрастания, т. е. при α>0 степенная функция возрастает на промежутке [0; оо). Примеры графиков степенной функции при различных а приведены на рисунке 1.

1. Практическое применение теории

Пример 1

Найдем производную функции 

Используем правило дифференцирования сложной функции и формулу производной степенной функции. Получаем  

  

IV. Решение упражнений

1.Учебник №558(а), 559(а), 560(г), 564(г), 565(в)

2. Найди верный ответ.

№

Найдите производные функций

Варианты ответов

1

2

3

4

1

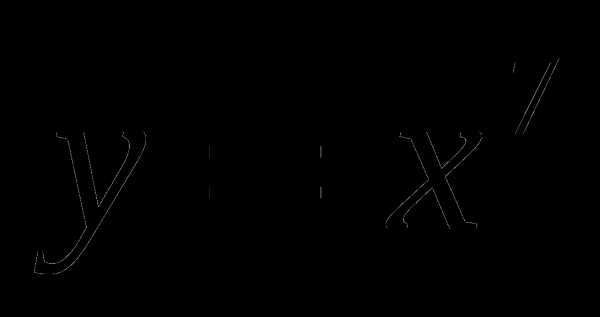
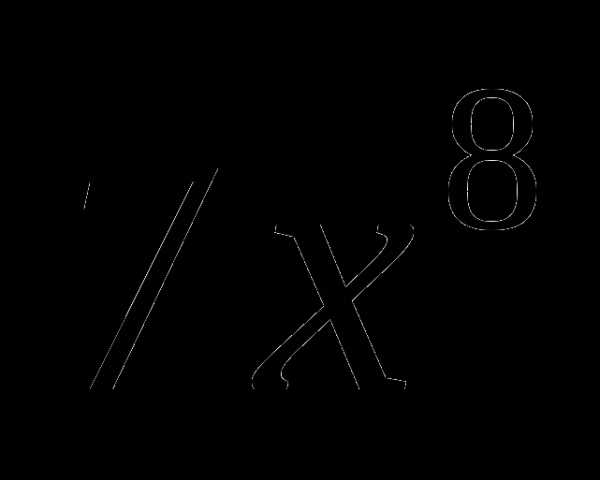
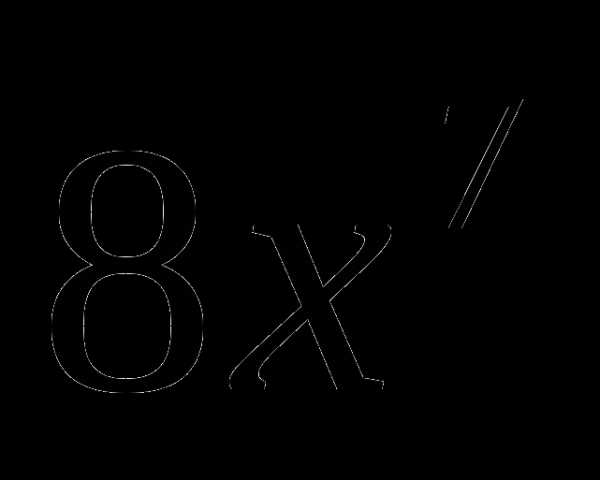
2

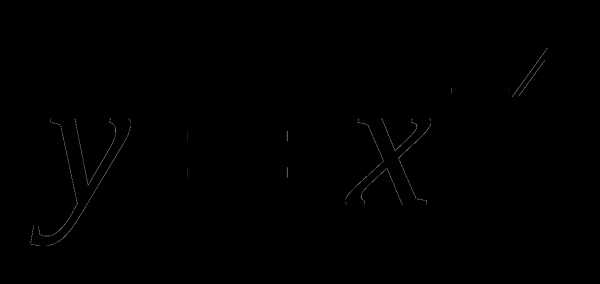
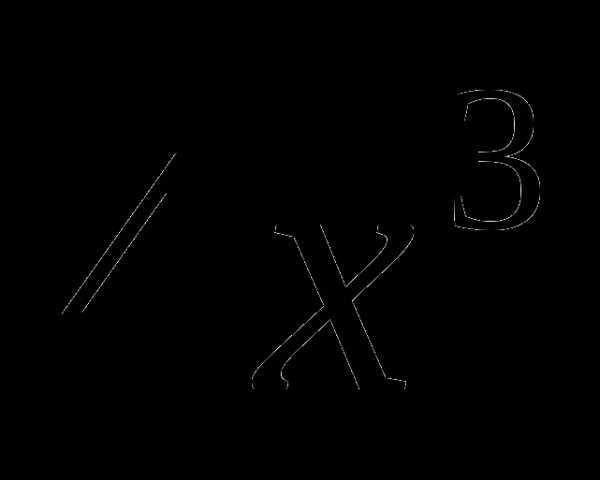
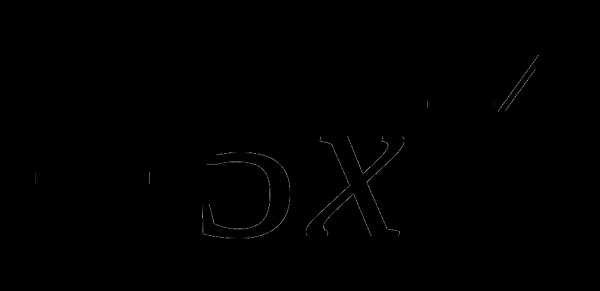
3

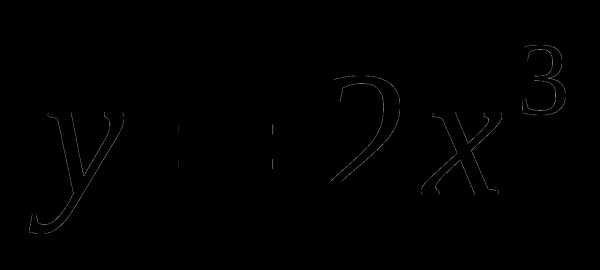
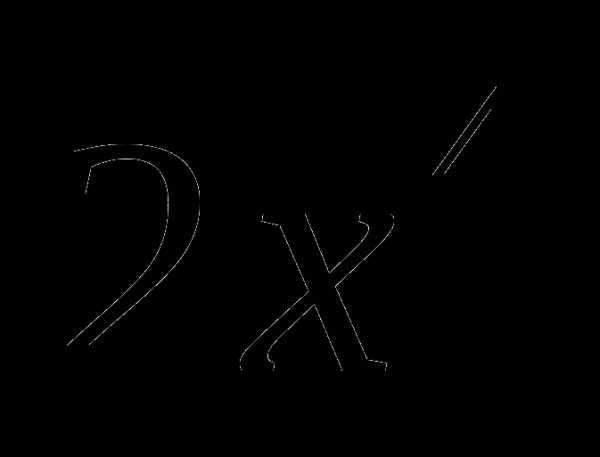
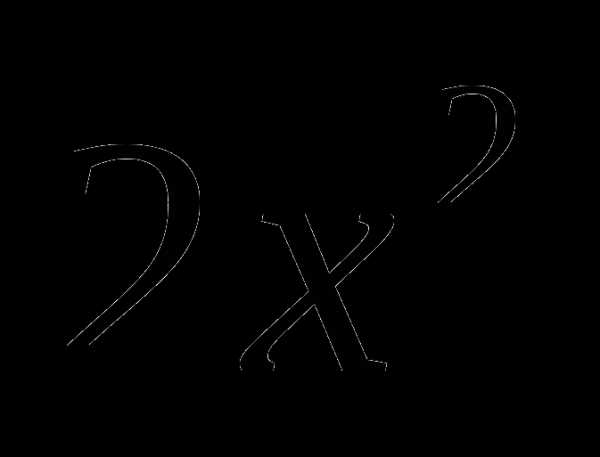
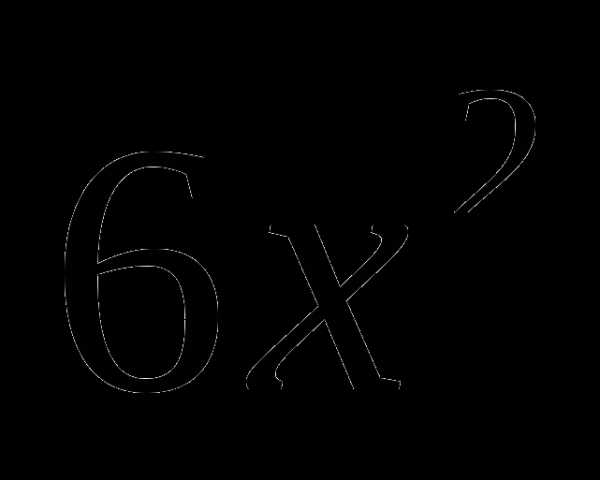
4

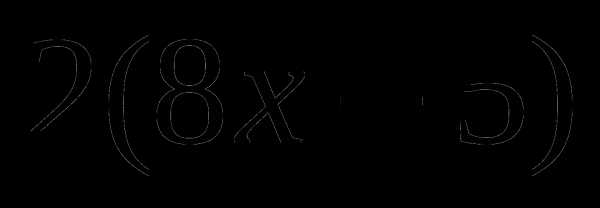
8

5

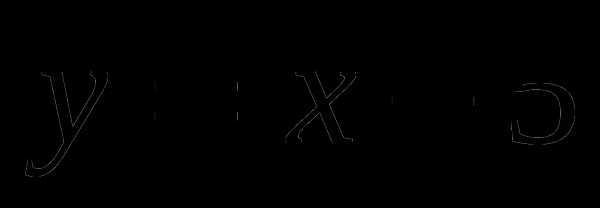
х-5

1

5х

0

6

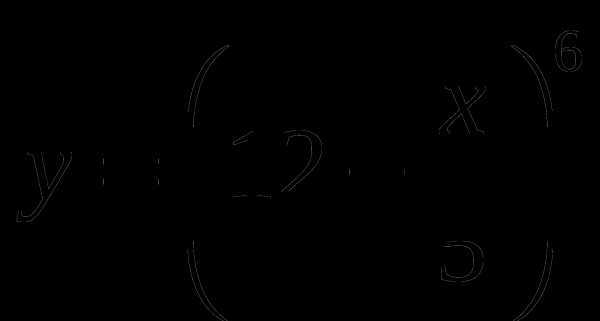
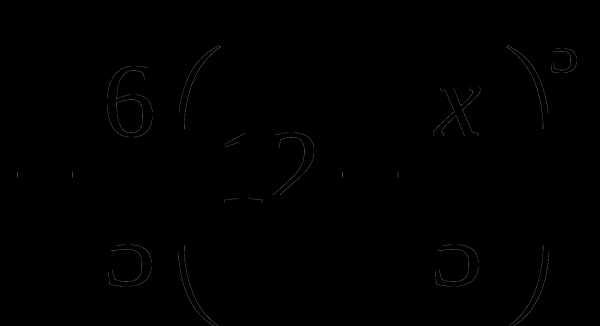
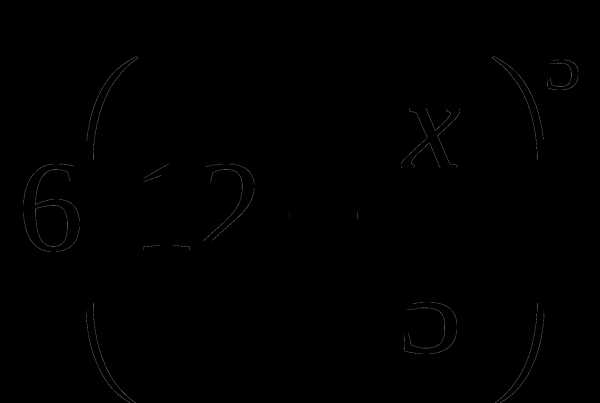
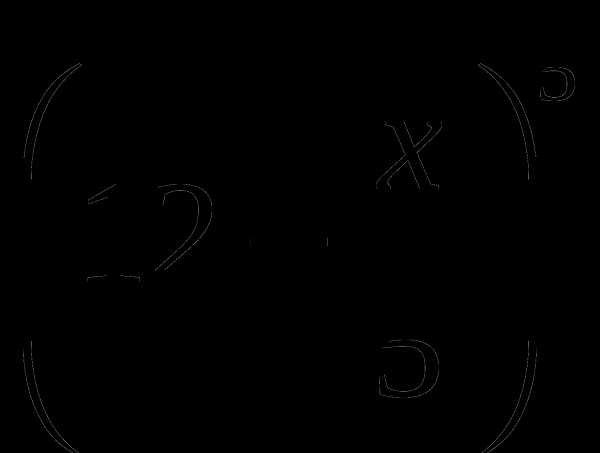
Ответы:

3.Подготовка к ЕГЭ задание из интернета на ноутбуке базовый уровень mathematichka.ru/ege/Demo_base.home

V. Контрольные вопросы

1. Дайте определение степенной функции.

2. Напишите формулу для производной степенной функции.

3. Приведите примеры графиков степенной функции.

VI. Домашнее задание

№558(в), 560(а,б), 564(а), 565(а,в)

VII. Подведение итогов урока. Рефлексия

infourok.ru

Самостоятельная работа по теме «Производная» I вариант 1

Documents войти Загрузить ×

1. Математика

advertisement advertisement

Related documents

Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №26»

239-827-274 Бондаренко Е.А. Приложение 4 Задачи к теме: «Геометрический смысл производной»

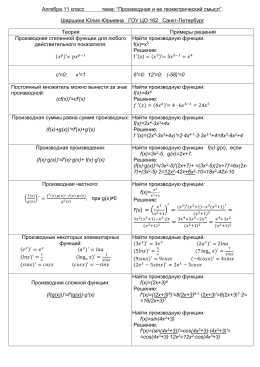
Алгебра 11 класс … Шаршина Юлия Юрьевна ГОУ ЦО 162 Санкт-Петербург

 

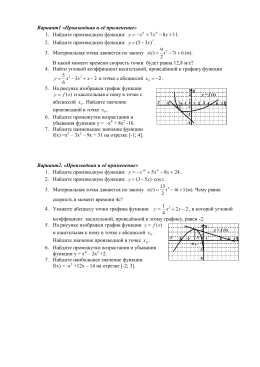
Вариант1 «Производная и её применение» Найдите

Задания для подготовки к экзамену 1 курс 1 семестр

2. Найти производную функции



Текст теста и сохранить

Открытый урок по теме: «Геометрический смысл производной».

11 класс Урок 84 Тема: «Применение производной к решению задач». Тип урока:

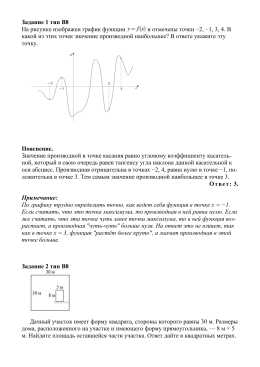
Задание 1 тип B8 На рисунке изображен график функции

Определение производной

studydoc.ru

Урок алгебры в 11 классе «Вычисление производных. Повторение»

Урок алгебры в 11 классе

Тема: «Вычисление производных»

Цели: обобщить и систематизировать основные понятия изучаемой темы; отработать и закрепить практические навыки решения ключевых задач; продолжить подготовку учащихся к ЕГЭ по математике; продолжить формирование логического мышления учащихся; продолжить формирование у учащихся навыков самостоятельной деятельности при подготовке к ЕГЭ; воспитывать коммуникативные компетенции;  продолжить формирование общей и математической культуры учащихся.

Краткая теоретическая справка

Производная сложной функции

Пусть задана сложная функция , тогда производная этой сложной функции находится по правилу:

  

иначе говоря, производная сложной функции берется по «правилу цепочки», то есть, сначала находится производная внешней функции, аргумент при этом не изменяется, а затем находится производная от её аргумента. Если же и он является сложной функцией, то процесс снова повторяется, пока не найдется производная от последнего независимого аргумента.

Пример 1. Вычислить производную функции  в точке 

Решение: 
Сначала находим производную:

На втором шаге вычислим значение производной в точке :

Ответ. 33

Пример 2. Найти производную сложной функции 

Решение. Используем правила дифференцирования и таблицу производных:

Ответ. 

Порядок выполнения работы.

1. Внимательно изучите теоретическую справку по теме и рассмотрите примеры решения некоторых заданий.

2. Выполните по учебнику следующие номера: стр. (на усмотрение учителя)

3. Выполните самостоятельную работу по вариантам.

Самостоятельная работа.

1 вариант

Задание №1. Найдите производные следующих функций:

y = 3sin x +2 x.

Задание №2. Найдите значение производной функции в точке

а) f (x) = 2x⁷ + 4 cos x в точке х₀ = 0.

б) y = в точке х₀ = 2.

Задание №3. Найдите производную сложной функции

2 вариант

Задание №1. Найдите производные следующих функций:

y = 3cos x + x²

+ lnx

Задание №2. Найдите значение производной функции в точке

а) f (x) = x⁹ + cos x в точке х₀ = 0.

б) y = в точке х₀ = 0,5.

Задание №3. Найдите производную сложной функции

3 вариант

Задание №1. Найдите производные следующих функций:

y = 3 — sin x +2 x.

Задание №2. Найдите значение производной функции в точке

а) в точке x₀ = .

б) y = в точке х₀ = -1.

Задание №3. Найдите производную сложной функции

4вариант

Задание №1. Найдите производные следующих функций:

y = 3x +2cos x -1

+ lnx

Задание №2. Найдите значение производной функции в точке

а) в точке x₀ = 0,5.

б) y = в точке х₀ = 2.

Задание №3. Найдите производную сложной функции

5 вариант

Задание №1. Найдите производные следующих функций:

y = x² + sin x

Задание №2. Найдите значение производной функции в точке

а) в точке x₀ = —.

б) y = в точке х₀ = -1.

Задание №3. Найдите производную сложной функции

6 вариант

Задание №1. Найдите производные следующих функций:

y = x⁶ – 4 sin x

y = x⁴∙ e^x

Задание №2. Найдите значение производной функции в точке

а) y = 2x + sin x в точке х₀ = π.

б) y = в точке х₀ = -1.

Задание №3. Найдите производную сложной функции

7 вариант

Задание №1. Найдите производные следующих функций:

y = x + sin x-1

Задание №2. Найдите значение производной функции в точке

а) в точке x₀=2.

б) y = в точке х₀ = -1.

Задание №3. Найдите производную сложной функции

8 вариант

Задание №1. Найдите производные следующих функций:

y =2 x⁶ – 4x+1

y = x∙ e^x

Задание №2. Найдите значение производной функции в точке

а) y = 2x + x³ в точке х₀ = 2.

б) y = в точке х₀ = 1.

Задание №3. Найдите производную сложной функции

4. Задание на дом: повторить теоретический материал по теме «Касательная к графику функции. Производная в физике и технике»

infourok.ru

Самостоятельная работа по теме «Производная сложной функции» 11 класс

Инфоурок › Алгебра › Тесты › Самостоятельная работа по теме «Производная сложной функции» 11 класс

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсемирная историяВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеДругоеДругойЕстествознаниеИЗО, МХКИзобразительное искусствоИностранные языкиИнформатикаИскусствоИспанский языкИсторияИстория РоссииИстория Средних вековИтальянский языкКлассному руководителюКультурологияЛитератураЛитературное чтениеЛогопедияМатематикаМировая художественная культураМузыкаМХКНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирОсновы безопасности жизнедеятельностиПриродоведениеРелигиоведениеРисованиеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФинский языкФранцузский языкХимияЧерчениеЧтениеШкольному психологуЭкология

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДБ-1265485

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

infourok.ru