Решение уравнений по физике – Уравнения математической физики, практикум по решению задач, учебное пособие, Емельянов В.М., Рыбакина Б.А., 2008

Уравнения математической физики, с примерами

Дифференциальные уравнения математической физики

Математические модели естественнонаучных явлений и процессов зачастую представляют собой задачи, содержащие дифференциальные уравнения с частными производными первого и второго порядков. Дифференциальные уравнения существенные для физики, механики техники называют дифференциальными уравнениями математической физики.

Каждое уравнение математической физики описывает бесконечное множество качественно аналогичных явлений или процессов, так как дифференциальные уравнения, которыми занимается математическая физика, имеют бесконечное множество частных решений. Конкретное решение, описывающее рассматриваемое физическое явление, выделяется из множества частных решений с помощью начальных и граничных условий.

Общий вид дифференциального уравнения в частных производных первого порядка относительно неизвестной искомой функции таков:

   

Если F является линейной функцией относительно старших производных, то есть:

   

   

данное уравнение называется квазилинейным дифференциальным уравнением.

Если функции не зависят от u, а зависимость P от u линейна, то есть , тогда уравнение (2) называется линейным. Если , то уравнение (2) называется однородным линейным дифференциальным уравнением в частных производных первого порядка.

Решений уравнений математической физики

Рассмотрим квазилинейное дифференциальное уравнение в частных производных первого порядка:

   

Для получения общего решения уравнения (3) рассматривают характеристическую систему обыкновенных дифференциальных уравнений:

   

Если с=0, то система сводится к одному уравнению .

Если общий интеграл уравнения, тогда – общее решение.

Само дифференциальное уравнение содержит в себе только самую общую информацию об описываемом процессе. Необходимо задание начальных и граничных условий, для конкретизации.

Дифференциальные уравнения математической физики второго порядка

Большое количество процессов и явлений в физике описывается с помощью дифференциальных уравнений второго порядка в частных производных, это связано с тем, что фундаментальные законы физики – законы сохранения – записываются в терминах вторых производных. Методы решения уравнений математической физики зависят от типа к которому принадлежит рассматриваемое уравнение. Выделяют три основных типа дифференциальных уравнений с частными производными второго порядка, поиск решения которых имеют качественные различия: уравнения параболического, гиперболического и эллиптического типов.

Рассмотрим линейное уравнение с частными производными второго порядка с двумя независимыми переменными:

   

где a, b, c некоторые функции от x, y, имеющие непрерывные производные до второго порядка включительно.

Уравнение (5) принадлежит в точке (x, y)

1. параболическому типу, если Канонический вид такого уравнения:

      

   где — независимые переменные. Кроме того — дважды дифференцируемая функция в рассматриваемой области. Уравнение (6) так же как и уравнение теплопроводности имеет только один член высшей производной.

2. гиперболическому типу, если Канонический вид такого уравнения:

   первая каноническая форма:

      

   где — независимые переменные,

   вторая каноническая форма:

      

   где . Левая часть уравнения (8) полностью совпадает с частью волнового уравнения.

3. эллиптическому типу, если Канонический вид такого уравнения:

      

   где — независимые переменные. Левая часть этого уравнения совпадает с левой частью уравнения Лапласа.

Для того чтобы привести уравнение (5) к каноническому виду, надо записать так называемое характеристическое уравнение (10):

   

которое распадается на два уравнения:

   

   

и найти их общие интегралы.

В общем случае линейное уравнение с частными производными второго порядка параболического типа с n независимыми переменными можно записать так:

   

где

   

   

Уравнения параболического типа описывают неустановившиеся тепловые, диффузионные процессы, которые зависят от времени.

Уравнение (13) называют однородным, если =0.

Довольно часто при решении уравнения (13) ставят так называемую задачу Коши. В которой, требуется найти функцию w, удовлетворяющую уравнению (13) (при -эвклидово пространство) и начальном условии w=f(x) при t=0 и граничному условию:

   

В общем случае — линейный дифференциальный оператор первого порядка по пространственным переменным, коэффициенты которого зависят от x и t.

Начальное условие называют однородным, если f(x)=0. Граничное условие называют однородным, если .

В общем случае линейное уравнение с частными производными второго порядка гиперболического типа с n независимыми переменными можно записать так:

   

где линейный дифференциальный оператор определен формулам (14). Уравнениями гиперболического типа описываются неустановившиеся волновые процессы, зависящие от времени.

При решении уравнения (15) ставят задачу Коши. В которой, требуется найти функцию w, удовлетворяющую уравнению (15) (при и начальным условиям:

   

   

Граничные условия задаются (14).

Уравнения эллиптического типа

В общем случае линейное уравнение с частными производными второго порядка эллиптического типа с n независимыми переменными можно записать в виде:

   

где

   

   

Уравнения эллиптического типа описывают установившиеся тепловые, диффузионные и другие процессы, которые не зависят от времени. Уравнение (18) называется однородным, если

Граничные условия для эллиптического уравнения записывают так:

   

В общем случае — линейный дифференциальный оператор первого порядка.

Наиболее часто в прикладных примерах при описании различных процессов, происходящих в изотропных средах коэффициенты

   

таковыми и мы будем считать коэффициенты .

Для любых уравнений в частных производных второго порядка в зависимости от вида граничных условий принято выделять четыре типа краевых задач.

Первая краевая задача. На границе области S функция w(x,t) принимает заданные значения:

   

Вторая краевая задача. На границе области S задается производная по (внешней) нормали:

   

Третья краевая задача. На границе области S задана линейная связь между искомой функцией и ее производной по нормали:

   

Чаще всего В задачах массопереноса, где w – концентрация, граничное условие (22) при описывает поверхностную химическую реакцию.

Смешанные краевые задачи. В этом случае на различных участках границы S задают различные граничные условия.

Методы решения уравнений математической физики

Все методы решения уравнений математической физики можно разделить на две большие группы:

1. аналитические методы решения уравнений, которые основаны на сведении уравнения в частных производных к обыкновенному или системе обыкновенных уравнений;
2. численные методы решения (с помощью ЭВМ).

Среди аналитических методов решения уравнений следует выделить:

1. Метод характеристик.
2. Метод разделения переменных.
3. Метод Фурье.
4. Метод Деламбера.
5. Метод интегральных преобразований.
6. Преобразование Лапласа.
7. Представление решений через функцию Грина.

Среди численных методов решения уравнений математической физики следует выделить:

1. метод сеток;
2. метод конечных разностей;
3. методы расщепления: метод переменных направлений, метод дробных шагов;
4. методы Эйлера;
5. методы Рунге-Кутта;
6. метод Адамса;
7. символьно-численный метод.

Примеры решения задач

ru.solverbook.com

Уравнения математической физики | Решатель

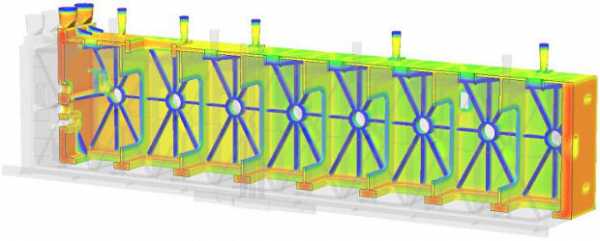
У физиков есть шутка с бородой: “Женщина-физик: еще не физик, но уже не женщина!”. С математической физикой примерно та же история. Это уже не чистая математика, а ее приложение к реальным физическим задачам. Однако, от привычной физики с ее экспериментами и рассуждениями, она тоже отличается.
 

Что касается масштабов бедствия, данная дисциплина охватывает почти все разделы физики, изложенные в 10 томах Ландау-Лифшица: электромагнетизм, гидро- и газодинамика, теория теплопереноса, упругости.
 

В рамках курса “уравнения математической физики”, очевидно, вы будете иметь дело с уравнениями, но не далеко не простыми. Забудьте о заданиях с уравнениями типа 2x+5=9. Да здравствуют дифференциальные уравнения с частными производными! А это вам не шутки.

 

В большинстве случаев вы будете рассматривать случай двух независимых переменных и уравнение второго порядка вида (хотя, конечно, для полноценного рассмотрения многих физических задач для реального мира необходимо рассматривать трехмерный случай):
 

 

Но не так страшно уравнение, каким оно кажется на первый вид. На самом деле далеко не каждое уравнение такого общего вида годится для моделирования физического явления, и вы будете сталкиваться с уравнениями одного и того же типа.
 

Итак, начнем наше знакомство с теми уравнениями, которые запишутся в ваш новый список друзей.
 

1) Одномерное волновое уравнение:

 

 

u(x,t) может быть, например, давлением или плотностью для упругих волн в газах, напряженностью электрического или магнитного поля,a a есть скорость распространения волн в рассматриваемой среде. Это уравнение является уравнением гиперболического типа; оно будет с вами, когда вы будете изучать процессы поперечных колебаний струны, электрических колебаний в проводе, колебаний газа и жидкости.

 

2) Ваш друг номер два:

 
 

Это уравнение параболического типа, известное в народе также как уравнение теплопроводности, где u(x,t)представляет собой температуру. С этим уравнением вы будете сталкиваться каждый раз, когда заинтересуетесь вопросом распространения тепла, фильтрации газа и жидкости.
 

3) Двумерное уравнение Лапласа:

 

 

Это уравнение эллиптического типа, которое необходимо при рассмотрении задач об электрических и магнитных полях (например, таким уравнением описывается потенциал электростатического поля при отсутствии зарядов), а также задач гидродинамики и диффузии.
 

Испугались? В действительности, не все так плохо. Уравнения такого типа можно научиться очень быстро решать, даже если вы перед этим не штудировали учебники по дифференциальным уравнениям.

 

Мы покажем на примере первого уравнения (2), как можно с ними дружить.
 

Мы можем заметить, что правая часть зависит только от t, а левая часть — только от x. Равенство между ними возможно только при условии, что обе части равны константе, это значит, что решение уравнения есть произведение одной функции от t и другой функции от x:
 

 

Подставив это выражение в исходное уравнение, получаем систему двух простых дифференциальных уравнений:
 

 

А для того, чтобы решить такие уравнения, достаточно знать, как решать квадратное уравнение (это под силу даже школьнику), ведь для решения подобного уравнения (дифференциального однородного уравнения второго порядка)
 

 

необходимо всего лишь решить квадратное уравнение
 

 

и тогда решение уравнения (7) есть:
 

 

В зависимости от условий конкретной физической задачи, вы будете иметь дело с определенными граничными условиями, например, f(x=0)=0, применяя которые, легко можно найти постоянную λ в системе уравнений (6) и постоянные A₁ и A₂ в каждом решении вида (9).
 

Хотите знать больше?

Тогда бегом в библиотеку за следующими учебниками:

• А.Н.Тихонов, А.А.Самарский, “Уравнения математической физики”. М. “Наука”, 1972.
• В.С. Владимиров “Уравнения математической физики”. М. “Наука”, 1988.
• Смирнов М.М. “Дифференциальные уравнения в частных производных второго порядка”. М. “Наука”, 1964.
• Полянин А.Д. “Справочник по линейным уравнениям математической физики”. М.: Физматлит, 2001.
• Полянин А.Д., Зайцев В.Ф. “Справочник по нелинейным уравнениям математической физики: Точные решения”. М.: Физматлит, 2002.

 
 

Хотите заказать решение у нас?

Автор данной статьи также берется за решение уравнений математической физики на заказ.
Узнать цену работы можно на странице заказа. Для этого нужно всего лишь прикрепить файл с заданием и указать сроки.

reshatel.org

Уравнения и формулы математической физики

Определение 1

Математическая физика (МФ) – это гипотеза математических моделей физических явлений, которые изучают сложные задачи на математическом уровне, а результаты исследований представляются в виде графиков, теорем и таблиц.

В математической физике характерно, что практически все общие методы, используемые для решения задач МФ, развились из способов решения физических заданий и в своем первоначальном виде не имели достаточной завершенности и математического обоснования. Все это относится к таким известным принципам решения задач МФ, как методы Галеркина и Ритца. Эффективное использование данных методов является причиной для их математического обобщения и обоснования.

Основным уравнением в математической физике принято считать дифференциальные показатели с частным производимым второго порядка. Например, формула волновой теории будет записываться следующим образом: $ \LARGE \frac {d^2 u}{dt^2}=a^2 \frac {d^2 u}{dx^2}$.

Уравнение теплопроводности ученые обозначают так: $\LARGE \frac {du}{dt}=a^2 \frac {d^2 u}{dx^2}$.

В создании формул физики изначально тщательно рассматривают элементы электромагнитного поля, а также его стационарное тепловое состояние.

Постановка задач в МФ заключается в построении математических моделей, которые описывают основные закономерности изучаемого класса физических явлений. Хорошим примером этого явления выступает уравнение Лапласа: $\LARGE \frac {d^2 u}{dx^2 } + \frac {d^2 u}{dy^2} = 0$.

Подобная постановка состоит из формул (интегральных, дифференциальных, алгебраических или интегро-дифференциальных), которые удовлетворяют величины, более тщательно характеризующие физический процесс.

Уравнения математической физики

Уравнения с частными производными первого порядка включают в себя: нелинейные уравнения с производными первого порядка; квазилинейные уравнения с производными первого порядка.

Линейные уравнения МФ:

• линейные задачи МФ для уравнений параболического типа;
• некоторые формулы, определения, решения и методы;
• линейные задачи МФ для уравнений эллиптического типа;
• линейные задачи МФ для уравнений гиперболического типа.

Нелинейные уравнения МФ:

• преобразования уравнений МФ;
• автомодельные решения и решения типа бегущей волны;
• метод подобия;
• метод функционального разделения переменных МФ;
• метод обобщенного разделения переменных МФ;
• классический метод исследования симметрий уравнений МФ;
• решение дифференциальных уравнений при помощи инвариантов;
• метод дифференциальных связей.

В целом, обобщённые функции в математической физике обладают рядом важных свойств, расширяющих возможности классического анализа.

Пример 1

Любая целостная функция оказывается бесконечно дифференцируемой и сходится в ряды из обобщённых понятий, которые возможно по отдельности дифференцировать бесконечное количество раз. Преобразование этого процесса всегда существует, поэтому применение техники комплексных функций существенно расширяет круг исследуемых задач и к тому же приводит к значительным упрощениям, автоматизируя элементарные операции.

Влияние математической физики на науку

Воздействие математической физики на разные разделы математики проявляется в том, что общее развитие математической физики, которая отражает в своих идеях требования естественных наук и часто меняющееся запросы практики, автоматически влечет за собой переориентацию направленности научных исследований в сложившихся разделах математики. Правильная постановка задач изучаемого течения в науке напрямую связана с разработкой новых моделей реальных физических процессов, и привела к кардинальному изменению главной проблематики гипотезы дифференциальных формул в стабильных производных. В результате появилась теория краевых задач, которая позволила ученым связать интегральные уравнения и вариационные методы, а также дифференциальные уравнения в частных производных.

Исследование математических моделей физики различными способами не только позволяет получить основные характеристики физических явлений, а еще и рассчитать с максимальной точностью ход реальных процессов, которые глубоко проникают в самую суть скрытых закономерностей, предсказания уникальных эффектов.

Стремление к более детализированному изучению физических явлений приводит физиков ко все большему усложнению математических моделей, которые способны описать происходящие процессы с помощью применения аналитических методов построения этих моделей. Это возможно объяснить еще и тем, что модели реальных физических процессов являются нелинейными. Для проведения точного исследования таких концепций успешно используются прямые количественные способы с применением компьютеров. Для типичных физических задач изучение численных методов сводится к частичной замене уравнений математической физики для обобщенных функций непрерывного аргумента посредством сеточных показателей, заданных на дискретном множестве точек. Другими словами, вместо непрерывной и стабильной модели внешней среды вводится ее дискретный аналог.

Применение таких методов в ряде случаев позволяет заменить трудоемкий и дорогостоящий эксперимент значительно более экономичным исследованием. Результативное математическое изучение является базой для выбора наиболее подходящих условий реального физического опыта, выбора правильных параметров сложных физических установок, выявление подходящих условий ля новых научных эффектов. Таким образом, численные методы в уравнениях математической физики расширяют сферу эффективного применения моделей физических явлений.

Решения уравнений математической физики

Для решения уравнений математической физики сначала необходимо рассмотреть структуру квазилинейной формулы в частных производных: $\LARGE a \frac {(х, у)(d^2w)}{dx^2 } + 2b(х,у)$ $\LARGE \frac {d^2w}{dxdy}=F (x,y,w dw/dx)$

Для получения общего и правильного решения уравнения исследователи рассматривают характеристическую концепцию обыкновенных дифференциальных уравнений: $\LARGE \frac {dx}{a} = \frac {dy}{b} = \frac {du}{c}$.

Если с=0, то система сводится к одному уравнению $\LARGE \frac {dх}{a}=\frac {dy}{b}$. Если $\LARGE f (х, у)=C$ общий интеграл уравнения, тогда $\LARGE u=w (f (х, у))$ – общее решение.

Сама дифференциальная формула содержит в себе только самую общую информацию об исследуемом процессе. Необходимо заранее получить задание граничных и начальных условий, для общей конкретизации.

На сегодняшний день ученые выделяют три основных типа дифференциальных уравнений, для которых поиск решения имеет существенные различия: уравнения гиперболического, параболического и эллиптического типов.

Большое количество физических процессов и явлений можно описать посредством дифференциальных уравнений в исследуемых частных производных. Это непосредственно связано с тем, что фундаментальные законы современной физики – принципы сохранения – записываются в определениях вторых производных. Способы решения задач математической физики зависят от конкретного типа, которому принадлежит само рассматриваемое уравнение.

spravochnick.ru

2. Уравнения математической физики

2.1. Классификация уравнений и постановка задач математической физики

Большинство физических процессов различной природы модели­руется дифференциальными уравнениями в частных производных. Наи­более часто при этом встречаются линейные уравнения второго по­рядка. Их изучение и составляет предмет математической физики.

Дифференциальным уравнением в частных производных называется соотношение между искомой функцией нескольких переменных, её частными производными и независимыми переменными.

Для двух независимых переменных x и y дифференциальное уравнение в частных производных второго порядка в общем случае имеет вид

.

Наивысший порядок частных производных, входящих в уравнение, определяет порядок дифференциального уравнения.

Уравнение называется линейным, если оно линейно относительно искомой функции и всех её производных. Линейное дифференци­альное уравнение в частных производных второго порядка с двумя независимыми переменными имеет следующий вид

. (2.1)

Коэффициенты линейного уравнения могут зависеть от переменных x, y. Тогда говорят, что уравнение (2.1) является уравнением с переменными коэффициентами. Если f(x, y) = 0, то уравнение (2.1) называется линейным однородным. В противном случае оно бу­дет линейным неоднородным.

Все многообразие уравнений математической физики может быть разделено на три класса. Уравнения каждого класса обладают общими свойствами ре­шений. В каждом из этих классов есть простейшее уравнение, назы­ваемое каноническим.

Принадлежность уравнения тому или иному классу определяется соотношением между коэффициентами при старших производных.

Если в некоторой области плоскости x0y дискриминант уравнения (2.1) , то говорят, что уравнение (2.1) будет в этой области уравнениемгиперболического типа.

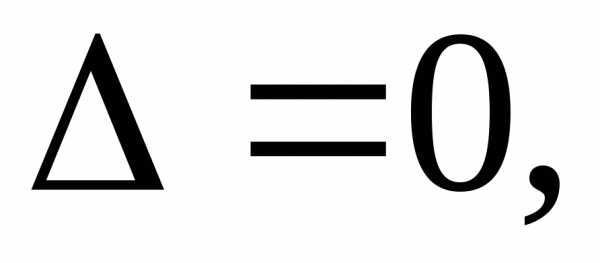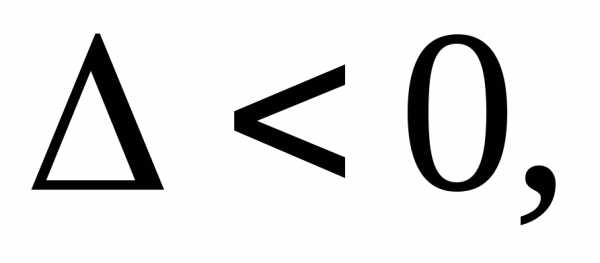Если в некоторой области плоскости x0y дискриминант то в этой области уравнение относится кпараболическому типу. Наконец, если в некоторой об­ласти то уравнение в этой области будет уравнениемэллиптического типа.

Основными уравнениями математической физики являются:

1). Волновое уравнение

.

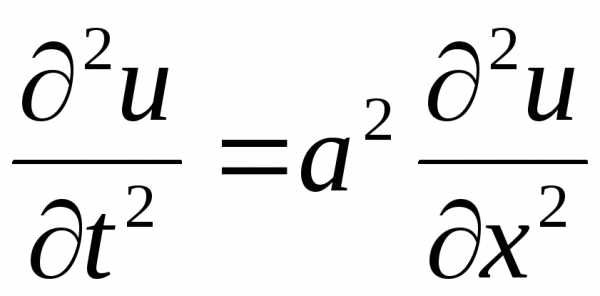Это однородное уравнение гиперболического типа. Оно описывает процессы поперечных колебаний струн, продольные колебания стержней, крутильные колебания валов, колебания тока и напряже­ния в проводах и другие динамические процессы (здесь и далее x ­– пространственная координата, t – время).

2). Уравнение теплопроводности

.

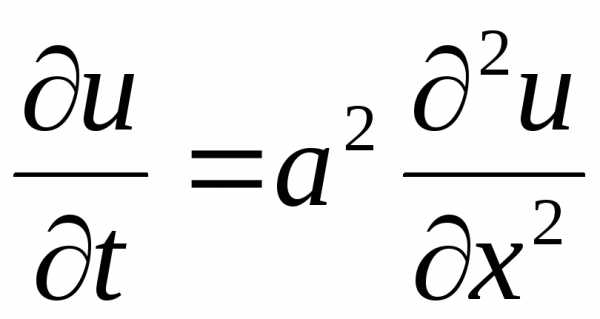Это однородное уравнение параболического типа. Оно описыва­ет процессы распространения тепла в стержнях, задачи фильтрации жидкостей и газов в пористых средах и др.

3). Уравнение Лапласа

.

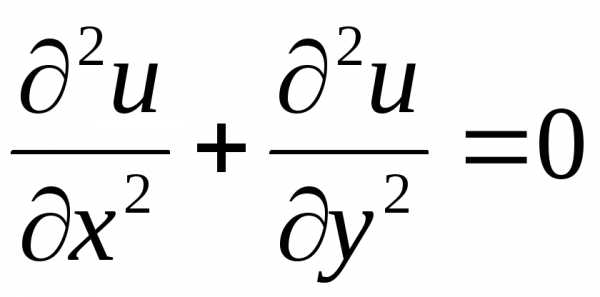Это однородное уравнение эллиптического типа. Уравнение Лапласа не содержит времени (x и y – пространственные координа­ты) и описывает стационарные процессы в электрических и магнит­ных полях, задачи стационарной теплопроводности, многие стацио­нарные задачи гидродинамики, диффузии, прочности и др.

Любое дифференциальное уравнение математической физики имеет бесчисленное множество решений. Для получения единственного решения необходимо задание дополнительных условий, которые поз­воляют однозначно описать конкретный физический процесс. Коли­чество и вид этих условий зависят от характера и порядка произ­водных, входящих в уравнение, от формы области, в которой ищется решение уравнения, от характера взаимодействия рассматриваемого тела (или процесса в выделенном теле) с окружающей средой.

В общем случае дополнительными условиями могут быть начальные и граничные условия.

Начальные условия описывают состояние системы в начальный момент времени. Для уравнения гиперболического типа ставятся два начальных условия соответственно второму порядку производной по времени, входящей в уравнение. Они характеризуют величины откло­нений и скоростей точек тела (струны, стержня и др.) в началь­ный момент времени. Для уравнения параболического типа ставится одно начальное условие, что соответствует первому порядку произ­водной по времени (если искомая функция в уравнении теплопро­водности u(x, t) – температура в произвольном сечении стержня в лю­бой момент времени t, то начальным условием задается распределе­ние температуры по длине стержня в начальный момент времени t = 0).

Граничные условия для волнового уравнения (если оно описы­вает, например, поперечные колебания струны конечных размеров) характеризуют поведение концов струны в процессе колебаний и за­висят от характера их закрепления.

Для уравнения теплопроводности стержня граничные условия имеют существенно различный вид в зависимости от характера теп­лообмена концов стержня с окружающей средой.

Для уравнения эллиптического типа, как и для уравнения па­раболического типа, также различают разные краевые задачи в за­висимости от условий на контуре рассматриваемой области.

Так, если на границе Г области задано значение искомой функции:

,

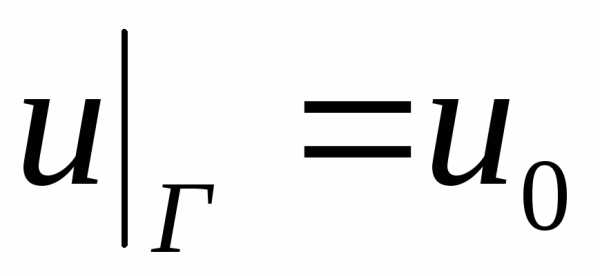то говорят, что для уравнения Лапласа поставлена первая краевая задача (задача Дирихле).

Если на границе области задано значение производной искомой функции по направлению нормали 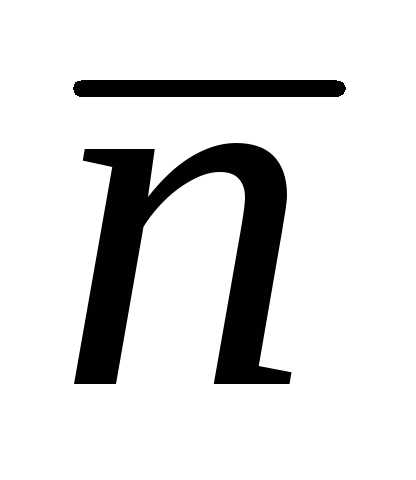к границе:

,

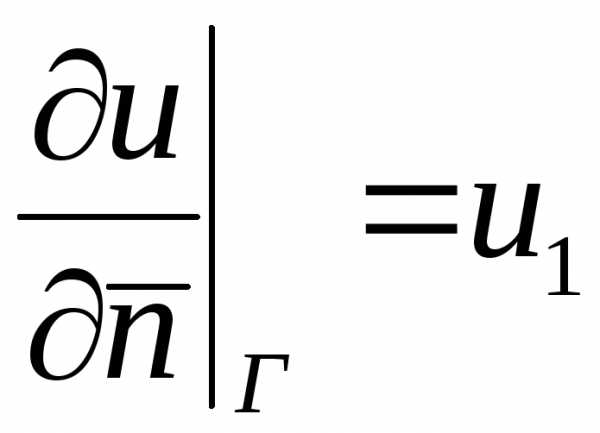то говорят, что для уравнения Лапласа поставлена вторая краевая задача (задача Неймана).

Если на границе области задано условие, связывающее искомую функцию и её производную

,

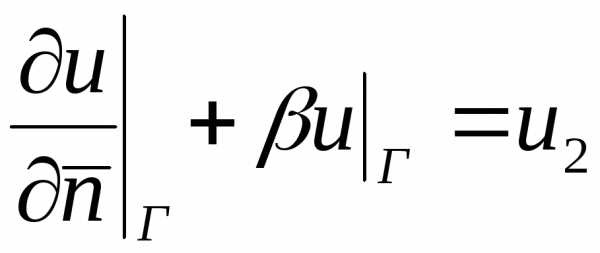то поставлена третья или смешанная краевая задача. Здесь u₀, u₁, u₂, – непрерывные функции, определённые на границе.

Итак, постановка задачи математической физики включает в себя задание дифференциального уравнения в частных производных, описывающего исследуемый процесс, а также в общем случае граничных и начальных условий, позволяющих получить единственное решение.

Если задача математической физики поставлена корректно, то её решение существует, единственно и устойчиво к малым изменениям исходных данных.

Ниже рассмотрены примеры решения основных уравнений матема­тической физики различного типа, аналогичных тем, которые встре­чаются в расчётно-графической работе. Решение задач строится ме­тодом Фурье (методом разделения переменных). Этот метод является одним из наиболее общих методов математической физики, пригодным для решения уравнений гиперболического, параболического и эллип­тического типов в различных областях.

studfiles.net

Решение волнового уравнения — fiziku5.ru

Контрольная работа

Задача 1. Решить первую смешанную задачу для волнового уравнения на отрезке.

Решение:

Запишем решение для волнового уравнения на отрезке длины для условий:

. Где ,

.

Для условий задачи после подстановки a и l будет следующее выражение:

, все равны нулю, т. к. .

.

= ===

=.

= = .

Ответ: .

Задача 2. Решить первую смешанную задачу для волнового уравнения в прямоугольнике.

.

Решение:

Запишем решение для волнового уравнения на прямоугольнике для условий:

;

=;

=;

=.

После подстановки условий задачи получится следующее выражение:

, так как ;

=;

==

==;

=

=.

Ответ: , где =.

Задача 3. Решить первую смешанную задачу для волнового уравнения в круге.

Решение:

Запишем решение для волнового уравнения в круге радиуса для условий :

;

=;

=;

Где =, — функция Бесселя первого рода, — корень с номером уравнения =(это уравнение имеет бесконечное число корней).

Так как .

Подставляем значения из условия задачи в выражения для , ,:

=

=;

=.

Ответ: =, где =,

=, — функция Бесселя первого рода, — корень с номером уравнения =

=.

Задача 4. Найти решение первой смешанной задачи для уравнения теплопроводности на отрезке.

; =; .

Решение:

Решим задачу для условий записанных ниже:

; ; .

Применим метод разделения переменных Фурье. Будем искать частное решение уравнения в виде

=. После преобразования, получим два дифференциальных уравнения:

1);

2).

Отыскание для второго уравнения представляет собой задачу Штурма – Луивилля, собственные значения которой , а собственные функции , где целое и .

Решение первого уравнения следующее (используется индекс k, так как каждому соответствует свой , и получается бесконечное счетное множество решений).

=, где частные решения уравнения . Из граничных условий следует, что и , обозначим =, и получим

=. Запишем общее решение как сумму частных =

==. определим из начальных условий :

= =. Отсюда видно, что являются коэффициентами разложения в ряд Фурье по синусам = .

Найдем для условий нашей задачи:

= +=

==

=.

Ответ: .

Задача 5. Найти решение первой смешанной задачи для уравнения теплопроводности в круге.

Решение:

Запишем решение для волнового уравнения в круге радиуса для условий в полярных координатах:

.

Будем искать частное решение в виде . Тогда ,

.Отсюда получаем два уравнения:

1)

2).

Решением задачи Штурма-Лиувилля для R будут собственные значения и собственные функции , где — функция Бесселя первого рода нулевого порядка,— корни уравнения , n – целое число n > 0.

Соответствующие решения уравнения будут такими: .

Тогда ==.

Общее решение будем искать в виде . Воспользуемся начальными условиями , подставив значение и получим:

— это коэффициенты Эйлера-Фурье разложения функции в ряд по

= , где — функция Бесселя первого рода первого порядка.

В результате мы имеем:

, = .

Подставим значения из условия задачи :

, =.

Ответ: , =.

Задача 6. Используя формулу Пуассона, найти решения задачи Коши для уравнения теплопроводности.

.

Решение:

Для условий формула Пуассона записывается в виде:

. У нас . После подстановки значений в интеграл, получим:

==.

Результатом вычисления интеграла , где — константы, является выражение:

= Для интеграла нашей задачи ; ; .

Тогда после преобразований =. Таким образом

==.

Ответ: =.

Задача 7. Найти общее решение уравнения.

.

Решение:

Приведем уравнение, данное в условиях, к каноническому виду. Для этого составим характеристическое уравнение . Разрешим его относительно dy. Получим два уравнения и . После интегрирования уравнения перейдут в

1)

2) .

Осуществим замену переменных .

Вычислим частные производные новых переменных по старым переменным: .

Так как выражаются линейно через , то получим:

;

;

;

Подставим значения производных:

= ;

=;

= .

Из условия задачи получаем 0==+=.

Общим решением полученного уравнения =0 (предполагается, что все вторые частные производные непрерывны) является функция линейная относительно переменных:

, где — произвольные константы. При возврате к независимым переменным x, y получится функция , где — произвольные константы.

Ответ: , где — произвольные константы.

Задача 8. Решить смешанную задачу.

Решение:

Запишем решение для волнового уравнения на отрезке длины в общем виде:

.

. Где ,

.

Для условий задачи после подстановки a и l будет следующее выражение:

.

Так как при =

=3. При .

Аналогично, для , получим ==1. При .

=

= =.

Ответ: .

fiziku5.ru

Уравнение движения в физике

Как получить уравнение движения?

Допустим, в какой-то момент времени мы знаем все параметры, определяющие состояние системы – например, скорости и координаты, — а также их производные по времени. Тогда мы можем рассчитать эти параметры и для момента времени, отстоящего от начального на малый промежуток времени. Если мы выберем малый, но конечный промежуток времени , мы можем приближенно оценить состояние системы в любой момент времени. Для получения точного уравнения движения нужно определить функцию, описывающую процесс: если временной шаг выбран достаточно малым, то приближенно вычисленные характеристики системы будут лежать к этой функции очень близко.

Для каждой области физики существуют свои уравнения движения

В классической механике эту функцию, в первую очередь, выполняют законы Ньютона. Их дополняют закон тяготения и кинематические законы, связывающие перемещение, скорость и ускорение. Так, второй закон Ньютона – это уравнение движения материальной точки массой , связывающий силу , приложенную к точке, и ускорение , которое точка вследствие этого приобрела:

   

В то время как законы движения классической механики определяют движение макроскопических материальных тел, то движение микроскопических частичек (например, в газе) описывается с помощью статистических распределений. К примеру, уравнение движение Больцмана позволяет найти распределение плотности частичек в пространстве f:

   

В этом уравнении – пространственная координата, – импульс, – масса частичек, – время, – поле действующих сил, а слагаемая учитывает столкновения частиц.

Движение сплошной среды описывают с помощью системы уравнений Коши, частными случаями которой являются уравнения Эйлера и Навье-Стокса:

   

   

В квантовой механике также существуют уравнения, которые характеризуют движение волновой функции (а элементарные частицы одновременно являются и волнами). Однако можно ли их называть уравнениями движения – спорный вопрос. Ведь квантовые системы неопределенны по своей природе, а значит, нельзя получить точное решение уравнения движения.

Примеры решения задач

ru.solverbook.com

Уравнения математической физики — это… Что такое Уравнения математической физики?

        дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные и т.д.), к которым приводит математический анализ физических явлений. Для теории У. м. ф. характерна постановка задач в таком виде, как это необходимо при исследовании физического явления. Круг У. м. ф. с расширением области применения математического анализа также неуклонно расширяется. При систематизации полученных результатов появляется необходимость включить в теорию У. м. ф. уравнения и задачи более общего вида, чем те, которые появляются при анализе конкретных явлений; однако и для таких уравнений и задач характерно то, что их свойства допускают более или менее наглядное физическое истолкование (см. Математическая физика).

         Классификация уравнений математической физики. Значительная часть У. м. ф. составляют линейные уравнения с частными производными 2-го порядка общего вида:

        

        , (1)

         где все коэффициенты a_ij (a_ij = a_ij), b_i, с и правая часть f представляют собой заданные функции независимых переменных x₁, x₂,…, х_п (n ≥ 2), а u – искомая функция тех же аргументов. Свойства решений уравнения (1) существенно зависят от знаков корней (алгебраического относительно λ) уравнения

        

         = 0, (2)

         и поэтому классификация уравнений (1) проводится в соответствии с этими знаками. Если все n корней уравнения (2) имеют одинаковый знак, то говорят, что уравнение (1) принадлежит к эллиптическому типу; если один из корней имеет знак, противоположный знаку остальных n – 1 корней, – к гиперболическому типу; наконец, если уравнение (2) имеет один нулевой корень, а прочие корни одинакового знака, – к параболическому типу. Если коэффициенты a_ij постоянны, то уравнение (1) принадлежит к определенному типу независимо от значений аргументов; если же эти коэффициенты зависят от x₁,…, х_п, то и корни уравнения (2) зависят от x₁,…, х_п, а потому уравнение (1) может принадлежать к разным типам при различных значениях аргументов. В последнем случае (уравнение смешанного типа) изучаемая область изменения аргументов состоит из зон, в которых тип уравнения (1) сохраняется. Если корень уравнения (2), переходя от положительных значений к отрицательным, обращается в нуль, то между зонами эллиптичности и гиперболичности расположены зоны параболичности (надо отметить, что и в ряде др. отношений параболического уравнения занимают промежуточное положение между эллиптическими и гиперболическими).

         Для линейных уравнений с частными производными выше 2-го порядка и для систем уравнений с несколькими искомыми функциями классификация более сложна.

         Основные примеры уравнений математической физики.

                  – простейшее уравнение гиперболического типа, а также соответствующие неоднородные уравнения (в правой части которых добавлены известные функции) – Телеграфное уравнение и т.д. Уравнения и системы этого типа появляются при анализе различных колебаний и волновых процессов. Свойства уравнений и систем гиперболического типа во многом аналогичны свойствам приведённых простейших таких уравнений.                   – простейшее уравнение эллиптического типа и соответствующее неоднородное уравнение – Пуассона уравнение. Уравнения и системы эллиптического типа появляются обычно при анализе стационарных состояний. Теплопроводности уравнение:         

         – простейший пример уравнения параболического типа. Уравнения и системы параболического типа появляются обычно при анализе процессов выравнивания.

         Первым примером уравнений смешанного типа явилось т. н. уравнение Трикоми:

                  Для этого уравнения полуплоскость у у = 0 – зоной параболичности.          Ряд задач математической физики приводит к интегральным уравнениям (См. Интегральные уравнения) различных типов. Так, например, интегральные уравнения Вольтерра возникают в тех задачах физики, в которых существует предпочтительное направление изменения независимого переменного (например, времени, энергии и т.д.). В задаче о крутильных колебаниях возникает некоторое интегро-дифференциальное уравнение (См. Интегро-дифференциальные уравнения).          Постановка задач и методы решения уравнений математической физики. На первом этапе развития теории У. м. ф. много усилий было затрачено на отыскание их общего решения. Уже Ж. Д’Аламбер (1747) получил общее решение волнового уравнения. Основываясь на подстановках, применявшихся Л. Эйлером (1770), П. Лаплас предложил (1773) «каскадный метод», дающий общее решение некоторых др. линейных однородных гиперболических уравнений 2-го порядка с двумя аргументами. Однако такое общее решение удалось найти в весьма редких случаях; в отличие от обыкновенных дифференциальных уравнений, для уравнений с частными производными не выделено ни одного сколько-нибудь значительного класса уравнений, для которых общее решение может быть получено в виде достаточно простой формулы. Кроме того, оказалось что при анализе физических процессов У. м. ф. обычно появляются вместе с дополнительными условиями, характер которых коренным образом влияет на направление исследования решения (см. Краевые задачи, Коши задача).          Широкое распространение получили методы приближённого решения краевых задач, в которых задача сводится к решению системы алгебраических (обычно линейных) уравнений (см. Ритца и Галёркина методы. Сеток метод). При этом за счёт увеличения числа неизвестных в системе можно достичь любой степени точности приближения.

         Лит.: Владимиров В. С., Уравнения математической физики, 2 изд., М., 1971; Годунове. К., Уравнения математической физики, М., 1971; Соболев С. Л., Уравнения математической физики, 4 изд., М., 1966; Тихонов А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972.

dic.academic.ru