Новая программа для решения Алгебры и Геометрии | AppleVesti.ru
Новая программа для решения Алгебры и Геометрии
 admin on 28.02.2014 — 19:29 en Обзор программ для iOS
admin on 28.02.2014 — 19:29 en Обзор программ для iOS
Все мы как-то обучались в школе, делали шпаргалки, пробовали списать кое-что у одноклассников. То же наиболее повторяется опять и опять, от школы до колледжей, ВУЗов, институтов и остальных образовательных учреждений, в каком месте уже требуются не обыкновенные шпаргалки, а функциональные ассистенты. А нежели у вас в кармашке лишь ваш телефон? Непременно, есть некие приложения, подсобляющие в учебе, но у всех их имеется одна неувязка – надобность в подключении к интернету. Предположим, вам очень срочно пригодилось подсчитать какой-нибудь пример, уравнение либо припомнить формулу. Тогда вы достаете собственный телефон, а интернета у вас или нет, или скорость ужасно медленная. Шанс решить пример или задачку был упущен и вы потеряете баллы.
В таковых вариантах на содействие прибывает очень нужное приложение под заглавием Evermath. Это точный вычислитель, который может улаживать большую часть алгебраических и геометрических задач, объясняя решениет и объясняя совершенное заключение. С его поддержкой вы сможете с легкостью улаживать алгебраические и геометрические уравнения, основывать графики, преобразовать примеры и даже улаживать матрицы и вычислять интегралы.
Запустив программу, мы сходу увидим логотип Evermath на бело-сером фоне. Тут же нам предложат выбрать, какой-никакой раздел программы, где мы желаем побывать. Раздела здесь 2: «Геометрия» и «Алгебра».
Полюбить в прибавление разрешено с главного взора: лёгкие изящные шрифты, калоритные, насыщенные цвета, полупрозрачность, плавные и прекрасные переходы, Все под начинать iOS 7.
Бесспорный плюс Evermath – это критерии вычисления, всяческие подсказки, формулы и объяснения решений. До этого чем отыскать, к примеру, меньшее сплошное кратное, нам дают припомнить, что это такое и для что это необходимо. При решении задач сообразно геометрии это в особенности актуально, так как почти все огромные аксиомы и характеристики тяжко уяснить. Кстати о аксиомах, им в прибавлении посвящён цельный раздел. В нём мы найдём приемник теорем курса геометрии с 7 сообразно 11 класс. Довольно нужная функция, способствует возместить позабытые познания. Наиболее основное, что всё это и почти все иное собрано в одном месте.
Милые сюрпризы в разделе «Геометрия» не кончаются, нежели нам необходимо вычислить объём, то мы жмем на заглавие подходящей нам фигуры и переходим на страницу решения, здесь нас ожидает 3D-модель самой фигуры, а еще ее чертёж.
Улаживать задачки сообразно алгебре и геометрии очень элементарно. Имеется все нужные шаблоны и формулы, вам остается лишь записать в поля смысла, и прибавление все само рассчитает. Таковым образом, мы экономим время, а еще, благодаря комфортным правилам вычисления, повторяем обойденный материал либо заучиваем новейший.
Обычное отображение и заключение задач, чрезвычайно прекрасное спецоформление, подробно отработанный интерфейс, а еще крутящиеся геометрические фигуры помогают проще и свободнее опознаться в программе. От себя разработчик обещает прибавить новейшие, наиболее трудные и достойные внимания функции в следующих версиях приложения, какие непременно посодействуют вам при решении математических задач.
Подключение к Интернету не требуется, следственно, для работы приложения довольно приобрести и запустить его. Evermath дозволит с легкостью постановить трудные математические задачки, вполне расписав ход решения, а еще показав разные методы получения верного итога.
App Store Apple
Следующая статья01.03.2014 — 01:21 Предыдущая статья
28.02.2014 — 19:16
applevesti.ru
Решебник по Геометрии
Решебники, ГДЗ
-
1 Класс
- Математика
- Русский язык
- Английский язык
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
-
2 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
- Технология
-
3 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Немецкий язык
- Литература
- Музыка
- Окружающий мир
-
4 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Немецкий язык
- Литература
- Человек и мир
- Основы здоровья
- Музыка
megaresheba.ru
Вся школьная геометрия — в одном калькуляторе
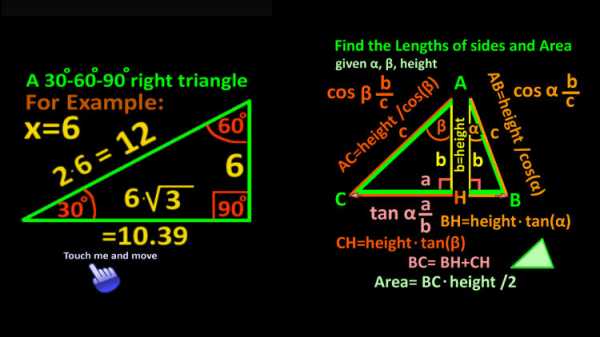
Родителям школьников порой не будет лишним освежить свои знания из давным-давно пройденного курса геометрии, чтобы помочь своим детям осваивать эту важную науку. В этом им поможет универсальный «геометрический калькулятор» Easy Geometry Calculator от разработчика DudiE — приложение для Android, которое можно загрузить из Google Play, позволяющее решать не только треугольники. В данном калькуляторе собрано многое из того, что может понадобиться изучающему геометрию школьнику.
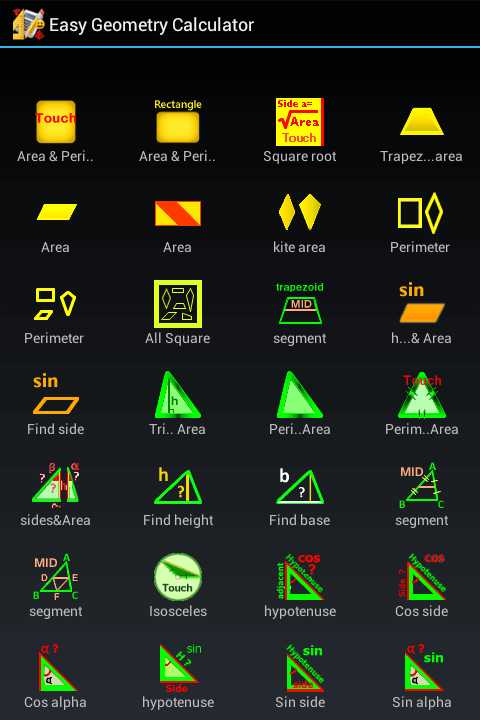
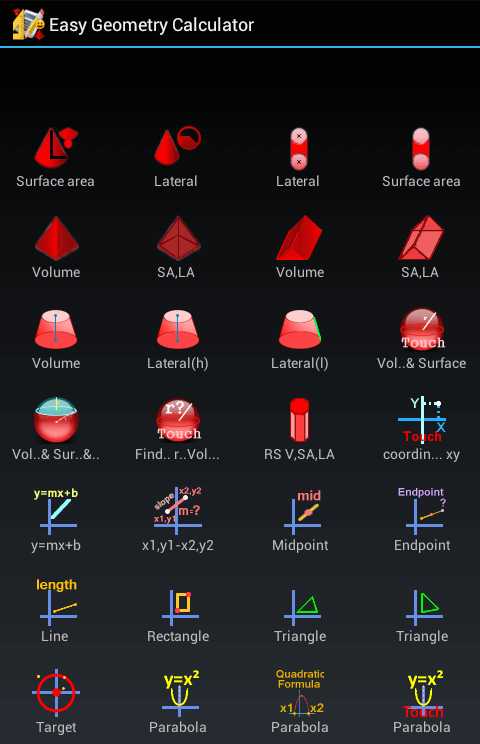
Данное приложение, хотя и является весьма функциональным, тем не менее относится к числу достаточно простых, поскольку ориентировано на базовый школьный курс геометрии и вряд ли подойдет для решения тех задач, которые стоят перед профессиональными математиками, что следует из его названия, которое переводится как «простой геометрический калькулятор». Но прост в нем только дизайн — классическая черная «школьная доска» и разноцветный «мел». И ничего лишнего, что отвлекало бы от геометрии.
Впрочем, рассматриваемое приложение не относится и к числу тех программных средств, которые выполняют всего одну задачу, ярким примером такого приложения является преобразователь градусов Фаренгейта в градусы Цельсия и наоборот. То, какое приложение лучше использовать, — «однозадачное» или комплексное — зависит и от набора решаемых задач и от предпочтений пользователя. Поэтому для ОС Android в огромном множестве созданы самые разнообразные программные инструменты. При необходимости планшет можно даже на время превратить в большой настольный калькулятор.
В любом случае в Easy Geometry Calculator собрана практически вся та геометрия, которая может потребоваться школьнику.


Главное окно приложения напоминает страницу приложений операционной системы Android. На ней располагаются ярлыки тех задач, которые оно умеет решать. Язык интерфейса приложения — английский. Для понимания того, для какой задачи предназначен каждый ярлык, будет вполне достаточно школьных знаний английского и некоторого представления о математической терминологии.
Кроме всего прочего, приложение позволяет производить также вычисления со стереометрическими фигурами. В качестве примера рассмотрим нахождение объема конуса. Для этого сначала найдем ярлык с изображением конуса и надписью «Volume». Для того чтобы приложением было осуществлено вычисление, необходимо ввести два параметра конуса: его радиус (radius) и высоту (height). Предположим, что радиус равен 10, а высота — 20. Введем значения в соответствующие поля ввода и коснемся кнопки «Calc».
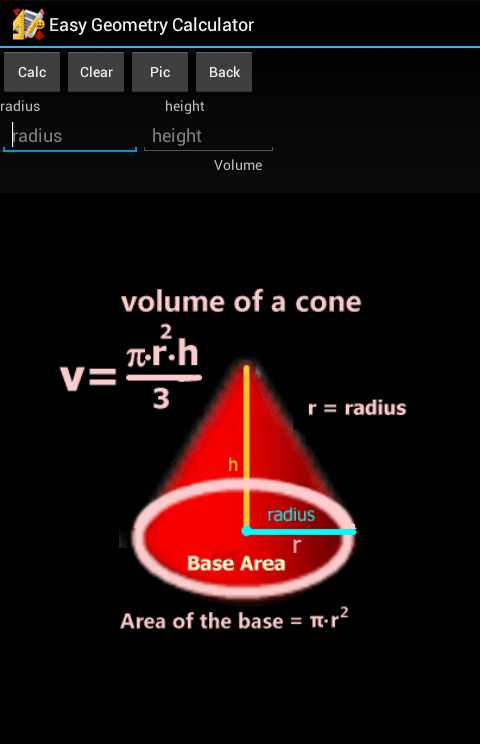
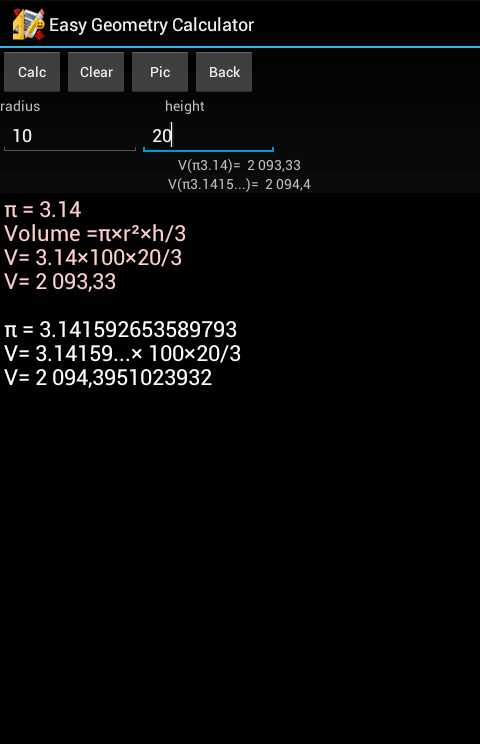
Приложение покажет не только объем конуса (V = 2093,33), но и ход решения задачи. На экран будет выведена формула вычисления объема конуса — π x r² x h/3 («число π, умноженное на радиус в квадрате и высоту, деленную на 3»), что применительно к данному конусу соответствует ~3,14 х 100 х 20/3. Следует отметить, что в первом, упрощенном, варианте вычисления значение числа π округлено до 3,14.
Ниже приложение выведет также более точный вариант данного вычисления — V = 2094,3951023932. Значение числа π в данном случае округлено до 15 знаков после запятой и составляет 3,141592653589793. Таким образом, приложение Easy Geometry Calculator предложит два варианта решения задачи.
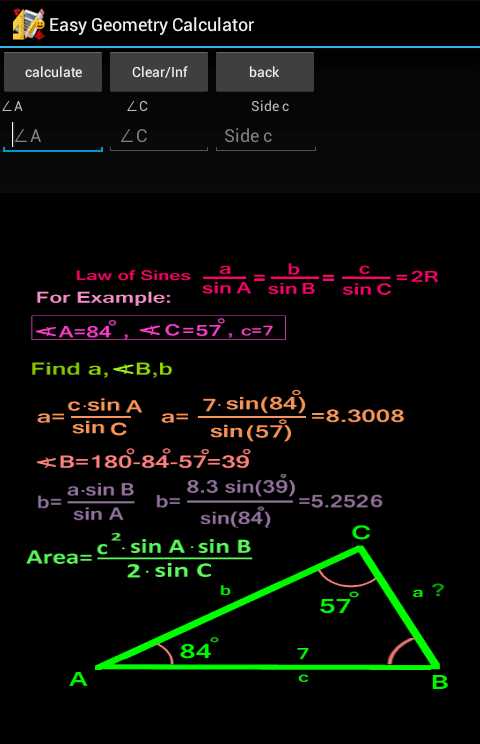

На этом примере становится ясно, каким образом данный «геометрический калькулятор» осуществляет вычисления. В каждом случае пользователь вводит необходимые приложению параметры геометрической фигуры и получает результат, который сопровождается выводом на экран смартфона или планшета формулы. Кроме того, на экран выводят
androidinsider.ru
Полезная геометрия | Наука и жизнь
В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.Вешаем зеркало
Вы решили повесить в прихожей зеркало. Тут же возникает вопрос: какой минимальной высоты должно быть зеркало, чтобы человек среднего роста мог видеть себя в нём целиком? И ещё: имеет ли при этом значение размер помещения, где будет висеть зеркало? Решение. Предмет и его отражение симметричны относительно плоскости зеркала. Построим в нём изображение человека (рис. 1): АВ — человек, А1В1 — его изображение, точка С — глаз, DE — зеркало. Из рисунка видно, что минимальная высота зеркала приблизительно равна половине роста человека, считая от уровня глаз. При этом высота Е нижнего края зеркала от пола должна быть вдвое меньше расстояния от пола до глаз. Легко понять, что, на каком бы расстоянии от такого зеркала ни находился человек, он сможет увидеть себя в нём с головы до ног, значит, размер помещения значения не имеет.Завариваем чай
Перед вами стеклянные чайники четырёх моделей одинаковой вместимости (рис. 2). В каком чайнике заваренный чай останется тёплым дольше? Решение. Из курса физики известно, что время охлаждения пропорционально площади поверхности тела. Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника, так как его форма близка к сфере (S = d2).Выдерживаем прямые углы
Если вы решили склеить коробку, сделать шкатулку или выложить плитку, важно, чтобы все детали были точными прямоугольниками или квадратами. В противном случае всё пойдёт наперекосяк. Как проверить, имеет ли деталь нужную «геометрию»? Решение. Чтобы проверить, у всех ли деталей, с которыми вы работаете, прямые углы и одинаковые линейные размеры, можно использовать строи-тельный угольник (рис. 3), а можно применить знания по геометрии. Убедитесь в том, что противоположные стороны четырёхугольника равны и при этом диагонали тоже имеют одинаковую длину. Как вы и сами знаете, сделать это можно с помощью линейки. Но вот вопрос: обязательно ли проверять и стороны и диагонали? Геометрия утверждает, что да! Например, на рис. 4 диагонали в четырёхугольнике слева равны, но очевидно, что его углы совсем не прямые. А в четырёхугольнике справа противоположные стороны равны, но это тоже не прямоугольник. Для проверки прямоугольности геометрия ещё советует убедиться в равенстве всех четырёх отрезков, на которые разбиваются диагонали в точке их пересечения.Строим прямой угол на земле
Известен старинный способ постро-ения прямого угла на поверхности земли. Его использовали ещё древние египтяне. Они строили прямой угол с помощью обычной верёвки, на которой через равные расстояния завязаны тринадцать узелков. Чтобы отрезки на верёвке были одинаковые, узелки завязывали вокруг колышков, вбитых в землю на равном расстоянии друг от друга. В чём состоит этот «верёвочный» способ? Решение. В древности при закладке храма такую верёвку с узелками использовали для определения направлений его стен. Концы верёвки на месте крайних узелков связывали, а затем натягивали её на три колышка так, как показано на рис. 5. Стороны при этом имели соотношение 3:4:5. В таком треугольнике один из углов получается прямым. Впоследствии этот факт был доказан в теореме Пифагора. Поэтому первых геометров называли ещё «натягивателями верёвок». Нужно отметить, что таким способом построения прямого угла на местности пользуются и сегодня, например при закладке фундамента небольшого строения.Проверяем перпендикулярность стен
Как проверить, перпендикулярны ли друг другу соседние стены в комнате, воспользовавшись верёвкой с узелками из предыдущей задачи? Решение. Если предположить, что стены в комнате вертикальны, а пол горизонтален, то проверку проводят так. От точки на полу в углу между стенами откладывают отрезки длиной 3 и 4 единицы (рис. 6). Если стены перпендикулярны, то расстояние между концами отрезков будет равно 5 единицам, так как построенный тре-угольник со сторонами 3, 4, 5 — прямоугольный.Отмеряем нужный объём
Часто в рецептуре того или иного блюда требуется взять четверть (или половину) стакана жидкости, муки либо какого-либо другого продукта. Как отмерить такой объём с наибольшей точностью, не прибегая к дополнительным измерительным средствам? Решение. Воспользуемся стаканом цилиндрической формы — это важно для точности измерений. Чтобы отмерить четверть стакана жидкости, надо из наполненного стакана вылить столько, чтобы оставшаяся в нём жидкость закрыла половину дна (рис. 7). Она займёт примерно четверть объёма стакана-цилиндра. Аналогично поступаем, если надо отмерить половину стакана. Наклоняем стакан так, чтобы оставшаяся в нём жидкость закрыла всё дно (рис. 8). А можно ли геометрическим способом узнать объём бутылки? Конечно! Для этого надо заполнить бутылку водой чуть меньше чем наполовину (рис. 9, слева) и измерить объём воды, умножив площадь дна бутылки на высоту налитой в неё воды (напомним, что объём цилиндра вычисляется как произведение площади основания на высоту). Затем нужно перевернуть бутылку горлышком вниз так, чтобы вода не вытекла, и измерить объём верхней цилиндрической части бутылки, оставшейся пустой (рис. 9, справа). Полный объём бутылки равен сумме найденных объёмов. Для точности можно учесть толщину стенок бутылки.Укрепляем калитку
Прямоугольная калитка (рис. 10, слева) со временем расшатывается и становится похожей на параллело-грамм. Этого можно избежать, прибив к ней ещё одну планку. Только надо знать, как это сделать. Решение. Выбор такого положения планки, как показано на рис. 10, справа, основан на свойстве жёсткости треугольника. Оно гласит: существует единственный треугольник с заданными длинами сторон. Планка и есть гипотенуза такого треугольника.Выбираем табурет
Если вы решили предыдущую задачу, то без труда определите, на какой табурет (рис. 11) можно сесть без риска оказаться на полу. Решение. Безопасный табурет изображён на правой картинке, так как его сиденье и ножки образуют треугольник.Исправляем ошибку кроя
Предположим, вам нужно вырезать для аппликации два разносторонних треугольника из цветной бумаги — «левый» и «правый». Вы случайно вырезали их одинаковыми — оба «левые». Можно ли, не используя новый кусок бумаги, исправить ошибку? Решение. Для исправления ошибки вы можете разрезать один из треугольников, например так, как показано на рис. 12, а затем сложить из него нужный треугольник.Находим середину
Как без всяких измерений найти середину негнущегося прута, доски или металлического стержня? Решение. Можно отмерить размеры стержня на шнуре, затем сложить его пополам и отложить полученную длину. А можно воспользоваться геометрическим построением середины отрезка с помощью циркуля и линейки, если, конечно, размеры позволяют это сделать. Ещё более рациональное решение даёт физика. Середину однородного стержня легко найти, используя понятие центра тяжести (рис. 13).Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
Наука и жизнь // Иллюстрации
‹
›
www.nkj.ru
Геометрия (Pocket Edition) — решение геометрических задачек
Геометрия – специальное приложение-справочник, которое может решать практически все задачи из школьного курса геометрии.
Основное меню программы располагается на нижней плашке. Первое время вам будут доступны лишь четыре раздела: Инструменты выделения, Инструменты рисования, Инструменты связи, а также Запуск решения/создание новой задачи/справки. После того как вы выберете раздел и нажмете на него, перед вами появиться окошко с дополнительным меню. Именно в этом меню и необходимо создать условия задачи, которую вам необходимо решить.

Программа Геометрия (Pocket Edition).
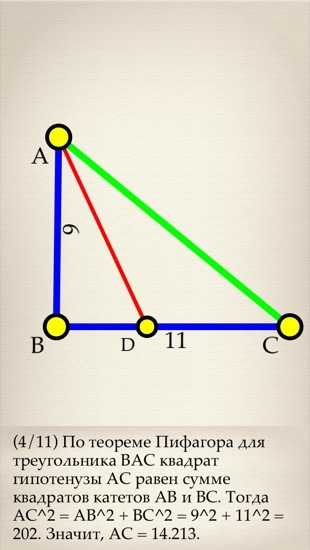
Быстрое решение геометрических задачек.
Разработчики сделали уникальный интерфейс, который позволяет создавать рисунки к геометрическим задачкам, которые попадаются как в домашнем задании, так и в контрольной работе.
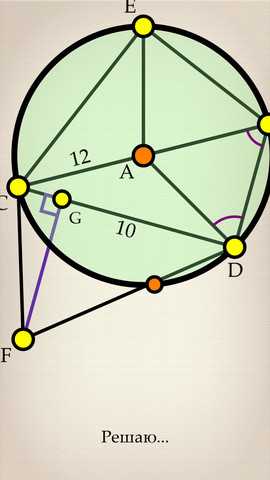
Объяснение теорем.
Решение задачки осуществляется в несколько логических этапов, каждый из которых заканчивается выводом и логическим продолжением. Каждый шаг в решении объясняется, доказывается и поясняется на рисунке. Благодаря этой концепции понять и выучить необходимую теорему или задачку не составит труда.
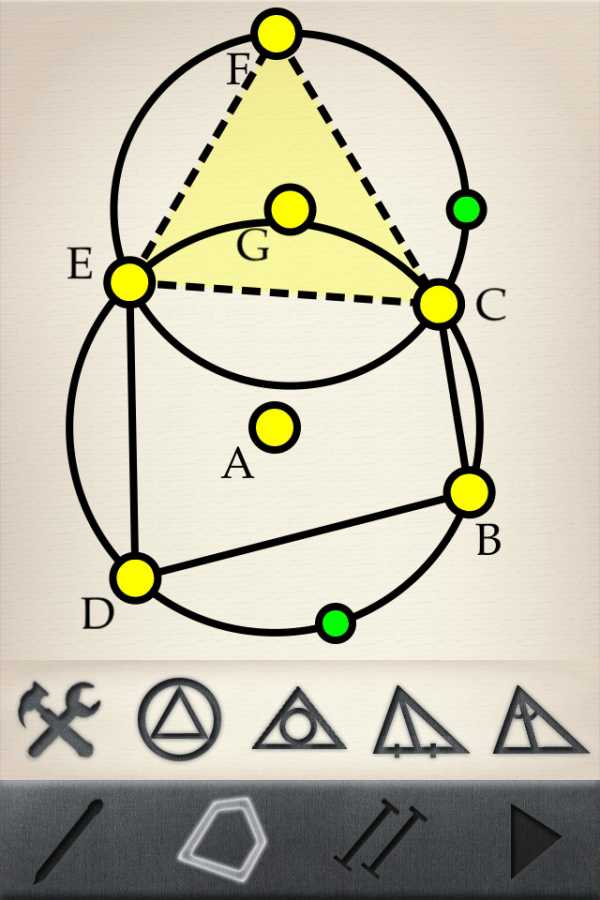
Графическое изображение задачек.
Однако решение задачек и доказывание теорем – это не единственная возможность приложения Геометрия, оно еще способно показать, как можно прийти к противоречию, а также какая теорема или свойство не выполняются.

Введение условий задачи.
Приложение Геометрия можно скачать как платно, так и бесплатно. Однако бесплатная версия программы ограничивается достаточно сильно: благодаря этой версии у вас есть возможность решить лишь одну геометрическую задачку, после этого будет ссылка на App Store, чтобы там приобрести платную версию программы.
Но этого вполне достаточно, чтобы ознакомиться с приложением и понять, нужно оно вам или нет. Сама программа сделана достаточно красиво и качественно, а разобраться в ее пользовании сможет любой школьник.
Скачать бесплатную версию приложения Геометрия можно по ссылке, а полную версию – по ссылке.
cuteiphone.ru
