Программа для решения квадратных уравнений – Исходник программы Паскаль, которая находит корни квадратного уравнения по заданным коэффициентам

Калькулятор онлайн — Решение показательных уравнений

Этот математический калькулятор онлайн поможет вам решить показательное уравнение. Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Вы можете посмотреть теорию о показательной функции и общие методы решения показательных уравнений.

Примеры подробного решения >>

Введите показательное уравнение

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Показательная функция, её свойства и график

Напомним основные свойства степени. Пусть а > 0, b > 0, n, m — любые действительные числа. Тогда
1) aⁿ a^m = a^n+m

2) \( \frac{a^n}{a^m} = a^{n-m} \)

3) (aⁿ)^m = a^nm

4) (ab)ⁿ = aⁿ bⁿ

5) \( \left( \frac{a}{b} \right)^n = \frac{a^n}{b^n} \)

6) aⁿ > 0

7) aⁿ > 1, если a > 1, n > 0

8) aⁿm, если a > 1, n

9) aⁿ > a^m, если 0

В практике часто используются функции вида y = a^x, где a — заданное положительное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Определение. Показательной функцией называется функция вида y = a^x, где а — заданное число, a > 0, \( a \neq 1\)

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a^x где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a^x = b, где а > 0, \( a \neq 1\), не имеет корней, если \( b \leq 0\), и имеет корень при любом b > 0.

3) Показательная функция у = a^x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 Это следует из свойств степени (8) и (9)

Построим графики показательных функций у = a^x при a > 0 и при 0 Использовав рассмотренные свойства отметим, что график функции у = a^x при a > 0 проходит через точку (0; 1) и расположен выше оси Oх.
Если х x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = a^x при 0 Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является горизонтальной асимптотой графика.

Если х

Показательные уравнения

Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени. Решение показательных уравнений часто сводится к решению уравнения a^x = a^b где а > 0, \( a \neq 1\), х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \( a \neq 1\) равны тогда и только тогда, когда равны их показатели.

Решить уравнение 2^3x • 3^x = 576
Так как 2^3x = (2³)^x = 8^x, 576 = 24², то уравнение можно записать в виде 8^x • 3^x = 24², или в виде 24^x = 24², откуда х = 2.

Ответ х = 2

Решить уравнение 3^{х + 1} — 2 • 3^{x — 2} = 25
Вынося в левой части за скобки общий множитель 3^{х — 2}, получаем 3^{х — 2}(3³ — 2) = 25, 3^{х — 2} • 25 = 25,
откуда 3^{х — 2} = 1, x — 2 = 0, x = 2
Ответ х = 2

Решить уравнение 3^х = 7^х
Так как \( 7^x \neq 0 \) , то уравнение можно записать в виде \( \frac{3^x}{7^x} = 1 \), откуда \( \left( \frac{3}{7} \right) ^x = 1 \), х = 0
Ответ х = 0

Решить уравнение 9^х — 4 • 3^х — 45 = 0
Заменой 3^х = t данное уравнение сводится к квадратному уравнению t² — 4t — 45 = 0. Решая это уравнение, находим его корни: t₁ = 9, t₂ = -5, откуда 3^х = 9, 3^х = -5.
Уравнение 3^х = 9 имеет корень х = 2, а уравнение 3^х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.
Ответ х = 2

Решить уравнение 3 • 2^{х + 1} + 2 • 5^{x — 2} = 5^х + 2^{х — 2}
Запишем уравнение в виде
3 • 2^{х + 1} — 2^{x — 2} = 5^х — 2 • 5^{х — 2}, откуда
2^{х — 2} (3 • 2³ — 1) = 5^{х — 2}( 5 ² — 2 )
2^{х — 2} • 23 = 5^{х — 2}• 23
\( \left( \frac{2}{5} \right) ^{x-2} = 1 \)
x — 2 = 0
Ответ х = 2

Решить уравнение 3^{|х — 1|} = 3^{|х + 3|}
Так как 3 > 0, \( 3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1)² = (х + 3)², откуда
х² — 2х + 1 = х² + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1

www.mathsolution.ru

Программа для решения квадратных уравнений

• 22.11.2012
• комментария 3
• Dimabiz

Сегодня я хочу представить вашему внимаю еще одну программку которую накидал на днях. Программа элементарная, предназначена для решения квадратных уравнений. Многие могут сказать “зачем изобретать велосипед, когда в интернете уже есть подобные программы”, но я вот захотел сделать свою программу, такой, какой вижу её я.

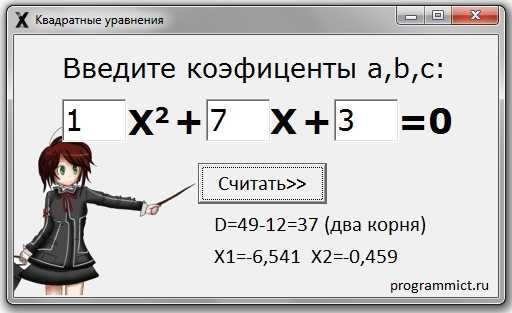
Выше размещен скриншот моей программки. Для вычисления уравнения нужно ввести коэффициенты a, b, c и нажать на кнопку считать. После чего программа выдаст результат под кнопкой с помощью Label. И все, это все что умеет делать программа) Чтобы окно программы не казалось слишком пустым добавил на задний план картинку. Программа очень простая, но как мне кажется удобная в использовании. На её создание в Delphi потратил около 20-30 минут, большую часть времени потратил на поиск картинки. Название придумывать не стал, просто подписал “Квадратные уравнения“. Следующие версии выпускать также не планирую, но всегда готов по вашим просьбам что-либо добавить в программу или сделать её более удобной, так что если есть идеи, пишите в комментариях и ли через форму обратной связи. Ну да ладно больше о этой элементарной программе писать нечего, поэтому мне остается только дать ссылку на её скачивание.

Скачать программу для решения квадратных уравнений

P.S. если честно, сделал эту программу в том числе и для того, чтобы в будущем мой блог мог выйти в топ поисковых систем по запросу “Программа для решения квадратных уравнений” и получат посетителей) Но это уже из области seo…

programmict.ru

Программа для решения квадратных уравнений второго порядка

Содержание

Введение

1. Определение требований

1.1 Постановка задачи

1.2 Требования к интерфейсу

2. Анализ, формальная постановка и выбор метода решения

2.1 Краткая характеристика операционной системы

2.2 Краткая характеристика языка программирования

2.3 Компоненты среды Delphi, использованные в программе

2.4 Методы решения

3. Проектирование

3.1 Требования к аппаратному обеспечению

3.2 Инструкция пользователя

3.3 Инструкция программиста

4. Реализация и тестирование

Заключение

Список использованных источников

Листинг программы

Введение

Нелинейные уравнения – уравнения вида F(x)=0. при построении графиков таких уравнений получается не ровная линия, а какая либо фигура, например, парабола. Здесь значения того или иного экстремума функции возрастают прямо пропорционально ее предыдущего значения.

Данная курсовая работа должна дать наглядное представление решений нелинейных уравнений на примере квадратных уравнений второго порядка.

Пояснительная записка курсовой работы состоит из нескольких разделов.

Первый раздел пояснительной записки включает в себя постановку задачи, требования, предъявляемые к разрабатываемым программам, цели работы.

Второй раздел включает в себя проектную часть продукта, в которой определяются названия объектов и их логические атрибуты, иногда статические связи между объектами.

Целью третьего раздела является принятие решений по структуре найденных абстракций и их взаимоотношения, а также создание механизмов связи между абстракциями, в виде логической модели системы, представимой диаграммой классов и объектов.

В четвертом разделе происходит собственно разработка программы с автономным тестированием частей и их интеграцией. Описываются тестовые сценарии, процедуры и метрики для измерения числа ошибок.

1. Определение требований

1.1 Постановка задачи

Целью создания курсового проекта является разработка программы для решения нелинейных уравнений различными численными методами.

Данный программный продукт должен реализовывать следующие основные возможности:

— решение уравнения с помощью дискриминанта;

— решение уравнения теоремой Виетта;

— решение квадратного уравнения с помощью таблицы Горнера;

Интерфейс программного продукта должен представлять собой удобную среду для ввода значений.

Получаемые ответы должны быть правильными и корректными.

Для наполнения окон интерфейса элементами управления необходимо чёткое понимание задач пользователя.

На этапе визуального дизайна нужно правильно использовать компоненты среды программирования, чтобы показать пользователю для чего нужно каждое окно и как им пользоваться. Хорошо выполненный дизайн выглядит чистым, простым и аккуратным. Его можно понять одним взглядом.

1.2 Описание требований к программе

Независимо от конкретности проблемы, можно выделить некоторые формальные требования, на которых защищается квалификация разработчика.

Устойчивость программы. Программа не должна терять работоспособности, ни при каких, даже некорректных, действиях пользователя. Всякие действия, грозящие потерей информации, выполняются только после повторного подтверждения. Вводимая информация там, где возможно, подвергается логическому контролю.

Функциональная полнота. В рамках согласованного с заказчиком подмножества функций все они должны быть реализованы.

Использование клавиатуры. На любом этапе нажатия любой клавиш (особенно функциональных) должно игнорироваться или вызывать предусмотренные действия (описанные в средствах помощи). Привязка действий к клавишам должна быть общепринятой.

2. Анализ, формальная постановка и выбор метода решения

2.1 Краткая характеристика операционной системы

Windows 7 — операционная система семейства Windows NT, следующая за Windows Vista. В линейке Windows NT система носит номер версии 6.1 (Windows 2000 — 5.0, Windows XP — 5.1, Windows Server 2003 — 5.2, Windows Vista и Windows Server 2008 — 6.0). Серверной версией является Windows Server 2008 R2, версией для интегрированных систем —Windows Embedded Standard 2011 (Quebec), мобильной —Windows Embedded Compact 2011 (Chelan, Windows CE 7.0).

Операционная система поступила в продажу 25 октября 2009 года, меньше чем через три года после выпуска предыдущей операционной системы, Windows Vista. Хотя изначально операционная система должна была поступить в продажу уже 31 августа 2009 года. Партнёрам и клиентам, обладающим лицензией Volume Licensing, доступ к RTM был предоставлен 24 июля 2009 года. Финальная нелицензионная версия (копия с дисков, которые потом пошли в продажу) была доступна всем с первых чисел августа 2009 года.

В состав Windows 7 вошли как некоторые разработки, исключённые из Windows Vista, так и новшества в интерфейсе и встроенных программах. Из состава Windows 7 были исключены игры Inkball, Ultimate Extras; приложения, имеющие аналоги в Windows Live (Почта Windows, Календарь Windows и пр.), технология Microsoft Agent, Windows Meeting Space; из меню «Пуск» исчезла возможность вернуться к классическому меню и автоматическая пристыковка браузера и клиента электронной почты…

Разработка Windows 7

Кодовое название Blackcomb принадлежало Windows NT 6.0, операционной системе, которая, как планировалось, станет следующей после Windows XP. Blackcomb должна была стать преемником этой ОС как для настольных, так и для серверных рабочих станций. В конце 2001 года выпуск Blackcomb запланировали на 2005 год, а в августе2002 года было объявлено о том, что промежуточной версией станет Windows Longhorn, которая будет обновлением ядра Windows NT 5.x. В течение разработки Windows Longhorn в неё были добавлены некоторые функции Blackcomb и присвоен номер 6.0. Blackcomb была окружена неразберихой, связанной с некоторыми сообщениями о том, что планы по маркетингу были сильно пересмотрены и что она должна быть серверной ОС Windows 6.x, но с улучшениями.

Vienna

В январе 2006 года Microsoft объявила, что новой клиентской ОС будет Vienna, выход которой был запланирован на 2010 год.

Fiji

В марте 2006 года стало известно, что наследницей Windows Vista будет Fiji, выход которой был запланирован на2008 год.

В 2008 году, в результате жалоб фиджийцев на то, что новая ОС будет носить имя их страны, стали известны новые сведения о Fiji. По словам фиджийцев, Бен Грин сказал, что в Fiji будут добавлены новые телевизионные форматы, поддержка интерактивных служб и улучшения пользовательского интерфейса для Windows Media Center. Вполне вероятно, во включённую в состав Windows 7 программу Windows Media Center уже добавлены изменения, которые должны были быть в Fiji.

Windows 7

24 июля 2007 года корпорация Microsoft официально сменила кодовое название Vienna на Windows 7. НомерWindows 7 в линейке NT, в которой она будет находиться — 6.1 (в своё время системы этого семейства получили номера: Windows 2000 — 5.0, Windows XP — 5.1, Windows Server 2003 — 5.2, Windows Vista — 6.0, Windows Server 2008 — 6.0).

13 октября 2008 года вице-президент Microsoft Майк Нэш сообщил, что кодовое имя Windows 7 и станет официальным названием новой версии.[9]

Начальная редакция (Windows 7 Starter) будет распространяться исключительно с новыми компьютерами, она не будет включать функциональной части для проигрывания H.264, AAC, MPEG-2. Домашняя базовая — предназначена исключительно для выпуска в развивающихся странах, в ней нет интерфейса Windows Aero с функциями Peek, Shake, общего доступа к подключению в интернет и некоторых других функций. Также в ней есть те же ограничения на просмотр, что и в начальной редакции. В профессиональной и максимальной версиях существует поддержка XP Mode (на некоторых процессорах).

Кроме этого, согласно требованиям Еврокомиссии, для продаж в Европе планировалась специальная версия всех редакций с индексом «Е» («Windows 7 Е») — без предустановленного браузера Internet Explorer, однако она снята с продажи. Одной из причин снятия с продаж является недовольство партнёров и OEM-производителей отсутствием браузера в изначальной комплектации. Всем, кто выполнил предзаказ версии с индексом «Е», было предложено заказать обновление или заказать полную версию с 1 сентября 2009 года.

Тем не менее, в течение 5 лет планируется заменить встроенный Internet Explorer опциональным. В настоящее время данная схема согласована с Еврокомиссией.

Все редакции, за исключением Начальной, существуют как в 32-битной, так и в 64-битной версиях.

Максимальный объём оперативной памяти для 32-битных версий ограничен 4 Гб, Начальная редакция поддерживает до 2 Гб. Однако на практике пользователю часто доступен меньший объём, из-за аппаратных ограничений часто невозможно реализовать функцию режима PAE. Поддержка более крупных объёмов памяти доступна только для 64-битных версий. Они поддерживают до 8 Гб («Домашняя базовая»), до 16 Гб («Домашняя расширенная»), все старшие версии могут адресовать до 192 Гб оперативной памяти.

Бесплатная 90-дневная версия Windows 7 Корпоративная доступна для ИТ-специалистов, желающих познакомиться с Windows 7 в рамках организации.

Операционная система обладает поддержкой мультитач-управления. Эта возможность была впервые продемонстрирована Microsoft на ежегодной конференции TechEd’08 в Орландо. В ходе демонстрации использовалась сборка системы 6.1.6856, а также опытная модель ноутбука с мультитач-экраном.

Сетевая технология Branch Cache позволяет кешировать содержимое интернет-трафика. Если пользователю в локальной сети потребуется файл, который уже был загружен кем-то из пользователей его сети, — он сможет получить его из локального кэш-хранилища, а не использовать канал с ограниченной пропускной способностью. Сетевой кеш может работать в двух режимах — Hosted Cache и Distributed Cache. В первом случае — файл хранится на выделенном локальном сервере под управлением Windows Server 2008 R2, во втором случае сервер не требуется, а кеш распределяется для хранения на компьютерах пользователей. Технология рассчитана на крупные сети и предлагается для внедрения на предприятиях в составе Корпоративной и Максимальной версий ОС.

В ОС также встроено около 120 фоновых рисунков, уникальных для каждой страны и языковой версии. Так, русская версия включает тему «Россия» с шестью уникальными обоями высокого разрешения. Все версии включают 50 новых шрифтов. Существующие шрифты доработаны для корректного отображения всех символов. Windows 7 — первая версия Windows, которая включает больше шрифтов для отображения нелатинских символов, чем для отображения латинских. Панель управления шрифтами также подверглась улучшению — по умолчанию, в ней будут отображаться только те шрифты, раскладка для которых установлена в системе. Реализована поддержкаUnicode 5.1.[ Панель поиска Instant Search теперь распознаёт больше языков.

mirznanii.com

Программа для решения квадратных уравнений РКУ v.1.0

Инфоурок › Алгебра › Другие методич. материалы › Программа для решения квадратных уравнений РКУ v.1.0

Выберите документ из архива для просмотра:

5.04 МБ РКУ v.1.0.exe

Курс повышения квалификации

Курс повышения квалификации

Курс профессиональной переподготовки

Учитель математики

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник: Все учебники

Выберите тему: Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала: ДA-015438

ВНИМАНИЮ ВСЕХ УЧИТЕЛЕЙ: согласно Федеральному закону N273-ФЗ «Об образовании в Российской Федерации» педагогическая деятельность требует от педагога наличия системы специальных знаний в области обучения и воспитания детей с ОВЗ. Поэтому для всех педагогов является актуальным повышение квалификации по этому направлению!

Дистанционный курс «Обучающиеся с ОВЗ: Особенности организации учебной деятельности в соответствии с ФГОС» от проекта «Инфоурок» даёт Вам возможность привести свои знания в соответствие с требованиями закона и получить удостоверение о повышении квалификации установленного образца (72 часа).

Подать заявку на курс

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

infourok.ru

2.4 Методы решения. Программа для решения квадратных уравнений второго порядка

Похожие главы из других работ:

Автоматизированное рабочее место производственно-технического отдела

1.5 Методы решения задачи

…

Задача о минимизации стоимости перегона транспортных средств

1.1 Математические методы решения задачи

Методы решения транспортных задач. Метод северно-западного угла (диагональный). Сущность метода заключается в том, что на каждом шаге заполняется левая верхняя (северо-западная) клетка оставшейся части таблицы…

Комбинаторные алгоритмы. Поиск кратчайшего пути на графе

Методы решения

Метод Эйлера Метод Эйлера состоит в том, что сначала конь двигается по произвольному маршруту, пока не исчерпает все возможные ходы. Затем оставшиеся не пройденными клетки добавляются в сделанный маршрут…

Комбинаторные алгоритмы. Поиск кратчайшего пути на графе

Методы решения и описание алгоритмов

Количество различных перестановок множества, состоящего из n элементов равно n!. В этом нетрудно убедиться: на первом месте в перестановке может стоять любой из n элементов множества, после того…

Применение линейного программирования для решения оптимизационных задач

1.2 Методы решения ЗЛП

линейный программирование оптимизационный задача Задачи линейного программирования решаются несколькими методами. В настоящей курсовой работе мы подробно рассмотрим графический метод решения метод решения в среде Exsel…

Программа для решения квадратных уравнений второго порядка

2.4 Методы решения

Квадратное уравнение — уравнение вида ax2 + bx + c= 0, где а не равно нулю…

Программирование и основы алгоритмизации (ведение в исследование операций)

2. Методы решения

Данная задача относится к типу целочисленных. Экстремальная задача, переменные которой принимают лишь целочисленные значения, называется задачей целочисленного программирования…

Программное средство нахождения кратчайших путей в графе

1.9 Методы решения

Классическую транспортную задачу можно решить симплекс-методом, но есть и другие подходы. Например, сначала ищется опорный план при помощи одного из ниже перечисленных методов: · «северо-западного угла», · «наименьшего элемента»…

Разработка инструментария по алгоритмической поддержке исследований асимметрии регионального развития

3 Методы решения

…

Разработка приложений для работы с базами данных

2.1 Анализ и методы решения задачи

2.1.1 Информация о приложении Целью приложения является работа с данными БД под управлением MS SQL Server. Пользователь подключается к базе данных «Нотариус». После подключения отображаются все таблицы БД с возможностью изменения данных в них. 2.1…

Разработка программы обработки массива данных с построением диаграммы (предметная область — «Садовод»)

3. Методы решения задач

Построение круговой диаграммы предполагает следующий алгоритм: 1) вычислить относительную частоту для каждого из интервалов в процентах Pj = 100 Fj / N; 2) вычертить окружность радиуса R < Yэ,max/2; 3) вычерчивать радиусы окружности…

Разработка проекта информационной системы учета и анализа трудозатрат на промышленном предприятии ОАО «КнААПО»

1.2 Возможные методы решения

Очевидно, что для решения возникших проблем можно пойти по двум пути. Путь первый это снижение нагрузки на работника за счет расширения штата бюро. Путь второй необходимо повысить производительность труда уже имеющегося персонала…

Реализация звуковых эффектов

3 методы решения поставленной задачи

В данном курсовом проекте реализованы методы, основанные на использовании задержки, а также основанные на частотном преобразовании. Рассмотрим подробнее данные методы. 3…

Решение системы линейных уравнений методом Гаусса и Жордана-Гаусса

Методы решения примененные в программе

…

Численные расчёты динамики генных сетей на основе редукции графов в рамках синхронной булевой модели

1.3 Существующие методы решения

1) SAT-подход. Основной минус SAT-подхода состоит в том, что с его помощью удается быстро найти одно конкретное решение SAT-задачи. При поиске новых решений (например, при перечислении неподвижных точек) информацию о найденных приходится учитывать…

prog.bobrodobro.ru