Принадлежность точки плоскости | Начертательная геометрия
Принадлежность точки плоскости на комплексном чертеже определяется согласно аксиоме инцидентности или отношения принадлежности между элементами евклидова пространства, которая гласит: — если точка E принадлежит прямой k, а прямая k принадлежит плоскости α, то точка E принадлежит плоскости α: E ∈ k ∧ k ∈ α ⇒ E ∈ α.
Задача на принадлежность точки плоскости может быть выражена следующим образом: — заключить точку E(E`, E») в; — провести через точку E(E`, E») плоскость α общего положения
Принадлежность точки плоскости
Положение плоскости α в пространстве определяется тремя точками — вершинами ΔABC. Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой k, которая принадлежит плоскости α, потому что две ее точки
Принадлежность точки плоскости
доказываем тем самым ее принадлежность заданной плоскости. Заключить точку M в плоскость α заданную параллельными прямыми a и b
Принадлежность точки плоскости
Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой k, которая принадлежит плоскости α, потому что две ее точки 1 и 2 принадлежат этой плоскости. Построение искомой плоскости α: — проводим прямую через точку M; — через точки 1 и 2 взятые на прямой k проводим взаимно параллельные прямые a и b соответственно.
Через точку M провести плоскость α заданную следами

Принадлежность точки плоскости
Здесь принадлежность точки плоскости α общего положения определяется ее принадлежностью прямой h, которая, в то же время, принадлежит плоскости α и является ее горизонталью. Построение искомой плоскости α: — проводим прямую h (горизонталь искомой плоскости) через точку K; — проводим горизонтальный след αH // h` ⇒ αx; — через точки αx и hV проводим фронтальный след αV.
+
2.3. Принадлежность точки и прямой плоскости
Признаки принадлежности хорошо известны из курса планиметрии. Наша задача рассмотреть их применительно к проекциям геометрических объектов.
Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.
Принадлежность прямой плоскости определяется по одному из двух признаков:
а) прямая проходит через две точки, лежащие в этой плоскости;
б) прямая проходит через точку и параллельна прямой, лежащим в этой плоскости.
Используя эти свойства, решим в качестве примера задачу. Пусть плоскость задана треугольником АВС. Требуется построить недостающую проекцию D1 точки D, принадлежащей этой плоскости. Последовательность построений следующая (рис. 2.5).
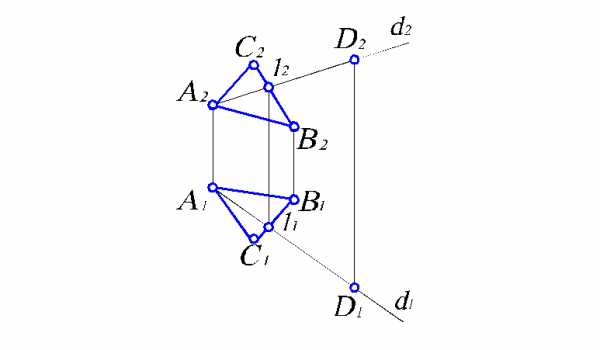
Рис. 2.5. К построению проекций точки, принадлежащей плоскости
Через точку D2 проводим проекцию прямой d, лежащей в плоскости АВС, пересекающую одну из сторон треугольника и точку А2. Тогда точка 12 принадлежит прямым А2D2 и C2В2. Следовательно, можно получить ее горизонтальную проекцию 11 на C1В1 по линии связи. Соединив точки 11 и А1, получаем горизонтальную проекцию d1. Ясно, что точка D1 принадлежит ей и лежит на линии проекционной связи с точкой D2.
Достаточно просто решаются задачи на определение принадлежности точки или прямой плоскости. На рис. 2.6 показан ход решения таких задач. Для наглядности изложения задачи плоскость задаем треугольником.
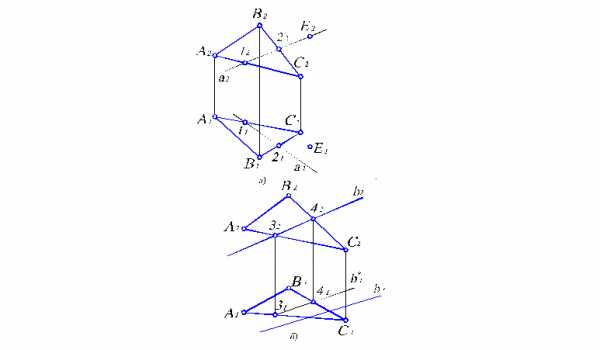
Рис. 2.6. Задачи на определение принадлежности точки и прямой плоскости.
Для того, чтобы определить принадлежит ли точка Е плоскости АВС, проведем через ее фронтальную проекцию Е2 прямую а2. Считая, что прямая а принадлежит плоскости АВС, построим ее горизонтальную проекцию а1 по точкам пересечения 1 и 2. Как видим (рис. 2.6, а), прямая а1 не проходит через точку Е1. Следовательно, точка Е АВС.
В задаче на принадлежность прямой в плоскости треугольника АВС (рис. 2.6, б), достаточно по одной из проекций прямой в2 построить другую в1* считая, что вАВС. Как видим, в1* и в1 не совпадают. Следовательно, прямая в АВС.
2.4. Линии уровня в плоскости
Определение линий уровня было дано ранее. Линии уровня, принадлежащие данной плоскости, называются главными. Эти линии (прямые) играют существенную роль при решении ряда задач начертательной геометрии.
Рассмотрим построение линий уровня в плоскости, заданной треугольником (рис. 2.7).
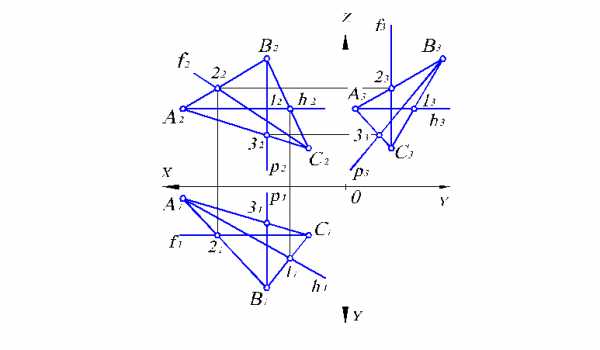
Рис. 2.7. Построение главных линий плоскости, заданной треугольником
Горизонталь плоскости АВС начинаем с вычерчивания ее фронтальной проекции h2, которая, как известно, параллельна оси ОХ. Поскольку эта горизонталь принадлежит данной плоскости, то она проходит через две точки плоскости
Фронталь плоскости АВС строится аналогично (рис. 2.7) с той лишь разницей, что ее вычерчивание начинается с горизонтальной проекции f1, так как известно, что она параллельна оси ОХ. Профильная проекция f3 фронтали должна быть параллельна оси ОZ и пройти через проекции С3, 23 тех же точек С и 2.
Профильная линия плоскости АВС имеет горизонтальную р1 и фронтальную р2 проекции, параллельные осям OY и OZ, а профильную проекцию р3 можно получить по фронтальной, используя точки пересечения В и 3 с АВС.
При построении главных линий плоскости необходимо помнить лишь одно правило: для решения задачи всегда нужно получить две точки пересечения с данной плоскостью. Построение главных линий, лежащих в плоскости, заданной иным способом, ничуть не сложнее рассмотренного выше. На рис. 2.8 показано построение горизонтали и фронтали плоскости, заданной двумя пересекающимися прямыми аив.
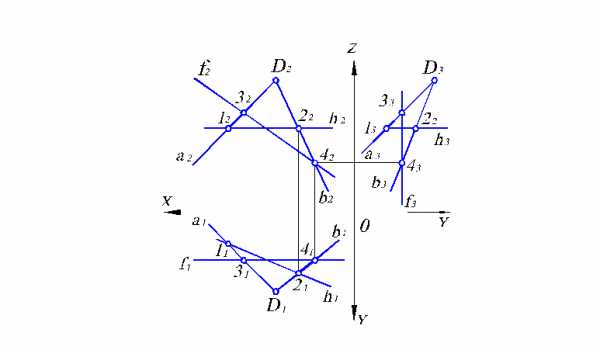
Рис. 2.8. Построение главных линий плоскости, заданной пересекающимися прямыми.
Принадлежность прямой и точки плоскости
Большинство задач на принадлежность точек и прямых плоскостям можно решить, руководствуясь двумя положениями.
1) Прямая принадлежит плоскости, если две точки прямой принадлежат этой плоскости или, если она имеет общую точку с плоскостью и параллельна прямой, лежащей в этой плоскости (рисунок 23, прямая l ).
2) Точка принадлежит плоскости, если она находится на некоторой прямой, находящейся в этой плоскости (рисунок 23, точки N и K ).
Проиллюстрируем эти положения примером.
Построить горизонтальную проекцию прямой l, лежащей в плоскости ∆АВС (рисунок 23).
Находим две общие точки для прямой l и плоскости ∆АВС. Это проекция точки A2и точки пересечения 12 проекции прямой l2 с проекцией стороны В2С 2 . Построив горизонтальную проекцию точки 11, проводим через неё искомую горизонтальную проекцию прямой l (l1).
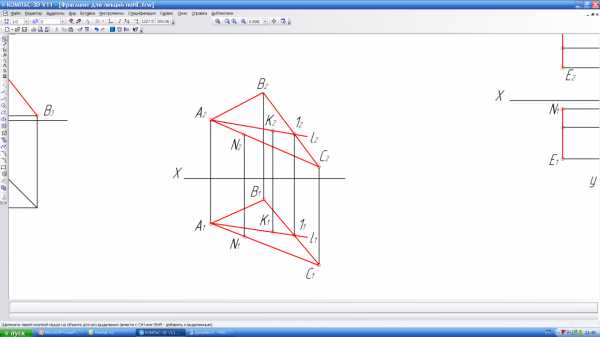
Рисунок 23
Главные линии плоскости или линии уровня плоскости (рисунок 24)
В плоскости можно провести бесчисленное множество горизонталей, фронталей и профильных прямых (см. задачу №16 в рабочей тетради по ИГ).
1) Фронталь(f) – прямая принадлежащая плоскости и //П2;
2)Горизонталь(h) – прямая принадлежащая плоскости и //П1;
3) Профильная(p) – прямая принадлежащая плоскости и //П3;
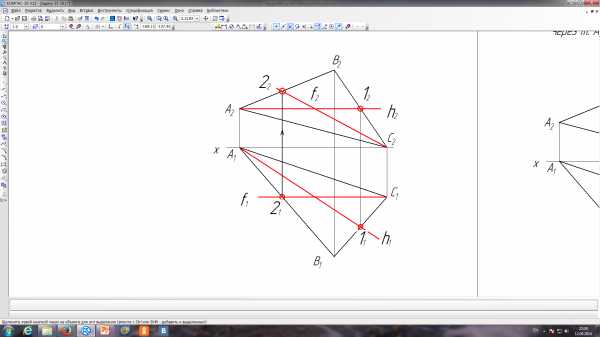
Рисунок 24
Взаимное положение прямых и плоскостей
Необходимо определять и строить на эпюре прямую параллельную плоскости и прямую, пересекающуюся с плоскостью, две параллельные плоскости и две пересекающиеся плоскости, прямые перпендикулярные плоскостям и перпендикулярные плоскости.
Похожие статьи:
poznayka.org
Принадлежность точки и прямой плоскости
Признаки принадлежности хорошо известны из курса планиметрии. Наша задача рассмотреть их применительно к проекциям геометрических объектов.
Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.
Принадлежность прямой плоскости определяется по одному из двух признаков:
а) прямая проходит через две точки, лежащие в этой плоскости;
б) прямая проходит через точку и параллельна прямой, лежащим в этой плоскости.
Используя эти свойства, решим в качестве примера задачу. Пусть плоскость задана треугольником АВС. Требуется построить недостающую проекцию D1 точки D, принадлежащей этой плоскости. Последовательность построений следующая (рис. 2.5).
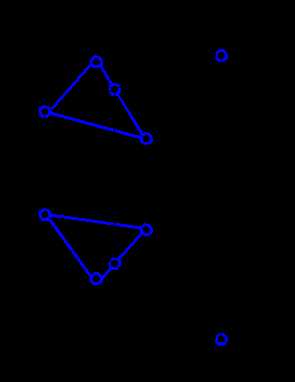
Через точку D2 проводим проекцию прямой d, лежащей в плоскости DАВС, пересекающую одну из сторон треугольника и точку А2. Тогда точка 12 принадлежит прямым А2D2 и C2В2. Следовательно, можно получить ее горизонтальную проекцию 11 на C1В1 по линии связи. Соединив точки 11 и А1, получаем горизонтальную проекцию d1. Ясно, что точка D1 принадлежит ей и лежит на линии проекционной связи с точкой D2.
Достаточно просто решаются задачи на определение принадлежности точки или прямой плоскости. На рис. 2.6 показан ход решения таких задач. Для наглядности изложения задачи плоскость задаем треугольником.
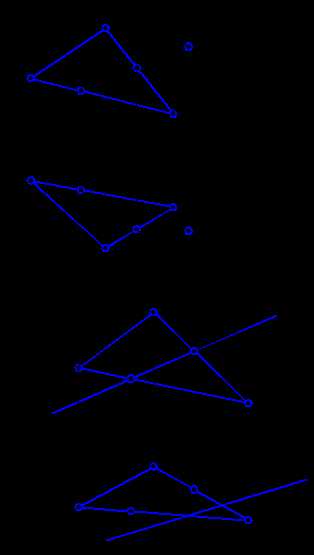
Рис. 2.6. Задачи на определение принадлежности точки и прямой плоскости.
Для того, чтобы определить принадлежит ли точка Е плоскости DАВС, проведем через ее фронтальную проекцию Е2 прямую а2. Считая, что прямая а принадлежит плоскости DАВС, построим ее горизонтальную проекцию а1 по точкам пересечения 1 и 2. Как видим (рис. 2.6, а), прямая а1 не проходит через точку Е1. Следовательно, точка Е ÏDАВС.
В задаче на принадлежность прямой в плоскости треугольника АВС (рис. 2.6, б), достаточно по одной из проекций прямой в2 построить другую в1* считая, что вÌDАВС. Как видим, в1* и в1 не совпадают. Следовательно, прямая в Ë DАВС.
Линии уровня в плоскости
Определение линий уровня было дано ранее. Линии уровня, принадлежащие данной плоскости, называются главными. Эти линии (прямые) играют существенную роль при решении ряда задач начертательной геометрии.
Рассмотрим построение линий уровня в плоскости, заданной треугольником (рис. 2.7).
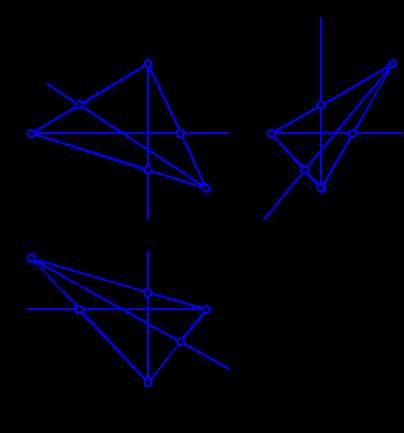
Рис. 2.7. Построение главных линий плоскости, заданной треугольником
Горизонталь плоскости DАВС начинаем с вычерчивания ее фронтальной проекции h2, которая, как известно, параллельна оси ОХ. Поскольку эта горизонталь принадлежит данной плоскости, то она проходит через две точки плоскости DАВС, а именно, точки А и 1. Имея их фронтальные проекции А2 и 12, по линии связи получим горизонтальные проекции (А1 уже есть) 11. Соединив точки А1 и 11, имеем горизонтальную проекцию h1 горизонтали плоскости DАВС. Профильная проекция h3 горизонтали плоскости DАВС будет параллельна оси ОХ по определению.
Фронталь плоскости DАВС строится аналогично (рис. 2.7) с той лишь разницей, что ее вычерчивание начинается с горизонтальной проекции f1, так как известно, что она параллельна оси ОХ. Профильная проекция f3 фронтали должна быть параллельна оси ОZ и пройти через проекции С3, 23 тех же точек С и 2.
Профильная линия плоскости DАВС имеет горизонтальную р1 и фронтальную р2 проекции, параллельные осям OY и OZ, а профильную проекцию р3 можно получить по фронтальной, используя точки пересечения В и 3 с D АВС.
При построении главных линий плоскости необходимо помнить лишь одно правило: для решения задачи всегда нужно получить две точки пересечения с данной плоскостью. Построение главных линий, лежащих в плоскости, заданной иным способом, ничуть не сложнее рассмотренного выше. На рис. 2.8 показано построение горизонтали и фронтали плоскости, заданной двумя пересекающимися прямыми а и в.
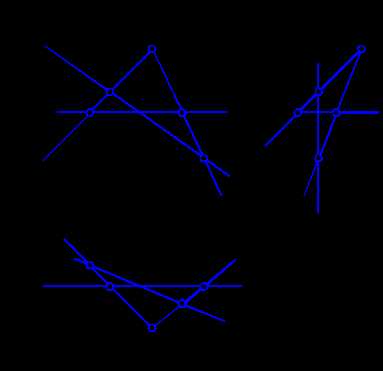
Рис. 2.8. Построение главных линий плоскости, заданной пересекающимися прямыми.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru
Принадлежность точки и прямой плоскости
Признаки принадлежности хорошо известны из курса планиметрии. Наша задача рассмотреть их применительно к проекциям геометрических объектов.
Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.
Принадлежность прямой плоскости определяется по одному из двух признаков:
а) прямая проходит через две точки, лежащие в этой плоскости;
б) прямая проходит через точку и параллельна прямой, лежащим в этой плоскости.
Используя эти свойства, решим в качестве примера задачу. Пусть плоскость задана треугольником АВС. Требуется построить недостающую проекцию D1 точки D, принадлежащей этой плоскости. Последовательность построений следующая (рис. 2.5).
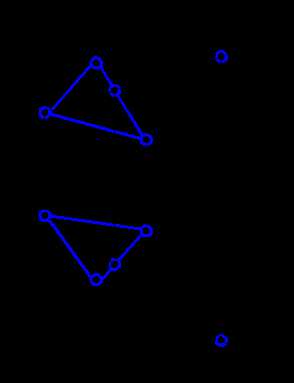
Через точку D2 проводим проекцию прямой d, лежащей в плоскости DАВС, пересекающую одну из сторон треугольника и точку А2. Тогда точка 12 принадлежит прямым А2D2 и C2В2. Следовательно, можно получить ее горизонтальную проекцию 11 на C1В1 по линии связи. Соединив точки 11 и А1, получаем горизонтальную проекцию d1. Ясно, что точка D1 принадлежит ей и лежит на линии проекционной связи с точкой D2.
Достаточно просто решаются задачи на определение принадлежности точки или прямой плоскости. На рис. 2.6 показан ход решения таких задач. Для наглядности изложения задачи плоскость задаем треугольником.
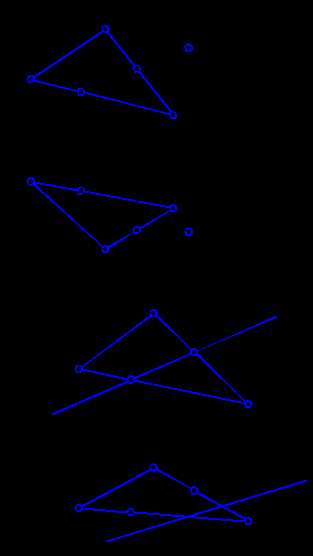
Рис. 2.6. Задачи на определение принадлежности точки и прямой плоскости.
Для того, чтобы определить принадлежит ли точка Е плоскости DАВС, проведем через ее фронтальную проекцию Е2 прямую а2. Считая, что прямая а принадлежит плоскости DАВС, построим ее горизонтальную проекцию а1 по точкам пересечения 1 и 2. Как видим (рис. 2.6, а), прямая а1 не проходит через точку Е1. Следовательно, точка Е ÏDАВС.
В задаче на принадлежность прямой в плоскости треугольника АВС (рис. 2.6, б), достаточно по одной из проекций прямой в2 построить другую в1* считая, что вÌDАВС. Как видим, в1* и в1 не совпадают. Следовательно, прямая в Ë DАВС.
Похожие статьи:
poznayka.org
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 | Program gold;
uses crt,graphABC;
const m=3;
nmax=100;
type mtr=array[1..nmax,1..m] of longint;
var b,c,d:boolean;{глобальные переменные для фиксации создания матрицы, круга и файла}
procedure matrix(var a:mtr;var n:integer);
var i:integer;
begin
clrscr;
randomize;
repeat
write('Количество проб до ',nmax,' n=');
readln(n);
until n in [1..nmax];
for i:=1 to n do
begin
a[i,1]:=1+random(640);
a[i,2]:=1+random(480);
a[i,3]:=random(50);
end;
b:=true;
end;
procedure krug(a:mtr;n:integer;var ox,oy,r:longint;var k:integer);
var i:integer;
begin
clrscr;
if not b then
begin
writeln('Матрица точек не создана, вернитесь к пункту 1');
readln;
exit
end;
repeat
write('Радиус круга от 10 до 200 r=');
readln(r);
until r in [10..200];
repeat
write('Координата Х центра круга от ',r,' до ',640-r,' x=');
readln(ox);
until(ox>=r)and(ox<=640-r);
repeat
write('Координата Y центра круга от ',r,' до ',480-r,' y=');
readln(oy);
until(oy>=r)and(ox<=480-r);
c:=true;
k:=0;
for i:=1 to n do
if sqr(ox-a[i,1])+sqr(oy-a[i,2])<r*r then k:=k+1;
writeln('В выделенный круг попало точек=',k);
readln
end;
procedure fail(a:mtr;n:integer;var f:text);
var nz:string;
i:integer;
begin
clrscr;
if not b then
begin
writeln('Матрица точек не создана, вернитесь к пункту 1');
readln;
exit
end;
assign(f,'data.txt');
rewrite(f);
for i:=1 to n do
begin
write(f,a[i,1]:4,a[i,2]:4,a[i,3]:3);
write('Введите название породы: ');
readln(nz);
writeln(f,' ',nz);
end;
close(f);
writeln('Данные записаны в файл data.txt');
d:=true;
readln
end;
procedure spisok(var f:text);
var a:array[1..nmax] of string[30];
m,i,k:integer;
s:string;
begin
clrscr;
if not d then
begin
writeln('Файл данных не создан, вернитесь к пункту 3');
readln;
exit
end;
reset(f);
readln(f,s);
while pos(' ',s)>0 do
delete(s,1,1);
m:=1;
a[m]:=s;
while not eof(f) do
begin
readln(f,s);
while pos(' ',s)>0 do
delete(s,1,1);
k:=0;
for i:=1 to m do
if a[i]=s then k:=1;
if k=0 then
begin
m:=m+1;
a[m]:=s;
end;
end;
close(f);
writeln('Список пород участка опробования');
for i:=1 to m do
writeln(a[i]);
readln
end;
procedure plan(a:mtr;n:integer;ox,oy,r:longint);
var g,d,i:integer;
begin
clrscr;
if not b then
begin
writeln('Матрица точек не создана, вернитесь к пункту 1');
readln;
exit
end;
if not c then
begin
writeln('Круг еще не задан, вернитесь к пункту 2');
readln;
exit
end;
g:=DETECT;
d:=VHAGI;
initgraph(g,d,'');
setcolor(14);
circle(ox,oy,r);
for i:=1 to n do
begin
if sqr(ox-a[i,1])+sqr(oy-a[i,2])<r*r then setcolor(12)
else setcolor(9);
circle(a[i,1],a[i,2],2);
end;
readln;
restorecrtmode
end;
var a:mtr;
n,k:integer;
ox,oy,r:longint;
f:text;
w:char;
begin
b:=false;
c:=false;
d:=false;
clrscr;
repeat
clrscr;
writeln('Выберите действие');
writeln('1-создание матрицы');
writeln('2-задать круг и определить число точек в нем');
writeln('3-создать файл');
writeln('4-показать список пород');
writeln('5-Показать план опробования');
writeln('другое выход');
readln(w);
case w of
'1':matrix(a,n);
'2':krug(a,n,ox,oy,r,k);
'3':fail(a,n,f);
'4':spisok(f);
'5': plan(a,n,ox,oy,r);
else exit
end;
until not(w in ['1'..'6']);
end. |
forundex.ru
ПРЯМАЯ И ТОЧКА, ПРИНАДЛЕЖАЩИЕ ПЛОСКОСТИ
Дом ПРЯМАЯ И ТОЧКА, ПРИНАДЛЕЖАЩИЕ ПЛОСКОСТИ просмотров — 130
1) Прямая принадлежит плоскости, если две ее точки принадлежат этой плоскости.
2) Прямая принадлежит плоскости, если она проходит через точку, принадлежащую данной плоскости, и параллельна прямой, находящейся в этой плоскости или параллельной ей.
3) Точка принадлежит плоскости, если она лежит на прямой, принадлежащей этой плоскости.
На рисунке 54 прямая 1-2 принадлежит плоскости треугольника АВС, так как она проходит через две точки, лежащие на сторонах треугольника АВС.
Точка К принадлежит плоскости треугольника АВС, так как расположена на прямой 1-2, принадлежащей плоскости треугольника АВС.
Рисунок 54.
Из первого свойства вытекает, что если плоскость задана следами, то прямая принадлежит плоскости, если следы прямой находятся на одноименных с ними следах плоскости (рисунок 55).
На основании этого вывода решаются задачи по определению следов плоскости, заданной другими способами.
Согласно второго свойства – прямая принадлежит плоскости, если она параллельна одному из следов этой плоскости и имеет с другим следом общую точку(рисунок 56). Такими прямыми являются главные линии плоскости. К ним относятся прямые частного положения и линия ската͵ принадлежащие плоскости. В плоскости можно провести множество главных линий.
Горизонталь плоскости —прямая, принадлежащая плоскости и параллельная горизонтальной плоскости проекций (рисунок 55).
Рисунок 55
Прямая h принадлежит плоскости Р (АВС)(точки 1 и 2 принадлежат плоскости Р) и параллельна горизонтальной плоскости П1. Сама горизонталь h и ее горизонтальная проекция h1 параллельны горизонтальному следу плоскости Р1, так как сам след является нулевой горизонталью. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, горизонталь плоскости определяет направление горизонтального следа плоскости (рисунок 55).
Фронталь плоскости– прямая, принадлежащая плоскости и параллельная фронтальной плоскости проекций П2 (рисунок 56)
Рисунок 56
Прямая f параллельна плоскости П2 и лежит в плоскости Р(АВС). Фронтальная проекция f2 и сама прямая f параллельны фронтальному следу Р2 , так как Р2 – нулевая фронталь.
.
Рисунок 57
Профильная прямая– прямая параллельная профильной плоскости проекций П3 и принадлежащая плоскости Г(АВС) (рисунок .57)
Прямая р параллельна плоскости П3 и лежит в плоскости . Профильная проекция р3 и сама прямая р параллельны профильному следу Г3.
Линия наибольшего скатаплоскости – прямая, лежащая в плоскости и перпендикулярная к ее горизонтальному следу (рисунок 58).
Рисунок 58
С помощью линии наибольшего ската плоскости определяют углы наклона плоскости общего положения к плоскостям проекций. На рисунке 58 определен угол наклона плоскости общего положения Р к горизонтальной плоскости проекций П1. Для этого проведена в плоскости Р произвольная прямая MN, принадлежащая плоскости Р и перпендикулярная горизонтальному следу Р1.Способом прямоугольного треугольника найдена истинная величина прямой MN и угол наклона ее к горизонтальной плоскости проекций. Этот угол и будет углом наклона плоскости Р к горизонтальной плоскости проекций.
oplib.ru
