Основные правила математики. Знать наизусть — Сайт учителя математики и финансовой грамотностиКосыхиной Н.В.
1
Натуральные числа
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.
Сравнение натуральных чисел
- Число 0 меньше любого натурального числа.
- Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.
- Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр.
Свойства сложения
Переместительный закон: а + b = b + а. Сочетательный закон: (а + b) + с = а + (b + с)
Формула пути
S = ⱱt, где s — пройденный путь, ⱱ — скорость движения, t — время, за которое пройден путь s.
Корень уравнения
Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.
Решение уравнений
Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.
2
Отрезок
Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)
Свойство длины отрезка
Если на отрезке АВ отметить точку С, то длина отрезка АВ равна сумме длин отрезков АС и СВ.
Равные отрезки
Два отрезка называют равными, если они совмещаются при наложении.
Свойство прямой
Через две точки проходит только одна прямая.
Измерить отрезок
Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается
Ломаная
Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом
Луч
Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.
Равные углы
Два угла называют равными, если они совмещаются при наложении.
Биссектриса угла
Луч, который делит угол на два равных угла, называется биссектрисой угла.
Свойство величины угла
Если между сторонами угла ABC провести луч BD, то градусная мера угла ABC равна сумме градусных мер углов ABD и DBC, то есть ∠ABC = ∠ABD+ ∠DBC.
Развернутый угол
Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.
Прямой угол
Угол, градусная мера которого равна 90°, называют прямым.
Острый угол
Угол, градусная мера которого меньше 90°, называют острым.
Тупой угол
Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.
Равные многоугольники
Два многоугольники называют равными, если они совмещаются при наложении.
Равные фигуры
Две фигуры называют равными, если они совмещаются при наложении.
Остроугольный треугольник
Если все углы треугольника острые, то его называют остроугольным треугольником.
Прямоугольный треугольник
Если один из углов треугольника прямой, то его называют прямоугольным треугольником.
Тупоугольный треугольник
Если один из углов треугольника тупой, то его называют тупоугольным треугольником.
Равнобедренный треугольник
Если две стороны треугольника равны, то его называют равнобедренным треугольником.
Равносторонний треугольник
Если три стороны треугольника равны, то его называют равносторонним треугольником.
Разносторонний треугольник
Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.
Периметр равностороннего треугольника
Если сторона равностороннего треугольника равна а, то его периметр Р вычисляют по формуле Р = 3а.
Прямоугольник
Если в четырехугольнике все углы прямые, то его называют прямоугольником.
Свойство прямоугольника
Противоположные стороны прямоугольника равны.
Периметр прямоугольника
Если соседние стороны прямоугольника равны а и b, то его периметр Р вычисляют по формуле Р = 2а + 2 b.
Квадрат
Прямоугольник, у которого все стороны равны, называют квадратом.
Периметр квадрата
Если сторона квадрата равна а, то его периметр Р вычисляют по формуле Р = 4а.
3
Умножение
• Произведением числа а на натуральное число b, которое не равно 1, называют сумму, состоящую из b слагаемых, каждый из которых равен а.
• В равенства а ∙ b = с числа а и b называют множителями, а число с и запись а ∙ b — произведением.
• Если один из двух множителей равен 1, то произведение равно второму множителю.
• Если один из множителей равен нулю, то произведение равно нулю.
• Если произведение равно нулю, то хотя бы один из множителей равен нулю.
Свойства умножения
• Переместительный закон умножения: ab = bа.
• Сочетательный закон умножения: (ab) с = а (bс).
• Распределительное свойство умножения относительно сложения:
a (b + с) = ab + ас.
• Распределительное свойство умножения относительно вычитания:
а (b — с) = аb — ас.
Деление
• Для натуральных чисел а, b и с равенство а : b = с является правильным, если является правильным равенство b ∙ с = а.
• В равенстве а : b = с число а называют делимым, число b — делителем, число с и запись a : b — частным от деления, отношением, долей.
• На ноль делить нельзя.
• Для любого натурального числа а правильными являются равенства: 0:а = 0; а:а=1; а:1 = а.
Деление с остатком
• а = bq + г, где а — делимое, b — делитель, q — неполное частное, r — остаток, r < b.
• Если остаток равен нулю, то говорят, что число а делится нацело на число b.
Свойства площади фигуры
1) Равные фигуры имеют равные площади;
2) площадь фигуры равна сумме площадей фигур, из которых она состоит.
Площадь прямоугольника
Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.
Площадь квадрата
S = а*a( a в квадрате), где S — площадь квадрата, а — длина его стороны.
Свойства объема фигуры
1) Равные фигуры имеют равные объемы;
2) объем фигуры равен сумме объемов фигур, из которых она состоит.
Объем прямоугольного параллелепипеда
V = abc, где V — объем параллелепипеда, а, b и с — его измерения, выраженные в одних и тех же единицах;
V = Sh, где S — площадь основания параллелепипеда, h — его высота.
Объем куба
V = а*a*a( a в кубе), где V — объем куба, а — длина его ребра.
4
Правильный дробь
Неправильная дробь
Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.
Сравнение дробей
• Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.
• Из двух дробей с одинаковыми числительнями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.
• Все правильные дроби меньше единицы, а неправильные — больше или равны единице.
• Любая неправильная дробь больше любой правильной дроби.
Сложение и вычитание дробей с одинаковыми знаменателями
• Чтобы найти сумму двух дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
• Чтобы найти разницу двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
Сложение и вычитание смешанных чисел
• Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.
• Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.
Преобразование неправильной дроби в смешанное число
Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно числитель разделить на знаменатель; полученный неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.
Преобразование смешанного числа в неправильную дробь — нужно целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в его знаменателе записать знаменатель дробной части смешанного числа.
5
Свойства десятичной дроби
• Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.
• Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.
Сравнение десятичных дробей
• Из двух десятичных дробей больше та, у которой целая часть больше.
• Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо с помощью приписывания нулей справа уравнять количество цифр в дробных частях, после чего сравнить полученные дроби поразрядно.
Округление десятичных дробей
Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо все следующие за этим разрядом цифры отбросить. Если при этом первая из цифр, которые отвергают равна 0, 1, 2, или 4, то последнюю из цифр, которые оставляют, не меняют; если же первая из цифр, которые отвергают, равна 5, 6, 7, 8 или 9, то последнюю из цифр, которые оставляют, увеличивают на единицу.
Сложение десятичных дробей
Чтобы найти сумму двух десятичных дробей, нужно:
1) уравнять количество цифр после запятых;
2) записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
3) сложить полученные числа так, как складывают натуральные числа;
4) поставить в полученной сумме запятую под запятыми.
Вычитание десятичных дробей
Чтобы найти разность двух десятичных дробей, нужно:
1) уравнять количество цифр после запятых;
2) записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
3) выполнить вычитание так, как вычитают натуральные числа;
4) поставить в полученной разности запятую под запятыми
Умножение десятичных дробей
Чтобы перемножить две десятичные дроби, надо:
1) перемножить их как натуральные числа, не обращая внимания на запятые;
2) в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.<.span>
Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.<.span>
Деление десятичных дробей
• Чтобы разделить десятичную дробь на десятичную, надо:
1) перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
2) выполнить деление на натуральное число.
Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.
Среднее арифметическое
Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.
Процент (процент)
Процентом (процентом) называют сотую часть величины или числа.
blackseaweb.ru
Татьяна Яковлевна Балашова Страница не найдена
ДЕНЬ ИМЕНИННИКА
Уроки радости
Ноябрь29
ПОЗДРАВЛЯЕМ ПАВЛА!!!
Ноябрь29
С днем рождения поздравляем,
Всего лучшего желаем.
Больше радости и смеха,
И во всех делах успеха.
Никогда не унывай,
Себя в обиду не давай.
Пусть сбудутся твои мечты,
И радость будет, там, где ты.
ПОЗДРАВЛЯЕМ АДЕЛИНУ!!!
Ноябрь26
Желаем здоровья, чтоб глазки сияли,
Чтоб ручки и ножки, как крылья, порхали,
Желаем тебе лишь с друзьями дружить
И самой счастливою девочкой быть!
Ура! Каникулы!
Ноябрь15
ПОЗДРАВЛЯЕМ!
Ноябрь5
Поздравляем наших ребят с победами в Неделе русского языка!
tbalashova.ru
Пособие по математике «Правила по математике»
Описание презентации по отдельным слайдам:
1 слайд
Описание слайда:ДРУЖОК правила по математике для начальных классов
2 слайд
Описание слайда:Дружок! Данное пособие содержит все основные правила по математике и составлено таким образом, чтобы тебе было легче и интереснее усвоить школьную программу.
3 слайд
Описание слайда:ЦИФРЫ И ЗНАКИ 0 1 2 3 4 5 6 7 8 9 Это арабские цифры. Их всего десять. I II III IV V VI VII VIII IX X … Это римские цифры. > больше + плюс < меньше — минус = равно или x умножение : деление
4 слайд
Описание слайда:СРАВНЕНИЕ ЧИСЕЛ 3 > 2 2 < 3 3 = 3 1+2 < 4+3 5+3 > 7 4 < 5 < 7 Число 5 больше 4, но меньше 7.
5 слайд
Описание слайда:ЧИСЛА ЧЁТНЫЕ И НЕЧЁТНЫЕ Числа, которые делятся на 2, называются ЧЁТНЫМИ: 2 4 6 8 10… Числа, которые не делятся на 2, называются НЕЧЁТНЫМИ: 1 3 5 7 9 11… При сложении чётных чисел получается чётное число, при сложении нечётных тоже получается чётное число: 4+2=6 3+5=8. Если складывают нечётное число с чётным, то в ответе будет нечётное число: 5+2=7.
6 слайд
Описание слайда:СЛОЖЕНИЕ 5 + 2 = 7 первое второе сумма слагаемое слагаемое a + b = c Прибавить 1 к какому-либо числу – значит назвать следующее за ним по порядку число 1 2 3 4 5 6 7 8 9 . . . 6 + 1 = 7
7 слайд
Описание слайда:ПЕРЕСТАНОВКА СЛАГАЕМЫХ От перестановки слагаемых сумма не изменяется a + b = b + a Если одно из слагаемых равно 0, то сумма равна другому слагаемому a + 0 = a 0 + a = a
8 слайд
Описание слайда:ВЫЧИТАНИЕ 5 — 3 = 2 уменьшаемое вычитаемое разность a – b = c Вычесть 1 из какого-либо числа – значит назвать предыдущее число 1 2 3 4 5 6 7 8 9 . . . 7 – 1 = 6
9 слайд
Описание слайда:СОСТАВ ЧИСЛА 2 = 1 + 1 3 = 1 + 2 = 1 + 1 + 1 4 = 1 + 3 = 2 + 2 5 = 1 + 4 = 2 + 3 6 = 1 + 5 = 2 + 4 = 3 + 3 7 = 1 + 6 = 2 + 5 = 3 + 4 8 = 1 + 7 = 2 + 6 = 3 + 5 = 4 + 4 9 = 1 + 8 = 2 + 7 = 3 + 6 = 4 + 5
10 слайд
Описание слайда:СЛОЖЕНИЕ И ВЫЧИТАНИЕ чисел с переходом через десяток Одно из слагаемых надо разложить так, чтобы одна из промежуточных сумм была равна 10. 7+5=7+(3+2)=(7+3)+2= 10+2=12 Таким же способом можно решать примеры на вычитание 15-7= 15-(5+2)=(15-5)-2=10-2=8
11 слайд
Описание слайда:ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ ПРИ РЕШЕНИИ ВЫРАЖЕНИЙ СО СКОБКАМИ Прибавить число к сумме, а также сумму к числу можно, складывая числа в любом порядке (а + b) + c (a + b) + c = a + (b + c) (a + b) + c = (a + c) + b a + (b + c) a + (b + c) = (a + b) + c a + (b + c) = (a + c) + b
12 слайд
Описание слайда:Вычесть из суммы число можно несколькими способами (a + b) – c (a + b) – c = (a – c) + b (a + b) – c = (b – c) + a Если перед скобкой в выражении стоит знак минус, то при раскрытии скобок знаки меняются на противоположные a – (b + c) = a – b – c a – (b – c) = a – b + c
13 слайд
Описание слайда:ПРОВЕРКА СЛОЖЕНИЯ Сложение можно проверить вычитанием. Для этого надо из суммы вычесть одно слагаемое. Если в результате получится другое слагаемое, значит сложение выполнено верно a + b = c c – a = b c – b = a
14 слайд
Описание слайда:ПРОВЕРКА ВЫЧИТАНИЯ Вычитание можно проверить сложением. Для этого надо к разности прибавить вычитаемое. Если в результате получится уменьшаемое, значит вычитание выполнено верно a – b = c c + b = a
15 слайд
Описание слайда:УМНОЖЕНИЕ 2 3 = 6 первый второй произведение множитель множитель a b = c От перестановки множителей произведение не меняется a b = b a
16 слайд
Описание слайда:Если один из множителей равен 0, то произведение равно 0. a 0 = 0 0 a = 0 Если один из множителей равен 1, то произведение равно другому множителю а 1 = а 1 а = а
17 слайд
Описание слайда:Умножение суммы на число (a + b) c (a + b) c = a c + b c a (b + c) a (b + c) = a b + a c
18 слайд
Описание слайда:Проверка умножения — деление Если произведение двух чисел разделить на один из множителей, то получится другой множитель a b = c c : b = a c : a = b
19 слайд
Описание слайда:ДЕЛЕНИЕ : 3 = 2 делимое делитель частное a : b = c Если делитель равен 1, то частное равно делимому а : 1 = а Если делимое равно делителю, то частное равно 1 а : а = 1 Если делимое равно 0, то частное равно 0 0 : а = 0 Делить на 0 нельзя! а : 0
20 слайд
Описание слайда:ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ На 2 делятся числа, оканчивающиеся на чётную цифру: 28:2=14 174:2=87 На 3 делятся числа, сумма цифр которых делится на 3: 225:3=75 (2+2+5=9. Число 9 делится на 3) На 4 делятся числа, если двузначное число, образованное двумя последними цифрами, делится на 4: 216:4=54 (две последние цифры делимого составляют число 16, которое делится на 4) На 5 делятся числа, оканчивающиеся на 5 или 0: 70:5=14 145:5=29
21 слайд
Описание слайда:ДЕЛЕНИЕ СУММЫ НА ЧИСЛО (a + b) : c (a + b) : c = a : c + b : c a : (b c) a : (b c) = (a : b) : c A : (b c) = (a : c) : b ДЕЛЕНИЕ ЧИСЛА НА ПРОИЗВЕДЕНИЕ
22 слайд
Описание слайда:ПРОВЕРКА ДЕЛЕНИЯ Если делимое разделить на частное, получится делитель а : b = c Проверка: а : с = b Если делитель умножить на частное, получится делимое a : b = c Проверка: с b = a
23 слайд
Описание слайда:ДЕЛЕНИЕ С ОСТАТКОМ Если делимое не делится на делитель, например 7 : 3, то надо подобрать ближайшее число, меньше 7, которое делится на 3 без остатка 7:3(6+1):36:3+12 (остаток 1) Остаток всегда должен быть меньше деления.
24 слайд
Описание слайда:ЗАПОМНИ Увеличить число на несколько единиц – значит прибавить a + b Увеличить число в несколько раз – значит умножить a b Уменьшить число на несколько единиц – значит вычесть a – b Уменьшить число в несколько раз – значит разделить а : b
25 слайд
Описание слайда:РЕШЕНИЕ УРАВНЕНИЙ Неизвестное число обозначается латинской буквой Х Х + а = с а – Х = с Х = с – а Х = а – с Х с = а с : Х = а Х = а : с Х = с : а
26 слайд
Описание слайда:ПЕРИМЕТР ФИГУРЫ Периметр – это сумма сторон геометрических фигур (квадрата, прямоугольника и т. д.), обозначается латинской буквой Р. Единицы измерения – миллиметры (мм), сантиметры (см), метры (м). Периметр прямоугольника Р = a+b+a+b = 2 a+2 b = 2 (a+b) Периметр квадрата Р = а + а + а + а = 4 а Периметр треугольника Р = a + b + c
27 слайд
Описание слайда:ПЛОЩАДЬ ФИГУРЫ Площадь – это внутренняя часть фигуры (прямоугольника, квадрата и т. д.), обозначается латинской буквой S. Единицы измерения – квадратные километры (км²), квадратные метры (м²), квадратные сантиметры (см²). Площадь прямоугольника S = a b Площадь квадрата S = a a
Курс повышения квалификации
Курс профессиональной переподготовки
Учитель начальных классов
Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Общая информация
Номер материала: ДВ-236127
ВНИМАНИЮ ВСЕХ УЧИТЕЛЕЙ: согласно Федеральному закону N273-ФЗ «Об образовании в Российской Федерации» педагогическая деятельность требует от педагога наличия системы специальных знаний в области обучения и воспитания детей с ОВЗ. Поэтому для всех педагогов является актуальным повышение квалификации по этому направлению!Дистанционный курс «Обучающиеся с ОВЗ: Особенности организации учебной деятельности в соответствии с ФГОС» от проекта «Инфоурок» даёт Вам возможность привести свои знания в соответствие с требованиями закона и получить удостоверение о повышении квалификации установленного образца (72 часа).
Подать заявку на курс
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарийinfourok.ru
Порядок выполнения математических действий | интернет проект BeginnerSchool.ru
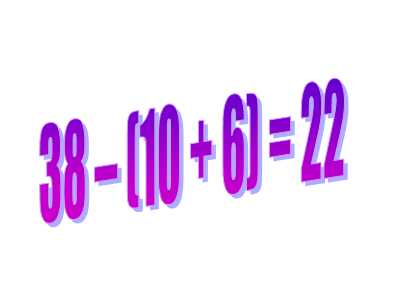Сегодня мы поговорим о порядке выполнения математических действий. Какие действия выполнять первыми? Сложение и вычитание, или умножение и деление. Странно, но у наших детей возникают проблемы с решением, казалось бы, элементарных выражений.
Итак, вспомним о том, что сначала вычисляются выражения в скобках
38 – (10 + 6) = 22;
1) в скобках: 10 + 6 = 16;
2) вычитание: 38 – 16 = 22.
Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.
10 ÷ 2 × 4 = 20;
Порядок выполнения действий:
1) слева направо, сначала деление: 10 ÷ 2 = 5;
2) умножение: 5 × 4 = 20;
10 + 4 – 3 = 11, т.е.:
1) 10 + 4 = 14;
2) 14 – 3 = 11.
Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.
18 ÷ 2 – 2 × 3 + 12 ÷ 3 = 7
Порядок выполнения действий:
1) 18 ÷ 2 = 9;
2) 2 × 3 = 6;
3) 12 ÷ 3 = 4;
4) 9 – 6 = 3; т.е. слева направо – результат первого действия минус результат второго;
5) 3 + 4 = 7; т.е. результат четвертого действия плюс результат третьего;
Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.
30 + 6 × (13 – 9) = 54, т.е.:
1) выражение в скобках: 13 – 9 = 4;
2) умножение: 6 × 4 = 24;
3) сложение: 30 + 24 = 54;
Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:
1) действия, заключенные в скобках;
2) умножение и деление;
3) сложение и вычитание.
Если вы хотите получать анонсы наших статей подпишитесь на рассылку “Новости сайта“.
Понравилась статья — поделитесь с друзьями:
Подпишитесь на новости сайта:
Оставляйте пожалуйста комментарии в форме ниже
beginnerschool.ru
Математика: арифметика, алгебра, геометрия
Математика – один из основных школьных предметов; наука о структурах, порядке и отношениях. Математика относится к точным наукам. Проект Infoogle.ru предлагает Вам статьи по математике: формулы, примеры, правила по математике – своеобразный урок математики для интернет пользователей.
Чтобы узнать нужную формулу, искомое правило, требуемые примеры, воспользуйтесь поиском на сайте.
Математика – это очень важная наука для любого человека. Она нужна с раннего детства. Мы считаем сдачу от покупки мороженного, количество человек в футбольной команде, сколько времени осталось до интересного мультфильма, количество опыта, необходимого для получения нового уровня в какой-нибудь онлайн-игрушке. Математика нужна и в старшем возрасте, чтобы рассчитать кредит или ипотеку, определить количество свободных денег с зарплаты после оплаты всех коммунальных платежей, рассчитать доход со своего сайта при различных параметрах и показателях.
Математика пригодится каждому!
Арифметика, алгебра и геометрия.
Если в начальных классах основой математики является арифметика, то в средних классах математика разделяется на два других больших раздела: алгебру и геометрию.
Арифметика – точная наука, большой раздел математики, изучающий числа, их отношения и свойства. На портале Infoogle.ru Вы сможете найти по арифметике всё, что Вам интересно.
Алгебра – точная наука, большой раздел математики, характеризующийся как обобщающий и расширяющий арифметику. На портале Infoogle.ru Вы можете найти правила и формулы по алгебре, примеры и методы их решения.
Геометрия – точная наука, большой раздел математики, изучающий пространственные структуры, отношения и их обобщения. На портале Infoogle.ru Вы можете найти теоремы и аксиомы геометрии.
infoogle.ru
Конспект урока для 1 класса «Правила по математике»
Правила по математике для 1 класса
1. Числа записывают с помощью цифр. Цифра — это знак для записи числа.
2. 4=4 Это равенство и читается так: «четыре равно четырем».
3. 9>6 6 < = — это знаки сравнения.
4. Числа, которые получают при счете предметов, называются натуральные числа. Число 0 — не натуральное.
1, 2, 3, 4, 5, 6 … — натуральный ряд чисел. Каждое следующее число натурального ряда больше предыдущего на 1. Если натуральный ряд начинается не с числа 1, а например, с 2 (2, 3, 4, 5, …) — это отрезок натурального ряда чисел.
5. Линия в математике, которая завершается в той же точке, с которой началась, называется замкнутой линией.
6. Сложение обозначают знаком +. Если между числами стоит такой знак, запись называют суммой чисел. Действие вычитания обозначают знаком минус ( — ). Если между числами стоит такой знак, запись называют разностью чисел.
7. Если в математике линию называют двумя буквами, то используют прописные буквы (АМ, ОК), если одной — строчную (а). Имена отрезков, в отличие от имен людей, читают в любом направлении.
8. Числа, которые складывают, называют слагаемые. Первое число при вычитании называют уменьшаемое, второе число называют вычитаемое.
9. Если слагаемые поменять местами, значение суммы не изменится. Это переместительное свойство сложения.
10. 5+4 7-2 9-6 — это выражения. Выражение — это запись, в которой числа соединены знаками действий. Знаков сравнения в выражениях нет.
11. Если одно слагаемое равно нулю, значение суммы равно другому слагаемому. Если из значения суммы вычесть одно слагаемое, получится другое слагаемое.
12. Числа 1, 2, 3 и т.д. — однозначные. Числа 10, 20, 30 и т. д. — двузначные.
13. 3 + Х = 9 Это уравнение, где Х — неизвестное число. Неизвестные числа могут обозначать и другими буквами латинского алфавита (например, Yy — игрек Zz — зет). Решить уравнение — значит найти число, при котором получается верное равенство.
14. (3+2)+5 Скобки в выражении показывают, какое действие нужно выполнять сначала.
15. Чтобы найти неизвестное слагаемое, нужно из значения суммы вычесть известное слагаемое. х + 5 = 7
16. Чтобы увеличить число на несколько единиц, нужно выполнить сложение. Чтобы уменьшить число на несколько единиц, нужно выполнить вычитание. Узнать, насколько одно число больше другого, можно действием вычитания.
17. Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть значение разности
globuss24.ru
Как быстро выучить правила по математике
Математика по праву считается среди детей одним из самых сложных школьных предметов. Способности к изучению математики обуславливаются несколькими факторами. В первую очередь это связано с предрасположенностью самого ребенка к точным или гуманитарным наукам. Во вторую очередь важна база, заложенная в начальных классах. В третью очередь имеет значение наличие желания у ребенка обучению.
Тем не менее, существуют методики, которые помогут быстрее выучить правила математики даже тем, кто считает себя абсолютно не предрасположенным к этой науке. Кроме того такие методики помогают в изучении не только математики, но и других предметов. На сегодняшний день существует много онлайн-ресурсов, предлагающих современные методики школьного образования, среди которых выделяется образовательный портал на сайте https://uchi.ru/.
Чтобы правильно организовать процесс изучения математики существует несколько способов, которые прошли проверку на практике.
Первый способ направлен на устранение пробелов в математических знаниях ближе к окончанию школы. При подготовке к экзамену по математике не нужно пытаться объять необъятное и повторить все сразу или за короткий срок выучить все темы. Во-первых, нужно определить конкретные темы, которые являются трудными для ученика. Это могут быть любые темы за любой предыдущий класс – в этом нет ничего страшного. Нужен конкретный перечень тем для повторения. Затем важно в выбранной теме изучить и понять основные определения. Важно именно понять, а не зазубрить. Далее нужно переходить к практическим заданиям, так как практика является самым лучшим способом усвоения математического материала.
Второй способ основан на четком планировании своей деятельности. В начале изучения ставится конкретная цель. Например, изучить квадратные уравнения. Затем, при необходимости можно разбить цель на подцели (если цель слишком большая). После этого нужно составить план, указав, что именно и в каике сроки нужно выучить. Математика – наука точная, поэтому и подходить к ее изучению нужно рационально и точно. Составление такого плана не только поможет быстрее выучить предмет, но и позволит научиться дисциплинированности и ответственности.
Вконтакте
Google+
Одноклассники
dettka.com
