Почему все реальные процессы необратимы – Законы классической термодинамики не могут установить, почему протекают необратимые процессы, почему все реальные

Лекция 16

Лекция 16. Второе начало термодинамики

ВВЕДЕНИЕ

Первое начало термодинамики устанавливает неизменность общего количества энергии в изолированной термодинамической системе и эквивалентность разных видов энергии при их превращениях в термодинамических процессах, но оно не накладывает никаких ограничений на направление процессов, происходящих в термодинамических системах, не описывает условий, при которых возможно то или иное превращение энергии.

Опыт показывает, что направления процессов не равновероятны. Условия, характеризующие возможное направление, протекающих в термодинамических системах процессов пределы возможного превращения теплоты в работу, определяются вторым началом термодинамики.

1. ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫ

Для обоснования второго начала термодинамики принципиальное значение имеют понятия обратимого и необратимого процессов.

Термодинамический процесс называется обратимым, если он может быть проведен обратно через те же состояния, что и в прямом направлении, и при возвращении системы в исходное состояние в окружающей среде не произошло никаких изменений.

Если по окончании процесса в окружающих телах иди самой термодинамической системе остались какие либо изменения, то такой процесс является необратимым.

Очевидно, что обязательным условием обратимости процесса является его равновесность. Примером обратимого процесса может служить адиабатный равновесный процесс сжатия газа в цилиндре под поршнем, при условии, что поршень в цилиндре движется без трения, то есть идеальный адиабатический процесс. Идеальные — изотермический, изобарический и изохорический процессы тоже являются обратимыми.

Все реальные процессы, как отмечалось ранее, неравновесны, в силу конечной скорости их протекания, и, следовательно, необратимы. Помимо конечной скорости протекания существуют и другие причины необратимости реальных процессов.

1. Превращение механической энергии в тепло при трении и других диссипативных процессах. Обратный процесс — превращение теплоты в механическую энергию (совершение работы за счет теплоты) может произойти только при идеальном изотермическом процессе, при котором силы трения должны отсутствовать.

2. Процесс теплообмена между двумя телами, имеющими различную температуру. Опыт показывает, что никогда не наблюдается нагревание одного тела за счет охлаждения другого тела, если первоначально оба, тела имели одинаковые температуры, Охлаждение тел в холодильных установках всегда требует затрат энергии.

3. Необратимыми являются процессы диффузии, выравнивания давления в соединенных емкостях и многие другие.

Таким образом, все реальные процессы необратимы.

2. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ

В результате необратимости все идущие в природе процессы имеют определенное направление и не могут самопроизвольно протекать в обратном направлении, хотя это и не противоречило бы первому началу термодинамики. Обобщение опытных данных позволило сформулировать закон, определяющий возможное направление реальных термодинамических процессов, который получил название второго начала термодинамики.

Существует несколько формулировок второго начала термодинамики. Остановимся на двух из них.

1. Невозможен процесс, единственным конечным результатом которого является передача энергии в форме теплоты от холодного тела к горячему (формулировка Р. Клаузиуса).

2. Невозможен процесс, единственным результатом которого является отнятие от некоторого тела энергии в форме теплоты и превращение этой энергии в эквивалентную ей работу

(формулировка В. Томсона).

Обе формулировки эквивалентны. Действительно, пусть существует процесс с помощью которого можно было-бы повысить температуру одного тела за счет охлаждения другого, при одинаковых начальных температурах обоих тел. Тогда, используя известные процессы, можно было бы превратить полученную разность температур в механическую энергию без каких либо изменений в состоянии окружающей среды.

Таким образом, если бы могли происходить процессы, запрещенные вторым началом термодинамики, то за счет отбора энергии в форме теплоты, например, от мирового океан, имелся бы практически неисчерпаемый источник механической энергии. Подобное устройство было бы равноценно вечному двигателю, Поэтому второе начало термодинамики иногда формулируют так: «Невозможен вечный двигатель второго рода».

Термодинамические циклы, Цикл Карно.

Циклом

или круговым процессом, как указывалось ранее, называется такой процесс, в результате которого термодинамическая система возвращается в исходное состояние.

Циклы используются во всех тепловых машинах: двигателях внутреннего сгорания, газотурбинных установках, холодильниках и т.п. Изучение циклов является одной из основных задач термодинамики.

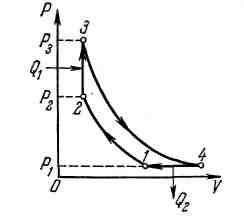
Рассмотрим произвольный цикл 1-а-2-6-1, изображенный на рис. 1 в переменных (P,V).

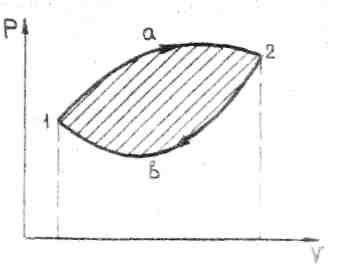
Рис. 1

Его можно разбить на два процесса: 1-а-2 — процесс расширения и 2-в-1 — процесс сжатия. На участке 1-а-2 совершается работа газа против внешних сил, которая равна площади под кривой процесса. На участке 2-в-1 наоборот внешние силы совершают работу, которая тоже равна площади под кривой процесса. Работа газа при расширении больше работы внешних сил при сжатии на величину равную площади кривой, ограниченной циклом и называемую — работой цикла

А_ц. При выбранном направлении цикла эта работа положительна. Такой цикл называется прямым и лежит в основе всех тепловых двигателей.

При обратном направлении цикла (1-в-2 — расширение газа, 2-а-1 — сжатие) работа расширения газа меньше работы внешних сил при сжатии газа и работа цикла станет отрицательной. Такие циклы используются для холодильных установок, а цикл называется обратным.

Тело, участвующее в цикле, называется рабочим телом.

КПД цикла. Поскольку рабочее тело при цикле возвращается в исходное состояние изменение его внутренней энергии . Уравнение первого начала термодинамики для такого цикла запишется как:

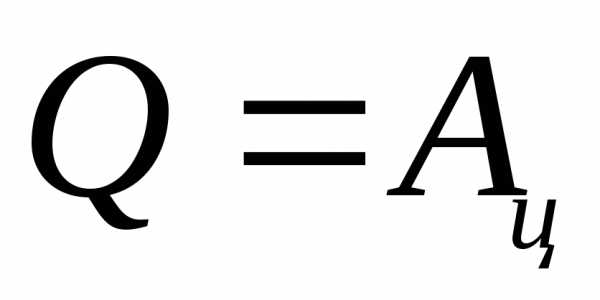. (1)

Однако выражение (1) противоречит второму началу термодинамики: Невозможен процесс, единственным результатом которого является отнятие от некоторого тела энергии в форме теплоты и превращение этой энергии в эквивалентную ей работу,

Для реализации цикла, в частности, изображенного на рис. 1, На одних участках необходимо передать рабочему телу теплоту Q₁ от внешнего источника тепла — нагревателя, а на других участках передать некоторое количество тепла 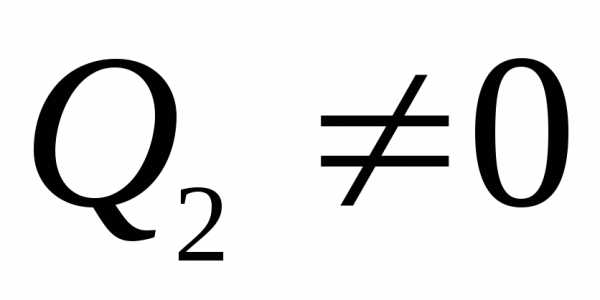от рабочего тела — другому менее нагретому телу — холодильнику, Только тогда рабочее тело может вернуться в исходное состояние. Суммарное количество теплоты, переданное рабочему телу равно:

и первое начало термодинамики запишется как:

(2)

Таким образом, реальные тепловые машины должны состоять, по крайней мере, из 3-х тел: нагревателя, рабочего тела и холодильника.

КПД тепловой машины. Назначение тепловой машины — совершать работу за счет использования энергии теплоты нагревателя, поэтому ее КПД можно записать как:

. (3)

Так как согласно второму началу термодинамики 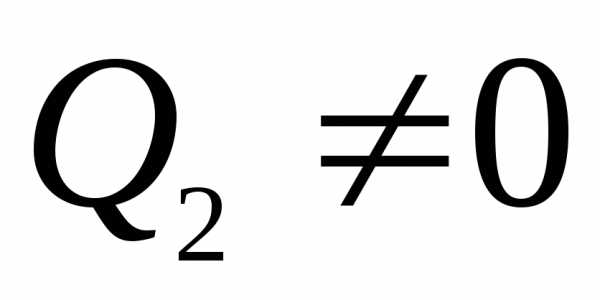, то КПД тепловой машины всегда меньше 1. Для повышения ее КПД необходимо увеличивать разницу между иQ_1.

Холодильный коэффициент. В холодильных установках рабочее тело отбирает тепло Q₂ у тела с более низкой температурой и отдавать телу с более высокой температурой теплоту

за счет работы, которую совершает внешняя сила. Эффективность холодильника тем выше, чем больше отношение Q₂ к А. Это отношение:

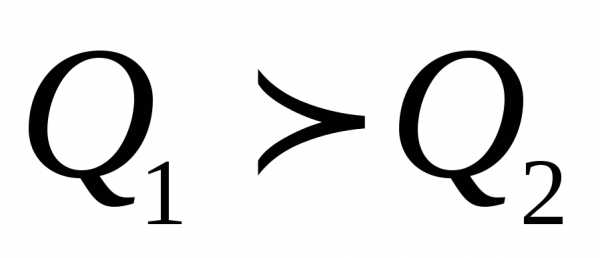
может превышать 1 и называется холодильным коэффициентом.

Эффективность теплового насоса, Обратный цикл может использоваться для обогрева. При этом теплота Q₂ забирается из внешней среды и ее часть Q₁ передается в обогреваемое помещение за счет работы внешней силы А. При этом Q₁>A

. (4)

Такое устройство называется тепловым насосом, Его эффективность может существенно превышать эффективность электрообогревателя в силу соотношения (2). Эффективность теплового насоса определяется как:

всегда больше единицы,

Цикл Карно. В термодинамике особое место занимает цикл, рассмотренный французским инженером Сади Карно в 1824 году. Цикл состоит из четырех обратимых процессов для идеального газа (рис. 2).

Рис. 2

Участок 1-2 — изотерма с температурой T₁, участок 2-3 адиабата, участок 3-4 — изотерма с температурой T₂ , участок 4-1 — адиабата (две изотермы и две адиабаты). Подвод теп­ла к рабочему телу осуществляется на участке 1-2, следовательно T₁ — температура нагревателя, а отвод тепла на участке 3-4, следовательно T₂ — температура холодильника. Карно доказал, что КПД этого цикла максимальный по сравнению со всеми другими возможными рабочими циклами в диапазоне температур T₁, T₂ не зависит от рода рабочего тела и определяется соот­ношением:

(5)

Таким образом, КПД всех возможных тепловых машин всегда меньше единицы.

В таблице 1 приведены для сравнения КПД различных современных тепловых машин.

КПД тепловых машин

Таблица 1

Вид машины	КПД
Паровозы	Менее 5%
Тепловозы	25%
Тепловые электростанции	35-40%
Двигатели внутреннего сгорания, в том числе дизельные	40-50%

Цикл Карно сыграл большую роль в развитии тепловых двигателей, Соотношение (5) показывает путь повышения КТТД реальных двигателей; повышение температуры рабочего тела и снижение температуры холодильника, Одновременно можно утверждать, что в рамках заданных T₁, T₂ этот цикл будет иметь больший КПД, который ближе к циклу Карно.

Наряду с циклом Карно существуют и другие термодинамические циклы, среди них приведены в таблице 2.

Теоретические термодинамические циклы

Таблица 2

Теоретические циклы поршневых двигателей
1. Цикл со сгоранием при V = const (цикл Отто)	1-2 – адиабатное сжатие, 2 — 3 – изохорное нагревание, 3 — 4 – адиабатное расширение, 4 — 1 – изохорное охлаждение.
2. Цикл со сгоранием при P = const (цикл Дизеля)	1 — 2 – адиабатное сжатие, 2 — 3 – изобарное нагревание, 3 — 4 – адиабатное расширение, 4 — 1 – изохорное охлаждение.
3. Смешанный цикл со сгоранием при V = const и P = const (цикл Тринклера—Сабатэ)	1 — 2 — адиабатное сжатие, 2 — 3′ – изохорное нагревание, 3′ -3 – изобарное нагревание, 3— 4 – адиабатное расширение, 4 -1 – изохорное охлаждение.
Теоретические циклы газовых турбин
1. Цикл со сгоранием при P = const	— 2 – адиабатное сжатие, — 3 – изобарное нагревание, 3 — 4 – адиабатное расширение, 4 — 1 – изобарное охлаждение.
2. Цикл со сгоранием при V = const	1 — 2 – адиабатное сжатие, — 3 – изохорное нагревание, — 4 – адиабатное расширение. 4 — 1 — изобарное охлаждение.

3. ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ СОСТОЯНИЯ

Термодинамические потенциалы. Подобно потенциальной энергии для механических систем, которая определяется только местонахождением механической системы и не зависит от пути, по которому механическая система оказалась в данном состоянии, в термодинамике тоже вводятся функции с размерностью энергии, называемые термодинамическими потенциалами. Как и потенциальная энергия в механике, термодинамические потенциалы характеризуют состояние системы и могут быть определены с точностью до некоторой постоянной, Так как изменения термодинамических потенциалов не зависят от пути перехода термодинамической системы из одного состояния в другое — они являются функциями состояния. Наиболее важными термодинамическими потенциалами являются внутренняя энергия и энтальпия. Внутренняя энергия термодинамической системы была рассмотрена выше. Рассмотрим понятие энтальпии на примере идеального газа,

Энтальпия I равная сумме внутренней энергии газа и произведения давления газа на его объем:

(6)

Так как P и V являются параметрами, состояния газа, a U — функция состояния, то и I — тоже функция состояния. Для идеального газа:

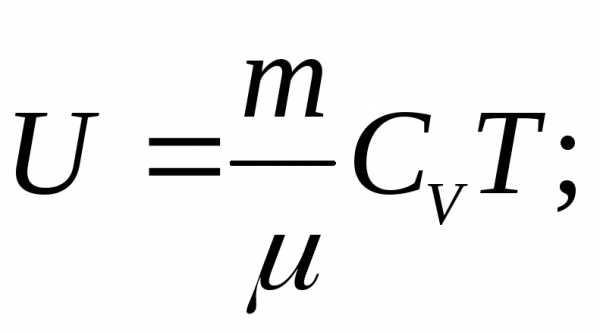
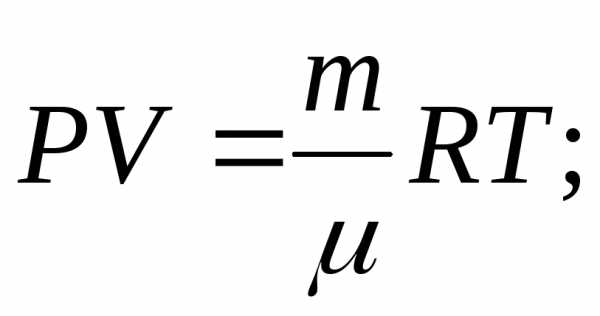то

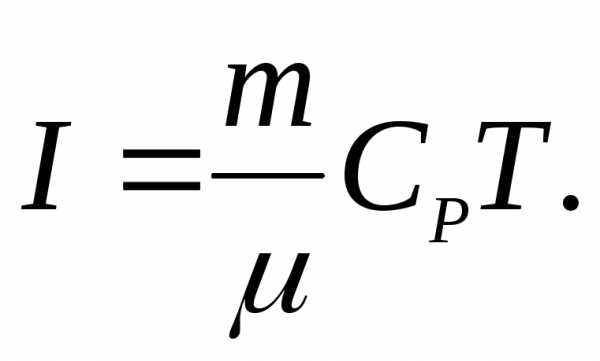(7)

Энтальпия играет большую роль в процессах расширения и сжатия газа.

Энтропия. В термодинамике большую роль играет еще одна функция состояния — энтропия S. Для обратимого процесса энтропия определяется как функция, дифференциал которой равен:

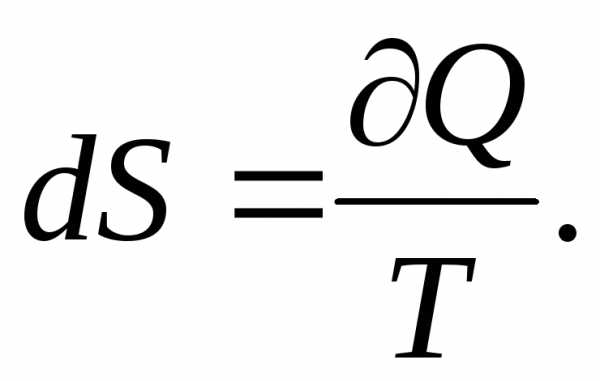(8)

Величина 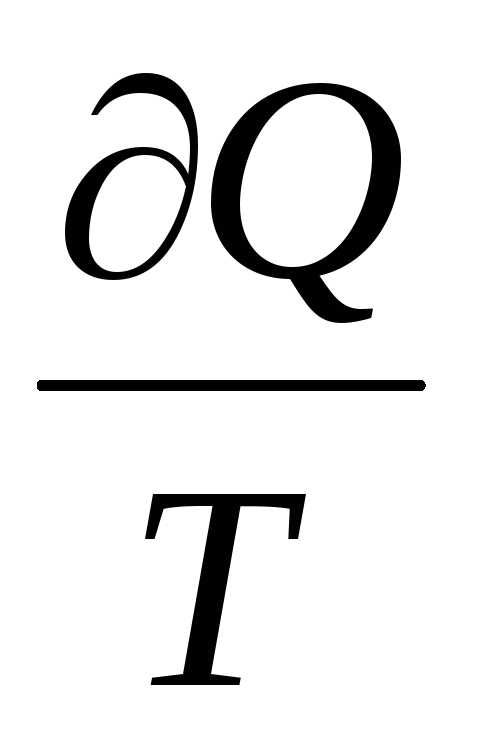называется приведенной теплотой. Из определения (8) следует, что если у системы в начальном состоянии 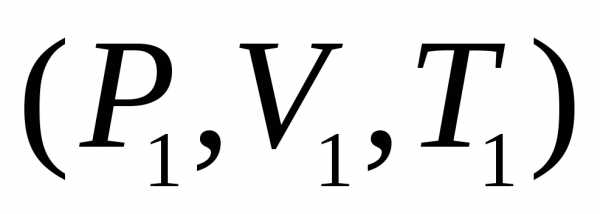была энтропияS₁, то при переходе в другое состояние при равновесном процессе ее энтропия буде равна:

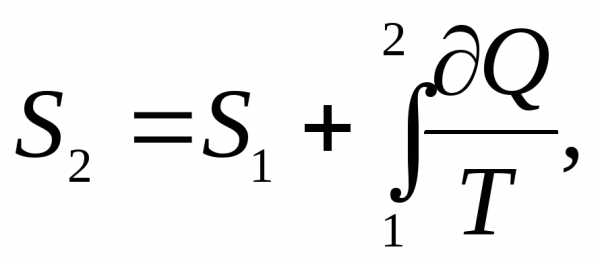(9)

Ранее было показано, что величина теплоты Q, подведенная к системе:

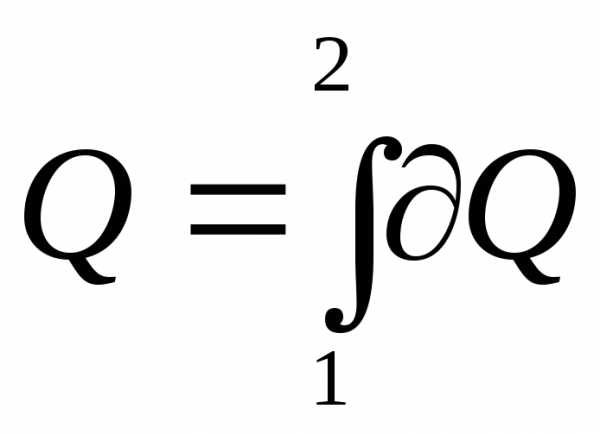
зависит от вида процесса, но изменение энтропии от вида процесса не зависит, если процесс был обратимым. Таким образом величина dS_, как и dU, является полным дифференциалом, в отличие от . Энтропию не относят к термодинамическим потенциалам, поскольку ее размерность не соответствует размерности энергии, а равна согласно (8) Дж/К. В термодинамике доказывается, что энтропия является функцией состояния любой термодинамической системы.

Рассмотрим некоторые свойства энтропии, выходящие из оп­ределения (8).

1. Энтропия нескольких тел равна сумме энтропии этих тел:

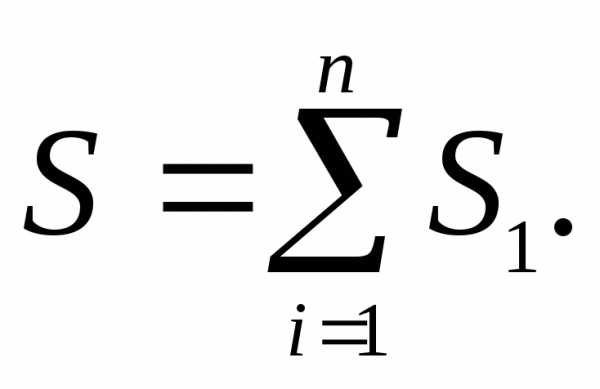
2. При равновесных процессах без передачи тепла (адиабатических процессах) энтропия системы не меняется.

S = const, если = 0.

3. Энтропия, как и все функции состояния, определяются с точностью до константы, поэтому измеримой величиной является только разность энтропии в начальном и конечном состояниях.

4. При постоянном объеме энтропия является функцией внутренней энергии тела. Действительно из первого начала термодинамики если dV=0, то , следовательно:

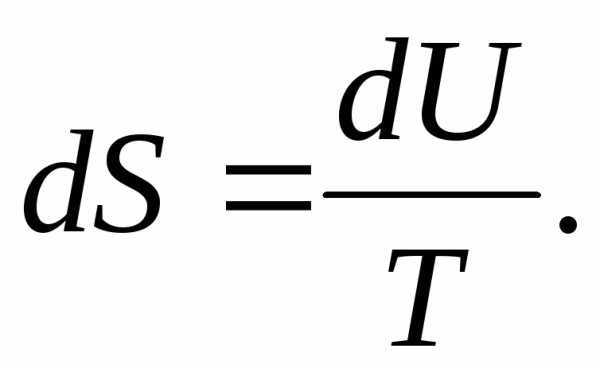
5. Для обратимых термодинамических циклов энтропия постоянна:

S = const.

Найдем значения энтропии, воспользовавшись уравнениями состояния и внутренней энергии для идеального газа, первым началом термодинамики и уравнением Майера;

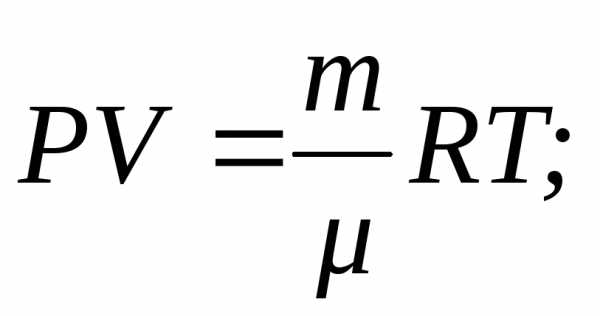
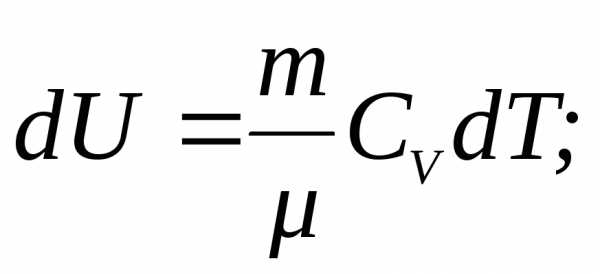
После интегрирования получим:

(10)

(11)

Энтропия изолированной системы. Выше отмечалось, что энтропия изолированной системы при обратимых процессах постоянна. Рассмотрим необратимый процесс теплопередачи в изолированной системе, Пусть два равных количества идеального газа с температурами T₁<Т₂ содержатся в изолированных одинаковых сосудах с жесткими стенками. Если создать тепловой контакт между этими сосудами, то через некоторое время газы в сосудах придут в термодинамическое равновесие и их температуры сравняются и будут равны .

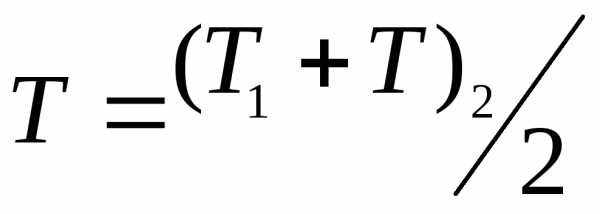Согласна (11) энтропия первого газа возрастет на;

энтропия второго газа изменится на:

Так как T<Т₂, то 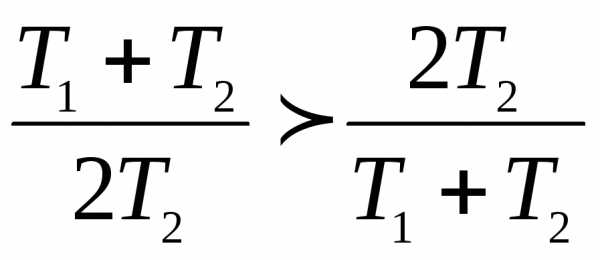, следовательно

Таким образом,

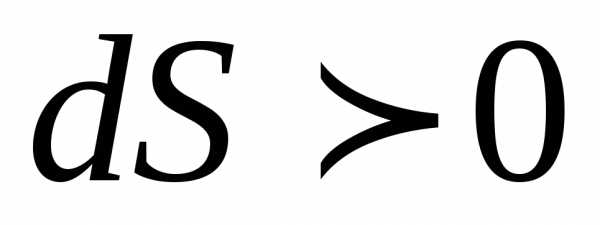. (12)

Энтропия любой изолированной системы не может убывать; она либо возрастает, либо остается постоянной.

Это утверждение является еще одной формулировкой второго начала термодинамики. Иногда (12) называют законом возрастания энтропии.

4. СТАТИСТИЧЕСКИЙ СМЫСЛ ЭНТРОПИИ

Приведенные выше формулировки энтропии и второго начала термодинамики связаны с макрохарактеристиками рабочего тела, Выше отмечалось, что все макрохарактеристики в конечном счете определяются микросостоянием (координатами и импульсами) всех входящих в термодинамическую систему частиц. Как уже отмечалось ранее/число частиц, входящих в реальные термодинамические системы очень большое (при нормальных условиях в 1 см³ газа содержится 3·10¹⁹ молекул). Поэтому, число возможных микросостояний для термодинамической системы соответствует громадному числу. Рассмотрим это утверждение на примере распределения частиц по объему.

Пусть в некотором сосуде находится газ в термодинамическом равновесии. Мысленно разделим этот сосуд на две половины I и II, Очевидно, что число молекул, находящихся в 1-й и II-й половинах одинаково. Молекулы подвижны, поэтому равновесие между частями I и II будет динамическим. Число молекул, перешедших из I в II, равно числу молекул, перешедших из II в I. С точки зрения макроскопических характеристик газа безразлично, какие молекулы находятся в I- части, а какие во 11-й. С точки зрения статистической физики все молекулы можно пометить и рассмотренному макросостоянию газа соответствует множество микрокомбинаций размещения конкретных молекул в частях I и II то есть множество микросостояний.

Число микросостояний, соответствующее конкретному макросостоянию термодинамической системы, Макс Планк предложил называть термодинамической вероятностью данного макросостояния. Обозначим термодинамическую вероятность буквой Ω. Нетрудно показать, что число всех возможных распределений N молекул по двум половинкам сосуда равно 2^N, а вероятность нахождения их всех в одной половине сосуда (I-й или II -й) равна 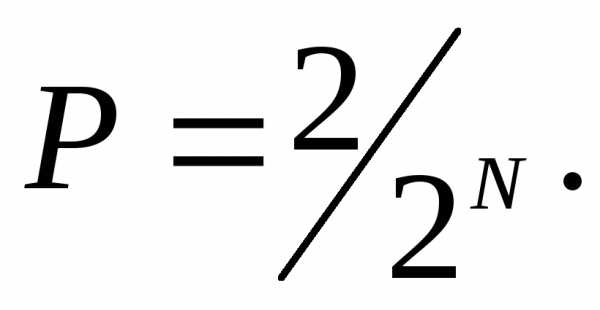ДляN — малых эта вероятность соответствует достаточно вероятному событию (N=2, P=1/2; N=4, P=2/16), но для реальных значений N — эта вероятность соответствует событию, которое практически невозможно. Вероятность равного количества молекул в частях I и II оказывается наиболее вероятной.

Из проведенного анализа следует, что второе начало термодинамики с точки зрения статистической физики можно сформулировать как: «Термодинамическая система всегда стремится занять наиболее вероятное макросостояние, то есть макросостояние с наибольшим числом возможных микросостояний или термодинамической вероятностью Ω. Это и является причиной необратимости термодинамических процессов. Необратимые процессы в изолированной термодинамической системе — это такие процессы, при которых система из менее вероятного макросостояния переходит в более вероятное.

Как отмечалось выше, при необратимых процессах растет энтропия системы S, То есть энтропия 5 и термодинамическая вероятность Ω растут при одних и тех же процессах. Эту связь установил Л. Больцман:

(13)

где k=1,38·10^-23 Дж/К — постоянная Больцмана. Соотношение (13) показывает статистический смысл энтропии.

11

studfiles.net

Необратимые процессы — Мегаэнциклопедия Кирилла и Мефодия — статья

Необрати́мые проце́ссы — термодинамические процессы, происходящие в изолированной системе, после которых система не может вернуться в первоначальное состояние без внешнего воздействия. Так как при протекании практически любого реального процесса изменяется внутренняя энергия тел, то самопроизвольно протекающие в природе процессы — необратимые. Самопроизвольный процесс — процесс, происходящий без воздействия внешних тел. Необратимость характерна лишь для макроскопических систем. Необратимые процессы — диффузия, теплопроводность, вязкое течение жидкости (газа) и другие физические процессы, которые могут самопроизвольно протекать только в одном направлении — в сторону равномерного распределения вещества, теплоты и т. д. Необратимые процессы характеризуются положительным производством энтропии.

В циклически действующем тепловом двигателе невозможно преобразовать все количество теплоты, полученное от нагревателя, в механическую работу.

Второй закон термодинамики — статистический, то есть замкунутая система многих частиц самопроизвольно переходит из более упорядоченного состояния в менее упорядоченное. Таким образом,

изолированная система самопроизвольно переходит из менее вероятного состояния в более вероятное.

Например, взаимная диффузия водорода и кислорода, находящихся до открытия перегородки в разных половинах объема, приводит к перемешиванию газов. Благодаря тепловому движению более легкий кислород поднимается вверх, а более легкий водород опускается вниз, несмотря на действие силы тяжести.

Явления, связанные с перемешиванием, с созданием беспорядка из порядка, увеличивают вероятность состояния.

Редактировать

Статистическое объяснение необратимости процессов в природе

Чисто механические процессы, без учета трения, обратимы, то есть инвариантны (не изменяются) при замене t → –t. Уравнения движения каждой отдельно взятой молекулы также инвариантны относительно преобразования времени, так как содержат только силы, зависящие от расстояния. Значит, причина необратимости процессов в природе в том, что макроскопические тела содержат очень большое количество частиц.

Макроскопическое состояние характеризуется несколькими термодинамическими параметрами (давление, объем, температура и т.д.). Микроскопическое состояние характеризуется заданием координат и скоростей (импульсов) всех частиц, составляющих систему. Одно макроскопическое состояние может быть реализовано огромным числом микросостояний.

Обозначим: N — полное число состояний системы, N₁ — число микросостояний, которые реализуют данное состояние, w — вероятность данного состояния. Тогда: \(w = {N_1 \over N}\)

Чем больше N₁, тем больше вероятность данного макросостояния, то есть тем большее время система будет находиться в этом состоянии. Эволюция системы происходит в направлении от маловероятных состояний к более вероятным. Так как механическое движение — хаотическое, то механическая энергия переходит в тепловую. При теплообмене состояние, в котором одно тело имеет более высокую температуру (молекулы имеют более высокую среднюю кинетическую энергию), менее вероятно, чем состояние, в котором температуры равны. Поэтому процесс теплообмена происходит в сторону выравнивания температур.

Все естественные процессы, происходящие в природе, — необратимые. В отличие от идеализированных процессов, которые обратимы.Газ занимает весь предоставленный ему объем. Этот процесс необратим: объем газа не будет уменьшаться без воздействия внешних сил.Процесс теплообмена необратим. Количество теплоты самопроизвольно передается от тела с большей температурой к телу с меньшей температурой. Теплопередача от холодного тела к более нагретому самопроизвольно не возникает, а достигается за счет дополнительной работы холодильной установки.Диффузия — это необратимый процесс.Так, молекулы чернил, проникая между молекулами воды, равномерно распределеяются по объему, открашивая сосуд. Обратная локализация чернил на поверхности воды практически невозможна.Процесс разрядки конденсатора через большое сопротивление, дросселирование газа, старение и смерть живых организмов — необратимые процессы.

1. Физика. 10 класс. В.А. Касьянов. Дрофа. 2002
2. Справочник школьника. Том 2. С.-Петербург. «Весь», 2006
3. Молекулы. Физика для всех. Л.Д. Ландау, А.И. Китайгородский. Москва, Наука. 1978.
4. Политехнический словарь. Советская энциклопедия. М: 1976

megabook.ru

2. Обратимые и необратимые процессы.

Подобно тому, как в первом начале термодинамики вводится функция состояния – внутренняя энергия, во втором начале – функция состояния, получившая название энтропия (S) (от греческого entropia – поворот, превращение). Рассмотрение изменения этой функции привело к разделению всех процессов на две группы: обратимые и необратимые (самопроизвольные) процессы.

Процесс называется обратимым, если его можно провести сначала в прямом, а затем в обратном направлении и так, что ни в системе, ни в окружающей среде не останется никаких изменений. Полностью обратимый процесс – абстракция, но многие процессы можно вести в таких условиях, чтобы их отклонение от обратимости было весьма мало. Для этого необходи мо, чтобы в каждой своей бесконечно малой стадии состояние системы, в которой этот процесс происходит, отвечало бы состоянию равновесия.

Состояние равновесия – особое состояние термодинамической системы, в которое она переходит в результате обратимого или необратимого процессов и может оставаться в нем бесконечно долго. Реальные процессы могут приближаться к обратимым, но для этого они должны совершаться медленно.

Процесс называется необратимым (естественным, спонтанным, самопроизвольным), если он сопровождается рассеянием энергии, т. е. равномерным распределением между всеми телами системы в результате процесса теплопередачи.

В качестве примеров необратимых процессов могут быть названы следующие:

• замерзание переохлажденной жидкости;

• расширение газа в вакуумированное пространство;

• диффузия в газовой фазе или в жидкости.

Систему, в которой произошел необратимый процесс, можно возвратить в исходное состояние, но для этого над системой нужно совершить работу.

К необратимым процессам относится большинство реальных процессов, так как они всегда сопровождаются работой против сил трения, в результате чего происходят бесполезные энергозатраты, сопровождающиеся рассеянием энергии.

Для иллюстрации понятий рассмотрим идеальный газ, находящийся в цилиндре под поршнем. Пусть начальное давление газа Р₁ при его объеме V₁ (рис. 4.1).

Д

авление газа уравновешено насыпанным на поршень песком. Совокупность равновесных состояний описывается уравнениемpV = const и графически изображается плавной кривой (1).

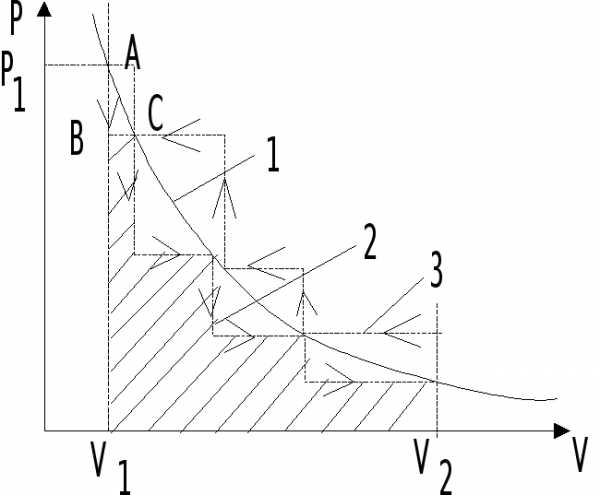
Если с поршня снять некоторое количество песка, то давление газа над поршнем резко снизится (от А до В) лишь после чего произойдет увеличение объема газа до равновесной величины (от В до С). Характер этого процесса – ломанная линия 2. Эта линия характеризует зависимость P=f (V) при необратимом процессе.

Рис. 4.1. Зависимость давления газа от его объема при обратимом (1) и необратимом процессах (2, 3).

Из рисунка видно, что при обратимом расширении газа совершаемая им работа (площадь под плавной кривой 1) больше, чем при любом необратимом его расширении.

Таким образом, любой термодинамический процесс характеризуется максимально возможной величиной работы, если он совершается в обратимом режиме. К аналогичному выводу можно прийти, если рассмотреть процесс сжатия газа. Только следует иметь ввиду, что в этом случае величина работы – отрицательная величина (рис. 4.1, ломаная 3).

studfiles.net

Обратимый необратимый процесс — Большая Энциклопедия Нефти и Газа, статья, страница 1

Обратимый необратимый процесс

Cтраница 1

Обратимые и необратимые процессы могут быть составлены из последовательности равновесных или неравновесных состояний рассматриваемой физической системы.  [1]

Обратимые и необратимые процессы имеют определенные свойства, позволяющие отличать одни процессы от других. Условиями обратимости процесса являются: бесконечно медленное изменение состояния тела, прохождение системы в процессе только через равновесные состояния, отсутствие в системе всякого трения и отсутствие процесса сгорания. Есл в процессах все эти условия или некоторые из них отсутствуют, то такие процессы становятся необратимыми.  [2]

Иногда обратимые и необратимые процессы поликонденсации называют соответственно равновесными и неравновесными.  [4]

Понятие обратимых и необратимых процессов является основным для термодинамики. Обратимыми называют процессы, протекающие с бесконечно малой скоростью, которые представляют собой как бы непрерывную смену равновесных состояний. Оно относится к основным понятиям классической термодинамики и является идеализированным представлением процессов, протекающих в естественных условиях.  [5]

Динамика обратимых и необратимых процессов намагничивания и перемагничивания представляет собой столь сложное явление, что теоретическое рассмотрение возможно в настоящее время только для некоторых частных случаев и весьма упрощенных моделей. Ниже рассмотрена в качестве иллюстрации динамика движения доменной стенки в тонкой ленте с прямоугольной петлей гистерезиса и показано ее влияние на форму динамической петли гистерезиса.  [6]

Чем отличаются обратимые и необратимые процессы. Почему все реальные процессы необратимы.  [7]

Анализируя понятия обратимых и необратимых процессов, мы путем некоторых общих, но еще недостаточно убедительных рассуждений, подтвержденных примерами, показали, что неравновесность процесса является признаком и причиной его необратимости. Теперь мы имеем возможность строго доказать это утверждение. Вспомним прежде всего, что понятия обратимого и необратимого процессов относятся к абсолютно изолированной системе.  [8]

Из определения обратимых и необратимых процессов следует, что работа, выполняемая системой при переходе из определенного начального состояния в определенное конечное состояние, в результате прохождения некоторого процесса в условиях, когда он является необратимым, заведомо меньше, чем когда этот процесс проводится в условиях, обеспечивающих его практическую обратимость.  [9]

Различие между квазистатическими обратимыми и необратимыми процессами заключается в конечном счете в том, что квазистатические обратимые процессы представляют собой последовательную цепь равновесных состояний, в то время как необратимые процессы представляют собой цепь неравновесных состояний.  [10]

Что подразумевается под обратимыми и необратимыми процессами.  [11]

Сравнивая работу при изотермическом обратимом и необратимом процессе ( уравнения ( 15 10) и ( 34 7)) видим, что работа при изотермическом необратимом процессе меньше, чем при обратимом.  [12]

В нее дают вклад обратимые и необратимые процессы намагничивания. Соответственно дифференциальная восприимчивость состоит из обратимой и необратимой восприимчивости.  [13]

Как изменяется энтропия для обратимых и необратимых процессов. Чему равно значение JdQ / T для обратимого и необратимого кругового процесса. Температура каких тел входит в этих случаях в знаменатель подынтегрального выражения.  [14]

В термодинамике существуют понятия обратимых и необратимых процессов. Обратимым называется процесс, после совершения которого в прямом, а затем в обратном направлении рабочее тело возвращается в свое первоначальное состояние без дополнительных затрат энергии.  [15]

Страницы:      1    2    3    4

www.ngpedia.ru

4.1 Обратимые и необратимые процессы

Для расширения представлений о термодинамических процессах уточним понятие обратимого процесса: процесс, совершаемый системой наз. обратимым, если после него можно возвратить систему и все тела, взаимодействующие с ней, в их начальное состояние таким образом, чтобы в других телах не возникало каких-либо остаточных изменений.

Необходимое условие обратимости терм. процесса – его равновесность, т.е. всякий обратимый процесс всегда является равновесным (квазистат). Однако не всякий равновесный процесс является обратимым. Например, квазистататический процесс равномерного движения по поверхности под действием силы тяжести и трения – процесс необратимый.

Пример обратимого процесса – незатухающие колебания тела, подвешенного на пружине в вакууме. Система тело-пружина консервативна. Ее механические колебания не вызывают никаких изменений в энергии теплового движения частиц системы. Изменение состояния системы связано с изменением ее конфигурации и скорости движения тела, которые полностью повторяются через период.

Пример необратимого процесса – торможение тела под действием силы трения. Если сила трения единственная сила, то скорость тела уменьшается и оно останавливается. При этом энергия мех движ. тела, как целого уменьш. и расходуется на увел. энергии тепл. движ. частиц тела и среды. Другими словами, за счет нач. кинет. эн. тела (W_к) растет внутрення энергия U тела и среды, нагревающихся при трении ΔU = W_к. Этот прямой процесс протекает самопроизвольно, он идет без каких либо процессов, происходящих с окружающими телами. Но для осуществления обратного процесса возвращения системы в исходное состояние необходимо, чтобы остановившееся тело вновь пришло в движение за счет энергии, выделившейся при его охлаждении и окружающей среды. Известно, что хаотическое движение тела, т.е., U не может самопроизвольно привести к упорядоченному движению всех частиц тела, как целого. Для реализации этого необходим дополнительный, так называемый компенсирующий процесс. Он заключается в охлаждении тела и окружающей среды до первоначальной Т, т.е., в отдаче ими некоторому другому телу теплоты Q = W_к и в совершении над рассматриваемым телом работы, равной W_к. Поэтому, хотя в результате прямого и обратного процесса система тело-среда возвратилась в исходное состояние, состояние внешних тел изменяется (меняется Т, затем совершается работа, т.е. меняются координаты). Следовательно, процессы сопровождающиеся трением необратимы.

Процесс теплообмена между двумя телами с разной Т приводит к выравниванию средних энергий тепл. движения частиц обоих тел. Энергия частиц более нагретого тела уменьшается, менее нагретого – увеличивается. В итоге Т₁ = Т₂. Процесс идет самопроизвольно, как только обеспечен контакт между телами. Обратный процесс – нагревание одного тела за счет охлаждения другого, имевшего вначале Т₁ = Т₂, самопроизвольно не протекает. Для него используется холодильное устройство, работа которого приводит к изменению состояния других внешних тел. Значит процесс теплообмен при конечной ΔТ является необратимым. Можно показать, что необратимыми являются процессы диффузии и растворения.

Из всех этих примеров необратимых процессов можно сделать общие выводы: Все они в прямом направлении происходят самопроизвольно, а для осуществл. обр. проц. требуется одновременное протекание компенсирующих процессов. Все реальные процессы идут с конечной скоростью и сопровождаются трением и теплообменом при конечной разности температур тел, находящихся в тепловом контакте, значит все реальные процессы, строго говоря, необратимы. Однако в некоторых случаях условия протекания процесса таковы, что их приближенно можно считать обратимыми.

studfiles.net

Необратимость тепловых процессов. Второй закон термодинамики. Понятие энтропии

Первый закон термодинамики – закон сохранения энергии для тепловых процессов – устанавливает связь между количеством теплотыQ, полученной системой, изменением ΔU еевнутренней энергиииработойA, совершенной над внешними телами:

 

Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Процессы, нарушающие первый закон термодинамики, никогда не наблюдались. На рис. 1.5.14 изображены устройства, запрещенные первым законом термодинамики.

1

Рисунок 1.5.14. Циклически работающие тепловые машины, запрещаемые первым законом термодинамики: 1 – вечный двигатель 1 рода, совершающий работу без потребления энергии извне; 2 – тепловая машина с коэффициентом полезного действия η > 1.

Первый закон термодинамики не устанавливает направление тепловых процессов. Однако, как показывает опыт, многие тепловые процессы могут протекать только в одном направлении. Такие процессы называются необратимыми. Например, при тепловом контакте двух тел с разными температурами тепловой поток всегда направлен от более теплого тела к более холодному. Никогда не наблюдается самопроизвольный процесс передачи тепла от тела с низкой температурой к телу с более высокой температурой. Следовательно, процесс теплообмена при конечной разности температур является необратимым.

Обратимымипроцессами называют процессы перехода системы из одного равновесного состояния в другое, которые можно провести в обратном направлении через ту же последовательность промежуточных равновесных состояний. При этом сама система и окружающие тела возвращаются к исходному состоянию.

Процессы, в ходе которых система все время остается в состоянии равновесия, называются квазистатическими. Все квазистатические процессы обратимы. Все обратимые процессы являются квазистатическими.

Если рабочее тело тепловой машины приводится в контакт с тепловым резервуаром, температура которого в процессе теплообмена остается неизменной, то единственным обратимым процессом будет изотермический квазистатический процесс, протекающий при бесконечно малой разнице температур рабочего тела и резервуара. При наличии двух тепловых резервуаров с разными температурами обратимым путем можно провести процессы на двух изотермических участках. Поскольку адиабатический процесс также можно проводить в обоих направлениях (адиабатическое сжатие и адиабатическое расширение), то круговой процесс, состоящий из двух изотерм и двух адиабат (цикл Карно) является единственным обратимым круговым процессом, при котором рабочее тело приводится в тепловой контакт только с двумя тепловыми резервуарами. Все остальные круговые процессы, проводимые с двумя тепловыми резервуарами, необратимы.

Необратимыми являются процессы превращения механической работы во внутреннюю энергию тела из-за наличия трения, процессы диффузии в газах и жидкостях, процессы перемешивания газа при наличии начальной разности давлений и т. д. Все реальные процессы необратимы, но они могут сколь угодно близко приближаться к обратимым процессам. Обратимые процессы являются идеализацией реальных процессов.

Первый закон термодинамики не может отличить обратимые процессы от необратимых. Он просто требует от термодинамического процесса определенного энергетического баланса и ничего не говорит о том, возможен такой процесс или нет. Направление самопроизвольно протекающих процессов устанавливает второй закон термодинамики. Он может быть сформулирован в виде запрета на определенные виды термодинамических процессов.

Английский физик У. Кельвин дал в 1851 г. следующую формулировку второго закона:

В циклически действующей тепловой машине невозможен процесс, единственным результатом которого было бы преобразование в механическую работу всего количества теплоты, полученного от единственного теплового резервуара.

Гипотетическую тепловую машину, в которой мог бы происходить такой процесс, называют «вечным двигателем второго рода». В земных условиях такая машина могла бы отбирать тепловую энергию, например, у Мирового океана и полностью превращать ее в работу. Масса воды в Мировом океане составляет примерно 10²¹кг, и при ее охлаждении на один градус выделилось бы огромное количество энергии (≈10²⁴Дж), эквивалентное полному сжиганию 10¹⁷кг угля. Ежегодно вырабатываемая на Земле энергия приблизительно в 10⁴раз меньше. Поэтому «вечный двигатель второго рода» был бы для человечества не менее привлекателен, чем «вечный двигатель первого рода», запрещенный первым законом термодинамики.

Немецкий физик Р. Клаузиус дал другую формулировку второго закона термодинамики:

Невозможен процесс, единственным результатом которого была бы передача энергии путем теплообмена от тела с низкой температурой к телу с более высокой температурой.

На рис. 1.5.15 изображены процессы, запрещаемые вторым законом, но не запрещаемые первым законом термодинамики. Эти процессы соответствуют двум формулировкам второго закона термодинамики.

2

Рисунок 1.5.15. Процессы, не противоречащие первому закону термодинамики, но запрещаемые вторым законом: 1 – «вечный двигатель второго рода»; 2 – самопроизвольный переход тепла от холодного тела к более теплому («идеальная холодильная машина»).

Следует отметить, что обе формулировки второго закона термодинамики эквивалентны. Если допустить, например, что тепло может самопроизвольно (то есть без затраты внешней работы) переходить при теплообмене от холодного тела к горячему, то можно прийти к выводу о возможности создания «вечного двигателя второго рода». Действительно, пусть реальная тепловая машина получает от нагревателя количество теплоты Q₁и отдает холодильнику количество теплоты Q₂. При этом совершается работа A = Q₁– |Q₂|. Если бы количество теплоты |Q₂| самопроизвольно переходило от холодильника к нагревателю, то конечным результатом работы реальной тепловой машины и «идеальной холодильной машины» было бы превращение в работу количества теплоты Q₁– |Q₂|, полученного от нагревателя без какого-либо изменения в холодильнике. Таким образом, комбинация реальной тепловой машины и «идеальной холодильной машины» равноценна «вечному двигателю второго рода». Точно также можно показать, что комбинация «реальной холодильной машины» и «вечного двигателя второго рода» равноценна «идеальной холодильной машине».

Второй закон термодинамики связан непосредственно с необратимостью реальных тепловых процессов. Энергия теплового движения молекул качественно отличается от всех других видов энергии – механической, электрической, химической и т. д. Энергия любого вида, кроме энергии теплового движения молекул, может полностью превратиться в любой другой вид энергии, в том числе и в энергию теплового движения. Последняя может испытать превращение в любой другой вид энергии лишь частично. Поэтому любой физический процесс, в котором происходит превращение какого-либо вида энергии в энергию теплового движения молекул, является необратимым процессом, то есть он не может быть осуществлен полностью в обратном направлении.

Общим свойством всех необратимых процессов является то, что они протекают в термодинамически неравновесной системе и в результате этих процессов замкнутая система приближается к состоянию термодинамического равновесия.

На основании любой из формулировок второго закона термодинамики могут быть доказаны следующие утверждения, которые называются теоремами Карно:

1. Коэффициент полезного действия тепловой машины, работающей при данных значениях температур нагревателя и холодильника, не может быть больше, чем коэффициент полезного действия машины, работающей по обратимому циклу Карно при тех же значениях температур нагревателя и холодильника.

2. Коэффициент полезного действия тепловой машины, работающей по циклу Карно, не зависит от рода рабочего тела, а только от температур нагревателя и холодильника.

Таким образом, коэффициент полезного действия машины, работающей по циклу Карно, максимален.

 

Знак равенства в этом соотношении соответствует обратимым циклам. Для машин, работающих по циклу Карно, это соотношение может быть переписано в виде

 

В каком бы направлении ни обходился цикл Карно (по или против часовой стрелки), величины Q₁и Q₂всегда имеют разные знаки. Поэтому можно записать

 

Это соотношение может быть обобщено на любой замкнутый обратимый процесс, который можно представить как последовательность малых изотермических и адиабатических участков (рис. 1.5.16).

3

Рисунок 1.5.16. Произвольный обратимый цикл как последовательность малых изотермических и адиабатических участков.

При полном обходе замкнутого обратимого цикла

где ΔQ_i= ΔQ_1i+ ΔQ_2i– количество теплоты, полученное рабочим телом на двух изотермических участках при температуре T_i. Для того, чтобы такой сложный цикл провести обратимым путем, необходимо рабочее тело приводить в тепловой контакт со многими тепловыми резервуарами с температурами T_i. Отношение ΔQ_i/ T_iназываетсяприведенным теплом. Полученная формула показывает, чтополное приведенное тепло на любом обратимом цикле равно нулю. Эта формула позволяет ввести новую физическую величину, которая называется энтропией и обозначается буквой S (Р. Клаузиус, 1865 г.). Если термодинамическая система переходит из одного равновесного состояния в другое, то ее энтропия изменяется.Разность значений энтропии в двух состояниях равна приведенному теплу, полученному системой при обратимом переходе из одного состояния в другое.

 

В случае обратимого адиабатического процесса ΔQ_i= 0 и, следовательно, энтропия S остается неизменной.

Выражение для изменения энтропии ΔS при переходе неизолированной системы из одного равновесного состояния (1) в другое равновесное состояние (2) может быть записано в виде

 

Энтропия определена с точностью до постоянного слагаемого, так же, как, например, потенциальная энергия тела в силовом поле. Физический смысл имеет разность ΔS энтропии в двух состояниях системы. Чтобы определить изменение энтропии в случае необратимого перехода системы из одного состояния в другое, нужно придумать какой-нибудьобратимыйпроцесс, связывающий начальное и конечное состояния, и найти приведенное тепло, полученное системой при таком переходе.

Рис. 1.5.17 иллюстрирует необратимый процесс расширения газа «в пустоту» в отсутствие теплообмена. Только начальное и конечное состояния газа в этом процессе являются равновесными, и их можно изобразить на диаграмме (p, V). Точки (a) и (b), соответствующие этим состояниям, лежат на одной изотерме. Для вычисления изменения ΔS энтропии можно рассмотреть обратимый изотермический переход из (a) в (b). Поскольку при изотермическом расширении газ получает некоторое количество теплоты от окружающих тел Q > 0, можно сделать вывод, что при необратимом расширении газа энтропия возросла: ΔS > 0.

4

Рисунок 1.5.17. Расширение газа в «пустоту». Изменение энтропии где A = Q – работа газа при обратимом изотермическом расширении.

Другой пример необратимого процесса – теплообмен при конечной разности температур. На рис. 1.5.18 изображены два тела, заключенные в адиабатическую оболочку. Начальные температуры тел T₁и T₂< T₁. При теплообмене температуры тел постепенно выравниваются. Более теплое тело отдает некоторое количество теплоты, а более холодное – получает. Приведенное тепло, получаемое холодным телом, превосходит по модулю приведенное тепло, отдаваемое горячим телом. Отсюда следует, что изменение энтропии замкнутой системы в необратимом процессе теплообмена ΔS > 0.

5

Рисунок 1.5.18. Теплообмен при конечной разности температур: a – начальное состояние; b – конечное состояние системы. Изменение энтропии ΔS > 0.

Рост энтропии является общим свойством всех самопроизвольно протекающих необратимых процессов в изолированных термодинамических системах. При обратимых процессах в изолированных системах энтропия не изменяется:

 

Это соотношение принято называть законом возрастания энтропии.

При любых процессах, протекающих в термодинамических изолированных системах, энтропия либо остается неизменной, либо увеличивается.

Таким образом, энтропия указывает направление самопроизвольно протекающих процессов. Рост энтропии указывает на приближение системы к состоянию термодинамического равновесия. В состоянии равновесия энтропия принимает максимальное значение. Закон возрастания энтропии можно принять в качестве еще одной формулировки второго закона термодинамики.

В 1878 году Л. Больцман дал вероятностнуютрактовку понятия энтропии. Он предложил рассматривать энтропию какмеру статистического беспорядка в замкнутой термодинамической системе. Все самопроизвольно протекающие процессы в замкнутой системе, приближающие систему к состоянию равновесия и сопровождающиеся ростом энтропии, направлены в сторону увеличения вероятности состояния.

Всякое состояние макроскопической системы, содержащей большое число частиц, может быть реализовано многими способами. Термодинамическая вероятностьW состояния системы – эточисло способов, которыми может быть реализовано данное состояние макроскопической системы, или числомикросостояний, осуществляющих данное макросостояние. По определению термодинамическая вероятность W >> 1.

Например, если в сосуде находится 1 моль газа, то возможно огромное число N способов размещения молекулы по двум половинкам сосуда: где –число Авогадро. Каждый из них является микросостоянием. Только одно из микросостояний соответствует случаю, когда все молекулы соберутся в одной половинке (например, правой) сосуда. Вероятность такого события практически равна нулю. Наибольшее число микросостояний соответствует равновесному состоянию, при котором молекулы равномерно распределены по всему объему. Поэтомуравновесное состояние является наиболее вероятным.Равновесное состояние с другой стороны является состоянием наибольшего беспорядка в термодинамической системе и состоянием с максимальной энтропией.

Согласно Больцману, энтропия S системы и термодинамическая вероятность W связаны между собой следующим образом:

где k = 1,38·10^–23Дж/К –постоянная Больцмана. Таким образом,энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы.

Вероятностная трактовка второго закона термодинамики допускает самопроизвольное отклонение системы от состояния термодинамического равновесия. Такие отклонения называются флуктуациями. В системах, содержащих большое число частиц, значительные отклонения от состояния равновесия имеют чрезвычайно малую вероятность.

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:

Установите температуры Т₁ и Т₂, указанные в табл.1 для вашей бригады. Для этого нажмите кнопку «ВЫБОР», переместите маркер мыши так, чтобы его остриё находилось на кнопках регуляторов термометровили. Последовательными короткими нажатиями на эти кнопки установите заданные температуры нагревателя и холодильника.

Нажмите мышью кнопку «СТАРТ» и наблюдайте перемещение точки по замкнутой кривой цикла Карно. Остановите процесс нажатием кнопки «СТОП» вблизи точки 1, обозначенной на рис.2, т.е. в месте перехода изотермического расширения газа в адиабатическое.

Запишите в табл.2 значение V₂, которое в момент остановки процесса в точке 1 будет обозначено в нижнем прямоугольнике окна опыта.

Аналогичные измерения проведите для точек 3,4 и 1 и запишите значения объёмов газа в соответствующие столбцы таблицы 2.

Установите вторые значения температуры нагревателя и холодильника, указанные в табл.1, и проделайте все измерения по п.п. 2- 4 ещё раз. Результаты опытов занесите в табл.3.

ОБРАБОТКА РЕЗУЛЬТАТОВ И ОФОРМЛЕНИЕ ОТЧЁТА:

1.Для любой произвольной точки цикла запишите значения давления, объёма и температуры, указанные в прямоугольнике окна опыта.

2. С помощью уравнения состояния идеального газа pV=определите число молей газа, находящихся в цилиндре под поршнем.

Используя уравнения: А₁₂=

А₃₄=.

А = А₁₂ + А₂₃ + А₃₄ + А₄₁= Q₁ + A₂₃ – Q₂ – А₂₃=Q₁ — Q₂.

рассчитайте Q₁,Q₂,Aи запишите эти значения в табл.2.

По формуле =.рассчитайте к.п.д. цикла Карно и сравните его со значением, приведённым в окне опыта.

Вычислите среднее значение работы цикла Карно и абсолютную погрешность измерения А.

Таблица 1. Значения температуры нагревателя Т₁ и холодильника Т₂

Номер бригады	1	2	3	4	5	6	7	8
Т1	400 500	410 510	420 520	430 530	440 540	450 550	460 560	470 570
Т2	270 350	280 340	290 330	300 320	310 310	320 300	330 290	340 280

Таблицы 2,3. Результаты измерений (количество измерений и строк = 3)

Номер измерения	V1 дм3	V2 дм3	V3 дм3	V4 дм3	Q1 кДж	Q2 кДж	A кДж	А кДж	
									%
1
2
3

Т₁= Т₂=

Вопросы и задания для самоконтроля

1. Какие устройства называют тепловыми двигателями?

2. Из каких основных элементов состоит тепловой двигатель?

3. Зачем в тепловом двигателе нужен холодильник?

4. Что является холодильником в двигателе внутреннего сгорания?

5. Чем отличаются обратимые и необратимые процессы? Почему все реальные процессы необратимы?

6. Дайте понятие энтропии (определение, размерность и математические выражения изменения энтропии для различных изопроцессов идеальных газов).

7. В каком направлении может изменяться энтропия замкнутой системы? незамкнутой системы?

8. В чём заключается теорема Карно?

9. Выведите формулу к.п.д. цикла Карно.

10. Изобразите в системе координат T-Sизотермический и адиабатический процессы и цикл Карно в целом.

11.Докажите, что к.п.д. теплового двигателя, работающего по произвольному обратимому циклу, всегда меньше, чем к.п.д. цикла Карно, работающего между максимальной и минимальной температурой этого цикла.

литература

1. Трофимова Т.И. Курс физики. М.: Высшая школа, 2001. Гл.23, §§ 179-180.

2. Детлаф А.А., Яворский Б.М. Курс физики. М.: Высшая школа, 2000. 543с.

ЛАБОРАТОРНАЯ РАБОТА № 1.5

ИССЛЕДОВНИЕ ЗАВИСИМОСТИ МОЩНОСТИ И К.П.Д. ИСТОЧНИКА ПОСТОЯННОГО ТОКА ОТ ВНЕШНЕЙ НАГРУЗКИ

Ознакомьтесь с теорией в конспекте и учебниках. Запустите программу «Электричество и магнетизм». Выберите: «Цепи постоянного тока». Нажмите вверху внутреннего окна кнопку с изображением страницы. Прочитайте краткие теоретические сведения. Необходимое запишите в свой конспект. (Если вы забыли, как работать с системой компьютерного моделирования, прочитайте ВВЕДЕНИЕ еще раз).

ЦЕЛЬ РАБОТЫ:

• Знакомство с компьютерным моделированием цепей постоянного тока.

• Исследование зависимости мощности и к.п.д. источника постоянного тока от сопротивления внешней цепи.

ТЕОРИЯ:

studfiles.net

57.Обратимые и необратимые процессы.

Первый закон термодинамики – закон сохранения энергии для тепловых процессов – устанавливает количественное соотношение при превращении теплоты в механическую работу: Q=ΔU+A. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую.

Человек с давних времён умел превращать запасную энергию или работу в теплоту. Первобытные люди добывали теплоту, сжигая различные виды топлива.

Используя обратный процесс (превращение теплоты в работу) люди овладели возможностью получать работу в требуемом кол-ве.

Первый закон термодинамики не устанавливает направление тепловых процессов. Однако, многие тепловые процессы могут протекать только в одном направлении. Такие процессы называются необратимыми. Например, при тепловом контакте двух тел с разными температурами тепловой поток всегда направлен от более теплого тела к более холодному. Никогда не наблюдается самопроизвольный процесс передачи тепла от тела с низкой температурой к телу с более высокой температурой. Следовательно, процесс теплообмена при конечной разности температур является необратимым.

Не смотря на то, что теплота самопроизвольно не переходит к более горячему телу, можно намеренно вызвать этот переход в противоестественном направлении. Так, холодильник работает за счёт того, что где-то сгорает уголь, падает поток воды или происходит деление ядра. Процессы перехода системы из одного равновесного состояния в другое, которые можно провести в обратном направлении через ту же последовательность промежуточных равновесных состояний, называют обратимыми процессами. При этом сама система и окружающие тела возвращаются к исходному состоянию.

Необратимыми являются процессы превращения механической работы во внутреннюю энергию тела из-за наличия трения, процессы диффузии в газах и жидкостях, процессы перемешивания газа при наличии начальной разности давлений и т. д. Все реальные процессы необратимы, но они могут сколь угодно близко приближаться к обратимым процессам. Обратимые процессы являются идеализацией реальных процессов.

58.Циклические процессы

Первым устр-вом, преобраз-им теплоту в работу, стала паровая машина. Двигателем назыв-сяустр-во, которое работает циклически и переодически возвращается в начальное положение. Двигатель должен работать сколь угодно долго, потребляя Е, поставляемую нагревателем, который в свою очередь питается энергией за счёт сгорания топлива. С помощью цикла Карнно можно воспроизвести рабочие процессы, происходящие в реальных машинах.

Цикл Карно имеет 3 стадии: изотерм-ое и адиабат-оерасширние газа, изотерм-ое и адиаб-ое сжатие газа. Начальное сост-ие двигателя А соотв-ет наличию контакта между цилиндром с газом и нагревателем. В этой точке поршень вдвинут в цилиндр, Vгаза мал,Tвысокая,pвелико. 1-й контакт цикла, в течение к-го цилиндр в контакте с нагревателем, состоит в расширении газа. Газ, имеющий высокое р, давит на поршень, стремясь вытолкнуть его из цилиндра. В рез-те поршень перемещ-ся, связанный с ним коленчатый вал поворачив-ся – совершается рабочий ход двигателя. Этот этап изотерм-ий. Чтобы преодолеть стремление газа к охлаждению при расширении, к нему необходимо подвести энергию от нагревателя. Чтобы цикл был полезным, необходимо уменьшить работу, совершаемую над газом при возвращению к исходным значениямVиp. Необходимо понизить р газа внутри цилиндра, чтобы на стадии сжатия требовалась меньшая работа, чем на стадии расширения. Один из способов понизить р газа стоит в понижении его температуры, т.е. охлаждении. Этого можно добиться, включив в цикл стадию адиабат-го расширения (В-С). Существенным этапом для цикла Карно явл-ся размыкание теплового контакта с нагревателем прежде, чем поршень окажется полностью выдвинутым. Коленчатый вал продолжает поворачиваться, а газ расширяться, но теперь это расширении происходит адиабат-ки, так что при этом падает р и Т газа. Он приходит в состояние, соответствующее точке С. Далее следует возвращение газа к исходному состоянию, т.е. необходимо вдвинуть поршень в цилиндр, уменьшитьVгаза до первонач-госост-ия. На этом этапе (С-D) газ приводится в тепловой контакт, но с холодильником, чтобы на сколько возможно понизить р, а следоват-но и умньшить работу по сжатию газа. В рез-те попадём в точкуDтеперьVпочти как в нач-ом сост-ии, но Т газа понизилась => прежде, чем коленчатый вал завершит полный оборот, нарушают тепловой контакт с холодильником и Т газа повышают за счёт работы, совершаемой над ним в процессе адиабат-го сжатия. Т.о., приходим к полностью замкнутому циклу, совершив ещё и полезную работу. В течение рабочего хода получили больше работы, чем затратили на этапах возврата в исходное сост-ие. Этой цели достигли, совершив сжатие при меньших значениях давления. Исключ-но важная роль принадлежит холодильнику. В отсутствие холод-ка мы совершим бесполезный цикл, неприводящий к выигрышу. Когда же обеспечили возможность передачи части энергии газа холод-ку, последов-ть процесса осталась циклической, но теперь она стала ещё и полезной с точки зрения совершения работы. Лишь при наличии холод-ка становиться возможным создать поток энергии от нагревателя к холод-ку и часть этой энергии превратить в работу. Цикл Карно – один из возможных способов получения работы с помощью теплоты.

studfiles.net