По геометрии 7 класс теория – Теория по геометрии 7 класс. Вопросы и ответы

Теория по геометрии 7 класс. Вопросы и ответы

Геометрия.

Аксиома.

3 аксиомы планиметрии о взаимном расположении точек и прямых.

IV аксиома планиметрии о трех точках прямой.

V аксиома планиметрии о точке прямой.

VI аксиома планиметрии о прямой на плоскости.

Отрезок.

Луч.

Угол.

Развернутый угол.

Равные фигуры.

Середина отрезка.

Биссектриса угла.

Измерение отрезков.

Свойства измерения отрезков.

Измерение углов.

Свойства измерения углов.

Прямой угол.

Острый угол.

Тупой угол.

Смежные углы.

Свойство смежных углов.

Вертикальные углы.

Свойство вертикальных углов.

Перпендикулярные прямые.

Свойство перпендикулярных прямых.

Треугольник.

Периметр треугольника.

Равные треугольники.

Теорема, доказательство теоремы.

Первый признак равенства треугольников.

Второй признак равенства треугольников.

Третий признак равенства треугольников.

Теорема о единственности опущенного перпендикуляра.

Медиана треугольника.

Биссектриса треугольника.

Высота треугольника.

Свойство о пересечении медиан, биссектрис и высот треугольников.

Равнобедренный треугольник.

Равносторонний треугольник.

Свойства равнобедренного треугольника.

Определение.

Определение окружности.

Хорда окружности.

Диаметр окружности.

Дуга окружности.

Круг.

Определение параллельных прямых.

Параллельные отрезки.

Секущая.

Углы при параллельных прямых и секущей.

3 признака параллельности двух прямых.

Аксиома параллельных прямых.

2 следствия из аксиомы параллельных прямых.

Обратная теорема.

Свойства параллельных прямых.

Свойство прямой, перпендикулярной к одной из двух параллельных прямых.

Сумма углов треугольника.

Внешний угол треугольника.

Свойства внешнего угла треугольника.

Виды треугольников.

Элементы прямоугольного треугольника.

Теорема о соотношениях между сторонами и углами треугольника.

2 следствия из теоремы о соотношениях между сторонами и углами треугольника.

Неравенства треугольника.

Свойства прямоугольных треугольников.

Признаки равенства прямоугольных треугольников.

Свойство двух параллельных прямых о равноудаленности точек.

Расстояние между параллельными прямыми.

Замечательные точки треугольника.

А₂: Имеются по крайней мере 3 точки, не лежащие на одной прямой.

А₃: Через любые 2 точки проходит прямая, и притом только одна.

А₄: Из трех точек прямой одна и только одна лежит между двумя другими.

А₅: Каждая точка О прямой разделяет её на 2 части (два луча) так, что любые две точки одного и того же луча лежат по одну сторону от точки О, а любые две точки разных лучей лежат по разные стороны от точки О.

А₆: Каждая прямая а разделяет плоскость на две части (две полуплоскости) так, что любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а, а любые две точки разных полуплоскостей лежат по разные стороны от прямой а.

Отрезок – это часть прямой, ограниченная двумя точками. Точки, ограничивающие отрезок, называются его концами. Отрезок обозначается двумя заглавными латинскими буквами. Например, АВ или ВА.

Луч – это часть прямой, ограниченная одной точкой. Эта точка называется началом луча. Луч обозначается двумя заглавными латинскими буквами или одной строчной латинской буквой. Например, луч АВ или луч m.

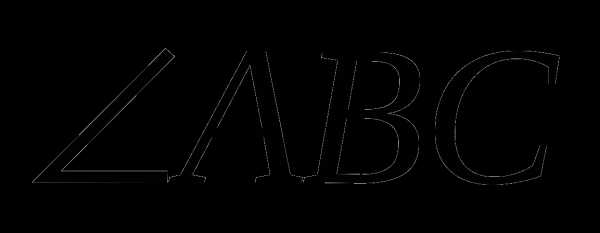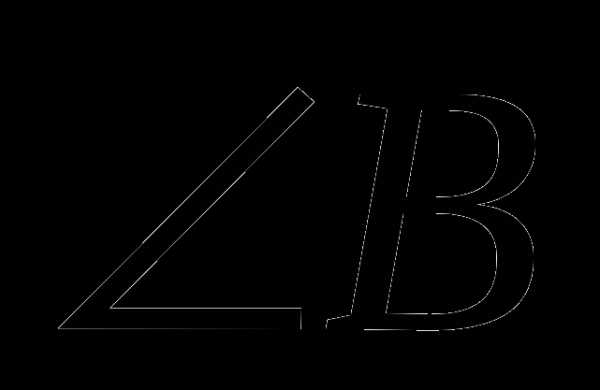Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало – вершиной угла. Угол обозначается тремя заглавными латинскими буквами или одной заглавной латинской буквой или двумя строчными латинскими буквами. Например, или или .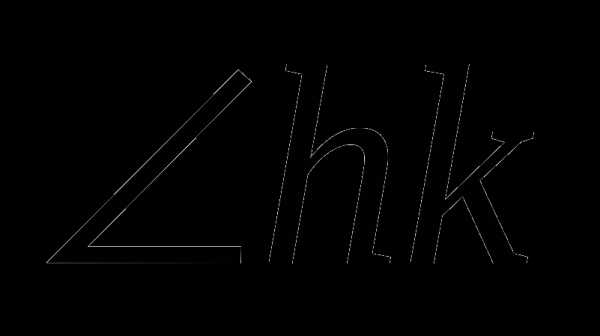

Угол называется развернутым, если обе его стороны лежат на одной прямой.

Две геометрические фигуры называются равными, если их можно совместить наложением.

Середина отрезка – это точка отрезка, делящая его пополам, т.е. на два равных отрезка.

Биссектриса угла – это луч, исходящий из вершины угла и делящий его на два равных угла.

Измерение отрезков. Выбрав единицу измерения, можно измерить любой отрезок, т.е. выразить его длину некоторым положительным числом.

Свойства измерения отрезков. 1) Равные отрезки имеют равные длины. 3) Меньший отрезок имеет меньшую длину. 3) Когда точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.

Измерение углов. Градусной мерой угла называется положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле.

Свойства измерения углов. 1) Равные углы имеют равные градусные меры.2) Меньший угол имеет меньшую градусную меру. 3) Развернутый угол равен 180 градусам. 4Неразвернутый угол меньше 180 градусов. 5) Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.

Прямой угол – угол, градусная мера которого равна 90 градусов.

Острый угол – угол, градусная мера которого меньше 90 градусов.

Тупой угол – угол, градусная мера которого больше 90 градусов, но меньше 180 градусов.

Смежные углы – два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.

Свойство смежных углов. Сумма смежных углов равна 180 градусов.

Вертикальные углы. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

Свойство вертикальных углов. Вертикальные углы равны.

Перпендикулярные прямые. Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.

Свойство перпендикулярных прямых. Две прямые, перпендикулярные к третьей, не пересекаются.

Треугольник – геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, соединенных отрезками. Три точки называются вершинами, а отрезки – сторонами треугольника.

Периметр треугольника – это сумма длин трех сторон треугольника.

Равные треугольники – треугольники, которые при наложении совмещаются. Если два треугольника равны, то элементы одного треугольника соответственно равны элементам другого треугольника.

Теорема, доказательство теоремы. Утверждение, справедливость которого устанавливается путем рассуждения, называется теоремой, а сами рассуждения называются доказательством теоремы.

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.

Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.

Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения также пересекаются в одной точке.

Треугольник называется равнобедренным, если его две стороны равны. Эти стороны называются боковыми, а третья – основанием.

Треугольник, все стороны которого равны, называется равносторонним.

В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Предложение, в котором разъясняется смысл того или иного выражения или названия, называется определением.

Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, ­­- радиусом окружности.

Отрезок, соединяющий две точки окружности, называется её хордой.

Хорда, проходящая через центр окружности, называется диаметром.

Часть окружности, ограниченная двумя точками, называется дугой окружности.

Часть плоскости, ограниченная окружностью, называется кругом.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Два отрезка называются параллельными, если они лежат на параллельных прямых.

Прямая с называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

Углы при параллельных прямых и секущей:

2)Если две прямые параллельны третьей прямой, то они параллельны.

2) обратно, против большего угла лежит большая сторона.

multiurok.ru

Теория по геометрии за 7 класс по учебнику Л.С. Атанасяна

Теория по геометрии за 7 класс по учебнику Л.С. Атанасяна

Доступные файлы (1):

n1.docx

Геометрия, теория 7 класс. Составила Аверкова Т.Е.

7 класс¹

Аксиома: через любые две точки можно провести прямую, и притом только одну.

Поэтому: две прямые либо имеют только одну общую точку, либо не имеют общих точек.

Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало — вершиной угла.

Любой угол разделяет плоскость на две части. Если угол неразвернутый, то одна из частей называется внутренней, а другая — внешней областью этого угла.

Если угол развернутый, то любую из двух частей, на которые он разделяет плоскость, можно считать внутренней областью угла. Фигуру, состоящую из угла и его внутренней области, также называют углом.

Две геометрические фигуры называются равными, если их можно совместить наложением.

Точка отрезка, делящая его пополам, т. е. на два равных отрезка, называется серединой отрезка.

Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.

Измерение отрезков основано на сравнении их с некоторым отрезком, принятым за единицу измерения (его называют также масштабным отрезком).

За единицу измерения можно принимать не только сантиметр, но и любой другой отрезок. Выбрав единицу измерения, можно измерить любой отрезок, т. е. выразить его длину некоторым положительным числом. Это число показывает, сколько раз единица измерения и ее части укладываются в измеряемом отрезке.

Если два отрезка равны, то единица измерения и ее части укладываются в этих отрезках одинаковое число раз, т. е. равные отрезки имеют равные длины. Если же один отрезок меньше другого, то единица измерения (или ее часть) укладывается в этом отрезке меньшее число раз, чем в другом, т. е. меньший отрезок имеет меньшую длину.

Когда точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.

Обычно за единицу измерения углов принимают градус — угол, равный -1/180 части развернутого угла.

Равные углы имеют равные градусные меры.

Меньший угол имеет меньшую градусную меру.

Развернутый угол равен 180°.

Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.

Угол называется прямым, если он равен 90°, острым, если он меньше 90°, т. е. меньше прямого угла, тупым, если он больше 90°, но меньше 180°, т. е. больше прямого, но меньше развернутого угла

Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными.

Сумма смежных углов равна 180°.

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.

Вертикальные углы равны.

Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.

Две прямые, перпендикулярные к третьей, не пересекаются.

Сумма длин трех сторон треугольника называется его периметром.

Признаки равенства треугольников:

1. 
   Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
   
2. 
   Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
   
3. 
   Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
   

Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности.

Отрезок, соединяющий две точки окружности, называется ее хордой. Хорда, проходящая через центр окружности, называется диаметром. Часть плоскости, ограниченная окружностью, называется кругом.

Рассмотрим прямую а и точку А, не лежащую на этой прямой. Соединим точку А отрезком с точкой Н прямой а. Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а, если прямые АН и а перпендикулярны. Точка Н называется основанием перпендикуляра.

Теорема: Из точки, не лежащей на прямой, можно провести перпендикуляр и только один.

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.

Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

В любом треугольнике медианы, высоты и биссектрисы пересекаются в одной точке.

Треугольник называется равнобедренным, если две его стороны равны.

Равные стороны называются боковыми сторонами, а третья сторона — основанием равнобедренного треугольника.

Треугольник, все стороны которого равны, называется равносторонним.

Теорема: В равнобедренном треугольнике углы при основании равны.

Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Признаки параллельности:

• 
  Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
  
• 
  Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
  
• 
  Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
  

Аксиомы:

• 
  через любые две точки проходит прямая, и притом только одна.
  
• 
  на любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
  
• 
  от любого луча в заданную сторону можно отложить угол, равный данному неразвернутому углу, и притом только один.
  
• 
  Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
  

Следствия из аксиом:

• 
  Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
  
• 
  Если две прямые параллельны третьей прямой, то они параллельны.
  

Обратные теоремы:

• 
  Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
  
• 
  Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
  
• 
  Если две параллельные прямые пересечены секущей, то соответственные углы равны.
  
• 
  Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
  

Сумма углов треугольника равна 180°.

Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.

Если все три угла треугольника острые, то треугольник называется остроугольным.

Если один из углов треугольника тупой, то треугольник называется тупоугольным.

Если один из углов треугольника прямой, то треугольник называется прямоугольным. Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны — катетами.

Теорема: В треугольнике: 1) против большей стороны лежит больший угол; 2) обратно, против большего угла лежит большая сторона.

Следствие 1: В прямоугольном треугольнике гипотенуза больше катета.

Следствие 2: Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).

Теорема о неравенстве треугольника: Каждая сторона треугольника меньше суммы двух других сторон.

Следствие: Для любых трех точек А, В и С, не лежащих на одной прямой, справедливы неравенства: АВ

Некоторые свойства прямоугольных треугольников:

1. 
   Сумма двух острых углов прямоугольного треугольника равна 90°.
   
2. 
   Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
   
3. 
   Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°.
   

Признаки равенства прямоугольных треугольников:

• 
  Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
  
• 
  Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
  
• 
  Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
  
• 
  Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
  

Перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой.

Длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой.

Все точки каждой из двух параллельных прямых равноудалены от другой прямой.

Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.

Медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.

perviydoc.ru

Вся теория по геометрии для подготовки к ОГЭ. 7 класс

Планиметрия – 7 класс. Теория

Определение

Планиметрия – это раздел геометрии, который изучает геометрические фигуры на плоскости.

Определение

Аксиома – это утверждение, принимающееся как истинное без доказательства. Аксиомы планиметрии – это основные свойства простейших геометрических фигур.

Основными понятиями в планиметрии являются точка, прямая.

1 Аксиомы принадлежности

1.1 Какова бы ни была прямая, существуют точки, принадлежащие ей и не принадлежащие ей.

1.2 Через любые две точки можно провести прямую и притом только одну.

2 Аксиомы расположения

2.1 Из трех точек на прямой одна и только одна лежит между двумя другими.

2.2 Прямая разбивает плоскость на две полуплоскости.

3

Аксиомы измерения

3.1 Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.

3.2 Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 180⁰. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

4

Аксиомы откладывания.

4.1 На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины и притом только один.

4.2 От любой полупрямой в заданную полуплоскость можно отложить угол, с заданной градусной мерой, меньшей 180⁰ и притом только один.

4.3 Каков бы ни был треугольник, существует треугольник, равный ему, в заданном расположении относительно данной полупрямой.

Определение

Прямые называются параллельными, если они не имеют общих точек.

5 Аксиома парал-ти

5.1 Через точку, не лежащую на данной прямой можно провести не более одной прямой, параллельной данной.

Теорема

Если две прямые параллельны третьей прямой, то они параллельны.

Теорема.(признак пар-ти)

Если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180 градусов, то прямые параллельны.

Теорема. (св-во углов при пересечении)

Если две параллельные прямые пересечены третьей прямой, то внутренние накрест лежащие углы равны и сумма внутренних односторонних углов равна 180 градусов.

Смежные и вертикальные углы

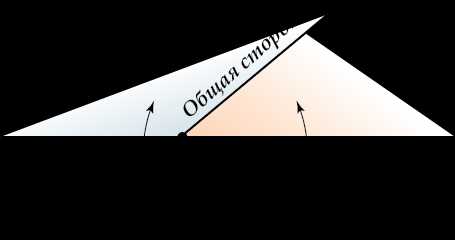
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами.

Теорема. 

Сумма смежных углов равна 180⁰.

 Если стороны одного угла являются дополнительными полупрямыми сторон другого угла, то такие углы называются вертикальными.

Теорема. 

Вертикальные углы равны.

Определение

Прямые называются перпендикулярными, если они пересекаются под прямым углом

Теорема. 

Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну.

Треугольник

Определение

Треугольник   —   это геометрическая фигура, состоящая из трех точек,  не лежащих на одной прямой, соединенных отрезками.  

Определение

Если треугольники   АВС   и   А1В1С1 можно совместить наложением,  то они являются равными.   У равных треугольников равны и их  соответствующие элементы.  

Определение

Высота треугольника – перпендикуляр, опущенный из данной вершины к противолежащей стороне треугольника.

Биссектриса треугольника – отрезок биссектрисы угла треугольника, проведенный из данной вершины к противолежащей стороне.

Медиана треугольника – отрезок, соединяющий данную вершину с серединой противолежащей стороны.

Признаки равенства треугольников

Первый признак равенства треугольников

Если две стороны и угол между этими сторонами одного треугольника равны соответственно двум сторонам и углу между этими сторонами другого треугольника, то такие треугольники равны. 

 Второй признак равенства треугольников

Если сторона и прилежащие к ней углы одного треугольника равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства треугольников

Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

Определение

Равнобедренный треугольник   —   треугольник  
у которого равны   две стороны.  

Равносторонний треугольник   —   треугольник  
у которого   все стороны   равны.  

Теорема. 

В равнобедренном треугольнике углы при основании равны;  

Теорема. 

В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;  

Свойства

• Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой.

• Биссектрисы, медианы и высоты, проведённые из углов, противолежащих равным сторонам треугольника, равны между собой.

• Биссектриса, медиана и высота, проведенные к основанию, совпадают между собой. 

• Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане (они совпадают) проведенных к основанию.

• Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.

Теорема. 

Сумма углов треугольника равна 180⁰.

Определение

Внешним углом треугольника при данной вершине, называется угол, смежный с углом треугольника при этой вершине

Теорема. 

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Теорема.

Средняя линия треугольника, которая соединяет середины двух данных сторон, параллельна третьей его стороне и равна ее половине.

Окружность

Определение

Окружностью называется фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки. Эта точка называется

центром окружности.

Радиус — расстояние от точек окружности до её центра.

Хорда- отрезок, соединяющий две точки окружности.

Диаметр – хорда, проходящая через центр.

Касательная к окружности — прямая, проходящая через точку окружности. Касательная всегда перпендикулярна радиусу.

Теорема.

Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров, опущенных на середины сторон данного треугольника.

Теорема.

Центр окружности, вписанной в треугольник, является точкой пересечения биссектрис, проведенных из его углов.

infourok.ru

Геометрия 7-9 класс — Всё для чайников

• Главная
• Видеотека
  • Естествознание
    • Физика
    • Математика
    • Химия
    • Биология
    • Экология
  • Обществознание
    • Обществознание — как наука
    • Иностранные языки
    • История
    • Психология и педагогика
    • Русский язык и литература
    • Культурология
    • Экономика
    • Менеджмент
    • Логистика
    • Статистика
    • Философия
    • Бухгалтерский учет
  • Технические науки
    • Черчение
    • Материаловедение
    • Сварка
    • Электротехника
    • АСУТП и КИПИА
    • Технологии
    • Теоретическая механика и сопромат
    • САПР
    • Метрология, стандартизация и сертификация
    • Геодезия и маркшейдерия
  • Программирование и сеть
    • Информатика
    • Языки программирования
    • Алгоритмы и структуры данных
    • СУБД
    • Web разработки и технологии
    • Архитектура ЭВМ и основы ОС
    • Системное администрирование
    • Создание программ и приложений
    • Создание сайтов
    • Тестирование ПО
    • Теория информации и кодирования
    • Функциональное и логическое программирование
  • Программы
    • Редакторы и компиляторы
    • Офисные программы
    • Работа с аудио видео
    • Работа с компьютерной графикой и анимацией
    • Автоматизация бизнеса
  • Прочие
    • Музыка
    • Природное земледелие
    • Рисование и живопись
• Библиотека
  • Естествознание
    • Физика
    • Математика
    • Химия
    • Биология
    • Экология
    • Астрономия
  • Обществознание
    • Иностранные языки
  • Технические науки
    • Теоретическая механика и сопромат
    • Сварка
    • Железная дорога
  • Паспорта и техническая документация
    • Металлообра-батывающие станки
    • Деревообра-батывающие станки
    • Сварочное оборудование
• Правила
• Контакты

forkettle.ru

Зачет по теории геометрия 7 класс

Вопросы для зачета.

Определение параллельных прямых. Какие два отрезка называются параллельными?

Что такое секущая? Назовите пары углов, которые образуются при пересечении двух прямых секущей.

Какие утверждения называются аксиомами?

Аксиома параллельных прямых

Какое утверждение называется следствием?

Какая теорема называется обратной данной теоремы? Примеры.

Теорема о сумме углов треугольника.

Какой угол называется внешним?

Какой треугольник называется остроугольным? Какой треугольник называется тупоугольным?

Какой треугольник называется прямоугольным? Как называют стороны прямоугольного треугольника?

Сформулируйте признак равенства прямоугольного треугольника по гипотенузе и острому углу.

Сформулируйте признак равенства прямоугольного треугольника по гипотенузе и катету.

Что называется расстоянием от точки до прямой?

Что называется расстоянием между параллельными прямыми.

Задачи к зачету.

Построение треугольника по двум сторонам и углу.

Построение треугольника по стороне и двум углам.

Построение треугольника по трем сторонам.

Построить равнобедренный треугольник по основанию по углу и боковой стороне.

Построить прямоугольный треугольник по гипотенузе и катету

В равнобедренном треугольнике ABC с основанием AC, равным 37, внешний угол при вершине В равен 60⁰. Найдите расстояние от вершины С до прямой АВ.

Один из углов прямоугольного треугольника равен 60⁰, а сумма гипотенузы и меньшего из катетов равна 26,4 см. Найдите гипотенузу треугольника.

Высота, проведенная к основанию равнобедренного треугольника, равна 7,6 см, а боковая сторона треугольника равна 15,2 см. найдите углы этого треугольника.

Угол, противолежащий основанию равнобедренного треугольника, равен 120⁰. Высота, проведенная к боковой стороне, равна 9 см. Найдите основание треугольника.

В прямоугольном треугольнике АВС с прямым углом С внешний угол при вершине А равен 120⁰, АС+АВ=18 см. Найдите АС и АВ.

Билет 6.

Билет 16.

multiurok.ru

Тест репетитора по математике для 7 класса. Определения и теоремы

Для успешного освоения геометрии в 7 классе репетитор по математике в той или иной форме отрабатывает с учеником определения, свойства и признаки изучаемых понятий. Предлагаю Вашему вниманию он-лайн вариант проверки уровня теоретических знаний школьника. Он рассчитан для работы с программой учебника Атанасяна. За исключением простейших вопросов на смежные / вертикальные углы и некоторых начальных сведений вводной части учебника тест позволяет репетитору по математике осуществить комплексную проверку всех основных фактов и понятий. Математика 7 класс он-лайн — Определения и теоремы.

Задание 1. Сопоставьте номера признаков равенства треугольников с их сокращенными формулировками.

---

Ответ:

1: …По двум сторонам и углу между нимиПо стороне и двум прилежащим к ней угламПо трем сторонам

2: …По двум сторонам и углу между нимиПо стороне и двум прилежащим к ней угламПо трем сторонам

3: …По двум сторонам и углу между нимиПо стороне и двум прилежащим к ней угламПо трем сторонам

Задание 2. Как называется отрезок, проведенный из вершины треугольника к потиволежащей стороне и делящий эту сторону пополам?

---

Выберите ответ:

Задание 3. Как называется отрезок, проведенный из вершины треугольника к противолежащей стороне под прямым углом?  

---

Выберите ответ:

Задание 4. Как называется отрезок, проведенный из вершины треугольника к противолежащей стороне и делящий угол пополам?

---

Выберите ответ:

Задание 5. Выберите неверное утверждение из списка.

---

Выберите ответ:

Задание 6. Выберите верное утверждение из списка.

---

Выберите ответ:

Задание 7. Выбирите неверное утверждение из списка.

---

Выберите ответ:

Задание 8. Треугольника называется равнобедренным, если у него …

---

Выберите ответ:

Задание 9. Укажите свойство медианы в равнобедренном треугольнике.

---

Выберите ответ:

Задание 10. Выберите верное продолжение фразы: в равнобедренном треугольнике… 

---

Выберите ответ:

Задание 11. Дайте название слудующему утверждению: если в треугольнике все углы равны, то он равносторонний. 

---

Выберите ответ:

Задание 12. Верно ли утверждение: в равнобедренном треугольнике медианы, проведенные с боковым стоонам равны?

---

Выберите ответ:

Задание 13. Как называются углы, изображенные на рисунке?

---

Выберите ответ:

Задание 14. Укажите верное утверждение. 

---

Выберите ответ:

Задание 15. Укажите верное название для следующего утверждения: если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. 

---

Выберите ответ:

Задание 16. Как называется сторона BC в прямоугольном треугольнике ABC с прямым углом А?

---

Выберите ответ:

Задание 17. Укажите верное свойство угла в 30 градусов в прямоугольном треугольнике.

---

Выберите ответ:

Задание 18. Выберите верное утверждение из списка.

---

Выберите ответ:

Задание 19. Укажите верно сформулированное неравенство треугольника.

---

Выберите ответ:

Задание 20. Укажите верно сформулированную теорему в внешнем угле треугольника.

---

Выберите ответ:

Задание 21. Чему равна сумма внутренних углов в треугольнике?

---

Выберите ответ:

Вопрос повышенной сложности: Чему  равна сумма внешних углов в треугольнике?

---

Выберите ответ:
Я хочу отправить результаты на почту

Меня зовут
и я хочу отправить свои результаты
на e-mail

Практически все задания расположены в хронологическом порядке их изучения в школьной программе. С удовольствием бы выдержал эту последовательность полностью, но пока, к сожалению, я не могу менять порядок номеров. Это техническая проблема составления теста, которая в скором времени, я надеюсь, будет решена.

Пройдите тест за 7 класс до начала занятий с предполагаемым репетитором по математике. Его результаты помогут быстрее оценить уровень Вашей подготовки к изучению последующей математики (геометрии) в 8 классе.

Методическое указание репетитора:
Отличие программ 7 класса по учебникам Атанасяна и Погорелова не настолько велико, чтобы репетитору по математике полностью отказаться от использования теста в работе с Погореловым. Главным образом эта разница касается раздела «начальные понятия планиметрии» (которая в тесте не представлена) и некоторых мелких тем, не имеющих тесной связи с дальнейшим изложением: «свойство угла в 30 градусов», «соотношение между углами и сторонами в треугольнике», пересечение медиан, биссектрис и высот … Существенную разницу в учебниках составляет материалы 8 — 9 классов. В присутствии преподавателя ученик может работать с данным тестом в ограниченном режиме, отвечая только на выбранные репетитором по математике вопросы. Удачных размышлений над заданиями!

Информация для преподавателей: составляйте и присылайте Ваши собственные тесты по любым темам за 5 — 11 класс (с вариантами ответов) мне на почту. Если в ответах или формулировках заданий имеются формулы, их можно сфотографировать или сканировать. С удовольствие опубликую лучшие работы.

С уважением, Александр Николаевич, репетитор по математике в Москве.

ankolpakov.ru

Тест по теории геометрия 7-9 класс

Вариант 1

1. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Один из углов тре­уголь­ни­ка все­гда не пре­вы­ша­ет 60 гра­ду­сов.

2) Диа­го­на­ли тра­пе­ции пе­ре­се­ка­ют­ся и де­лят­ся точ­кой пе­ре­се­че­ния по­по­лам.

3) Все диа­мет­ры окруж­но­сти равны между собой.

2. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Впи­сан­ные углы, опи­ра­ю­щи­е­ся на одну и ту же хорду окруж­но­сти, равны.

2) Если ра­ди­у­сы двух окруж­но­стей равны 5 и 7, а рас­сто­я­ние между их цен­тра­ми равно 3, то эти окруж­но­сти не имеют общих точек.

3) Если ра­ди­ус окруж­но­сти равен 3, а рас­сто­я­ние от цен­тра окруж­но­сти до пря­мой равно 2, то эти пря­мая и окруж­ность пе­ре­се­ка­ют­ся.

4) Если впи­сан­ный угол равен 30°, то дуга окруж­но­сти, на ко­то­рую опи­ра­ет­ся этот угол, равна 60°.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

3. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Около лю­бо­го пра­виль­но­го мно­го­уголь­ни­ка можно опи­сать не более одной окруж­но­сти.

2) Центр окруж­но­сти, опи­сан­ной около тре­уголь­ни­ка со сто­ро­на­ми, рав­ны­ми 3, 4, 5, на­хо­дит­ся на сто­ро­не этого тре­уголь­ни­ка.

3) Цен­тром окруж­но­сти, опи­сан­ной около квад­ра­та, яв­ля­ет­ся точка пе­ре­се­че­ния его диа­го­на­лей.

4) Около лю­бо­го ромба можно опи­сать окруж­ность.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

4. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Су­ще­ству­ет квад­рат, ко­то­рый не яв­ля­ет­ся пря­мо­уголь­ни­ком.

2) Если два угла тре­уголь­ни­ка равны, то равны и про­ти­во­ле­жа­щие им сто­ро­ны.

3) Внут­рен­ние на­крест ле­жа­щие углы, об­ра­зо­ван­ные двумя па­рал­лель­ны­ми пря­мы­ми и се­ку­щей, равны.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

5. Какое из сле­ду­ю­щих утвер­жде­ний верно?

1) Пло­щадь па­рал­ле­ло­грам­ма равна по­ло­ви­не про­из­ве­де­ния его диа­го­на­лей.

2) Сумма углов пря­мо­уголь­но­го тре­уголь­ни­ка равна 90 гра­ду­сам.

3) Бис­сек­три­сы тре­уголь­ни­ка пе­ре­се­ка­ют­ся в цен­тре впи­сан­ной в него окруж­но­сти.

6. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Пра­виль­ный ше­сти­уголь­ник имеет шесть осей сим­мет­рии.

2) Пря­мая не имеет осей сим­мет­рии.

3) Цен­тром сим­мет­рии ромба яв­ля­ет­ся точка пе­ре­се­че­ния его диа­го­на­лей.

4) Рав­но­бед­рен­ный тре­уголь­ник имеет три оси сим­мет­рии.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

7. Какое из сле­ду­ю­щих утвер­жде­ний верно?

1) Если два угла од­но­го тре­уголь­ни­ка равны двум углам дру­го­го тре­уголь­ни­ка, то такие тре­уголь­ни­ки по­доб­ны.

2) Диа­го­на­ли ромба равны.

3) Тан­генс лю­бо­го остро­го угла мень­ше еди­ни­цы.

8. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Если катет и ги­по­те­ну­за пря­мо­уголь­но­го тре­уголь­ни­ка равны со­от­вет­ствен­но 6 и 10, то вто­рой катет этого тре­уголь­ни­ка равен 8.

2) Любые два рав­но­бед­рен­ных тре­уголь­ни­ка по­доб­ны.

3) Любые два пря­мо­уголь­ных тре­уголь­ни­ка по­доб­ны.

4) Тре­уголь­ник ABC, у ко­то­ро­го AB = 3, BC = 4, AC = 5, яв­ля­ет­ся ту­по­уголь­ным.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

9. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Если два угла од­но­го тре­уголь­ни­ка равны двум углам дру­го­го тре­уголь­ни­ка, то такие тре­уголь­ни­ки по­доб­ны.

2) Вер­ти­каль­ные углы равны.

3) Любая бис­сек­три­са рав­но­бед­рен­но­го тре­уголь­ни­ка яв­ля­ет­ся его ме­ди­а­ной.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

10. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Пло­щадь тре­уголь­ни­ка мень­ше про­из­ве­де­ния двух его сто­рон.

2) Сред­няя линия тра­пе­ции равна сумме её ос­но­ва­ний.

3) Если два угла од­но­го тре­уголь­ни­ка равны двум углам дру­го­го тре­уголь­ни­ка, то такие тре­уголь­ни­ки по­доб­ны.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

11. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Цен­тры впи­сан­ной и опи­сан­ной окруж­но­стей рав­но­сто­рон­не­го тре­уголь­ни­ка сов­па­да­ют.

2) Су­ще­ству­ет квад­рат, ко­то­рый не яв­ля­ет­ся ром­бом.

3) Сумма углов лю­бо­го тре­уголь­ни­ка равна 180° .

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

12. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Смеж­ные углы равны.

2) Любые две пря­мые имеют ровно одну общую точку.

3) Если угол равен 108°, то вер­ти­каль­ный с ним равен 108°.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

13. Какие из дан­ных утвер­жде­ний верны? За­пи­ши­те их но­ме­ра.

1) Во­круг лю­бо­го тре­уголь­ни­ка можно опи­сать окруж­ность.

2) Если в па­рал­ле­ло­грам­ме диа­го­на­ли равны и пер­пен­ди­ку­ляр­ны, то этот па­рал­ле­ло­грамм — квад­рат.

3) Пло­щадь тра­пе­ции равна про­из­ве­де­нию сред­ней линии на вы­со­ту.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

14.Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Пло­щадь мно­го­уголь­ни­ка, опи­сан­но­го около окруж­но­сти, равна про­из­ве­де­нию его пе­ри­мет­ра на ра­ди­ус впи­сан­ной окруж­но­сти.

2) Если диа­го­на­ли ромба равна 3 и 4, то его пло­щадь равна 6.

3) Пло­щадь тра­пе­ции мень­ше про­из­ве­де­ния суммы ос­но­ва­ний на вы­со­ту.

4) Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка мень­ше про­из­ве­де­ния его ка­те­тов.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

15. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Окруж­ность имеет бес­ко­неч­но много цен­тров сим­мет­рии.

2) Пря­мая не имеет осей сим­мет­рии.

3) Пра­виль­ный пя­ти­уголь­ник имеет пять осей сим­мет­рии.

4) Квад­рат не имеет цен­тра сим­мет­рии.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

16. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Квад­рат любой сто­ро­ны тре­уголь­ни­ка равен сумме квад­ра­тов двух дру­гих сто­рон без удво­ен­но­го про­из­ве­де­ния этих сто­рон на синус угла между ними.

2) Если ка­те­ты пря­мо­уголь­но­го тре­уголь­ни­ка равны 5 и 12, то его ги­по­те­ну­за равна 13.

3) Тре­уголь­ник ABC, у ко­то­ро­го AB = 5, BC = 6, AC = 7, яв­ля­ет­ся ост­ро­уголь­ным.

4) В пря­мо­уголь­ном тре­уголь­ни­ке квад­рат ка­те­та равен раз­но­сти квад­ра­тов ги­по­те­ну­зы и дру­го­го ка­те­та.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

17. Какие из дан­ных утвер­жде­ний верны? За­пи­ши­те их но­ме­ра.

1) Каж­дая из бис­сек­трис рав­но­бед­рен­но­го тре­уголь­ни­ка яв­ля­ет­ся его ме­ди­а­ной.

2) Диа­го­на­ли пря­мо­уголь­ни­ка равны.

3) У любой тра­пе­ции бо­ко­вые сто­ро­ны равны.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

18. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой со­от­вет­ствен­ные углы равны 65°, то эти две пря­мые па­рал­лель­ны.

2) Любые две пря­мые имеют не менее одной общей точки.

3) Через любую точку про­хо­дит более одной пря­мой.

4) Любые три пря­мые имеют не менее одной общей точки.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

19. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Если три сто­ро­ны од­но­го тре­уголь­ни­ка про­пор­ци­о­наль­ны трём сто­ро­нам дру­го­го тре­уголь­ни­ка, то тре­уголь­ни­ки по­доб­ны.

2) Сумма смеж­ных углов равна 180°.

3) Любая вы­со­та рав­но­бед­рен­но­го тре­уголь­ни­ка яв­ля­ет­ся его бис­сек­три­сой.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

20. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Любые три пря­мые имеют не более одной общей точки.

2) Если угол равен 120°, то смеж­ный с ним равен 120°.

3) Если рас­сто­я­ние от точки до пря­мой боль­ше 3, то и длина любой на­клон­ной, про­ведённой из дан­ной точки к пря­мой, боль­ше 3.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

obrazbase.ru