Плавающей операции точкой с – Всё, точка, приплыли! Учимся работать с числами с плавающей точкой и разрабатываем альтернативу с фиксированной точностью десятичной дроби / Блог компании Журнал Хакер / Хабрахабр

Блок операций с плавающей точкой

Компания Weitek также выпускала математические сопроцессоры для платформ 68000 и

Устройство FPU

Модуль операций с плавающей запятой представляет собой стековый калькулятор, работающий по принципу обратной польской записи. Перед операцией аргументы помещаются в LIFO-стек, при выполнении операции необходимое количество аргументов снимается со стека. Результат операции помещается в стек, где может быть использован в дальнейших вычислениях или может быть снят со стека для записи в память. Также поддерживается и прямая адресация аргументов в стеке относительно вершины.

Внутри FPU числа хранятся в 80-битном формате с плавающей запятой, для записи же или чтения из памяти могут использоваться:

• один из трёх форматов с плавающей точкой (32, 64 и 80 бит),
• целочисленные форматы (16, 32 и 64 бита),
• 80-битный BCD-формат.

Поддерживаемые математические операции: арифметические операции, сравнение, деление по модулю, округление, смена знака, модуль, квадратный корень, синус, косинус, частичный тангенс, частичный арктангенс, загрузка константы (0, 1, число пи, log

2(10), log₂(e), lg(2), ln(2)) и некоторые другие специфические операции.

FPU умеет обрабатывать пограничные состояния с помощью специальных значений, представимых форматом с плавающей запятой:

• денормализованное число (число, близкое к переполнению; при дальнейшем возрастании модуля денормализованное число становится бесконечностью),
• бесконечность (положительная и отрицательная), возникает при делении на нуль ненулевого значения а также при переполнениях,
• англ. not-a-number (NaN)). Нечисла могут определять такие случаи, как:
  • неопределённость (IND), возникает при комплексном результате (например, при вычислении квадратного корня из отрицательного числа) и в некоторых других случаях,
  • недействительное значение (qNaN, sNaN) — может использоваться компилятором (для предотвращения использования неинициализированных переменных) или отладчиком,
• нуль — в формате с плавающей запятой, нуль также считается специальным значением.

В зависимости от флагов FPU, специальные значения могут инициировать обработку исключения операционной системой.

См. также

dic.academic.ru

Блок операций с плавающей точкой Википедия

Математический сопроцессор — сопроцессор для расширения командного множества центрального процессора и обеспечивающий его функциональностью модуля операций с плавающей запятой, для процессоров, не имеющих интегрированного модуля.

Модуль операций с плавающей запятой (или с плавающей точкой; англ. floating point unit (FPU)) — часть процессора для выполнения широкого спектра математических операций над вещественными числами.

Простым «целочисленным» процессорам для работы с вещественными числами и математическими операциями требуются соответствующие процедуры поддержки и время для их выполнения. Модуль операций с плавающей запятой поддерживает работу с ними на уровне примитивов — загрузка, выгрузка вещественного числа (в/из специализированных регистров) или математическая операция над ними выполняется одной командой, за счёт этого достигается значительное ускорение таких операций.

Сопроцессоры

Основная статья: X87

x87 — это специальный набор инструкций для работы с математическими вычислениями, являющийся подмножеством архитектуры процессоров x86. Такое название он получил, потому что первоначальные отдельные математические сопроцессорные чипы имели названия, заканчивающиеся на 87. Как и другие расширения базового набора инструкций процессора, эти инструкции не являются строго необходимыми для построения рабочей программы, но будучи аппаратно реализованными, общие математические задачи они позволяют выполнять гораздо быстрее. Например, в наборе инструкций

x87 присутствуют команды для расчёта значений синуса или косинуса.

Сопроцессоры Intel семейства x86

Для процессоров семейства x86 с 8086/8088 по 386 модуль операций с плавающей запятой был выделен в отдельную микросхему, называемую математическим сопроцессором. Для установки сопроцессора на плате компьютера предусматривался отдельный разъём.

Сопроцессор не является полноценным процессором, так как не умеет делать многих необходимых для этого операций (например, не умеет работать с программой и вычислять адреса памяти), являясь всего лишь придатком центрального процессора.

Одна из схем взаимодействия центрального процессора и сопроцессора, применяемая, в частности, в x86-сопроцессорах, реализуется следующим образом:

• Сопроцессор подключен к шинам центрального процессора, а также имеет несколько специальных сигналов для синхронизации процессоров между собой.
• Часть командных кодов центрального процессора зарезервирована для сопроцессора, он следит за потоком команд, игнорируя другие команды. Центральный процессор, наоборот, игнорирует команды сопроцессора, занимаясь только вычислением адреса в памяти, если команда предполагает к ней обращение. Центральный процессор делает цикл фиктивного считывания, позволяя сопроцессору считать адрес с адресной шины. Если сопроцессору необходимо дополнительное обращение к памяти (для чтения или записи результатов), он выполняет его через захват шины.
• После получения команды и необходимых данных сопроцессор начинает её выполнение. Пока сопроцессор выполняет команду, центральный процессор выполняет программу дальше, параллельно с вычислениями сопроцессора. Если следующая команда также является командой сопроцессора, процессор останавливается и ожидает завершения выполнения сопроцессором предыдущей команды.
• Также существует специальная команда ожидания (FWAIT), принудительно останавливающая процессор до завершения вычислений (если для продолжения программы необходимы их результаты). В настоящее время команда используется лишь для обработки исключений при работе с плавающей точкой, работа процессора и сопроцессора синхронизируется прозрачно для программиста
  [1].

Начиная с процессора Intel486DX модуль операций с плавающей запятой был интегрирован в центральный процессор и назван FPU. В линейке Intel486SX модуль FPU отключался (поначалу в эту линейку попадали процессоры с бракованным FPU). Для процессоров Intel486SX также выпускался «сопроцессор» Intel487SX, но фактически он являлся процессором Intel486DX, и при его установке процессор Intel486SX отключался.

Несмотря на интеграцию, FPU в процессорах i486 представляет собой неизменный сопроцессор, выполненный на том же кристалле, более того, схема FPU i486 полностью идентична сопроцессору предыдущего поколения 387DX вплоть до тактовой частоты (в два раза меньшей, чем частота центрального процессора). Настоящая интеграция FPU c центральным процессором началась только в процессорах Pentium модели MMX.

Сопроцессоры x86 от сторонних производителей

Широкое распространение в соответствующий период получили сопроцессоры для платформы x86, выпускавшиеся компанией Weitek — ею были выпущены 1167, 2167 в виде набора микросхем и микросхемы 3167, 4167, для процессоров 8086, 80286, 80386, 80486, соответственно. По сравнению с сопроцессорами от Intel они обеспечивали в 2—3 раза большую производительность, но обладали несовместимым программным интерфейсом, реализованным через технологию memory-mapping. Она сводилась к тому, что основной процессор должен был записывать информацию в те или иные области памяти, контролируемые Weitek-овским сопроцессором (собственной оперативной памяти там не было). Конкретный адрес, куда производилась запись, интерпретировался в качестве той или иной команды. Несмотря на несовместимость, сопроцессоры от Weitek были широко поддержаны как разработчиками ПО, так и производителями материнских плат, предусматривавших на них гнёзда для установки такой микросхемы.

Ряд других компаний также выпускал различные несовместимые математические сопроцессоры, реализуя интерфейс к ним через порты ввода-вывода или прерывания BIOS, но они не получили такого широкого распространения.

Компании-производители клонов выпускали совместимые с 80287 80387 сопроцессоры, работавшие быстрее аналогичных интеловских. Среди этих компаний можно упомянуть Cyrix, AMD, Chips & Technologies (C&T). Иногда система команд этих сопроцессоров расширялась несколькими несовместимыми, например, аналог 80287 от C&T содержал команды для работы с вектором из четырёх значений с плавающей точкой. Серьёзной поддержки от производителей ПО эти расширенные команды не получили.

Процессоры EMC87 от фирмы Cyrix могли работать как в режиме программной совместимости с Intel 80387, так и в собственном несовместимом режиме программирования. Для них обеспечивалась аппаратная совместимость с разъёмом 80387-го сопроцессора.

В СССР выпускалась микросхема (КМ)1810ВМ87, которая являлась аналогом 8087.

Другие платформы

Аналогично, материнские платы ПК, построенных на процессорах Motorola, до разработки этой фирмой процессора MC68040 (в который сопроцессор был встроен) содержали математический сопроцессор. Как правило, в качестве FPU использовался сопроцессор 68881 16 МГц или 68882 25 МГц. Практически любой современный процессор имеет встроенный сопроцессор.

Компания Weitek также выпускала математические сопроцессоры для платформ 68000 и MIPS.

Устройство FPU

Все процессоры Intel и AMD, начиная с 486DX, имеют встроенный математический сопроцессор, и в отдельном сопроцессоре не нуждаются (за исключением Intel486SX). Тем не менее, термин x87 всё ещё используется для выделения той части инструкций процессора, которая занимается вычислениями с использованием плавающей запятой; компиляторы могут использовать эти инструкции для производства кода, который работает быстрее, нежели тот, что использует вызовы к библиотекам для выполнения операций с плавающей запятой.

Инструкции x87 совместимы со стандартом IEEE-754. Однако x87 выполняют операции не в строгом соответствии с форматами IEEE-754, из-за использования более широких регистров. Поэтому последовательность арифметических операций может выполняться несколько по-разному на наборе x87 и на процессоре, строго следующем формату IEEE-754.

x87 организует свои регистры не как массив, как большинство других архитектур, а как регистровый стек, работающий по принципу обратной польской записи. Это означает, что в один момент времени только два верхних регистра доступны для проведения операций, а доступ к другим регистрам требует манипуляций со стеком. Хотя такая организация получается и удобной для программистов, она делает трудоёмким построение эффективного кода x87 для компиляторов.

Начиная с Pentium III, вычисления с помощью инструкций SSE осуществляются с одинарной точностью, а в более поздних версиях — с двойной точностью форматов IEEE-754. После появления SSE2 использование

x87 в значительной степени умалчивается в 64-разрядных архитектурах x86-64 и связанных с ней 64-битных реализациях операционных систем, таких, как Microsoft Windows, Mac OS X, Solaris, FreeBSD и Linux, хотя он по-прежнему хорошо поддерживается для полной совместимости со старыми приложениями.

Модуль операций с плавающей запятой^[2][3] представляет собой стековый калькулятор, работающий по принципу обратной польской записи. Перед операцией аргументы помещаются в LIFO-стек, при выполнении операции необходимое количество аргументов снимается со стека. Результат операции помещается в стек, где может быть использован в дальнейших вычислениях или может быть снят со стека для записи в память. Также поддерживается и прямая адресация аргументов в стеке относительно вершины.

Форматы данных

Внутри FPU числа хранятся в 80-битном формате с плавающей запятой, для записи же или чтения из памяти могут использоваться:

• Вещественные числа в трёх форматах: коротком (32 бита), длинном (64 бита) и расширенном (80 бит).
• Двоичные целые числа в трёх форматах: 16, 32 и 64 бита.
• Упакованные целые десятичные числа (BCD) числа — длина максимального числа составляет 18 упакованных десятичных цифр (72 бита).

FPU также поддерживает специальные численные значения:

• Денормализованные вещественные числа — числа, которые меньше минимального нормализованного числа. При формировании такого значения в некотором регистре стека в соответствующем этому регистру теге регистра TWR формируется специальное значение (10).
• Бесконечность (положительная и отрицательная), возникает при делении на нуль ненулевого значения, а также при переполнениях. При формировании такого значения в некотором регистре стека в соответствующем этому регистру теге регистра TWR формируется специальное значение (10).
• нечисло (англ. not-a-number (NaN)). Различают два вида нечисел:
  • SNaN (Signaling Non a Number) — сигнальные нечисла. Сопроцессор реагирует на появление этого числа в регистре стека возбуждением исключения недействительной операции. Сопроцессор не формирует сигнальных чисел. Программисты формируют такие числа преднамеренно, чтобы возбудить в нужной ситуации исключение.
  • QNaN (Quiet Non a Number) — спокойные (тихие) нечисла. Сопроцессор может формировать спокойные нечисла в качестве реакции на определённые исключения, например, число вещественной неопределённости.
• Нуль (положительный и отрицательный), который с точки зрения формата с плавающей запятой также считается специальным значением.
• Неопределённости и неподдерживаемые форматы. Существует много битовых наборов, которые можно представить в расширенном формате вещественного числа. Для большинства их значений формируется исключение недействительной операции.

Регистры

В FPU можно выделить три группы регистров:

• Стек процессора: регистры R0..R7. Размерность каждого регистра: 80 бит.
• Служебные регистры
  • Регистр состояния процессора SWR (Status Word Register) — информация о текущем состоянии сопроцессора. Размерность: 16 бит.
  • Управляющий регистр сопроцессора CWR (Control Word Register) — управление режимами работы сопроцессора. Размерность: 16 бит.
  • Регистр слова тегов TWR (Tags Word Register) — контроль над регистрами R0..R7 (например, для определения возможности записи). Размерность: 16 бит.
• Регистры указателей
  • Указатель данных DPR (Data Point Register). Размерность: 48 бит.
  • Указатель команд IPR (Instruction Point Register). Размерность: 48 бит.

Система команд сопроцессора

Система включает около 80 команд. Их классификация:

• Команды передачи данных
  • Вещественные данные
  • Целочисленные данные
  • Десятичные данные
  • Загрузка констант (0, 1, число Пи, log₂(10), log₂(e), lg(2), ln(2))
  • Обмен
  • Условная пересылка (Pentium II/III)
• Команды сравнения данных
  • Вещественные данные
  • Целочисленные данные
  • Анализ
  • С нулём
  • Условное сравнение (Pentium II/III)
• Арифметические команды
  • Вещественные данные: сложение, вычитание, умножение, деление
  • Целочисленные данные: сложение, вычитание, умножение, деление
  • Вспомогательные арифметические команды (квадратный корень, модуль, изменение знака, выделение порядка и мантиссы)
• Трансцендентные команды
  • Тригонометрия: синус, косинус, тангенс, арктангенс
  • Вычисление логарифмов и степеней
• Команды управления
  • Инициализация сопроцессора
  • Работа со средой
  • Работа со стеком
  • Переключение режимов

См. также

Примечания

1. ↑ Intel 64 and IA-32 Architectures Software Developer’s Manual. Volume 2A and 2B: Instruction Set Reference. Order numbers #253666, #253667
2. ↑ Intel 64 and IA-32 Architectures Software Developer’s Manual. Volume 1: Basic Architecture. Order number #253665
3. ↑ AMD64 Architecture Programmer’s Manual. Volume 1: Application Programming. Publication number #24592

wikiredia.ru

Глава 5. Операции над числами с плавающей точкой.

I. Для представления чисел с фиксированной точкой положение точки фиксируется в определенном месте относительно разрядов модуля числа в разрядной сетке (ячейке).

а) Точка фиксируется перед старшим цифровым разрядом числа

.

В этом случае могут быть представлены числа, по модулю меньше единицы. При занесении числа в ячейку, свободные младшие разряды заполняются нулями. А если число значащих разрядов модуля больше числа (n-1), то младшие разряды теряются, что приводит к погрешности меньшей единицы младшего разряда.

б) Точка фиксируется перед младшим цифровым разрядом

По сложившейся традиции нумерация разрядов сетки в больших машинах ведется слева направо, а в малых – справа налево.

В этом случае модулем числа является только целое число. При занесении числа в ячейку, число разрядов которого превышает число (n-2), теряются старшие разряды, которые могут дать погрешность до 100 %.

II. Числа с плавающей точкой.

В этом случае формат представления числа иной.

Вобщем случае представление числа с плавающей точкой имеет вид:, гдеq  1, S^P — характеристика числа, p – порядок числа, S – основание характеристики.

Формат разрядной сетки:

Числа с плавающей точкой могут быть представлены и в других форматах: с основанием 8 и 16.

Число называютнормализованным, если мантисса q удовлетворяет следующему соотношению: 1/S.

В процессе вычисления может получиться ненормализованное число (в старших разрядах появляются нули). Тогда машина автоматически нормализует число.

Например: получен результат, в котором r старших разрядов – нулевые.

Нормализация заключается в сдвиге мантиссы q на r разрядов влево и одновременном уменьшении порядка на r единиц. При этом в младшие r разрядов мантиссы записываются нули. После этой операции число не меняется, а условие нормализации выполняется.

Поскольку арифметическое действие над числами с плавающей точкой требуют отдельных операций над мантиссами и порядками чисел, то операции над порядками сводят к операциям над целыми положительными числами, применяя представление чисел со смещенным порядком. Для этого при записи числа в ячейку памяти к порядку p прибавляется целое число смещения N=2^k, где k – число двоичных разрядов, используемых для расположения порядка в разрядной сетке. Тогда смещенный порядок будет равен: p_см=p+N. Этот смещенный порядок всегда будет положительным, и будет при этом занимать то же число разрядов.

Свойство смещенного порядка: если p‘ > p», то p‘_см  p»_см

Это говорит о том, что смещение порядка не влияет на операции над числами.

§ 5.1 Сложение и вычитание чисел с плавающей точкой.

Сложение и вычитание чисел плавающей точкой производится по формуле:

, пусть x > y

Алгоритм сложения / вычитания:

1) Производится выравнивание порядков чисел:

порядок меньшего по модулю числа принимается равным порядку большего числа, а мантисса меньшего сдвигается влево на S-ичных разрядов, равных разности порядков.

2) Производится сложение / вычитание мантисс, и получается сумма / разность мантисс.

3) Порядок суммы / разности принимается равным порядку большего числа.

4) Полученный результат нормализуется.

Арифметическое действие над порядками и мантиссами выполняется либо отдельными устройствами, либо последовательно одним устройством.

Операция сложения / вычитания состоит из следующих этапов:

1) прием операндов

2) выравнивание порядков со сдвигом мантисс

3) сложение / вычитание мантисс

4) нормализация результата

1) Прием операндов:

Прием слагаемого / вычитаемого х в регистр RG3. Фиксация знака числа (из ₀) в триггере знака Тзн1. Установка регистра RG3 в ноль.

Прием второго слагаемого / вычитаемого y в RG1. Фиксация знака в триггере знака Тзн2. Установка регистра RGA в .

2) Операции над порядками:

Значение порядков из разрядов ₁  ₇ регистров RG1 и RG3 подаются в регистры RGC и RGD.

Далее в блоке обработки порядков происходит их сравнение, по результатам которого мантисса с меньшим порядком сдвигается вправо на число разрядов, равное разности порядков. За порядок результата операции принимается больший из порядков.

При сравнении порядков возможны пять случаев их соотношения:

• P_x – P_y  m, где m – число разрядов мантиссы, за результат в этом случае принимается слагаемое х, так как при сдвиге мантиссы слагаемого y все ее разряды примут нулевое значение.

• P_y – P_x  m, за результат принимается мантисса y.

• P_x – P_y = 0, производится суммирование / вычитание мантиссы.

• P_x – P_y = K1 (K1  m), мантисса y сдвигается на K1 разрядов.

• P_y – P_x = K2 (K2  m), мантисса x сдвигается на K2 разрядов.

Процесс сдвига мантиссы заключается в следующем: в счетчик циклов из блока обработки порядков заносится число разрядов K1 или K2, на которые ее надо сдвинуть. По мере сдвига мантиссы содержимое счетчика циклов уменьшается, и когда счетчик циклов становится равным нулю, сдвиг прекращается.

Полученные модули мантисс хранятся в регистрах RG1 и RG3 в разрядах ₈₃₁, их знаки – в триггерах знака Тзн1 и Тзн2, а принятый порядок хранится в регистре счетчика RGСч1.

3) Сложение / вычитание мантисс:

а) при одинаковых знаках чисел модули мантисс передаются в RGA и RGB и складываются в сумматоре.

Если в сумматоре в разряде ₇ окажется единица, то возникло переполнение разрядной сетки, поэтому сумма сдвигается на разряд вправо, а порядок увеличивается на единицу, т.е. RG1 := RGСч1 + 1.

Если окажется, что в сумматоре в разряде ₀ находится единица, то произошло переполнение порядка, поэтому вырабатывается сигнал прерывания вычислительного процесса.

Если переполнения порядка нет, то в регистр сумматора в разряды ₁  ₇ заносится порядок из регистра счетчика RGСч1, в разряд ₀ в регистр сумматора заносится знак мантиссы, а в разряды сумматора ₈  ₃₁ заносится мантисса суммы.

Таким образом, в регистре сумматора полностью сформирован результат.

б) при разных знаках мантисс отрицательный из них передается на входной регистр RGA или RGB, в обратном коде производится суммирование с дальнейшим подсуммированием единицы.

Знак результата фиксируется в триггере знака. Если полученный результат нормализован, т.е. в разряде сумматора ₈ находится единица, то в регистр сумматора заносится: знак результата – в ₀, порядок – в ₁  ₇, модуль мантиссы – в разряды ₈  ₃₁.

Если результат не нормализован, т.е. в ₈ находится ноль, и нет исчезновения мантиссы ([₈  ₃₁]  0), производится нормализация сдвигом мантиссы влево с одновременным уменьшением порядка.

При отрицательном переполнении порядка, т.е. если RGСч1[0]=1, формируется признак исчезновения порядка, т.е. результат равен нулю.

Если нормализация происходит без исчезновения порядка, то формируется результат из кодов знака, порядка и мантиссы.

Примечание: в операциях с плавающей точкой сложение и вычитание выполняется приближенно, т.к. при выравнивании порядка может происходить потеря младших разрядов одного из слагаемых.

Погрешность в этом случае всегда отрицательна и может доходить до единицы младшего разряда. Поэтому применяется округление результата, для чего используется дополнительный разряд сумматора, в который после суммирования добавляется единица.

studfiles.net

ОПЕРАЦИИ НАД ЧИСЛАМИ С ПЛАВАЮЩЕЙ ТОЧКОЙ МК AVR

Для выполнения арифметических операций над числами с плавающей точкой в микроконтроллерах необходимо разрабатывать довольно сложные подпрограммы. Исходные числа в формате с плавающей точкой представлены знаком, мантиссой и порядком. Мантисса является правильной дробью, разряды которой представляют значащие разряды числа, порядок показывает фактическое положение точки в записи мантиссы.

Для представления чисел с плавающей точкой разработан и введен стандарт IEEE-754, включающий базовый одинарный, базовый двойной, расширенный одинарный и расширенный двойной форматы, отличающиеся количеством разрядов и способами представления мантиссы и порядка. На рис. 3.8 приведена структура полей базового 32-разрядного одинарного формата. Формат содержит знаковый разряд S, 8-разрядное поле для смещенного порядка В и 23-разрядное поле для мантиссы F.

Рис. 3.8. Базовый одинарный формат

В этом формате при изображении порядка используется смещение, равное 127, скрытый бит целой части мантиссы Fq, содержащий 1. Минимальный (Е = 0) и максимальный (В = 255) порядки

зарезервированы для представления специальных чисел. Диапазон

± 38

представления чисел в этом формате составляет ±10 , а точность 6-7 десятичных разрядов. Приведем несколько примеров кодирования чисел в этом формате:

В рассмотренных далее алгоритмах для 8-разрядных микроконтроллеров принимается представление истинного нуля нулевым набором (знак, порядок, мантисса). Специальные числовые значения из стандарта (на изображения бесконечности, неопределенности) учитывать не будем.

Во всех приводимых программах арифметических операций для микроконтроллеров AVR принято размещение исходных операндов и результатов во второй половине регистров общего назначения (R16…R31). Первый операнд, символически обозначаемый А, размещается в четырех регистрах А: рА (порядок), шАН, тАМ, rtiAL (старший, средний и младший байты мантиссы). Второй операнд, символически обозначаемый В, размещается в регистрах В: рВ (порядок), тВН, шВМ, mBL (мантисса). Результат помещается перед выходом из процедуры в регистры рА, шАН, тАМ, mAL.

Сложение

Процедура сложения чисел с плавающей точкой одного знака включает следующие действия:

•    определяется разность порядков слагаемых Ар = (рА – рВ). При неравенстве порядков, если разность порядков больше О, сдвигается мантисса числа В вправо до тех пор, пока порядок меньшего числа В не станет равным большему; если разность порядков меньше О, сдвигается мантисса числа А вправо;

•    после выравнивания порядков слагаемых при Ар = О производится сложение мантисс. В качестве порядка суммы принимается рА или рВ;

•     проверяется мантисса суммы на возможность нарушения нормализации. При сложении чисел с одинаковыми знаками возможно нарушение нормализации только влево на один разряд. Чтобы получить нормализованную мантиссу, необходимо сдвинуть ее вправо. Порядок увеличивается на единицу, что может привести к переполнению.

На рис. 3.9 приведена схема алгоритма сложения чисел А и В с плавающей точкой и одинаковыми знаками. Каждое слагаемое представлено однобайтовым порядком и трехбайтовой мантиссой в стандартном формате: знак числа, 8-разрядный смещенный порядок, 23-разрядная мантисса со скрытой единицей (всего 32 разряда). Число А перед началом операции размещено в регистрах рА, тАН, шАМ, mAL, число В – в регистрах рВ, рВИ, рВМ, pBL. Результат операции сохраняется на месте первого операнда А.

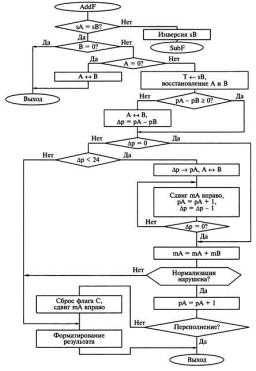
Рис. 3.9. Схема алгоритма сложения с плавающей точкой

Процедура сложения с плавающей точкой AddF начинается с проверки знаков слагаемых. Если знаки операндов не совпадают, знак второго операнда изменяется на противоположный и выполняется переход к процедуре вычитания чисел SubF. Если исходные операнды имеют один знак, каждый из них проходит проверку на равенство 0. Если один из операндов равен О, сложение не проводится, а результат принимается равным другому операнду. При этом в случае равенства О первого операнда регистры А и В обмениваются операндами. На этом операция заканчивается. Преобразование результата в стандартный формат не проводится.

Если оба операнда ненулевые, в однобитовом флаге Т регистра состояния микроконтроллера SREG сохраняется общий знак операндов и выполняется их восстановление из базового формата. Поскольку для этого используется одна и та же процедура гес из библиотеки вспомогательных процедур, настроенная на работу с регистрами А, перед вторым восстановлением проводится обмен операндами.

Далее вычитают порядки. При получении отрицательной разности выполняется обмен операндами и вычитание повторяется. При равенстве порядков, когда их разность Ар = О, выполняется переход к сложению мантисс. В противном случае предварительно разность Ар сравнивается с длиной мантиссы. Если разность превысит 24, то при выравнивании порядков со сдвигом вправо мантиссы меньшего числа она покинет разрядную сетку, происходит потеря значимости. В качестве результата принимается операнд, который в этот момент находится в регистрах первого операнда (рА, шА). Если разность меньше 24, переходим к сдвигу мантиссы меньшего числа, поместив ее в регистры (тАН, шАМ, mAL), разность порядков – в регистре рВ, меньший порядок – в регистре рА. Сдвиг мантиссы вправо сопровождается увеличением порядка в регистре рА, уменьшением в регистре рВ и продолжается до тех пор, пока в регистре рВ не получим 0.

Сложив побайтно мантиссы, проверяем признак переноса, который свидетельствует о нарушении нормализации. При отсутствии его (С = 0) выполняется переход к преобразованию числа в базовый формат. При С = 1 мантиссу суммы сдвигаем вправо и порядок увеличиваем на 1. Выполняем проверку переполнения. Если образовался порядок, равный О, это означает превышение максимального порядка 255. Программа завершается с установленным флагом переполнения С. Полученный в регистрах рА, шА результат считается неопределенным и не форматируется. При отсутствии переполнения флаг С сбрасывается и выполняется преобразование в базовый формат.

Алгоритм сложения чисел с одинаковым знаком представлен листингом программы 3.3. Программа позволяет выполнить алгебраическое сложение чисел с учетом знаков слагаемых. В том случае, когда слагаемые имеют разные знаки, происходит обращение к модулю вычитания. С помощью директивы .include «flsub.asm» подключают программный модуль вычитания чисел с плавающей точкой одинаковых знаков. Это позволяет в дальнейшем выполнить посредством одной и той же программы не только сложение, но и вычитание чисел.

В начале общей программы сложения;вычитания выполняют проверку кода выполняемой операции: 1 – для сложения (+), 2 – для вычитания (-). В зависимости от заданной операции и знаков операндов запускают процедуру сложения или вычитания беззнаковых чисел (табл. 3.4). При необходимости производится перемена мест операндов. В итоге можно применить одну из двух процедур: сложение или вычитание модулей чисел.

Таблица 3.4. Выполняемые операции

Программа 3.3

;Программа 3.3 сложения;вычитания чисел с плавающей точ- ; кой.

;Первый операнд находится в регистрах рА, гпАН, шАМ, mAL, ;второй – в регистрах рВ,тВН, тВМ, mBL. Результат ;возвращается в регистры первого операнда. При переполне- ;нии флаг С устанавливается в 1. Вызываемые процедуры

;расположены в файлах flsub.asm (модуль вычитания) и ;fllib.asm (библиотечные модули)

.include «8515def.inc» ;файл определений для AT90S8515 ;.include «m8515def.inc» ;файл определений для ATmega8515 .def temp = г1б                          ;временный регистр

.def асс = г17            ;регистр аккумулятор

.def сор = г18            ;код операции:

; 1 – сложение, 2 – вычитание .def рА = г20 ;операнд А (рА – байт порядка),

.def mAH = г21            ;(mAH, mAM, mAL – байты мантиссы)

.def mAM = г22 .def mAL = г23

.def pB = r24             ;операнд В (рВ – байт порядка),

.def тВН = г25            ;(тВН, тВМ, mBL – байты мантиссы)

.def тВМ = г2б .def mBL = г27

.org $000

Idi temp, low(RAMEND) ;инициализация указателя стека

out spl, temp

Idi temp, high(RAMEND)

out sph, temp

cpi cop,0x01              ;проверка кода операции

breq AddF rjmp SubF

;модуль сложения чисел с плавающей точкой ; с одинаковым знаком AddF: mov асс,рА eor асс,рВ brpl AddFl

Idi temp,0x80             ;изменение знака

add pB,temp rjmp SubF

AddFl: rcall cp_B_0       ;сравнение В с 0

breq Quit

rcall cp_A_0              ;сравнение A с 0

brne AddF2

rcall swapAB              ;обмен A и В

rjmp Quit

AddF2: bst pB, 7          ;сохранение знака Т=рВ.7

rcall rec                 ;восстановление

rcall swapAB              ; чисел через регистры A

rcall rec

mov acc,pA                ;вычитание порядков

sub асс,рВ

brpl AddF3         ;переход, если больше О,

rcall swapAB       ; иначе обмен и

mov асс,рА            ; снова вычитание sub асс,рВ

AddF3: breq AddF6     ;переход, если порядки равны

cpi асс,24            ;сравниваем brmi AddF4

rjmp AddF7         ;переход при потере значимости

AddF4: mov рА,асс     ;разность порядков в рА

rcall swapAB       ;разность теперь в рВ

AddFS: rcall shift    ;сдвиг в регистрах тА

inc рА             ;увеличиваем порядок меньшего числа

dec рВ                ;уменьшаем разность порядков brne AddFS

AddF6: add mAL,mBL        ;сложение мантисс adc mAM,mBM adc mAH,mBH

brcc AddFV         ;проверка нарушения нормализации

inc pA             ;корректируем порядок

breq Quit          ;выход с флагом переполнения

rcall shift        ;сдвиг мантиссы вправо

AddF7: rcall pack     ;форматирование результата Quit: rjmp Quit

.include «flsub.asm» ;подключение модуля вычитания .include «fllib.asm» ; и библиотечных процедур

Типовые процедуры, используемые алгоритмами сложения;вычитания, помещены в библиотеку, подключаемую директивой .include «fllib.asm». Библиотека fllib содержит процедуры восстановления операнда из базового формата гес, упаковки в базовый формат раек, обмен операндов swapAB, сдвига мантиссы вправо на один разряд shift, логического сложения 24-разрядной мантиссы для сравнения с нулем.

Восстановление числа из базового формата производится с помощью четырех операций, как показано на рис. 3.10, а. Вначале при помощи логического сдвига влево ф младший бит порядка из регистра старшего байта мантиссы шАН выталкивается на флаг переноса С. Затем выполняется циклический сдвиг влево содержимого регистра порядка рА Благодаря этому 8-разрядный порядок полностью оказывается в регистре рА. Далее мантисса шАН сдвигается вправо @ и в разряд 7 регистра шАН восстанавливается скрытая 1

Рис. зло. Схема восстановления числа из базового формата {а) и преобразования в базовый формат {б)

Преобразование результата операции, помещаемого после обработки в регистры А, в базовый формат выполняется по схеме на рис. 3.10, б. Вначале сохраняем порядок рА в одном из регистров, например рВ ф. Затем знак результата, сохраняемый на флаге Т, переносим на флаг С Выполняя сдвиг вправо регистра порядка рА, вводим знак числа в разряд 7 регистра рА Передачу младшего бита порядка в старший разряд мантиссы шАН выполняем за два шага: сначала из разряда О регистра рВ в Т затем из Т в разряд 7 регистра шАН ® на место старшего разряда мантиссы.

Обмен 32-разрядных операндов в регистрах А и В осуществляется с использованием логической функции Исключающее ИЛИ. Действительно, получив сначала А <— А Ф В, выполняем далее В<-ВФАиА<-АФВ. Эти операции повторяют отдельно для каждого байта порядка и мантиссы (всего 12 операций). Используемые библиотечные процедуры с комментариями представлены в листинге программы 3.4.

Программа 3.4

;Модуль 3.4 библиотечных процедур fllib.asm

;Восстановление операнда из базового формата гес: Isl mAH   ;младший разряд порядка в С

го1 рА             ;восстановление порядка

Isr mAH            ;сдвиг вправо мантиссы

ori mAH, 0x80       ;восстановление скрытой 1

ret

;Упаковка в базовый формат раек: mov pb,pa     ;сохраняем рА

с1с

brtc m2            ;проверяем знак

sec

m2: ror рА                 ;вводим знак в рА.7

bst pb,0           ;младший разряд порядка

bid mAH,7          ; переносим в АН.7

ret

;Обмен операндов swapAB:

еог рА,рВ           ;обмен регистров

еог рВ,рА           ; рА и рВ

еог рА,рВ           ; за три операции

еог mAL,mBL еог mBL,mAL еог mAL,mBL еог тАМ,тВМ еог тВМ,тАМ еог тАМ,тВМ

еог тАН,тВН еог тВН,тАН еог тАН,тВН

ret

;Сложение для сравнения А(В) с О ср_А_0: mov асс,рА or acc,mAH or acc,mAM

or acc,mAL       ;при A=0 возвращает флаг Z=1

ret             ;при A^O – Z=0

cp_B_0: mov acc,pB or acc,mBH or acc,mBM

or acc,mBL       ;при B=0 возвращает флаг Z=1

ret             ;при     – Z=0

;Сдвиг вправо 24-разрядной мантиссы mA shift: Isr mAH ror mAM ror mAL clc ret

Вычитание

Операция начинается с проверьси знаков слагаемых (рис. 3.11). Если знаьси операндов не совпадают, знак вычитаемого изменяется на противоположный и выполняется переход к процедуре сложения чисел AddF. Если исходные операнды с одним знаком, каждый

Рис. 3.11. Схема алгоритма вычитания с плавающей точкой

проходит проверку на равенство 0. Если один из операндов равен О, вычитание не проводится, а результат принимается равным другому операнду, при необходимости корректируется знак результата.

Если оба операнда не равны О, в Т сохраняется знак уменьшаемого и восстанавливают оба числа. При этом восстановлению числа В предшествует регистровый обмен А<->В. Затем выполняют сравнение порядков. Если порядки равны, сравнивают мантиссы, при их равенстве результат операции считается равным 0. Выявляется большее число без учета знака, которое помещается в регистры В. Если при этом выполняется обмен регистров, то хранимый в Т знак меняется на противоположный.

Дальнейшие действия связаны с выравниванием порядков и сдвигом вправо мантиссы меньшего числа, которое находится в регистрах А. После выравнивания порядков выполняется вычитание мантисс и формирование результата в регистрах А. При вычитании мантисс с одинаковым знаком может возникнуть нарушение нормализации вправо, т. е. появление одного или нескольких нулей в старших разрядах мантиссы разности. Устранение нарушения нормализации выполняется путем сдвига мантиссы разности влево и уменьшения порядка результата рА на единицу при каждом сдвиге. Если при уменьшении порядка возникнет антипереполнение (при изменении порядка от минимально допустимого значения 0x00 к максимальному значению OxFF), выполняется выход из процедуры с установленным флагом С = 1 и возврат в головной модуль программы с неопределенным результатом. После устранения нарушения нормализации выполняется форматирование результата в регистрах А и выход из процедуры вычитания в основную программу.

Программа модуля вычитания, согласно описанному алгоритму, представлена в листинге программы 3.5. В ней, как и в предыдущем случае, использованы стандартные библиотечные процедуры для сдвига мантиссы, обмена операндов, преобразования форматов. Следует отметить, что использование команд с условным переходом, выполняемых по механизму относительной адресации, привело к необходимости выполнения длинных переходов за два шага: сначала на близко расположенную локальную метку QuitS, а затем с помощью команды безусловного перехода rjmp на метку выхода Quit.

Программа 3.5

;Программа 3.5 модуля вычитания чисел с плавающей точкой ;с одинаковым знаком выполняет вычитание из 1-го числа А,

;размещенного в регистрах (рА,тА), 2-го числа, размещенного ;в регистрах (рВ,МВ).

;Исходные операнды представлены в базовом формате. ;Результат операции возвращается в регистры 1-го числа ;(рА,тА) в базовом формате.

;Программный модуль размещается в файле flsub.asm и ;подключается к основной программе с помощью директивы ; .include «flsub.asm»

SubF: mov acc,pA          ;сравнение знаков чисел

eor асс,рВ brpl SubFl

Idi temp,0x80             ;при неравных знаках смена

add pB,temp               ;знака 2-го числа

rjmp AddF

SubFl: rcall cp_B_0       ;проверка В на 0

breq Quit

rcall cp_A_0              ;проверка A на 0

brne SubF2

rcall swapAB              ;обмен операндов

Idi temp,0x80

add pA,temp               ; со сменой знака результата

Quits: rjmp Quit

SubF2: bst pA, 7          ;сохранение знака в Т

rcall rec                 ;восстановление числа А

rcall swapAB              ;теперь в рА порядок 2-го числа

rcall rec                 ;восстановление числа В

mov асс,рВ                ;из порядка 1-го вычитаем

sub асс,рА                ; порядок 2-го

brne SubF3

ср mBH,mAH                ;при равенстве порядков

brne SubF3                ; сравниваем мантиссы

ср тВМ,тАМ

brne SubF3

ср mBL,mAL

brne SubF3

clr pA                    ;если числа равны,

clr mAH                   ; результат равен О

clr таМ clr mAL rjmp Quit

SubF3: brcc SubF4         ;переход, если 1-е число

; (оно в pB,mB) больше, rcall swapAB ; иначе обмен числами

brbc 6,s2                 ; и изменение знака в Т

rjmp s3 s2: set

rjmp SubF4 s3: clt

SubF4: mov acc,pB         ;снова вычитание порядков

sub acc,pA

breq SubF7             ;переход при одинаковых порядках

cpi асс,24 brmi SubF6

rcall swapAB           ;передача большего числа

; в (pA,mA) перед rjmp SubF9  ; форматированием результата

SubF6: rcall shift ;сдвиг мантиссы меньшего числа dec асс       ; в тА, пока

brne SubF6             ; разность порядков не равна О

;Вычитание мантисс и сохранение разности в тА

SubF7:     sub mBL,mAL

mov     mAL,mBL

sbc     mBM,mAM        ;вычитание с заемом

mov     mAM,mBM

sbc     mBH,mAH        ;вычитание с заемом

mov     mAH,mBH

mov     pA,pB          ;передача порядка результата в рА

SubF8: sbrc шАН,7         ;проверка нарушения нормализации

rjmp SubF9             ;переход, если нарушения нет,

dec рА                 ; иначе, не сдвигая мантиссу,

cpi рА,Oxff            ; проверяем антипереполнение,

sec                    ; заранее установив флаг в 1,

breq Quits            ;при антипереполнении выходим

; с флагом 1, иначе

Isl mAL                ; сдвигаем мантиссу шА влево го1 тАМ го1 шАН

с1с                    ; и сбрасываем флаг

rjmp SubFB             ;повторяем проверку

SubF9: rcall pack         ;форматируем результат

rjmp Quit              ;выход из процедуры вычитания

Следует заметить, что описанные здесь алгоритмы и программы сложения и вычитания не являются полностью оптимальными. Например, восстановленные операнды можно с учетом заданной операции и операндов представить в дополнительных кодах со знаковым разрядом; в дальнейшем проводить операции сложения мантисс в дополнительных кодах, исключив тем самым необходимость перестановки операндов (табл. 3.5).

Таблица 3.5. Операции в дополнительных кодах

В рамках практикума не предполагалось получение оптимального кода по времени исполнения и по размеру, а требовалось лишь достижение результативности алгоритмов. Тем не менее предложенные программные решения могут оказаться достаточно эффективными в целом ряде приложений.

Умножение

Алгоритм умножения чисел с плавающей точкой С = А

Практическая часть

Задание 1. Открыв AVR Studio 4, создать проект. Загрузить программу 3.3 для проверки операций сложения и вычитания чисел с плавающей точкой. Привести ряд примеров с разными значениями операндов, воспользовавшись ручной загрузкой операндов в регистры окна НО. Подобрать операнды с равными и максимально различающимися порядками. Выполнить операции, фиксируя время их исполнения.

Задание 2. Создать проект и загрузить программу 3.6 для умножения чисел с плавающей точкой. Привести ряд примеров с разными значениями операндов. Оценить время выполнения операции умножения. Заменить программу умножения программой деления 3.7 и проверить ее работу.

Задания для самостоятельного программирования

1.  Изменить модуль эмуляции арифметического устройства базовой программы, включив в него дополнительно одну из логических и(или) арифметических операций.

2.   Для микроконтроллера ATmega8515 проверить работу операций умножения по их описанию, открыв файл помощи по AVR Ассемблеру, используя команды меню: Help;A VR Tools User Guide. В окне Html Help щелчком открыть А VR Assembler, выбрать Parts и затем ATmega8515. Подробное описание каждой из команд умножения можно найти в разделе А VR Assembler;Instructions.

3.  Рассмотреть операцию умножения дробных чисел на примерах. Проверить результаты с помощью симулятора AVR Studio 4.

4.  Написать процедуру сложения (вычитания) 2-байтовых операндов для проверки с помощью STK500. Сформировать признаки результата, как признаки 2-байтовой суммы (разности).

5.   Написать макрос для двоично-десятичной коррекции при сложении, равноценный команде DA А в системе команд микроконтроллеров MCS-51.

6.  Написать процедуру сложения (вычитания) двух 4-байтовых упакованных двоично-десятичных чисел.

nauchebe.net

Арифметические операции над числами с плавающей точкой / Хабрахабр

Все читатели Хабра так или иначе связаны с ИТ направлением. Будь ты программист или работаешь с железом, сетями и так далее, все мы знаем общие концепции.

Когда-то на втором курсе университета я познакомился как раз с одной из вещей, которую, по-моему, должен знать каждый из нас, ну или хотя бы услышать о ней вот в такой статье. Это стандарт представления чисел в формате с плавающей точкой(в других источниках с плавающей запятой). Как же въелось мне это название: стандарт IEEE-754.

Уверен, что каждый из айтишников хоть раз но слышал с числами в формате плавающей точкой, но для меня впервые это показалось полной чушью. И не с проста: ведь предмет, на котором мы изучали стандарт, назывался «Архитектура ЭВМ» да и преподаватель был, да и сейчас есть живой легендой. Ну, это оффтоп.

Итак, что же такое этот стандарт IEEE-754? Скажу сразу, что нам в университете дали его в электронном виде на русском, но в интернете я не смог его найти, даже дойдя до 30-й страницы гугла. Был пример на английском, в котором автор писал его в 4:36 АМ. Я даже нашёл сайт, в котором говориться, что если бы Сатана решил захватить Землю медленно, он бы создал этот стандарт. Но его создали люди, такие же, как и мы с вами.

Сам стандарт представляет собой описание операций двоичной арифметики с числами в формате с плавающей точкой. Так же там описаны исключительные ситуации, возникающие в таких случаях, запись в такой формат и многое другое. Естественно, прочитав его, да ещё и с таким трудом, я не понял ничего! Ведь я совсем ничего не знал про формат с плавающей точкой. А ведь это грубо, говоря дробная часть любого числа, только точность надо знать.

По этому предмету в университете у нас рассчитывалась РГР (Расчётно-Графическая работа) и почему то тогда я понял, что стоит ей уделить больше времени, чем чему-либо и оказался прав. Это, наверное, был переломный момент моей учёбы. Я сидел ночами над этим стандартом и над конкретно поставленной передо мной задачей: «Деление двух чисел в формате с плавающей точкой двойной точности с заменой цепочек непрерывных единиц нулями и с округлением до ближайшего чётного». Тогда это нельзя было понять. И стандарт IEEE-754 всегда следовал рядом с этим заданием. На самом деле там было всё, абсолютно всё, что мне нужно было.

Ну, а теперь подробнее собственно, о стандарте IEEE-754. Он представляет собой несколько глав, которые я хотел бы описать поподробнее.
Всё как всегда начинается с введения. О том, что существуют программы, намного сложнее чем то, что я видел. Рассказывается об истории создания стандарта. Ведь программы становятся всё сложнее и сложнее, а ЦВМ стареет и следует заменить её новой архитектурой. Это послужило причиной тому, что IEEE (Институт инженеров по электротехнике и электронике США) в конце 70-х годов создал комиссию, рассмотревшую множество предложений. Результатом работы комиссии явился стандарт IEEE 754 ≪Двоичная арифметика с плавающей точкой≫ (1985г.), ставший международным. Его основы разработал профессор математики университета Беркли William Kahan.
В последующие годы на базе IEEE 754 – 1985 были разработаны стандарты:

— IEEE 854 – 1987, покрывающий десятичную арифметику также как и двоичную;

— IEC 60559 — 1989 IEC ≪Двоичная арифметика с плавающей точкой для
микропроцессорных систем≫ (IEC — International Electrotechnical Commission).

Стандарт IEEE 754 не обязывает, а рекомендует применение пакета оговоренных в нем форматов, способов кодирования данных, округления результатов и многое другое. Задача выбора формата для конструктора универсальной ЦВМ предельно упростилась, и с этого времени фирмы стали производить универсальные ЦВМ с арифметикой с плавающей точкой удовлетворяющей рекомендациям стандарта. Задача программистов также несколько упростилась, т.к. нет необходимости изучать особенности двоичной арифметики с плавающей точкой разных ЦВМ, достаточно овладеть знанием стандарта.
Но нужно помнить, что стандарты консервативны, но не вечны. И, тем не менее, этим стандартом пользуемся все мы с вами, коллеги.

Стандарт поддерживает несколько форматов: одинарная точность(32 разряда), двойная(64 разряда) и двойная расширенная точность. Так же предусмотрены другие форматы для предотвращения ошибок округления и т.д. В стандарте описаны случаи возникновения исключительных ситуаций: Nan, бесконечность, деление на ноль и т.д. Ничего не напоминает? Очень важную роль играет округление чисел в формате с плавающей точкой. Это тоже описано в стандарте.

И наконец-то, главный раздел – Выполнение операций над числами в формате с плавающей точкой. В этом разделе описаны все арифметические операции от сравнения до деления, а так же все нюансы при выполнении таких операций. Про этот раздел нельзя сказать вот так, «в двух словах». Скажу лишь, что это настоящая морока и передо мной встала задача понять, как это происходит.
Опишу вкратце свой алгоритм работы «Деление в формате с плавающей точкой». После того, как мы получили операнды А и В, нужно было проверить их на все возможные случаи возникновения исключительных ситуаций. Это и деление на ноль и Nan и бесконечность. Немного ниже, на таблице, изображены типы представления чисел, которые поддерживает формат:

Если операнды действительно являлись числами в формате IEEE-754, начинался второй этап выполнения операции: приведение порядков. Ни для кого не секрет, что числа в формате с плавающей точкой выглядят примерно так:

Это представление числа в формате с одинарной точностью.
Порядок числа в ЦВМ – это, в моём понимании, порядковый номер числа в ЦВМ, то есть его порядок. Наверняка есть научное определение, но оно лишь запутает ещё больше. Так вот, раз числа имеют разные порядки, их нельзя делить. Следует сначала привести порядки к одному виду смещением порядков. Но для этого требовалось проанализировать порядки на min и маx значение. А когда происходит смещение порядков, мантиссы тоже сдвигаются. Если порядки уравнены, нужно проверить мантиссы, не вылетели ли они за границы и не заполнились ли они нулями и т.д. Закончив ряд проверок, можно приступать к самому главному: наконец-то делить мантиссы. Ну, тут всё просто, как и вся двоичная арифметика. Я делил делитель на делимое, а остаток записывал в регистр и складывал. Там ещё есть несколько способов деления: с восстановление и без восстановления остатка. Да и это ещё не всё! В конце следовало округлить полученный результат по нужному условию и определить знак частного.

Это всего лишь на словах, хоть и звучит страшно, на деле выглядит куда лучше. Тогда я откровенно запал на этот стандарт, что принесло мне не только более глубокие знания в ЦВМ и двоичной арифметике, но и удовольствие что я смог это сделать, удовольствие осознавать то, что я знаю что-то очень важное.
У меня всё, на самом деле тема очень интересная и увлекательная. Кто заинтересовался, с удовольствием скину стандарт IEEE-754 и отвечу на ваши вопросы.

Спасибо.

habr.com

Операции с плавающей точкой

Правило сложения (вычитания):

пусть,– два нормализованных двоичных числа, и(в противном случае мы можем просто поменять их местами). В результате их сложения или вычитания будет получено следующее выражение:

_.

Последовательность вычислений следующая:

1. Порядки чисел A и B выравниваются по большему из них (в нашем случае это n_A). Для этого мантисса числа B сдвигается на n_A—n_B разрядов вправо (часть значащих цифр при этом могут оказаться утерянными), а его порядок становится равным n_A.

2. Выполняется операция сложения (вычитания) над мантиссами с округлением по значению n+1-ой значащей цифры результата.

3. Мантисса результата должна быть нормализована (получившийся после нормализации порядок может отличаться от n_A как в меньшую, так и в большую сторону).

Если порядки равны, сложение-вычитание выполняется следующим образом:

A₁ = m₁pⁿ

A₂ = m₂pⁿ

Тогда:

A₁ + A₂ = m₁pⁿ + m₂pⁿ = (m₁ + m₂)pⁿ

A₁ — A₂ = m₁pⁿ — m₂pⁿ = (m₁ — m₂)pⁿ

Если порядки отличаются, то необходимо вначале их выровнять:

A₁ = m₁ pⁿ¹

A₂ = m₂ pⁿ²

Тогда A₁ + A₂ = m₁ pⁿ¹ + m₂ pⁿ² = (m₁ + m₂p^n2-n1) pⁿ¹

После чего нужно привести m₂p^n2-n1 к нормальному (т.е. к обычному, без показателя степени) виду, сложить с m₁, полученный результат и будет мантиссой суммы, а порядком суммы будет n1.

Умножение-деление

A₁ = m₁pⁿ¹; A₂ = m₂pⁿ²

Тогда:

A₁ * A₂ = m₁pⁿ¹ * m₂pⁿ²= m₁ * m₂ * pⁿ¹* pⁿ² = (m₁ * m₂) * pⁿ¹⁺ⁿ²

A₁ / A₂ = m₁pⁿ¹ / m₂pⁿ² = m₁ / m₂ * pⁿ¹ / pⁿ² = (m₁ / m₂) * p^n1-n2

То есть, при умножении нужно перемножить мантиссы и сложить показатели степени, при делении – разделить мантиссы и вычесть из показателя степени делимого показатель степени делителя. Например:

(1,2·10⁵) · (2·10^-2) = (1,2 · 2) ·10^5-2 =2,4·10³

5. Основные понятия алгебры высказываний. Логические операции

Логические операции

Компьютер выполняет не только арифметические, но и логические операции, используя понятие истины (1, True, T) или ложь (0, False, F). Большое количество технических устройств компьютера, а также программных систем (экспертных, поддержки управленческих решений, интеллектуальных и т.д.) работают на основании математической логики, из всех разделов которой наибольшую популярность приобрели исчисление высказываний и исчисление предикатов.

Исчисление высказываний.

Цель исчисления высказываний состоит в определении их истинности или ложности на основании исходных посылок. В основе такого рода исчислений находится понятие «высказывание», связном повествовательном предложении, о котором можно сказать, истинно оно или ложно. Например, среди следующих предложений:

1. Два умножить на три равно шесть.

2. 5 > 7.

3. Река Волга впадает в Балтийское море.

4. Какая завтра будет погода?

высказываниями являются 1, 2 и 3 предложения и среди них лишь 1 будет истинным. Пример 4 не является высказыванием, так как нельзя сказать истинно оно или ложно.

Логику высказываний не интересует то, о чем идет речь в высказывании. Ее интересует лишь его истинность или ложность, так как она необходима для рассмотрения суждений без учета их внутренней структуры. Логика высказываний использует содержательные символы – выражения языка, имеющие смысл даже в том случае, если они взяты сами по себе. Высказывания обозначаются большими буквами латинского алфавита. Если высказывание A истинно, то пишут A = 1, если ложно, то используют запись A = 0.

На естественном языке из простых связных повествовательных предложений с помощью некоторых стандартных связок можно образовывать составные предложения. В логике высказываний таким связкам соответствуют логические операции.

Операция отрицания

Операция логического отрицания осуществляется над одним высказыванием. Выполнить операцию логического отрицания (обозначается ) – значит получить из данного высказывания новое, присоединяя слова «неверно, что …» ко всему высказыванию. Например, если А = «Луна спутник Земли», то = «неверно, что Луна спутник Земли», что ложно. Истинность высказывания определяется таблицей:

Отрицание
А
1	0
0	1

Отсюда следует, что отрицание высказывания истинно тогда и только тогда, когда высказывание А ложно.

Операция конъюнкции

Конъюнкция (логическое умножение) соответствует союзу ‘и’ в русском языке. Конъюнкция двух высказываний истинна тогда и только тогда, когда оба составляющих высказывания истинны. Например, пусть у нас есть два истинных высказывания А= «Земля круглая» и В= «Луна –спутник Земли», тогда их конъюнкцией будет так же истинное высказывание «Земля круглая и Луна – спутник Земли» (А=1, В=1; 1·1=1). В случае, если хотя бы одно из высказываний ложно, например В = «Марс — спутник Земли», их конъюнкция «Земля круглая и Марс – спутник Земли» так же будет ложным высказыванием (А=1, В=0; 1·0)=0. Истинность конъюнкции определяется таблицей:

Конъюнкция
А	В	АВ
0	0	0
0	1	0
1	0	0
1	1	1

Операция дизъюнкции

Дизъюнкция (логическое сложение) соответствует союзу ‘или’ в русском языке.

Например, высказывание A – «Декабрь – зимний месяц», В – «В январе сильный мороз», определим высказывание A+B как «Декабрь – зимний месяц или в январе сильный мороз» (А=1; В=1 или В=0; 1+1=1 или 1+0=1). Дизъюнкция истинна, если хотя бы одно из высказываний истинно. Установить истинность логической суммы можно с помощью следующей таблицы:

Дизъюнкция
А	В	А+В
0	0	0
0	1	1
1	0	1
1	1	1

То есть дизъюнкция двух высказываний ложна тогда и только тогда, когда оба высказывания ложны.

Эквиваленция высказываний А, В — это высказывание, обозначаемое и определяемое следующей таблицей:

Эквиваленция истинна тогда и только тогда, когда образующие её высказывания А, В имеют одинаковые значения.

Импликация

Импликации соответствуют конструкции ‘Если …, то … ‘ (‘ Из … следует …’).

Импликация высказываний А и В обозначается как . Ее истинность определяется следующей таблицей:

Импликация
А	В
0	0	1
1	0	0
0	1	1
1	1	1

Импликация ложна тогда и только тогда, когдаА — истина, В — ложь.

Допустим А = «Цены высоки» и В = «Товаров продано мало». Тогда импликация является истинным. Элементы высказывания, образующего импликацию, имеют специальные названия:А — посылка (гипотеза, антецедент), В — заключение (вывод, консеквент ).

Формулы исчисления высказываний. Таблицы истинности

Формулы исчисления высказываний – это высказывания, которые могут быть получены из элементарных высказываний (например A, B, 1, 0) посредством применения логических операций отрицания, конъюнкции, дизъюнкции, импликации и эквиваленции. Формулы необходимы для исчисления истинности или ложности составных высказываний, то есть решения логических задач.

Особое значение в логике исчисления высказываний имеют тождественные высказывания и эквивалентные высказывания (формулы де Моргана). Если высказывания в таблице истинности характеризуются либо одними единицами, либо только нулями, то это означает, что они, либо всегда истинны, либо ложны, независимо от истинности входящих в них высказываний. Например, высказывание всегда истинно, а высказывание всегда ложно. Сложные высказывания, истинные при любых значениях входящих в них других высказываний, называются тождественно истинными, а высказывания, ложные при любых значениях входящих в них других высказываний, называются тождественно ложными. Правила де Моргана имеют вид:

;

.

Полезными также являются следующие законы:

(закон склеивания),

(закон поглощения),

(закон обобщенного склеивания).

Тождественно истинные или тождественно ложные высказывания, если они встречаются в формулах, заменяются в них, соответственно единицей или нулем:

, .

Среди высказываний встречаются также и такие, в которых таблицы истинности совпадают. Эти высказывания называются эквивалентными. Эквивалентными являются, например, высказывания и .

studfiles.net

Операции с плавающей точкой

Правило сложения (вычитания):

пусть, – два нормализованных двоичных числа, и (в противном случае мы можем просто поменять их местами). В результате их сложения или вычитания будет получено следующее выражение:

.

Последовательность вычислений следующая:

1. Порядки чисел A и B выравниваются по большему из них (в нашем случае это n_A). Для этого мантисса числа B сдвигается на n_A—n_B разрядов вправо (часть значащих цифр при этом могут оказаться утерянными), а его порядок становится равным n_A.

2. Выполняется операция сложения (вычитания) над мантиссами с округлением по значению n+1-ой значащей цифры результата.

3. Мантисса результата должна быть нормализована (получившийся после нормализации порядок может отличаться от n_A как в меньшую, так и в большую сторону).

Если порядки равны, сложение-вычитание выполняется следующим образом:

A₁ = m₁pⁿ A₂ = m₂pⁿ

Тогда:

A₁ + A₂ = m₁pⁿ + m₂pⁿ = (m₁ + m₂)pⁿ A₁ — A₂ = m₁pⁿ — m₂pⁿ = (m₁ — m₂)pⁿ

Если порядки отличаются, то необходимо вначале их выровнять:

A₁ = m₁ pⁿ¹A₂ = m₂ pⁿ²Тогда A₁ + A₂ = m₁ pⁿ¹ + m₂ pⁿ² = (m₁ + m₂p^n2-n1) pⁿ¹

После чего нужно привести m₂p^n2-n1 к нормальному (т.е. к обычному, без показателя степени) виду, сложить с m₁, полученный результат и будет мантиссой суммы, а порядком суммы будет n1.

Умножение-деление

A₁ = m₁pⁿ¹; A₂ = m₂pⁿ²

Тогда:

A₁ * A₂ = m₁pⁿ¹ * m₂pⁿ²= m₁ * m₂ * pⁿ¹* pⁿ² = (m₁ * m₂) * pⁿ¹⁺ⁿ² A₁ / A₂ = m₁pⁿ¹ / m₂pⁿ² = m₁ / m₂ * pⁿ¹ / pⁿ² = (m₁ / m₂) * p^n1-n2

То есть, при умножении нужно перемножить мантиссы и сложить показатели степени, при делении – разделить мантиссы и вычесть из показателя степени делимого показатель степени делителя. Например:

(1,2·10⁵) · (2·10^-2) = (1,2 · 2) ·10^5-2 =2,4·10³

 

Основные понятия алгебры высказываний. Логические операции

Похожие статьи:

poznayka.org