Частота колебаний | Все формулы
Частота колебаний — величина, обратная периоду колебаний, т. е. равная числу периодов колебаний (числу колебаний), совершаемых в единицу времени.
Разновидность частот колебаний :
Циклическая частота
Частота колебаний физического маятника
Частота пружинного маятника
Частота математического маятника
Частота электромагнитных колебаний
Частота колебаний крутильного маятника
В Формуле мы использовали :
— Частота колебаний
— Циклическая частота
— Период колебаний маятника
— Масса груза, или масса маятника
— Жесткость пружины
— Длина подвеса
— Ускорение свободного падения
— Момент инерции маятника относительно оси вращения
— Расстояние от оси вращения до центра масс
— Момент инерции тела
— Вращательный коэффициент жёсткости маятника
Период колебаний — Википедия
Материал из Википедии — свободной энциклопедии
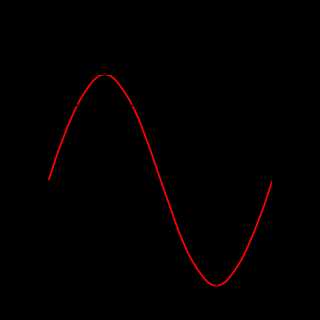
Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние[1], в котором он находился в первоначальный момент, выбранный произвольно).
В принципе совпадает с математическим понятием периода функции, но имея в виду под функцией зависимость физической величины, совершающей колебания, от времени.
Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическими колебаниям (а приближенно — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).
В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.
Обозначения: обычное стандартное обозначение периода колебаний: T{\displaystyle T} (хотя могут применяться и другие, наиболее часто это τ{\displaystyle \tau }
ru.wikipedia.org
Частота колебаний | Все формулы
Частота колебаний — величина, обратная периоду колебаний, т. е. равная числу периодов колебаний (числу колебаний), совершаемых в единицу времени.
Разновидность частот колебаний :
Циклическая частота
Частота колебаний физического маятника
Частота пружинного маятника
Частота математического маятника
Частота электромагнитных колебаний
Частота колебаний крутильного маятника
В Формуле мы использовали :
— Частота колебаний
— Циклическая частота
— Период колебаний маятника
— Масса груза, или масса маятника
— Жесткость пружины
— Длина подвеса
— Ускорение свободного падения
— Момент инерции маятника относительно оси вращения
— Расстояние от оси вращения до центра масс
— Момент инерции тела
— Вращательный коэффициент жёсткости маятника
xn--b1agsdjmeuf9e.xn--p1ai
Период, частота, амплитуда и фаза переменного тока
Период и частота переменного тока
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
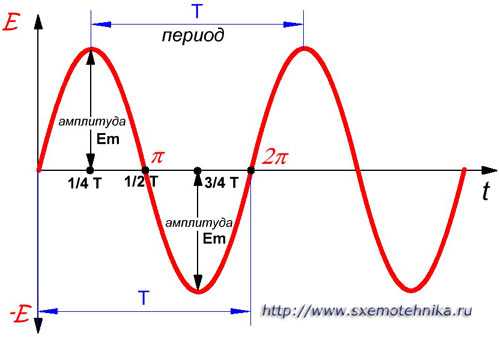
Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мс =0,001сек =10-3сек.
1 мкс=0,001 мс = 0,000001сек =10-6сек.
1000 мкс = 1 мс.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 103 Гц = 1 кГц;
1000 000 Гц = 106 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 109 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
Амплитуда переменного тока
Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно буквами
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.
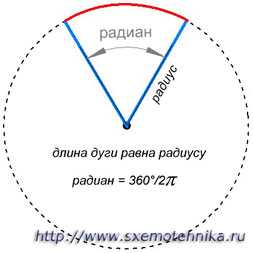
Рисунок 2. Радиан.
Тогда,
1рад = 360°/2
Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ?.
Итак,
?= 6,28*f = 2f
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
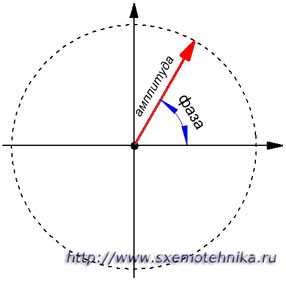
Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
www.sxemotehnika.ru
Колебания: частота, период
Прежде, чем начинать решать “серьезные” задачи, нужно хорошо освоить терминологию, основу. Поэтому вводная статья посвящена определению периода, частоты, циклической частоты колебаний, амплитуды и общей записи закона колебаний.
Колебания
Задача 1. Грузик на пружине за с совершил колебаний. Найти период и частоту колебаний.
Период – время одного полного колебания:
Частота колебаний
Ответ: c, Гц.
Задача 2. Груз на пружине за мин совершает колебаний. Определить период колебаний и циклическую частоту.
Период – время одного полного колебания:
Циклическая частота (угловая частота) равна:
Ответ: c, рад/с.
Задача 3. За 1 с комар совершает 600 взмахов крыльями, а период колебаний крыльев шмеля 5 мс. Какое из насекомых и на сколько сделает в полете большее количество взмахов за 1 мин?
Частота колебаний крыльев комара – 600 Гц. Частота колебаний крыльев шмеля равна:
Следовательно, комар делает на 400 взмахов за 1 с больше, чем шмель, а за 1 минуту – на 24000 взмахов.
Ответ: комар, на 24000.
Задача 4. Крылья пчелы колеблются с частотой Гц. Сколько взмахов крыльями сделает пчела, пока долетит до цветочного поля, расположенного на расстоянии в 500 м, если она летит со скоростью м/с?
Если скорость полета пчелы известна и известно расстояние, определим время полета:
Тогда количество взмахов за это время равно:
Ответ: 30 000.
Задача 5. Найти амплитуду, период и частоту колебаний, если закон колебаний материальной точки имеет вид (см).
Амплитуда – первое число в законе колебаний, то есть . Циклическая частота – множитель при , . Тогда период
А частота:
Ответ: с, Гц.
easy-physic.ru
опыты, формулы, задачи :: SYL.ru
Что такое период колебаний? Что это за величина, какой физический смысл она имеет и как ее рассчитать? В этой статье мы разберемся с этими вопросами, рассмотрим различные формулы, по которым можно рассчитать период колебаний, а также выясним, какая связь имеется между такими физическими величинами, как период и частота колебаний тела/системы.
Определение и физический смысл
Периодом колебаний называется такой промежуток времени, при котором тело или система совершают одно колебание (обязательно полное). Параллельно можно отметить параметр, при выполнении которого колебание может считаться полным. В роли такого условия выступает возвращение тела в его первоначальное состояние (к первоначальной координате). Очень хорошо проводится аналогия с периодом функции. Ошибочно, кстати, думать, что она имеет место исключительно в обыкновенной и высшей математике. Как известно, эти две науки неразрывно связаны. И с периодом функций можно столкнуться не только при решении тригонометрических уравнений, но и в различных разделах физики, а именно речь идет о механике, оптике и прочих. При переносе периода колебаний из математики в физику под ним нужно понимать просто физическую величину (а не функцию), которая имеет прямую зависимость от проходящего времени.
Какие бывают колебания?
Колебания подразделяются на гармонические и ангармонические, а также на периодические и непериодические. Логично было бы предположить, что в случае гармонических колебаний они совершаются согласно некоторой гармонической функции. Это может быть как синус, так и косинус. При этом в деле могут оказаться и коэффициенты сжатия-растяжения и увеличения-уменьшения. Также колебания бывают затухающими. То есть, когда на систему действует определенная сила, которая постепенно “тормозит” сами колебания. При этом период становится меньше, в то время как частота колебаний неизменно увеличивается. Очень хорошо демонстрирует такую вот физическую аксиому простейший опыт с использованием маятника. Он может быть пружинного вида, а также математического. Это неважно. Кстати, период колебаний в таких системах будет определяться разными формулами. Но об этом чуточку позже. Сейчас же приведем примеры.
Опыт с маятниками
Взять первым можно любой маятник, разницы никакой не будет. Законы физики на то и законы физики, что они соблюдаются в любом случае. Но почему-то больше по душе математический маятник. Если кто-то не знает, что он собой представляет: это шарик на нерастяжимой нити, который крепится к горизонтальной планке, прикрепленной к ножкам (или элементам, которые играют их роль – держать систему в равновесном состоянии). Шарик лучше всего брать из металла, чтобы опыт был нагляднее.
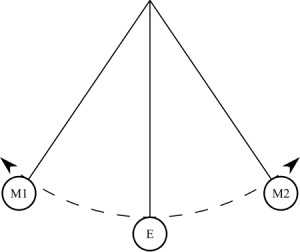
Итак, если вывести такую систему из равновесия, приложить к шару какую-то силу (проще говоря, толкнуть его), то шарик начнет раскачиваться на нити, следуя определенной траектории. Со временем можно заметить, что траектория, по которой проходит шар, сокращается. В то же время шарик начинает все быстрее сновать туда-сюда. Это говорит о том, что частота колебаний увеличивается. А вот время, за которое шарик возвращается в начальное положение, уменьшается. А ведь время одного полного колебания, как мы выяснили ранее, и называется периодом. Если одна величина уменьшается, а другая увеличивается, то говорят об обратной пропорциональности. Вот мы и добрались до первого момента, на основании которого строятся формулы для определения периода колебаний. Если же мы возьмем для проведения пружинный маятник, то там закон будет наблюдаться немного в другом виде. Для того чтобы он был наиболее наглядно представлен, приведем систему в движение в вертикальной плоскости. Чтобы было понятнее, сначала стоило сказать, что собой представляет пружинный маятник. Из названия понятно, что в его конструкции должна присутствовать пружина. И это действительно так. Опять же таки, у нас есть горизонтальная плоскость на опорах, к которой подвешивается пружина определенной длины и жесткости. К ней, в свою очередь, подвешивается грузик. Это может быть цилиндр, куб или другая фигурка. Это может быть даже какой-то сторонний предмет. В любом случае, при выведении системы из положения равновесия, она начнет совершать затухающие колебания. Наиболее четко просматривается увеличение частоты именно в вертикальной плоскости, без всякого отклонения. На этом с опытами можно закончить.
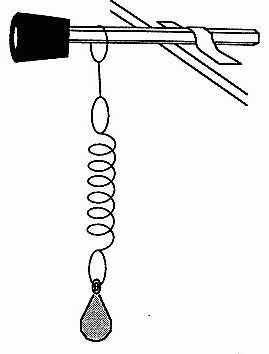
Итак, в их ходе мы выяснили, что период и частота колебаний это две физические величины, которые имеют обратную зависимость.
Обозначение величин и размерности
Обычно период колебаний обозначается латинской буквой T. Гораздо реже он может обозначаться по-другому. Частота же обозначается буквой µ (“Мю”). Как мы говорили в самом начале, период это не что иное, как время, за которое в системе происходит полное колебание. Тогда размерностью периода будет секунда. А так как период и частота обратно пропорциональны, то размерностью частоты будет единица, деленная на секунду. В записи задач все будет выглядеть таким образом: T (с), µ (1/с).
Формула для математического маятника. Задача №1
Как и в случае с опытами, я решил первым делом разобраться с маятником математическим. Подробно вдаваться в вывод формулы мы не будем, поскольку такая задача поставлена изначально не была. Да и вывод сам по себе громоздкий. Но вот с самими формулами ознакомимся, выясним, что за величины в них входят. Итак, формула периода колебаний для математического маятника имеет следующий вид:

Где l – длина нити, п = 3,14, а g – ускорение свободного падения (9,8 м/с^2). Никаких затруднений формула вызывать не должна. Поэтому без дополнительных вопросов перейдем сразу к решению задачи на определение периода колебания математического маятника. Металлический шар массой 10 грамм подвешен на нерастяжимой нити длиной 20 сантиметров. Рассчитайте период колебания системы, приняв ее за математический маятник. Решение очень простое. Как и во всех задачах по физике, необходимо максимально упростить ее за счет отброса ненужных слов. Они включаются в контекст для того чтобы запутать решающего, но на самом деле никакого веса абсолютно не имеют. В большинстве случаев, разумеется. Здесь можно исключить момент с “нерастяжимой нитью”. Это словосочетание не должно вводить в ступор. А так как маятник у нас математический, масса груза нас интересовать не должна. То есть слова о 10 граммах тоже просто призваны запутать ученика. Но мы ведь знаем, что в формуле масса отсутствует, поэтому со спокойной совестью можем приступать к решению. Итак, берем формулу и просто подставляем в нее величины, поскольку определить необходимо период системы. Поскольку дополнительных условий не было задано, округлять значения будем до 3-его знака после запятой, как и принято. Перемножив и поделив величины, получим, что период колебаний равен 0,886 секунд. Задача решена.
Формула для пружинного маятника. Задача №2
Формулы маятников имеют общую часть, а именно 2п. Эта величина присутствует сразу в двух формулах, но разнятся они подкоренным выражением. Если в задаче, касающейся периода пружинного маятника, указана масса груза, то избежать вычислений с ее применение невозможно, как это было в случае с математическим маятником. Но пугаться не стоит. Вот так выглядит формула периода для пружинного маятника:
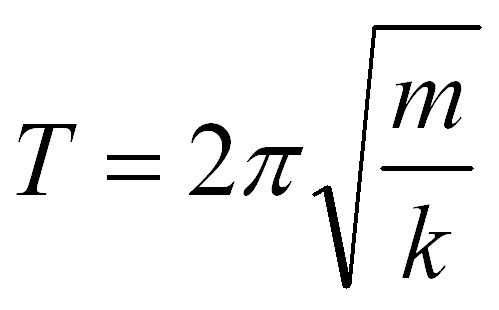
В ней m – масса подвешенного к пружине груза, k – коэффициент жесткости пружины. В задаче значение коэффициента может быть приведено. Но если в формуле математического маятника особо не разгуляешься – все-таки 2 величины из 4 являются константами – то тут добавляется 3 параметр, который может изменяться. И на выходе мы имеем 3 переменных: период (частота) колебаний, коэффициент жесткости пружины, масса подвешенного груза. Задача может быть сориентирована на нахождение любого из этих параметров. Вновь искать период было бы слишком легко, поэтому мы немного изменим условие. Найдите коэффициент жесткости пружины, если время полного колебания составляет 4 секунды, а масса груза пружинного маятника равна 200 граммам.
Для решения любой физической задачи хорошо бы сначала сделать рисунок и написать формулы. Они здесь – половина дела. Записав формулу, необходимо выразить коэффициент жесткости. Он у нас находится под корнем, поэтому обе части уравнения возведем в квадрат. Чтобы избавиться от дроби, умножим части на k. Теперь оставим в левой части уравнения только коэффициент, то есть разделим части на T^2. В принципе, задачку можно было бы еще немного усложнить, задав не период в числах, а частоту. В любом случае, при подсчетах и округлениях (мы условились округлять до 3-его знака после запятой), получится, что k = 0, 157 Н/м.
Период свободных колебаний. Формула периода свободных колебаний
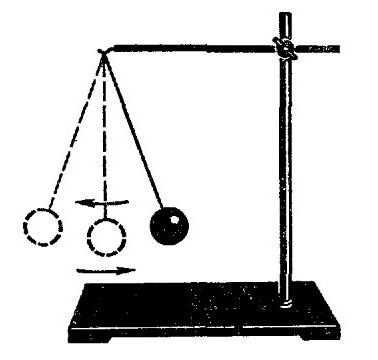
Под формулой периода свободных колебаний понимают те формулы, которые мы разобрали в двух ранее приведенных задачах. Составляют также уравнение свободных колебаний, но там речь идет уже о смещениях и координатах, а этот вопрос относится уже к другой статье.
Советы для решения задач, связанных с периодом
1) Прежде чем браться за задачу, запишите формулу, которая с ней связана.
2) Простейшие задачи не требуют рисунков, но в исключительных случаях их нужно будет сделать.
3) Старайтесь избавляться от корней и знаменателей, если это возможно. Записанное в строчку уравнение, не имеющее знаменателя, решать гораздо удобнее и проще.
www.syl.ru
Период математического маятника | Все формулы
Период математического маятника — период колебания математического маятника зависит от длины нити: с уменьшением длины нити период колебания уменьшается
Для математического маятника выполняются некоторые законы:
1 закон. Если, сохраняя одну и ту же длину маятника, подвешивать разные грузы (например 5кг и 100 кг), то период колебаний получится один и тот же, хотя массы грузов сильно различаются. Период математического маятника не зависит от массы груза.
2 закон. Если маятник отклонять на разные, но маленькие углы, то он будет колебаться с одним и тем же периодом, хотя и с разными амплитудами. Пока амплитуда маятника будут малы, колебания и по своей форме будут похожи на гармонические, и тогда период математического маятника не зависит от амплитуды колебаний. Это свойство приняло название изохронизмом..
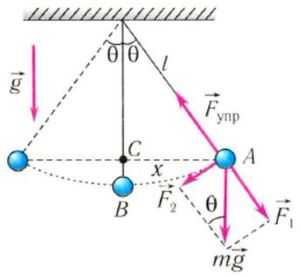
Давайте выведем формулу периода математического маятника.
На груз m математического маятника действуют сила тяжести mg и сила упругости нити Fynp. Ось 0Х направим вдоль касательной к траектории движения вверх. Запишем второй закон Ньютона для данного случая:
С проецируем все на ось ОХ:
При малых углах
Сделав замены и маленькие преобразования у нас получается, что уравнение имеет вид:
Сравнивая полученное выражение с уравнением гармонических колебаний у нас получается:
Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:
Тогда период математического маятника будет равен:
Период математического маятника зависит только от ускорения свободного падения g и от длины маятника l. Из полученной формулы следует, что период маятника не зависит от его массы и от амплитуды (при условии, что она достаточно мала). Так же мы установили количественную зависимость между периодом маятника, его длиной и ускорением свободного падения. Период математического маятника пропорционален корню квадратному из отношения длины маятника к ускорению свободного падения. Коэффициент пропорциональности равен 2p
Так же есть:
Период пружинного маятника
Период физического маятника
Период крутильного маятника
В Формуле мы использовали :
— Период математического маятника
— Длина подвеса
— Ускорение свободного падения
— Циклическая частота пружинного маятника
— Сила упругости
— Длина дуги АВ
xn--b1agsdjmeuf9e.xn--p1ai
