Олимпиада по математике школьный этап 11 класс с ответами – Олимпиадные задания по математике (11 класс) на тему: Задания по математике для школьного этапа олимпиады 11 класс Учитель Колесникова М.Г | скачать бесплатно

Если x<0, то (x²-3)² ≥ 0, а x(4x²+3)<0, значит, полученное равенство при любом отрицательном значении x будет неверным. Следовательно, отрицательных корней нет.

Критерии проверки

• “+” – приведено полное обоснованное решение
• “±” –  приведено верное в целом рассуждение, содержащее незначительные пробелы или неточности (например, утверждается, что (x²-3)² > 0 при всех значениях x)
• “–” – приведен только ответ
• “–” – задача не решена или решена неверно

Задание 2

Вася вписал в клетки таблицы 4×18 (4 строки, 18 столбцов) натуральные числа от 1 до 72 в некотором одному ему известном порядке. Сначала он нашел произведение чисел, стоящих в каждом столбце, а затем у каждого из восемнадцати полученных произведений вычислил сумму цифр. Могли ли все получившиеся суммы оказаться одинаковыми?

Ответ: нет.

Решение

Предположим, что каждая из указанных сумм цифр равна S. Так как некоторые из произведений содержат множители кратные девяти, то такие произведения делятся на 9, значит, их сумма цифр также делится на 9. Следовательно, число S должно быть кратно девяти.

Таким образом, произведение чисел в каждом столбце должно быть кратно девяти.

Оно может быть кратно девяти только в двух случаях:

• если содержит хотя бы один множитель, кратный девяти;
• если содержит не менее двух множителей, кратных трем, но не кратных девяти.

Среди чисел от 1 до 72 восемь чисел делятся на 9 и 16 чисел делятся на 3, но не делятся на 9. Следовательно, произведений, кратных девяти, может оказаться не больше, чем 8 + 8 = 16, то есть на 9 могут делится не больше, чем 16 сумм их цифр. Так как в таблице – 18 столбцов, то получено противоречие.

Критерии проверки

• “+” – приведено полное обоснованное решение
• “±” – приведено верное в целом рассуждение, содержащее незначительные пробелы или неточности
• “ ±” – присутствует идея делимости на 9, но решение не доведено до конца или содержит ошибки
• “–” – рассмотрены только частные случаи или конкретные примеры
• “–” – приведен только ответ
• “–” – задача не решена или решена неверно

Задание 3

Правильный пятиугольник и правильный двадцатиугольник вписаны в одну и ту же  окружность. Что больше: сумма квадратов длин всех сторон пятиугольника или сумма квадратов длин всех сторон двадцатиугольника?

Ответ: сумма квадратов длин сторон правильного пятиугольника больше.

Решение

Заметим, что в правильном двадцатиугольнике вершины, взятые через одну, образуют правильный десятиугольник, а вершины этого десятиугольника, взятые через одну, образуют правильный пятиугольник. Следовательно, достаточно сравнить две величины:4(a₂₀)² и (a₅)², где a₂₀ и a₅ – длины сторон правильных двадцатиугольника и пятиугольника соответственно. Рассмотрим соответствующий фрагмент и введем обозначения вершин так, как показано на

Первый способ

Воспользуемся тем, что при  n  > 4  угол любого правильного  n-угольника  –  тупой.

Рассмотрим  треугольник А₁А₂А₃ с тупым углом А₂  (см. рис.11.3а).

Рис.11.3а

По следствию из теоремы косинусов 2(a₂₀)² < (a₅)² ⇔ 4(a₂₀)² < 2(a₁₀)². Аналогично, из треугольника  А₁А₃А₅  получим, 2(a₁₀)² < (a₅)². Таким образом, 4(a₂₀)² < (a₅)², откуда следует, что квадрат стороны пятиугольника больше.

Второй способ

Опустим перпендикуляры А₂В и А₃С на А₁А₅, а также проведем перпендикуляр А₂D к А₃С (см. рис. 11.3б). Пусть А₁В = x, А₂

так как косинус убывает на промежутке (0; 90°).

Тогда

откуда и следует ответ.

Третий способ

Рис.11.3б

Воспользуемся формулой для вычисления длин сторон правильных n-угольников, вписанных в окружность радиуса  R:

Критерии проверки

• “+” – приведено полное обоснованное решение
• “±” – приведено верное в целом рассуждение, содержащее незначительные пробелы или неточности
• “–” – приведен только ответ
• “–” – задача не решена или решена неверно

Задание 4

Дана треугольная пирамида ABCD с плоскими прямыми углами при вершине D, в которой CD=AD+DB. Докажите, что сумма плоских углов при вершине C равна 90°

Решение

Введем обозначения: ∠ACD=α, ∠BCD=β, ∠BCA=γ, DA=a,DB=b. По условию: CD=a+b, а доказать требуется, что α+ β+ γ=90°

Первый способ

Пусть  CA=m, CB=n  (см. рис. 11.4а).

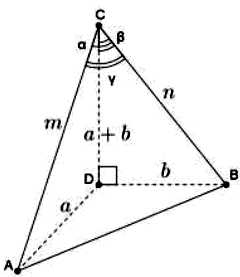
Рис. 11.4а

Сначала докажем, что углы α+β и γ  –  острые. Действительно, в прямоугольных треугольниках ACD и ВCD стороны AD и BD – наименьшие, значит, α<45° и β<45°. Следовательно, α+β<90°, тогда и γ <α+β<90°. Теперь достаточно доказать, что sin(α+β)=cos γ.

Заметим, что

sin(α+β)=sinαcosβ + cosαsinβ=

С другой стороны, из треугольника  ABC  по теореме косинусов: AB²=m²+n²-2mn∙cosγ. Учитывая, что AB² = a²+b², получим:

cosγ = (m²+n²-a²-b²)/2mn = ((a+b)²+(a+b)²)/2mn = (a+b)²/mn

Таким образом, sin(α+β) = cosγ, значит α+β+γ=90⁰

Вычисление cosγ можно упростить, если воспользоваться формулой трех косинусов:

cosγ = cosα∙cosβ = (a+b)/m∙(a+b)/n = (a+b)²/mn

Второй способ

Заметим, что при фиксированных длинах ребер DA и DB  существует единственная пирамида  ABCD, удовлетворяющая условию задачи.

Рассмотрим квадрат СD₁TD₂  со стороной a+b  и отложим на его сторонах  TD₁  и  TD₂  отрезки  TA  = b и  TB  = a соответственно  (см. рис. 11.4б).

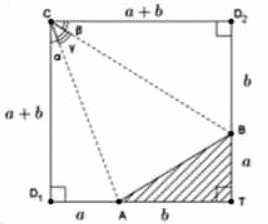
Рис. 11.4б

Тогда пятиугольник ABD₂CD₁ является разверткой боковой поверхности данной пирамиды, а треугольник  ATB  равен треугольнику  ADB  ее основания. Таким образом, выполняются все условия задачи, значит α+β+γ=90⁰

Критерии проверки

• “+” – приведено полное обоснованное решение
• “±”  –  приведено верное в целом рассуждение, содержащее незначительные пробелы или неточности (например, при первом способе решения не обосновано, что углы α+β и γ   – острые, или при втором способе решения не указано, что условие задачи однозначно задает пирамиду, и т. п.)
• “–” – задача не решена или решена неверно

Формулу трех косинусов школьники могут использовать без доказательства.

Задание 5

Функция f(x) определена для всех действительных чисел, причем для любого x выполняются равенства: f(x+2) = f(2-x) и f(x+7)=f(7-x). Докажите, что f(x) – периодическая функция.

Решение

Докажем, что данная функция имеет период 10. Можно рассуждать по-разному.

Первый способ

Учитывая, что  f(x) определена везде, достаточно доказать, что, для любого действительного x выполняется равенство

 f(x+10) = f(x).

Последовательно используя второе и первое равенство из условия, получим:

f((x+3)+7) = f(7-(x+3)) = f(4-x) = f(2+(2-x)) = f(2-(2-x)) = f(x)

Второй способ

Пусть x₁ = x + 2, x₂ = 2 – x.

Тогда x₀ = (x₁+x₂)/2=2. Это означает, что точки графика  f(x) с координатами (x₁; f(x₁)) и (x₂; f(x₂)) симметричны относительно прямой x = 2, то есть такая прямая является осью симметрии этого графика. Аналогично, из второго равенства в условии следует, что прямая x = 7 также является осью симметрии графика данной функции.

Теперь воспользуемся теоремой: композиция двух симметрий с параллельными осями является параллельным переносом на вектор, перпендикулярный этим осям, модуль которого равен удвоенному расстоянию между осями. В нашем случае расстояние между осями равно 5, поэтому график f(x) перейдет в себя при параллельном переносе на вектор (0 ; 10). Следовательно, функция f(x) – периодическая с периодом 10.

Отметим, что 10 может оказаться не наименьшим положительным периодом данной функции. 

Критерии проверки

• “+” – приведено полное обоснованное решение
• “±” – приведено верное в целом рассуждение, содержащее незначительные пробелы или неточности
• “±” – при первом способе решения проведены выкладки, использующие оба данных равенства, но из-за вычислительных ошибок получен период, не кратный десяти
• “–” – задача не решена или решена неверно

Задание 6

Каждое целое число на координатной прямой покрашено в один из двух цветов  –  белый или черный, причем числа 2016 и 2017 покрашены разными цветами. Обязательно ли можно найти три одинаково покрашенных целых числа, сумма которых равна нулю?

Ответ: обязательно.

Решение

Предположим таких целых чисел нет. Пусть, для определенности, число 2016 покрашено в черный цвет, а число 2017 – в белый. Рассмотрим два случая:

1-й случай

Число 0 покрашено в белый цвет. Так как числа 0 и 2017 – белые, то число –2017 покрашено в черный цвет.

Из того, что числа –2017 и 2016 – черные и –2017 + 2016 + 1 = 0 следует, что число 1 – белое. Аналогично, так как числа 0 и 1 – белые, то число –1 должно быть черным. Далее, числа –1 и 2016 – черные, значит, число –2015 – белое, тогда число 2015 – черное. Числа –2015 и 2017 – белые, 2017 + (–2015) + (–2) = 0, поэтому число –2 – черное, тогда число 2 – белое.

Таким образом, числа 1 и 2 покрашены в белый цвет. Пусть число n – наименьшее натуральное число, покрашенное в черный цвет, тогда число –n покрашено в белый цвет. Так как 1 + (n – 1) + (–n) = 0, n > 2 и эти три числа – белые, то получено противоречие.

2-й случай

Число 0 покрашено в черный цвет. Так как числа 0 и 2016 – черные, то число –2016 покрашено в белый цвет. Из того, что числа –2016 и 2017 – белые и –2016 + 2017 +  (–1) = 0 следует, что число –1 – черное.

Аналогично, так как числа 0 и –1 – черные, то число 1 должно быть белым. Далее, числа 1  и –2016 – белые, значит, число 2015 – черное, тогда число –2015 – белое. Числа –2015 и 2017 – белые, (–2015) + 2017 + (–2) = 0, поэтому число –2 – черное.

Таким образом, числа –1 и –2 покрашены в черный цвет. Пусть число –m – наибольшее целое отрицательное число, покрашенное в белый цвет, тогда число m покрашено в черный цвет. Так как –1 + (–m + 1) + m = 0, –m < –2 и эти три числа – черные, то получено противоречие.

Допустимо не разбирать второй случай подробно, указав, что он аналогичен первому, но указав при этом, в чем конкретно он будет отличаться

Критерии проверки

• “+” – приведено полное обоснованное решение
• “±” – верно и полностью разобран только один из возможных случаев
• “±” – присутствует верная идея получения противоречия, но допущены ошибки или решение не доведено до конца
• “–” – приведен только ответ
• “–” – задача не решена или решена неверно

olimpiadnye-zadanija.ru

Олимпиада по математике 5-11 классы

Решение заданий олимпиады по математике (школьный тур)

5 класс

1. Сколько всего трехзначных чисел? Ответ. 900

Решение. Первое трехзначное число 100, последнее – 999. Всего

999 чисел от 1 до 999, из них нам не нужны 99 чисел – от 1 до 99. Поэтому нужных 999-99=900.

Комментарий. Можно было посчитать, использую комбинаторику:

для первой цифры 9 вариантов, для второй 10, для третьей 10, итого 9*10*10=900 комбинаций.

2. Календарь представляет собой два кубика, у каждого кубика на всех гранях написано по цифре. Дату (день месяца) составляют, используя один или два кубика. Придумайте, как написать цифры

на кубиках, чтобы можно было получить любую дату от 1 до 31. (В ответе напишите, какие цифры должны быть на одном кубике, а какие – на другом.)

Решение. Например, на одном кубике написаны цифры 0, 1, 2, 4, 5, 6 а на другом 1, 2, 3, 7, 8, 9. Замечание. Существуют и другие примеры. Для проверки правильности примера, достаточно проверить, что 1) в каждой группе по 6 цифр, 2) все цифры встречаются, 3) можно составить числа 11, 22 и 30 (т.е. в каждой группе есть цифры 1 и 2, а цифры 0 и 3 находятся в разных группах).

3. Разрежьте фигуру на рисунке справа на 4 равные части.

4. Три математика ехали в разных вагонах одного поезда. Когда поезд подъезжал к станции, математики насчитали на перроне 7, 12 и 15 скамеек. А когда поезд отъезжал, один из них насчитал еще 2 скамейки. Сколько насчитали остальные?

Ответ. 5 и 10 скамеек. Решение. Очевидно, что тот, кто до остановки проехал большую часть перрона, насчитал большее число скамеек. Пусть первый насчитал 15 скамеек, второй 12, третий 7. Так как первый насчитал на 3 скамейки больше, чем второй, то, когда поезд будет отъезжать, второй увидит эти 3 скамейки, т.е. насчитает на 3 скамейки больше, чем первый. Аналогично третий насчитает на 8 скамеек больше, чем первый. Раз кто-то насчитал 2 скамейки, то это мог быть только первый. Значит, остальные насчитали 2+3=5 и 2+8=10 скамеек.

5. Дедка вдвое сильнее Бабки, Бабка втрое сильнее Внучки, Внучка вчетверо сильнее Жучки, Жучка впятеро сильнее Кошки, Кошка вшестеро сильнее Мышки. Без Мышки все остальные не могут вытащить репку, а вместе с Мышкой – могут. Сколько мышек надо собрать вместе, чтобы эти мышки смогли вытащить репку сами?

Ответ. 1237 мышек. Решение. Кошка = 6 мышек; жучка = 5 кошек = 30 мышек; внучка = 4 жучки = 120 мышек; бабка = 3 внучки = 360 мышек; дедка = 2 бабки = 720 мышек.

Все вместе дедка+бабка+внучка+жучка+кошка+мышка = 720+360+120+30+6+1=1237 мышек.

6. Мальчик Сережа увидел двоих двухголовых дракончиков, головы которых спутались. Драконы бывают либо правдивые, т.е. обе головы говорят только правду, либо лживые, т.е. обе головы

всегда лгут. Сережа решил помочь дракончикам распутать головы. Но для этого ему надо знать, где чья голова. Он спросил это у дракончиков, на что головы ответили:

первая: «я – правдивая голова»;

вторая: «третья голова – моя родная голова»;

третья: «вторая голова – не родная мне голова»;

четвертая: «третья голова – лживая».

Какие головы принадлежат каким дракончикам?

Ответ. Третья и первая головы от одного (правдивого) дракона, а вторая и четвертая – от другого (лживого).

Решение. Вторая и третья головы противоречат друг другу, значит, они не родные (родные головы либо обе скажут, что они родные, либо обе скажут, что они не родные). А значит, третья голова сказала правду (т.е. она правдивая), а вторая солгала (т.е. она лживая). Значит, четвертая голова солгала, сказав, что третья лживая, т.е. родная второй голове. А тогда третья родная первой.

Комментарии по проверке

Каждая задача оценивается из 7 баллов. Каждая оценка – целое число от 0 до 7. Ниже приведены некоторые указания к проверке. При оценке решения нужно исходить из того, является ли приведенное решение в целом верным (хотя, может, и с недостатками) – тогда решение

оценивается не менее чем в 4 балла. Или оно неверное (хотя, может, и с существенными продвижениями) – в этом случае оценка должна быть не выше 3 баллов.

Задача 1. Правильный ответ без обоснования – 3 балла. Выражение 999-99=900 или 999100+1=900 является достаточным обоснованием. Выражение 1000-100=900 без дополнительных пояснений обоснованием не считается.

Задача 2. Правильное распределение – 7 баллов. Голый неправильный пример – 0 баллов. Сказано, что 1 и 2 должны быть на обоих кубиках, т.к. есть числа 11 и 22, а дальше пример

неправильный из-за того, что 0 и 3 поместили на один кубик – 2 балла.

Задача 3. Правильное разрезание – 7 баллов. Разрезание на равные по площади, но не равные части – 0 баллов.

Задача 4. Ответ без обоснования – 2 балла.

Задача 5. Есть идея все выражать в мышках, но не доведено до конца или неправильно доведено (например, посчитано, что дедка — это 720 мышек и в ответ записано 720 ) – 2 балла. Вычислительная ошибка – минус 1 балл (если вычислительных ошибок несколько, соответственно вычитается больше).

Задача 6. Правильный ответ 1 балл. Правильный ответ и проверка – все равно 1 балл. Неполный перебор, какие головы кому принадлежат, добавляет не больше 2 баллов.

6 класс

1. Календарь представляет собой два кубика, у каждого кубика на всех гранях написано по цифре. Дату (день месяца) составляют, используя один или два кубика. Придумайте, как написать цифры

на кубиках, чтобы можно было получить любую дату от 1 до 31. (В ответе напишите, какие цифры должны быть на одном кубике, а какие – на другом)

Решение. Например, на одном кубике написаны цифры 0, 1, 2, 4, 5, 6 а на другом 1, 2, 3, 7, 8, 9.

Замечание. Существуют и другие примеры. Для проверки правильности примера, достаточно проверить, что 1) в каждой группе по 6 цифр, 2) все цифры встречаются, 3) можно составить

числа 11, 22 и 30 (т.е. в каждой группе есть цифры 1 и 2, а цифры 0 и 3 находятся в разных группах).

2. Одной черепахе 300 лет, а другой 15 лет. Через сколько лет первая черепаха будет вдвое старше второй? Ответ. Через 270 лет.

Решение. Разница между черепахами всегда 300-15=285 лет. Одна будет вдвое старше другой, когда второй будет столько лет, какова разница, т.е. 285. А 285 лет второй черепахе исполнится через 285-15=270 лет.

3. Сад разбит на квадраты. Садовник начал обход с верхнего правого квадрата, обошел весь сад и

вернулся в тот же угловой квадрат. В закрашенных квадратиках он не был (там располагаются пруды). Во всех остальных квадратиках он побывал по одному разу, причем через вершины квадратов он не проходил. Начертите возможный путь садовника.

Ответ. Один из возможных примеров обхода приведен на рисунке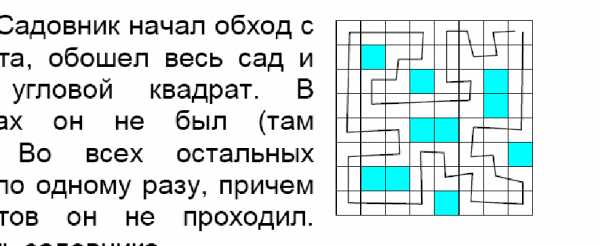

(возможны и другие пути).

4. На некотором острове каждый житель либо всегда лжет, либо всегда говорит правду. Трое островитян А, Б, В сказали следующее:

А: «Б – лжец»; Б: «ровно один из А и В лжец»; В: «у меня есть крокодил». Есть ли у В крокодил?

Ответ. Да, есть. Решение. Первый способ. 1) Пусть А говорит правду. Тогда Б – лжец.

Тогда А и В оба лжецы или оба «правдивцы», но т.к. А –

«правдивец», то и В «правдивец», т.е. крокодил у него есть.

2) Пусть А – лжец. Тогда Б – «правдивец». Тогда ровно один из А

и В лжец, но т.к. А лжец, то В – «правдивец». Т.е. крокодил у него есть.

Таким образом, в обоих случаях получаем, что у В есть крокодил.

Второй способ. 1) Пусть Б «правдивец». Тогда ровно один из А и В лжец, но т.к. А говорит, что Б лжец, то А – лжец = В «правдивец» = крокодил у него есть.

2) Пусть Б лжец. Тогда оба А и В «правдивцы», или оба лжецы. Но А говорит, что Б лжец, т.е. говорят правду = они оба (А и В) «правдивцы», т.е. у В есть крокодил.

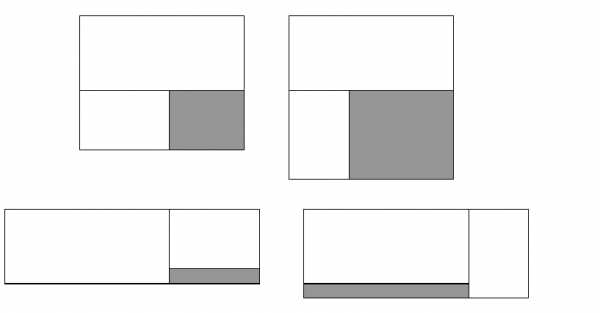
5. Прямоугольник разрезали на три прямоугольника, два из которых имеют размеры 5×11 и 4×6. Какие размеры мог иметь третий прямоугольник? (Найдите все возможности.)

Ответ. 5×4, 7×6, 1×6, 1×11.

Решение. Посмотрим, как могут прилегать прямоугольники друг к другу.

Прямоугольник 4×6 может примыкать к стороне 5 или к стороне 11, при этом прилегать он может стороной 4 или стороной 6, т.е. всего 4 варианта: Из них получаем размеры третьего прямоугольника: 5×4, 7×6, 1×6, 1×11.

6. Винни-Пуху дали полную тарелку манной каши. Он съел половину и положил в тарелку еще столько же меда. Затем он съел треть содержимого тарелки (каши с медом) и снова доложил мед. Потом съел четверть содержимого и опять доложил медом, после чего с аппетитом все съел. Чего в итоге Винни-Пух съел больше: каши или меда?

Ответ. Меда он съел больше.

Решение. Видно, что Пух в итоге съел тарелку каши. Посчитаем, сколько он съел меда: 1/2+1/3+1/4 = 13/121.

Комментарии по проверке

Каждая задача оценивается из 7 баллов. Каждая оценка – целое число от 0 до 7.

При оценке решения нужно исходить из того, является ли приведенное решение в целом верным (хотя, может, и с недостатками) – тогда решение оценивается не менее чем в 4 балла. Или оно неверное (хотя, может, и с существенными продвижениями) – в этом случае оценка должна быть не выше 3 баллов.

Задача 1. Правильное распределение – 7 баллов. Только неправильный пример – 0 баллов. Сказано, что 1 и 2 должны быть на обоих кубиках т.к. есть числа 11 и 22, а дальше пример

неправильный из-за того, что 0 и 3 поместили на один кубик – 2 балла.

Задача 2. Только ответ без всяких пояснений – 2 балла.

Задача 3. Правильный пример – 7 баллов. Пример незамкнутого пути или пути не по всем клеткам – 0 баллов.

Задача 4. Голый ответ «Да, есть» – 0 баллов. Разобран только один случай, например, что А – «правдивец» – 1 балл.

Задача 5. Найдены все варианты (подтверждены картинками), но нет никаких объяснений, почему это именно ВСЕ варианты – 5 баллов.

Найдены только три из четырех вариантов – 2 балла. Найдено два

варианта – 1 балл. Найден только один вариант – 0 баллов.

Задача 6. Голый ответ 0 баллов.

7 класс

1. Замените буквы цифрами так, чтобы получилось верное равенство: О + Л + И + М + П + И + А = ДА (Одинаковые буквы надо заменять одинаковыми цифрами, разные – разными, ДА – двузначное число)

Ответ. Например, О=3, Л=4, И=0, М=5, П=8, Д=2, А=9.

Решение. Вычтем из обоих частей уравнения А, получим, что сумма цифр О+Л+И+М+П+И должна заканчиваться на ноль. Попробуем подобрать цифры так, чтобы например она была

равна 20 (т.е. Д=2). Это легко сделать, например 3+4+0+5+8+0 =20. т.е. О=3, Л=4, И=0, М=5, П=8, Д=2, А=9

Комментарий. Возможно много других решений. При этом Д может равняться 2, 3, 4.

2. На каждой перемене Робин-Бобин-Барабек съедает по конфете. За неделю (с понедельника по субботу) было 30 уроков. Сколько всего конфет съел Робин на переменах?

Ответ. 24 конфеты.

Решение. Если бы все эти уроки произошли в один день, то Робин съел бы 29 конфет (количество промежутков между 30 уроками). Но так как между последним уроком какого-то дня и первым

уроком следующего дня конфета не съедается, то нужно еще вычесть 5 конфет (по количеству промежутков между шестью днями), т.е. итого получается, что Робин съел 30 – 5=24 конфеты.

3. Из двух одинаковых железных проволок кузнец сковал по железной цепи. Первая содержит 80 звеньев, а вторая – 100. Каждое звено первой цепи на 5 граммов тяжелее каждого звена

второй цепи. Какова масса цепей?

Ответ. 2 кг.

Первое решение. Пусть x г – масса каждого звена второй цепи, тогда (x+5) г – масса каждого звена первой цепи. Тогда масса проволоки, с одной стороны, равна 100x, а с другой 80(x+5) г. Из

равенства 100x=80(x+5) следует, что x=20, а масса одной проволоки 100*20 г = 2 кг.

Второе решение. Т.к. массы цепей одинаковы, то, «забрав» у каждого звена первой цепи по 5 г, мы получим 80 кусочков по массе таких же, как звенья второй цепи, а из излишков должны

получиться оставшиеся 20 звеньев. Т.е. 20 звеньев весят 5*80=400 г, а одно звено второй цепи весит 400:20=20 г. Поэтому все 100 звеньев весят 100*20=2000 г, т.е. 2 кг.

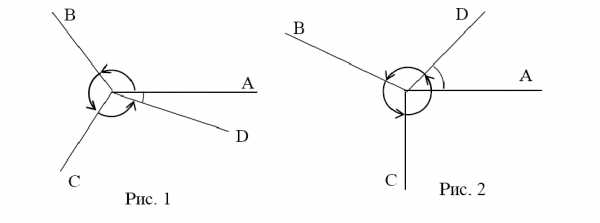
4. Углы АОВ, ВОС и СОD равны между собой, а угол АОD втрое меньше каждого из них. Все лучи ОА, ОВ, ОС, ОD различны. Найдите величину угла AOD (перечислите все возможные варианты).

Ответ. 36, 45 градусов.

Решение. Углы АОВ, ВОС и СОD следуют друг за другом в одном направлении (т.к. никакие лучи не совпадают). При этом их сумма может быть меньше 360(см. рис 1) и больше 360 (см. рис. 2).

Обозначим величину угла АОD через x. Тогда каждый из углов АОВ, ВОС и СОD равен 3x. В первом случае получается, что 3x+3x+3x+x=360, откуда x=36. Во втором 3x+3x+3x-x=360, откуда x=45.

5. На некотором острове каждый житель либо всегда лжет, либо всегда говорит правду. Трое островитян А, Б, В сказали следующее: А: «Б – лжец»; Б: «ровно один из А и В лжец»;

В: «у меня есть крокодил». Есть ли у В крокодил?

Ответ. Да, есть.

Решение. Первый способ. 1) Пусть А говорит правду. Тогда Б – лжец. Тогда А и В оба лжецы или оба «правдивцы», но т.к. А – «правдивец», то и В «правдивец», т.е. крокодил у него есть.

2) Пусть А – лжец. Тогда Б – «правдивец». Тогда ровно один из А и В лжец, но т.к. А лжец, то В – «правдивец». Т.е. крокодил у него есть.

Таким образом, в обоих случаях получаем, что у В есть крокодил.

Второй способ. 1) Пусть Б «правдивец». Тогда ровно один из А и В лжец, но т.к. А говорит, что Б лжец, то А – лжец = В «правдивец» = крокодил у него есть.

2) Пусть Б лжец. Тогда оба А и В «правдивцы», или оба лжецы. Но А говорит, что Б лжец, т.е. говорят правду = они оба (А и В) «правдивцы», т.е. у В есть крокодил.

6. Имеется 6 гирь: по паре зеленых, красных и белых. В каждой паре одна гиря тяжелая, а другая – легкая, причем все легкие весят одинаково и все тяжелые весят одинаково. Можно ли определить

3 тяжелые гири за два взвешивания на чашечных весах? (Чашечные весы показывают, равны ли веса грузов на чашках, а если не равны, то какая чашка тяжелее.)

Ответ. Да.

Решение. Обозначим зеленые гири З1 и З2, аналогично гири других цветов К1, К2, Б1, Б2. Первое взвешивание: (К1+Б1) =? (К2+З1) 1) (К1+Б1) = (К2+З1). Возможные варианты:

а) К1К2 и Б1З1. Вторым взвешиванием сравниваем Б1 и З1 и выясняем какая из них тяжелая, какая легкая и соответственно какая легкая, а какая тяжелая из К1 и К2.

2) (К1+Б1) Б1 – легкая, З1 – легкая; Б1=З2 = Б1 и З1 разные, т.е. Б1 легкая, т.е. легкие Б1 и З2; Б1З2 = Б2, З2 – легкие. 3) (К1+Б1) (К2+З1). Аналогично случаю 2)

Комментарии по проверке

Каждая задача оценивается из 7 баллов. Каждая оценка – целое число от 0 до 7. Ниже приведены некоторые указания к проверке. Естественно, всех случаев жюри предвидеть не может. При оценке решения нужно исходить из того, является ли приведенное решение в целом верным (хотя, может, и с недостатками) – тогда решение оценивается не менее чем в 4 балла. Или оно неверное (хотя, может, и с существенными продвижениями) – в этом случае оценка должна быть не выше 3 баллов.

Задача 1. Правильный пример – 7 баллов. Если есть идея подбирать сумму О+Л+И+М+П+И так, чтобы она заканчивалась на 0: 2 балла.

Задача 2. Только ответ – 1 балл. Ответ на примере – 2 балла. Далее в зависимости от полноты обоснований – от 3 до 7 баллов.

Задача 3. Только ответ – 1 балл. Верный ответ с проверкой (сказано, сколько должно весить каждое звено) – 3 балла. Верно составлено уравнение, которое затем решается подбором – не более 5 баллов.

Задача 4. За один из ответов 360 или 450, снабженный пояснениями (хотя бы в виде чертежей). – 3 балла. Только один из ответов без пояснений 1 балл. Оба ответа написаны, но нет никаких пояснений, – 3 балла.

Задача 5. Только ответ «Да» – 0 баллов. Разобран только один случай, например, что А – «правдивец»: 1 балл.

Задача 6. Приведены верные взвешивания, из которых делаются правильные выводы какие гирьки тяжелые/легкие – 7 баллов. Если хотя бы одно из взвешиваний неправильное (в итоге нельзя сделать однозначного вывода, какие гирьки какие) – 0 баллов. Приведена только верная последовательность взвешиваний, но никаких выводов и пояснений, почему она работает, нет – 4 балла.

8 класс

1. Числитель дроби увеличили на 5, а знаменатель – на 2 (числитель и знаменатель – целые положительные числа). При этом значение дроби уменьшилось. Приведите пример, как такое могло произойти. Ответ. Например, 10/3.

Комментарий. Подойдет любая дробь, большая чем 5/2.

2. Дано трехзначное число ABB. Если перемножить его цифры, то получится двузначное число АС, а если перемножить цифры АС, то получится С. Найдите исходное число.

Ответ. 144.

Решение. Так как А*С=С, то А=1 или С=0.

Первый случай: А=1. Тогда А*В*В=В²=1С, но есть только один квадрат между 10 и 20 – это 16, т.е. С=6. Откуда В=4. Т.е. исходное число 144: А=1, В=4, С=6.

Второй случай: С=0. Тогда А*В*В=А0=10А. Т.к. А – первая цифра, то А.0, можем сократить на А. Получим В²=10 – нет решения. Таким образом, ответ единственный.

3. Три математика ехали в разных вагонах одного поезда. Когда поезд подъезжал к станции, математики насчитали на перроне 7, 12 и 15 скамеек. Когда поезд отъезжал, каждый из них насчитал еще несколько скамеек, причем один из них насчитал в три раза больше, чем другой. А сколько насчитал третий?

Ответ. 7 скамеек.

Решение. Очевидно, что тот, кто до остановки проехал большую часть перрона, насчитал большее число скамеечек. Пусть первый насчитал 15 скамеек, второй 12, третий 7. Так как первый насчитал на 3 скамейки больше, чем второй, то, когда поезд будет отъезжать, второй увидит эти 3 скамейки, т.е. насчитает на 3 скамейки больше, чем первый. Аналогично третий насчитает на 8 скамеек больше, чем первый, и на 5 скамеек больше, чем второй. Раз кто-то насчитал в 3 раза больше, чем другой, то разница между насчитанными ими скамейками – четное

число (3x-x=2x). В нашем случае разность насчитанных скамеек четна только между первым и третьим и она равна 8. Значит, первый насчитал 8:2=4 скамейки, тогда второй 4+3=7 скамеек.

Замечание. Можно было обойтись и без четности. Пусть первый насчитал x скамеек. Тогда второй x+3, а третий x+8. А дальше составить всевозможные пары и решить получившиеся три уравнения (один насчитал в три раза больше, чем другой в паре): 3x=x+3, 3x=x+8, 3(x+5)=x+8. Только одно из них имеет целое решение.

4. В треугольнике АВС (см. рисунок) CD – биссектриса угла ACB, АВ=ВС, BD=BK, BL=CL. Докажите, что BF – биссектриса угла CBE.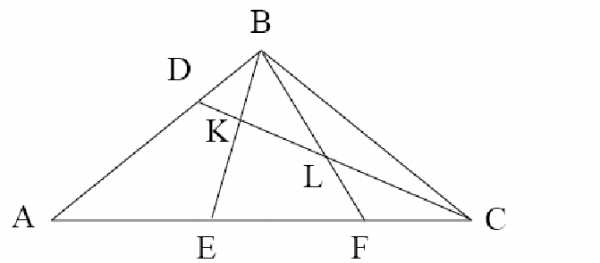

Решение. Обозначим (треугольник BDK – равнобедренный)

CBE.

5. Имеется 6 гирь: по паре зеленых, красных и белых. В каждой паре одна гиря тяжелая, а другая – легкая, причем все легкие весят одинаково и все тяжелые весят одинаково. Можно ли определить 3 тяжелые гири за два взвешивания на чашечных весах?

Ответ. Да.

Решение. Обозначим зеленые гири З1 и З2, аналогично гири других цветов К1, К2, Б1, Б2. Первое взвешивание: (К1+Б1) =? (К2+З1) 1) (К1+Б1) = (К2+З1). Возможные варианты:

а) К1К2 и Б1З1. Вторым взвешиванием сравниваем Б1 и З1 и выясняем какая из них тяжелая, какая легкая и соответственно какая легкая, а какая тяжелая из К1 и К2.

2) (К1+Б1) Б1 – легкая, З1 – легкая;

Б1=З2 = Б1 и З1 разные, т.е. Б1 легкая, т.е. легкие Б1 и З2; Б1З2 = Б2, З2 – легкие

3) (К1+Б1) (К2+З1). Аналогично случаю 2)

6. У каждого трехзначного числа нашли произведение его цифр. Получилось 900 произведений от 1*0*0 до 9*9*9 . Чему равна их сумма?

Ответ. 45³=91125.

Решение. Достаточно заметить, что если мы раскроем скобки в произведении (1+2+…+9)·(0+1+2+…+9)·(0+1+2+…+9), то получим как раз 900 перечисленных в условии слагаемых, а все три суммы, стоящие в скобках, равны 45.

Комментарии по проверке

Каждая задача оценивается из 7 баллов. Каждая оценка – целое

число от 0 до 7. При оценке решения нужно исходить из того, является ли приведенное решение

в целом верным (хотя, может, и с недостатками) – тогда решение оценивается не менее чем в 4 балла. Или оно неверное (хотя, может, и с существенными продвижениями) – в этом случае оценка должна быть не выше 3 баллов.

Задача 1. Правильный пример дроби – 7 баллов.

Задача 2. Правильный ответ – 1 балл.

Верно разобран случай А=1, случай С=0 потерян – 3 балла.

Случай А разобран верно, в обосновании невозможности случая С=0 есть те или иные погрешности 4-6 баллов.

Задача 3. Голый ответ – 2 балла. Решение перебором по возможным парам (кто насчитал в три раза больше, чем другой), но какая-то пара из трех потеряна – не более 3 баллов.

Задача 5. Приведены верные взвешивания, из которых делаются правильные выводы какие гирьки тяжелые/легкие – 7 баллов. Если хотя бы одно из взвешиваний неправильное (в итоге нельзя сделать однозначного вывода, какие гирьки какие) – 0 баллов. Приведена

только верная последовательность взвешиваний, но никаких выводов и пояснений, почему она работает, нет – 4 балла.

Задача 6. За ответ без обоснования – 3 балла. С другой стороны, не надо требовать более подробного обоснования, чем в приведенном решении. Вычислять 45³ не требуется.

9 класс

1. Придумайте такое нецелое число, что 15% и 33% от него – целые числа.

Ответ. Например, 100/3.

2. Туристам-байдарочникам нужны восемь одинаковых «сидушек» – мягких ковриков длиной не менее 35 см и шириной не менее 20 см. В спортивном магазине продаются большие коврики длиной 110 см и шириной 56 см. Хватит ли большого коврика на восемь «сидушек»?

Ответ. Да, хватит.

Решение. Разрежем большой коврик на два куска размерами 110×20 и 110×36. Из первого куска можно вырезать 3 «сидушки» размером 35×20 (и даже 36×20), а из второго куска – 5 «сидушек»

размером 35×20 (и даже 36×22).

Комментарий. Подсчет и сравнение площадей: 110*56=6160 – площадь большого ковра, 8*(35*20)=5600 – суммарная площадь маленьких, 61605600 – обоснованием не является. Например, большой ковер мог быть шириной 10 см, а длиной – километр.

Его площади хватило бы, однако ни одной «сидушки» из него вырезать нельзя.

3. Бумажный треугольник разрезали на два многоугольника прямолинейным разрезом, один из полученных многоугольников вновь разрезали на два и т. д. Какое наименьшее количество разрезов следует произвести, чтобы суммарное количество вершин у полученных многоугольников стало равно 400? Как это сделать?

Ответ. 100 разрезов.

Решение. Все получающиеся многоугольники выпуклые. Каждый разрез может идти:

а) из вершины в вершину;

б) из вершины к стороне;

в) от стороны к стороне.

В первом случае суммарное число вершин увеличивается на две, во втором – на три, в третьем – на 4. Таким образом, за один разрез общее число вершин может увеличиться максимум на 4.

Изначально у нас есть 3 вершины. Если разрезов было 99 или меньше, то общее число вершин будет 3+99*4=399

Комментарий. Возможны и другие способы разрезания.

4. У разбойников есть 13 слитков золота. Имеются весы, с помощью которых можно узнать суммарный вес любых двух слитков. Придумайте, как за 8 взвешиваний выяснить суммарный вес всех слитков.

Решение. Возьмем три первых слитка и взвесим их попарно: С1+С2, С1+С3, С2+С3, затратив три взвешивания. Сложив результаты этих взвешиваний и поделив пополам, найдем суммарный вес этих трех слитков: ((С1+С2)+(С1+С3)+(С2+С3))/2 = С1+С2+С3. За оставшиеся пять взвешиваний найдем вес остальных 10 слитков: объединим их в 5 пар и взвесим каждую пару.

5. У каждого трехзначного числа нашли произведение его цифр. Получилось 900 произведений от 1*0*0 до 9*9*9 . Чему равна их сумма?

Ответ. 45³=91125.

Решение. Достаточно заметить, что если мы раскроем скобки в произведении (1+2+…+9)·(0+1+2+…+9) ·(0+1+2+…+9), то получим как раз 900 перечисленных в условии слагаемых, а все три суммы, стоящие в скобках, равны 45.

6. Шестиугольник ABCDEF вписан в окружность. Докажите, что если AB||DE, AF||DC, то и BC||EF.

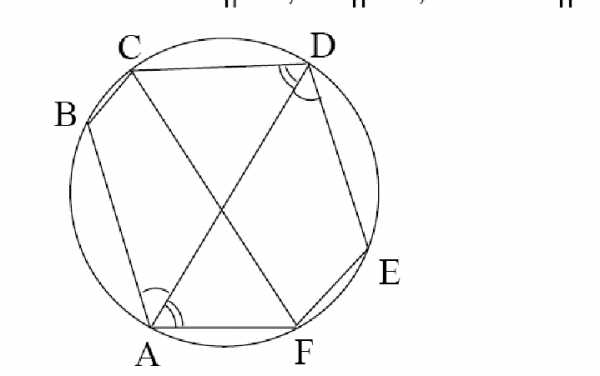
Решение. Так как АВ||DE, то

Так как четырехугольник ABCF – вписанный, то

Замечание. Можно было не использовать вписанные четырехугольники, а просто выразить оба угла BCF и CFE через дуги.

Комментарии по проверке

Каждая задача оценивается из 7 баллов. Каждая оценка – целое число от 0 до 7. При оценке

решения нужно исходить из того, является ли приведенное решение в целом верным (хотя, может, и с недостатками) – тогда решение оценивается не менее чем в 4 балла. Или оно неверное (хотя, может, и с существенными продвижениями) – в этом случае оценка должна быть не выше 3 баллов.

Задача 1. Правильный пример – 7 баллов.

Задача 2. Ответ без обоснования или с обоснованием, что площади хватает – 0 баллов. Ответ с объяснением, как резать – 7 баллов.

Задача 3. В задаче нужно сделать две вещи: 1) доказать оценку – что меньшим числом разрезаний не обойтись; 2) привести пример на данное число разрезаний. Если сделана только какая-то одна из этих двух вещей – 3 балла.

Только ответ «100 разрезаний» – 1 балл.

Задача 4. Правильные взвешивания и объяснение, как по их результатам узнать суммарный вес слитков – 7 баллов. Если используется запрещенное взвешивание (например, в какой-то момент взвешивается только один слиток) – 0 баллов.

Задача 5. За ответ без обоснования – 3 балла. С другой стороны, не надо требовать более подробного обоснования, чем в приведенном решении. Вычислять 45³ не требуется.

10 класс

1. Придумайте такое нецелое число, что 15% и 33% от него – целые числа.

Ответ. Например, 100/3.

2. Найдите сумму: 100²–99²+98²–97²+…+2²–1².

Решение.

По формуле разности квадратов 100²–99² = 100+99; 98²–97²=98+97; …

Поэтому 100²–99²+98²–97²+…+2²–1² = 100+99+98+97+96+95+..+2+1=(100+1)*100/2=5050.

Комментарий. Возможны и другие способы подсчета.

3. Встретились несколько друзей. Каждый из них обменялся рукопожатием с каждым, кроме Федота Бурчеева, который, будучи не в духе, некоторым пожал руку, а некоторым – нет.

Всего было сделано 197 рукопожатий. Сколько рукопожатий сделал Федот?

Ответ. 7 рукопожатий.

Решение. Если каждый из n человек пожмет руки всем остальным, то все сделают по n-1 рукопожатий, а всего рукопожатий будет сделано n(n-1)/2, ибо в каждом из них

участвуют двое. Посмотрим, сколько могло быть людей, кроме Федота. Заметим, что если 20 человек пожмут руки друг другу, то всего будет сделано 190 рукопожатий. Т.е. Федоту останется сделать 7 рукопожатий. Если же без Федота было менее 20 человек, то они сделали без него не более 19*18/2=171 рукопожатие, т.е. на долю Федота осталось бы не менее 26 рукопожатий, а человек, кому он мог бы пожать руку – не более 19 – противоречие. Если же без Федота было больше 20 человек, то только они одни в сумме сделали бы больше 197 рукопожатий (21*20/2=210197). Таким образом, ответ единственный – Федот сделал 7 рукопожатий.

4. На круглой арене цирка (но не в ее центре) стоит тумба, на которой сидит лев. По команде укротителя лев спрыгивает с тумбы и бежит по прямой. Добежав до бортика, он поворачивает на 90градусов, снова добегает до бортика, поворачивает на 90градусов и т.д. Докажите, что на арене (но не на тумбе) можно положить кусочек мяса так, что, независимо от первоначального направления движения, лев съест мясо. (Лев съедает мясо, если его путь проходит через точку, в которой оно лежит.)

Ответ. Мясо надо положить в точку, симметричную тумбе относительно центра окружности.

Решение. Пусть тумба находится в точке T. Тогда лев движется вдоль ломаной TABC (см. рисунок). Продолжим AT до пересечения с окружностью в точке D. Так как хорды ВС и АD перпендикулярны хорде АВ, они симметричны относительно центра окружности. (Действительно, АС – диаметр, т.к. он виден из точки В под прямым углом. Аналогично ВD диаметр. Значит, точка их пересечения – центр окружности и центр симметрии прямоугольника ABCD.) Следовательно, независимо от начального направления, лев пройдет через точку U, симметричную точке T относительно центра окружности.

5. У каждого трехзначного числа нашли произведение его цифр. Получилось 900 произведений от 1*0*0 до 9*9*9 . Чему равна их сумма?

Ответ. 45³=91125.

Решение. Достаточно заметить, что если мы раскроем скобки в произведении (1+2+…+9)·(0+1+2+…+9) ·(0+1+2+…+9), то получим как раз 900 перечисленных в условии слагаемых, а все три суммы, стоящие в скобках, равны 45.

6. Был квадратный трехчлен x²+10x+12. За один ход разрешается менять на единицу свободный член или коэффициент при x. После нескольких таких операций получили трехчлен x²+12x+10. Докажите, что в некоторый момент был трехчлен с целым корнем.

Решение. Заметим, что -1 является корнем квадратного трехчлена x²+(n+1)x+n, т.е. приведенного трехчлена, у которого коэффициент при x на 1 больше свободного члена. В изначальном трехчлене коэффициент при x меньше свободного члена, а в конечном – больше. А так как изменять мы можем только один из них на единицу, значит, в некоторый момент коэффициент при x был на 1 больше.

Комментарии по проверке

Каждая задача оценивается из 7 баллов. Каждая оценка – целое число от 0 до 7.

При оценке решения нужно исходить из того, является ли приведенное решение в целом верным (хотя, может, и с недостатками) – тогда решение оценивается не менее чем в 4 балла. Или оно неверное (хотя, может, и с существенными продвижениями) – в этом случае оценка должна быть не выше 3 баллов.

Задача 1. Правильный пример – 7 баллов.

Задача 2. Только ответ без обоснования, как он найден, – 2 балла. За представление выражения в виде суммы арифметической прогрессии – 2 балла. После этого арифметическая ошибка (но не

ошибка при подсчете количества слагаемых/пар и не ошибка в формуле, которые арифметическими не считаются) – 5 баллов.

Задача 3. Только ответ «7» без обоснования – 1 балл. Ответ с проверкой – 3 балла.

Задача 4. Ответ: «мясо нужно положить в точку, симметричную тумбе относительно центра арены», без достаточных обоснований, почему она годится – 3 балла.

Задача 5. За ответ без обоснования – 3 балла. С другой стороны, не надо требовать более подробного обоснования, чем в приведенном решении. Вычислять 45³ не требуется, если такое вычисление есть и в нем допущена ошибка, оценка не снижается.

Задача 6. Сказано, что обязательно будет корень -1, но не сказано почему – 2 балла.

11 класс

1. Придумайте такое нецелое число, что 15% и 33% от него – целые числа.

Ответ. Например, 100/3.

2. Найдите сумму: 100²–99²+98²–97²+…+2²–1².

Решение.

По формуле разности квадратов 100²–99² = 100+99; 98²–97²=98+97; …

Поэтому 100²–99²+98²–97²+…+2²–1² = 100+99+98+97+96+95+..+2+1=(100+1)*100/2=5050.

Комментарий. Возможны и другие способы подсчета.

3. Встретились несколько друзей. Каждый из них обменялся рукопожатием с каждым, кроме Федота Бурчеева, который, будучи не в духе, некоторым пожал руку, а некоторым – нет.

Всего было сделано 197 рукопожатий. Сколько рукопожатий сделал Федот?

Ответ. 7 рукопожатий.

Решение. Если каждый из n человек пожмет руки всем остальным, то все сделают по n-1 рукопожатий, а всего рукопожатий будет сделано n(n-1)/2, ибо в каждом из них

участвуют двое. Посмотрим, сколько могло быть людей, кроме Федота. Заметим, что если 20 человек пожмут руки друг другу, то всего будет сделано 190 рукопожатий. Т.е. Федоту останется сделать 7 рукопожатий. Если же без Федота было менее 20 человек, то они сделали без него не более 19*18/2=171 рукопожатие, т.е. на долю Федота осталось бы не менее 26 рукопожатий, а человек, кому он мог бы пожать руку – не более 19 – противоречие. Если же без Федота было больше 20 человек, то только они одни в сумме сделали бы больше 197 рукопожатий (21*20/2=210197). Таким образом, ответ единственный – Федот сделал 7 рукопожатий.

4. Докажите, что для любых x и y справедливо неравенство: sinxcosy+1≥sinx+cosy

Решение. Преобразуем: sinx(cosy-1)+1-cosy≥0. Последнее неравенство всегда верно, ибо cosy, sinx≤1.

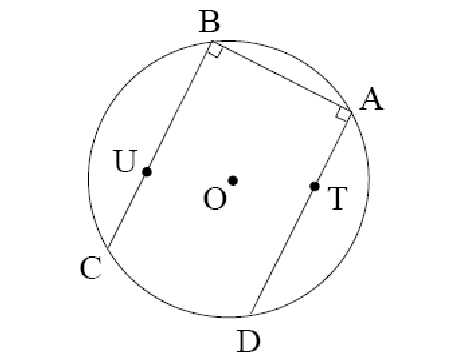
5. В четырехугольнике АВСD углы А и С – прямые. Из точек В и D опустили перпендикуляры на диагональ АC и получили соответственно точки M и N. Докажите, что AM=CN.

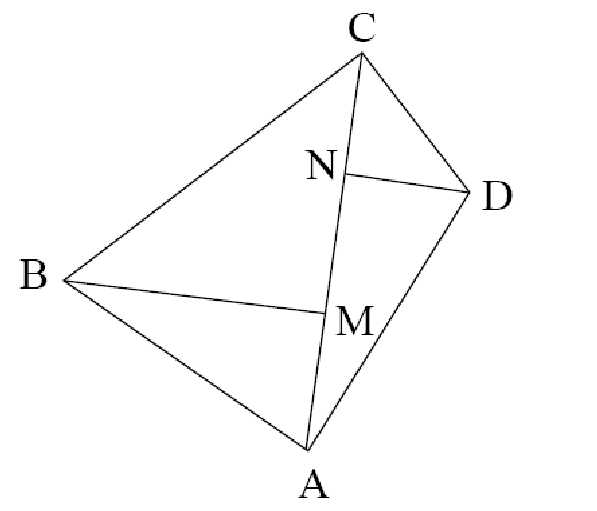
Решение. Треугольники BMC и CND – прямоугольные, при этом их острые углы BCN и DCN в сумме дают 90, следовательно

считая от точки А, а другая, считая от точки С. Значит, соответствующие отрезки AM и CN равны. Можно также вывести это явно: CM·NC =AN·MA = (AC-AM)NC=(AC-CN)MA =

AC·NC =AC·MA =NC=MA.

Второе решение. Обозначим середину отрезка NM через Q. Нетрудно видеть, что утверждение задачи равносильно тому, что Q – середина и отрезка AC. Заметим, что по теореме Фалеса точка Q есть основание перпендикуляра OQ, опущенного на CA из середины отрезка BD. Но, так как отрезок BD виден из точек A и C под прямыми углами, AC – хорда окружности с центром в точке O. А значит, OQ действительно делит отрезок AC пополам (как радиус, перпендикулярный хорде).

6. Существует ли одиннадцатигранник (не обязательно выпуклый), у которого каждая грань – многоугольник с четным числом сторон?

Ответ. Да, существует.

Решение.

Заметим, что если из куба вырезать кубик поменьше (оба куба имеют общий трехгранный угол) – см. рисунок 1, получится 9-гранник, у которого все грани – чётноугольники. А чтобы получился 11-гранник вместо большого куба возьмем шестиугольную призму – см. рисунок 2.

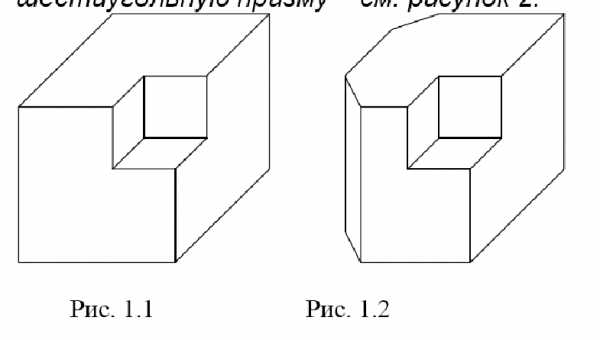
Другой пример. Рассмотрим многогранник в виде объемной буквы Т – см. рис.1. Срежем у него часть «ножки», как показано на рисунке 2. Получим 11-гранник, у которого нижняя грань

8-угольник, а остальные грани четырехугольные.

Комментарий. Кроме многогранников, изображенных на рис. 1.2 и 2.2 есть и другие примеры.

Комментарии по проверке

Каждая задача оценивается из 7 баллов. Каждая оценка – целое число от 0 до 7. При оценке

решения нужно исходить из того, является ли приведенное решение в целом верным (хотя, может, и с недостатками) – тогда решение оценивается не менее чем в 4 балла. Или оно неверное (хотя, может, и с существенными продвижениями) – в этом случае оценка должна быть не выше 3 баллов.

Задача 1. Правильный пример – 7 баллов.

Задача 2. Только ответ без обоснований, как он найден, – 2 балла.

За представление выражения в виде суммы арифметической прогрессии – 2 балла. После этого арифметическая ошибка (но не ошибка при подсчете количества слагаемых/пар или ошибка в

формуле, которые арифметическими не считаются) – 5 баллов.

Задача 3. Только ответ «7» без обоснования – 1 балл. Ответ с проверкой – 3 балла.

Задача 6. Ответ «Да» – 0 баллов. У многогранника могут быть грани, являющиеся «многоугольниками с дырками», оценка за это не снижается.

multiurok.ru

Олимпиада по математике 11 класс городской этап с ответами |

Можно ли провести в городе 10 автобусных маршрутов и установить на них остановки так, что для любых 8 маршрутов найдётся остановка, не лежащая ни на одном из них, а любые 9 маршрутов проходят через все остановки?

Ответ: можно.

Решение. Рассмотрим, например, 10 прямых плоскости. Никакие две из которых не параллельны и никакие три не пересекаются в одной точке. Будем считать, что прямые – это автобусные маршруты, а их точки пересечения – остановки. При этом с каждой остановки можно проехать на любую другую: если остановки лежат на одной прямой, то без пересадки, а если нет, то с одной пересадкой. Далее, если даже отбросить в этой схеме одну прямую, то всё ещё останется возможность проехать с каждой остановки на любую другую, сделав в пути не больше одной пересадки. Однако если отбросить две прямые, то одна остановка (точка пересечения этих прямых) уже вовсе не будет обслуживаться оставшимися маршрутами и с неё будет невозможно проехать на какую- либо другую.

Сколько существует четырехзначных чисел, не делящихся на 1000, у которых первая и последняя цифры чётны?

Ответ: 1996.

Решение. Первая цифра числа может быть любой из четырёх (2,4,6 или 8), вторая и третья – любой из десяти каждая, а четвёртая, если отказаться от условия « не делящихся на тысячу», — любой из пяти ( 0,2, 4,6 или 8). Следовательно, четырёхзначных чисел, в записи которых первая и последняя цифры чётны, всего имеется 4+10+10+5= 2000; так как среди них четыре числа (2000, 4000, 6000, 8000) делятся на 1000, то чисел, удовлетворяющих условию задачи, окажется 2000 – 4 = 1996.

3. На доске через запятую выписаны числа 1, 2, 3, … 99. Двое играющих по очереди заменяют одну из имеющихся запятых на знак «+» или «» (умножить). После того как запятых не останется, игроки вычисляют значение полученного выражения. Если результат является нечётным числом, то выигрывает первый, а если чётным – второй. Кто выигрывает при правильной игре?

Ответ: выигрывает второй игрок.

Решение. Для достижения успеха второй игрок может пользоваться симметричной стратегией: если первый ставит какой – то знак между числами к и к+1, то второй ставит такой же знак между числами 99-к и 100-к. Выражение, которое получится в конце игры, будет содержать несколько слагаемых – произведений, причём слагаемое, содержащее число 50, является чётным, а остальные слагаемые естественным образом разобьются на пары «симметричных» слагаемых одинаковой чётности. Таким образом, выражение, полученное в конце игры, окажется чётным.

4. Расположите натуральные числа от 1 до 100 в строку так, чтобы разность между любыми двумя соседними числами была равна 2 или 3.

Решение. Например, так:1, 3, 5, 2, 4, 6, 8,10, 7, 9 , 11, … , 96, 98, 100,97, 99 (в каждой пятёрке порядок расположения чисел 5к+1, 5к+3, 5к+5, 5к+2, 5к+4)

5. На какое наибольшее число натуральных слагаемых можно разложить число 96 так, чтобы все слагаемые были больше 1 и попарно взаимно просты?

Ответ: на семь слагаемых.

Решение. Приведём пример разбиения числа 96 на семь слагаемых:

9 6 = 2 + 5 + 7 + 11 + 13 + 17 + 41.

Если слагаемых больше, то среди них не менее восьми нечётных ( если их семь, то сумма нечётна). Заменим каждое из них на наименьший простой сомножитель. При этом сумма не увеличится, и все слагаемые будут различны. Но сумма восьми наименьших нечётных простых чисел равна 98.

6. Докажите, что числа от 1 до 16 можно записать в строку, но нельзя записать по кругу так, чтобы сумма любых двух соседних чисел была квадратом натурального числа.

Решение. Если рядом с числом 16 стоит число х, то 16 + 1  16 +х =а2  16 + 15, откуда а2 = 25 и х = 9. поэтому у числа 16 не может быть более одного соседа и удовлетворяющее условию расположение чисел по кругу невозможно. Пример расположения в строку:

16, 9, 7, 2, 14, 11, 5, 4, 12, 13, 3, 6, 10, 15, 1, 8.

7. Правильный 1997-угольник разбит непересекающимися диагоналями на треугольники. Докажите, что среди них ровно один — остроугольный.

Решение. Окружность, описанная около правильного 1997- угольника, является описанной и для любого треугольника данного разбиения. Так как центр окружности, описанной около правильного 1997- угольника, не лежит на диагонали, то он попадает внутрь какого-то одного треугольника.

Треугольник является остроугольным, если центр описанной окружности лежит внутри него, и тупоугольным, если центр описанной окружности лежит вне его. Следовательно, треугольник, в который попал центр описанной окружности, — остроугольный, все остальные – тупоугольные.

8. В классе 33 человека. У каждого ученика спросили, сколько у него в классе тёзок и сколько однофамильцев (включая родственников). Оказалось, что среди названных чисел встретились все целые, от 0 до 10 включительно. Докажите что в классе есть два ученика с одинаковыми именем и фамилией.

Решение. Объединим учеников в группы по фамилиям и в группы по именам (возможны группы, состоящие из одного человека, — например, ученик, не имеющий однофамильцев).

Каждый войдёт в две группы – по фамилии и по имени. Из условия задачи следует, что в классе ровно 11 групп. Действительно, есть группы, состоящие из 1, 2, …, 11 человек, поэтому групп не менее 11, но 1 + 2 + … + 11 = 66 = 2 .33, т. е. мы уже сосчитали каждого ученика дважды, значит, больше групп нет.

Рассмотрим группу из 11 человек ( скажем, однофамильцев). Остальных групп и, в частности, групп тёзок не более десяти. Поэтому какие – то двое из11 входят в одну группу тёзок, т. е. у них одинаковы и имя, и фамилия.

9. На листе бумаги проведено 11 горизонтальных и 11 вертикальных прямых, точки пересечения которых называются узлами. Звеном мы будем называть отрезок, соединяющий два соседних узла одной прямой. Какое наименьшее число звеньев надо стереть, чтобы после этого в каждом узле сходилось не более трёх звеньев?

Ответ: 41 звено.

Решение. Звенья следует стирать через одно.

10. В классе не менее 95,5% и не более 96,5% учеников учатся без двоек. При каком наименьшем числе учеников это возможно?

Ответ: 23.

Решение. Исходя из условия задачи заключаем, что хотя бы один двоечник в классе есть. Понятно, что меньше всего учеников будет в классе, где двоечник только один. Поскольку двоечников – не более 4,5% от общего числа учеников, то всего в классе не менее 1 : 0,045 =22 29 человек, т. е. не менее 23 человек. Класс из 23 учеников, среди которых ровно один двоечник, удовлетворяет условию задачи.

11. Двое по очереди закрашивают клетки таблицы 8  8. одним ходом разрешается закрасить одну или несколько клеток, расположенных либо в одной строке, либо в одном столбце таблицы. Клетки закрашенные ранее, закрашивать вторично запрещается, проигравшим считается тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре: начинающий или его партнёр?

Ответ: выигрывает партнёр начинающего.

Решение. Для того чтобы победить, он должен каждым своим ходом закрашивать клетки, симметричные клеткам, закрашенным предыдущим ходом начинающего (относительно центра доски или одной из осей симметрии доски, параллельной её краям).

12. Решить в целых числах систему уравнений

ху + z = 94,

х + уz = 95.

Ответ: х = 95, у = 0, z = 94 или х = 31, у = 2, z = 32.

Решение. Вычтя из второго уравнения первое, получим (х — z)(1 — у) = 1.

По условию, х, у, z целые, тогда возможны два случая:

1) х– z = 1, 1 – у = 1, т. е. у = 0. Подставив значение у в систему, получим: z =94, x=95.

2) х –z = -1, 1 – у = — 1, т. е. z = х +1, у = 2. Подставим найденные значения у и z в первое уравнение, получим 2х + х +1 = 94, х = 31. Отсюда z = 32.

13. Докажите, что если а2 +в2 + ав + вс + са  0, то а2 +в2  с2.

Решение. Домножим обе части неравенства на 2 и преобразуем его следующим образом:

2а2+2в2+2(ав+вс+са)0,

а2+в2+с2+2(ав+вс+са)+а2+в2с20,

(а+в+с)2+а2+в2с20,

а2+в2с2(а+в+с)20.

Отсюда а2+в2с20, или а2+в2 с2.

14. На кубе отмечены вершины и центры граней, а также проведены диагонали всех граней. Можно ли по отрезкам этих диагоналей обойти все отмеченные точки, побывав в каждой из них ровно по одному разу?

Ответ: нельзя.

Решение. Двигаясь по отрезкам диагоналей, мы проходим поочерёдно через вершины и центры граней. Но у куба 8 вершин и только 6 граней.

Можно ли на плоскости расположить бесконечное множество одинаковых кругов так, чтобы любая прямая пересекала не более двух кругов?

Ответ: можно.

Решение. Например, круги можно расположить далеко друг от друга так, чтобы их центры лежали на параболе у=х2.

Литература.

1.Н. Х. Агаханов, Д. А. Терешин, Г. М.Кузнецова ,,Школьные математические олимпиады ,, — М. : Дрофа , 2002.

2. Г.А. Гальперин, А.К.Толпыго ,,Московские математические олимпиады,, -М.: Просвещение, 1986.

3. журнал ,, Математика в школе,, №4 1995г.

urok-na-temu.ru

Разработка «Олимпиада по математике — 11 класс (школьный тур)

Школьный этап всероссийской олимпиады школьников

2016-2017 учебный год

МАТЕМАТИКА – 11 КЛАСС

Время выполнения – 90 минут

Максимальное количество баллов – 31.

1. Какое из чисел больше: или (5 баллов)

2. Постройте график функции (5 баллов)

3. Убирая детскую комнату к приходу гостей, мама нашла 9 носков. Среди любых четырёх носков хотя бы два принадлежат одному хозяину. А среди любых пяти носков не больше трёх имеют одного хозяина. Сколько детей разбросало носки, и сколько носков принадлежит каждому ребенку?

(7 баллов)

4. Дан куб. А, В и С — середины его ребер (см. рисунок). Чему равен угол ABC?

(7 баллов)

5. Сколько существует натуральных чисел п, для которых —15 является квадратом целого числа? (7 баллов)

Олимпиада, 11 класс

Решения

1. Какое из чисел больше: или

Ответ. Второе число больше.

Решение.

7¹⁰ >7² >11, поэтому 7¹¹=77¹⁰ > 7 11=77. Отсюда следует, что

Критерии проверки.

Верный ответ и доказательство — 5 баллов.

Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение- 3—4 балла

Верное рассуждение и в конце неверный ответ — 2 балла.

Только ответ — 1 балл.

2. Постройте график функции

Ответ. См. рисунок.

Решение. Используя определение модуля, получаем, что

В точках, где sin х=0, функция не определена.

Критерии проверки.

Верный график с объяснениями — 5 баллов.

График с частично выколотыми точками — 4 балла

График без выколотых точек – 3 балла

График функции, принимающей значения 1 и -1, но на неверных промежутках — 1-2 балла.

3. Убирая детскую комнату к приходу гостей, мама нашла 9 носков. Среди любых четырёх носков хотя бы два принадлежат одному хозяину. А среди любых пяти носков не больше трёх имеют одного хозяина. Сколько детей разбросало носки, и сколько носков принадлежит каждому ребенку?

Ответ. Детей трое, каждому принадлежит по три носка.

Решение. Ни одному из детей не принадлежало более трех носков, так как в противном случае условие «среди любых пяти носков не больше трех имели одного хозяина» было бы не выполнено. Всего носков 9, поэтому детей не менее трех. С другой стороны среди любых четырех носков есть два носка одного ребенка, поэтому детей меньше четырех. Таким образом, в семье трое детей, причем каждый разбросал не более трех носков, а всего носков 9. Значит, каждому ребенку принадлежит 3 носка из найденных мамой.

Критерии проверки.

Полный ответ с верным объяснением — 7 баллов.

Обосновано, что детей трое – 5-6 баллов.

Верно доказано, что детей не больше трех или что меньше четырех- 3-4 балла

Верные соображения, но решение не доведено до конца — 1-2 балла.

Ответ без обоснования — 0 баллов.

4. Дан куб. А, В и С — середины его ребер (см. рисунок). Чему равен угол ABC?

Ответ. 120°.

Решение. 1 способ. Проведем диагонали DE //ВС и EF//AB и пусть К — точка на продолжении диагонали DE за точку Е (см. рис.). Тогда угол ABC равен углу FEK. Но треугольник DEF — равносторонний, поэтому угол DEF равен 60°, а значит, угол FEK равен 120°.

2 способ.

Введем систему координат с началом в точке О, осями Ох, Оу и Oz, сонаправленными

векторам , OF и OD соответственно и пусть ребро куба равно 2.

Тогда А(0;0;1), В( 1;0;2), С(2;1;2). Поэтому ВА(-1; 0; -1), / B A / =,

ВС(1; 1; 0), /В С / = .

Теперь найдем двумя способами скалярное произведение векторов ВА и ВС

ВА ВС =(-1)1+01+(-1) 0= -1 и ВА ВС = cos ABC.

Из этих двух равенств получается, что cos АВС = -0,5, т.е. угол ABC равен 120°.

3 способ. Пусть ребро куба равно 1.

Тогда по теореме Пифагора АВ=ВС= , D C = и АС= = . Теперь по теореме косинусов из треугольника ABC находим, что cos ABC = -0,5.

Критерии проверки.

Получен верный ответ со всеми обоснованиями — 7 баллов.

Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение – 6 баллов

Решение содержит незначительные ошибки, пробелы в обоснованиях, но в целом верно и может стать полностью правильным после небольших исправлений – 5 баллов

Ход решения правильный, но ответ неверен из-за арифметической ошибки — 4 баллов.

Получен ответ 60° — 3 балла.

Доказаны некоторые утверждения – 1-2 балла

Только ответ (в том числе — верный) — 0 баллов.

5. Сколько существует натуральных чисел п, для которых —15 является квадратом целого числа?

Ответ. Два.

Решение. Пусть -15= , причем х — целое число. Очевидно, что х#0. Если х — отрицательно, то также равно -15; поэтому дальше будем считать, -15= , причем х — натуральное. Из равенства получаем: 15, а используя формулу для разложения разности квадратов на множители: (2^п-х)(2^п+х)=15. Т.к. х — натуральное число, то второй множитель слева в последнем равенстве положителен, но тогда положительным должен быть и первый множитель. Число 15 можно разложить на натуральные множители двумя способами:

15=3• 5=1 15. При этом, т.к. х > 0, то 2^п +х > 2^п-х. Таким образом, возможны только два случая:

или

Решая первую систему уравнений (удобнее всего просто сложить уравнения), получаем, что 2=16, т.е. п=3. Аналогично из второй системы получается, что п=2.

Можно не ограничиваться при решении натуральными значениями х, но тогда число систем, подлежащих рассмотрению, возрастает, т.к. возможны еще варианты

15=(-1) (-15)=(-3) (-5).

Критерии проверки.

Получен верный ответ с полным обоснованием — 7 баллов

Не рассмотрены случаи разложения 15 на отрицательные множители без обоснования,

почему можно не рассматривать отрицательные — 6 баллов.

Верно составлены системы для определения п, но не проверено, что они имеют

натуральные решения — 5 баллов.

Из двух возможностей разложения числа 15 на множители рассмотрен только один — 4

балла.

Разумные соображения, не приведшие к решению 1-2 балла.

Максимальный балл – 31.

infourok.ru

Олимпиада по математике 11 класс с ответами 2017-2018 школьный этап

1. Постройте график функции: .

2. Докажите, что 2а +>3 при 0<а<1.

3.  

4. Две окружности касаются сторон KL и MN четырехугольника KLMN: первая в точках A и B,  вторая – в точках C и D соответственно. На отрезке AC взята точка E, а на отрезке CD – точка F так, что отрезок EF касается обеих окружностей: первой – в точке G, а второй в точке H. Найдите EC, если AE=BF+9 и BD=13.

5. Дано:  Найти косинус угла между векторами и .

Решения (11 класс)

1. Графиком функции будет прямая, заданная уравнением у=4.

      =

  =

2. Найдем производную функции f(a)= 2a +  

<0 при  Значит, f(a) убывает на   (0;1), а поэтому f(0)>f(1),

где   f(1=3, то есть        2a +   >3 при      

3.Ответ: .

4.  При построении не

будем проводить стороны

KN и LM, a проведем только

KL и MN.

Так как длины касательных,

проведенных из одной точки

к одной окружности, равны,

то OC=OD, OA=OB, значит

AC=BD=13.

Обозначим EC=EH=x,

BF=FG=а, и

AE=EG=а+9 и FH=FD=у.

Тогда АС=а+9+х=13. Для отрезка ЕF запишем два выражения. С одной стороны ЕF=FH+HE=x+y, с другой стороны ЕF=EG+EF=a+a+9=2a+9, откуда получаем уравнение x+y=2a+9.

Таким образом получили систему уравнений  Решив систему, запишем а=2, х=2=ЕС.         Ответ: ЕС=2.

5. Ответ: .

konspekt-v-gruppe.ru