Обратимый процесс необратимый процесс – Процесс термодинамический необратимый обратимый — Энциклопедия по машиностроению XXL

Обратимый процесс — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 июня 2013; проверки требуют 19 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 июня 2013; проверки требуют 19 правок.

Обратимый процесс — равновесный термодинамический процесс, который может проходить как в прямом, так и в обратном направлении, проходя через одинаковые промежуточные состояния, причем система возвращается в исходное состояние без затрат энергии, и в окружающей среде не остается макроскопических изменений. Количественным критерием обратимости/необратимости процесса служит возникновение энтропии — эта величина равна нулю при отсутствии необратимых процессов в термодинамической системе и положительна при их наличии^[1][2].

Обратимый процесс можно в любой момент заставить протекать в обратном направлении, изменив какую-либо независимую переменную на бесконечно малую величину.

Обратимые процессы имеют максимальный КПД. Бо́льший КПД от системы получить невозможно. Это придает обратимым процессам теоретическую важность. На практике обратимый процесс реализовать невозможно. Он протекает бесконечно медленно, и можно только приблизиться к нему.

В термодинамике примером тепловой машины, работающей только по обратимым процессам, является машина Карно, состоящая из двух адиабат и двух изотерм. В адиабатических процессах никакого обмена энергией с окружающей средой не происходит. В изотермических процессах теплообмен между окружающей средой (нагревателем, при расширении, и холодильником, при сжатии) и рабочим телом проходит между телами, имеющими одну и ту же температуру. Это важный момент, так как если теплообмен происходит между телами с разной температурой, он является необратимым (второе н

ru.wikipedia.org

Обратимые и необратимые процессы

Первый закон термодинамики – закон сохранения энергии для тепловых процессов – устанавливает связь между количеством теплоты Q, полученной системой, изменением ΔU ее внутренней энергии и работой A, совершенной над внешними телами:

Q = ΔU + A.

Количество теплоты, сообщенное системе, идёт на изменение её внутренней энергии и на совершение работы протии внешних сил.

Процессы, нарушающие первый закон термодинамики, никогда не наблюдались. Однако, этот закон не дает никаких сведений о том, в каком направлении развиваются процессы, удовлетворяющие принципу сохранения энергии.

Различают обратимые и необратимые термодинамические процессы.

Обратимым термодинамическим процессом называется процесс, допускающий возможность возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения.

При осуществлении обратимого процесса система переходит из одного равновесного состояния в другое. Процессы, в ходе которых система все время остается в состоянии равновесия, называются квазистатическими. Все квазистатические процессы обратимы. Все обратимые процессы являются квазистатическими.

Если рабочее тело тепловой машины приводится в контакт с тепловым резервуаром, температура которого в процессе теплообмена остается неизменной, то единственным обратимым процессом будет изотермический квазистатический процесс, протекающий при бесконечно малой разнице температур рабочего тела и резервуара. При наличии двух тепловых резервуаров с разными температурами обратимым путем можно провести процессы на двух изотермических участках. Поскольку адиабатический процесс также можно проводить в обоих направлениях (адиабатическое сжатие и адиабатическое расширение), то круговой процесс, состоящий из двух изотерм и двух адиабат (

цикл Карно) является единственным обратимым круговым процессом, при котором рабочее тело приводится в тепловой контакт только с двумя тепловыми резервуарами.

Первый закон термодинамики не устанавливает направление тепловых процессов. Однако, как показывает опыт, многие тепловые процессы могут протекать только в одном направлении. Такие процессы называются необратимыми.

Необратимым термодинамическим процессом называется процесс, не допускающий возможности возвращения системы в первоначальное состояние без того, чтобы в окружающей среде остались какие-либо изменения. Такой процесс в прямом направлении протекает самопроизвольно, а для осуществления его в обратном направлении так, чтобы система вернулась в первоначальное состояние, требуется компенсирующий процесс во внешних телах, в результате которого состояние этих тел оказывается отличным от первоначальных.

Например, при тепловом контакте двух тел с разными температурами тепловой поток всегда направлен от более теплого тела к более холодному. Никогда не наблюдается самопроизвольный процесс передачи тепла от тела с низкой температурой к телу с более высокой температурой. Следовательно, процесс теплообмена при конечной разности температур является необратимым.

Все остальные круговые процессы, проводимые с двумя тепловыми резервуарами, необратимы. Необратимыми являются процессы превращения механической работы во внутреннюю энергию тела из-за наличия трения, процессы диффузии в газах и жидкостях, процессы перемешивания газа при наличии начальной разности давлений и т. д.

Все реальные процессы необратимы, но они могут сколь угодно близко приближаться к обратимым процессам. Обратимые процессы являются идеализацией реальных процессов.

Односторонняя направленность макроскопических процессов психологически воспринимается как однонаправленность времени.

Второй закон термодинамики

Опыт показывает, что разные виды энергии неравноценны в отношении способности превращаться в другие виды энергии. Механическую энергию можно целиком превратить во внутреннюю энергию любого тела. Для обратных превращений внутренней энергии в другие виды энергии существуют определенные ограничения: запас внутренней энергии ни при каких условиях не может превратиться целиком в другие виды энергии. С отмеченными особенностями энергетических превращений связано протекание процессов в природе.

Второй закон термодинамики связан непосредственно с необратимостью реальных тепловых процессов. Энергия теплового движения молекул качественно отличается от всех других видов энергии – механической, электрической, химической и т. д. Энергия любого вида, кроме энергии теплового движения молекул, может полностью превратиться в любой другой вид энергии, в том числе и в энергию теплового движения. Последняя может испытать превращение в любой другой вид энергии лишь частично. Поэтому любой физический процесс, в котором происходит превращение какого-либо вида энергии в энергию теплового движения молекул, является необратимым процессом, то есть он не может быть осуществлен полностью в обратном направлении. Общим свойством всех необратимых процессов является то, что они протекают в термодинамически неравновесной системе и в результате этих процессов

замкнутая система приближается к состоянию термодинамического равновесия.

Направление самопроизвольно протекающих процессов устанавливает второй закон (начало) термодинамики. Он может быть сформулирован в виде запрета на определенные виды термодинамических процессов.

Этот закон представляет собой результат обобщения огромного числа опытных данных.

Формулировки второго начала термодинамики:

1) по Карно: наибольший КПД тепловой машины не зависит от рода рабочего тела и вполне определяется предельными температурами, между которыми машина работает.

2) по Клаузиусу: невозможен процесс единственным результатом1 которого является передача энергии в форме теплоты от тела, менее нагретого, к телу, более нагретому.

Второе начало термодинамики не запрещает переход теплоты от менее нагретого тела к более нагретому, такой переход осуществляется в холодильной машине, но при этом внешние силы совершают работу над системой, т.е. этот переход не является единственным результатом процесса.

3) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.

На первый взгляд может показаться, что такой формулировке противоречит процесс изотермического расширения идеального газа. Действительно, все полученное идеальным газом от какого-то тела тепло превращается полностью в работу. Однако получение тепла и превращение его в работу не единственный конечный результат процесса; кроме того, в результате процесса происходит изменение объема газа.

4) по Оствальду: осуществление вечного двигателя второго рода невозможно.

Вечным двигателем второго рода называется периодически действующее устройство, которое совершает работу только за счет охлаждения одного источника теплоты.

Примером такого двигателя мог бы служить судовой двигатель, получающий тепло из моря и использующий его для движения судна. Такой двигатель был бы практически вечным, т.к. запас энергии в окружающей среде практически безграничен.

Все формулировки второго закона термодинамики эквивалентны.

Эквивалентность этих формулировок легко показать. В самом деле, допустим, что постулат Клаузиуса неверен, то есть существует процесс, единственным результатом которого была бы передача тепла от более холодного тела к более горячему. Тогда возьмем два тела с различной температурой (нагреватель и холодильник) и проведем несколько циклов тепловой машины, забрав тепло у нагревателя, отдав холодильнику и совершив при этом работу . После этого воспользуемся процессом Клаузиуса и вернем тепло от холодильника нагревателю. В результате получается, что мы совершили работу только за счет отъёма теплоты от нагревателя, то есть постулат Томсона тоже неверен.

С другой стороны, предположим, что неверен постулат Томсона. Тогда можно отнять часть тепла у более холодного тела и превратить в механическую работу. Эту работу можно превратить в тепло, например, с помощью трения, нагрев более горячее тело. Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса. Таким образом, постулаты Клаузиуса и Томсона эквивалентны.

Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.

С точки зрения статистической физики второе начало термодинамики имеет статистический характер: оно справедливо для наиболее вероятного поведения системы. Существование флуктуаций препятствует точному его выполнению, однако вероятность сколь-нибудь значительного нарушения крайне мала.

Энтропия

Энтропия (от греч. entropía — поворот, превращение), понятие, впервые введенное в термодинамику Р. Клаузиусом (1865) для определения меры необратимого рассеяния энергии, позволило строго математически сформулировать второй закон термодинамики. Энтропию можно определить с помощью двух эквивалентных подходов – статистического и термодинамического.

Термодинамический подход

Энтропия, функция состояния S термодинамической системы2, изменение которой dS для бесконечно малого обратимого изменения состояния системы равно отношению количества теплоты полученного системой в этом процессе (или отнятого от системы), к абсолютной температуре Т:

, (1)

.где dS – приращение энтропии; δQ3 – минимальная теплота, подведенная к системе; T – абсолютная температура процесса.

Величина dS является полным дифференциалом, т.е. ее интегрирование по любому произвольно выбранному пути дает разность между значениями энтропии в начальном (А) и конечном (В) состояниях:

. (2)

Теплота не является функцией состояния, поэтому интеграл от δQ зависит от выбранного пути перехода между состояниями А и В.

Энтропия измеряется в Дж/(моль·К).

Выражения (1) и (2) справедливы только для обратимых процессов.

Для необратимых процессов выполняется неравенство:

, (3)

из которого следует возрастания энтропии в этих процессах.

Свойства энтропии:

1. Энтропия — величина аддитивная, т.е. энтропия системы из нескольких тел является суммой энтропий каждого тела: S = ∑S_{i .}

2. В равновесных процессах без передачи тепла энтропия не меняется. Поэтому равновесные адиабатические процессы (δQ = 0) называется изоэнтропийным.

3. Энтропия определяется только с точностью до произвольной постоянной.

Действительно, согласно формуле (2) измеренной является лишь разность энтропий в двух состояниях.

Абсолютное значение энтропии можно установить с помощью третьего начала термодинамики (теоремы Нернста): энтропия любого тела стремится к нулю при стремлении к абсолютному нулю его температуры: lim S = 0 при Т → 0К.

Т.о., за начальную точку отсчета энтропии принимают

S₀ = 0 при Т→ 0 К.

Энтропия – функция, устанавливающая связь между макро- и микро- состояниями; единственная функция в физике, которая показывает направленность процессов.

Энтропия – в естественных науках мера беспорядка системы, состоящей из многих элементов. В частности, в статистической физике – мера вероятности осуществления какого-либо макроскопического состояния; в теории информации – мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации; в исторической науке, для экспликации феномена альтернативности истории (инвариантности и вариативности исторического процесса). Энтропия в информатике – степень неполноты, неопределённости знаний.

Понятие энтропии как показал впервые Э. Шрёдингер (1944), существенно и для понимания явлений жизни. Живой организм с точки зрения протекающих в нём физико-химических процессов можно рассматривать как сложную открытую систему, находящуюся в неравновесном, но стационарном состоянии. Для организмов характерна сбалансированность процессов, ведущих к росту энтропии и процессов обмена, уменьшающих её. Однако жизнь не сводится к простой совокупности физико-химических процессов, ей свойственны сложные процессы саморегулирования. Поэтому с помощью понятия энтропии нельзя охарактеризовать жизнедеятельность организмов в целом.

Закон возрастания энтропии

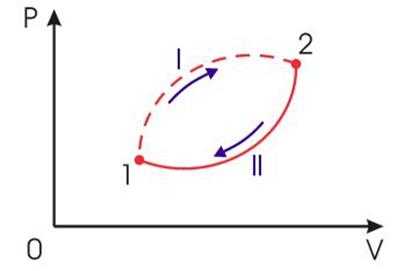
Рис.2.
Необратимый круговой термодинамический процесс

Применим неравенство (3) для описания необратимого кругового термодинамического процесса, изображенного на рис 2.

Пусть процесс будет необратимым, а процесс — обратимым. Тогда неравенство (3) для этого случая примет вид:

(4)

Так как процесс является обратимым, для него можно воспользоваться соотношением (2), которое дает:

(5)

Подстановка этой формулы в неравенство (4) позволяет получить выражение:

(6)

Сравнение выражений (2) и (6) позволяет записать следующее неравенство:

(7)

в котором знак равенства имеет место в случае, если процесс является обратимым, а знак больше, если процесс – необратимый.

Неравенство (7) может быть также записано и в дифференциальной форме:

(8)

Если рассмотреть адиабатически изолированную термодинамическую систему, для которой , то выражение (8) примет вид: ΔS = S₂ – S₁ ≥ 0

или в интегральной форме:

/dS ≥ 0 (9)

Из формулы (9) следует: S₂ ≥ S₁.

Полученные неравенства выражают собой закон возрастания энтропии, который можно сформулировать следующим образом:

В адиабатически изолированной термодинамической системе энтропия не может убывать: она или сохраняется, если в системе происходят только обратимые процессы, или возрастает, если в системе протекает хотя бы один необратимый процесс.

Записанное утверждение является ещё одной формулировкой второго начала термодинамики.

Таким образом, изолированная термодинамическая система стремится к максимальному значению энтропии, при котором наступает состояние термодинамического равновесия.

Термодинамическому равновесию адиабатической системы соответствует состояние с максимумом энтропии. Энтропия может иметь не один, а несколько максимумов, при этом система будет иметь несколько состояний равновесия. Равновесие, которому соответствует наибольший максимум энтропии называется абсолютно устойчивым (стабильным). Из условия максимальности энтропии адиабатические системы в состоянии равновесия вытекает важное следствие: температура всех частей системы в состоянии равновесия одинакова.

Рост энтропии является общим свойством всех самопроизвольно протекающих необратимых процессов в изолированных термодинамических системах. В состоянии равновесия энтропия принимает максимальное значение. В состоянии с максимальной энтропией макроскопические необратимые процессы невозможны.

При обратимых процессах в изолированных системах энтропия не изменяется.

Необходимо отметить, что если система не является изолированной, то в ней возможно уменьшение энтропии. Примером такой системы может служить, например, обычный холодильник, внутри которого возможно уменьшение энтропии. Но для таких открытых систем это локальное понижение энтропии всегда компенсируется возрастанием энтропии в окружающей среде, которое превосходит локальное ее уменьшение.

Статистический подход

В 1878 году Л. Больцман дал вероятностную трактовку понятия энтропии. Он предложил рассматривать энтропию как меру статистического беспорядкав замкнутой термодинамической системе. При этом Л. Больцман исходил из общего положения: природа стремится от состояний менее вероятных к состояниям более вероятным.

Все самопроизвольно протекающие процессы в замкнутой системе, приближающие систему к состоянию равновесия и сопровождающиеся ростом энтропии, направлены в сторону увеличения вероятности состояния. Всякое состояние макроскопической системы, содержащей большое число частиц, может быть реализовано многими способами.

Термодинамическая вероятность W состояния системы – это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние.

По определению термодинамическая вероятность W >> 1.

Например, если в сосуде находится 1 моль газа, то возможно огромное число N способов размещения молекулы по двум половинкам сосуда: N = 2 ^NAгде N_A – число Авогадро.

Каждый из них является микросостоянием. Только одно из микросостояний соответствует случаю, когда все молекулы соберутся в одной половинке (например, правой) сосуда. Вероятность такого события практически равна нулю. Наибольшее число микросостояний соответствует равновесному состоянию, при котором молекулы равномерно распределены по всему объему. Поэтому равновесное состояние является наиболее вероятным. Равновесное состояние с другой стороны является состоянием наибольшего беспорядка в термодинамической системе и состоянием с максимальной энтропией.

Согласно Больцману, энтропия S системы и термодинамическая вероятность W связаны между собой следующим образом:

S = k lnW,

где k = 1,38·10^–23 Дж/К – постоянная Больцмана.

Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы.

Вероятностная трактовка второго закона термодинамики допускает самопроизвольное отклонение системы от состояния термодинамического равновесия. Такие отклонения называются флуктуациями4. В системах, содержащих большое число частиц, значительные отклонения от состояния равновесия имеют чрезвычайно малую вероятность. Наличие флуктуаций показывает, что закон возрастания энтропии выполняется только статистически: в среднем для большого промежутка времени.



infopedia.su

Обратимые и необратимые процессы в термодинамике

Определение 1

Обратимый процесс считается в физике процессом, который возможен для проведения в обратном направлении таким образом, что система будет подвержена прохождению тех же состояний, но в обратных направлениях.

Рисунок 1. Обратимые и необратимые процессы. Автор24 — интернет-биржа студенческих работ

Определение 2

Необратимый процесс считается процессом, самопроизвольно протекающим исключительно в одном направлении.

Термодинамический процесс

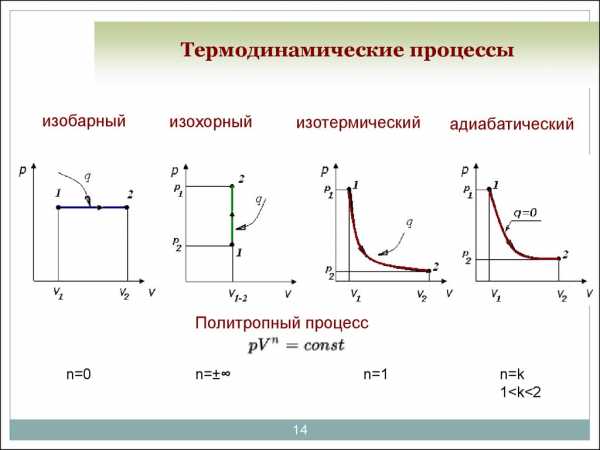
Рисунок 2. Термодинамические процессы. Автор24 — интернет-биржа студенческих работ

Термодинамический процесс представляет непрерывное изменение состояний системы, которое происходит в итоге ее взаимодействий с окружающей средой. Внешним признаком процесса будет считаться в таком случае изменение хотя бы одного параметра состояния.

Реальные процессы изменения состояния проистекают при условии присутствия значительных скоростей и разностей потенциалов (давлений и температур), существующих между системой и средой. В подобных условиях появится сложное неравномерное распределение параметров и функций состояния, исходя из объема системы, пребывающей в неравновесном состоянии. Термодинамические процессы, предусматривающие прохождение системы через ряд неравновесных состояний, будут называться неравновесными.

Изучение неравновесных процессов считается сложнейшей для ученых задачей, поскольку разработанные в рамках термодинамики методы приспособлены в основном для исследования равновесных состояний. К примеру, неравновесный процесс весьма сложно рассчитывается посредством уравнений состояния газа, применимых для равновесных условий, в то время, как в отношении всего объема системы давление и температура обладают равными значениями.

Возможно было бы выполнять приближенный расчет неравновесного процесса путем подстановки в уравнение средних значений параметров состояния, но в большинстве случаев осреднение параметров по объему системы становится невозможным.

В технической термодинамике в рамках исследования реальных процессов условно принимают распределение параметров состояния равномерным образом. Это, в свою очередь, позволяет воспользоваться уравнениями состояния и иными расчетными формулами, полученными с целью равномерного распределения в системе параметров.

В некоторых конкретных случаях погрешности, обусловленные подобным упрощением, незначительны и при расчете реальных процессов их возможно не учитывать. Если в результате неравномерности процесс ощутимо отличается от идеальной равновесной модели, то в расчет внесут соответствующие поправки.

Условия равномерно распределенных параметров в системе при изменении ее состояния, по существу подразумевают взятие идеализированного процесса в качестве объекта исследования. Подобный процесс при этом состоит из бесконечно большого количества равновесных состояний.

Такой процесс возможно представить в формате протекающего настолько медленно, что в каждый конкретный момент времени в системе установится практически равновесное состояние. Степень приближения такого процесса к равновесному окажется тем большей, чем меньшей будет при этом скорость изменения системы.

В пределе мы приходим к бесконечно медленному процессу, предоставившему непрерывную смену для состояний равновесия. Подобный процесс равновесного изменения состояния будет называться квазистатическим (или как бы статическим). Такому виду процесса будет соответствовать бесконечно малая разность потенциалов между системой и окружающей средой.

Определение 3

При обратном направлении квазистатического процесса система будет проходить через состояния, аналогичные тем, что происходят в прямом процессе. Такое свойство квазистатических процессов называют обратимостью, а сами процессы при этом являются обратимыми.

Обратимый процесс в термодинамике

Рисунок 3. Обратимый процесс в термодинамике. Автор24 — интернет-биржа студенческих работ

Определение 4

Обратимый процесс (равновесный) – представляет термодинамический процесс, способный к прохождению и в прямом, и в обратном направлении (за счет прохождения через одинаковые промежуточные состояния), система при этом возвращается в исходное состояние без энергетических затрат, а в окружающей среде не остается никаких макроскопических изменений.

Обратимый процесс возможно в абсолютно любой момент времени заставить протекать в обратном направлении, за счет изменения какой-либо независимой переменной на бесконечно малую величину. Обратимые процессы могут давать наибольшую работу. Большую работу от системы получить невозможно ни при каких условиях. Это придает теоретическую важность обратимым процессам, реализовать которые на практике также нереально.

Такие процессы протекают бесконечно медленно, и становится возможным лишь приблизиться к ним. Важно отметить существенное отличие термодинамической обратимости процесса от химической. Химическая обратимость будет характеризовать направление процесса, а термодинамическая – способ, при котором он будет проводиться.

Понятия обратимого процесса и равновесного состояния играют очень значимую роль в термодинамике. Так, каждый количественный вывод термодинамики будет применим исключительно в отношении равновесных состояний и обратимых процессов.

Необратимые процессы термодинамики

Необратимый процесс невозможен к проведению в противоположном направлении посредством все тех же самых промежуточных состояний. Все реальные процессы считаются в физике необратимыми. В качестве примеров таких процессов выступают следующие явления:

• диффузия;
• термодиффузия;
• теплопроводность;
• вязкое течение и др.

Переход кинетической энергии (для макроскопического движения) в теплоту через трение (во внутреннюю энергию системы) будет представлять собой необратимый процесс.

Все осуществляемые в природе физические процессы подразделяются на обратимые и необратимые. Пусть изолированная система вследствие некоего процесса осуществит переход из состояния А в состояние В и затем возвратится в свое изначальное состояние.

Процесс, в таком случае, станет обратимым в условиях вероятного осуществления обратного перехода из состояния В в А через аналогичные промежуточные состояния таким путем, чтобы при этом не оставалось совершенно никаких изменений в окружающих телах.

Если осуществление подобного перехода невозможно и при условии сохранения по окончании процесса в окружающих телах или внутри самой системы каких-либо изменений, то процесс окажется необратимым.

Любой процесс, сопровождающийся явлением трения, станет необратимым, поскольку, в условиях трения, часть работы всегда превратится в тепло, оно рассеется, в окружающих телах сохранится след процесса – (нагревание), что превратит процесс (с участием трения) в необратимый.

Пример 1

Идеальный механический процесс, выполняемый в консервативной системе (без сил трения), стал бы обратимым. Примером подобного процесса можно считать колебания на длинном подвесе тяжеловесного маятника. По причине незначительной степени сопротивления среды, амплитуда маятниковых колебаний становится практически неизменной на протяжении продолжительного времени, кинетическая энергия колеблющегося маятника при этом оказывается полностью переходящей в его потенциальную энергию и обратно.

В качестве важнейшей принципиальной особенности всех тепловых явлений (где участвует громаднейшее количество молекул), будет выступать их необратимый характер. Примером процесса такого характера можно считать расширение газа (в частности, идеального) в пустоту.

Итак, в природе наблюдается существование двух видов принципиально различных процессов:

• обратимых;
• необратимых.

Согласно заявлению М. Планка, сделанного однажды, различия между такими процессами, как необратимые и обратимые, будут лежать значительно глубже, чем, к примеру, между электрическими и механическими разновидностями процессов. По этой причине, его с большим основанием (сравнительно с любым другим признаком) имеет смысл выбирать как первейший принцип в рамках рассмотрения физических явлений.

spravochnick.ru

3.2. Обратимые и необратимые процессы

Глава 3 . ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ

Важно отчетливо представлять себе, что состояние равновесия в системе может быть достигнуто посредством осуществления в этой системе как обратимых, так и необратимых процессов.

На основе сказанного выше нетрудно прийти к выводу о том, что работа может производиться системой только до тех пор, пока система не придет в состояние равновесия. В самом деле, ранее было отмечено, что в любом тепловом двигателе работа может быть получена только тогда, когда имеются минимум два источника теплоты — горячий и холодный. Если же температуры горячего и холодного источников сравняются, т.е. система, включающая в себя горячий источник, рабочее тело и холодный источник, придет в тепловое равновесие, то перенос рабочим телом теплоты от горячего источника к холодному (как будет показано в дальнейшем, этот перенос теплоты может осуществляться

иобратимо, и необратимо) прекратится и работа производиться не будет.

Впроцессе перетекания воды из одного резервуара в другой (с более низким уровнем воды) может быть произведена работа, если заставить поток воды вращать колесо гидротурбины. Понятно, что работа будет совершаться рассматриваемой системой до тех пор, пока уровни воды в обоих резервуарах не сравняются.

Расширяющийся газ, перемещающий поршень в цилиндре, будет производить работу против сил внешнего давления, действующих на поршень извне, до тех пор, пока давление газа над поршнем не станет равным внешнему давлению. После этого в системе цилиндр с газом — внешняя среда установится равновесие1), поршень остановится и работа производиться не будет.

Электромотор, получающий питание от аккумулятора, будет производить работу до тех пор, пока аккумулятор не разрядится, т.е. пока потенциалы на зажимах аккумулятора не сравняются и, следовательно, разность потенциалов не станет равной нулю.

Когда мы говорим о работе, то имеем в виду работу, совершаемую против любых внешних сил, в том числе, разумеется, и против сил трения. Работа на преодоление сил трения, конечно, тоже совершается только до тех пор, пока система не придет в состояние равновесия. Так, в рассмотренном выше примере с шариком, движущимся по наклонным плоскостям, энергия шарика будет расходоваться на преодоление сил трения до тех пор, пока шарик не остановится в точке 3.

Из рассмотренных нами примеров видно, что отсутствие равновесия в системе характеризуется наличием в этой системе разности некоторых характерных величии; это может быть либо разность температур в различных частях системы, либо разность давлений, либо разность высот (и, следовательно, разность потенциальных энергий) различных частей этой системы, либо разность электрических потенциалов и т.д. Все эти, казалось бы, столь разные понятия могут быть объединены одним общим понятием, которое было введено ранее в § 2.3 — понятием обобщенной силы.

Чрезвычайно важно подчеркнуть следующее. Как уже отмечалось выше, степень необратимости того или иного необратимого процесса может быть различной. В принципе, можно представить себе степень необратимости настолько малой, что процесс будет осуществляться практически обратимо (т.е. неизбежная в любом реальном процессе необратимость будет неуловимо малой). В этой связи полезно использовать понятие о равновесных (квазистатических) и неравновесных процессах, введенное в гл. 1.

В § 1.3 было показано, что любой неравновесный процесс становится равновесным, если скорость осуществления этого процесса стремится к нулю. В то же время любой неравновесный процесс является необратимым и, наоборот, всякий равновесный процесс является процессом обратимым. Иными словами, при-

1) Условимся называть механическим равновесием равенство давлений тел, термическим (или тепловым) равновесием — равенство температур тел.

studfiles.net

§56. Круговой процесс (цикл). Обратимые и необратимые процессы

Круговым процессом (или циклом) называется процесс, при котором система, пройдя через ряд состояний, возвращается в исходное. На диаграмме процессов цикл изображается замкнутой кривой (рис.84). Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1—2) и сжатия (2—1) газа. Работа расширения (определяется площадью фигуры 1a2V₂V₁1) положительна (dV>0), работа сжатия (определяется площадью фигуры 2b1V₁V₂2) отрицательна (dV<0), Следовательно, работа, совершаемая газом за цикл, определяется площадью, охватываемой замкнутой кривой. Если за цикл совершается положительная работа (цикл протекает по часовой стрелке), то он называется прямым (рис. 84, а), если за цикл совершается отрицательная работа (цикл протекает против часовой стрелки), то он называется обратным (рис. 84,б).

Прямой цикл используется в тепловых двигателях — периодически действующих двигателях, совершающих работу за счет полученной извне теплоты. Обратный цикл

используется в холодильных машинах — периодически действующих установках, в которых за счет работы внешних сил теплота переносится к телу с более высокой температурой.

В результате кругового процесса система возвращается в исходное состояние и, следовательно, полное изменение внутренней энергии газа равно нулю. Поэтому первое начало термодинамики (51.1) для кругового процесса

Q=U+A=A, (56.1)

т. е. работа, совершаемая за цикл, равна количеству полученной извне теплоты. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому

Q=Q₁-Q₂,

где Q₁— количество теплоты, полученное системой, q₂ — количество теплоты, отданное системой. Поэтому термический коэффициент полезного действия для кругового процесса

Термодинамический процесс называется обратимым, если он может происходить как в прямом, так и в обратном направлении, причем если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяющий этим условиям, является необратимым.

Любой равновесный процесс является обратимым. Обратимость равновесного процесса, происходящего в системе, следует из того, что ее любое промежуточное состояние есть состояние термодинамического равновесия; для него «безразлично», идет процесс в прямом или обратном направлении. Реальные процессы сопровождаются диссипацией энергии (из-за трения, теплопроводности и т.д.), которая нами не обсуждается. Обратимые процессы — это идеализация реальных процессов. Их рассмотрение важно по двум при-

97

чинам: 1) многие процессы в природе и технике практически обратимы; 2) обратимые процессы являются наиболее экономичными; имеют максимальный термический коэффициент полезного действия, что позволяет указать пути повышения к. п. д. реальных тепловых двигателей.

§ 57. Энтропия, ее статистическое толкование и связь с термодинамической вероятностью

Понятие энтропии введено в 1865г. Р. Клаузиусом. Для выяснения физического содержания этого понятия рассматривают отношение теплоты Q, полученной телом в изотермическом процессе, к температуре Т теплоотдающего тела, называемое приведенным количеством теплоты.

Приведенное количество теплоты, сообщаемое телу на бесконечно малом участке процесса, равно Q/T. Строгий теоретический анализ показывает, что приведенное количество теплоты, сообщаемое телу в любом обратимом круговом процессе, равно нулю:

Из равенства нулю интеграла (57.1), взятого по замкнутому контуру, следует, что подынтегральное выражение Q/T есть полный дифференциал некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние. Таким образом,

Функция состояния, дифференциалом которой является Q/T, называется энтропией и обозначается S.

Из формулы (57.1) следует, что для обратимых процессов изменение энтропии

S=0. (57.3)

В термодинамике доказывается, что энтропия системы, совершающей необратимый цикл, возрастает:

S>0. (57.4)

Выражения (57.3) и (57.4) относятся только к замкнутым системам, если же система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом. Соотношения (57.3) и (57.4) можно представить в виде неравенства Клаузиуса

S0, (57.5)

т. е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).

Если система совершает равновесный переход из состояния 1 в состояние 2, то, согласно (57.2), изменение энтропии

где подынтегральное выражение и пределы интегрирования надо выразить через величины, характеризующие исследуемый процесс. Формула (57.6) определяет энтропию лишь с точностью до аддитивной постоянной. Физический смысл имеет не сама энтропия, а разность энтропии.

Исходя из выражения (57.6), найдем изменение энтропии в процессах идеального газа. Так как dU=(m/M)C_v dT,

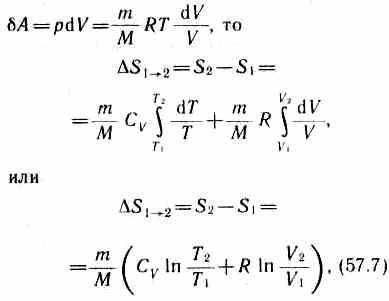
т. е. изменение энтропии S_12 идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса перехода 12.

Так как для адиабатического процесса Q = 0, то S=0 и, следовательно, S=const, т. е. адиабатический обратимый

98

процесс протекает при постоянной энтропии. Поэтому его часто называют изоэнтропийным процессом. Из формулы (57.7) следует, что при изотермическом процессе (T₁=T₂)

при изохорном процессе (V₁=V₂)

Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропии тел, входящих в систему. Свойством аддитивности обладают также внутренняя энергия, масса, объем (температура и давление таким свойством не обладают).

Более глубокий смысл энтропии вскрывается в статистической физике, энтропия связывается с термодинамической вероятностью состояния системы. Термодинамическая вероятность W состояния системы — это число способов, которыми может быть реализовано данное состояние макроскопической системы, или ‘число микросостояний, осуществляющих данное макросостояние (по определению, W1, т. е. термодинамическая вероятность не есть вероятность в математическом смысле (последняя 1!)).

Согласно Больцману (1872), энтропия S системы и термодинамическая вероятность связаны между собой следующим образом:

S = klnW, (57.8)

где k — постоянная Больцмана. Таким образом, энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Формула Больцмана (57.8) позволяет дать энтропии следующее статистическое толкование: энтропия является мерой неупорядоченности системы. В самом деле, чем больше число микросостояний, реализующих данное макросостояние, тем больше энтропия. В состоянии

равновесия — наиболее вероятного состояния системы — число микросостояний максимально, при этом максимальна и энтропия.

Так как реальные процессы необратимы, то можно утверждать, что все процессы в замкнутой системе ведут к увеличению ее энтропии — принцип возрастания энтропии. При статистическом толковании энтропии это означает, что процессы в замкнутой системе идут в направлении увеличения числа микросостояний, иными словами, от менее вероятных состояний к более вероятным, до тех пор пока вероятность состояния не станет максимальной.

Сопоставляя выражения (57.5) и (57.8), видим, что энтропия и термодинамическая вероятность состояний замкнутой системы могут либо возрастать (в случае необратимых процессов), либо оставаться постоянными (в случае обратимых процессов).

Отметим, однако, что эти утверждения имеют место для систем, состоящих из очень большого числа частиц, но могут нарушаться в системах с малым числом частиц. Для «малых» систем могут наблюдаться флуктуации, т. е. энтропия и термодинамическая вероятность состояний замкнутой системы на определенном отрезке времени могут убывать, а не возрастать, или оставаться постоянными.

studfiles.net

Обратимые и необратимые процессы

Задание: Тело массы $m_1$, удельной теплоемкости при постоянном объеме $c_{V1}$, c температурой $T_1$ приведено в тепловой контакт с телом массы $m_2$, удельной теплоемкости при постоянном объеме $c_{V2}$, c температурой $T_2$. Теплообмен происходит при постоянном объеме тел. Получите формулу, для расчета изменения энтропии. $c_{V1},\ c_{V2}$ считать независящими от температуры. $T_1>T_2$.

Решение:

Вычисление энтропии в необратимом процессе основывается на том, что она является функцией состояния. То есть если система перешла из состояния 1 в состояние 2 посредством необратимого процесса, то мы можем гипотетически перевести ее из 1 в 2 с помощью обратимого процесса и рассчитать изменение $S$.

При тепловом контакте тел их температуры выравниваются.

Запишем уравнение теплового баланса для этих тел:

\[m_1c_{V1}\left(T_1-T\right)=m_2c_{V2}\left(T{-T}_2\right)\ \left(1.1\right),\]

где T — температура тел, после установления теплового равновесия.

Из (1.1) выразим температуру:

\[T=\frac{m_1c_{V1}T_1+m_2c_{V2}T_2}{m_1c_{V1}+m_2c_{V2}}\ \left(1.2\right),\]

Опишем процесс передачи тепла с точки зрения обратимого и необратимого процесса. В необратимом процессе мы имеем ситуацию из условий задачи. А именно: два тела были изолированы друг от друга и имели разную температуру. Потом их приводят в тепловой контакт. В результате теплообмена их температура выравнивается и становится равной T (1.2). Однако переход из состояния 1 в состояние 2 можно совершить с помощью обратимых процессов. А именно: будем считать, что тела изолированы, и каждое из них обратимым процессом переводится в состояние при температуре T. После этого они приводятся в контакт, но это уже не меняет их состояние. В первом и втором процессах (обратимом и необратимом) начальные и конечные состояния одинаковы, следовательно, одинаково будет и изменение энтропии. Рассчитаем его с помощью формулы (изменения энтропии для обратимого процесса):

\[\triangle S=\int\limits^{\left(2\right)}_{\left(1\right)}{\frac{\delta Q}{T}}=m_1c_{V1}\int\limits^T_{T_1}{\frac{\delta Q}{T}}+m_2c_{V2}\int\limits^{T_2}_T{\frac{\delta Q}{T}}\ \left(1.3\right),\]

где

\[\delta Q=mc_VdT\ \left(1.4\right).\]

Подставим (1.4) для каждого тела в (1.3), получим:

\[\triangle S=m_1c_{V1}\int\limits^T_{T_1}{\frac{dT\ }{T}}+m_2c_{V2}\int\limits^{T_2}_T{\frac{dT\ }{T}}=m_1c_{V1}ln\frac{T}{T_1}+\ m_2c_{V2}ln\frac{T_2}{T}\left(1.5\right),\]

Подставим в (1.5) T из (1.2), сравним с нулем:

\[\triangle S=m_1c_{V1}ln\frac{m_1c_{V1}T_1+m_2c_{V2}T_2}{T_1(m_1c_{V1}+m_2c_{V2})}+m_2c_{V2}ln\frac{(m_1c_{V1}+m_2c_{V2})T_2}{m_1c_{V1}T_1+m_2c_{V2}T_2}\ \left(1.6\right).\]

Очевидно, что $\triangle S>0.$ Энтропия в теплообмене увеличивается.

Ответ: Изменение энтропии в данном необратимом процессе $\triangle S=m_1c_{V1}ln\frac{m_1c_{V1}T_1+m_2c_{V2}T_2}{T_1(m_1c_{V1}+m_2c_{V2})}+m_2c_{V2}ln\frac{(m_1c_{V1}+m_2c_{V2})T_2}{m_1c_{V1}T_1+m_2c_{V2}T_2}$.

spravochnick.ru

Круговой процесс (цикл). Обратимые и необратимые процессы.

Круговой процесс (цикл) — процесс, при котором система, проходя через ряд состояний, возвращается в исходное состояние. На диаграмме р-V равновесный круговой процесс изображают замкнутой кривой. Прямой цикл используют в тепловых двигателях — двигателях, действуют периодически и выполняют работу за счет полученной извне
теплоты. Обратная цикл используют в холодильных машинах — установках, действующих также периодически, но в которых за счет работы внешних сил теплота переносится в тел с высокой температурой от менее нагретых тел.

В результате кругового процесса система возвращается в исходное состояние и, значит, полное изменение внутренней энергии газа есть нуль. Поэтому первое начало термодинамики для кругового процесса

(1)

т. е. работа, которая совершается за цикл, равна количеству теплоты, полученной извне. Однако в результате кругового процесса система может теплоту как получать, так и отдавать, поэтому

где Q₁ — количество теплоты, которая получила система, Q₂ — количество теплоты, которое отдала система. Поэтому термический коэффициент полезного действия для кругового процесса

(2)

Первый закон термодинамики выражает закон сохранения и превращения энергии применительно термодинамических процессов и не позволяет определить направление протекания процессов. Чтобы в дальнейшем обсудить возможные направления протекания термодинамических процессов, разделим все процессы, которые могут происходить реально, на два класса: обратимые и необратимые.

Термодинамический процесс называют обратимым, если он может происходить как в прямом, так и в обратном направлении, причем если такой процесс происходит сначала в прямом, а затем в обратном направлении и система возвращается в исходное состояние, то в окружающей среде и в этой системе не происходит никаких изменений. Всякий процесс, не удовлетворяет этим условиям, является необратимым.

Понятие оборотного процесса можно отнести только к замкнутой системы (совокупность тел, на которые отсутствуют внешние энергетические действия и отделены от окружающих тел адиабатно оболочкой). Примерами обратимых процессов могут служить столкновения упругих тел, незатухающие колебания маятника, т.. Конечно, все процессы в реальных системах необратимы. Так, маятник через какое-то время остановится, ибо каким бы трения не было малым, но оно всегда присутствует между частями маятника и между маятником и средой.

Если перейти к тепловых процессов, то все тепловые процессы необратимы. Известно, что теплообмен всегда происходит от горячего тела к холодному, причем до тех пор, пока температуры тел не станут
одинаковыми. Например, горячий кофе, налитое в чашку, постепенно охлаждается, нагревая воздух. Но теплая кофе в чашке никогда не закипит при охлаждении окружающего воздуха. Итак, энергия всегда передается сама собой от тел с высокой температурой к телам с низкой температурой, то есть только в одном направлении. Таким образом, необратимые процессы — процессы, которые могут протекать в одном, определенном направлении.

Любой обратимый процесс является равновесным. Оборачиваемость равновесного процесса, что происходит в системе, исходит из того, что ее промежуточный состояние является состоянием термодинамического равновесия, для него «все равно», идет процесс в прямом или обратном направлении. Очевидно, что неравновесный процесс не может быть обратимым, он всегда необратим. Обратимые процессы — это идеализация реальных процессов. Но в конкретных случаях условия протекания термодинамических процессов такие, которые приблизительно можно считать обратимыми.

Энтропия.

От греческого entropia — поворот, превращение. Понятие энтропии впервые было введено в термодинамике для определения меры необратимого рассеяния энергии. Энтропия широко применяется и в других областях науки: в статистической физике как мера вероятности осуществления какого — либо макроскопического состояния; в теории информации — мера неопределенности какого-либо опыта (испытания), который может иметь разные исходы. Все эти трактовки энтропии имеют глубокую внутреннюю связь.

Энтропия — это функция состояния, то есть любому состоянию можно сопоставить вполне определенное (с точность до константы — эта неопределенность убирается по договоренности, что при абсолютном нуле энтропия тоже равна нулю) значение энтропии.

Для обратимых (равновесных) процессов выполняется следующее математическое равенство (следствие так называемого равенства Клаузиуса)

,

где — подведенная теплота, — температура, и — состояния, и — энтропия, соответствующая этим состояниям (здесь рассматривается процесс перехода из состояния в состояние ).

Для необратимых процессов выполняется неравенство, вытекающее из так называемого неравенства Клаузиуса

,

где — подведенная теплота, — температура, и — состояния, и — энтропия, соответствующая этим состояниям.

Поэтому энтропия адиабатически изолированной (нет подвода или отвода тепла) системы при необратимых процессах может только возрастать.

Используя понятие энтропии Клаузиус (1876) дал наиболее общую формулировку 2-го начала термодинамики: при реальных (необратимых) адиабатических процессах энтропия возрастает, достигая максимального значения в состоянии равновесия (2-ое начало термодинамики не является абсолютным, оно нарушается при флуктуациях).

Второе начало термодинамики

Используя понятие энтропии и неравенство Клаузиуса (см. §57),второе начало термодинамики можно сформулировать как закон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает.

Можно дать более краткую формулировку второго начала термодинамики:

в процессах, происходящих в замкнутой системе, энтропия не убывает. Здесь существенно, что речь идет о замкнутых системах, так как в незамкнутых системах энтропия может вести себя любым образом (убывать, возрастать, оставаться постоянной). Кроме того, отметим еще раз, что энтропия остается постоянной в замкнутой системе только при обратимых процессах. При необратимых процессах в замкнутой системе энтропия всегда возрастает.

Формула Больцмана (57.8) позволяет объяснить постулируемое вторым началом термодинамики возрастание энтропии в замкнутой системе при необратимых процессах: возрастание энтропии означает переход системы из менее вероятных в более вероятные состояния. Таким образом, формула Больцмана позволяет дать статистическое толкование второго начала термодинамики. Оно, являясь статистическим законом, описывает закономерности хаотического движения большого числа частиц, составляющих замкнутую систему.

Укажем еще две формулировки второго начала термодинамики:

1)по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу;

2)по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.

Можно довольно просто доказать (предоставим это читателю) эквивалентность формулировок Кельвина и Клаузиуса. Кроме того, показано, что если в замкнутой системе провести воображаемый процесс, противоречащий второму началу термодинамики в формулировке Клаузиуса, то он сопровождается уменьшением энтропии. Это же доказывает эквивалентность формулировки Клаузиуса (а следовательно, и Кельвина) и статистической формулировки, согласно которой энтропия замкнутой системы не может убывать.

Рекомендуемые страницы:

lektsia.com