Угол между прямой и плоскостью онлайн
С помощью этого онлайн калькулятора можно найти угол между прямой и плоскостью. Дается подробное решение с пояснениями. Для вычисления угла между прямой и плоскостью введите элементы уравнения и плоскости в ячейки и нажимайте на кнопку «Решить». Теоретическую часть смотрите ниже.
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Угол между прямой и плоскостью − теория, примеры и решения
В данной статье мы рассмотрим задачу определения угла φ между прямой L, заданной каноническим уравнением
| (1) |
и плоскостью P, заданной общим уравнением
где q=(
Нормальный вектор плоскости n и направляющий вектор прямой q могут составить острый угол, прямой угол и тупой угол.
Вариант 1. Угол ψ между нормальным вектором плоскости n и направляющим вектором прямой q острый (Рис.1):ψ<90°. Тогда имеем:
| cosψ=cos(90−φ)=sinφ. | (3) |
 |
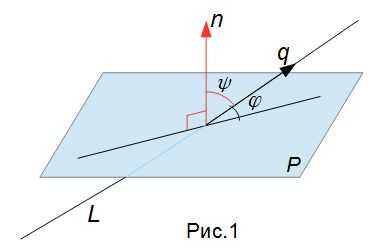Вариант 2.Угол ψ между нормальным вектором плоскости n и направляющим вектором прямой q:ψ=90°. Тогда имеем:
Вариант 3.Угол ψ между нормальным вектором плоскости n и направляющим вектором прямой q тупой (Рис.2):ψ>90°.
Тогда имеем:
| cosψ=cos(90+φ )=−sinφ. | (4) |
 |
Поскольку угол φ между прямой и плоскостью всегда меньше или равно 90°, то
Из определения скалярного произведения векторов имеем:
| (6) |
Из уравнений (5) и (6) можно найти синус угла φ
| (7) |
или
| (8) |
Из формулы (8) можно найти угол между прямой L и плоскостью P.
Пример 1. Найти угол между прямой L:
и плоскостью P:
Решение.
Направляющий вектор прямой L имеет вид q=(m, p, l)=(1, 3, 2). Нормальный вектор плоскости P имеет вид n=(A, B, C)=(2, 6, 1).
Поскольку угол φ между прямой L и плоскостью P является дополнительным к углу
Подставляя значения A, B, C, m, p, l в (11), получим:
Упростим и решим:
Найдем угол φ:
Ответ:
Пример 2. Найти угол между прямой L:
и плоскостью P:
Решение.
Направляющий вектор прямой L имеет вид q=(m, p, l)=(4, 1, 3). Нормальный вектор плоскости P имеет вид n=(A, B, C)=(8, 2, 6).
Поскольку угол φ между прямой L и плоскостью P является дополнительным к углу ψ между направляющим вектором прямой q=(m,p,l) и нормальным вектором плоскости n=(A,B,C), то cosψ=sinφ
. Из определения скалярного произведения (q,n)=|q||n|cosψ. Тогда для угла между прямой L и плоскостью P получим следующую формулу:Подставляя значения A, B, C, m, p, l в (14), получим:
Упростим и решим:
Найдем угол φ:
Ответ:
Замечание. Мы могли бы избежать вышеизложенных вычислений, если заметили, что векторы n и q коллинеарны. Действительно:
В этом случае прямая L и плоскость P перпендикулярны, т. е. угол между ними равен 90°.
matworld.ru
Угол между прямой и плоскостью. Метод координат. Задание 14
В этой статье я расскажу, как находить угол между прямой и плоскостью c помощью методом координат.
Для этого нам, как обычно, понадобятся некоторые теоретические сведения.
1. Уравнение плоскости имеет вид
2. Важно! В этом уравнении плоскости коэффициенты — координаты вектора нормали к плоскости (то есть вектора, перпендикулярного плоскости).
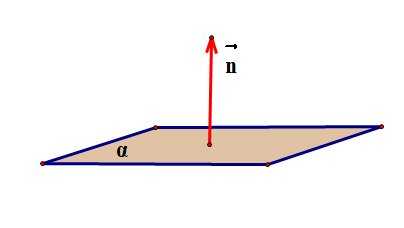
3. Косинус угла между векторами и вычисляется по формуле:
4. Любой ненулевой вектор , лежащий на прямой , или параллельный прямой , называется направляющим вектором прямой.
5. Синус угла между прямой и плоскостью равен косинусу угла между нормалью () к плоскости и направляющим вектором прямой (), поскольку
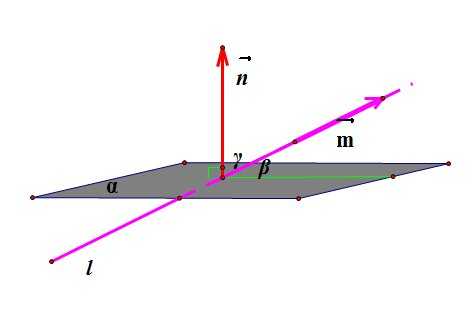То есть синус угла между прямой, направляющий вектор которой имеет координаты и плоскостью, заданной уравнением вычисляется по формуле:
Решим задачу:
В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите синус угла между прямой BD и плоскостью SBC.
Введем систему координат:
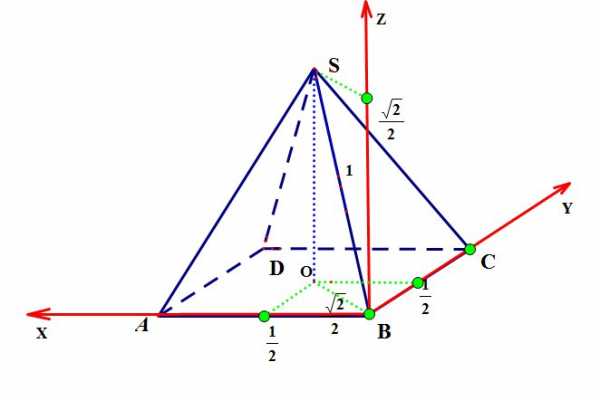
Начало координат поместим в точку В, поэтому все координаты этой точки равны нулю.
Запишем уравнение плоскости SBC. Для этого найдем координаты точек S, B и C и подставим их в уравнение плоскости
(все ребра пирамиды равны 1)
Чтобы найти координаты точки S сначала найдем координаты ее проекции на плоскость основания, а затем ее координаты по оси OZ:
Так как плоскость SBC проходит через начало координат, ,
Получим систему уравнений:
Отсюда , .
Уравнение плоскости имеет вид:
. Разделим обе части равенства на с, получим:
.
Таким образом, вектор нормали к плоскости SBC имеет координаты:
Найдем координаты направляющего вектора прямой BD. Для этого найдем координаты точек B и D, а затем из координат конца вычтем координаты начала.
D(1;1;0)
B(0;0;0),
Ответ:
И.В. Фельдман, репетитор по математике.
ege-ok.ru
Прямой и плоскостью | Начертательная геометрия
Найти угол между прямой и плоскостью — это означает найти угол между этой прямой и ее проекцией на данную плоскость.
Пространственная модель иллюстрирующая задачу найти угол между прямой и плоскостью представлена на рисунке.
Найти угол между прямой и плоскостью
План решения задачи: 1. Из произвольной точки A∈a опускаем перпендикуляр на плоскость α; 2. Определим точку встречи этого перпендикуляра с плоскостью α
. Точка Aα — ортогональная проекция A на плоскость α; 3. Находим точку пересечения прямой a с плоскостью α. Точка aα — след прямой a на плоскости α; 4. Проводим (Aαaα) — проекцию прямой a на плоскость α; 5. Определяем действительную величину ∠AaαAα, т. е. ∠φ.Решение задачи найти угол между прямой и плоскостью может быть значительно упрощено, если определять не ∠φ между прямой и плоскостью, а дополняющий до 90° ∠γ. В этом случае отпадает необходимость в определении проекции точки A и проекции прямой a на плоскость α. Зная величину γ, вычисляем по формуле:
Определение угла между прямой a и плоскостью α, заданной параллельными прямыми m и n.
Найти угол между прямой и плоскостью
Из произвольной точки на прямой a опускаем перпендикуляр к плоскости α Вращением вокруг горизонтали заданной точками 5 и 6 определяем натуральную величину ∠γ. Зная величину γ, вычисляем по формуле:
Определение угла между прямой a и плоскостью α, заданной треугольником BCD.
Найти угол между прямой и плоскостью
Из произвольной точки на прямой a опускаем перпендикуляр к плоскости α Вращением вокруг горизонтали заданной точками 3 и 4 определяем натуральную величину ∠γ. Зная величину γ, вычисляем по формуле:
Определение угла между прямой a и плоскостью α, заданной следами.
Найти угол между прямой и плоскостью
Из произвольной точки на прямой a опускаем перпендикуляр к плоскости α Вращением вокруг горизонтали заданной точками 1 и 2 определяем натуральную величину ∠γ. Зная величину γ, вычисляем по формуле:
+
ngeo.fxyz.ru
Построение угла между прямой и плоскостью
Углом между прямой и плоскостью называется угол, который прямая образует со своей проекцией на данную плоскость. Его величина может быть определена графически в соответствии с приведенным ниже алгоритмом.
Алгоритм построения
- Из произвольной точки, взятой на прямой, проводят перпендикуляр к заданной плоскости.
- Способом вращения вокруг линии уровня определяют величину угла β° между построенным перпендикуляром и прямой.
- Вычисляют искомый угол α° = 90° – β°.
Задача 1
Рассмотрим, как осуществляется описанный нами алгоритм на практике. На рисунке ниже приведены построения, с помощью которых вычислен угол α° между прямой a и плоскостью γ, заданной параллельными прямыми c и d.
Решение
- Строим проекции фронтали f и горизонтали h плоскости γ. Для этого используем вспомогательные точки 1 и 2, 3 и 4.
- Из произвольной точки K, лежащей на прямой a, опускаем перпендикуляр b на плоскость γ. Как видно на рисунке, проекция b’⊥h’, а b»⊥f».
- Определяем величину угла β° между прямыми a и b способом поворота вокруг линии уровня. Для этого сначала строим горизонталь h1 и перпендикулярно её проекции h’1 проводим луч K’O’. Центр поворота O’ = K’O’ ∩ h’1.
Определяем радиус вращения R как гипотенузу прямоугольного треугольника K0K’O’, катет которого K0K’ равен величине ZO – ZK. После этого по дуге окружности переводим точку K0 в положение K’1, как это показано на рисунке выше. Угол β° находится при вершине K’1. - Вычисляем значение искомого ∠α° = 90° – ∠β°.
Задача 2
В данном примере прямая e занимает общее положение, а плоскость γ задана следами. В отличие от предыдущей задачи здесь нет необходимости достраивать горизонталь и фронталь, поскольку их роль выполняют следы h0γ и f0γ.
Решение
- На прямой e возьмем произвольную точку N и из неё опустим перпендикуляр m на плоскость γ. Проекцию m’ нужно провести перпендикулярно h0γ, а m»⊥f0γ соответственно.
- Определяем величину угла β° между прямыми m и е способом вращения вокруг линии уровня, в качестве которой в нашей задаче была использована горизонталь h.
- Вычисляем величину искомого ∠α° = 90° – ∠β°.
Похожие задачи:
ngeometry.ru
Угол между прямой и плоскостью– определение, примеры нахождения. — Стереометрия
|
Начнем эту статью с определения угла между прямой и плоскостью. После этого покажем, как находится угол между прямой и плоскостью методом координат, подробно разберем решения характерных примеров и задач.
Навигация по странице.
- Угол между прямой и плоскостью — определение.
- Нахождение угла между прямой и плоскостью.
Угол между прямой и плоскостью — определение.
Прежде чем говорить об определении угла между прямой и плоскостью, рекомендуем освежить в памяти понятие прямой линии в пространстве и понятие плоскости.
Чтобы определить угол между прямой и плоскостью нам потребуется несколько вспомогательных определений. Дадим эти определения.
Прямая и плоскость пересекаются, если они имеют одну единственную общую точку, которую называют точкой пересечения прямой и плоскости.
При этом прямая, которая пересекает плоскость, может быть перпендикулярна к этой плоскости.
Прямая перпендикулярна к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Проекцией прямой a на плоскость называют множество проекций всех точек прямой a на плоскость .
Очевидно, что проекцией прямой, перпендикулярной к плоскости , на плоскость является их точка пересечения. Также достаточно очевидно, что проекцией прямой a, которая пересекает плоскость и не перпендикулярна к этой плоскости, на плоскость является прямая линия, лежащая в плоскости и проходящая через точку пересечения прямой a и плоскости .
Теперь нам достаточно сведений, чтобы дать определение угла между прямой и плоскостью.
Угол между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, — это угол между прямой и ее проекцией на эту плоскость.
Определение угла между прямой и плоскостью позволяет заключить, что угол между прямой и плоскостью представляет собой угол между двумя пересекающимися прямыми: самой прямой и ее проекцией на плоскость. Следовательно, угол между прямой и плоскостью есть острый угол.
Угол между перпендикулярными прямой и плоскостью считают равным , а угол между параллельными прямой и плоскостью либо не определяют вовсе, либо считают равным .
К началу страницы
Нахождение угла между прямой и плоскостью.
Условия задач, в которых приходится отыскивать угол между прямой и плоскостью, достаточно разнообразны. В зависимости от исходных данных, приходится подбирать соответствующий метод решения. Часто справиться с задачей нахождения угла между прямой и плоскостью помогают признаки равенства или подобия фигур, теорема косинусов и определения синуса, косинуса и тангенса угла. Также можно найти угол между прямой и плоскостью методом координат. Остановимся на нем подробнее.
Пусть в трехмерном пространстве введена прямоугольная система координат Oxyz , в ней задана прямая a, которая пересекает плоскость в точке M и не перпендикулярна плоскости , и требуется найти угол между прямой a и плоскостью .
Начнем с начальных данных, от которых мы будем отталкиваться при определении угла между прямой и плоскостью методом координат.
Прямой a в заданной прямоугольной системе координат Oxyz соответствуют некоторыеуравнения прямой в пространстве и направляющий вектор прямой в пространстве, а плоскости — уравнение плоскости некоторого вида и нормальный вектор плоскости. Пусть — направляющий вектор прямой a, — нормальный вектор плоскости . Итак, будем считать, что нам известны координаты направляющего вектора прямой a и координаты нормального вектора плоскости (если известны уравнения прямой aи плоскости , то координаты векторов и определяются по этим уравнениям).
Осталось получить формулу, которая позволят вычислять угол между прямой и плоскостью по известным координатам направляющего вектора прямой и нормального вектора плоскости.
Отложим векторы и от точки пересечения прямой a и плоскости . В зависимости от координат векторов и возможны четыре варианта расположения этих векторов относительно заданных прямой и плоскости. Изобразим их на чертеже.
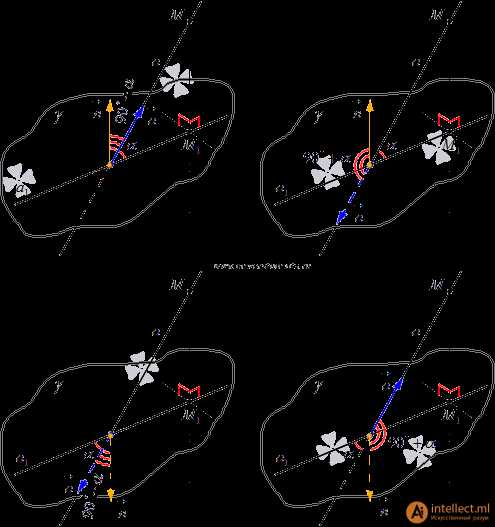
Очевидно, если угол между векторами и (обозначим его ) острый, то он дополняет искомый угол между прямой и плоскостью до прямого угла, то есть, . Если же , то .
Так как косинусы равных углов равны, то последние равенства можно записать следующим образом:
Формулы приведения приводят нас к равенствам , которые после преобразований принимают вид
То есть, синус угла между прямой и плоскостью равен модулю косинуса угла между направляющим вектором прямой и нормальным вектором плоскости.
В разделе нахождение угла между двумя векторами мы выяснили, что угол между векторами равен отношению скалярного произведения векторов и произведения длин этих векторов, тогда для вычисления синуса угла между прямой и плоскостью справедлива формула .
Следовательно, формула для вычисления угла между прямой и плоскостью по координатам направляющего вектора прямой и нормального вектора плоскости имеет вид .
Основное тригонометрическое тождество позволяет найти косинус угла при известном синусе. Так как угол между прямой и плоскостью острый, то косинус этого угла является положительным числом и вычисляется по формуле .
Теперь мы можем находить синус угла, косинус угла и сам угол между прямой и плоскостью по полученным формулам. Решим несколько характерных примеров.
Найдите угол, синус и косинус угла между прямой и плоскостью .
На векторах построена пирамида. Найдите угол между прямой AD и плоскостью ABC.
intellect.ml
Угол между прямой и плоскостью. Видеоурок. Геометрия 10 Класс
Наверняка вы слышали такое выражение: «Солнечный луч падает под углом…». (См. Рис. 1.)
Рис. 1. Падает солнечный луч
По сути, здесь идет речь об угле между прямой, частью которой является луч, и «плоскостью» земной поверхности (хотя она, конечно, не совсем плоская).
Мы привыкли, что угол бывает между двумя лучами (см. Рис. 2) или прямыми (см. Рис. 3).
Рис. 2. Угол между лучами
Рис. 3. Угол между прямыми
Как же определить угол между прямой и плоскостью?
Углом между прямой и плоскостью называют угол между прямой и ее проекцией на эту плоскость.
Чтобы построить проекцию прямой на плоскость, достаточно опустить из любых двух ее точек перпендикуляры на плоскость (спроектировать эти точки), после чего провести через них прямую – это и будет проекция (см. Рис. 4).
Рис. 4. Угол между прямой и плоскостью
Так, проекции всех точек данной прямой будут лежать на одной прямой.
Доказательство
Пусть – точка пересечения прямой и плоскости , и – точки на прямой , и – их проекции на плоскость . Докажем, что , и лежат на одной прямой . (См. Рис. 5.)
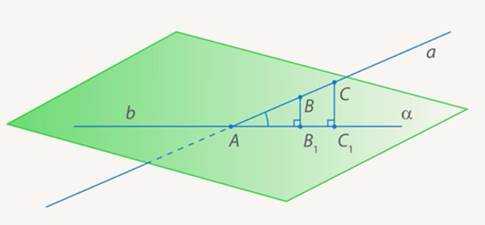
Рис. 5. Иллюстрация к доказательству
Заметим, что , так как , . Значит если рассмотреть плоскость , то точки и будут принадлежать ей. Но плоскость пересекает исходную плоскость по некоторой прямой. (См. Рис. 6.)
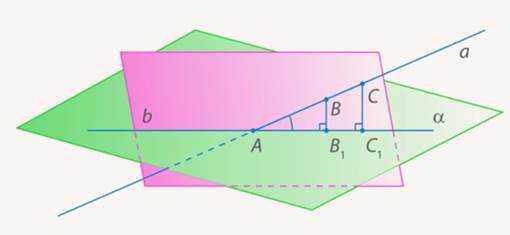
Рис. 6. Пересечение плоскостей
Значит раз точки , и принадлежат обеим плоскостям, то они лежат на этой прямой, что и требовалось доказать.
То есть мы свели новое определение к углу между прямыми, который мы уже знаем.
Обратите внимание на частую ошибку, которую допускают ученики. Углом между прямой и плоскостью называется угол именно между прямой и ее проекцией, а не между прямой и любой прямой в плоскости. Потому как такие углы могут быть разными.
Рассмотрим куб .
Решение
А) Найдите угол между прямой и плоскостью . (См. Рис. 7.)
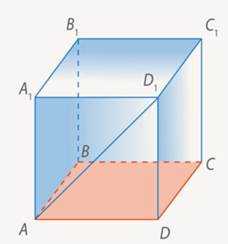
Рис. 7. Иллюстрация к примеру А
Как мы знаем, искомый угол – это угол между самой прямой и ее проекцией.
Чтобы построить проекцию прямой на плоскость, достаточно взять две точки. Одной из них будет точка пересечения прямой и плоскости – точка . Второй – проекция точки – точка , т. к. боковое ребро куба перпендикулярно плоскости основания. (См. Рис. 8.)
Рис. 8. , следовательно, точка – проекция точки на плоскость
Значит, искомый угол – это угол (см. Рис. 9), а он равен , так как это угол между диагональю и стороной квадрата.
Рис. 9. Искомый угол
Обратите внимание, что если взять вместо другую прямую из плоскости основания, например , то угол будет другим – в данном случае , так как треугольник равносторонний (все стороны – диагонали граней). (См. Рис. 10.)
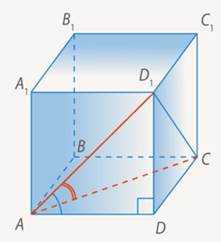
Рис. 10. Угол в равностороннем треугольнике
Так что угол между прямой и плоскостью – это совсем не угол между прямой и любой прямой в плоскости.
Б) Чему равен угол между и ? (См. Рис. 11.)
Рис. 11. Иллюстрация к примеру Б
Как мы знаем, искомый угол – это угол между самой прямой и ее проекцией.
Чтобы построить проекцию прямой на плоскость, достаточно взять две точки. Одной из них будет точка пересечения прямой и плоскости – точка . Второй – проекция точки – точка , т. к. боковое ребро куба перпендикулярно плоскости основания (см. Рис. 12).
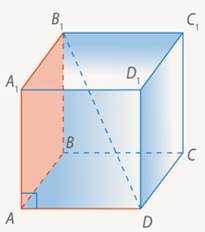
Рис. 12. , следовательно, точка – проекция точки на плоскость
Значит, искомый угол – (см. Рис. 13).
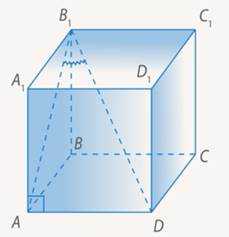
Рис. 13. Искомый угол
Его можно найти из треугольника (см. Рис. 14).
Рис. 14. Треугольник
Треугольник прямоугольный, т. к. , , значит, (см. Рис. 15).
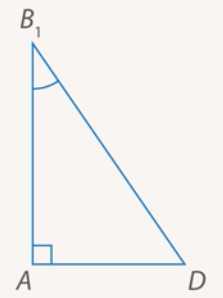
Рис. 15. Выносной рисунок треугольника
Если взять сторону куба за , тогда , и .
Ответ: , .
Вспомните, что расстояние от точки до плоскости – это кратчайший из отрезков, соединяющий исходную точку с точкой плоскости. Подобное верно и для угла: угол между прямой и плоскостью – наименьший из углов между прямой и произвольной прямой в плоскости.
Доказательство
Пусть прямая пересекает плоскость в точке , – проекция на плоскость, а – произвольная прямая в плоскости, проходящая через . Пусть также
interneturok.ru
Угол между прямой и плоскостью.
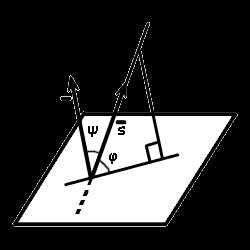
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость
Формула вычисления угла между прямой и плоскостью
Если в пространстве заданы направляющий вектор прямой L
s
={l
;m
;n}
и уравнение плоскости Ax
+ By
+ Cz
+ D = 0, то угол между этой прямой и плоскостью можно найти используя формулуsin φ = |
| A · l + B ·m + C ·n | |
| √ A2 + B2 + C2 · √ |
Вывод формулы для вычисления угла между прямой и плоскостью
Из уравнения прямой можно найти направляющий вектор прямой
s
={l
;m
;n}
Из уравнения плоскости вектор нормали плоскости имеет вид
q
= {A; B; C}Из формул скалярного произведения векторов найдем косинус угла между нормалью к плоскости и направляющим вектором прямой
cos ψ = |
| q ·s | |
| | s | · |q | |
Так как
φ
= 90° —ψ
, то синус угла между прямой и плоскостьюsin φ
=cos ψ
.Расписав скалярное произведение векторов и модуль векторов через их координаты, получим формулу для вычисления угла между прямой и плоскостью.
Пример вычисления угла между прямой и плоскостью
Пример. Найти угол между прямой
x — 4 |
= | y + 2 |
= — | z — 6 |
| 2 | 6 | 3 |
x
— 2y
+ 3z
+ 4 = 0.Решение.
Из уравнения прямой найдем направляющий вектор прямой
s
= {2; 6; -3}Из уравнения плоскости найдем вектор нормали плоскости
q
= {1; -2; 3}Воспользовавшись формулой, найдем угол между прямой и плоскостью
sin φ = |
| 2 · 1 + 6 · (-2) + (-3) · 3 | | = |
| √ 22 + 62 + (-3)2 · √12 + (-2)2 + 32 |
sin φ = |
| 2 — 12 — 9 | | = | 19 | = | 19 |
| √ 4 + 36 + 9 · √1 + 4 + 9 |
√ 49 · √14 |
7√ 14 |
o-math.com
