Логические основы компьютера – Логические основы компьютера — Логические основы устройства компьютера — Основы логики — Каталог статей

Основные логические элементы и схемы их построения

Логические основы работы компьютера

Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых “ложь” и “истина”. Таким предметом, имеющим два фиксированных состояния, может быть электрический ток.

Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если “отсутствует” электрический сигнал, и 1, если “имеется” электрический сигнал.

Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».

 

Логический элемент «НЕ» (инвертор)

Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.

У этого элемента один вход и один выход

. На функциональных схемах он обозначается:

Говорят также, что элемент «НЕ» инвертирует значение входной двоичной переменной.

 

 

Проверь соответствие логического элемента “НЕ” логическому элементу “НЕ”. Воспользуйся тренажером Логические элементы.xlsx

 

Логический элемент «И» (конъюнктор)

Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.

Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:

Сигнал на выходе конъюнктора появляется тогда и только тогда, когда поданы сигналы на все входы. На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей. Известным примером последовательного соединения проводников является елочная гирлянда: она горит, когда все лампочки исправны. Если же хотя бы одна из лампочек перегорела, то гирлянда не работает.

 Проверь соответствие логического элемента “И” логическому элементу “И”.  Воспользуйся тренажером Логические элементы.xlsx

 

Логический элемент «ИЛИ» (дизъюнктор)

Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:

Сигнал на выходе дизъюнктора не появляется тогда и только тогда, когда на все входы не поданы сигналы.

 

 

На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.

Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.

Проверь соответствие логического элемента “ИЛИ” логическому элементу “ИЛИ”.  Воспользуйся тренажером

Логические элементы.xlsx

 

Пример 1.
Составьте логическую схему для логического выражения: F=A \/ B /\ A.

1.                  Две переменные – А и В.

2.                  Две логические операции: 1-/\, 2-\/.

3.                  Строим схему:

 

 

 

 

Пример 2.
Постройте логическую схему, соответствующую логическому выражению F=А/\В\/ ¬(В\/А). Вычислить значения выражения для А=1,В=0.

1.  Переменных две: А и В; 1 4 3 2

2.  Логических операций три: /\ и две \/; А/\В\/ ¬ (В\/ А).

3.  Схему строим слева направо в соответствии с порядком логических операций:

 

 

 

 

 

 

4.  Вычислим значение выражения: F=1 /\ 0 \/ ¬(0 \/ 1)=0

mir-logiki.ru

Логические основы построения компьютера

Разделы: Информатика

---

1. Понятие, суждение, умозаключение.

Логика изучает внутреннюю структуру процесса мышления, который реализуется в таких естественно сложившихся формах мышления как понятие, высказывание и умозаключение.

Мышление всегда осуществляется через понятия, высказывания и умозаключения.

Понятие – это форма мышления, которая выделяет существенные признаки предмета или класса предметов, позволяющие отличать их от других.

Существенными называются такие признаки, каждый из которых, взятый отдельно, необходим, а все вместе достаточны, чтобы с их помощью отличить данный предмет от всех остальных и сделать обобщение, объединив однородные предметы в множество.

Примеры понятий:

Единичные понятия: самая высокая гора в Европе, этот стол, Москва и т.д.

Общие понятия: красота, металл, доброта, глупость, лес, коллектив и т.д.

Абстрактные понятия: вес, жесткость, цвет, вселенная, человечество и т.д.

Конкретные понятия: круг, дом, пламя, битва и т.д.

Любое понятие характеризуется содержанием и объемом.

Содержание понятия – совокупность (множество) его признаков.

Объем понятия – множество предметов, к которым прилагается понятие.

Высказывание – это формулировка своего понимания окружающего мира. Высказывание является повествовательным предложением, в котором что-либо утверждается или отрицается. По поводу высказывания можно сказать, истинно оно или ложно. В русском языке высказывания выражаются повествовательными предложениями:

Алупкинский дворец находится в Крыму.

Кащей Бессмертный – скупой и жадный.

В русском языке высказывания выражаются повествовательными предложениями:

в математической логике – утверждение, истинность которого (в общем случае) зависит от значений входящих в него переменных.

Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение.

Рассуждение – цепочка фактов, общих положений и умозаключений. Умозаключение представляет собой переход от сведений, которыми мы располагаем до рассуждения (посылок или условий), к выводам. Правильный способ умозаключений из истинных посылок всегда ведет к истинным выводам.

Примеры индуктивных рассуждений:

Правильны ли полученные выводы?

1)
    1 – нечетное и простое число,
    3 – нечетное и простое число.

    5 – нечетное и простое число
Вывод: все нечетные – простые числа.

2). 1=1,1+3=4,1+3+5=9,1+3+5+7=16,1+3+5+7+9=25, и т.д.

Вывод: квадрат любого числа К равен сумме К первых нечетных чисел.

3). Fe, Си, Zn. Pt – твердые тела
Вывод: все металлы-твердые.

4) В Аргентине, Эквадоре, Венесуэле говорят по-испански.
Вывод: все страны Латинской Америки – испаноязычные

2. Алгебра логики

– определяет правила записи, вычисления значений, упрощения и преобразования высказываний.

В алгебре логики высказывания обозначают буквами и называют логическими переменными.

Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей (А = 1), а если ложно – нулём (В = 0).

0 и 1 называются

логическими значениями.

Высказывания бывают простые и сложные.

Высказывание называется простым, если никакая его часть сама не является высказыванием.

Сложные (составные) высказывания строятся из простых с помощью логических операций.

Логические операции.

Конъюнкция – логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Другое название: логическое умножение.

Дизъюнкция – логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.

Другое название:

логическое сложение.

Обозначения: V, |, ИЛИ, +.

Инверсия – логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.

Другое название: логическое отрицание.

Обозначения: НЕ, ¬ , ¯ .

Импликация – это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

В естественном языке – “Если A, то B”;

Обозначение –

Логическая эквивалентность (равнозначность) – это логическая операция, ставящая в соответствие каждым двум высказываниям составное высказывание, являющееся

истинным тогда и только тогда, когда оба исходных высказывания одновременно истины или одновременно ложны.

В естественном языке – “Тогда и только тогда и в том и только том случае”;

Обозначение – ↔

Логические операции имеют следующий приоритет:

инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность

Задача.

В 10-х классах учатся 50 человек. Факультатив по математике посещают 36 человек, по физике – 20 человек, на тот и другой факультатив записаны 10 учеников.

Какое количество учащихся не посещают факультативы?

36 – 10 = 26 – число учеников посещающих математику, и не посещающих физику.

20 + 26 = 46 – число учеников, посещающих математику или физику.

50 – 46 = 4 – число учеников, которые не посещают никаких факультативов.

3. Построение таблиц истинности сложных высказываний.

Свойства логических операций.

Пример:

Справочный материал:

Решение логических задач упрощением логических выражений.

На соревнованиях по легкой атлетике Андрей, Боря, Сережа и Володя заняли первые четыре места. Но когда девочки стали вспоминать, как эти места распределились между победителями, то мнения разошлись:

Даша: Андрей был первым, а Володя – вторым.

Галя: Андрей был вторым, а Борис – третьим.

Лена: Боря был четвертым, а Сережа – вторым.

Известно, что каждая девочка в одном утверждении ошиблась, а в другом была права. Кто из мальчиков какое место занял?

Введем обозначения:

А1 – Андрей первый, А2 – Андрей второй, Б4 – Борис четвертый,

В2 – Володя второй, Б3 – Борис третий, С2 – Сережа второй

4. Базовые логические элементы компьютера

Дискретный преобразователь, который после обработки входных двоичных сигналов выдает на выходе сигнал, являющийся значением одной из логических операций, называется логическим элементом.

Базовые логические элементы реализуют три базовые логические операции:

• логический элемент “И” (конъюнктор) – логическое умножение;
• логический элемент “ИЛИ” (дизъюнктор)
– логическое сложение;
• логический элемент “НЕ” (инвертор)
– логическое отрицание.

Любая логическая операция может быть представлена в виде комбинации трех базовых, поэтому любые устройства компьютера, производящие обработку и хранение информации, могут быть собраны из базовых логических элементов.

Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы.

Есть импульс – логическое значение сигнала 1, нет импульса – значение 0.

Анализ электронной схемы.

Какой сигнал должен быть на выходе при каждом возможном наборе сигналов на входах?

Решение. Все возможные комбинации сигналов на входах А и В внесём в таблицу истинности. Проследим преобразование каждой пары сигналов при прохождении их через логические элементы и запишем полученный результат в таблицу.

Заполненная таблица истинности полностью описывает рассматриваемую электронную схему.

В инвертор поступает сигнал от входа В. В конъюнктор поступают сигналы от входа А и от инвертора. Таким образом, F= А & ¬ B

Полусумматор и сумматор.

Арифметико-логическое устройство процессора (АЛУ) содержит в своем составе
такие элементы как сумматоры. Они позволяют складывать двоичные числа.
Сложение в пределах одного разряда (без учета возможной пришедшей
единицы из младшего разряда) можно реализовать схемой, которая называется
полусумматором. У полусумматора два входа (для слагаемых) и два выхода
(для суммы и переноса).

В отличие от полусумматора сумматор учитывает перенос из предыдущего
разряда, поэтому имеет не два, а три входа.

Триггер.

(trigger-защелка, спусковой крючок) – это устройство, позволяющее запоминать, хранить и считывать информацию.

Каждый триггер хранит 1 бит информации, те он может находиться в одном из двух устойчивых состояний –логический “О” или логическая “1”.

Триггер способен почти мгновенно переходить из одного электрического состояния в другое и наоборот

Логическая схема триггера выглядит следующим образом:

Входы триггера расшифровываются следующим образом – S (от английского Set – установка) и R (Reset – сброс). Они используются для установки триггера в единичное состояние и сброса в нулевое. В связи с этим такой триггер называется RS-триггер.

Выход Q называется прямым, а противоположный – инверсный. Сигналы на прямом и инверсном выходах, конечно же, должны быть противоположны.

Пусть для определенности на вход S подан единичный сигнал, a R=0. Тогда независимо от состояния другого входа, который подсоединен к выходу Q (иначе говоря, вне зависимости от предыдущего состояния триггера), верхний по схеме элемент ИЛИ-НЕ получит на выходе 0 (результат ИЛИ равен 1, но его инверсия – 0). Этот нулевой сигнал передается на вход другого логического элемента, где на втором входе R тоже установлен 0. В итоге после выполнения логических операций ИЛИ-НЕ над двумя входными нулями этот элемент получает на выходе 1, которую возвращает первому элементу на соответствующий вход. Последнее обстоятельство очень важно: теперь, когда на этом входе установилась 1, состояние другого входа (S) больше не играет роли. Иными словами, если даже теперь убрать входной сигнал S, внутреннее распределение уровней сохранится без изменения.

Поскольку Q = 1, триггер перешел в единичное состояние, и, пока не придут новые внешние сигналы, сохраняет его. Итак, при подаче сигнала на вход S триггер переходит в устойчивое единичное состояние.

При противоположной комбинации сигналов R = 1 и S = 0 вследствие полной симметрии схемы все происходит совершенно аналогично, но теперь на выходе Q уже получается 0. Иными словами, при подаче сигнала на R-триггер сбрасывается в устойчивое нулевое состояние.

Таким образом, окончание действия сигнала в обоих случаях приводит к тому, что R = 0 и S = 0.

(Приложение 1)

xn--i1abbnckbmcl9fb.xn--p1ai

Логические основы компьютера — Логические основы устройства компьютера — Основы логики — Каталог статей

Логические основы устройства компьютера

      Компьютер работает на электричестве,  т.е. логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс – логический смысл сигнала – 1, нет импульса – 0. На входы логического элемента поступают
сигналы-значения аргументов, на выходе появляется сигнал-значение функции.

      Преобразование сигнала логическим элементом является таблицей состояния, которая фактически является таблицей истинности, соответствующей логической функции.

     Базовые логические элементы реализуют рассмотренные выше три основные логические операции:
• логический элемент «И» — логическое умножение;
• логический элемент «ИЛИ» — логическое сложение;
• логический элемент «НЕ» — инверсию.
    

     Поскольку любая логическая операция может быть представлена в виде комбинаций трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из «кирпичиков».

      Логический элемент «И». 

     На выходы А и В логического элемента (рис1)  подаются два сигнала (00,01,10 или 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического умножения.

 

      Логический элемент «ИЛИ».
 
     На входы А и В логического элемента (рис2) подаются два сигнала (00, 01, 10 или 11). На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности операции логического сложения.

 

 

Логический элемент «НЕ».

На вход А логического элемента (рис3) подается сигнал 0 или 1. На выходе получается сигнал 0 или 1 в соответствии с таблицей истинности инверсии.

 

СУММАТОР ДВОИЧНЫХ ЧИСЕЛ
ПРЕЗЕНТАЦИЯ ПО ТЕМЕ

dpk-info.ucoz.ru

Логические основы компьютера — Мегаобучалка

Алгебра логики и логические основы компьютера

Что такое алгебра логики?

Алгебра логики (булева алгебра) – это раздел математики, возникший в XIX веке благодаря усилиям английского математика Дж. Буля. Поначалу булева алгебра не имела никакого практического значения. Однако уже в XX веке ее положения нашли применение в описании функционирования и разработке различных электронных схем. Законы и аппарат алгебры логики стал использоваться при проектировании различных частей компьютеров (память, процессор). Хотя это не единственная сфера применения данной науки.

Что же собой представляет алгебра логики? Во-первых, она изучает методы установления истинности или ложности сложных логических высказываний с помощью алгебраических методов. Во-вторых, булева алгебра делает это таким образом, что сложное логическое высказывание описывается функцией, результатом вычисления которой может быть либо истина, либо ложь (1, либо 0). При этом аргументы функции (простые высказывания) также могут иметь только два значения: 0, либо 1.

Что такое простое логическое высказывание? Это фразы типа «два больше одного», «5.8 является целым числом». В первом случае мы имеем истину, а во втором ложь. Алгебра логики не касается сути этих высказываний. Если кто-то решит, что высказывание «Земля квадратная» истинно, то алгебра логики это примет как факт. Дело в том, что булева алгебра занимается вычислениями результата сложных логических высказываний на основе заранее известных значений простых высказываний.

Логические операции. Дизъюнкция, конъюнкция и отрицание(инверсия)

Так как же связываются между собой простые логические высказывания, образуя сложные? В естественном языке мы используем различные союзы и другие части речи. Например, «и», «или», «либо», «не», «если», «то», «тогда». Пример сложных высказываний: «у него есть знания и навыки», «она приедет во вторник, либо в среду», «я буду играть тогда, когда сделаю уроки», «5 не равно 6». Как мы решаем, что нам сказали правду или нет? Как-то логически, даже где-то неосознанно, исходя из предыдущего жизненного опыта, мы понимает, что правда при союзе «и» наступает в случае правдивости обоих простых высказываний. Стоит одному стать ложью и все сложное высказывание будет лживо. А вот, при связке «либо» должно быть правдой только одно простое высказывание, и тогда все выражение станет истинным.

Булева алгебра переложила этот жизненный опыт на аппарат математики, формализовала его, ввела жесткие правила получения однозначного результата. Союзы стали называться здесь логическими операторами.

Алгебра логики предусматривает множество логических операций. Однако три из них заслуживают особого внимания, т.к. с их помощью можно описать все остальные, и, следовательно, использовать меньше разнообразных устройств при конструировании схем. Такими операциями являются конъюнкция (И), дизъюнкция (ИЛИ) и отрицание (НЕ). Часто конъюнкцию обозначают &, дизъюнкцию — ||, а отрицание — чертой над переменной, обозначающей высказывание.

При конъюнкции истина сложного выражения возникает лишь в случае истинности всех простых выражений, из которых состоит сложное. Во всех остальных случаях сложное выражение будет ложно.

При дизъюнкции истина сложного выражения наступает при истинности хотя бы одного входящего в него простого выражения или двух сразу. Бывает, что сложное выражение состоит более, чем из двух простых. В этом случае достаточно, чтобы одно простое было истинным и тогда все высказывание будет истинным.

Отрицание – это унарная операция, т.к выполняется по отношению к одному простому выражению или по отношению к результату сложного. В результате отрицания получается новое высказывание, противоположное исходному.

Таблицы истинности

Логические операции удобно описывать так называемыми таблицами истинности, в которых отражают результаты вычислений сложных высказываний при различных значениях исходных простых высказываний. Простые высказывания обозначаются переменными (например, A и B).

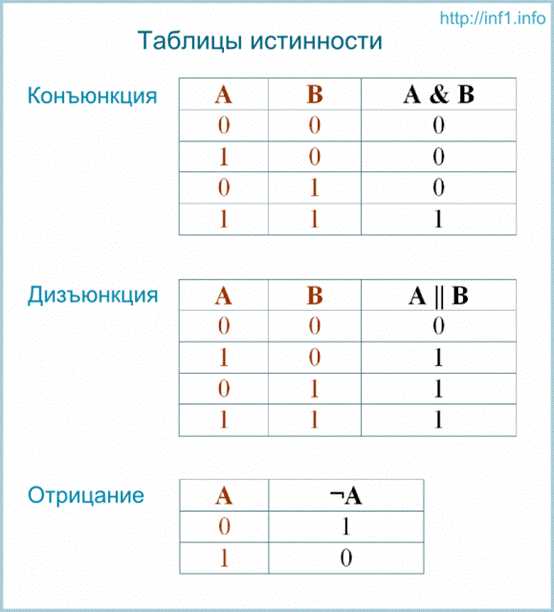
Логические основы компьютера

В ЭВМ используются различные устройства, работу которых прекрасно описывает алгебра логики. К таким устройствам относятся группы переключателей, триггеры, сумматоры.

Кроме того, связь между булевой алгеброй и компьютерами лежит и в используемой в ЭВМ системе счисления. Как известно она двоичная. Поэтому в устройствах компьютера можно хранить и преобразовывать как числа, так и значения логических переменных.

megaobuchalka.ru

Логические основы компьютера

              ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА.

Что такое алгебра логики?

Алгебра логики— это  раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности ) и логических операций над  ними.

Алгебра логики возникла в середине 19в. в трудах английского математика Джорджа Буля. Ее создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.

Логическое высказывание-это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно или ложно.

Так например, предложение «6- четное число» следует считать высказыванием, так как оно истинное. Предложение «Рим- столица Франции» тоже высказывание, так как оно ложное.

Разумеется, не всякое предложение является логическим высказыванием.

Высказывательная  форма— это повествовательное предложение, которое прямо или косвенно содержит  хотя бы одну переменную или становится высказыванием, когда все переменные замешаются своими  значениями.

Алгебра логики рассматривает любое высказывание  только с одной точки зрения- является оно ли истинным или ложным. Употребляемые в обычной речи слова и словосочетания «не», «и», «или», «если…, то», «тогда и только тогда» и др. позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.

Высказывания, образованныеиз других высказываний с помощью логических связок,называются составными. Высказывания, не являющиеся составными, называются элементарными.

Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначения:

1.Операция, выражаемая словом «не», называется отрицанием и обозначается чертой над высказыванием.

2.Операция, выражаемая связкой «и», называется конъюкцией (от лат.-соединение) или логическим умножением  и обозначается точкой.

3. Операция, выражаемая связкой «или»,называется дизъюнкцией или логическим сложением и обозначается плюсом+.

4. Операция, выражаемая связками «если …., то», «из … слудует», «…влечет …», называется импликацией и обозначается знаком→.

5. Операция, выражаемая связками «тогда и только тогда», «необходимо и достаточно», «… равносильно …», называется эквиваленцией или двойной импликацией и обозначается знаком ↔.

                Что такое логическая формула.

С помощью логических переменных и символов логических операций любое высказывание можно формализовать, т.е заменить формулой. Дадим определение логической формуле:

1. Всякая логическая переменная и символы «истинна» («1») и ложь («0»)- формулы.

2.Если А и В — формулы, то А, (А*В), (А+В), (А→В),(А↔В) — формулы.

3.Никаких других формул в алгебре логики нет.

В пункте 1 определены элементарные формулы, в пункте 2 даны правила образования из любых данных формул новых формул.

         Что такое логический элемент компьютера.

Логический элемент компьютера— часть электронной логической схемы, которая реализует элементарную логическую функцию.

Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и др. (называемые также вентилями), а также триггер.

С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода. Чтобы представить два логических состояния «1» и «0» в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт.

Высокий уровень обычно соответствует значению «истина» («1»), а низкий- значению «ложь» (0). Каждый логический элемент  имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем. Работу логических элементов описывают с помощью таблиц истинности.

Таблица истинности- это табличное представление логической схемы, в котором перечислены все возможные сочетания значений истинности входных сигналов вместе со значением истинности выходного сигнала для каждого из этих сочетаний.

         Что такое схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ.

1)Схема И реализует конъюнкцию двух или более логических значений.

Условное обозначение на структурных схемах схемы И с двумя входами представлено, а таблица истинности — в таблице 1

Таблица 1

Х	У	Х*У
0	0	0
0	1	0
1	0	0
1	1	1

2) Схема ИЛИ реализует дизъюнкцию двух или более логических значений.

Когда хотя бы на одном входе схемы ИЛИ будет единица, на ее выходе также будет единица. Таблица истинности 2

Х	У	Х+У
0	0	0
0	1	1
1	0	1
1	1	1

 3)Схема НЕ(инвертор) реализует операцию отрицания.

Таблица2

 4)Схема И-НЕ состоит из элемента И и инвертора и осуществляет отрицание результата схемы И.

 Таблица3

Х	У	Х*У
0	0	1
0	1	1
1	0	1
1	1	0

 5)Схема ИЛИ-НЕ состоит из элемента ИЛИ и инвертора и осуществляет отрицание результата схемы ИЛИ.

 Таблица4

Х	У	Х+У
0	0	1
0	1	0
1	0	0
1	1	0

                                    Что такое триггер.

Триггер- Это электронная схема, широко применяемая в регистрах компьютера для надежного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует  двоичной еденице, а другое — двоичному нулю.

Термин  «триггер» происходит от английского слова ТРИГГЕР-защелка, спусковой крючок. Самый распространенный тип триггера  — так называемый  РС — триггер. Он имеет 2 симметричных входа С и Р.

                                    Что такое сумматор.

Сумматор- это электронная логическая схема, выполняющая суммирование двоичных чисел.

Сумматор служит прежде всего центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и других устройствах машины. Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядовых двоичных чисел, представляет собой комбинацию одноразрядовых сумматоров, с рассмотрения которых мы и начнем. Одноразрядовый  двоичный сумматор есть устройство с тремя входами и двумя выходами,работа которого может быть описана следующей таблицей истинности:

	Входы			Выходы
Первое слагаемое	Второе слагаемое	перенос		сумма	перенос
0	0	0		0	0
0	0	1		1	0
0	1	0		1	0
0	1	1		0	1
1	0	0		1	0
1	0	1		0	1
1	1		0	0	1
1	1		1	1	1

 Если требуется складывать двоичные слова длиной два и более бит, то можно использовать последовательное соединение таких сумматоров, причем для двух соседних сумматоров выход переноса одного сумматора  является входом для другого.  

                     Что такое переключательная схема.

Переключательная схема-это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников , а так же из входов и выходов, на которые подается и с которых снимается электрический сигнал.

Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Две схемы называются равносильными, если через одну из них проходит ток тогда и только тогда, когда он проходит через другую. Из двух равносильных схем более простой считается та схема, функция проводимости которой содержит меньшее число логических операций или переключателей. При рассмотрении переключательных схем возникают две основные задачи: синтез и анализ схемы. Синтез схемы по заданным условиям ее работы сводится к следующим трем этапам:

—составление функции проводимости по таблице истинности, отражающей эти условия;

-упрощение этой функции;

-построение соответствующей схемы.

Анализ схемы сводится к:

-определению значений ее функции проводимости при всех возможных наборах входящих в эту функцию переменных;

-получению упрощенной формулы.

                             Решение логических задач.

Разнообразие логических задач очень велико. Способов решения тоже не мало. Но наибольшее распространение получили следующие три способа решения логических задач: средствами алгебры логики; табличный; с помощью рассуждений.

 Решение логических задач средствами алгебры логики

 Обычно используется следующая схема решения:

-изучается условие задачи;

-вводится система обозначений для логических высказываний;

-конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;

-определяются значения истинности этой логической формулы;

-из полученных значений истинности формулы определяются значения истинности введенных логических высказываний, на основании которых делается заключение о решении.

coolreferat.com

Основы логики и логические основы компьютера

Разделы: Информатика

---

Изучение темы рассчитано на 6 часов в 10-х классах.

При объяснении нового материала используется презентация (Приложение 1).

Основные цели:

1. Познакомить учащихся с основными понятиями алгебры логики: логические константы, переменные, функции, элементарные логические операции, логические выражения.
2. Научить строить таблицу истинности по заданному логическому выражению.
3. Изучить законы алгебры логики.

• Логика – наука о формах и способах мышления
• Логика изучает внутреннюю структуру процесса мышления
• Алгебра логики – булева алгебра. Цель алгебры логики – описание поведения и структуры логических схем

Формы мышления

Понятие		Суждение		Умозаключение	Доказательство
Отражает наиболее существенные свойства предмета		Высказывание строится на основе понятий		На основе известных фактов делается вывод	Мыслительный существенные процесс, направленный на подтверждение или опровержение кого-либо положения
Содержание	Объем	Истинное	Ложные
Совокупность существенных признаков предметов	Совокупность предметов, на которые данное понятие распространяется	Простое, сложное

Истинные высказывания правильно отражают свойства и отношения реальных вещей.

Ложные высказывания не соответствуют реальной действительности.

Алгебра высказываний

• Объекты алгебры логики – высказывания.
• Высказывания обозначаются заглавными латинскими буквами.
• Каждому логическому высказыванию ставится в соответствие логическая переменная, которое принимает значение “истина” или “ложь”. А=1 – истина, В=0 – ложь.
• Составные высказывания образуются из простых с помощью союзов “и”, “или”, которые в алгебре логики заменяются на логические операции.

Высказывания:

• Истинное высказывание правильно отражает свойства и отношение реальных вещей (2*2=4).
• Ложное высказывание
не соответствует реальной действительности (2*2=5).

Виды высказываний:

1. Простые и сложные.
2. Истинные и ложные.

Логические операции

• Логическое умножение – И – коньюнкция – AND.
• Логическое сложение – ИЛИ – дизъюнкция –OR.
• Логическое отрицание – НЕ – NOT.

Логические операции задаются таблицами истинности.

Операция “ИЛИ” – “OR” – операция логического сложения:

A	B	A OR B
0	0	0
0	1	1
1	0	1
1	1	1

Операция “И” – “AND” – операция логического умножения:

A	B	A AND B
0	0	0
0	1	0
1	0	0
1	1	1

Операция “НЕ” – “NOT” – операция логического отрицания:

Импликация – логическое следование:

A	B	A -> B
0	0	1
0	1	1
1	0	0
1	1	1

Составное высказывание, образованное с помощью операции логического следования (импликации) ложно тогда и только тогда, когда из истинной посылки (первого высказывания) следует ложный вывод (второе высказывание)

Эквиваленция – равнозначность:

A	B	A <-> B
0	0	1
0	1	0
1	0	0
1	1	1

Составное высказывание, образованное с помощью логической операции эквивалентности, истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.

Логические выражения и таблицы истинности

• Логическое выражение – это выражение, которое включает в себя логические переменные, объединенные логическими операциями
• Таблица истинности определяет истинность или ложность составного высказывания

Пример

Определить истинность или ложность логического высказывания:

A AND B OR C AND A

A & B OR C & A

A ^ B OR C ^ A

Алгоритм построения таблицы истинности, по логическому выражению:

1. Посчитать кол-во переменных в лог. Выражении n=
2. Определить число строк в таблице, которое равно m=2ⁿ
3. Посчитать кол-во логических операций k=
4. Определить кол-во столбцов в таблице k 2=n+k=
5. Заполнить столбцы входными переменными.
6. Ввести название столбцов, с учётом порядка действий:

Инверсия, логическое умножение, логическое сложение.

A	B	C	A and B	C and A	A and B or C and A
0	0	0	0	0	0
0	0	1	0	0	0
0	1	0	0	0	0
0	1	1	0	0	0
1	0	0	0	0	0
1	0	1	0	1	1
1	1	0	1	0	1
1	1	1	1	1	1

Логическая функция.

Любое логическое выражение можно рассматривать как логическую функцию.

Логической функцией называют функцию F(x₁, x₂, …x_n) – функция от логических переменных, которая может принимать значения либо логического “0”, либо логической “1”. Для каждой логической функции имеется таблица истинности логической функции.

Логическая функция может быть задана табличным способом или в виде соответствующих формул.

Каждая логическая функция 2-х аргументов имеет 4 возможных набора значений аргументов: 00, 01, 10, 11.

N = 2⁴ = 16 различных логических функций.

Законы алгебры логики:

Закон тождества

A = A

Закон непротиворечия

A & not A = 0

Закон исключения третьего

A and not A = 1

Закон двойного отрицания

Not (not A) =1

Закон Де Моргана

• Not (A & B) = not A or not B
• Not (A or B) = not A & not B

Правила коммутативности:

• A & B = B & A
• A or B = B or A

Правила ассоциативности

• (A & B) & C = A & (B & C)
• (A or B) or C = A or (B or C)

Правила дистрибутивности

• (A & B) OR (A & C) = A & (B OR C)
• (A or B) & (A or C) = A or (B & C)

Правила равносильности

Правила исключения констант

• A or 1 = 1
• A or 0 = A
• A & 1 = A
• A & 0 = 0

Вопросы по теме: “Основы логики и логические основы компьютера”:

1. Что такое логика?
2. Основные формы мышления.
3. Что такое высказывание. Какие высказывания существуют?
4. Какие значения могут принимать логические переменные?
5. Что такое логическое выражение?
6. Перечислить основные логические операции и таблицы истинности.
7. При построении таблицы истинности чему равно а) количество строк, б) количество столбцов?
8. Что такое логическая функция?
9. Какие значения может принимать логическая функция?
10. Каким образом может быть задана логическая функция?

Практические задания по теме

Построить таблицу истинности по булеву выражению:

1. F(x1, x2, x3) = x3 \/ (2 & x1 & x3)

2. F(x1, x2, x3) = 1 & 2 \/ x2 \/ x1 & x3

3. F(x1, x2, x3) = 1 & x2 & x3 \/ 1 \/ x2 \/ x3

Используемая литература:

1. Информатика и ИКТ. Профильный уровень: учебник для 10 класса / Н.Д. Угринович.

Презентация

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai

Логические основы компьютера

Перейти к основному содержанию

Breadcrumbs

You are here:

1. Главная
2. Теория информатики

• Алгебра логики и логические основы компьютера
• Законы алгебры логики
• Логические элементы. Вентили
• Сумматор и полусумматор
• Триггер как элемент памяти. Схема RS-триггера
• Практическое значение алгебры логики
• Битовые операции

Перекрёстные ссылки книги для Логические основы компьютера

• RGB модель
• Вверх
• Алгебра логики и логические основы компьютера

Теория

• Информатика
• Информация
• Системы счисления
• Кодирование информации
• Логические основы компьютера
  • Алгебра логики и логические основы компьютера
  • Законы алгебры логики
  • Логические элементы. Вентили
  • Сумматор и полусумматор
  • Триггер
  • Практическое значение алгебры логики
  • Битовые операции
• Теория алгоритмов
• Аппаратное обеспечение
• Программное обеспечение
• Компьютерное моделирование
• Вирусы и безопасность
• Программирование
• Компьютерные сети

Решение задач ЕГЭ

• Кодирование и измерение информации
• Системы счисления
• Логические выражения

Программирование в КуМир

• Линейные алгоритмы
• Условный оператор
• Циклы
• Массивы
• Строки
• Функции
• Файлы

Footer menu

• Контакт

inf1.info