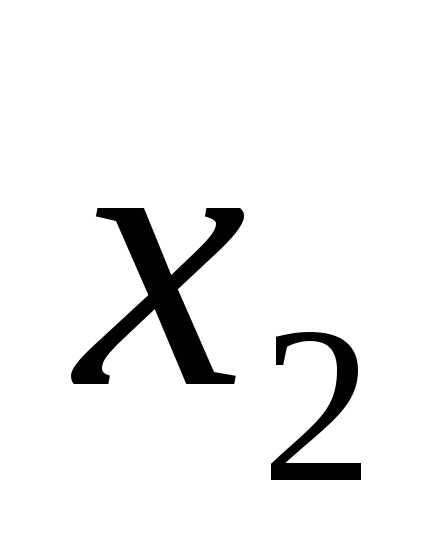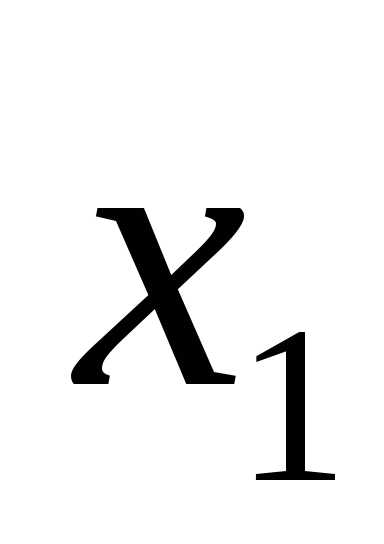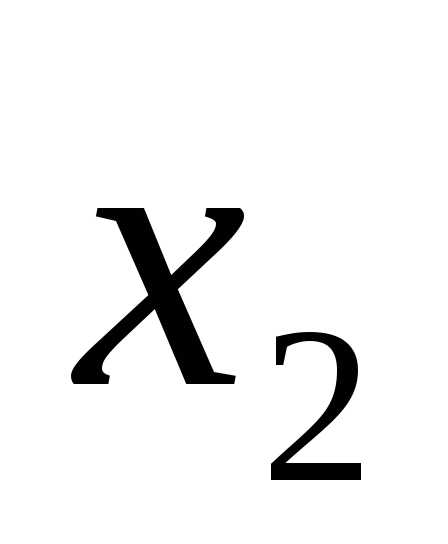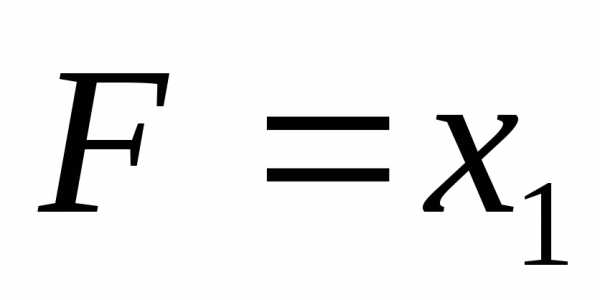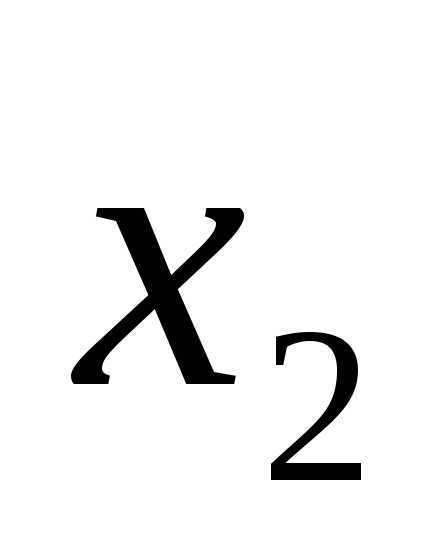Основные логические функции и элементы
Логический элемент — графическое представление элементарной логической функции.
Функция «НЕ» — инвертор (‾)
Правило инверсии: проходя через инвертор, сигнал меняет свое значение на противоположное.
Таблица истинности инвертора
Обозначается
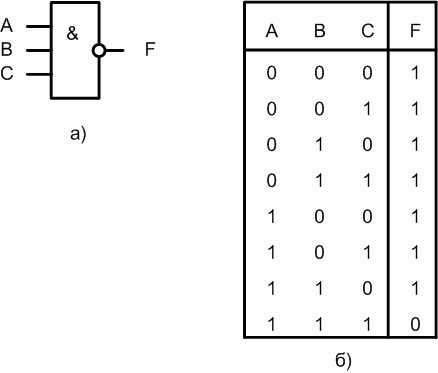
Функция «2И» — логическое умножение (&)
Правило логического умножения :если на вход логического элемента И подается хотя бы один логический 0, то на его выходе будет логический 0.
Таблица истинности логической функции 2И
|
X1 |
X2 |
F |
|
0 | 0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Обозначается
Функция «ИЛИ» — логическое сложение (V)
Правило логического сложения: если на вход логического элемента ИЛИ подается хотя бы одна логическая 1, то на его выходе будет логическая 1.
Таблица истинности логической функции 2ИЛИ
|
X1 |
X2 |
F |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Обозначается
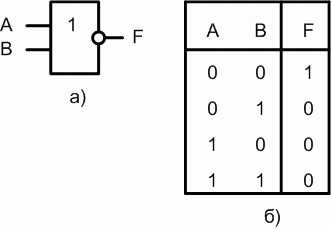
Логическая функция и элемент И-НЕ
Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1.
Логическая функция и элемент ИЛИ-НЕ
Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0
Комбинированные цифровые схемы. Построение цифровой схемы по произвольной таблице истинности (сднф)
СДНФ — Совершенная дизъюктивная нормальная форма
Для реализации таблицы истинности при помощи логических элементов «И» (СДНФ) достаточно рассмотреть только те строки таблицы истинности, которые содержат логические «1» в выходном сигнале. Строки, содержащие в выходном сигнале логический 0 в построении цифровой схемы не участвуют. Каждая строка, содержащая в выходном сигнале логическую «1», реализуется схемой логического элемента «И» с количеством входов, совпадающим с количеством входных сигналов в таблице истинности.
Входные сигналы, описанные в таблице истинности логической единицей, подаются на вход этого логического элемента непосредственно, а входные сигналы, описанные в таблице истинности логическим нулем, подаются на вход этого же логического элемента «И» через инверторы. Объединение сигналов с выходов логических элементов «И», реализующих отдельные строки таблицы истинности, производится при помощи логического элемента «ИЛИ». Количество входов в логическом элементе «ИЛИ» определяется количеством строк в таблице истинности, в которых в выходном сигнале присутствует логическая единица.
Рассмотрим конкретный пример. Пусть необходимо реализовать таблицу истинности, приведенную на рисунке 1:

Рисунок 1. Произвольная таблица истинности.
Для синтеза цифровой схемы, реализующей сигнал Out0, достаточно рассмотреть строки, выделенные красным цветом. В таблице истинности три строки, содержащие единицу в выходном сигнале Out0, поэтому в формуле СДНФ будет содержаться три произведения входных сигналов —термов, а точнее минтермов:
Так как количество переменных в каждом терме (ранг терма) данного логического выражения равно, то такое логическое выражение называется совершенным. (Совершенная Дизъюнктивная Нормальная Форма — СДНФ)
Полученное логическое выражение реализуются микросхемой D2 в схеме, приведенной на рисунке 2. Как и в формуле, каждая строка (терм) реализуется своим логическим элементом «И», затем выходы этих логических элементов объединяются при помощи логического элемента «ИЛИ». Количество входов логического элемента «И» (дизъюнкция) в СДНФ однозначно определяется количеством входных сигналов в таблице истинности. Количество этих элементов, а значит и количество входов в логическом элементе «ИЛИ» определяется количеством строк с единичным сигналом на реализуемом выходе цифровой схемы.
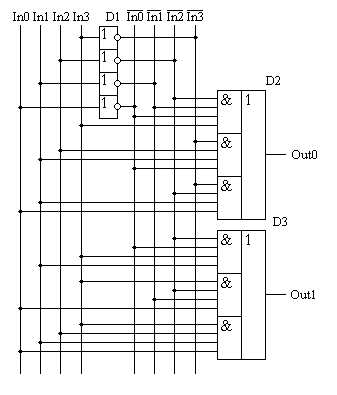 Рисунок 2.
Принципиальная схема, реализующая
таблицу истинности, приведенную на
рисунке 1
Рисунок 2.
Принципиальная схема, реализующая
таблицу истинности, приведенную на
рисунке 1
Для построения схемы, реализующей сигнал Out1, достаточно рассмотреть строки, выделенные зеленым цветом. Эти строки реализуются микросхемой D3. Принцип построения этой схемы не отличается от примера, рассмотренного выше. В таблице истинности присутствуют всего три строки, содержащие единицу в выходном сигнале Out1, поэтому в формуле СДНФ выхода Out1 будет содержаться три произведения входных сигналов:
Обычно при построении цифровых схем после реализации таблицы истинности производится минимизация схемы, но для упрощения понимания материала сейчас минимизация производиться не будет. Это оправдано еще и с той точки зрения, что неминимизированные схемы обычно обладают максимальным быстродействием. При реализации схемы на ТТЛ микросхемах быстродействие всего узла будет равно быстродействию одиночного инвертора (см. описание ТТЛ микросхем).
По СДНФ форме логического выражения обычно строятся современные микросхемы большой интеграции — программируемые логические интегральные схемы (ПЛИС), такие какпрограммируемые логические матрицы (ПЛМ), программируемые матрицы логики ПМЛ или CPLD.
studfiles.net
Логические функции если, и, или
ЕСЛИ
Синтаксис:
ЕСЛИ(логическое_выражение; значение_если_истина; значение_если_ложь).
Предназначение: Функция ЕСЛИвыполняет то («Значение если ИСТИНА») или иное («Значение если ЛОЖЬ»)действие в зависимости от того, выполняется (равно ИСТИНА) условие или нет (равно ЛОЖЬ).
аргумент1. Логическое выражение: Все, что даёт в результате логические значения ЛОЖЬ или ИСТИНА. Обычно либо выражения отношения (A1>=12) либо функции, возвращающие логические значения (И, ИЛИ).
аргумент2. Значение если ИСТИНА: любое допустимое в Excel выражение.
аргумент3. Значение если ЛОЖЬ:
любое допустимое в Excel выражение.возвращаемое значение: может возвращать значения любых типов, в зависимости от аргументов 2 и 3.
Функция ЕСЛИ позволяет организовать в формуле ветвление. Вспомните сказки: налево пойдешь — коня потеряешь, прямо пойдешь — в болото попадешь, направо пойдешь — засосёт в чёрную дыру. Использование функций ЕСЛИ, И, ИЛИ граничит с программированием. Неудивительно, что для многих людей разобраться, как они работают, очень сложно. В голове должен быть чёткий алгоритм решения задачи и требуется хорошее понимание понятия «тип данных»

Алгоритм перехода через дорогу на светофор
И
Синтаксис:
Логич_знач И( логич_знач1; логич_знач2; … ; логич_знач30 )
Предназначение: Функция И используется тогда, когда нужно проверить, выполняются ли несколько условий ОДНОВРЕМЕННО. Одно из наиболее часто используемых применений функции И — проверка, попадает ли число x в диапазон от x1 до x2.
аргументы: Функция И принимает от 1 до 30 аргументов (в Office 2007 — до 256), каждый из которых является логическим значением ЛОЖЬ или ИСТИНА, либо любым выражением или функцией, которое в результате дает ЛОЖЬ или ИСТИНА.
возвращаемое значение: Функция И возвращает логическое значение. Если ВСЕ аргументы функции И равны ИСТИНА, возвращает ИСТИНА. Если хотя бы один аргумент имеет значение ЛОЖЬ, возвращает ЛОЖЬ.Примечание: Функция И почти никогда не используется сама по себе, обычно её используют в качестве аргумента других функций, например, ЕСЛИ.
ИЛИ
Синтаксис:
Логич_знач ИЛИ( логич_знач1; логич_знач2; … ; логич_знач30 )
Предназначение: Функция ИЛИ используется тогда, когда нужно проверить, выполняется ли ХОТЯ-БЫ ОДНО из многих условий.
аргументы: Функция ИЛИ принимает от 1 до 30 аргументов (в Office 2007 — до 256), каждый из которых является логическим значением ЛОЖЬ или ИСТИНА, либо любым выражением или функцией, которое в результате дает ЛОЖЬ или ИСТИНА.
возвращаемое значение: Функция ИЛИ возвращает логическое значение. Если ХОТЯ БЫ ОДИН аргумент имеет значение ИСТИНА, возвращает ИСТИНА. Если ВСЕ аргументы имеют значение ЛОЖЬ, возвращает ЛОЖЬ.
Примечание: Функция ИЛИ почти никогда не используется сама по себе, обычно её используют в качестве аргумента других функций, например, ЕСЛИ.
Функция впр (Вертикальное Первое Равенство)
Для функции необходимо внести следующие данные: какое значение искать (указывается ячейка содержащее значение), массив, в котором происходит поиск, иномер столбца, в котором находится значение, номер повторного значения в массиве, значение которого и будет использовано , которое надо вернуть. Очень удобная Функция значительно расширяет свои возможности при использовании её в паре с логической функцией ЕСЛИ().
Объясняю, как пользоваться функцией: = ВПР (что ищем, таблица где ищем, из какого столбца взять значение, булевская переменная единица или ноль альтернативой или ИСТИНА ЛОЖЬ, параметр 0/ЛОЖЬ ставится, если значения первого столбца не отсортированы). К примеру = ВПР(A1;B:D;2;ЛОЖЬ) В этом примере ищется значение находящееся в ячейке A1 и возвращается значение из столбца C диапазона B:D Эту функцию используют, когда необходимо найти соответствие в определенном столбце для значения, находящегося в первом столбце. Функция как-бы вытаскивает значение из указанного столбца. Допустим, есть таблица вида: ФИО и табельный номер. Функция ВПР() позволяет получить табельный номер по указанной фамилии и инициалам (в вышеприведенном примере фамилия должна находиться в ячейке A1).
Примечание: ВПР выбирает первое сверху вниз значение. Это означает, что если в списке работников будет более одной одинаковой фамилии, то функция вернет табельный номер для той фамилии, которая идет сверху вниз раньше.
studfiles.net
Основные логические функции
Лабораторная работа №3
Решение логических задач школьного курса повышенной сложности
Алгебра логики – раздел математической логики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними. Алгебра логики возникла в середине 19 века в трудах Дж. Буля и развивалась затем в работах Ч. Пирса, П. С. Порецкого, Б. Рассела, Д. Гильберта и др. Создание алгебры логики представляло собой попытку решать традиционные логические задачи алгебраическими методами. С появлением теории множеств (70-е гг. 19 в.) и дальнейшим развитием математической логики (последняя четверть 19 в. — 1-я половина 20 в.), предмет алгебры логики значительно изменился. Основным предметом алгебры логики стали высказывания. Под высказыванием понимается каждое предложение, относительно которого имеет смысл утверждать, истинно оно или ложно. Примеры высказываний: «кит — животное», «все углы — прямые» и т.п. Первое из этих высказываний является, очевидно, истинным, а второе — ложным. Употребляемые в обычной речи логические связки «и», «или», «если…, то…», «эквивалентно», частица «не» и т. д. позволяют из уже заданных высказываний строить новые, более «сложные» высказывания. Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как операций над высказываниями.
В отличие от обычной алгебры, изучающей математические функции, алгебра логики изучает логические функции. Известно, что функция — это закон соответствия между переменными. Следовательно, логическая функция— это закон соответствия между логическими переменными.Логическая переменная— это такая переменная, которая может принимать одно из двух возможных значений: 0 («ложь») и 1 («истина»).
Логическим выражением называется выражение, о котором можно сказать истинно оно или ложно.
Примеры:
«5>8» — логическое выражение, т.к. о нем можно сказать, что оно ложно.
«Эту девочку зовут Юля» — логическое выражение.
«Подайте книгу» — это не логическое выражение, т.к. о нем нельзя сказать, истинно оно или ложно
Логическая функция может также принимать два значения.
Таким образом, логические переменные и функции определены на множестве двух значений — {0,1}.
ЭВМ строятся из компонентов с двумя устойчивыми состояниями. Одно состояние обозначается нулем, другое — единицей. На такие компоненты воздействуют двоичные сигналы. Под воздействием сигналов компоненты изменяют свои состояния, т. е. состояние компонентов или значения их выходных сигналов зависят от значений воздействующих сигналов. Очевидно, что функционирование компонентов ЭВМ следует описывать логическими функциями. По этой причине алгебра логики находит непосредственное и широкое применение при разработке и использовании средств электронной вычислительной техники.
Логические функции характеризуются (задаются) так называемыми таблицами истинности, или соответствия. Таблица истинности— это таблица, устанавливающая соответствие между возможными наборами значений логических переменных и значениями функций.
Функция отрицания
Отрицание – это логическая функция от одной переменной, которая принимает единичное значение при нулевом значении переменной и наоборот. Запись этой функции:
F= .
.
Конъюнкция может быть обозначена следующими символами:
¬,¯, не, not.
Черта над переменной xявляется признаком отрицания (инверсии). Таблица истинности этой функции представлена на рис. 1а. Функция логического отрицания описывает функционирование логического элемента НЕ (рис. 1б).
Условно-графическое обозначение элемента НЕ приведено на рис. 1в. Единичный сигнал на выходе элемента НЕ появляется при нулевом сигнале на входе (x=0,F=1) и, наоборот, нулевой сигнал на выходе появляется при единичном сигнале на входе (x=1,F=0). Графически отрицание можно представить с помощью кругов Эйлера (рис. 2).
а) б) в)
Рис. 1. Элемент НЕ
Рис. 2. Графическое представление отрицания на множестве
Функция логического умножения (конъюнкция)
Логическое умножение – это логическая функция, по крайней мере, от двух переменных, которая принимает единичное значение при единичных значениях всех переменных. Эта функция называется также конъюнкцией. Элементарная конъюнкция зависит от двух переменных. Она принимает единичное значение только тогда, когда и первая переменная и вторая переменная равны единице. Возможны различные варианты записи конъюнкции:
F=
 ;F=
;F=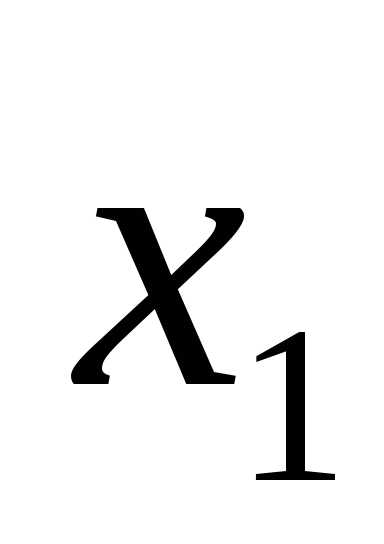 •
• ;F=
;F=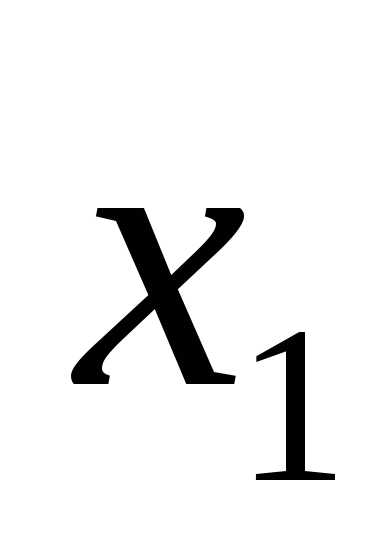
 ;F=
;F=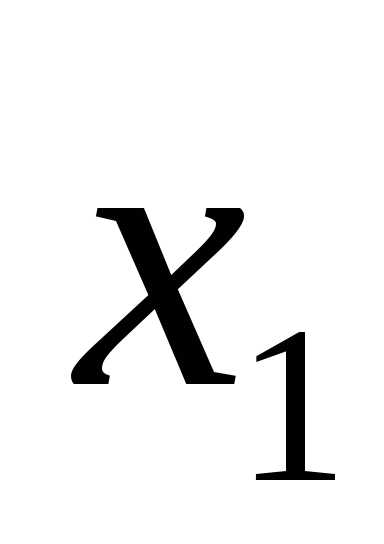 &
&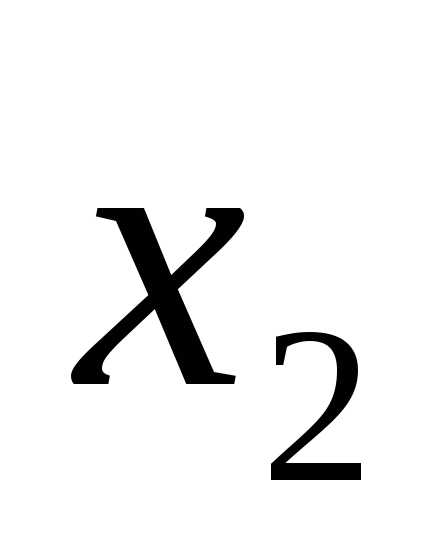 .
.
Конъюнкция может быть обозначена следующими символами:
, &, •, ∩, and, и.
Конъюнкция характеризуется таблицей истинности, представленной на рис. 3а. Из рассмотрения таблицы следует, что эта функция принимает единичное значение на наборе 4. Логическое умножение описывает работу элемента И (рис. 3б). Графически конъюнкцию можно представить с помощью кругов Эйлера (рис. 4).
а) б) в)
|
|
|
F |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Рис. 3. Элемент И
Рис. 4. Графическое представление конъюнкции на множествах
Конъюнкция на числовых множествах (операция пересечения): {a,b,c} {b,c,d,e}={b,c}.
Единичный сигнал появляется на выходе этого элемента только при наличии единичного сигнала и на входе 1, и на входе 2.
В общем случае элемент И может иметь n входов (рис. 3в). При этом он реализует конъюнкцию от n переменных, т.е.:
F=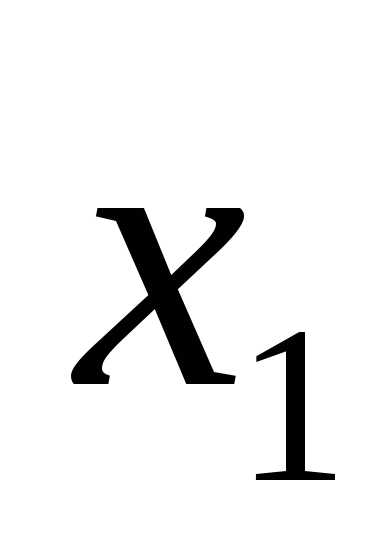 •
•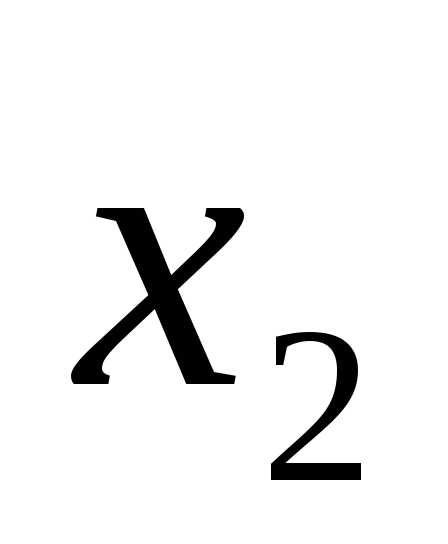 •
•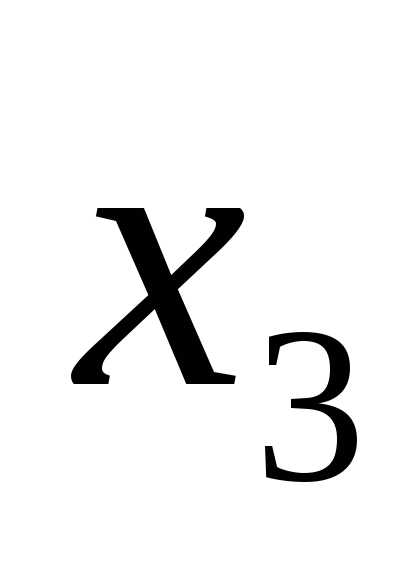 •…•
•…•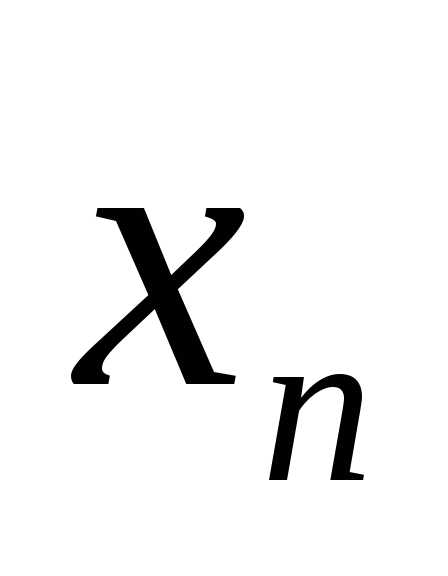 .
.
Функция логического сложения (дизъюнкция)
Логическое сложение – это логическая
функция, по крайней мере, от двух
переменных, которая принимает нулевое
значение при нулевых значениях всех
переменных. Эта функция называется
также дизъюнкцией. Таблица истинности
элементарной дизъюнкции представлена
на рис. 3а. Элементарная дизъюнкция
принимает единичное значение на наборах
1, 2, 3 и нулевое значение – только на
наборе 0. Функция записывается в одном
из двух видов: F=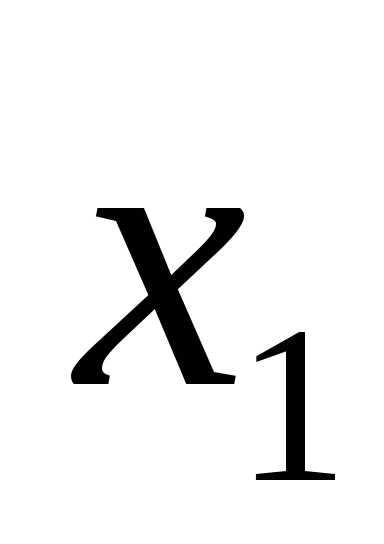
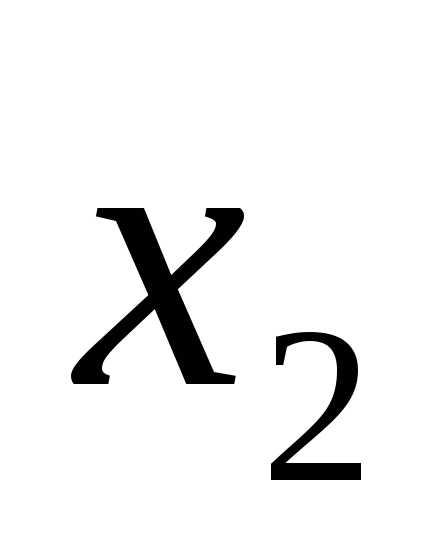 илиF=
илиF=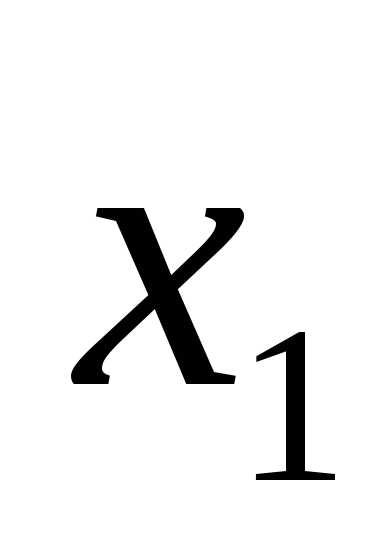 +
+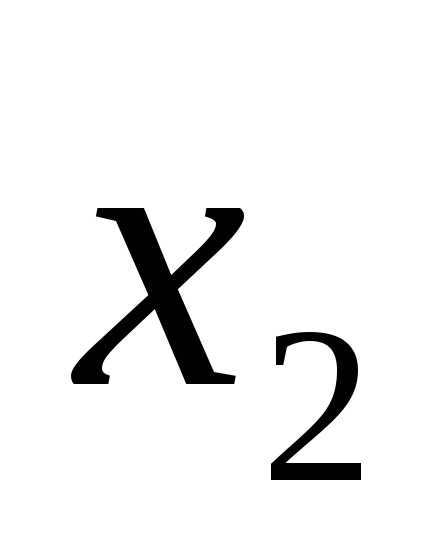 .
.
Знак «плюс» не является алгебраическим,
т.к. при
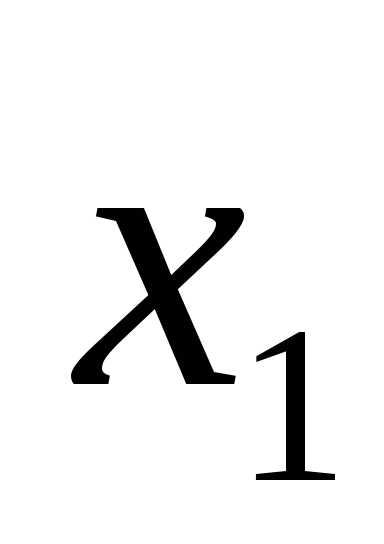 =1,
=1,
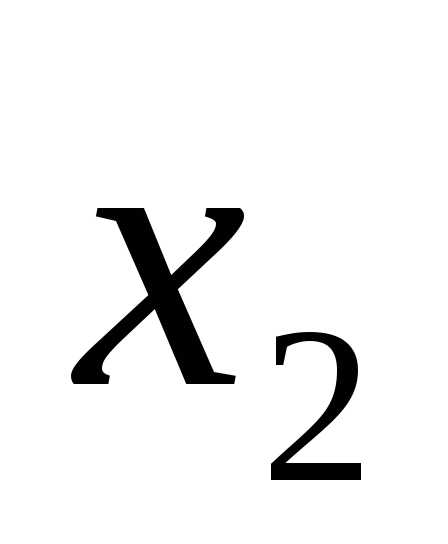 =1
дизъюнкцияF=
=1
дизъюнкцияF=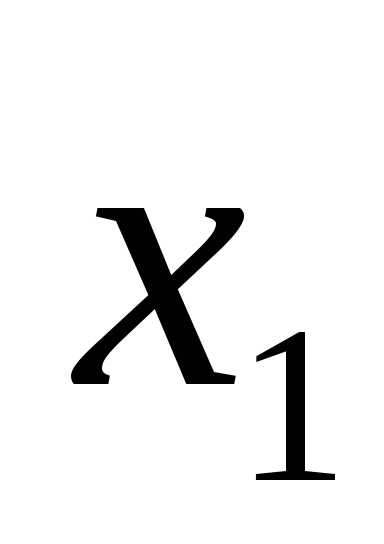 +
+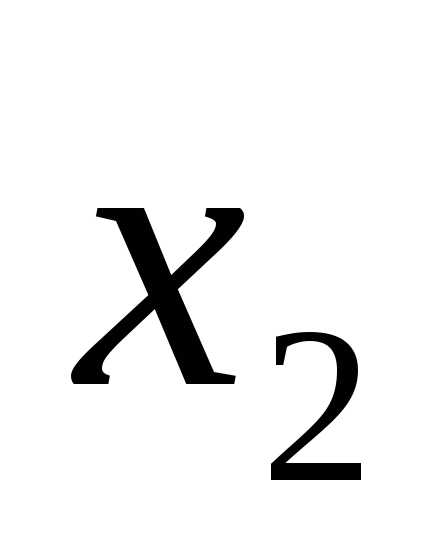 =1
=1
Дизъюнкция может быть обозначена следующими символами:
,
+, ,
or, или.
,
or, или.
Дизъюнкция описывает функционирование элемента ИЛИ (рис. 5б). Единичный сигнал на выходе этого элемента возникает тогда, когда или на входе 1, или на входе 2, или на двух входах единичные сигналы. И только в том случае, когда на оба входа поступают нулевые сигналы, на выходе элементов появляется нулевой сигнал.
В общем случае элемент ИЛИ может иметь n входов (рис. 5в). При этом он реализует дизъюнкцию от n переменных.
а) б) в)
|
|
|
F |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |
Рис. 5. Элемент ИЛИ
Рис. 6. Графическое представление дизъюнкции на множествах
Дизъюнкция на числовых множествах (операция объединения): {a,b,c}{b,c,d,e}={a,b,c,d,e}.
Равнозначность (эквиваленция)
Равнозначность – это логическая функция от двух переменных, которая принимает единичное значение при одинаковых значениях переменных. Одинаковые по значению переменные называются равнозначными, поэтому функция носит название «равнозначность».
Запись функции:
F=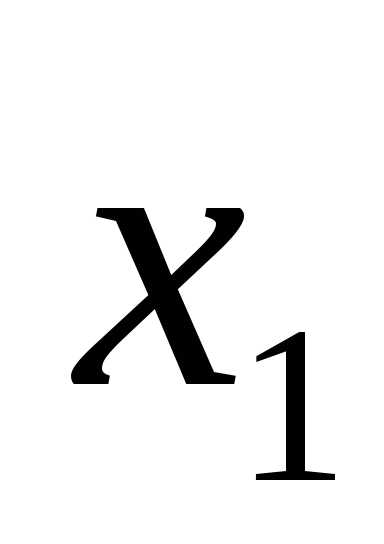
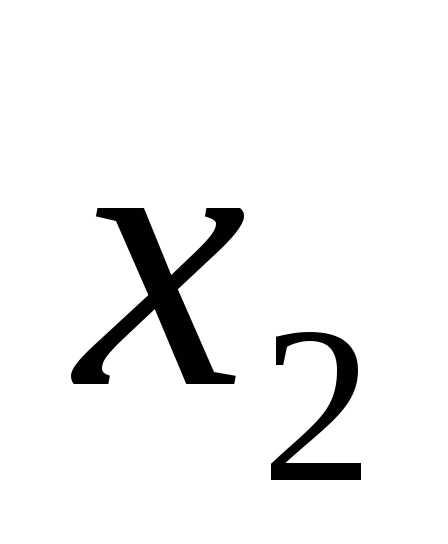 +
+
 .
.
Таблица истинности функции равнозначности представлена на рис. 7а. Эта функция реализуется элементом равнозначности (сравнения), который показан на рис. 7б.
Эквиваленция может быть обозначена следующими символами:
~,
, ,
, .
.
Элемент используется для сравнения двоичных сигналов.
|
|
|
F |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
а) б)
Рис. 7. Элемент равнозначности
Логическое следование (импликация)
Обозначение логического следования:
F=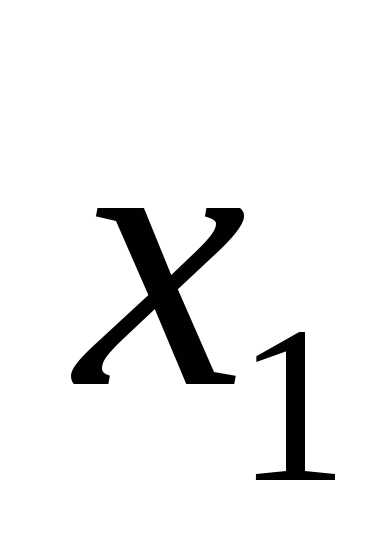 →
→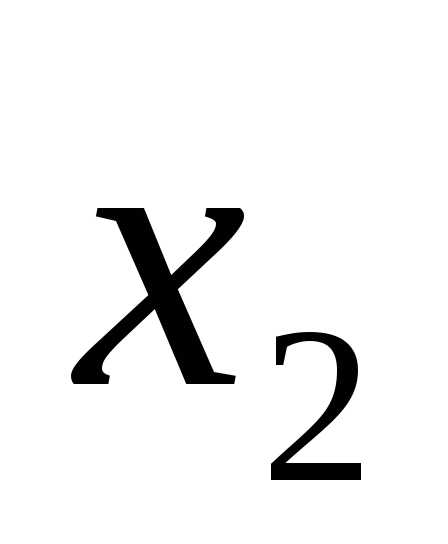 .
.
Высказывание F=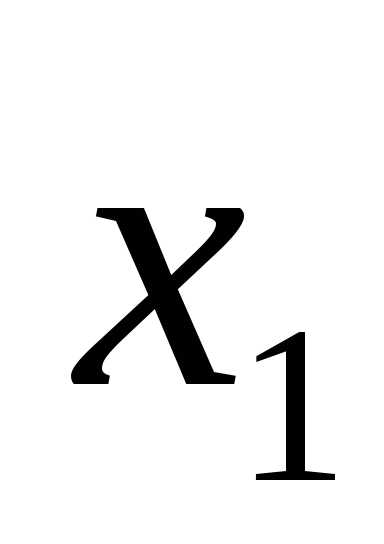 →
→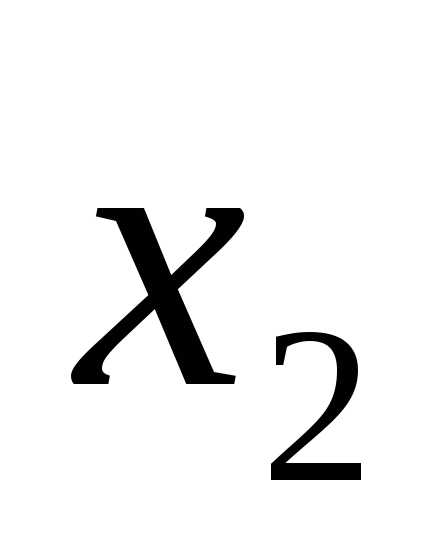 будем
считать истинным во всех случаях, кроме
случая, когда
будем
считать истинным во всех случаях, кроме
случая, когда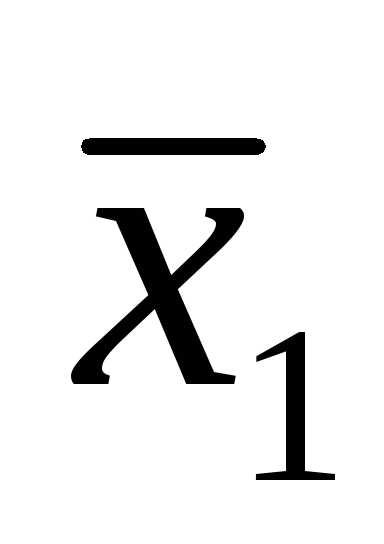 истинно, а
истинно, а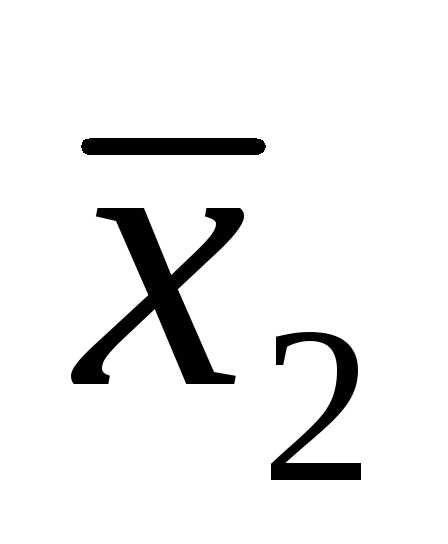 ложно. Таблица истинности представлена
на рис. 8.
ложно. Таблица истинности представлена
на рис. 8.
|
|
|
F= |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Рис. 8. Элемент импликации
Импликация может быть обозначена следующими символами:→, ,.
Элемент (штрих) Шеффера
Обозначение:

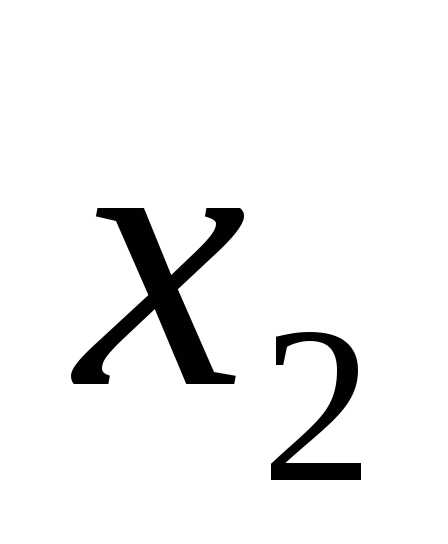 ;.
;.
Другое название этой функции: «И-НЕ».
Высказывание
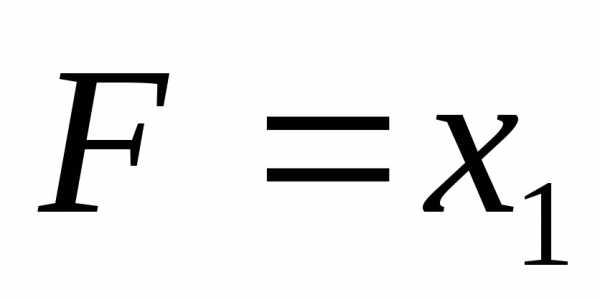
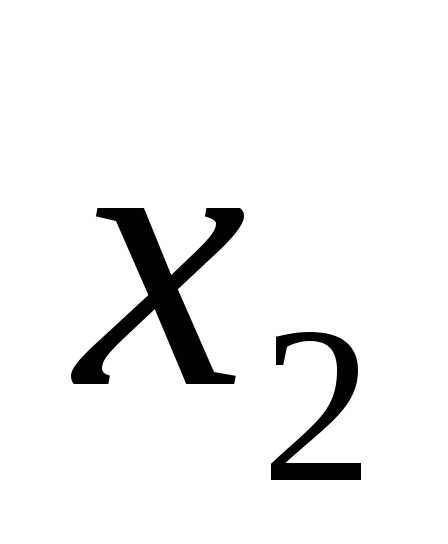 будем считать ложным, когда
будем считать ложным, когда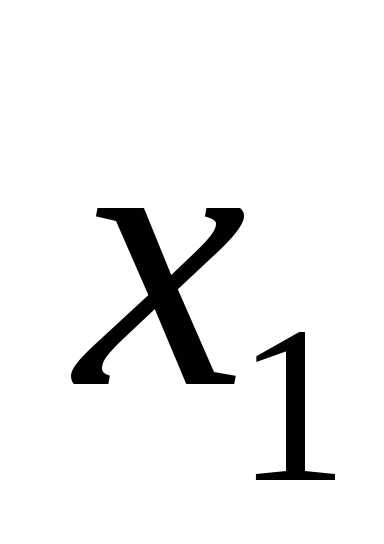 и
и равны единице. Таблица истинности
представлена на рис. 9.
равны единице. Таблица истинности
представлена на рис. 9.
|
|
|
|
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Рис. 9. Элемент (штрих) Шеффера
Элемент Вебба (стрелка Пирса)
Обозначение:
;.
Высказывание
будем считать истинным только тогда,
когда оба операнда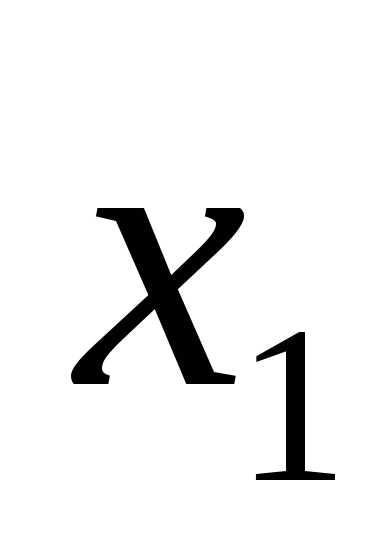 и
и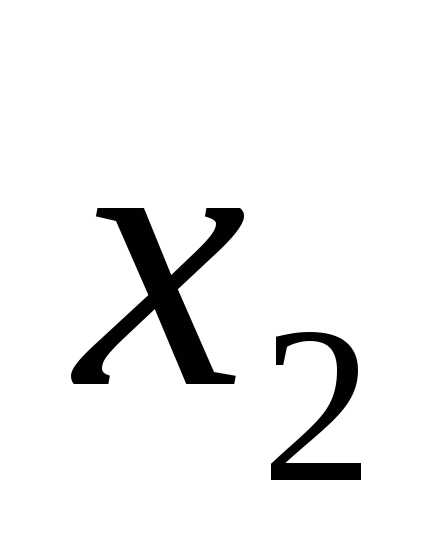 равны нулю. Таблица истинности представлена
на рис.10.
равны нулю. Таблица истинности представлена
на рис.10.
Другое название этой функции: «ИЛИ-НЕ».
Рис. 10. Элемент Вебба (стрелка Пирса)
Сложение по модулю 2.
Обозначение:
;;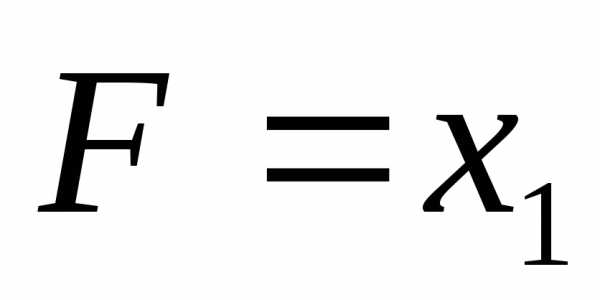 XOR
XOR
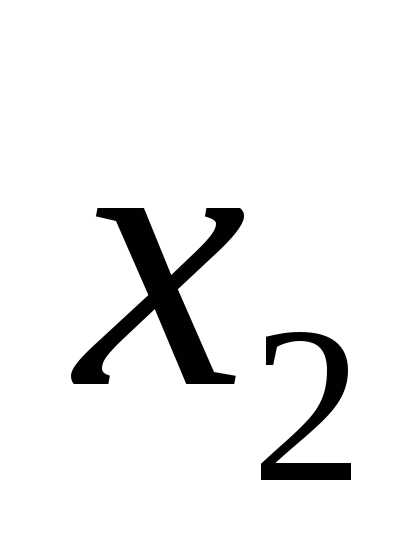 .
.
Высказывание
будем считать истинным, если первый
операнд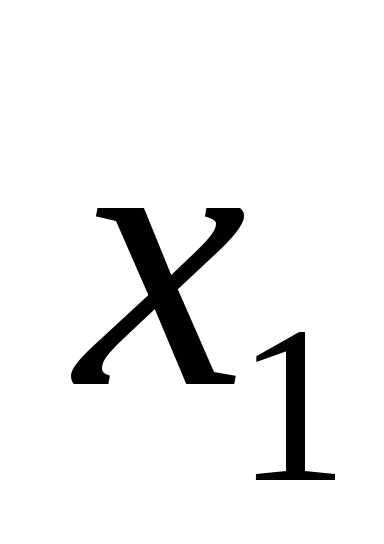 не равен второму операнду
не равен второму операнду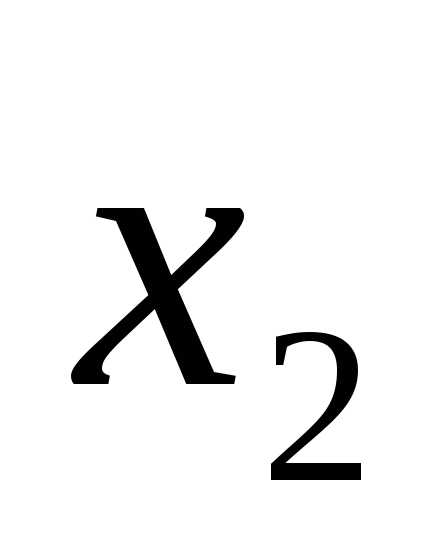 .
Таблица истинности представлена на
рис. 11.
.
Таблица истинности представлена на
рис. 11.
Другие названия этой функции: «исключающее ИЛИ», «логическое ЛИБО», «неравносильность», «неэквивалентность», «логическое сложение», «булево сложение».
Рис. 11. Сложение по модулю 2
Коимпликация
Обозначение:
; .
.
Высказывание
будем считать истинным, если первый
операнд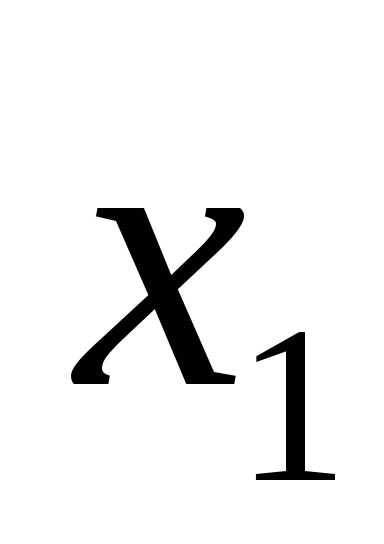 равен 1, а второй операнд
равен 1, а второй операнд
 равен 0. Таблица истинности представлена
на рис. 12.
равен 0. Таблица истинности представлена
на рис. 12.
Рис. 12 Таблица истинности функции коимпликация
Приоритет операций в логическом выражении, не содержащем скобок:
Отрицание.
Конъюнкция, *, /, div,mod.
Дизъюнкция, +, -.
Операция отношения.
Для усиления операции используются скобки.
studfiles.net
Логические функции если, и, или
ЕСЛИ
Синтаксис:
ЕСЛИ(логическое_выражение; значение_если_истина; значение_если_ложь).
Предназначение: Функция ЕСЛИвыполняет то («Значение если ИСТИНА») или иное («Значение если ЛОЖЬ»)действие в зависимости от того, выполняется (равно ИСТИНА) условие или нет (равно ЛОЖЬ).
аргумент1. Логическое выражение: Все, что даёт в результате логические значения ЛОЖЬ или ИСТИНА. Обычно либо выражения отношения (A1>=12) либо функции, возвращающие логические значения (И, ИЛИ).
аргумент2. Значение если ИСТИНА: любое допустимое в Excel выражение.
аргумент3. Значение если ЛОЖЬ: любое допустимое в Excel выражение.
возвращаемое значение: может возвращать значения любых типов, в зависимости от аргументов 2 и 3.
Функция ЕСЛИ позволяет организовать в формуле ветвление. Вспомните сказки: налево пойдешь — коня потеряешь, прямо пойдешь — в болото попадешь, направо пойдешь — засосёт в чёрную дыру. Использование функций ЕСЛИ, И, ИЛИ граничит с программированием. Неудивительно, что для многих людей разобраться, как они работают, очень сложно. В голове должен быть чёткий алгоритм решения задачи и требуется хорошее понимание понятия «тип данных»

Алгоритм перехода через дорогу на светофор
И
Синтаксис:
Логич_знач И( логич_знач1; логич_знач2; … ; логич_знач30 )
Предназначение: Функция И используется тогда, когда нужно проверить, выполняются ли несколько условий ОДНОВРЕМЕННО. Одно из наиболее часто используемых применений функции И — проверка, попадает ли число x в диапазон от x1 до x2.
аргументы: Функция И принимает от 1 до 30 аргументов (в Office 2007 — до 256), каждый из которых является логическим значением ЛОЖЬ или ИСТИНА, либо любым выражением или функцией, которое в результате дает ЛОЖЬ или ИСТИНА.
возвращаемое значение: Функция И возвращает логическое значение. Если ВСЕ аргументы функции И равны ИСТИНА, возвращает ИСТИНА. Если хотя бы один аргумент имеет значение ЛОЖЬ, возвращает ЛОЖЬ.Примечание: Функция И почти никогда не используется сама по себе, обычно её используют в качестве аргумента других функций, например, ЕСЛИ.
ИЛИ
Синтаксис:
Логич_знач ИЛИ( логич_знач1; логич_знач2; … ; логич_знач30 )
Предназначение: Функция ИЛИ используется тогда, когда нужно проверить, выполняется ли ХОТЯ-БЫ ОДНО из многих условий.
аргументы: Функция ИЛИ принимает от 1 до 30 аргументов (в Office 2007 — до 256), каждый из которых является логическим значением ЛОЖЬ или ИСТИНА, либо любым выражением или функцией, которое в результате дает ЛОЖЬ или ИСТИНА.
возвращаемое значение: Функция ИЛИ возвращает логическое значение. Если ХОТЯ БЫ ОДИН аргумент имеет значение ИСТИНА, возвращает ИСТИНА. Если ВСЕ аргументы имеют значение ЛОЖЬ, возвращает ЛОЖЬ.
Примечание: Функция ИЛИ почти никогда не используется сама по себе, обычно её используют в качестве аргумента других функций, например, ЕСЛИ.
Функция впр (Вертикальное Первое Равенство)
Для функции необходимо внести следующие данные: какое значение искать (указывается ячейка содержащее значение), массив, в котором происходит поиск, иномер столбца, в котором находится значение, номер повторного значения в массиве, значение которого и будет использовано , которое надо вернуть. Очень удобная Функция значительно расширяет свои возможности при использовании её в паре с логической функцией ЕСЛИ().
Объясняю, как пользоваться функцией: = ВПР (что ищем, таблица где ищем, из какого столбца взять значение, булевская переменная единица или ноль альтернативой или ИСТИНА ЛОЖЬ, параметр 0/ЛОЖЬ ставится, если значения первого столбца не отсортированы). К примеру = ВПР(A1;B:D;2;ЛОЖЬ) В этом примере ищется значение находящееся в ячейке A1 и возвращается значение из столбца C диапазона B:D Эту функцию используют, когда необходимо найти соответствие в определенном столбце для значения, находящегося в первом столбце. Функция как-бы вытаскивает значение из указанного столбца. Допустим, есть таблица вида: ФИО и табельный номер. Функция ВПР() позволяет получить табельный номер по указанной фамилии и инициалам (в вышеприведенном примере фамилия должна находиться в ячейке A1).
Примечание: ВПР выбирает первое сверху вниз значение. Это означает, что если в списке работников будет более одной одинаковой фамилии, то функция вернет табельный номер для той фамилии, которая идет сверху вниз раньше.
studfiles.net
Логические базисы и-не, или-не
Булевый базис не является единственной функционально полной системой логических функций. Среди других наибольшее распространение получили базис И-НЕ и базис ИЛИ -НЕ.
Чтобы доказать логическую полноту любого базиса, достаточно показать, что в этом базисе можно реализовать базовые функции И, ИЛИ, НЕ.
Для базиса И-НЕ в качестве базового элемента используется элемент приведенный на рисунке рис.1.2.10,а.
a b
Рис. 1.2.9
Реализация с помощью функции И-НЕ базовых функций алгебры Буля осуществляется следующим образом.
ИЛИ:
И:
Функция НЕ реализуется с помощью схемы И -НЕ с одним входом.
На рис.1.2.11 риведена схемная реализация функций И, ИЛИ, НЕ в базисе И — НЕ.
Рис. 1.2.10
Реализация с помощью логической функции ИЛИ-НЕ базовых функций алгебры Буля осуществляется следующим образом.
ИЛИ:
И:
Функция НЕ реализуется с помощью схемы ИЛИ -НЕ с одним входом.
На рис.1.2.12 приведена схемная реализация операции И, ИЛИ, НЕ в базисе ИЛИ – НЕ
И ИЛИ НЕ
Рис. 1.2.11.
При синтезе логических схем в заданном базисе логических элементов (например, в базисе И-НЕ, или ИЛИ — НЕ) целесообразно предварительно исходное выражение привести к форме, в которой в выражении будут использованы только логические операции, соответствующие используемым логическим элементам в заданном базисе.
Пример
Синтезировать логическую схему в базисе И — НЕ, соответствующую выражению
.
Решение
Используя правило де Моргана преобразуем исходное выражение таким образом, чтобы последней операцией было отрицание и в выражение были бы только операции И.
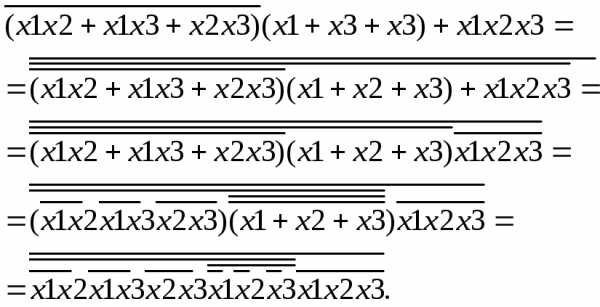
Полученное выражение, представленное в виде вложенных операции И-НЕ, позволяет синтезировать соответствующую логическую схему в заданном базисе, которая приведена на рис.1.2.13.
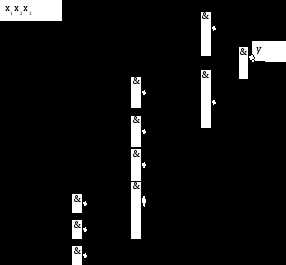
Рис. 1.2.12
Пример
Синтезировать логическую схему в базисе ИЛИ — НЕ, соответствующую выражению
Решение
Используя правило де Моргана преобразуем исходное выражение таким образом, чтобы последней операцией было отрицание и в выражение были бы только операции ИЛИ.
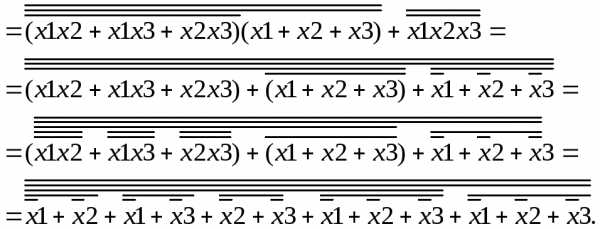
Полученное выражение, представленное в виде вложенных операций ИЛИ-НЕ, позволяет легко синтезировать соответствующую логическую схему в заданном базисе, которая приведена на рисунке рис.1.2.14.

Рис. 1.2.13
studfiles.net
Урок N 16. Логические элементы и логические функции.
Урок N 16
Логические элементы и логические функции.
Элементы математической логики.
Логическая функция — это функция логических переменных, которая
может принимать только два значения : 0 или 1. В свою очередь,
сама логическая переменная (аргумент логической функции) тоже может
принимать только два значения : 0 или 1.
Логический элемент — это устройство, реализующее ту или иную
логическую функцию.
Y=f(X1,X2,X3,…,Xn) — логическая функция, она может быть задана
таблицей, которая называется таблицей истинности.
Число строк в таблице — это число возможных наборов значений
аргументов. Оно равно 2n, где n — число переменных.
Число различных функций n переменных равно 22^n.
Логические функции одной переменной
Таблица истинности функции одной переменной Y=f(X) содержит всего
2 строки, а число функций одной переменной равно 4.
1. Функция константа 0, Y=0. Техническая реализация этой функции —
соединение вывода Y с общей шиной с нулевым потенциалом.
Таблица истинности функции константа 0 имеет вид:
2. Функция Y=f(X)=X — функция повторения. Техническая реализация
этой функции — соединение между собой выводов X и Y.
Таблица истинности функции повторения имеет вид:
3. Функция Y=f(X)=NOT(X) — отрицание НЕ или инверсия (NOT(X) — это НЕ X).
Техническая реализация этой функции — инвертор на любом транзисторе
или логическом элементе, или транзисторный ключ.
Таблица истинности функции отрицания имеет вид:
Логический элемент НЕ обозначается на схемах следующим образом:
(пишется X c чертой сверху)
4. Функция константа 1, Y=1. Техническая реализация этой функции —
соединение вывода Y с источником питания.
Таблица истинности функции константа 1 имеет вид:
Важнейшей функцией одной переменной является отрицание НЕ,
остальные функции являются тривиальными.
Логические функции двух переменных
Таблица истинности функции двух переменных Y=f(X1,Х2) содержит 4
строки, а число функций двух переменных равно 16.
Мы рассмотрим только несколько основных функций двух переменных.
1. Логическое ИЛИ (логическое сложение, дизъюнкция):
Y= X1 + X2 = X1VX2
Техническая реализация этой функции — два параллельно соединенных
ключа:
Таблица истинности логического ИЛИ имеет вид:
Логический элемент ИЛИ обозначается на схемах следующим образом:
2. Логическое И (логическое умножение, конъюнкция, схема совпаде-
ний): Y = X1X2 = X1&X2
Техническая реализация этой функции — два последовательно сое-
диненных ключа:
Таблица истинности логического И имеет вид:
Логический элемент И обозначается на схемах следующим образом:
3. Функция стрелка Пирса (ИЛИ-НЕ): Y = NOT(X1+X2)
Таблица истинности функции ИЛИ-НЕ имеет вид:
Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом
:
4. Функция штрих Шеффера (И-НЕ): Y = X1|X2 = NOT(X1X2)
Таблица истинности функции И-НЕ имеет вид:
Логический элемент И-НЕ обозначается на схемах следующим образом:
Есть ещё три логические функции двух переменных, имеющие специ-
альные названия: импликация, эквивалентность, неравнозначность
(исключающее ИЛИ, сложение по модулю 2). Последние две функции
являются взаимно обратными, также как, например, функция И и
функция штрих Шеффера.
Элемент памяти — RS-триггер
Триггер — это логическое устройство, способное хранить 1 бит ин-
формации. К триггерам относятся устойства, имеющие два устойчивых
состояния. Простейший триггер — RS-триггер, образован из двух
элементов И-НЕ (или ИЛИ-НЕ). Он позволяет запоминать 1 бит инфор-
мации, поскольку информация в компьютере представляется в двоич-
ном виде. Его схема приведена ниже.
Действие RS-триггера поясняется в приведенной ниже таблице ис-
тинности. S-вход установки (Set), R-вход сброса (Reset).
В обычном (исходном) состоянии на входы триггера поданы 1. Для
записи информации на вход R подан 0. Для сброса информации и под-
готовки к приёму новой информации на вход S подается 0 и триггер
вернётся в исходное состояние.
Поскольку один триггер запоминает 1 бит информации, то для запо-
минания 1 байта (8 бит) нужно 8 триггеров, для запоминания 1 Кб
(1024 байт) надо 8192 триггеров. Современные микросхемы ОЗУ спо-
собны запоминать десятки мегабайт информации.
Элементы математической логики
Существуют такие наборы логических функций, с помощью которых
можно выразить любые другие логические функции. Они называются
функционально полными или базисами. Наиболее известный базис —
это набор функций И, ИЛИ, НЕ. Функция штрих Шеффера является ба-
зисной, также как и функция стрелка Пирса. Поэтому, с помощью ло-
гических элементов ИЛИ-НЕ или И-НЕ можно собрать любую логическую
схему. На таких элементах собран микропроцессор компьютера и дру-
гие логические устройства. Логические схемы состоят из логических
элементов, осуществляющих логические операции.
Логика — наука, изучающая методы установления истинности или лож-
ности одних высказываний на основе истинности или ложности других
высказываний (утверждений). Логика изучает методы доказательств и
опровержений. Логика составляет основу всякого управления, в том
числе технологическими процессами.
Математическая логика — современная форма логики, опирающаяся на
формальные математические методы.
Основные объекты логики — высказывания, то есть предложения, ко-
торые могут быть либо истинными, либо ложными. Существуют два
подхода установления истинности высказываний: эмпирический (опыт-
ный) и логический. При эмпирическом подходе истинность высказыва-
ний устанавливается на основе наблюдений, экспериментов, докумен-
тов и других фактов. При логическом подходе истинность высказыва-
ний доказывается на основе истинности других высказываний, то
есть чисто формально, на основе рассуждений без обращения к фак-
там.
В языках программирования QBasic и Turbo Pascal логические функ-
ции И, ИЛИ, НЕ реализуются в виде логических операций OR (ИЛИ),
AND (И), NOT (НЕ).
Множество всех логических функций, на котором определены три ло-
гические операции И, ИЛИ, НЕ называется булевой алгеброй (по име-
ни основоположника математической логики английского математика
Джорджа Буля). Упрощение формул в булевой алгебре производится на
основе эквивалентных преобразований, опирающихся на следующие ос-
новные законы (эквивалентные соотношения):
Кроме того, применяются ещё три соотношения:
Законы 1,2,3,7 показывают, что свойства конъюнкции очень похожи
на свойства умножения, поэтому её часто называют логическим умно-
жением. Из законов 6 и 8 следует, что используя отрицание, дизъ-
юнкцию можно выразить через конъюнкцию, и наоборот:
Это означает, что наборы И-НЕ и ИЛИ-НЕ также являются функцио-
нально полными или базисными.
Вопросы
1. Что такое логическая функция и логический элемент?
2. Что такое таблица истинности и сколько в ней строк?
3. Какие функции одной переменной Вы знаете? Какая из них являет-
ся важнейшей?
4. Как зависит число функций от числа переменных?
5. Что такое конъюнкция и дизъюнкция? Как они реализуются?
6. Что такое функция стрелка Пирса? Какова её таблица истинности?
7. Что такое функция штрих Шеффера? Какова её таблица истинности?
8. Что такое базисная функция и какие базисы Вы знаете?
9. Что такое логика? Какие два подхода существуют в логике?
10. Как доказывается истинность или ложность высказываний? Приве-
дите примеры из практики.
11. Что такое булева алгебра?
12. Какие законы булевой алгебры Вы знаете? Где они применяются?
13. Что такое триггер? Как работает RS-триггер?
14. Сколько надо триггеров, чтобы запомнить 1 Мб информации?
marklv.narod.ru
НОУ ИНТУИТ | Лекция | Логические основы ЭВМ
Аннотация: Рассматриваются основные логические элементы и принципы их соединения в логические схемы.
Любая цифровая вычислительная машина состоит из логических схем — таких схем, которые могут находиться только в одном из двух возможных состояний — либо «логический ноль», либо «логическая единица». За логический 0 и логическую 1 можно принять любое выражение, в том числе и словесное, которое можно характеризовать как «истина» и «ложь». В вычислительной технике логические 0 и 1 — это состояние электрических схем с определенными параметрами. Так, для логических элементов и схем, выполненных по технологии транзисторно-транзисторной логики (ТТЛ-схемы), логический 0 — это напряжение в диапазоне 0 … + 0,4 В, а логическая 1 — это напряжение в диапазоне + 2,4 … + 5 В [1]. Работа логических схем описывается посредством специального математического аппарата, который называется логической (булевой) алгеброй или алгеброй логики. Булева алгебра была разработана Джорджем Булем (1815 — 1864 гг.), она является основой всех методов упрощения булевых выражений.
Логические переменные и логические функции — это такие переменные и функции, которые могут принимать только два значения — либо логический 0, либо логическая 1.
Основные логические функции и элементы
Логический элемент — графическое представление элементарной логической функции.
Логическое умножение (конъюнкция) — функция И
Рассмотрим ключевую схему представленную на рис. 1.1,а. Примем за логический 0 [2]:
- на входе схемы разомкнутое состояние соответствующего ключа, например, ;
- на выходе схемы ( ) — такое ее состояние, когда через сопротивление R ток не протекает.
Таблица истинности — это таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции.

Рис. 1.1. Трёх-входовой логический элемент И
Таблица истинности для логической схемы, представленной на рис. 1.1,б, состоит из 8 строк, поскольку данная схема имеет три входа — , и . Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1. Соответственно количество сочетаний этих переменных равно . Очевидно, что через сопротивление R ток протекает только тогда, когда замкнуты все три ключа — и , и , и . Отсюда еще одно название логического умножения — логический элемент И. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.1,в.
Правило логического умножения :если на вход логического элемента И подается хотя бы один логический 0, то на его выходе будет логический 0.
Уровень логического 0 является решающим для логического умножения .
В логических выражениях применяется несколько вариантов обозначения логического умножения. Так, для приведенного на рис. 1.1,в трёх-входового элемента И, логическое выражение можно представить в виде:
Логическое сложение (дизъюнкция) — функция ИЛИ
Рассмотрим ключевую схему, представленную на рис. 1.2,а. Таблица истинности для данной логической схемы (рис. 1.2,б) состоит из 4 строк, поскольку данная схема имеет два входа — и . Количество сочетаний этих переменных равно . Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или , или . Отсюда еще одно название логического сложения — логическое ИЛИ. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.
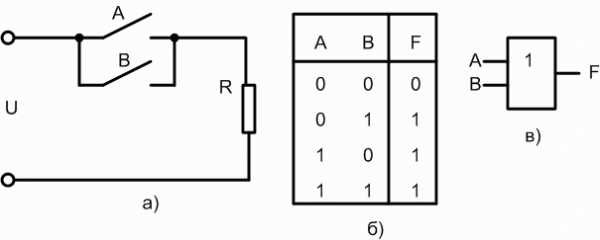
Рис. 1.2. Логический элемент ИЛИ на два входа
Правило логического сложения: если на вход логического элемента ИЛИ подается хотя бы одна логическая , то на его выходе будет логическая 1.
Для логического сложения решающим является уровень логической 1.
В логических выражениях применяется два варианта обозначения логического сложения. Так, для приведенного двух-входового элемента ИЛИ, логическое выражение можно представить в виде:
- либо , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
- либо — с использованием знака дизъюнкции.
Логическое отрицание (инверсия) — функция НЕ
Рассмотрим ключевую схему, представленную на рис. 1.3,а. Таблица истинности для данной схемы (рис. 1.3,б) самая простая и состоит всего из 2 строк, поскольку она (единственная из всех логических элементов) имеет только один вход — . Количество вариантов для единственной логической переменной равно . Очевидно, что через сопротивление R ток протекает ( ) тогда, когда не замкнут, т.е. . Еще одно название этой логической функции — отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.
Рис. 1.3. Логический элемент НЕ
Правило инверсии: проходя через инвертор, сигнал меняет свое значение на противоположное.
В логических выражениях применяется единственный вариант обозначения инверсии:
К основным логическим элементам относятся еще два элемента, которые являются комбинацией элементов И, ИЛИ и НЕ: элемент И-НЕ и ИЛИ-НЕ.
Логическая функция и элемент И-НЕ
Данная функция производит логическое умножение значений входных сигналов, а затем инвертирует результат этого умножения. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.4,а. Таблица истинности приведена на рис. 1.4,б.
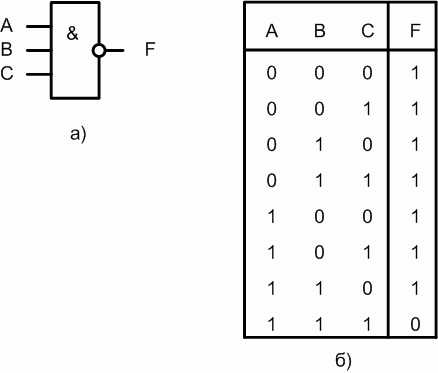
Рис. 1.4. Логический элемент И-НЕ на три входа
Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1.
В логических выражениях применяются обозначения:
- либо , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
- либо ;
- либо ;
- либо .
Логическая функция и элемент ИЛИ-НЕ
В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.5,а. Таблица истинности приведена на рис. 1.5,б.
Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0.В логических выражениях применяются обозначения:
- либо , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
- либо .
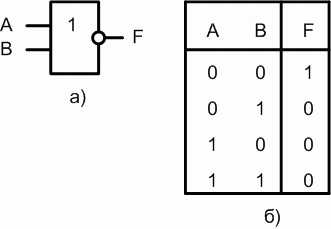
Рис. 1.5. Логический элемент ИЛИ-НЕ на два входа
www.intuit.ru


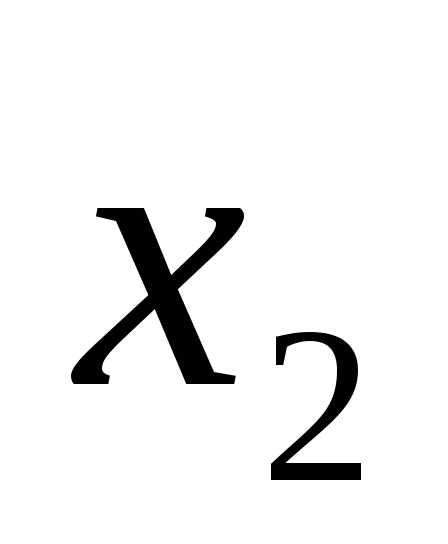
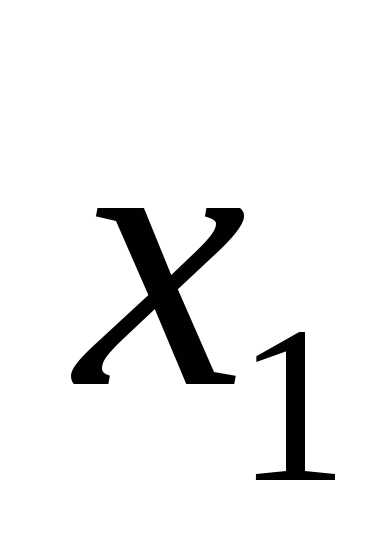

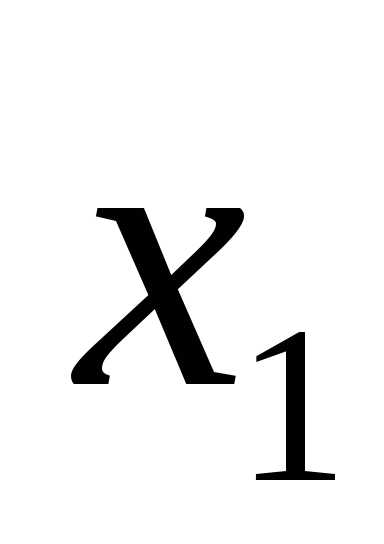
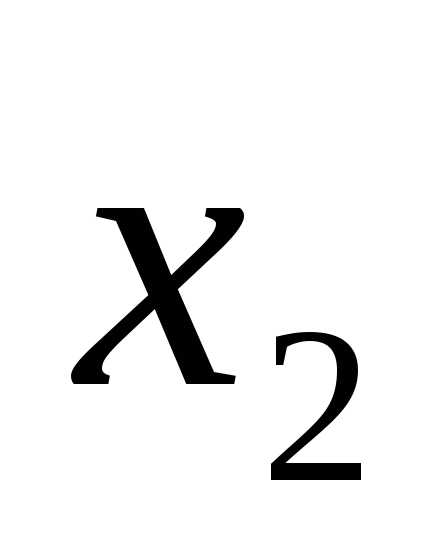
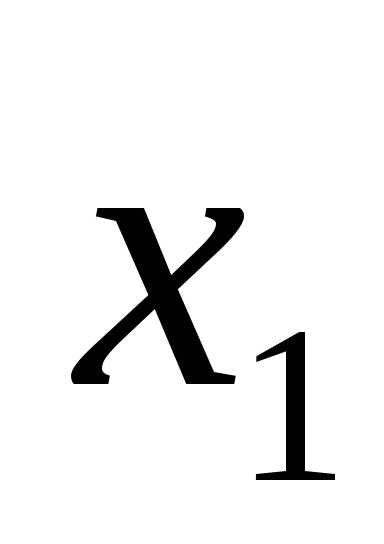
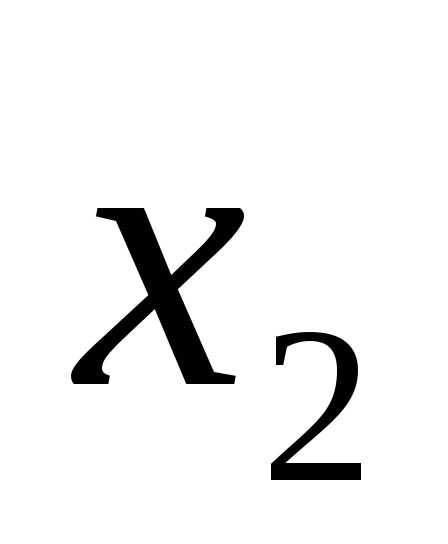
 →
→