Тестовые контрольные работы по алгебре и началам анализа, 10–11-е классы
Разделы: Математика
Проблемой первостепенной важности в процессе реформирования системы образования становится унификация требований к уровню знаний учащихся. Возможно, поэтому важнейшими критериями при введении ЕГЭ были:
- Необходимость унификации требований к уровню знаний учащихся;
- Возможность последующего использования результатов ЕГЭ в качестве основного критерия при приёме абитуриентов в ВУЗ.
Однако ЕГЭ позволяет установить субъективность оценки уровня знаний учеников лишь на конечном этапе его обучения. Для текущего контроля представляется актуальным создание единой согласованной системы тематических контрольных работ, соответствующей минимальным требованиям к содержанию образования, федеральному компоненту государственного стандарта математики.
В пределах соответствующего уровня изложения материала тематические контрольные работы должны быть приспособлены для работы с любым учебником, входящим в Федеральный перечень.
Контрольная работа традиционно ассоциируется с
- Огромной подготовительной работой учителя, скурпулёзно отбирающего разноуровневый, многовариантный тематический материал;
- Значительным стрессом учащихся, которым предстоит не только продемонстрировать достаточный уровень усвоения текущего материала, но и быть уверенным в объективности итоговой отметки.
Наличие ряда программ, учебников по математике, неизбежная субъективность требований учителей, связанная с различием уровня предварительной подготовленности школьников, в конечном итоге приводит к значительной неоднородности уровня подготовки выпускника и его оценки в пределах региона.
Для заблаговременной адаптации школьников к режиму проведения и требованиям ЕГЭ структура контрольных работ должна быть сходной со структурой ЕГЭ. Мы в своей школе группой учителей составили контрольные работы по всем темам 10 и 11 классов в 4-х — 6-и вариантах. Уровень тестов и задач соответствует Федеральному компоненту Государственного стандарта, а также уровням А и В единого государственного экзамена по математике.
Тесты по темам «Тригонометрические функции» и «Свойства функций» включают в себя 10 заданий уровней А и В, все они содержат 4 ответа, один из которых верный. Это первые контрольные работы в 10 классе в форме ЕГЭ, поэтому задания уровня С каждый учитель добавляет сам в зависимости от состава класса и изученного материала.
Тест по теме «Тригонометрические уравнения и неравенства» тоже содержат 10 заданий, но уже 8 заданий с выбором ответа и 2 задания более сложные.
Для ознакомления со структурой ЕГЭ подготовлена годовая контрольная работа в 10 классе, состоящая из трёх частей: 10 заданий части А, 6 заданий части В, 4 задания части С.
Аналогично составлены контрольные работы по темам:
- «Тригонометрические функции»
- «Свойства функции»
- «Тригонометрические уравнения и неравенства»
- «Производная. Применение производной»
- «Применение непрерывности и производной»
- Итоговая работа в 10 классе
- «Первообразная и интеграл»
- «Обобщение понятия степени»
- «Показательная функция. Показательные уравнения и неравенства»
- «Логарифмическая функция. Логарифмические уравнения и неравенства»
- «Производная и первообразная показательной и логарифмической функций»
- Контрольная работа за полугодие в 11 классе.
В апреле проводится пробный экзамен для одиннадцатиклассников, задания для него готовит администрация школы.
При проведении работ оговаривается с ребятами заранее количество баллов за каждое задание и соответствующая оценка за работу.
Со временем видна положительная динамика усвоения ребятами курса, они привыкают к жёсткому временному контролю тестирования.
Контрольные работы могут быть использованы при работе с любым учебником, соответствующим Федеральному компоненту. Они способствуют улучшению контроля уровня усвоения материала курса «Алгебра и начала анализа» учащимися, являются рациональной тематической имитацией ЕГЭ.
Аналогичная структура контрольных и ЕГЭ, а также принципиальное организационное разделение времени на ответы на сравнительно простые тесты и на решение традиционных задач, должны помочь учащимся в подготовке к ЕГЭ.
Мы предлагаем для коллег тексты всех контрольных работ (См. приложение).
21.07.2009
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Контрольные работы по алгебре для 10 класса по уч. Ю. Колягина
Просмотр содержимого документа
«К. Р. № 8 Тригоном. уравнения НН»
Просмотр содержимого документа
«К. Р. № 6 Логарифмическая функция НН»
Просмотр содержимого документа
«К. Р. №4 Степенная функция Колягин»
А – 10 (Ю.М. Колягин) Базовый уровень Контрольная работа №4
Степенная функция
Вариант 1
1. Найти область определения функции .
2. Изобразить эскиз графика функции у = х7
1) сравнить с единицей (0,95)7;
2) сравнить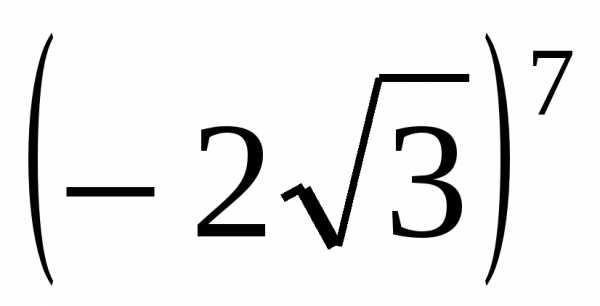 
и 
.
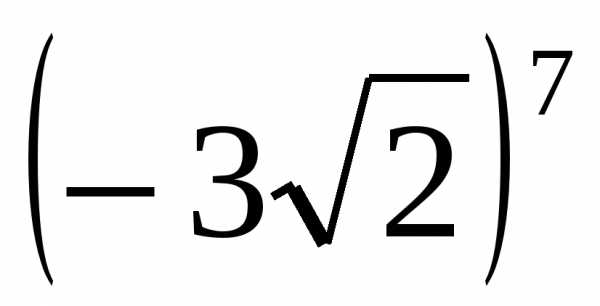3. Решить уравнение:
1) 2) .
3)
4. Установить, равносильны ли неравенства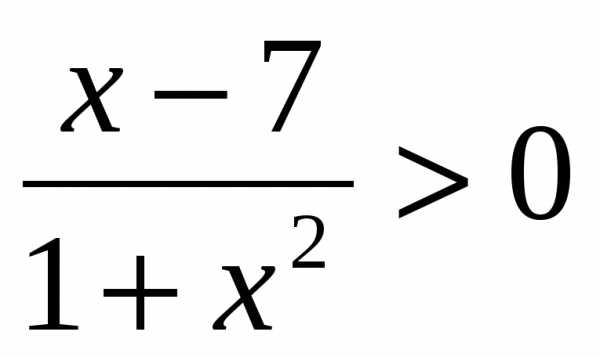 
и
5. Найти функцию, обратную к функции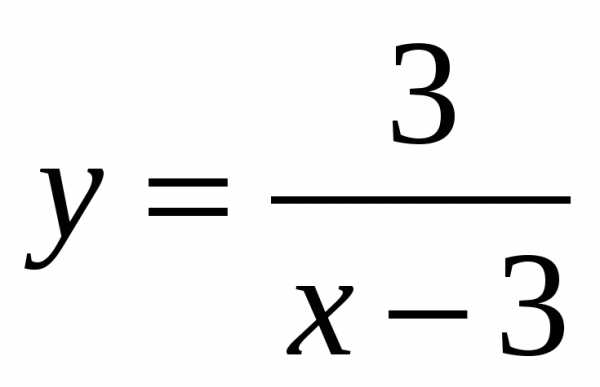 
. Указать её область определения и множество значений. Является ли эта функция ограниченной?
Контрольная работа №4
Степенная функция
Вариант 2
1. Найти область определения функции .
2. Изобразить эскиз графика функции у = х 6 и перечислить её основные свойства. Пользуясь свойствами этой функции:
1) сравнить с единицей (1,001)6;
2) сравнить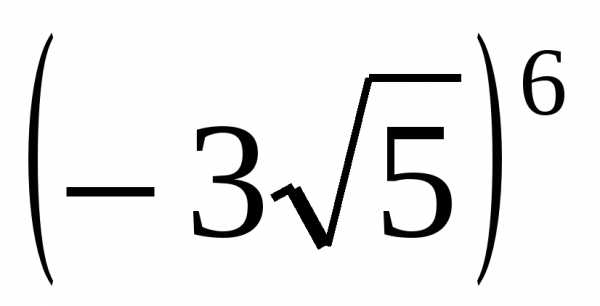 
и 
.
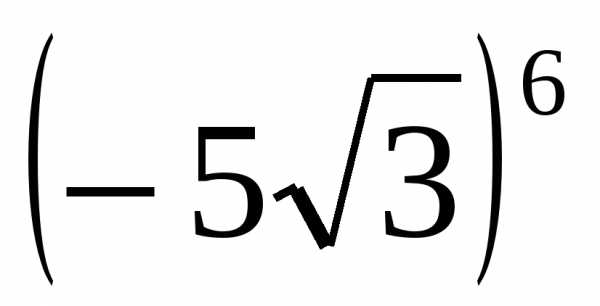3. Решить уравнение:
1) 2) .
3)
4. Установить, равносильны ли неравенства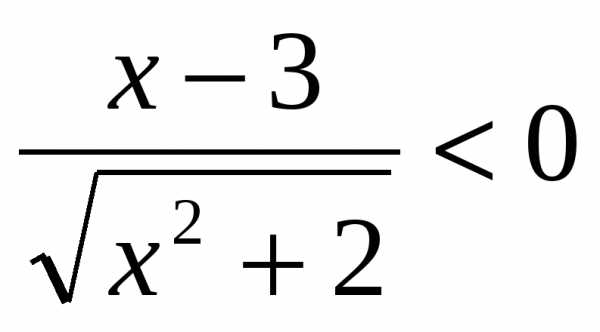 
и .
5. Найти функцию, обратную к функции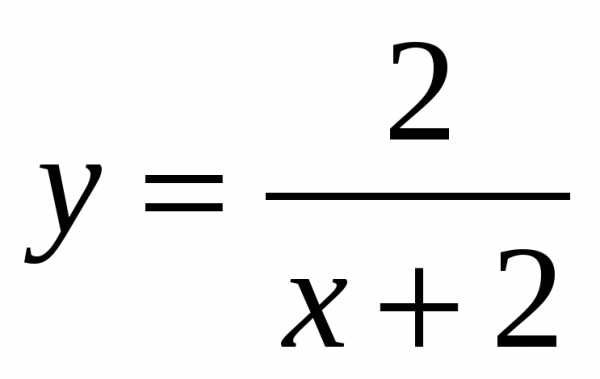 
. Указать её область определения и множество значений. Является ли эта функция ограниченной?
Просмотр содержимого документа
«К.Р. №3 Степень с действительным показателем по Колягину»
Просмотр содержимого документа
«К.Р. №5 Показательная функция по Колягину»
Просмотр содержимого документа
«К.Р. №7 Тригонометрические формулы»
multiurok.ru
10 класс, Ш.А.Алимов Итоговый тест по алгебре и началам анализа 2008-2009 учебный год ВАРИАНТ 1 ЧАСТЬ 1 ЧАСТЬ 2
10 класс, Ш.А.Алимов Итоговый тест по алгебре и началам анализа 2008-2009 учебный год ВАРИАНТ 2 ЧАСТЬ 1
ЧАСТЬ 2
10 класс, Ш.А.Алимов Итоговый тест по алгебре и началам анализа 2008-2009 учебный год ВАРИАНТ 3 ЧАСТЬ 1 ЧАСТЬ 2
10 класс, Ш.А.Алимов Итоговый тест по алгебре и началам анализа 2008-2009 учебный год ВАРИАНТ 4 ЧАСТЬ 1 ЧАСТЬ 2
10 класс, Ш.А.Алимов Итоговый тест по алгебре и началам анализа 2008-2009 учебный год ВАРИАНТ 5 ЧАСТЬ 1 ЧАСТЬ 2
10 класс, Ш.А.Алимов Итоговый тест по алгебре и началам анализа 2008-2009 учебный год ВАРИАНТ 6 ЧАСТЬ 1 ЧАСТЬ 2
|
uch.znate.ru
Контрольная работа по алгебре 10 класс Алимов
1. Напишите первый, тридцатый и сотый члены последовательности, если
ее n-й член задается формулой .
2. Исследуйте последовательность на ограниченность
и на монотонность.
3. Вычислите: а) ; б) .
4. Пользуясь определением, выведите формулу дифференцирования
функции .
5. Пользуясь правилами и формулами дифференцирования, найдите
производную функции:
.
6. Найдите абсциссу точки графика функции , в которой
касательная к нему параллельна прямой .
___________________________________________________________
7. Дана функция . Найдите , если .
___________________________________
8. Найдите площадь треугольника, образованного осью ординат и двумя
касательными, к графику функции , проведенными из
точки
Контрольная работа № 8 (2 часа)
Вариант 1
- Исследуйте функцию на монотонность и экстремумы.
- Постройте график функции .
- Найдите наименьшее и наибольшее значения функции
на отрезке .
- В полукруг радиуса 6 см вписан прямоугольник. Чему равна его наибольшая площадь?
___________________________________________________________
- Докажите, что при справедливо неравенство .
___________________________________
- При каких значениях параметра функция
убывает на всей числовой прямой?
kontrolnaya-s-otvetami.ru
Контрольная работа по алгебре 10 класс Алимов
ВАРИАНТ 1.
Часть I.
- Укажите наименьшее значение функции у = 2 – 5sin x.
Ответ:
- Найдите производную функции у = 2х + cos х.
- у = 2х – sin x 3) у = x 2х-1 + cos x
- у = 2х ln 2 – sin x 4) у = 2х ln 2 – cos x
На рисунке изображены график функции у = f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0. |
На рисунке изображен график производной функции у = f(x), определённой на (-10; 4). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них. |
5.
На рисунке изображен график производной функции у = f(x), определённой на (-5; 5). В какой точке отрезка [-4; -1] f(x) принимает наибольшее значение. |
ВАРИАНТ 2.
Часть I.
- Укажите наибольшее значение функции у = — 3 – 2cos x.
Ответ:
- Найдите производную функции у = е – х + х2.
- у = — е – х + х2 3) у = — е – х + 2х
- у = е – х + 2х 4) у = е – х — 2х
На рисунке изображен график функции у = f(x), определённой на (-2; 12). Найдите количество точек, в которых касательная к графику функции параллельна прямой у = -5. |
На рисунке изображен график производной функции у = f(x), определённой на (-8; 3). Найдите точку экстремума функции f(x) на отрезке [-5; 2]. |
На рисунке изображен график производной функции у = f(x), определённой на (-5; 7). В какой точке отрезка [-4; 2] f(x) принимает наименьшее значение. |
Часть II. Запишите обоснованное решение и ответ.
- Найдите первообразную F(x) функции f(x) = + 2х, если график первообразной проходит через точку М(3; 13).
- В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
- Тело движется прямолинейно по закону х(t) = 2t4 — 3t3 – 5t2 (x в метрах, t в секундах). Найдите его скорость в момент времени t = 10c.
- Касательная к графику функции f(x) = 2×3 – 3×2 – 4 параллельна прямой у = 12х + 1. Найдите абсциссу точки касания.
- Дана функция f(x) = 8×2 – x4 . Найдите:
А) промежутки возрастания и убывания функции;
Б) точки максимума и минимума функции;
В) наибольшее и наименьшее значения функции
на отрезке [-1; 3] .
- Найдите площадь фигуры, ограниченной графиком функции
f(x) = -x2 + 6x — 5, прямыми х = 2, х = 3 и осью абсцисс, изобразив рисунок.
- Найдите все решения уравнения cos 2x + sin x = cos2 x, принадлежащие отрезку [0; 2π].
konspekt-v-gruppe.ru
